Comparison of Marine Gravity Measurements from Shipborne and Satellite Altimetry in the Arctic Ocean
Abstract
:1. Introduction
2. Data
3. Data Comparison and Analysis
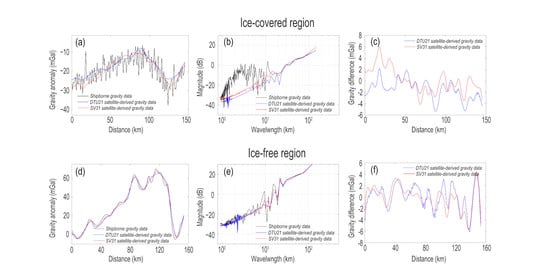
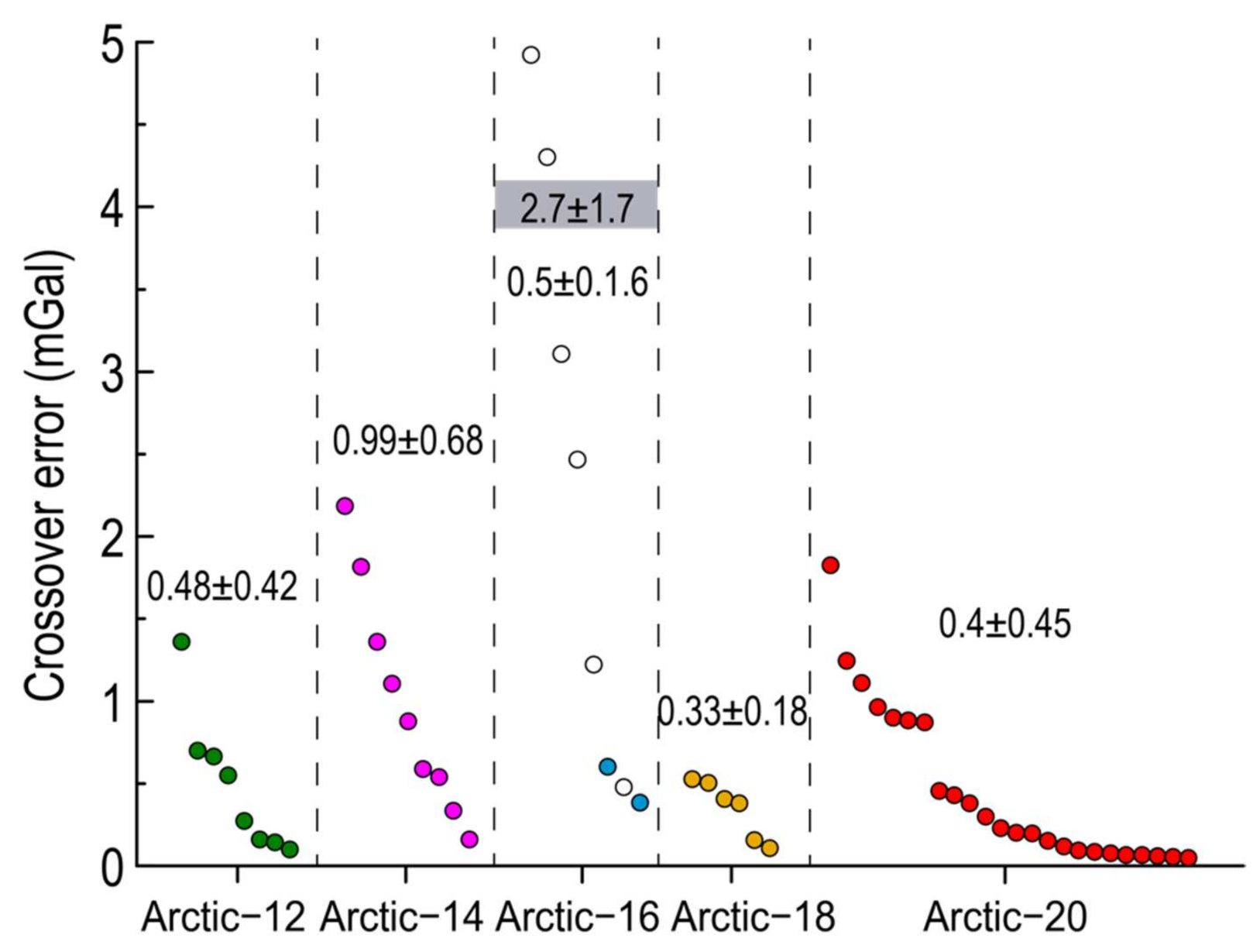
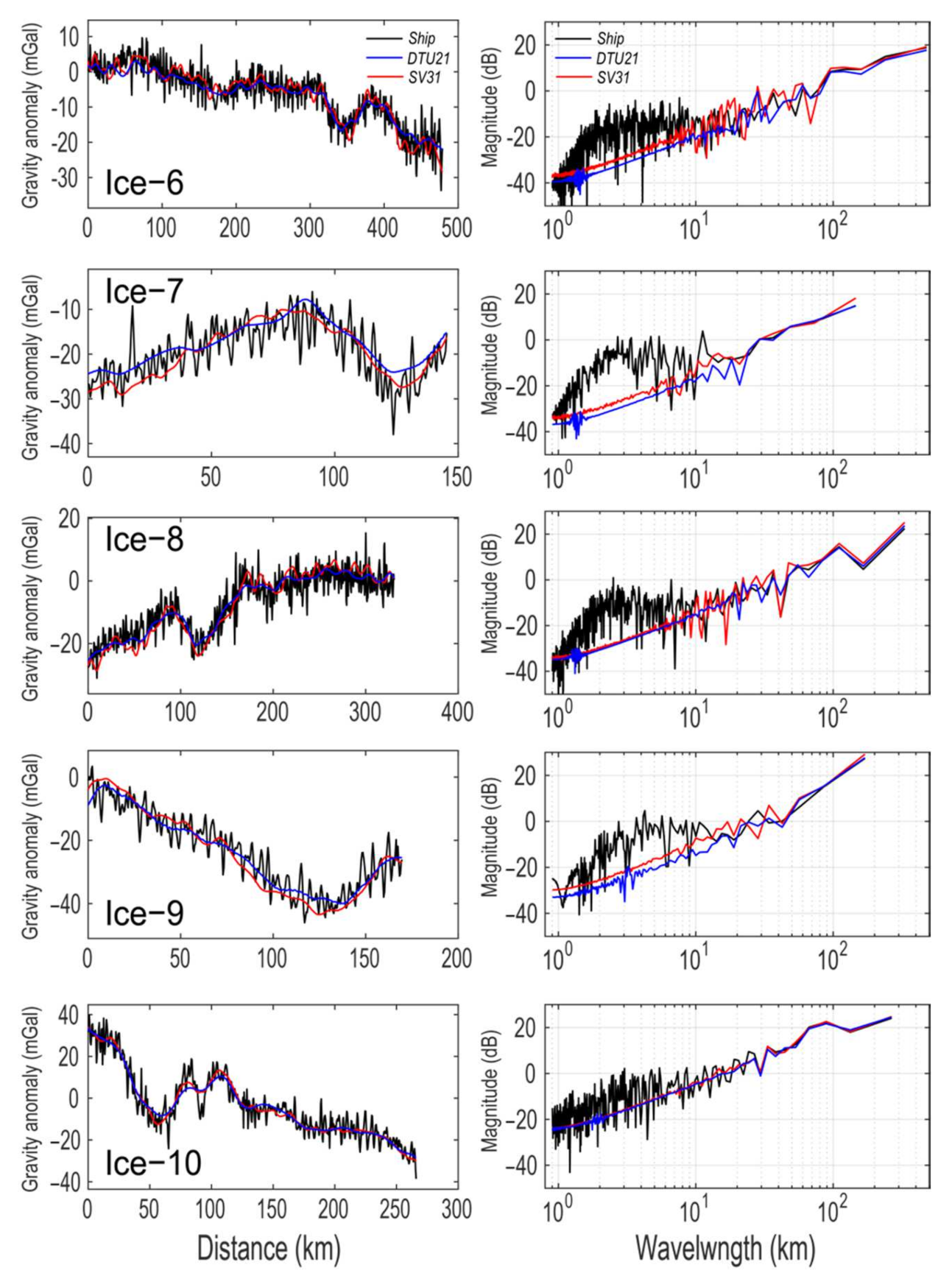
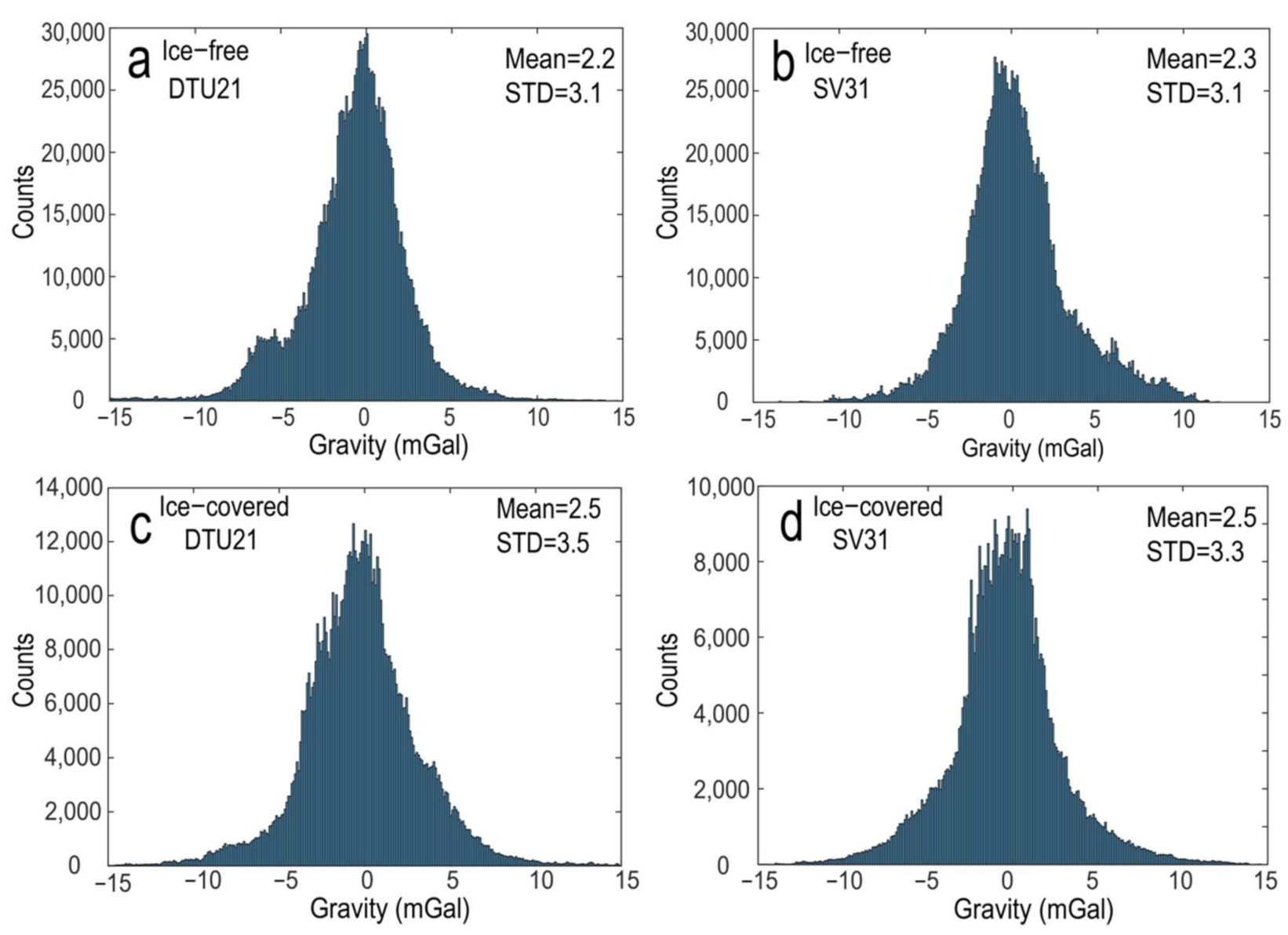
3.1. One-Dimensional Analysis
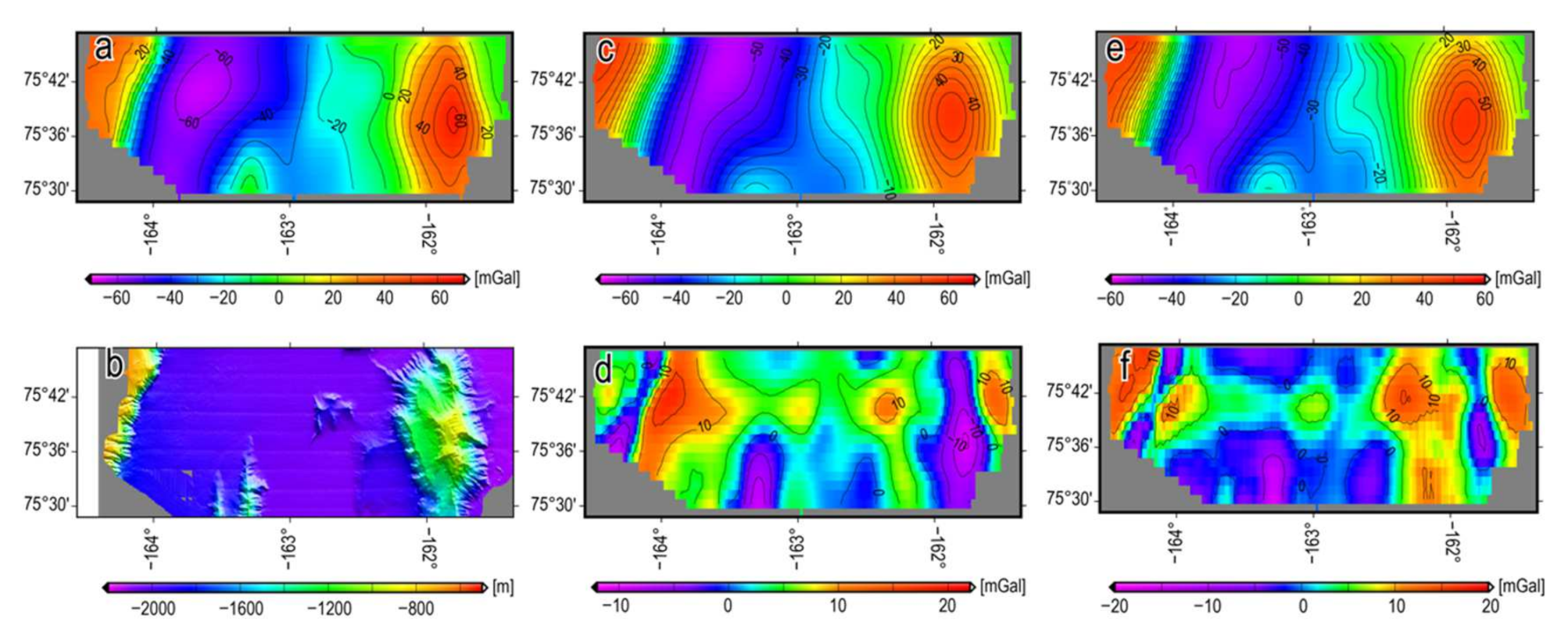
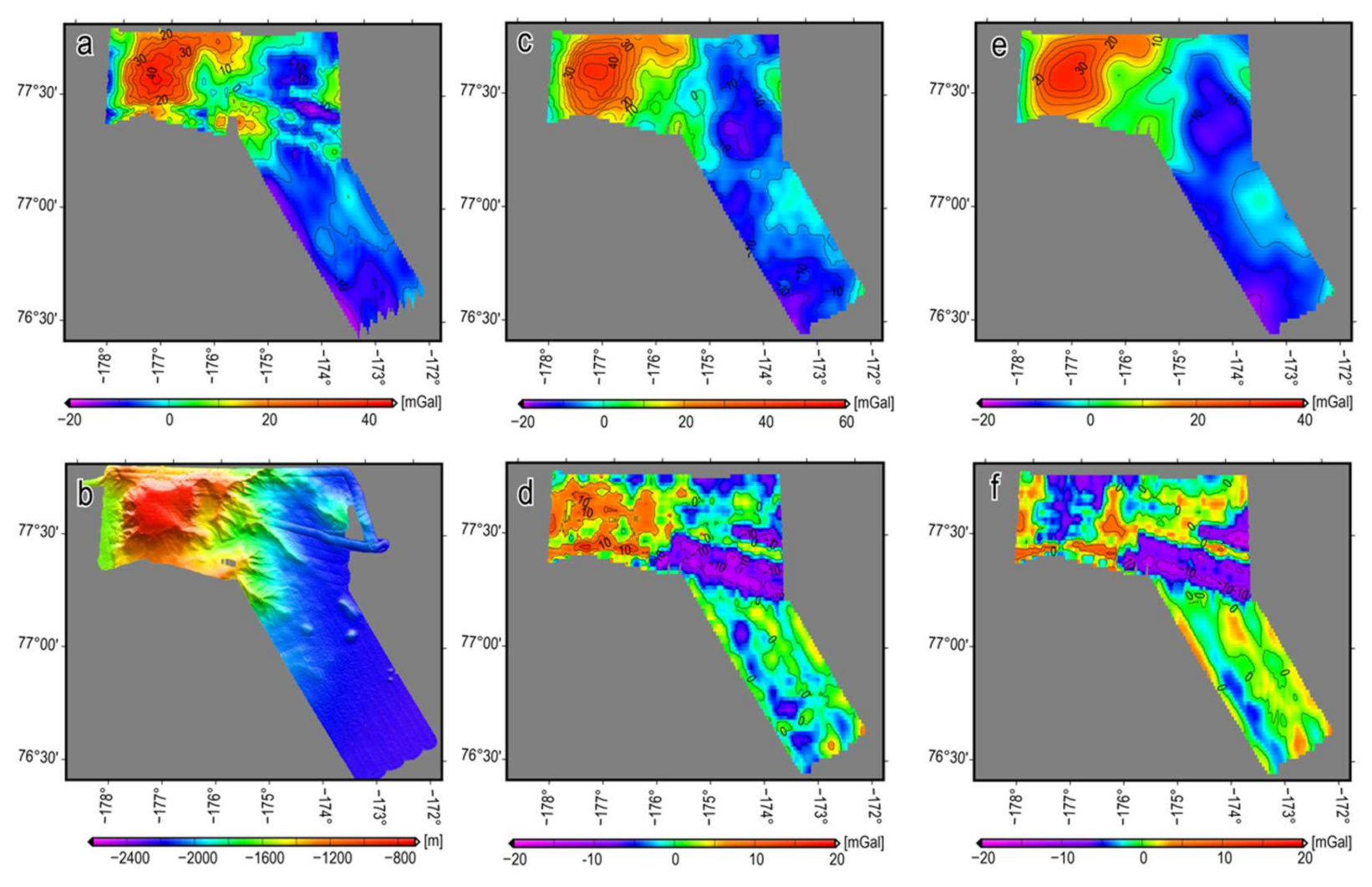
3.2. Two-Dimensional Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Blackman, D.K.; Forsyth, D.W. Isostatic compensation of tectonic features of the Mid-Atlantic Ridge: 25–27°30′ S. J. Geophys. Res. Solid Earth 1991, 22, 883–892. [Google Scholar] [CrossRef]
- Kuo, B.Y.; Forsyth, D.W. Gravity anomalies of the ridge-transform system in the South Atlantic between 31 and 34.5° S: Upwelling centers and variations in the crustal thickness. Mar. Geophys. Res. 1988, 96, 11741–11758. [Google Scholar] [CrossRef]
- Lin, J.; Purdy, G.M.; Schouten, H.; Sempéré, J.C.; Zervas, C. Evidence from gravity data for focused magmatic accretion along the Mid-Atlantic Ridge. Nature 1990, 344, 627–632. [Google Scholar] [CrossRef]
- Morris, E.; Detrick, R.S. Three-dimensional analysis of gravity anomalies in the MARK area, Mid-Atlantic Ridge 23° N. J. Geophys. Res. Solid Earth 1991, 96, 4355–4366. [Google Scholar] [CrossRef]
- Kwok, R. Simulated Effects of a Snow Layer on Retrieval of CryoSat-2 Sea Ice Freeboard. Geophys. Res. Lett. 2014, 41, 5014–5020. [Google Scholar] [CrossRef]
- Hector, H.S.; Pierre, Q.; Fabrice, A. Assessment of SARAL/AltiKa Wave Height Measurements Relative to Buoy, Jason-2, and Cryosat-2 Data. Mar. Geod. 2015, 38, 449–465. [Google Scholar] [CrossRef] [Green Version]
- Shen, X.; Ke, C.Q.; Xie, H.; Li, M.; Xia, W. A comparison of Arctic sea ice freeboard products from Sentinel-3A and CryoSat-2 data. Int. J. Remote Sens. 2020, 41, 2789–2806. [Google Scholar] [CrossRef]
- Christensen, A.N.; Andersen, O.B. Comparison of Satellite Altimetric Gravity and Ship-borne Gravity—Offshore Western Australia. In Proceedings of the ASEG-PESA-AIG 2016, Adelaide, Australis, 21–24 August 2016. [Google Scholar] [CrossRef] [Green Version]
- Andersen, O.B.; Forsberg, R.; Knudsen, P.; Laxon, S.; McAdoo, D. Comparison of Altimetric and Ship borne Marine Gravity over Ice-free and Ice-covered polar Seas. In Geodesy on the Move-Gravity, Geoid, Geodynamics and Antarctica; Forsberg, R., Feissel, M., Dietrich, R., Eds.; Springer: Berlin/Heidelberg, Germany, 1998; Volume 119, pp. 492–497. ISBN 978-3-642-72245-5. [Google Scholar]
- Laxon, S.W.; McAdoo, D. Arctic Ocean Gravity Field Derived From ERS-1 Satellite Altimetry. Science 1994, 265, 621–624. [Google Scholar] [CrossRef]
- Urlaub, M.; Schmidt-Aursch, M.C.; Jokat, W.; Kaul, N. Gravity crustal models and heat flow measurements for the Eurasia Basin, Arctic Ocean. Mar. Geophys. Res. 2009, 30, 277–292. [Google Scholar] [CrossRef]
- Sandwell, D.T.; Müller, R.D.; Smith, W.H.; Garcia, E.; Francis, R. New global marine gravity model from CryoSat-2 and Jason-1 reveals buried tectonic structure. Science 2014, 346, 65–67. [Google Scholar] [CrossRef]
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008). J. Geophys. Res. Solid Earth 2012, 117, B04406. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Rothrock, D.A. Modeling global sea ice with a thickness and enthalpy distribution model in generalized curvilinear coordinates. Mon. Weather. Rev. 2003, 131, 681–697. [Google Scholar] [CrossRef] [Green Version]
- Lindsay, R.W.; Zhang, J.; Schweiger, A.; Steele, M.A. Seasonal predictions of ice extent in the Arctic Ocean. J. Geophys. Res. Atmos. 2008, 113, C02023. [Google Scholar] [CrossRef] [Green Version]
- Schweiger, A.R.; Lindsay, J.; Zhang, J.; Steele, M.A.; Stern, H. Uncertainty in modeled arctic sea ice volume. J. Geophys. Res. 2011, 116, C00D06. [Google Scholar] [CrossRef] [Green Version]
- Andersen, O.B.; Knudsen, P. The DTU17 Global Marine Gravity Field: First Validation Results. In Fiducial Reference Measurements for Altimetry; Mertikas, S., Pail, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; Volume 150, pp. 83–87. ISBN 978-3-030-39437-0. [Google Scholar]
- Pérez-Gussinyé, M.; Metois, M.; Fernández, M.; Vergés, J.; Fullea, J.; Lowry, A.R. Effective elastic thickness of Africa and its relationship to other proxies for lithospheric structure and surface tectonics. Earth Planet. Sci. Lett. 2009, 287, 152–167. [Google Scholar] [CrossRef]
- Kirby, J.F.; Swain, C.J. An accuracy assessment of the fan wavelet coherence method for elastic thickness estimation. Geochem. Geophys. Geosyst. 2008, 9, Q03022. [Google Scholar] [CrossRef] [Green Version]
- Neumann, G.A.; Forsyth, D.; Sandwell, S.T. Comparison of marine gravity from shipboard and high-density satellite altimetry along the Mid-Atlantic Ridge, 30.5°–35.5° S. Geophys. Res. Lett. 1993, 20, 1639–1642. [Google Scholar] [CrossRef] [Green Version]




| Survey Lines | Number of Observations | Length (km) | Minimum (mGal) | Maximum (mGal) | Mean (mGal) | Standard Deviation (mGal) | |
|---|---|---|---|---|---|---|---|
| Arctic−12 | 29 | 906,789 | 11,062 | −49.6 | 129.3 | 2.9 | 22.3 |
| Arctic−14 | 20 | 717,961 | 2124 | −72.4 | 59.3 | −6.3 | 19.1 |
| Arctic−16 | 15 | 375,841 | 2239 | −78.8 | 39.9 | −10.9 | 16.6 |
| Arctic−18 | 15 | 180,014 | 1088 | −58.6 | 69.8 | 5.6 | 36.8 |
| Arctic−20 | 40 | 652,418 | 4486 | −42.9 | 44.1 | 4.0 | 17.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ling, Z.; Zhao, L.; Zhang, T.; Zhai, G.; Yang, F. Comparison of Marine Gravity Measurements from Shipborne and Satellite Altimetry in the Arctic Ocean. Remote Sens. 2022, 14, 41. https://doi.org/10.3390/rs14010041
Ling Z, Zhao L, Zhang T, Zhai G, Yang F. Comparison of Marine Gravity Measurements from Shipborne and Satellite Altimetry in the Arctic Ocean. Remote Sensing. 2022; 14(1):41. https://doi.org/10.3390/rs14010041
Chicago/Turabian StyleLing, Zilong, Lihong Zhao, Tao Zhang, Guojun Zhai, and Fanlin Yang. 2022. "Comparison of Marine Gravity Measurements from Shipborne and Satellite Altimetry in the Arctic Ocean" Remote Sensing 14, no. 1: 41. https://doi.org/10.3390/rs14010041
APA StyleLing, Z., Zhao, L., Zhang, T., Zhai, G., & Yang, F. (2022). Comparison of Marine Gravity Measurements from Shipborne and Satellite Altimetry in the Arctic Ocean. Remote Sensing, 14(1), 41. https://doi.org/10.3390/rs14010041