Abstract
Mountain ecosystems provide environmental goods, which can be threatened by climate change. Near-Surface Temperature Lapse Rate (NSTLR) is an essential factor used for thermal and hydrological analysis in mountain ecosystems. The aims of the present study were to estimate NSTLR and to identify its relationship with aspect, Local solar zenith angle (LSZA) and Evaporative Stress Index (ESI) for two seasons of the year in a mountain ecosystem at the North of Mexico. Normalized Land Surface Temperature (NLST) was estimated using environmental and topographical variables. LSZA was calculated from slope to consider the effect of solar position. NSTLR was estimated through simple linear models. Observed NSTLR was 9.4 °C km−1 for the winter and 14.3 °C km−1 for the summer. Our results showed variation in NSTLR by season. In addition, aspect, LSZA and ESI also influenced NSTLR regulation. In addition, Northwest and West aspects exhibited the highest NSTLR. LSZA angles closest to 90° were related with a decrease in NSTLR for both seasons. Finally, ESI values associated with less evaporative stress were related to lower NSTLR. These results suggest potential of Landsat-8 LST and ECOSTRESS ESI to capture interactions of temperature, topography, and water stress in complex ecosystems.
1. Introduction
Mountain ecosystems are characterized by being located at high elevations and showing environmental heterogeneity within their altitudinal gradient [1,2]. Mountain ecosystems provide a large quantity of ecosystem services [3,4]. One of most important ecosystem services is water supply, it is estimated more than half of water resources for human consumption are directly or indirectly from these areas [5,6,7]. In addition, forested areas and grasslands within the altitudinal gradient of mountain ecosystems are important for the processes of climatic regulation, net primary productivity, and soil conservation [5,7,8,9,10].
These ecosystems and the environmental processes occurring within them are very sensitive to climate change and other impacts from human activities, such as deforestation and overgrazing [8,11]. Globally, mountain ecosystems are threatened by human activities, including land use change degradation and human-caused climate change, which is affecting forests distribution [12,13]. For examples, changes in forest and glacier distribution related to climate change have been documented in Himalayan ecosystems [13,14]. These processes modify the humidity, precipitation and temperature patterns throughout the altitudinal gradient and affect water availability, endangering water reserves for human population, and affecting fauna and flora [14,15]. In spite of the importance and fragility of these ecosystems, research on climatic processes in mountain areas has been limited by accessibility constraints [11,16].
The analysis of mountain ecosystems trough a thermal approach could provide information about environmental dynamics of these ecosystems. An essential variable to studied thermal and climatic conditions in mountainous area is near-surface temperature lapse rate (NSTLR), defined as the rate of change in temperature by elevation [17]. NSTLR is defined as inverse relationship between elevation and temperature [17,18,19]. It is generally assumed to have a value of 6.5 °C km−1, inferred from the NSTLR of the atmospheric column within the troposphere [20,21], and is generally the constant value of NSTLR in mountain areas. Nevertheless, several studies have concluded that the NSTLR is locally variable, depending on the region and season, with varying results of the thermal gradient value and the factors affecting it [18,22,23,24]. There is consequently a need to further analyse the factors influencing the seasonal and spatial variability in NSTLR.
NSTLR can be affected by topographic variables, such as aspect and slope and other variables such as evapotranspiration (ET) [1,25], although many questions remain regarding the environmental drivers of NSTLR. The characterization of NSTLR in mountain ecosystems is limited by the availability and spatial distribution of weather stations, often limiting a spatially detailed characterization of climatic data [24,26,27].
Higher resolution DEM and satellite climate information offers a new opportunity to better analyze thermal and hydric processes in mountain ecosystems [13,28]. Remote sensing techniques utilizing satellite images from passive remote sensors can be a useful alternative to study mountain ecosystems, since they can provide information in areas without water stations data and areas under low accessibility conditions, providing historical data at regional and global scales [29]. The thermal dynamics can be monitored from land surface temperature (LST) data estimated from satellite images, which provide spectral information about the processes of energy exchange between solar radiation and the terrestrial surface [30].
Several studies have been utilized satellite information to estimate and analyze the NSTLR in mountain ecosystems, using the relationship between LST and a digital elevation model (DEM) [8,18,26,31,32,33]. Nevertheless, it has been observed that some environmental variables (i.e., solar incidence, moisture, land cover characteristics) cause interference of NSTLR estimated from LST data [18,34]. Therefore, it has been suggested normalizing LST data with respect to environmental variables, potentially improving the accuracy of estimation of NSTLR from satellite information [8,35]. This approach has been less explored and requires further evaluation, particularly for the relatively less utilized medium resolution sensors. In particular, studies using Landsat Land Surface Temperature product to analyse factors driving thermal gradients in forest ecosystems are still relatively scarce [18,26,36]. In the present study, we used LST derived from Landsat-8 TIRS, which was normalized using random forests to obtain NSTLR information. This information allowed us to analyze the variability of NSTLR with respect to biophysical parameters, such as evapotranspiration (ET) and topographic characteristics.
The knowledge about NSTLR and the factors influencing it at a regional scale can allow to improve the understanding the thermal and hydric dynamics of mountain ecosystems [18] and could be used to develop climatic models, hydrological models and analysis of soil moisture [37]. For example, the effect of slope which depends on solar radiation flux incidence on the terrestrial surface; it can be quantified through the Local Solar Zenith Angle (LSZA). This parameter is calculated considering the interaction of the slope relative to sun position at time of satellite pass [38].
In addition to the previously documented contrasting effects of vegetation and topography on NSTLR [18,26], other parameters potentially affecting thermal gradients have received less attention. For example, very few studies have analysed the variation of thermal gradients with respect to remotely sensed evapotranspiration (ET) indices, particularly from medium resolution sensors.
ET is a key hydrologic component for the energy balance of terrestrial surface, influencing water availability [39]. Until recently, there remained a large gap in our ability to monitor ET concurrently at both fine spatial and fine temporal scales globally [40]. The relatively recently launched (June 2018) ECOSTRESS sensor provides a good opportunity for monitoring daily ET at medium (70 m) resolution globally [40,41]. There remains a need to evaluate ECOSTRESS mission performance, particularly the ET estimates in humid, temperate, mountainous areas [41]. In addition, to our best knowledge, no previous study has analysed the variations Landsat-derived NSTLR against ECOSTRESS ET indices such as the Evaporative Stress Index (ESI).
Therefore, the aim of current study was to examine the variability of NSTLR for two contrasting year seasons (winter-summer) in a forest management area at the Sierra Madre Occidental (SMO) in Durango State, Mexico and to analyze the influence of topography and other biophysical factors such as evaporative stress, through Landsat-8 and ECOSTRESS images. The study had following hypotheses: (1) NSTLR in the study area is different than the constant value (6.5 °C km−1), (2) NSTLR is influenced by different topographic and biophysical characteristics (LSZA, aspect and ESI). Improved NSTLR characterization could contribute to ecological modeling and water management planning, including water balances assessment [31,42]. Furthermore, understanding the effects of topography on temperature gradients could contribute to ongoing fire risk analysis e.g., [43,44].
2. Materials and Methods
2.1. Study Area
The area of study was the management unit UMAFOR 1001, in the central part of the SMO, at the North of Durango State, Mexico (Figure 1). The SMO is the highest mountain range in México, it has a one of the main forest reserves in Mexico, which gives it great economic and ecological relevance given the wide variety of environmental services it provides [45,46,47]. UMAFOR 1001 is bounded between 25.57° and 26.84°N latitude and 105.05° and 106.55°W longitude with an approximate 11,336 km2 of area. The average elevation of study area is 2131 m above the mean sea level. The vegetation includes more than 75 species of pine and oak forests in the upper and middle elevations [48]. Among these species, Quercus sideroxyla Humb and Bonpl, Pinus durangensis Martínez, Quercus grisea Liebm and Pinus teocote Humb and Bonpl stand out [49], while mid-slopes and flat terrains are characterized by semiarid vegetation, such as shrublands, chaparral, natural grasslands and induced pasturelands [47]. Climate ranges from subhumid to semiarid, with an annual precipitation average of 664 mm and mean temperatures ranging from 8.7 (average of coldest month) to 16.1 °C (average of the warmest month), with an annual average of 11.1 °C [48,50]. UMAFOR 1001 has a variable topography ranging from undulating to rugged topography and altitudinal characteristics that make it valuable to analyze regional thermal processes.
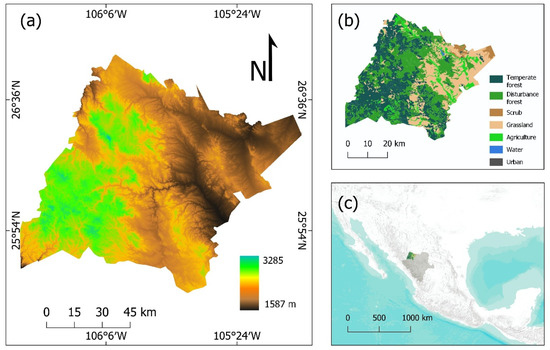
Figure 1.
Study area. (a) Elevation; (b) Vegetation. The data on land use and vegetation were taken from information from the National Institute of Statistics and Geography of Mexico [50]. Temperate forests include pine forests, oak forests, and mixed forests. The disturbance forest classification corresponds to forests that suffered some alteration and are under a natural regeneration process; (c) Location of study area.
2.2. Images Acquisition
The Digital Elevation Model (DEM) from the Shuttle Radar Topography Mission (SRTM), with a resolution of 30 m, was downloaded from the US Geological Service webpage (https://earthexplorer.usgs.gov) (accessed on 25 July 2020). Slope and aspect were obtained from the DEM, using QGIS 3.14 [51].
Google Earth Engine (GEE) platform was used to visualize, process, and download Landsat-8 OLI/TIRS (with a 30 m resolution) [52]. The GEE allows processing large datasets in a cloud-based platform, accessing satellite data such as Landsat collections. The images correspond to LANDSAT/LC08/C01/T1_SR collection from winter and summer of 2019 (Table 1). In addition, a cloud and cloud shadow mask from Quality assessment band (BQA) band was applied to remove pixels where attributes might be altered by climatic conditions; this process is a prerequisite to perform a more trustable thermal analysis; this process that must be considered every time that satellite images are processed [53,54].

Table 1.
Path/Row and acquisition dates of Landsat-8 images.
2.3. Spectral Indices Estimation
The spectral indices had estimated employing Landsat-8 bands. These indices were estimated using the Equations (1)–(3) in the GEE platform and was used for the normalization LST.
where NDVI is the Normalized difference vegetation index developed by Rouse, et al. [55], which is used for analyzing the photosynthetic activity in the terrestrial surface. NDVI was estimated using red band (B4) and Near infrared band (B5). Whereas NDBI is the Normalized difference built-up index (NDBI), this index allows emphasizing the impervious surfaces such as bare and built-up land [56]. NDBI was calculated with the Equation (2), using the Shortwave-infrared band (B6) and Near infrared (B5) data of Landsat-8. Finally, the Normalized difference water index (NDWI) provides wetness information, as soil moisture, vegetation, and built-up land [57]. The NSWI was calculated using B3 (green band) and B5 (Near infrared band).
2.4. Land Surface Temperature Estimation
LST was estimated using the inversion of Planck’s function (Equation (4)). Where, TB is brightness temperature, defined as the temperature of blackbody. TB values come from band 10 coming from Google Earth Engine Landsat collection, λ is wavelength in radiance values, and is a constant value of 14,380.
Land surface emissivity (ε) was calculated using the methodology of Sobrino and Raissouni [58], as shown in Equation (5), using the constants predefined according to the sensor (0.986 and 0.0004) and NDVI, NDVImin, NDVImax calculated in previously step.
The LST obtained was in Kelvin and it was converted to Celsius by subtracting 273.15. LST images was processed in the GEE platform using the code developed by Ermida, et al. [59] applying the methodology previously described.
2.5. Local Solar Zenith Angle
In order to analyze the effect of slope relative to sun position at the moment of satellite pass, LSZA, the angle between the zenith vertical and solar radiation (ranging from 0° to 90°) was calculated. The local LSZA was calculated utilizing Equation (6), which was developed by Dozier and Frew [60].
where Ɵ is LSZA, Zs and As are the solar zenith angle and azimuth angle, respectively, and A and S are the aspect and slope of terrain, in degrees, obtained from the DEM.
2.6. Evaporative Stress Index
Evaporative stress index (ESI) is an ECOSTRESS product, which is a useful tool to analyze drought processes in areas where precipitation data are limited. It is based on evapotranspiration and potential evapotranspiration obtained from satellite thermal bands and some auxiliary products, i.e., vapor pressure data and relative humidity [61]. ESI can range between 0 and 1, where 0 is an area with high hydric stress, while 1 represents an area without hydric stress [39]. Likewise, ECOSTRESS products have a spatial resolution of 70 × 70 m [40] and its products include information for geometric correction and cloud detection [62]. Raster data was downloaded from the LP DAAC platform from US Geological Service (https://lpdaac.usgs.gov) (accessed on 19 August 2020). Images were downloaded for the UMAFOR 1001 polygon; the selected images were those which had the highest number of quality pixels for winter (24 February 2019) and summer (21 June 2019).
2.7. Near-Surface Temperature Lapse Rate Estimation
The NSTLR estimation trough the LST-DEM linear regression has a well-known error, which is due of effect of surface characteristics [8,63,64]. To solve this effect the LST obtained from Landsat-8 was normalized relative to biophysical characteristics and solar incidence angle. We used the approach developed for Firozjaei, Fathololoumi, Alavipanah, Kiavarz, Vaezi and Biswas [8], through a normalization of LST relative to the surface biophysical characteristics and the solar incidence angle (Equation (7)).
where NLST is LST modeled based on the surface biophysical characteristics and solar incidence angle, is non-linear linking model. Random Forest regression method was used to build the non-linear linking model between LST obtained and the predictors (NDVI, NDBI, NDWI and LSZA). Finally, NSTLR was calculated by a simple linear regression between NLST (dependent variable) and DEM (independent variable), where regression slope represents the NSTLR value [8,33].
The raster layers (NLST, Aspect, LSZA and ESI) were aligned and aggregated to the same spatial context; this process was made with Bicubic interpolation raster algorithm. A database was constructed extracting information for every pixel, these processes were performed using QGIS 3.14 [51]. The NSTLR was analyzed separately to each aspect (i.e., N, NE, E, SE, S, SW, W, NW), while for LSZA, values were divided in different ranges with an interval of 15° (i.e., 0–15°, 15–30°, 30–45°, 45–60°, 60–75°, 75–90°). Likewise, the ESI values were divided into five ranges (i.e., 0–0.2, 0.2–0.4, 0.4–0.6, 0.6–0.8, 0.8–1). We applied linear regressions of NLST against elevation to determine the NSTLR (Equation (8)) for each one of the data ranges analyzed for aspect, slope and ESI (Table 2). The goodness of fit of the 19 fitted linear models was evaluated by the coefficient of determination (R2) and root square mean error (RMSE).
where b and m are coefficients of the linear regression between NLST and elevation (DEM); m is the slope value of linear regression, which represents the NSTLR.

Table 2.
Descriptive data of normalized surface temperature in winter and summer (NLSTw and NLSTs), and of evaporative stress index in winter and summer (ESIw and ESIs). Q1 and Q3 are quartiles of the data series.
Finally, an overview of the workflow described in the previous sections is presented in Figure 2.
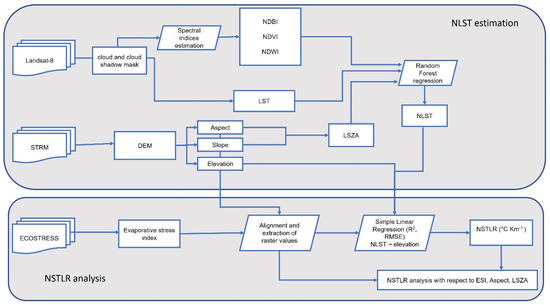
Figure 2.
Flow diagram of data analysis.
3. Results
The accuracy of Random Forest model to normalization LST data were to winter and summer were 0.71 R2 and 0.86 R2, respectively. Meanwhile, the mean winter NLST of the study area ranged between 5.8 and 26.7 °C, with an average value of 17.4 °C. Mean summer LST ranged in the study area between 18.1 and 47.8 °C, with an average value of 34.3 °C. ESI values ranged for the study area between 0.03 and 0.7 in winter and between 0.3 and 0.9 in summer (Table 2).
NLST maps for winter and summer show the LST distribution in the study area, where the LST decreasing in the zones with highest elevation, while in the lower areas was found higher temperature (Figure 3). Linear regression between LST and elevation for winter had an R2 of 0.74, with a RMSE of 1.9 °C; for summer, R2 was 0.81 and RMSE 2.4 °C. Linear models showed that elevation influenced LST more in summer. The observed dispersion of data from the linear regression in both seasons (Figure 4) suggests that there is a complex relationship where interacting multiple factors, in addition to elevation. The complementary factors which affect the NSTLR can be related to land cover, wetness of soil and amount of solar radiation, caused by slope and angle.
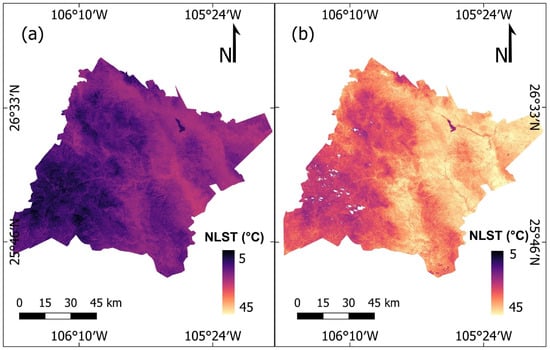
Figure 3.
NLST estimated for two seasons of year. (a) winter; (b) summer.
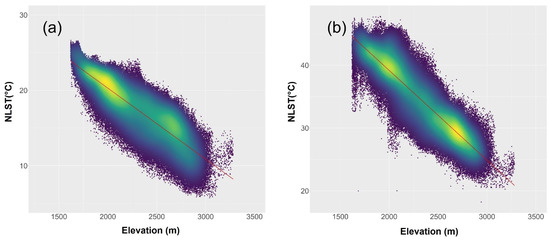
Figure 4.
Point density plots of elevation (meters above sea level) against Normalized Land Surface Temperature at two seasons (a) winter and (b) summer. The red line is the linearly fitted line.
The NSTLR in the areas with different features of aspect, LSZA and ESI, was calculated the DEM-NLST lineal regression model separately and the results is showed in Table 3. The goodness of fit of the 19 fitted linear models shown R2 above 0.5 in almost all variables. However, the differences in R2 values suggest that ESI condition strongly affects the DEM-NLST relationship.

Table 3.
Metrics of simple regression models. R2: coefficient of determination; RMSE: root mean square error; LSZA: Local solar zenith angle; ESI: Evaporative Stress Index. The gaps in the ESI data (-) are shown where there are not data of these ranges in this season of year.
Temperature Lapse Rate
In our study area, observed NSTLR was 9.4 °C km−1 for winter and 14.3 °C km−1 for summer. Likewise, the NSTLR values was different in the different aspects, the summer ranged between 14.2 and 15.1, while summer shows NSTLR ranged between 9.2 and 10.8. The highest NSTLR was found for Northweast aspect and the lowest for Southeast aspect at both seasons of the year (Figure 5).
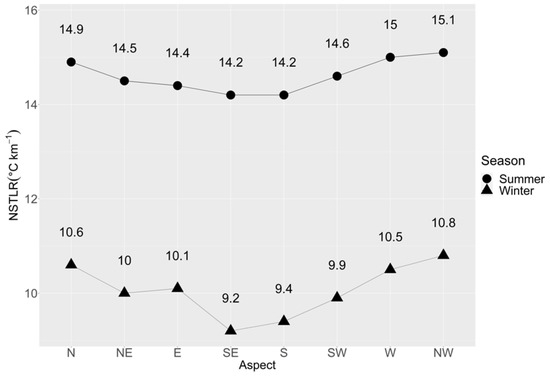
Figure 5.
Temperature lapse rate of the two seasons against aspect.
We utilized the LSZA equation to quantify the effect of solar position on the terrain slope at acquisition time, since the solar position changes the angle and intensity of the solar energy above the terrain [65,66]. NSTLR decreased with increasing LSZA for both seasons, possibly caused by a less direct impact of sunlight at higher LSZA, with a difference between seasons of more than 5 °C km−1 (Figure 6).
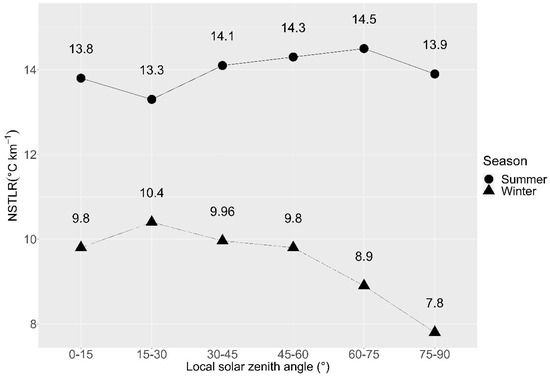
Figure 6.
Temperature lapse rate of the two seasons at different Local solar zenith angle.
NSTLR against ESI ranges are shown in Figure 7. Observed ESI ranges were 0.2–1 for summer and 0–0.8 for winter (Figure 7). Observed NSTLR in our study was lower in areas with higher ESI for both seasons. These results suggest that areas with the higher water availability have lower thermal gradients and this effect is stronger in summer season.
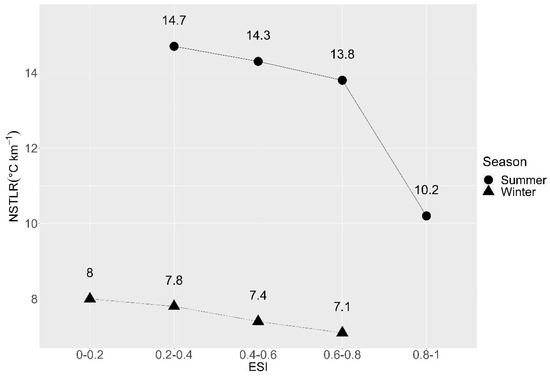
Figure 7.
Temperature lapse rate of the two seasons at different ESI ranges.
4. Discussion
In areas with a low availability of field weather stations, satellite data can provide an alternative information, capturing a higher degree of variability caused by interactions of climate with topography or evaporative processes, the latter influenced by land cover properties. NSTLR have been shown to have a middle uncertainty when estimated from satellite data, nevertheless the methodology developed by Firozjaei et al. [8] allows estimating NSTLR with more accuracy.
There is a clear difference of NLST between both seasons of year (winter and summer) explained by amount of energy received in summer, that is two times more than in winter [67]. In addition, biophysical and topographical features were key factors to NLST distribution, the effect of these variables seems to be stronger in winter. He at al. [18] noted that NLST was also influenced by aspect, slope, and solar radiation. On the order hand, the relative fine resolution scale of thermal satellite information might be evincing the topographic influences more accurately and cause the dispersion data observed in density plots of elevation-NLST.
The most widely accepted altitudinal NSTLR value is 6.5 °C km−1. This value is given as a function of temperature in a vertical atmospheric column of wet air is frequently accepted as a NSTLR constant in mountainous environments [20,24,68]. This general value does not address the particularities of every study area and might be inexact in some specific locations [69]. For example, Soto Molina and Delgado Granados [70] found NSTLR to vary between locations in their analysis in Nevado de Toluca, Mexico, and consequently suggested that it should be quantified at each location. The seasonal and spatial variation observed in our study supports the importance to analyze NSTLR at a regional and season level. Our observed NSTLR were higher than the values previously reported by several studies [32,42,71]; this could be related to the influence of the land use types analysed on the thermal characteristics of the land Surface. Future studies could focus on analysing NSTLR variations against land use categories [72].
In the present study, the NSTLR was higher in summer, this agrees with higher NSTLR observed in summer in previous studies, such as Tang and Fang [27] study in a mountainous location in China or Navarro-Serrano, López-Moreno, Azorin-Molina, Alonso-González, Tomás-Burguera, Sanmiguel-Vallelado, Revuelto and Vicente-Serrano [71] analysis in the main mountain ranges in Spain. In contrast, Li et al. [73] observed a more marked NSTLR in winter season in Northern China mountain areas. This discrepancy could be related to our study area being dominated by semiarid ecosystems, with pasturelands in the lower slopes. It could also possibly be explained by the precipitation regimes characteristic of the area of study, receiving precipitation in summer season [74], therefore having lower evaporative stress in spite of the high temperatures. On the other hand, lower precipitation in winter resulted in lower water availability for evapotranspiration and a higher hydric stress. Conversely, studies reporting higher NSTLR in winter than in summer are generally associated with mountain ecosystems with higher humidity conditions [24,27,73,75]. These results confirm the utility of accounting for evaporative stress in understanding the seasonal and spatial variations of the thermal gradient.
More specifically, our study reveals the potential of the relatively recent ECOSTRESS sensor to characterize the impact of vegetation evaporative stress on thermal gradients from the Landsat sensor at relatively fine spatial scales. The high variation observed in summer NSTLR across ESI intervals, with a range from wetter areas with lower NSTLR, to areas with higher water stress and with higher NSTLR values, might be related to contrasting interactions of vegetation cover and water stress conditions. Areas with high vegetation cover limit sunlight incidence on terrain surface, cooling surfaces through evapotranspiration, while bare ground areas are associated to high surface temperatures; this might result in high NSTLR, mainly in summer season, where the solar radiation has higher effects [18,26]. While our findings agree with previous studies reporting effects of water availability on LST in environments with altitudinal variability (e.g., [1,27]), such previous analyses were conducted utilizing other water availability variables such as NDVI [1], unlike the ECOSTRESS ESI data utilized here.
The aspect was an important characteristic for the NSTLR values, it had higher values in the Northwest aspect of the two seasons studied (winter and summer). In the north hemisphere, southern and eastern aspects generally present a more homogeneous temperature through the altitudinal gradient. That agrees with, Liu and Li [76] in a study in China mountains where observed a higher NSTLR in North and West aspects, which are opposite to solar radiation direction. Aspect plays a key role in thermal processes in mountain areas; the higher NSTLR observed for N and NW aspects for both seasons might be related to a non-homogeneous heating process in aspects opposed to solar radiation, as opposed to a more homogeneous heating in aspects oriented towards solar radiation (i.e., S and SE) [18]. In the north hemisphere, southern and eastern aspects generally present a more homogeneous temperature through the altitudinal gradient.
Meanwhile, higher NSTLR in the 0–15° LSZA range are very possibly a consequence of a higher solar radiation, which in turns affects moisture conditions [75], which also affects NSTLR (i.e., higher NSTLR under water stress conditions) (e.g., [77]). This supports the effect of solar angle and slope interactions on the thermal conditions in mountain ecosystems observed by several authors [18,24,69].
These results suggest sensitivity of NLST derived of Landsat-8 thermal information. Besides, ECOSTRESS product, ESI allows to analyze dynamics of vegetation water stress and temperature in our study area across an altitudinal gradient, possibly capturing variations between vegetation types and tree cover characteristics, a point that deserves further analysis. NSTLR analysis can help to understand the altitudinal migration of forest species that has been reported in several locations globally as a consequence of climate change [78,79,80,81]. Detailed NSTLR and ESI maps might aid in identifying fire-prone areas [82,83]. Future studies might explore the inclusion of local relationships of topographic effects on temperature (e.g., [84]) to refine ongoing research of fire risk (e.g., [43,44,85,86,87]) or biomass or tree growth modeling (e.g., [88,89]) in these diverse and complex ecosystems.
5. Conclusions
Near-surface temperature lapse rate (NSTLR) is one of the main features to understand climatic dynamics in mountain environments. Our results showed variation in NSTLR, quantified from NLST derived of Landsat-8 surface temperature and environmental variables, by season. Winter and summer NSTLR were different than the global average constant value widely utilized (6.5 °C km−1). NSTLR also varied widely between aspects, with the highest value observed for Northwest aspect in both seasons. In addition, Local solar zenith angle (LSZA) and evapotranspiration also influenced NSTLR regulation. The areas with greater LSZA showed lower NSTLR in both seasons. Evaporative Stress Index (ESI) showed a negative relation with NSTLR values, suggesting a role of water stress in increasing the NSTLR, this being more marked in summer season.
The results from the current study suggest potential of Landsat-8 LST and ECOSTRESS ESI to capture the interactions of topographic factors and vegetative stress on NSTLR gradients at relatively fine spatial scales, which can aid in water management planning and conservation planning. Further factors, such as vegetation types and tree cover are possibly influencing these water stress-topography-temperature gradient interactions, a point that should be further analyzed in future studies. Furthermore, future studies might focus on a multitemporal analysis of thermal gradients, including further quantifying topography and water stress interactions with vegetation and fuel characteristics, which might be beneficial for enhancing fire risk or tree growth predictions in these complex ecosystems.
Author Contributions
P.M.L.-S. and M.R.-C. planned and designed the research; M.R.-C. and P.M.L.-S. contributed to data analysis; and P.M.L.-S. led the manuscript with contributions from M.R.-C. and D.J.V.-N.; M.R.-C. writing—original draft preparation, J.C.H.-D., C.W. and D.J.V.-N. writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors are grateful to Mexican National Science and Technology Council (CONACYT) for supporting the studies of the first author. We are also grateful for the careful review and valuable comments by the anonymous reviewers.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bindajam, A.A.; Mallick, J.; AlQadhi, S.; Singh, C.K.; Hang, H.T. Impacts of Vegetation and Topography on Land Surface Temperature Variability over the Semi-Arid Mountain Cities of Saudi Arabia. Atmosphere 2020, 11, 762. [Google Scholar] [CrossRef]
- Naud, L.; Måsviken, J.; Freire, S.; Angerbjörn, A.; Dalén, L.; Dalerum, F. Altitude effects on spatial components of vascular plant diversity in a subarctic mountain tundra. Ecol. Evol. 2019, 9, 4783–4795. [Google Scholar] [CrossRef]
- Daw, T.M.; Hicks, C.C.; Brown, K.; Chaigneau, T.; Januchowski-Hartley, F.A.; Cheung, W.W.L.; Rosendo, S.; Crona, B.; Coulthard, S.; Sandbrook, C.; et al. Elasticity in ecosystem services: Exploring the variable relationship between ecosystems and human well-being. Ecol. Soc. 2016, 21. [Google Scholar] [CrossRef]
- Pastur, G.J.M.; Perera, A.H.; Peterson, U.; Iverson, L.R. Ecosystem Services from Forest Landscapes: An Overview. In Ecosystem Services from Forest Landscapes; Springer: Singapore, 2018; pp. 1–10. [Google Scholar]
- Liu, L.; Wang, Z.; Wang, Y.; Zhang, Y.; Shen, J.; Qin, D.; Li, S. Trade-off analyses of multiple mountain ecosystem services along elevation, vegetation cover and precipitation gradients: A case study in the Taihang Mountains. Ecol. Indic. 2019, 103, 94–104. [Google Scholar] [CrossRef]
- Mengist, W.; Soromessa, T.; Legese, G. Ecosystem services research in mountainous regions: A systematic literature review on current knowledge and research gaps. Sci. Total Environ. 2020, 702, 134581. [Google Scholar] [CrossRef] [PubMed]
- Spehn, E.M.; Rudmann-Maurer, K.; Körner, C. Mountain biodiversity. Plant Ecol. Divers. 2011, 4, 301–302. [Google Scholar] [CrossRef]
- Firozjaei, M.K.; Fathololoumi, S.; Alavipanah, S.K.; Kiavarz, M.; Vaezi, A.R.; Biswas, A. A new approach for modeling near surface temperature lapse rate based on normalized land surface temperature data. Remote Sens. Environ. 2020, 242, 111746. [Google Scholar] [CrossRef]
- Grêt-Regamey, A.; Brunner, S.H.; Kienast, F. Mountain Ecosystem Services: Who Cares? Mt. Res. Dev. 2012, 32, S23–S34. [Google Scholar] [CrossRef]
- Hagedorn, F.; Mulder, J.; Jandl, R. Mountain soils under a changing climate and land-use. Biogeochemistry 2009, 97, 1–5. [Google Scholar] [CrossRef]
- Beniston, M. Climatic Change in Mountain Regions: A Review of Possible Impacts. Clim. Chang. 2003, 59, 5–31. [Google Scholar] [CrossRef]
- Sigdel, S.R.; Zhang, H.; Zhu, H.; Muhammad, S.; Liang, E. Retreating Glacier and Advancing Forest Over the Past 200 Years in the Central Himalayas. J. Geophys. Res. Biogeosci. 2020, 125, 005751. [Google Scholar] [CrossRef]
- Zeng, Z.; Wang, D.; Yang, L.; Wu, J.; Ziegler, A.D.; Liu, M.; Ciais, P.; Searchinger, T.D.; Yang, Z.-L.; Chen, D.; et al. Deforestation-induced warming over tropical mountain regions regulated by elevation. Nat. Geosci. 2021, 14, 23–29. [Google Scholar] [CrossRef]
- Sakai, A.; Fujita, K. Contrasting glacier responses to recent climate change in high-mountain Asia. Sci. Rep. 2017, 7, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Tuladhar, D.; Dewan, A.; Kuhn, M.; Corner, R.J. Spatio-temporal rainfall variability in the Himalayan mountain catchment of the Bagmati River in Nepal. Theor. Appl. Clim. 2019, 139, 599–614. [Google Scholar] [CrossRef]
- Li, Y.; Zeng, Z.; Zhao, L.; Piao, S. Spatial patterns of climatological temperature lapse rate in mainland China: A multi-time scale investigation. J. Geophys. Res. Atmos. 2015, 120, 2661–2675. [Google Scholar] [CrossRef]
- Fang, J.-Y.; Yoda, K. Climate and vegetation in China (I). Changes in the altitudinal lapse rate of temperature and distribution of sea level temperature. Ecol. Res. 1988, 3, 37–51. [Google Scholar] [CrossRef]
- He, J.; Zhao, W.; Li, A.; Wen, F.; Yu, D. The impact of the terrain effect on land surface temperature variation based on Landsat-8 observations in mountainous areas. Int. J. Remote Sens. 2019, 40, 1808–1827. [Google Scholar] [CrossRef]
- Vuille, M.; Bradley, R.S. Mean annual temperature trends and their vertical structure in the tropical Andes. Geophys. Res. Lett. 2000, 27, 3885–3888. [Google Scholar] [CrossRef]
- Barry, R.G.; Richard, J.C. Atmosphere, Weather and Climate, 1st ed.; Taylor & Francis Group: London, UK, 2009. [Google Scholar]
- Kattel, D.B.; Yao, T.; Panday, P.K. Near-surface air temperature lapse rate in a humid mountainous terrain on the southern slopes of the eastern Himalayas. Theor. Appl. Clim. 2018, 132, 1129–1141. [Google Scholar] [CrossRef]
- Guo, X.; Wang, L.; Tian, L. Spatio-temporal variability of vertical gradients of major meteorological observations around the Tibetan Plateau. Int. J. Clim. 2016, 36, 1901–1916. [Google Scholar] [CrossRef]
- Harlow, R.C.; Burke, E.J.; Scott, R.; Shuttleworth, W.J.; Brown, C.M.; Petti, J.R. Research Note:Derivation of temperature lapse rates in semi-arid south-eastern Arizona. Hydrol. Earth Syst. Sci. 2004, 8, 1179–1185. [Google Scholar] [CrossRef]
- Minder, J.R.; Mote, P.W.; Lundquist, J.D. Surface temperature lapse rates over complex terrain: Lessons from the Cascade Mountains. J. Geophys. Res. Space Phys. 2010, 115, 115. [Google Scholar] [CrossRef]
- Hais, M.; Kučera, T. The influence of topography on the forest surface temperature retrieved from Landsat TM, ETM+ and ASTER thermal channels. ISPRS J. Photogramm. Remote Sens. 2009, 64, 585–591. [Google Scholar] [CrossRef]
- Firozjaei, M.K.; Fathololuomi, S.; Alavipanah, S.K.; Kiavarz, M.; Vaezi, A.; Biswas, A.; Ghorbani, A. Modeling the impact of surface characteristics on the near surface temperature lapse rate. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII-4/W18, 395–399. [Google Scholar] [CrossRef]
- Tang, Z.; Fang, J. Temperature variation along the northern and southern slopes of Mt. Taibai, China. Agric. For. Meteorol. 2006, 139, 200–207. [Google Scholar] [CrossRef]
- Veh, G.; Korup, O.; Walz, A. Hazard from Himalayan glacier lake outburst floods. Proc. Natl. Acad. Sci. USA 2020, 117, 907–912. [Google Scholar] [CrossRef]
- Muradyan, V.; Tepanosyan, G.; Asmaryan, S.; Saghatelyan, A.; Dell’Acqua, F. Relationships between NDVI and climatic factors in mountain ecosystems: A case study of Armenia. Remote Sens. Appl. Soc. Environ. 2019, 14, 158–169. [Google Scholar] [CrossRef]
- García-Santos, V.; Cuxart, J.; Martínez-Villagrasa, D.; Jiménez, M.A.; Simó, G. Comparison of Three Methods for Estimating Land Surface Temperature from Landsat 8-TIRS Sensor Data. Remote Sens. 2018, 10, 1450. [Google Scholar] [CrossRef]
- Jain, S.K.; Goswami, A.; Saraf, A.K. Determination of land surface temperature and its lapse rate in the Satluj River basin using NOAA data. Int. J. Remote Sens. 2008, 29, 3091–3103. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, L.; Li, X.; Chen, D. Temporal and spatial changes in estimated near-surface air temperature lapse rates on Tibetan Plateau. Int. J. Clim. 2018, 38, 2907–2921. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, F.; Zhang, G.; Che, T.; Yan, W. How Accurately Can the Air Temperature Lapse Rate Over the Tibetan Plateau Be Estimated From MODIS LSTs? J. Geophys. Res. Atmos. 2018, 123, 3943–3960. [Google Scholar] [CrossRef]
- Peters, J.; Van Doninck, J.; Verhoest, N.E.C.; De Baets, B.; De Clercq, E.M.; Ducheyne, E. Influence of topographic normalization on the vegetation index–surface temperature relationship. J. Appl. Remote Sens. 2012, 6, 063518. [Google Scholar] [CrossRef]
- Qin, Y.; Ren, G.; Zhai, T.; Zhang, P.; Wen, K. A New Methodology for Estimating the Surface Temperature Lapse Rate Based on Grid Data and Its Application in China. Remote Sens. 2018, 10, 1617. [Google Scholar] [CrossRef]
- Penton, D.J.; Neumann, L.E.; Karki, R.; Nepal, S. Verifying Temperature Lapse Rates in the Eastern Himalayas using Landsat 7 and 8. In Proceedings of the 21st International Congress on Modelling and Simulation, Gold Coast, Australia, 29 Novembe–4 December 2015. [Google Scholar]
- Zhuang, Y.; Liu, X.; Nguyen, T.; He, Q.; Hong, S. Global remote sensing research trends during 1991–2010: A bibliometric analysis. Science 2013, 96, 203–219. [Google Scholar] [CrossRef]
- Martinez-Gracia, A.; Arauzo, I.; Uche, J. Chapter 5-Solar energy availability. In Solar Hydrogen Production; Calise, F., D’Accadia, M.D., Santarelli, M., Lanzini, A., Ferrero, D., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 113–149. [Google Scholar]
- Anderson, M.C.; Hain, C.R.; Wardlow, B.; Pimstein, A.; Mecikalski, J.R.; Kustas, W.P. Evaluation of Drought Indices Based on Thermal Remote Sensing of Evapotranspiration over the Continental United States. J. Clim. 2011, 24, 2025–2044. [Google Scholar] [CrossRef]
- Fisher, J.B.; Lee, B.; Purdy, A.J.; Halverson, G.H.; Dohlen, M.B.; Cawse-Nicholson, K.; Wang, A.; Anderson, R.G.; Aragon, B.; Arain, M.A.; et al. ECOSTRESS: NASA’s Next Generation Mission to Measure Evapotranspiration From the International Space Station. Water Resour. Res. 2020, 56, e2019WR026058. [Google Scholar] [CrossRef]
- Liu, N.; Oishi, A.C.; Miniat, C.F.; Bolstad, P. An evaluation of ECOSTRESS products of a temperate montane humid forest in a complex terrain environment. Remote Sens. Environ. 2021, 265, 112662. [Google Scholar] [CrossRef]
- Moradi, M.; Salahi, B.; Masoodian, S.A. On the relationship between MODIS Land Surface Temperature and topography in Iran. Phys. Geogr. 2018, 39, 354–367. [Google Scholar] [CrossRef]
- Briones-Herrera, C.I.; Vega-Nieva, D.J.; Monjarás-Vega, N.A.; Flores-Medina, F.; Lopez-Serrano, P.M.; Corral-Rivas, J.J.; Carrillo-Parra, A.; Pulgarin-Gámiz, M.Á.; Alvarado-Celestino, E.; González-Cabán, A.; et al. Modeling and Mapping Forest Fire Occurrence from Aboveground Carbon Density in Mexico. Forests 2019, 10, 402. [Google Scholar] [CrossRef]
- Monjarás-Vega, N.A.; Briones-Herrera, C.I.; Vega-Nieva, D.J.; Calleros-Flores, E.; Corral-Rivas, J.J.; López-Serrano, P.M.; Pompa-García, M.; Rodríguez-Trejo, D.A.; Carrillo-Parra, A.; González-Cabán, A.; et al. Predicting forest fire kernel density at multiple scales with geographically weighted regression in Mexico. Sci. Total Environ. 2020, 718, 137313. [Google Scholar] [CrossRef]
- Aragón-Piña, E.E.; Garza-Herrera, A.; González-Elizondo, M.S.; Luna-Vega, I. Composición y estructura de las comunidades vegetales del rancho El Durangueño, en la Sierra Madre Occidental, Durango, México. Rev. Mex. Biodivers. 2010, 81, 771–787. [Google Scholar] [CrossRef]
- González-Elizondo, M.S.; González-Elizondo, M.; Tena-Flores, J.A.; Ruacho-González, L.; López-Enríquez, I.L. Vegetación de la Sierra Madre Occidental, México: Una síntesis. Acta Botánica Mex. 2012, 100, 351–403. [Google Scholar] [CrossRef]
- Hernandez-Díaz, J.C.; Prieto-Ruiz, J.A. Estudio Regional Forestal Caso UMAFOR 1001; Secretaría de Medio Ambiente y Recursos Naturales (SEMARNAT): Durango, Mexico, 2007. [Google Scholar]
- Wehenkel, C.; Reyes-Martínez, A.; Martínez-Guerrero, J.H.; Pinedo-Alvarez, C.; Lopez-Sanchez, C.A. The bird species diversity in the wintering season is negatively associated with precipitation, tree species diversity and stand density in the Sierra Madre Occidental, Durango, Mexico. Community Ecol. 2017, 18, 63–71. [Google Scholar] [CrossRef]
- Silva-Flores, R.; Pérez-Verdín, G.; Wehenkel, C. Patterns of Tree Species Diversity in Relation to Climatic Factors on the Sierra Madre Occidental, Mexico. PLoS ONE 2014, 9, e105034. [Google Scholar] [CrossRef]
- INEGI. Conjunto de Datos Vectoriales de Uso del Suelo y Vegetación Escala 1:250,000, Series VI. Available online: http://www.conabio.gob.mx/informacion/metadata/gis/usv250s6gw.xml?_httpcache=yes&_xsl=/db/metadata/xsl/fgdc_html.xsl&_indent=no (accessed on 5 October 2021).
- QGIS Development Team. QGIS Geographic Information System. Open Source Geospatial Foundation Project. 2016. Available online: http://qgis.osgeo.org (accessed on 22 November 2020).
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Parastatidis, D.; Mitraka, Z.; Chrysoulakis, N.; Abrams, M. Online Global Land Surface Temperature Estimation from Landsat. Remote Sens. 2017, 9, 1208. [Google Scholar] [CrossRef]
- Dewan, A.; Kiselev, G.; Botje, D. Diurnal and seasonal trends and associated determinants of surface urban heat islands in large Bangladesh cities. Appl. Geogr. 2021, 135, 102533. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the great plains with ERTS. NASA Spec. Publ. 1973, 351, 309–317. [Google Scholar]
- Zha, Y.; Gao, J.; Ni, S. Use of normalized difference built-up index in automatically mapping urban areas from TM imagery. Int. J. Remote Sens. 2003, 24, 583–594. [Google Scholar] [CrossRef]
- Gao, B.-C. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Raissouni, N. Toward remote sensing methods for land cover dynamic monitoring: Application to Morocco. Int. J. Remote Sens. 2000, 21, 353–366. [Google Scholar] [CrossRef]
- Ermida, S.L.; Soares, P.; Mantas, V.; Göttsche, F.-M.; Trigo, I.F. Google Earth Engine Open-Source Code for Land Surface Temperature Estimation from the Landsat Series. Remote Sens. 2020, 12, 1471. [Google Scholar] [CrossRef]
- Dozier, J.; Frew, J. Rapid calculation of terrain parameters for radiation modeling from digital elevation data. IEEE Trans. Geosci. Remote Sens. 1990, 28, 963–969. [Google Scholar] [CrossRef]
- Nguyen, H.; Wheeler, M.C.; A Otkin, J.; Cowan, T.; Frost, A.J.; Stone, R.C. Using the evaporative stress index to monitor flash drought in Australia. Environ. Res. Lett. 2019, 14, 064016. [Google Scholar] [CrossRef]
- Fisher, J.B. Level-4 Evaporative Stress Index L4(ESI_PT-JPL) Algorithm Theoretical Basis Document; JPL: Pasadena, CA, USA, 2018; p. 13. [Google Scholar]
- Hutengs, C.; Vohland, M. Downscaling land surface temperatures at regional scales with random forest regression. Remote Sens. Environ. 2016, 178, 127–141. [Google Scholar] [CrossRef]
- Sismanidis, P.; Keramitsoglou, I.; Bechtel, B.; Kiranoudis, C.T. Improving the Downscaling of Diurnal Land Surface Temperatures Using the Annual Cycle Parameters as Disaggregation Kernels. Remote Sens. 2016, 9, 23. [Google Scholar] [CrossRef]
- Bennie, J.; Hill, M.O.; Baxter, R.; Huntley, B. Influence of slope and aspect on long-term vegetation change in British chalk grasslands. J. Ecol. 2006, 94, 355–368. [Google Scholar] [CrossRef]
- Weiss, D.J.; Walsh, S.J. Remote Sensing of Mountain Environments. Geogr. Compass 2008, 3, 1–21. [Google Scholar] [CrossRef]
- Fu, P.; Rich, P.M. A geometric solar radiation model with applications in agriculture and forestry. Comput. Electron. Agric. 2002, 37, 25–35. [Google Scholar] [CrossRef]
- Maurer, E.P.; Wood, A.W.; Adam, J.C.; Lettenmaier, D.P.; Nijssen, B. A Long-Term Hydrologically Based Dataset of Land Surface Fluxes and States for the Conterminous United States. J. Clim. 2002, 15, 3237–3251. [Google Scholar] [CrossRef]
- Córdova, M.; Célleri, R.; Shellito, C.J.; Orellana-Alvear, J.; Abril, A.; Carrillo-Rojas, G. Near-Surface Air Temperature Lapse Rate Over Complex Terrain in the Southern Ecuadorian Andes: Implications for Temperature Mapping. Arct. Antarct. Alp. Res. 2016, 48, 673–684. [Google Scholar] [CrossRef]
- Molina, V.H.S.; Granados, H.D. Estimación de la temperatura del aire en la alta montaña mexicana mediante un modelo de elevación del terreno: Caso del volcán Nevado de Toluca (México)/Estimation of the air temperature in the Mexican high mountain environment by means of a model of elevation of the terrain, case of the Nevado de Toluca volcano (Mexico). Ería 2020, 2, 167–182. [Google Scholar] [CrossRef]
- Navarro-Serrano, F.; Lopez-Moreno, I.; Azorin-Molina, C.; González, E.A.; Tomás-Burguera, M.; Sanmiguel-Vallelado, A.; Revuelto, J.; Vicente-Serrano, S.M. Estimation of near-surface air temperature lapse rates over continental Spain and its mountain areas. Int. J. Clim. 2018, 38, 3233–3249. [Google Scholar] [CrossRef]
- Rolland, C. Spatial and Seasonal Variations of Air Temperature Lapse Rates in Alpine Regions. J. Clim. 2003, 16, 1032–1046. [Google Scholar] [CrossRef]
- Li, X.; Wang, L.; Chen, D.; Yang, K.; Xue, B.; Sun, L. Near-surface air temperature lapse rates in the mainland China during 1962–2011. J. Geophys. Res. Atmos. 2013, 118, 7505–7515. [Google Scholar] [CrossRef]
- Echeverría, C.; Huber, A.; Taberlet, F. Estudio comparativo de los componentes del balance hídrico en un bosque nativo y una pradera en el sur de Chile. Bosque (Valdivia) 2007, 28, 271–280. [Google Scholar] [CrossRef][Green Version]
- Blandford, T.R.; Humes, K.S.; Harshburger, B.J.; Moore, B.C.; Walden, V.P.; Ye, H. Seasonal and Synoptic Variations in Near-Surface Air Temperature Lapse Rates in a Mountainous Basin. J. Appl. Meteorol. Clim. 2008, 47, 249–261. [Google Scholar] [CrossRef]
- Liu, Y.; Li, F. A preliminary approach on the land surface temperature (LST) lapse rate of mountain area using MODIS data. In Proceedings of the Remote Sensing and Space Technology for Multidisciplinary Research and Applications, Beijing, China, 19 May 2006; Volume 6199, p. 619907. [Google Scholar]
- Kattel, D.B.; Yao, T.; Yang, K.; Tian, L.; Yang, G.; Joswiak, D. Temperature lapse rate in complex mountain terrain on the southern slope of the central Himalayas. Theor. Appl. Clim. 2013, 113, 671–682. [Google Scholar] [CrossRef]
- Joshi, R.; Sambhav, K. Near Surface Temperature Lapse Rate for Treeline Environment in Western Himalaya and Possible Impacts on Ecotone Vegetation; ResearchGate: Berlin, Germany, 2018. [Google Scholar]
- Lute, A.C.; Abatzoglou, J.T. Best practices for estimating near-surface air temperature lapse rates. Int. J. Clim. 2021, 41, E110–E125. [Google Scholar] [CrossRef]
- Gheyret, G.; Mohammat, A.; Tang, Z.-Y. Elevational patterns of temperature and humidity in the middle Tianshan Mountain area in Central Asia. J. Mt. Sci. 2020, 17, 397–409. [Google Scholar] [CrossRef]
- Kidane, Y.O.; Steinbauer, M.J.; Beierkuhnlein, C. Dead end for endemic plant species? A biodiversity hotspot under pressure. Glob. Ecol. Conserv. 2019, 19, e00670. [Google Scholar] [CrossRef]
- Holden, Z.A.; Jolly, W.M.; Swanson, A.; Warren, D.A.; Jencso, K.; Maneta, M.; Burgard, M.; Gibson, C.; Hoylman, Z.; Landguth, E.L. TOPOFIRE: A Topographically Resolved Wildfire Danger and Drought Monitoring System for the Conterminous United States. Bull. Am. Meteorol. Soc. 2019, 100, 1607–1613. [Google Scholar] [CrossRef]
- Havel, A.; Tasdighi, A.; Arabi, M. Assessing the hydrologic response to wildfires in mountainous regions. Hydrol. Earth Syst. Sci. 2018, 22, 2527–2550. [Google Scholar] [CrossRef]
- Holden, Z.A.; Jolly, W.M. Modeling topographic influences on fuel moisture and fire danger in complex terrain to improve wildland fire management decision support. For. Ecol. Manag. 2011, 262, 2133–2141. [Google Scholar] [CrossRef]
- Flores-Medina, F.; Vega Nieva, D.J.; Monjarás-Vega, N.; Briones-Herrera, C.I.; Corral-Rivas, J.J. Mapping fuel loads and fire behavior from Sentinel in Durango, NW Mexico. In Proceedings of the 6th International Fire Behavior and Fuels Conference, Albuquerque, NM, USA, 29 April–3 May 2019. [Google Scholar]
- Vega-Nieva, D.J.; Briseño-Reyes, J.; Nava-Miranda, M.G.; Calleros-Flores, E.; López-Serrano, P.M.; Corral-Rivas, J.J.; Montiel-Antuna, E.; Cruz-López, M.I.; Cuahutle, M.; Ressl, R.; et al. Developing Models to Predict the Number of Fire Hotspots from an Accumulated Fuel Dryness Index by Vegetation Type and Region in Mexico. Forests 2018, 9, 190. [Google Scholar] [CrossRef]
- Vega-Nieva, D.J.; Nava-Miranda, M.G.; Calleros-Flores, E.; López-Serrano, P.M.; Briseño-Reyes, J.; López-Sánchez, C.; Corral-Rivas, J.J.; Montiel-Antuna, E.; Cruz-Lopez, M.I.; Ressl, R.; et al. Temporal patterns of active fire density and its relationship with a satellite fuel greenness index by vegetation type and region in Mexico during 2003–2014. Fire Ecol. 2019, 15, 28. [Google Scholar] [CrossRef]
- Briseño-Reyes, J.; Corral-Rivas, J.J.; Solis-Moreno, R.; Padilla-Martínez, J.R.; Vega-Nieva, D.J.; López-Serrano, P.M.; Vargas-Larreta, B.; Diéguez-Aranda, U.; Quiñonez-Barraza, G.; López-Sánchez, C.A. Individual Tree Diameter and Height Growth Models for 30 Tree Species in Mixed-Species and Uneven-Aged Forests of Mexico. Forests 2020, 11, 429. [Google Scholar] [CrossRef]
- López-Serrano, P.M.; Cárdenas-Domínguez, J.L.; Corral-Rivas, J.J.; Jiménez, E.; López-Sánchez, C.A.; Vega-Nieva, D.J. Modeling of Aboveground Biomass with Landsat 8 OLI and Machine Learning in Temperate Forests. Forests 2019, 11, 11. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).