A Novel Weighted Amplitude Modulation (WAM) System for Ambiguity Suppression of Spaceborne Hybrid Quad-Pol SAR
Abstract
:1. Introduction
2. Hybrid Quad-Pol SAR
2.1. Ambiguity-to-Signal Ratio
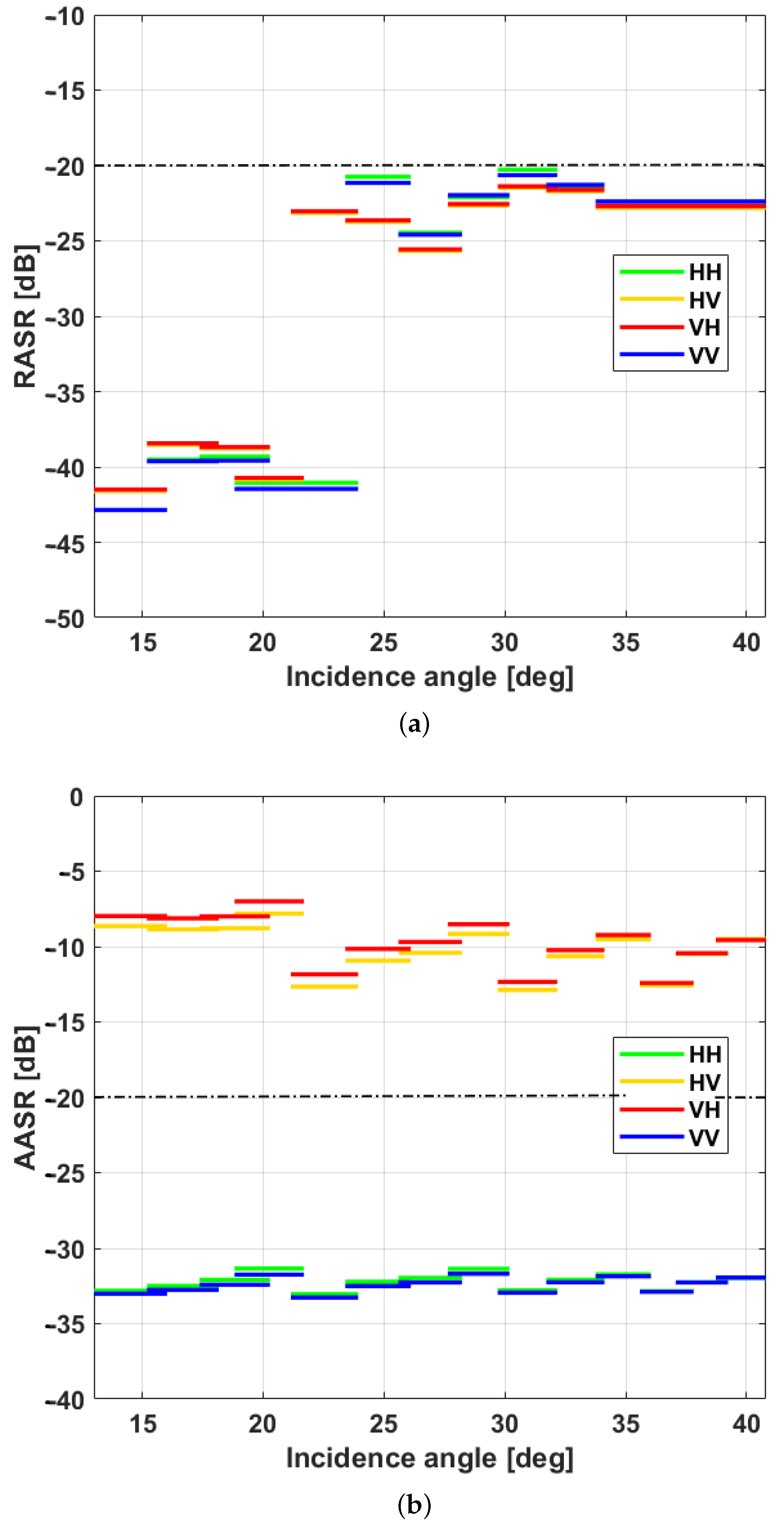
2.2. Performance Analysis
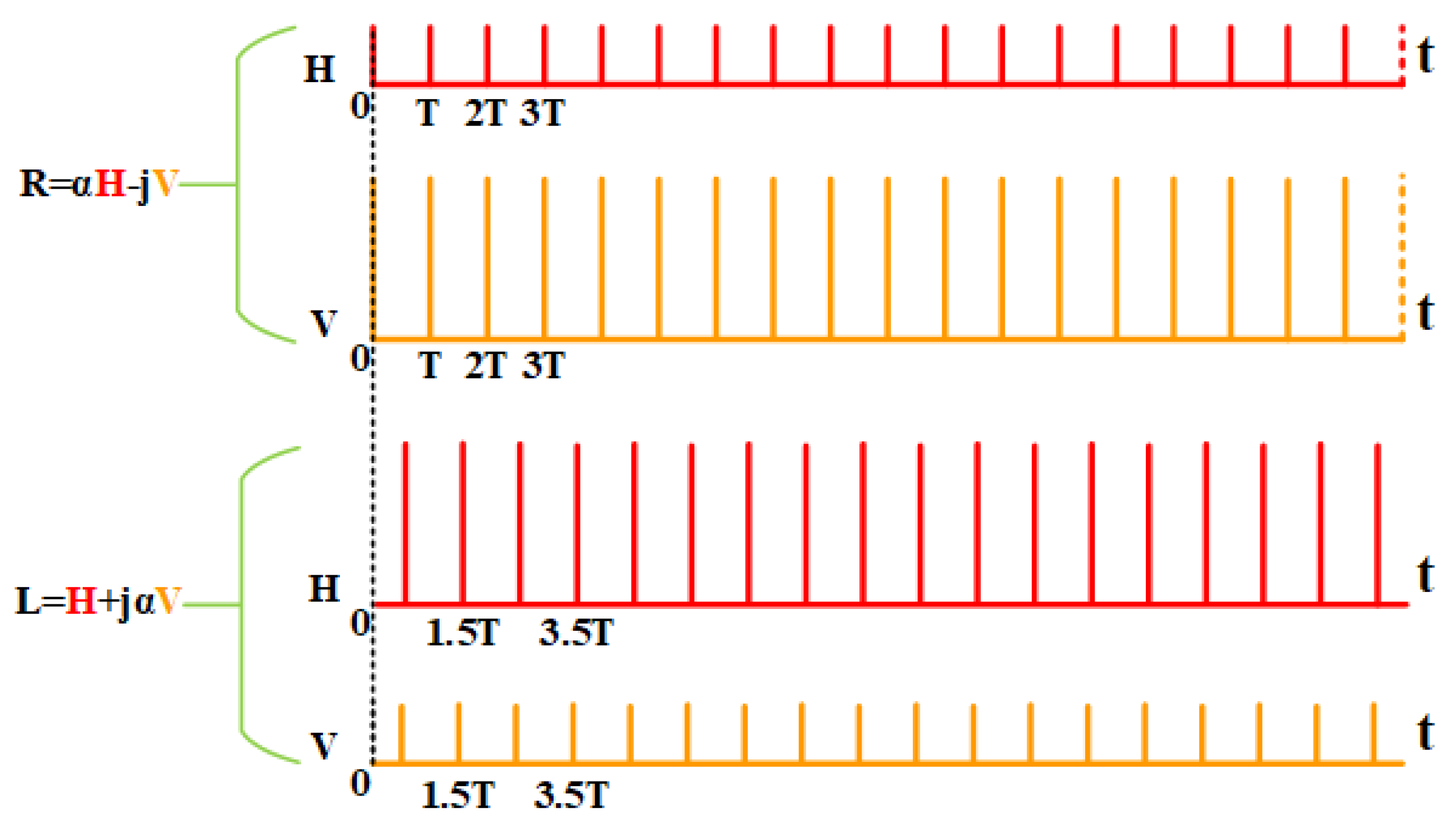
3. WAM Full-Pol SAR
3.1. The First Imaging Mode
3.2. The Second Imaging Mode
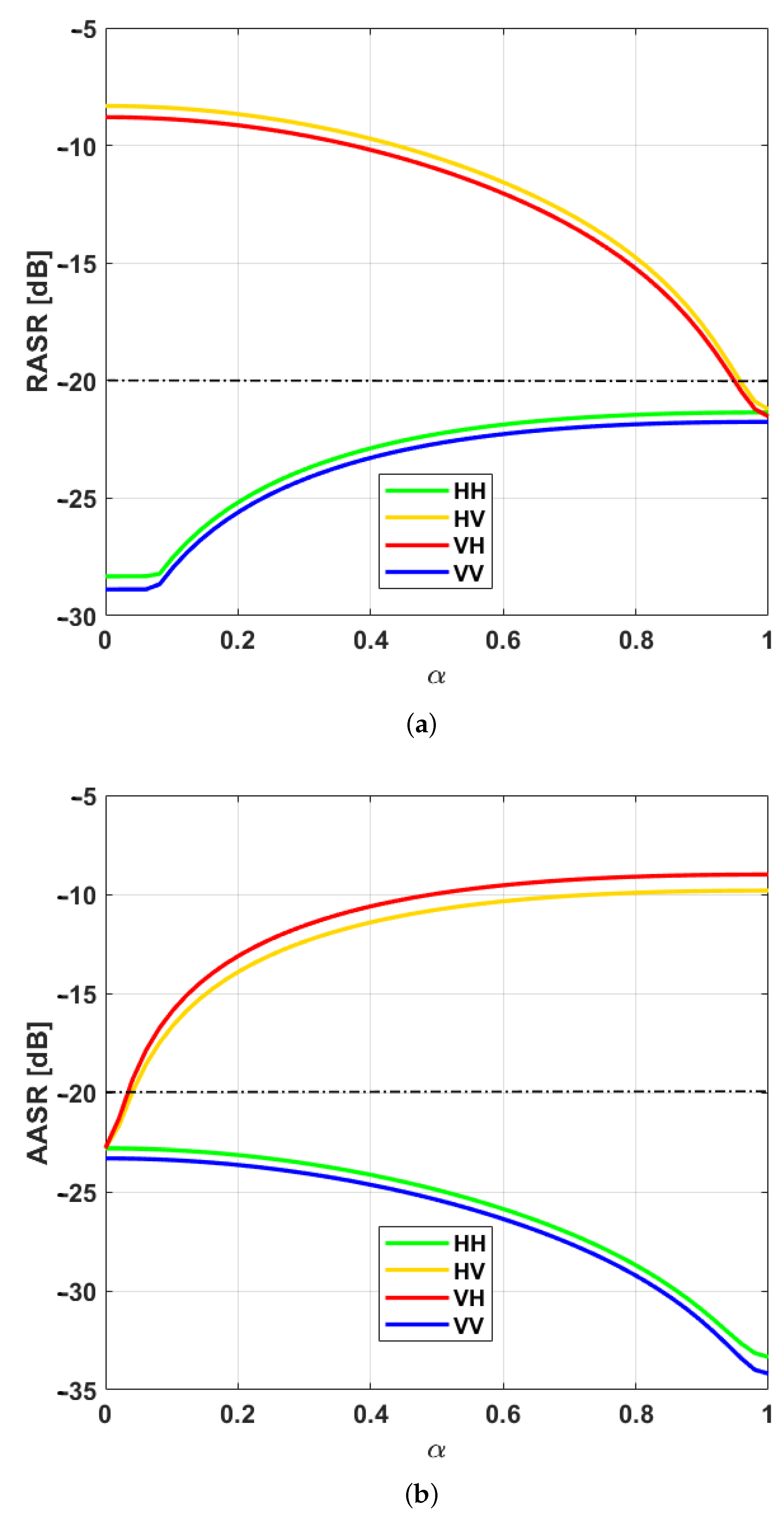
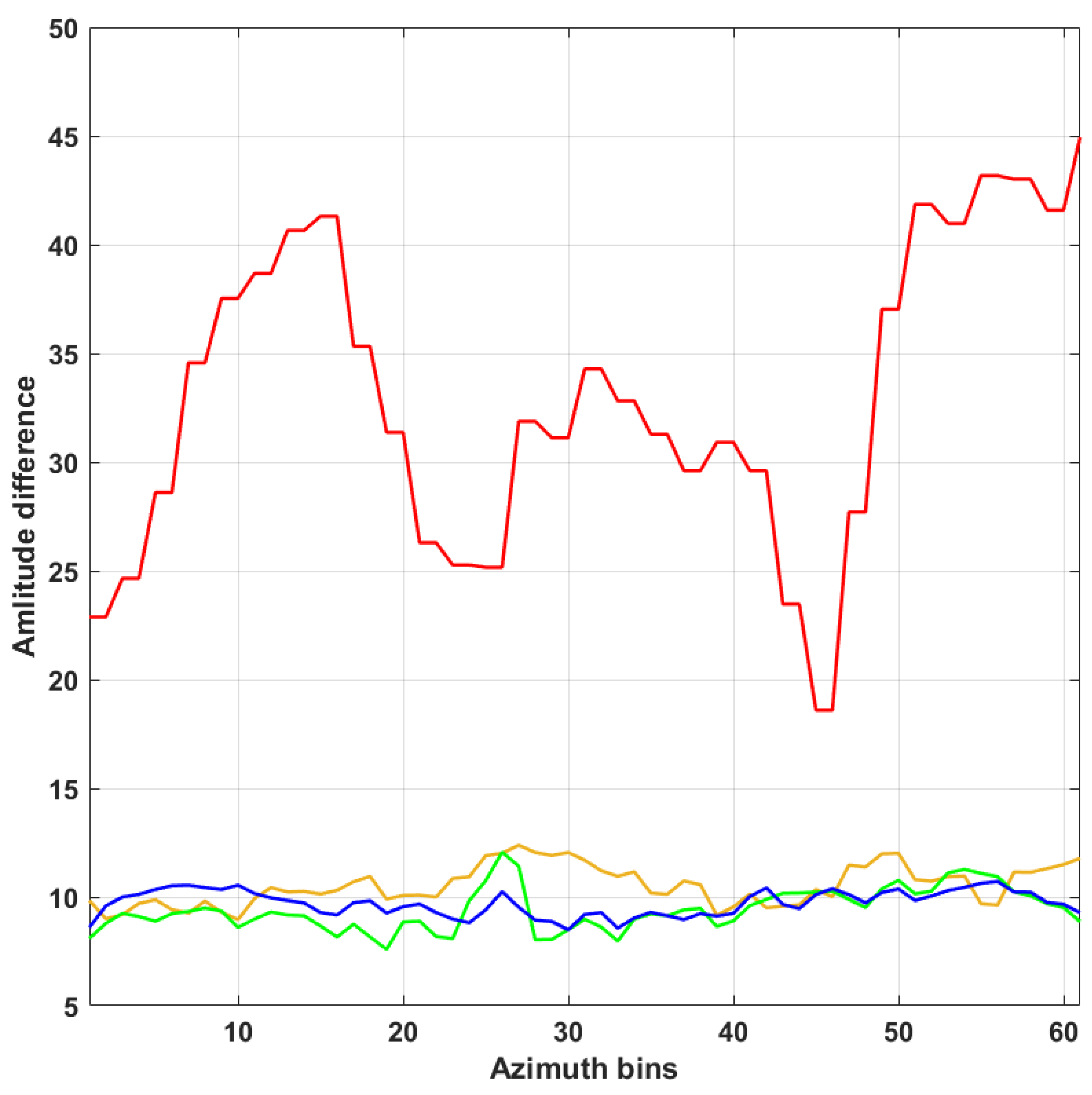
4. Simulations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Raney, R.K. Hybrid-Polarity SAR Architecture. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3397–3404. [Google Scholar] [CrossRef] [Green Version]
- Raney, R.K. Hybrid-quad-pol SAR. In Proceedings of the IGARSS 2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 8–11 July 2008; Volume 4, pp. 491–493. [Google Scholar]
- Blunt, S.D.; Mokole, E.L. Overview of radar waveform diversity. IEEE Aerosp. Electron. Syst. Mag. 2016, 31, 2–42. [Google Scholar] [CrossRef]
- Sadjadi, F. Improved target classification using optimum polarimetric SAR signatures. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 38–49. [Google Scholar] [CrossRef]
- Aldhubaib, F.; Shuley, N.V. Radar Target Recognition Based on Modified Characteristic Polarization States. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 1921–1933. [Google Scholar] [CrossRef]
- Touzi, R.; Hurley, J.; Vachon, P.W. Optimization of the Degree of Polarization for Enhanced Ship Detection Using Polarimetric RADARSAT-2. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5403–5424. [Google Scholar] [CrossRef]
- McCormick, P.; Jakabosky, J.; Blunt, S.D.; Allen, C.; Himed, B. Joint polarization/waveform design and adaptive receive processing. In Proceedings of the 2015 IEEE Radar Conference, Arlington, VA, USA, 10–15 May 2015; pp. 1382–1387. [Google Scholar]
- Fritz, J.P.; Chandrasekar, V. A Fully Polarimetric Characterization of the Impact of Precipitation on Short Wavelength Synthetic Aperture Radar. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2037–2048. [Google Scholar] [CrossRef]
- Lim, S.; Chandrasekar, V.; Bringi, V.N. Hydrometeor classification system using dual-polarization radar measurements: Mode improvements and in situ verification. IEEE Trans. Geosci. Remote Sens. 2005, 43, 792–801. [Google Scholar] [CrossRef]
- Bringi, V.N.; Chandrasekar, V. Polarimetric Doppler Weather Radar: Principles and Applications; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Li, P.; Zhao, F.; Liu, D.; Ou, N.; Cao, C.; Liu, X.; Zhang, Y.; Deng, Y.; Wang, R. First Demonstration of Hybrid Quad-Pol SAR Based on P-Band Airborne Experiment. IEEE Trans. Geosci. Remote Sens. 2021. [Google Scholar] [CrossRef]
- Zhang, R.; Wang, Y.; Hu, J.; Yang, W.; Chen, J.; Zhu, X.X. SAR4LCZ-Net: A Complex-valued Convolutional Neural Network for Local Climate Zones Classification Using Gaofen-3 Quad-pol SAR Data. IEEE Trans. Geosci. Remote Sens. 2021. [Google Scholar] [CrossRef]
- Campbell, B.A. Scale-dependent surface roughness behavior and its impact on empirical models for radar backscatter. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3480–3488. [Google Scholar] [CrossRef]
- Truong-Loi, M.-L.; Saatchi, S.; Jaruwatanadilok, S. Soil moisture estimation under tropical forests using UHF radar polarimetry. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1718–1727. [Google Scholar] [CrossRef]
- Yang, Z.; Xu, H.; Huang, P.; Liu, A.; Tian, M.; Liao, G. Preliminary Results of Multichannel SAR-GMTI Experiments for Airborne Quad-Pol Radar System. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3822–3840. [Google Scholar] [CrossRef]
- Hoang, H.K.; Bernier, M.; Duchesne, S.; Tran, Y.M. Rice Mapping Using RADARSAT-2 Dual- and Quad-Pol Data in a Complex Land-Use Watershed: Cau River Basin (Vietnam). IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2016, 9, 3082–3096. [Google Scholar] [CrossRef] [Green Version]
- Raney, R.K.; Freeman, A.; Jordan, R.L. Improved Range Ambiguity Performance in Quad-Pol SAR. IEEE Trans. Geosci. Remote Sens. 2012, 50, 349–356. [Google Scholar] [CrossRef]
- Villano, M.; Krieger, G.; Moreira, A. New Insights Into Ambiguities in Quad-Pol SAR. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3287–3308. [Google Scholar] [CrossRef]
- Li, J.; Ji, Y.; Zhang, Y.; Zhang, Q.; Dong, Z. Effects of Ionosphere Polarimetric Dispersion on Lower-Frequency Spaceborne SAR. In Proceedings of the 2018 IEEE 3rd International Conference on Signal and Image Processing (ICSIP), Shenzhen, China, 13–15 July 2018; pp. 510–515. [Google Scholar]
- Villano, M.; Krieger, G. Impact of Azimuth Ambiguities on Interferometric Performance. IEEE Geosci. Remote Sens. Lett. 2012, 9, 896–900. [Google Scholar] [CrossRef] [Green Version]
- Di Martino, G.; Iodice, A.; Riccio, D.; Ruello, G. Filtering of Azimuth Ambiguity in Stripmap Synthetic Aperture Radar Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3967–3978. [Google Scholar] [CrossRef] [Green Version]
- Cloude, S.R. A General Elliptical Formulation of Hybrid-POLSAR System Ambiguities. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1066–1069. [Google Scholar] [CrossRef]
- Krieger, G.; Gebert, N.; Moreira, A. Multidimensional waveform encoding for spaceborne synthetic aperture radar systems. In Proceedings of the 2007 International Waveform Diversity and Design Conference, Pisa, Italy, 4–8 June 2007; pp. 282–286. [Google Scholar]
- Krieger, G.; Gebert, N.; Moreira, A. Multidimensional Waveform Encoding: A New Digital Beamforming Technique for Synthetic Aperture Radar Remote Sensing. IEEE Trans. Geosci. Remote Sens. 2008, 46, 31–46. [Google Scholar] [CrossRef] [Green Version]
- Krieger, G.; Gebert, N.; Moreira, A. Multidimensional radar waveforms a new paradigm for the design and operation of highly performant spaceborne synthetic aperture radar systems. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007; pp. 4937–4941. [Google Scholar]
- Krieger, G.; Gebert, N.; Moreira, A. Multidimensional waveform encoding for synthetic aperture radar remote sensing. In Proceedings of the 2007 IET International Conference on Radar Systems, Edinburgh, UK, 15–18 October 2007; pp. 1–5. [Google Scholar]
- Krieger, G.; Gebert, N.; Younis, M.; Moreira, A. Advanced synthetic aperture radar based on digital beamforming and waveform diversity. In Proceedings of the 2008 IEEE Radar Conference, Rome, Italy, 26–30 May 2008; pp. 1–6. [Google Scholar]
- Yang, C.; Ou, N.; Deng, Y.; Liu, D.; Zhang, Y.; Wang, N.; Wang, R. Pattern Synthesis Algorithm for Range Ambiguity Suppression in the LT-1 Mission via Sequential Convex Optimizations. IEEE Trans. Geosci. Remote Sens. 2021. [Google Scholar] [CrossRef]
- Zhang, L.; Li, H.; Qiao, Z.; Xu, Z. A Fast BP Algorithm With Wavenumber Spectrum Fusion for High-Resolution Spotlight SAR Imaging. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1460–1464. [Google Scholar] [CrossRef]
- Raney, R.K.; Runge, H.; Bamler, R.; Cumming, I.G.; Wong, F.H. Precision SAR processing using chirp scaling. IEEE Trans. Geosci. Remote Sens. 1994, 32, 786–799. [Google Scholar] [CrossRef]
- Duan, S.; Li, J. High Squint SAR Processing Using Modified Extended Chirp Scaling. In Proceedings of the First International Conference on Innovative Computing, Information and Control (ICICIC’06), Beijing, China, 30 August–1 September 2006; Volume 1, pp. 358–361. [Google Scholar]
- Moreira, A.; Mittermayer, J.; Scheiber, R. Extended chirp scaling algorithm for air- and spaceborne SAR data processing in stripmap and ScanSAR imaging modes. IEEE Trans. Geosci. Remote Sens. 1996, 34, 1123–1136. [Google Scholar] [CrossRef]
- Hui, K.; Jie, C.; Wei, Y. A modified chirp-scaling algorithm for spaceborne squinted sliding spotlight SAR data processing. In Proceedings of the 2015 IEEE 5th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Singapore, 1–4 September 2015; pp. 459–461. [Google Scholar]
- Dudczyk, J.; Kawalec, A. Optimizing the minimum cost flow algorithm for the phase unwrapping process in sar radar. Bulletin of the Polish Academy of Sciences. Tech. Sci. 2014, 62, 511–516. [Google Scholar]
- Jin, G.; Aubry, A.; De Maio, A.; Wang, R.; Wang, W. Quasi-Orthogonal Waveforms for Ambiguity Suppression in Spaceborne Quad-Pol SAR. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5204617. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, W.; Deng, Y.; Zhang, Z.; Wang, R. Ambiguity Suppression of Cross-Pol Signals by DPCA With DBF Reflector for Hybrid/±π/4 Quad-Pol SAR. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5202613. [Google Scholar] [CrossRef]
- Zhao, P.; Deng, Y.; Wang, W.; Zhang, Y.; Wang, R. Ambiguity Suppression Based on Joint Optimization for Multichannel Hybrid and ±π/4 Quad-Pol SAR Systems. Remote Sens. 2021, 13, 1907. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Dobson, M.C. Handbook of Radar Scattering Statistics for Terrain; Artech House: Norwood, MA, USA, 1989. [Google Scholar]
- Freeman, A.; Johnson, W.T.K.; Hunecutt, B.; Jordan, R.; Hensley, S.; Siqueira, P.; Curlander, J. The “Myth” of the minimum SAR antenna area constraint. IEEE Trans. Geosci. Remote Sens. 2000, 38, 320–324. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Zhang, Y.; Deng, Y.; Chang, S.; Liu, D.; Wang, R. A Quad-Pol SAR Imaging Mode with Sound Azimuth Ambiguity. In Proceedings of the 2020 IEEE Radar Conference (RadarConf20), Florence, Italy, 21–25 September 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Van Trees, H.L. Optimum Array Processing; John Wiley & Sons: Hoboken, NJ, USA, 2004; ISBN 978-0471463832. [Google Scholar]





| Parameters | Value |
|---|---|
| Satellite height | 607 Km |
| Carrier frequency | 1.26 GHz |
| Signal bandwidth | 80 MHz |
| Pulse width | 20 us |
| Antenna length | 9.8 m |
| Antenna height | 3.4 m |
| Peak power | 15,840 W |
| Antenna efficiency | 75% |
| Resolution/Width | 6 m/30 km |
| Look angle | 12∼33 deg |
| Squint angle | 0 deg |
| Duty cycle | 16% |
| Weighting factor | 0.02 |
| Backscattering coefficient | [38] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Chang, S.; Wang, R.; Li, P.; Zhang, Y.; Deng, Y. A Novel Weighted Amplitude Modulation (WAM) System for Ambiguity Suppression of Spaceborne Hybrid Quad-Pol SAR. Remote Sens. 2022, 14, 155. https://doi.org/10.3390/rs14010155
Zhang Y, Chang S, Wang R, Li P, Zhang Y, Deng Y. A Novel Weighted Amplitude Modulation (WAM) System for Ambiguity Suppression of Spaceborne Hybrid Quad-Pol SAR. Remote Sensing. 2022; 14(1):155. https://doi.org/10.3390/rs14010155
Chicago/Turabian StyleZhang, Yanyan, Sheng Chang, Robert Wang, Peng Li, Yongwei Zhang, and Yunkai Deng. 2022. "A Novel Weighted Amplitude Modulation (WAM) System for Ambiguity Suppression of Spaceborne Hybrid Quad-Pol SAR" Remote Sensing 14, no. 1: 155. https://doi.org/10.3390/rs14010155
APA StyleZhang, Y., Chang, S., Wang, R., Li, P., Zhang, Y., & Deng, Y. (2022). A Novel Weighted Amplitude Modulation (WAM) System for Ambiguity Suppression of Spaceborne Hybrid Quad-Pol SAR. Remote Sensing, 14(1), 155. https://doi.org/10.3390/rs14010155









