An Objective Method with a Continuity Constraint for Improving Surface Velocity Estimates from the Geostationary Ocean Color Imager
Abstract
:1. Introduction
2. Data and Methods
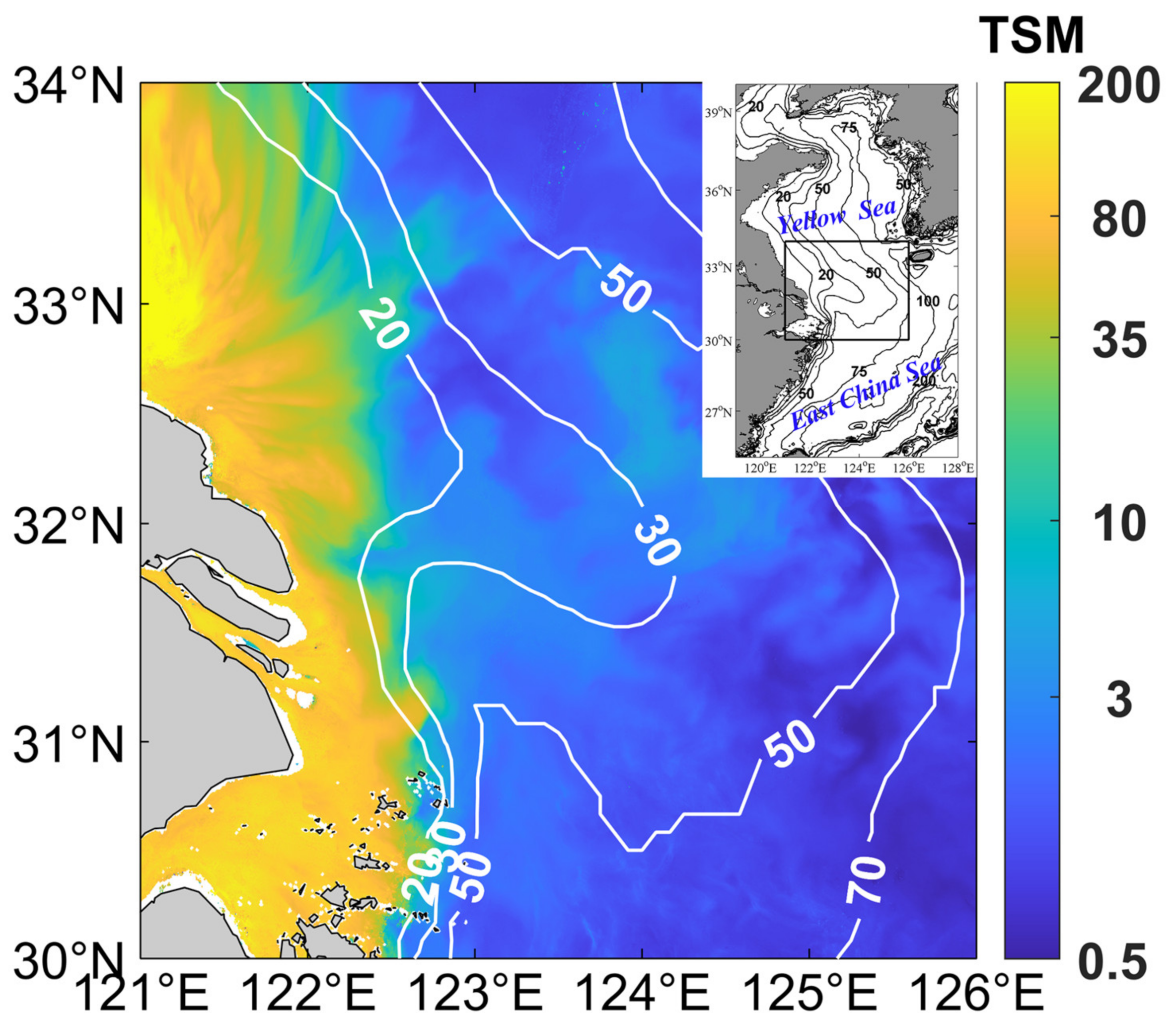
2.1. GOCI Data
2.2. Ocean Model Data
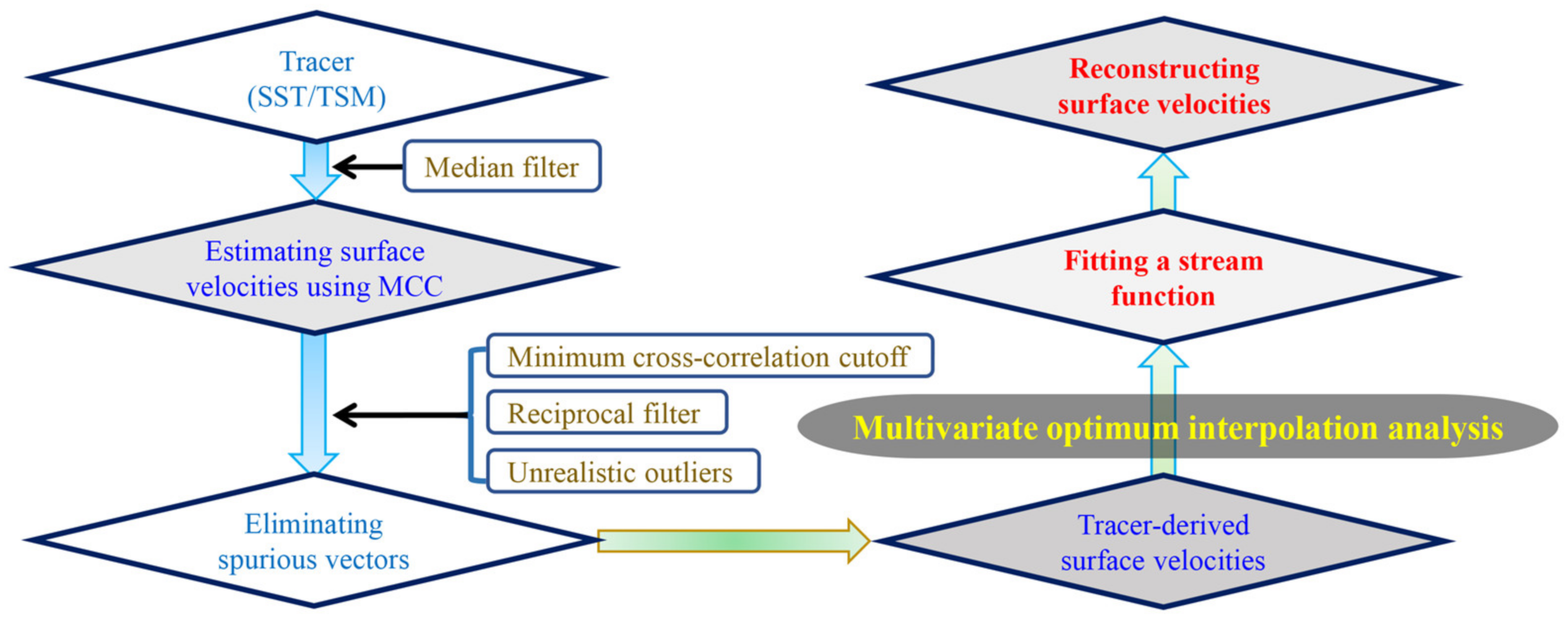
2.3. MCC Method
2.4. Multivariate Optimum Interpolation Analysis
3. Synthetic Tests
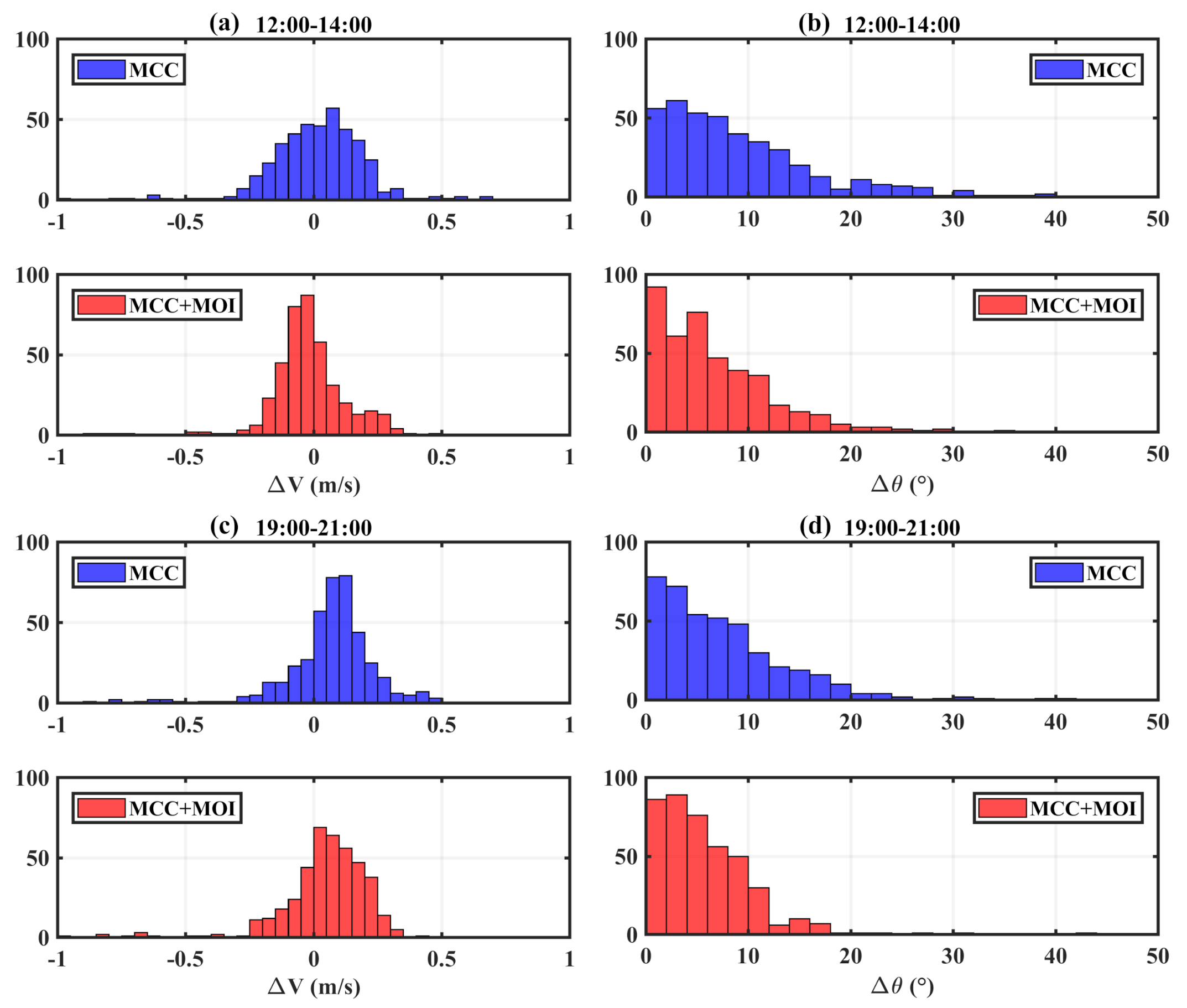
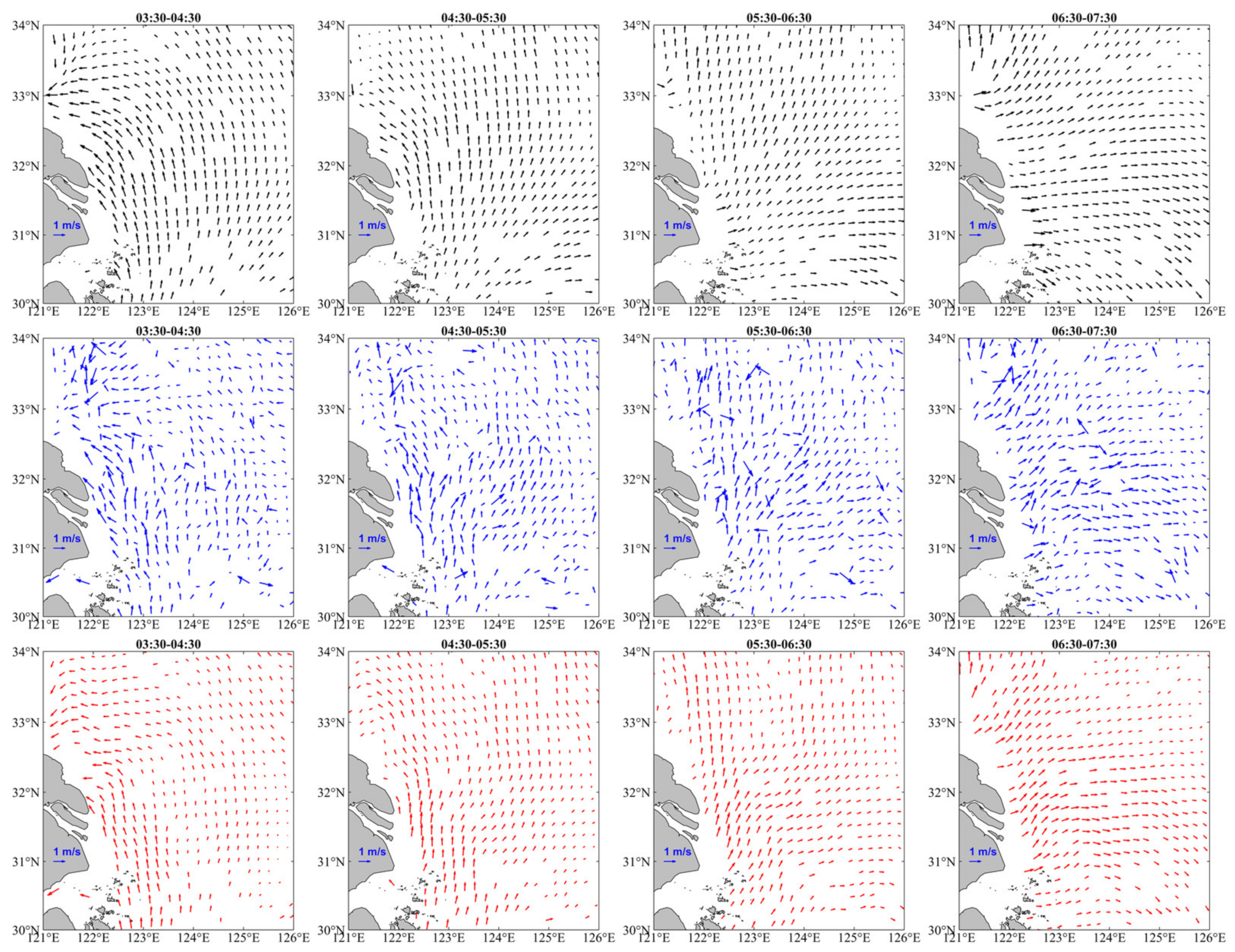
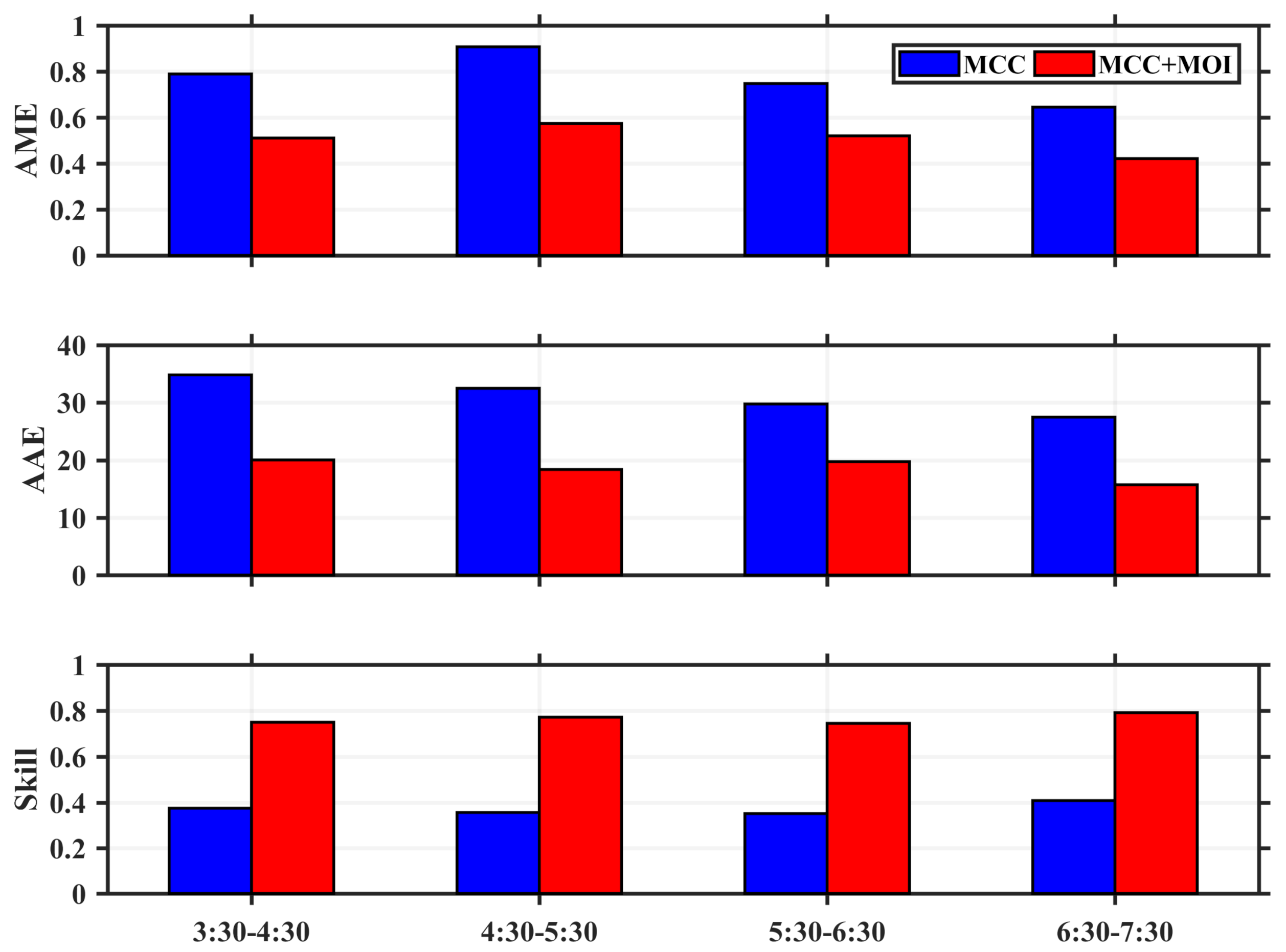
4. Application to GOCI Images
5. Discussions and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bowen, M.M.; Emery, W.J.; Wilkin, J.L.; Tildesley, P.C.; Barton, I.J.; Knewtson, R. Extracting multiyear surface currents from sequential thermal imagery using the maximum cross-correlation technique. J. Atmos. Ocean. Technol. 2002, 19, 1665–1676. [Google Scholar] [CrossRef] [Green Version]
- Emery, W.J.; Thomas, A.C.; Collins, M.J.; Crawford, W.R.; Mackas, D.L. An objective method for computing advective surface velocities from sequential infrared satellite images. J. Geophys. Res. Oceans 1986, 91, 12865–12878. [Google Scholar] [CrossRef] [Green Version]
- Domingues, C.M.; Goncalves, G.A.; Ghisolfi, R.D.; Garcia, C.A.E. Advective surface velocities derived from sequential infrared images in the southwestern Atlantic Ocean. Remote Sens. Environ. 2000, 73, 218–226. [Google Scholar] [CrossRef]
- Yang, H.; Choi, J.-K.; Park, Y.-J.; Han, H.-J.; Ryu, J.-H. Application of the Geostationary Ocean Color Imager (GOCI) to estimates of ocean surface currents. J. Geophys.Res. Oceans 2014, 119, 3988–4000. [Google Scholar] [CrossRef]
- Keating, S.R.; Smith, K.S. Upper ocean flow statistics estimated from superresolved sea-surface temperature images. J. Geophys. Res. Oceans 2015, 120, 1197–1214. [Google Scholar] [CrossRef]
- Yang, H.P.; Arnone, R.; Jolliff, J. Estimating advective near-surface currents from ocean color satellite images. Remote Sens. Environ. 2015, 158, 1–14. [Google Scholar] [CrossRef]
- Chen, J.; Chen, J.; Cao, Z.; Shen, Y. Improving Surface Current Estimation From Geostationary Ocean Color Imager Using Tidal Ellipse and Angular Limitation. J. Geophys. Res. Oceans 2019, 124, 4322–4333. [Google Scholar] [CrossRef]
- Crocker, R.I.; Matthews, D.K.; Emery, W.J.; Baldwin, D.G. Computing coastal ocean surface currents from infrared and ocean color satellite imagery. IEEE Trans. Geosci. Remote Sens. 2007, 45, 435–447. [Google Scholar] [CrossRef]
- Kelly, K.A.; Strub, P.T. Comparison of velocity estimates from advanced very high resolution radiometer in the Coastal Transition Zone. J. Geophys. Res. Oceans 1992, 97, 9653–9668. [Google Scholar] [CrossRef]
- Warren, M.A.; Quartly, G.D.; Shutler, J.D.; Miller, P.I.; Yoshikawa, Y. Estimation of ocean surface currents from maximum cross correlation applied to GOCI geostationary satellite remote sensing data over the Tsushima (Korea) Straits. J. Geophys. Res. Oceans 2016, 121, 6993–7009. [Google Scholar] [CrossRef] [Green Version]
- Choi, J.K.; Park, Y.J.; Ahn, J.H.; Lim, H.S.; Eom, J.; Ryu, J.H. GOCI, the world’s first geostationary ocean color observation satellite, for the monitoring of temporal variability in coastal water turbidity. J. Geophys. Res. Oceans 2012, 117. [Google Scholar] [CrossRef]
- Jiang, L.; Wang, M. Diurnal Currents in the Bohai Sea Derived From the Korean Geostationary Ocean Color Imager. IEEE Trans. Geosci. Remote Sens. 2016, 55, 1437–1450. [Google Scholar] [CrossRef]
- Choi, J.K.; Yang, H.; Han, H.J.; Ryu, J.H.; Park, Y.J. Quantitative estimation of suspended sediment movements in coastal region using GOCI. J. Coast. Res. 2013, 1367–1372. [Google Scholar] [CrossRef]
- Hu, Z.; Qi, Y.; He, X.; Wang, Y.-H.; Wang, D.-P.; Cheng, X.; Liu, X.; Wang, T. Characterizing surface circulation in the Taiwan Strait during NE monsoon from Geostationary Ocean Color Imager. Remote Sens. Environ. 2019, 221, 687–694. [Google Scholar] [CrossRef]
- Hu, Z.; Wang, D.-P.; He, X.; Li, M.; Wei, J.; Pan, D.; Bai, Y. Episodic surface intrusions in the Yellow Sea during relaxation of northerly winds. J. Geophys. Res. Oceans 2017, 122, 6533–6546. [Google Scholar] [CrossRef]
- Hu, Z.; Wang, D.-P.; Pan, D.; He, X.; Miyazawa, Y.; Bai, Y.; Wang, D.; Gong, F. Mapping surface tidal currents and Changjiang plume in the East China Sea from Geostationary Ocean Color Imager. J. Geophys. Res. Oceans 2016, 121, 1563–1572. [Google Scholar] [CrossRef] [Green Version]
- Hu, Z.; Pan, D.; He, X.; Bai, Y. Diurnal Variability of Turbidity Fronts Observed by Geostationary Satellite Ocean Color Remote Sensing. Remote Sens. 2016, 8, 147. [Google Scholar] [CrossRef] [Green Version]
- Hu, Z.; Pan, D.; He, X.; Song, D.; Huang, N.; Bai, Y.; Xu, Y.; Wang, X.; Zhang, L.; Gong, F. Assessment of the MCC method to estimate sea surface currents in highly turbid coastal waters from GOCI. Int. J. Remote Sens. 2017, 38, 572–597. [Google Scholar] [CrossRef]
- Notarstefano, G.; Poulain, P.-M.; Mauri, E. Estimation of surface currents in the Adriatic Sea from sequential infrared satellite images. J. Atmos. Ocean. Technol. 2008, 25, 271–285. [Google Scholar] [CrossRef]
- Barton, I.J. Tidal streams observed with sequential AVHRR images. Int. J. Remote Sens. 2004, 25, 1785–1790. [Google Scholar] [CrossRef]
- Forget, G.; Campin, J.M.; Heimbach, P.; Hill, C.N.; Ponte, R.M.; Wunsch, C. ECCO version 4: An integrated framework for non-linear inverse modeling and global ocean state estimation. Geosci. Model Dev. Discuss. 2015, 8, 3653–3743. [Google Scholar] [CrossRef] [Green Version]
- Rocha, C.B.; Chereskin, T.K.; Gille, S.T.; Menemenlis, D. Mesoscale to Submesoscale Wavenumber Spectra in Drake Passage. J. Phys. Oceanogr. 2016, 46, 601–620. [Google Scholar] [CrossRef]
- Egbert, G.D.; Bennett, A.F.; Foreman, M.G.G. TOPEX/POSEIDON tides estimated using a global inverse model. J. Geophys. Res. Oceans 1994, 99, 24821–24852. [Google Scholar] [CrossRef] [Green Version]
- Egbert, G.D.; Erofeeva, S.Y. Efficient Inverse Modeling of Barotropic Ocean Tides. J. Atmos. Ocean. Technol. 2002, 19, 183–204. [Google Scholar] [CrossRef] [Green Version]
- Lie, H.-J.; Lee, S.; Cho, C.-H. Computation methods of major tidal currents from satellite-tracked drifter positions, with application to the Yellow and East China Seas. J. Geophys. Res. Oceans 2002, 107, 3-1-3-22. [Google Scholar] [CrossRef] [Green Version]
- Barton, I.J. Ocean currents from successive satellite images: The reciprocal filtering technique. J. Atmos. Ocean. Technol. 2002, 19, 1677–1689. [Google Scholar] [CrossRef]
- Bretherton, F.P.; Davis, R.E.; Fandry, C.B. A technique for objective analysis and design of oceanographic experiments applied to MODE-73. Deep Sea Res. Oceanogr. Abstr. 1976, 23, 559–582. [Google Scholar] [CrossRef]
- Wang, Y.; Jan, S.; Wang, D. Transports and tidal current estimates in the Taiwan Strait from shipboard ADCP observations (1999–2001). Estuar. Coast. Shelf Sci. 2003, 57, 193–199. [Google Scholar] [CrossRef]
- Chen, W. Surface velocity estimation from satellite imagery using displaced frame central difference equation. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2791–2801. [Google Scholar] [CrossRef]
- Doronzo, B.; Taddei, S.; Brandini, C.; Fattorini, M. Extensive analysis of potentialities and limitations of a maximum cross-correlation technique for surface circulation by using realistic ocean model simulations. Ocean Dyn. 2015, 65, 1183–1198. [Google Scholar] [CrossRef]
- Tokmakian, R.; Strub, P.T.; McClean-Padman, J. Evaluation of the maximum cross-correlation method of estimating sea surface velocities from sequential satellite images. J. Atmos. Ocean. Technol. 1990, 7, 852–865. [Google Scholar] [CrossRef] [Green Version]
- Wahl, D.D.; Simpson, J.J. Physical processes affecting the objective determination of near-surface velocity from satellite data. J. Geophys. Res. Oceans 1990, 95, 13511–13528. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Z.; Li, L.; Zhao, J.; Wang, D. An Objective Method with a Continuity Constraint for Improving Surface Velocity Estimates from the Geostationary Ocean Color Imager. Remote Sens. 2022, 14, 14. https://doi.org/10.3390/rs14010014
Hu Z, Li L, Zhao J, Wang D. An Objective Method with a Continuity Constraint for Improving Surface Velocity Estimates from the Geostationary Ocean Color Imager. Remote Sensing. 2022; 14(1):14. https://doi.org/10.3390/rs14010014
Chicago/Turabian StyleHu, Zifeng, Lan Li, Jun Zhao, and Dongxiao Wang. 2022. "An Objective Method with a Continuity Constraint for Improving Surface Velocity Estimates from the Geostationary Ocean Color Imager" Remote Sensing 14, no. 1: 14. https://doi.org/10.3390/rs14010014
APA StyleHu, Z., Li, L., Zhao, J., & Wang, D. (2022). An Objective Method with a Continuity Constraint for Improving Surface Velocity Estimates from the Geostationary Ocean Color Imager. Remote Sensing, 14(1), 14. https://doi.org/10.3390/rs14010014








