Abstract
Although a variety of ocean mesoscale eddy datasets are available for researchers to study eddy properties throughout the global ocean, subtle differences in how these datasets are produced often lead to large differences between one another. This study compares the Global Ocean Mesoscale Eddy Atmospheric-Oceanic-Biological interaction Observational Dataset (GOMEAD) with the well-recognized Mesoscale Eddy Trajectory Atlas in four regions with strong eddy activity: the Northwest Pacific Subtropical Front (SF), Kuroshio Extension (KE), South China Sea (SCS), and California Coastal Current (CC), and assesses the relative advantages and disadvantages of each. It was identified that while there is a slight difference in the total number of eddies detected in each dataset, the frequency distribution of eddy radii presents a right-skewed normal distribution, tending towards larger radii eddies, and there are more short- than long-lived eddies. Interestingly, the total number of GOMEAD eddies is 8% smaller than in the META dataset and this is most likely caused by the GOMEAD dataset’s underestimation of total eddy numbers and lifespans due to their presence near islands, and the tendency to eliminate eddies from its database if their radii are too small to be adequately detected. By contrast, the META dataset, due to tracking jumps in detecting eddies, may misidentify two eddies as a single eddy, reducing total number of eddies detected. Additionally, because the META dataset is reliant on satellite observations of sea surface level anomalies (SLAs), when SLAs are weak, the META dataset struggles to detect eddies. The GOMEAD dataset, by contrast, is reliant on applying vector geometry to detect and track eddies, and thus, is largely insulated from this problem. Thus, although both datasets are excellent in detecting and characterizing eddies, users should use the GOMEAD dataset when the region of interest is far from islands or when SLAs are weak but use the META dataset if the region of interest is populated by islands, or if SLAs are intense.
1. Introduction
Mesoscale eddies are one of the most important geophysical phenomena and are ubiquitous in the global ocean. They possess lifespans ranging from several days to several months and cover spatial scales from tens to hundreds of kilometers [1,2,3,4]. Due to their dynamic properties which are controlled by strong nonlinear effects, mesoscale eddies play important roles in transporting heat, mass, salt, and nutrients in the world’s oceans [5,6,7].
Due to the high cost and difficulty of field observations, eddy studies are usually based on remotely sensed (e.g., from observations of satellite altimeter-derived sea level anomalies, or sea surface temperature observed by microwave/infrared platforms), in situ observations, or numerical modelling. In the era of big data, manual detection can no longer satisfactorily process many tens of thousands of observations and consequently, automatic eddy detection algorithm development is an intense area of research. This development has kept pace with development of satellite observation technology and increases in available computing power [8]. These provide a greater understanding in the classification of eddy characteristics, their movement, and spatiotemporal distribution. Eddy detection can be achieved through a variety of variables and methods. A full summary is provided by [9] categorized algorithms into three categories: physical parameter-based [10,11], geometric velocity field-based [12] and hybrid, which is the combination of the former two methods [13,14,15]. From these methods, several relatively mature datasets such as those produced by [2,16,17] are available. Although these can make the study of eddies more efficient, their accuracy is also confronted with great challenges. For example, utilized data, methods and definitions used by different datasets differ to some extent [18]. These parameters may include how eddy center and boundaries are identified, how they are tracked over time, and the definitions of eddy parameters [15].
Previous studies have shown that in the comparison between physical parameter-based and geometry-based methodologies, the former has some limitations where they often fail to detect quite recognizable eddies and may even treat non-eddy structures as eddies [19]. Presently, the Mesoscale Eddy Trajectory Atlas [2] (hereinafter referred to as the META dataset) is one of the most widely used datasets and was recently updated following improvements to the eddy detection and tracking method [20]. Additionally, the temporal resolution was increased from 1 week to 1 day. Since, the dataset has been applied in multiple regions [21,22,23]. Recently, refs. [24,25] developed an eddy dataset (hereinafter referred to as the GOMEAD dataset) based on identifying the eddy geometric velocity field. Since then, the dataset has also been used in several studies [26,27].
Although both datasets are widely used in eddy studies, their specific characteristics, and the differences between them have yet to be assessed, motivating the present study. Here, both datasets are compared and their similarities/differences, advantages/disadvantages are rigorously investigated so that other users of either the GOMEAD or META datasets would have a deeper understanding of their efficacy and limitations in specific studies.
The remainder of this paper are arranged as follows. Section 2 introduces the data and methods used in this study. Section 3 describes the basic features of two eddy datasets. Section 4 discusses the possible reasons for the difference between the two datasets and Section 5 summarizes the main findings.
2. Data and Methods
2.1. Data
2.1.1. Satellite Remote Sensing Data
The two datasets used for comparison in this work both detect and track eddies using observations of sea level anomalies (SLA). Satellite altimetry data was acquired from Archiving, Validation, and Interpretation of Satellite Oceanographic Data (AVISO). It merges multiple satellite data from The European Remote Sensing (ERS) Satellites 1 and 2, the Environmental Satellite (ENVISAT), the GEOSAT Follow-On (GFO), and Jason−1, etc. The data provides historical data from 1 January 1993 to the present (it will be about 5 months behind real time) with a temporal resolution of 1 day and a spatial resolution of 0.25° 0.25°. The latest version of this data (vDT2021) from 1 January 1993 to 31 December 2019 is employed to detect eddies. Data can be acquired at https://cds.climate.copernicus.eu/cdsapp#!/dataset/satellite-sea-level-global?tab=overview, accessed on 11 November 2021.
2.1.2. Mesoscale Eddy Trajectory Atlas Product Version 2.0 (META v2.0)
The META v2.0 (delayed-time) dataset is available on the AVISO website and was last updated in December 2020. The algorithm for detecting and tracking eddies is provided by [1,2,20]. The META dataset uses an SLA based automatic eddy detection algorithm. The time and spatial resolution of the data are consistent with the SLA data, and eddy position, radius, type, amplitude can be provided, but there is no information of eddy contour. The data can be acquired at https://www.aviso.altimetry.fr/en/data/products/value-added-products/global-mesoscale-eddy-trajectory-product/meta2-0-dt.html (accessed on 11 November 2021) by FTP.
2.1.3. Global Ocean Mesoscale Eddy Atmospheric-Oceanic-Biological Interaction Observational Dataset 1.0 (GOMEAD v1.0)
The other dataset is an eddy dataset based on the geostrophic velocity anomaly, which is one of GOMEAD’s five sub-datasets [28]. Based on identifying eddies through studying the oceanic geometric velocity field as derived from the AVISO SLA dataset, the GOMEAD dataset [24,25] was interpolated to a spatial resolution to 0.15° 0.15° for enhanced eddy detection capabilities. This dataset is global, with a daily resolution. The dataset can provide the latitude and longitude of the eddy center, radius, type, and contour information. The dataset can be acquired through reasonable requests from https://dx.doi.org/10.11922/sciencedb.01190 accessed on 11 November 2021. Identical to the META dataset, data is acquired from 1 January 1993 to 31 December 2019.
2.2. Eddy Detection Schemes
2.2.1. META Eddy Detection
After the SLA is processed by high-pass filtering, the location and polarity of the eddies are determined by finding the local extremum point. This is where the maximum value corresponds to anticyclonic eddies (AEs), and the minimum value corresponds to cyclonic eddies (CEs) [20].
In the “Growing Method”, starting from the pixels of the local extreme value of SLA, each time “growing”, all the neighboring pixels within the threshold increment successively are found. This “growing” will continue until any one of the following four conditions is violated.
- The amplitude of the test area must be equal to or smaller than that of the area already defined.
- The distance between the two remotest points must be less than a maximum diameter for a given eddy. Distance max = 700 km for latitudes lower than 25°, or 400 km for latitudes higher than 25°.
- No more than 2000 pixels.
- No latitude holes on the edges and no holes within the interior of the area.
An additional constraint is that eddies amplitude must be greater than 1 cm.
After detecting, calculating the parameters of the eddy is an important step in forming the dataset. The eddy centroid is regarded as the eddy center. The longitude (xc) and latitude (yc) of the centroid are defined as:
where E is an eddy, i and j are rows and columns of pixels of the eddy. x and y are longitude and latitude of a pixel. h is the sea surface height. Each “growth” forms an SLA contour, and the outermost SLA contour satisfying the conditions is the eddy edge. In all SLA contours formed in the detection process, the subset of pixels surrounded by the SLA contour with maximum mean geostrophic current is called speed core. The radius of a circle whose area is equal to the speed core is the speed-based radius, which is the radius provided by the META dataset. The amplitude is the difference between the SLA extremum within the eddy range, and the mean SLA of the eddy edge pixels. For more details, see https://www.aviso.altimetry.fr/fileadmin/documents/data/tools/hdbk_eddytrajectory_META2.0_DT.pdf, accessed on 11 November 2021.
2.2.2. GOMEAD Eddy Detection
In the GOMEAD dataset, a vector geometry-based automatic eddy detection algorithm developed by [9] was used for eddy detection. The methodology has been successfully applied in several areas [25,29,30,31,32,33,34,35,36,37,38]. In this method, the SLA field needs to be converted into geostrophic velocity anomaly field. The zonal and meridional components and of the geostrophic velocity anomaly can be calculated as:
where g, and f are the gravitational acceleration and the Coriolis parameter, respectively, and h’ is SLA. Based on the vector geometry algorithm, geostrophic velocity anomalies were used to detect eddies. In eddy detection, the point meeting the following constraints is defined as the eddy center [9]:
- The velocity component u’ in the north–south direction have opposite signs on both sides of the eddy center, and their absolute value increases as they move away from the center.
- The velocity component v’ in the east–west direction have opposite signs on both sides of the eddy center, and their absolute value increases as they move away from the center.
- The minimum velocity point within the selected range is the undetermined eddy center.
- The direction of the two adjacent velocity vectors around the eddy center must be close to each other and must be in the same or adjacent quadrants to ensure the same direction of rotation.
As there is no unified definition of eddy boundaries, the results obtained by different methods may vary significantly. In this algorithm, the contour of the outermost closed flow function around the eddy center is defined as the eddy edge. The determination of the eddy boundary is closely related to parameters a and b. Here, a = 4 and b = 3. Parameter a defines the minimum range of grid points of detection. That is, 2a grid points extend in each direction from the eddy center. In this work, a = 4 corresponds to the grid area of 17 × 17. If the range of the eddy is larger than the grid area, then the position of the contour is too close to the edge of the detection area, then expand the grid area in this direction for a grids and the stream function and eddy edge are computed in the larger area. Parameter b works in the third constraint, which determines the range of the search area for the point of minimum eddy current velocity. If the search area exceeds the eddy range and there is a small velocity value outside the eddy, the eddy center will not satisfy the third constraint. Therefore, when the value of parameter b is large, only large radii eddies can be detected.
Eddy parameters are estimated as follows. The radius of the eddy is defined as the average distance from the center to each point on the edge of the eddy. There is no specific definition of eddy amplitude. Here, the definition in the META dataset is referred to and the absolute difference between the SLA extreme value in the eddy range, and the SLA average value at the edge of the eddy as the eddy amplitude is utilized.
2.2.3. Similarities and Differences of Two Datasets
The main similarities and differences between the two data sets are summarized in Table 1. Although the raw data used in both datasets is the same SLA data, the types of the data directly used in detection are different, the resolutions are different, and the methods used for eddy detection are different.

Table 1.
Similarities and differences of the META and GOMEAD datasets.
The eddy parameters are also defined differently in the two datasets, such as the eddy center and radius. Additionally, the META dataset does not provide the eddy edge, which is important eddy information. The GOMEAD dataset does not provide the amplitude, but it can be readily calculated from other information. Some unique parameters of the two datasets can also cause differences in the final results.
2.3. Eddy Tracking Method
2.3.1. META Dataset Eddy Tracking Method
For an eddy at day D, it is detected at day D + 1 in a circle with the eddy center at day D0 as the starting point and radius R (determined by latitude). If no target eddy is detected at day D + 1, the search radius at day D + 2 increases to 1.33R and so on, 1.66R at day D + 3 and 2R at day D + 4. If the target eddy is still not found at day D + 4, the eddy is considered to have terminated. The eddy lifespan can be defined as the day number from the first day of finding the eddy to the day of the eddy termination.
2.3.2. GOMEAD Dataset Eddy Tracking Method
After an eddy is identified using the vector geometry method, eddy centers are tracked in time. If it can be established that two eddy centers at t1 and t2 are in fact of the same eddy, but that eddy has simply moved, the algorithm follows that eddy and tracks it over time.
To make the data comparison scientific and fair, the tracking method of GOMEAD made reference to the parameters of the META dataset for tracking settings and set the same allowable missing days as the META dataset (3 days), and used the same search radius as the META dataset.
2.4. Introduction to the Study Area
Eddy kinetic energy (EKE), the kinetic energy of the time-varying component of the sea current velocity [39], is used to characterize eddy activity intensities. EKE can be calculated by the following equation:
where flow zonal and meridional components are given by u′ and v′, respectively. u′ and v′ can be calculated by Equations (3) and (4) based on the AVISO SLA data.
Based on the average EKE of the North Pacific from 1993 to 2019 (Figure 1), four regions with high EKE in the North Pacific were selected as research areas. These include the Northwest Pacific Subtropical Front (SF), Kuroshio Extension (KE), South China Sea (SCS), and California Coastal Current (CC) regions (Table 2). In addition, due to the low intensity of the Coriolis effect when calculating the eddy geostrophic velocities, the detection of the eddy in the equatorial region is not reliable, so the region within 5° of the equator is usually not studied [19,40]. The SF consists of two high EKE zones: the subtropical countercurrent zone [41] and the leeward side of the Hawaii Islands [42]. According to Figure 1, it can be seen that the areas with the highest average EKE in the North Pacific are the SF and KE. While eddy occurrence probability in the two areas is high, the eddy generation mechanism in the two regions is different. The main generation mechanisms of SF eddies are frontal instability in the west, but wind curl and ocean current shear in the east [31]. In KE, by contrast, the main mechanism for eddy generation is baroclinic instability [43]. Compared with surrounding areas, the mean EKE of the SCS and CC regions is also significantly higher. The SCS is affected by a variety of factors, and the eddy activity is more active [35,44]. Areas west of Luzon Island and East Vietnam are high incidence areas of eddy occurence [45,46,47].
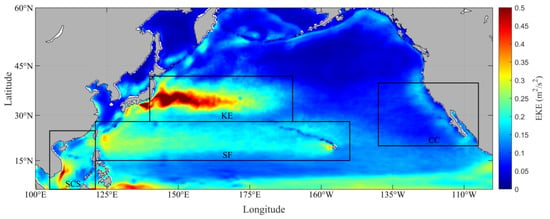
Figure 1.
Mean value of EKE during 1993 to 2019. The black lines delineate the four study regions.

Table 2.
Research regions and their geographical ranges.
3. Results
3.1. Eddy Characteristics Statistics
To investigate the characteristics of the two datasets, eddy number, radii, and lifespans in the four study regions of the North Pacific Ocean were analyzed and compared during the period of 1993 to 2019 (Figure 2, Table 3). The Lagrangian method is employed in estimating eddy statistics, and it considers the eddy throughout its life as one eddy. Firstly, the overall parameters of the four regions are compared and analyzed. There is little difference in the total number of eddies between the two datasets, but it can be noted that the GOMEAD dataset reports slightly fewer eddies than does the META dataset. Specifically, the total number of eddies in GOMEAD is 8% fewer than that in META. Both datasets report more CEs than AEs. The GOMEAD dataset reports approximately 5.5% more CEs than AEs, while for the META dataset, that dataset reports 7.7% more CEs than AEs.
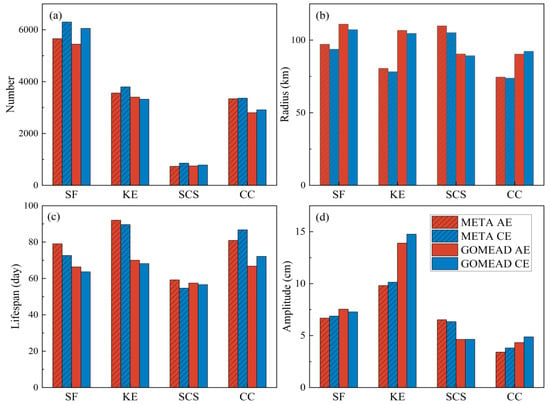
Figure 2.
Comparison of eddy number (a), radius (b), lifespan (c) and Amplitude (d) in four regions. AE and CE, respectively, represent anticyclonic and cyclonic eddies.

Table 3.
Comparison of the META and GOMEAD datasets statistics in the four study areas. Mean values (standard deviations) are shown outside (inside) the brackets.
In terms of average radius, GOMEAD dataset eddies are about 15 km larger than that of those in the META dataset, but it can also be noted that AEs generally have larger radii than CEs. Eddy lifespans as recorded by the GOMEAD dataset for AEs (CEs) were measured at 66.9 days (66.3 days). These were shorter than AEs (CEs) of the META dataset that was measured at 81.9 days (79.4 days). The mean amplitude of eddies in the GOMEAD dataset was larger than that of those in the META dataset. The amplitude of AE (CE) was 0.92 cm (1.07 cm) larger than that of those in the META dataset. Both datasets report that CEs are generally larger than AEs.
The eddy parameters of each region are compared and analyzed. To facilitate comparison, the eddy number, and mean parameters (including mean radius, lifespan, and amplitude) in the four regions of the two datasets were represented in the form of bar graphs. Figure 2a shows the number of eddies in the four regions. The number of eddies in the two datasets is very close in the four areas, and the number of eddies in the GOMEAD dataset is slightly less than that in the META dataset. The distribution of the mean eddy radius in the four regions is shown in Figure 2b. It can be seen that the mean eddy radius of the GOMEAD dataset is larger in the three regions except for the SCS. The mean eddy radius in the SCS of the META dataset is not only larger than that of other regions, but also about 15 km larger than that of the GOMEAD dataset in the SCS. The mean eddy lifespans of the GOMEAD dataset are shorter than that of those in the META dataset in all four regions, with the difference reaching about 20 days in the KE regions and about 10 days in the SF and CC regions. The mean eddy lifespans of the two datasets were closest in the SCS region, and both were similar to the results calculated by [48]. Except for the SCS region, the eddy amplitude of the GOMEAD dataset is larger in the other three regions, in which the difference in the KE region is the largest, about 4 cm, and that in the SF and CC regions is about 1 cm.
It was identified that the SCS was most statistically different from the remaining regions, but differences amongst those (i.e., SF, KE, CC), were minor. Specifically, META eddy radii are larger in the SCS than the remaining regions and this may be because of parameter settings. The SCS is located at 0–25°N, and because the META dataset’s eddy detection method allows the distance of two farthest points in the eddy to be 700 km at most, this is much larger than the 400 km distance north of 25°N. Another possible reason is that the SLA is negligible in the SCS, which weakens that dataset’s ability to detect small eddies. As fewer small radii eddies are detected, the mean eddy radius is artificially increased. This may also be the reason why eddy lifespans in the META dataset are shorter in regions other than the SCS. During the eddy generation and termination stages, the eddy is not as intense as it can be in its mature phase. Due to weak SLAs, eddies are more difficult to detect and thus this may also lead to abnormally short eddy lifespans. By contrast, eddy detection in the GOMEAD dataset is dependent on vector geometry, rather than SLA, and thus, weak SLAs have an extremely minor, if any, effect on the GOMEAD’s eddy detection ability. Here, it can be noted that the amplitude of a given eddy is related to its radius, and so, statistical results of amplitude would naturally be similar to those of eddy radii.
Standard deviation (STD) reflects the degree of fluctuation of data. The larger the value is, the greater the individual difference of data is. In general, compared with the META dataset, the GOMEAD dataset has higher STDs in eddy radii, lifespan, and amplitude. Distinct from other regions, STDs for those variables in the SCS is noticeably smaller in the GOMEAD dataset than the META dataset.
Figure 3 provides histograms of eddy radius distribution. It can be seen that the eddy radius of the two datasets in the four regions possess a biased normal distribution and the eddy radius of eddies in the GOMEAD dataset is generally larger. AEs (CEs) with radii of 30–80 km in the GOMEAD dataset account for 42% (42%) of the totals, while they account for 60% (64%) in the META dataset. The GOMEAD dataset reports fewer small-radii eddies. In the GOMEAD dataset, there are 11% (10%) AE (CE) with a radius greater than 150 km, and 3% (2%) in the META dataset. The GOMEAD dataset has significantly more large radii eddies.
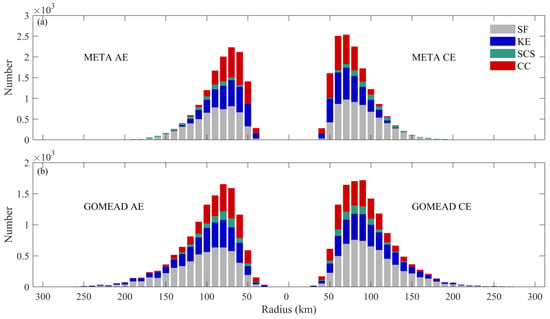
Figure 3.
Histograms of eddy radii of (a) META and (b) GOMEAD datasets.
According to the statistics of eddy lifespan (Figure 4), both datasets have more short-life eddies than longer-lived eddies. The number of each type of eddy decreases with increases in lifespan. When eddies develop, the energy required to sustain this development is continuously dispersed into the environment. Thus, over longer frames of time, the eddy would find it harder to maintain its coherent structure, thus dissipating, such as its energy, into the environment. Generally, eddy lifespans in the GOMEAD dataset are significantly shorter than that of those in the META dataset. The eddies with lifespan of 4–10 weeks in the GOMEAD dataset accounted for 78% (78%) of AEs (CEs), while that of the META dataset accounted for 65% (67%). The two datasets differ greatly in the number of eddies over 20 weeks, with only 5% (5%) of AEs (CEs) lifespan for the GOMEAD dataset and 13% (12%) for the META dataset.
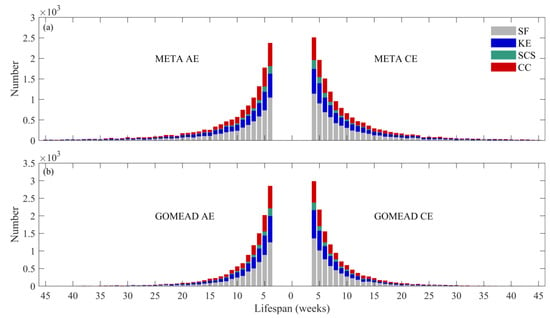
Figure 4.
Histograms of eddy lifespans, (a) META; (b) GOMEAD.
As shown in Figure 5, the frequency distribution of the eddy amplitudes shows a biased normal distribution, which tends to the large amplitude. The AE (CE) amplitude between 0 and 10 cm was 76% (77%) in the GOMEAD dataset, and 86% (86%) in the META dataset.
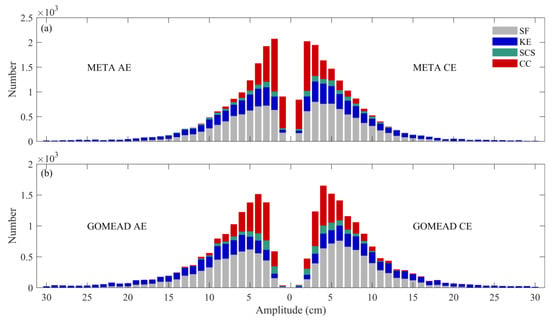
Figure 5.
Histograms of eddy amplitudes, (a) META; (b) GOMEAD.
AEs (CEs) with amplitudes greater than 20 cm accounted for 6% (5%) in the GOMEAD dataset and 3% (3%) in the META dataset. The amplitudes of eddies in the CC region and SCS region are both small. In the CC region, the META dataset has more small-amplitude eddies, while the SCS region contains more small-amplitude eddies as reported by the GOMEAD dataset.
3.2. Temporal Distribution
To understand the law of eddy generation and termination, the first recorded moment when an eddy is detected is taken as the generation moment, and the last recorded moment is taken as the time of its termination. Figure 6 shows the interannual variation in the number of eddy generation and termination in the SF region. Although the numbers of eddy generation in the two datasets is somewhat different, the variation trend is basically the same (Figure 6a,b). Correlation coefficients calculated between AEs (CEs) in the datasets were measured at 0.70 (0.71). Here, because the number of eddies terminating varies greatly from year to year (Figure 6c,d), the correlation of AEs (CEs) in each dataset decreases to 0.41 (0.50) The results indicate that the two datasets are consistent in the detection of eddy generation, but due to the difference in eddy lifespan in the two datasets, the eddy termination time is not. Other regions are generally similar and will not be shown individually.
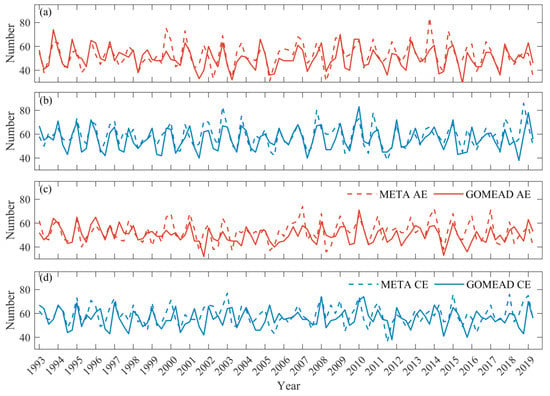
Figure 6.
Interannual variation of the number of generated (a) AEs and (b) CEs and terminated (c) AEs and (d) CEs in the SF region. The time resolution is three months.
The monthly variation of the number of eddy generation in the SF region showed a more consistent trend than the annual variation (Figure 7a,b), with the eddy generation peak around March and the minimum around September. Due to differences in eddy lifespan between the two datasets, the monthly variation trend of eddy terminated in the two datasets is somewhat different, with the peak of eddies in the META dataset from March to May, and the peak of eddies in the GOMEAD dataset from May to July (Figure 7c,d).
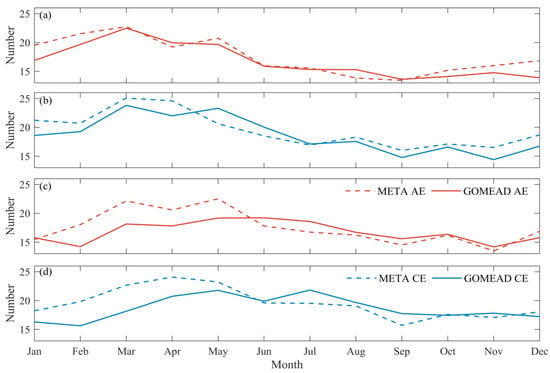
Figure 7.
Seasonal variation of the number of generated (a) AEs and (b) CEs and with the corresponding terminated (c) AEs and (d) CEs in the SF region.
The eddy radius of the GOMEAD dataset is larger than that of the META dataset on the whole, but the interannual variation trend of the eddy radius of the GOMEAD and META dataset is basically the same (Figure 8). Their correlation coefficients calculated between AEs (CEs) in the datasets were measured at 0.71 (0.53). Variability in the monthly mean eddy radius between the two datasets is the same: there is a decreasing eddy radius trend in June that continues until a minimum in March/April before rising again steadily after May to peak in the fall and winter months (August–December).
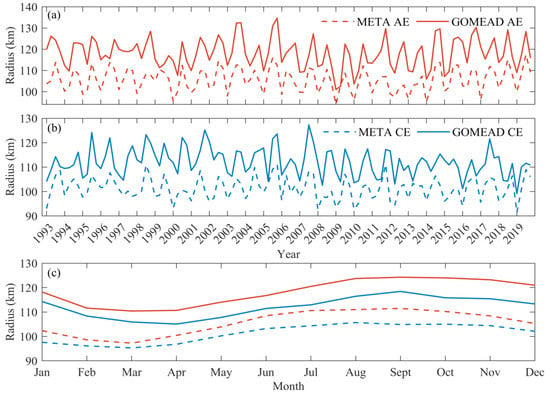
Figure 8.
Variation of the eddy radius in the SF region. Eddy radius annual time series of (a) AE and (b) CE, and (c) the monthly variation of four regions. The time resolution of annual time series is 3 months.
3.3. Spatial Distribution
Here, a 1° 1° grid was used to divide statistical areas, and the spatial distribution of the number of eddy generation and termination in the two datasets was statistically analyzed. The results are shown in Figure 9 and Figure 10. To avoid the statistics of eddy outside the study area, it is required that the eddy must generate and terminate within the study area.
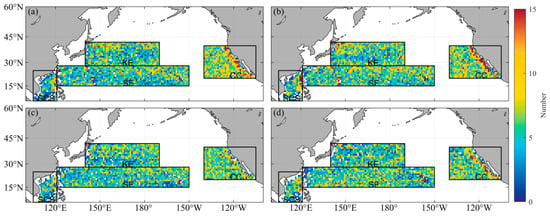
Figure 9.
Number of eddy generation. AEs and CEs detected by the META dataset are given in (a) and (b), respectively. Identically, AEs and CEs detected by the GOMEAD dataset are given in (c) and (d), respectively.
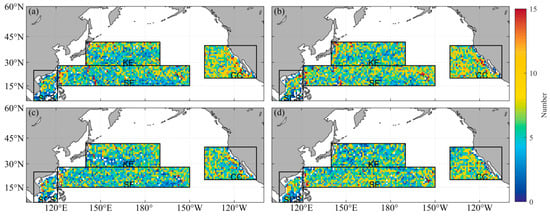
Figure 10.
Number of eddy termination. AEs and CEs detected by the META dataset are given in (a) and (b), respectively. Identically, AEs and CEs detected by the GOMEAD dataset are given in (c) and (d), respectively.
Figure 9 shows the spatial distribution of the number of eddy generation. On the whole, the number of eddy generation in the GOMEAD dataset is less than that in the META dataset, but in many regions, they have a good corresponding relationship. In the SF and KE regions, there are fewer eddies generated in the middle and more eddies generated in the north and south parts. In the west of the Hawaiian islands, both show a small area of a lot of eddies are generated in the two datasets. This is due to the wind curl and ocean current shear in the lee region [31]. There are more eddies generated in the east of the SCS region (the western Luzon Strait and the western Philippines), which is consistent with the results obtained by [49] using the META dataset and model data in the SCS regions. In addition, the number of eddies in the two datasets near the central axis from northeast to southwest is large in the SCS regions, and the number of eddies in the GOMEAD dataset near 120°W is slightly less than that in the META dataset. That site is an area that generates eddies. Eddies in that area would be characterized by small radii, and thus, would often be missed by the GOMEAD dataset. In the CC region, high frequency of eddy generation in both datasets is located on the east coast. It can be clearly seen from Figure 10 that the number of eddy termination in the SF, KE and SCS regions is relatively large at the western boundary, which is consistent with the studies of [31,50,51]. The number of eddy termination is smaller than that of generation in the eastern coast of the SCS and CC region.
In order to understand the spatial variation of eddy radius, the Eulerian method was used to categorize eddy radii. Same as the above research, divide the research area into 1° × 1° bins, and the value of each bin is the mean radius of eddies of a given pixel. The eddy radius of the GOMEAD dataset is larger than the META dataset in the three study regions except for the SCS region. There are more large-radius eddies in the middle of the SF, KE, and SCS. When identifying eddies closer to the equator, the META dataset shows a tendency of artificially increasing eddy radii. Such a trend does not exist in the GOMEAD dataset. As can be seen from Figure 11a,b, the eddy radius of META shows an obvious change process around 20–25°N, which may be related to the threshold of the META detection scheme. In the Northern Hemisphere, META limits the maximum distance between the two points in the eddy to 700 km from 0–25°N and 400 km beyond this geographical range.
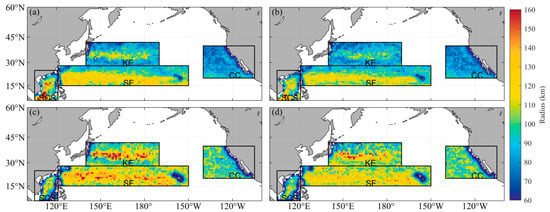
Figure 11.
Distribution of eddy radii. AEs and CEs detected by the META dataset are given in (a) and (b), respectively. Identically, AEs and CEs detected by the GOMEAD dataset are given in (c) and (d), respectively.
The Eulerian method was also used to estimate eddy amplitude. As shown in Figure 12, the distribution of eddy amplitudes in the two datasets is very similar. Both AEs and CEs have the largest amplitudes in the central and western KE region, followed by the western SF region. Due to the existence of Kuroshio, the sea surface velocity in the KE region is higher than that in the SF, leading to greater sea surface amplitudes. Therefore, eddy amplitude of the KE region is higher. The eddy amplitudes of GOMEAD are larger in three of the four regions except for the SCS. In addition, AEs amplitude of both datasets decreases along the CC region from northwest to southeast (Figure 12a,c), while CEs do not change significantly (Figure 12b,d).
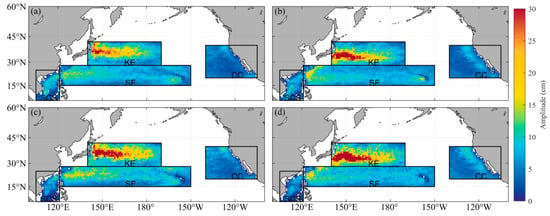
Figure 12.
Distribution of eddy amplitude. AEs and CEs detected by the META dataset are given in (a) and (b), respectively. Identically, AEs and CEs detected by the GOMEAD dataset are given in (c) and (d), respectively.
3.4. Time Evolution
In order to understand the variation process of the eddy characteristic parameters in the whole eddy lifespan, eddy parameters are normalized. If the whole lifespan of eddy is viewed from 0 to 1, then the generation time is 0 and the termination time is 1. During this process, the eddy goes through four stages: generation (~10%), intensification (~20%), maturation (~50%) and termination (20%). The percentage indicates the percentage of each stage of the eddy to the total lifespan. The radius, EKE and amplitude of eddy with a lifespan of no less than 28 days are normalized by this method. EKE refers to the average EKE within the eddy range.
In both datasets, whether AE or CE, the eddy radius normalization curves have a similar convex shape in all four regions (Figure 13a–d). In the KE and CC, the variation amplitude of the normalization eddy radius curves in the GOMEAD dataset is significantly smaller than that of the META dataset, which reflects that the eddy radius of the GOMEAD dataset has a smaller fluctuation in its lifespan. Variability in the amplitude of the GOMEAD dataset normalized eddy radii curves are much smaller than the META dataset. This indicates that differences in eddy radii are small over an eddy’s lifespan. This is due to the fact that small radii eddies may be unintentionally missed by the vector geometry method employed by the GOMEAD dataset. Specifically, when eddies are generated or they die, their radii are often very small and this may lead to the GOMEAD dataset to detect eddies only when they grow larger (and hence not necessarily when they are initially generated) or remove eddies from its catalogue too early (that is, the algorithm thinks the eddy has dissipated when in actuality, its radius has shortened beneath its detection threshold). Thus, the GOMEAD dataset is sparsely populated by small radii eddies, thus causing small amplitudes in normalized eddy radii curves and relatively flat normalized evolution curves.
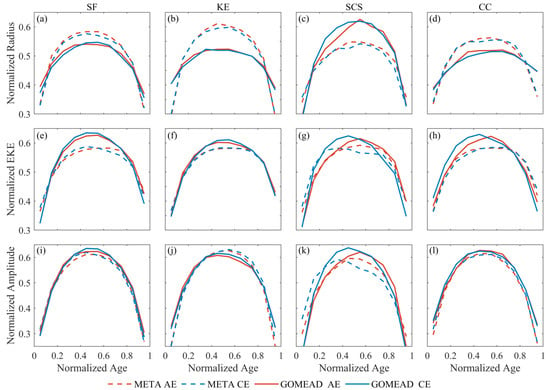
Figure 13.
Time evolution of the mean normalized (a–d) radius, (e–h) EKE and (i–l) amplitude. The four columns from left to right represent the normalized parameters of SF, KE, SCS, and CC regions, respectively.
The mean eddy EKE and amplitude normalized curves of the two datasets are basically the same (Figure 13e–l). The variation range of the eddy EKE normalized curve of the GOMEAD dataset is slightly higher than that of the META dataset in all four regions. This may be due to the GOMEAD dataset missing some small eddies their lifespans. The GOMEAD dataset normalized amplitude is higher in the maturation stage in the SCS region, which may be related to the definition and the accuracy of detection of eddy edge. The curves of the three normalized parameters all changed sharply in the generation and termination stages, while they changed gently in the intensification and maturation stages. Generally, the variation amplitude of AE normalized eddy parameters curves in both datasets are slightly smaller than that of CE normalized eddy parameters.
3.5. Eddy Movement
In order to understand and compare the movement of eddies in the two datasets, the movement speed and direction of eddies along the zonal and meridional directions, respectively, are calculated.
According to the zonal statistics, both AEs and CEs have basically the same mean eddy moving direction, and the difference of mean eddy moving velocity is less than 0.5 cm/s except for some regions of SCS (Figure 14 and Figure 15).
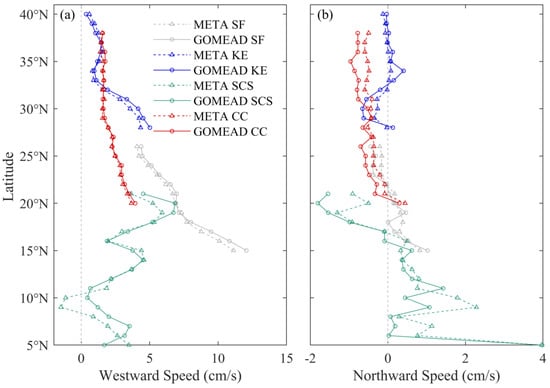
Figure 14.
Variations of (a) westward speeds and (b) northward speed of AEs by latitude. Dashed and solid lines represent results from the META and GOMEAD datasets, respectively.
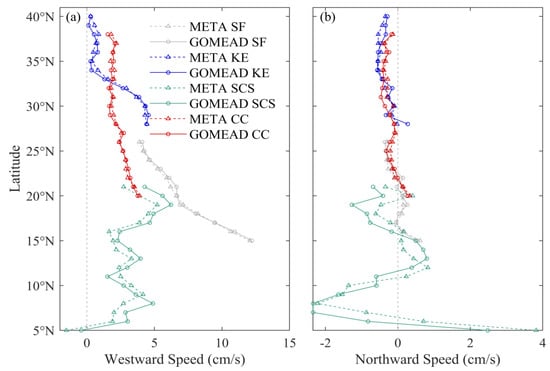
Figure 15.
Variations of (a) westwards and (b) northwards speeds of CEs by latitude. Dashed and solid lines represent results from the META and GOMEAD datasets, respectively.
In the zonal direction, eddies within the four regions is basically westward, and only at 9–10°N in the SCS, the direction in the META dataset move eastward, which is inconsistent with GOMEAD. The results of GOMEAD are similar to those of [35]. Meridionally, the mean moving direction of AEs in the four regions is basically the same, and the moving speed of GOMEAD in the SF and CC region is about 0.3 cm/s faster than that of META. The difference in moving speed is more obvious in the SCS region, and the difference is about 1 cm/s between 5–10°N and 20–21°N. This may be related to the presence of more landmasses. In the SF and CC regions, AEs move southward in the north of about 21°N and move northward in the south of about 21°N, which is similar to the research results of [52]. In the KE region of about 32°N, the westward velocity in both data decreased significantly, due to the influence of the eastward flow field on the main axis of the KE current [27].
According to Figure 15, it can be seen that the CEs speed variation trend of the two datasets is consistent. However, by comparing Figure 14 and Figure 15, it can be seen that the westward movement of AEs and CEs has the same trend, but the northward movement is different. For example, AEs and CEs in the CC region both move southwards, but CEs move at an overall lower speed. One reason is that due to the β-effect of Earth’s rotation, AEs and CEs move westwards, and they also tend to move towards the equator and the pole, respectively. Another reason is the influence of the local background flow field.
According to the meridional statistics, eddies in both datasets are basically the same in terms of movement direction and speed (Figure 16 and Figure 17). In the western SF and the western KE, eddies move more slowly westward and faster northward. This is thought to be due to the existence of Kuroshio. Background flow northward drives the eddy movement. Combined with Figure 14, AEs in the SF region north of about 21°N will propagate towards the equator, but those south of about 21°N will move towards the pole in the northern hemisphere. From the latitudinal perspective, the northward movement speed of the SF region is basically zero to the east of 125°E, indicating that the northward movement speed of the SF region is symmetrically distributed along the latitude line of 21°N and generally moves toward 21°N with basically the same movement rate.
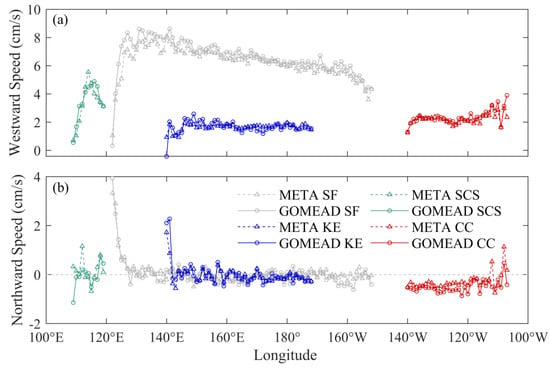
Figure 16.
Variations of (a) westward speeds and (b) northward speed of AEs by longitude. Dashed and solid curves represent the META and GOMEAD datasets, respectively.
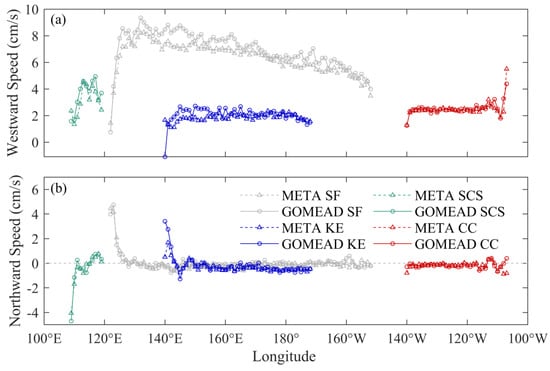
Figure 17.
Variations of (a) westwards and (b) northwards speeds of CEs by longitude. Dashed and solid curves represent the META and GOMEAD datasets, respectively.
4. Discussion
4.1. Eddy Center Difference
Although the difference of eddy centers in the eddy detection algorithms cannot be directly reflected in the above statistical results, its value affects dataset reliability. In the GOMEAD dataset, vector geometry is used to detect eddies and as the eddy center is the minimum velocity point in the surrounding area, eddies can be detected more accurately than the META dataset. Starting from the eddy center, this study calculates tangential components of streamlines in the four cardinal directions to verify the accuracy of eddy detection (Figure 18). It can be seen that the eddy center in the two examples is located at the minimum velocity point.
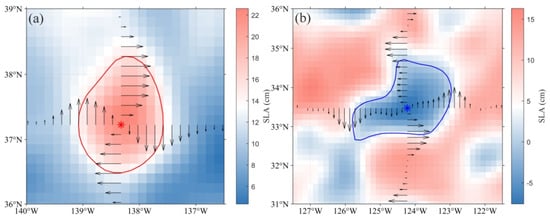
Figure 18.
Eddies centers of (a) AE and (b) CE as estimated in the GOMEAD dataset in the KE region on 1 January 2019. Red and blue curves represent contours of selected AE and CE, respectively. The stars represent eddy centers. Arrows indicate flow direction.
In the META eddy detection algorithm, the eddy center is determined according to the centroid of the eddy range, which has a good effect on simple regular eddies. In practice, however, eddies are complex, with irregular eddies occurring when two or more eddies come within close proximity of each other. The center of detected eddies may then be offset from real value. An example is presented in Figure 19a where it can be clearly seen that the eddy center is located at the edge of the eddy, far away from the true center of the eddy. That’s because the eddy is shaped similar to the letter C, and the centroid is not at the center of the eddy. Figure 19b is an example similar to Figure 19a.
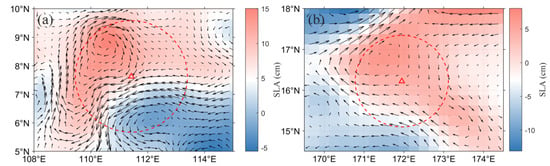
Figure 19.
Two cases of irregular eddies in the META dataset in (a) the SF region on 14 January 2019, and (b) the SCS region on 28 February 2019, respectively. The red triangle is the calculated eddy center, and the dashed curves represent the circle corresponding to the eddy radius of the META dataset. Arrows indicate flow direction.
In addition, when two eddies of the same polarity are close to each other, the eddy center detected by the META algorithm may appear at their barycenters (Figure 20). This is the track jumping intrinsic to the META dataset. Similarly, if eddies of the same polarity, the low-value regions of local SLA are connected to each other. Since the META algorithm does not consider the segmentation of eddies, the algorithm will identify the two eddies as one, resulting in their centroid appearing in between the eddies, leading to deviations between real and estimated eddy centers.
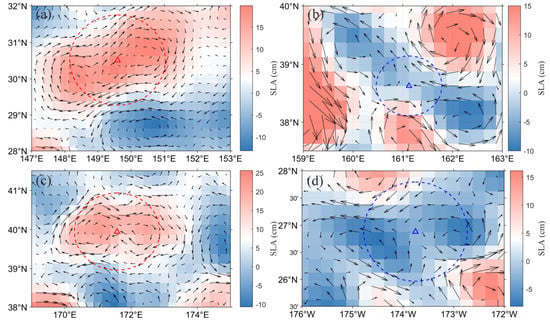
Figure 20.
Four cases of the close of two eddies. Red (blue) curves represent AEs (CEs). (a) 14 February 2019, in KE region, (b) 14 March 2019, in KE region, (c) 6 March 2019, in KE region, and (d) 17 April 2019, in SF region.
4.2. Eddy Number Difference
One possible reason why the eddy number recorded by the GOMEAD dataset is lower than that of the META dataset may be related to the setting of eddy detection parameters. A possible reason is that the META eddy detection algorithm often misidentifies oceanic structures as eddies as it is dependent on detecting local extreme points to identify possible eddies from SLA data. The existence of SLA extreme points does not necessarily represent the occurrence of eddies, and the rotation direction of eddy vectors must be consistent near the center of eddies. As shown in Figure 21, there are only curved flow fields, and the rotation directions of velocity vectors are not consistent, but they are nevertheless identified as eddies by the META algorithm.
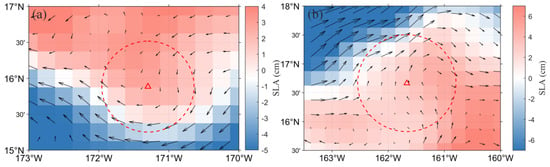
Figure 21.
Snapshots of eddy identification errors as identified by the META dataset on (a) 5 January 2019, and (b) 24 March 2019, in the SF region. The triangle represents the center of the META eddy. Dashed curves represent the circle corresponding to the eddy radius of the META dataset.
Another possible reason is that the GOMEAD may miss some eddies with a radius of less than 0.6°. In the GOMEAD dataset, the minimum scale of eddy detection is controlled by parameters a and b. Moreover, as the GOMEAD dataset is a global eddy dataset, and when a = 4, b = 3 are selected, the best results can be obtained. However, this parameter selection greatly reduces the possibility of detecting eddies with radii with fewer than 4 grid points (i.e., 0.6°), which is clearly reflected in the statistical results. For example, the number of eddies with radii below 70 km in the GOMEAD dataset is only about 15%, while that of the META dataset, this value is about 30%.
4.3. Eddy Radius Difference
The difference in the mean radius of eddies between the two datasets reaches about 17 km, which may be caused by the following reasons.
As mentioned above, the parameter setting of the GOMEAD dataset may result in fewer smaller-radius eddies. Therefore, the parameter setting is one of the important reasons for the larger mean eddy radius in the GOMEAD dataset.
The radius of META was limited by the detection parameter. The GOMEAD dataset has 1.89% (1.45%) AEs (CEs) with radii of over 200 km, while the META dataset has only 0.1% (0.07%). In the two examples of Figure 22, the two farthest points of the eddy are more than 400 km apart in the GOMEAD dataset. In the META algorithm, distances are limited to less than 400 km (north of 25°N), but the GOMEAD dataset possesses no such limit.
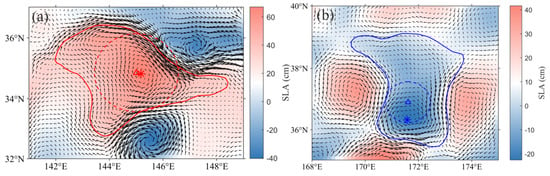
Figure 22.
Comparison of eddies’ boundaries on (a) 1 January 2019 and (b) 7 March 2019 in the KE region. Dashed (solid) curves represent the META (GOMEAD) datasets. Red (blue) curves represent the AE (CE). The triangle (star) represents the eddy center of the META (GOMEAD) dataset.
In addition, the eddy amplitude difference is similar to the eddy radius difference. For an eddy, the larger the eddy detection range, the greater its amplitude is. Due to the larger radius, the amplitude of the GOMEAD dataset is greater. So, the amplitude difference is no longer analyzed separately.
4.4. Eddy Lifespan Difference
The difference in lifespan may be related to the fact that META’s algorithm jumps from one eddy to another during eddy tracking. Eddy detection anomalies may occur when two eddies with the same polarity are close to each other. Jumping thus occurs. The jumping process is divided into three steps. Firstly, an ordinary single-core eddy is detected (‘eddy A’). Secondly, another but stronger eddy (‘eddy B’) approaches eddy A. The META algorithm then misidentifies the two eddies as a single eddy with a radius larger than either and its center at the ‘barycenter’ of both eddies. Third and finally, after eddy A weakens, the detection algorithm will ‘jump’ to identify the center of eddy B.
In Figure 23a, the identified eddy gradually moved eastward after 13 February 2019. On 22 February 2019 (Figure 23b), it reached the center of two eddies. On 26 February 2019 (Figure 23c), the identified eddy center completely changed to another eddy. This jumping phenomenon causes the detected eddies to artificially live longer. A similar situation is presented in another example presented in Figure 23d–f.
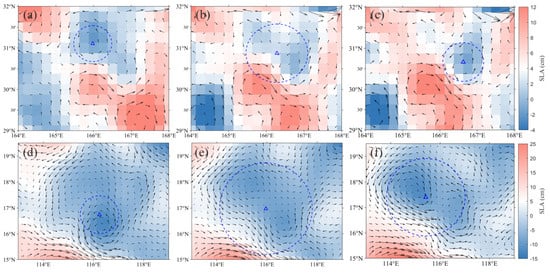
Figure 23.
Two cases of tracking error of the META dataset. The jumping process of the first case in the KE region: (a) Before jumping (13 February 2019), (b) jumping (22 February 2019) and (c) after jumping (26 February 2019). Another jumping process in the SF region: (d) Before jumping (3 February 2019), (e) jumping (11 February 2019) and (f) after jumping (18 February 2019).
5. Conclusions
The identification, classification, and study of eddies and their properties have important implications for a variety of atmospheric, oceanic, and climatic phenomena and processes. Thus, the selection of an appropriate eddy dataset has strong effects on the results of relevant research. This study compares the traditional META eddy dataset with the GOMEAD dataset in four regions of the North Pacific Ocean. Eddy properties such as spatiotemporal distributions, evolution, and movement characteristics are examined. Results illustrate that the total eddy number of the GOMEAD dataset is 8% smaller than that of the META dataset. The mean eddy radius and lifespan in the GOMEAD dataset are, respectively, 17 km larger and 15 days shorter than in the META dataset. Using the SF as an example, both datasets possess similar annual trends in eddy generation, but the consistency of the number of eddy termination has some differences. In terms of monthly variation, eddy generation numbers in the GOMEAD and META datasets are roughly the same, but the peak of eddy termination occurs about one month later in the GOMEAD dataset than does the META dataset. The spatial distribution of eddy generation is roughly the same between both datasets. Large radii eddies tend to appear in the middle of the SF, KE, and SCS regions. Eddy amplitudes as estimated by the GOMEAD dataset are generally larger than the META dataset, but both datasets have similar eddy amplitude distribution trends. The evolution of eddy parameters with lifespan (including radius, EKE, and amplitude) can fully reflect the whole process of eddy formation, growth, maturation, and termination. Eddy movement is consistent between the two datasets. Generally, eddy movement speeds and directions are virtually the same in other regions except for the SCS, with the difference of the mean eddy velocity is less than 0.5 cm/s.
The reasons for the difference between the two datasets are analyzed. The number of eddies in the GOMEAD dataset is smaller than that of the META dataset. It is thought that this is partly because the eddy detection scheme of the META dataset may not be completely accurate as some flows that do not form closed circulation are detected as eddies. An overestimation of eddy numbers consequently occurs. Furthermore, parameter selection reduces the chances for eddy with radii of < 0.6° to be detected, which results in an underestimation of the eddy number of the GOMEAD dataset. The parameter selection ensures that the GOMEAD dataset preferentially identifies large radii eddies by neglecting small radii eddies. Eddy lifespans in the GOMEAD dataset are notably shorter than those in the META dataset. This may be caused by the tracking jumps inherent to the META dataset. The inaccurate detection of some eddy centers in META results in the phenomenon that some eddy centers jump from one eddy to other eddy during the tracking process, resulting in abnormal long-lifespan eddies are detected.
The advantages and disadvantages of the two datasets are reflected in different aspects. The GOMEAD dataset can provide accurate eddy center and eddy edge, while META can’t provide eddy edge and its eddy center is usually not the point with a minimum of an eddy. What’s more, in the META dataset, some unclosed currents are detected as eddies. Therefore, it is better to use the GOMEAD dataset when eddy edge and precise eddy center are important in studies. The detection parameter (a = 4) of GOMEAD reduces its ability to detect eddies smaller than 0.6°. Small eddies, such as those near coastlines or between islands, maybe partially missed in the GOMEAD dataset. The META dataset is more advantageous in detecting small radii eddies. Therefore, the META dataset is potentially more suitable for the detection of a region with small eddies, such as those with archipelagos such as Japan, the Philippines, the Aleutian Archipelago, or the Caribbean Sea, however further research is required.
Although both datasets use the same raw data, their parameter definitions and methods are somewhat different, so the two datasets have a lot, but not everything in common. Since there is no so-called “truth value” for eddies, it is difficult to quantitatively judge which dataset is better. Using this study as a benchmark as it has discussed the relative advantages and disadvantages of each dataset, and specifically, where each dataset can or cannot be used, users are encouraged to carefully weigh the advantages and disadvantages of either dataset for their specific applications.
Author Contributions
Conceptualization, Z.Y. and C.D.; methodology, Z.Y., C.D. and L.L.; software, Z.Y., L.L. and B.J.B.; formal analysis, Z.Y.; investigation, Z.Y. and B.J.B.; data curation, Y.Z and B.J.B.; writing—original draft preparation, Z.Y.; writing—review and editing, Z.Y., L.L. and B.J.B.; visualization, Z.Y.; supervision, C.D.; funding acquisition, C.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Key Research and Development Program of China under contract No.2017YFA0604100, 2016YFA0601803, and 2016YFC1401407; the National Natural Science Foundation of China under contract No. 41490643 and 41706008.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The altimeter product was produced by SSALTO/DUACS and distributed by AVISO, with support from the Copernicus Marine Environment Monitoring Service (CMEMS) (https://cds.climate.copernicus.eu/cdsapp#!/dataset/satellite-sea-level-global?tab=overview, accessed on 11 November 2021). The META dataset in this study was provided by Oregon State University algorithm (in collaboration with Chelton D.B.), and is available on the AVISO website (https://www.aviso.altimetry.fr/en/data/products/value-added-products/global-mesoscale-eddy-trajectory-product/meta2-0-dt.html, accessed on 11 November 2021) as “Mesoscale Eddy Trajectory Atlas Product version 2.0” product by FTP. The GOMEAD dataset used during the study is developed by Dong C. et al. [28] and is available from https://dx.doi.org/10.11922/sciencedb.01190, accessed on 11 November 2021.
Acknowledgments
The authors would like to thank the creators and archivers of the META dataset used in this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M.; de Szoeke, R.A. Global observations of large oceanic eddies. Geophys. Res. Lett. 2007, 34, L15606. [Google Scholar] [CrossRef]
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M. Global observations of nonlinear mesoscale eddies. Prog. Oceanogr. 2011, 91, 167–216. [Google Scholar] [CrossRef]
- Frenger, I.; Münnich, M.; Gruber, N.; Knutti, R. Southern ocean eddy phenomenology. J. Geophys. Res. Ocean. 2015, 120, 7413–7449. [Google Scholar] [CrossRef] [Green Version]
- Tian, F.; Wu, D.; Yuan, L.; Chen, G. Impacts of the efficiencies of identification and tracking algorithms on the statistical properties of global mesoscale eddies using merged altimeter data. Int. J. Remote Sens. 2019, 41, 2835–2860. [Google Scholar] [CrossRef]
- Dandapat, S.; Chakraborty, A. Mesoscale eddies in the Western Bay of Bengal as observed from satellite altimetry in 1993–2014: Statistical characteristics, variability and three-dimensional properties. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 5044–5054. [Google Scholar] [CrossRef]
- Cui, W.; Wang, W.; Zhang, J.; Yang, J. Multicore structures and the splitting and merging of eddies in global oceans from satellite altimeter data. Ocean Sci. 2019, 15, 413–430. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Liang, Y.; Zhang, J.; Yang, J.; Song, P.; Cui, W. A new automatic oceanic mesoscale eddy detection method using satellite altimeter data based on density clustering. Acta Oceanol. Sin. 2019, 38, 134–141. [Google Scholar] [CrossRef]
- Amores, A.; Monserrat, S.; Melnichenko, O.; Maximenko, N. On the shape of sea level anomaly signal on periphery of mesoscale ocean eddies. Geophys. Res. Lett. 2017, 44, 6926–6932. [Google Scholar] [CrossRef]
- Nencioli, F.; Dong, C.; Dickey, T.; Washburn, L.; McWilliams, J.C. A vector geometry–based eddy detection algorithm and its application to a high-resolution numerical model product and high-frequency radar surface velocities in the Southern California Bight. J. Atmos. Ocean. Technol. 2010, 27, 564–579. [Google Scholar] [CrossRef]
- Halo, I.; Backeberg, B.; Penven, P.; Ansorge, I.; Reason, C.; Ullgren, J.E. Eddy properties in the mozambique channel: A comparison between observations and two numerical ocean circulation models. Deep Sea Res. Part II Top. Stud. Oceanogr. 2014, 100, 38–53. [Google Scholar] [CrossRef]
- Pegliasco, C.; Chaigneau, A.; Morrow, R.; Dumas, F. Detection and tracking of mesoscale eddies in the Mediterranean Sea: A comparison between the Sea Level Anomaly and the Absolute Dynamic Topography fields. Adv. Space Res. 2021, 68, 401–419. [Google Scholar] [CrossRef]
- Sun, W.; Dong, C.; Tan, W.; Liu, Y.; He, Y.; Wang, J. Vertical structure anomalies of oceanic eddies and eddy-induced transports in the South China Sea. Remote Sens. 2018, 10, 795. [Google Scholar] [CrossRef] [Green Version]
- Yi, J.; Du, Y.; He, Z.; Zhou, C. Enhancing the accuracy of automatic eddy detection and the capability of recognizing the multi-core structures from maps of sea level anomaly. Ocean Sci. 2014, 10, 39–48. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Li, H.; Liu, S.; Shao, L.; Zhao, Z.; Liu, H. Automatic detection of oceanic eddies in reanalyzed SST images and its application in the East China Sea. Sci. China Earth Sci. 2015, 58, 2249–2259. [Google Scholar] [CrossRef]
- Le Vu, B.; Stegner, A.; Arsouze, T. Angular momentum eddy detection and tracking algorithm (AMEDA) and its application to coastal eddy formation. J. Atmos. Ocean. Technol. 2018, 35, 739–762. [Google Scholar] [CrossRef]
- Faghmous, J.H.; Frenger, I.; Yao, Y.; Warmka, R.; Lindell, A.; Kumar, V. A daily global mesoscale ocean eddy dataset from satellite altimetry. Sci. Data 2015, 2, 150028. [Google Scholar] [CrossRef] [Green Version]
- Mason, E.; Pascual, A.; McWilliams, J.C. A new sea surface height–based code for oceanic mesoscale eddy tracking. J. Atmos. Ocean. Technol. 2014, 31, 1181–1188. [Google Scholar] [CrossRef] [Green Version]
- Meng, Y.; Liu, H.; Lin, P.; Ding, M.; Dong, C. Oceanic mesoscale eddy in the Kuroshio extension: Comparison of four datasets. Atmos. Ocean. Sci. Lett. 2021, 14, 100011. [Google Scholar] [CrossRef]
- Chaigneau, A.; Gizolme, A.; Grados, C. Mesoscale eddies off Peru in altimeter records: Identification algorithms and eddy spatio-temporal patterns. Prog. Oceanogr. 2008, 79, 106–119. [Google Scholar] [CrossRef]
- Schlax, M.G.; Chelton, D.B. The “Growing Method” of Eddy Identification and Tracking in Two and Three Dimensions. 2016. Available online: https://www.aviso.altimetry.fr/fileadmin/documents/data/products/value-added/Schlax_Chelton_2016.pdf (accessed on 11 November 2021).
- Dilmahamod, A.F.; Aguiar-González, B.; Penven, P.; Reason, C.J.C.; De Ruijter, W.P.M.; Malan, N.; Hermes, J.C. SIDDIES corridor: A major east-west pathway of long-lived surface and subsurface eddies crossing the subtropical south indian ocean. J. Geophys. Res. Ocean. 2018, 123, 5406–5425. [Google Scholar] [CrossRef] [Green Version]
- Gaube, P.J.; McGillicuddy, D.; Moulin, A.J. Mesoscale eddies modulate mixed layer depth globally. Geophys. Res. Lett. 2019, 46, 1505–1512. [Google Scholar] [CrossRef] [Green Version]
- Melnichenko, O.; Hacker, P.; Müller, V. Observations of mesoscale eddies in satellite SSS and inferred eddy salt transport. Remote Sens. 2021, 13, 315. [Google Scholar] [CrossRef]
- Ji, J.; Dong, C.; Zhang, B.; Liu, Y. An oceanic eddy statistical comparison using multiple observational data in the Kuroshio Extension region. Acta Oceanol. Sin. 2017, 36, 1–7. [Google Scholar] [CrossRef]
- Ji, J.; Dong, C.; Zhang, B.; Liu, Y.; Zou, B.; King, G.P.; Xu, G.; Chen, D. Oceanic eddy characteristics and generation mechanisms in the Kuroshio Extension region. J. Geophys. Res. Ocean. 2018, 123, 8548–8567. [Google Scholar] [CrossRef]
- Wang, S.; Zhu, W.; Ma, J.; Ji, J.; Yang, J.; Dong, C. Variability of the Great Whirl and its impacts on atmospheric processes. Remote Sens. 2019, 11, 322. [Google Scholar] [CrossRef] [Green Version]
- Ji, J.; Ma, J.; Dong, C.; Chiang, J.; Chen, D. Regional dependence of atmospheric responses to oceanic eddies in the North Pacific Ocean. Remote Sens. 2020, 12, 1161. [Google Scholar] [CrossRef] [Green Version]
- Dong, C.; Liu, L.; Nencioli, F.; Xia, C.; Xu, G.; Ma, J.; Liu, Y.; Sun, W.; Ji, J. Global Ocean Mesoscale Eddy Atmospheric-Oceanic-Biological Interaction Observational Dataset (GOMEAD) (V1); Science Data Bank: Beijing, China, 2021. [Google Scholar] [CrossRef]
- Couvelard, X.; Caldeira, R.M.A.; Araújo, I.B.; Tomé, R. Wind mediated vorticity-generation and eddy-confinement, leeward of the Madeira Island: 2008 numerical case study. Dynam. Atmos. Ocean. 2012, 58, 128–149. [Google Scholar] [CrossRef]
- Dong, C.; Lin, X.; Liu, Y.; Nencioli, F.; Chao, Y.; Guan, Y.; Chen, D.; Dickey, T.; McWilliams, J.C. Three-dimensional oceanic eddy analysis in the Southern California Bight from a numerical product. J. Geophys. Res. Ocean. 2012, 117, C00H14. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Dong, C.; Guan, Y.; Chen, D.; McWilliams, J.; Nencioli, F. Eddy analysis in the subtropical zonal band of the North Pacific Ocean. Deep Sea Res. Part I Oceanogr. Res. Pap. 2012, 68, 54–67. [Google Scholar] [CrossRef]
- Amores, A.; Monserrat, S.; Marcos, M. Vertical structure and temporal evolution of an anticyclonic eddy in the Balearic Sea (western Mediterranean). J. Geophys. Res. Ocean. 2013, 118, 2097–2106. [Google Scholar] [CrossRef] [Green Version]
- Peliz, A.; Boutov, D.; Teles-Machado, A. The Alboran Sea mesoscale in a long term high resolution simulation: Statistical analysis. Ocean Model. 2013, 72, 32–52. [Google Scholar] [CrossRef]
- Dong, C.; McWilliams, J.C.; Liu, Y.; Chen, D. Global heat and salt transports by eddy movement. Nat. Commun. 2014, 5, 3294. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, X.; Dong, C.; Chen, D.; Liu, Y.; Yang, J.; Zou, B.; Guan, Y. Three-dimensional properties of mesoscale eddies in the South China Sea based on eddy-resolving model output. Deep Sea Res. Part I 2015, 99, 46–64. [Google Scholar] [CrossRef]
- Qin, D.; Wang, J.; Liu, Y.; Dong, C. Eddy analysis in the Eastern China Sea using altimetry data. Front. Earth Sci. 2015, 9, 709–721. [Google Scholar] [CrossRef]
- Xu, G.; Cheng, C.; Yang, W.; Xie, W.; Kong, L.; Hang, R.; Ma, F.; Dong, C.; Yang, J. Oceanic eddy identification using an AI scheme. Remote Sens. 2019, 11, 1349. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.; Xu, G.; Liu, Y.; Sun, W.; Xia, C.; Dong, C. Multi-source data analysis of mesoscale eddies and their effects on surface chlorophyll in the Bay of Bengal. Remote Sens. 2020, 12, 3485. [Google Scholar] [CrossRef]
- Quattrocchi, G.; Cucco, A.; Cerritelli, G.; Mencacci, R.; Comparetto, G.; Sammartano, D.; Ribotti, A.; Luschi, P. Testing a novel aggregated methodology to assess hydrodynamic impacts on a high-resolution marine turtle trajectory. Front. Mar. Sci. 2021, 8, 699580. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, G.; Sun, M.; Liu, S.; Tian, F. A parallel SLA-based algorithm for global mesoscale eddy identification. J. Atmos. Ocean. Technol. 2016, 33, 2743–2754. [Google Scholar] [CrossRef]
- Kang, L.; Wang, F.; Chen, Y. Eddy generation and evolution in the North Pacific Subtropical Countercurrent (NPSC) zone. Chin. J. Oceanol. Limnol. 2010, 28, 968–973. [Google Scholar] [CrossRef]
- Yoshida, S.; Qiu, B.; Hacker, P. Wind-generated eddy characteristics in the lee of the island of Hawaii. J. Geophys. Res. 2010, 115, C03019. [Google Scholar] [CrossRef]
- Xu, C.; Shang, X.-D.; Huang, R.X. Estimate of eddy energy generation/dissipation rate in the world ocean from altimetry data. Ocean Dynam. 2011, 61, 525–541. [Google Scholar] [CrossRef]
- Zhang, Z.; Tian, J.; Qiu, B.; Zhao, W.; Chang, P.; Wu, D.; Wan, X. Observed 3D structure, generation, and dissipation of oceanic mesoscale eddies in the South China Sea. Sci. Rep. 2016, 6, 24349. [Google Scholar] [CrossRef]
- Chen, G.; Hou, Y.; Zhang, Q.; Chu, X. The eddy pair off eastern Vietnam: Interannual variability and impact on thermohaline structure. Cont. Shelf Res. 2010, 30, 715–723. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, W.; Qiu, B.; Tian, J. Anticyclonic eddy sheddings from Kuroshio loop and the accompanying cyclonic eddy in the Northeastern South China Sea. J. Phys. Oceanogr. 2017, 47, 1243–1259. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Du, Y.; Liang, F.; Sun, Y.; Yi, J. A census of the 1993–2016 complex mesoscale eddy processes in the South China Sea. Water 2019, 11, 1208. [Google Scholar] [CrossRef] [Green Version]
- Chen, G.; Hou, Y.; Chu, X. Mesoscale eddies in the South China Sea: Mean properties, spatiotemporal variability, and impact on thermohaline structure. J. Geophys. Res. 2011, 116, C06018. [Google Scholar] [CrossRef]
- Xie, J.; De Vos, M.; Bertino, L.; Zhu, J.; Counillon, F. Impact of assimilating altimeter data on eddy characteristics in the South China Sea. Ocean Model. 2020, 155, 101704. [Google Scholar] [CrossRef]
- Xing, T.; Yang, Y. Three mesoscale eddy detection and tracking methods: Assessment for the South China Sea. J. Atmos. Ocean. Technol. 2021, 38, 243–258. [Google Scholar] [CrossRef]
- Zhai, X.; Johnson, H.L.; Marshall, D.P. Significant sink of ocean-eddy energy near western boundaries. Nat. Geosci. 2010, 3, 608–612. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, W.; Qiu, B. Oceanic mass transport by mesoscale eddies. Science 2014, 345, 322–324. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).