Hyperspectral Snapshot Compressive Imaging with Non-Local Spatial-Spectral Residual Network
Abstract
1. Introduction
- we propose a non-local spatial-spectral attention module to represent the HSI data, and both the spatial structure and the global correlations between spectral channels are exploited to improve the reconstruction quality;
- we design a compound loss, consisting of the reconstruction loss, the measurement loss and the cosine loss, to supervise the network learning. In particular, the cosine loss can further enhance the fidelity of the reconstructed spectral signatures;
- and experimental results demonstrate that the proposed model achieves better performance on simulation and real datasets, which proves the effectiveness and superiority of the proposed network.
2. Related Work
3. CASSI Forward Model
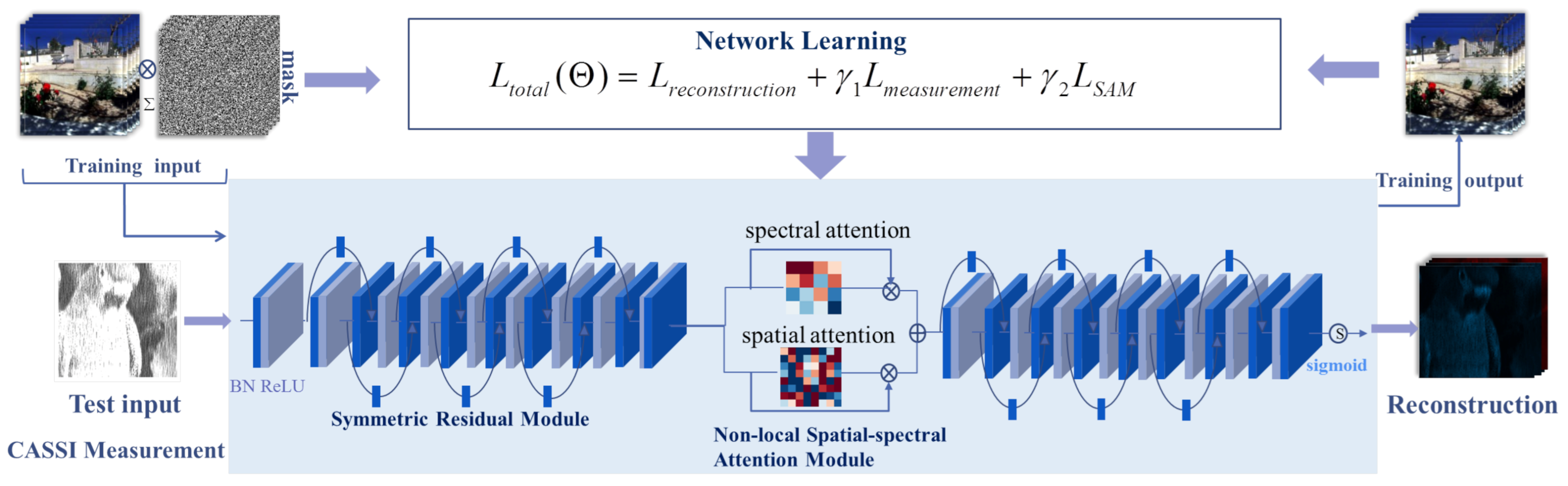
4. The Proposed Method
4.1. Non Local Spatial-Spectral Residual Reconstruction Network
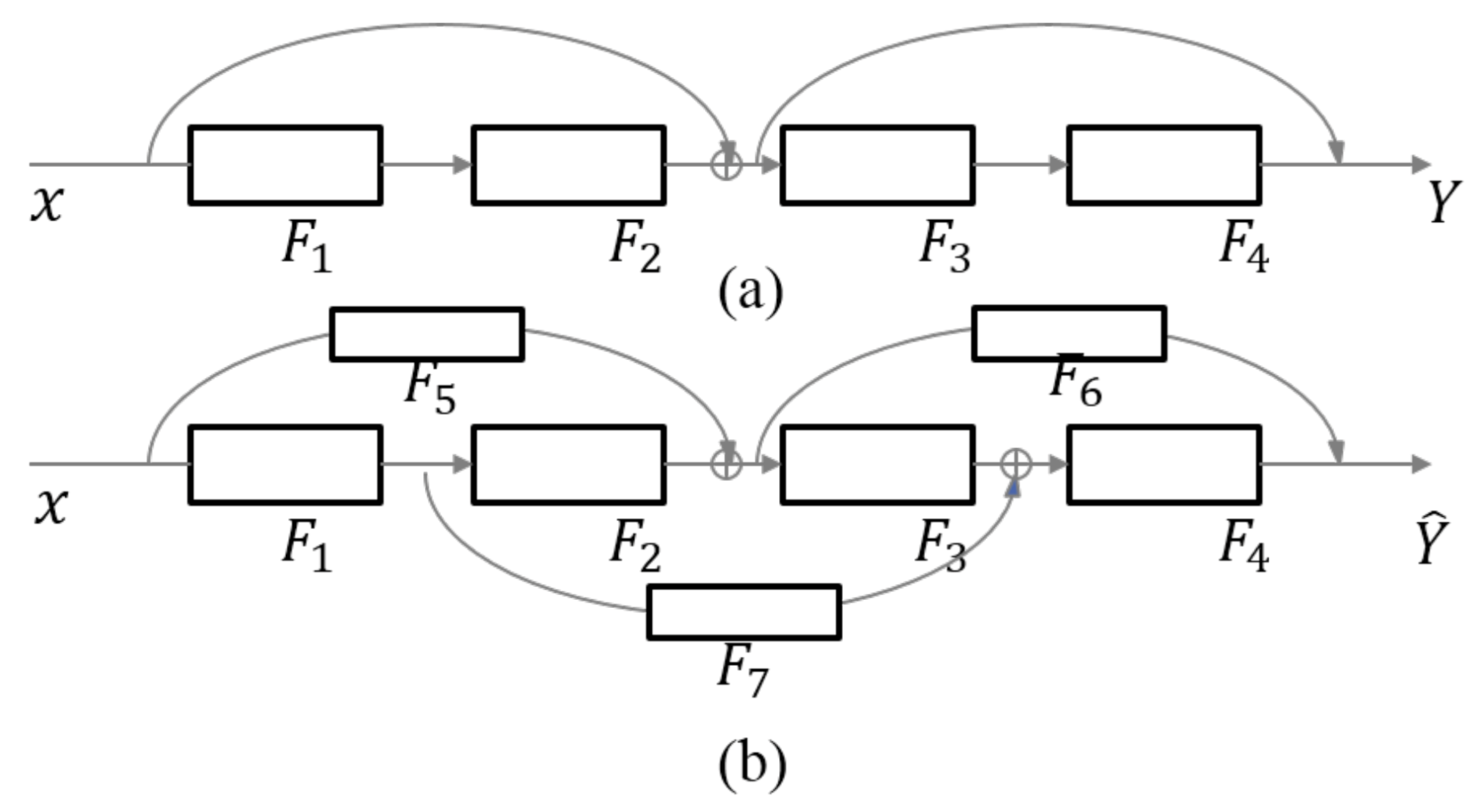
4.1.1. The Symmetric Residual Module
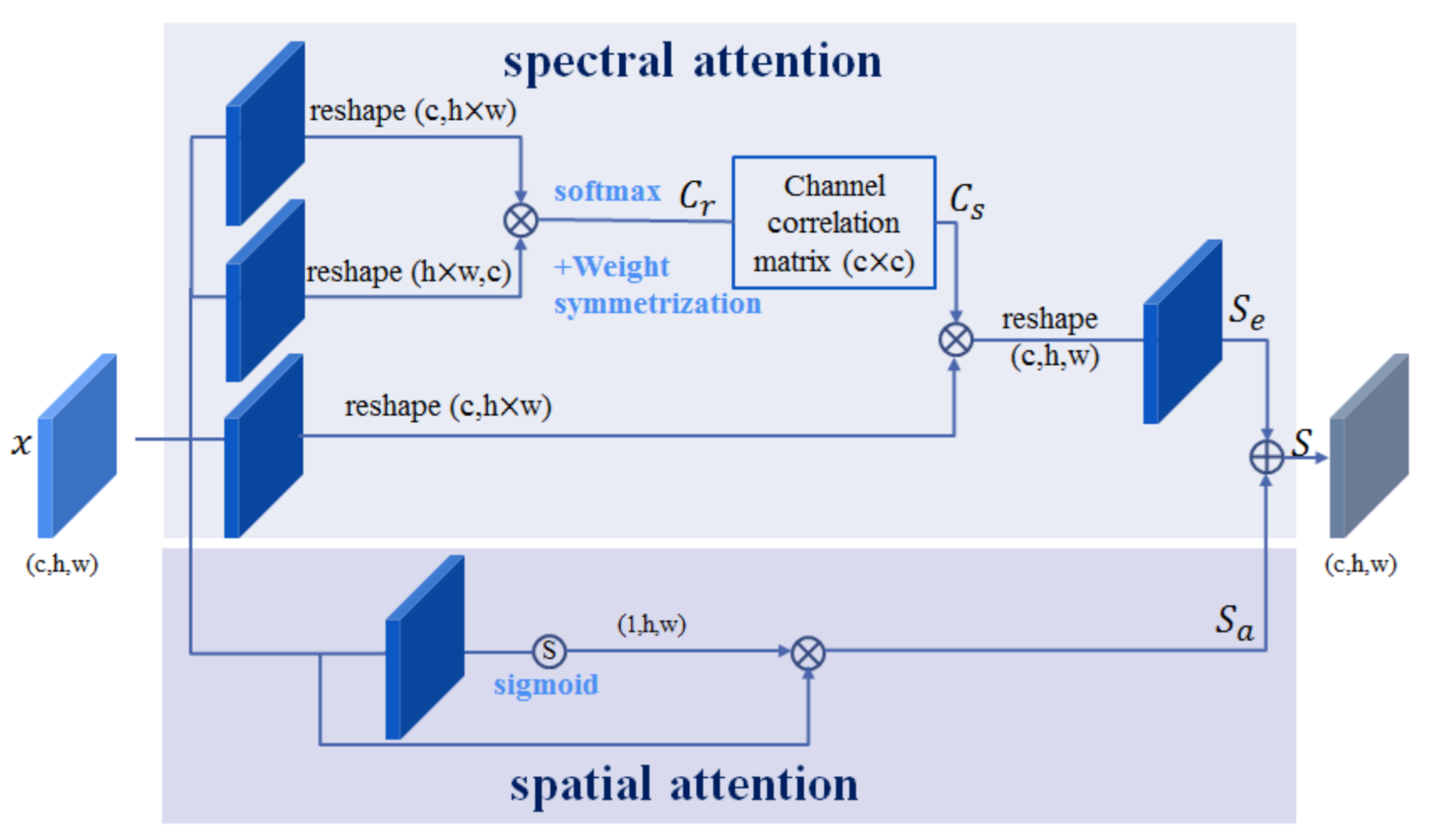
4.1.2. The Non-Local Spatial-Spectral Attention Module
4.1.3. Loss Function
5. Experiments
5.1. Experimental Setting
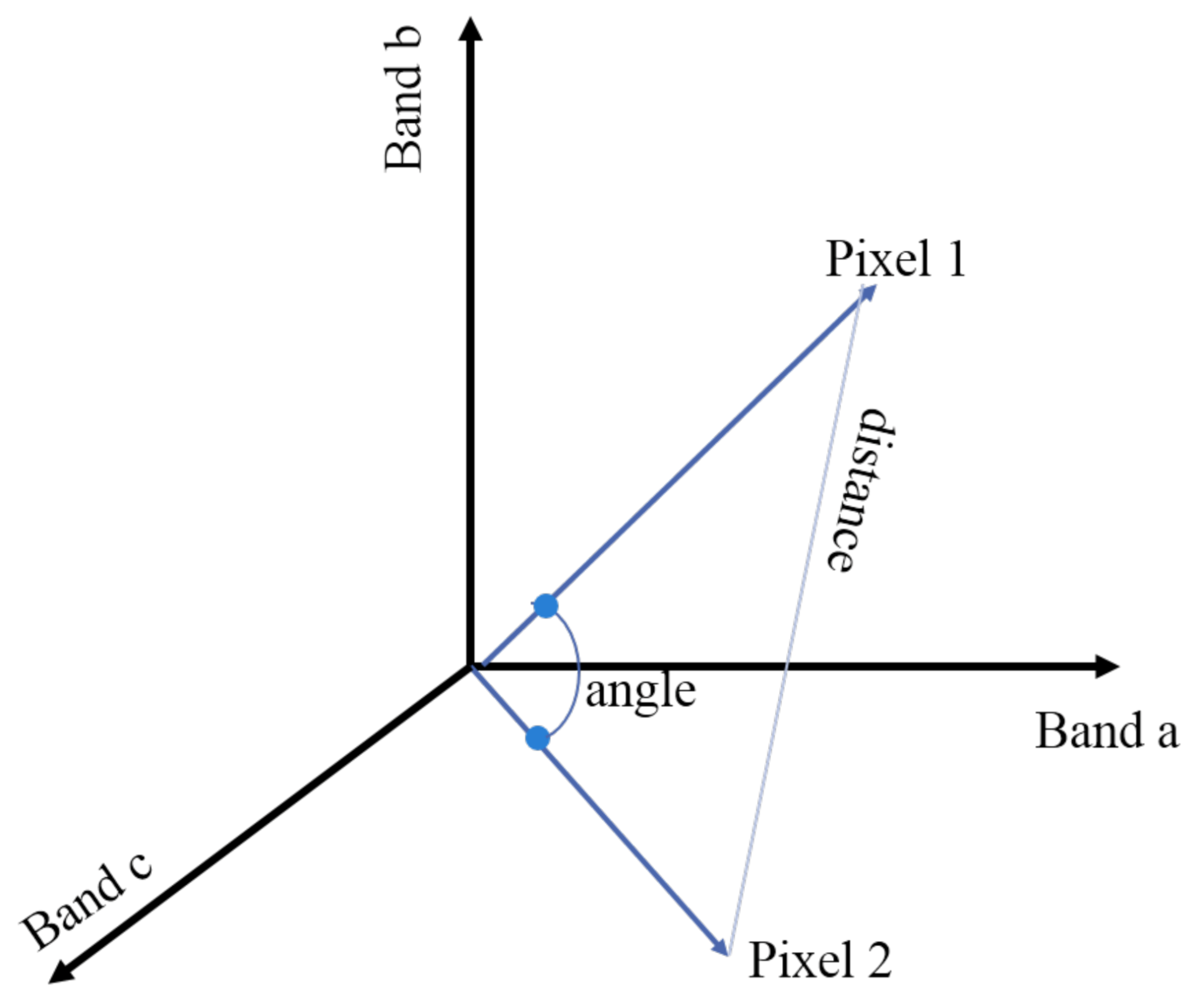
5.2. Evaluation Metrics
5.3. Ablation Studies
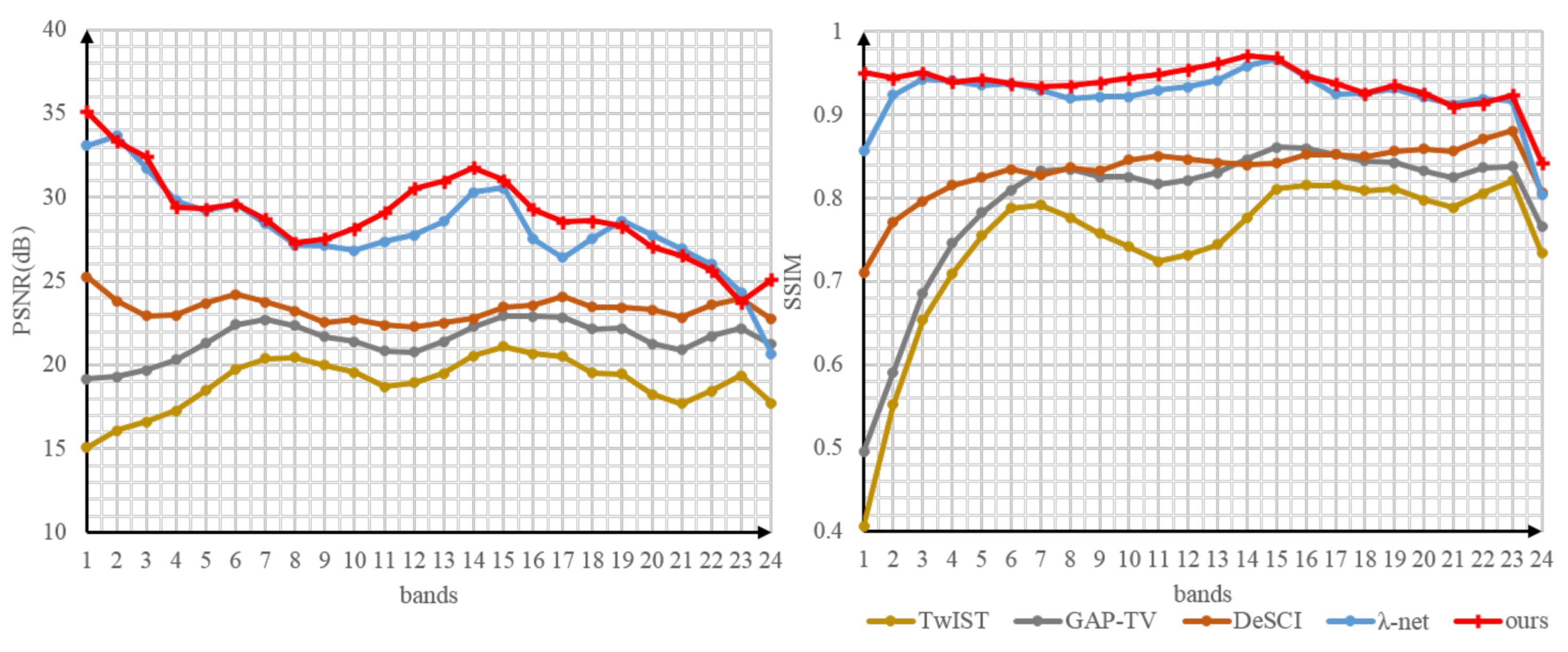
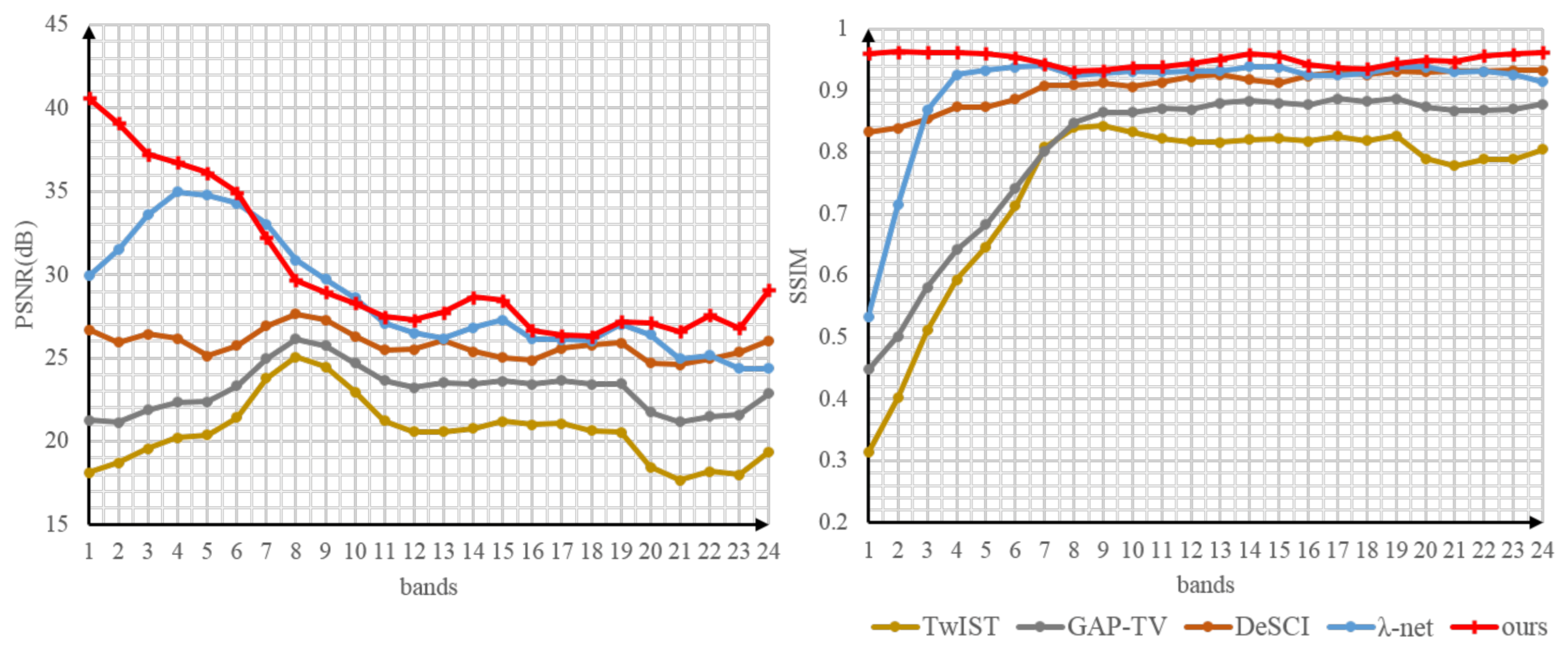
5.4. Simulation Data Results
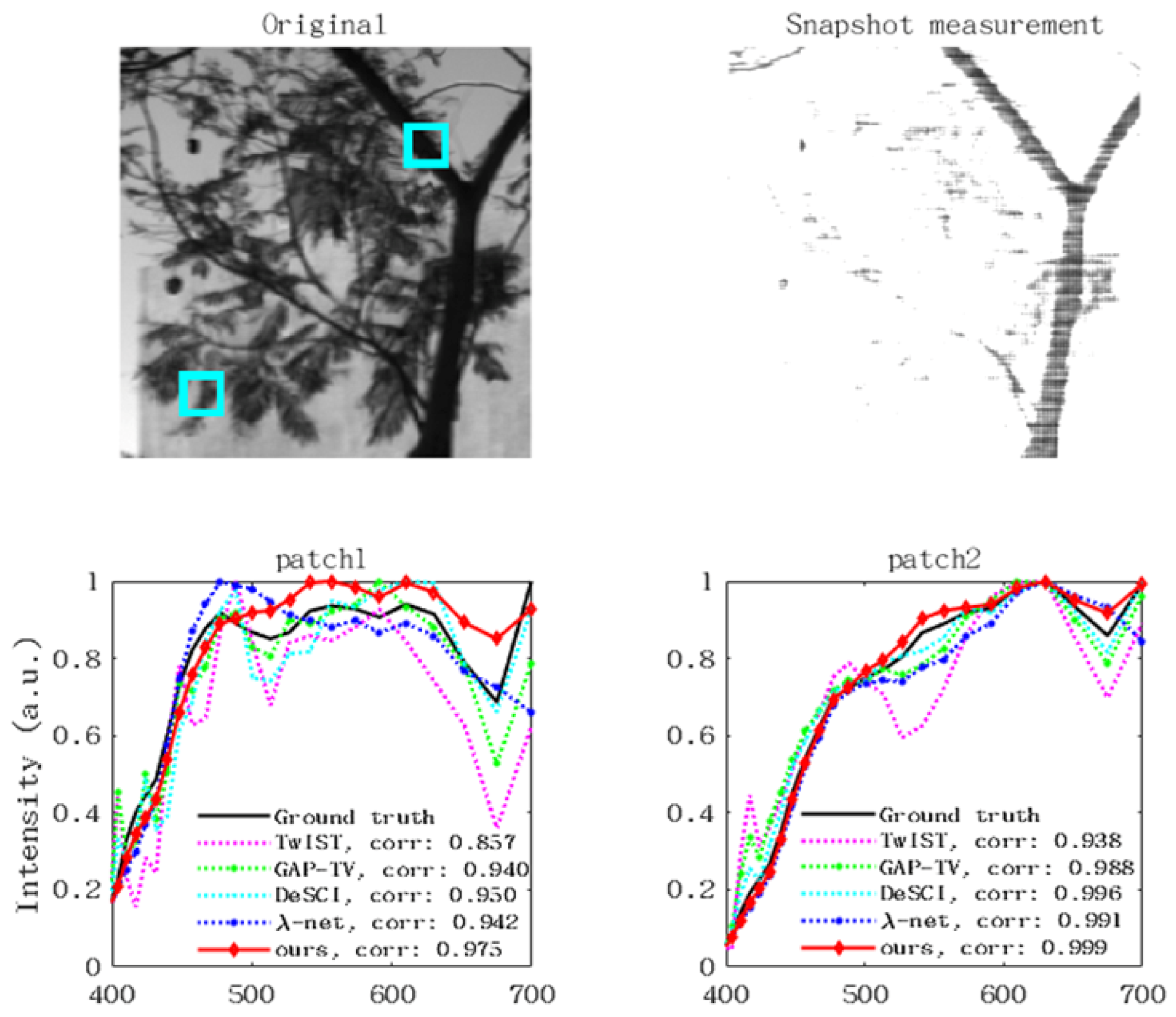
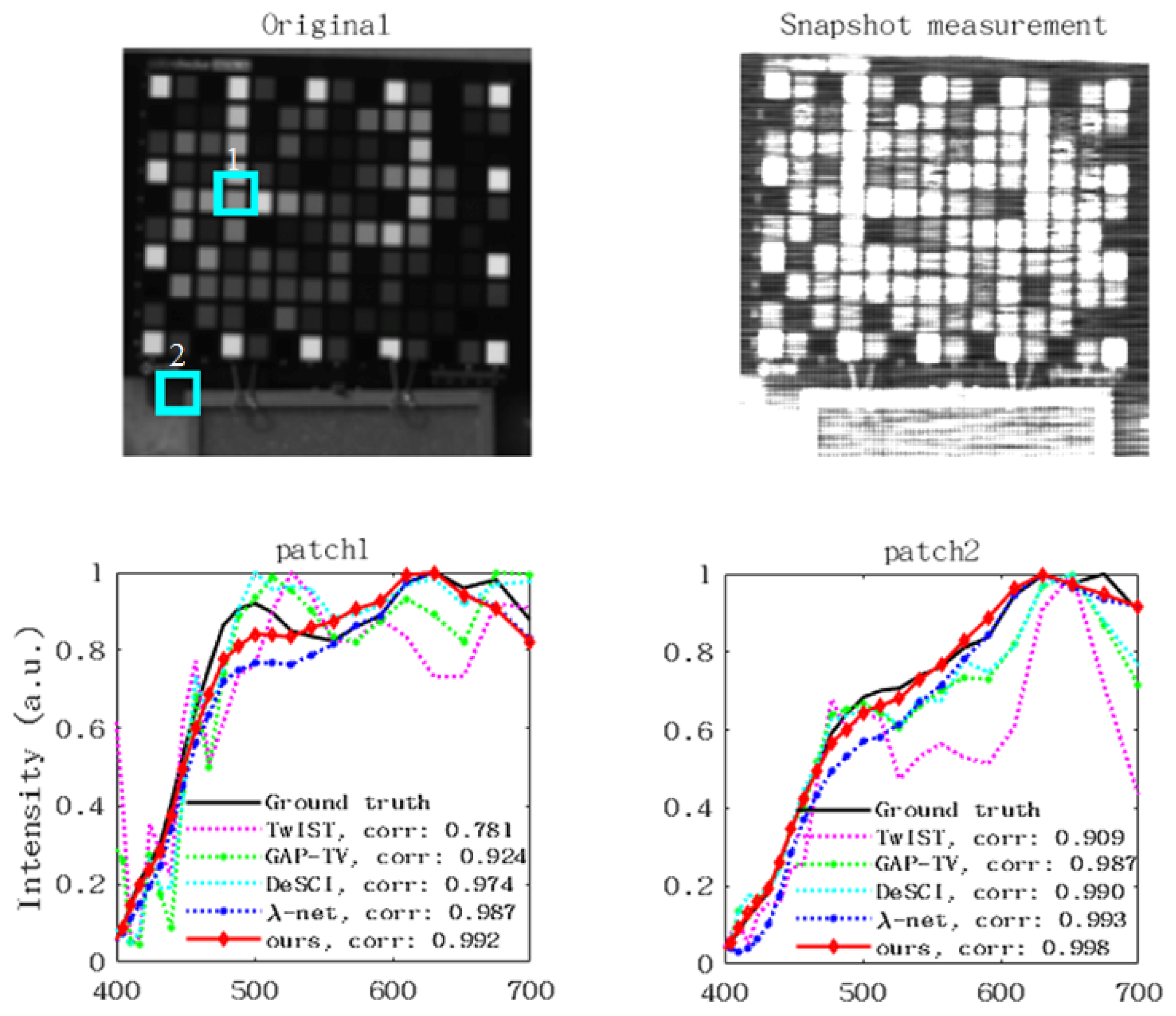
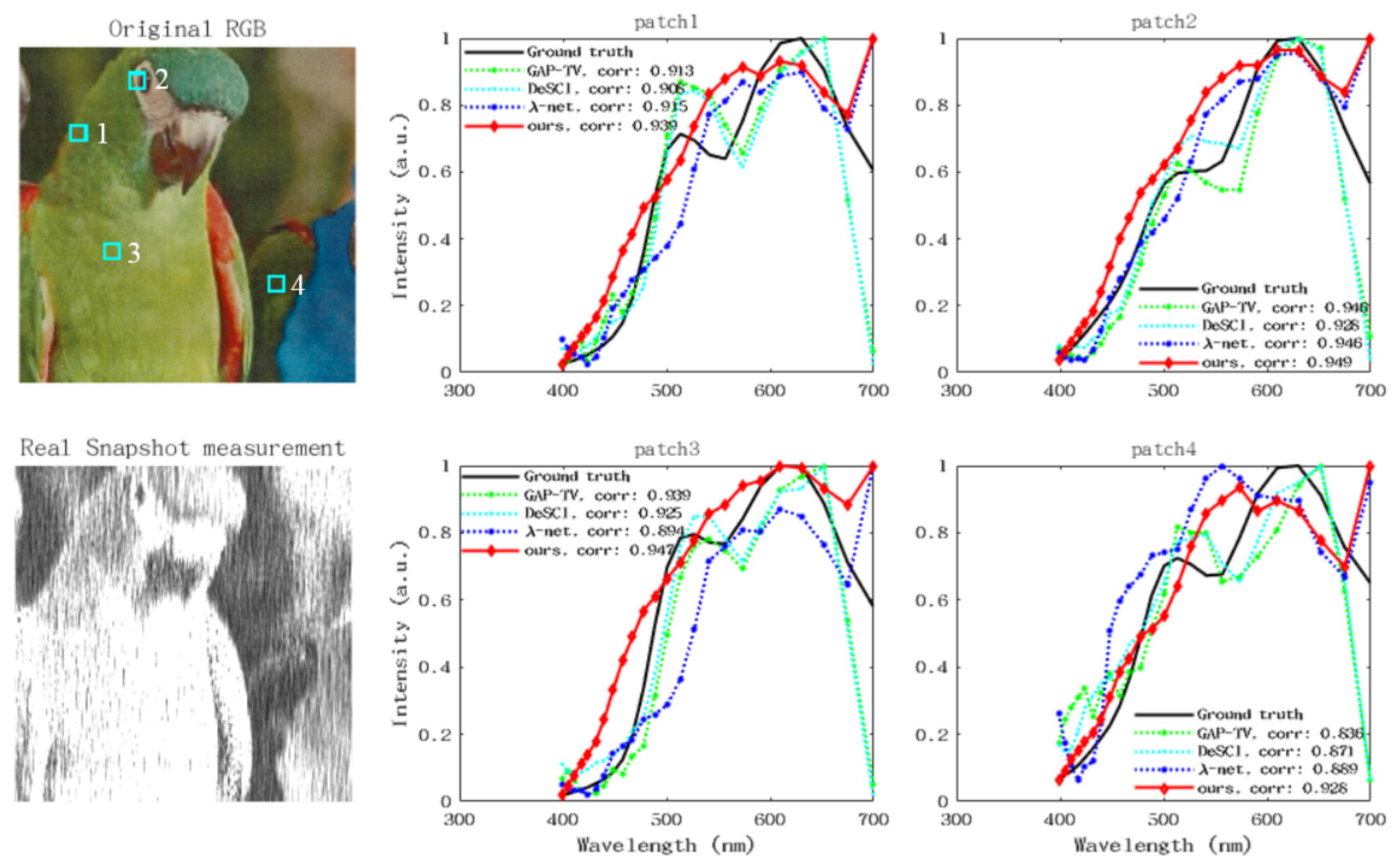
5.5. Real Data Results
5.6. Time Complexity Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chakrabarti, A.; Zickler, T. Statistics of real-world hyperspectral images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Colorado Springs, CO, USA, 20–25 June 2011; pp. 193–200. [Google Scholar]
- Tu, B.; Zhou, C.; Liao, X.; Zhang, G.; Peng, Y. Spectral-Spatial Hyperspectral Classification via Structural-Kernel Collaborative Representation. IEEE Geosci. Remote Sens. Lett. 2020, 18, 861–865. [Google Scholar] [CrossRef]
- Ojha, L.; Wilhelm, M.B.; Murchie, S.L.; McEwen, A.S.; Wray, J.J.; Hanley, J.; Massé, M.; Chojnacki, M. Spectral evidence for hydrated salts in recurring slope lineae on Mars. Nat. Geosci. 2015, 8, 829–832. [Google Scholar]
- Cao, X.; Zhou, F.; Xu, L.; Meng, D.; Xu, Z.; Paisley, J. Hyperspectral image classification with markov random fields and a convolutional neural network. IEEE Trans. Image Process. 2018, 27, 2354–2367. [Google Scholar] [CrossRef] [PubMed]
- Fauvel, M. Advances in spectral-spatial classification of hyperspectral images. Proc. IEEE 2012, 101, 652–675. [Google Scholar] [CrossRef]
- Mouroulis, P.; Green, R.O.; Chrien, T.G. Design of pushbroom imaging spectrometers for optimum recovery of spectroscopic and spatial information. Appl. Opt. 2000, 39, 2210–2220. [Google Scholar] [CrossRef]
- Wehr, A.; Lohr, U. Airborne laser scanning-an introduction and overview. ISPRS J. Photogramm. Remote Sens. 1999, 54, 68–82. [Google Scholar] [CrossRef]
- Shogenji, R.; Kitamura, Y.; Yamada, K. Multispectral imaging using compact compound optics. Opt. Express 2004, 12, 1643–1655. [Google Scholar] [CrossRef]
- Arce, G.; Brady, D.; Carin, L.; Arguello, H.; Kittle, D. Compressive coded aperture spectral imaging: An introduction. IEEE Signal Process. Mag. 2014, 31, 105–115. [Google Scholar] [CrossRef]
- Wagadarikar, A.; John, R.; Willett, R.; Brady, D. Single disperser design for coded aperture snapshot spectral imaging. OSA Appl. Opt. 2008, 47, 44–51. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, J.; Yin, W.; Zhang, Y. A new alternating minimization algorithm for total variation image reconstruction. SIAM J. Imaging Sci. 2008, 1, 248–272. [Google Scholar] [CrossRef]
- Buades, A.; Coll, B.; Morel, J.-M. A non-local algorithm for image denoising. IEEE Conf. Comput. Vis. Pattern Recognit. 2005, 2, 60–65. [Google Scholar]
- Elad, M.; Aharon, M. Image denoising via sparse and redundant representations over learned dictionaries. IEEE Trans. Image Process. 2006, 15, 3736–3745. [Google Scholar] [CrossRef]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Kittle, D.; Choi, K.; Wagadarikar, A.; Brady, D.J. Multiframe image estimation for coded aperture snapshot spectral imagers. Appl. Opt. 2010, 49, 6824–6833. [Google Scholar] [CrossRef]
- Wang, L.; Xiong, Z.; Shi, G.; Wu, F.; Zeng, W. Adaptive nonlocal sparse representation for dual-camera compressive hyperspectral imaging. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2104–2111. [Google Scholar] [CrossRef]
- Yuan, X. Generalized alternating projection based total variation minimization for compressive sensing. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 2990–3006. [Google Scholar]
- Blumensath, T.; Davies, M.E. Iterative hard thresholding for compressed sensing. Appl. Comput. Harmon. Anal. 2009, 27, 265–274. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, J.; Liu, Q.; Liu, B.; Guo, G. Dual-Path Attention Network for Compressed Sensing Image Reconstruction. IEEE Trans. Image Process. 2020, 29, 9482–9495. [Google Scholar] [CrossRef]
- Sun, Y.; Yang, Y.; Liu, Q.; Chen, J.; Yuan, X.-T.; Guo, G. Learning Non-Locally Regularized Compressed Sensing Network With Half-Quadratic Splitting. IEEE Trans. Multimed. 2020, 22, 3236–3248. [Google Scholar] [CrossRef]
- Xiong, Z.; Shi, Z.; Li, H.; Wang, L.; Liu, D.; Wu, F. Hscnn: Cnn-based hyperspectral image recovery from spectrally undersampled projections. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 518–525. [Google Scholar]
- Choi, I.; Jeon, D.S.; Nam, G.; Gutierrez, D.; Kim, M.H. High-quality hyperspectral reconstruction using a spectral prior. ACM Trans. Graph. 2017, 36, 218. [Google Scholar] [CrossRef]
- Wang, L.; Sun, C.; Zhang, M.; Fu, Y.; Huang, H. DNU: Deep Non-Local Unrolling for Computational Spectral Imaging. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 1658–1668. [Google Scholar]
- Zheng, S.; Liu, Y.; Meng, Z.; Qiao, M.; Tong, Z.; Yang, X.; Han, S.; Yuan, X. Deep plug-and-play priors for spectral snapshot compressive imaging. Photonics Res. 2021, 9, B18–B29. [Google Scholar] [CrossRef]
- Miao, X.; Yuan, X.; Pu, Y. lambda-net: Reconstruct Hyperspectral Images from a Snapshot Measurement. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 4058–4068. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N. FAttention is all you need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5998–6008. [Google Scholar]
- Sun, H.; Zheng, X.; Lu, X.; Wu, S. Spectral–Spatial Attention Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3232–3245. [Google Scholar] [CrossRef]
- Sellami, A.; Abbes, A.B.; Barra, V. Fused 3-D spectral-spatial deep neural networks and spectral clustering for hyperspectral image classification. Pattern Recognit. Lett. 2020, 138, 594–600. [Google Scholar] [CrossRef]
- Sellami, A.; Abbes, A.B.; Barra, V. Hyperspectral Image Classification Based on 3-D Octave Convolution With Spatial–Spectral Attention Network. IEEE Trans. Geosci. Remote Sens. 2021, 59, 2430–2447. [Google Scholar]
- Zhang, X.; Huang, W.; Wang, Q.; Li, X. SSR-NET: Spatial-Spectral Reconstruction Network for Hyperspectral and Multispectral Image Fusion. IEEE Trans. Geosci. Remote Sens. 2020, 1–13. [Google Scholar] [CrossRef]
- Meng, Z.; Ma, J.; Yuan, X. End-to-end low cost compressive spectral imaging with spatial-spectral self-attention. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 187–204. [Google Scholar]
- Wang, X.; Girshick, R.; Gupta, A.; He, K. Non-local Neural Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 7794–7803. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Liu, X.; Suganuma, M.; Sun, Z.; Okatani, T. Dual Residual Networks Leveraging the Potential of Paired Operations for Image Restoration. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 7000–7009. [Google Scholar]
- Hu, X.S.; Zagoruyko, S.; Komodakis, N. Exploring Weight Symmetry in Deep Neural Networks. arXiv 2018, arXiv:1812.11027. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Figueiredo, M.A. A new twist: Two-step iterative shrinkage/thresholding algorithms for image restoration. IEEE Trans. Image Process. 2007, 16, 2992–3004. [Google Scholar] [CrossRef]
- Liu, Y.; Yuan, X.; Suo, J.; Brady, D.; Dai, Q. Rank minimization for snapshot compressive imaging. IEEE Int. Conf. Image Process. 2016, 16, 2539–2543. [Google Scholar] [CrossRef]
- Diederik, P.K.; Jimmy, B. Adam: A method for stochastic optimization. In Proceedings of the 33rd International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015; pp. 1–15. [Google Scholar]
- Liu, X.; Yang, C. A Kernel Spectral Angle Mapper algorithm for remote sensing image classification. In Proceedings of the International Congress on Image and Signal Processing (CISP), Beijing, China, 14–16 July 2013; pp. 814–818. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]




| Configuration | PSNR ↑ | SSIM ↑ | SAM↓ |
|---|---|---|---|
| without Non-local Module | 34.019 (±0.141) | 0.967 (±0.0020) | 0.091 (±0.0005) |
| without Cosine Loss | 34.303 () | 0.970 () | 0.092 () |
| NSSR-Net | 34.764 () | 0.972 () | 0.089 () |
| Methods | Metrics | Scene 1 | Scene 2 | Scene 3 | Scene 4 | Scene 5 | Scene 6 | Scene 7 | Scene 8 | Scene 9 | Scene 10 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TwIST | PSNR | 25.621 | 18.413 | 21.750 | 21.240 | 23.784 | 20.579 | 24.232 | 20.202 | 27.014 | 18.921 | 22.140 |
| SSIM | 0.856 | 0.826 | 0.826 | 0.828 | 0.799 | 0.744 | 0.870 | 0.784 | 0.888 | 0.747 | 0.817 | |
| SAM | 0.160 | 0.175 | 0.192 | 0.197 | 0.235 | 0.335 | 0.173 | 0.199 | 0.226 | 0.241 | 0.213 | |
| GAP-TV | PSNR | 30.666 | 22.410 | 23.499 | 22.273 | 26.985 | 23.090 | 24.859 | 22.913 | 29.105 | 21.502 | 24.730 |
| SSIM | 0.892 | 0.869 | 0.863 | 0.829 | 0.792 | 0.802 | 0.877 | 0.841 | 0.912 | 0.796 | 0.847 | |
| SAM | 0.207 | 0.185 | 0.302 | 0.184 | 0.330 | 0.334 | 0.166 | 0.186 | 0.225 | 0.213 | 0.233 | |
| DeSCI | PSNR | 31.147 | 26.443 | 24.741 | 29.251 | 29.372 | 25.814 | 28.401 | 24.424 | 34.411 | 23.331 | 27.732 |
| SSIM | 0.937 | 0.947 | 0.898 | 0.949 | 0.907 | 0.906 | 0.921 | 0.872 | 0.971 | 0.834 | 0.914 | |
| SAM | 0.168 | 0.081 | 0.263 | 0.105 | 0.229 | 0.262 | 0.148 | 0.186 | 0.175 | 0.190 | 0.181 | |
| -Net | PSNR | 36.109 | 32.054 | 33.341 | 29.598 | 35.403 | 28.573 | 35.219 | 32.355 | 33.418 | 28.204 | 32.427 |
| SSIM | 0.949 | 0.975 | 0.974 | 0.937 | 0.942 | 0.902 | 0.969 | 0.951 | 0.916 | 0.924 | 0.944 | |
| SAM | 0.098 | 0.043 | 0.091 | 0.100 | 0.129 | 0.205 | 0.071 | 0.099 | 0.200 | 0.113 | 0.115 | |
| NSSR-Net (ours) | PSNR | 40.044 | 36.557 | 34.632 | 29.225 | 38.474 | 30.002 | 38.298 | 33.886 | 37.217 | 28.924 | 34.726 |
| SSIM | 0.988 | 0.989 | 0.972 | 0.953 | 0.984 | 0.944 | 0.985 | 0.966 | 0.987 | 0.937 | 0.971 | |
| SAM | 0.055 | 0.027 | 0.073 | 0.114 | 0.081 | 0.198 | 0.046 | 0.075 | 0.123 | 0.107 | 0.090 |
| Methods | TwIST | GAP-TV | DeSCI | -Net | NSSR-Net |
|---|---|---|---|---|---|
| Times (s) | 70.96 | 25.8 | 3594.5 | 4.28 | 1.19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Xie, Y.; Chen, X.; Sun, Y. Hyperspectral Snapshot Compressive Imaging with Non-Local Spatial-Spectral Residual Network. Remote Sens. 2021, 13, 1812. https://doi.org/10.3390/rs13091812
Yang Y, Xie Y, Chen X, Sun Y. Hyperspectral Snapshot Compressive Imaging with Non-Local Spatial-Spectral Residual Network. Remote Sensing. 2021; 13(9):1812. https://doi.org/10.3390/rs13091812
Chicago/Turabian StyleYang, Ying, Yong Xie, Xunhao Chen, and Yubao Sun. 2021. "Hyperspectral Snapshot Compressive Imaging with Non-Local Spatial-Spectral Residual Network" Remote Sensing 13, no. 9: 1812. https://doi.org/10.3390/rs13091812
APA StyleYang, Y., Xie, Y., Chen, X., & Sun, Y. (2021). Hyperspectral Snapshot Compressive Imaging with Non-Local Spatial-Spectral Residual Network. Remote Sensing, 13(9), 1812. https://doi.org/10.3390/rs13091812





