Next Article in Journal
In-Season Interactions between Vine Vigor, Water Status and Wine Quality in Terrain-Based Management-Zones in a ‘Cabernet Sauvignon’ Vineyard
Previous Article in Journal
Astrape: A System for Mapping Severe Abiotic Forest Disturbances Using High Spatial Resolution Satellite Imagery and Unsupervised Classification
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 13
Issue 9
10.3390/rs13091635
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Improving Accuracy of Unmanned Aerial System Thermal Infrared Remote Sensing for Use in Energy Balance Models in Agriculture Applications

by
Mitchell S. Maguire
1,*,
Christopher M. U. Neale
1,2 and
Wayne E. Woldt
1
1
Department of Biological Systems Engineering, University of Nebraska Lincoln, Lincoln, NE 68583, USA
2
Daugherty Water for Food Global Institute, University of Nebraska, Lincoln, NE 68588, USA
*
Author to whom correspondence should be addressed.
Remote Sens. 2021, 13(9), 1635; https://doi.org/10.3390/rs13091635
Submission received: 15 March 2021 / Revised: 14 April 2021 / Accepted: 20 April 2021 / Published: 22 April 2021
Browse Figures
Versions Notes

Abstract

:
Unmanned aerial system (UAS) remote sensing has rapidly expanded in recent years, leading to the development of several multispectral and thermal infrared sensors suitable for UAS integration. Remotely sensed thermal infrared imagery has been used to detect crop water stress and manage irrigation by leveraging the increased thermal signatures of water stressed plants. Thermal infrared cameras suitable for UAS remote sensing are often uncooled microbolometers. This type of thermal camera is subject to inaccuracies not typically present in cooled thermal cameras. In addition, atmospheric interference also may present inaccuracies in measuring surface temperature. In this study, a UAS with integrated FLIR Duo Pro R (FDPR) thermal camera was used to collect thermal imagery over a maize and soybean field that contained twelve infrared thermometers (IRT) that measured surface temperature. Surface temperature measurements from the UAS FDPR thermal imagery and field IRTs corrected for emissivity and atmospheric interference were compared to determine accuracy of the FDPR thermal imagery. The comparison of the atmospheric interference corrected UAS FDPR and IRT surface temperature measurements yielded a RMSE of 2.24 degree Celsius and a R2 of 0.85. Additional approaches for correcting UAS FDPR thermal imagery explored linear, second order polynomial and artificial neural network models. These models simplified the process of correcting UAS FDPR thermal imagery. All three models performed well, with the linear model yielding a RMSE of 1.27 degree Celsius and a R2 of 0.93. Laboratory experiments also were completed to test the measurement stability of the FDPR thermal camera over time. These experiments found that the thermal camera required a warm-up period to achieve stability in thermal measurements, with increased warm-up duration likely improving accuracy of thermal measurements.

Graphical Abstract

1. Introduction

Unmanned aerial system (UAS) remote sensing has gained significant traction in the last decade, leading to the development of various UAS and sensor payloads. Typical remote sensing platforms like satellite and manned aircraft have limitations due to the lack of spatiotemporal resolution and high cost. UASs provide a less expensive method of remote sensing and offer greater opportunity and flexibility to collect high resolution data usable in various applications. Satellite and manned aircraft remote sensing have previously provided data shown to be beneficial to agronomic applications. These data have been used to predict various crop biophysical characteristics such as leaf area index (LAI), crop height, fraction of vegetative cover, crop coefficient, crop evapotranspiration (ET) and phenotyping. Multispectral reflectance and vegetation indices have been used to model LAI, canopy height and fraction of vegetative cover [1,2,3,4,5]. Neale et al. [6] used canopy reflectance measured with portable radiometers and the normalized difference vegetation index (NDVI) to develop a reflectance-based crop coefficient model providing a more real-time crop coefficient which improved estimating actual crop ET. In addition to modeling crop characteristics, remotely sensed thermal infrared data has been used to model the surface energy balance fluxes. Norman et al. [7] proposed the two-source energy balance (TESB) model that uses remotely sensed multispectral reflectance and surface temperature measurements to partition the canopy and soil surfaces into their respective energy balance fluxes. Several others have explored similar energy balance parameterizations utilizing remotely sensed data [8,9,10,11,12,13,14]. Many of these models require accurately calibrated canopy/surface temperatures as inputs to estimate the energy balance fluxes. The energy balance approach has been used to estimate actual crop ET which provides information necessary for irrigation management. Neale et al. [15] developed a hybrid model combining the TSEB and reflectance-based crop coefficient models for determining actual crop ET with higher accuracy. This hybrid approach has been used for managing variable rate irrigation of maize and soybean fields [16,17,18]. While agronomic research has utilized remote sensing extensively, UASs are beginning to provide additional insight through very high-resolution remote sensing of vegetation previously not feasible with satellite and manned aircraft platforms.
Thermal information is often used to detect crop water stress due to different factors. DeJonge et al. [19] found plant canopy temperature measured with thermal infrared radiometers (IRT) to be highly correlated with leaf water potential, affirming that plant water stress can be evaluated using thermal infrared thermography techniques. Given that IRT measurements can be used to detect crop water stress, studies have applied similar techniques with UAS thermal imagery. Bian et al. [20] used UAS thermal infrared imagery and a simplified crop water stress index (CWSIsi) to determine water stress of cotton, finding that the CWSIsi had higher correlation with stomatal conductance and transpiration rate. With current research using UAS-based thermal data for agricultural applications, studies using thermal cameras for crop monitoring are becoming more frequent.
Common sensors used in agriculturally related remote sensing include multispectral reflectance and thermal infrared cameras. Multispectral cameras are typically less complex than thermal cameras due to the simpler detector required to measure the shortwave portion of the electromagnetic spectrum. Thermal camera sensors often are cooled to a specific temperature to maintain measurement accuracy. However, cooled thermal cameras are large and heavy for typical UASs. Uncooled microbolometer thermal cameras are better suited for UAS remote sensing due to their small lightweight design. A downside to an uncooled sensor is the stability and accuracy in thermal measurements, as microbolometer sensors are less sensitive and accurate than cooled sensor systems. Uncooled thermal cameras are subject to measurement drift due to changing camera body and sensor temperature. Ribeiro-Gomes et al. [21] discussed various corrections needed for uncooled thermal cameras including corrections for non-uniformity, defective pixel, shutter, radiometric and temperature dependency. While some radiometric thermal cameras are capable of accounting for some of these corrections, non-radiometric cameras require additional corrections for accurate thermal imaging. Prior research has noted that thermal calibration is crucial for uncooled sensors [22]. Several studies have been conducted to determine the accuracy of uncooled thermal cameras, with some developing calibration models intended to increase thermal measurement accuracy. Ribeiro-Gomes et al. [21] developed a neural network calibration model that improved UAS thermal remote sensing accuracy while Jensen et al. [23] demonstrated two calibration approaches involving ground-based thermal measurements and temperature-controlled pools for improving UAS-based thermal imaging. Kelly et al. [24] developed a simple empirical line calibration for a non-radiometric FLIR Vue Pro 640 camera, finding that their calibration performed well under stable laboratory conditions with a decline in accuracy under changing ambient conditions typically experienced during UAS flights. Their findings also suggested that the thermal camera required a warm-up period before measurements stabilized.
In addition to the inaccuracies of the cameras themselves, atmospheric interference may play a role in settings such as remote sensing of agricultural fields. Modeling the atmospheric profile and applying corrections may help remove the effects of atmospheric interference [25]. This approach has been used in previous research with Landsat satellite thermal imagery [16,17]. A downside to modeling the atmospheric profile and interference is the need for the radiative transfer code MODTRAN, a licensed software [26]. MODTRAN uses the modeled atmospheric profile to determine the transmission and the upwelling and downwelling radiance that affect thermal infrared measurements. Acquiring MODTRAN software may not be feasible for all UAS thermal remote sensing users. A potential alternative is to develop a calibration model using similar parameters used in modeling the atmospheric profile. The Barsi et al. [25] online atmospheric profile calculator offers optional inputs for surface condition parameters including atmospheric pressure, air temperature and relative humidity. A model using these parameters may be sufficient for determining the atmospheric interference for low altitude UAS remote sensing and, hence, lead to a simplified method for correcting UAS thermal images.
Surface emissivity also plays a role in accurately estimating surface temperature using thermal infrared radiometers and/or imagers. Emissivity ranges from zero to one and is the ratio of emission of a surface to that of a perfect emitter (blackbody) at a given temperature [2]. Several thermal cameras used in UAS remote sensing provide the user the ability to set the target emissivity. In agricultural applications, the surface often measured consists of a mix of vegetation and soil which have different emissivity values. The actual surface emissivity is then a combination of vegetation and soil emissivity based on the fraction of the two surfaces present in the sensor field of view (FOV), or the fraction of vegetation cover. In typical agricultural fields, the fraction of vegetative cover changes over time as the crop grows leading to changes in surface emissivity. This change in emissivity should be accounted for when collecting thermal imagery of agricultural fields over a growing season. Brunsell and Gillies [2] provided a method for calculating surface emissivity of vegetated areas using NDVI. This approach has been used with high-resolution airborne thermal imagery in numerous applications [27,28].
While uncalibrated or non-radiometric UAS thermal imagery may be adequate for identifying spatial patterns in the crop canopy for agronomic management, applications requiring surface or canopy temperature for crop stress indices or energy balance models requires a highly accurate determination of canopy temperature. Thermal imagery used in various models for detecting crop water stress and estimating crop ET highlights the need to confirm UAS thermal camera measurement accuracy. Many thermal cameras available today for UAS remote sensing are radiometric sensors claiming accurate temperature measurements within a certain error tolerance. The error tolerance of these cameras often does not meet the accuracy needed for use in energy balance models. The idea of developing a universal calibration model to increase the accuracy of UAS remote sensing thermal cameras is ideal but likely unfeasible from a research standpoint due to the need to collect remotely sensed thermal imagery with different thermal cameras at various climates and remote sensing altitudes. A more concentrated approach for increasing accuracy of UAS remotely sensed thermal imagery may be easier and provide high quality data for use in applications like energy balance modeling.
The objective of this study was to determine the accuracy of a FLIR Duo Pro R (FDPR) thermal infrared camera integrated with a DJI Matric 600 (M600) UAS in measuring canopy temperature of an agricultural field. The objectives of this research were: (1) determine duration of warm-up period needed for FDPR thermal camera to achieve stabilized measurements; (2) correct UAS thermal imagery for emissivity and atmospheric interference using the modeled atmospheric profile and MODTRAN and assess accuracy of corrected UAS thermal imagery by comparing to IRT surface temperature measurements; (3) develop simplified FDPR thermal camera calibration models using IRT surface temperature measurements.

2. Materials and Methods

2.1. Laboratory Test

This research included laboratory and field testing of the FDPR thermal camera. Laboratory testing of the thermal camera was conducted in a controlled indoor environment to minimize atmospheric effects. The laboratory work consisted of collecting FDPR thermal imagery over a temperature-controlled water bath that was heated from 3 to 50 degrees Celsius using two hot plates and was kept well mixed using a magnetic stir bar. Two factory calibrated Apogee Instruments ST-100 thermistors connected to a Campbell Scientific CR200 data logger measured water bath and surrounding air temperatures. The thermistor used for measuring water temperature was submerged just below the surface of the water. Thermal imagery was collected over the water bath every ten seconds with water and air temperatures collected every minute by the thermistors. The built-in flat field correction (FFC) of the FDPR camera was operated based on the camera’s default algorithm for determining FFC events. The FDPR camera allows the user to set the target emissivity, surrounding air temperature and humidity, which were set to one, twenty degrees Celsius and thirty percent, respectively. The emissivity of water was assumed to be 0.98, which required emissivity corrections for the FDPR thermal imagery. Equation (1) was used to correct the FDPR thermal images, where Lsens is the radiance measured by the sensor, τ is the atmospheric transmission, ε is the surface emissivity, Lsfc is the radiance of a blackbody target of a temperature in Kelvin, Lu is the upwelling atmospheric path radiance and Ld is the downwelling sky radiance. This equation was simplified into Equation (2) as the Lu and Ld terms were assumed to be zero and τ was assumed to be one since thermal images were collected in a controlled indoor environment and at close proximity to the water bath. To correct for emissivity, the FDPR thermal images were converted from temperature to radiance using Plank’s equation and the center wavelength of the full width half max (FWHM) spectral response of the FDPR camera. After emissivity corrections, the radiance images were converted back to temperature using the inverse of Plank’s equation.
Lsens = τεLsfc + Lu + τ(1 − ε)Ld
Lsens = εLsfc
FDPR water bath temperature measurements were obtained by averaging the inner fifty percent of the individual emissivity corrected FDPR thermal images to avoid the image vignetting effects. Water and air temperature measurements collected by the thermistors were interpolated in time to match when FDPR images were collected. The averaged emissivity corrected thermal images were compared against water temperature measured from the thermistor. Tests were conducted three times at different ambient air temperatures to capture how air temperature may affect FDPR thermal measurements.

2.2. Field Test

The field research was conducted at a 53-ha irrigated field site containing maize and soybean located at the Eastern Nebraska Research and Extension Center near Mead, NE. The field contained twelve factory calibrated Apogee SI-111 IRTs that measured a spectral range of 8 to 14 microns with a view angle of 44 degrees. IRTs were mounted on tripods and positioned nadir to the ground surface where each IRT measured canopy temperature on continuous one-minute averages with measurements recorded to Campbell Scientific data loggers. The IRTs located in the soybean were consistently positioned 2 m above ground level (AGL) while IRTs located in maize were initially positioned at 2 m AGL and raised to a greater height mid-season so that the distance between the IRT and maize canopy was no less than 1 m. As the distance between the IRT and canopy changed, the IRT FOV also changed. Throughout the growing season, the IRT FOV was assumed to be constant as a 1 m diameter circle.
The UAS remote sensing platform used to collect imagery consisted of a DJI M600 with integrated FDPR thermal infrared (Table 1) and MicaSense RedEdge multispectral cameras (Table 2). Both cameras were mounted on a gimbal and positioned to view the ground surface from nadir during image acquisition flights. Remotely sensed images were collected over the field using the M600 UAS at an altitude of 240 m AGL with image overlap of seventy percent or more along the flight line and in parallel flight lines. The typical flight duration for covering the 53 ha field was approximately ten minutes with images collected once per second. UAS imagery was collected on cloud free days to ensure shadowing did not negatively affect image quality. The FDPR camera was powered on for a minimum of thirty minutes before collecting imagery to allow the camera to thermally stabilize. During flights, the FFC event was manually triggered every ten seconds to recalibrate the FDPR camera. When collecting thermal imagery of the field, the FDPR camera settings including target emissivity, ambient air temperature and relative humidity were set to one, twenty degrees Celsius and thirty percent, respectively. FDPR target emissivity, air temperature and humidity settings were held constant throughout the growing seasons even if they did not represent actual conditions. The FDPR camera provides the user the ability to supply numerical values for emissivity and air temperature while relative humidity was limited to a categorical setting (i.e., low, medium, or high). Given that the categorical setting for relative humidity did not provide accurate representation of actual relative humidity, the authors chose to hold this value, along with emissivity and air temperature, constant. While changes in set target emissivity is automatically adjusted in the acquired thermal images by the camera, the adjustments by the camera for selected air temperature and relative humidity were undetermined. Air temperature and relative humidity measurements are used in determining the thermal path transmittance, where increases in air temperature and relative humidity results in decreased transmittance of the thermal infrared signal. To help minimize any potential path transmittance corrections applied by the camera, air temperature and relative humidity were held constant at twenty degrees Celsius and thirty percent (low), respectively. By minimizing the potential path transmittance corrections by the camera, the corrections discussed in Section 2.4 provide a better assessment of how path transmittance affects the acquired thermal imagery without correcting for path transmittance effects twice.
The thermal and multispectral images collected over the field were processed into ortho-images using Pix4D [29] with Figure 1 providing a typical set of processed images. The MicaSense RedEdge multispectral imagery was calibrated using reflectance panel images collected before and after flights. A total of twenty-five UAS flights were conducted over the research field during the 2018 and 2019 growing seasons (Table 3), which encompassed the various growth stages and fraction of vegetation covers of maize and soybean.

2.3. Emissivity Corrections

Emissivity ranges between zero and one, with vegetation and soil having emissivity values of 0.98 and 0.96, respectively [2,30]. The FDPR image emissivity corrections consider the surface being measured, with corrections based on the difference between set camera emissivity and actual surface emissivity. Varying field emissivity values were present throughout the growing season due to changes in fraction of vegetation cover. The FDPR thermal infrared ortho-images were corrected using the actual surface emissivity of the surface being imaged (vegetation and soil). Brunsell and Gillies [2] proposed a method to calculate emissivity based on multispectral reflectance imagery, where fraction of cover derived from NDVI is used to calculate a weighted emissivity value based on the emissivity values of vegetation and soil. Fraction of cover derived from NDVI was calculated using Equation (3),
fc = [(NDVI − NDVImin)/(NDVImax − NDVImin)]2
where NDVImin and NDVImax are the NDVI values of bare soil and full vegetative cover, respectively and NDVI is the calculated surface NDVI. NDVImin and NDVImax values of 0.1 and 0.89 were used to follow that of Li et al. [5]. Actual surface emissivity was calculated using Equation (4), where εv and εs are emissivity of vegetation and soil, respectively, fc is fraction of cover from Equation (3) and εi is surface emissivity.
εi = fc × εv + (1 − fc) × εs
The calibrated MicaSense multispectral reflectance imagery was used to calculate NDVI for deriving fraction of cover in Equation (3). Similar emissivity corrections were applied to the field IRTs, where the MicaSense multispectral reflectance imagery once again was used to calculate the fraction of cover in the IRT’s FOV.

2.4. Atmospheric Interference Corrections

Additional procedures were considered to include atmospheric interference corrections to the FDPR thermal imagery and IRT surface temperature measurements. Based on the atmospheric conditions, the thermal infrared signal may be enhanced or attenuated by the atmosphere. The online atmospheric profile calculator from Barsi et al. [25] was used to determine the atmospheric profiles interpolated in space and time to the field location and scene center time of the UAS flights. MODTRAN was used with the modeled atmospheric profiles to generate values for Lu, Ld and τ for an atmospheric profile from the surface to the UAS altitude and for a spectrum from 6.5 to 15 microns. These values were weighted and summed over the FWHM spectral responses of the FDPR thermal camera and IRT using Planck’s equation and the center wavelength of the FDPR and IRT FWHM spectrums resulting in a single atmospheric Ld, Lu and τ values specific to the spectral response of each sensor. To apply the atmospheric corrections to the FDPR thermal ortho-images and IRT measurements, the calculated Lu, Ld and τ terms and calculated emissivity values from Equation (4) for a given image date or IRT measurement were used in Equation (1). This method includes corrections for differences in set target emissivity and surface emissivity. Using Equation (1) and the modeled atmospheric parameters and calculated surface emissivity values, the FDPR surface temperature ortho-images and IRT measurements expressed as radiance were corrected by solving for Lsfc. After solving for Lsfc, the newly corrected radiance ortho-images and IRT measurements were converted back to temperature using the inverse of Plank’s equation.

2.5. FLIR Duo Pro R Calibration Models

The method for correcting atmospheric interference discussed Section 2.3 and Section 2.4 may be restrictive for certain users. The online atmospheric profile calculator from Barsi et al. [25] is open access; however, MODTRAN is a licensed software that must be purchased. This method also requires several steps that include converting surface temperature to radiance, applying the corrections and converting radiance back to surface temperature. This method was originally proposed for correcting Landsat 5 and Landsat 7 thermal bands [25] that are affected by the entire atmospheric profile due to their high altitudes. Given that UASs are typically operated significantly closer to the earth’s surface, using this method may be unwarranted. While atmospheric parameters like pressure, air temperature and relative humidity change with altitude, UAS operating at low altitudes are subject to less variability in these parameters with relation to changes in altitude. While the atmospheric profile between the ground surface and the altitude of the UAS may be relatively constant, atmospheric interference is present. Given that the atmosphere is relatively constant between the ground surface and typical operating altitudes of UAS, the need for modeling the entire atmospheric profile may be unnecessary. In addition, atmospheric parameters like air pressure, temperature and relative humidity used in modeling the atmospheric profile are often measured with typical weather stations and are widely available. With the atmospheric conditions considered constant, a model using these atmospheric parameters may be sufficient to account for atmospheric interference in UAS thermal remote sensing.
Three different models were developed to correct UAS thermal imagery for differences in set target and actual surface emissivity and atmospheric interference. The three models developed were: (1) linear model (Equation (5)), (2) second order polynomial (Equation (6)) and (3) artificial neural network (ANN). The three models included similar parameters used in modeling the atmospheric profile in the Barsi et al. [25] online calculator. Model independent variables included UAS non-corrected surface temperature measurements (UAS), modeled surface emissivity (ε), atmospheric pressure (P), air temperature (Tair) and relative humidity (RH) measured at the time of UAS flights. The IRT surface temperature measurements corrected for atmospheric interference (IRTatm) as discussed in Section 2.4 were considered as actual surface temperature and used as the models’ dependent variable.
IRTatm = β0 + β1UAS + β2Tair + β3RH + β4P
IRTatm = β0 + β1UAS + β2Tair + β3RH + β4P + β5ε + β6UAS2 + β7(UAS)(Tair) +
β8(UAS)(RH) + β9(UAS)(P) + β10(UAS)(ε) + β11Tair2 + β12(Tair)(RH) + β13(Tair)(P) +
β14(Tair)(ε) + β15RH2 + β16(RH)(P) + β17(RH)(ε) + β18P2 + β19 (P)(ε) + β20ε2
The ANN model was developed using the Keras Python library [31]. ANNs consist of input, hidden and output layers, with the potential to contain several hidden layers. The ANN model used the same independent and dependent variables from the linear and second order polynomial models as input and output layers. The model contained three hidden layers that used linear, rectified linear unit and sigmoid activation functions. The input and output layer data were scaled between zero and one, as ANNs tend to perform better with scaled or normalized data. The data used in model development were divided into training and testing datasets, with seventy percent of the data used for training. The models were fitted or trained using the training data and evaluated against the testing data.
Given that all UAS thermal images in this study were collected at an altitude of 240 m AGL, the calibration models developed in this section may not be useful at different remote sensing altitudes and locations. To better understand how atmospheric interference changes with respect to remote sensing altitude, the modeled atmospheric profile and MODTRAN were used to characterize atmospheric interference at different altitudes typically used in UAS remote sensing. This provided information to quantify the potential error if the calibration models described in this section were used with thermal imagery collected at different altitudes.

3. Results

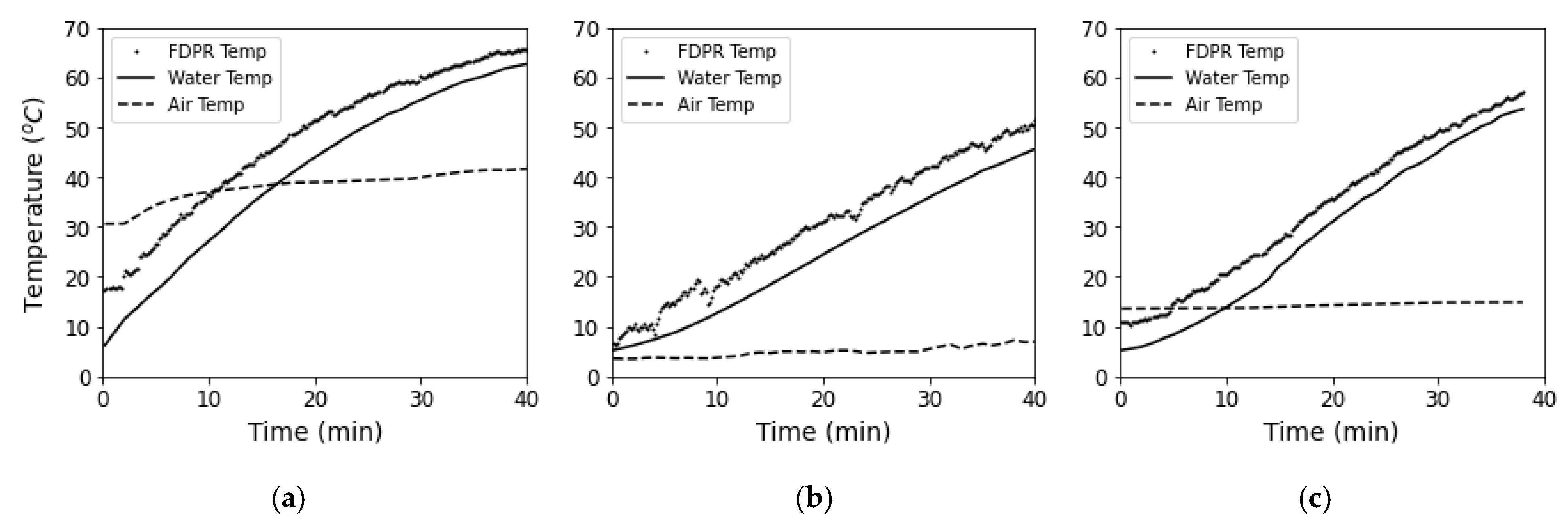
The water bath experiments conducted with the FDPR thermal camera helped gauge the accuracy and stability of the thermal camera over time. Water temperature was measured with the FDPR camera and thermistor on regular intervals as the water was heated. The results showed large differences in measured water temperature between the FDPR thermal camera and thermistor for all three tests conducted at different air temperatures (Figure 2). These differences were greater than the FDPR accuracy specification listed in Table 1. In addition, FDPR measured water temperature was more variable early in the tests similar to what previous studies have noted.
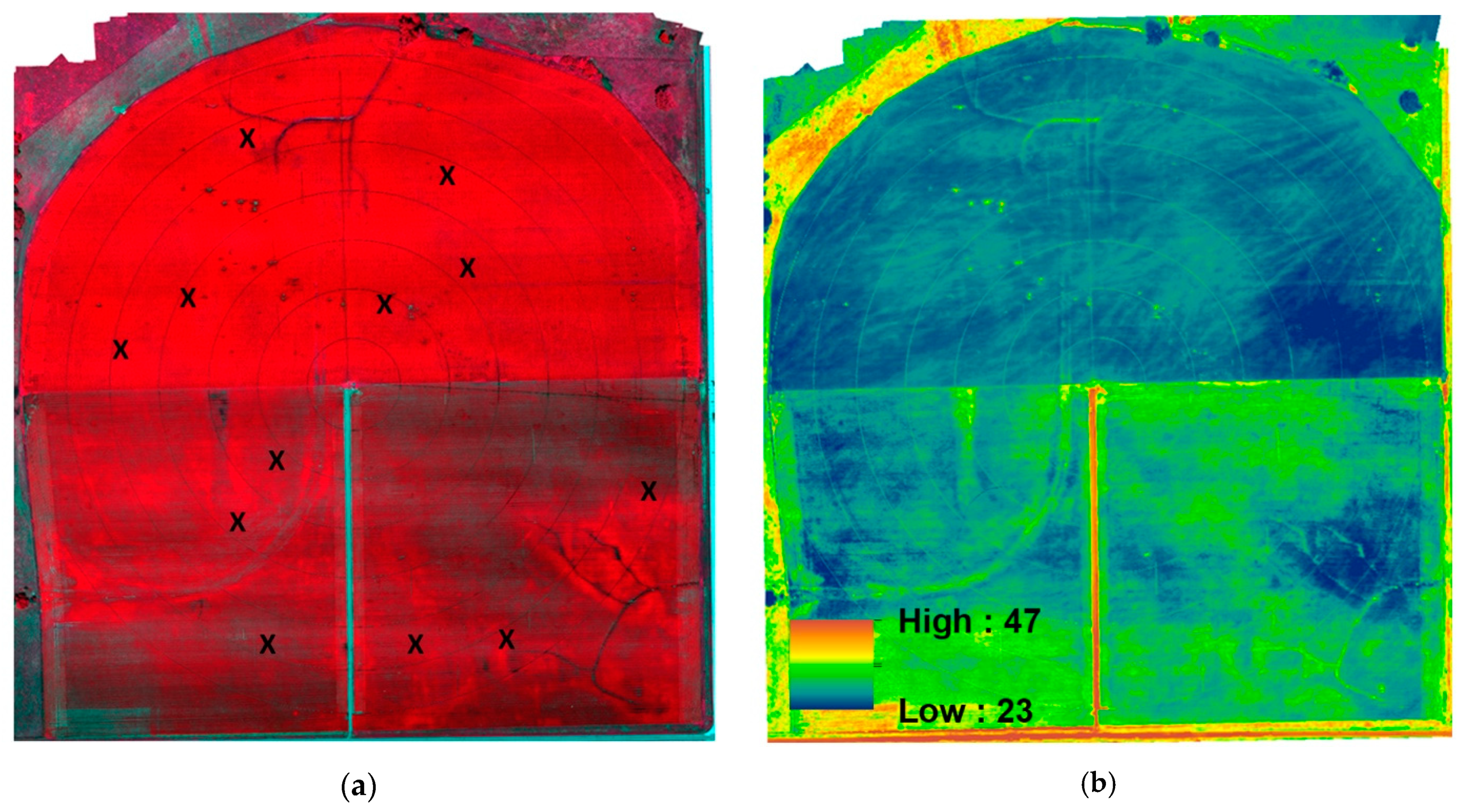
The comparison of surface temperature measurements from the UAS FDPR thermal imagery and field IRTs consisted of correcting both thermal imagery and IRT measurements for set target and actual surface emissivity differences and atmospheric interference. The IRT surface temperature measurements of the maize and soybean fields corrected for atmospheric interference were considered as actual surface temperature and most accurate. UAS FDPR and IRT surface temperature measurements were corrected at three different levels and compared (Table 4, Figure 3). The three levels of corrections were no corrections, corrections for emissivity differences between set sensor emissivity and actual surface emissivity and corrections for atmospheric interference which included corrections for emissivity. Of the nine comparisons, the non-corrected IRT and emissivity corrected UAS thermal measurements had the highest agreement with a RMSE of 1.76 degree Celsius and a R2 of 0.90. The actual surface temperature measurements (IRT measurements corrected for atmosphere interference) compared best with the emissivity corrected FDPR thermal imagery (RMSE: 2.15, R2: 0.86) while comparisons with the FDPR thermal measurements corrected for atmospheric interference yielded a RMSE of 2.24 and a R2 of 0.85.
Three different UAS FDPR calibration models were developed and assessed based on comparison of surface temperature measurements from the UAS FDPR and field IRTs (Figure 4). The linear and second order polynomial model coefficients are listed in Table 5. All three calibration models performed well improving UAS thermal measurement accuracy (Table 6). The ANN model performed best in comparison to the IRT surface temperature measurements corrected for atmospheric interference (RMSE: 1.12, R2: 0.94).
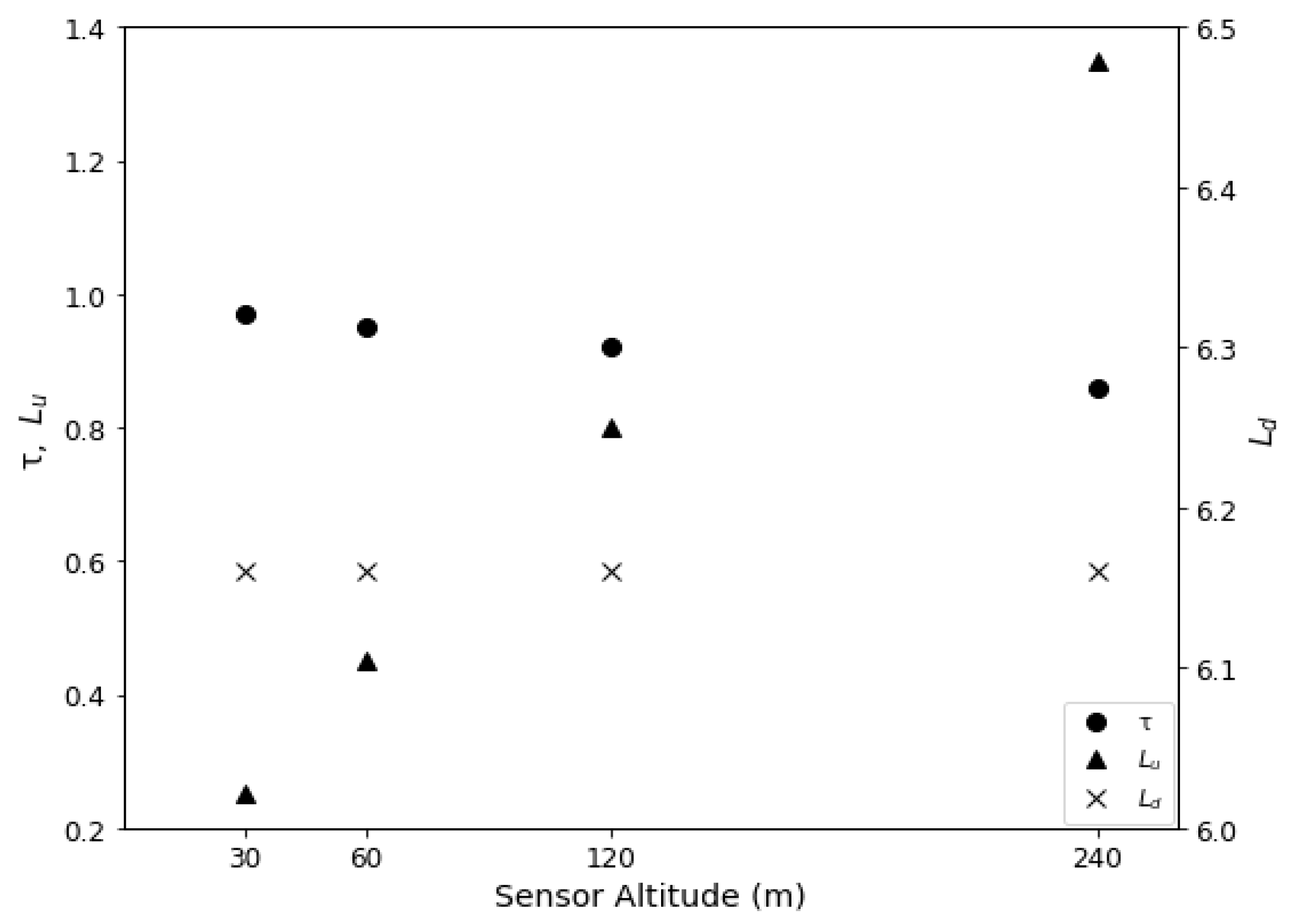
The UAS thermal images used in this study were collected at 240 m AGL, which limited the testing and development of the thermal calibration models discussed in Section 2.5 to a single sensor altitude. The atmospheric interference on thermal imagery is dependent on both atmospheric conditions and the altitude at which remotely sensed thermal imagery is collected. Figure 5 depicts the changes in atmospheric Lu, Ld and τ on 9 August 2018, at the field site in relation to changes in remote sensing altitude. It is apparent in Figure 5 that sensor altitude affects the Lu and τ terms while Ld is unaffected. As sensor altitude decreases, Lu decreases and τ increases both contributing to less interference by the atmosphere. 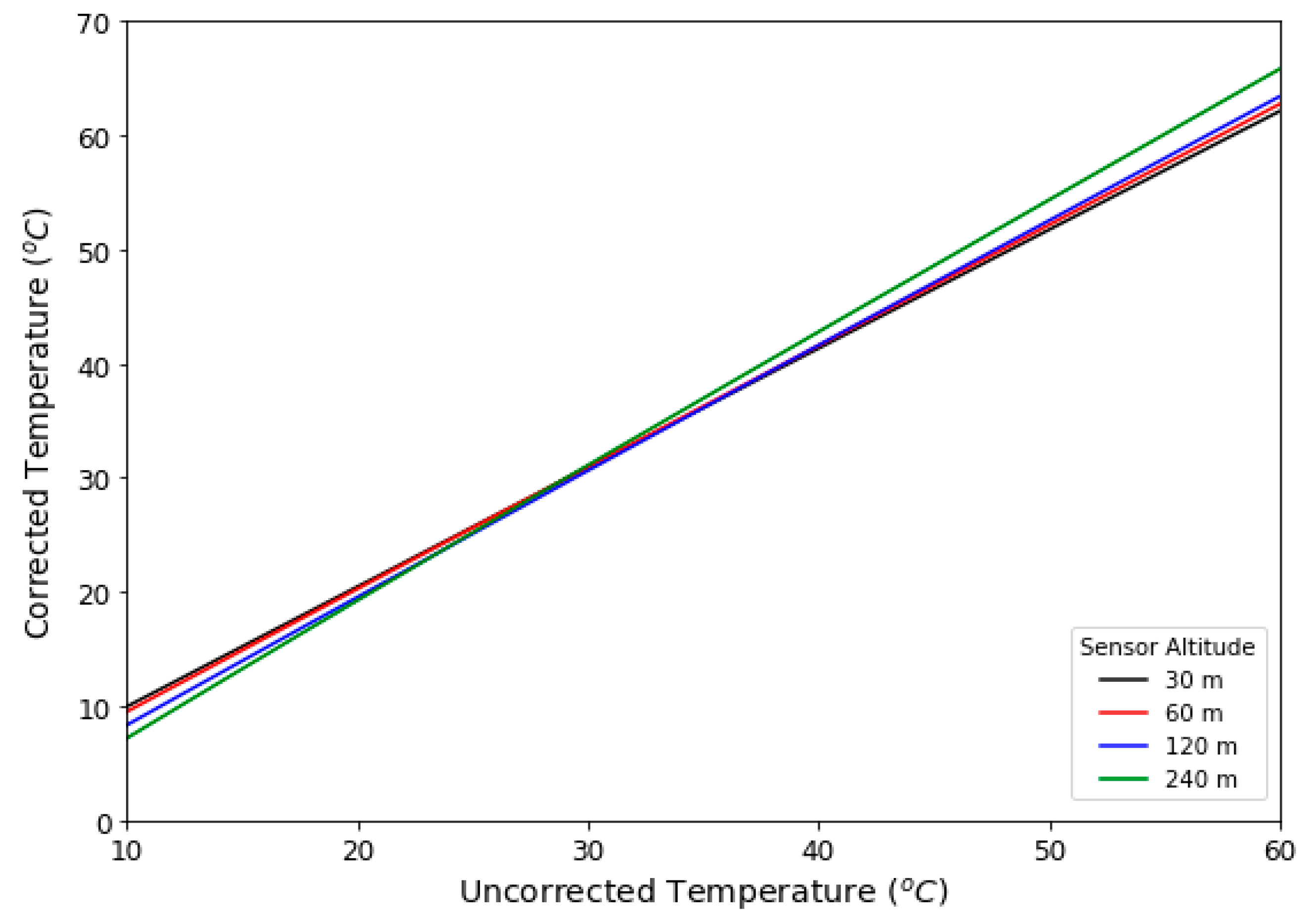Figure 6 shows the differences in atmospherically corrected thermal imagery collected at four different altitudes. MODTRAN was used to determine atmospheric interference at each altitude based on the modeled atmospheric profile at the field site on 9 August 2018. Figure 6 demonstrates that thermal imagery collected at different altitudes is affected differently by the atmosphere given that the slopes and intercepts of the corrected versus uncorrected temperature lines are different. It also is apparent that there is a range of measured temperatures where the effects of atmospheric interference are not largely different at different sensor altitudes for this given day. 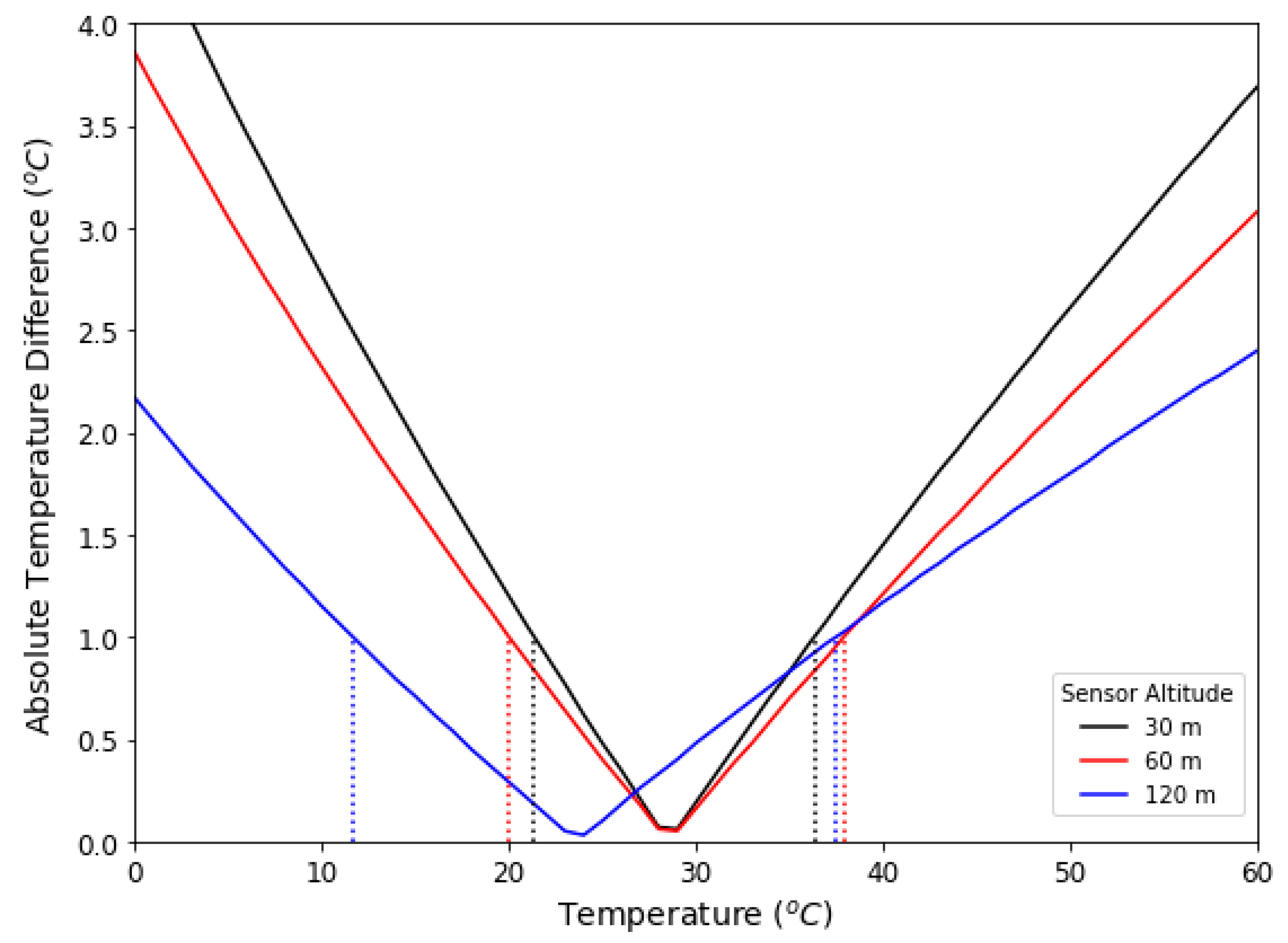Figure 7 shows the absolute temperature differences between atmospherically corrected thermal imagery collected at 240 m AGL and corrected thermal imagery collected at 30 m, 60 m and 120 m AGL. The vertical dashed lines in Figure 7 depict an absolute one-degree Celsius difference between the atmospherically corrected thermal imagery collected at 240 m AGL and corrected thermal imagery collected at 30 m, 60 m and 120 m AGL. For example, if thermal imagery collected at a remote sensing altitude of 120 m AGL were corrected using the calibration models described in Section 2.5, measured temperatures between 11 and 37 degrees Celsius should have no more than an additional one-degree Celsius error compared to imagery collected and corrected at a remote sensing altitude of 240 m AGL.

4. Discussion

The water bath tests conducted in a controlled environment demonstrated some of the working capabilities and accuracy of the FDPR camera. The differences in measured water bath temperature between the FDPR camera and thermistor were often outside the specified accuracy of the FDPR camera (+/−5 degrees Celsius). These tests also identified instability in FDPR thermal measurements for a duration after powering the camera on, where the FDPR camera recorded fluctuations in temperatures not truly present. It appeared that the FDPR accuracy increased as the camera was powered on longer, which is supported in Figure 2. Other studies have presented similar findings [21,24], which poses an issue for previous studies that have used these types of cameras and assumed an adequate measurement accuracy. While the FDPR measurement inaccuracy is troubling, the instability of the FDPR camera may be improved through the camera’s FFC event or calibration shutter, which is meant to re-calibrate the sensor array by accounting for changes in camera body temperature and individual pixel drift. This calibration event takes place automatically based on internal camera parameters and can also be manually initiated. In the case of the water bath experiments, the FFC event was automatically completed by the camera. Given the fluctuations of temperatures measured by the FDPR in the minutes following power-up, the FFC event may not have occurred often enough to address the measured fluctuations, especially during the minutes after initial power-up where the sensor begins to warm. Completing the FFC event more regularly either through a modified firmware from the manufacturer or manually may minimize the fluctuations in measured temperatures. The results of the water bath experiment raise concerns on the accuracy of the FDPR camera that may need to be addressed in further research or by the manufacturer.
The FDPR camera performed better in the field experiments in terms of accurately measuring surface temperature when compared to IRT measurements. In the field analysis, the FDPR camera and IRTs were subject to atmospheric interference which can enhance or attenuate the thermal infrared signal. The FDPR and IRT temperature comparison analysis assumed the IRT measurements corrected for atmospheric interference provided actual surface temperature measurements. The IRT measurements were corrected for atmospheric interference using the Barsi et al. [25] online atmospheric profile calculator and MODTRAN to model the Ld, Lu and τ parameters used to characterize the atmospheric profile. This method may raise some concern as it was originally intended to correct thermal imagery acquired with satellites. In modeling the Ld, Lu and τ parameters using this method, the assumption that the Lu and τ terms were negligible (Lu = 0, τ = 1) in contributing to atmospheric interference minimized the potential error associated with correcting atmospheric interference using this method. The Ld term is unaffected by path length (distance from sensor to surface measured) assuming τ = 1, while the Lu and τ terms are dependent on path length, which was small for the IRT in comparison to the path length of the UAS when collecting thermal imagery. In addition, the effects of the Ld term on the thermal infrared signal are relatively small compared to the Lu and τ terms, as the contributing interference due to Ld is attributed to the reflected downwelling longwave radiation or (1 − ε)Ld (see Equation (1)). Overall, the assumption that the IRT measurements corrected for atmospheric interference most accurately represented actual surface temperature provided greater confidence in the comparisons with UAS acquired thermal imagery.
The comparison of atmospherically corrected UAS and IRT surface temperature measurements using the modeled atmospheric profile and MODTRAN presented some of the limitations of this method. While there were slight improvements in surface temperature comparisons from no correction (RMSE: 2.50, R2: 0.79) to full atmospheric interference corrections (RMSE: 2.24, R2: 0.85), the desired accuracy of UAS surface temperature measurements needed for various applications is not met. The lack of accuracy may be attributed to the limitation on modeling the atmospheric profile at low altitudes and the overall short path length in UAS remote sensing compared to that of a satellite. The modeled atmospheric profile and MODTRAN method was originally used in correcting thermal imagery from satellites, where the entire atmospheric profile affects the thermal infrared signal. With UAS remote sensing, there is far less atmosphere affecting the thermal infrared signal, however, the low altitude atmosphere contains the most variation in air temperature and humidity which are important factors contributing to atmospheric interference. In Figure 5, the rate of change for the Lu and τ terms vary based on altitude, showing that atmospheric interference is more prominent at lower altitudes. The method using MODTRAN may not be able to accurately distinguish the fine yet present changes in these parameters at low altitudes typically seen in UAS remote sensing. The apparent bias in the comparisons (Table 4, Figure 3), where UAS temperature measurements were overall lower than IRT measurements may also present an argument on the limitations of this method for correcting UAS thermal imagery.
Given the results of correcting FDPR remotely sensed thermal imagery using the modeled atmospheric profile and MODTRAN, a different method of obtaining increased accuracy in UAS-based surface temperature measurements was desirable. The linear, second order polynomial and ANN models proposed and tested in this study all performed better at correcting UAS FDPR measurements when compared to IRT measurements corrected for atmospheric interference. These additional models offered increased FDPR measurement accuracy and a simplified approach that does not require modeling the atmospheric profile and MODTRAN. While the calibration models discussed in Section 2.5 use common atmospheric parameters including air temperature, relative humidity and atmospheric pressure as explanatory variables, the models may not properly characterize atmospheric interference at other UAS remote sensing altitudes and locations. Figure 7 provides insight on quantifying the potential error if the proposed calibration models from Section 2.5 are used at different remote sensing altitudes; however, the information provided in Figure 5, Figure 6 and Figure 7 are specific to a certain location, time and sensor. While these models are easier to implement, they have potential to account for atmospheric interference and sensor bias simultaneously, whereas the method using MODTRAN had no specific capabilities for correcting sensor bias.
The methods used in this research for correcting UAS thermal imagery may be restrictive for certain users or yield lower accuracy in corrected imagery based on location and sensor. The MODTRAN radiative transfer code is a licensed software that must be purchased, which limits its use by a wide audience constricting the potential to further test this method as a viable means for correcting UAS-based thermal imagery. The calibration models presented in Section 2.5 were developed at a specific location using a single thermal infrared camera, which may limit their use at different locations, altitudes and sensors. In addition, the potential sensor bias present with the FDPR used in this study may not be present in other thermal cameras, further decreasing the usefulness of the models presented in Section 2.5. Other means for correcting thermal imagery may involve direct measurements of the components needed in Equation (1), similar to Berni et al. [32], who modeled the Lu and τ components using MODTRAN and measured the Ld component with a thermal sensor. Preliminary work has shown that there is a strong linear correlation between Ld and the Lu and τ parameters when using the modeled atmospheric profile and MODTRAN for a satellite like Landsat [33]. Further work is needed to determine if direct measurements of Ld contains a similar correlation to Lu and τ at typical UAS remote sensing altitudes and sensors.

5. Conclusions

Thermal infrared remote sensing is used in various agricultural applications and models for determining water stress and plant health. Satellite and manned aircraft remote sensing platforms have been the primary means for collecting remotely sensed imagery while UAS have recently gained a greater foothold in remote sensing due to their flexibility and lower cost. Several thermal cameras are available as UAS payloads capable of collected non-radiometric and radiometric thermal imagery. This study assessed a FLIR Duo Pro R, a radiometric thermal camera, and determined methods for increasing thermal measurement accuracy in agricultural applications. The assessment included laboratory and field-based testing. The water bath test results showed that the FDPR thermal camera had a degree of measurement instability that lasted several minutes after power-up. In addition, the FDPR water bath temperature measurements were consistently outside the manufacturer’s stated measurement error tolerance when compared to the thermistor-based water temperature measurements, with differences between FDPR and thermistor water temperature measurements typically decreasing with time. A warm-up period is recommended to surpass the instability of the FDPR camera after power-up, with longer warm-up periods likely enhancing FDPR measurement accuracy.
Surface temperature measurements from the UAS FDPR thermal imagery and field IRTs were compared to verify accuracy of remotely sensed thermal measurements. Corrections for emissivity differences between set sensor emissivity and actual surface emissivity along with atmospheric interference were applied to both the UAS FDPR thermal imagery and IRT surface temperature measurements. Comparisons were made at different levels of corrections including no corrections, corrections for emissivity differences only and corrections for atmospheric interference. Nine different comparisons were made at the various levels of corrections with the IRT surface temperature measurements corrected for atmospheric interference considered most accurate or as the actual surface temperature. While the initial assumption would be that the UAS FDPR thermal imagery and IRT measurements corrected for atmospheric interference would compare best, the UAS FDPR thermal imagery corrected for emissivity only had the strongest agreement with the atmospherically corrected IRT measurements.
Three additional FDPR calibration models were developed as an alternative method of correcting UAS FDPR thermal imagery. The linear, second order polynomial and ANN calibration models developed to improve accuracy of the UAS FDPR thermal imagery all performed similarly. Model development was based on using similar parameters used in modeling the atmospheric profile with the Barsi et al. [25] online atmospheric profile calculator. All three models performed better at correcting UAS FDPR thermal imagery compared to the method using the modeled atmospheric profile and MODTRAN. These calibration models provided a simple yet accurate means of correcting UAS FDPR thermal imagery without the need of a licensed software like MODTRAN. While the newly developed calibration models performed well, they may not perform similarly to UAS thermal imagery collected at different altitudes and locations. The calibration models developed in this study are likely not suitable as a universal calibration approach, but rather sheds light on the process of obtaining accurate UAS remotely sensed surface temperature measurements.
This study provided a better understanding of the accuracy and stability of the FDPR thermal camera, demonstrating the need for atmospheric interference corrections and camera warm-up period before collecting imagery. With thermal imagery often used in monitory vegetative conditions and water stress, the need for accurate surface temperature measurements is imperative. The UAS FDPR calibration models developed and tested in this study provided an additional and simplified approach to correcting thermal imagery for atmospheric interference while increasing FDPR thermal measurement accuracy. By increasing the accuracy of UAS thermal remote sensing, the various agricultural applications that utilize this data will benefit greatly and may lead to better decisions with managing agricultural systems.

Author Contributions

Conceptualization, M.S.M., C.M.U.N., and W.E.W.; methodology, M.S.M.; validation, M.S.M.; formal analysis, M.S.M.; investigation, M.S.M.; data curation, M.S.M.; writing—original draft preparation, M.S.M.; writing—review and editing, all authors; supervision, C.M.U.N. and W.E.W.; project administration, C.M.U.N. and W.E.W.; funding acquisition, C.M.U.N. and W.E.W. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the USDA-NIFA Foundational program (Award# 2017-67021-26249) and the Daugherty Water for Food Global Institute, University of Nebraska.

Acknowledgments

The authors would like to thank the support from the USDA-NIFA Foundational program and the Daugherty Water for Food Global Institute, University of Nebraska. In addition, we would like to thank Jasreman Singh for collecting and providing infrared thermometer data.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

References

  1. Choudhury, B.J.; Ahmed, N.U.; Idso, S.B.; Reginato, R.J.; Daughtry, C.S.T. Relations between Evaporation Coefficients and Vegetation Indices Studied by Model Simulations. Remote Sens. Environ. 1994, 50, 1–17. [Google Scholar] [CrossRef]
  2. Brunsell, N.A.; Gillies, R.R. Incorporating Surface Emissivity into a Thermal Atmospheric Correction. Photogramm. Eng. Remote Sens. 2002, 68, 1263–1269. [Google Scholar]
  3. Anderson, M.C.; Neale, C.M.U.; Li, F.; Norman, J.; Kustas, W.; Jayanthi, H.; Chavez, J. Upscaling Ground Observations of Vegetation Water Content, Canopy Height, and Leaf Area Index during SMEX02 Using Aircraft and Landsat Imagery. Remote Sens. Environ. 2004, 92, 447–464. [Google Scholar] [CrossRef]
  4. Anderson, M.C.; Norman, J.M.; Kustas, W.P.; Li, F.; Prueger, J.H.; Mecikalski, J.R. Effects of Vegetation Clumping on Two–Source Model Estimates of Surface Energy Fluxes from an Agricultural Landscape during SMACEX. J. Hydrometeorol. 2005, 6, 892–909. [Google Scholar] [CrossRef]
  5. Li, F.; Kustas, W.P.; Prueger, J.H.; Neale, C.M.U.; Jackson, T.J. Utility of Remote Sensing–Based Two-Source Energy Balance Model under Low- and High-Vegetation Cover Conditions. J. Hydrometeorol. 2005, 6, 878–891. [Google Scholar] [CrossRef]
  6. Neale, C.M.U.; Bausch, W.C.; Heermann, D.F. Development of Reflectance-Based Crop Coefficients for Corn. Trans. ASAE 1989, 32, 1891. [Google Scholar] [CrossRef]
  7. Norman, J.M.; Kustas, W.P.; Humes, K.S. Source Approach for Estimating Soil and Vegetation Energy Fluxes in Observations of Directional Radiometric Surface Temperature. Agric. For. Meteorol. 1995, 77, 263–293. [Google Scholar] [CrossRef]
  8. Kustas, W.P.; Norman, J.M. Use of Remote Sensing for Evapotranspiration Monitoring over Land Surfaces. Hydrol. Sci. J. 1996, 41, 495–516. [Google Scholar] [CrossRef]
  9. Kustas, W.P.; Norman, J.M. A Two-Source Approach for Estimating Turbulent Fluxes Using Multiple Angle Thermal Infrared Observations. Water Resour. Res. 1997, 33, 1495–1508. [Google Scholar] [CrossRef]
  10. Anderson, M.C.; Norman, J.M.; Diak, G.R.; Kustas, W.P.; Mecikalski, J.R. A Two-Source Time-Integrated Model for Estimating Surface Fluxes Using Thermal Infrared Remote Sensing. Remote Sens. Environ. 1997, 60, 195–216. [Google Scholar] [CrossRef]
  11. Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A Remote Sensing Surface Energy Balance Algorithm for Land (SEBAL). 1. Formulation. J. Hydrol. 1998, 212–213, 198–212. [Google Scholar] [CrossRef]
  12. Tasumi, M.; Allen, R.G.; Trezza, R.; Wright, J.L. Satellite-Based Energy Balance to Assess Within-Population Variance of Crop Coefficient Curves. J. Irrig. Drain Eng. 2005, 131, 94–109. [Google Scholar] [CrossRef]
  13. Sánchez, J.M.; Kustas, W.P.; Caselles, V.; Anderson, M.C. Modelling Surface Energy Fluxes over Maize Using a Two-Source Patch Model and Radiometric Soil and Canopy Temperature Observations. Remote Sens. Environ. 2008, 112, 1130–1143. [Google Scholar] [CrossRef]
  14. Neale, C.M.U.; Geli, H.M.E.; Kustas, W.P.; Alfieri, J.G.; Gowda, P.H.; Evett, S.R.; Prueger, J.H.; Hipps, L.E.; Dulaney, W.P.; Chávez, J.L.; et al. Soil Water Content Estimation Using a Remote Sensing Based Hybrid Evapotranspiration Modeling Approach. Adv. Water Resour. 2012, 50, 152–161. [Google Scholar] [CrossRef]
  15. Neale, C.M.U.; Vinukollu, R.K.; Ramsey, R.D. A Hybrid Surface Energy Balance Approach for the Estimation of Evapotranspiration in Agricultural Areas. In Proceedings of the AIP, Naples, Italy, 10–11 November 2005; D’Urso, G., Osann Jochum, M.A., Moreno, J., Eds.; American Institute of Physics: College Park, MD, USA, 2006; Volume 852, pp. 138–145. [Google Scholar] [CrossRef]
  16. Barker, J.B.; Neale, C.M.U.; Heeren, D.M.; Suyker, A.E. Evaluation of a Hybrid Reflectance-Based Crop Coefficient and Energy Balance Evapotranspiration Model for Irrigation Management. Trans. ASABE 2018, 61, 533–548. [Google Scholar] [CrossRef] [Green Version]
  17. Barker, J.B.; Heeren, D.M.; Neale, C.M.U.; Rudnick, D.R. Evaluation of Variable Rate Irrigation Using a Remote-Sensing-Based Model. Agric. Water Manag. 2018, 203, 63–74. [Google Scholar] [CrossRef] [Green Version]
  18. Bhatti, S.; Heeren, D.M.; Barker, J.B.; Neale, C.M.U.; Woldt, W.E.; Maguire, M.S.; Rudnick, D.R. Site-Specific Irrigation Management in a Sub-Humid Climate Using a Spatial Evapotranspiration Model with Satellite and Airborne Imagery. Agric. Water Manag. 2020, 230, 105950. [Google Scholar] [CrossRef] [Green Version]
  19. DeJonge, K.C.; Taghvaeian, S.; Trout, T.J.; Comas, L.H. Comparison of Canopy Temperature-Based Water Stress Indices for Maize. Agric. Water Manag. 2015, 156, 51–62. [Google Scholar] [CrossRef]
  20. Bian, J.; Zhang, Z.; Chen, J.; Chen, H.; Cui, C.; Li, X.; Chen, S.; Fu, Q. Simplified Evaluation of Cotton Water Stress Using High Resolution Unmanned Aerial Vehicle Thermal Imagery. Remote Sens. 2019, 11, 267. [Google Scholar] [CrossRef] [Green Version]
  21. Ribeiro-Gomes, K.; Hernández-López, D.; Ortega, J.; Ballesteros, R.; Poblete, T.; Moreno, M. Uncooled Thermal Camera Calibration and Optimization of the Photogrammetry Process for UAV Applications in Agriculture. Sensors 2017, 17, 2173. [Google Scholar] [CrossRef]
  22. Gómez-Candón, D.; Virlet, N.; Labbé, S.; Jolivot, A.; Regnard, J.-L. Field Phenotyping of Water Stress at Tree Scale by UAV-Sensed Imagery: New Insights for Thermal Acquisition and Calibration. Precis. Agric. 2016, 17, 786–800. [Google Scholar] [CrossRef]
  23. Jensen, A.M.; McKee, M.; Chen, Y. Calibrating Thermal Imagery from an Unmanned Aerial System—AggieAir. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium—IGARSS, Melbourne, Australia, 21–26 July 2013; pp. 542–545. [Google Scholar] [CrossRef]
  24. Kelly, J.; Kljun, N.; Olsson, P.-O.; Mihai, L.; Liljeblad, B.; Weslien, P.; Klemedtsson, L.; Eklundh, L. Challenges and Best Practices for Deriving Temperature Data from an Uncalibrated UAV Thermal Infrared Camera. Remote Sens. 2019, 11, 567. [Google Scholar] [CrossRef] [Green Version]
  25. Barsi, J.A.; Barker, J.L.; Schott, J.R. An Atmospheric Correction Parameter Calculator for a Single Thermal Band Earth-Sensing Instrument. In Proceedings of the IGARSS 2003 IEEE International Geoscience and Remote Sensing Symposium, Proceedings (IEEE Cat. No.03CH37477), Toulouse, France, 21–25 July 2003; Volume 5, pp. 3014–3016. [Google Scholar] [CrossRef]
  26. Berk, A.; Conforti, P.; Kennett, R.; Perkins, T.; Hawes, F.; van den Bosch, J. MODTRAN® 6: A Major Upgrade of the MODTRAN® Radiative Transfer Code. In Proceedings of the 2014 6th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Lausanne, Switzerland, 24–27 June 2014; IEEE: Lausanne, Switzerland, 2014; pp. 1–4. [Google Scholar] [CrossRef]
  27. Chávez, J.; Neale, C.M.U.; Hipps, L.E.; Prueger, J.H.; Kustas, W.P. Comparing Aircraft-Based Remotely Sensed Energy Balance Fluxes with Eddy Covariance Tower Data Using Heat Flux Source Area Functions. J. Hydrometeorol. 2005, 6, 923–940. [Google Scholar] [CrossRef]
  28. Neale, C.M.U.; Jaworowski, C.; Heasler, H.; Sivarajan, S.; Masih, A. Hydrothermal Monitoring in Yellowstone National Park Using Airborne Thermal Infrared Remote Sensing. Remote Sens. Environ. 2016, 184, 628–644. [Google Scholar] [CrossRef] [Green Version]
  29. Pix4D. Available online: https://www.pix4d.com/ (accessed on 1 March 2020).
  30. Houborg, R.; Anderson, M.C.; Norman, J.M.; Wilson, T.; Meyers, T. Intercomparison of a ‘Bottom-up’ and ‘Top-down’ Modeling Paradigm for Estimating Carbon and Energy Fluxes over a Variety of Vegetative Regimes across the U.S. Agric. For. Meteorol. 2009, 149, 1875–1895. [Google Scholar] [CrossRef]
  31. Chollet, F. Keras. GitHub. Available online: https://github.com/fchollet/keras (accessed on 1 March 2020).
  32. Berni, J.; Zarco-Tejada, P.J.; Suarez, L.; Fereres, E. Thermal and Narrowband Multispectral Remote Sensing for Vegetation Monitoring from an Unmanned Aerial Vehicle. IEEE Trans. Geosci. Remote Sens. 2009, 47, 722–738. [Google Scholar] [CrossRef] [Green Version]
  33. Barker, J.B.; University of Nebraska Lincoln, Lincoln, NE, USA. Personal communication, 2018.
Remotesensing 13 01635 g001 550
Figure 1. (a) UAS multispectral color infrared ortho-images; (b) thermal infrared (°C) ortho-images. Color infrared image depicts location of IRT sensors denoted with X.
Figure 1. (a) UAS multispectral color infrared ortho-images; (b) thermal infrared (°C) ortho-images. Color infrared image depicts location of IRT sensors denoted with X.
Remotesensing 13 01635 g001
Remotesensing 13 01635 g002 550
Figure 2. FDPR and thermistor measured water bath temperature at different ambient air temperatures: (a) high ambient air temperature; (b) low ambient air temperature; (c) mid ambient air temperature (room temperature).
Figure 2. FDPR and thermistor measured water bath temperature at different ambient air temperatures: (a) high ambient air temperature; (b) low ambient air temperature; (c) mid ambient air temperature (room temperature).
Remotesensing 13 01635 g002
Remotesensing 13 01635 g003 550
Figure 3. Comparison of surface temperature measurements from UAS FDPR thermal camera and field IRTs at different correction levels: (a) non-corrected IRT and UAS FDPR; (b) non-corrected IRT and emissivity corrected UAS FDPR; (c) non-corrected IRT and atmospherically corrected UAS FDPR; (d) emissivity corrected IRT and non-corrected UAS FDPR; (e) emissivity corrected IRT and UAS FDPR; (f) emissivity corrected IRT and atmospherically corrected UAS FDPR; (g) atmospherically corrected IRT and non-corrected UAS FDPR; (h) atmospherically corrected IRT and emissivity corrected UAS FDPR; (i) atmospherically corrected IRT and UAS FDPR.
Figure 3. Comparison of surface temperature measurements from UAS FDPR thermal camera and field IRTs at different correction levels: (a) non-corrected IRT and UAS FDPR; (b) non-corrected IRT and emissivity corrected UAS FDPR; (c) non-corrected IRT and atmospherically corrected UAS FDPR; (d) emissivity corrected IRT and non-corrected UAS FDPR; (e) emissivity corrected IRT and UAS FDPR; (f) emissivity corrected IRT and atmospherically corrected UAS FDPR; (g) atmospherically corrected IRT and non-corrected UAS FDPR; (h) atmospherically corrected IRT and emissivity corrected UAS FDPR; (i) atmospherically corrected IRT and UAS FDPR.
Remotesensing 13 01635 g003
Remotesensing 13 01635 g004 550
Figure 4. Comparison of (a) linear, (b) second order polynomial and (c) ANN calibrated UAS FDPR thermal imagery with field IRT surface temperature measurements corrected for atmospheric interference.
Figure 4. Comparison of (a) linear, (b) second order polynomial and (c) ANN calibrated UAS FDPR thermal imagery with field IRT surface temperature measurements corrected for atmospheric interference.
Remotesensing 13 01635 g004
Remotesensing 13 01635 g005 550
Figure 5. Modeled Lu, Ld and τ at the UAS scene center time on 9 August 2018 at different sensor altitudes.
Figure 5. Modeled Lu, Ld and τ at the UAS scene center time on 9 August 2018 at different sensor altitudes.
Remotesensing 13 01635 g005
Remotesensing 13 01635 g006 550
Figure 6. Corrected temperature at different sensor altitudes based on modeled Lu, Ld and τ at the scene center time on 9 August 2018 using the modeled atmospheric profile and MODTRAN.
Figure 6. Corrected temperature at different sensor altitudes based on modeled Lu, Ld and τ at the scene center time on 9 August 2018 using the modeled atmospheric profile and MODTRAN.
Remotesensing 13 01635 g006
Remotesensing 13 01635 g007 550
Figure 7. Absolute temperature differences in atmospherically corrected thermal imagery collected at 240 m AGL and thermal imagery collected at 30 m, 60 m and 120 m AGL based on MODTRAN modeled atmospheric interference on 9 August 2018. Vertical dashed lines represent a potential one-degree Celsius error for each sensor altitude compared to atmospherically corrected thermal imagery collected at 240 m AGL.
Figure 7. Absolute temperature differences in atmospherically corrected thermal imagery collected at 240 m AGL and thermal imagery collected at 30 m, 60 m and 120 m AGL based on MODTRAN modeled atmospheric interference on 9 August 2018. Vertical dashed lines represent a potential one-degree Celsius error for each sensor altitude compared to atmospherically corrected thermal imagery collected at 240 m AGL.
Remotesensing 13 01635 g007
Table
Table 1. FLIR Duo Pro R thermal camera specifications.
Table 1. FLIR Duo Pro R thermal camera specifications.
Spectral Band7.5–13.5 µm
Thermal Frame Rate30 Hz
Thermal ImagerUncooled VOx Microbolometer
Focal Length13 mm
Field of View45° × 37°
Thermal Sensitivity<50 mK
Thermal Sensor Resolution640 × 512
Measurement Accuracy+/− 5 °C or 5% of readings in the −25 °C to +135 °C range
+/− 20 °C or 20% of readings in the −40 °C to +550 °C range
Table
Table 2. MicaSense RedEdge multispectral camera specifications.
Table 2. MicaSense RedEdge multispectral camera specifications.
Band NameCenter Wavelength (nm)Bandwidth FWHM (nm)
Blue47520
Green56020
Red66810
Near IR84040
Red Edge71710
Ground Sampling Distance8.2 cm/pixel at 120 m AGL
Lens Focal Length (mm)5.5
Lens Field of View (degrees 1 HFOV)47.2
Imager Size (mm)4.8 × 3.6
Image Resolution (pixels)1280 × 960
1 Horizontal field of view
Table
Table 3. Dates of UAS image acquisition.
Table 3. Dates of UAS image acquisition.
5 June 201824 July 201831 May 201923 July 2019
18 June 20181 August 20187 June 20194 August 2019
27 June 20189 August 201813 June 20196 August 2019
2 July 201829 August 201824 June 201913 August 2019
6 July 201817 September 201828 June 201919 August 2019
11 July 2018 11 July 201928 August 2019
18 July 20196 September 2019
Table
Table 4. Comparison results of measured surface temperature from UAS FDPR and field IRTs at different levels of corrections.
Table 4. Comparison results of measured surface temperature from UAS FDPR and field IRTs at different levels of corrections.
IRT Calibration
Method		UAS FDPR Calibration MethodMAEMBERMSER2
NoneNone1.98−1.222.500.79
Nonee1.37−0.031.760.90
NoneAtm1.42−0.351.800.89
eNone3.19−2.993.900.57
ee2.15−1.802.670.80
eAtm2.36−2.132.860.77
AtmNone2.52−2.013.180.70
Atme1.65−0.822.150.86
AtmAtm1.78−1.142.240.85
None—no corrections; e—corrections for emissivity differences; Atm—corrections for atmospheric interference (includes emissivity corrections).
Table
Table 5. Linear (Equation (5)) and second order polynomial (Equation (6)) FDPR calibration model coefficients.
Table 5. Linear (Equation (5)) and second order polynomial (Equation (6)) FDPR calibration model coefficients.
Linear Model CoefficientsSecond Order Polynomial Model Coefficients
β0569.6453β0−12,192.8655β7−0.0196β14−0.4039
β10.4236β125.9004β8−0.030β15−0.0041
β20.4062β2−20.1826β9−0.0252β16−0.0123
β3−0.0098β315.9142β100.6130β17−3.8417
β40.0080β417.4669β110.0024β18−0.0020
β5−583.0948β56804.1218β120.0415β19−13.9106
β60.01377β130.0595β203899.6337
Table
Table 6. Statistical performance of UAS FDPR thermal calibration models.
Table 6. Statistical performance of UAS FDPR thermal calibration models.
ModelMAEMBERMSER2
Linear1.000.461.270.93
Second Order Polynomial0.910.141.240.94
Artificial Neural Network0.88−0.081.120.94
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Maguire, M.S.; Neale, C.M.U.; Woldt, W.E. Improving Accuracy of Unmanned Aerial System Thermal Infrared Remote Sensing for Use in Energy Balance Models in Agriculture Applications. Remote Sens. 2021, 13, 1635. https://doi.org/10.3390/rs13091635

AMA Style

Maguire MS, Neale CMU, Woldt WE. Improving Accuracy of Unmanned Aerial System Thermal Infrared Remote Sensing for Use in Energy Balance Models in Agriculture Applications. Remote Sensing. 2021; 13(9):1635. https://doi.org/10.3390/rs13091635

Chicago/Turabian Style

Maguire, Mitchell S., Christopher M. U. Neale, and Wayne E. Woldt. 2021. "Improving Accuracy of Unmanned Aerial System Thermal Infrared Remote Sensing for Use in Energy Balance Models in Agriculture Applications" Remote Sensing 13, no. 9: 1635. https://doi.org/10.3390/rs13091635

APA Style

Maguire, M. S., Neale, C. M. U., & Woldt, W. E. (2021). Improving Accuracy of Unmanned Aerial System Thermal Infrared Remote Sensing for Use in Energy Balance Models in Agriculture Applications. Remote Sensing, 13(9), 1635. https://doi.org/10.3390/rs13091635

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop