Robust Multipath-Assisted SLAM with Unknown Process Noise and Clutter Intensity
Abstract
1. Introduction
2. Environment Map and Signal Model
3. System Model with Unknown Process Noise and Clutter Intensity
3.1. UE State and PF States
3.2. Markov Chain Modeling of the Process Noise and the Clutter Intensity
3.3. State Evolution with Unknown Process Noise
3.4. Prior Distributions with Unknown Clutter Intensity
3.5. Measurement Model and Likelihood Function
4. The Proposed Algorithm
4.1. Detection and Estimation
4.2. Joint Posterior Distribution and Factor Graph
4.3. BP Message Passing Algorithm
- Prediction.
- 2.
- Measurement evaluation of legacy PFs.
- 3.
- Measurement evaluation of new PFs.
- 4.
- Iterative DA
- 5.
- Measurement update for legacy PFs
- 6.
- Measurement update for new PFs
- 7.
- Calculation of beliefs
5. Simulation Results and Discussions
5.1. Simulation Parameters
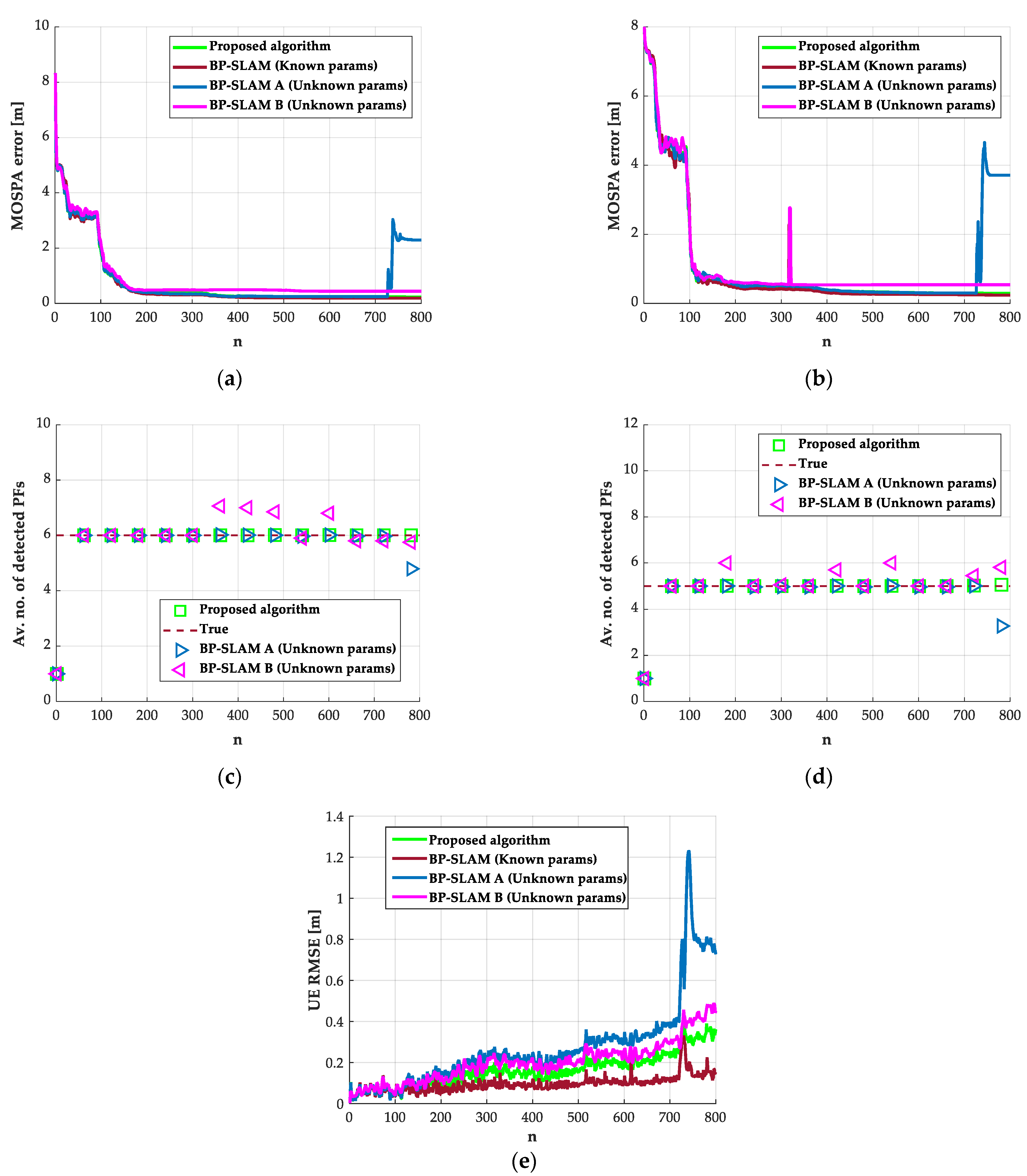
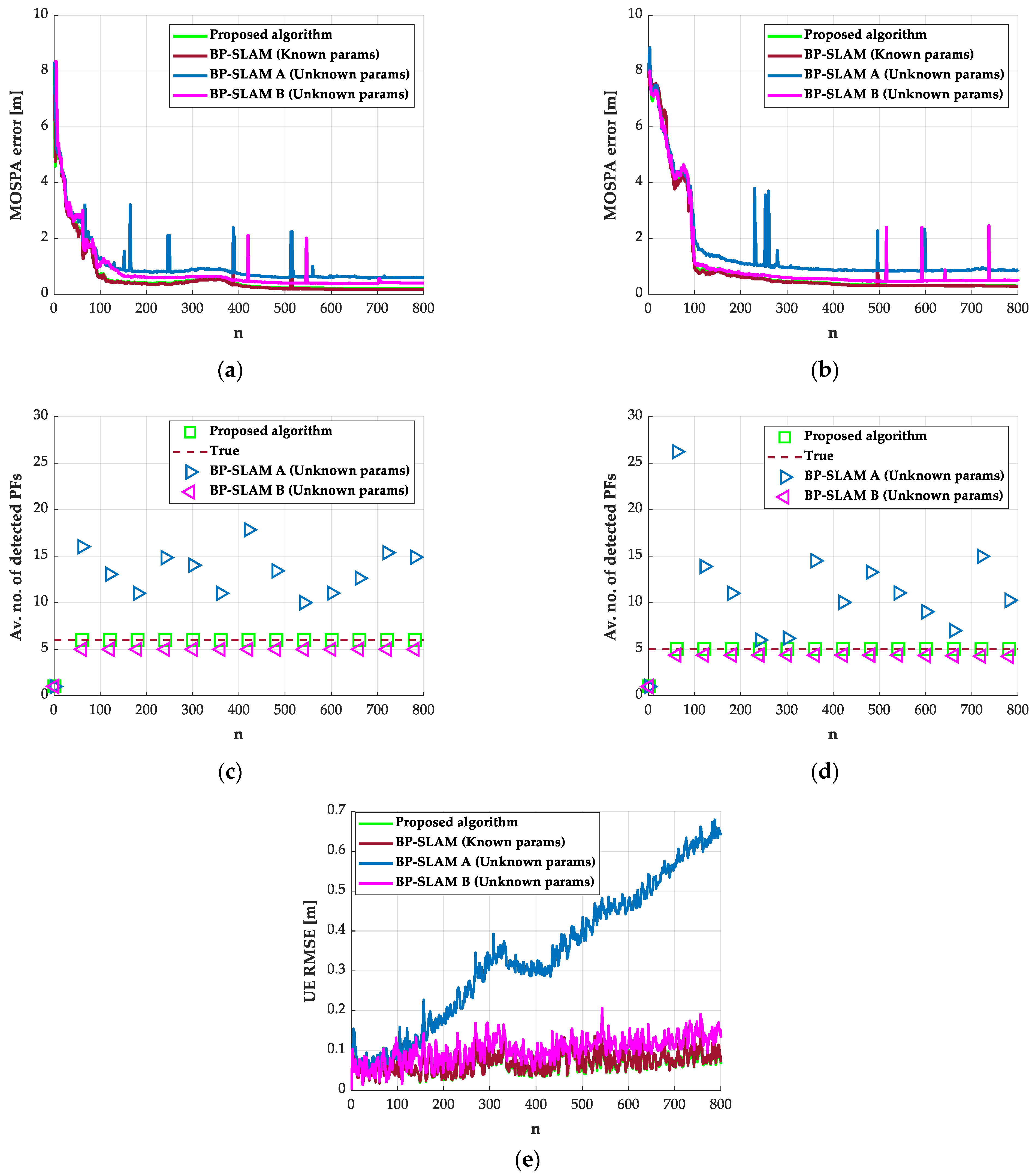
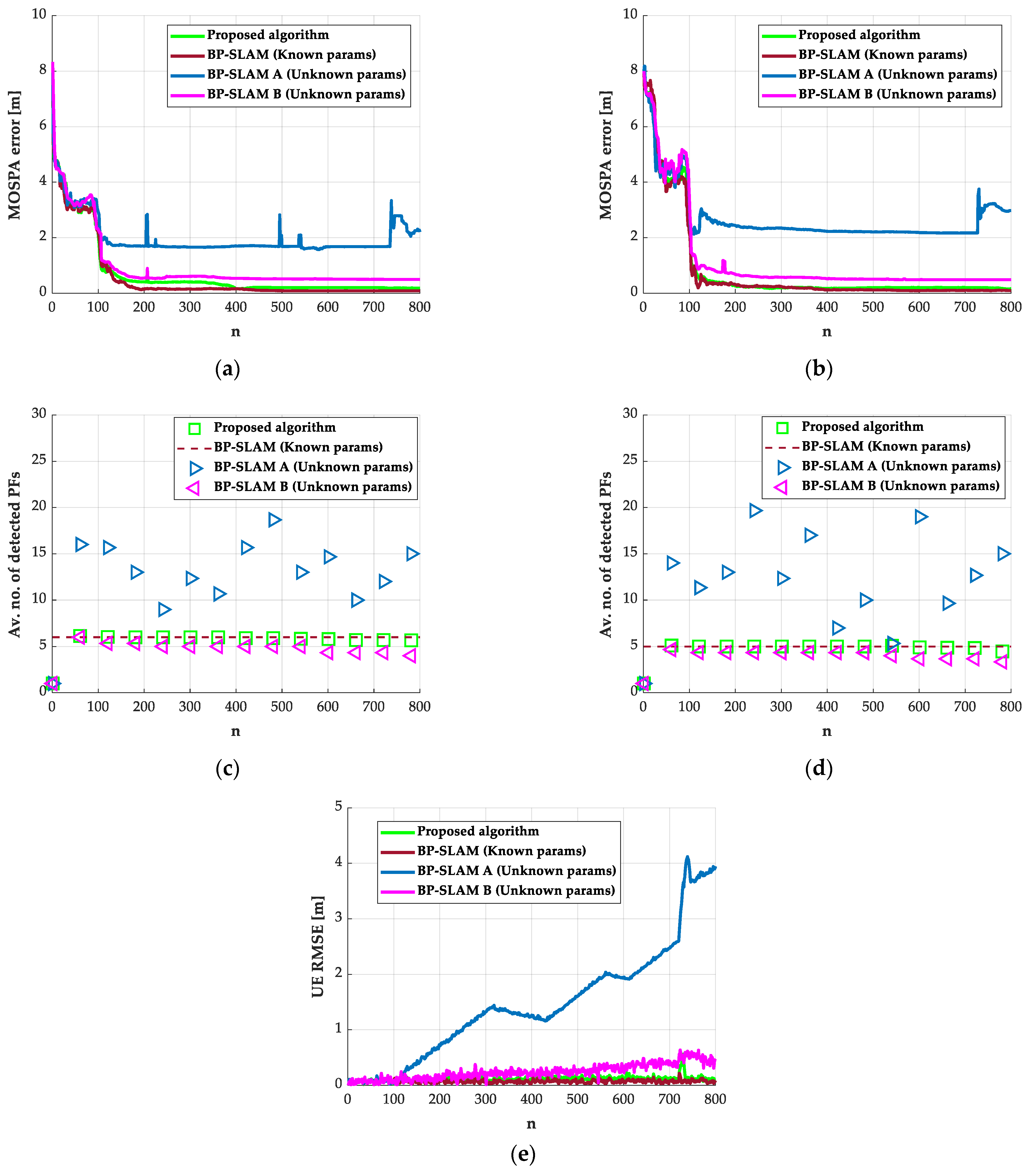
5.2. First Scenario: Unknown Process Noise Only
5.3. Second Scenario: Unknown Clutter Intensity Only
5.4. Third Scenario: Unknown Process Noise and Clutter Intensity
5.5. Calculation Complexity Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Durrant-Whyte, H.; Bailey, T. Simultaneous localization and mapping: Part I. IEEE Robot. Autom. Mag. 2006, 13, 99–110. [Google Scholar] [CrossRef]
- Bailey, T.; Durrant-Whyte, H. Simultaneous localization and mapping (SLAM): Part II. IEEE Robot. Autom. Mag. 2006, 13, 108–117. [Google Scholar] [CrossRef]
- Lajoie, P.Y.; Ramtoula, B.; Chang, Y. DOOR-SLAM: Distributed, Online, and Outlier Resilient SLAM for Robotic Teams. IEEE Robot. Autom. Lett. 2020, 5, 1656–1663. [Google Scholar] [CrossRef]
- Chiang, K.W.; Tsai, G.J.; Chu, H.J. Performance Enhancement of INS/GNSS/Refreshed-SLAM Integration for Acceptable Lane-Level Navigation Accuracy. IEEE Trans. Veh. Technol. 2020, 69, 2463–2476. [Google Scholar] [CrossRef]
- Mendrzik, R.; Meyer, F.; Bauch, G. Enabling Situational Awareness in Millimeter Wave Massive MIMO Systems. IEEE J. Sel. Top. Signal Process. 2019, 13, 1196–1211. [Google Scholar] [CrossRef]
- Chen, Z.; Zhu, G.; Wang, S. M3: Multipath Assisted Wi-Fi Localization with a Single Access Point. IEEE Trans. Mob. Comput. 2021, 20, 588–602. [Google Scholar] [CrossRef]
- Ulmschneider, M.; Gentner, C.; Jost, T. Association of Transmitters in Multipath-Assisted Positioning. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Singapore, 4–8 December 2017. [Google Scholar]
- Li, Z.; Tian, Z.; Wang, Z. Multipath-Assisted Indoor Localization Using a Single Receiver. IEEE Sens. J. 2021, 21, 692–705. [Google Scholar] [CrossRef]
- Li, Z.; Tian, Z.; Wang, Z. Multipath-Assisted Indoor Localization: Turning Multipath Signal from Enemy to Friend. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Waikoloa, HI, USA, 9–13 December 2019. [Google Scholar]
- Wielandt, S.; Strycker, L.D. Indoor Multipath Assisted Angle of Arrival Localization. Sensors 2017, 17, 2522. [Google Scholar] [CrossRef]
- Witrisal, K.; Meissner, P.; Leitinger, E. High-accuracy localization for assisted living: 5G systems will turn multipath channels from foe to friend. IEEE Signal Process. Mag. 2016, 33, 59–70. [Google Scholar] [CrossRef]
- Guidi, F.; Closas, P.; Dardari, D. Personal mobile radars with millimeter-wave massive arrays for indoor mapping. IEEE Trans. Mobile Comput. 2016, 15, 1471–1484. [Google Scholar] [CrossRef]
- Guerra, A.; Guidi, F.; Dardari, D. Occupancy grid mapping for personal radar applications. In Proceedings of the IEEE Statistical Signal Processing Workshop (SSP), Freiburg, Germany, 10–13 June 2018. [Google Scholar]
- Zhang, H.; Tan, S.Y. TOA based indoor localization and tracking via single-cluster PHD filtering. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Singapore, 4–8 December 2017. [Google Scholar]
- Kim, H.; Granström, K.; Gao, L. 5G mmWave Cooperative Positioning and Mapping Using Multi-Model PHD Filter and Map Fusion. IEEE Trans. Wirel. Commun. 2020, 19, 3782–3795. [Google Scholar] [CrossRef]
- Mendrzik, R.; Wymeersch, H.; Bauch, G. Joint Localization and Mapping through Millimeter Wave MIMO in 5G Systems. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Abu Dhabi, United Arab Emirates, 9–13 December 2018. [Google Scholar]
- Leitinger, E.; Meissner, P.; Rudisser, C. Evaluation of position-related information in multipath components for indoor positioning. IEEE J. Sel. Areas Commun. 2015, 33, 2313–2328. [Google Scholar] [CrossRef]
- Leitinger, E.; Meissner, P.; Witrisal, K. Simultaneous localization and mapping using multipath channel information. In Proceedings of the IEEE International Conference on Communication Workshop (ICCW), London, UK, 8–12 June 2015. [Google Scholar]
- Gentner, C.; Ma, B.; Ulmschneider, M. Simultaneous localization and mapping in multipath environments. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium (PLANS), Savannah, GA, USA, 11–14 April 2016. [Google Scholar]
- Li, Z.; Tian, Z.; Wang, Z. WalkAround: Multipath-assisted Indoor Localization and Mapping Using a Single Receiver. In Proceedings of the IEEE International Conference on Communications (ICC), Dublin, Ireland, 7–11 June 2020. [Google Scholar]
- Ulmschneider, M.; Gentner, C. Multipath assisted positioning for pedestrians using LTE signals. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium (PLANS), Savannah, GA, USA, 11–14 April 2016. [Google Scholar]
- Gentner, C.; Jost, T.; Wang, W. Multipath Assisted Positioning with Simultaneous Localization and Mapping. IEEE Trans. Wirel. Commun. 2016, 15, 6104–6117. [Google Scholar] [CrossRef]
- Karásek, R.; Gentner, C. Stochastic Data Association for Multipath Assisted Positioning Using a Single Transmitter. IEEE Access 2020, 8, 46735–46752. [Google Scholar] [CrossRef]
- Liu, Y.; Lian, B.; Zhou, T. Gaussian message pasing-based cooperative localization with node selection scheme in wireless networks. Signal Process. 2019, 156, 166–176. [Google Scholar] [CrossRef]
- Leitinger, E.; Meyer, F.; Hlawatsch, F. A Belief Propagation Algorithm for Multipath-Based SLAM. IEEE Trans. Wirel. Commun. 2019, 18, 5613–5629. [Google Scholar] [CrossRef]
- Leitinger, E.; Meyer, F.; Tufvesson, F. Factor Graph Based Simultaneous Localization and Mapping Using Multipath Channel Information. In Proceedings of the IEEE International Conference on Communications Workshops (ICC Workshops), Paris, France, 21–25 May 2017. [Google Scholar]
- Leitinger, E.; Grebien, S.; Li, X. On the Use of Mpc Amplitude Information in Radio Signal Based SLAM. In Proceedings of the IEEE Statistical Signal Processing Workshop (SSP), Freiburg, Germany, 10–13 June 2018. [Google Scholar]
- Leitinger, E.; Grebien, S.; Witrisal, K. Multipath-based SLAM Exploiting AoA and Amplitude Information. In Proceedings of the IEEE International Conference on Communications Workshops (ICC Workshops), Shanghai, China, 20–24 May 2019. [Google Scholar]
- Bar-Shalom, Y.; Li, X.-R. Multitarget-Multisensor Tracking: Principles and Techniques; Yaakov Bar-Shalom: Storrs, CT, USA, 1995; pp. 1–4. [Google Scholar]
- Mahler, R.P.S.; Vo, B.T.; Vo, B.N. CPHD Filtering with Unknown Clutter Rate and Detection Profile. IEEE Trans. Signal. Process. 2011, 59, 3497–3513. [Google Scholar] [CrossRef]
- Vo, B.T.; Vo, B.N.; Hoseinnezhad, R. Robust multi-Bernoulli filtering. IEEE J. Sel. Top. Signal Process. 2013, 7, 399–409. [Google Scholar] [CrossRef]
- Ristic, B.; Clark, D.; Vo, B.T.; Vo, B.N. Adaptive target birth intensity for PHD and CPHD filters. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 1656–1668. [Google Scholar] [CrossRef]
- Soldi, G.; Meyer, F.; Braca, P.; Hlawatsch, F. Self-Tuning Algorithms for Multisensor-Multitarget Tracking Using Belief Propagation. IEEE Trans. Signal. Process. 2019, 67, 3922–3937. [Google Scholar] [CrossRef]
- Kschischang, F.R.; Frey, B.J.; Loeliger, H.-A. Factor graphs and the sum-product algorithm. IEEE Trans. Inf. Theory 2001, 47, 498–519. [Google Scholar] [CrossRef]
- Salmi, J.; Richter, A.; Koivunen, V. Detection and tracking of MIMO propagation path parameters using state-space approach. IEEE Trans. Signal. Process. 2009, 57, 1538–1550. [Google Scholar] [CrossRef]
- Mahler, R.P.S. Statistical Multisource-Multitarget Information Fusion; Artech House: Norwood, MA, USA, 2007. [Google Scholar]
- Jo, K.; Chu, K.; Sunwoo, M. Interacting Multiple Model Filter-Based Sensor Fusion of GPS With In-Vehicle Sensors for Real-Time Vehicle Positioning. IEEE Trans. Intell. Transp. 2012, 13, 329–343. [Google Scholar] [CrossRef]
- Meyer, F.; Braca, P.; Willett, P.; Hlawatsch, F. A scalable algorithm for tracking an unknown number of targets using multiple sensors. IEEE Trans. Signal. Process. 2017, 65, 3478–3493. [Google Scholar] [CrossRef]
- Wymeersch, H.; Seco-Granados, G. Adaptive Detection Probability for mmWave 5G SLAM. In Proceedings of the IEEE 2nd 6G Wireless Summit (6G SUMMIT), Levi, Finland, 17–20 March 2020. [Google Scholar]
- Williams, J.L.; Lau, R. Approximate evaluation of marginal association probabilities with belief propagation. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 2942–2959. [Google Scholar] [CrossRef]
- Meyer, F.; Kropfreiter, T.; Williams, J.L. Message passing algorithms for scalable multitarget tracking. Proc. IEEE 2018, 106, 221–259. [Google Scholar] [CrossRef]
- Meyer, F.; Hlinka, O.; Wymeersch, H.; Hlawatsch, F. Distributed localization and tracking of mobile networks including noncooperative objects. IEEE Trans. Signal Inf. Process. Netw. 2016, 2, 57–71. [Google Scholar] [CrossRef]
- Li, X.R.; Jilkov, V.P. Survey of maneuvering target tracking. part I. dynamic models. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1333–1364. [Google Scholar] [CrossRef]
- Horridge, P.; Maskell, S. Using a probabilistic hypothesis density filter to confirm tracks in a multi-target environment. In Proceedings of the Informatik Schafft Communities (INFORMATIK-11), Berlin, Germany, 4–7 July 2011. [Google Scholar]
- Schuhmacher, D.; Vo, B.T.; Vo, B.N. A consistent metric for performance evaluation of multi-object filters. IEEE Trans. Signal Process. 2008, 56, 3447–3457. [Google Scholar] [CrossRef]


| Simulation Runs | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 10−4 m | 10−3 m | 6 | 0.1 m | 0.95 | 10−4 | 0.999 | 0.5 | 10−4 | 10,000 | 100 |
| Algorithm | UE RMSE | MOSPA | No. of PFs |
|---|---|---|---|
| BP-SLAM A | 0.2891 m | 1.1143 m | 0.1090 |
| BP-SLAM B | 0.1984 m | 1.0442 m | 0.2564 |
| Proposed algorithm | 0.1605 m | 0.8759 m | 0.0005 |
| BP-SLAM (known params) | 0.0949 m | 0.7739 m | 0 (True) |
| Algorithm | UE RMSE | MOSPA | No. of PFs |
|---|---|---|---|
| BP-SLAM A | 0.3768 m | 1.2199 m | 8.0151 |
| BP-SLAM B | 0.1083 m | 1.0006 m | 0.8329 |
| Proposed algorithm | 0.0741 m | 0.7659 m | 0.0678 |
| BP-SLAM (known params) | 0.0714 m | 0.7376 m | 0 (True) |
| Algorithm | UE RMSE | MOSPA | No. of PFs |
|---|---|---|---|
| BP-SLAM A | 1.4636 m | 2.2396 m | 8.4696 |
| BP-SLAM B | 0.2452 m | 1.0713 m | 0.8099 |
| Proposed algorithm | 0.1121 m | 0.7659 m | 0.0628 |
| BP-SLAM (known params) | 0.0699 m | 0.6738 m | 0 (True) |
| Algorithm | Complexity Order | CPU Run Time |
|---|---|---|
| BP-SLAM (unknown params) | 0.0645 s | |
| Proposed algorithm | 0.0761 s | |
| BP-SLAM (known params) | 0.0652 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dan, Z.; Lian, B.; Tang, C. Robust Multipath-Assisted SLAM with Unknown Process Noise and Clutter Intensity. Remote Sens. 2021, 13, 1625. https://doi.org/10.3390/rs13091625
Dan Z, Lian B, Tang C. Robust Multipath-Assisted SLAM with Unknown Process Noise and Clutter Intensity. Remote Sensing. 2021; 13(9):1625. https://doi.org/10.3390/rs13091625
Chicago/Turabian StyleDan, Zesheng, Baowang Lian, and Chengkai Tang. 2021. "Robust Multipath-Assisted SLAM with Unknown Process Noise and Clutter Intensity" Remote Sensing 13, no. 9: 1625. https://doi.org/10.3390/rs13091625
APA StyleDan, Z., Lian, B., & Tang, C. (2021). Robust Multipath-Assisted SLAM with Unknown Process Noise and Clutter Intensity. Remote Sensing, 13(9), 1625. https://doi.org/10.3390/rs13091625







