Assessing the Effects of Spatial Scales on Regional Evapotranspiration Estimation by the SEBAL Model and Multiple Satellite Datasets: A Case Study in the Agro-Pastoral Ecotone, Northwestern China
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Datasets and Processing
2.2.1. Remote Sensing Datasets
2.2.2. Meteorological and Flux Data
2.2.3. Other Data
2.3. Methods
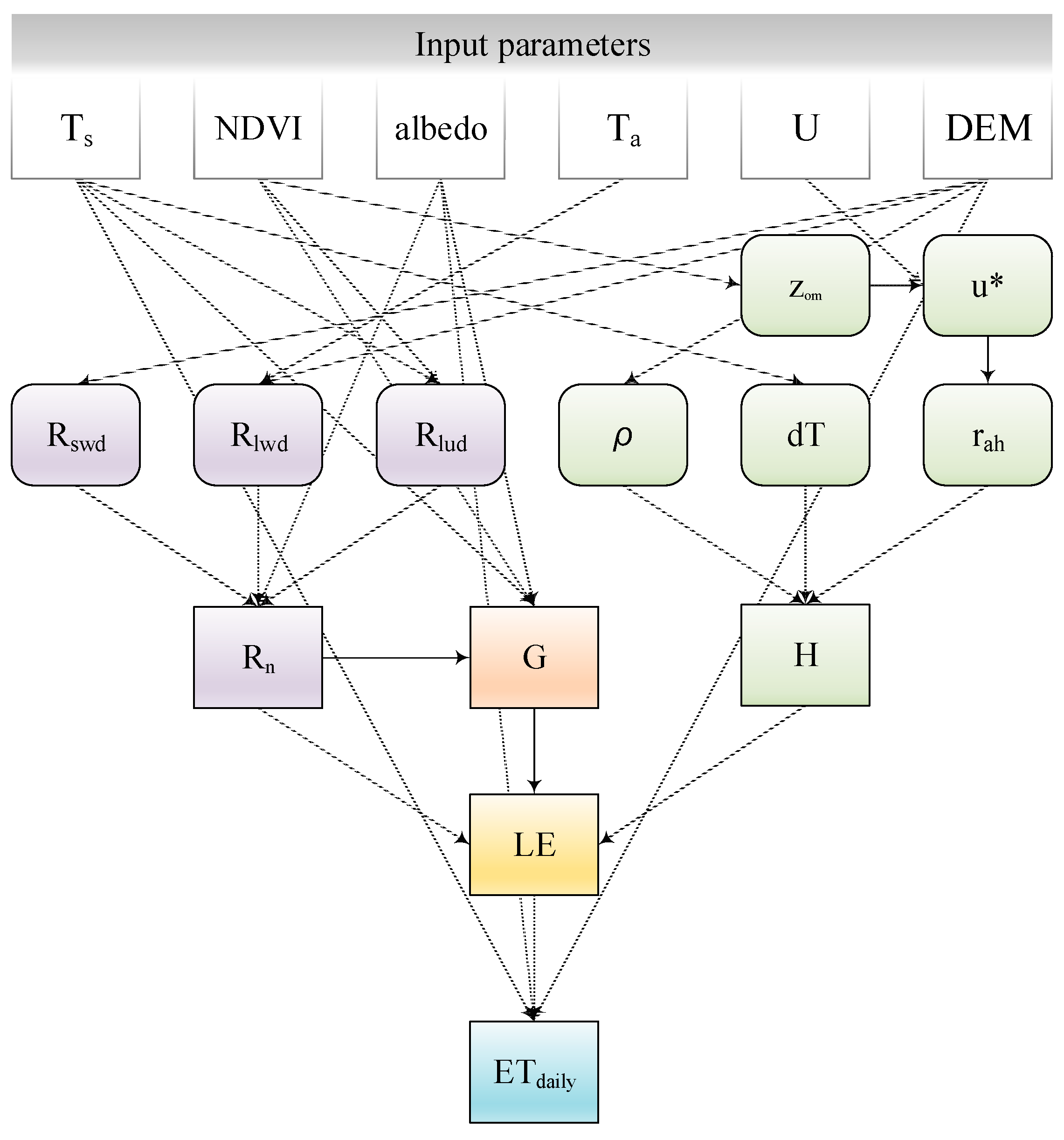
2.3.1. SEBAL Model
2.3.2. Aggregation Process and Statistical Indicators
2.3.3. Determination of Homogeneous and Heterogeneous Area
3. Results
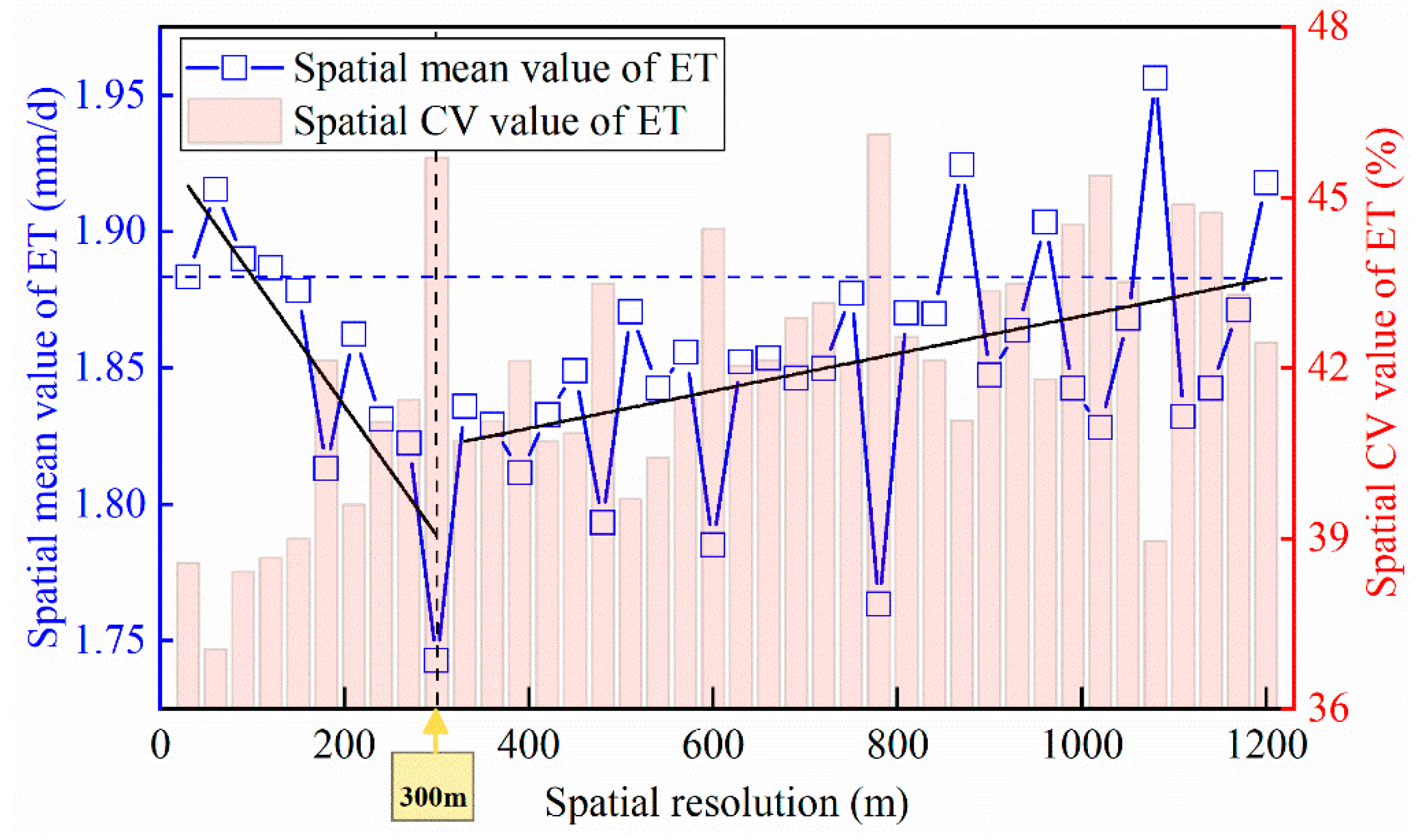
3.1. Assessment of the ET Estimates from the Different Satellite Datasets
3.1.1. Validation of the ET Simulations from the Different Satellite Sensors
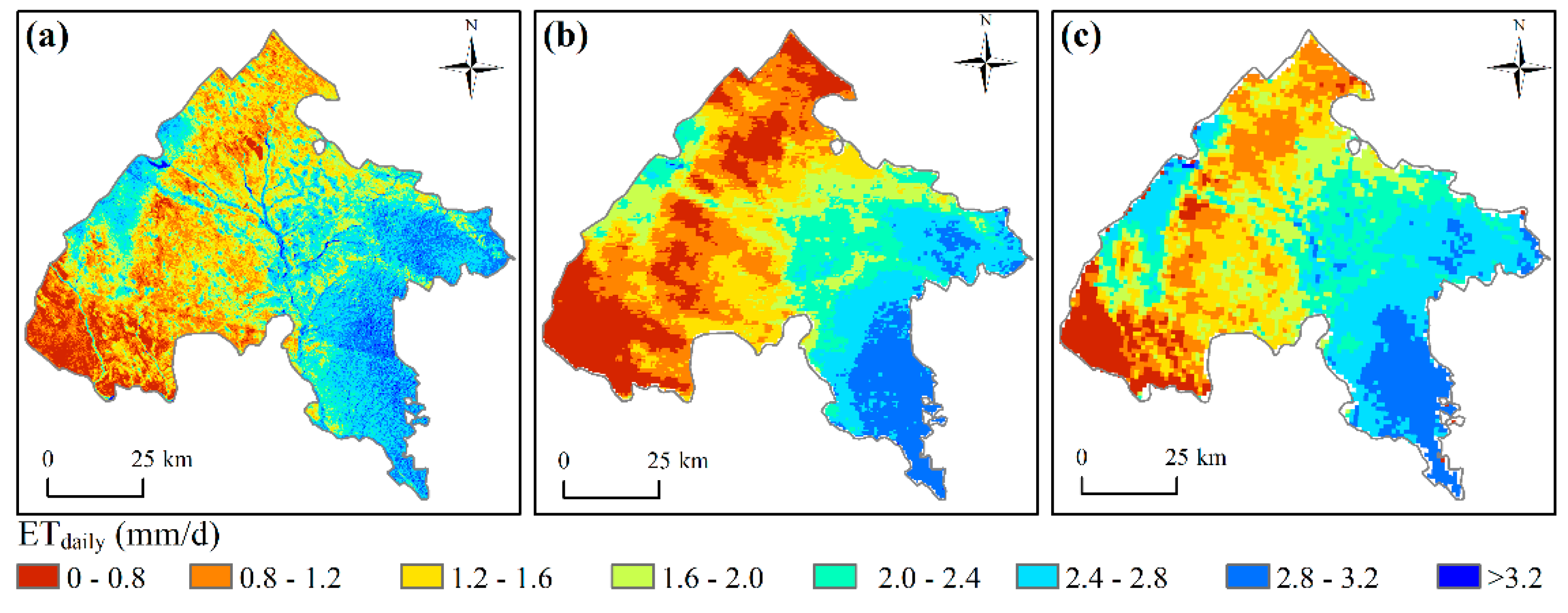
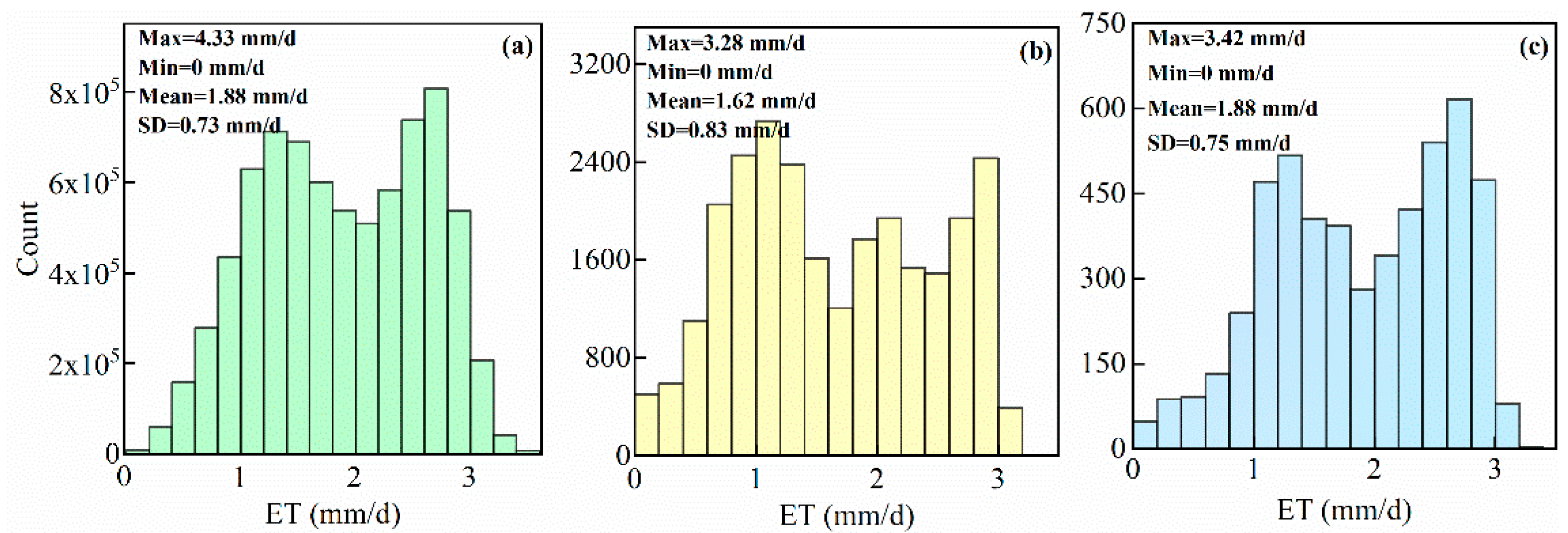
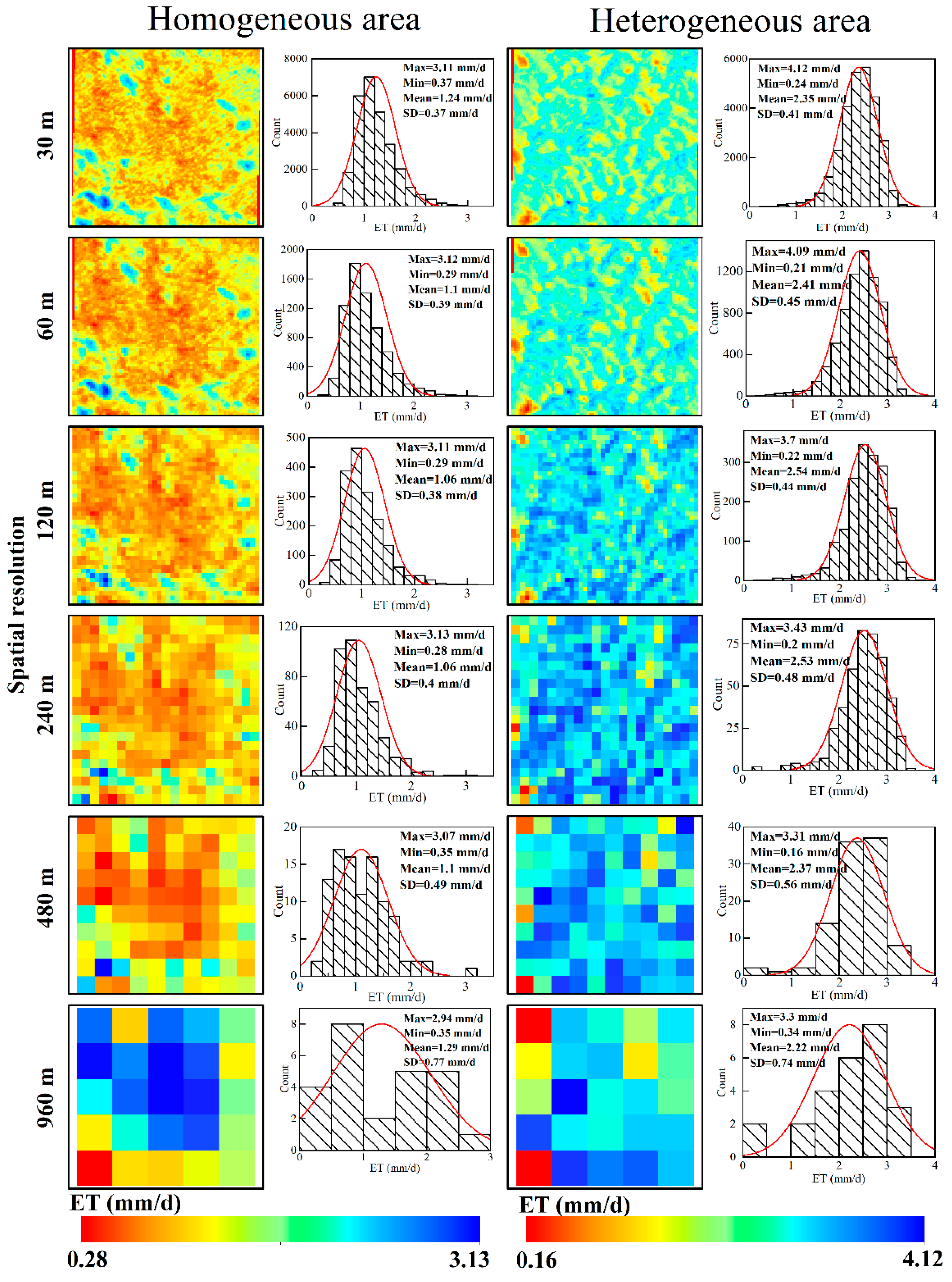
3.1.2. Spatial Patterns and Statistical Characteristics of the Simulated ET from the Different Datasets
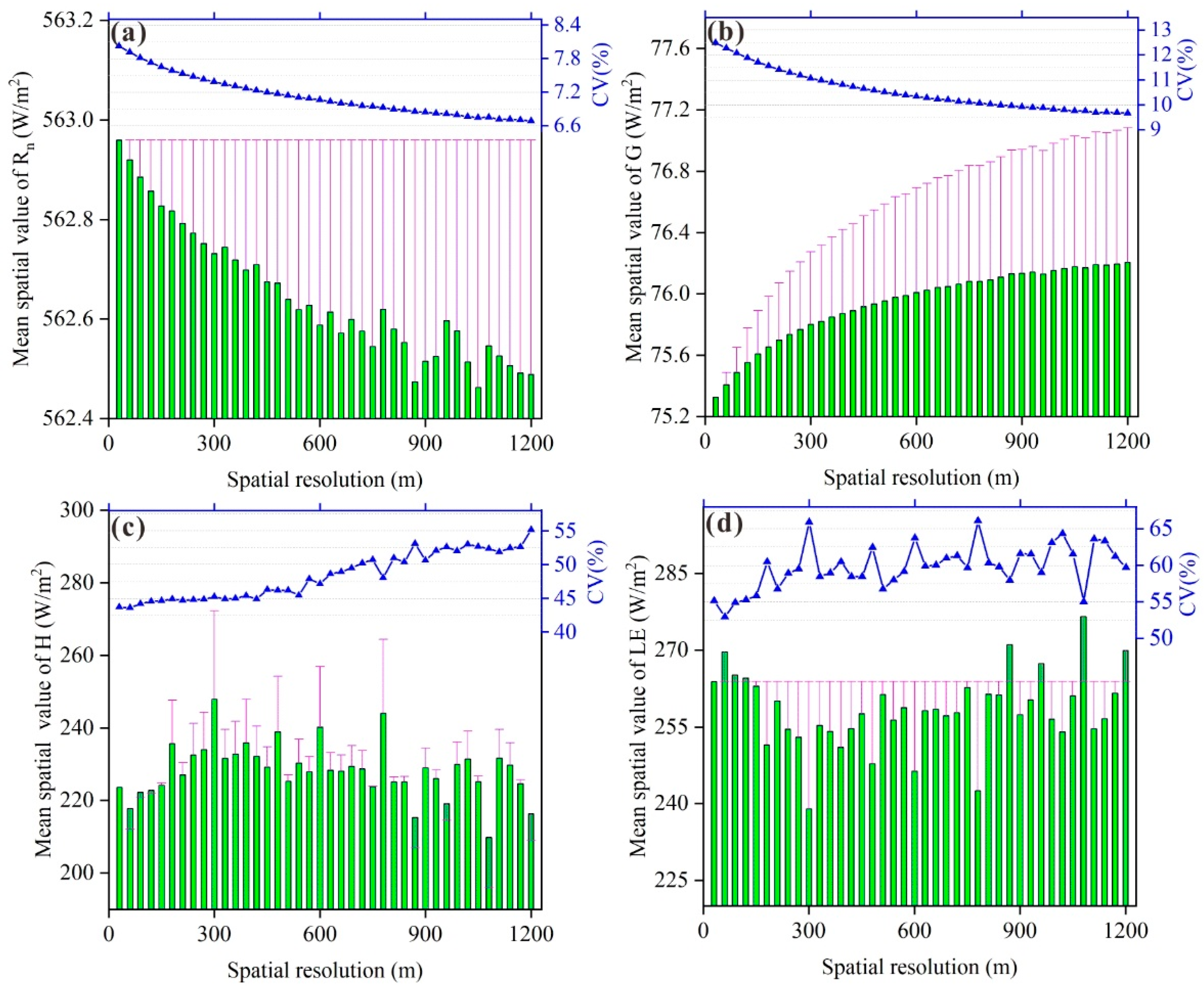
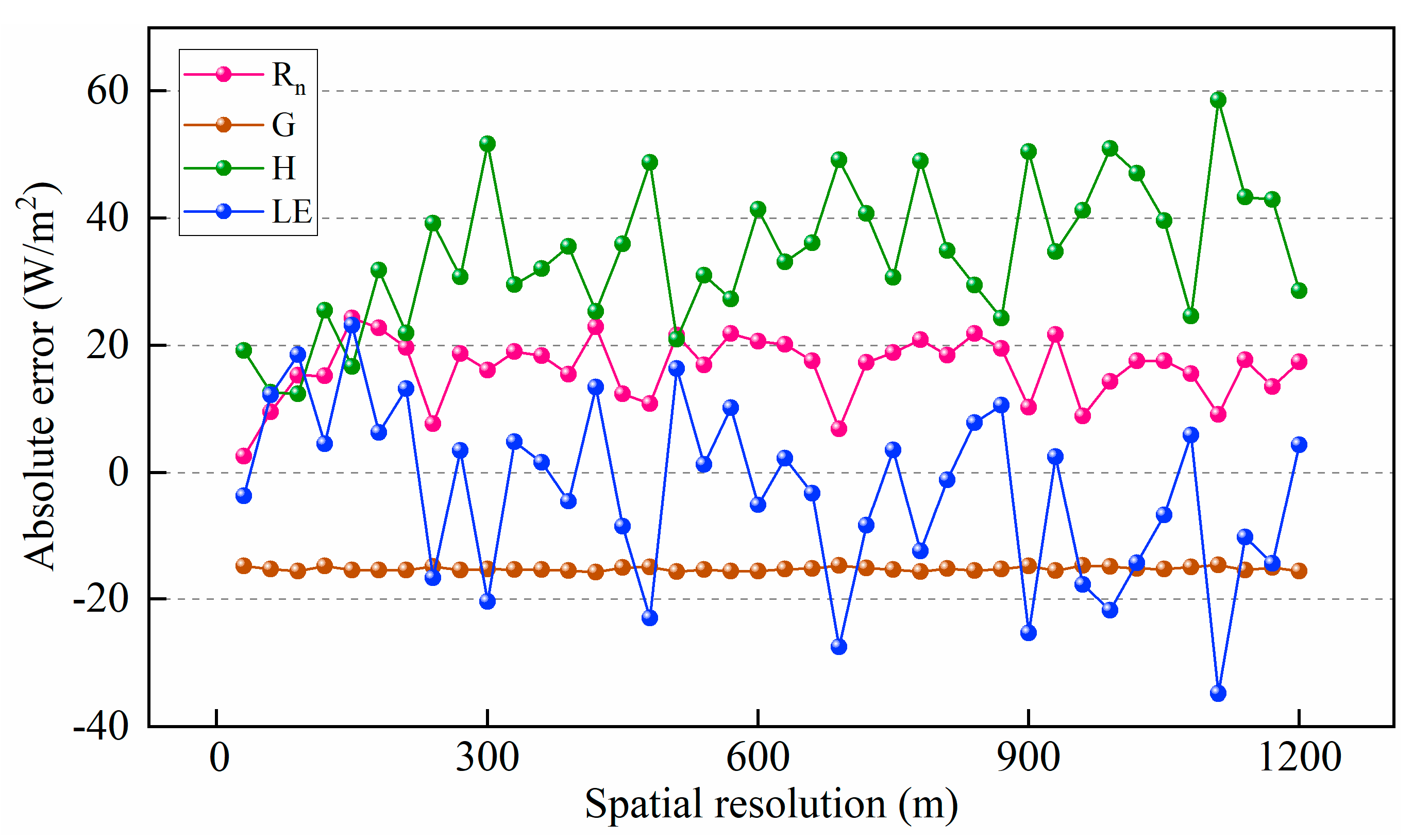
3.2. Effects of Aggregation on the Energy Balance Components and ET Estimation
3.3. The Effects of Land Use/Cover Pattern on the ET Estimation during the Aggregation Process
4. Discussion
4.1. Estimation of the ET from the Three Different Satellite Sensors
4.2. Aggregation Effects on the Energy Balance Flux Simulation
4.3. Influence of the Land Use/Cover Pattern on the ET Estimates during the Aggregation Process
4.4. Limitations and Outlook
5. Conclusions
- The spatial distribution patterns of the ET estimates using Landsat TM, MODIS, and AVHRR datasets were similar, with MODIS having the largest uncertainties. The validation of the simulated ET must consider matching spatial scales of the satellite datasets.
- With scale aggregation, the spatial average values of the Rn decreased slightly, while the G increased, and the spatial variabilities of both Rn and G all decreased. The spatial mean values of the H and LE were relatively larger, but the relative error was less than 20%. This was due to the changes in the selection of the locations of the hot and cold pixels in the model mechanisms as well as the NDVI and surface albedo input parameters in the SEBAL model.
- Surface heterogeneity affected the spatial scale aggregation results, and differences in the land use/cover pattern led to the different aggregation results. However, the scale errors caused by the SEBAL model mechanisms were larger than that contributed by the land use/cover pattern during the scale aggregation.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wood, E.F.; Sivapalan, M.; Beven, K.; Band, L. Effects of spatial variability and scale with implications to hydrologic modeling. J. Hydrol. 1988, 102, 29–47. [Google Scholar] [CrossRef]
- Goodrich, D.C.; Lane, L.J.; Shillito, R.M.; Miller, S.N.; Syed, K.H.; Woolhiser, D.A. Linearity of basin response as a function of scale in a semiarid watershed. Water Resour. Res. 1997, 33, 2951–2965. [Google Scholar] [CrossRef]
- Brunsell, N.A.; Gillies, R.R. Scale issues in land–atmosphere interactions: Implications for remote sensing of the surface energy balance. Agric. Forest Meteorol. 2003, 117, 203–221. [Google Scholar] [CrossRef]
- Sridhar, V.; Elliott, R.L.; Chen, F. Scaling effects on modeled surface energy-balance components using the NOAH-OSU land surface model. J. Hydrol. 2003, 280, 105–123. [Google Scholar] [CrossRef]
- Brunsell, N.A.; Anderson, M.C. Characterizing the multi–scale spatial structure of remotely sensed evapotranspiration with information theory. Biogeosciences 2011, 8, 2269–2280. [Google Scholar] [CrossRef]
- Schulze, R. Transcending scales of space and time in impact studies of climate and climate change on agrohydrological responses. Agric. Ecosyst. Environ. 2000, 82, 185–212. [Google Scholar] [CrossRef]
- Wallender, W.W.; Grismer, M.E. Irrigation hydrology: Crossing scales. J. Irrig. Drain. Eng. 2002, 128, 203–211. [Google Scholar] [CrossRef]
- Simic, A.; Chen, J.M.; Liu, J.; Csillag, F. Spatial scaling of net primary productivity using subpixel information. Remote Sens. Environ. 2004, 93, 246–258. [Google Scholar] [CrossRef]
- Yu, Z.; Lu, Q.; Zhu, J.; Yang, C.; Ju, Q.; Yang, T.; Chen, X.; Sudicky, E.A. Spatial and temporal scale effect in simulating hydrologic processes in a watershed. J. Hydrol. Eng. 2014, 19, 99–107. [Google Scholar] [CrossRef]
- Oki, T.; Kanae, S. Global hydrological cycles and world water resources. Science 2006, 313, 1068–1072. [Google Scholar] [CrossRef] [PubMed]
- Batra, N.; Islam, S.; Venturini, V.; Bisht, G.; Jiang, L. Estimation and comparison of evapotranspiration from MODIS and AVHRR sensors for clear sky days over the southern great plains. Remote Sens. Environ. 2006, 103, 1–5. [Google Scholar] [CrossRef]
- Fisher, J.B.; Melton, F.; Middleton, E.; Hain, C.; Anderson, M.; Allen, R.; Kilic, A. The future of evapotranspiration: Global requirements for ecosystem functioning, carbon and climate feedbacks, agricultural management, and water resources. Water Resour. Res. 2017, 53, 2618–2626. [Google Scholar] [CrossRef]
- Xu, X.F.; Li, X.L.; Wang, X.J.; He, C.S.; Tian, W.; Tian, J.; Yang, L.X. Estimating daily evapotranspiration in the agricultural-pastoral ecotone in Northwest China: A comparative analysis of the Complementary Relationship, WRF-CLM4.0, and WRF-Noah methods. Sci. Total Environ. 2020, 138635. [Google Scholar] [CrossRef] [PubMed]
- Mauser, W.; Schädlich, S. Modelling the spatial distribution of evapotranspiration on different scales using remote sensing data. J. Hydrol. 1998, 212–213, 250–267. [Google Scholar] [CrossRef]
- Zhang, K.; Kimball, J.S.; Nemani, R.R.; Running, S.W. A continuous satellite-derived global record of land surface evapotranspiration from 1983 to 2006. Water Resour. Res. 2010, 46, W09522. [Google Scholar] [CrossRef]
- Yang, Y.T.; Long, D.; Shang, S.H. Remote estimation of terrestrial evapotranspiration without using meteorological data. Geophys. Res. Lett. 2013, 40, 3026–3030. [Google Scholar] [CrossRef]
- Hong, S.H.; Hendrickx, J.M.H.; Borchers, B. Up-scaling of SEBAL derived evapotranspiration maps from Landsat (30 m) to MODIS (250 m) scale. J. Hydrol. 2009, 370, 122–138. [Google Scholar] [CrossRef]
- Sharma, V.; Kilic, A.; Irmak, S. Impact of scale/resolution on evapotranspiration from Landsat and MODIS images. Water Resour. Res. 2016, 52, 1800–1819. [Google Scholar] [CrossRef]
- Peng, Z.Q.; Xin, X.; Jiao, J.J.; Zhou, T.; Liu, Q. Remote sensing algorithm for surface evapotranspiration considering landscape and statistical effects on mixed pixels. Hydrol. Earth Syst. Sci. 2016, 20, 4409–4438. [Google Scholar] [CrossRef]
- Gebremichael, M.; Wang, J.; Sammis, T.W. Dependence of remote sensing evapotranspiration algorithm on spatial resolution. Atmos. Res. 2010, 96, 489–495. [Google Scholar] [CrossRef]
- Tang, R.; Li, Z.; Chen, K.; Jia, Y.; Li, C.; Sun, X. Spatial-scale effect on the SEBAL model for evapotranspiration estimation using remote sensing data. Agric. For. Meteorol. 2013, 174–175, 28–42. [Google Scholar] [CrossRef]
- Wang, S.; Li, X.; Ge, Y.; Jin, R.; Ma, M.; Liu, Q.; Wen, J.; Liu, S. Validation of regional-scale remote sensing products in China: From Site to Network. Remote Sens. 2016, 8, 980. [Google Scholar] [CrossRef]
- Liu, S.; Xu, Z.; Song, L.; Zhao, Q.; Ge, Y.; Xu, T.; Ma, Y.; Zhu, Z.; Jia, Z.; Zhang, F. Upscaling evapotranspiration measurements from multi-site to the satellite pixel scale over heterogeneous land surfaces. Agric. For. Meteorol. 2016, 230–231, 97–113. [Google Scholar] [CrossRef]
- Liang, S. Quantitative Remote Sensing of Land Surfaces; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2004. [Google Scholar]
- Hong, S.H.; Hendrickx, J.M.H.; Borchers, B. Effect of scaling transfer between evapotranspiration maps derived from Landsat 7 and MODIS images. In targets and backgrounds XI: Characterization and representation. Int. Soc. Opt. Photonic 2005, 5811, 147–158. [Google Scholar]
- Sun, Z.; Gebremichael, M.; Ardo, J.; Nickless, A.; Caquet, B.; Merboldh, L.; Kutschi, W. Estimation of daily evapotranspiration over Africa using MODIS/Terra and SEVIRI/MSG data. Atmos. Res. 2012, 112, 35–44. [Google Scholar] [CrossRef]
- Ramírez-Cuesta, J.M.; Allen, R.G.; Zarcotejada, P.J.; Kilic, A.; Santos, C.; Lorite, I.J. Impact of the spatial resolution on the energy balance components on an open-canopy olive orchard. Int. J. Appl. Earth Obs. Geoinf. 2019, 88–102. [Google Scholar] [CrossRef]
- Gao, X.; Sun, M.; Luan, Q.; Zhao, X.; Wang, J.; He, G.; Zhao, Y. The spatial and temporal evolution of the actual evapotranspiration based on the remote sensing method in the Loess Plateau. Sci. Total Environ. 2020, 708, 135111. [Google Scholar] [CrossRef]
- Weng, Q. Remote sensing of impervious surfaces in the urban area: Requirements, methods: And trends. Remote Sens. Environ. 2012, 117, 34–49. [Google Scholar] [CrossRef]
- Ershadi, A.; Mccabe, M.F.; Evans, J.P.; Walker, J.P. Effects of spatial aggregation on the multi-scale estimation of evapotranspiration. Remote Sens. Environ. 2013, 131, 51–62. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Xiong, Y.J.; Qiu, G.Y.; Zhang, Q. Is scale really a challenge in evapotranspiration estimation? A multi-scale study in the Heihe oasis using thermal remote sensing and the three-temperature model. Agric. Forest Meteorol. 2016, 230–231, 128–141. [Google Scholar] [CrossRef]
- Henderson-Sellers, A.; Wilson, M.F.; Thomas, G. The effect of spatial resolution on archives of land cover type. Clim. Change. 1985, 7, 391–402. [Google Scholar] [CrossRef]
- Moran, M.S.; Humes, K.S.; Pinter, P.J. The scaling characteristics of remotely-sensed variables for sparsely-vegetated heterogeneous landscapes. J. Hydrol. 1997, 190, 337–362. [Google Scholar] [CrossRef]
- Su, Z.; Pelgrum, H.; Menenti, M. Aggregation effects of surface heterogeneity in land surface processes. Hydrol. Earth Syst. Sci. 1999, 3, 549–563. [Google Scholar] [CrossRef]
- Liang, S. Numerical experiments on the spatial scaling of land surface albedo and leaf area index. Remote Sens. Rev. 2000, 19, 225–242. [Google Scholar] [CrossRef]
- Long, D.; Singh, V.P.; Li, Z.L. How sensitive is SEBAL to changes in input variables, domain size and satellite sensor? J. Geophys. Res. Atmos. 2011, 116, D21107. [Google Scholar] [CrossRef]
- McCabe, M.F.; Wood, E.F. Scale influences on the remote estimation of evapotranspiration using multiple satellite sensors. Remote Sens. Environ. 2006, 105, 271–285. [Google Scholar] [CrossRef]
- Semmens, K.A.; Anderson, M.C.; Kustas, W.P.; Gao, F.; Alfieri, J.G.; Mckee, L.; Prueger, J.H.; Hain, C.R.; Cammalleri, C.; Yang, Y.; et al. Monitoring daily evapotranspiration over two California vineyards using Landsat 8 in a multi-sensor data fusion approach. Remote Sens. Environ. 2016, 185, 155–170. [Google Scholar] [CrossRef]
- Vinukollu, R.K.; Wood, E.F.; Ferguson, C.R.; Fisher, J.B. Global estimates of evapotranspiration for climate studies using multi-sensor remote sensing data: Evaluation of three process-based approaches. Remote Sens. Environ. 2011, 115, 801–823. [Google Scholar] [CrossRef]
- Elhaddad, A.; Garcia, L.A.; Chavez, J.L. Using a surface energy balance model to calculate spatially distributed actual evapotranspiration. J. Irrig. Drain. Eng. 2011, 137, 17–26. [Google Scholar] [CrossRef]
- Su, Z. The Surface Energy Balance System (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–100. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.; Menenti, M.; Feddes, R.A.; Holtslag, A.A. A remote sensing surface energy balance algorithm for land (SEBAL); 1 formulation. J. Hydrol. 1998, 212, 198–212. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-based energy balance for mapping evapotranspiration with internalized calibration (MERTIC)-model. J. Irrig. Drain. Eng. 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Norman, J.M.; Kustas, W.P.; Humes, K.S. Source approach for estimating soil and vegetation energy fluxes in observations of directional radiometric surface temperature. Agric. For. Meteorol. 1995, 77, 263–293. [Google Scholar] [CrossRef]
- Kustas, W.P.; Li, F.; Jackson, T.J.; Prueger, J.H.; Macpherson, J.I.; Wolde, M. Effects of remote sensing pixel resolution on modeled energy flux variability of croplands in Iowa. Remote Sens. Environ. 2004, 92, 535–547. [Google Scholar] [CrossRef]
- Roerink, G.; Su, Z.; Menenti, M. S-SEBI: A simple remote sensing algorithm to estimate the surface energy balance. Phys. Chem. Earth B Hydrol. Ocean. Atmos. 2000, 25, 147–157. [Google Scholar] [CrossRef]
- Gaur, N.; Mohanty, B.P.; Kefauver, S.C. Effect of observation scale on remote sensing based estimates of evapotranspiration in a semi-arid row cropped orchard environment. Prec. Agric. 2017, 18, 762–778. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.; Noordman, E.J.; Pelgrum, H.; Davids, G.; Thoreson, B.; Allen, R.G. SEBAL model with remotely sensed data to improve water-resources management under actual field conditions. J. Irrig. Drain. Eng. 2005, 131, 85–93. [Google Scholar] [CrossRef]
- Mo, X.G.; Liu, S.X.; Chen, D.; Lin, Z.H.; Guo, R.P.; Wang, K. Grid-size effects on estimation of evapotranspiration and gross primary production over a large Loess Plateau basin, China. Hydrol. Sci. J. 2009, 54, 160–173. [Google Scholar] [CrossRef]
- Xue, Y.Y.; Zhang, B.Q.; He, C.S.; Shao, R. Detecting vegetation variations and main drivers over the agropastoral ecotone of northern china through the ensemble empirical mode decomposition method. Remote Sens. 2019, 11, 1860. [Google Scholar] [CrossRef]
- Wang, X.J.; Zhang, B.Q.; Xu, X.F.; Tian, J.; He, C.S. Regional water-energy cycle response to land use/cover change in the agro-pastoral ecotone, Northwest China. J. Hydrol. 2020, 580, 124246. [Google Scholar] [CrossRef]
- Han, Z.B.; Zhang, B.Q.; Yang, L.X.; He, C.S. Assessment of the impact of future climate change on maize yield and water use efficiency in agro-pastoral ecotone of Northwestern China. J. Agro. Crop. Sci. 2021, 207, 1–15. [Google Scholar] [CrossRef]
- Gong, T.T.; Lei, H.M.; Yang, D.W.; Jiao, Y.; Yang, H.B. Monitoring the variations of evapotranspiration due to land use/cover change in a semiarid shrubland. Hydrol. Earth Syst. Sci. 2017, 21, 863–877. [Google Scholar] [CrossRef]
- Matthew, M.W.; Adler-Golden, S.M.; Berk, A.; Felde, G.; Anderson, G.P.; Gorodestzky, D.; Paswaters, S.; Shippert, M. Atmosphere correction of spectral imagery. Evaluation of the FLAASH algorithm with AVIRIS data. Presented at the SPIE Proceeding, Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery IX, Washington, DC, USA, 16–18 October 2002. [Google Scholar]
- Nemani, R.R.; Running, S.W. Estimation of regional surface resistance to evapotranspiration from NDVI and Thermal-IR AVHRR data. J. Appl. Meteorol. 1989, 28, 276–284. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M. SEBAL-based sensible and latent heat fluxes in the irrigated Gediz Basin, Turkey. J. Hydrol. 2000, 229, 87–100. [Google Scholar] [CrossRef]
- Allen, R.G.; Irmak, A.; Trezza, R.; Hendrickx, J.M.; Bastiaanssen, W.G.; Kjaersgaard, J. Satellite-based ET estimation in agriculture using SEBAL and METRIC. Hydrol. Proc. 2011, 25, 4011–4027. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Requirements; FAO Irrigation and Drainage Paper 56; Food and Agricultural Organization of the U.N.: Rome, Italy, 1998. [Google Scholar]
- Clothier, B.E.; Clawson, K.L.; Pinter, J.P.J.; Moran, M.S.; Reginato, R.J.; Jackson, R.D. Estimation of soil heat flux from net radiation during growth of alfalfa. Agric. For. Meteorol. 1986, 37, 319–329. [Google Scholar] [CrossRef]
- Brutsaert, W. Evaporation into the Atmosphere; D. Reidel Pub. Co.: Dordrecht, The Netherlands, 1982. [Google Scholar] [CrossRef]
- Su, Z.; Jacobs, C. ENVISAT: Actual Evaporation. BCRS Report 2001: USP-2 Report 2001; Publication of the National Remote Sensing Board (BCRS): Delft, The Netherlans, 2001. [Google Scholar]
- Shuttleworth, W.J.; Gurney, R.J.; Hsu, A.Y.; Ormsby, J.P. Fife: The variation in energy partition at surface flux sites. IAHS Publ. 1989, 186, 67–74. [Google Scholar]
- Crago, R.D. Conservation and variability of the evaporative fraction during the daytime. J. Hydrol. 1996, 180, 173–194. [Google Scholar] [CrossRef]
- Bian, L.; Butler, R. Comparing effects of aggregation methods on statistical and spatial properties of simulated spatial data. Photogram. Eng. Remote Sens. 1999, 65, 73–84. [Google Scholar] [CrossRef]
- Famiglietti, J.S.; Wood, E.F. Multiscale modelling of spatially variable water and energy balance processes. Water Resour. Res. 1994, 30, 3061–3078. [Google Scholar] [CrossRef]
- Willmott, C.J. Some comments on the evaluation of model performance. Bull. Am. Meteorol. Soc. 1982, 63, 1309–1369. [Google Scholar] [CrossRef]
- Yu, D.; Li, X.; Cao, Q.; Hao, R.; Qiao, J. Impacts of climate variability and landscape pattern change on evapotranspiration in a grassland landscape mosaic. Hydrol. Proc. 2020, 34, 1035–1051. [Google Scholar] [CrossRef]
- McGarigal, K.; Cushman, S.A.; Neel, M.C.; Ene, E. FRAGSTATS: Spatial Pattern Analysis Program for Categorical Maps. Computer Software Program Produced by the Authors at the University of Massachusetts, Amherst. 2002. Available online: http://www.umass.edu/landeco/research/fragstats/fragstats.html (accessed on 23 March 2020).
- Twine, T.E.; Kustas, W.P.; Norman, J.M.; Cook, D.R.; Houser, P.R.; Meyers, T.P.; Prueger, J.H.; Starks, P.J.; Wesely, M.L. Correcting eddy-covariance flux underestimates over a grassland. Agric. For. Meteorol. 2000, 103, 279–300. [Google Scholar] [CrossRef]
- Jia, Z.; Liu, S.; Xu, Z.; Chen, Y.; Zhu, M. Validation of remotely sensed evapotranspiration over the Hai River Basin, China. J. Geophys. Res. 2012, 117, D13113. [Google Scholar] [CrossRef]
- Tian, H.; Wen, J.; Wang, C.; Liu, R.; Lu, D. Effect of pixel scale on evapotranspiration estimation by remote sensing over oasis areas in north-western China. Environ. Earth Sci. 2012, 67, 2301–2313. [Google Scholar] [CrossRef]
- Wang, J.; Sammis, T.W.; Gutschick, V.P.; Gebremichael, M.; Miller, D.R. Sensitivity analysis of the surface energy balance algorithm for land (SEBAL). Trans. ASABE 2009, 52, 801–811. [Google Scholar] [CrossRef]




| Band Name | Wavelength (µm) | ||
|---|---|---|---|
| Landsat TM | MODIS | AVHRR | |
| Blue | 0.45–0.52 | 0.459–0.470 | 0.55–0.68 |
| Green | 0.52–0.60 | 0.545–0.560 | |
| Red | 0.63–0.69 | 0.630–0.690 | |
| Near infrared | 0.76–0.90 | 0.841–0.870 | 0.75–1.00 |
| Shortwave infrared 1 | 1.55–1.75 | 1.550–1.750 | 1.58–1.64 |
| Shortwave infrared 2 | 2.08–2.35 | 2.105–2.115 | 3.55–3.93 |
| Thermal infrared | 10.40–12.50 | 3.66–14.385 (16 thermal infrared bands) | 10.5–11.3 11.5–12.5 |
| Landscape Pattern Indices | Formula | Value Range | Meanings |
|---|---|---|---|
| NP | is the number of patches in the landscape of patch type (class) i. | NP ≥ 1 | NP = 1 when the landscape contains only one patch of the corresponding patch type. |
| SHAPE | is the perimeter (m) of patch ij. is the area (m2) of patch ij. | SHAPE ≥ 1 | SHAPE = 1 when the patch is a square and increases without limit as the patch shape becomes more irregular. |
| CONTAG | Pi is the proportion of the landscape occupied by patch type (class) i. gik is the number of adjacencies (joins) between pixels of patch types (classes) i and k based on the double-count method. m is the number of patch types (classes) present in the landscape, including the landscape border if present. | 0 < CONTAG ≤ 100 | CONTANG approaches 0 when the patch types are maximally disaggregated and interspersed. CONTAG = 100 when all patches are maximally aggregated. |
| LPI | is the area (m2) of patch ij. A is the total landscape area (m2) | 0 < LPI < 100 | LPI = 0 when the largest patch of the corresponding patch type is small. LPI = 100 when the entire landscape consists of a single patch. |
| SHDI | is the proportion of the landscape occupied by patch type (class) i. | SHDI ≥ 0 | Larger the value of SHDI, the greater the diversity. |
| PR | m is the number of patch types (classes) present in the landscape, excluding the landscape border if present. | PR ≥ 1 | PR is 1, this indicates the simplest landscape in terms of landscape composition. |
| Landscape Pattern Indices | Proportion of Land Cover Types (%) | NP | LPI (%) | SHAPE_MN | CONTAG | SHDI | PR |
|---|---|---|---|---|---|---|---|
| Homogeneous area | Farmland: 2.72 Grassland: 15.53 Barren land: 81.75 | 23 | 81.70 | 1.64 | 68.50 | 0.55 | 3 |
| Heterogeneous area | Farmland: 47.90 Wood land: 0.35 Grassland: 50.80 Built-up land: 0.51 Barren land: 0.44 | 43 | 28.17 | 2.25 | 65.24 | 0.76 | 5 |
| Types | Simulated ET Value (mm/d) | Absolute Error (mm/d) | Relative Error (%) | |
|---|---|---|---|---|
| Measured data | 1.40 | |||
| Simulated data | ETLandsat | 1.23 | −0.17 | 11.98 |
| ETMODIS | 0.94 | −0.46 | 32.90 | |
| ETAVHRR | 1.35 | −0.05 | 3.60 | |
| Homogeneous Area | Heterogeneous Area | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rn | AE | G | AE | H | AE | LE | AE | Rn | AE | G | AE | H | AE | LE | AE | |
| 30 m | 512.75 | - | 81.64 | - | 293.64 | - | 137.47 | - | 603.16 | - | 65.88 | - | 164.35 | - | 372.93 | - |
| 60 m | 512.61 | −0.14 | 81.7 | 0.06 | 317.5 | 23.86 | 113.41 | −24.06 | 603.14 | −0.02 | 65.98 | 0.10 | 153.07 | −11.28 | 384.09 | 11.16 |
| 120 m | 512.49 | −0.26 | 81.8 | 0.16 | 325.48 | 31.84 | 105.21 | −32.26 | 603.02 | −0.14 | 66.12 | 0.24 | 128.36 | −35.99 | 408.54 | 35.61 |
| 240 m | 512.44 | −0.31 | 81.89 | 0.25 | 327.42 | 33.78 | 103.13 | −34.34 | 602.93 | −0.23 | 66.26 | 0.38 | 129.78 | −34.57 | 406.89 | 33.96 |
| 480 m | 511.32 | −1.43 | 81.95 | 0.31 | 315.98 | 22.34 | 113.39 | −24.08 | 603.3 | −0.14 | 66.34 | 0.46 | 160.51 | −3.84 | 376.45 | 3.52 |
| 960 m | 511.26 | −1.49 | 82.00 | 0.36 | 283.22 | −10.42 | 146.04 | 8.57 | 603.37 | 0.21 | 66.39 | 0.51 | 189.37 | 25.02 | 347.61 | −25.32 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Xu, X.; Wang, X.; Xu, S.; Tian, W.; Tian, J.; He, C. Assessing the Effects of Spatial Scales on Regional Evapotranspiration Estimation by the SEBAL Model and Multiple Satellite Datasets: A Case Study in the Agro-Pastoral Ecotone, Northwestern China. Remote Sens. 2021, 13, 1524. https://doi.org/10.3390/rs13081524
Li X, Xu X, Wang X, Xu S, Tian W, Tian J, He C. Assessing the Effects of Spatial Scales on Regional Evapotranspiration Estimation by the SEBAL Model and Multiple Satellite Datasets: A Case Study in the Agro-Pastoral Ecotone, Northwestern China. Remote Sensing. 2021; 13(8):1524. https://doi.org/10.3390/rs13081524
Chicago/Turabian StyleLi, Xuliang, Xuefeng Xu, Xuejin Wang, Shaoyuan Xu, Wei Tian, Jie Tian, and Chansheng He. 2021. "Assessing the Effects of Spatial Scales on Regional Evapotranspiration Estimation by the SEBAL Model and Multiple Satellite Datasets: A Case Study in the Agro-Pastoral Ecotone, Northwestern China" Remote Sensing 13, no. 8: 1524. https://doi.org/10.3390/rs13081524
APA StyleLi, X., Xu, X., Wang, X., Xu, S., Tian, W., Tian, J., & He, C. (2021). Assessing the Effects of Spatial Scales on Regional Evapotranspiration Estimation by the SEBAL Model and Multiple Satellite Datasets: A Case Study in the Agro-Pastoral Ecotone, Northwestern China. Remote Sensing, 13(8), 1524. https://doi.org/10.3390/rs13081524







