R-DFS: A Coverage Path Planning Approach Based on Region Optimal Decomposition
Abstract
1. Introduction
- A method capable of completely decomposing a concave polygonal region into convex polygonal sub-regions.
- A DFS algorithm that merges sub-regions, thereby reducing the number of UAV turns.
- Characterizing the TSP problem by the centers of gravity of the convex polygonal sub-regions.
2. CPP of a Convex Polygon Region
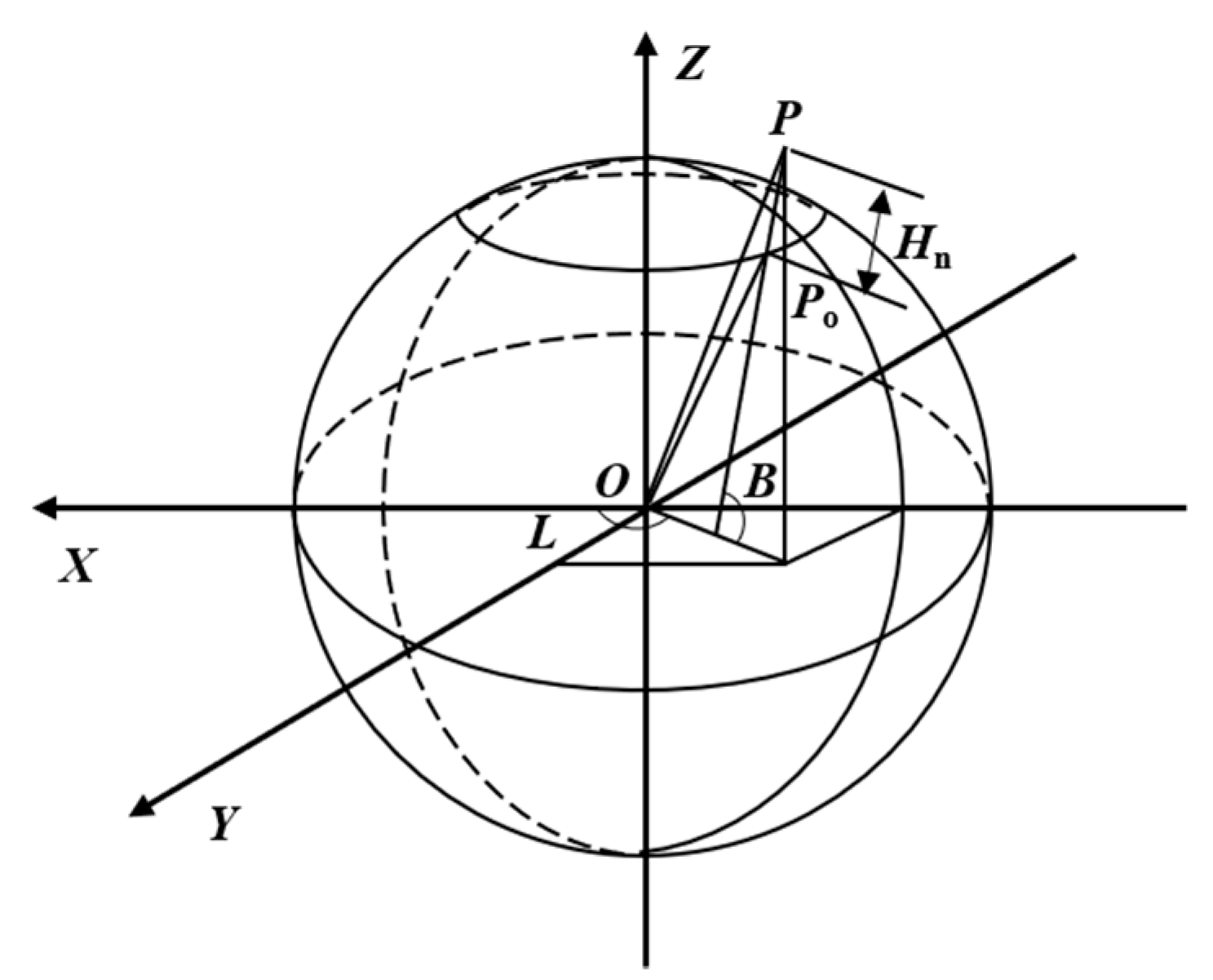
2.1. Environmental Modeling
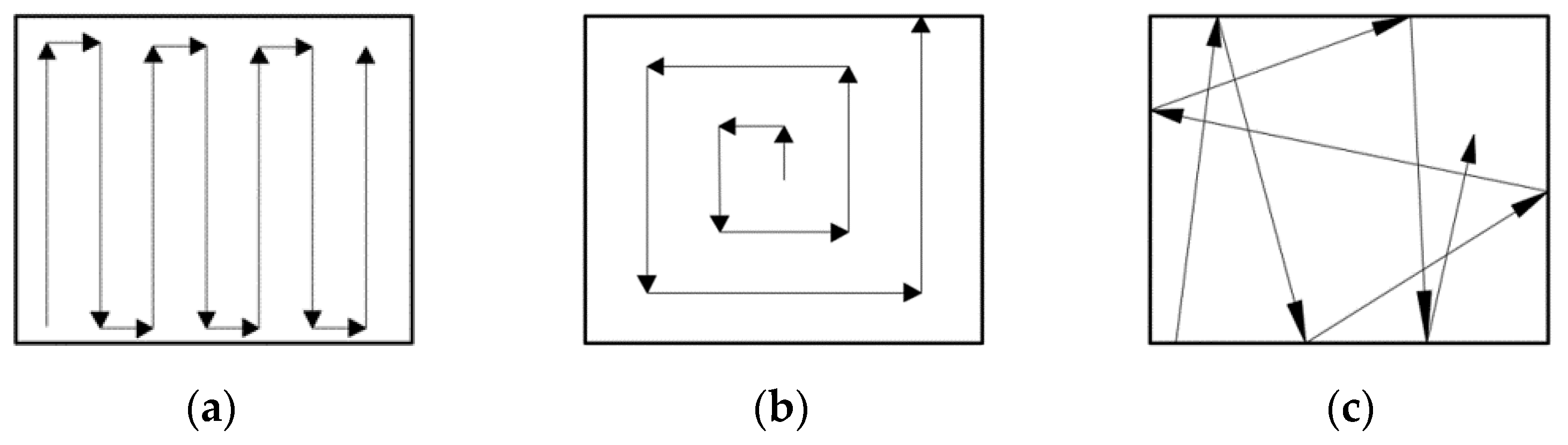
2.2. Selection of Coverage Pattern
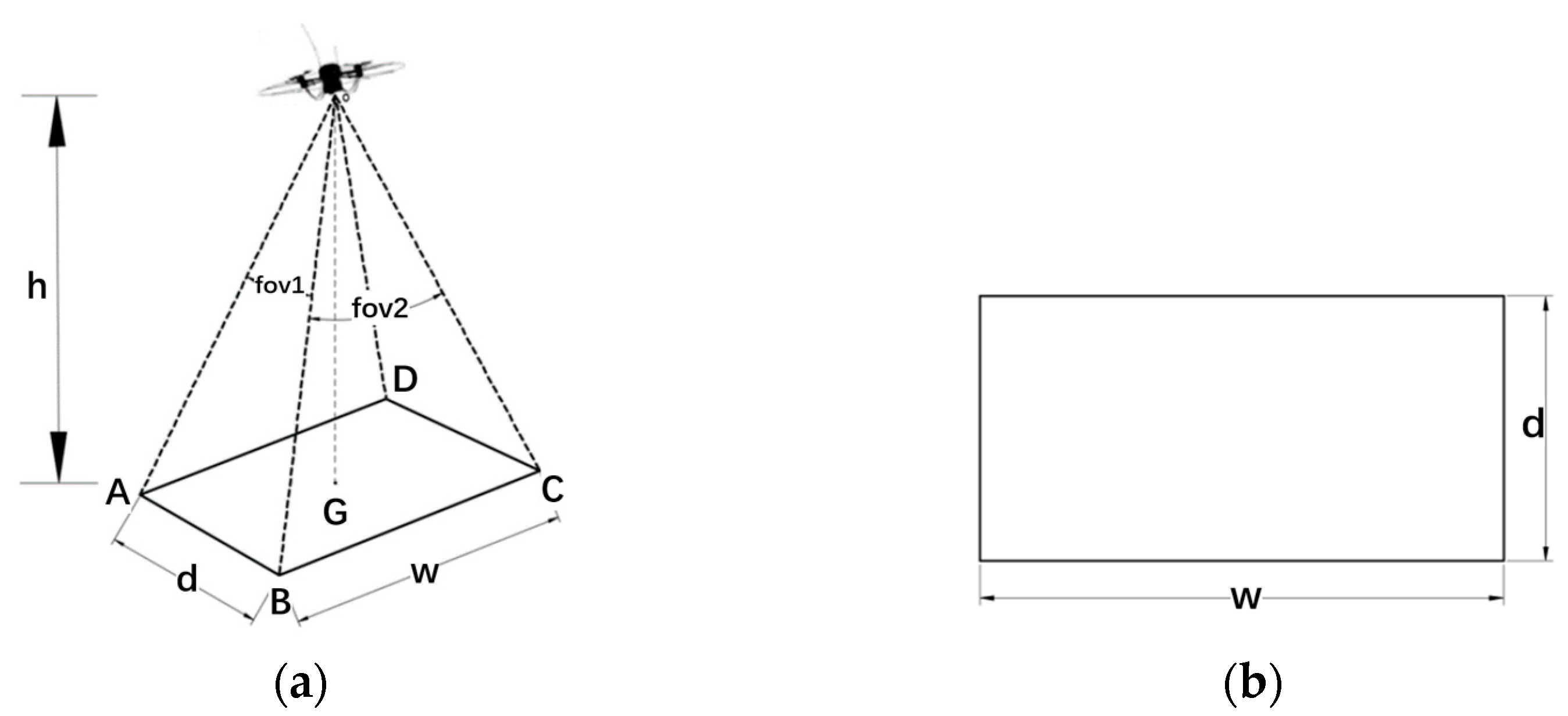
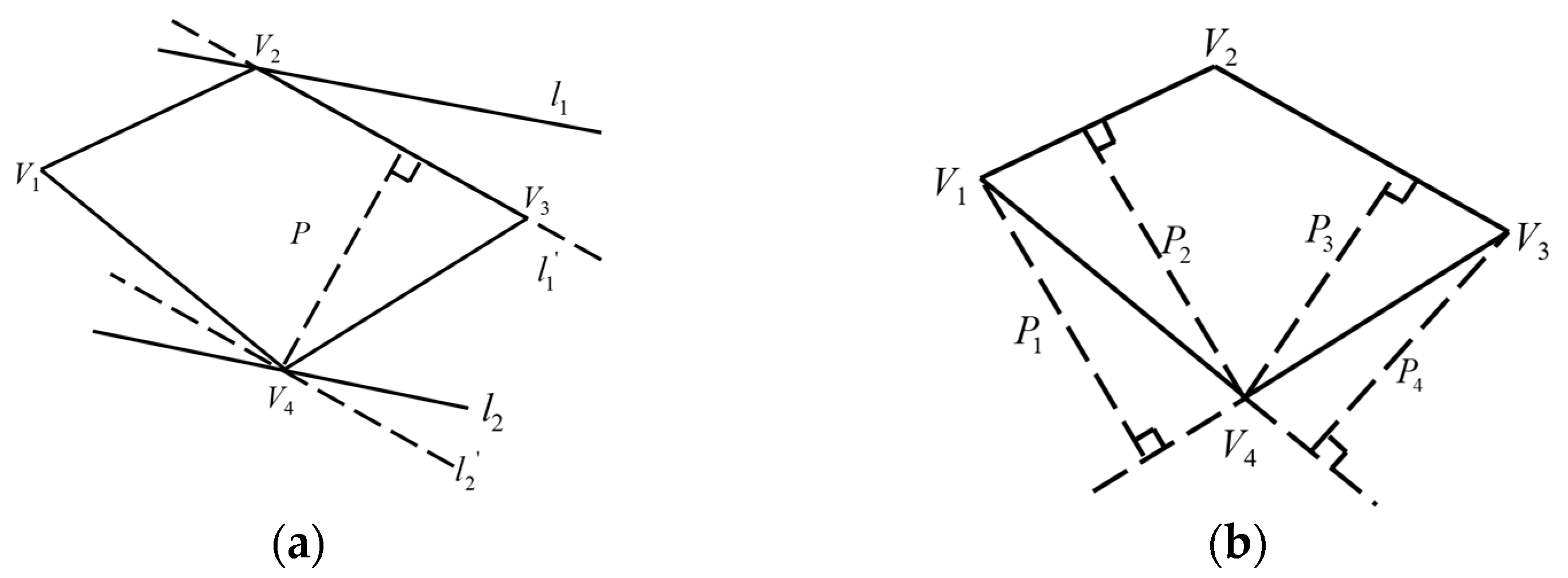
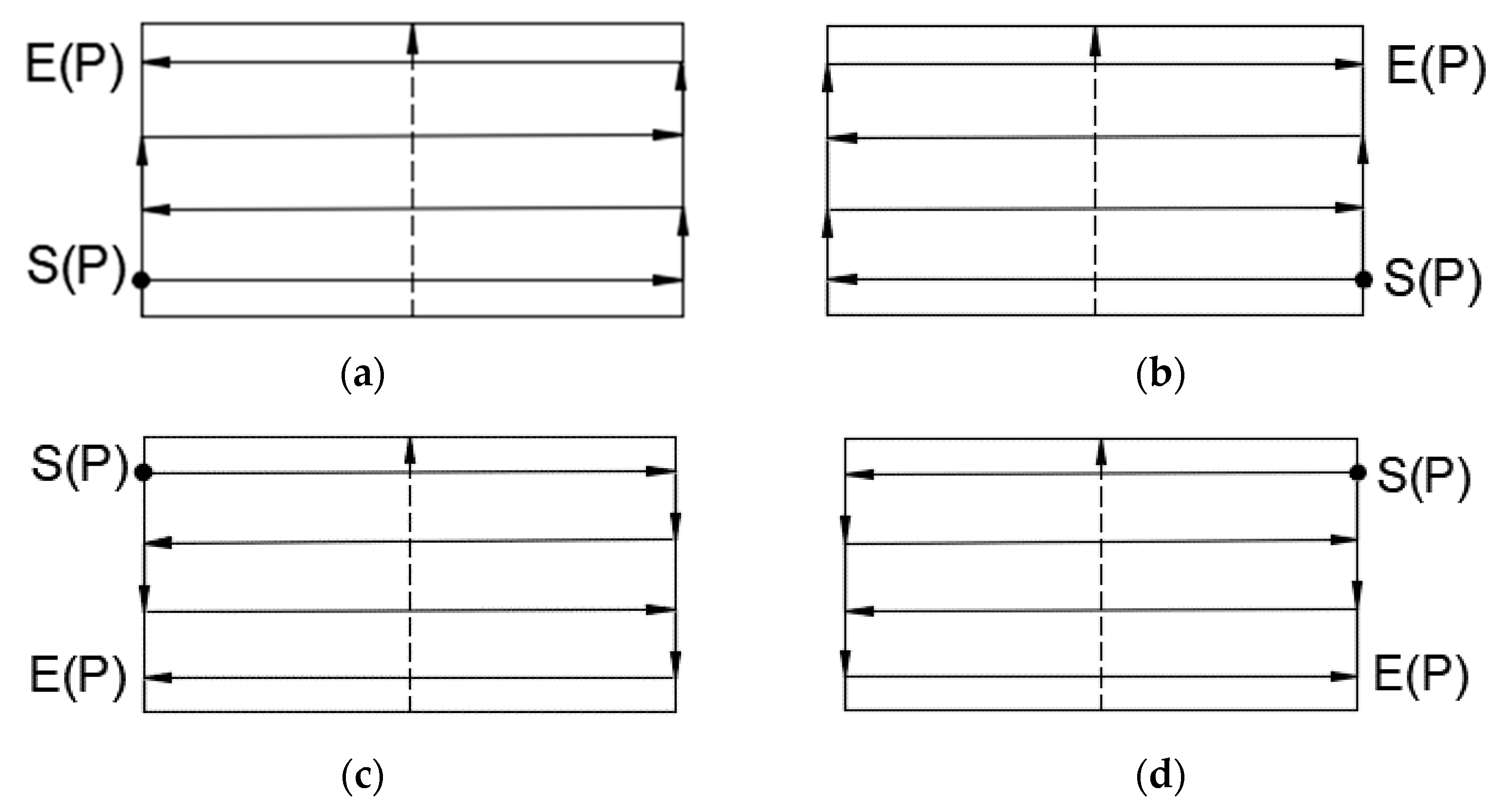
2.3. Determination of Projected Width
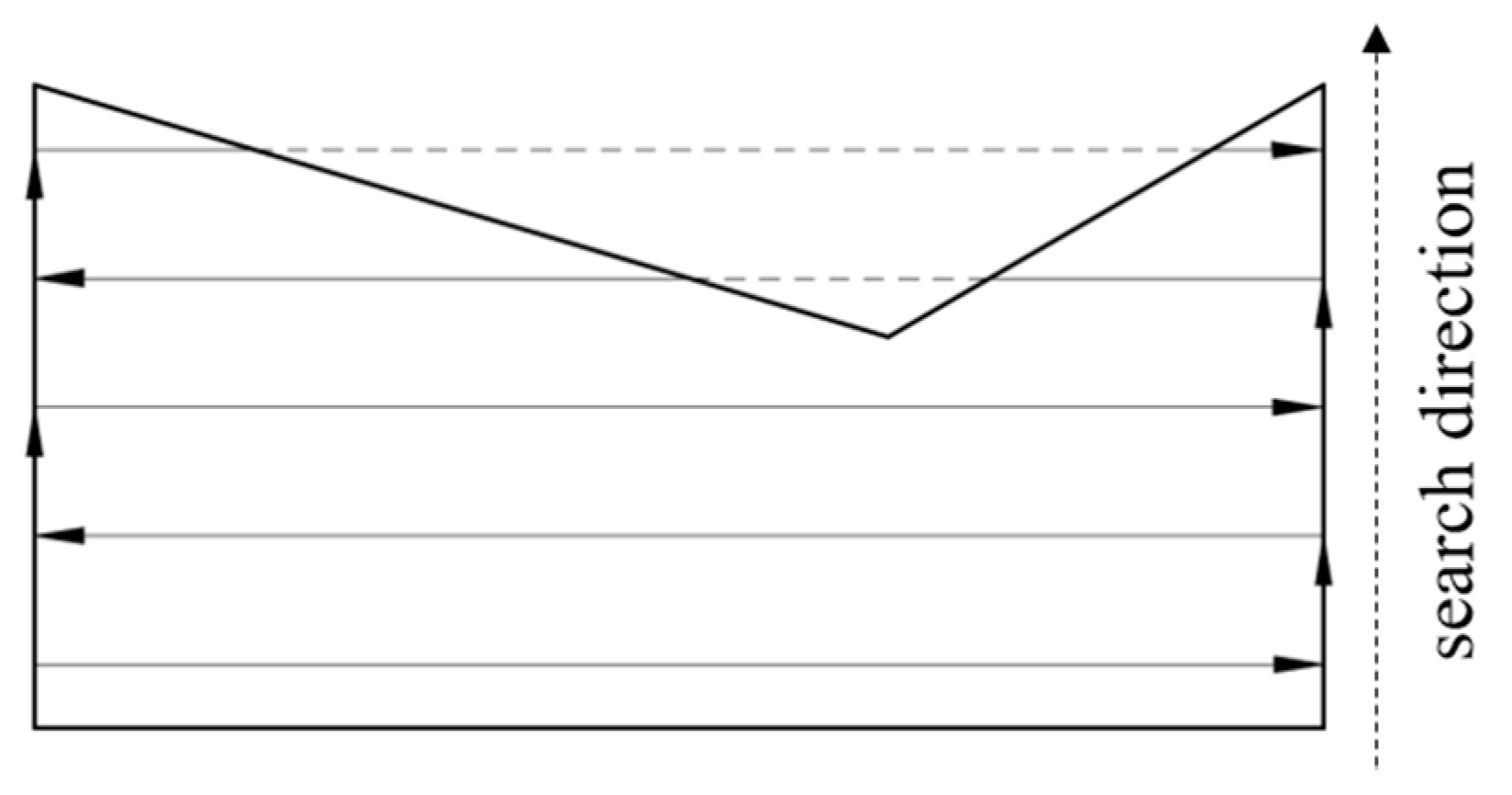
2.4. UAV Search Direction
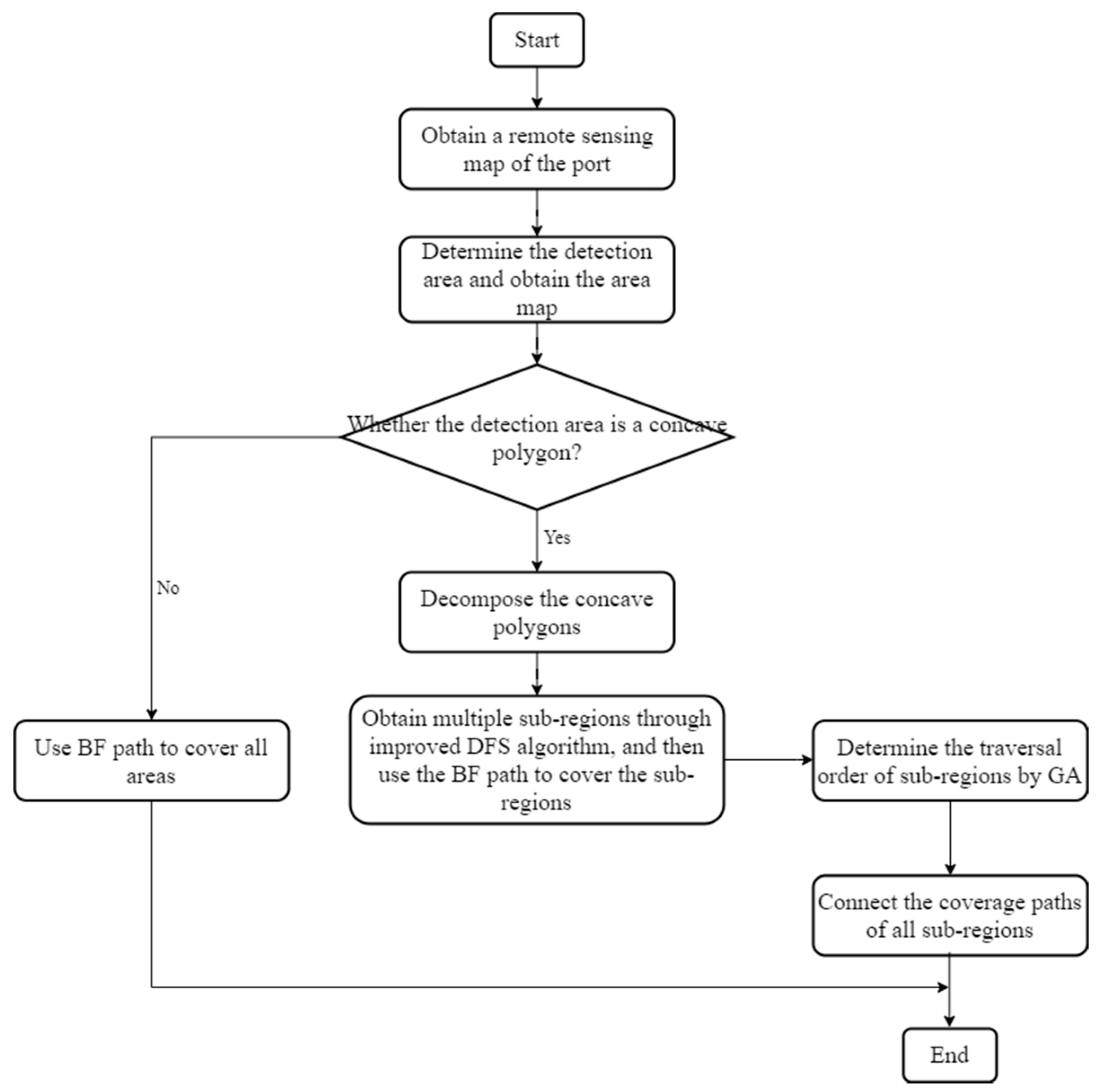
3. CPP of Concave Polygon Area
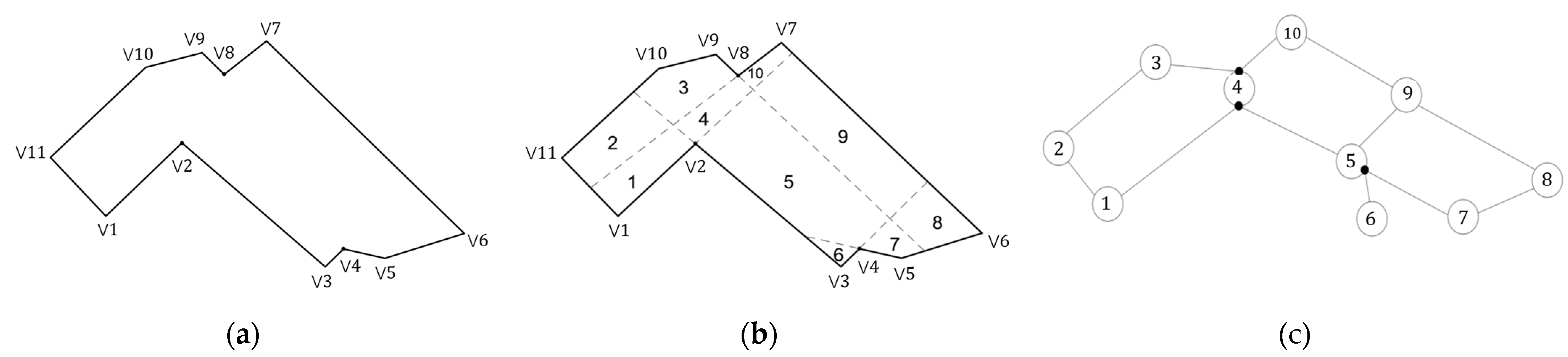
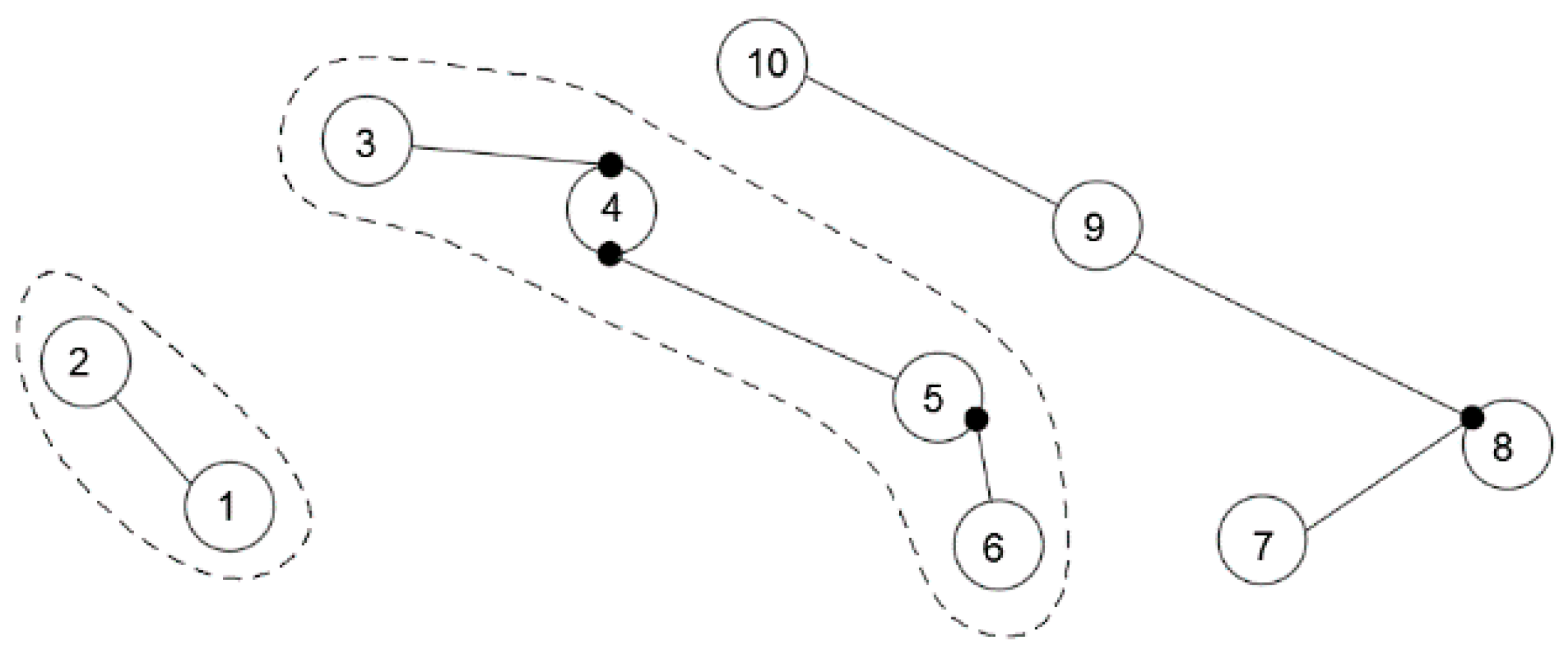
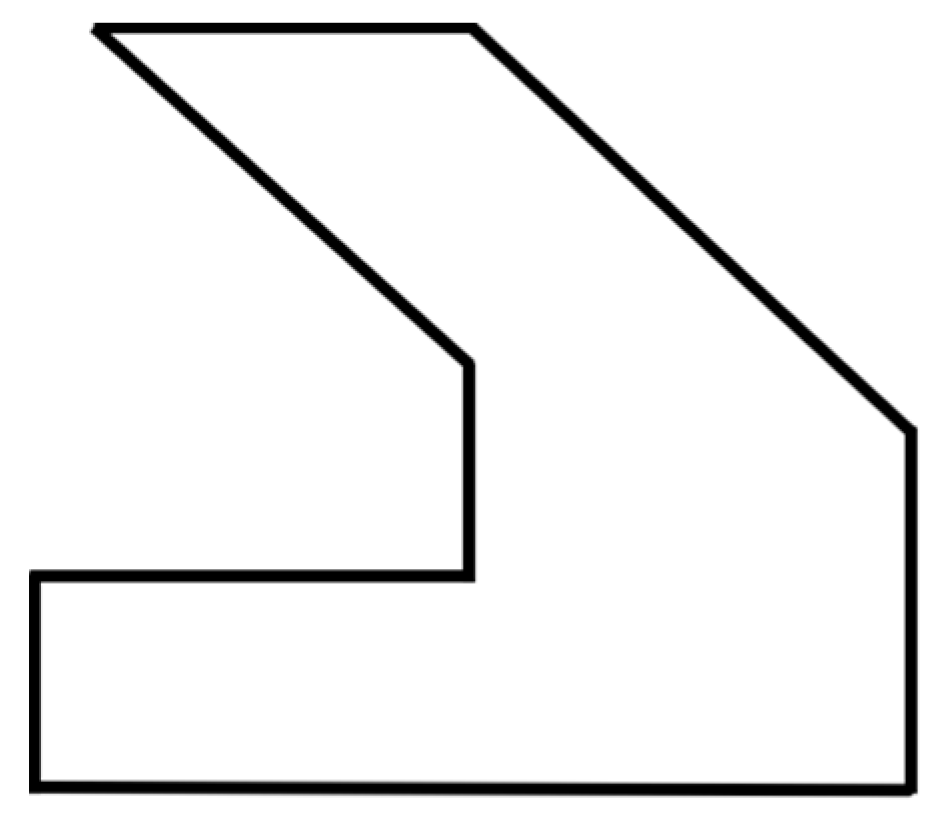
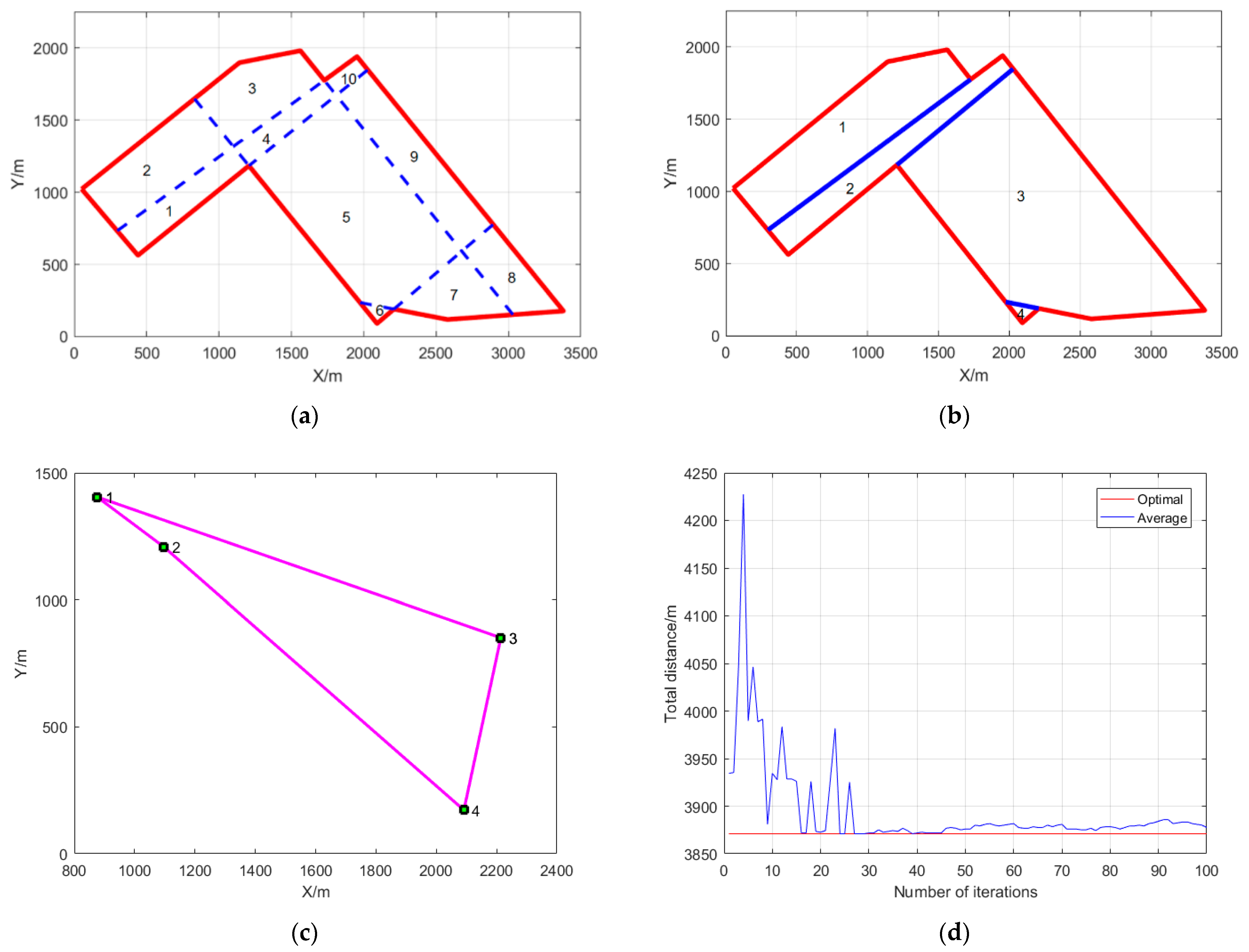
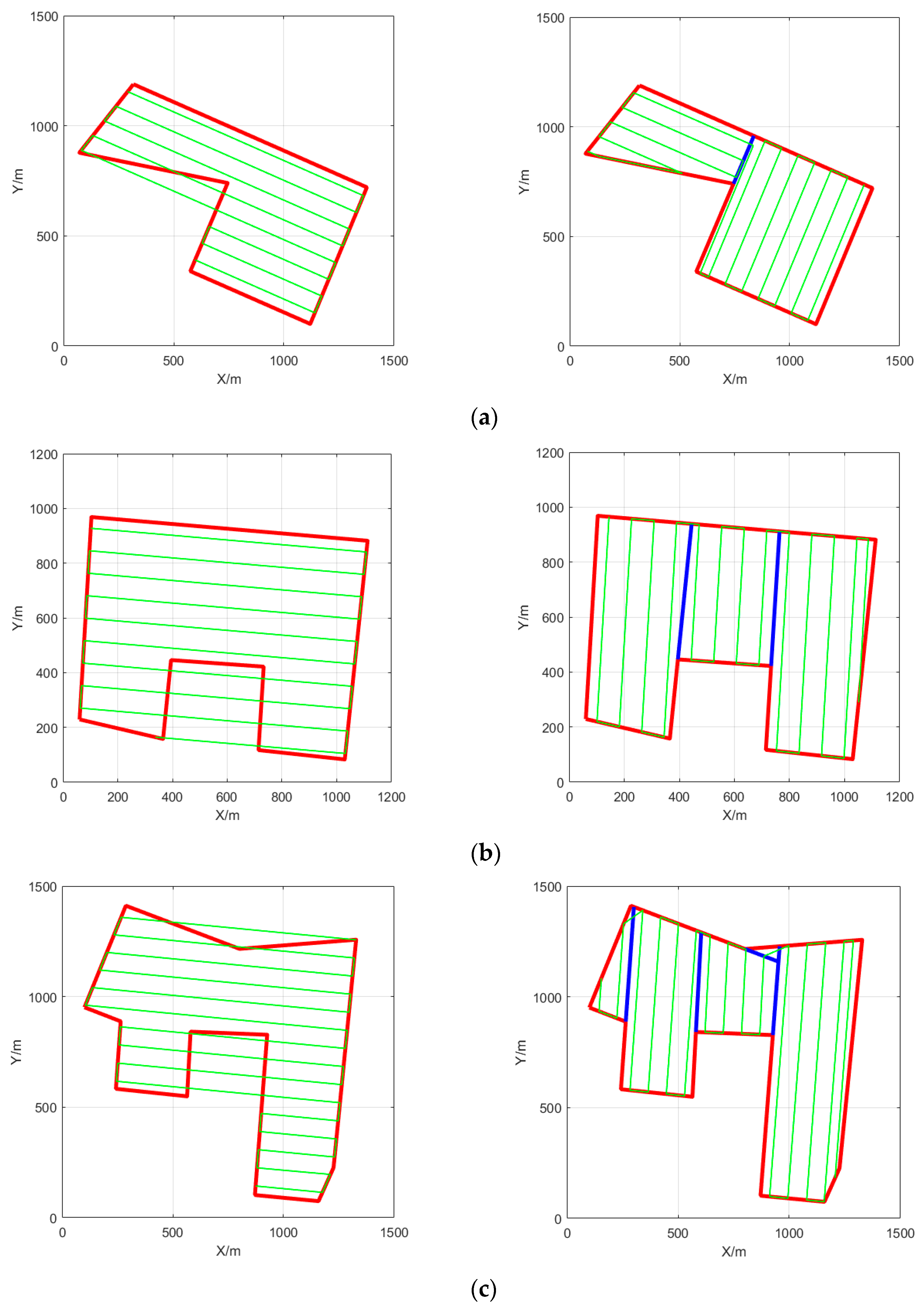
3.1. Decomposition of Concave Polygon Area
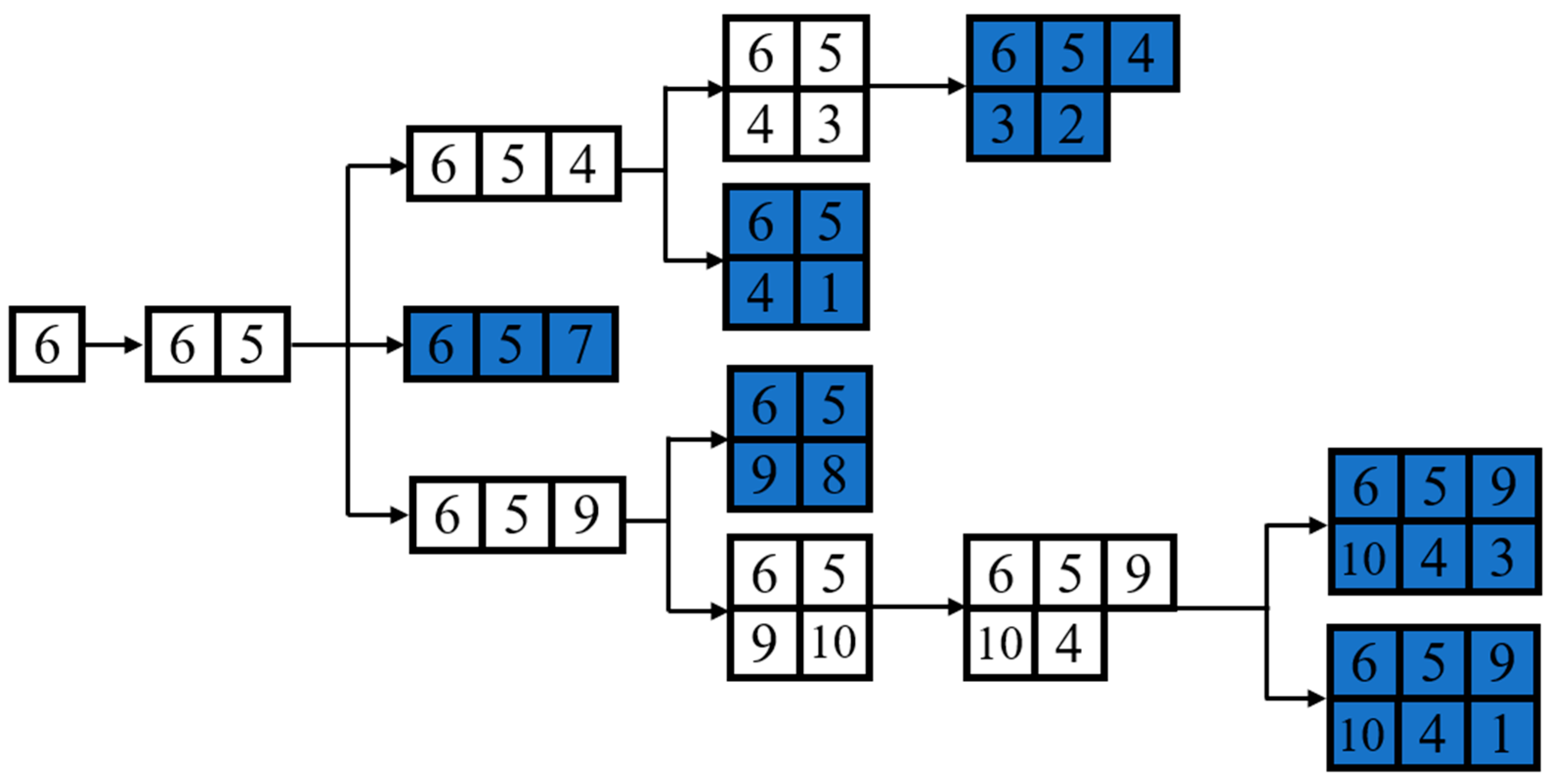
3.2. Improved DFS Algorithm
3.3. Algorithms Comparison
4. Traversal Order between Sub-Regions
4.1. Determination of the Traversal Order of Sub-Regions
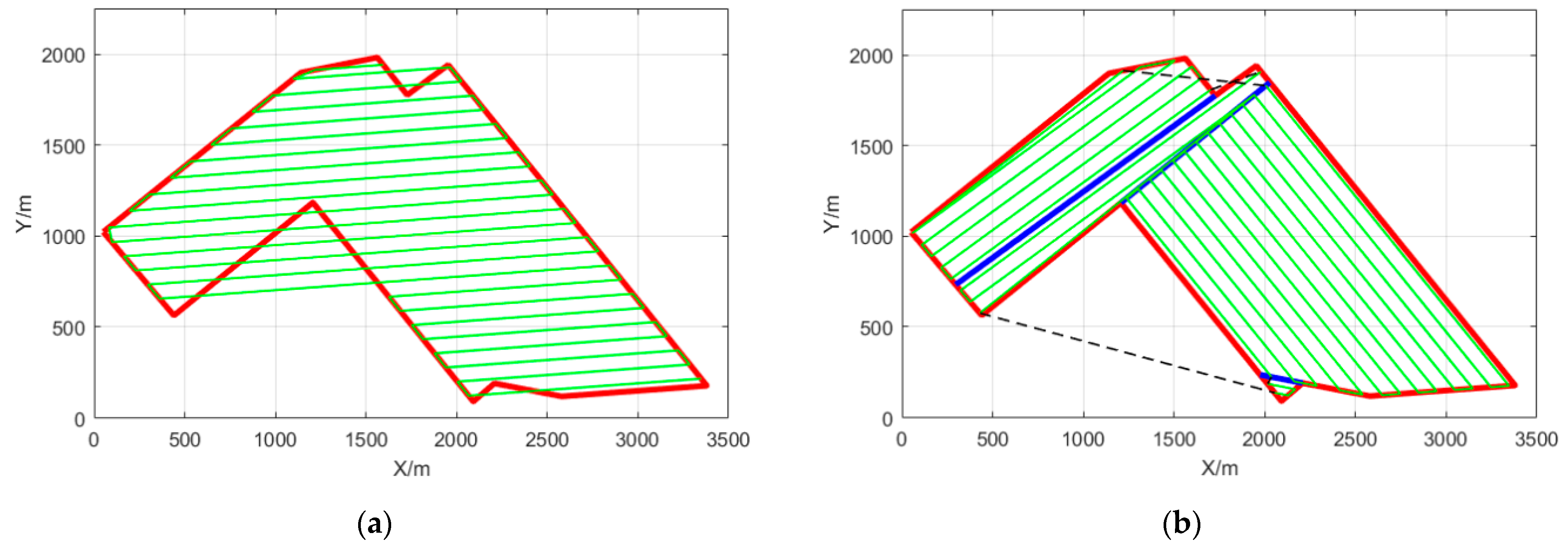
4.2. Coverage Strategy for Subregions
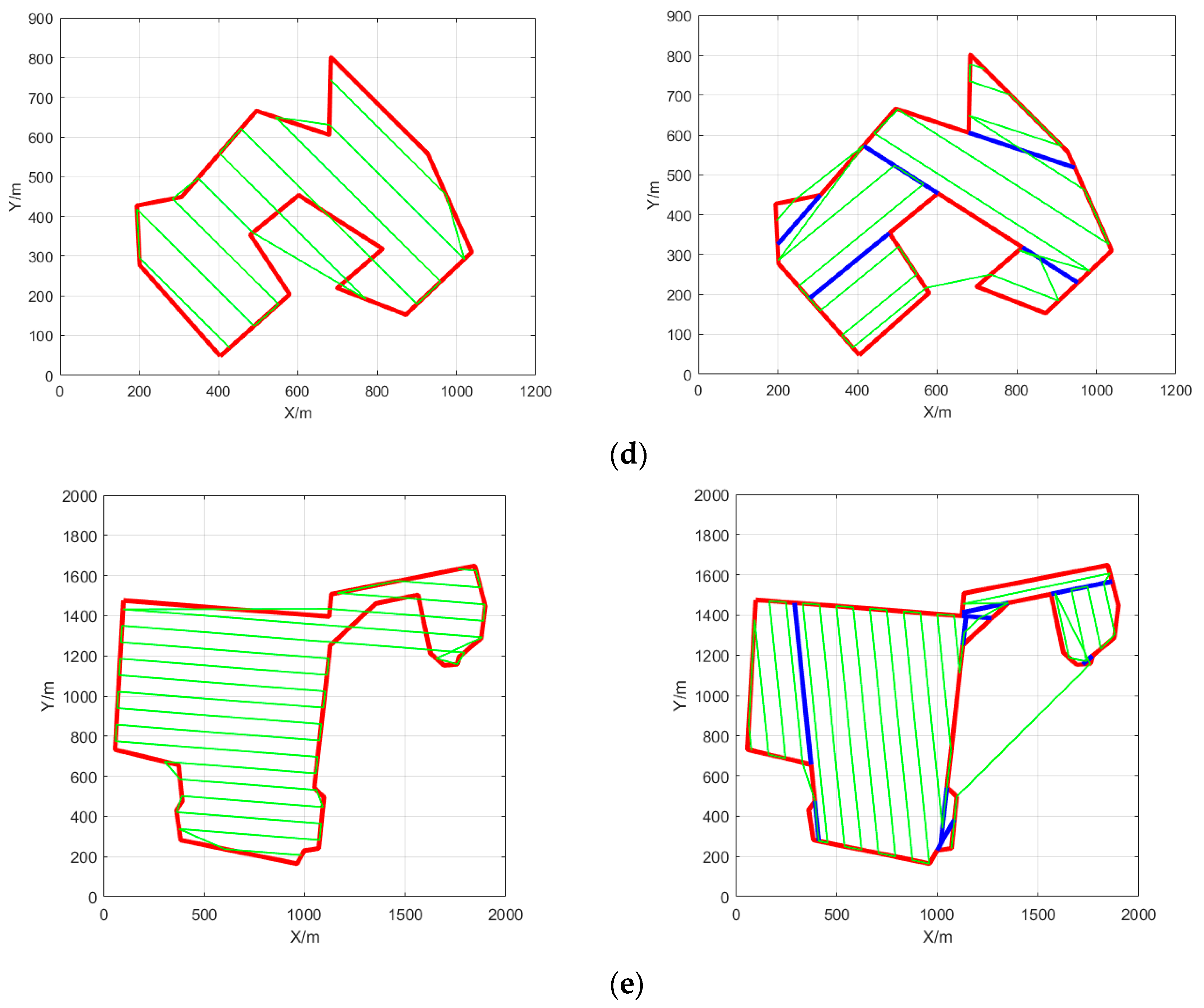
5. Simulation and Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Floreano, D.; Wood, R.J. Science, technology and the future of small autonomous drones. Nature 2015, 521, 460–466. [Google Scholar] [CrossRef] [PubMed]
- Comba, L.; Biglia, A.; Ricauda Aimonino, D.; Gay, P. Unsupervised detection of vineyards by 3D point-cloud UAV photogrammetry for precision agriculture. Comput. Electron. Agric. 2018, 155, 84–95. [Google Scholar] [CrossRef]
- Battulwar, R.; Winkelmaier, G.; Valencia, J.; Naghadehi, M.Z.; Peik, B.; Abbasi, B.; Parvin, B.; Sattarvand, J. A Practical Methodology for Generating High-Resolution 3D Models of Open-Pit Slopes Using UAVs: Flight Path Planning and Optimization. Remote Sens. 2020, 12, 2283. [Google Scholar] [CrossRef]
- Erdelj, M.; Saif, O.; Natalizio, E.; Fantoni, I. UAVs that fly forever: Uninterrupted structural inspection through automatic UAV replacement. Ad. Hoc. Netw. 2019, 94, 101612. [Google Scholar] [CrossRef]
- Yao, P.; Xie, Z.; Ren, P. Optimal UAV Route Planning for Coverage Search of Stationary Target in River. IEEE Trans. Control Syst. Technol. 2019, 27, 822–829. [Google Scholar] [CrossRef]
- Devaurs, D.; Simeon, T.; Cortes, J. Optimal Path Planning in Complex Cost Spaces with Sampling-Based Algorithms. IEEE Trans. Autom. Sci. Eng. 2016, 13, 415–424. [Google Scholar] [CrossRef]
- Ellefsen, K.O.; Lepikson, H.A.; Albiez, J.C. Multiobjective coverage path planning: Enabling automated inspection of complex, real-world structures. Appl. Soft Comput. 2017, 61, 264–282. [Google Scholar] [CrossRef]
- Krishna Lakshmanan, A.; Elara Mohan, R.; Ramalingam, B.; Vu Le, A.; Veerajagadeshwar, P.; Tiwari, K.; Ilyas, M. Complete coverage path planning using reinforcement learning for Tetromino based cleaning and maintenance robot. Autom. Constr. 2020, 112, 103078. [Google Scholar] [CrossRef]
- Macleod, C.N.; Dobie, G.; Pierce, S.G.; Summan, R.; Morozov, M. Machining-Based Coverage Path Planning for Automated Structural Inspection. IEEE Trans. Autom. Sci. Eng. 2018, 15, 202–213. [Google Scholar] [CrossRef]
- Hameed, I.A.; La Cour-Harbo, A.; Osen, O.L. Side-to-side 3D coverage path planning approach for agricultural robots to minimize skip/overlap areas between swaths. Robot. Autonom. Syst. 2016, 76, 36–45. [Google Scholar] [CrossRef]
- Cabreira, T.; Brisolara, L.; Ferreira, P.R., Jr. Survey on Coverage Path Planning with Unmanned Aerial Vehicles. Drones 2019, 3, 4. [Google Scholar] [CrossRef]
- Vasquez-Gomez, J.I.; Marciano-Melchor, M.; Valentin, L.; Herrera-Lozada, J.C. Coverage Path Planning for 2D Convex Regions. J. Intell. Robot. Syst. 2020, 97, 81–94. [Google Scholar] [CrossRef]
- Torres, M.; Pelta, D.A.; Verdegay, J.L.; Torres, J.C. Coverage path planning with unmanned aerial vehicles for 3D terrain reconstruction. Expert Syst. Appl. 2016, 55, 441–451. [Google Scholar] [CrossRef]
- Wu, C.; Dai, C.; Gong, X.; Liu, Y.-J.; Wang, J.; Gu, X.D.; Wang, C.C.L. Energy-Efficient Coverage Path Planning for General Terrain Surfaces. IEEE Robot. Autom. Lett. 2019, 4, 2584–2591. [Google Scholar] [CrossRef]
- Cabreira, T.M.; Franco, C.D.; Ferreira, P.R.; Buttazzo, G.C. Energy-Aware Spiral Coverage Path Planning for UAV Photogrammetric Applications. IEEE Robot. Autom. Lett. 2018, 3, 3662–3668. [Google Scholar] [CrossRef]
- Jensen, M.F.; Bochtis, D.; Sørensen, C.G. Coverage planning for capacitated field operations, part II: Optimisation. Biosyst. Eng. 2015, 139, 149–164. [Google Scholar] [CrossRef]
- Bogaerts, B.; Sels, S.; Vanlanduit, S.; Penne, R. A Gradient-Based Inspection Path Optimization Approach. IEEE Robot. Autom. Lett. 2018, 3, 2646–2653. [Google Scholar] [CrossRef]
- Nilsson, R.S.; Zhou, K. Method and bench-marking framework for coverage path planning in arable farming. Biosyst. Eng. 2020, 198, 248–265. [Google Scholar] [CrossRef]
- Samaniego, F.; Sanchis, J.; García-Nieto, S.; Simarro, R. Recursive Rewarding Modified Adaptive Cell Decomposition (RR-MACD): A Dynamic Path Planning Algorithm for UAVs. Electronics 2019, 8, 306. [Google Scholar] [CrossRef]
- Nair, V.G.; Guruprasad, K.R. MR-SimExCoverage: Multi-robot Simultaneous Exploration and Coverage. Comput. Electr. Eng. 2020, 85, 106680. [Google Scholar] [CrossRef]
- Guastella, D.C.; Cantelli, L.; Giammello, G.; Melita, C.D.; Spatino, G.; Muscato, G. Complete coverage path planning for aerial vehicle flocks deployed in outdoor environments. Comput. Electr. Eng. 2019, 75, 189–201. [Google Scholar] [CrossRef]
- Song, J.; Gupta, S. ε*: An Online Coverage Path Planning Algorithm. IEEE Trans. Robot. 2018, 34, 526–533. [Google Scholar] [CrossRef]
- Kan, X.; Teng, H.; Karydis, K. Online Exploration and Coverage Planning in Unknown Obstacle-Cluttered Environments. IEEE Robot. Autom. Lett. 2020, 5, 5969–5976. [Google Scholar] [CrossRef]
- Bircher, A.; Kamel, M.; Alexis, K.; Burri, M.; Oettershagen, P.; Omari, S.; Mantel, T.; Siegwart, R. Three-dimensional coverage path planning via viewpoint resampling and tour optimization for aerial robots. Auton. Robots 2016, 40, 1059–1078. [Google Scholar] [CrossRef]
- Ghaddar, A.; Merei, A.; Natalizio, E. PPS: Energy-Aware Grid-Based Coverage Path Planning for UAVs Using Area Partitioning in the Presence of NFZs. Sensors 2020, 20, 3742. [Google Scholar] [CrossRef]
- Xie, L.; Xue, S.; Zhang, J.; Zhang, M.; Tian, W.; Haugen, S. A path planning approach based on multi-direction A* algorithm for ships navigating within wind farm waters. Ocean Eng. 2019, 184, 311–322. [Google Scholar] [CrossRef]
- Han, G.; Zhou, Z.; Zhang, T.; Wang, H.; Liu, L.; Peng, Y.; Guizani, M. Ant-Colony-Based Complete-Coverage Path-Planning Algorithm for Underwater Gliders in Ocean Areas with Thermoclines. IEEE Trans. Veh. Technol. 2020, 69, 8959–8971. [Google Scholar] [CrossRef]
- Coombes, M.; Fletcher, T.; Chen, W.-H.; Liu, C. Optimal Polygon Decomposition for UAV Survey Coverage Path Planning in Wind. Sensors 2018, 18, 2132. [Google Scholar] [CrossRef]
- Nielsen, L.D.; Sung, I.; Nielsen, P. Convex Decomposition for a Coverage Path Planning for Autonomous Vehicles: Interior Extension of Edges. Sensors 2019, 19, 4165. [Google Scholar] [CrossRef]
- Jensen-Nau, K.R.; Hermans, T.; Leang, K.K. Near-Optimal Area-Coverage Path Planning of Energy-Constrained Aerial Robots with Application in Autonomous Environmental Monitoring. IEEE Trans. Autom. Sci. Eng. 2020. [Google Scholar] [CrossRef]
- Huang, W.H. Optimal line-sweep-based decompositions for coverage algorithms. In Proceedings of the 2001 ICRA IEEE International Conference on Robotics and Automation, Seoul, Korea, 21–26 May 2001. [Google Scholar]
- Li, Y.; Chen, H.; Joo Er, M.; Wang, X. Coverage path planning for UAVs based on enhanced exact cellular decomposition method. Mechatronics 2011, 21, 876–885. [Google Scholar] [CrossRef]
- Bolourian, N.; Hammad, A. LiDAR-equipped UAV path planning considering potential locations of defects for bridge inspection. Autom. Constr. 2020, 117, 103250. [Google Scholar] [CrossRef]
- Mansouri, S.S.; Kanellakis, C.; Georgoulas, G.; Kominiak, D.; Gustafsson, T.; Nikolakopoulos, G. 2D visual area coverage and path planning coupled with camera footprints. Control Eng. Pract. 2018, 75, 1–16. [Google Scholar] [CrossRef]
- Phung, M.D.; Quach, C.H.; Dinh, T.H.; Ha, Q. Enhanced discrete particle swarm optimization path planning for UAV vision-based surface inspection. Autom. Constr. 2017, 81, 25–33. [Google Scholar] [CrossRef]










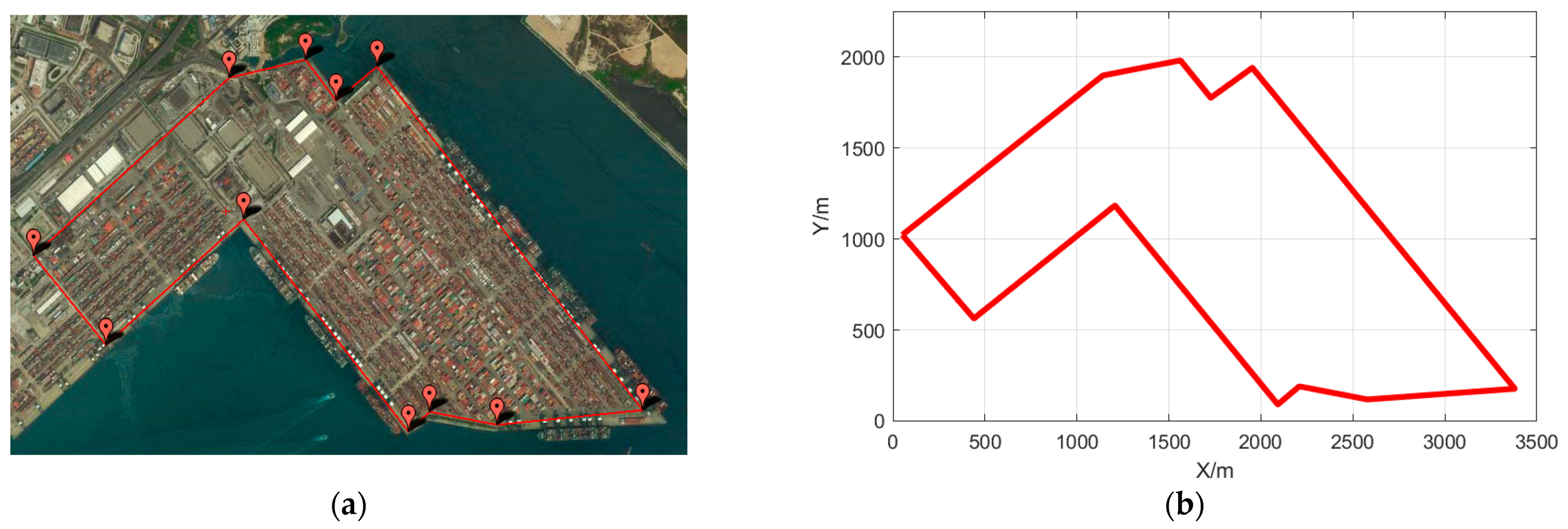

| Vertex | ||
|---|---|---|
| 30.598914 | 122.130204 | |
| 30.597834 | 122.130161 | |
| 30.596985 | 122.131277 | |
| 30.596736 | 122.132810 | |
| 30.597059 | 122.133250 | |
| 30.598914 | 122.134119 | |
| 30.600769 | 122.131598 |
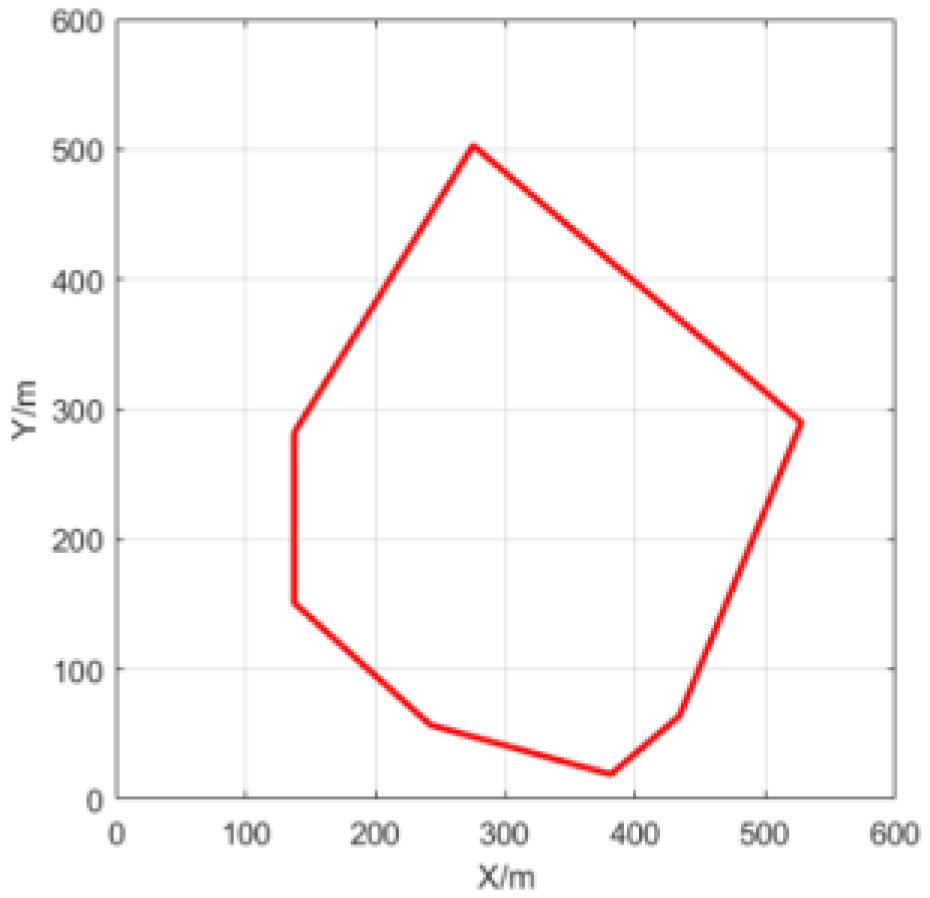
| Vertex | ||
|---|---|---|
| 137.041 | 282.073 | |
| 137.041 | 151.113 | |
| 242.181 | 57.954 | |
| 381.024 | 19.121 | |
| 434.281 | 64.257 | |
| 528.112 | 290.218 | |
| 275.239 | 503.332 |
| Serial Number | Accessible Node Queue |
|---|---|
| 1 | 6-5-4-3, 1-2, 8-9-10, 7 |
| 2 | 6-5-4-3, 1-2, 7-8, 9-10 |
| 3 | 6-5-9-10-4, 2-3, 1, 7-8 |
| 4 | 6-5-9-10-4, 1-2, 3, 7-8 |
| 5 | 1-2-3-4, 5-6-9, 7-8, 10 |
| 6 | 1-2-3-4, 10, 5-9-8-7, 6 |
| 7 | 1-2-3-4, 6, 8-9-10, 5-7 |
| 8 | 1-2-3-4, 7, 5-6, 8-9-10 |
| 9 | 1-4-10, 2-3, 5-7-8-9, 6 |
| 10 | 1-4-10, 2-3, 6-5-9, 7-8 |
| 11 | 3-4-5-7, 6, 1-2, 8-9-10 |
| 12 | 4-5-7-8-9-10, 6, 1-2, 3 |
| 13 | 4-5-7-8-9-10, 6, 2-3, 1 |
| Parameters | Line Sweep | MSA | Enhanced Exact Cellular Decomposition | Improved DFS |
|---|---|---|---|---|
| Number of sub-regions | 1 | 6 | 8 | 6 |
| Types of sub-region combinations | 3 | 9 | 10 | 7 |
| Minimum height of the sub-region | 5.31 | 4.405 | 4.845 | 4.405 |
| Serial Number | Number of Turns |
|---|---|
| 1 | 56 |
| 2 | 62 |
| 3 | 62 |
| 4 | 72 |
| 5 | 64 |
| 6 | 48 |
| 7 | 44 |
| 8 | 56 |
| 9 | 44 |
| 10 | 62 |
| 11 | 44 |
| 12 | 56 |
| 13 | 44 |
| Parameter | Set Value | Influence of Set Value |
|---|---|---|
| Population size | 20~100 | The is too small, errors will easily occur; the is too large, the stability will decrease. |
| Maximum iteration times | 100~500 | The is too small, it is not easy to converge; the is too large, it will cause waste. |
| Crossover probability | 0.4~0.99 | The is too small, the population cannot be updated effectively; the is too large, the randomness will increase. |
| Mutation probability | 0.0001~0.1 | The is too small, the population diversity will deteriorate; the is too large, the higher-order mode will be destroyed. |
| Serial Number | Distance/m |
|---|---|
| 7 | 4358.76 |
| 9 | 3817.02 |
| 11 | 4578.41 |
| 13 | 4153.53 |
| Camera Specifications | Camera Detail |
|---|---|
| Camera | Sony A6000 |
| Camera dimension | 120.0 mm × 66.9 mm × 45.1 mm |
| Camera weight | 285 g |
| Mega pixels | 24.3 |
| Type of camera sensor | 23.5 mm × 15.6 mm (APS-C) |
| Speed of shutter | 0.00025 to 30 s |
| Speed of flash sync | 0.00625 s |
| Path Parameters | Before ROD | After ROD | Percentage Reduction/% |
|---|---|---|---|
| Number of turns | 46 | 44 | 4.34 |
| Working distance/m | 39,616.87 | 39,263.83 | 0.89 |
| Non-Working distance/m | 4014.84 | 2813.81 | 29.91 |
| Total distance/m | 43,631.71 | 42,077.64 | 3.56 |
| Search time/s | 3635.98 | 3506.47 | 3.56 |
| Coverage rate/% | 90.8 | 93.3 | −2.5 |
| Area Number | Path Parameters | Before ROD | After ROD | Percentage Reduction/% |
|---|---|---|---|---|
| A | Number of turns | 14 | 23 | −64.29 |
| Working distance/m | 7527.26 | 7593.36 | 0.88 | |
| Non-working distance/m | 844.60 | 0 | - | |
| Total distance/m | 8371.86 | 7593.36 | 9.30 | |
| Search time/s | 697.66 | 632.78 | 9.31 | |
| Coverage rate/% | 89.9 | 100 | 10.1 | |
| B | Number of turns | 18 | 24 | −33.33 |
| Working distance/m | 9184.59 | 9517.80 | 3.63 | |
| Non-working distance/m | 1378.85 | 0 | - | |
| Total distance/m | 10,563.44 | 9517.80 | 9.90 | |
| Search time/s | 880.29 | 793.15 | 9.91 | |
| Coverage rate/% | 86.9 | 100 | 13.1 | |
| C | Number of turns | 28 | 28 | 0 |
| Working distance/m | 11,553.49 | 11,524.43 | 0.25 | |
| Non-working distance/m | 2232.88 | 0 | - | |
| Total distance/m | 13,786.37 | 11,524.43 | 16.41 | |
| Search time/s | 1148.86 | 960.36 | 16.41 | |
| Coverage rate/% | 83.8 | 100 | 16.2 | |
| D | Number of turns | 16 | 26 | −62.5 |
| Working distance/m | 4134.82 | 4159.71 | −0.60 | |
| Non-working distance/m | 890.19 | 553.88 | 37.78 | |
| Total distance/m | 5025.01 | 4713.59 | 6.20 | |
| Search time/s | 418.75 | 392.80 | 6.21 | |
| Coverage rate/% | 82.3 | 100 | 17.7 | |
| E | Number of turns | 37 | 42 | −13.5 |
| Working distance/m | 18,654.90 | 18,574.66 | 0.43 | |
| Non-working distance/m | 2069.05 | 1137.09 | 45.04 | |
| Total distance/m | 20,723.95 | 19,711.75 | 4.88 | |
| Search time/s | 1726.99 | 1642.65 | 4.88 | |
| Coverage rate/% | 90 | 100 | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, G.; Tang, C.; Zhou, H.; Claramunt, C.; Men, S. R-DFS: A Coverage Path Planning Approach Based on Region Optimal Decomposition. Remote Sens. 2021, 13, 1525. https://doi.org/10.3390/rs13081525
Tang G, Tang C, Zhou H, Claramunt C, Men S. R-DFS: A Coverage Path Planning Approach Based on Region Optimal Decomposition. Remote Sensing. 2021; 13(8):1525. https://doi.org/10.3390/rs13081525
Chicago/Turabian StyleTang, Gang, Congqiang Tang, Hao Zhou, Christophe Claramunt, and Shaoyang Men. 2021. "R-DFS: A Coverage Path Planning Approach Based on Region Optimal Decomposition" Remote Sensing 13, no. 8: 1525. https://doi.org/10.3390/rs13081525
APA StyleTang, G., Tang, C., Zhou, H., Claramunt, C., & Men, S. (2021). R-DFS: A Coverage Path Planning Approach Based on Region Optimal Decomposition. Remote Sensing, 13(8), 1525. https://doi.org/10.3390/rs13081525







