Wetlands Cool Land Surface Temperature in Tropical Regions but Warm in Boreal Regions
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
2.1.1. Land Use and Landcover Data
2.1.2. LST Data
2.1.3. Albedo Data
2.1.4. ET Data
2.1.5. Air Temperature, Radiation, and Elevation Data
2.2. Methods
3. Results
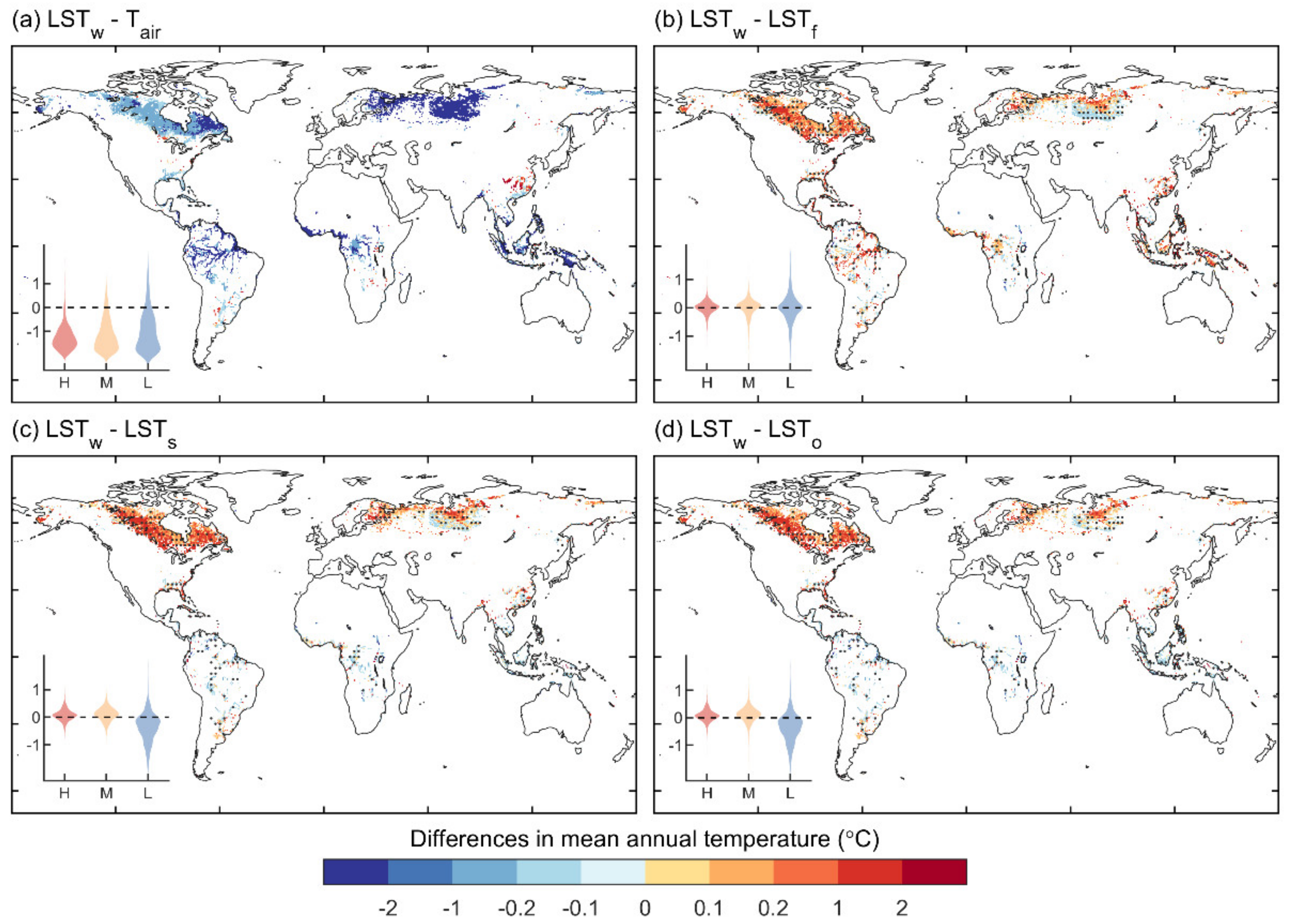
3.1. Spatial Patterns of Mean Annual ΔLST
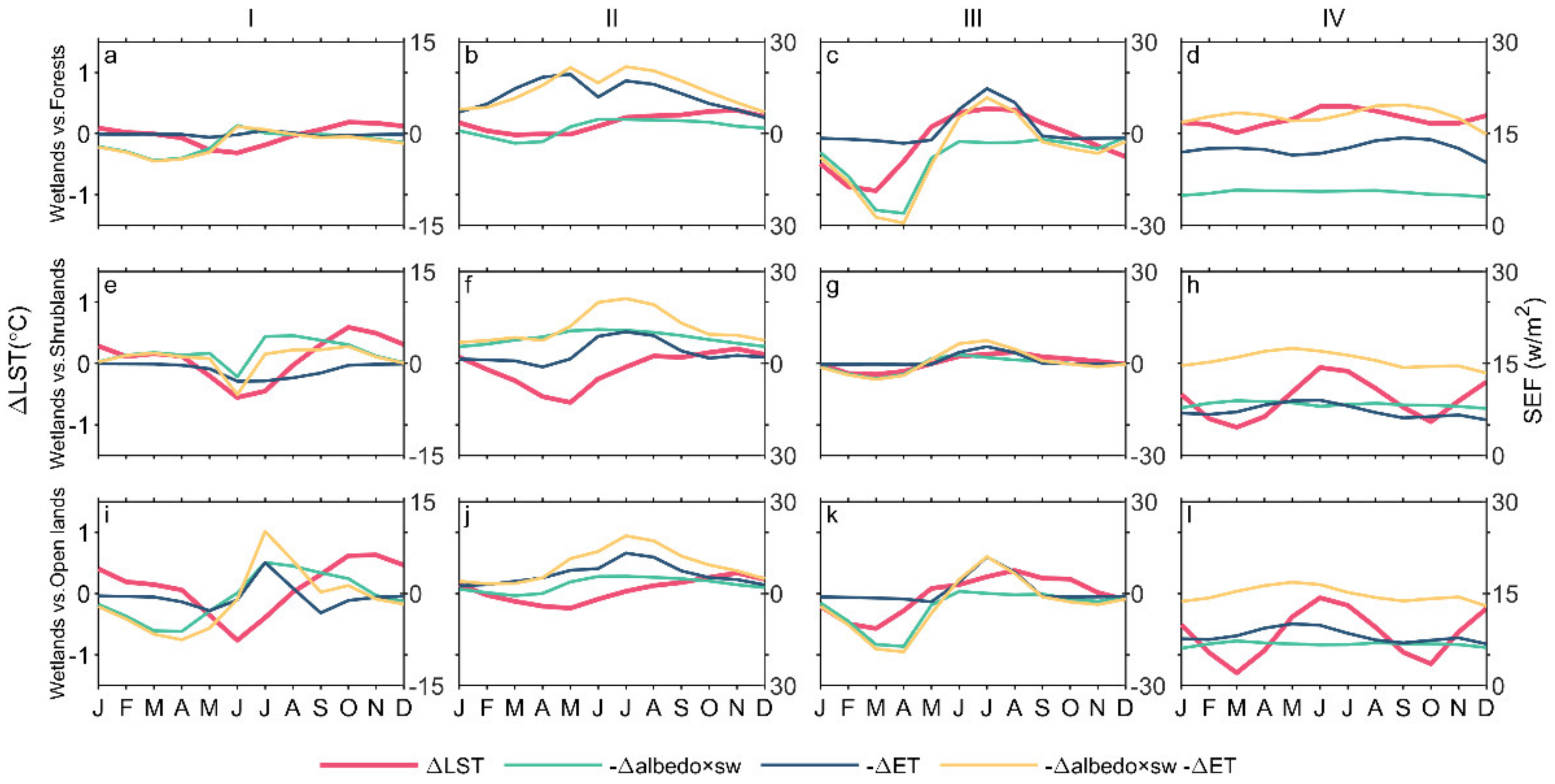
3.2. Spatial Patterns of Seasonal ΔLST
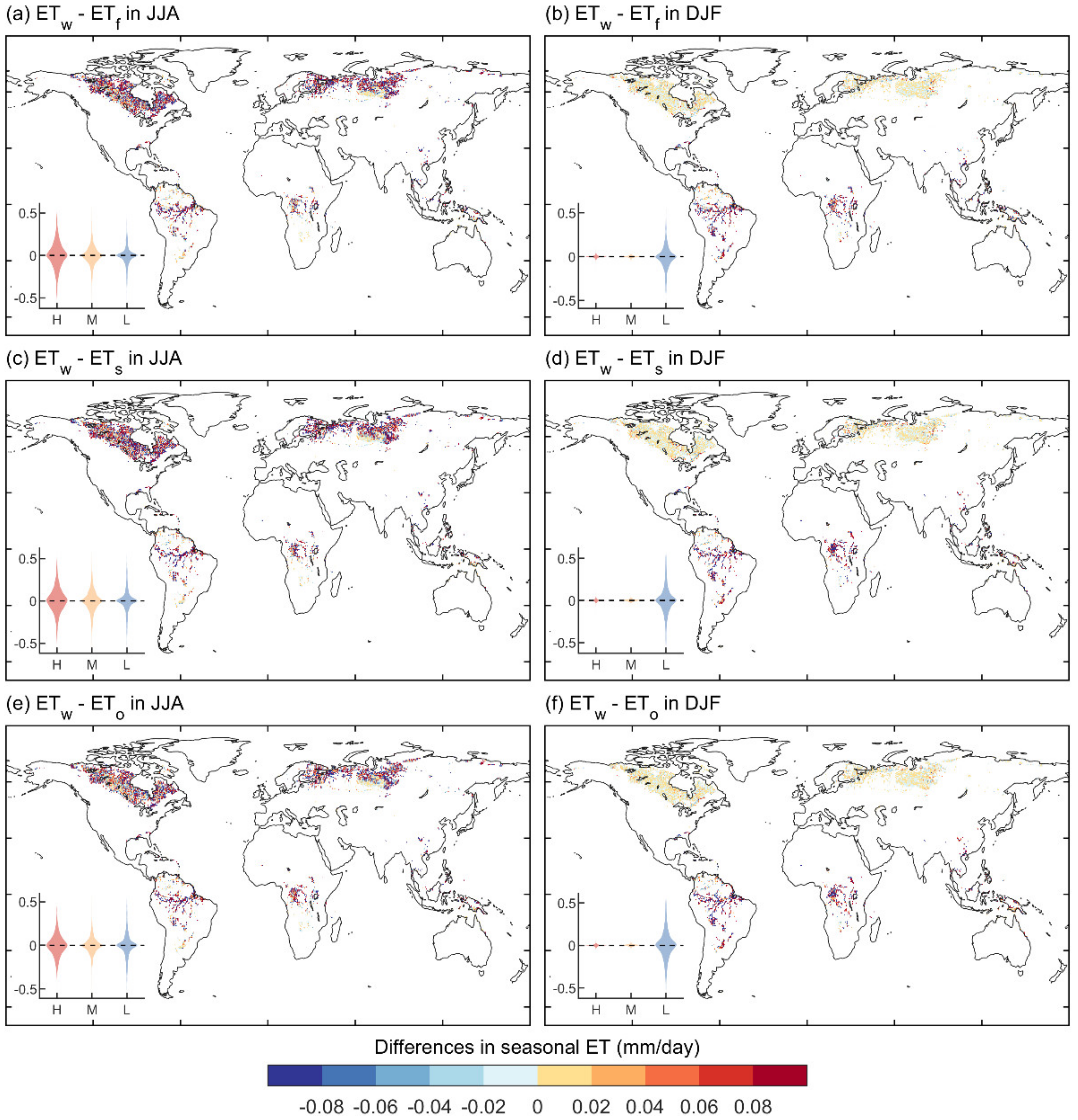
3.3. Spatial Patterns of Seasonal Δalbedo and ΔET
4. Discussion
4.1. The Cooling or Warming Effect of Wetlands
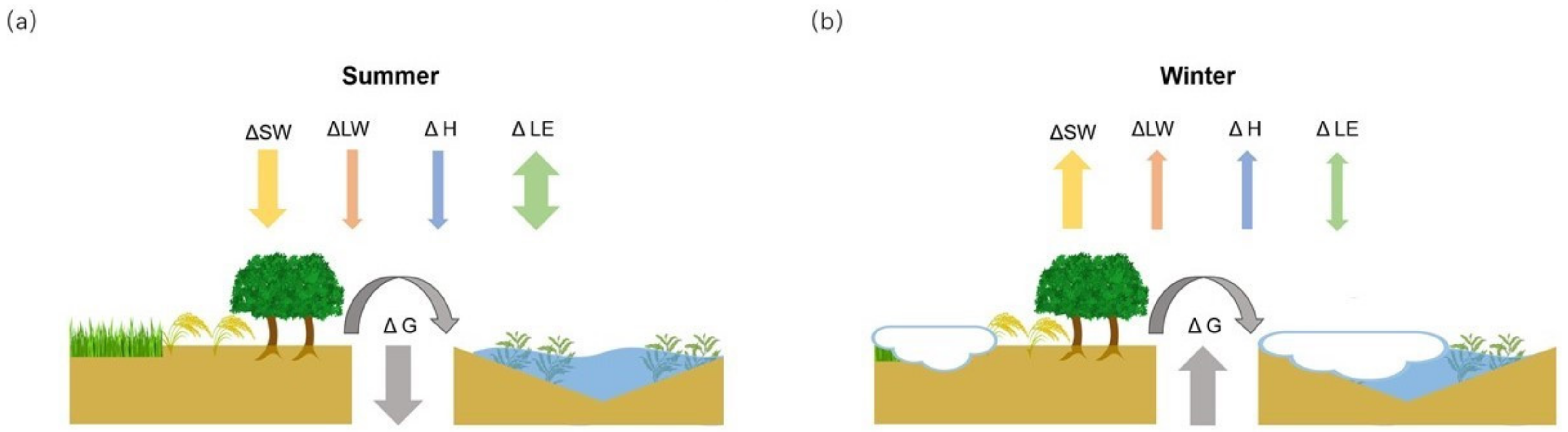
4.2. Mechanisms of the Warming or Cooling Effects of Wetlands
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tootchi, A.; Jost, A.; Ducharne, A. Multi-source global wetland maps combining surface water imagery and groundwater constraints. Earth Syst. Sci. Data 2019, 11, 189–220. [Google Scholar] [CrossRef]
- Zedler, J.B.; Kercher, S. Wetland resources: Status, trends, ecosystem services, and restorability. Annu. Rev. Environ. Resour. 2005, 30, 39–74. [Google Scholar] [CrossRef]
- Finlayson, M.; Cruz, R.D.; Davidson, N.; Alder, J.; Cork, S.; de Groot, R.S.; Lévêque, C.; Milton, G.R.; Peterson, G.; Pritchard, D.; et al. Millennium Ecosystem Assessment: Ecosystems and Human Well-Being: Wetlands and Water Synthesis; Island Press: Washington, DC, USA, 2005. [Google Scholar]
- Gardner, R.; Finlayson, M. Global Wetland Outlook: State of the World’s Wetlands and their Services to People; Ramsar: Gland, Switzerland, 2018. [Google Scholar]
- Russi, D.; ten Brink, P.; Farmer, A.; Badura, T.; Coates, D.; Förster, J.; Kumar, R.; Davidson, N. The Economics of Ecosystems and Biodiversity for Water and Wetlands; IEEP: Bruxelles, Belgium, 2012. [Google Scholar]
- Prigent, C.; Jimenez, C.; Bousquet, P. Satellite-Derived Global Surface Water Extent and Dynamics Over the Last 25 Years (GIEMS-2). J. Geophys. Res. Atmos. 2020, 125, 125. [Google Scholar] [CrossRef]
- Jensen, K.; McDonald, K. Surface Water Microwave Product Series Version 3: A Near-Real Time and 25-Year Historical Global Inundated Area Fraction Time Series From Active and Passive Microwave Remote Sensing. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1402–1406. [Google Scholar] [CrossRef]
- Prigent, C.; Papa, F.; Aires, F.; Jimenez, C.; Rossow, W.B.; Matthews, E. Changes in land surface water dynamics since the 1990s and relation to population pressure. Geophys. Res. Lett. 2012, 39, L08403. [Google Scholar] [CrossRef]
- UN. General Assembly Resolution A/RES/70/1. Transforming Our World, the 2030 Agenda for Sustainable Development; UN: New York, NY, USA, 2015. [Google Scholar]
- Xu, X.; Chen, M.; Yang, G.; Jiang, B.; Zhang, J. Wetland ecosystem services research: A critical review. Glob. Ecol. Conserv. 2020, 22, e01027. [Google Scholar] [CrossRef]
- Chapin, F.S., III; Matson, P.A.; Vitousek, P. Principles of Terrestrial Ecosystem Ecology, 2nd ed.; Springer: New York, NY, USA, 2011. [Google Scholar]
- Sumner, D.M.; Wu, Q.; Pathak, C.S. Variability of Albedo and Utility of the MODIS Albedo Product in Forested Wetlands. Wetlands 2011, 31, 229–237. [Google Scholar] [CrossRef]
- Georg, W.; Albin, H.; Georg, N.; Katharina, S.; Enrico, T.; Peng, Z. On the energy balance closure and net radiation in complex terrain. Agric. For. Meteorol. 2016, 226-227, 37–49. [Google Scholar] [CrossRef] [PubMed]
- Hemes, K.S.; Eichelmann, E.; Chamberlain, S.D.; Knox, S.H.; Oikawa, P.Y.; Sturtevant, C.; Verfaillie, J.; Szutu, D.; Baldocchi, D.D. A Unique Combination of Aerodynamic and Surface Properties Contribute to Surface Cooling in Restored Wetlands of the Sacramento-San Joaquin Delta, California. J. Geophys. Res. Biogeosci. 2018, 123, 2072–2090. [Google Scholar] [CrossRef]
- Worrall, F.; Boothroyd, I.M.; Gardner, R.L.; Howden, N.J.K.; Burt, T.P.; Smith, R.; Mitchell, L.; Kohler, T.; Gregg, R. The Impact of Peatland Restoration on Local Climate: Restoration of a Cool Humid Island. J. Geophys. Res. Biogeosci. 2019, 124, 1696–1713. [Google Scholar] [CrossRef]
- Bai, J.; Lu, Q.; Zhao, Q.; Wang, J.; Ouyang, H. Effects of Alpine Wetland Landscapes on Regional Climate on the Zoige Plateau of China. Adv. Meteorol. 2013, 2013, 1–7. [Google Scholar] [CrossRef]
- Zheng, H.Z.; Chen, Y.H.; Pan, W.B.; Zheng, P.; Cai, Y.B. Land surface temperature fluctuation characteristics and key influencing factors in estuarine wetland. Shengtaixue Zazhi 2018, 37, 2463–2473. [Google Scholar]
- Peng, S.-S.; Piao, S.; Zeng, Z.; Ciais, P.; Zhou, L.; Li, L.Z.X.; Myneni, R.B.; Yin, Y.; Zeng, H. Afforestation in China cools local land surface temperature. Proc. Natl. Acad. Sci. USA 2014, 111, 2915–2919. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Zhao, M.; Motesharrei, S.; Mu, Q.; Kalnay, E.; Li, S. Local cooling and warming effects of forests based on satellite observations. Nat. Commun. 2015, 6, 6603. [Google Scholar] [CrossRef]
- Friedl, M.A.; Sulla-Menashe, D.; Tan, B.; Schneider, A.; Ramankutty, N.; Sibley, A.; Huang, X. MODIS Collection 5 global land cover: Algorithm refinements and characterization of new datasets. Remote Sens. Environ. 2010, 114, 168–182. [Google Scholar] [CrossRef]
- Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Trans. Geosci. Remote. Sens. 1996, 34, 892–905. [Google Scholar] [CrossRef]
- Lian, X.; Zeng, Z.; Yao, Y.; Peng, S.; Wang, K.; Piao, S. Spatiotemporal variations in the difference between satellite-observed daily maximum land surface temperature and station-based daily maximum near-surface air temperature. J. Geophys. Res. Atmos. 2017, 122, 2254–2268. [Google Scholar] [CrossRef]
- Wan, Z. New refinements and validation of the collection-6 MODIS land-surface temperature/emissivity product. Remote. Sens. Environ. 2014, 140, 36–45. [Google Scholar] [CrossRef]
- Mira, M.; Weiss, M.; Baret, F.; Courault, D.; Hagolle, O.; Gallego-Elvira, B.; Olioso, A. The MODIS (collection V006) BRIDF/albedo product MCD43D: Temporal course evaluated over agricultural landscape. Remote Sens. Environ. 2015, 170, 216–228. [Google Scholar] [CrossRef]
- Cescatti, A.; Marcolla, B.; Vannan, S.K.S.; Pan, J.Y.; Román, M.O.; Yang, X.; Ciais, P.; Cook, R.B.; Law, B.E.; Matteucci, G.; et al. Intercomparison of MODIS albedo retrievals and in situ measurements across the global FLUXNET network. Remote Sens. Environ. 2012, 121, 323–334. [Google Scholar] [CrossRef]
- Kalma, J.D.; McVicar, T.R.; Matthew, F. UNSW Faculty of Engineering Matthew Francis McCabe Estimating Land Surface Evaporation: A Review of Methods Using Remotely Sensed Surface Temperature Data. Surv. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]
- Kim, H.W.; Hwang, K.; Mu, Q.; Lee, S.O.; Choi, M. Validation of MODIS 16 global terrestrial evapotranspiration products in various climates and land cover types in Asia. KSCE J. Civ. Eng. 2012, 16, 229–238. [Google Scholar] [CrossRef]
- Harris, I.; Osborn, T.J.; Jones, P.; Lister, D. Version 4 of the CRU TS monthly high-resolution gridded multivariate climate dataset. Sci. Data 2020, 7, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Budescu, D.V. Dominance Analysis—A New Approach to the Problem of Relative Importance of Predictors in Multiple-Regression. Psychol. Bull. 1993, 114, 542–551. [Google Scholar] [CrossRef]
- Cui, E.; Huang, K.; Arain, M.A.; Fisher, J.B.; Huntzinger, D.N.; Ito, A.; Luo, Y.; Jain, A.K.; Mao, J.; Michalak, A.M.; et al. Vegetation Functional Properties Determine Uncertainty of Simulated Ecosystem Productivity: A Traceability Analysis in the East Asian Monsoon Region. Glob. Biogeochem. Cycles 2019, 33, 668–689. [Google Scholar] [CrossRef]
- Yu, L.; Liu, T.; Zhang, S. Temporal and Spatial Changes in Snow Cover and the Corresponding Radiative Forcing Analysis in Siberia from the 1970s to the 2010s. Adv. Meteorol. 2017, 2017, 1–11. [Google Scholar] [CrossRef]
- Zheng, H.; Chen, Y.; Pan, W.; Cai, Y.; Chen, Z. Impact of Land Use/Land Cover Changes on the Thermal Environment in Urbanization: A Case Study of the Natural Wetlands Distribution Area in Minjiang River Estuary, China. Pol. J. Environ. Stud. 2019, 28, 3025–3041. [Google Scholar] [CrossRef]
- Muro, J.; Strauch, A.; Heinemann, S.; Steinbach, S.; Thonfeld, F.; Waske, B.; Diekkrüger, B. Land surface temperature trends as indicator of land use changes in wetlands. Int. J. Appl. Earth Obs. Geoinf. 2018, 70, 62–71. [Google Scholar] [CrossRef]
- Turner, J.; Desai, A.R.; Thom, J.; Wickland, K.P.; Olson, B. Wind Sheltering Impacts on Land-Atmosphere Fluxes Over Fens. Front. Environ. Sci. 2019, 7, 179. [Google Scholar] [CrossRef]
- Xiao, J.; Zhuang, Q.; Law, B.E.; Chen, J.; Baldocchi, D.D.; Cook, D.R.; Oren, R.; Richardson, A.D.; Wharton, S.; Siyan USA (host institution) IN 47907 West Lafayette Purdue University Purdue Climate Change Research Center Department of Earth & Atmospheric Sciences. A continuous measure of gross primary production for the conterminous United States derived from MODIS and AmeriFlux data. Remote. Sens. Environ. 2010, 114, 576–591. [Google Scholar] [CrossRef]
- Wang, Y.; Lu, Y.; Horton, R.; Ren, T. Specific Heat Capacity of Soil Solids: Influences of Clay Content, Organic Matter, and Tightly Bound Water. Soil Sci. Soc. Am. J. 2019, 83, 1062–1066. [Google Scholar] [CrossRef]
- Lehner, B.; Döll, P. Development and validation of a global database of lakes, reservoirs and wetlands. J. Hydrol. 2004, 296, 1–22. [Google Scholar] [CrossRef]
- Huryna, H.; Brom, J.; Pokorný, J. The importance of wetlands in the energy balance of an agricultural landscape. Wetl. Ecol. Manag. 2013, 22, 363–381. [Google Scholar] [CrossRef]
- Tsuang, B.-J. Ground Heat Flux Determination according to Land Skin Temperature Observations from In Situ Stations and Satellites. J. Hydrometeorol. 2005, 6, 371–390. [Google Scholar] [CrossRef]
- Sulla-Menashe, D.; Gray, J.M.; Abercrombie, S.P.; Friedl, M.A. Hierarchical mapping of annual global land cover 2001 to present: The MODIS Collection 6 Land Cover product. Remote Sens. Environ. 2019, 222, 183–194. [Google Scholar] [CrossRef]
- Cheng, F.Y.; Van Meter, K.J.; Byrnes, D.K.; Basu, N.B. Maximizing US nitrate removal through wetland protection and restoration. Nat. Cell Biol. 2020, 588, 625–630. [Google Scholar] [CrossRef]
- Kroeger, K.D.; Crooks, S.; Moseman-Valtierra, S.; Tang, J. Restoring tides to reduce methane emissions in impounded wetlands: A new and potent Blue Carbon climate change intervention. Sci. Rep. 2017, 7, 1–12. [Google Scholar] [CrossRef] [PubMed]
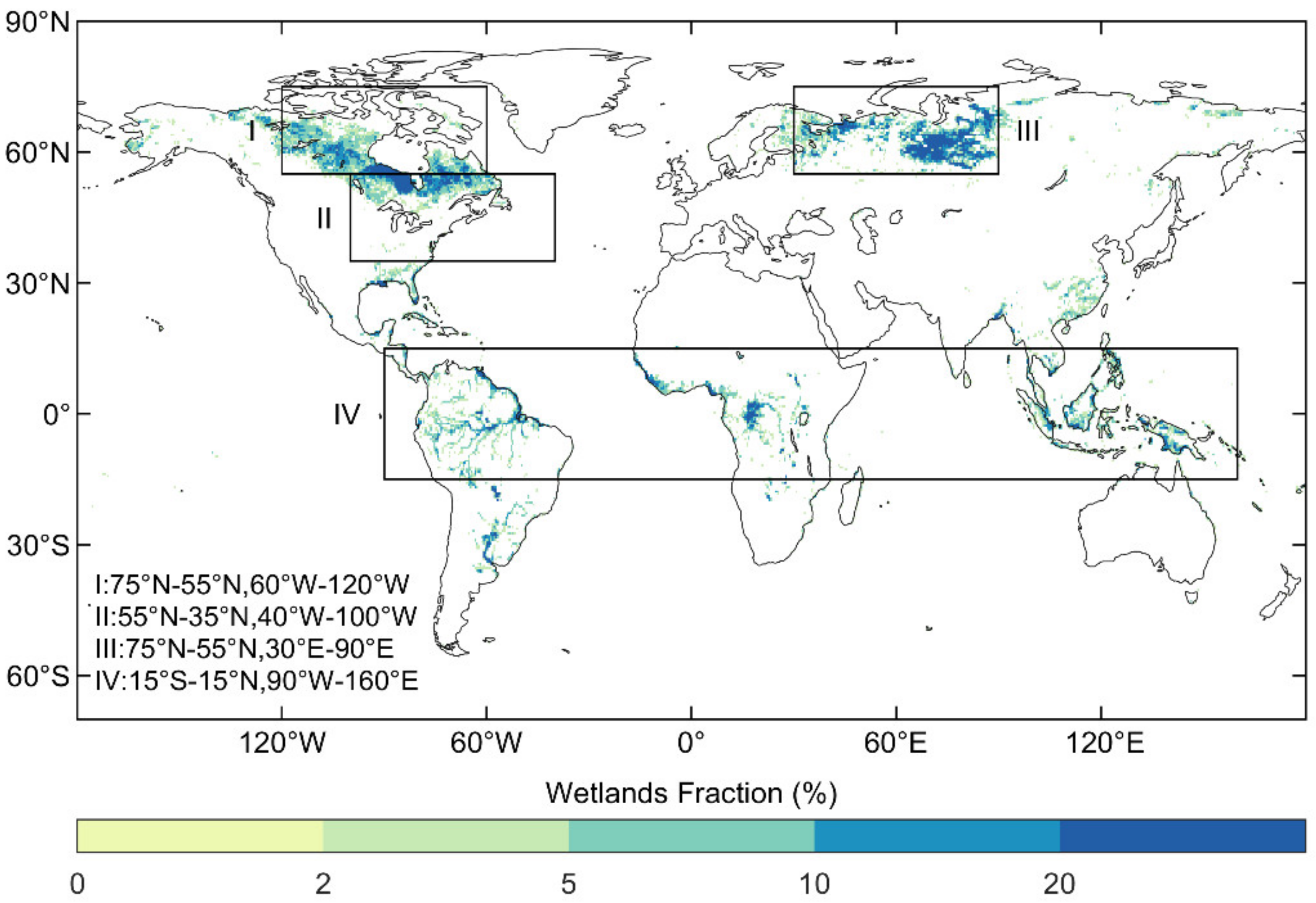

| Number | Class | Extent (Million km2) | Percentage of the Land Surface | IGBP |
|---|---|---|---|---|
| 1 | Wetland | 1.1 | 0.7% | Permanent Wetlands |
| 2 | Forest | 22.3 | 14.9% | Evergreen needleleaf forests, evergreen broadleaf forests, deciduous needleleaf forests, deciduous broadleaf forest, mixed forests |
| 3 | Shrubland | 39 | 26.2% | Closed shrublands, open shrublands, woody savannas, savannas |
| 4 | Open land | 34.5 | 23.1% | Grasslands, croplands, cropland—natural vegetation mosaic |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Xi, Y.; Feng, M.; Peng, S. Wetlands Cool Land Surface Temperature in Tropical Regions but Warm in Boreal Regions. Remote Sens. 2021, 13, 1439. https://doi.org/10.3390/rs13081439
Wu Y, Xi Y, Feng M, Peng S. Wetlands Cool Land Surface Temperature in Tropical Regions but Warm in Boreal Regions. Remote Sensing. 2021; 13(8):1439. https://doi.org/10.3390/rs13081439
Chicago/Turabian StyleWu, Yuxuan, Yi Xi, Maoyuan Feng, and Shushi Peng. 2021. "Wetlands Cool Land Surface Temperature in Tropical Regions but Warm in Boreal Regions" Remote Sensing 13, no. 8: 1439. https://doi.org/10.3390/rs13081439
APA StyleWu, Y., Xi, Y., Feng, M., & Peng, S. (2021). Wetlands Cool Land Surface Temperature in Tropical Regions but Warm in Boreal Regions. Remote Sensing, 13(8), 1439. https://doi.org/10.3390/rs13081439






