Ambient PM2.5 Estimates and Variations during COVID-19 Pandemic in the Yangtze River Delta Using Machine Learning and Big Data
Abstract
1. Introduction
2. Data and Methods
2.1. Data
2.1.1. PM2.5 Data
2.1.2. Aerosol Optical Depth (AOD) Data
2.1.3. POIs Data
2.1.4. Meteorological Data
2.1.5. Elevation Data
2.1.6. Boundary and Road Network Data
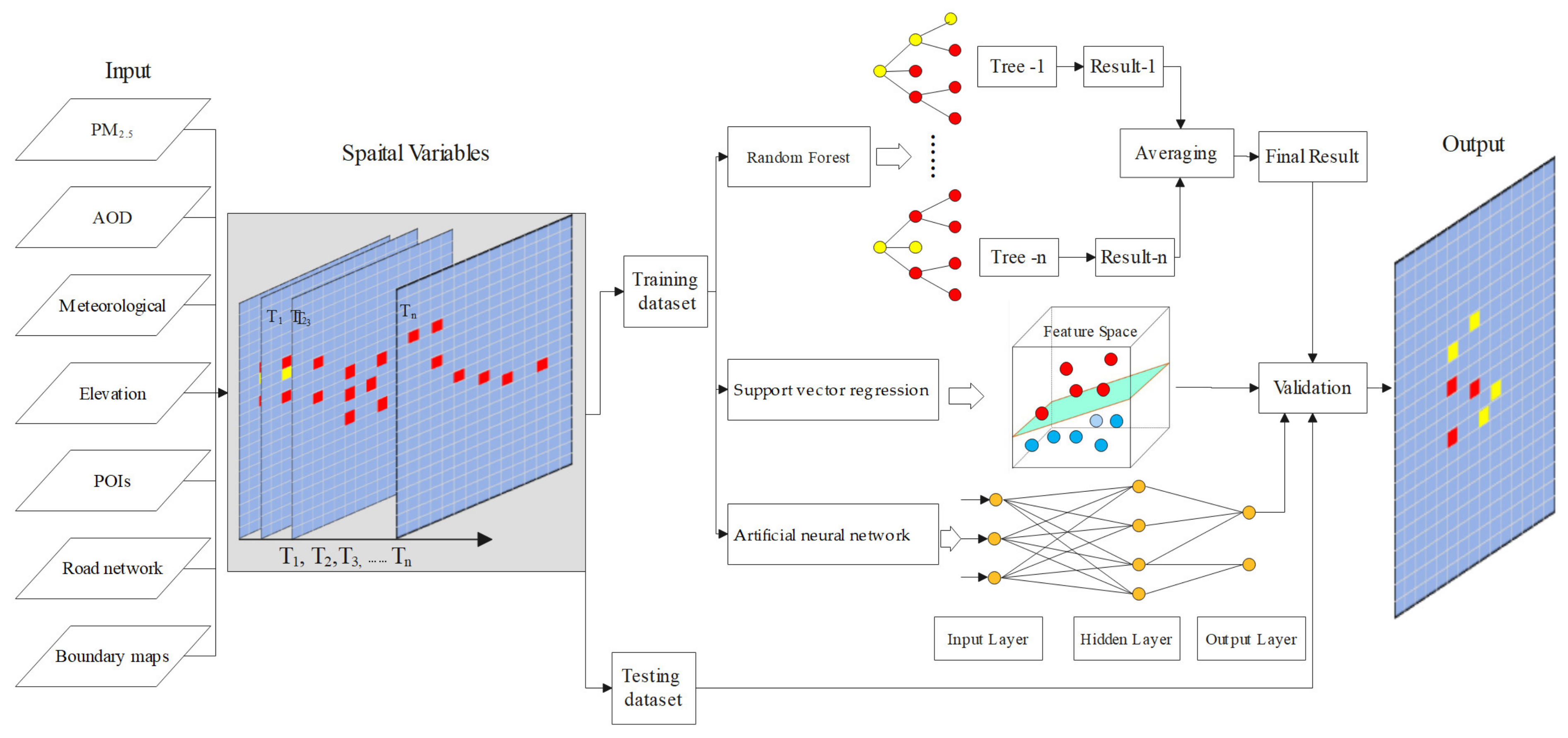
2.2. Model Structure and Validation
2.2.1. Random Forest Model
2.2.2. Support Vector Regression Model
2.2.3. Back Propagation Artificial Neural Network
2.2.4. Cross Validated Model Accuracy
3. Results and Analysis
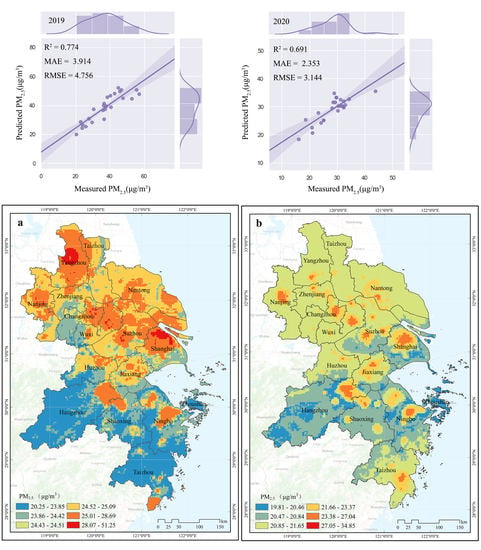
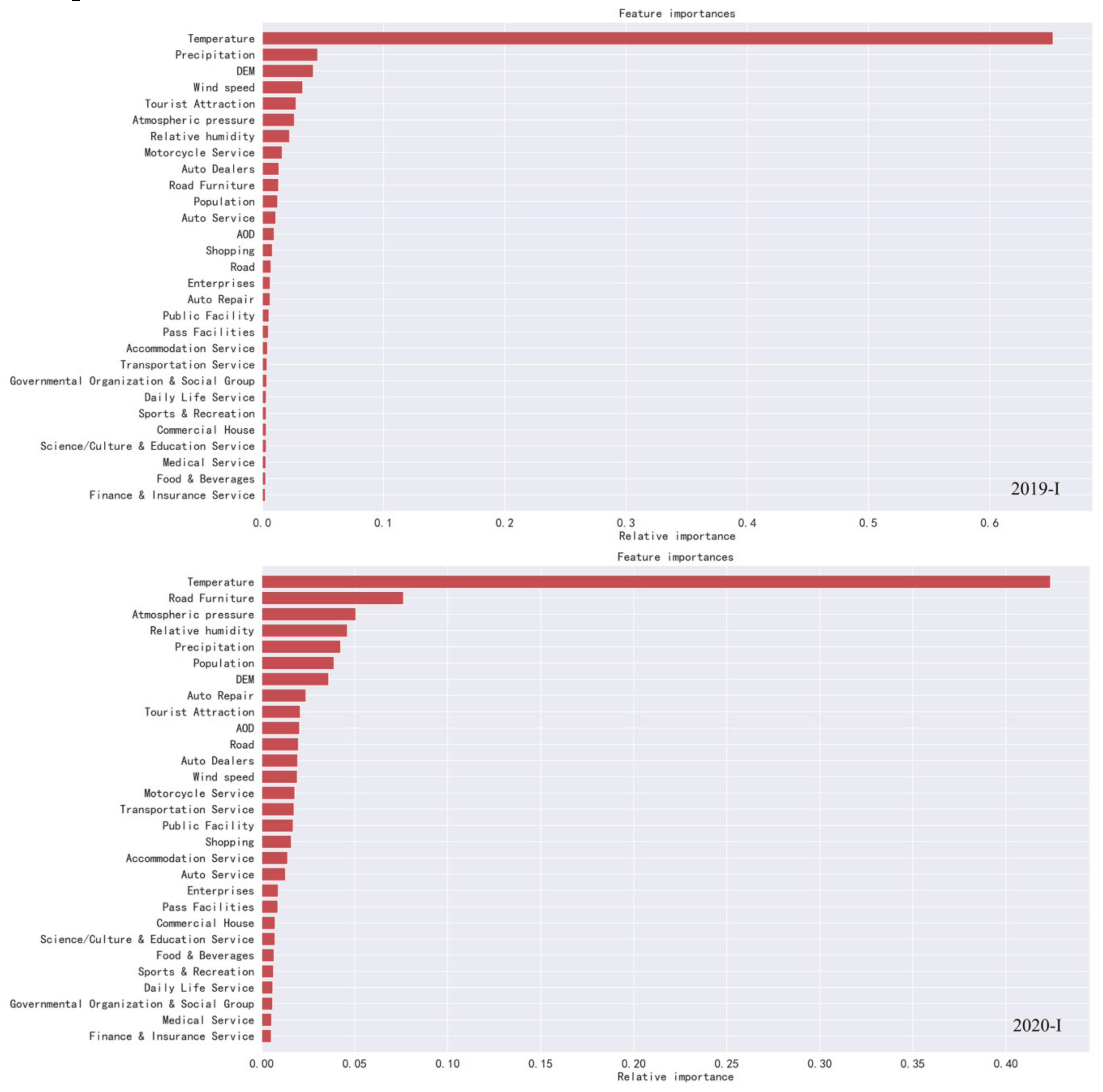
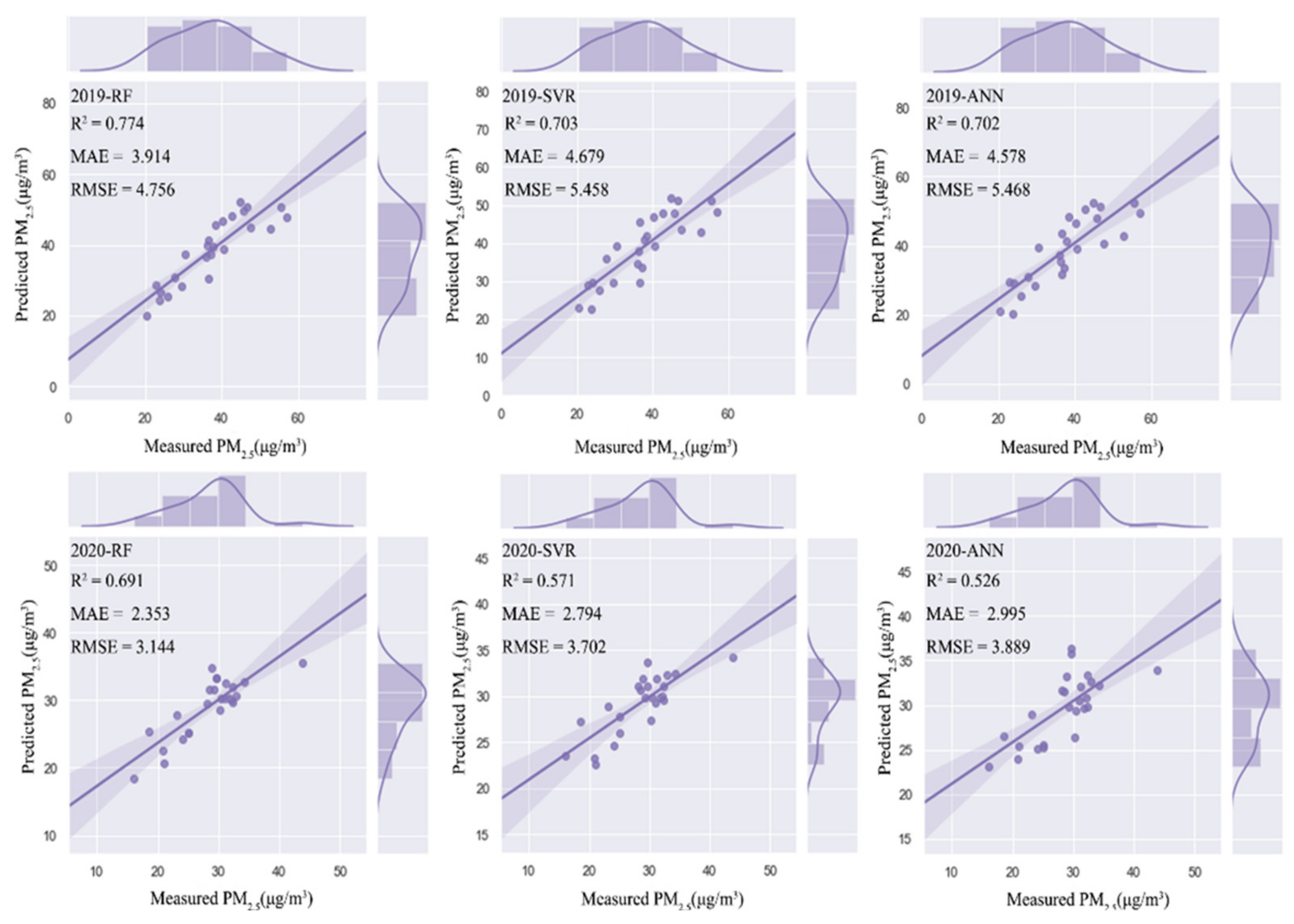
3.1. Model Performance
3.2. Cross Validated Model Accuracy
3.3. PM2.5 Estimates during COVID-19
3.4. PM2.5 Variations during COVID-19
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sulaymon, I.D.; Zhang, Y.; Hopke, P.K.; Zhang, Y.; Hua, J.; Mei, X. COVID-19 pandemic in Wuhan: Ambient air quality and the relationships between criteria air pollutants and meteorological variables before, during, and after lockdown. Atmos. Res. 2021, 250, 105362. [Google Scholar] [CrossRef]
- Guan, D.; Wang, D.; Hallegatte, S.; Davis, S.J.; Huo, J.; Li, S.; Bai, Y.; Lei, T.; Xue, Q.; Coffman, D.; et al. Global supply-chain effects of COVID-19 control measures. Nat. Hum. Behav. 2020, 4, 577–587. [Google Scholar] [CrossRef]
- Coker, E.S.; Cavalli, L.; Fabrizi, E.; Guastella, G.; Lippo, E.; Parisi, M.L.; Pontarollo, N.; Rizzati, M.; Varacca, A.; Vergalli, S. The Effects of Air Pollution on COVID-19 Related Mortality in Northern Italy. Environ. Resour. Econ. 2020, 1–24. [Google Scholar] [CrossRef]
- Ming, W.; Zhou, Z.; Ai, H.; Bi, H.; Zhong, Y. COVID-19 and Air Quality: Evidence from China. Emerg. Mark. Financ. Trade 2020, 56, 2422–2442. [Google Scholar] [CrossRef]
- Liu, S.; Kong, G.; Kong, D. Effects of the COVID-19 on Air Quality: Human Mobility, Spillover Effects, and City Connections. Environ. Resour. Econ. 2020, 1–19. [Google Scholar] [CrossRef]
- Brimblecombe, P.; Lai, Y. Effect of sub-urban scale lockdown on air pollution in Beijing. Urban Clim. 2020, 34, 100725. [Google Scholar] [CrossRef]
- Chakraborty, I.; Maity, P. COVID-19 outbreak: Migration, effects on society, global environment and prevention. Sci. Total Environ. 2020, 728, 138882. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Wang, T.; Xie, M.; Li, S.; Zhuang, B.; Fu, Q.; Zhao, M.; Wu, H.; Liu, J.; Saikawa, E.; et al. Drivers for the poor air quality conditions in north China Plain during the COVID-19 outbreak. Atmos. Environ. 2020, 118103. [Google Scholar] [CrossRef]
- Pei, Z.; Han, G.; Ma, X.; Su, H.; Gong, W. Response of major air pollutants to COVID-19 lockdowns in China. Sci. Total Environ. 2020, 743, 140879. [Google Scholar] [CrossRef] [PubMed]
- Feng, S.; Jiang, F.; Wang, H.; Wang, H.; Ju, W.; Shen, Y.; Zheng, Y.; Wu, Z.; Ding, A. NO x Emission Changes Over China During the COVID-19 Epidemic Inferred from Surface NO2 Observations. Geophys. Res. Lett. 2020, 47, e2020GL090080. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Q.; Qi, B.; Hu, D.; Wang, J.; Zhang, J.; Yang, H.; Zhang, S.; Liu, L.; Xu, L.; Li, W. Spatiotemporal variations and reduction of air pollutants during the COVID-19 pandemic in a megacity of Yangtze River Delta in China. Sci. Total Environ. 2021, 751, 141820. [Google Scholar] [CrossRef] [PubMed]
- Han, Y.; Lam, J.C.K.; Li, V.O.K.; Guo, P.; Zhang, Q.; Wang, A.; Crowcroft, J.; Wang, S.; Fu, J.; Gilani, Z.; et al. The Effects of Outdoor Air Pollution Concentrations and Lockdowns on Covid-19 Infections in Wuhan and Other Provincial Capitals in China. Preprints 2020. [Google Scholar] [CrossRef][Green Version]
- Bao, R.; Zhang, A. Does lockdown reduce air pollution? Evidence from 44 cities in northern China. Sci. Total Environ. 2020, 731, 139052. [Google Scholar] [CrossRef] [PubMed]
- Fang, X.; Zou, B.; Liu, X.; Sternberg, T.; Zhai, L. Satellite-based ground PM2.5 estimation using timely structure adaptive modeling. Remote Sens. Environ. 2016, 186, 152–163. [Google Scholar] [CrossRef]
- Wang, S.; Zhou, C.; Wang, Z.; Feng, K.; Hubacek, K. The characteristics and drivers of fine particulate matter (PM2.5) distribution in China 2016. J. Clean. Prod. 2017, 142, 1800–1809. [Google Scholar] [CrossRef]
- Chen, G.; Li, S.; Knibbs, L.D.; Hamm, N.A.S.; Cao, W.; Li, T.; Guo, J.; Ren, H.; Abramson, M.J.; Guo, Y. A machine learning method to estimate PM2.5 concentrations across China with remote sensing, meteorological and land use information. Sci. Total Environ. 2018, 636, 52–60. [Google Scholar] [CrossRef] [PubMed]
- Ma, Z.; Hu, X.; Sayer, A.M.; Levy, R.; Zhang, Q.; Xue, Y.; Tong, S.; Bi, J.; Huang, L.; Liu, Y. Satellite-Based Spatiotemporal Trends in PM2.5 Concentrations: China, 2004-2013. Environ. Health Perspect. 2016, 124, 184–192. [Google Scholar] [CrossRef] [PubMed]
- Xue, W.; Zhang, J.; Zhong, C.; Ji, D.; Huang, W. Satellite-derived spatiotemporal PM2.5 concentrations and variations from 2006 to 2017 in China. Sci. Total Environ. 2020, 712, 134577. [Google Scholar] [CrossRef]
- Ma, Z.; Hu, X.; Huang, L.; Bi, J.; Liu, Y. Estimating ground-level PM2.5 in China using satellite remote sensing. Environ. Sci. Technol. 2014, 48, 7436–7444. [Google Scholar] [CrossRef]
- Lu, D.; Xu, J.; Yang, D.; Zhao, J. Spatio-temporal variation and influence factors of PM2.5 concentrations in China from 1998 to 2014. Atmos. Pollut. Res. 2017, 8, 1151–1159. [Google Scholar] [CrossRef]
- Zhai, L.; Zou, B.; Fang, X.; Luo, Y.; Wan, N.; Li, S. Land Use Regression Modeling of PM2.5 Concentrations at Optimized Spatial Scales. Atmosphere 2017, 8, 1. [Google Scholar] [CrossRef]
- Brokamp, C.; Jandarov, R.; Hossain, M.; Ryan, P. Predicting Daily Urban Fine Particulate Matter Concentrations Using a Random Forest Model. Environ. Sci. Technol. 2018, 52, 4173–4179. [Google Scholar] [CrossRef] [PubMed]
- Wei, J.; Huang, W.; Li, Z.; Xue, W.; Peng, Y.; Sun, L.; Cribb, M. Estimating 1-km-resolution PM2.5 concentrations across China using the space-time random forest approach. Remote Sens. Environ. 2019, 231, 111221. [Google Scholar] [CrossRef]
- Stafoggia, M.; Bellander, T.; Bucci, S.; Davoli, M.; de Hoogh, K.; de’ Donato, F.; Gariazzo, C.; Lyapustin, A.; Michelozzi, P.; Renzi, M.; et al. Estimation of daily PM10 and PM2.5 concentrations in Italy, 2013–2015, using a spatiotemporal land-use random-forest model. Environ. Int. 2019, 124, 170–179. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Lu, D.; Xu, J.; Ye, C.; Zhao, J.; Tian, G.; Wang, X.; Zhu, N. Predicting spatio-temporal concentrations of PM2.5 using land use and meteorological data in Yangtze River Delta, China. Stoch. Environ. Res. Risk Assess. 2018, 32, 2445–2456. [Google Scholar] [CrossRef]
- Di, Q.; Amini, H.; Shi, L.; Kloog, I.; Silvern, R.; Kelly, J.; Sabath, M.B.; Choirat, C.; Koutrakis, P.; Lyapustin, A.; et al. An ensemble-based model of PM2.5 concentration across the contiguous United States with high spatiotemporal resolution. Environ. Int. 2019, 130, 104909. [Google Scholar] [CrossRef]
- Wei, J.; Li, Z.; Lyapustin, A.; Sun, L.; Peng, Y.; Xue, W.; Su, T.; Cribb, M. Reconstructing 1-km-resolution high-quality PM2.5 data records from 2000 to 2018 in China: Spatiotemporal variations and policy implications. Remote Sens. Environ. 2021, 252, 112136. [Google Scholar] [CrossRef]
- Wei, J.; Li, Z.; Xue, W.; Sun, L.; Fan, T.; Liu, L.; Su, T.; Cribb, M. The ChinaHighPM10 dataset: Generation, validation, and spatiotemporal variations from 2015 to 2019 across China. Environ. Int. 2021, 146, 106290. [Google Scholar] [CrossRef]
- Meng, X.; Hand, J.L.; Schichtel, B.A.; Liu, Y. Space-time trends of PM2.5 constituents in the conterminous United States estimated by a machine learning approach, 2005–2015. Environ. Int. 2018, 121, 1137–1147. [Google Scholar] [CrossRef]
- Huang, K.; Xiao, Q.; Meng, X.; Geng, G.; Wang, Y.; Lyapustin, A.; Gu, D.; Liu, Y. Predicting monthly high-resolution PM2.5 concentrations with random forest model in the North China Plain. Environ. Pollut. 2018, 242, 675–683. [Google Scholar] [CrossRef]
- Kashima, S.; Yorifuji, T.; Tsuda, T.; Doi, H. Application of land use regression to regulatory air quality data in Japan 2009. Sci. Total Environ. 2009, 407, 3055–3062. [Google Scholar] [CrossRef] [PubMed]
- Ryan, P.H.; Lemasters, G.K.; Biswas, P.; Levin, L.; Hu, S.; Lindsey, M.; Bernstein, D.I.; Lockey, J.; Villareal, M.; Khurana Hershey, G.K.; et al. A comparison of proximity and land use regression traffic exposure models and wheezing in infants. Environ. Health Perspect. 2007, 115, 278–284. [Google Scholar] [CrossRef] [PubMed]
- Thompson, B. Stepwise Regression and Stepwise Discriminant Analysis Need Not Apply here: A Guidelines Editorial. Educ. Psychol. Meas. 1995, 55, 525–534. [Google Scholar] [CrossRef]
- Lu, D.; Xu, J.; Yue, W.; Mao, W.; Yang, D.; Wang, J. Response of PM2.5 pollution to land use in China. J. Clean. Prod. 2020, 244, 118741. [Google Scholar] [CrossRef]
- Hino, M.; Benami, E.; Brooks, N. Machine learning for environmental monitoring. Nat. Sustain 2018, 1, 583–588. [Google Scholar] [CrossRef]
- Mao, W.; Lu, D.; Hou, L.; Liu, X.; Yue, W. Comparison of Machine-Learning Methods for Urban Land-Use Mapping in Hangzhou City, China. Remote Sens. 2020, 12, 2817. [Google Scholar] [CrossRef]
- Yang, L.; Xu, H.; Yu, S. Estimating PM2.5 concentrations in Yangtze River Delta region of China using random forest model and the Top-of-Atmosphere reflectance. J. Environ. Manag. 2020, 272, 111061. [Google Scholar] [CrossRef]
- Hu, X.; Belle, J.H.; Meng, X.; Wildani, A.; Waller, L.A.; Strickland, M.J.; Liu, Y. Estimating PM2.5 Concentrations in the Conterminous United States Using the Random Forest Approach. Environ. Sci. Technol. 2017, 51, 6936–6944. [Google Scholar] [CrossRef]
- Yang, W.; Deng, M.; Xu, F.; Wang, H. Prediction of hourly PM2.5 using a space-time support vector regression model. Atmos. Environ. 2018, 181, 12–19. [Google Scholar] [CrossRef]
- Gupta, P.; Christopher, S.A. Particulate matter air quality assessment using integrated surface, satellite, and meteorological products: 2. A neural network approach. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef]
- Wei, J.; Li, Z.; Peng, Y.; Sun, L.; Yan, X. A regionally robust high-spatial-resolution aerosol retrieval algorithm for MODIS images over Eastern China. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4748–4757. [Google Scholar] [CrossRef]
- Liu, N.; Zou, B.; Feng, H.; Wang, W.; Tang, Y.; Liang, Y. Evaluation and comparison of multiangle implementation of the atmospheric correction algorithm, Dark Target, and Deep Blue aerosol products over China. Atmos. Chem. Phys. 2019, 19, 8243–8268. [Google Scholar] [CrossRef]
- Lyapustin, A.; Wang, Y.; Korkin, S.; Huang, D. MODIS collection 6 MAIAC algorithm. Atmos. Meas. Tech. 2018, 11, 5741–5765. [Google Scholar] [CrossRef]
- Breiman, L.I.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Wadsworth: Belmont, CA, USA, 1984; p. 40. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Liu, Y.; Cao, G.; Zhao, N.; Mulligan, K.; Ye, X. Improve ground-level PM2.5 concentration mapping using a random forests-based geostatistical approach. Environ. Pollut. 2018, 235, 272–282. [Google Scholar] [CrossRef] [PubMed]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Drucker, H.; Burges, C.J.C.; Kaufman, L.; Chris, J.C.; Kaufman, B.L.; Smola, A.; Vapnik, V. Support Vector Regression Machines. Adv. Neural Inf. Process. Syst. 1997, 28, 779–784. [Google Scholar]
- Rumelhart, D.E.; Mcclelland, J.L. Parallel Distributed Processing; The MIT Press: Cambridge, MA, USA, 1986; pp. 45–76. [Google Scholar]
- Ma, Z.; Liu, Y.; Zhao, Q.; Liu, M.; Zhou, Y.; Bi, J. Satellite-derived high resolution PM2.5 concentrations in Yangtze River Delta Region of China using improved linear mixed effects model. Atmos. Environ. (1994) 2016, 133, 156–164. [Google Scholar] [CrossRef]
- Jiang, M.; Sun, W.; Yang, G.; Zhang, D. Modelling Seasonal GWR of Daily PM2.5 with Proper Auxiliary Variables for the Yangtze River Delta. Remote Sens. 2017, 9, 346. [Google Scholar] [CrossRef]
- She, Q.; Choi, M.; Belle, J.H.; Xiao, Q.; Bi, J.; Huang, K.; Meng, X.; Geng, G.; Kim, J.; He, K.; et al. Satellite-based estimation of hourly PM2.5 levels during heavy winter pollution episodes in the Yangtze River Delta, China. Chemosphere 2020, 239, 124678. [Google Scholar] [CrossRef]
- Chen, K.; Wang, M.; Huang, C.; Kinney, P.L.; Anastas, P.T. Air pollution reduction and mortality benefit during the COVID-19 outbreak in China. Lancet Planet. Health 2020, 4, e210–e212. [Google Scholar] [CrossRef]
- Li, L.; Li, Q.; Huang, L.; Wang, Q.; Zhu, A.; Xu, J.; Liu, Z.; Li, H.; Shi, L.; Li, R.; et al. Air quality changes during the COVID-19 lockdown over the Yangtze River Delta Region: An insight into the impact of human activity pattern changes on air pollution variation. Sci. Total Environ. 2020, 732, 139282. [Google Scholar] [CrossRef] [PubMed]
- Xian, T.; Li, Z.; Wei, J. Changes in air pollution following the COVID-19 epidemic in Northern China: The role of meteorology. Front. Environ. Sci. 2021, 1–9. [Google Scholar] [CrossRef]
- Wang, M.; Liu, F.; Zheng, M. Air quality improvement from COVID-19 lockdown: Evidence from China. Air Qual. Atmos. Health 2020, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Mahato, S.; Pal, S.; Ghosh, K.G. Effect of lockdown amid COVID-19 pandemic on air quality of the megacity Delhi, India. Sci. Total Environ. 2020, 730, 139086. [Google Scholar] [CrossRef]
- Chauhan, A.; Singh, R.P. Decline in PM2.5 concentrations over major cities around the world associated with COVID-19. Environ. Res. 2020, 187, 109634. [Google Scholar] [CrossRef]


| Datasets | Format | Source |
|---|---|---|
| PM2.5 | Table | Ministry of Ecology and Environment, China |
| AOD | Grid | 1-km MODIS MAIAC AOD |
| Meteorological | Table | China Meteorological Administration |
| Elevation | Grid | Geospatial data cloud of China |
| POIs | Point features | Gaode Map Services, China |
| Road network | Line features | Open Street Map |
| Boundary maps | Line features | Open Street Map |
| Category | Counts | Category | Counts |
|---|---|---|---|
| Food & Beverages | 962,507 | Auto Service | 127,669 |
| Road Furniture | 3619 | Auto Repair | 53,193 |
| Tourist Attraction | 35,668 | Auto Dealers | 25,941 |
| Public Facility | 79,557 | Commercial House | 242,212 |
| Enterprises | 874,211 | Daily Life Service | 836,412 |
| Shopping | 1,959,948 | Sports & Recreation | 109,452 |
| Transportation Service | 349,160 | Pass Facilities | 393,393 |
| Finance & Insurance Service | 85,445 | Medical Service | 138,940 |
| Science/Culture & Education Service | 244,247 | Governmental Organization & Social Group | 232,836 |
| Motorcycle Service | 10,517 | Accommodation Service | 106,669 |
| RF | SVR | ANN | |||||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | MAE | RMSE | R2 | MAE | RMSE | R2 | MAE | RMSE | |
| 2019-I | 0.938 | 1.663 | 2.696 | 0.740 | 2.148 | 5.522 | 0.739 | 3.582 | 5.538 |
| 2020-I | 0.917 | 1.026 | 1.413 | 0.705 | 1.521 | 2.663 | 0.559 | 2.476 | 3.258 |
| Related Study | Model | Model Fitting | Model Validation | Spatial Resolution | ||||
|---|---|---|---|---|---|---|---|---|
| R2 | MAE | RMSE | R2 | MAE | RMSE | |||
| Ma et al. (2016) | LME | 0.771 | - | 16.72 | 0.725 | - | 18.30 | 3 km |
| Jiang et al. (2017) | GWR | 0.838 (spring) | - | 12.84 | 0.753 (spring) | - | 16.12 | 10 km |
| 0.85 (summer) | - | 6.18 | 0.74 (summer) | - | 8.29 | |||
| 0.915 (autumn) | - | 9.86 | 0.882 (autumn) | - | 12.33 | |||
| 0.867 (winter) | - | 16.34 | 0.785 (winter) | - | 21.15 | |||
| Yang et al. (2018) | STM | 0.86 | - | 8.15 | 0.63 | - | 4.22 | 3 km |
| She et al. (2020) | T-SSM | - | - | - | 0.72 | - | 23 | 6 km |
| Out study | RF | 0.938 (2019-I) | 1.663 | 2.696 | 0.77 (2019-I) | 3.914 | 4.756 | 1km |
| 0.917 (2020-I) | 1.026 | 1.413 | 0.691 (2020-I) | 2.353 | 3.144 | 1km |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, D.; Mao, W.; Zheng, L.; Xiao, W.; Zhang, L.; Wei, J. Ambient PM2.5 Estimates and Variations during COVID-19 Pandemic in the Yangtze River Delta Using Machine Learning and Big Data. Remote Sens. 2021, 13, 1423. https://doi.org/10.3390/rs13081423
Lu D, Mao W, Zheng L, Xiao W, Zhang L, Wei J. Ambient PM2.5 Estimates and Variations during COVID-19 Pandemic in the Yangtze River Delta Using Machine Learning and Big Data. Remote Sensing. 2021; 13(8):1423. https://doi.org/10.3390/rs13081423
Chicago/Turabian StyleLu, Debin, Wanliu Mao, Lilin Zheng, Wu Xiao, Liang Zhang, and Jing Wei. 2021. "Ambient PM2.5 Estimates and Variations during COVID-19 Pandemic in the Yangtze River Delta Using Machine Learning and Big Data" Remote Sensing 13, no. 8: 1423. https://doi.org/10.3390/rs13081423
APA StyleLu, D., Mao, W., Zheng, L., Xiao, W., Zhang, L., & Wei, J. (2021). Ambient PM2.5 Estimates and Variations during COVID-19 Pandemic in the Yangtze River Delta Using Machine Learning and Big Data. Remote Sensing, 13(8), 1423. https://doi.org/10.3390/rs13081423