Abstract
We manually mapped particles ranging in longest axis from 0.3 cm to 95 m on (101955) Bennu for the Origins, Spectral Interpretation, Resource Identification, and Security–Regolith Explorer (OSIRIS-REx) asteroid sample return mission. This enabled the mission to identify candidate sample collection sites and shed light on the processes that have shaped the surface of this rubble-pile asteroid. Building on a global survey of particles, we used higher-resolution data from regional observations to calculate particle size-frequency distributions (PSFDs) and assess the viability of four candidate sites for sample collection (presence of unobstructed particles ≤ 2 cm). The four candidate sites have common characteristics: each is situated within a crater with a relative abundance of sampleable material. Their PSFDs, however, indicate that each site has experienced different geologic processing. The PSFD power-law slopes range from −3.0 ± 0.2 to −2.3 ± 0.1 across the four sites, based on images with a 0.01-m pixel scale. These values are consistent with, or shallower than, the global survey measurements. At one site, Osprey, the particle packing density appears to reach geometric saturation. We evaluate the uncertainty in these measurements and discuss their implications for other remotely sensed and mapped particles, and their importance to OSIRIS-REx sampling operations.
1. Introduction
Particles formed from geologic processes, from dust to boulders, typically have a scale-invariant and fractal frequency versus size relationship due to the natural process of fragmentation [1]. This relationship can be modeled with a fractal (power-law), Weibull, exponential, or log-normal distribution, with varying success depending on the dataset.
In planetary science, the methods for calculating particle size-frequency distributions (PSFDs) are similar to those for calculating crater size-frequency distributions, which have long been used to estimate the ages of many planetary surfaces (e.g., [2,3]). The goal of determining PSFDs is often to assess candidate landing or sampling sites (e.g., [4,5,6,7]) and to understand the geophysical processes responsible for shaping a planetary surface (e.g., [8,9,10,11,12,13]). For example, on the Moon, PSFDs have been used to understand rock breakdown and regolith evolution rates (e.g., [14,15]). PSFDs are also often used to understand impact processes, including the formation of secondary craters (e.g., [16,17,18]). Much of this work is done through remote sensing by mapping and measuring particles that appear in images (apart from the Apollo samples returned to Earth, which were sieved; e.g., [19]). Particles are measured either by their longest axis, their two longest axes, all three axes, or a full polygonal outline of the visible extent.
NASA’s OSIRIS-REx sample return mission [20] conducted particle size measurements on asteroid (101955) Bennu. These measurements were needed to assess the feasibility of sample collection by the OSIRIS-REx Touch-And-Go Sample Acquisition Mechanism (TAGSAM; [21,22]). These measurements also enabled us to draw conclusions about the geophysical processes on Bennu and make comparisons with other planetary bodies. The importance of PSFDs became more crucial after arrival at Bennu revealed a surface dense with boulders and less sampleable material than anticipated [23].
A global PSFD of Bennu’s surface was calculated by DellaGiustina and Emery et al. [24] using images acquired during the spacecraft’s approach to the asteroid. Regional-scale (local) PSFDs were used to estimate the amount of sampleable material at four candidate sample sites on Bennu and to refine the coordinates for spacecraft targeting during the Touch-And-Go sampling maneuver [24,25]. The global and local analyses for sample-site selection relied on two assumptions: that the PSFD calculated from meter-sized particles could be extrapolated to constrain the PSFD of centimeter-sized particles, and that remotely sensed measurements could accurately reproduce ground truth measurements.
Here, we present local PSFDs from high-resolution images, in context with the global results, with particle sizes ranging in longest axis from 0.3 cm to 95 m. Our results provide insight into the differing geologic processes at work on Bennu’s surface. These data were also key in the selection of Nightingale crater as the OSIRIS-REx primary site. Lastly, we comment on improvements that could be made in the future by similar missions.
2. Materials and Methods
2.1. Background
The OSIRIS-REx TAGSAM [21] was designed to ingest particles smaller than 2 cm in the longest dimension, defined here as sampleable regolith. Larger particles would reduce the efficiency of collection (particles > 5 cm in longest dimension) or block the sampling mechanism completely (particles > 21 cm in longest dimension, [21]). With the mission’s requirement of returning at least 60 g of regolith from Bennu to Earth, it was imperative to map particles on the surface to identify regions of interest (ROIs). We define particles as features of positive relief with a well-defined perimeter, characterized by an elongated shadow at large phase angles (consistent with the definition in [24]; Figure 1). Much like asteroid (162173) Ryugu [26], the target of the JAXA Hayabusa2 mission, particles on Bennu have varied geomorphic characteristics and many are partially buried, which makes identifying particle perimeters difficult. Furthermore, mapping performed on lower-spatial-resolution data will miss particles that can only be identified in higher-spatial-resolution images (see Figure 1).

Figure 1.
Close-up examples of images of Bennu’s surface with and without mapped particles. This example falls within the Nightingale region. Illumination conditions and pixel resolution are included for context. We define incidence as the angle between the light vector and the surface normal (Sun-Bennu-surface normal), emission as the angle between the observation vector and the surface normal (OCAMS-Bennu-surface normal), and phase as the angle between the light vector and observation vector (Sun-Bennu-OCAMS).
2.2. Mapped Image Datasets
Particle mapping was performed on images that were radiometrically calibrated [27] and registered to shape models of the asteroid and to each other [28], but not map-projected. A summary of the image datasets used is provided in Table 1. In most cases, multiple images were required to map all of the particles in a given scene, and the lowest emission-angle images were prioritized to minimize foreshortening and other projection effects. Particles were mapped on individual images first, then the particle measurement data were combined and cartographically projected onto an image mosaic for visualization.

Table 1.
Summary of the image datasets used for particle mapping. Image datasets are grouped by global or sample site location. The number of unique image/user pairs (when greater than 1) denotes when images were mapped by more than one user. In cases where this value does not match the total number of images mapped, a modified DBSCAN clustering algorithm was used to combine and reduce the dataset.
DellaGiustina and Emery et al. [24] mapped particles at a global scale (~0.42 m/px) on images taken by the OSIRIS-REx Camera Suite (OCAMS) PolyCam panchromatic imager [29] during the Approach phase of the mission [20,30] (Figure 2a). This image dataset allowed the OSIRIS-REx team to identify ROIs on Bennu’s surface that warranted more study before being classified as candidate sample sites. As the team obtained higher-resolution imagery throughout the subsequent mission phases, the size and location of the ROIs used for particle mapping varied (Figure 2b). These variations were partly driven by mission schedule—as image resolution increased, there were more particles to count. Refinements were also made to optimize sample collection and avoid unsafe terrain and large hazardous particles (boulders).
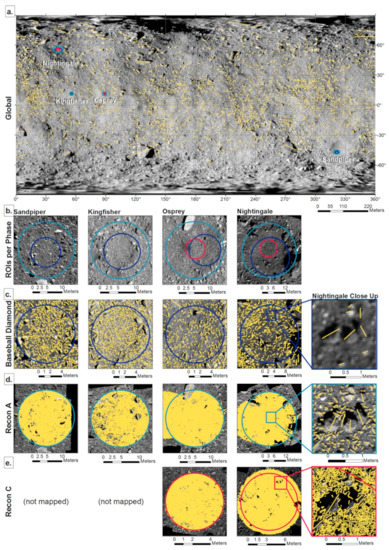
Figure 2.
Compilation of mapped particles in each mission phase. (a). Global counts re-produced from DellaGiustina and Emery et al. [24] with the four candidate sample sites are shown. (b). Change in the region of interest (ROI) size and location per imaging campaign is plotted on Baseball Diamond (BBD) images used for particle mapping for each of the four candidate sample sites. (c). Particles mapped during the BBD imaging campaign for each of the four candidate sample sites. (d). Particles mapped during the Recon A imaging campaign for each of the four candidate sample sites. (e). Particles mapped during the Recon C imaging campaign for each of the four candidate sample sites. The panels on the far right of (c–e) show close-ups of the counts made for Nightingale.
The Detailed Survey phase [20,30] of the mission included the Baseball Diamond (BBD) imaging campaign, which provided global image data at ~0.05 m/px [25,31]. We performed detailed mapping of 16 ROIs. Analyses of these particle measurements, together with other data products and logistical information, informed the selection of four candidate sample sites, named Nightingale, Osprey, Sandpiper, and Kingfisher [30]. The particles mapped during BBD for each of the candidate sites are shown in Figure 2c.
After selection of these final four candidate sites came the Reconnaissance (Recon) phase [20,30] of the mission, which included two imaging campaigns specific to particle mapping: Recon A and Recon C. Recon A mapping efforts (Figure 2d) demonstrated a notable improvement over the mapping performed during BBD due to higher image resolution with a pixel scale of 0.01 m/px, which allowed mappers to more easily discern particle edges than in BBD images, thus assisting the team in the final selection of the primary and backup sample sites: Nightingale and Osprey. Recon C mapping was only performed for Nightingale and Osprey, and the collected particle measurements helped the team confirm the presence of sampleable regolith at both sites as the pixel scale (~0.004 m) allowed for the identification of particles that could be ingested by TAGSAM (Figure 2e).
2.3. Particle Mapping Team and GIS Environment
For each mission phase, particles were manually identified by their longest axis dimension with polylines using ArcMap, part of the Environmental Systems Research Institute’s (ESRI) [32] geospatial information system (GIS) software. The GIS environment enabled us to explore the geospatial connection between the mapped particles and the geometry layers, included as backplanes in a multilayer image cube file, using the Integrated Software for Imagers and Spectrometers 3 (ISIS3) [33]. Pixel backplane values were assigned using ISIS3′s spiceinit routine and the approved shape model version in use in each mission phase. The values were refined using manual and automated photogrammetric registration [28]. Particle long-axis length was calculated using the Cartesian distance formula with the endpoints determined from the geometry backplanes. The decision to measure particles only by longest axis dimension was due to the tight operational schedule, which could not accommodate the increased time needed to map more detailed particle shapes.
The membership of the particle mapping team changed over the course of the mission. As a result, the team composition was not consistent across mission phases or sample site regions. To account for the uncertainty introduced by different mappers [34], we developed mapping criteria for identifying particles and relied on expert verification of all mapped images. After a member of the particle mapping team completed an image, an expert mapper reviewed the image to evaluate whether all visible particles ≥4 pixels across were identified and to remove any incorrect identifications. Generally, a minimum of 4 pixels across is required to identify a feature [35]. Where there was overlap between mappers on images, we employed a modified DBSCAN [36] clustering algorithm to combine and reduce the dataset.
We used the GIS environment to calculate the reference surface area of each mapped region from shape models of Bennu. This value allows us to derive a cumulative frequency of particles normalized by area, providing the ability to make meaningful comparisons among regions with varying sizes of mapped areas. The shape models created for Bennu represent the surface with triangular facets where each vertex has a body-fixed Cartesian coordinate [37,38]. The high-resolution (5-cm grid spacing) regional models are uniformly spaced grids of height values above a planar surface averaged over the region. They were converted to triangular facets using the gridded heights as vertices. To calculate surface area, we identified all facets intersecting the mapped image set. Since the shape is uniformly spaced on a projected plane, all facets have the same projected area. We report the projected grid areas of the facets with points falling within the surface area mapped. This process avoids having the facet resolution and small-scale tilts affect the computed surface area.
2.4. Evaluating Particle Measurements and Calculating the PSFD
To assess the completeness of the particle measurements and to make predictions about the proportion of unresolved fine-particulate material at a given ROI, we calculated the PSFDs and their best fit distribution. Relying on the assumption that PSFDs calculated from meter-sized particles could constrain the PSFDs of centimeter-sized particles due to their fractal frequency versus size relationship, we used a fractal distribution (a power law) to model PSFDs of Bennu. Previous work has demonstrated that this is an acceptable assumption [39], and DellaGiustina and Emery et al. [24] showed that a power law provides a reasonable fit to the global cumulative PSFD of Bennu. Power-law fits are common in planetary science because the straightforward relationship allows for streamlined analysis and comparison with other planetary bodies (e.g., [4,10,11,40,41,42,43]). Power-law PSFDs have the form
where NC is the cumulative number of particles greater than or equal to D per surface area unit, D is the longest axis particle measurement, a is the power-law index, and c is the coefficient of proportionality.
NC = cD−a,
We can also evaluate PSFDs by plotting the binned frequency of particle measurements as opposed to the cumulative unbinned frequency. This is referred to as a differential frequency plot. We can fit a power law to the differential frequency data that has the form
where dN/dD is the number of particles in the given size bin per surface area, b is the power-law index, and k is the coefficient of proportionality. As the differential frequency plot is the derivative of the cumulative frequency plot, these two power-law fits are connected through their exponent, and, therefore, we expect b = a + 1, though this is rarely seen in practice due to variation within naturally occurring phenomena such as particle size. In this work, we use bin widths that progressively increase by √2 m, with the first bin edge starting at 0.2 cm. This allows us to account for the disproportionate number of particles at small scales.
dN/dD = kD−b,
A third way to evaluate PSFDs involves plotting the differential frequency normalized by a power law with an index of −3. This is known as a relative frequency or R plot. This type of plot can be used to gauge the spatial density of a given particle size bin. Here, we use the same binning scheme as the differential frequency plot. For crater size-frequency distributions, this type of plot is used to evaluate the level of crater saturation (e.g., [44]).
In a double-logarithmic plot, a power law appears as a straight line, where the slope of the line is equal to the power-law index. Power laws are generally fit between a given particle-size range as smaller particles tend to be undersampled. The smallest meaningful measurement in the data set defines the completeness limit. In a double-logarithmic plot, this value often occurs where the particle measurement data appear to ‘roll over’ and depart from the power-law fit, but not always. This limit may or may not be a real attribute of the PSFD. Ultimately, it is constrained by image spatial resolution limits, human factors in identifying small features, and illumination conditions (which can reduce edge contrast) [39,45].
We use the Clauset et al. [46] technique for fitting a power law and identifying the completeness limit. In this method the completeness limit is determined using the Kolmogorov–Smirnov statistic, minimizing the difference between the data and the best-fit power law. Then, the power-law index is determined by method of maximum likelihood. Uncertainty for both of these values is the standard error, determined through a non-parametric bootstrap. DeSouza et al. [47] demonstrated the improved performance of the Clauset et al. [46] technique for PSFDs calculated for asteroid Itokawa.
We also assume that particle frequency follows a Poisson detection distribution as suggested by the Crater Analysis Techniques Working Group [48]. This assumption allows us to capture the uncertainty in particle frequency by plotting the square root of NC for each particle measurement. Presenting our results in this manner facilitates comparison with previously calculated PSFDs of other solar system bodies.
2.5. Connecting Remotely Sensed Measurements to Ground Truth
To evaluate our assumption that remotely sensed measurements could accurately reproduce ground truth measurements, we prepared analog surface rock trays with predetermined PSFDs described by power laws with indices between −3 to −2 to conduct a small laboratory study. Rocks were manually layered in several trays from largest to smallest, glued in place, and spray-painted matte black to simulate asteroid surface conditions. We imaged these trays to simulate illumination conditions with 40° incidence (angle between the light vector and the surface normal, i.e., Sun-Bennu-surface normal), 0° emission (angle between the observation vector and the surface normal, i.e., OCAMS-Bennu-surface normal), and 40° phase (angle between the light vector and observation vector, i.e., Sun-Bennu-OCAMS) to provide a test data set for remote measurements. Nearly every mapper involved in our study (13 total) mapped particles in at least one of the trays to determine the accuracy of their remotely sensed particle measurements as compared to ground-truth caliper measurements (Figure 3).

Figure 3.
Rock Tray 1 from the OSIRIS-REx particle measurement uncertainty analysis with remotely measured counts overlaid. Counts were performed in the same ArcMap mapping environment used for mission operations. Counters who mapped in ArcMap mapped the full image, but ground-truth caliper measurements were only collected for 85 of these rocks (shown in light blue).
The team mapped the particles in these trays at different points in the mission, resulting in varying levels of detail. An initial group tested mapping and data flow processes with one of the tray images prior to the OSIRIS-REx spacecraft’s arrival at Bennu. A second group of mappers performed this task after mapping particles on Bennu. The two groups differed only in the total number of mapped particles identified per mapper, where experience with mapping on Bennu led to an increased number of particle identifications in the rock tray. It is worth re-iterating that all particle mapping performed on Bennu was verified by at least one independent, experienced mapper.
We collected 85 caliper measurements from a random subset of the particles within the tray by viewing the tray from an approximately nadir position (camera pointed directly down, centered over the tray such that the lens is parallel with the plane of the rock tray) and then measuring the visible longest axis. Two separate mappers performed this step, averaging the results to obtain ground truth. Then, we manually clustered the ‘remotely sensed’ particles in ArcMap based on spatial location to compare with these ground truth caliper measurements. We estimated particle lengths using the image pixel scale, which we then compared to the ground truth caliper measurements (Figure 4).
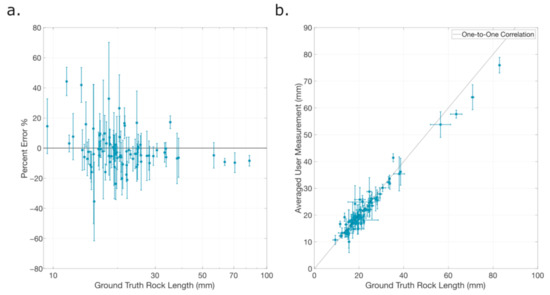
Figure 4.
(a). Percent error between remotely sensed and ground-truth measurements. (b). Correlation plot between caliper measurements and remotely sensed measurements. Both panels demonstrate the slight trend of overestimating the measurement of small particles and underestimating the measurement of large particles. Vertical error bars represent the uncertainty in the remote measurements amongst all of the counters. Horizontal error bars represent the uncertainty in the caliper measurements.
We found that a majority of particles (~68%) were underestimated in size by the remotely-sensed mapping. For the most part this difference was small, with ~69% of particle measurements falling within 5% error of the ground truth measurement and ~89% of particle measurements falling within 20% error of the ground truth measurement. We also compared the PSFDs between the two measurement sets (Figure 5). The power-law fits applied to the data have similar completeness limits, but the power-law index for the remotely sensed data is shallower than that of the ground truth data, though it falls within the uncertainty.
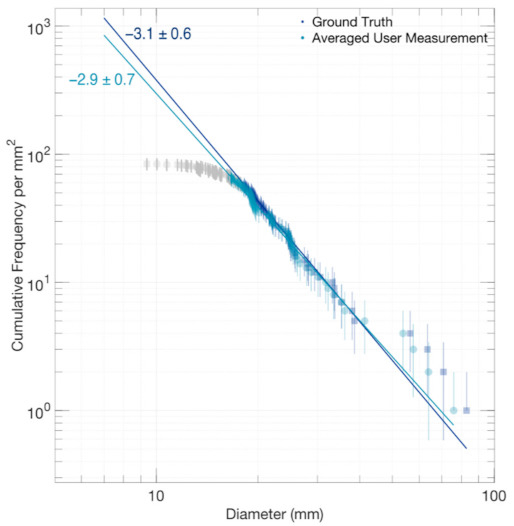
Figure 5.
Cumulative PSFDs of caliper measurements and remotely sensed measurements. Light gray points indicate particle measurements that were smaller than the completeness limit. Error bars represent Poisson detection distribution uncertainty (square root of NC).
Given that these power-law uncertainties overlap, we cannot conclusively state whether a measurement bias exists or would be strong enough to impact the PSFD determined through remotely-sensed measurements.
3. Results
The global set of particle measurements from the OSIRIS-REx Approach phase presented in DellaGiustina and Emery et al. [24] included 3136 unique particles (Figure 2a). We identified between 269 and 556 unique particles for each of the candidate sample sites during BBD (Figure 2c) and between 5111 and 17,867 unique particles during Recon A (Figure 2d). During Recon C (Figure 2e), we identified 26,171 unique particles at Nightingale and 28,929 unique particles at Osprey. Using the approach described in Section 2, we calculated the PSFDs and identified the best-fitting power laws, which involved determining the completeness of each dataset. Table 2 summarizes the particle mapping effort performed during each mission phase and the resulting best fit power-law parameters. Figure 6 presents the cumulative PSFDs of the four candidate sample sites as calculated for BBD, Recon A, and (only Nightingale and Osprey) Recon C.

Table 2.
Summary of particles mapped for each of the four candidate sample sites at various mission phases. Recon C mapping was only performed for the primary and back-up sample sites, Nightingale and Osprey. The surface area mapped for the global set of particle measurements has been updated from that reported in DellaGiustina et al. [24]. Unlike [24] we included the Roc (95 m) which slightly improved the estimated completeness limit.
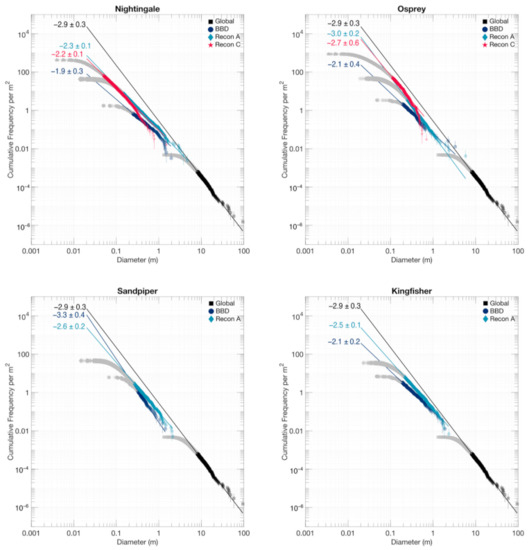
Figure 6.
Cumulative PSFDs of Bennu for the four candidate sample sites as calculated at several key mission phases. Recon C mapping was only performed for the primary and back-up sample sites, Nightingale and Osprey. The global PSFD calculated from early OSIRIS-REx images of Bennu by DellaGiustina and Emery et al. [24] is included as a reference. Light gray points indicate particle measurements that were smaller than the completeness limit.
The global PSFD of Bennu from DellaGiustina and Emery et al. [24], which included particles measuring between 1 and 58 m in longest axis with a best fitting power-law index of −2.9 ± 0.3 applying for particles 8 m and larger, is included for reference with a correction to the value used for area normalization to reflect the true surface area mapped as opposed to the surface area of the full global surface. We also updated these particle measurements to include the Roc (95 m; the largest cogent feature on the surface), which was previously excluded as its full particle extent could not be ascertained in lower-resolution imagery.
The power-law indices of the candidate sample sites across different mission phases suggests the use of the global PSFD to constrain expectations for site-specific PSFDs was reasonable, despite local variability. The power-law fit to the global set of measurements consistently overestimated the number of small particles present at each of the candidate sample sites. This observation is not surprising given that power-law fits are only applicable for particle sizes larger than the completeness limit and these four candidate sample sites were selected for their relative scarcity of large (hazardous) particles. However, the global power-law index provides an upper bound for all four-local power-law indices. The uncertainties in the power-law indices obtained for particles mapped during BBD are relatively high, likely as a consequence of the proportionally fewer counts; less than 600 particles were identified for each candidate sample site. At the time, these datasets were sufficient for mission operational decisions by making relative comparisons and assuming consistent mapping coverage.
Based on the detailed mapping performed during Recon A, we see a shallower power-law index for Nightingale (−2.3 ± 0.1), Kingfisher (−2.5 ± 0.1), and Sandpiper (−2.6 ± 0.2), whereas Osprey (−3.0 ± 0.2) has a power-law index closer to that of the global surface (−2.9 ± 0.3). However, accounting for uncertainty in the power-law index, the PSFD power-law fits determined for Sandpiper and Kingfisher fall within the uncertainty of the PSFD power-law fit determined for global Bennu. Recon C measurements produced PSFDs with similar power-law indices to those calculated for Recon A for Nightingale (−2.2 ± 0.1) and Osprey (−2.7 ± 0.6), yet both distributions visibly depart from the power-law fit (the distribution is more curved than linear), suggesting that a single power law may not fully describe the distribution of particles in these regions at this scale. In particular, the large uncertainty in Osprey’s power-law index supports this conclusion. A similar effect was observed on asteroid Itokawa for particle sizes smaller than 1 m [39] and comparable trends have been observed on other bodies (e.g., [5,49,50,51]).
Plotting the same data in the differential frequency version of the PSFD plot (Figure 7) shows that the completeness limit identified through the Clauset et al. [46] method only aligns with the peak of the differential frequency data in the case of BBD, which had the smallest number of particle measurements. The Clauset et al. [46] technique identifies a completeness limit that maximizes the goodness of fit for the resulting power-law function. Thus, we cannot use this limit to distinguish between observation bias (e.g., image resolution) and physical processes (e.g., size sorting) as the cause for PSFDs departing from the power-law fit at small particle sizes.
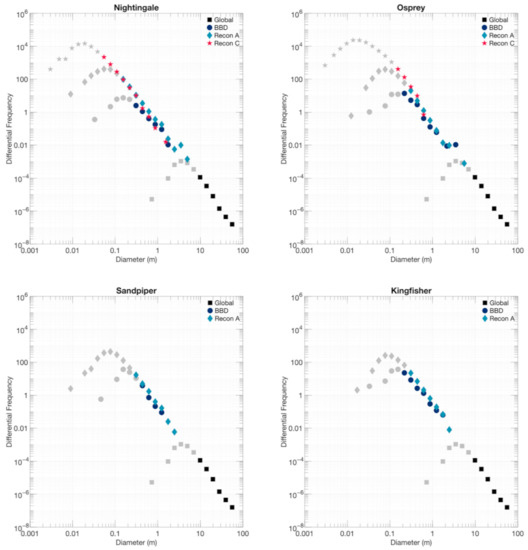
Figure 7.
Differential PSFDs of Bennu for the four candidate sample sites as calculated at several key mission phases. Recon C mapping was only performed for the primary and back-up sample sites, Nightingale and Osprey. The global PSFD calculated from early OSIRIS-REx images of Bennu by DellaGiustina and Emery et al. [24] is included as a reference. Light gray points indicate particle measurements that were smaller than the completeness limit.
The Recon C Osprey PSFD exhibits distinct behavior when plotted in relative frequency (Figure 8). For the global measurements and all measurements performed at Nightingale, Sandpiper, and Kingfisher, relative frequency (R) values level off, with R around 0.4. Kingfisher exhibits a slight increase in relative frequency with the peak occurring around an R of 0.5. Osprey, however, does not level off; its R exceeds 1 for particles measured in Recon C images. It appears that Osprey is geometrically saturated with particles measuring between 10 and 30 cm in longest axis. This is further discussed in Section 4.2.
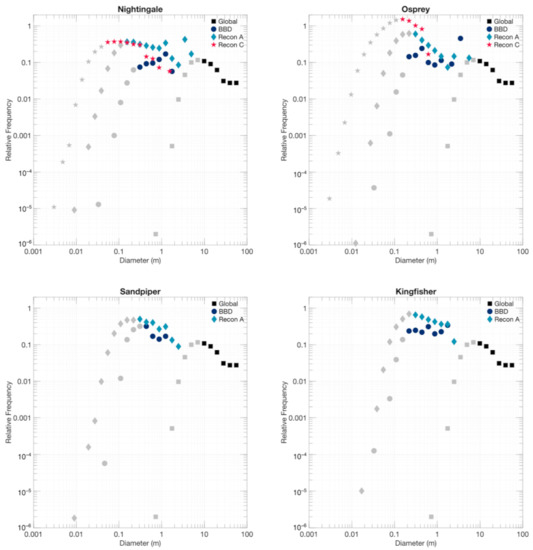
Figure 8.
Relative PSFDs of Bennu for the four candidate sample sites as calculated at several key mission phases. Recon C mapping was only performed for the primary and back-up sample sites, Nightingale and Osprey. The global PSFD calculated from early OSIRIS-REx images of Bennu by DellaGiustina and Emery et al. [24] is included as a reference. Light gray points indicate particle measurements that were smaller than the completeness limit.
For discussion purposes, we also present merged datasets in the cumulative PSFD plot type. We present this in two stages for clarity: a merged dataset for each mission phase (Figure 9) and a single merged dataset (Figure 10). To obtain a merged dataset for each mission phase, we combined the counts made for each of the candidate sample sites and normalized by their cumulative area. Then, to obtain a single merged dataset, we combine counts as follows: the minimum measurement from Recon C to the largest measurement smaller than the completeness limit for merged Recon A, the completeness limit for merged Recon A to the largest measurement smaller than the completeness limit for the global counts, and the completeness limit for the global counts to the Roc (95 m). We exclude merged BBD as the counts in this size range are better captured by the merged Recon A data.
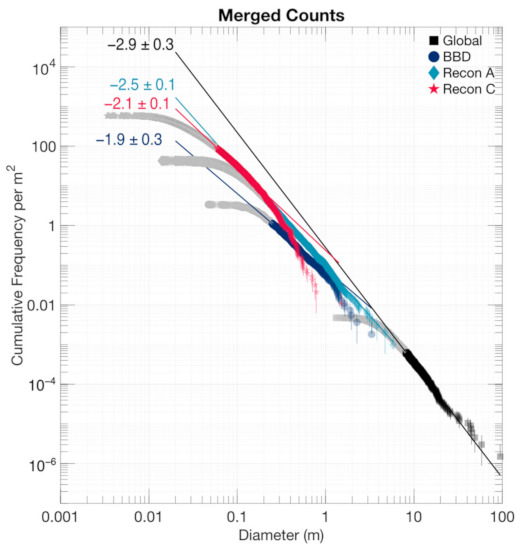
Figure 9.
Cumulative PSFDs of Bennu using merged measurements based on the four key mission phases. The global PSFD calculated from early OSIRIS-REx images of Bennu by DellaGiustina and Emery et al. [24] is included as a reference. Light gray points indicate particle measurements that were smaller than the completeness limit.
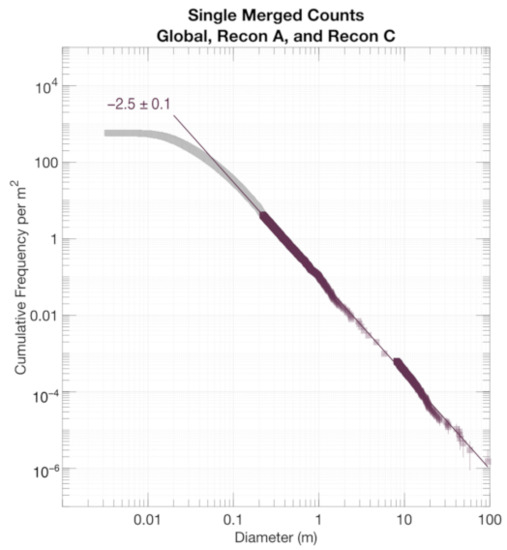
Figure 10.
Cumulative PSFD of Bennu based on measurements merged into a single dataset. Light gray points indicate particle measurements that were smaller than the completeness limit.
The goal of this presentation is to simplify variation among the different sites and present a single, representative PSFD of Bennu. Though interesting for discussion, this PSFD likely represents only the lower bound of Bennu’s full surface particle frequency distribution as each of the sample sites was chosen for its scarcity of large particles. Notably, this dataset is lacking in measurements between 3 to 7 m, which can be attributed to the way data was culled from the four mission phases in our analysis to produce the single merged dataset, which prioritized the completeness of measurement data. The power-law index of the single merged dataset is −2.5 ± 0.1.
Particle densities also vary across each of the four sites. In Recon A we observed particle densities (particles per square meter) for Nightingale, Osprey, Sandpiper, and Kingfisher to be 1.4, 2.0, 2.1, and 2.9, respectively, for particles greater than 30 cm. For Recon C, Nightingale and Osprey had particle densities of 6.0 and 24.7, respectively, for particles greater than 15 cm. Particle density also varied within each of the four sample sites, as evidenced in Figure 2b. For example, the area directly south of the Recon C ROI for Nightingale would have increased particle density based on the presence of the four large particles alone. The team calculated particle densities and localized power-law fits within each of the sample sites in order to optimize potential sample coordinates to prioritize spacecraft safety and the likelihood of sampling success. The relatively low particle density of Nightingale was one reason this site was ultimately chosen for sampling.
4. Discussion
4.1. Properties of Bennu Discernable from the PSFDs
On the basis of Bennu’s relatively shallow global power-law index, the observation of very large, intact particles, and comparisons with asteroids (25143) Itokawa and (162173) Ryugu, DellaGiustina and Emery et al. [24] proposed that the largest particles (boulders ≥20 m) on Bennu’s surface were left over from the catastrophic parent body disruption [52,53,54] and that smaller particles (<20 m) were likely broken down by surface impacts [55] and degradation processes due to thermal fatigue [56,57]. With the detailed mapping performed for the candidate sample sites during Recon A and the primary and backup sites (Nightingale and Osprey) during Recon C, we further analyze the processes responsible for the generation and degradation of smaller particles. However, given that the four candidate sample sites were chosen specifically for their expected higher-than-average abundance of sampleable regolith, the geophysical processes active at these sites may not be representative of those active across the global asteroid surface.
Processes observed on Bennu include space weathering [58]; thermal fracturing [57]; impact cratering at large [52,59] and small [55] scales; mass movement due to surface slope changes, which likely results in abrasion and breakdown at large scales and equatorial deposition [60]; and particle ejection events [23,61]. Each of these physical mechanisms can result in particle fragmentation, thereby influencing the PSFD observed for particles at different size ranges. In early observations of Bennu, DellaGiustina and Emery et al. [24] found evidence of a multimodal particle population having distinct normal albedo ranges and PSFDs. Recent work has confirmed the presence of at least two distinct particle populations on the basis of spectral, geomorphologic [58], and thermal [62] analyses: (i) a high-reflectance, high-thermal-inertia population of smooth, angular particles, all of which are smaller than ~20 m, and (ii) a more common low-reflectance, low-thermal-inertia population of rough, hummocky particles that spans the full-size range of measured objects (up to ~100 m). Both are present within the candidate sample sites (Figure 11) [63] suggesting that Bennu’s heterogeneity [58] extends to small scales (<1 m). This heterogeneity likely influences the observed PSFD as fragmentation may affect the two particle populations on different time scales.
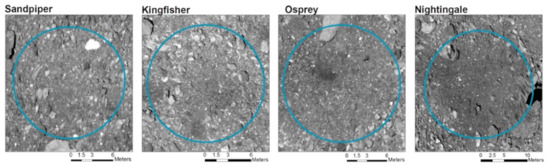
Figure 11.
Close-ups of the four candidate sample sites from a global normal albedo map of Bennu [64] showing that both comparatively bright and dark materials are present. ROIs shown (blue circles) are from Recon A.
Each of the candidate sample sites are situated within an impact crater [30,52,59], which likely influenced the PSFD in the region. Turcotte [1] compiled the power-law indices of common terrestrially fragmented objects, with most types of fragmentation resulting in a power-law index between −2.0 and −3.0. The power-law indices identified for the candidate sample site PSFDs generally fall within this range. Nightingale’s power-law index is the closest to −2.0 of the four candidate sample sites (on the basis of Recon A and Recon C PSFDs). Power-law indices closer to −2.0 have been associated with time-dependent disaggregation (as opposed to impact-generated disaggregation; [2]); however, it is not clear that this type of process is what drives the PSFD at Nightingale given the low gravity environment of Bennu and the geomorphological setting of the site. Indeed, Nightingale is situated within a freshly exposed crater [58] and thus would be expected to have a power-law index indicative of recent impact cratering (between −2.5 to −3.0; [64]). This potential discrepancy in interpreting the geologic processes present at Nightingale based on the obtained power-law index, whether due to the relatively young age of the crater or specific local properties of the underlying site, will be resolved following analysis of the returned sample.
On the other hand, Osprey is closest to −3.0, a value which Hartmann [2] attributed to grinding and compound fragmentation processes. Osprey is a redder-than-average crater and thus also hypothesized to be geologically young [58]. Though its power-law index is in line with the expectations for a surface that experienced impact cratering, Osprey’s location on the equatorial ridge implies that equatorial deposition [60] has likely influenced the particle distribution, perhaps explaining the overabundance of particles between 10 and 30 cm in longest axis as compared to the other sites.
Using the merged datasets presented in Figure 9 and Figure 10, we can also attempt to translate these PSFDs based on particle diameter into PSFDs based on particle surface area assuming a notional boulder ellipticity of 0.7 [65]. The goal of this presentation is to understand what the average boulder surface area size would be on Bennu. This value also has implications for interpreting cratering regimes on asteroids [66]. In Figure 12 and Figure 13 we present the merged PSFDs of particle surface area with the y-axis scaled to fractional coverage. Average particle measurements (where cumulative surface coverage reaches 50%) is between 12 to 18 cm in longest axis based on the merged datasets of Recon A and Recon C (Figure 12) or is 23 cm based on the single merged dataset (Figure 13). These results could be refined by determining the true average ellipticity of particles on Bennu. Notably, the fractional surface coverage estimated in Figure 13 exceeds 1, which we attribute to overestimating particle size with ellipses (many particles on Bennu are angular) as well as measurements of partially buried particles.
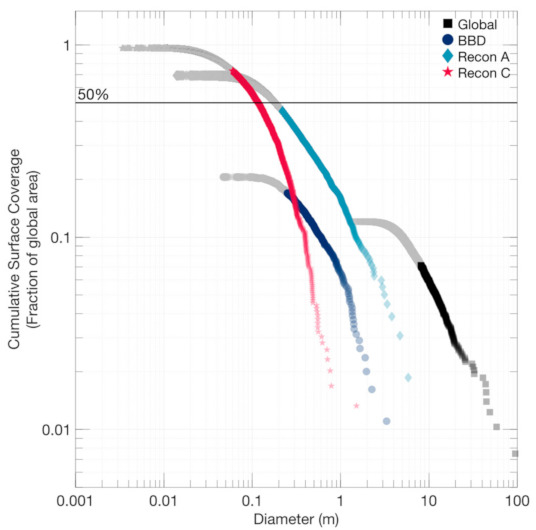
Figure 12.
Cumulative surface coverage of PSFDs of Bennu using merged measurements based on the four key mission phases. The global PSFD calculated from early OSIRIS-REx images of Bennu by DellaGiustina and Emery et al. [24] is included as a reference. Light gray points indicate particle measurements that were smaller than the completeness limit. The black line denotes where 50% surface coverage is achieved.
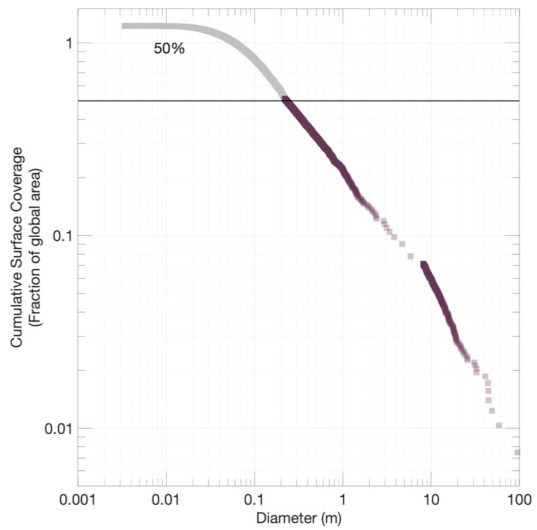
Figure 13.
Cumulative surface coverage of PSFD of Bennu based on measurements merged into a single dataset. Light gray points indicate particle measurements that were smaller than the completeness limit. The black line denotes where 50% surface coverage is achieved.
For each of the cumulative PSFDs (Figure 6), particle measurements depart from the power-law fit at small scales. This indicates that there is either an identification bias or a depletion mechanism affecting the frequency of smaller particles within the candidate sample sites based on a fractal frequency nature of particles. An identification bias could be systematic as a result of mappers not being able to identify features at the image resolution limit. For Recon A, this would roughly translate to 4-cm particles. In every case, however, this minimum resolvable feature size is much smaller than the completeness limits we identified with the Clauset et al. [46] technique. This is not surprising as the Clauset et al. [46] technique aims to maximize the goodness of fit between the power-law and the data set above a given particle size; however, it means we cannot differentiate between identification bias and a possible small particle depletion mechanism.
4.2. Comparison to Ryugu
Michikami et al. [26] similarly found that the power-law index becomes shallower as particle sizes decrease for five localized regions on Ryugu. These five regions had power-law fits with indices between 1.65 and 2.07, thus indicating there is a lesser degree of fragmentation on Ryugu than is observed on Bennu (see [2,43]). Michikami et al. [26] noted that this observation conflicted with the high number density of large particles, which suggests that a high degree of fragmentation occurred during catastrophic disruption of the parent body, and attributed it to particle burial, which could result in a shallower power-law index.
Particle burial has also been observed on Bennu either as regolith grains overlaying larger particles or as densely packed, similar-sized particles [60]. The latter is visible at Osprey, which appears more densely packed with large particles than Nightingale (Figure 14).

Figure 14.
Close-ups of Nightingale (left) and Osprey (right) highlighting regions densely packed with counted particles. Nightingale has a larger proportion of sampleable particles (≤2.0 cm) than Osprey, which appears to be saturated with particles ~10.0 cm and larger.
This is reflected in the relative frequency plot shown in Figure 8, which suggests that a physical process, such as particle saturation, is influencing the observable PSFD at this location. Examples of particle saturation are scarce in the space science literature despite the interest received by craters (e.g., [44,67]), but this is likely due to the limited availability of high-resolution images across rubble-pile bodies. Michikami et al. [26] observed particle saturation in the five local sites studied on Ryugu, though the observed R values (~0.1–0.2) are slightly shallower due to the particle range being larger. It remains to be seen whether particle saturation (assuming it is present) is unique to rubble-pile asteroids such as Bennu and Ryugu, or if there is simply a lack of observations from analog features (e.g., lag deposits) on larger planetary bodies.
Recently, Grott et al. [68] proposed that Ryugu’s PSFD is better described by a Weibull distribution of the form
where D is the mean horizontal particle diameter, NT is the total number of particles, and λ and β define the Weibull shape. A Weibull distribution provides an improved fit to the small diameters and is better able to capture changes in the PSFD over a larger range of particle sizes. Other studies have also proposed Weibull distributions or an exponential variation as opposed to a power-law fit (e.g., [4,5,50,51,69]. Using the merged dataset presented in Figure 10, we fit a Weibull distribution (Figure 15) and, similarly, find this fit very suitable. In terms of applicability for future missions undertaking similar particle mapping work, the power-law fitting technique provides a superior estimate for gauging the completeness of measurements by providing an upper bound or conservative estimate of the completeness limit based on the fractal nature of particles; however, a Weibull fit may be a better predictor of overall particle frequency.
N(D) = NT exp(−3(D/λ)β/β),
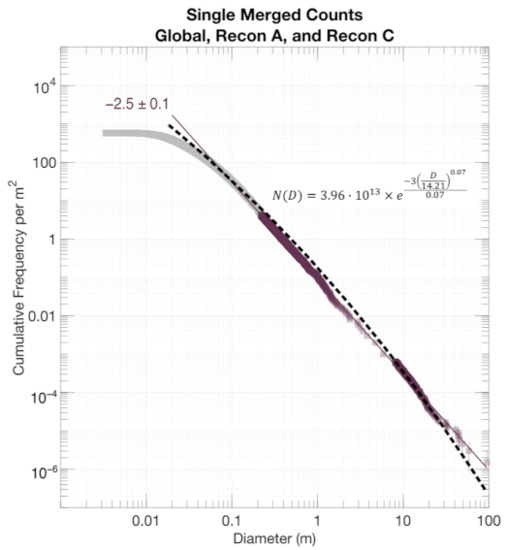
Figure 15.
Same plot as Figure 10, but with a Weibull fit (displayed as black dashed line).
4.3. Limitations of the Rock Tray Study
Although the rock tray study is helpful for evaluating the accuracy of remote measurements, there are limitations to the conclusions we can draw for the PSFDs calculated for Bennu. Most importantly, we conducted the rock tray analysis with a relatively small sample size (n = 85) when compared to the number of particles measured at the candidate sample sites on Bennu (n ≥ 269). Considering that the lower particle counts from BBD images were poor indicators of later PSFDs calculated with higher-resolution data, we are hesitant to conclude that a measurement bias would be as pronounced, or even present, for particles mapped on Bennu. Additionally, the two distinct particle populations [24,58] on Bennu may have different measurement uncertainties due to their different physical properties. Higher-contrast boulders (bright and very dark particles) are easier to detect against Bennu’s average terrain and thus likely do not suffer from as many missed detections as particles with average reflectance. Angular and smooth particles likely have improved accuracy and consistency between mappers in terms of identifying the longest axis and particle edges correctly, relative to the rougher and more hummocky particles. The rock tray study does not account for these factors. Similarly, as the rock tray study was developed in the Earth gravity environment, it does not account for patterns due to particle reorganization in Bennu’s micro-gravity environment. For simplicity, we assumed that mappers would correctly identify the longest axis of particles a majority of the time. This assumption only holds true if, for a majority of particles, gravity orients the particles such that the longest axis is visible to the mapper from a roughly nadir viewing position and if mappers are able to correctly discern the longest particle axis. Michikami et al. [70] demonstrated that on Itokawa, smaller particles were generally oriented with the smallest axis measurement (c-axis) perpendicular to the surface, whereas larger particles were more likely to resist gravity- or friction-induced orientation. A more thorough study should be conducted to fully assess the extent of potential measurement bias that may be present in remotely sensed particle measurements. Nonetheless, the controlled study performed here highlights the types of errors that may be introduced when working with remotely sensed images of particles on a planetary surface.
5. Conclusions
Particle measurements enable quantitative comparisons with other planetary surfaces, influencing the conclusions that can be drawn about the geophysical processes that cause fragmentation and disaggregation on those surfaces. Though an individual power-law fit to a PSFD cannot solely convey the geologic history, in tandem with other evidence, we used these data to make inferences on the origin of surface particles. Each of the four candidate Bennu sample sites likely experienced complex particle fragmentation as a result of multiple processes and appears to have a distinct geologic history.
We identified over 100,000 particles ≥ 1 cm in the longest axis dimension across the four candidate sample sites of the OSIRIS-REx mission. On the basis of PSFD power-law indices, we infer that the primary sample site, Nightingale, is characterized more closely by processes related to disaggregation in spite of its geologically recent impact cratering history, though this cannot be fully resolved without a returned sample. Osprey maintains a PSFD consistent with its geologically recent impact cratering history except for a saturation of particles between 10 and 30 cm that could be due to equatorial deposition.
We validated our assumption that the PSFD calculated from meter-sized particles could constrain the PSFD of centimeter-sized particles, though this assumption may not hold for other localized regions on the asteroid or other planetary bodies. We determined, that at least on Bennu, particle sample sizes must be large (>600 particle measurements, likely closer to thousands) to effectively estimate particle frequency at small scales when using a power-law model. The Weibull distribution appears to be a better predictor of particle frequency than power-laws, though smaller sample sizes of particle measurements could lead to an underestimation of the frequency of smaller particles. In practice, it may be best to use both of these distributions to model the full range of potential PSFDs.
Through our laboratory study to connect ground truth measurements to remotely sensed measurements, we found that a possible systematic bias present for remotely measured particles may cause smaller particles to be overestimated in size and larger particles to be underestimated, though this did not have a statistically significant impact on the PSFD. This should be further explored for missions that require high particle measurement accuracy.
For the OSIRIS-REx mission, particle mapping was pivotal to spacecraft safety. The use of a GIS environment enabled us to tie particle measurements to real coordinates on Bennu, which enabled the identification of candidate sample sites and helped the spacecraft to avoid large particle hazards during sample collection.
On 20 October 2020, OSIRIS-REx successfully contacted the surface of Bennu at the Nightingale sample site [30]. Image analysis and event reconstructions suggest that more than 60 g of material were collected from the asteroid. The successful sample collection event on an asteroid with very limited unobstructed sampleable material at the surface underscores the value of using PSFDs to incrementally estimate the frequency of particles of a given size.
Author Contributions
Conceptualization, K.N.B., D.N.D., C.A.B., E.B.B., K.J.W. and M.P.; methodology, K.N.B., D.N.D., C.A.B., K.J.W., M.P., E.B.B. and M.C.N.; software, K.N.B., C.A.B., E.B.B., K.J.W. and M.C.N.; validation, K.N.B., D.N.D., K.J.W., M.P. and E.B.B.; formal analysis, K.N.B., D.N.D., K.J.W., M.P. and E.B.B.; investigation, K.N.B., D.N.D., C.A.B., K.J.W., E.B.B., M.P., J.I.B., H.C.C.J., J.P.D., R.H.H., E.R.J., J.O.N., J.P., S.J.R., E.M.S. and S.J.S.; resources, D.N.D., C.A.B., M.C.N., W.V.B., H.L.E., E.M.S. and D.S.L.; data curation, K.N.B., C.A.B. and K.J.W.; writing—original draft preparation, K.N.B., D.N.D., C.A.B., K.J.W., M.P. and M.C.N.; writing—review and editing, K.N.B., D.N.D., C.A.B., K.J.W., M.P., M.C.N., H.C.C.J., J.D.P.D., J.P.D., C.M.E., D.R.G., R.H.H., E.R.J., T.J.M., P.M., J.L.M., B.R., S.J.R., E.M.S., P.H.S., H.C.M.S. and D.S.L.; visualization, K.N.B. and K.J.W.; supervision, D.N.D., C.A.B., E.B.B., K.J.W., M.P., M.C.N., D.R.G. and P.H.S.; project administration, K.N.B., D.N.D. and C.A.B.; funding acquisition, D.N.D., M.C.N., W.V.B., P.H.S., H.L.E. and D.S.L. All authors have read and agreed to the published version of the manuscript.
Funding
This material is based upon work supported by NASA under Contract NNM10AA11C issued through the New Frontiers Program. E.B. Bierhaus acknowledges funding support through Lockheed Martin under contract NNG12FD66C. M. Pajola was supported for this research by the Italian Space Agency (ASI) under the ASI-INAF agreement no. 2017-37-H.0. J.P. Dworkin acknowledges funding support through NASA GSFC under contract NNH09ZDA007O. J.D.P. Deshapriya and P. Michel acknowledge funding support from CNES. P. Michel also acknowledges funding support from the European Union’s Horizon 2020 research and innovation program under grant agreement No 870377 (project NEO-MAPP), and from Academies of Excellence of the IDEX JEDI of the Université Côte d’Azur. C.M. Elder, J.L. Molaro, and M. Pajola were supported by the OSIRIS-REx Participating Scientist Program.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
OCAMS images used for particle counting are available via the Planetary Data System (PDS) [71]. Data are delivered to the PDS according to the OSIRIS-REx Data Management Plan available in the OSIRIS-REx PDS archive [72]. Shape models of Bennu are available via the Small Body Mapping Tool at http://sbmt.jhuapl.edu/ (accessed on 26 March 2021). The particle measurement data are available upon request (knburke@email.arizona.edu).
Acknowledgments
This research made use of the U.S. Geological Survey’s (USGS) Integrated Software for Imagers and Spectrometers (ISIS) and the Environmental Systems Research Institute’s (ESRI) ArcMap Software system. Some of this research was carried out at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration (80NM0018D0004). We are grateful to the entire OSIRIS-REx Team for making the encounter with Bennu possible. K.N. Burke thanks, in particular, C.W.V. Wolner for her help editing and guiding this paper to submission, as well as N. Habib and N.A. Porter for their support throughout the fruition of this work. The particle mapping team referred to in this work includes: R.K. Bandrowski, C.A. Bennett, J.I. Brodbeck, K.N. Burke, M. Chojnacki, H.C. Connolly Jr., J.P. Dworkin, R.H. Hoover, E.R. Jawin, M. Luján, D. McCarty, R. Melikyan, V. Morrison, J.O. Nolau, J. Padilla, M. Pajola, S.J. Robbins, S. Salazar, S.A. Sandford, N.K. Schultz, S.J. Stewart, N. Wagner, and Z. Zeszut.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Turcotte, D.L. Fractals and Chaos in Geology and Geophysics; Cambridge University Press (CUP): Cambridge, UK, 1997. [Google Scholar]
- Hartmann, W.K. Terrestrial, lunar, and interplanetary rock fragmentation. Icarus 1969, 10, 201–213. [Google Scholar] [CrossRef]
- Michel, P.; O’Brien, D.; Abe, S.; Hirata, N. Itokawa’s cratering record as observed by Hayabusa: Implications for its age and collisional history. Icarus 2009, 200, 503–513. [Google Scholar] [CrossRef]
- Golombek, M.; Rapp, D. Size-frequency distributions of rocks on Mars and Earth analog sites: Implications for future landed missions. J. Geophys. Res. Space Phys. 1997, 102, 4117–4129. [Google Scholar] [CrossRef]
- Golombek, M.P.; Haldemann, A.F.C.; Forsberg-Taylor, N.K.; DiMaggio, E.N.; Schroeder, R.D.; Jakosky, B.M.; Mellon, M.T.; Matijevic, J.R. Rock size-frequency distributions on Mars and implications for Mars Exploration Rover landing safety and operations. J. Geophys. Res. Space Phys. 2003, 108. [Google Scholar] [CrossRef]
- Pajola, M.; Lucchetti, A.; Fulle, M.; Mottola, S.; Hamm, M.; Da Deppo, V.; Penasa, L.; Kovacs, G.; Massironi, M.; Shi, X.; et al. The pebbles/boulders size distributions on Sais: Rosetta’s final landing site on comet 67P/Churyumov–Gerasimenko. Mon. Not. R. Astron. Soc. 2017, 469, S636–S645. [Google Scholar] [CrossRef]
- Pajola, M.; Rossato, S.; Baratti, E.; Pozzobon, R.; Quantin, C.; Carter, J.; Thollot, P. Boulder abundances and size-frequency distributions on Oxia Planum-Mars: Scientific implications for the 2020 ESA ExoMars rover. Icarus 2017, 296, 73–90. [Google Scholar] [CrossRef]
- Miyamoto, H.; Yano, H.; Scheeres, D.J.; Abe, S.; Barnouin-Jha, O.; Cheng, A.F.; Demura, H.; Gaskell, R.W.; Hirata, N.; Ishiguro, M.; et al. Regolith Migration and Sorting on Asteroid Itokawa. Science 2007, 316, 1011–1014. [Google Scholar] [CrossRef] [PubMed]
- Michikami, T.; Nakamura, A.M.; Hirata, N.; Gaskell, R.W.; Nakamura, R.; Honda, T.; Honda, C.; Hiraoka, K.; Saito, J.; Demura, H.; et al. Size-frequency statistics of boulders on global surface of asteroid 25143 Itokawa. Earth Planets Space 2008, 60, 13–20. [Google Scholar] [CrossRef]
- Mazrouei, S.; Daly, M.; Barnouin, O.; Ernst, C.; DeSouza, I. Block distributions on Itokawa. Icarus 2014, 229, 181–189. [Google Scholar] [CrossRef]
- Pajola, M.; Vincent, J.-B.; Güttler, C.; Lee, J.-C.; Bertini, I.; Massironi, M.; Simioni, E.; Marzari, F.; Giacomini, L.; Lucchetti, A.; et al. Size-frequency distribution of boulders ≥7 m on comet 67P/Churyumov-Gerasimenko. Astron. Astrophys. 2015, 583, A37. [Google Scholar] [CrossRef]
- Pajola, M.; Lucchetti, A.; Bertini, I.; Marzari, F.; A’Hearn, M.F.; La Forgia, F.; Lazzarin, M.; Naletto, G.; Barbieri, C. Size-frequency distribution of boulders ≥10 m on comet 103P/Hartley 2. Astron. Astrophys. 2015, 585, A85. [Google Scholar] [CrossRef]
- Connolly, H.C.; Lauretta, D.S.; Walsh, K.J.; Tachibana, S.; Bottke, W.F. Towards understanding the dynamical evolution of asteroid 25143 Itokawa: Constraints from sample analysis. Earth Planets Space 2015, 67, 12. [Google Scholar] [CrossRef]
- Basilevsky, A.; Head, J.W.; Horz, F. Survival times of meter-sized boulders on the surface of the Moon. Planet. Space Sci. 2013, 89, 118–126. [Google Scholar] [CrossRef]
- Watkins, R.N.; Jolliff, B.L.; Mistick, K.; Fogerty, C.; Lawrence, S.J.; Singer, K.N.; Ghent, R.R. Boulder Distributions Around Young, Small Lunar Impact Craters and Implications for Regolith Production Rates and Landing Site Safety. J. Geophys. Res. Planets 2019, 124, 2754–2771. [Google Scholar] [CrossRef]
- Bart, G.D.; Melosh, H.J. Using lunar boulders to distinguish primary from distant secondary impact craters. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Bart, G.D.; Melosh, H. Distributions of boulders ejected from lunar craters. Icarus 2010, 209, 337–357. [Google Scholar] [CrossRef]
- Singer, K.N.; McKinnon, W.B.; Nowicki, L. Secondary craters from large impacts on Europa and Ganymede: Ejecta size–velocity distributions on icy worlds, and the scaling of ejected blocks. Icarus 2013, 226, 865–884. [Google Scholar] [CrossRef]
- Butler, J.C.; King, E.A., Jr. Analysis of the grain size-frequency distributions of lunar fines. In Lunar and Planetary Science Conference Proceedings; Lunar and Planetary Institute: Houston, TX, USA, 1974; Volume 5, pp. 829–841. [Google Scholar]
- Lauretta, D.S.; Balram-Knutson, S.S.; Beshore, E.; Boynton, W.V.; D’Aubigny, C.D.; DellaGiustina, D.N.; Enos, H.L.; Gholish, D.R.; Hergenrother, C.W.; Howell, E.S.; et al. OSIRIS-REx: Sample Return from Asteroid (101955) Bennu. Space Sci. Rev. 2017, 212, 925–984. [Google Scholar] [CrossRef]
- Bierhaus, E.B.; Clark, B.C.; Harris, J.W.; Payne, K.S.; Dubisher, R.D.; Wurts, D.W.; Hund, R.A.; Kuhns, R.M.; Linn, T.M. The OSIRIS-REx Spacecraft and the Touch-and-Go Sample Acquisition Mechanism (TAGSAM). Space Sci. Rev. 2018, 214, 107. [Google Scholar] [CrossRef]
- Bierhaus, E.; Songer, J.; Clark, B.; Dubisher, R.; Deden, S.; Payne, K.; Wurts, D.; McMahon, J.; Rozitis, B.; Lauretta, D. Bennu regolith mobilized by TAGSAM: Expectations for the OSIRIS-REx sample collection event and application to understanding naturally ejected particles. Icarus 2021, 355, 114142. [Google Scholar] [CrossRef]
- Lauretta, D.S.; DellaGiustina, D.N.; Bennett, C.A.; Golish, D.R.; Becker, K.J.; Balram-Knutson, S.S.; Barnouin, O.S.; Becker, T.L.; Bottke, W.F.; Boynton, W.V.; et al. The unexpected surface of asteroid (101955) Bennu. Nat. Cell Biol. 2019, 568, 55–60. [Google Scholar] [CrossRef]
- DellaGiustina, D.N.; Emery, J.P.; Golish, D.R.; Rozitis, B.; Bennett, C.A.; Burke, K.N.; Ballouz, R.-L.; Becker, K.J.; Christensen, P.R.; the OSIRIS-REx Team; et al. Properties of rubble-pile asteroid (101955) Bennu from OSIRIS-REx imaging and thermal analysis. Nat. Astron. 2019, 3, 341–351. [Google Scholar] [CrossRef]
- DellaGiustina, D.N.; Bennett, C.A.; Becker, K.; Golish, D.R.; Le Corre, L.; Cook, D.A.; Edmundson, K.L.; Chojnacki, M.; Sutton, S.S.; Milazzo, M.P.; et al. Overcoming the Challenges Associated with Image-Based Mapping of Small Bodies in Preparation for the OSIRIS-REx Mission to (101955) Bennu. Earth Space Sci. 2018, 5, 929–949. [Google Scholar] [CrossRef]
- Michikami, T.; Honda, C.; Miyamoto, H.; Hirabayashi, M.; Hagermann, A.; Irie, T.; Nomura, K.; Ernst, C.M.; Kawamura, M.; Sugimoto, K. Boulder size and shape distributions on asteroid Ryugu. Icarus 2019, 331, 179–191. [Google Scholar] [CrossRef]
- Golish, D.R.; D’Aubigny, C.D.; Rizk, B.; DellaGiustina, D.N.; Smith, P.H.; Becker, K.; Shultz, N.; Stone, T.; Barker, M.K.; Mazarico, E.; et al. Ground and in-flight Calibration of the OSIRIS-REx Camera Suite. Space Sci. Rev. 2020, 216, 1–31. [Google Scholar] [CrossRef] [PubMed]
- Edmundson, K.L.; Becker, K.J.; Becker, T.L.; Bennett, C.A.; DellaGiustina, D.N.; Golish, D.R.; Porter, N.A.; Rizk, B.; D’Aubigny, C.D.; Daly, M.G.; et al. Photogrammetric processing of OSIRIS-REx images of asteroid (101955) BENNU. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 5, 587–594. [Google Scholar] [CrossRef]
- Rizk, B.; D’Aubigny, C.D.; Golish, D.; Fellows, C.; Merrill, C.; Smith, P.; Walker, M.S.; Hendershot, J.E.; Hancock, J.; Bailey, S.H.; et al. OCAMS: The OSIRIS-REx Camera Suite. Space Sci. Rev. 2018, 214, 26. [Google Scholar] [CrossRef]
- Lauretta, D.S.; Enos, H.L.; Polit, A.T.; Roper, H.L.; Wolner, C.W.V. OSIRIS-REx at Bennu: Overcoming Challenges to Collect a Sample of the Early Solar System, in Sample Return Missions; Longobardo, A., Ed.; Elsevier: Amsterdam, The Netherlands, 2020; Chapter 8; in press. [Google Scholar] [CrossRef]
- Bennett, C.; DellaGiustina, D.; Becker, K.; Becker, T.; Edmundson, K.; Golish, D.; Bennett, R.; Burke, K.; Cue, C.; Clark, B.; et al. A high-resolution global basemap of (101955) Bennu. Icarus 2020, 357, 113690. [Google Scholar] [CrossRef]
- ESRI. ArcGIS Desktop: Release 10; Environmental Systems Research Institute: Redlands, CA, USA, 2011. [Google Scholar]
- Keszthelyi, L.; Becker, T.L.; Sides, S.; Barrett, J.; Cook, D.; Lambright, S.; Lee, E.; Milazzo, M.; Oyama, K.; Richie, J.; et al. Support and future vision for the integrated software for imagers and spectrometers (ISIS). In Proceedings of the 44th Lunar and Planetary Science Conference, The Woodlands, TX, USA, 18–22 March 2013; Volume 44, p. 2546. [Google Scholar]
- Robbins, S.J.; Antonenko, I.; Kirchoff, M.R.; Chapman, C.R.; Fassett, C.I.; Herrick, R.R.; Singer, K.; Zanetti, M.; Lehan, C.; Huang, D.; et al. The variability of crater identification among expert and community crater analysts. Icarus 2014, 234, 109–131. [Google Scholar] [CrossRef]
- Nyquist, H. Certain Topics in Telegraph Transmission Theory. Trans. Am. Inst. Electr. Eng. 1928, 47, 617–644. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A Density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining KDD-96, Portland, OR, USA, 2–4 August 1996; Volume 96, pp. 226–231. [Google Scholar]
- Barnouin, O.S.; Daly, M.G.; Palmer, E.E.; Gaskell, R.W.; Weirich, J.R.; Johnson, C.L.; Al Asad, M.M.; Roberts, J.H.; Perry, M.E. Shape of (101955) Bennu indicative of a rubble pile with internal stiffness. Nat. Geosci. 2019, 12, 247–252. [Google Scholar] [CrossRef]
- Barnouin, O.; Daly, M.; Palmer, E.; Johnson, C.; Gaskell, R.; Al Asad, M.; Bierhaus, E.; Craft, K.; Ernst, C.; Espiritu, R.; et al. Digital terrain mapping by the OSIRIS-REx mission. Planet. Space Sci. 2020, 180, 104764. [Google Scholar] [CrossRef]
- Rodgers, D.J.; Ernst, C.M.; Barnouin, O.S.; Murchie, S.L.; Chabot, N.L. Methodology for finding and evaluating safe landing sites on small bodies. Planet. Space Sci. 2016, 134, 71–81. [Google Scholar] [CrossRef]
- Dombard, A.J.; Barnouin, O.S.; Prockter, L.M.; Thomas, P.C. Boulders and ponds on the Asteroid 433 Eros. Icarus 2010, 210, 713–721. [Google Scholar] [CrossRef]
- Krishna, N.; Kumar, P.S. Impact spallation processes on the Moon: A case study from the size and shape analysis of ejecta boulders and secondary craters of Censorinus crater. Icarus 2016, 264, 274–299. [Google Scholar] [CrossRef]
- Küppers, M.; Moissl, R.; Vincent, J.-B.; Besse, S.; Hviid, S.F.; Carry, B.; Grieger, B.; Sierks, H.; Keller, H.U.; Marchi, S. Boulders on Lutetia. Planet. Space Sci. 2012, 66, 71–78. [Google Scholar] [CrossRef]
- Thomas, P.C.; Veverka, J.; Robinson, M.S.; Murchie, S. Shoemaker crater as the source of most ejecta blocks on the asteroid 433 Eros. Nat. Cell Biol. 2001, 413, 394–396. [Google Scholar] [CrossRef]
- Hartmann, W.K. Does crater “saturation equilibrium” occur in the solar system? Icarus 1984, 60, 56–74. [Google Scholar] [CrossRef]
- Michael, G.; Neukum, G. Planetary surface dating from crater size–frequency distribution measurements: Partial resurfacing events and statistical age uncertainty. Earth Planet. Sci. Lett. 2010, 294, 223–229. [Google Scholar] [CrossRef]
- Clauset, A.; Shalizi, C.R.; Newman, M.E.J. Power-Law Distributions in Empirical Data. SIAM Rev. 2009, 51, 661–703. [Google Scholar] [CrossRef]
- DeSouza, I.; Daly, M.; Barnouin, O.; Ernst, C.; Bierhaus, E. Improved techniques for size–frequency distribution analysis in the planetary sciences: Application to blocks on 25143 Itokawa. Icarus 2015, 247, 77–80. [Google Scholar] [CrossRef]
- Standard techniques for presentation and analysis of crater size-frequency data. Icarus 1979, 37, 467–474. [CrossRef]
- Golombek, M.P.; Huertas, A.; Marlow, J.; McGrane, B.; Klein, C.; Martinez, M.; Arvidson, R.E.; Heet, T.; Barry, L.; Seelos, K.; et al. Size-frequency distributions of rocks on the northern plains of Mars with special reference to Phoenix landing surfaces. J. Geophys. Res. Space Phys. 2008, 113. [Google Scholar] [CrossRef]
- Pajola, M.; Pozzobon, R.; Lucchetti, A.; Rossato, S.; Baratti, E.; Galluzzi, V.; Cremonese, G. Abundance and size-frequency distribution of boulders in Linné crater’s ejecta (Moon). Planet. Space Sci. 2019, 165, 99–109. [Google Scholar] [CrossRef]
- Schröder, S.E.; Carsenty, U.; Hauber, E.; Schulzeck, F.; Raymond, C.A.; Russell, C.T. The Boulder Population of Asteroid 4 Vesta: Size-Frequency Distribution and Survival Time. Earth Space Sci. 2021, 8, e2019EA000941. [Google Scholar] [CrossRef]
- Walsh, K.J.; Jawin, E.R.; Ballouz, R.-L.; Barnouin, O.S.; Bierhaus, E.B.; Connolly, H.C., Jr.; Molaro, J.L.; McCoy, T.J.; Delbo’, M. Craters, boulders and regolith of (101955) Bennu indicative of an old and dynamic surface. Nat. Geosci. 2019, 12, 242–246. [Google Scholar] [CrossRef]
- Michel, P. Collisions and Gravitational Reaccumulation: Forming Asteroid Families and Satellites. Science 2001, 294, 1696–1700. [Google Scholar] [CrossRef] [PubMed]
- Michel, P.; Ballouz, R.-L.; Barnouin, O.S.; Jutzi, M.; Walsh, K.J.; May, B.H.; Manzoni, C.; Richardson, D.C.; Schwartz, S.R.; Sugita, S.; et al. Collisional formation of top-shaped asteroids and implications for the origins of Ryugu and Bennu. Nat. Commun. 2020, 11, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Ballouz, R.-L.; Walsh, K.J.; Barnouin, O.S.; DellaGiustina, D.N.; Al Asad, M.; Jawin, E.R.; Daly, M.G.; Bottke, W.F.; Michel, P.; Avdellidou, C.; et al. Bennu’s near-Earth lifetime of 1.75 million years inferred from craters on its boulders. Nat. Cell Biol. 2020, 587, 205–209. [Google Scholar] [CrossRef]
- Delbo, M.; Libourel, G.; Wilkerson, J.; Murdoch, N.; Michel, P.; Ramesh, K.T.; Ganino, C.; Verati, C.; Marchi, S. Thermal fatigue as the origin of regolith on small asteroids. Nat. Cell Biol. 2014, 508, 233–236. [Google Scholar] [CrossRef]
- Molaro, J.L.; Hergenrother, C.W.; Chesley, S.R.; Walsh, K.J.; Hanna, R.D.; Haberle, C.W.; Schwartz, S.R.; Ballouz, R.; Bottke, W.F.; Campins, H.J.; et al. Thermal Fatigue as a Driving Mechanism for Activity on Asteroid Bennu. J. Geophys. Res. Planets 2020, 125. [Google Scholar] [CrossRef]
- DellaGiustina, D.N.; Burke, K.N.; Walsh, K.J.; Smith, P.H.; Golish, D.R.; Bierhaus, E.B.; Ballouz, R.-L.; Becker, T.L.; Campins, H.; Tatsumi, E.; et al. Variations in color and reflectance on the surface of asteroid (101955) Bennu. Science 2020, 370, eabc3660. [Google Scholar] [CrossRef] [PubMed]
- Bierhaus, E.B.; Trang, D.; Barnouin, O.S.; Walsh, K.J.; Daly, R.T.; Pajola, M.; Jawin, E.R.; McCoy, T.J.; Connolly, H.C., Jr.; Hamilton, V.E.; et al. Impact craters on Bennu: Their morphology, size-frequency distribution, and correlation with other data sets. LPI Contrib. 2019, 2189, 2129. [Google Scholar]
- Jawin, E.R.; Walsh, K.J.; Barnouin, O.S.; McCoy, T.J.; Ballouz, R.; DellaGiustina, D.N.; Connolly, H.C., Jr.; Marshall, J.; Beddingfield, C.; Nolan, M.C.; et al. Global Patterns of Recent Mass Movement on Asteroid (101955) Bennu. J. Geophys. Res. Planets 2020, 125, e2020JE006549. [Google Scholar] [CrossRef]
- Hergenrother, C.W.; Adam, C.D.; Chesley, S.R.; Lauretta, D.S. Introduction to the Special Issue: Exploration of the Activity of Asteroid (101955) Bennu. J. Geophys. Res. Planets 2020, 125, e2020JE006549. [Google Scholar] [CrossRef]
- Rozitis, B.; Ryan, A.J.; Emery, J.P.; Christensen, P.R.; Hamilton, V.E.; Simon, A.A.; Reuter, D.C.; Al Asad, M.; Ballouz, R.-L.; Bandfield, J.L.; et al. Asteroid (101955) Bennu’s weak boulders and thermally anomalous equator. Sci. Adv. 2020, 6, eabc3699. [Google Scholar] [CrossRef] [PubMed]
- Golish, D.; Shultz, N.; Becker, T.; Becker, K.; Edmundson, K.; DellaGiustina, D.; D’Aubigny, C.D.; Bennett, C.; Rizk, B.; Barnouin, O.; et al. A high-resolution normal albedo map of asteroid (101955) Bennu. Icarus 2021, 355, 114133. [Google Scholar] [CrossRef]
- Hirata, N.; Nakamura, A.M. Secondary craters of Tycho: Size-frequency distributions and estimated fragment size–velocity relationships. J. Geophys. Res. Space Phys. 2006, 111. [Google Scholar] [CrossRef]
- Biele, J.; Burke, K.; Grott, M.; Ryan, A.; DellaGiustina, D.; Rozitis, B.; Michel, P.; Schröder, S.; Neumann, W. macroporosity and grain density of rubble pile asteroid (101955) Bennu. In Proceedings of the AGU Fall Meeting, San Francisco, CA, USA, 10 December 2020. [Google Scholar]
- Tatsumi, E.; Sugita, S. Cratering efficiency on coarse-grain targets: Implications for the dynamical evolution of asteroid 25143 Itokawa. Icarus 2018, 300, 227–248. [Google Scholar] [CrossRef]
- Turrini, D. The primordial collisional history of Vesta: Crater saturation, surface evolution and survival of the basaltic crust. Planet. Space Sci. 2014, 103, 82–95. [Google Scholar] [CrossRef]
- Grott, M.; Biele, J.; Michel, P.; Sugita, S.; Schröder, S.; Sakatani, N.; Neumann, W.; Kameda, S.; Michikami, T.; Honda, C. Macroporosity and Grain Density of Rubble Pile Asteroid (162173) Ryugu. J. Geophys. Res. Planets 2020, 125. [Google Scholar] [CrossRef]
- Mastropietro, M.; Pajola, M.; Cremonese, G.; Munaretto, G.; Lucchetti, A. Boulder Analysis on the Oxia Planum ExoMars 2022 Rover Landing Site: Scientific and Engineering Perspectives. Sol. Syst. Res. 2020, 54, 504–519. [Google Scholar] [CrossRef]
- Michikami, T.; Nakamura, A.M.; Hirata, N. The shape distribution of boulders on Asteroid 25143 Itokawa: Comparison with fragments from impact experiments. Icarus 2010, 207, 277–284. [Google Scholar] [CrossRef]
- Rizk, B.; d’Aubigny, C.D.; Golish, D.; DellaGiustina, D.N.; Lauretta, D.S. Origins, Spectral Interpretation, Resource Identification, Security, Regolith Explorer (OSIRIS-REx): OSIRIS-REx Camera Suite (OCAMS) Bundle. NASA Planetary Data System, urn:nasa:pds:orex.ocams. 2019. Available online: https://sbn.psi.edu/pds/resource/orex/ocams.html (accessed on 26 March 2021).
- Crombie, M.K.; Selznick, S. Origins, Spectral Interpretation, Resource Identification, Security, Regolith Explorer (OSIRIS-REx): Mission Bundle. NASA Planetary Data System, urn: Nasa: Pds: Orex. Mission. 2019. Available online: https://sbn.psi.edu/pds/resource/orex/orexmission.html (accessed on 26 March 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).