Knowledge and Spatial Pyramid Distance-Based Gated Graph Attention Network for Remote Sensing Semantic Segmentation
Abstract
1. Introduction
2. Related Work
2.1. Geographic Object-Based Image Analysis (GEOBIA)
2.2. Remote Sensing with GNN
3. Methodology
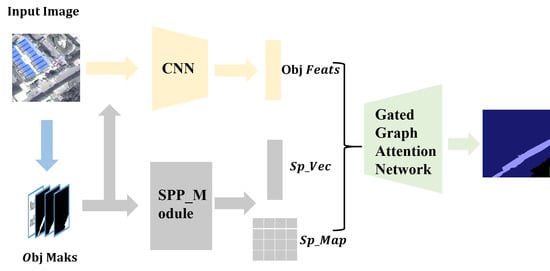
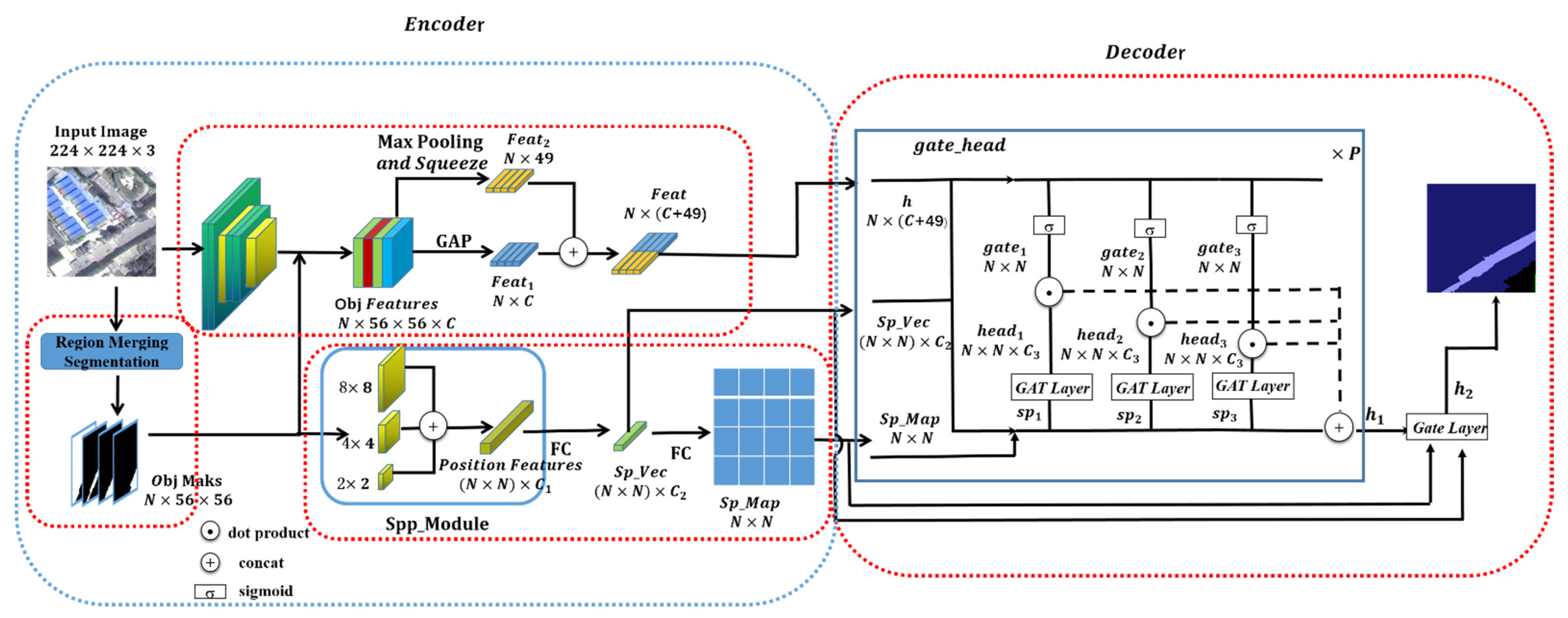
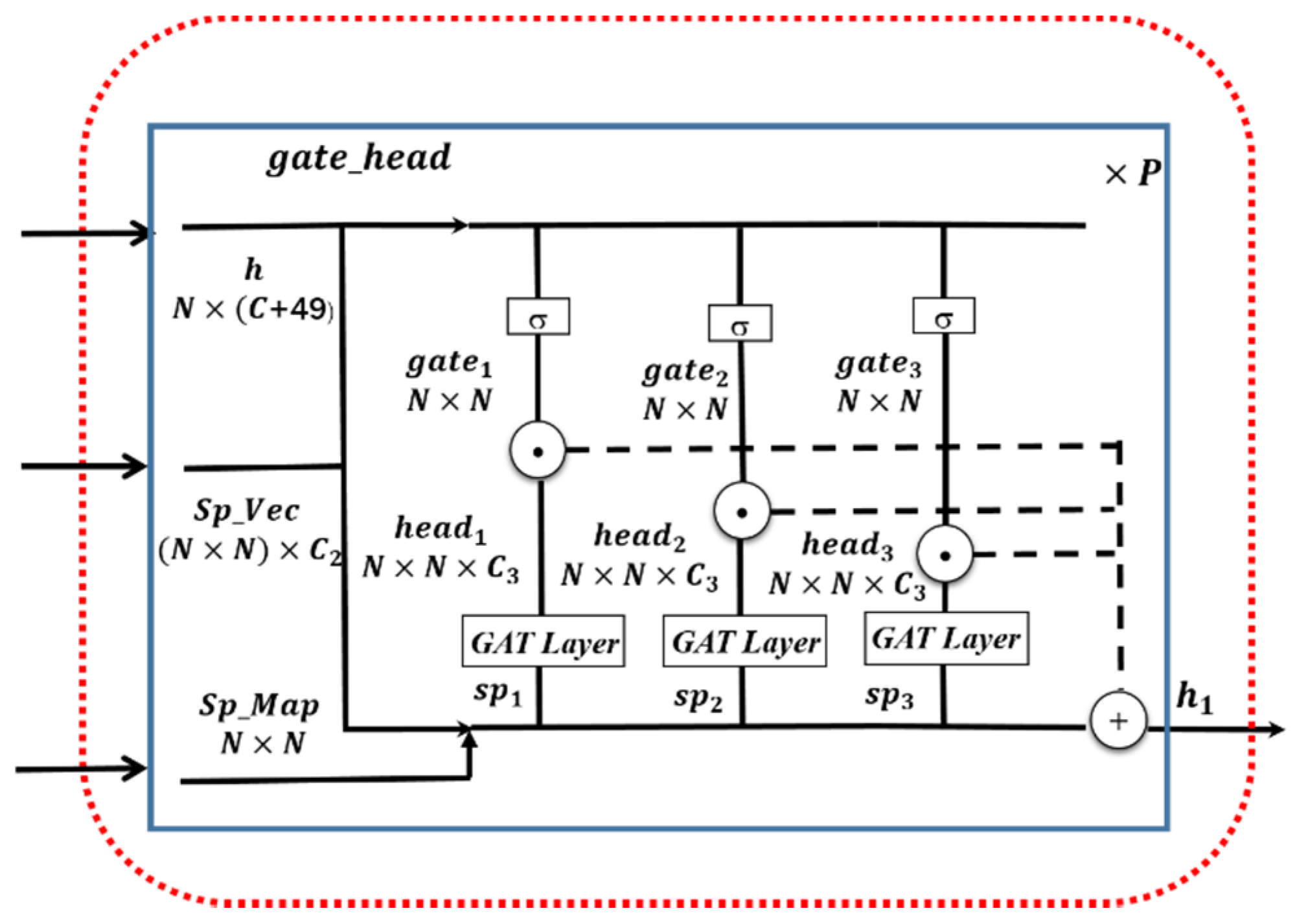
3.1. Network Structure
3.1.1. Superpixel Clustering Module
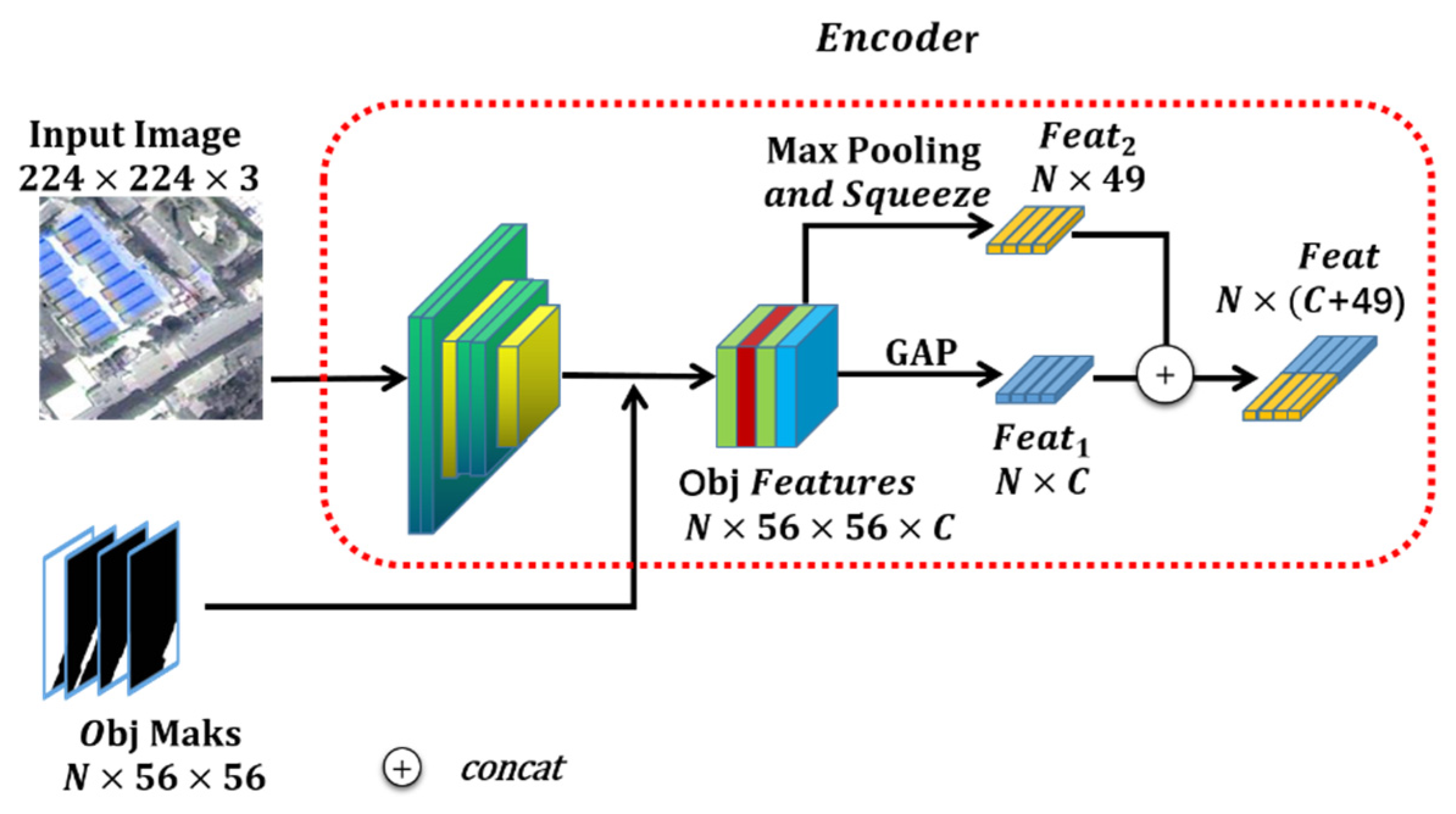
3.1.2. Feature Extraction Module
3.1.3. Spatial Correlation Recognition Algorithm Based on Spatial Pyramid Distance and Multi-Source Attention Mechanism
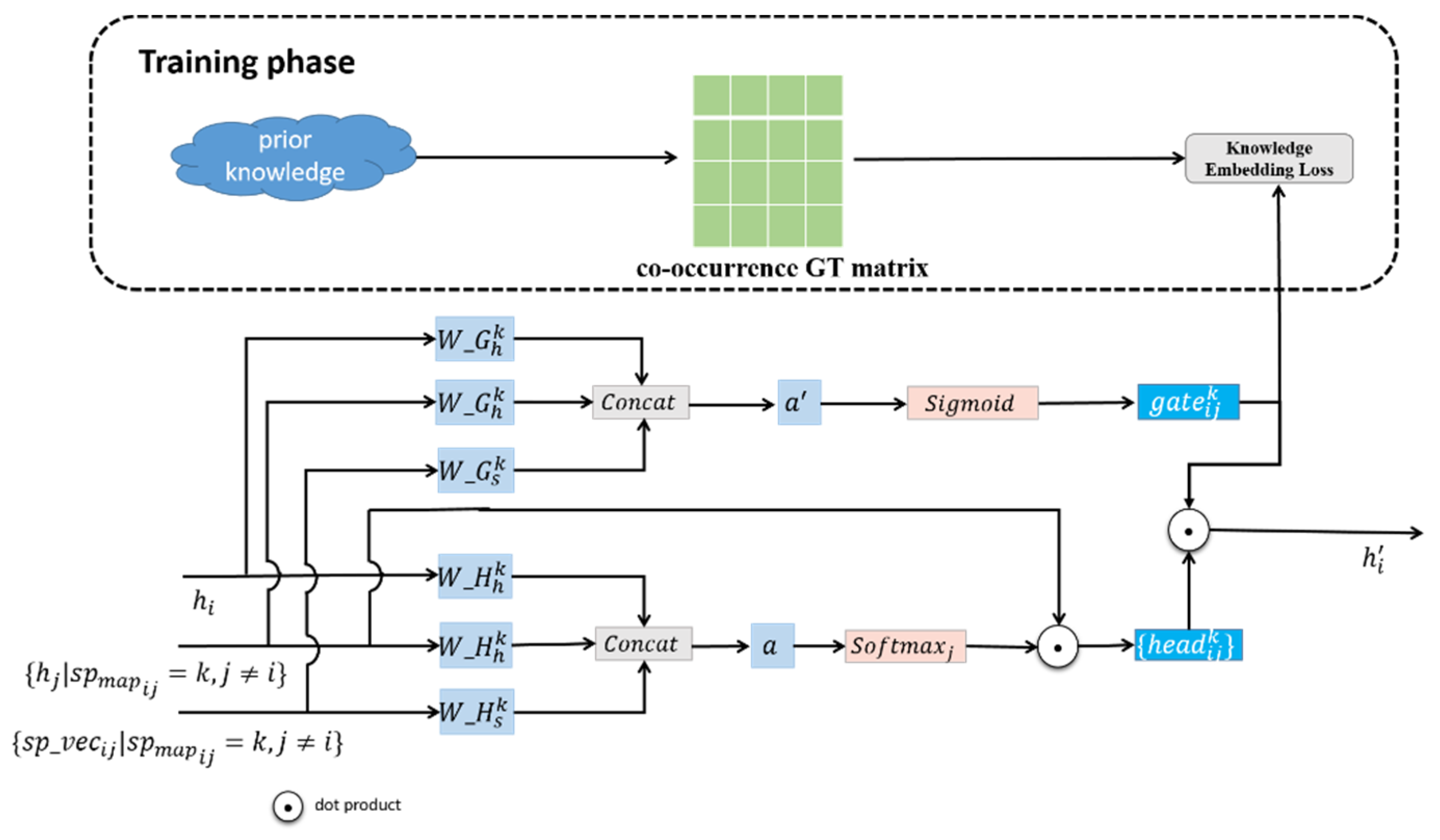
3.1.4. Gating Mechanism Based on Prior Knowledge of Category Co-Occurrence
3.2. Superpixel Clustering Module and Feature Extraction Module
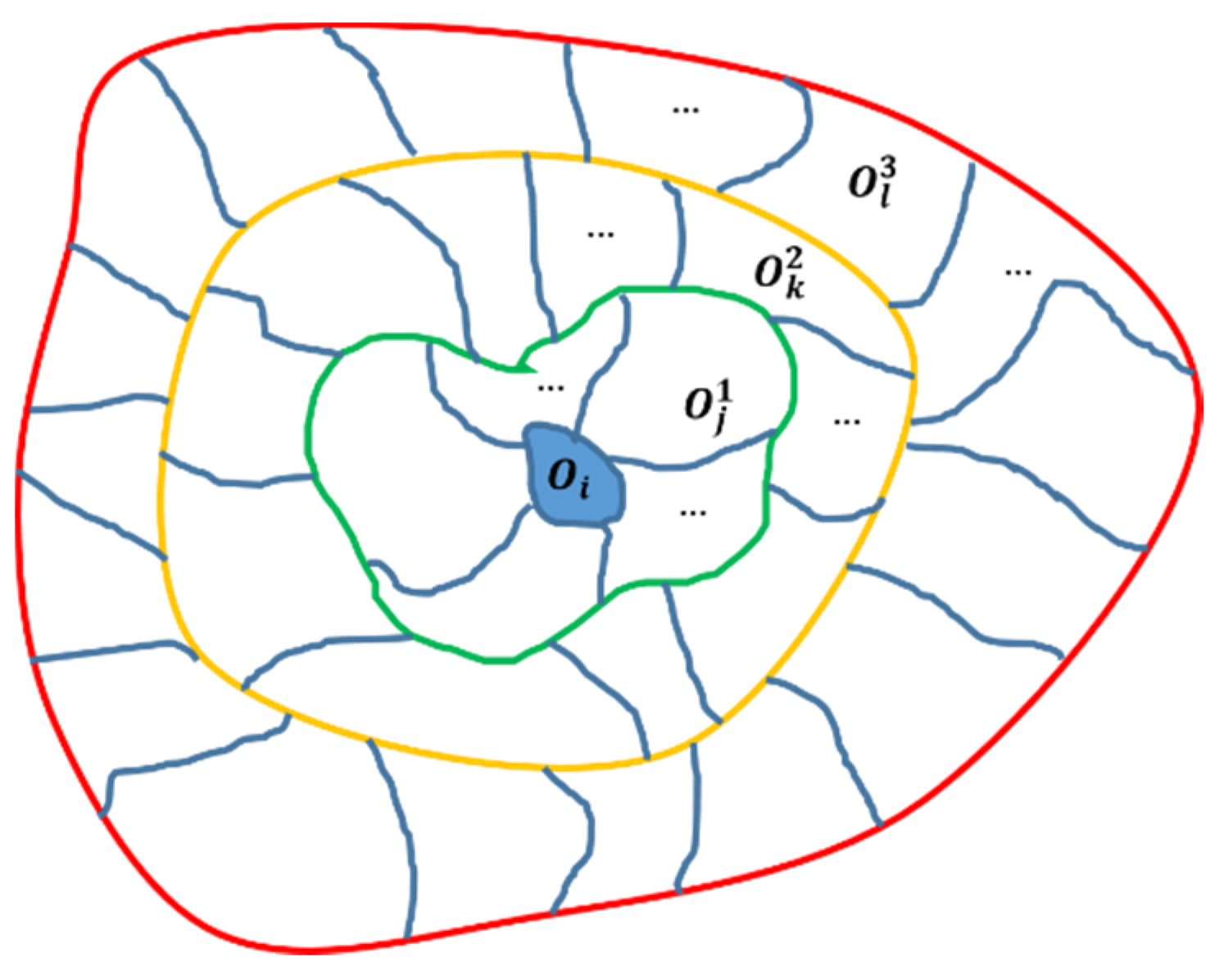
3.3. The Spatial Correlation between Objects: The Spatial Pyramid Distance
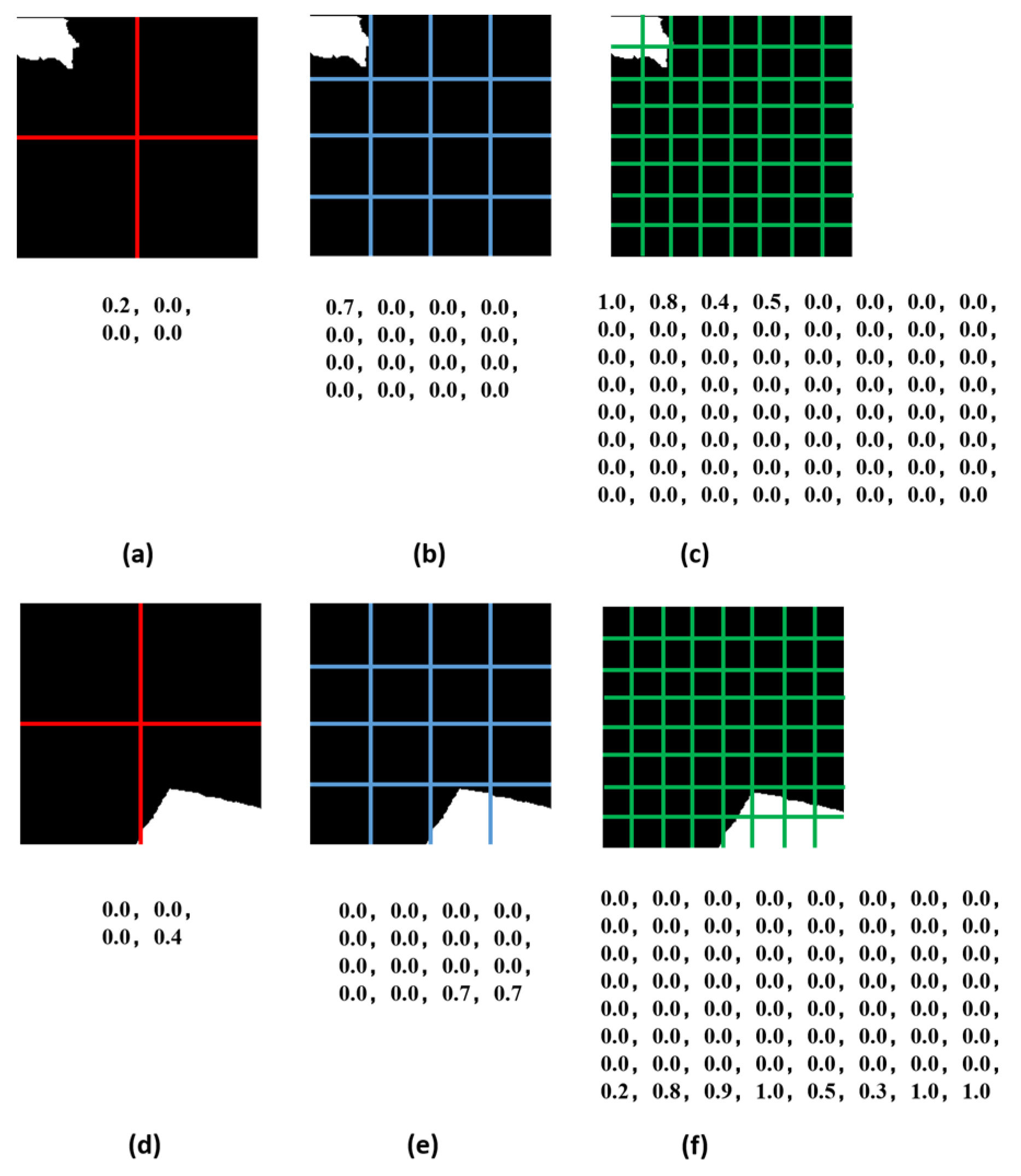
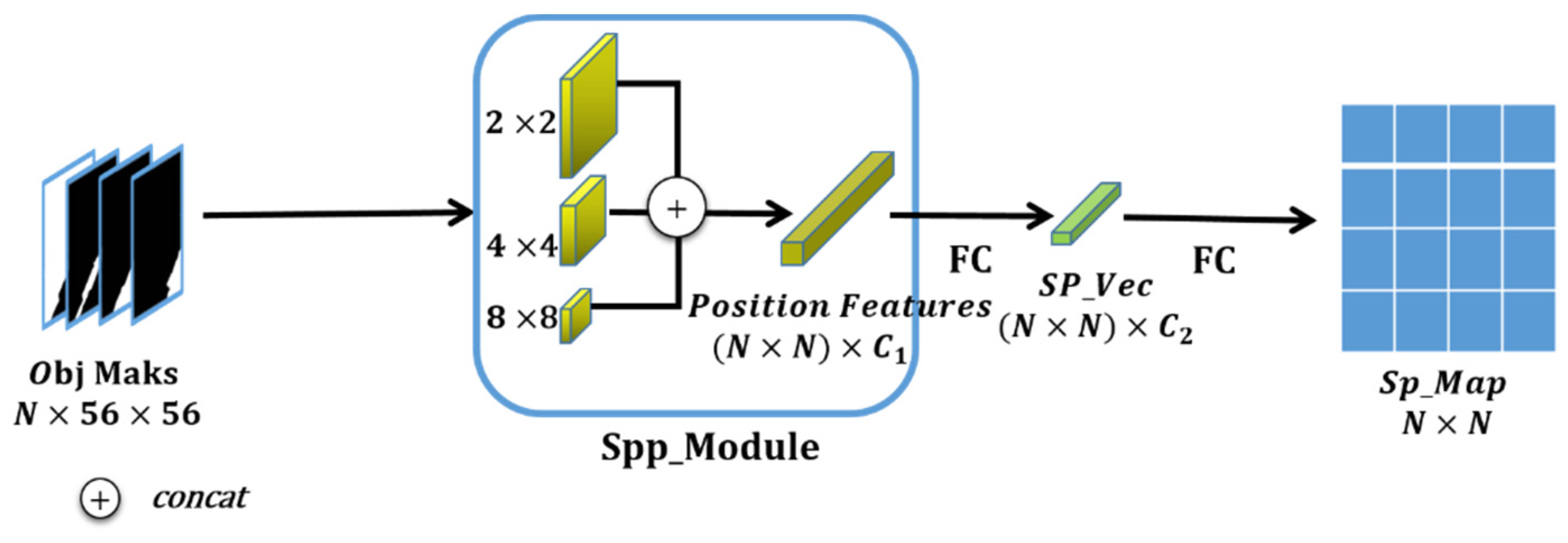
3.3.1. The Location Encoding Method Based on Pyramid Pooling
3.3.2. Spatial Pyramid Distance
3.3.3. The Spatial Correlation Recognition Algorithm Based on Spatial Pyramid Distance
| Algorithm 1 For recognizing the spatial pyramid distance |
| Input: mask of object , mask of object |
| Output: distance feature vector , spatial pyramid distance |
| 1 Begin |
| 2 For t 1 to 3 step 1; do |
| 3 ; // calculate the pooling size k |
| 4 ; // encode the position vector of with pooling size k |
| 5 ; // encode the position vector of with pooling size k |
| 6 End For |
| 7 all to obtain the multiscale location features of ; |
| 8 all to obtain the multiscale location features of ; |
| 9 ; // subtract the position encoding vectors of and |
| 10 ; |
| 11 ; |
| 12 Return , ; |
| 13 End |
3.4. Multi-source Attention Mechanism Based on Similarity of Spectral Features and Spatial Relationships of Geographic Objects
3.4.1. Attention Mechanism in the Baseline GAT
3.4.2. Multi-Source Attention Mechanism Based on Geographic Object Feature Similarity and Pyramid Distance
3.5. Knowledge-Based Gating Mechanism
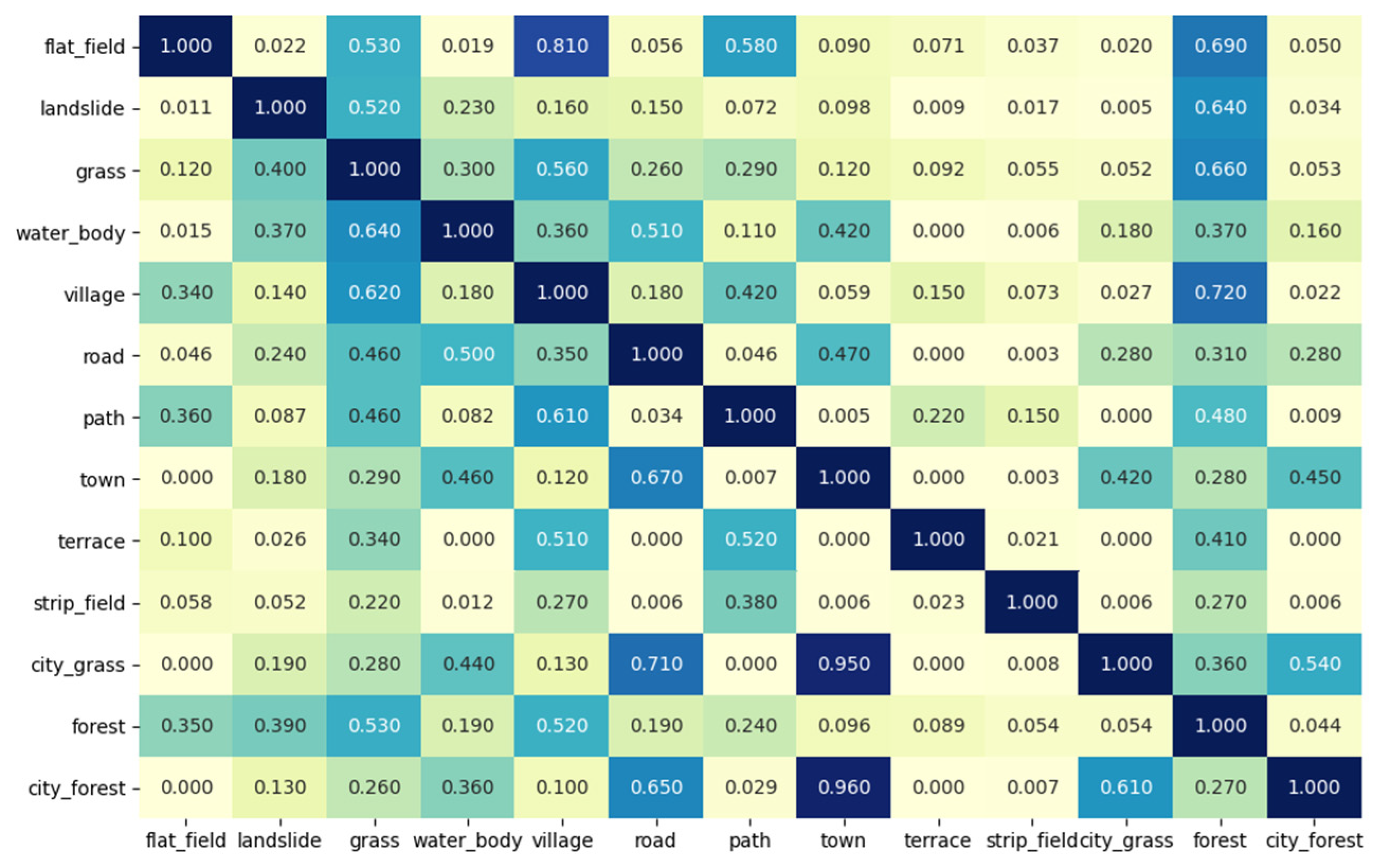
3.5.1. Category Co-Occurrence Knowledge in the Sample Set
3.5.2. Gated Graph Attention Network Based on Category Co-Occurrence Prior Knowledge
3.6. Network Depth (Number of Aggregation) and Loss Function
3.6.1. Depth of KSPGAT Network
3.6.2. Co-Occurrence Knowledge Embedding Loss
4. Experiment
4.1. Introduction of Research Areas and Samples
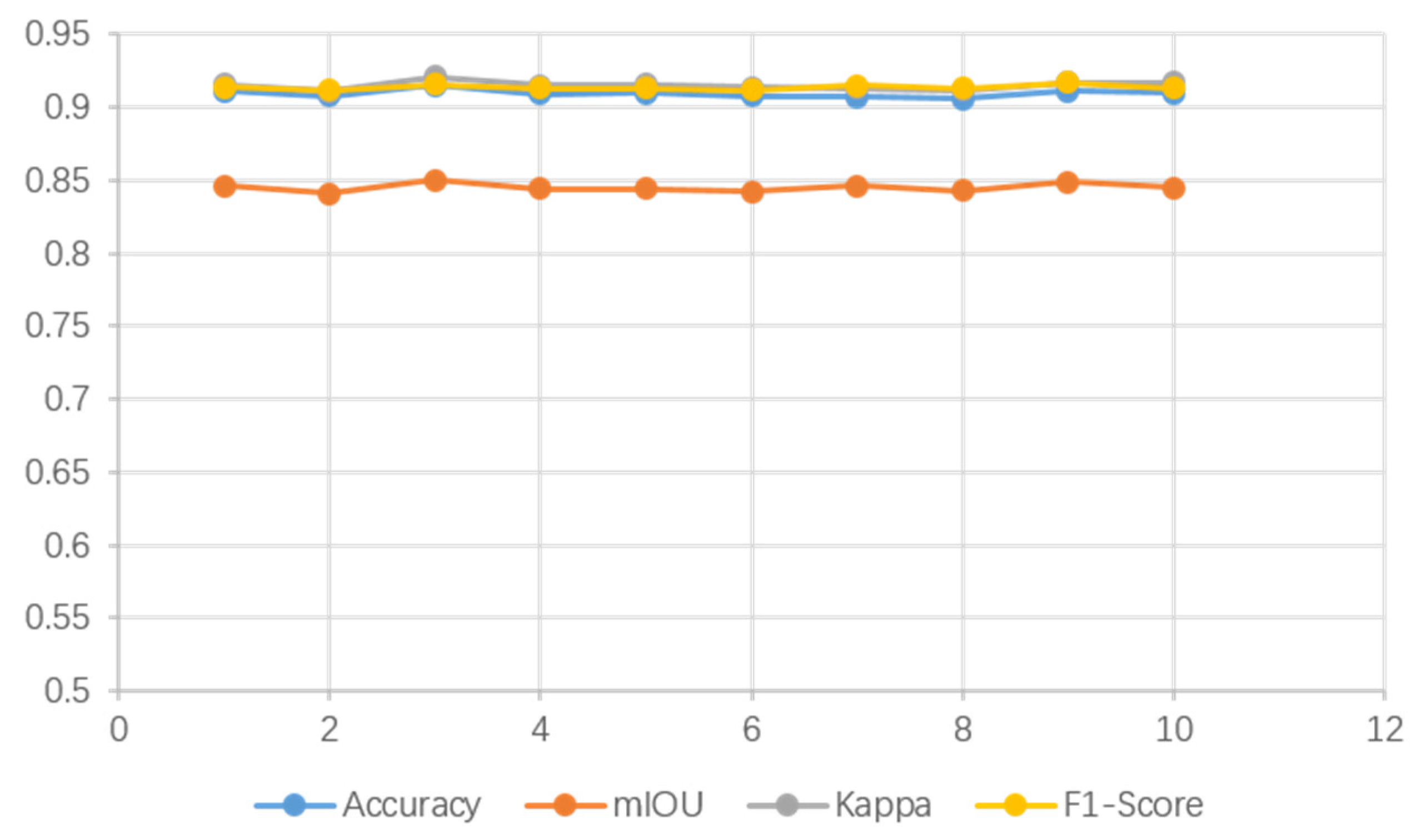
4.2. Network Parameters
4.3. Overall Accuracy Comparison
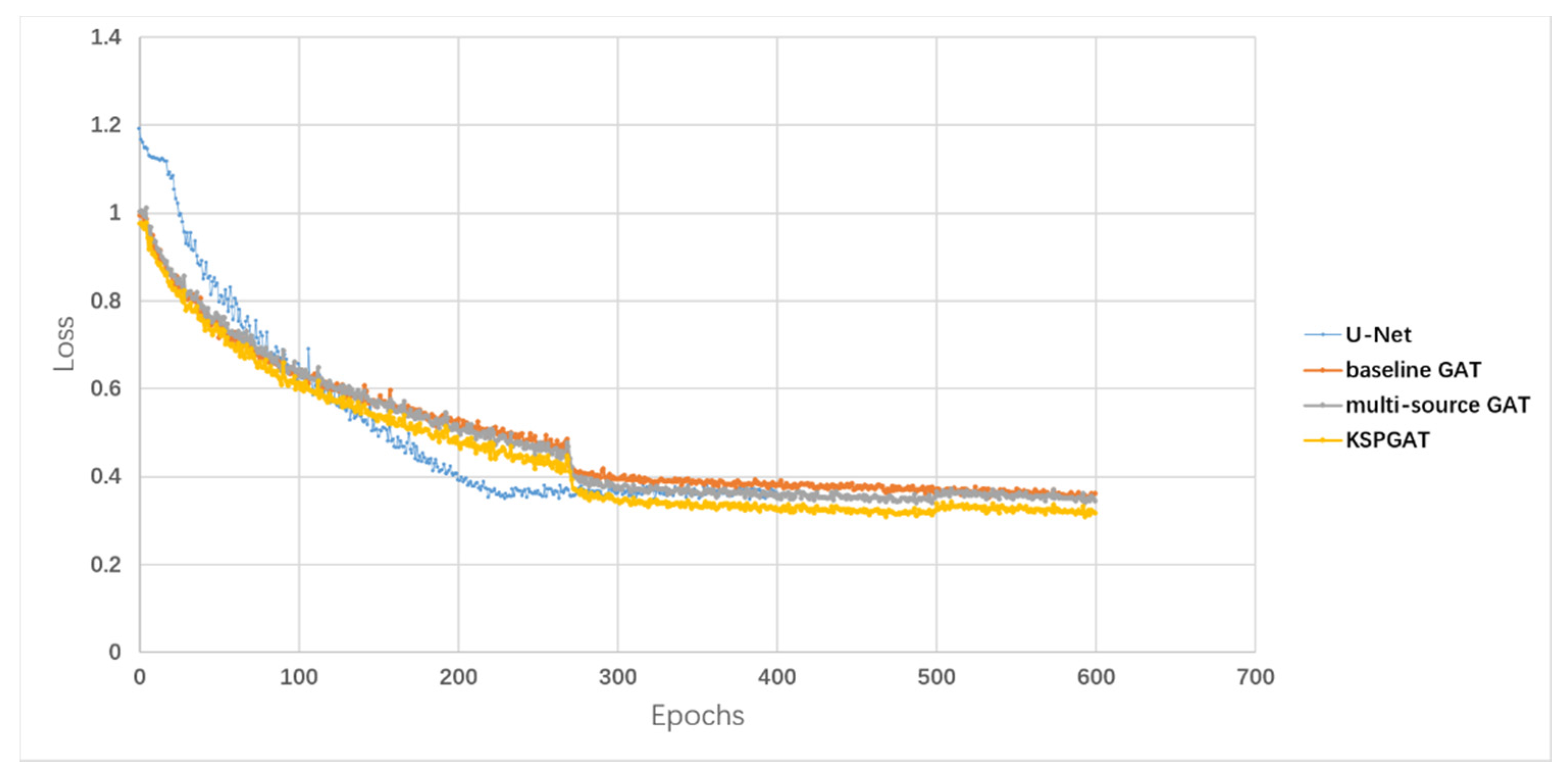
4.4. Training Process and Loss Curve
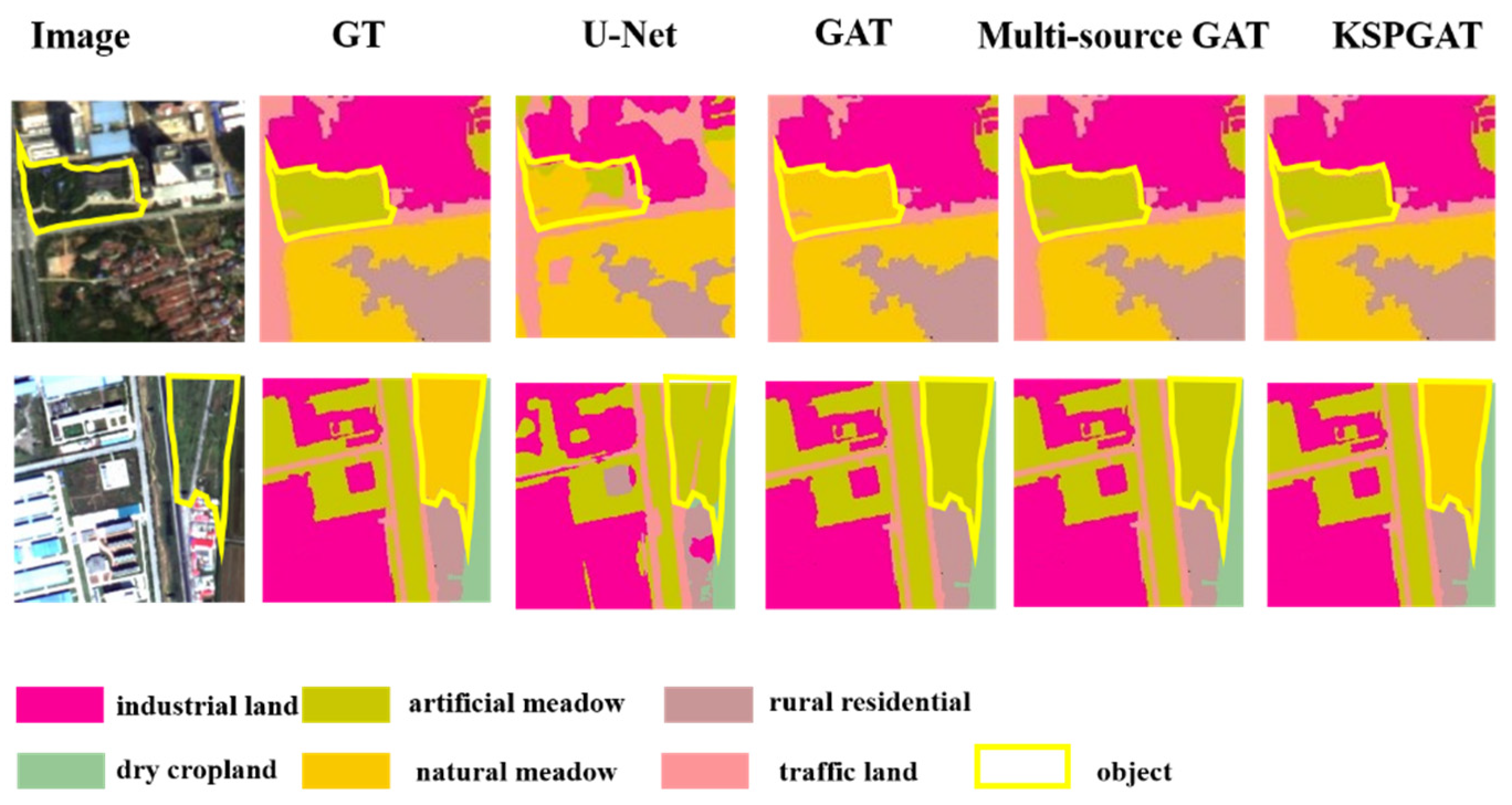
5. Results
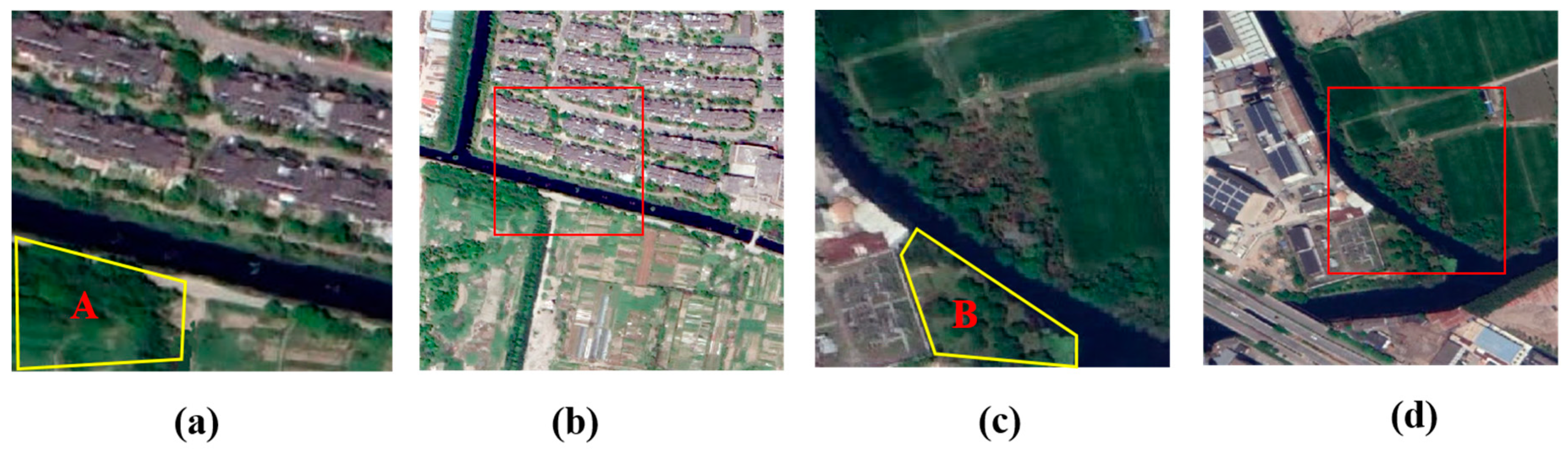
5.1. The Problem of “Different Objects with the Same Spectrum” in Sample III, IV
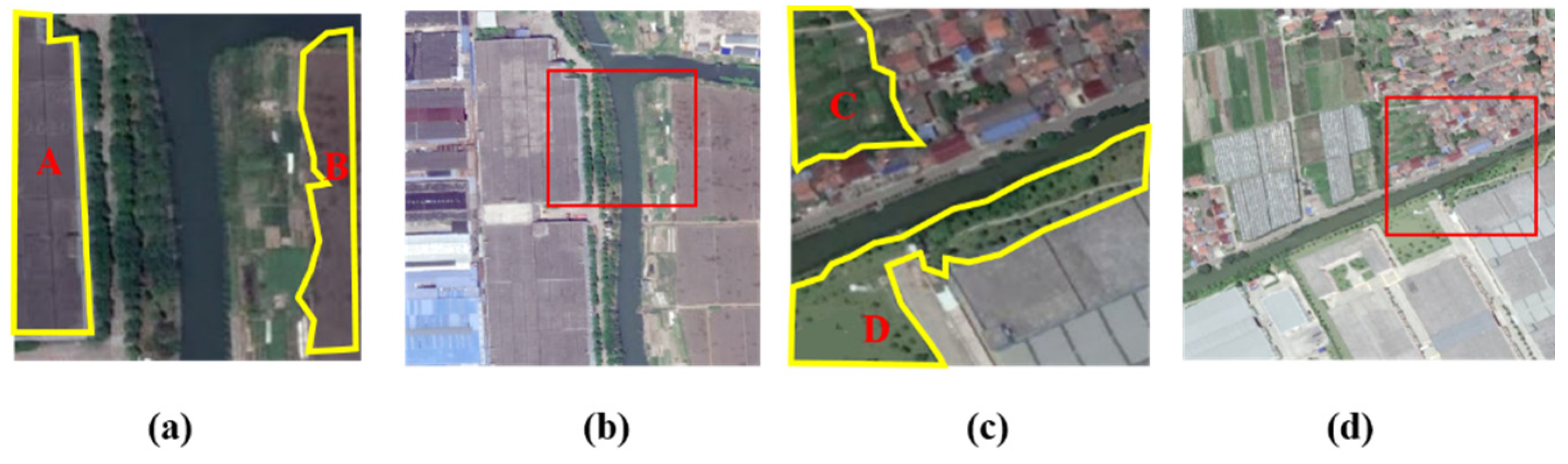
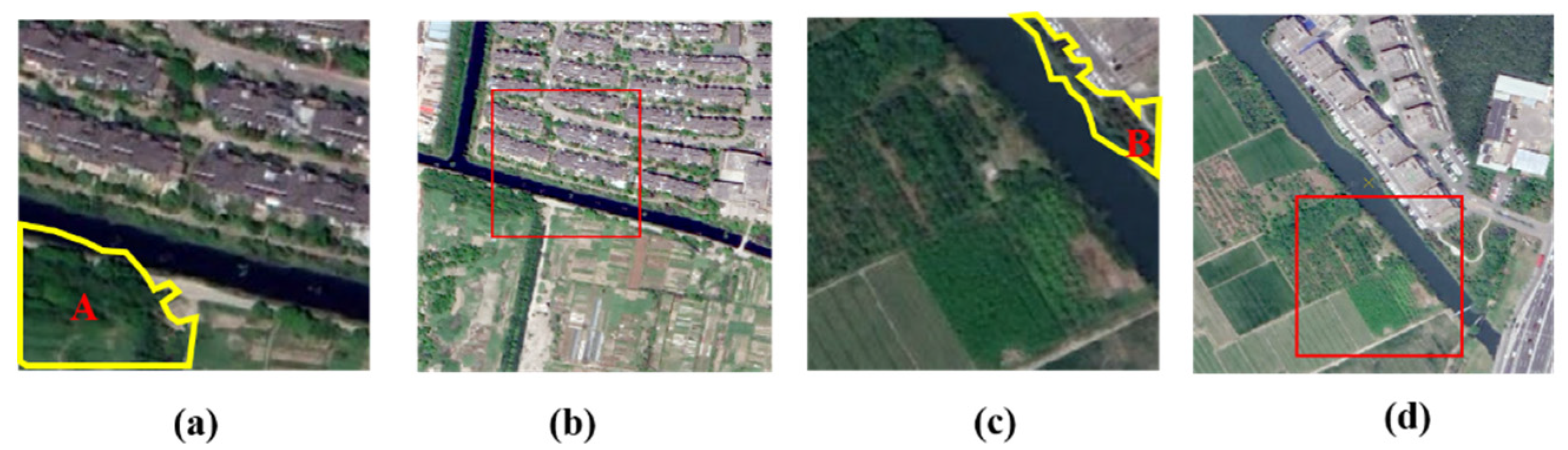
5.2. The Problem of “Violating the First Law of Geography” in Sample V and VI
5.3. Analysis of the Problem “Different Objects with the Same Spectrum”
5.3.1. Analysis of the Baseline GAT Network
5.3.2. Analysis of the Multi-Source GAT Network
5.3.3. Analysis of the KSPGAT Network
5.4. Analysis of the Problem “Violating the First Law of Geography”
5.4.1. Analysis of the Baseline GAT Network
5.4.2. Analysis of the Multi-Source GAT Network
5.4.3. Analysis of the KSPGAT Network
5.5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cui, W.; Wang, F.; He, X.; Zhang, D.; Xu, X.; Yao, M.; Wang, Z.; Huang, J. Multi-Scale Semantic Segmentation and Spatial Relationship Recognition of Remote Sensing Images Based on an Attention Model. Remote Sens. 2019, 11, 1044. [Google Scholar] [CrossRef]
- Yi, Y.; Zhang, Z.; Zhang, W.; Zhang, C.; Li, W.; Zhao, T. Semantic Segmentation of Urban Buildings from VHR Remote Sensing Imagery Using a Deep Convolutional Neural Network. Remote Sens. 2019, 11, 1774. [Google Scholar] [CrossRef]
- Shao, Z.; Tang, P.; Wang, Z.; Saleem, N.; Yam, S.; Sommai, C. BRRNet: A Fully Convolutional Neural Network for Automatic Building Extraction From High-Resolution Remote Sensing Images. Remote Sens. 2020, 12, 1050. [Google Scholar] [CrossRef]
- He, C.; Li, S.; Xiong, D.; Fang, P.; Liao, M. Remote Sensing Image Semantic Segmentation Based on Edge Information Guidance. Remote Sens. 2020, 12, 1501. [Google Scholar] [CrossRef]
- Xu, Z.; Zhang, W.; Zhang, T.; Li, J. HRCNet: High-Resolution Context Extraction Network for Semantic Segmentation of Remote Sensing Images. Remote Sens. 2020, 13, 71. [Google Scholar] [CrossRef]
- Liu, W.; Rabinovich, A.; Berg, A.C. ParseNet: Looking Wider to See Better. arXiv 2015, arXiv:1506.04579. [Google Scholar]
- Luo, W.; Li, Y.; Urtasun, R.; Zemel, R. Understanding the Effective Receptive Field in Deep Convolutional Neural Networks. arXiv 2017, arXiv:1701.04128. [Google Scholar]
- Wang, X.; Girshick, R.; Gupta, A.; He, K. Non-Local Neural Networks. arXiv 2018, arXiv:1711.07971. [Google Scholar]
- Yu, F.; Koltun, V. Multi-Scale Context Aggregation by Dilated Convolutions. arXiv 2016, arXiv:1511.07122. [Google Scholar]
- Li, D.; Shen, X.; Yu, Y.; Guan, H.; Li, J.; Zhang, G.; Li, D. Building Extraction from Airborne Multi-Spectral LiDAR Point Clouds Based on Graph Geometric Moments Convolutional Neural Networks. Remote Sens. 2020, 12, 3186. [Google Scholar] [CrossRef]
- Ma, F.; Gao, F.; Sun, J.; Zhou, H.; Hussain, A. Attention Graph Convolution Network for Image Segmentation in Big SAR Imagery Data. Remote Sens. 2019, 11, 2586. [Google Scholar] [CrossRef]
- Zhao, W.; Emery, W.; Bo, Y.; Chen, J. Land Cover Mapping with Higher Order Graph-Based Co-Occurrence Model. Remote Sens. 2018, 10, 1713. [Google Scholar] [CrossRef]
- Tobler, W.R. A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 1970, 46, 234. [Google Scholar] [CrossRef]
- Hay, G.J.; Marceau, D.J.; Dubé, P.; Bouchard, A. A Multiscale Framework for Landscape Analysis: Object-Specific Analysis and Upscaling. Landsc. Ecol. 2001, 16, 471–490. [Google Scholar] [CrossRef]
- Huang, H.; Chen, J.; Li, Z.; Gong, F.; Chen, N. Ontology-Guided Image Interpretation for GEOBIA of High Spatial Resolution Remote Sense Imagery: A Coastal Area Case Study. IJGI 2017, 6, 105. [Google Scholar] [CrossRef]
- Merciol, F.; Faucqueur, L.; Damodaran, B.; Rémy, P.-Y.; Desclée, B.; Dazin, F.; Lefèvre, S.; Masse, A.; Sannier, C. GEOBIA at the Terapixel Scale: Toward Efficient Mapping of Small Woody Features from Heterogeneous VHR Scenes. IJGI 2019, 8, 46. [Google Scholar] [CrossRef]
- Zhou, Z.; Ma, L.; Fu, T.; Zhang, G.; Yao, M.; Li, M. Change Detection in Coral Reef Environment Using High-Resolution Images: Comparison of Object-Based and Pixel-Based Paradigms. IJGI 2018, 7, 441. [Google Scholar] [CrossRef]
- Knevels, R.; Petschko, H.; Leopold, P.; Brenning, A. Geographic Object-Based Image Analysis for Automated Landslide Detection Using Open Source GIS Software. IJGI 2019, 8, 551. [Google Scholar] [CrossRef]
- Mishra, N.; Mainali, K.; Shrestha, B.; Radenz, J.; Karki, D. Species-Level Vegetation Mapping in a Himalayan Treeline Ecotone Using Unmanned Aerial System (UAS) Imagery. IJGI 2018, 7, 445. [Google Scholar] [CrossRef]
- Lefèvre, S.; Sheeren, D.; Tasar, O. A Generic Framework for Combining Multiple Segmentations in Geographic Object-Based Image Analysis. IJGI 2019, 8, 70. [Google Scholar] [CrossRef]
- Alganci, U. Dynamic Land Cover Mapping of Urbanized Cities with Landsat 8 Multi-Temporal Images: Comparative Evaluation of Classification Algorithms and Dimension Reduction Methods. IJGI 2019, 8, 139. [Google Scholar] [CrossRef]
- Cui, W. Geographical Ontology Modeling Based on Object-Oriented Remote Sensing Technology; The Science Publishing Compan: Beijing, China, 2016; ISBN 978-7-03-050323-7. [Google Scholar]
- Cui, W.; Zheng, Z.; Zhou, Q.; Huang, J.; Yuan, Y. Application of a Parallel Spectral–Spatial Convolution Neural Network in Object-Oriented Remote Sensing Land Use Classification. Remote Sens. Lett. 2018, 9, 334–342. [Google Scholar] [CrossRef]
- Hamedianfar, A.; Gibril, M.B.A.; Hosseinpoor, M.; Pellikka, P.K.E. Synergistic Use of Particle Swarm Optimization, Artificial Neural Network, and Extreme Gradient Boosting Algorithms for Urban LULC Mapping from WorldView-3 Images. Geocarto Int. 2020, 1–19. [Google Scholar] [CrossRef]
- Bronstein, M.M.; Bruna, J.; LeCun, Y.; Szlam, A.; Vandergheynst, P. Geometric Deep Learning: Going beyond Euclidean Data. IEEE Signal. Process. Mag. 2017, 34, 18–42. [Google Scholar] [CrossRef]
- Zhou, J.; Cui, G.; Zhang, Z.; Yang, C.; Liu, Z.; Wang, L.; Li, C.; Sun, M. Graph Neural Networks: A Review of Methods and Applications. arXiv 2019, arXiv:1812.08434. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. arXiv 2017, arXiv:1609.02907. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Liò, P.; Bengio, Y. Graph Attention Networks. arXiv 2018, arXiv:1710.10903. [Google Scholar]
- Hechtlinger, Y.; Chakravarti, P.; Qin, J. A Generalization of Convolutional Neural Networks to Graph-Structured Data. arXiv 2017, arXiv:1704.08165. [Google Scholar]
- Liu, Q.; Kampffmeyer, M.; Jenssen, R.; Salberg, A.-B. Self-Constructing Graph Convolutional Networks for Semantic Labeling. arXiv 2020, arXiv:2003.06932. [Google Scholar]
- Chen, Y.; Rohrbach, M.; Yan, Z.; Yan, S.; Feng, J.; Kalantidis, Y. Graph-Based Global Reasoning Networks. arXiv 2018, arXiv:1811.12814. [Google Scholar]
- Lu, Y.; Chen, Y.; Zhao, D.; Chen, J. Graph-FCN for Image Semantic Segmentation. arXiv 2020, arXiv:2001.00335. [Google Scholar]
- Abu-El-Haija, S.; Kapoor, A.; Perozzi, B.; Lee, J. N-GCN: Multi-Scale Graph Convolution for Semi-Supervised Node Classification. arXiv 2018, arXiv:1802.08888. [Google Scholar]
- Hamilton, W.L.; Ying, R.; Leskovec, J. Inductive Representation Learning on Large Graphs. arXiv 2018, arXiv:1706.02216. [Google Scholar]
- Chiang, W.-L.; Liu, X.; Si, S.; Li, Y.; Bengio, S.; Hsieh, C.-J. Cluster-GCN: An Efficient Algorithm for Training Deep and Large Graph Convolutional Networks. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 25 July 2019; ACM: New York, NY, USA, 2019; pp. 257–266. [Google Scholar] [CrossRef]
- Rong, Y.; Huang, W.; Xu, T.; Huang, J. DropEdge: Towards Deep Graph Convolutional Networks on Node Classification. arXiv 2020, arXiv:1907.10903. [Google Scholar]
- Wang, G.; Ying, R.; Huang, J.; Leskovec, J. Direct Multi-Hop Attention Based Graph Neural Network. arXiv 2020, arXiv:2009.14332. [Google Scholar]
- Kampffmeyer, M.; Chen, Y.; Liang, X.; Wang, H.; Zhang, Y.; Xing, E.P. Rethinking Knowledge Graph Propagation for Zero-Shot Learning. arXiv 2019, arXiv:1805.11724. [Google Scholar]
- Singh, K.K.; Divvala, S.; Farhadi, A.; Lee, Y.J. DOCK: Detecting Objects by Transferring Common-Sense Knowledge. arXiv 2018, arXiv:1804.01077. [Google Scholar]
- Marino, K.; Salakhutdinov, R.; Gupta, A. The More You Know: Using Knowledge Graphs for Image Classification. arXiv 2017, arXiv:1612.04844. [Google Scholar]
- Hou, J.; Wu, X.; Zhang, X.; Qi, Y.; Jia, Y.; Luo, J. Joint Commonsense and Relation Reasoning for Image and Video Captioning. AAAI 2020, 34, 10973–10980. [Google Scholar] [CrossRef]
- You, R.; Guo, Z.; Cui, L.; Long, X.; Bao, Y.; Wen, S. Cross-Modality Attention with Semantic Graph Embedding for Multi-Label Classification. arXiv 2020, arXiv:1912.07872. [Google Scholar] [CrossRef]
- Xie, Y.; Xu, Z.; Kankanhalli, M.S.; Meel, K.S.; Soh, H. Embedding Symbolic Knowledge into Deep Networks. arXiv 2019, arXiv:1909.01161. [Google Scholar]
- Chen, T.; Yu, W.; Chen, R.; Lin, L. Knowledge-Embedded Routing Network for Scene Graph Generation. arXiv 2019, arXiv:1903.03326. [Google Scholar]
- Li, M.; Stein, A. Mapping Land Use from High Resolution Satellite Images by Exploiting the Spatial Arrangement of Land Cover Objects. Remote Sens. 2020, 12, 4158. [Google Scholar] [CrossRef]
- Li, Y.; Chen, R.; Zhang, Y.; Zhang, M.; Chen, L. Multi-Label Remote Sensing Image Scene Classification by Combining a Convolutional Neural Network and a Graph Neural Network. Remote Sens. 2020, 12, 4003. [Google Scholar] [CrossRef]
- Iddianozie, C.; McArdle, G. Improved Graph Neural Networks for Spatial Networks Using Structure-Aware Sampling. IJGI 2020, 9, 674. [Google Scholar] [CrossRef]
- Jimenez-Sierra, D.A.; Benítez-Restrepo, H.D.; Vargas-Cardona, H.D.; Chanussot, J. Graph-Based Data Fusion Applied to: Change Detection and Biomass Estimation in Rice Crops. Remote Sens. 2020, 12, 2683. [Google Scholar] [CrossRef]
- Niu, Y.; Wang, B. A Novel Hyperspectral Anomaly Detector Based on Low-Rank Representation and Learned Dictionary. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 5860–5863. [Google Scholar]
- Liu, J.; Xiao, Z.; Chen, Y.; Yang, J. Spatial-Spectral Graph Regularized Kernel Sparse Representation for Hyperspectral Image Classification. IJGI 2017, 6, 258. [Google Scholar] [CrossRef]
- Zhu, D.; Wang, B.; Zhang, L. Airport Target Detection in Remote Sensing Images: A New Method Based on Two-Way Saliency. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1096–1100. [Google Scholar] [CrossRef]
- Hu, Z.; Zhang, Q.; Zou, Q.; Li, Q.; Wu, G. Stepwise Evolution Analysis of the Region-Merging Segmentation for Scale Parameterization. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2461–2472. [Google Scholar] [CrossRef]
- Hu, Z.; Li, Q.; Zhang, Q.; Zou, Q.; Wu, Z. Unsupervised Simplification of Image Hierarchies via Evolution Analysis in Scale-Sets Framework. IEEE Trans. Image Process. 2017, 26, 2394–2407. [Google Scholar] [CrossRef]
- Hu, Z.; Li, Q.; Zou, Q.; Zhang, Q.; Wu, G. A Bilevel Scale-Sets Model for Hierarchical Representation of Large Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7366–7377. [Google Scholar] [CrossRef]
- Tong, X.-Y.; Xia, G.-S.; Lu, Q.; Shen, H.; Li, S.; You, S.; Zhang, L. Land-Cover Classification with High-Resolution Remote Sensing Images Using Transferable Deep Models. arXiv 2019, arXiv:1807.05713. [Google Scholar] [CrossRef]
- Hao, W.; Zhen, L.; Clarke, K.C.; Wenzhong, S.; Linchuan, F.; Anqi, L.; Jie, Z. Examining the sensitivity of spatial scale in cellular automata Markov chain simulation of land use change. Int. J. Geogr. Inf. Sci. 2019, 33, 1040–1061. [Google Scholar]
- Wang, H.; Huang, J.; Zhou, H.; Deng, C.; Fang, C. Analysis of Sustainable Utilization of Water Resources Based on the Improved Water Resources Ecological Footprint Model: A Case Study of Hubei Province, China. J. Environ. Manag. 2020, 262, 110331. [Google Scholar] [CrossRef] [PubMed]





| Interval_Number | 0 | 1 | 2 |
|---|---|---|---|
| 1 | 2 | 3 |
| Flat_Field | Landslide | Grass | Water_Body | Village | Road | Path | Town | Terrace | Strip_Field | City_Grass | Forest | City_Forest | Total | Accuracy | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| flat_field | 1,522,988 | 1761 | 10,916 | 0 | 21,115 | 56 | 8087 | 12,167 | 46,621 | 2532 | 0 | 19,944 | 0 | 1,646,187 | 0.925 |
| landslide | 9 | 1,441,605 | 63,309 | 11,620 | 5523 | 9968 | 3634 | 3114 | 745 | 0 | 165 | 40,069 | 99 | 1,579,860 | 0.912 |
| grass | 44,886 | 111,517 | 1,773,678 | 35,181 | 67,345 | 9393 | 11,356 | 5950 | 45,618 | 9585 | 8035 | 207,006 | 1093 | 2,330,643 | 0.761 |
| water_body | 95 | 7086 | 6587 | 1,275,542 | 287 | 4245 | 0 | 10,837 | 1068 | 0 | 1698 | 3310 | 189 | 1,310,944 | 0.973 |
| village | 59,839 | 2092 | 57,893 | 1604 | 1,161,845 | 2680 | 9702 | 22,002 | 4922 | 2768 | 663 | 73,881 | 587 | 1,400,478 | 0.830 |
| road | 552 | 2807 | 5170 | 4909 | 1601 | 188,614 | 1596 | 26,785 | 0 | 1 | 1358 | 1811 | 1869 | 237,073 | 0.796 |
| path | 11,322 | 7683 | 23,383 | 475 | 17,715 | 6661 | 159,216 | 579 | 9580 | 1559 | 14 | 6077 | 1204 | 245,468 | 0.649 |
| town | 0 | 1324 | 3321 | 4454 | 31,313 | 20,874 | 0 | 1,245,303 | 0 | 0 | 6980 | 5228 | 28,086 | 1,346,883 | 0.925 |
| terrace | 8778 | 2907 | 47,851 | 96 | 7420 | 0 | 5965 | 0 | 1,289,477 | 4212 | 0 | 27,968 | 0 | 1,394,674 | 0.925 |
| strip_field | 623 | 17 | 31,937 | 0 | 9170 | 38 | 3230 | 0 | 22,178 | 1,269,693 | 0 | 32,061 | 0 | 1,368,947 | 0.927 |
| city_grass | 0 | 47 | 50,235 | 8668 | 3552 | 5134 | 0 | 36,330 | 0 | 0 | 50785 | 6649 | 15,850 | 177,250 | 0.287 |
| forest | 35,186 | 38,047 | 147,480 | 4885 | 112,987 | 2267 | 6824 | 2144 | 31,645 | 29,314 | 5671 | 2,622,081 | 43,532 | 3,082,063 | 0.851 |
| city_forest | 0 | 2 | 1687 | 521 | 282 | 1373 | 0 | 33,044 | 0 | 0 | 4891 | 19,977 | 124,953 | 186,730 | 0.669 |
| Flat_Field | Landslide | Grass | Water_Body | Village | Road | Path | Town | Terrace | Strip_Field | City_Grass | Forest | City_Forest | Total | Accuracy | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| flat_field | 1,497,918 | 5368 | 37,417 | 0 | 12,107 | 0 | 1464 | 8576 | 60,709 | 0 | 0 | 22,628 | 0 | 1,646,187 | 0.910 |
| landslide | 0 | 1,493,644 | 42,332 | 2465 | 2364 | 2441 | 8373 | 0 | 0 | 0 | 0 | 28,241 | 0 | 1,579,860 | 0.945 |
| grass | 39,959 | 47,384 | 1,714,643 | 21,551 | 32,807 | 19,009 | 4677 | 11,330 | 61,819 | 49,820 | 2131 | 325,513 | 0 | 2,330,643 | 0.736 |
| water_body | 0 | 496 | 14,003 | 1,280,572 | 6246 | 1434 | 0 | 6808 | 1143 | 0 | 0 | 242 | 0 | 1,310,944 | 0.977 |
| village | 21,213 | 391 | 25,327 | 0 | 1,236,790 | 6110 | 3582 | 81,193 | 2081 | 0 | 0 | 23,791 | 0 | 1,400,478 | 0.883 |
| road | 0 | 3417 | 14,214 | 7371 | 1635 | 177,481 | 8300 | 23,935 | 0 | 0 | 0 | 0 | 720 | 237,073 | 0.7494 |
| path | 1934 | 6058 | 13,628 | 0 | 18,281 | 7886 | 192,288 | 0 | 2649 | 349 | 0 | 2395 | 0 | 245,468 | 0.783 |
| town | 0 | 5669 | 5939 | 4084 | 104,789 | 3982 | 0 | 1,217,621 | 0 | 0 | 0 | 4799 | 0 | 1,346,883 | 0.904 |
| terrace | 0 | 6172 | 74,527 | 0 | 13,514 | 0 | 1460 | 0 | 1,192,926 | 25,437 | 0 | 80,638 | 0 | 1,394,674 | 0.855 |
| strip_field | 0 | 0 | 36,866 | 0 | 7389 | 0 | 0 | 0 | 30,479 | 1,232,888 | 0 | 61,325 | 0 | 1,368,947 | 0.901 |
| city_grass | 0 | 0 | 67,416 | 7811 | 2894 | 5496 | 0 | 24,842 | 0 | 0 | 44,491 | 19,276 | 5024 | 177,250 | 0.251 |
| forest | 8882 | 10,758 | 66,926 | 893 | 35,673 | 189 | 0 | 1766 | 29,678 | 3823 | 111 | 2,844,492 | 78,872 | 3,082,063 | 0.923 |
| city_forest | 0 | 0 | 918 | 0 | 0 | 376 | 0 | 17,526 | 0 | 0 | 2103 | 52,228 | 113,579 | 186,730 | 0.608 |
| Flat_Field | Landslide | Grass | Water_Body | Village | Road | Path | Town | Terrace | Strip_Field | City_Grass | Forest | City_Forest | Total | Accuracy | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| flat_field | 1,495,321 | 5352 | 37,568 | 0 | 20,719 | 0 | 776 | 7016 | 59,349 | 0 | 0 | 20,086 | 0 | 1,646,187 | 0.908 |
| landslide | 0 | 1,489,063 | 23,094 | 36,682 | 2053 | 8936 | 3014 | 0 | 0 | 0 | 0 | 17,018 | 0 | 1,579,860 | 0.943 |
| grass | 88,916 | 28,921 | 1,804,551 | 111,075 | 44,028 | 11,017 | 1918 | 6400 | 12,386 | 7627 | 25,182 | 188,622 | 0 | 2,330,643 | 0.774 |
| water_body | 0 | 11,756 | 1237 | 1,275,417 | 7651 | 10,003 | 0 | 3495 | 1143 | 0 | 0 | 242 | 0 | 1,310,944 | 0.973 |
| village | 7751 | 17,833 | 17,275 | 0 | 1,306,466 | 141 | 2577 | 28,931 | 763 | 0 | 0 | 18,741 | 0 | 1,400,478 | 0.933 |
| road | 0 | 6939 | 4834 | 10,380 | 1701 | 176,319 | 2504 | 33,676 | 0 | 0 | 720 | 0 | 0 | 237,073 | 0.744 |
| path | 2805 | 6256 | 20,833 | 2349 | 15,913 | 1610 | 191,704 | 2061 | 0 | 204 | 0 | 1733 | 0 | 245,468 | 0.781 |
| town | 0 | 0 | 5095 | 3700 | 5355 | 2426 | 0 | 1,325,508 | 0 | 0 | 0 | 0 | 4799 | 1,346,883 | 0.984 |
| terrace | 6476 | 0 | 113,601 | 0 | 39,116 | 0 | 1460 | 0 | 1,185,165 | 0 | 0 | 48,856 | 0 | 1,394,674 | 0.85 |
| strip_field | 6295 | 0 | 60,435 | 0 | 26,636 | 0 | 0 | 0 | 8035 | 1,226,985 | 0 | 40,561 | 0 | 1,368,947 | 0.896 |
| city_grass | 0 | 0 | 44,935 | 25,513 | 2753 | 1727 | 0 | 23,810 | 0 | 0 | 61,003 | 17,509 | 0 | 177,250 | 0.344 |
| forest | 35,937 | 13,158 | 149,580 | 5965 | 57,858 | 111 | 0 | 1163 | 12,448 | 44,238 | 2876 | 2,739,376 | 19,353 | 3,082,063 | 0.889 |
| city_forest | 0 | 0 | 556 | 2574 | 0 | 192 | 0 | 15,869 | 0 | 0 | 4053 | 26,114 | 137,372 | 186,730 | 0.736 |
| Flat_Field | Landslide | Grass | Water_Body | Village | Road | Path | Town | Terrace | Strip_Field | City_Grass | Forest | City_Forest | Total | Accuracy | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| flat_field | 1,513,767 | 5368 | 32,466 | 0 | 13,237 | 0 | 835 | 0 | 26,629 | 0 | 0 | 53,885 | 0 | 1,646,187 | 0.920 |
| landslide | 0 | 1,521,801 | 32,219 | 2465 | 2053 | 5848 | 3014 | 0 | 0 | 0 | 0 | 12,460 | 0 | 1,579,860 | 0.963 |
| grass | 117,598 | 30,654 | 1,952,874 | 20,567 | 27,580 | 7058 | 1918 | 4559 | 9703 | 13,820 | 0 | 144,312 | 0 | 2,330,643 | 0.838 |
| water_body | 0 | 21,993 | 11,606 | 1,266,012 | 6773 | 0 | 0 | 3417 | 1143 | 0 | 0 | 0 | 0 | 1,310,944 | 0.966 |
| village | 10,230 | 17,833 | 33,818 | 0 | 1,304,349 | 141 | 2513 | 16,684 | 1376 | 0 | 0 | 13,534 | 0 | 1,400,478 | 0.931 |
| road | 0 | 4452 | 12,347 | 5339 | 1701 | 180,157 | 4704 | 26,947 | 0 | 0 | 706 | 0 | 720 | 237,073 | 0.760 |
| path | 3018 | 11,413 | 18,784 | 0 | 15,118 | 0 | 194,203 | 0 | 663 | 204 | 0 | 2065 | 0 | 245,468 | 0.791 |
| town | 0 | 0 | 961 | 588 | 1244 | 1957 | 0 | 1,337,157 | 0 | 0 | 0 | 0 | 4976 | 1,346,883 | 0.993 |
| terrace | 6476 | 0 | 100,720 | 0 | 39,459 | 0 | 1460 | 0 | 1,202,918 | 0 | 0 | 43,641 | 0 | 1,394,674 | 0.863 |
| strip_field | 0 | 0 | 55,674 | 0 | 13,425 | 0 | 0 | 0 | 18,693 | 1,246,394 | 0 | 34,761 | 0 | 1,368,947 | 0.910 |
| city_grass | 0 | 0 | 26,947 | 0 | 5647 | 7387 | 0 | 19,435 | 0 | 0 | 109,700 | 2754 | 5380 | 177,250 | 0.619 |
| forest | 12,194 | 10,738 | 115,220 | 1026 | 30,842 | 7301 | 4871 | 122 | 8783 | 10,476 | 1684 | 2,873,886 | 4920 | 3,082,063 | 0.932 |
| city_forest | 0 | 0 | 556 | 2212 | 0 | 192 | 0 | 18,220 | 0 | 0 | 362 | 5204 | 159,984 | 186,730 | 0.857 |
| Accuracy | mIOU | Kappa | F1-Score | |
|---|---|---|---|---|
| U-Net | 0.867 | 0.699 | 0.850 | 0.806 |
| Baseline GAT | 0.873 | 0.799 | 0.883 | 0.885 |
| Multi-source GAT | 0.886 | 0.829 | 0.897 | 0.900 |
| KSPGAT | 0.911 | 0.846 | 0.916 | 0.914 |
| City_Grass | City_Forest | Grass | Forest | Path | |
|---|---|---|---|---|---|
| U-Net | 28.7% | 66.9% | 76.1% | 85.1% | 64.9% |
| Baseline GAT | 25.1% | 60.8% | 73.6% | 92.3% | 78.3% |
| Multi-source GAT | 34.4% | 73.6% | 77.4% | 88.9% | 78.1% |
| KSPGAT | 61.9% | 85.7% | 83.8% | 93.2% | 79.1% |
| Model | Params (M) | Mem (GB) | FLOPs (G) | Inf Time (FPS) |
|---|---|---|---|---|
| U-Net | 8.64 | 8.88 | 12.60 | 43.01 |
| Baseline GAT | 0.02 | 1.47 | 0.31 | 85.56 |
| Multi-source GAT | 0.02 | 1.48 | 0.31 | 84.31 |
| KSPGAT | 0.02 | 1.47 | 0.31 | 90.07 |
| Accuracy | mIOU | Kappa | F1-Score | |
|---|---|---|---|---|
| U-Net | 0.898 | 0.706 | 0.882 | 0.873 |
| Baseline GAT | 0.906 | 0.761 | 0.886 | 0.889 |
| Multi-source GAT | 0.928 | 0.801 | 0.912 | 0.907 |
| KSPGAT | 0.941 | 0.839 | 0.927 | 0.919 |
| Model | Predict | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Baseline GAT | town | 1 | 0.25 | 0.21 | 0.28 | 0.34 | 0.24 | 0.29 | 0.89 |
| Multi-source GAT | flat_field | 1 | 0.67 | 0.39 | 0.21 | 0.14 | 0.12 | 0.14 | 0.32 |
| KSPGAT | flat_field | 1 | 0.65 | 0.03 | 0.03 | 0 | 0 | 0.01 | 0.02 |
| Distance | 0 | 1 | 1 | 2 | 3 | 3 | 3 | 3 |
| Co-occurrence probability | 1 | 1 | 0.02 | 0.05 | 0.06 | 0.05 | 0.05 | 0.09 |
| Multi-source attention | 1 | 0.68 | 0.36 | 0.23 | 0.12 | 0.13 | 0.13 | 0.30 |
| Gate | 1 | 0.95 | 0.09 | 0.14 | 0.03 | 0.01 | 0.10 | 0.08 |
| Aggregation weight in KSPGAT | 1 | 0.65 | 0.03 | 0.03 | 0 | 0 | 0.01 | 0.02 |
| Model | Predict | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Baseline GAT | city_forest | 1 | 0.22 | 0.13 | 0.11 | 0.43 | 0.09 | 0.39 | 0.06 | 0.15 | 0.04 | 0.41 | 0.02 | 0.05 | 0.39 |
| Multi-source GAT | city_forest | 1 | 0.49 | 0.20 | 0.14 | 0.36 | 0.07 | 0.32 | 0.04 | 0.02 | 0.02 | 0.22 | 0.02 | 0.01 | 0.28 |
| KSPGAT | forest | 1 | 0.49 | 0.01 | 0.02 | 0.01 | 0 | 0.03 | 0 | 0 | 0 | 0.02 | 0 | 0 | 0.02 |
| Order | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Objects in Sample V | city_forest | flat_field | road | water_body | town | |
| Accumulation weight | 1 | 1.62 | 0.22 | 0.21 | 0.11 | 0.39 |
| Order | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Objects of Sample V | city_forest | flat_field | road | water_body | town | |
| Accumulation weight | 1 | 1.06 | 0.49 | 0.26 | 0.14 | 0.12 |
| Distance | 0 | 1 | 1 | 1 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| Co-occurrence probability | 1 | 0.69 | 0.31 | 0.37 | 0.04 | 0.10 | 0.04 | 0.31 | 0.10 | 0.10 | 0.04 | 0.31 | 0.10 | 0.04 |
| Multi-source attention | 1 | 0.50 | 0.18 | 0.15 | 0.35 | 0.08 | 0.34 | 0.05 | 0.01 | 0.02 | 0.23 | 0.01 | 0.01 | 0.25 |
| Gate | 1 | 0.98 | 0.08 | 0.12 | 0.02 | 0.04 | 0.08 | 0.05 | 0.04 | 0.02 | 0.09 | 0.02 | 0.05 | 0.08 |
| Aggregation weight in KSPGAT | 1 | 0.49 | 0.01 | 0.02 | 0.01 | 0 | 0.03 | 0 | 0 | 0 | 0.02 | 0 | 0 | 0.02 |
| Order | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Objects of Sample V | flat_field | city_forest | water_body | road | town | |
| Accumulation weight | 1 | 0.49 | 0.08 | 0.02 | 0.01 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, W.; He, X.; Yao, M.; Wang, Z.; Hao, Y.; Li, J.; Wu, W.; Zhao, H.; Xia, C.; Li, J.; et al. Knowledge and Spatial Pyramid Distance-Based Gated Graph Attention Network for Remote Sensing Semantic Segmentation. Remote Sens. 2021, 13, 1312. https://doi.org/10.3390/rs13071312
Cui W, He X, Yao M, Wang Z, Hao Y, Li J, Wu W, Zhao H, Xia C, Li J, et al. Knowledge and Spatial Pyramid Distance-Based Gated Graph Attention Network for Remote Sensing Semantic Segmentation. Remote Sensing. 2021; 13(7):1312. https://doi.org/10.3390/rs13071312
Chicago/Turabian StyleCui, Wei, Xin He, Meng Yao, Ziwei Wang, Yuanjie Hao, Jie Li, Weijie Wu, Huilin Zhao, Cong Xia, Jin Li, and et al. 2021. "Knowledge and Spatial Pyramid Distance-Based Gated Graph Attention Network for Remote Sensing Semantic Segmentation" Remote Sensing 13, no. 7: 1312. https://doi.org/10.3390/rs13071312
APA StyleCui, W., He, X., Yao, M., Wang, Z., Hao, Y., Li, J., Wu, W., Zhao, H., Xia, C., Li, J., & Cui, W. (2021). Knowledge and Spatial Pyramid Distance-Based Gated Graph Attention Network for Remote Sensing Semantic Segmentation. Remote Sensing, 13(7), 1312. https://doi.org/10.3390/rs13071312