Analysis of Land Development Drivers Using Geographically Weighted Ridge Regression
Abstract
1. Introduction
2. Background
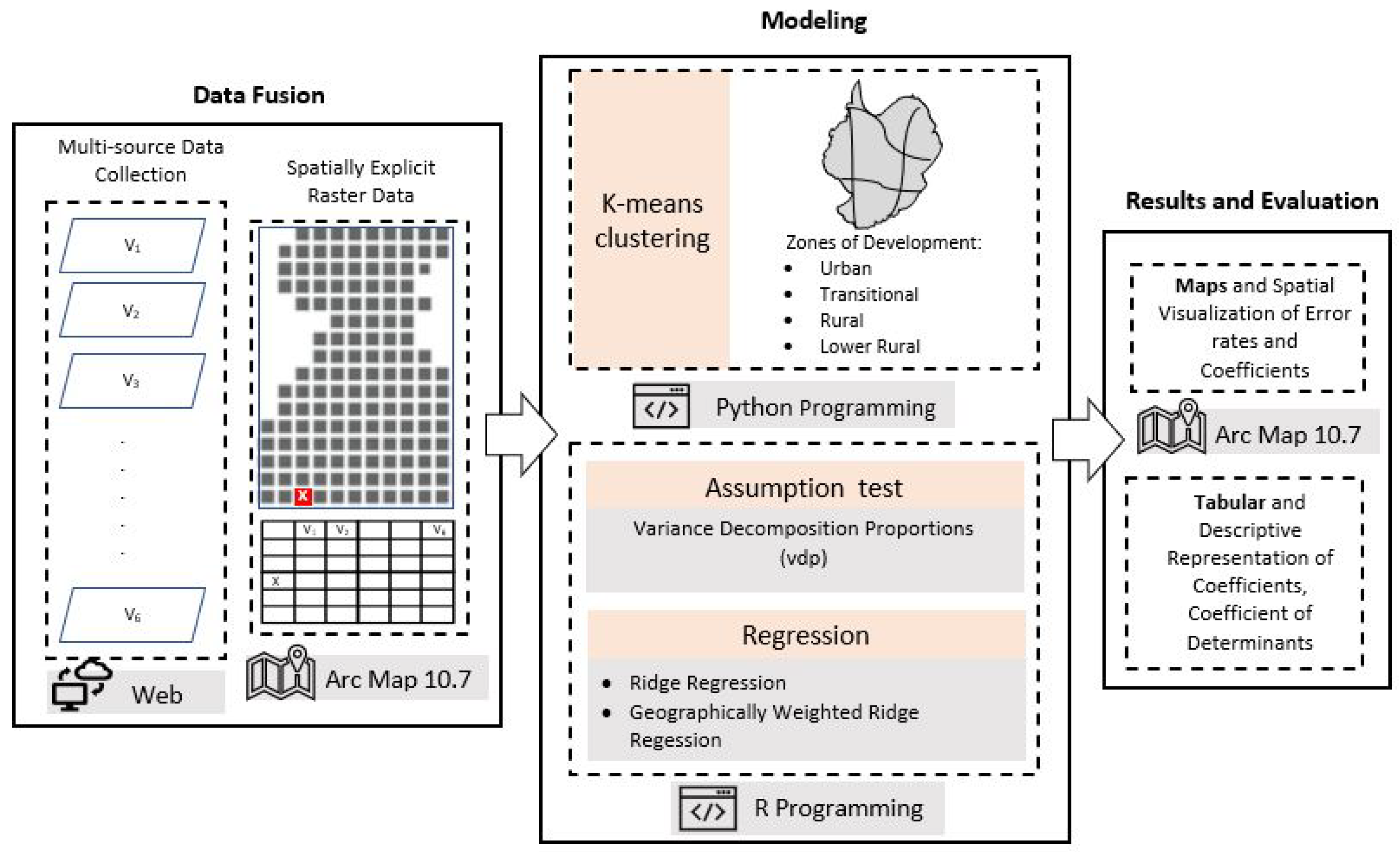
2.1. Data Fusion
2.2. Assumption Test
2.3. Regression Models
3. Materials and Methods
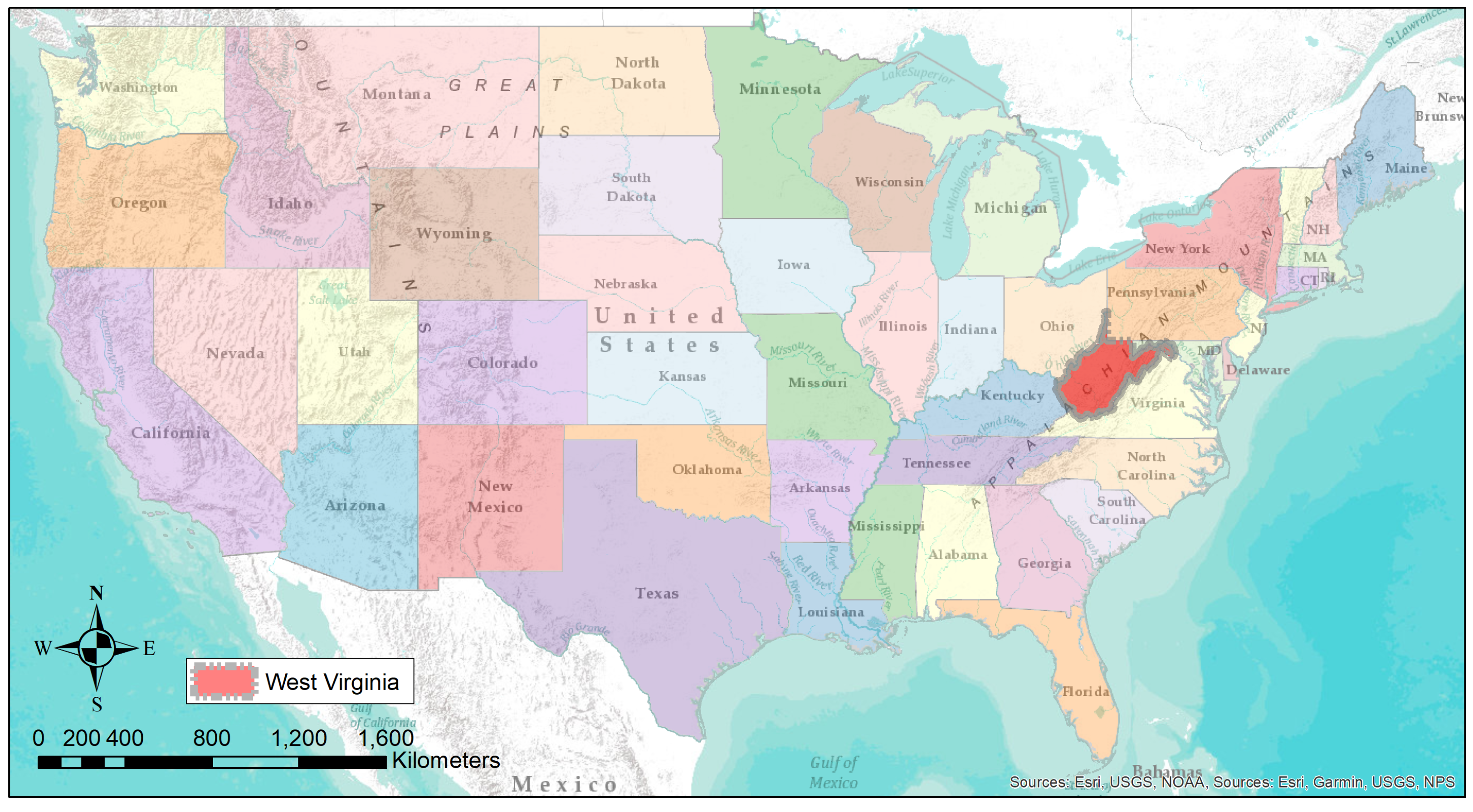
3.1. Study Area
3.2. Variables
3.3. Assumption Test and Modeling
3.4. Model Evaluation
3.4.1. Zones of Development
4. Results
4.1. Global Ridge Regression Model
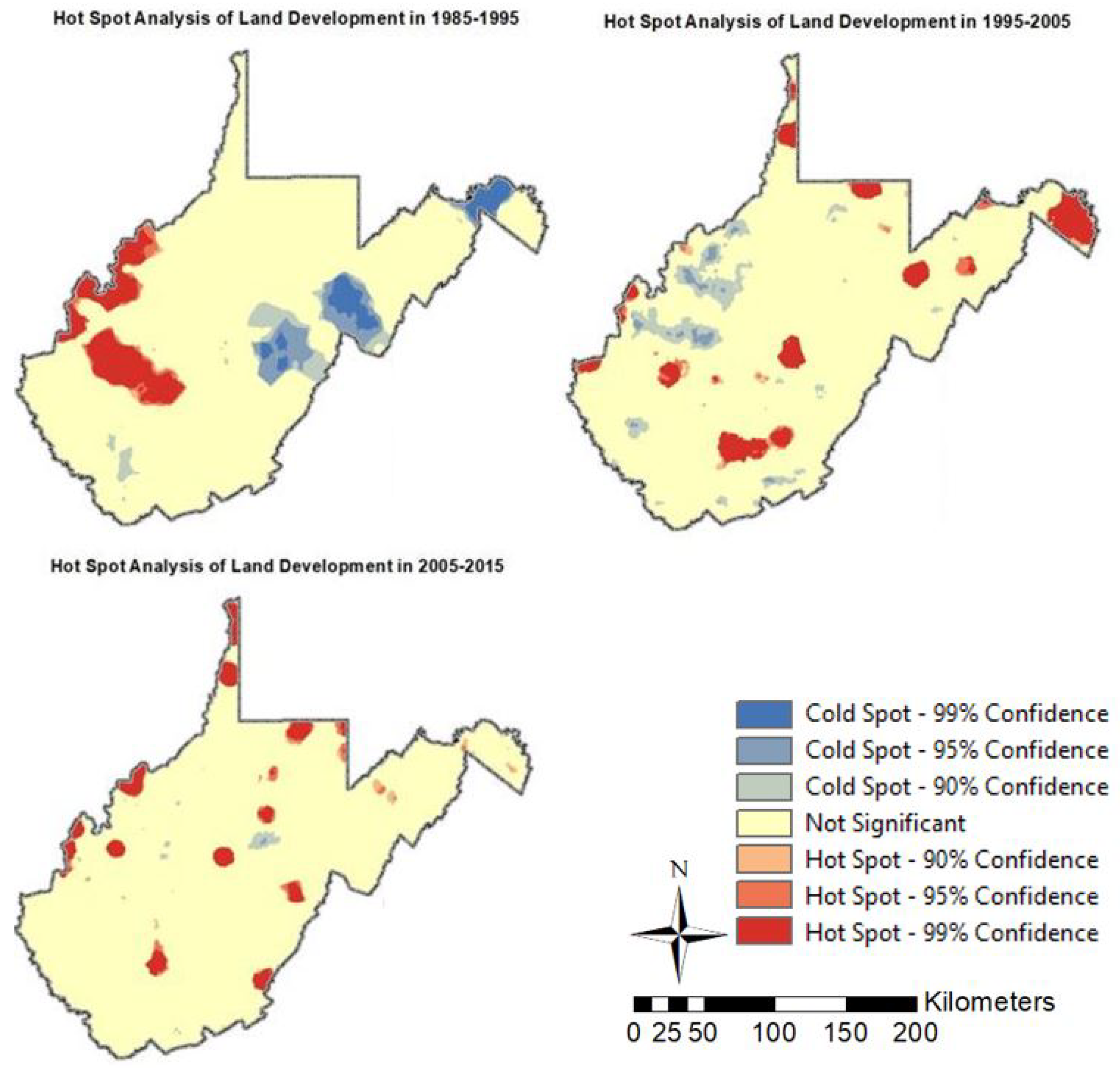
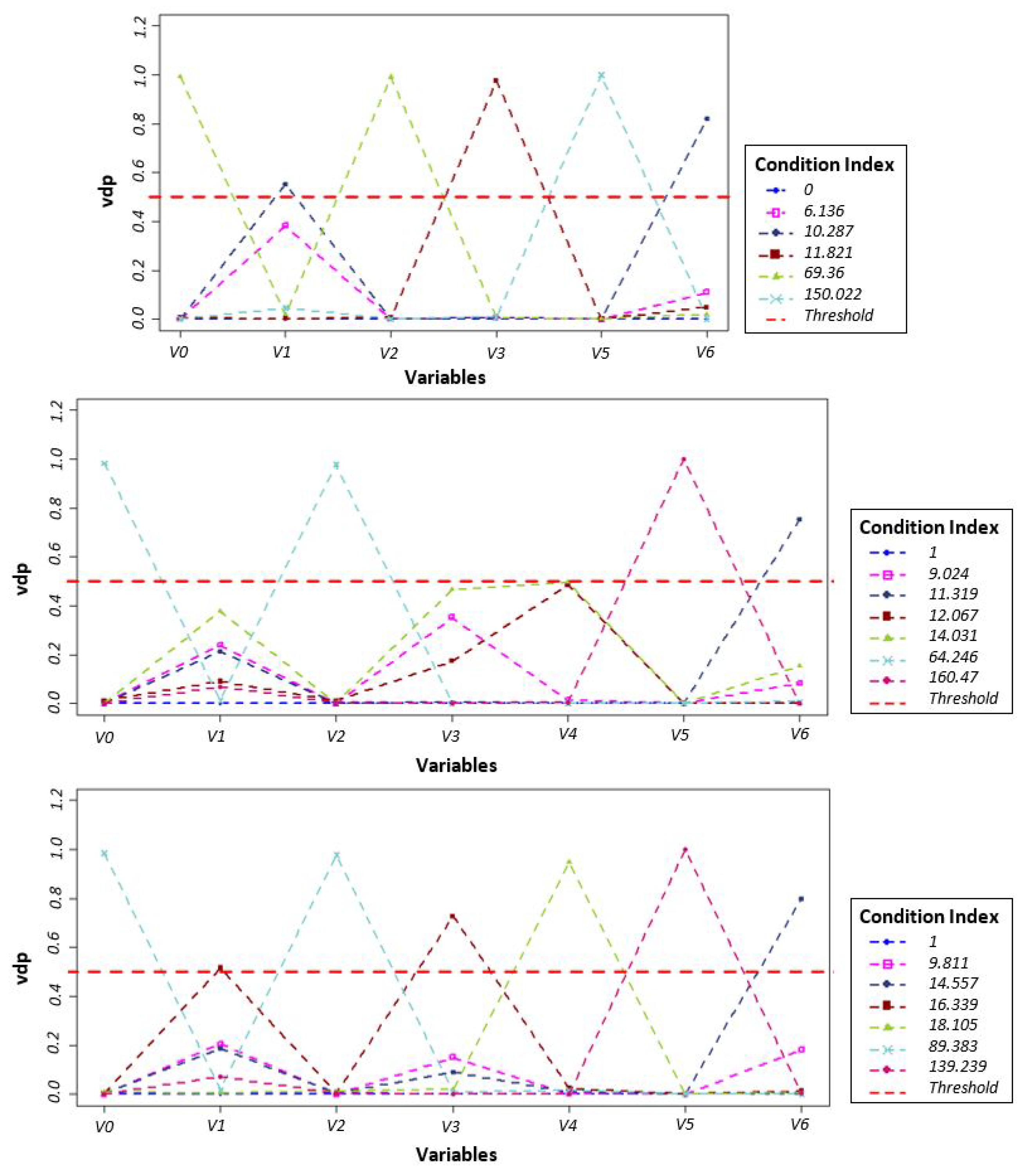
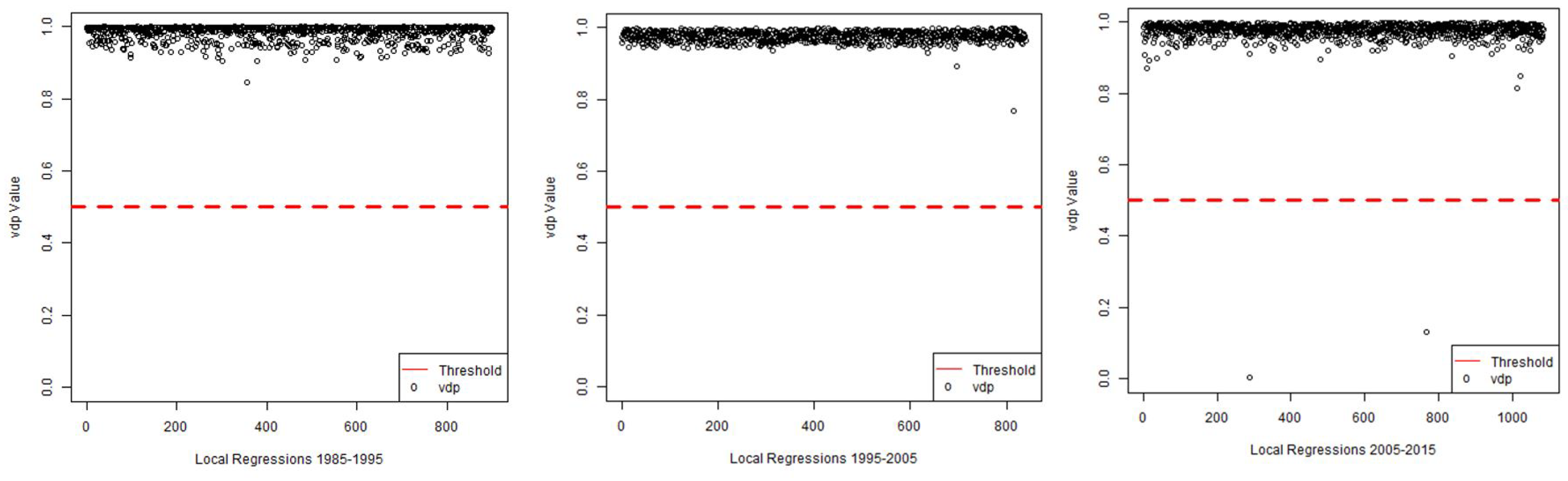
4.2. Geographically Weighted Ridge Regression Model Results and Visual Assessment
5. Discussions
5.1. Study Findings
5.2. Implications
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- De Groot, R. Function-analysis and valuation as a tool to assess land use conflicts in planning for sustainable, multi-functional landscapes. Landsc. Urban Plan. 2006, 75, 175–186. [Google Scholar] [CrossRef]
- Foley, J.A.; DeFries, R.; Asner, G.P.; Barford, C.; Bonan, G.; Carpenter, S.R.; Chapin, F.S.; Coe, M.T.; Daily, G.C.; Gibbs, H.K.; et al. Global consequences of land use. Science 2005, 309, 570–574. [Google Scholar] [CrossRef] [PubMed]
- Bürgi, M.; Hersperger, A.M.; Schneeberger, N. Driving forces of landscape change-current and new directions. Landsc. Ecol. 2005, 19, 857–868. [Google Scholar] [CrossRef]
- Anderson, J.R. A Land Use and Land Cover Classification System for Use with Remote Sensor Data; US Government Printing Office: Washington, DC, USA, 1976; Volume 964.
- NLCD Classes of Landcover. Available online: https://www.mrlc.gov/data/legends/national-land-cover-database-2016-nlcd2016-legend (accessed on 29 March 2021).
- Lambin, E.F.; Turner, B.L.; Geist, H.J.; Agbola, S.B.; Angelsen, A.; Bruce, J.W.; Coomes, O.T.; Dirzo, R.; Fischer, G.; Folke, C.; et al. The causes of land-use and land-cover change: Moving beyond the myths. Glob. Environ. Chang. 2001, 11, 261–269. [Google Scholar] [CrossRef]
- Wheeler, D.C. Diagnostic tools and a remedial method for collinearity in geographically weighted regression. Environ. Plan. A 2007, 39, 2464–2481. [Google Scholar] [CrossRef]
- Getis, A.; Ord, J.K. The analysis of spatial association by use of distance statistics. In Perspectives on Spatial Data Analysis; Springer: Berlin/Heidelberg, Germany, 2010; pp. 127–145. [Google Scholar]
- Sheehan, K.R.; Strager, M.P.; Welsh, S.A. Advantages of geographically weighted regression for modeling benthic substrate in two Greater Yellowstone ecosystem streams. Environ. Model. Assess. 2013, 18, 209–219. [Google Scholar] [CrossRef]
- Ren, Y.; Lü, Y.; Fu, B.; Comber, A.; Li, T.; Hu, J. Driving Factors of Land Change in China’s Loess Plateau: Quantification Using Geographically Weighted Regression and Management Implications. Remote Sens. 2020, 12, 453. [Google Scholar] [CrossRef]
- Maimaitijiang, M.; Ghulam, A.; Sandoval, J.O.; Maimaitiyiming, M. Drivers of land cover and land use changes in St. Louis metropolitan area over the past 40 years characterized by remote sensing and census population data. Int. J. Appl. Earth Obs. Geoinf. 2015, 35, 161–174. [Google Scholar] [CrossRef]
- Mennis, J. Mapping the results of geographically weighted regression. Cartogr. J. 2006, 43, 171–179. [Google Scholar] [CrossRef]
- Huang, X.; Huang, X.; Liu, M.; Wang, B.; Zhao, Y. Spatial-temporal dynamics and driving forces of land development intensity in the western China from 2000 to 2015. Chin. Geogr. Sci. 2020, 30, 16–29. [Google Scholar] [CrossRef]
- Aguayo, M.I.; Wiegand, T.; Azócar, G.D.; Wiegand, K.; Vega, C.E. Revealing the driving forces of mid-cities urban growth patterns using spatial modeling: A case study of Los Ángeles, Chile. Ecol. Soc. 2007, 12, 13. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: Cham, Switzerland, 2013; Volume 112. [Google Scholar]
- Klein, L.A. Sensor and Data Fusion: A Tool for Information Assessment and Decision Making; SPIE Press: Bellingham, WA, USA, 2004; Volume 138. [Google Scholar]
- Zhu, A.X.; Band, L.E. A knowledge-based approach to data integration for soil mapping. Can. J. Remote Sens. 1994, 20, 408–418. [Google Scholar] [CrossRef]
- Blasch, E.; Lambert, D.A. High-Level Information Fusion Management and Systems Design; Artech House: Norwood, MA, USA, 2012. [Google Scholar]
- Warner, T.; Almutairi, A. Chapetr 33: Remote sensing and land cover change. In The SAGE Handbook of Remote Sensing; SAGE: Thousand Oaks, CA, USA, 2009; pp. 459–472. [Google Scholar]
- Cornell, J.A. Classical and Modern Regression with Applications; Taylor & Francis Group: Oxfordshire, UK, 1987. [Google Scholar]
- Callaghan, K.J.; Chen, J. Revisiting the collinear data problem: An assessment of estimator’Ill-Conditioning’in linear regression. Pract. Assess. Res. Eval. 2008, 13, 5. [Google Scholar]
- Esri, National Atlas of the United States, United States Geological Survey, Department of Commerce, Census Bureau, Geography Division, USA. Available online: https://www.arcgis.com/ (accessed on 29 March 2021).
- Appalachia Regional Commission, USA. Available online: https://www.arc.gov/research (accessed on 29 March 2021).
- Annual report of the United Nations High Commissioner for Human Rights and reports of the Office of the High Commissioner and the Secretary-General. In Economic Impact of Energy and Environmental Policy in Appalachia; Appalachian Regional Commission: Washington, DC, USA, 2011.
- US Geological Survey, USA. Available online: https://waterdata.usgs.gov/wv/nwis/current (accessed on 29 March 2021).
- U.S. CensusUS Geological Survey, USA. Available online: https://www.census.gov/ (accessed on 29 March 2021).
- Ghadimi, H. Sustainable Economic Development Planning in Energy Rich Regions. J. Energy Dev. 2015, 41, 68–84. [Google Scholar]
- GIS Tech Center at West Virginia University, Morgantown, WV, USA. Available online: http://wvgis.wvu.edu/ (accessed on 29 March 2021).
- Verburg, P.H. Simulating feedbacks in land use and land cover change models. Landsc. Ecol. 2006, 21, 1171–1183. [Google Scholar] [CrossRef]
- Huang, Z.; Wei, Y.D.; He, C.; Li, H. Urban land expansion under economic transition in China: A multi-level modeling analysis. Habitat Int. 2015, 47, 69–82. [Google Scholar] [CrossRef]
- Liu, J.; Li, T.; Xie, P.; Du, S.; Teng, F.; Yang, X. Urban big data fusion based on deep learning: An overview. Inf. Fusion 2020, 53, 123–133. [Google Scholar] [CrossRef]
- Pato, R.L.; Castro, P.; Tavares, A.O. The relevance of physical forces on land-use change and planning process. J. Environ. Plan. Manag. 2016, 59, 607–627. [Google Scholar] [CrossRef]
- USGS Earth Explorer, USA. Available online: https://earthexplorer.usgs.gov/ (accessed on 29 March 2021).
- U.S. Bureau of Labor, USA. Available online: https://www.bls.gov/ (accessed on 29 March 2021).
- Pourmohammadi, P.; Adjeroh, D.A.; Strager, M.P. Mapping the Land Development Processes Using Data Transformation and Clustering Methods. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 2775–2778. [Google Scholar] [CrossRef]
- Mitchell, A. The ESRI Guide to GIS Analysis (Volume 2); Esri Press: Redlands, CA, USA, 2005. [Google Scholar]
- De Smith, M.J.; Goodchild, M.F.; Longley, P. Geospatial Analysis: A Comprehensive Guide to Principles, Techniques and Software Tools; Troubador Publishing Ltd.: Kibworth, UK, 2007. [Google Scholar]
- Scott, L.M.; Janikas, M.V. Spatial statistics in ArcGIS. In Handbook of Applied Spatial Analysis; Springer: Berlin/Heidelberg, Germany, 2010; pp. 27–41. [Google Scholar]



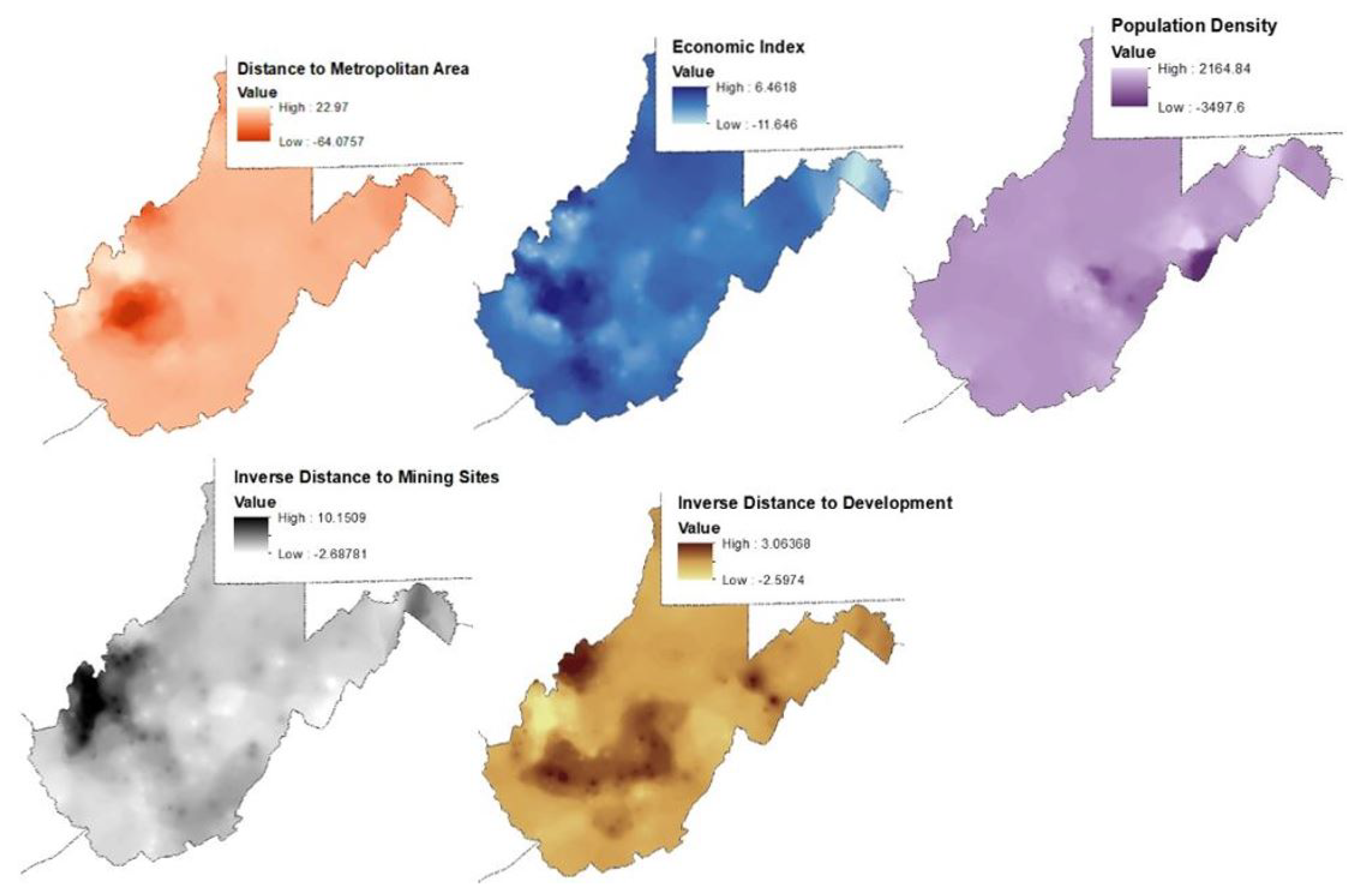
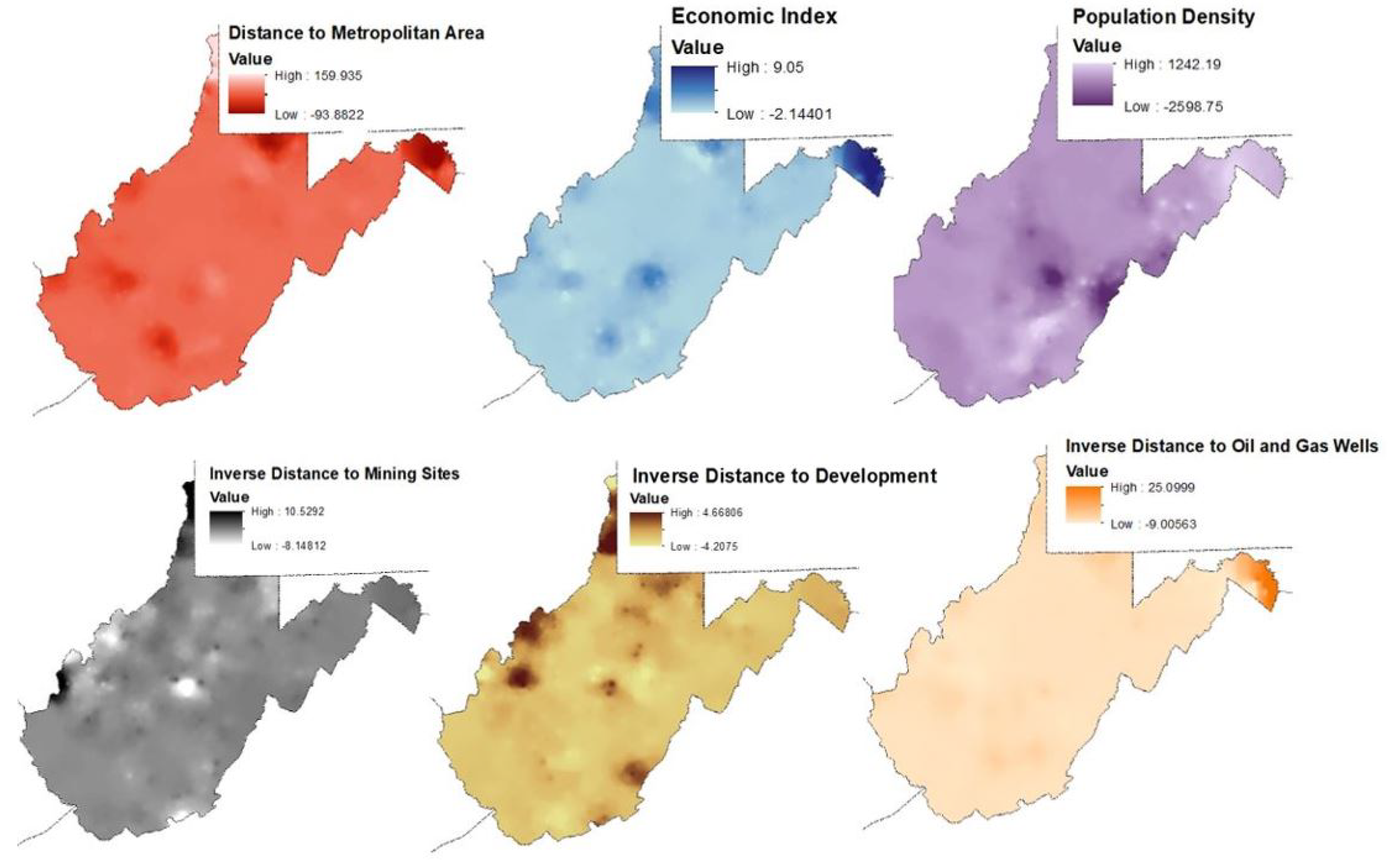
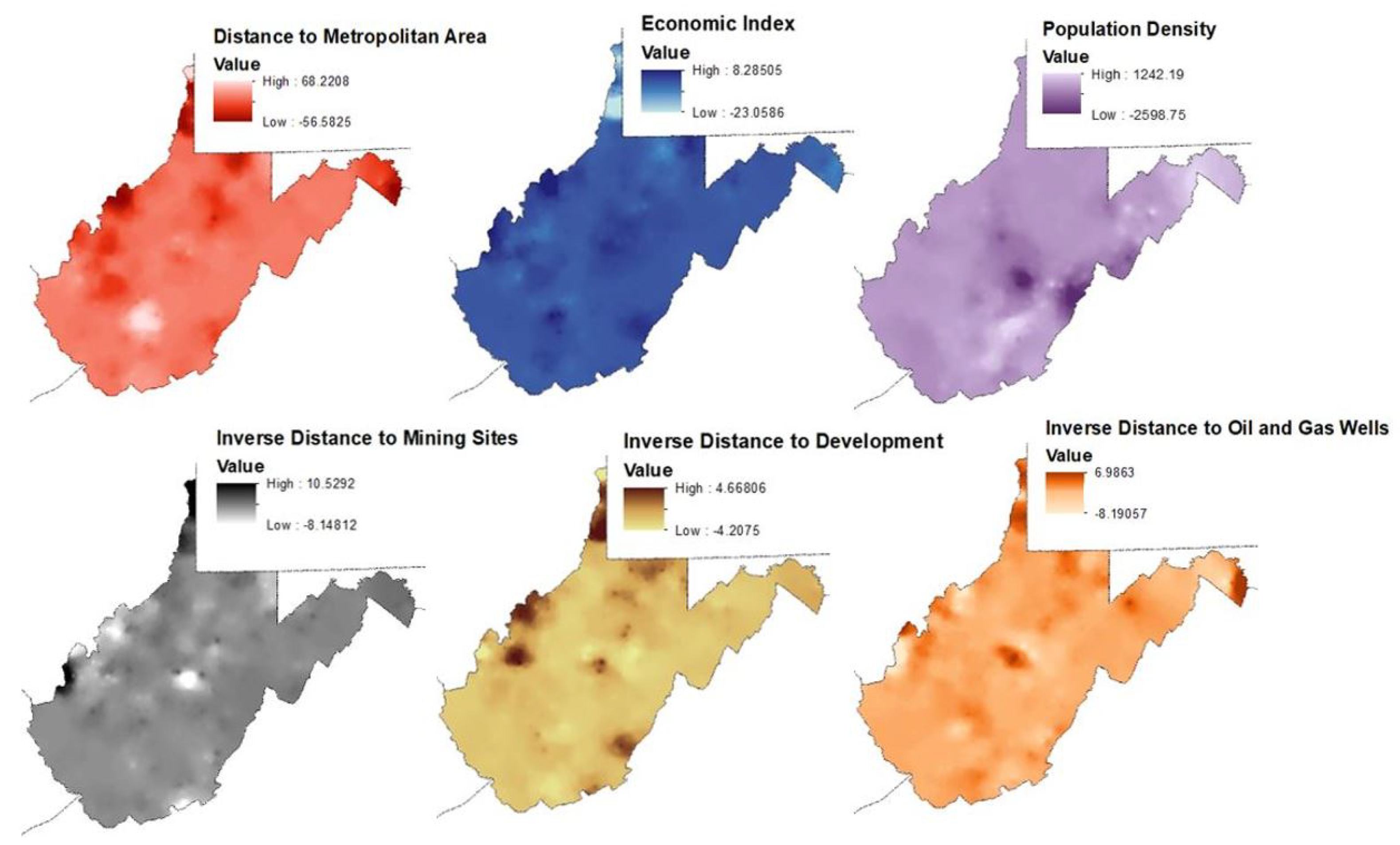
| Variable | Data | Source of Data |
|---|---|---|
| Distance to MSA (m) | Census Data | US Decennial Census Data [26] |
| Distance to Developed Land (m) | Developed Land Historical Trends | Obtained from Landsat [33] |
| Distance to Mining Sites (m) | Mining Permits | WVU GIS Tech Center [28] |
| Distance to Oil and Gas Wells (m) | Shale Gas Points | WVU GIS Tech Center [28] |
| Population Density (per sq. mile) | Census Tract Population | US Decennial Census Data [26] |
| Economic Index (at County Level) | Household Poverty Rate (Percentage) | US Decennial Census Data and |
| Per-Capita Income (US $) | U.S. Bureau of Labor [26,34] | |
| Unemployment Rate (Percentage) |
| 1985−1995 | ||||||
| Variable | Data Type | Min. | Max | Mean | Std. Dev | |
| Distance to MSA | Raster | 0 | 40,752.16 | 8661.12 | 8648.79 | |
| Distance to Developed Lands | Raster | 0 | 4092.55 | 379.29 | 397.15 | |
| Distance to Mining Sites | Raster | 0 | 157,531 | 63,558.0 | 41,038.9 | |
| Population Density | Vector | 1.15 | 9.57 | 3.90 | 2.26 | |
| Household Poverty Rate | Tabular/Vector | 11.1% | 36.33% | 20.97% | 0.06 | |
| E.I. | Per-Capita Income | Tabular/Vector | 9422.50 | 18,706.00 | 13,353.41 | 2158.46 |
| Unemployment Rate | Tabular/Vector | 2.96% | 9.12% | 5.25% | 0.02 | |
| 1995−2005 | ||||||
| Variable | Data Type | Min. | Max | Mean | Std. Dev | |
| Distance to MSA | Raster | 0 | 65,662.27 | 15,375.24 | 11,838.02 | |
| Distance to Developed Lands | Raster | 0 | 4092.55 | 377.20 | 395.75 | |
| Distance to Mining Sites | Raster | 0 | 42,648.5 | 8540.92 | 8097.55 | |
| Distance to Oil and Gas Wells | Raster | 0 | 167,898.67 | 54,125.02 | 30,187.83 | |
| Population Density | Vector | 1.13 | 9.70 | 3.90 | 2.18 | |
| Household Poverty Rate | Tabular/Vector | 9% | 33.07% | 17.28% | 0.05 | |
| E.I. | Per-Capita Income | Tabular/Vector | 15,241.10 | 31,342.20 | 20,537.79 | 3464.27 |
| Unemployment Rate | Tabular/Vector | 3.14% | 12.45% | 6.56% | 0.02 | |
| 2005−2015 | ||||||
| Variable | Data Type | Min. | Max | Mean | Std. Dev | |
| Distance to MSA | Raster | 0 | 64,963.97 | 14,732.04 | 12,163.08 | |
| Distance to Developed Lands | Raster | 0 | 4069.95 | 359.53 | 383.87 | |
| Distance to Mining Sites | Raster | 0 | 42,648.5 | 8111.38 | 7476.66 | |
| Distance to Oil and Gas Wells | Raster | 0 | 111,511.03 | 15,148.23 | 17,683.43 | |
| Population Density | Vector | 1.06 | 9.62 | 3.95 | 2.18 | |
| Household Poverty Rate | Tabular/Vector | 10.30% | 35.23% | 19.19% | 0.05 | |
| E.I. | Per-Capita Income | Tabular/Vector | 19,009.50 | 44,424.10 | 30,078.96 | 4651.86 |
| Unemployment Rate | Tabular/Vector | 5.18% | 13.15% | 9.17% | 0.02 |
| Model | Bandwidth |
|---|---|
| GWRR 1985−1995 | 5801 m |
| GWRR 1995−2005 | 4337 m |
| GWRR 2005−1015 | 4319 m |
| Df | Pillai’s Trace | Approx F | num Df | den Df | Pr (>F) | Residuals | |
|---|---|---|---|---|---|---|---|
| Zones of Development 1985 | 1 | 0.787 | 859.05 | 2 | 465 | <2.2 × 10 *** | 466 |
| Zones of Development 1995 | 1 | 0.76166 | 768.56 | 2 | 481 | <2.2 × 10 *** | 482 |
| Zones of Development 2005 | 1 | 0.72351 | 629.34 | 2 | 481 | <2.2 × 10 *** | 482 |
| 1985−1995 | ||||
| Scaled Estimate | Std. Error (scaled) | t value (scaled) | Pr () | |
| Distance to MSA | −1.3638 | 0.01706 | 79.95 | <2 × 10 *** |
| Inverse Distance to Development | 0.13904 | 0.0147 | 9.462 | <2 × 10 *** |
| Inverse Distance to Mining Sites | 0.55096 | 0.01463 | 37.647 | <2 × 10 *** |
| Inverse Distance to Oil and Gas Wells | - | - | - | - |
| Population Density (per sq. mile) | 0.16899 | 0.01475 | 11.455 | <2 × 10 *** |
| Economic Index | −0.69773 | 0.01687 | 41.358 | <2 × 10 *** |
| Ridge parameter: 8.69 Degrees of freedom: model 4.997, variance 4.994, residual 5 | ||||
| Significance codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 | ||||
| 1995−2005 | ||||
| Scaled Estimate | Std. Error (scaled) | t value (scaled) | Pr () | |
| Distance to MSA | −40.33322 | 0.008175 | 40.76 | <2 × 10 *** |
| Inverse Distance to Development | 0.140729 | 0.007529 | 18.69 | <2 × 10 *** |
| Inverse Distance to Mining Sites | 0.341333 | 0.008027 | 42.52 | <2 × 10 *** |
| Inverse Distance to Oil and Gas Wells | 0.42451 | 0.008035 | 52.83 | <2 × 10*** |
| Population Density (per sq. mile) | 0.447566 | 0.00777 | 57.6 | <2 × 10 *** |
| Economic Index | −0.1587 | 0.007668 | 20.7 | <2 × 10 *** |
| Ridge parameter: 38.5 Degrees of freedom: model 5.995, variance 5.991, residual 6 | ||||
| Significance codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 | ||||
| 2005−2015 | ||||
| Scaled Estimate | Std. Error (scaled) | t value (scaled) | Pr () | |
| Inverse Distance to MSA | −0.4493 | 0.007628 | 58.9 | <2 × 10 *** |
| Inverse Distance to Development | 0.04935 | 0.006631 | 7.442 | 9.95 × 10 *** |
| Inverse Distance to Mining Sites | 0.007491 | 0.007286 | 1.028 | |
| Inverse Distance to Oil and Gas Wells | 0.0409 | 0.0091 | 4.495 | 6.94 × 10 *** |
| Population Density (in sq mi) | 0.400434 | 0.006916 | 57.897 | <2 × 10 *** |
| Economic Index | −0.31697 | 0.006992 | 45.333 | <2 × 10 *** |
| Ridge parameter: 65.49 Degrees of freedom: model 5.994, variance 5.987, residual 6 | ||||
| Significance codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 | ||||
| Model | |
|---|---|
| GWRR 1985−1995 | 0.982 |
| GWRR 1995−2005 | 0.956 |
| GWRR 2005−1015 | 0.961 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pourmohammadi, P.; Strager, M.P.; Dougherty, M.J.; Adjeroh, D.A. Analysis of Land Development Drivers Using Geographically Weighted Ridge Regression. Remote Sens. 2021, 13, 1307. https://doi.org/10.3390/rs13071307
Pourmohammadi P, Strager MP, Dougherty MJ, Adjeroh DA. Analysis of Land Development Drivers Using Geographically Weighted Ridge Regression. Remote Sensing. 2021; 13(7):1307. https://doi.org/10.3390/rs13071307
Chicago/Turabian StylePourmohammadi, Pariya, Michael P. Strager, Michael J. Dougherty, and Donald A. Adjeroh. 2021. "Analysis of Land Development Drivers Using Geographically Weighted Ridge Regression" Remote Sensing 13, no. 7: 1307. https://doi.org/10.3390/rs13071307
APA StylePourmohammadi, P., Strager, M. P., Dougherty, M. J., & Adjeroh, D. A. (2021). Analysis of Land Development Drivers Using Geographically Weighted Ridge Regression. Remote Sensing, 13(7), 1307. https://doi.org/10.3390/rs13071307