A Novel Recursive Model Based on a Convolutional Long Short-Term Memory Neural Network for Air Pollution Prediction
Abstract
1. Introduction
2. Materials and Methods
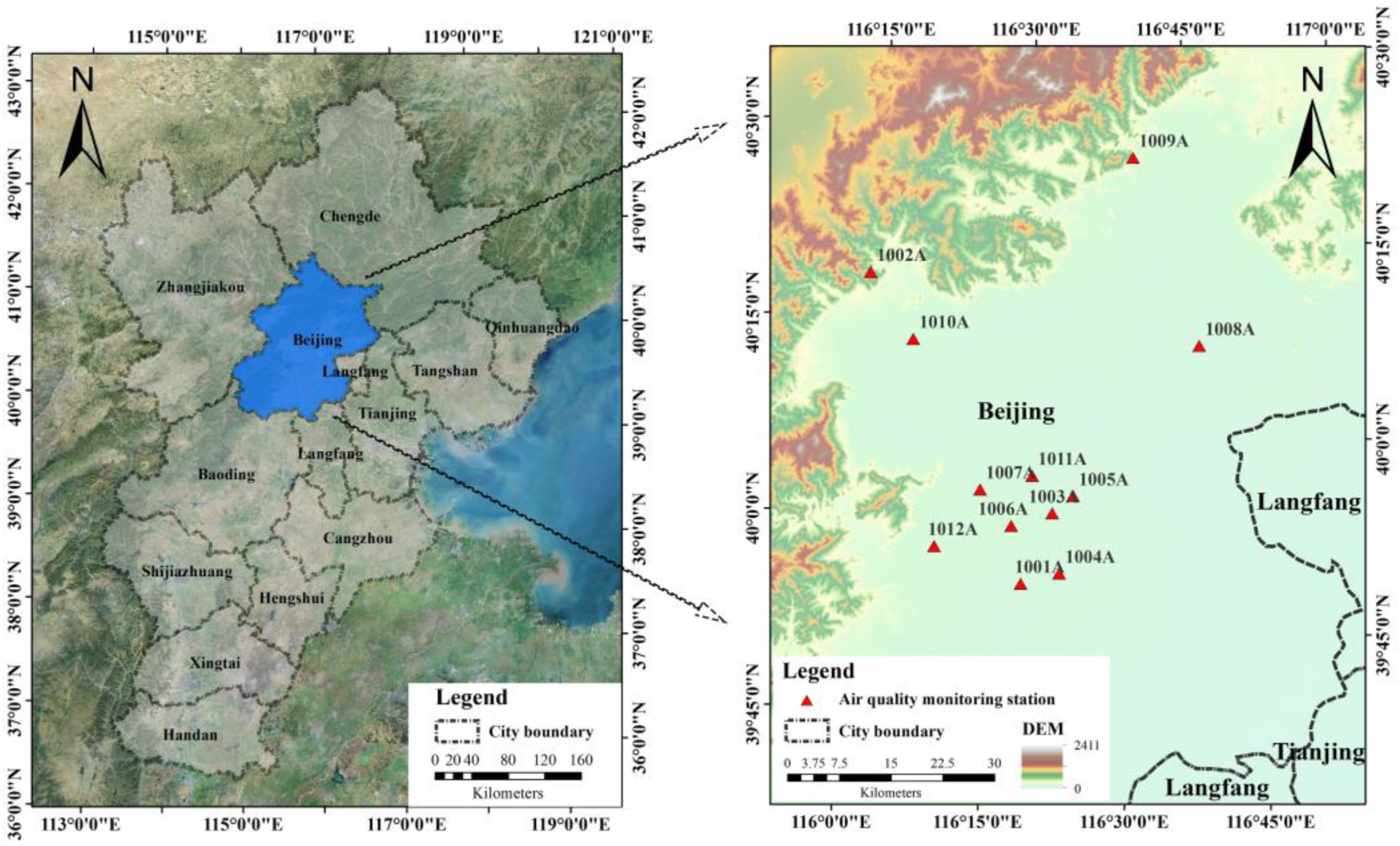
2.1. Study Area and Data Source
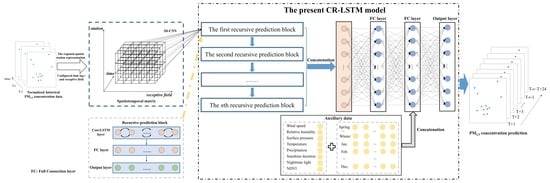
2.2. CR-LSTM Model
2.2.1. The Regional Spatial Station Representation Method
2.2.2. The LSTM Neural Network
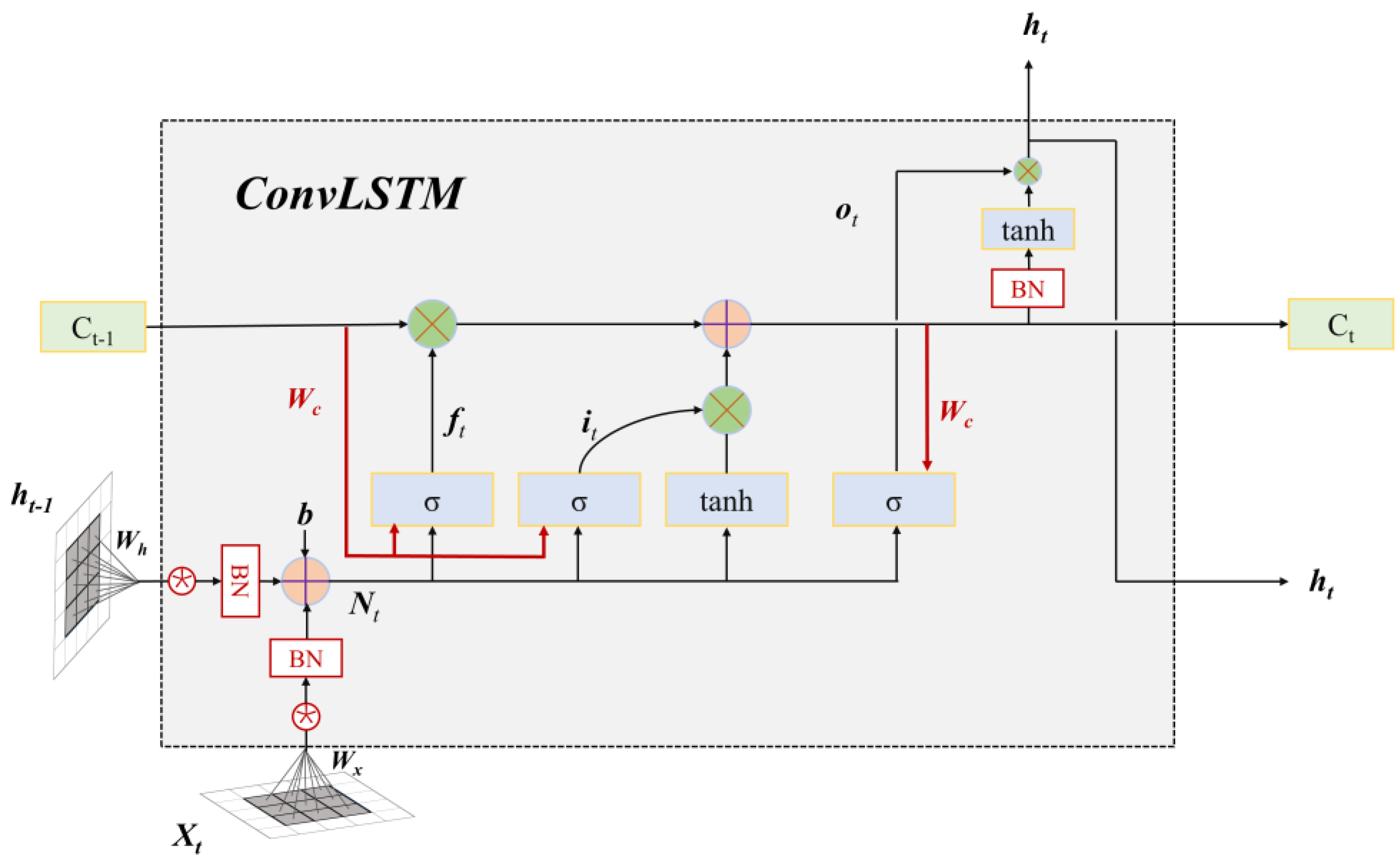
2.2.3. The ConvLSTM Neural Network
2.2.4. The CR-LSTM Model
3. Results and Analysis
3.1. Pre-Processing of the Model
3.2. CR-LSTM Model Performance
4. Discussion
4.1. Comparison of the Experiments
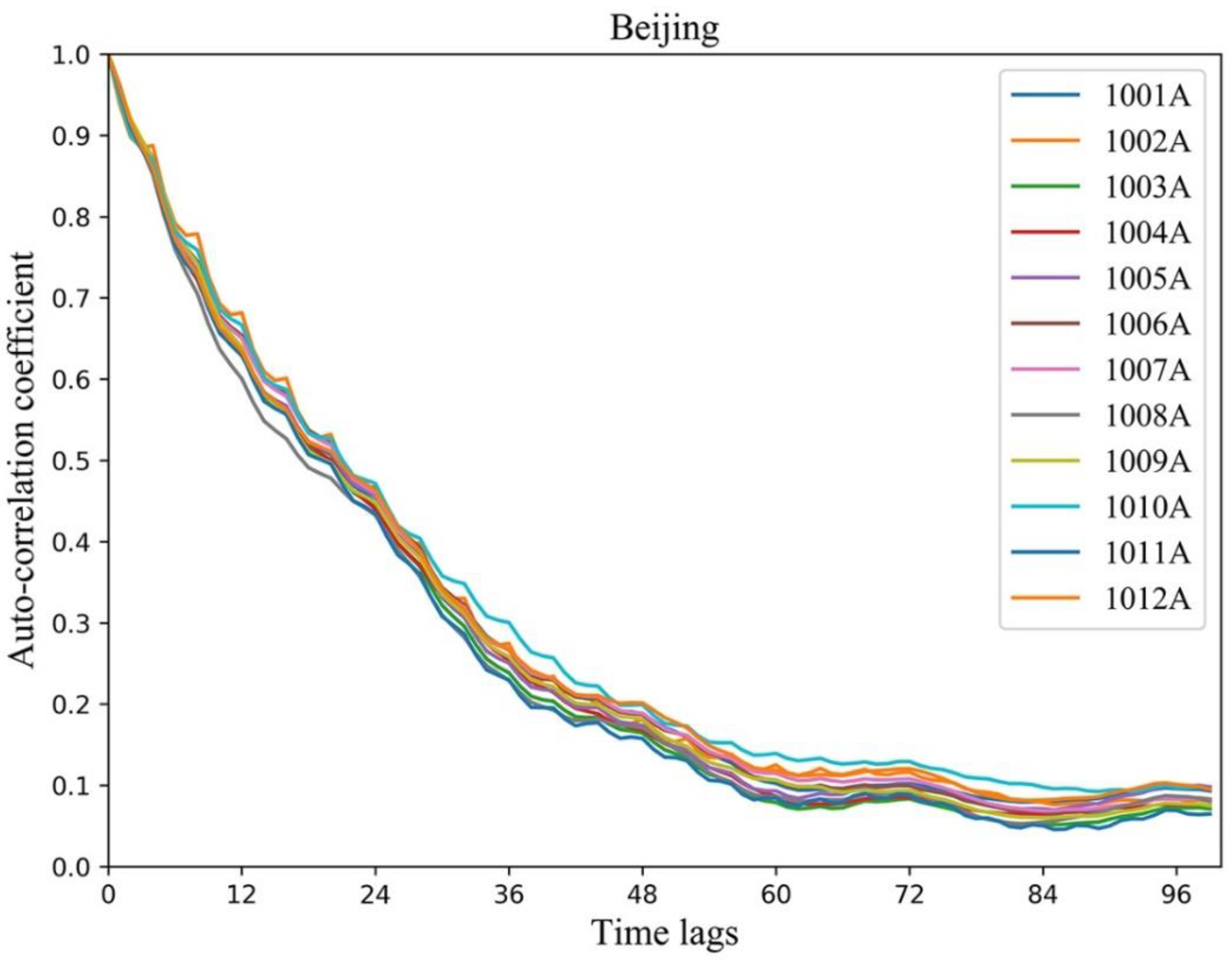
4.2. Rationality of Time Lag r Derived from the Temporal Correlation
4.3. Sensitivity of the Spatiotemporal Dynamics Related to Meteorological Dynamics
4.4. Contributions and Limitations
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Barzeghar, V.; Sarbakhsh, P.; Hassanvand, M.S.; Faridi, S.; Gholampour, A. Long-term trend of ambient air PM10, PM2.5, and O3 and their health effects in Tabriz city, Iran, during 2006–2017. Sustain. Cities Soc. 2020, 54, 101988. [Google Scholar] [CrossRef]
- Kampa, M.; Castanas, E. Human health effects of air pollution. Environ. Pollut. 2008, 151, 362–367. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Zhao, S.; Jiao, L.; Taylor, M.; Zhang, B.; Xu, G.; Hou, H. Estimation of PM2.5 concentrations in china using a spatial back propagation neural network. Sci. Rep. 2019, 9, 13788. [Google Scholar] [CrossRef] [PubMed]
- Lelieveld, J.; Evans, J.S.; Fnais, M.; Giannadaki, D.; Pozzer, A. The contribution of outdoor air pollution sources to premature mortality on a global scale. Nature 2015, 525, 367–371. [Google Scholar] [CrossRef]
- Madrigano, J.; Kloog, I.; Goldberg, R.; Coull, B.A.; Mittleman, M.A.; Schwartz, J. Long-term exposure to PM2.5 and incidence of acute myocardial infarction. Environ. Health Persp. 2013, 121, 192–196. [Google Scholar] [CrossRef]
- Zhang, Q.; Jiang, X.; Tong, D.; Davis, S.J.; Zhao, H.; Geng, G.; Feng, T.; Zheng, B.; Lu, Z.; Streets, D.G. Transboundary health impacts of transported global air pollution and international trade. Nature 2017, 543, 705–709. [Google Scholar] [CrossRef]
- Nel, A. Air pollution-related illness: Effects of particles. Science 2005, 308, 804–806. [Google Scholar] [CrossRef]
- National Urban Air Quality Report of China. 2019. Available online: http://www.mee.gov.cn/hjzl/dqhj/cskqzlzkyb/201908/P020190821498490317309.pdf (accessed on 2 July 2019).
- Li, T.; Shen, H.; Zeng, C.; Yuan, Q.; Zhang, L. Point-surface fusion of station measurements and satellite observations for mapping PM2.5 distribution in China: Methods and assessment. Atmos. Environ. 2017, 152, 477–489. [Google Scholar] [CrossRef]
- Wen, C.; Liu, S.; Yao, X.; Peng, L.; Li, X.; Hu, Y.; Chi, T. A novel spatiotemporal convolutional long short-term neural network for air pollution prediction. Sci. Total Environ. 2019, 654, 1091–1099. [Google Scholar] [CrossRef]
- Mao, W.; Wang, W.; Jiao, L.; Zhao, S.; Liu, A. Modeling air quality prediction using a deep learning approach: Method optimization and evaluation. Sustain. Cities Soc. 2020, 65, 102567. [Google Scholar] [CrossRef]
- Geng, G.; Zhang, Q.; Martin, R.V.; van Donkelaar, A.; Huo, H.; Che, H.; Lin, J.; He, K. Estimating long-term PM2.5 concentrations in China using satellite-based aerosol optical depth and a chemical transport model. Remote Sens. Environ. 2015, 166, 262–270. [Google Scholar] [CrossRef]
- Stern, R.; Builtjes, P.; Schaap, M.; Timmermans, R.; Vautard, R.; Hodzic, A.; Memmesheimer, M.; Feldmann, H.; Renner, E.; Wolke, R. A model inter-comparison study focussing on episodes with elevated PM10 concentrations. Atmos. Environ. 2008, 42, 4567–4588. [Google Scholar] [CrossRef]
- Wang, J.; Bai, L.; Wang, S.; Wang, C. Research and application of the hybrid forecasting model based on secondary denoising and multi-objective optimization for air pollution early warning system. J. Clean. Prod. 2019, 234, 54–70. [Google Scholar] [CrossRef]
- Pan, L.; Sun, B.; Wang, W. City air quality forecasting and impact factors analysis based on grey model. Procedia Engineering. 2011, 12, 74–79. [Google Scholar] [CrossRef]
- Li, T.; Shen, H.; Yuan, Q.; Zhang, L. Geographically and temporally weighted neural networks for satellite-based mapping of ground-level PM2.5. ISPRS J. Photogramm. Remote Sens. 2020, 167, 178–188. [Google Scholar] [CrossRef]
- Yuan, Q.; Shen, H.; Li, T.; Li, Z.; Li, S.; Jiang, Y.; Xu, H.; Tan, W.; Yang, Q.; Wang, J.; et al. Deep learning in environmental remote sensing: Achievements and challenges. Remote Sens. Environ. 2020, 241, 111716. [Google Scholar] [CrossRef]
- Lv, B.; Cai, J.; Xu, B.; Bai, Y. Understanding the rising phase of the PM2.5 concentration evolution in large China cities. Sci. Rep. 2017, 7, 46456. [Google Scholar] [CrossRef]
- Gupta, P.; Christopher, S.A. Particulate matter air quality assessment using integrated surface, satellite, and meteorological products: 2. A neural network approach. J. Geophys. Res. Atmos. 2009, 114, 1–14. [Google Scholar] [CrossRef]
- Zhang, G.; Lu, H.; Dong, J.; Poslad, S.; Li, R.; Zhang, X.; Rui, X. A framework to predict high-resolution spatiotemporal PM2.5 distributions using a deep-learning model: A case study of Shijiazhuang, China. Remote Sens. 2020, 12, 2825. [Google Scholar] [CrossRef]
- Fan, Z.; Zhan, Q.; Yang, C.; Liu, H.; Bilal, M. Estimating PM2.5 concentrations using spatially local Xgboost based on full-covered SARA AOD at the urban scale. Remote Sens. 2020, 12, 3368. [Google Scholar] [CrossRef]
- Shen, H.; Jiang, Y.; Li, T.; Cheng, Q.; Zeng, C.; Zhang, L. Deep learning-based air temperature mapping by fusing remote sensing, station, simulation and socioeconomic data. Remote Sens. Environ. 2020, 240, 111692. [Google Scholar] [CrossRef]
- Wan, R.; Mei, S.; Wang, J.; Liu, M.; Yang, F. Multivariate temporal convolutional network: A deep neural networks approach for multivariate time series forecasting. Electronics 2019, 8, 876. [Google Scholar] [CrossRef]
- Qi, Y.; Li, Q.; Karimian, H.; Liu, D. A hybrid model for spatiotemporal forecasting of PM2.5 based on graph convolutional neural network and long short-term memory. Sci. Total Environ. 2019, 664, 1–10. [Google Scholar] [CrossRef]
- Shen, H.; Li, T. Progress of remote sensing mapping of atmospheric PM2.5. Acta Geodaetica et Cartographica Sinica 2019, 48, 1426–1635. [Google Scholar]
- Han, L.; Zhao, J.; Gao, Y.; Gu, Z.; Xin, K.; Zhang, J. Spatial distribution characteristics of PM2.5 and PM10 in Xi’an city predicted by land use regression models. Sustain. Cities Soc. 2020, 61, 102329. [Google Scholar] [CrossRef] [PubMed]
- Stadlober, E.; Hörmann, S.; Pfeiler, B. Quality and performance of a PM10 daily forecasting model. Atmos. Environ. 2008, 42, 1098–1109. [Google Scholar] [CrossRef]
- Perez, P.; Reyes, J. An integrated neural network model for PM10 forecasting. Atmos. Environ. 2006, 40, 2845–2851. [Google Scholar] [CrossRef]
- Suárez Sánchez, A.; García Nieto, P.J.; Riesgo Fernández, P.; Del Coz Díaz, J.J.; Iglesias-Rodríguez, F.J. Application of an SVM-based regression model to the air quality study at local scale in the Avilés urban area (Spain). Math. Comput. Model. 2011, 54, 1453–1466. [Google Scholar] [CrossRef]
- Gariazzo, C.; Carlino, G.; Silibello, C.; Renzi, M.; Finardi, S.; Pepe, N.; Radice, P.; Forastiere, F.; Michelozzi, P.; Viegi, G.; et al. A multi-city air pollution population exposure study: Combined use of chemical-transport and random-forest models with dynamic population data. Sci. Total Environ. 2020, 724, 138102. [Google Scholar] [CrossRef] [PubMed]
- Danesh Yazdi, M.; Kuang, Z.; Dimakopoulou, K.; Barratt, B.; Suel, E.; Amini, H.; Lyapustin, A.; Katsouyanni, K.; Schwartz, J. Predicting fine particulate matter (PM2.5) in the greater London area: An ensemble approach using machine learning methods. Remote Sens. 2020, 12, 914. [Google Scholar] [CrossRef]
- Schneider, R.; Vicedo-Cabrera, A.M.; Sera, F.; Masselot, P.; Stafoggia, M.; de Hoogh, K.; Kloog, I.; Reis, S.; Vieno, M.; Gasparrini, A. A satellite-based spatio-temporal machine learning model to reconstruct daily PM2.5 concentrations across Great Britain. Remote Sens. 2020, 12, 3803. [Google Scholar] [CrossRef]
- Zhou, Q.; Jiang, H.; Wang, J.; Zhou, J. A hybrid model for PM2.5 forecasting based on ensemble empirical mode decomposition and a general regression neural network. Sci. Total Environ. 2014, 496, 264–274. [Google Scholar] [CrossRef]
- Chang-Hoi, H.; Park, I.; Oh, H.; Gim, H.; Hur, S.; Kim, J.; Choi, D. Development of a PM2.5 prediction model using a recurrent neural network algorithm for the Seoul metropolitan area, Republic of Korea. Atmos. Environ. 2021, 245, 118021. [Google Scholar] [CrossRef]
- Abirami, S.; Chitra, P. Regional air quality forecasting using spatiotemporal deep learning. J. Clean. Prod. 2021, 283, 125341. [Google Scholar] [CrossRef]
- Zhang, B.; Zou, G.; Qin, D.; Lu, Y.; Jin, Y.; Wang, H. A novel Encoder-Decoder model based on read-first LSTM for air pollutant prediction. Sci. Total Environ. 2021, 765, 144507. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Ding, Y.; Cheng, J.C.P.; Jiang, F.; Gan, V.J.L.; Xu, Z. A Lag-FLSTM deep learning network based on Bayesian optimization for multi-sequential-variant PM2.5 prediction. Sustain. Cities Soc. 2020, 60, 102237. [Google Scholar] [CrossRef]
- Yan, R.; Liao, J.; Yang, J.; Sun, W.; Nong, M.; Li, F. Multi-hour and multi-site air quality index forecasting in Beijing using CNN, LSTM, CNN-LSTM, and spatiotemporal clustering. Expert Syst. Appl. 2021, 169, 114513. [Google Scholar] [CrossRef]
- Leng, X.; Wang, J.; Ji, H.; Wang, Q.; Li, H.; Qian, X.; Li, F.; Yang, M. Prediction of size-fractionated airborne particle-bound metals using MLR, BP-ANN and SVM analyses. Chemosphere 2017, 180, 513–522. [Google Scholar] [CrossRef]
- Li, X.; Peng, L.; Yao, X.; Cui, S.; Hu, Y.; You, C.; Chi, T. Long short-term memory neural network for air pollutant concentration predictions: Method development and evaluation. Environ. Pollut. 2017, 231, 997–1004. [Google Scholar] [CrossRef]
- Zhou, Y.; Chang, F.; Chang, L.; Kao, I.; Wang, Y. Explore a deep learning multi-output neural network for regional multi-step-ahead air quality forecasts. J. Clean. Prod. 2019, 209, 134–145. [Google Scholar] [CrossRef]
- Huang, C.; Kuo, P. A deep CNN-LSTM model for particulate matter (PM2.5) forecasting in Smart Cities. Sensors 2018, 18, 2220. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Shen, H.; Yuan, Q.; Zhang, X.; Zhang, L. Estimating ground-level PM2.5 by fusing satellite and station observations: A geo-intelligent deep learning approach. Geophys. Res. Lett. 2017, 44, 911–985, 993. [Google Scholar] [CrossRef]
- Li, T.; Wang, Y.; Yuan, Q. Remote sensing estimation of regional NO2 via space-time neural networks. Remote Sens. 2020, 12, 2514. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.; Wong, W.; Woo, W. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. Adv. Neural Inf. Process. Syst. 2015, 28, 802–810. [Google Scholar]
- Ministry of Ecology and Environment of the People’s Republic of China. Ambient Air Quality Standards. 2012. Available online: http://www.mee.gov.cn/ywgz/fgbz/bz/bzwb/dqhjbh/dqhjzlbz/201203/t20120302_224165.shtml (accessed on 29 February 2012).
- Centre for Research on Energy and Clean Air. 2020. Air Pollution in China (2019). Available online: https://energyandcleanair.org/wp/wp-content/uploads/2020/01/CREA-brief-China2019-Zh.pdf (accessed on 31 January 2020).
- Tobler, W.R. A computer movie simulating urban growth in the Detroit region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- He, J.; Li, X.; Yao, Y.; Hong, Y.; Jinbao, Z. Mining transition rules of cellular automata for simulating urban expansion by using the deep learning techniques. Int. J. Geogr. Inf. Sci. 2018, 32, 2076–2097. [Google Scholar] [CrossRef]
- Wu, C.; Li, Q.; Hou, J.; Karimian, H.; Chen, G. PM2.5 concentration prediction using convolutional neural networks. Sci. Surv. Mapp. 2018, 43, 68–75. [Google Scholar]
- Xu, G.; Jiao, L.; Zhao, S.; Cheng, J. Spatial and temporal variability of PM2.5 concentration in China. Wuhan Univ. J. Nat. Sci. 2016, 21, 358–368. [Google Scholar] [CrossRef]
- Xu, G.; Jiao, L.; Zhang, B.; Zhao, S.; Ma, Y.; Gu, Y.; Liu, J.; Tang, X. Spatial and temporal variability of the PM2.5/PM10 ratio in Wuhan, Central China. Aerosol Air Qual. Res. 2017, 17, 1–11. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, X.; Ding, Y.; Liu, Y.; Zhang, H.; Wang, Y.; Zhong, J. The impact of meteorological changes from 2013 to 2017 on PM2.5 mass reduction in key regions in China. Sci. China Earth Sci. 2019, 62, 1885–1902. [Google Scholar] [CrossRef]
- Huang, B.; Wu, B.; Barry, M. Geographically and temporally weighted regression for modeling spatio-temporal variation in house prices. Int. J. Geogr. Inf. Sci. 2010, 24, 383–401. [Google Scholar] [CrossRef]






| Variables | Unit | Range | Mean | Variance |
|---|---|---|---|---|
| PM2.5 | μg/m3 | [1, 1000] | 64.16 | 69.89 |
| WS | m/s | [0.4, 25.68] | 2 | 2.38 |
| RHU | % | [4.27, 94.94] | 42.14 | 21.5 |
| PRS | hPa | [930.20, 1037.73] | 975.14 | 28.25 |
| TEM | °C | [−18.09, 32.27] | 12.9 | 11.35 |
| PRE | mm | [0, 159.63] | 1.51 | 5.75 |
| SSD | h | [0, 13.82] | 6.84 | 3.74 |
| Nighttime light | N/A | [0.36, 62.10] | 26.65 | 16.54 |
| NDVI | N/A | [0.27, 0.90] | 0.53 | 0.20 |
| Season | N/A | [1, 4] | One-hot encoding | |
| Month | N/A | [1, 12] | ||
| Station | RMSE (μg/m3) | MAE (μg/m3) | R2 |
|---|---|---|---|
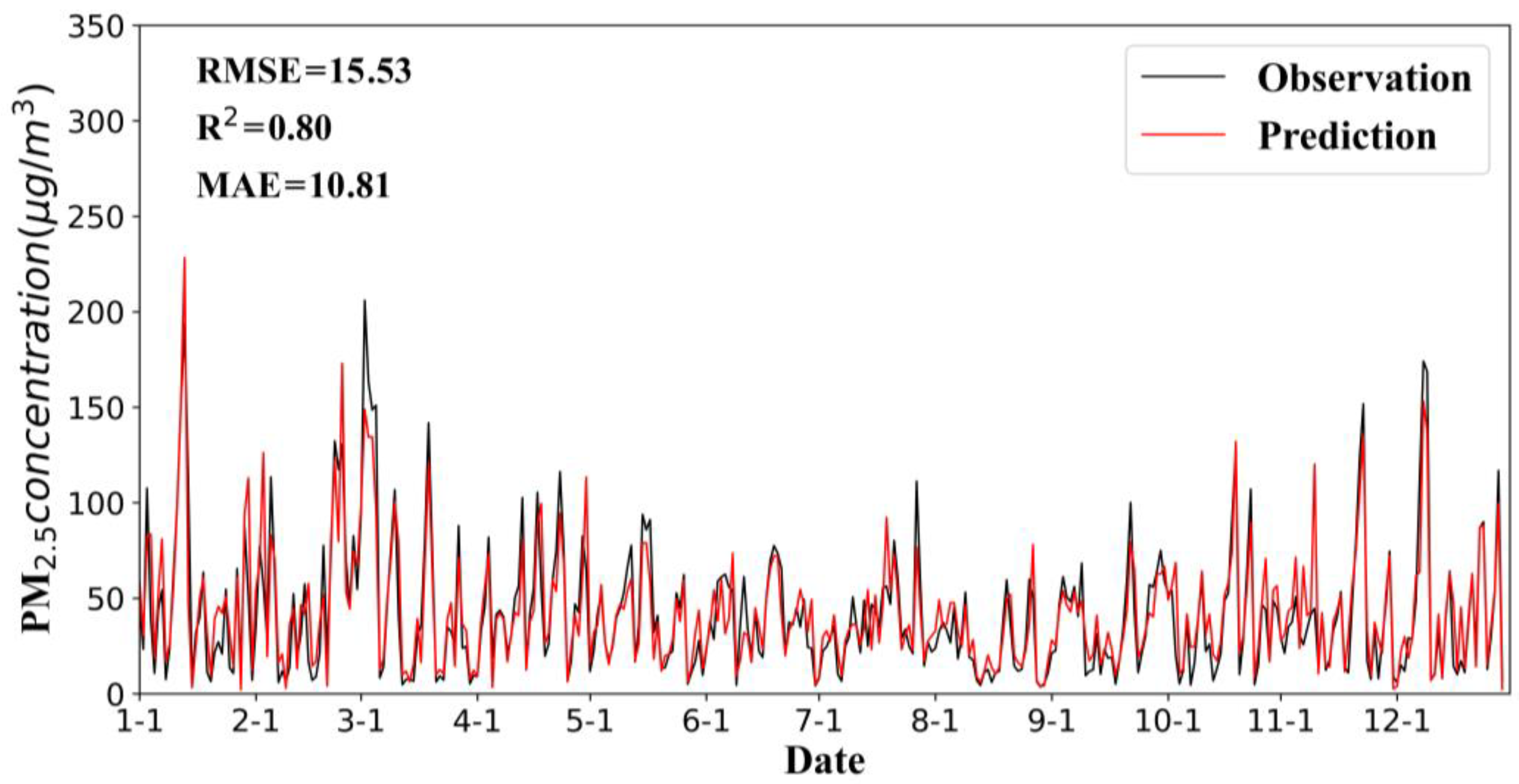
| Beijing | 18.96 | 12.89 | 0.74 |
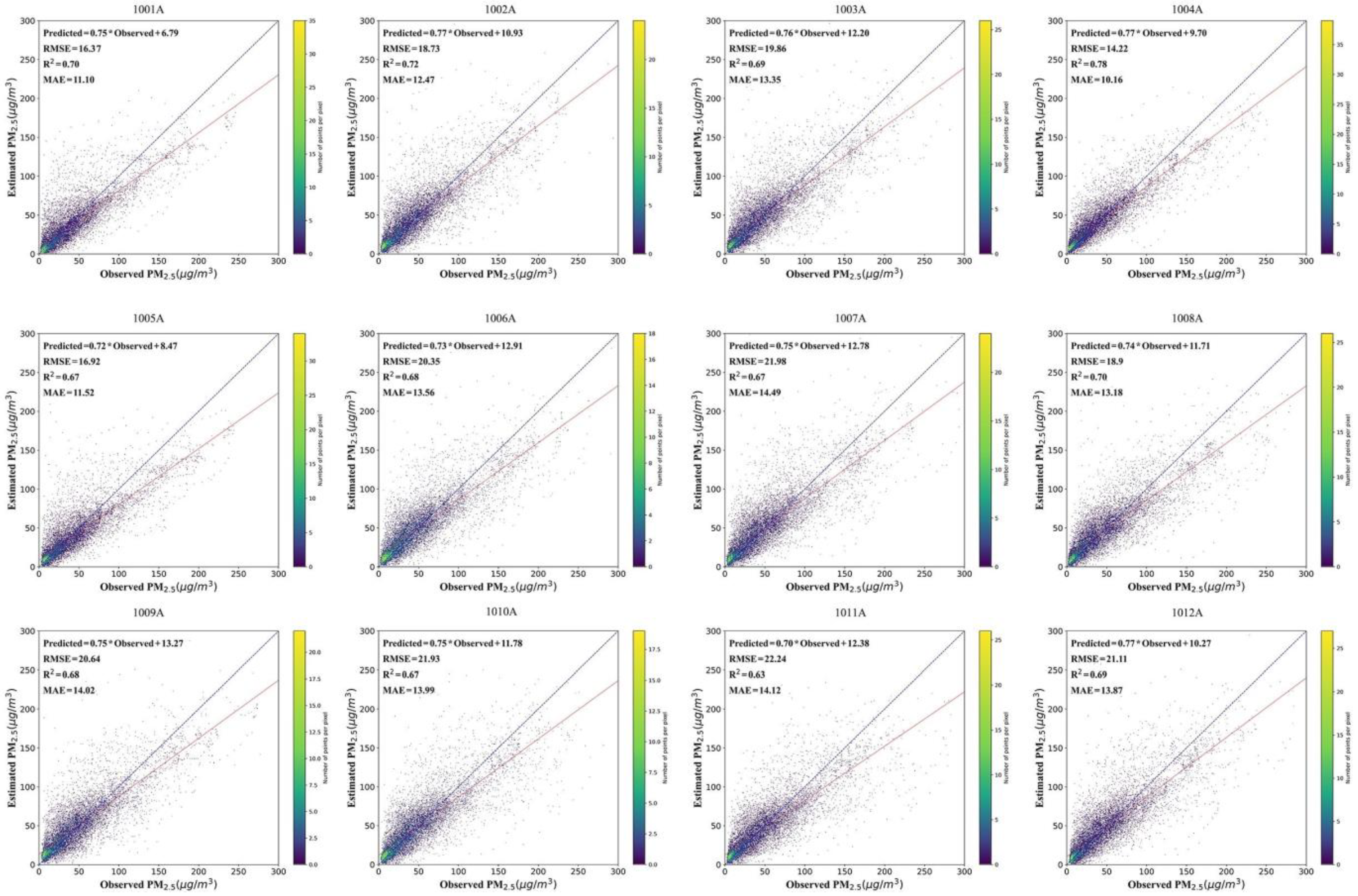
| 1001A | 16.52 | 11.01 | 0.70 |
| 1002A | 18.71 | 12.45 | 0.72 |
| 1003A | 19.82 | 13.35 | 0.69 |
| 1004A | 14.21 | 10.16 | 0.78 |
| 1005A | 16.82 | 11.52 | 0.67 |
| 1006A | 20.15 | 13.56 | 0.68 |
| 1007A | 21.98 | 14.75 | 0.68 |
| 1008A | 18.75 | 13.18 | 0.70 |
| 1009A | 20.62 | 14.01 | 0.68 |
| 1010A | 21.52 | 13.99 | 0.67 |
| 1011A | 22.12 | 14.38 | 0.64 |
| 1012A | 21.11 | 13.69 | 0.69 |
| Model | RMSE (μg/m3) | MAE (μg/m3) | R2 |
|---|---|---|---|
| MLR | 44.16 | 29.32 | 0.37 |
| SVR | 46.74 | 31.21 | 0.33 |
| LSTM | 24.84 | 17.76 | 0.51 |
| LSTME | 24.66 | 17.24 | 0.53 |
| TS-LSTME | 19.87 | 13.24 | 0.72 |
| CR-LSTM | 8.96 | 12.89 | 0.74 |
| Time Lag (r) | Temporal Correlation | Structure of ConvLSTM Unit | Number of Recursive Iterations | RMSE (μg/m3 ) | MAE (μg/m3) | R2 |
|---|---|---|---|---|---|---|
| 4 | 0.85–0.89 | 1–4 h→5–8 h→9–12 h→13–16→17–20 h→21–24 h average | 6 | 25.17 | 14.64 | 0.54 |
| 6 | 0.77–0.80 | 1–6 h→7–12 h→13–18 h→19–24 h average | 4 | 23.72 | 14.65 | 0.62 |
| 8 | 0.70–0.78 | 1–8 h→9–16 h→17–24 h average | 3 | 21.63 | 14.12 | 0.67 |
| 12 | 0.59–0.68 | 1–12 h→13–24 h average | 2 | 18.96 | 12.89 | 0.74 |
| 24 | 0.44–0.48 | 1–24 h | 1 | 24.75 | 17.26 | 0.53 |
| Scenes | Variables | RMSE (μg/m3) | MAE (μg/m3) | R2 |
|---|---|---|---|---|
| 1 | PM2.5 | 24.66 | 17.24 | 0.53 |
| 2 | PM2.5 + RHU+ PRS+ TEM + PRE + SSD (without WS) | 22.03 | 13.54 | 0.69 |
| 3 | PM2.5 + WS+ PRS+ TEM + PRE + SSD (without RHU) | 22.58 | 15.80 | 0.68 |
| 4 | PM2.5 + WS+ RHU+ TEM + PRE + SSD (without PRS) | 20.97 | 13.17 | 0.72 |
| 5 | PM2.5 + WS+ RHU+ PRS+ PRE + SSD (without TEM) | 22.37 | 15.06 | 0.68 |
| 6 | PM2.5 + WS+ RHU+ PRS+ TEM + SSD (without + PRE) | 22.01 | 13.51 | 0.69 |
| 7 | PM2.5 + WS+ RHU+ PRS+ TEM + PRE (without SSD) | 21.63 | 13.51 | 0.70 |
| 8 | PM2.5 + WS+ RHU+ PRS+ TEM + PRE + SSD | 18.96 | 12.89 | 0.74 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Mao, W.; Tong, X.; Xu, G. A Novel Recursive Model Based on a Convolutional Long Short-Term Memory Neural Network for Air Pollution Prediction. Remote Sens. 2021, 13, 1284. https://doi.org/10.3390/rs13071284
Wang W, Mao W, Tong X, Xu G. A Novel Recursive Model Based on a Convolutional Long Short-Term Memory Neural Network for Air Pollution Prediction. Remote Sensing. 2021; 13(7):1284. https://doi.org/10.3390/rs13071284
Chicago/Turabian StyleWang, Weilin, Wenjing Mao, Xueli Tong, and Gang Xu. 2021. "A Novel Recursive Model Based on a Convolutional Long Short-Term Memory Neural Network for Air Pollution Prediction" Remote Sensing 13, no. 7: 1284. https://doi.org/10.3390/rs13071284
APA StyleWang, W., Mao, W., Tong, X., & Xu, G. (2021). A Novel Recursive Model Based on a Convolutional Long Short-Term Memory Neural Network for Air Pollution Prediction. Remote Sensing, 13(7), 1284. https://doi.org/10.3390/rs13071284