Experimental Study on the Thermal Infrared Spectral Variation of Fractured Rock
Abstract
1. Introduction
2. Materials and Methods
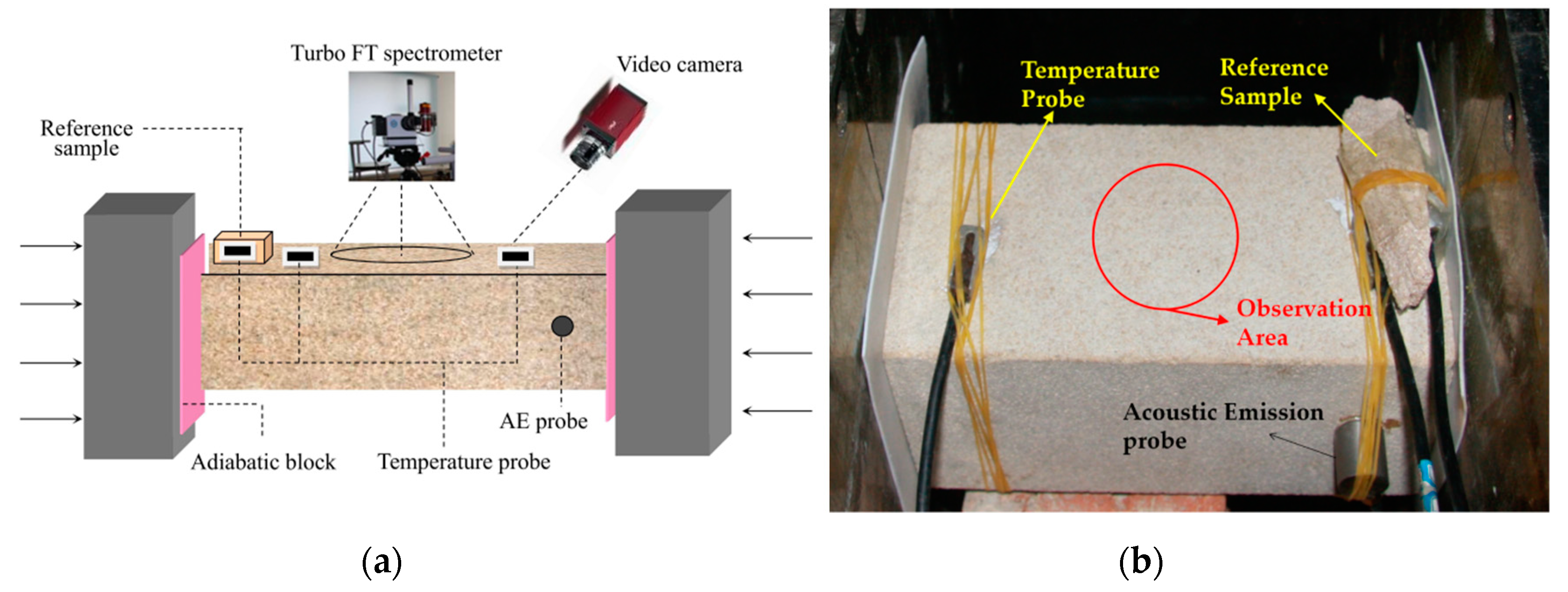
2.1. Experimental System
2.2. Experimental Method
3. Results
3.1. Fracturing Mode
3.1.1. Extensional Fissures
3.1.2. Local Bulging
3.2. Preprocessing Method for Radiance
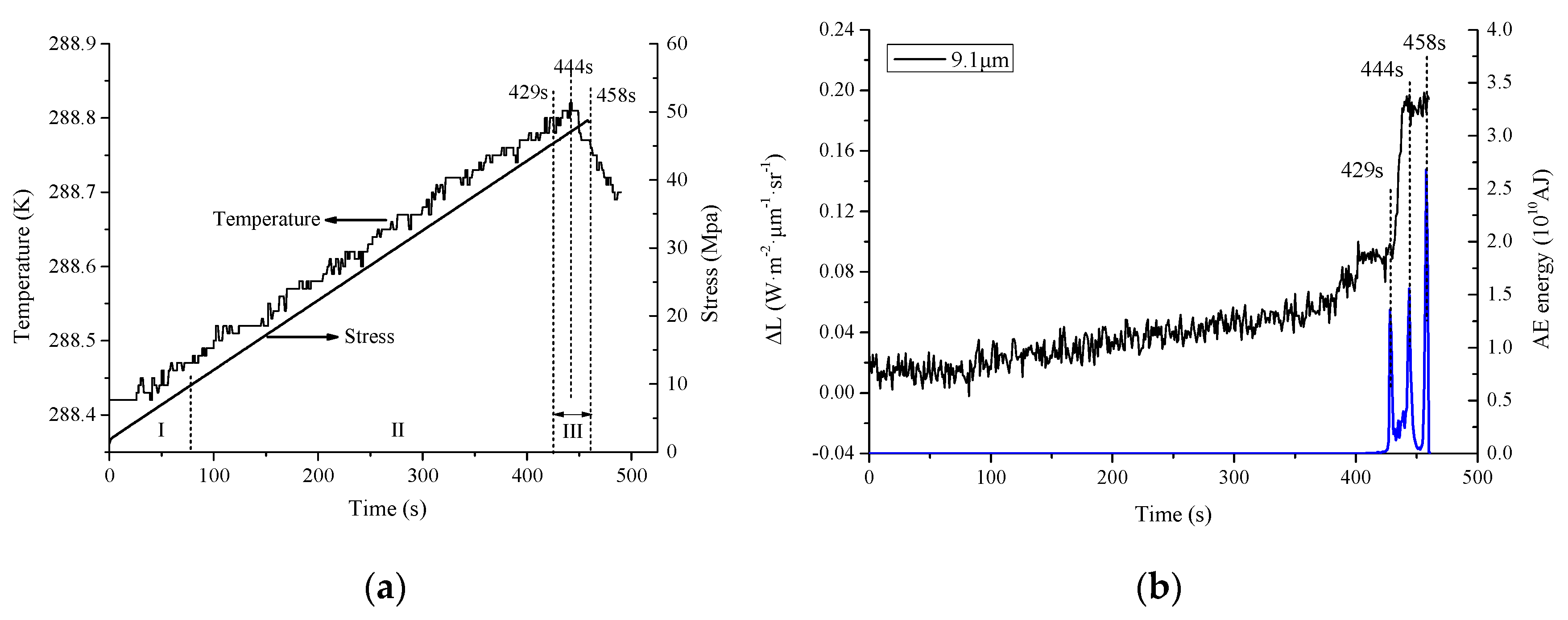
3.3. Stages Division
3.4. Analysis of the Spectral Radiance Variation
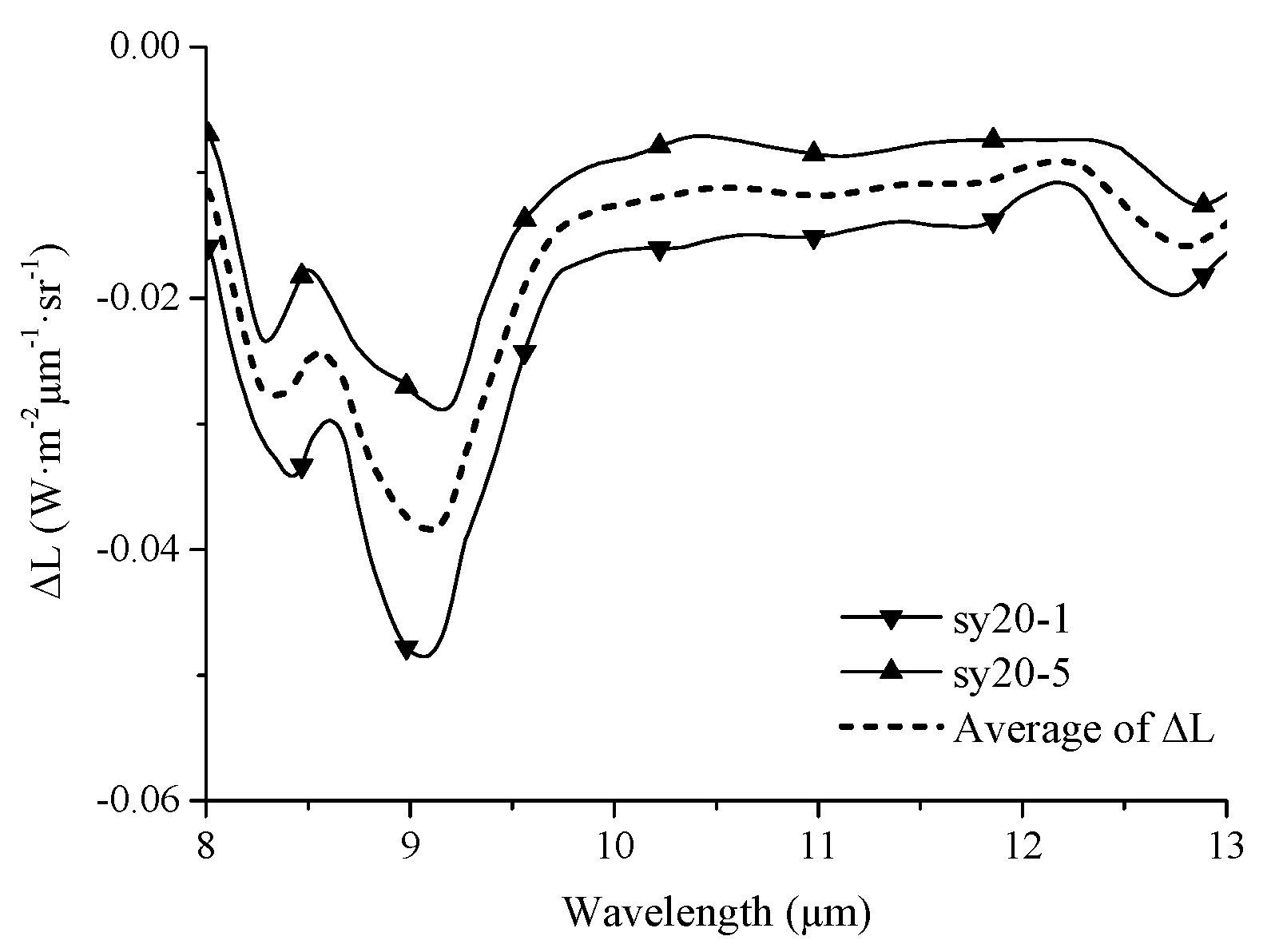
3.4.1. Extensional Fissures
3.4.2. Local Bulging
4. Discussion
4.1. Theoretical Analysis of the Energy Components Reaching the Spectrometer
4.2. The Mechanism of Radiance Variation for Extensional Fissures
4.3. The Mechanism of Radiance Variation for Local Bulging
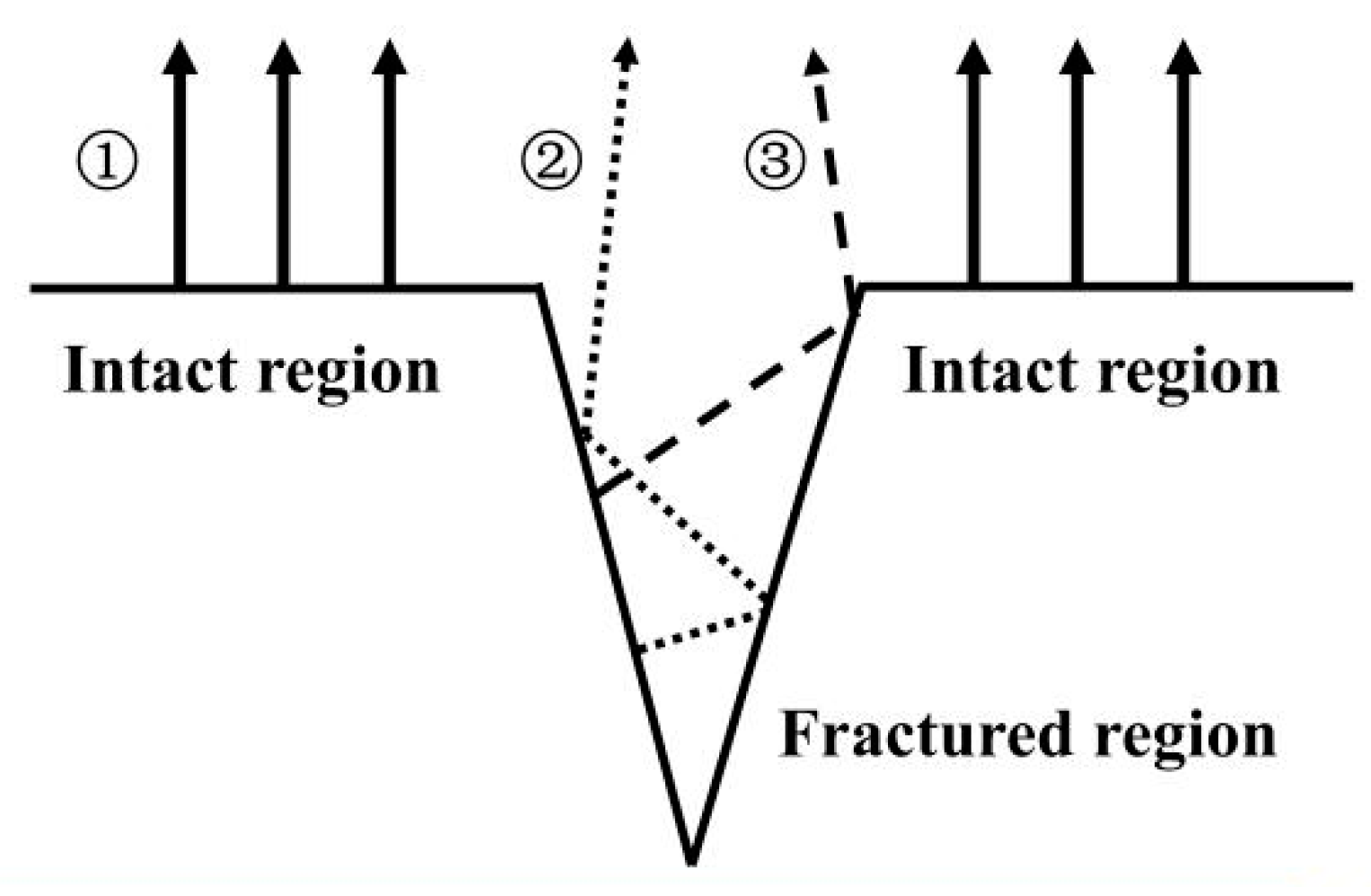
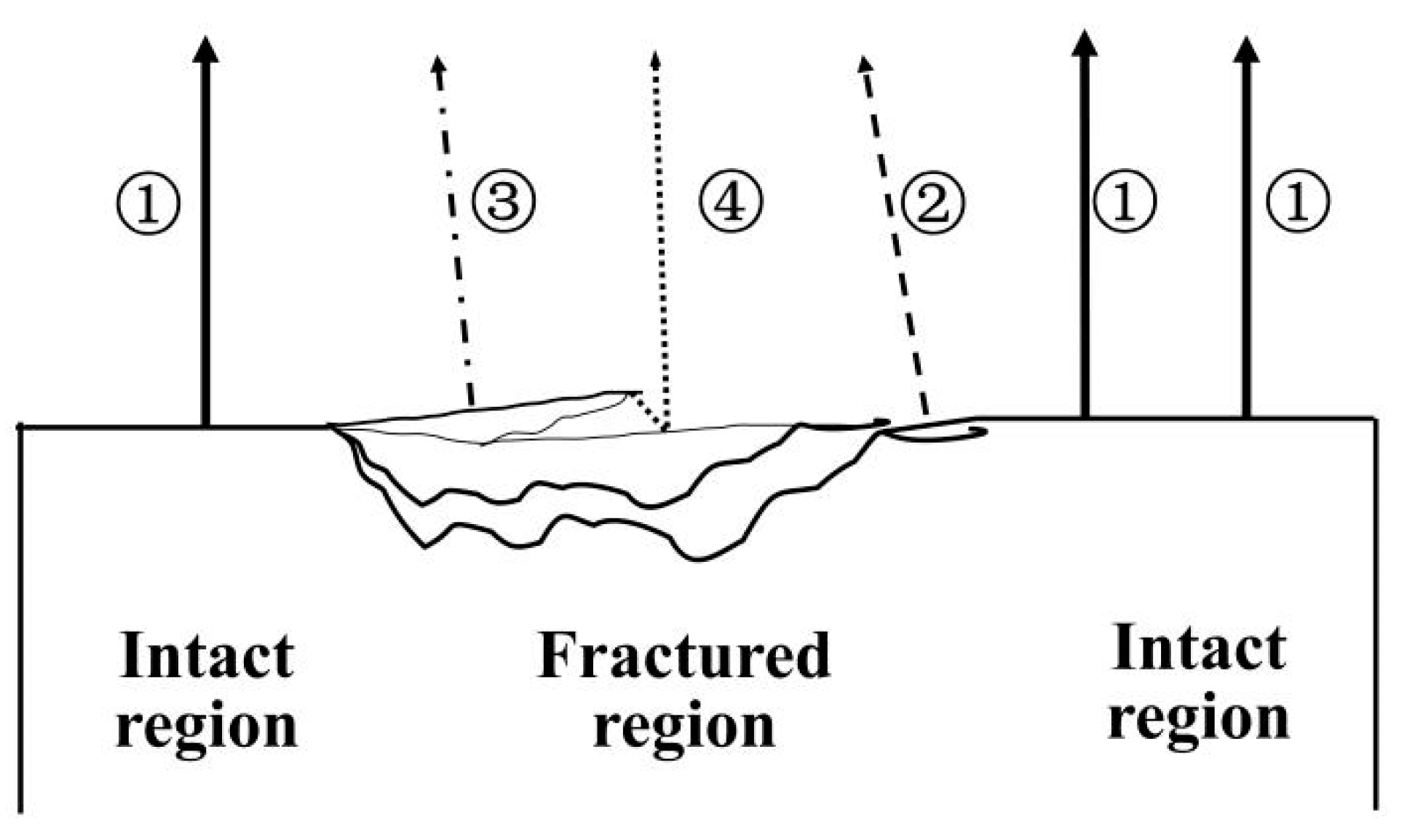
- The radiance received at the initial moment travels perpendicularly to the sample surface, which is labeled ① in Figure 10.
- Compared to the perpendicular radiation, the local bulging could lead to a change in the observation angle θt on the flat inclined surface and raised surface, which is labeled ② and ③ in Figure 10, respectively. The raised surface can be regarded as multiple continuous smooth facets with different inclined angles. The change in θt lead to a decrease in ε(λ) [34,35], resulting in a decrease in radiance.
- There could be multiple fracture layers leading to different heights, resulting in the interaction. The change in radiance propagation can decrease the received radiance. The shadow and shelter effect [55] by the interaction between the fractured and intact regions can affect the received radiance, which is labeled ④ in Figure 10. It is noted that the cavity effect can also result by the interaction of multiple inclined surfaces. The enhanced radiance emitted at a large angle cannot be received by the sensor.
- According to the thermoelastic effect, the stress relaxation in the fractured region causes a decrease in temperature. The contact area between the sample and the environment increased when local bulging appeared. The improvement of the heat dissipation area can lead to a decrease in the temperature as well.
4.4. The Potential Significance of Emissivity Changes in the Fracturing Stage For the Experimental Condition
4.4.1. The Contribution of the Emissivity Change
4.4.2. Sensitive Waveband Selection for Satellite Observation Conditions
4.5. The Difficulty for Further Application
5. Conclusions
- Different fracturing modes can lead to different patterns of radiance change. The fracturing mode has an important influence on the characteristics of the radiance variation.
- The radiance increased considerably, with peaks in the range of 8.0–9.7 μm on the radiance variation curve, when extensional fissures appeared on the sample surface. The emissivity change caused by the cavity effect is the main factor leading to the radiance variation.
- When local bulging appeared on the sample surface, the radiance decreased, with local valleys in the range of 8.0–9.7 μm. The diverse morphological changes related to bulging can lead to complex radiance variation.
- The radiance variation is the combined effect of changes in both temperature and emissivity. The different types of emissivity changes during the fracturing stage are the main causes of the differences in the radiance change.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Caponier, P.; Molnar, P. Active faulting and tectonics in China. J. Geophys. Res. 1977, 82, 2905–2930. [Google Scholar] [CrossRef]
- Wesnousky, S.G. Displacement and Geometrical Characteristics of Earthquake Surface Ruptures: Issues and Implications for Seismic-Hazard Analysis and the Process of Earthquake Rupture. Bull. Seismol. Soc. Am. 2008, 98, 1609–1632. [Google Scholar] [CrossRef]
- Ren, Z.; Lin, A. Deformation characteristics of co-seismic surface ruptures produced by the 1850 M 7.5 Xichang earthquake on the eastern margin of the Tibetan Plateau. J. Asian Earth Sci. 2010, 38, 1–13. [Google Scholar] [CrossRef]
- Pan, J.W.; Li, H.B.; Wu, F.Y.; Li, N.; Guo, R.Q.; Zhang, W. Surface rupture characteristics, rupture mechanics, and rupture process of the Yushu earthquake (Ms7.1), 14/04/2010. Acta Petrol. Sin. 2011, 27, 3449–3459. (In Chinese) [Google Scholar] [CrossRef]
- Lin, A. Structural features and seismotectonic implications of coseismic surface ruptures produced by the 2016 Mw 7.1 Kumamoto earthquake. J. Seismol. 2017, 21, 1079–1100. [Google Scholar] [CrossRef]
- Sugito, N.; Goto, H.; Yasuhiro, K. Surface fault ruptures associated with the 14 april foreshock (mj 6.5) of the 2016 kumamoto earthquake sequence, southwest japan. Earth Planets Space 2016, 68, 170–178. [Google Scholar] [CrossRef]
- Li, S.P.; Tao, T.Y.; Gao, F.; Qu, X.C.; Zhu, Y.C.; Huang, J.W.; Wang, Q. Interseismic Coupling beneath the Sikkim-Bhutan Himalaya Constrained by GPS Measurements and Its Implication for Strain Segmentation and Seismic Activity. Remote Sens. 2020, 12, 2202. [Google Scholar] [CrossRef]
- Feng, W.; Samsonov, S.; Qiu, Q.; Wang, Y.; Zhang, P.; Li, T.; Zheng, W. Orthogonal fault rupture and rapid postseismic deformation following 2019 Ridgecrest, California, earthquake sequence revealed from geodetic observations. Geophys. Res. Lett. 2020, 47, e2019GL086888. [Google Scholar] [CrossRef]
- Shen, X.H.; Zhang, X.M.; Cui, J.; Zhou, X.; Jiang, W.L.; Gong, L.X.; Li, Y.S.; Liu, Q.Q. Remote sensing application in earthquake science research and geophysical fields exploration satellite mission in China. J. Remote Sens. 2018, 22, 1–16. (In Chinese) [Google Scholar] [CrossRef]
- Gorny, V.I.; Sal’Man, A.G.; Tronin, A.A.; Shilin, B.V. Outgoing infrared radiation of the earth as an indicator of seismic activity. Proc. Acad. Sci. USSR 1988, 301, 67–69. [Google Scholar]
- Qiang, Z.J.; Xu, X.D.; Ning, C.G. Abnormal infrared thermal of satellite-forewarning of earthquakes. Chin. Sci. Bull. 1990, 35, 1324–1327. (In Chinese) [Google Scholar]
- Ouzounov, D.; Liu, D.F.; Kang, C.L.; Cervone, G.; Kafatos, M.; Taylor, P. Outgoing long wave radiation variability from IR satellite data prior to major earthquakes. Tectonophysics 2007, 431, 211–220. [Google Scholar] [CrossRef]
- Wu, L.X.; Qin, K.; Liu, S.J. GEOSS-based thermal parameters analysis for earthquake anomaly recognition. Proc. IEEE 2012, 100, 2891–2907. [Google Scholar] [CrossRef]
- Wu, L.X.; Qin, K.; Liu, S.J. Progress in analysis to remote sensed thermal abnormity with fault activity and seismogenic process. Acta Geod. Cartogr. Sin. 2017, 46, 1470–1481. (In Chinese) [Google Scholar] [CrossRef]
- Luong, M.P. Infrared observations of failure processes in plain concrete. Durab. Build. Mater. Compon. 1987, 4, 870–878. [Google Scholar] [CrossRef]
- Luong, M.P. Infrared thermovision of damage processes in concrete and rock. Eng. Fract. Mech. 1990, 35, 291–301. [Google Scholar] [CrossRef]
- Geng, N.G.; Cui, C.Y.; Deng, M.D. Remote sensing detection in rock fracture experiment and the beginning of remote sensing rock mechanics. Acta Seismol. Sin. 1992, 14, 645–652. (In Chinese) [Google Scholar]
- Wu, L.X.; Cui, C.Y.; Geng, N.G.; Wang, J.Z. Remote sensing rock mechanics (RSRM) and associated experimental studies. Int. J. Rock Mech. Min. Sci. 2000, 37, 879–888. [Google Scholar] [CrossRef]
- Wu, L.X. Remote sensing rock mechanics and its recent achievements and future development. Chin. J. Rock Mech. Eng. 2001, 20, 139–146. (In Chinese) [Google Scholar] [CrossRef]
- Ren, Y.Q.; Ma, J.; Liu, P.X.; Chen, S.Y. Experimental study of thermal field evolution in the short-impending stage before earthquakes. Pure Appl. Geophys. 2017, 175, 2527–2539. [Google Scholar] [CrossRef]
- Salami, Y.; Dano, C.; Hicher, P.Y. Infrared thermography of rock fracture. Géotechnique Lett. 2017, 7, 36–40. [Google Scholar] [CrossRef]
- Wu, L.X.; Liu, S.J.; Wu, Y.H.; Wang, C.Y. Precursors for rock fracturing and failure-part I: IRR image abnormalities. Int. J. Rock Mech. Min. Sci. 2006, 43, 473–482. [Google Scholar] [CrossRef]
- Wu, L.X.; Liu, S.J.; Wu, Y.H.; Wang, C.Y. Precursors for rock fracturing and failure-part II: IRRT-curve abnormalities. Int. J. Rock Mech. Min. Sci. 2006, 43, 483–493. [Google Scholar] [CrossRef]
- Liu, S.J.; Wu, L.X.; Wu, Y.H. Infrared radiation of rock at failure. J. Rock Mech. Min. Sci. 2006, 43, 972–979. [Google Scholar] [CrossRef]
- Ma, L.Q.; Sun, H. Spatial-temporal infrared radiation precursors of coal failure under uniaxial compressive loading. Infrared Phys. Technol. 2018, 93, 144–153. [Google Scholar] [CrossRef]
- Wang, C.L.; Lu, Z.J.; Liu, L.; Chuai, X.S.; Lu, H. Predicting points of the infrared precursor for limestone failure under uniaxial compression. Int. J. Rock Mech. Min. Sci. 2016, 88, 34–43. [Google Scholar] [CrossRef]
- Ma, J.; Ma, S.P.; Liu, P.X.; Liu, L.Q. Thermal field indicators for identifying active fault and its instability from laboratory experiments. Seismol. Geol. 2008, 30, 363–382. (In Chinese) [Google Scholar]
- Lyon, R.J.P. Analysis of rocks by spectral infrared emission (8 to 25 microns). Econ Geol. 1965, 60, 715–736. [Google Scholar] [CrossRef]
- Ruff, S.W.; Christensen, P.R.; Barbera, P.W.; Anderson, D.L. Quantitative thermal emission spectroscopy of minerals: A laboratory technique for measurement and calibration. J. Geophys. Res. 1997, 102, 14899–14913. [Google Scholar] [CrossRef]
- Salvaggio, C.; Miller, C.J. Methodologies and protocols for the collection of midwave and longwave infrared emissivity spectral using a portable field spectrometer. Proc. SPIE Int. Soc. Opt. Eng. 2001, 4381, 539–548. [Google Scholar] [CrossRef]
- Christensen, P.R.; Bandfield, J.L.; Hamilton, V.E.; Howard, D.A.; Lane, M.D.; Piatek, J.L.; Ruff, S.W.; Stefanov, W.L. A thermal emission spectral library of rock-forming minerals. J. Geophys. Res. 2000, 105, 9735–9739. [Google Scholar] [CrossRef]
- Walter, L.S.; Salisbury, J.W. Spectral characterization of igneous rocks in the 8 to 12 μm region. J. Geophys. Res. 1989, 94, 9203–9212. [Google Scholar] [CrossRef]
- Kerekes, J.P.; Strackerjan, K.E.; Salvaggio, C. Spectral reflectance and emissivity of man-made surfaces contaminated with environmental effects. Opt. Eng. 2008, 47, 1065–1074. [Google Scholar] [CrossRef]
- Labed, J.; Stoll, M.P. Angular variation of land surface spectral emissivity in the thermal infrared: Laboratory investigations on bare soils. Int. J. Remote Sens. 1991, 12, 2299–2310. [Google Scholar] [CrossRef]
- Laurel, K.; Kenneth, H.; Eric, K.; Paul, A.; John, S.; John, H.; Allan, T. First use of an airborne thermal infrared hyperspectral scanner for compositional mapping. Remote Sens. Environ. 2002, 80, 447–459. [Google Scholar] [CrossRef]
- Bandfield, J.L. Effects of surface roughness and graybody emissivity on Martian thermal infrared spectra. Icarus 2009, 202, 414–428. [Google Scholar] [CrossRef]
- Osterloo, M.M.; Hamilton, V.E.; Anderson, F.S. A laboratory study of the effects of roughness on the thermal infrared spectra of rock surfaces. Icarus 2012, 220, 404–426. [Google Scholar] [CrossRef]
- Araújo, A. Analysis of multi-band pyrometry for emissivity and temperature measurements of gray surfaces at ambient temperature. Infrared Phys. Technol. 2016, 76, 365–374. [Google Scholar] [CrossRef]
- Araújo, A. Dual-band pyrometry for emissivity and temperature measurements of gray surfaces at ambient temperature: The effect of pyrometer and background temperature uncertainties. Measurement 2016, 94, 316–325. [Google Scholar] [CrossRef]
- Li, T.Z.; Liu, S.J. A Study on the Effects of Roughness on Thermal Infrared Spectral Unmixing of Rock. Spectrosc. Spectr. Anal. 2017, 37, 3051–3057. (In Chinese) [Google Scholar] [CrossRef]
- Cui, C.Y.; Deng, M.D.; Geng, N.G. Rock spectral radiation signatures under different pressures. Sci. Bull. 1993, 38, 1377–1382. (In Chinese) [Google Scholar]
- Yin, J.Y.; Fang, Z.F.; Qian, J.D.; Deng, M.D.; Geng, N.G.; Hao, J.S.; Wang, Z.; Ji, Q.Q. Research on the application of infrared remote sensing in earthquake prediction and its physical mechanism. Earthq. Res. China 2000, 16, 140–148. (In Chinese) [Google Scholar]
- Liu, S.J.; Wu, L.X.; Feng, Z.; Xu, Z.Y. Thermal infrared spectral variation and sensitive waveband of quartzy sandstone under pressure. Spectrosc. Spectr. Anal. 2012, 32, 78–82. (In Chinese) [Google Scholar] [CrossRef]
- Xu, Z.Y.; Liu, S.J.; Wu, L.X.; Feng, Z. Stress-related thermal infrared spectral variation and sensitive waveband of granite. J. Infrared Millim. Waves 2013, 32, 44–49. (In Chinese) [Google Scholar] [CrossRef]
- Freund, F.T.; Takeuchi, A.; Lau, B.W.S.; Al-Manaseer, A.; Fu, C.C.; Bryant, N.A.; Ouzounov, D. Stimulated infrared emission from rocks: Assessing a stress indicator. eEarth 2007, 2, 7–16. [Google Scholar] [CrossRef]
- Freund, F.T. Pre-earthquake signals: Underlying physical processes. J. Asian Earth Sci. 2011, 41, 383–400. [Google Scholar] [CrossRef]
- Freund, F.T.; Freund, M.M. Paradox of Peroxy Defects and Positive Holes in RocksPart I: Effect of Temperature. J. Asian Earth Sci. 2015, 114, 373–383. [Google Scholar] [CrossRef]
- Scoville, J.; Freund, F.T.; Bobrovskiy, V. Stress-Activated Infrared Emission from Rock Surfaces in the Thermal Infrared (TIR) Window. In Proceedings of the AGU Fall Meeting 2016, San Francisco, CA, USA, 12–16 December 2016. [Google Scholar]
- Huang, J.W.; Liu, S.J.; Xu, Z.Y.; Ma, C.Y.; Wu, L.X. Experimental study on the influence of the radiation background on the variation in thermal infrared radiance of loaded rock. Spectrosc. Spectr. Anal. 2018, 38, 4222–4225. (In Chinese) [Google Scholar] [CrossRef]
- Huang, J.W.; Liu, S.J.; Gao, X.; Yang, Z.C.; Qiang, N.; Wu, L.X. Experimental study of the thermal infrared emissivity variation of loaded rock and its significance. Remote Sens. 2018, 10, 818. [Google Scholar] [CrossRef]
- Liu, S.J.; Xu, Z.Y.; Wei, J.L.; Huang, J.W.; Wu, L.X. Experimental study on microwave radiation from deforming and fracturing rock under loading outdoor. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5578–5587. [Google Scholar] [CrossRef]
- Huang, J.W.; Liu, S.J.; Qiang, N.; Mao, W.F.; Gao, X. Experimental Study of Extracting Weak Infrared Signals of Rock Induced by Cyclic Loading under the Strong Interference Background. Appl. Sci. 2018, 8, 1458. [Google Scholar] [CrossRef]
- Salisbury, J.W.; D’Aria, D.M. Emissivity of terrestrial materials in the 8-14 μm atmospheric window. Remote Sens. Environ. 1992, 42, 83–106. [Google Scholar] [CrossRef]
- Feng, J.; Rivard, B.; Rogge, D.; Sánchez-Azofeifa, A. The longwave infrared (3–14 μm) spectral properties of rock encrusting lichens based on laboratory spectra and airborne SEBASS imagery. Remote Sens. Environ. 2013, 131, 173–181. [Google Scholar] [CrossRef]
- Fraden, J. AIP Handbook of Modern Sensors; American Institute of Physics, Advanced Monitors Corporation: San Diego, CA, USA, 1994; pp. 136–138. [Google Scholar] [CrossRef]
- Shan, X.J.; Qu, C.Y.; Ma, J. Satellite thermal infrared observation and analysis on alternate activity of different segments of seismogenic fault. J. Geod. Geodyn. 2005, 25, 58–62. (In Chinese) [Google Scholar] [CrossRef]
- Bhardwaj, A.; Singh, S.; Sam, L.; Bhardwaj, A.; Martín-Torres, F.J.; Singh, A.; Kumar, R. MODIS-based estimates of strong snow surface temperature anomaly related to high altitude earthquakes of 2015. Remote Sens. Environ. 2017, 188, 1–8. [Google Scholar] [CrossRef]
- Jing, F.; Shen, X.H.; Zhang, T.B.; Pan, X.; Sun, K. Variation characteristics in infrared radiation of active fault zone related to earthquakes. Remote Sens. Land Resour. 2013, 25, 56–60. (In Chinese) [Google Scholar] [CrossRef]
- Wu, L.X.; Mao, W.F.; Liu, S.J.; Xu, Z.Y.; Li, Z.W.; Qi, Y.; Miao, Z.L. Mechanisms of Altering Infrared-Microwave Radiation from Stressed Rock and Key Issues on Crust Stress Remote Sensing. J. Remote Sens. 2018, 22, 146–161. (In Chinese) [Google Scholar] [CrossRef]
- Ren, H.Z.; Yan, G.J.; Chen, L.; Li, Z. Angular effect of MODIS emissivity products and its application to the split-window algorithm. ISPRS J. Photogramm. Remote Sens. 2011, 66, 498–507. [Google Scholar] [CrossRef]
- Ren, H.; Liu, R.; Yan, G.; Mu, X.; Li, Z.L.; Nerry, F.; Qiang, N. Angular normalization of land surface temperature and emissivity using multiangular middle and thermal infrared data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4913–4931. [Google Scholar] [CrossRef]
- Mao, W.F.; Wu, L.X.; Liu, S.J.; Gao, X.; Huang, J.W.; Xu, Z.Y.; Qi, Y. Additional Microwave Radiation From Experimentally Loaded Granite Covered With Sand Layers: Features and Mechanisms. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5008–5022. [Google Scholar] [CrossRef]





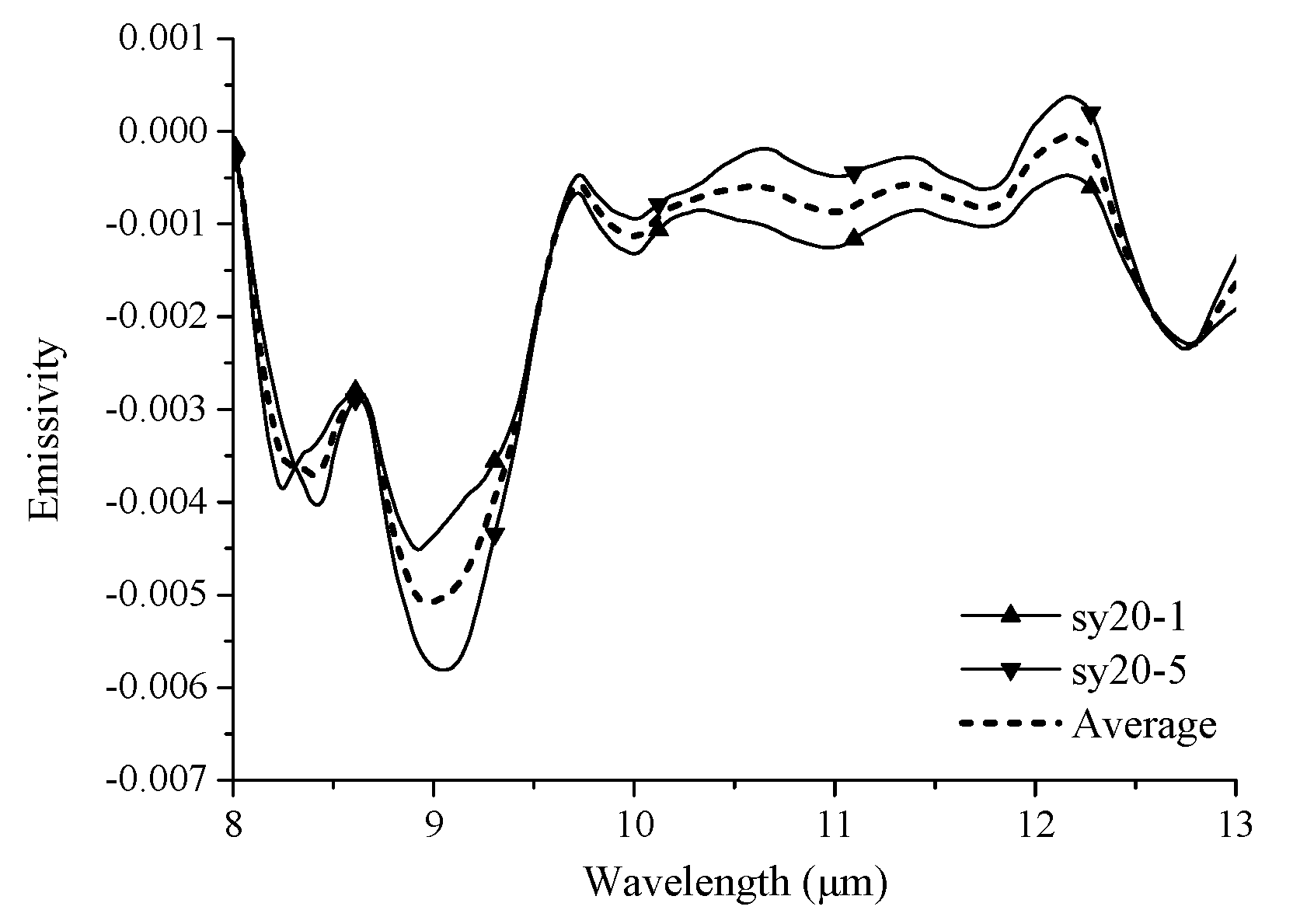
| Specimen | Similarity Coefficient |
|---|---|
| sy20–2 | 0.99 |
| sy20–3 | 0.91 |
| sy20–4 | 0.96 |
| sy20–6 | 0.99 |
| sy20–7 | 0.98 |
| sy20–8 | 0.96 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, J.; Liu, S.; Liu, W.; Zhang, C.; Li, S.; Yu, M.; Wu, L. Experimental Study on the Thermal Infrared Spectral Variation of Fractured Rock. Remote Sens. 2021, 13, 1191. https://doi.org/10.3390/rs13061191
Huang J, Liu S, Liu W, Zhang C, Li S, Yu M, Wu L. Experimental Study on the Thermal Infrared Spectral Variation of Fractured Rock. Remote Sensing. 2021; 13(6):1191. https://doi.org/10.3390/rs13061191
Chicago/Turabian StyleHuang, Jianwei, Shanjun Liu, Wenfang Liu, Chunju Zhang, Shuiping Li, Min Yu, and Lixin Wu. 2021. "Experimental Study on the Thermal Infrared Spectral Variation of Fractured Rock" Remote Sensing 13, no. 6: 1191. https://doi.org/10.3390/rs13061191
APA StyleHuang, J., Liu, S., Liu, W., Zhang, C., Li, S., Yu, M., & Wu, L. (2021). Experimental Study on the Thermal Infrared Spectral Variation of Fractured Rock. Remote Sensing, 13(6), 1191. https://doi.org/10.3390/rs13061191








