Forest Fuel Loads Estimation from Landsat ETM+ and ALOS PALSAR Data
Abstract
1. Introduction
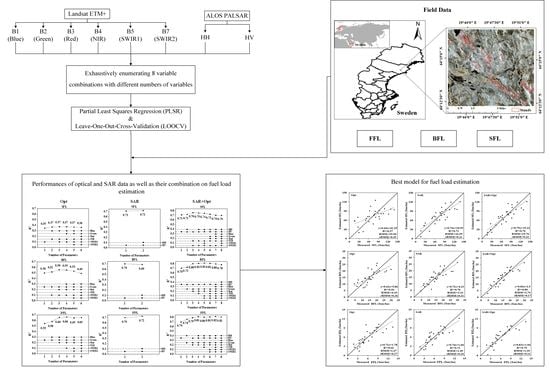
2. Materials and Methods
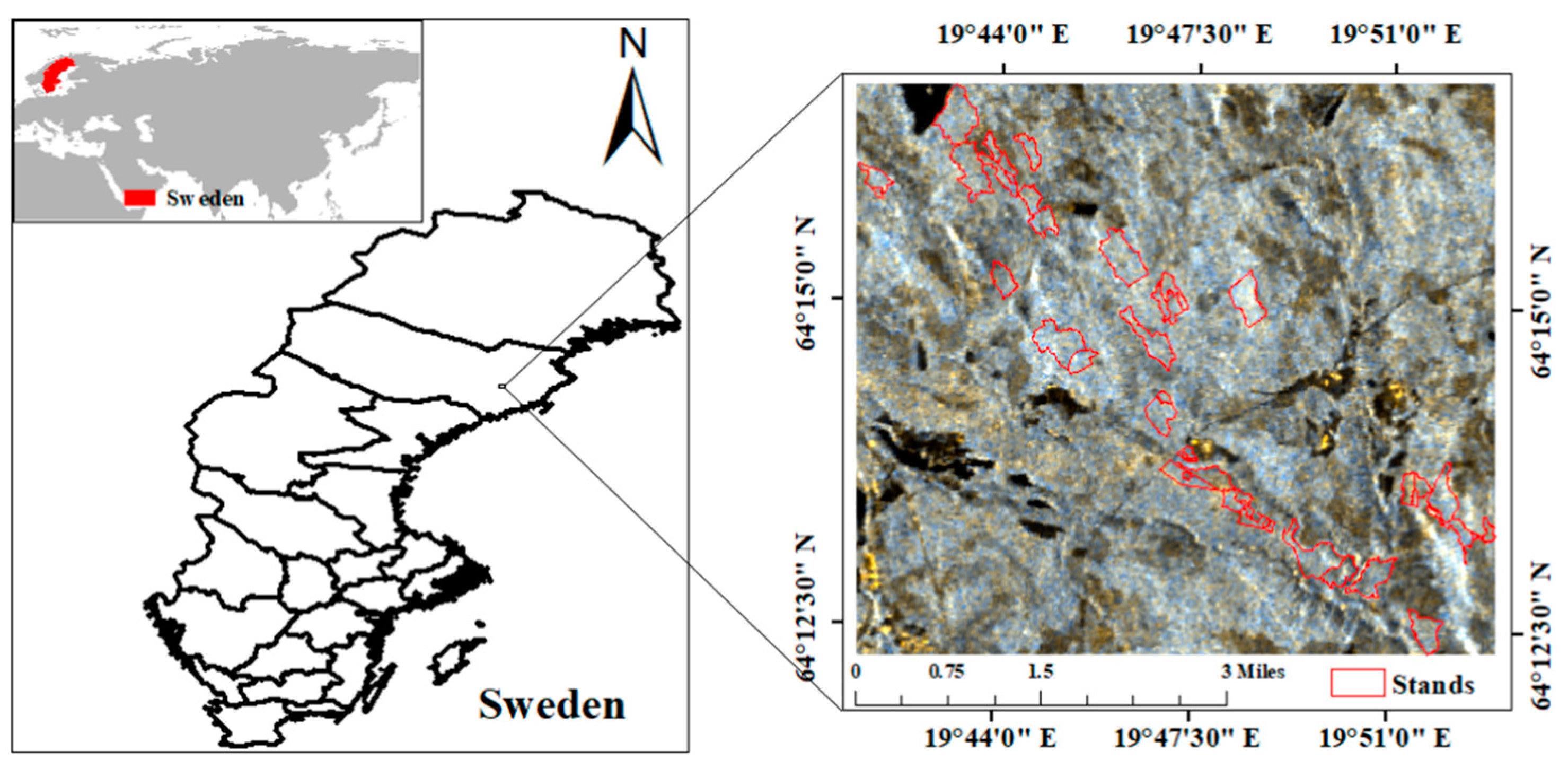
2.1. StudyAarea and Field Measurements
2.2. Satellite Data
2.3. Modeling Algorithms
2.4. Model Evaluation
3. Results
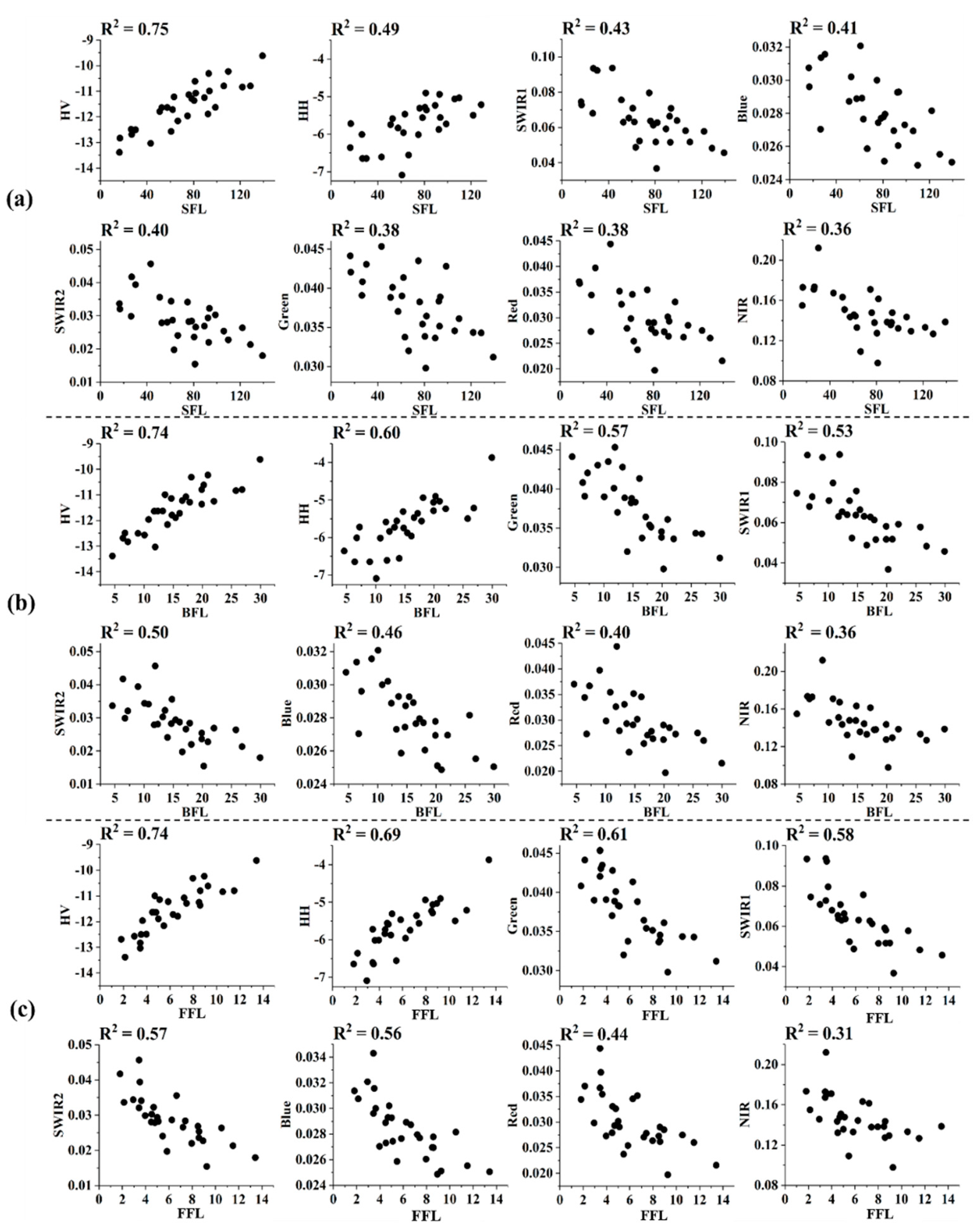
3.1. Correlation Analysis between Single Parameters and Fuel Loads
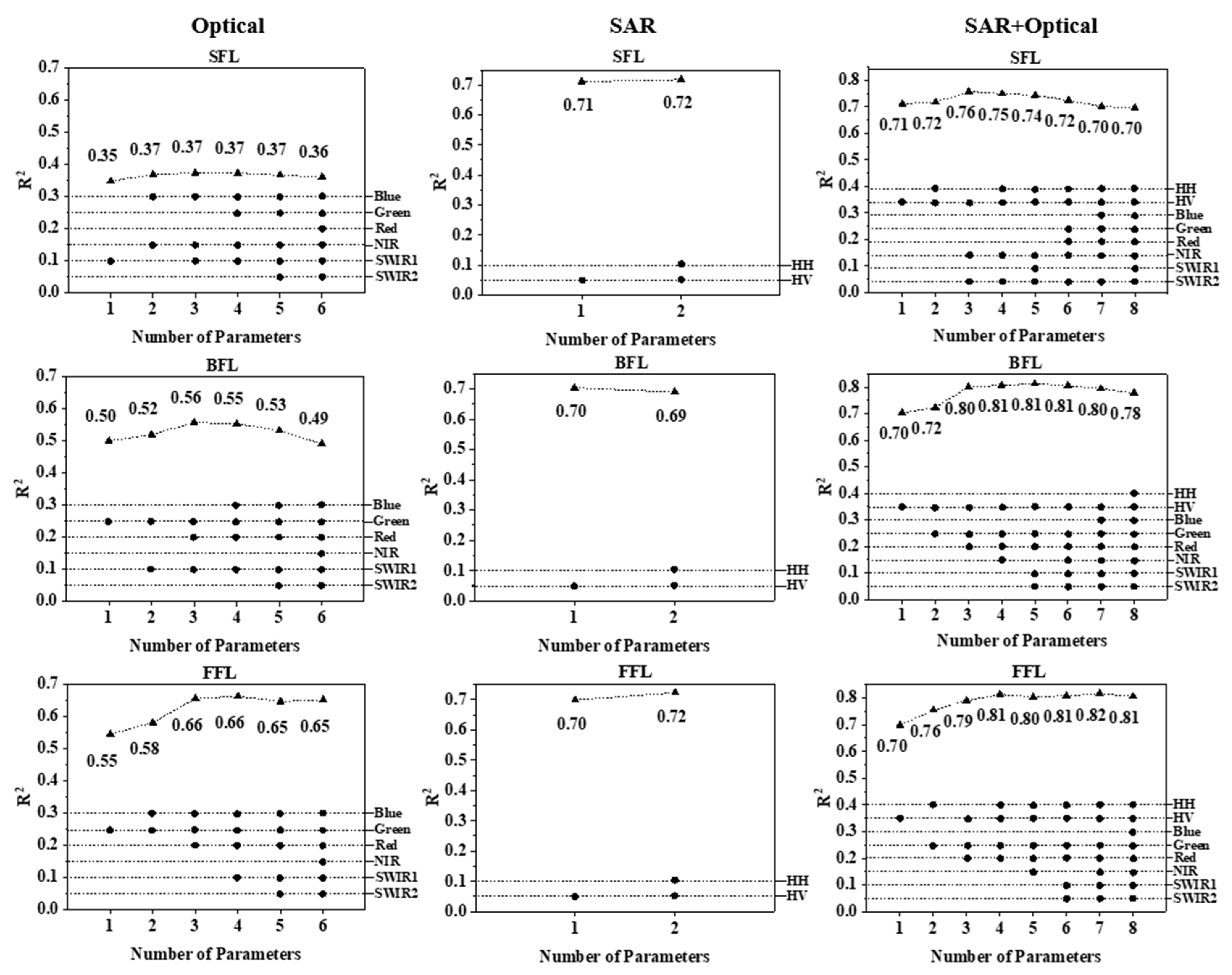
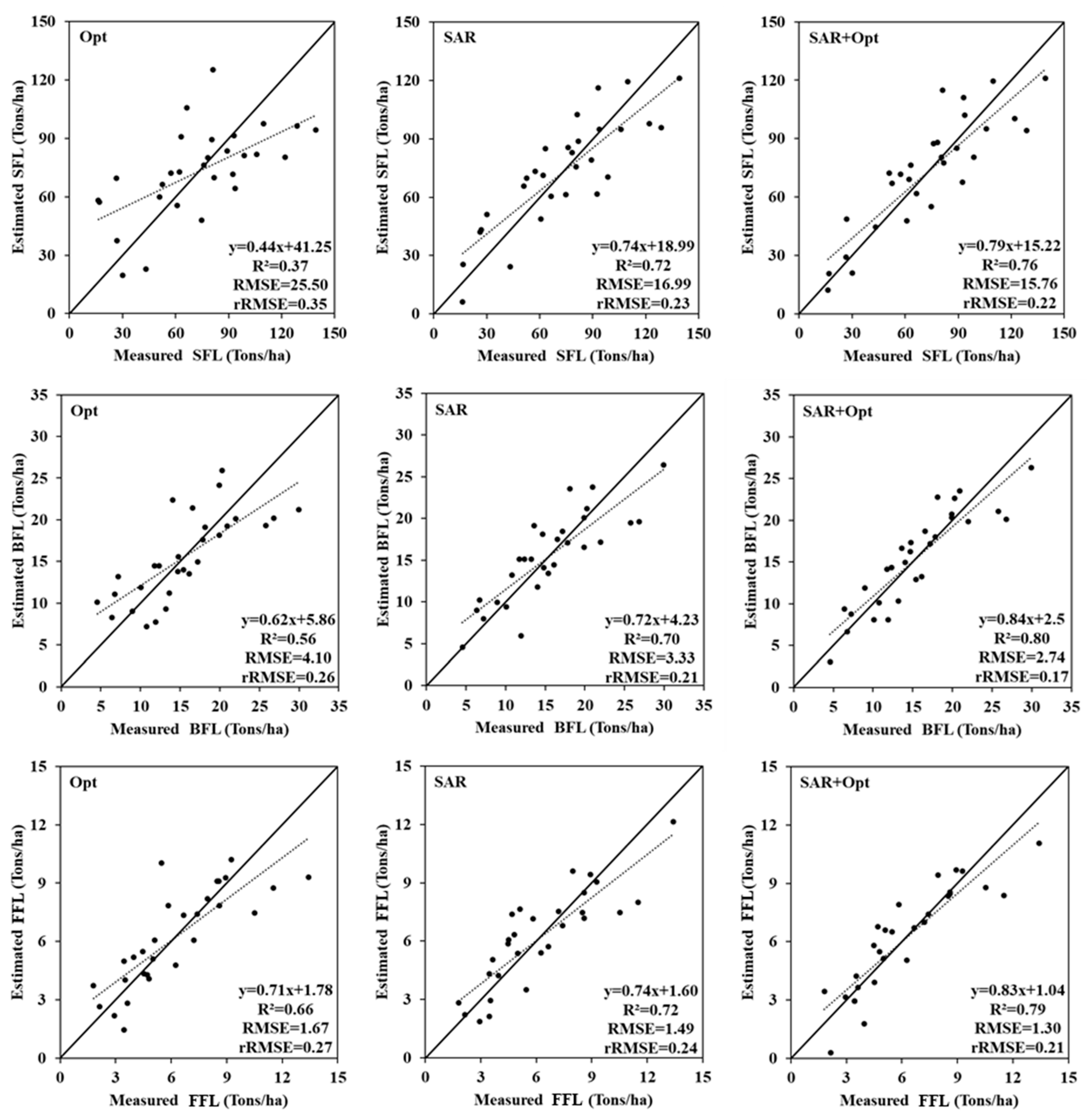
3.2. Fuel Load Estimation from Satellite Data
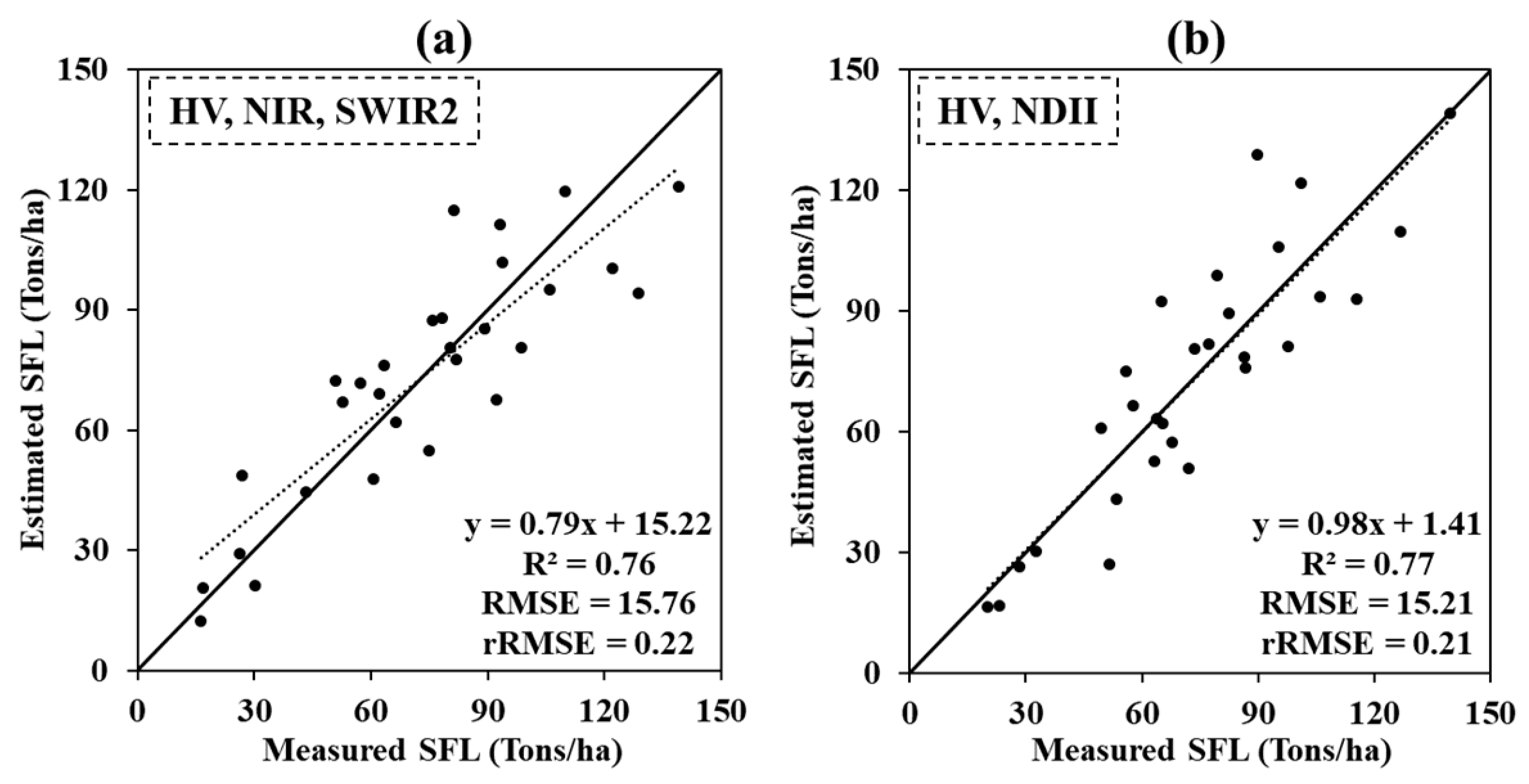
3.3. Comparison between VI and Spetral Bands
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bowman, D.M.B.; Balch, J.K.; Artaxo, P.; Bond, W.J.; Carlson, J.M.; Cochrane, M.A.; D’Antonio, C.M.; Defries, R.S.; Doyle, J.C.; Harrison, S.P.; et al. Fire in the earth system. Science 2009, 324, 481–484. [Google Scholar] [CrossRef]
- Pausas, J.G.; Keeley, J.E. Wildfires as an ecosystem service. Front. Ecol. Environ. 2019, 17, 289–295. [Google Scholar] [CrossRef]
- Yebra, M.; Chuvieco, E.; Riaño, D. Estimation of live fuel moisture content from MODIS images for fire risk assessment. Agric. For. Meteorol. 2008, 148, 523–536. [Google Scholar] [CrossRef]
- Bowman, D.M.J.S.; Moreira-Muñoz, A.; Kolden, C.A.; Chávez, R.O.; Muñoz, A.A.; Salinas, F.; González-Reyes, Á.; Rocco, R.; De La Barrera, F.; Williamson, G.J.; et al. Human–environmental drivers and impacts of the globally extreme 2017 Chilean fires. Ambio 2019, 48, 350–362. [Google Scholar] [CrossRef]
- Jolly, W.M.; Cochrane, M.A.; Freeborn, P.H.; Holden, Z.A.; Brown, T.J. Climate-induced variations in global wildfire danger from 1979 to 2013. Nature Commun. 2015, 6, 1–11. [Google Scholar] [CrossRef]
- David, B. Wildfire science is at a loss for comprehensive data. Nature 2018, 560, 7–8. [Google Scholar]
- Keeley, J.E.; Van Mantgem, P.; Falk, D.A. Fire, climate and changing forests. Nat. Plants 2019, 5, 774–775. [Google Scholar] [CrossRef]
- Byram, G. Combustion of forest fuels. In Forest Fire Forest Fire: Control Use; McGraw-Hill: New York, NY, USA, 1959; pp. 61–89. [Google Scholar]
- Thomas, P. The size of flames from natural fires. Symp. (Int.) Combust. 1963, 9, 844–859. [Google Scholar] [CrossRef]
- Stocks, B.J.; Wotton, B.M.; Stefner, C.N.; Flannigan, M.D.; Taylor, S.W.; Lavoie, N.; Mason, J.A.; Hartley, G.R.; Maffey, M.E.; Dalrymple, G.N.; et al. Crown fire behaviour in a northern jack pine–black spruce forest. Can. J. Forest Res. 2004, 34, 1548–1560. [Google Scholar] [CrossRef]
- Pollet, J.; Omi, P.N. Effect of thinning and prescribed burning on crown fire severity in ponderosa pine forests. Int. J. Wildland Fire 2002, 11, 1–10. [Google Scholar] [CrossRef]
- Andersen, H.-E.; McGaughey, R.J.; Reutebuch, S.E. Estimating forest canopy fuel parameters using LIDAR data. Remote Sens. Environ. 2005, 94, 441–449. [Google Scholar] [CrossRef]
- Brandis, K.; Jacobson, C. Estimation of vegetative fuel loads using Landsat TM imagery in New South Wales, Australia. Int. J. Wildland Fire 2003, 12, 185–194. [Google Scholar] [CrossRef]
- Mitsopoulos, I.D.; Dimitrakopoulos, A.P. Allometric equations for crown fuel biomass of Aleppo pine (Pinus halepensis Mill.) in Greece. Int. J. Wildland Fire 2007, 16, 642–647. [Google Scholar] [CrossRef]
- Keane, R.E.; Burgan, R.; van Wagtendonk, J. Mapping wildland fuels for fire management across multiple scales: Integrating remote sensing, GIS, and biophysical modeling. Int. J. Wildland Fire 2001, 10, 301–309. [Google Scholar] [CrossRef]
- Mallinis, G.; Mitsopoulos, Ι.; Stournara, P.; Patias, P.; Dimitrakopoulos, A.; Mitsopoulos, I. Canopy Fuel Load Mapping of Mediterranean Pine Sites Based on Individual Tree-Crown Delineation. Remote Sens. 2013, 5, 6461–6480. [Google Scholar] [CrossRef]
- Lucas, R.; Van De Kerchove, R.; Otero, V.; Lagomasino, D.; Fatoyinbo, L.; Omar, H.; Satyanarayana, B.; Dahdouh-Guebas, F. Structural characterisation of mangrove forests achieved through combining multiple sources of remote sensing data. Remote Sens. Environ. 2020, 237, 111543. [Google Scholar] [CrossRef]
- Kganyago, M.; Shikwambana, L. Assessment of the Characteristics of Recent Major Wildfires in the USA, Australia and Brazil in 2018–2019 Using Multi-Source Satellite Products. Remote Sens. 2020, 12, 1803. [Google Scholar] [CrossRef]
- Baysal, I.; Yurtgan, M.; Küçük, Ö.; Öztürk, N. Estimation of Crown Fuel Load of Suppressed Trees in Non-treated Young Calabrian Pine (Pinus brutia Ten.) Plantation Areas. Kast. Üniversitesi Orman Fakültesi Derg. 2019, 19, 351–360. [Google Scholar] [CrossRef]
- Kucuk, O.; Bilgili, E.; Sağlam, B. Estimating crown fuel loading for calabrian pine and Anatolian black pine. Int. J. Wildland Fire 2008, 17, 147–154. [Google Scholar] [CrossRef]
- Kucuk, O.; Saglam, B.; Bilgili, E. Canopy Fuel Characteristics and Fuel Load in Young Black Pine Trees. Biotechnol. Biotechnol. Equip. 2007, 21, 235–240. [Google Scholar] [CrossRef][Green Version]
- Arellano-Pérez, S.; Castedo-Dorado, F.; López-Sánchez, C.A.; González-Ferreiro, E.; Yang, Z.; Díaz-Varela, R.A.; Álvarez-González, J.G.; Vega, J.A.; Ruiz-González, A.D. Potential of Sentinel-2A Data to Model Surface and Canopy Fuel Characteristics in Relation to Crown Fire Hazard. Remote Sens. 2018, 10, 1645. [Google Scholar] [CrossRef]
- Scott, J.H.; Reinhardt, E.D.; Station, R.M.R. Assessing Crown Fire Potential by Linking Models of Surface and Crown Fire Behavior; U.S. Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2001. [CrossRef]
- Güngöroglu, C.; Serttaş, A.; Sari, A.; Güney, Ç.O. Predicting crown fuel biomass of Turkish red pine (Pinus brutia Ten.) for the Mediterranean regions of Turkey. Šumarski List 2018, 142, 610. [Google Scholar] [CrossRef]
- Reich, R.M.; Lundquist, J.E.; Bravo, V.A. Spatial models for estimating fuel loads in the Black Hills, South Dakota, USA. Int. J. Wildland Fire 2004, 13, 119–129. [Google Scholar] [CrossRef]
- Stow, D.; Hope, A.; McKinsey, D.; Pray, H. Deriving dynamic information on fire fuel distributions in southern Californian chaparral from remotely sensed data. Landsc. Urban. Plan. 1993, 24, 113–127. [Google Scholar] [CrossRef]
- Chen, Y.; Zhu, X.; Yebra, M.; Harris, S.; Tapper, N. Development of a predictive model for estimating forest surface fuel load in Australian eucalypt forests with LiDAR data. Environ. Model. Softw. 2017, 97, 61–71. [Google Scholar] [CrossRef]
- González-Ferreiro, E.; Arellano-Pérez, S.; Castedo-Dorado, F.; Hevia, A.; Vega, J.A.; Vega-Nieva, D.J.; Álvarez-González, J.G.; Ruiz-González, A.D. Modelling the vertical distribution of canopy fuel load using national forest inventory and low-density airbone laser scanning data. PLoS ONE 2017, 12, e0176114. [Google Scholar] [CrossRef]
- Michel, U.; Schulz, K.; Ehlers, M.; Nikolakopoulos, K.G.; Civco, D.; Chen, Y.; Zhu, X.; Yebra, M.; Harris, S.; Tapper, N. Estimation of forest surface fuel load using airborne lidar data. In Proceedings of the Earth Resources and Environmental Remote Sensing/GIS Applications VII, Edinburgh, UK, 27–29 September 2016. [Google Scholar]
- Skowronski, N.; Clark, K.; Nelson, R.; Hom, J.; Patterson, M. Remotely sensed measurements of forest structure and fuel loads in the Pinelands of New Jersey. Remote Sens. Environ. 2007, 108, 123–129. [Google Scholar] [CrossRef]
- Jin, S.; Chen, S.-C. Application of QuickBird imagery in fuel load estimation in the Daxinganling region, China. Int. J. Wildland Fire 2012, 21, 583–590. [Google Scholar] [CrossRef]
- Lai, X.Q.Y.L.B.H.G.C.G. Application of Landsat ETM+ and OLI Data for Foliage Fuel Load Monitoring Using Radiative Transfer Model and Machine Learning Method. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 99, 1. [Google Scholar]
- Saatchi, S.; Halligan, K.; Despain, D.G.; Crabtree, R.L. Estimation of Forest Fuel Load From Radar Remote Sensing. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1726–1740. [Google Scholar] [CrossRef]
- Cho, M.A.; Mathieu, R.; Asner, G.P.; Naidoo, L.; Van Aardt, J.; Ramoelo, A.; Debba, P.; Wessels, K.; Main, R.; Smit, I.P.; et al. Mapping tree species composition in South African savannas using an integrated airborne spectral and LiDAR system. Remote Sens. Environ. 2012, 125, 214–226. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Hudak, A.T.; Cohen, W.B.; Acker, S. Geographic variability in lidar predictions of forest stand structure in the Pacific Northwest. Remote Sens. Environ. 2005, 95, 532–548. [Google Scholar] [CrossRef]
- Cartus, O.; Santoro, M.; Kellndorfer, J. Mapping forest aboveground biomass in the Northeastern United States with ALOS PALSAR dual-polarization L-band. Remote Sens. Environ. 2012, 124, 466–478. [Google Scholar] [CrossRef]
- Evans, J.P.; Guojie, W. Recent reversal in global terrestrial biomass loss. Nat. Clim. Chang. 2015, 5, 470–474. [Google Scholar]
- Massetti, A.; Rüdiger, C.; Yebra, M.; Hilton, J. The Vegetation Structure Perpendicular Index (VSPI): A forest condition index for wildfire predictions. Remote Sens. Environ. 2019, 224, 167–181. [Google Scholar] [CrossRef]
- Bai, X.; He, B.; Li, X.; Zeng, J.; Wang, X.; Wang, Z.; Zeng, Y.; Su, Z. First Assessment of Sentinel-1A Data for Surface Soil Moisture Estimations Using a Coupled Water Cloud Model and Advanced Integral Equation Model over the Tibetan Plateau. Remote Sens. 2017, 9, 714. [Google Scholar] [CrossRef]
- Wang, L.; Quan, X.; He, B.; Yebra, M.; Xing, M.; Liu, X. Assessment of the Dual Polarimetric Sentinel-1A Data for Forest Fuel Moisture Content Estimation. Remote Sens. 2019, 11, 1568. [Google Scholar] [CrossRef]
- Castillo, J.A.A.; Apan, A.A.; Maraseni, T.N.; Salmo, S.G. Estimation and mapping of above-ground biomass of mangrove forests and their replacement land uses in the Philippines using Sentinel imagery. ISPRS J. Photogramm. Remote Sens. 2017, 134, 70–85. [Google Scholar] [CrossRef]
- Debastiani, A.B.; Sanquetta, C.R.; Corte, A.P.D.; Pinto, N.S.; Rex, F.E. Evaluating SAR-optical sensor fusion for aboveground biomass estimation in a Brazilian tropical forest. Ann. For. Res. 2019, 62, 109–122. [Google Scholar] [CrossRef]
- Li, X.; Li, L.; Liu, X. Collaborative inversion heavy metal stress in rice by using two-dimensional spectral feature space based on HJ-1 A HSI and radarsat-2 SAR remote sensing data. Int. J. Appl. Earth Obs. Geoinf. 2019, 78, 39–52. [Google Scholar] [CrossRef]
- Nuthammachot, N.; Askar, A.; Stratoulias, D.; Wicaksono, P. Combined use of Sentinel-1 and Sentinel-2 data for improving above-ground biomass estimation. Geocarto Int. 2020, 10, 1–11. [Google Scholar] [CrossRef]
- Laudon, H.; Sjöblom, V.; Buffam, I.; Seibert, J.; Mörth, M. The role of catchment scale and landscape characteristics for runoff generation of boreal streams. J. Hydrol. 2007, 344, 198–209. [Google Scholar] [CrossRef]
- Petersson, H. Biomassafunktioner for trädfraktioner av tall, gran och björk i sverige. SLU Inst. Skoglig Resur. Och Geomatik Arbetsrapport 1999, 59. [Google Scholar]
- Hajnsek, I.; Scheiber, R.; Keller, M.; Horn, R.; Lee, S.; Ulander, L.; Gustavsson, A.; Sandberg, G.; Le Toan, T.; Tebaldini, S.; et al. BIOSAR 2008: Final Report. ESA-ESTEC Noordwijk Neth. Tech. Rep. 2009, 8, 22052. [Google Scholar]
- Thapa, R.B.; Watanabe, M.; Motohka, T.; Shimada, M. Potential of high-resolution ALOS–PALSAR mosaic texture for aboveground forest carbon tracking in tropical region. Remote Sens. Environ. 2015, 160, 122–133. [Google Scholar] [CrossRef]
- Shimada, M.; Ohtaki, T. Generating Large-Scale High-Quality SAR Mosaic Datasets: Application to PALSAR Data for Global Monitoring. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 637–656. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Shimada, M.; Itoh, T.; Motooka, T.; Watanabe, M.; Shiraishi, T.; Thapa, R.; Lucas, R. New global forest/non-forest maps from ALOS PALSAR data (2007–2010). Remote Sens. Environ. 2014, 155, 13–31. [Google Scholar] [CrossRef]
- Scaramuzza, P.; Barsi, J. Landsat 7 scan line corrector-off gap-filled product developme. Proc. Pecora 2005, 16, 23–27. [Google Scholar]
- Hardisky, M.A.; Klemas, V.; Smart, R.M. The influence of soil salinity, growth form, and leaf moisture on the spectral radiance of Spartina Alterniflora canopies. Photogramm. Eng. Remote Sens. 1983, 49, 77–84. [Google Scholar]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Adjorlolo, C.; Mutanga, O.; Cho, M.A. Predicting C3 and C4 grass nutrient variability using in situ canopy reflectance and partial least squares regression. Int. J. Remote Sens. 2015, 36, 1743–1761. [Google Scholar] [CrossRef]
- Rapaport, T.; Hochberg, U.; Shoshany, M.; Karnieli, A.; Rachmilevitch, S. Combining leaf physiology, hyperspectral imaging and partial least squares-regression (PLS-R) for grapevine water status assessment. ISPRS J. Photogramm. Remote Sens. 2015, 109, 88–97. [Google Scholar] [CrossRef]
- Kiala, Z.; Odindi, J.; Mutanga, O.; Peerbhay, K. Comparison of partial least squares and support vector regressions for predicting leaf area index on a tropical grassland using hyperspectral data. J. Appl. Remote Sens. 2016, 10, 036015. [Google Scholar] [CrossRef]
- Ryan, K.; Ali, K. Application of a partial least-squares regression model to retrieve chlorophyll-a concentrations in coastal waters using hyper-spectral data. Ocean. Sci. J. 2016, 51, 209–221. [Google Scholar] [CrossRef]
- Guo, Y.-J.; Han, J.-J.; Zhao, X.; Dai, X.-Y.; Zhang, H. Understanding the Role of Optimized Land Use/Land Cover Components in Mitigating Summertime Intra-Surface Urban Heat Island Effect: A Study on Downtown Shanghai, China. Energies 2020, 13, 1678. [Google Scholar] [CrossRef]
- Fernandes, P.; Loureiro, C.; Botelho, H.; Ferreira, A.; Fernandes, M. Avaliação Indirecta da Carga de Combustível em Pinhal Bravo. Silva Lusit. 2002, 10, 73–90. [Google Scholar]
- Jiménez, E.; Vega, J.A.; Fernández-Alonso, J.M.; Vega-Nieva, D.; Álvarez-González, J.G.; Ruiz-González, A.D. Allometric equations for estimating canopy fuel load and distribution of pole-size maritime pine trees in five Iberian provenances. Can. J. For. Res. 2013, 43, 149–158. [Google Scholar] [CrossRef]
- Amini, J.; Sumantyo, J.T.S. Employing a Method on SAR and Optical Images for Forest Biomass Estimation. IEEE Trans. Geosci. Remote Sens. 2009, 47, 4020–4026. [Google Scholar] [CrossRef]
- Svoray, T.; Shoshany, M. Herbaceous biomass retrieval in habitats of complex composition: A model merging sar images with unmixed landsat tm data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1592–1601. [Google Scholar] [CrossRef]
- Reese, H.; Nilsson, M.; Olsson, H. Comparison of Resourcesat-1 AWiFS and SPOT-5 data over managed boreal forest stands. Int. J. Remote Sens. 2009, 30, 4957–4978. [Google Scholar] [CrossRef]
- Féret, J.-B.; Le Maire, G.; Jay, S.; Berveiller, D.; Bendoula, R.; Hmimina, G.; Cheraiet, A.; Oliveira, J.; Ponzoni, F.; Solanki, T.; et al. Estimating leaf mass per area and equivalent water thickness based on leaf optical properties: Potential and limitations of physical modeling and machine learning. Remote Sens. Environ. 2019, 231, 110959. [Google Scholar] [CrossRef]
- Blomberg, E.; Ferro-Famil, L.; Soja, M.J.; Ulander, L.M.H.; Tebaldini, S. Forest Biomass Retrieval From L-Band SAR Using Tomographic Ground Backscatter Removal. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1030–1034. [Google Scholar] [CrossRef]
- Askne, J.I.; Soja, M.J.; Ulander, L.M. Biomass estimation in a boreal forest from TanDEM-X data, lidar DTM, and the interferometric water cloud model. Remote Sens. Environ. 2017, 196, 265–278. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, C.; Zhu, J.; Fu, H.; Xie, Q.; Shen, P. Forest Above-Ground Biomass Estimation Using Single-Baseline Polarization Coherence Tomography with P-Band PolInSAR Data. Forests 2018, 9, 163. [Google Scholar] [CrossRef]
- Huang, X.; Ziniti, B.; Torbick, N.; Ducey, M.J. Assessment of Forest above Ground Biomass Estimation Using Multi-Temporal C-band Sentinel-1 and Polarimetric L-band PALSAR-2 Data. Remote Sens. 2018, 10, 1424. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E.; Olofsson, P. Continuous monitoring of forest disturbance using all available Landsat imagery. Remote Sens. Environ. 2012, 122, 75–91. [Google Scholar] [CrossRef]
- Ye, S.; Rogan, J.; Zhu, Z.; Eastman, J.R. A near-real-time approach for monitoring forest disturbance using Landsat time series: Stochastic continuous change detection. Remote Sens. Environ. 2021, 252, 112167. [Google Scholar] [CrossRef]
- Liao, Z.; He, B.; Quan, X.; Van Dijk, A.I.; Qiu, S.; Yin, C. Biomass estimation in dense tropical forest using multiple information from single-baseline P-band PolInSAR data. Remote Sens. Environ. 2019, 221, 489–507. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Y.; Ren, C.; Zhang, B.; Wang, Z. Optimal Combination of Predictors and Algorithms for Forest Above-Ground Biomass Mapping from Sentinel and SRTM Data. Remote Sens. 2019, 11, 414. [Google Scholar] [CrossRef]


| Sensor | Parameters | Description |
|---|---|---|
| ALOS PALSAR | HH | HH channel |
| HV | HV channel | |
| Landsat ETM+ | Band 1 | Blue, 485 nm |
| Band 2 | Green, 560 nm | |
| Band 3 | Red, 660 nm | |
| Band 4 | NIR, 830 nm | |
| Band 5 | SWIR1, 1650 nm | |
| Band 7 | SWIR2, 2215 nm |
| Number of Variables | Combination Situation | Number of Combinations |
|---|---|---|
| 1 | (a)(b)…(h) | 8 |
| 2 | (a, b)(a, c)…(g, h) | 28 |
| 3 | (a, b, c)(a, b, d)…(f, g, h) | 56 |
| 4 | (a, b, c, d)(a, b, c, e)...(e, f, g, h) | 70 |
| 5 | (a, b, c, d, e)(a, b, c, d, f)...(d, e, f, g, h) | 56 |
| 6 | (a, b, c, d, e, f)…(c, d, e, f, g, h) | 28 |
| 7 | (a, b, c, d, e, f, g)…(b, c, d, e, f, g, h) | 8 |
| 8 | (a, b, c, d, e, f, g, h) | 1 |
| Blue | Green | Red | NIR | SWIR1 | SWIR2 | HH | HV | |
| Blue | -- | |||||||
| Green | 0.62 | -- | ||||||
| Red | 0.69 | 0.85 | -- | |||||
| NIR | 0.44 | 0.53 | 0.53 | -- | ||||
| SWIR1 | 0.76 | 0.72 | 0.76 | 0.72 | -- | |||
| SWIR2 | 0.78 | 0.72 | 0.78 | 0.58 | 0.96 | -- | ||
| HH | 0.59 | 0.42 | 0.40 | 0.20 | 0.54 | 0.59 | -- | |
| HV | 0.61 | 0.55 | 0.54 | 0.30 | 0.58 | 0.61 | 0.78 | -- |
| Fuel Load | Variable Source | Model | R2 | RMSE (Tons/ha) | rRMSE |
| SFL | Optical | 0.37 | 25.50 | 0.35 | |
| SAR | 0.72 | 17.00 | 0.23 | ||
| SAR+Optical | 0.76 | 15.76 | 0.22 | ||
| BFL | Optical | 0.56 | 4.10 | 0.26 | |
| SAR | 0.70 | 3.33 | 0.21 | ||
| SAR+Optical | 0.80 | 2.74 | 0.17 | ||
| FFL | Optical | 0.66 | 1.67 | 0.27 | |
| SAR | 0.72 | 1.49 | 0.24 | ||
| SAR+Optical | 0.79 | 1.30 | 0.21 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Quan, X.; Liao, Z.; He, B. Forest Fuel Loads Estimation from Landsat ETM+ and ALOS PALSAR Data. Remote Sens. 2021, 13, 1189. https://doi.org/10.3390/rs13061189
Li Y, Quan X, Liao Z, He B. Forest Fuel Loads Estimation from Landsat ETM+ and ALOS PALSAR Data. Remote Sensing. 2021; 13(6):1189. https://doi.org/10.3390/rs13061189
Chicago/Turabian StyleLi, Yanxi, Xingwen Quan, Zhanmang Liao, and Binbin He. 2021. "Forest Fuel Loads Estimation from Landsat ETM+ and ALOS PALSAR Data" Remote Sensing 13, no. 6: 1189. https://doi.org/10.3390/rs13061189
APA StyleLi, Y., Quan, X., Liao, Z., & He, B. (2021). Forest Fuel Loads Estimation from Landsat ETM+ and ALOS PALSAR Data. Remote Sensing, 13(6), 1189. https://doi.org/10.3390/rs13061189