A Novel Digital IQ Demodulation for Interferometric Radiometers
Abstract
1. Introduction
2. Materials and Methods
2.1. Visibility and Correlation
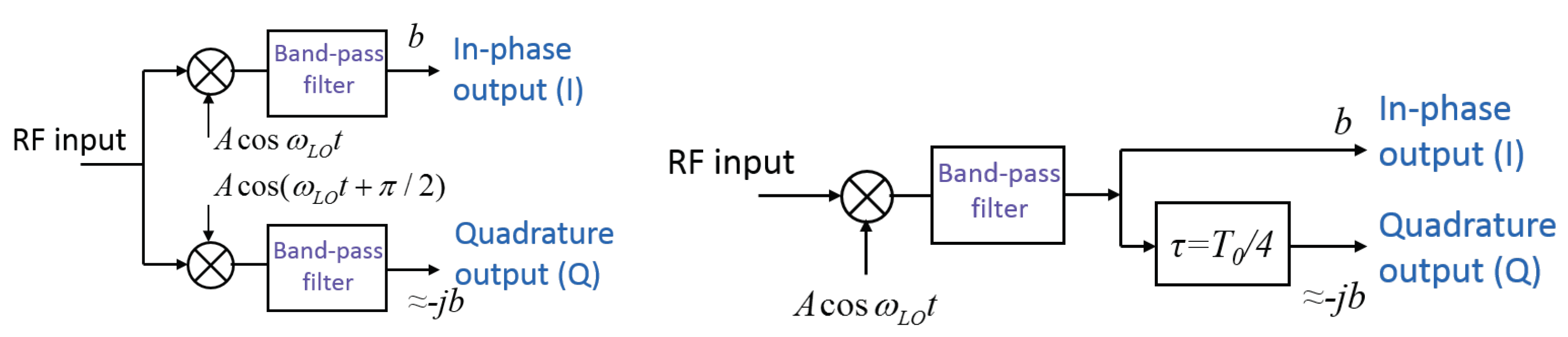
2.2. In-Phase and Quadrature
2.3. Normalized Cross-Correlation Function
2.4. Data Processing
2.4.1. Decorrelation of the Imaginary Part
2.4.2. Center Frequency Error
2.5. Fringe Washing Function Shape
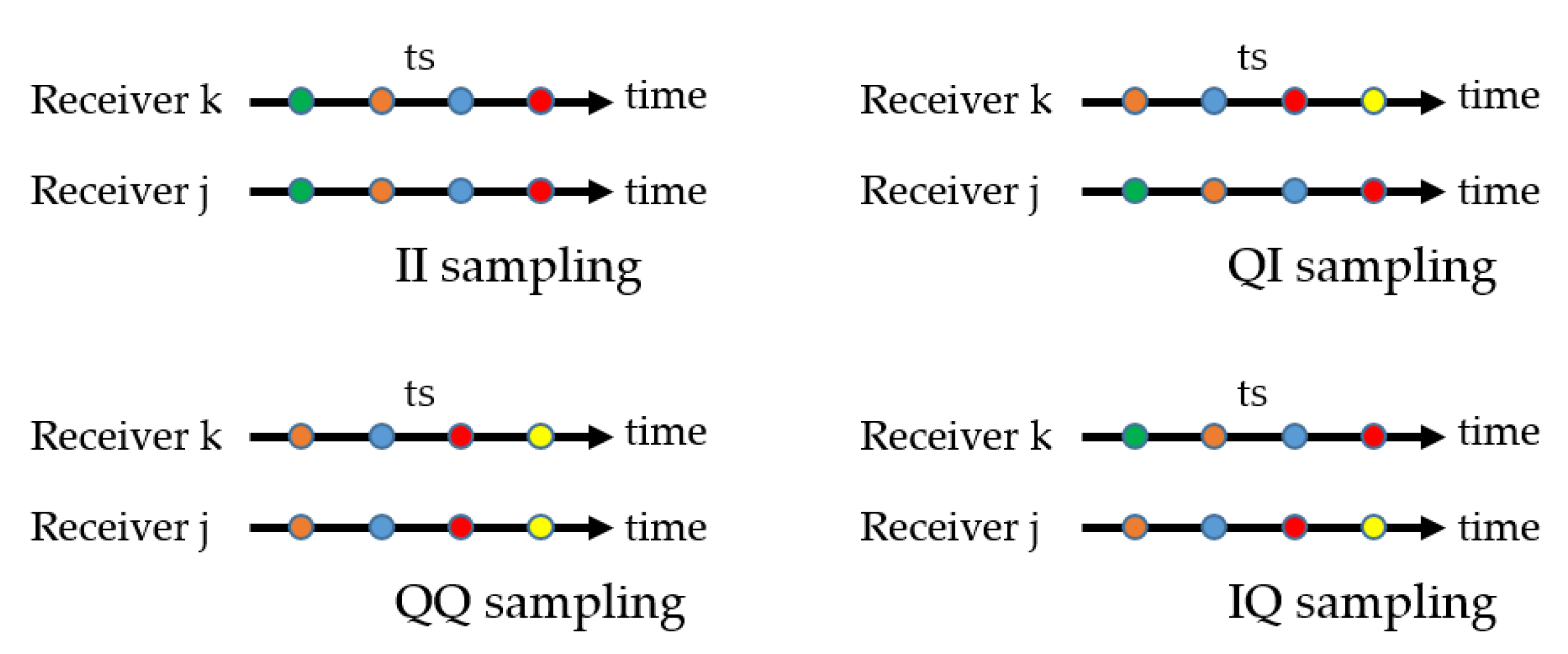
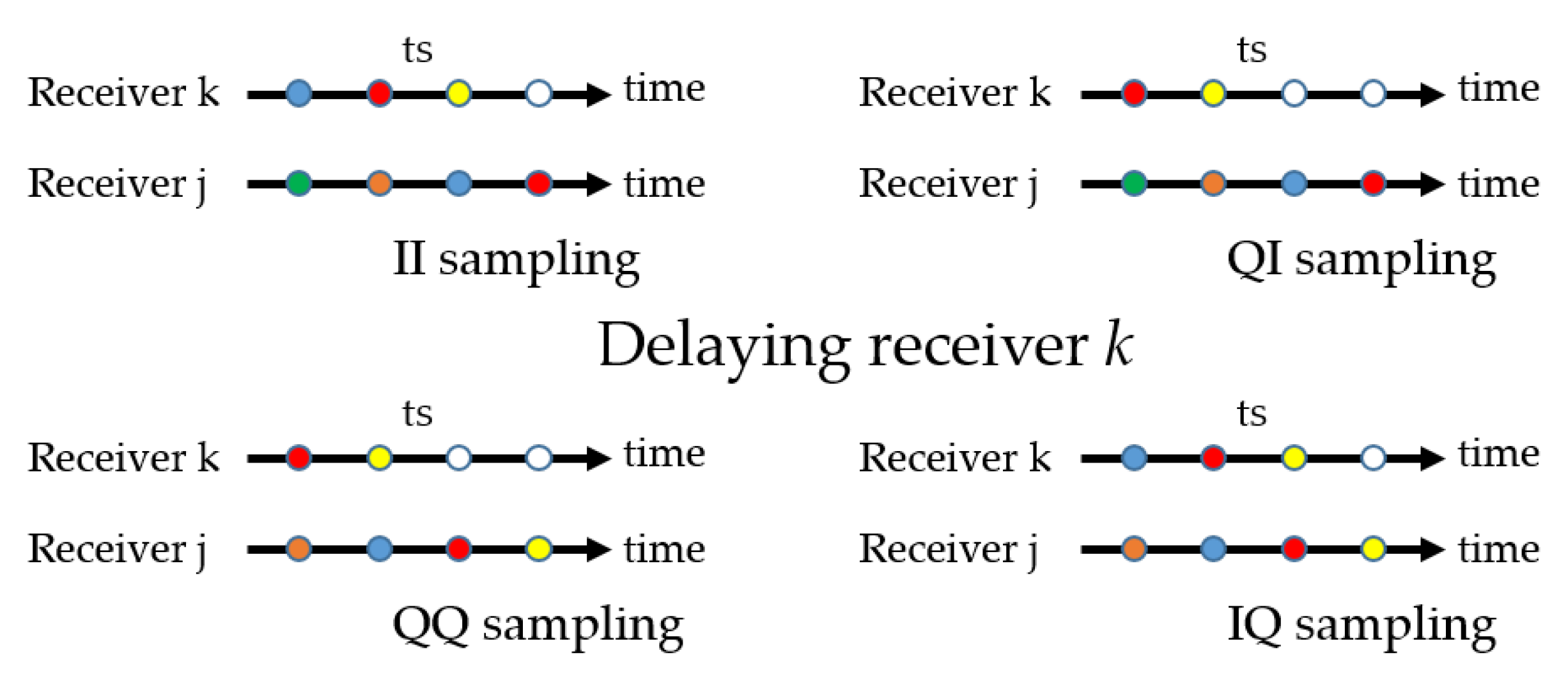
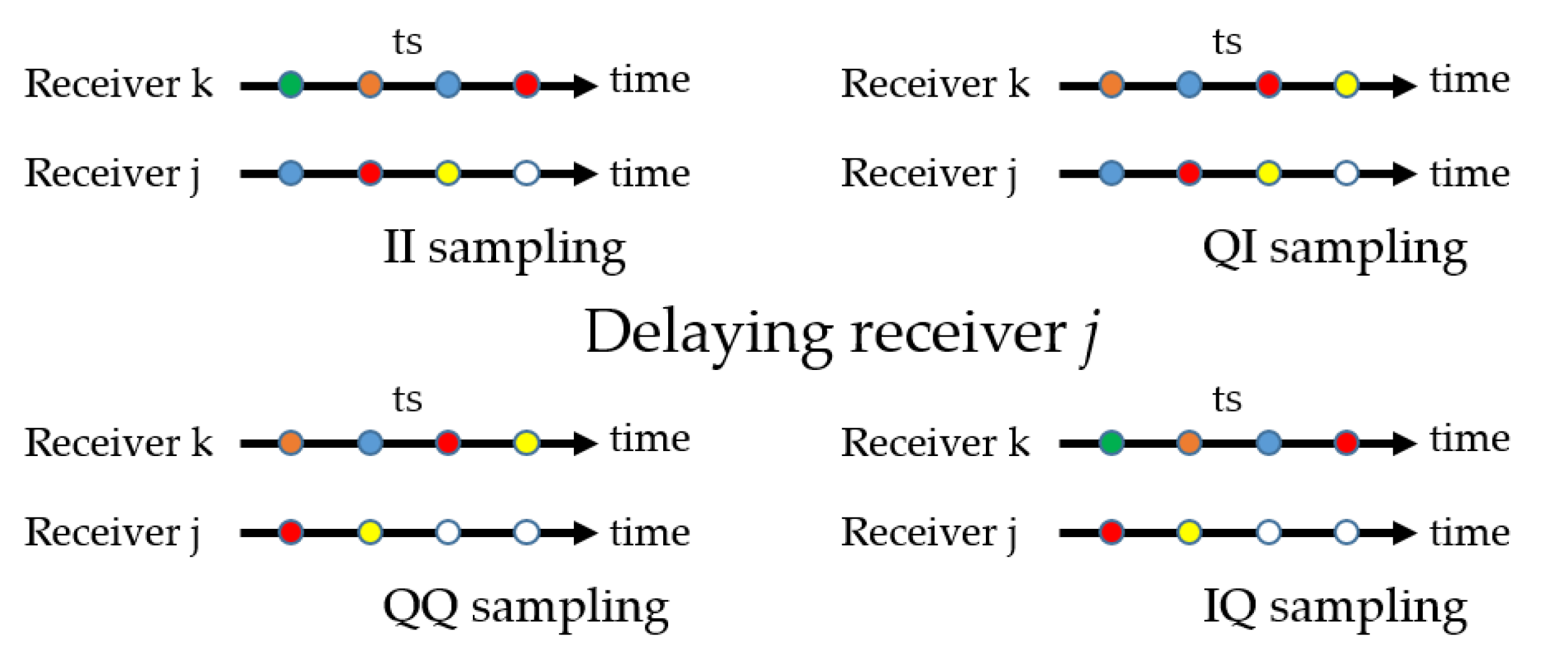
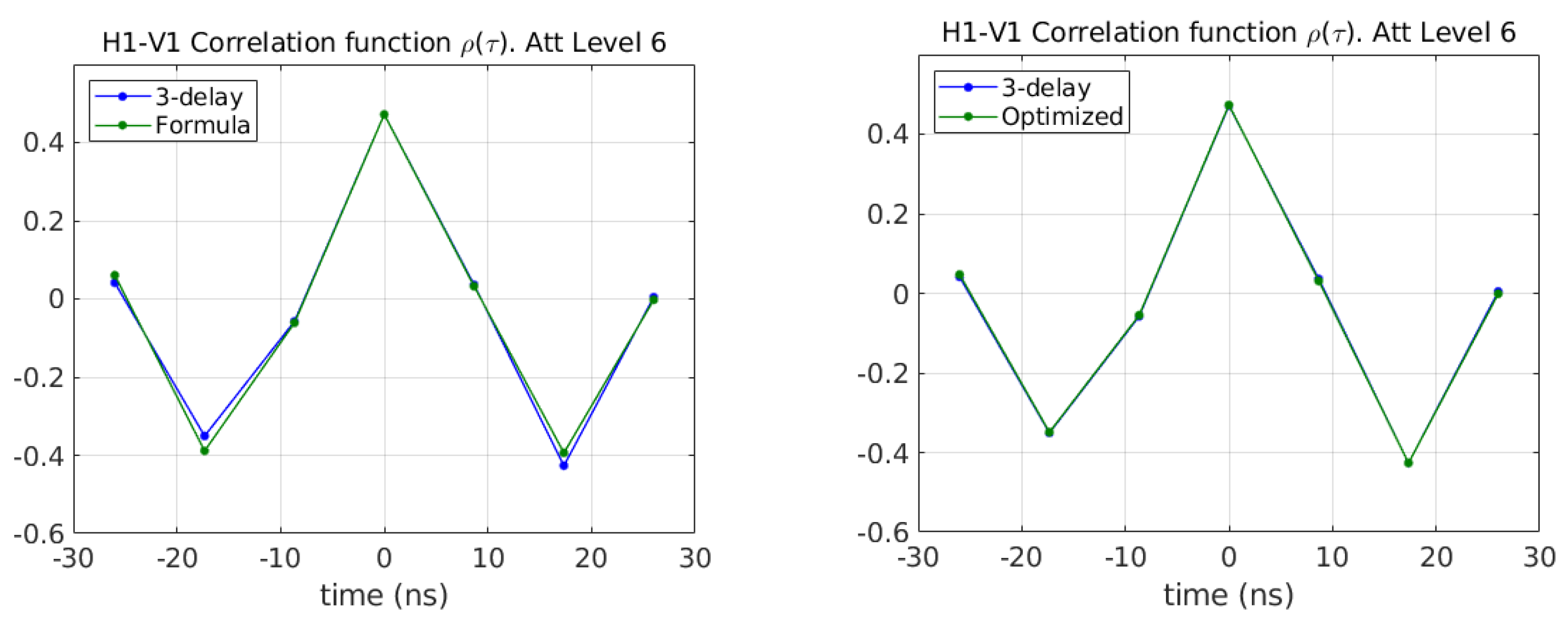
2.5.1. Three-Delay Measurements
- Delaying receiver k (Figure 3):
- Delaying receiver j (Figure 4).
2.5.2. The system of Equations
3. Results
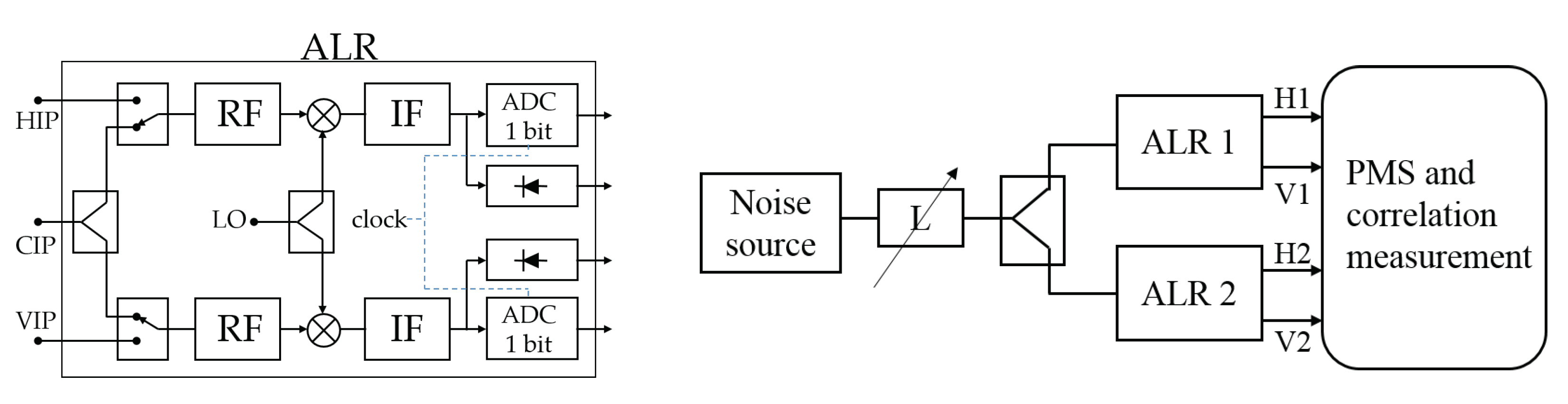
3.1. Power Measurements
3.2. Correlation Measurements
3.2.1. Self-IQ Correlation
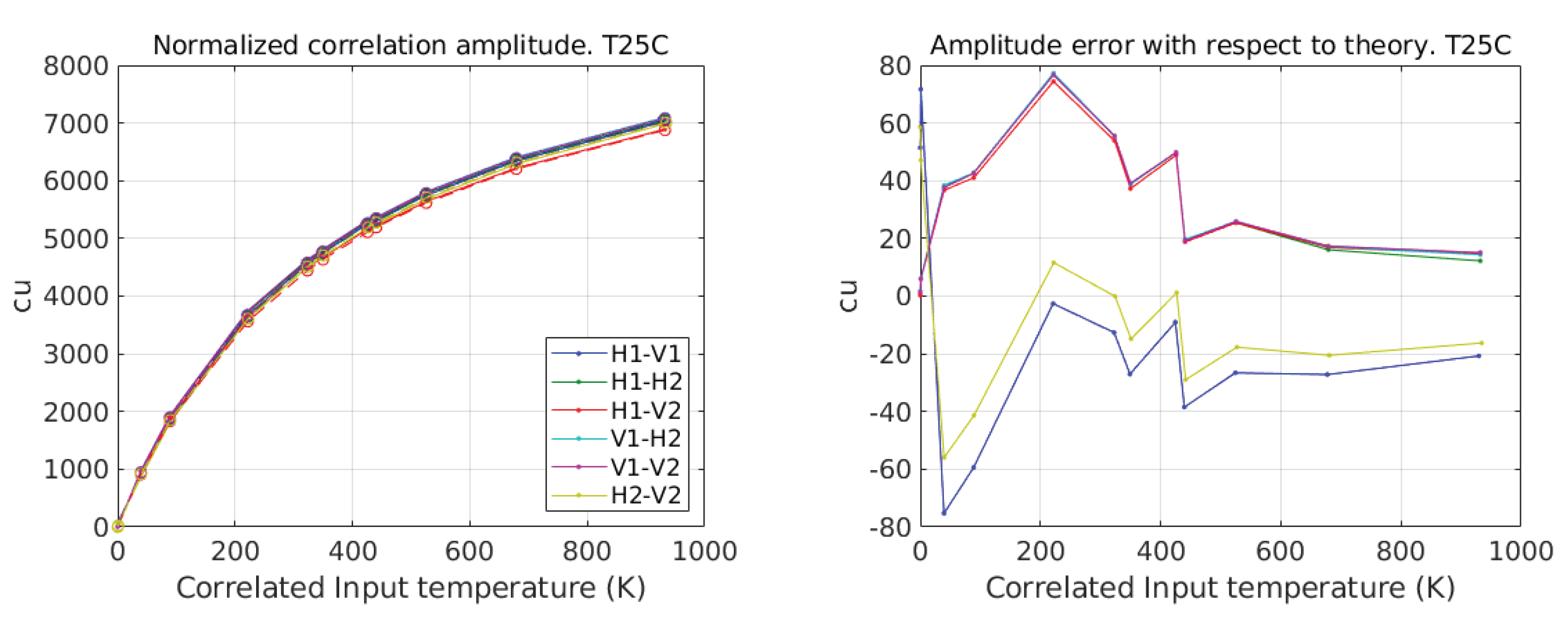
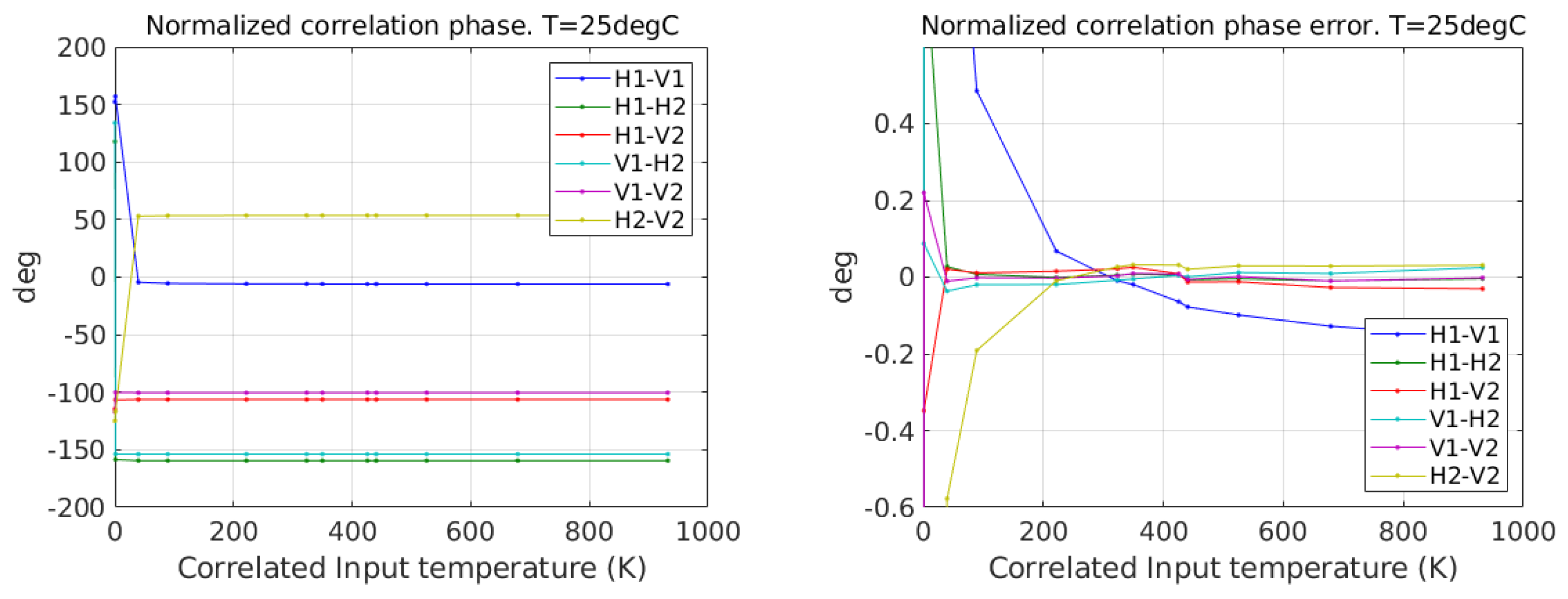
3.2.2. Cross-Correlation
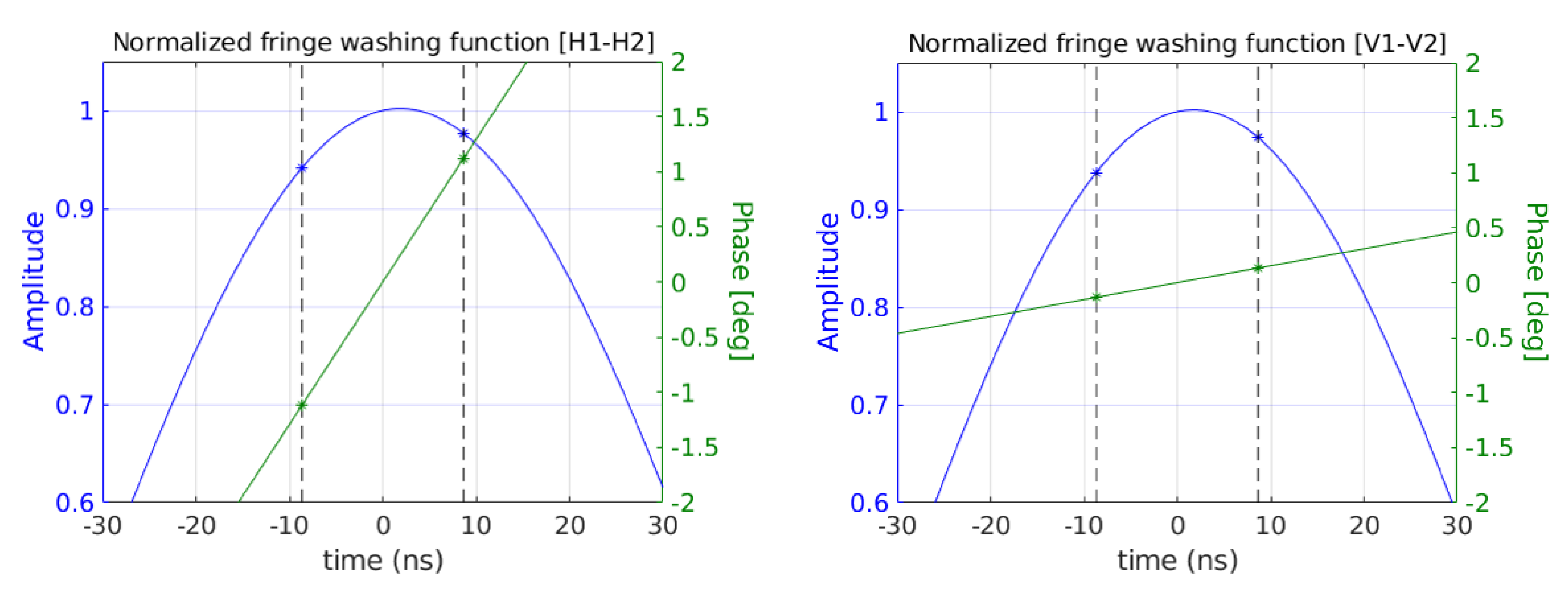
3.2.3. Fringe Washing Function Shape
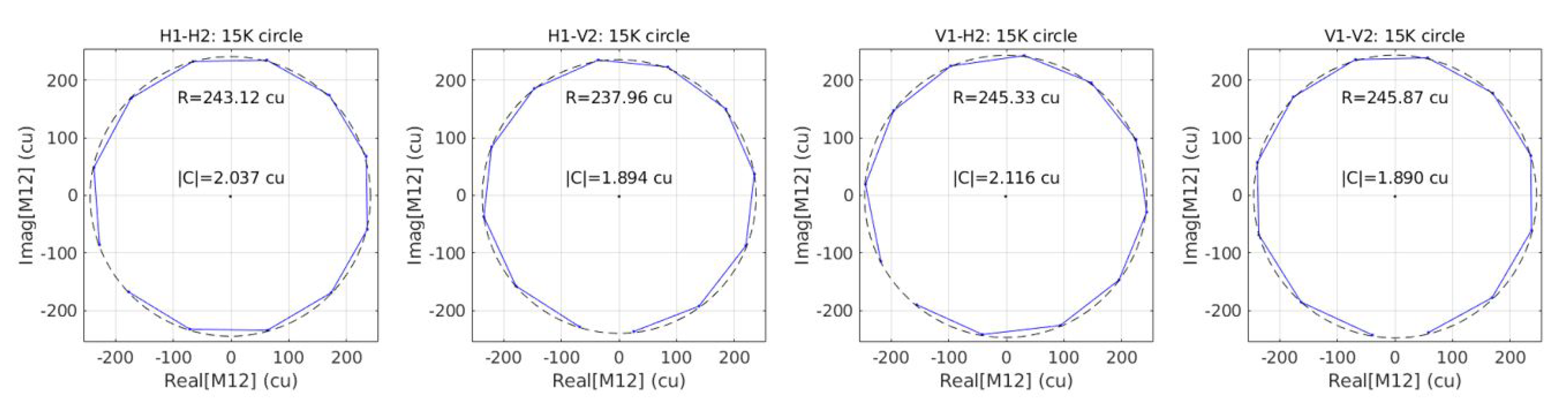
3.2.4. Sensitivity Circles
3.3. Effective Integration Time
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ALR | Advanced Receiver for the Future L-Band Radiometer |
| DUT | Device Under Test |
| ESA | European Space Agency |
| EBB | Elegant Breadboard |
| IF | Intermediate Frequency |
| IQ | In-phase and Quadrature |
| LICEF | Lightweight Cost-Effective Front-end |
| LO | Local Oscillator |
| MIRAS | Microwave Imaging Radiometer with Aperture Synthesis |
| NOSU | Noise Source |
| PMS | Power Measurement System |
| RF | Radio Frequency |
| SMOS | Soil Moisture and Ocean Salinity |
Appendix A. The Fringe Washing Function
- If the product is real, then , so the real part is even and the imaginary part odd. This happens either if both receivers have identical frequency responses or if a single receiver is considered (the case of or ).
- If both frequency responses are symmetrical around the reference frequency (that is, if ), then the fringe washing function is real.
- A group delay difference between both receivers, defined as , is equivalent to a linear phase shift in the frequency domain. As a consequence, the integrand of (A1) can be written as the product of two filter responses with equal group delay multiplied by . After some mathematical operations, it is easily found that the fringe washing function becomes:where is the fringe washing function corresponding to filters with equal group delay. As expected, this result is compatible with adding a delay of to (8).
- Changing the reference frequency of the fringe washing function only adds a linear term to the phase, with no change in the amplitude:
- If the product can be approximated by a rectangular function of width B centered at , then the fringe washing function referenced to this frequency becomes:simplifying to just if . For filters centered at another frequency, (A5) applies.
- Independent of the reference frequency, the fringe washing function at the origin is:which is complex in general and normally has an amplitude close to unity (if the filters are similar enough).
References
- Barré, H.; Duesmann, B.; Kerr, Y. SMOS: The mission and the system. IEEE Trans. Geosci. Remote Sens. 2008, 46, 587–593. [Google Scholar] [CrossRef]
- McMullan, K.; Brown, M.; Martín-Neira, M.; Rits, W.; Ekholm, S.; Marti, J.; Lemanzyk, J. SMOS: The payload. IEEE Trans. Geosci. Remote Sens. 2008, 46, 594–605. [Google Scholar] [CrossRef]
- Martín-Neira, M.; Oliva, R.; Corbella, I.; Torres, F.; Duffo, N.; Durán, I.; Kainulainen, J.; Closa, J.; Zurita, A.; Cabot, F.; et al. SMOS instrument performance and calibration after six years in orbit. Remote Sens. Environ. 2016, 180, 19–39. [Google Scholar] [CrossRef]
- Martín-Neira, M.; Goutoule, J.M. MIRAS A Two-Dimensional Aperture-Synthesis Radiometer for Soil Moisture and Ocean Salinity Observations. ESA Bull. 1997, 95–104. [Google Scholar]
- Zurita, A.M.; Corbella, I.; Martín-Neira, M.; Plaza, M.A.; Torres, F.; Benito, F.J. Towards a SMOS Operational Mission: SMOSOps-Hexagonal. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1769–1780. [Google Scholar] [CrossRef]
- Corbella, I.; Duffo, N.; Vall-llossera, M.; Camps, A.; Torres, F. The visibility function in interferometric aperture synthesis radiometry. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1677–1682. [Google Scholar] [CrossRef]
- Dugundji, J. Envelopes and Pre-Envelopes of Real Waveforms. IRE Trans. Inf. Theory 1958, 4, 53–57. [Google Scholar] [CrossRef]
- Franks, L.E. Signal Theory; Prentice Hall, Inc.: Upper Saddle River, NJ, USA, 1969. [Google Scholar]
- Corbella, I.; Torres, F.; Camps, A.; Colliander, A.; Martín-Neira, M.; Ribó, S.; Rautiainen, K.; Duffo, N.; Vall-llossera, M. MIRAS End-to-End Calibration. Application to SMOS L1 Processor. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1126–1134. [Google Scholar] [CrossRef]
- Corbella, I.; Torres, F.; Duffo, N.; Martín-Neira, M.; González-Gambau, V.; Camps, A.; Vall-llossera, M. On-Ground Characterization of the SMOS Payload. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3123–3133. [Google Scholar] [CrossRef]
- Corbella, I.; Torres, F.; Duffo, N.; Duran, I.; González-Gambau, V.; Martín-Neira, M. Wide Field of View Microwave Interferometric Radiometer Imaging. Remote Sens. 2019, 11, 682. [Google Scholar] [CrossRef]
- Camps, A.; Torres, F.; Corbella, I.; Bará, J.; Monzón, F. Automatic calibration of channels frequency response in interferometric radiometers. Electron. Lett. 1999, 35, 115–116. [Google Scholar] [CrossRef]
- Hagen, J.B.; Farley, D.T. Digital-correlation techniques in radio science. Radio Sci. 1973, 8, 775–784. [Google Scholar] [CrossRef]
- Corbella, I.; Camps, A.; Torres, F.; Bará, J. Analysis of noise injection networks for interferometric radiometer calibration. IEEE Trans. Microw. Theory Tech. 2000, 48, 545–552. [Google Scholar] [CrossRef]
- Piironen, P. PMS Offset Determination Using an IF Attenuator; Technical Note 14629/00/NL/SF; ESA-ESTEC: Noordwijk, The Netherlands, 2002. [Google Scholar]
- Torres, F.; Corbella, I.; Camps, A.; Duffo, N.; Vall-llossera, M.; Beraza, S.; Martín-Neira, M. Denormalization of Visibilities for In-orbit Calibration of Interferometric Radiometers. In Proceedings of the International Geoscience and Remote Sensing Symposium, IGARSS 2005, Seoul, Korea, 25–29 July 2005; Volume VIII, pp. 5554–5557. [Google Scholar]
- Corbella, I.; Torres, F.; Camps, A.; Bará, J.; Duffo, N.; Vall-llossera, M. L-band aperture synthesis radiometry: Hardware requirements and system performance. In Proceedings of the International Geoscience and Remote Sensing Symposium, IGARSS 2000, Honolulu, HI, USA, 24–28 July 2000; Volume 7, pp. 2975–2977. [Google Scholar]
- Brown, M.; Torres, F.; Corbella, I.; Colliander, A. SMOS calibration. IEEE Trans. Geosci. Remote Sens. 2008, 46, 646–658. [Google Scholar] [CrossRef]




| DUT | Offset (Hz) | Gain (Hz/K) | Noise Figure (dB) |
|---|---|---|---|
| ALR01 H | 8503 | 9.56 | 1.02 |
| ALR01 V | 7143 | 11.59 | 0.99 |
| ALR02 H | 7399 | 9.58 | 1.20 |
| ALR02 V | 7306 | 7.92 | 1.18 |
| Baseline | Amplitude | Phase (deg) |
|---|---|---|
| H1-V1 | 0.9876 | −6.13 |
| H1-H2 | 0.9939 | −159.44 |
| H1-V2 | 0.9694 | −106.37 |
| V1-H2 | 0.9982 | −153.75 |
| V1-V2 | 0.9961 | −100.42 |
| H2-V2 | 0.9928 | 53.67 |
| Baseline | A-1 (cu) | B (MHz) | C (ns) | E (kHz) |
|---|---|---|---|---|
| H1-V1 | 100.163 | 19.688 | 3.945 | 600.290 |
| H1-H2 | 19.602 | 18.398 | 1.875 | 359.365 |
| H1-V2 | 191.575 | 18.733 | 5.723 | 177.256 |
| V1-H2 | 29.676 | 18.976 | −2.236 | 173.539 |
| V1-V2 | 18.610 | 19.112 | 1.759 | 42.783 |
| H2-V2 | 104.440 | 19.036 | 4.166 | −99.463 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Corbella, I.; Martín Neira, M.; Vilaseca, R.; Catalan, A.; Torres, F.; Suess, M. A Novel Digital IQ Demodulation for Interferometric Radiometers. Remote Sens. 2021, 13, 1156. https://doi.org/10.3390/rs13061156
Corbella I, Martín Neira M, Vilaseca R, Catalan A, Torres F, Suess M. A Novel Digital IQ Demodulation for Interferometric Radiometers. Remote Sensing. 2021; 13(6):1156. https://doi.org/10.3390/rs13061156
Chicago/Turabian StyleCorbella, Ignasi, Manuel Martín Neira, Roger Vilaseca, Albert Catalan, Francesc Torres, and Martin Suess. 2021. "A Novel Digital IQ Demodulation for Interferometric Radiometers" Remote Sensing 13, no. 6: 1156. https://doi.org/10.3390/rs13061156
APA StyleCorbella, I., Martín Neira, M., Vilaseca, R., Catalan, A., Torres, F., & Suess, M. (2021). A Novel Digital IQ Demodulation for Interferometric Radiometers. Remote Sensing, 13(6), 1156. https://doi.org/10.3390/rs13061156







