Unsupervised Building Instance Segmentation of Airborne LiDAR Point Clouds for Parallel Reconstruction Analysis
Abstract
1. Introduction
2. Building Instance Segmentation
2.1. Definition of Building Types
2.2. Building Point Clouds Segmentation
2.2.1. The Improved kd Tree Shared Nearest Neighbor Clustering Algorithm
2.2.2. Model Consistency Evaluation Method
2.2.3. The Improved Minimum Bounding Rectangle (MBR) Algorithm
| Algorithm 1. The improved minimum bounding rectangle (MBR) algorithm. |
| 1. Notation: |
| 2. : current building point cloud instance |
| 3. : current rotation angle |
| 4. : The degree of increase or decrease for each rotation |
| 5. : area of building point cloud cluster bounding rectangle without rotation |
| 6. : area of last rotated building point cloud cluster bounding rectangle |
| 7. : area of next rotated building point cloud cluster bounding rectangle |
| 8. , : improved MBR length and width |
| 9. Input: |
| 10. Output: , |
| 1 initialization: , |
| 2 Calculate area of building point cloud cluster bounding rectangle |
| 3 Rotate point cloud degrees and calculate area of rotated point cloud cluster bounding rectangle |
| 4 if do |
| 5 for to 90 do |
| 6 Rotate point cloud degrees and calculate area of current rotated building point cloud cluster; |
| 7 if do |
| 8 ; |
| 9 else |
| 10 ; Rotate point cloud degrees and calculate length and width of building point cloud cluster bounding rectangle |
| 11 ; |
| 12 end if |
| 13 end for |
| 14 else |
| 15 for −90 do |
| 16 Rotate point cloud degrees and calculate area by current building point cloud cluster |
| 17 if do |
| 18 ; |
| 19 else |
| 20 ; Rotate point cloud degrees and calculate length and width of building point cloud cluster bounding rectangle |
| 21 ; |
| 22 end if |
| 23 end for |
| 24 end if |
2.3. Merging of Building Façade Point Clouds

2.4. Recognition and Merging of Roof Detail Instance
2.5. Merging of Isolated Point Cloud Clusters
3. Experiments and Analysis
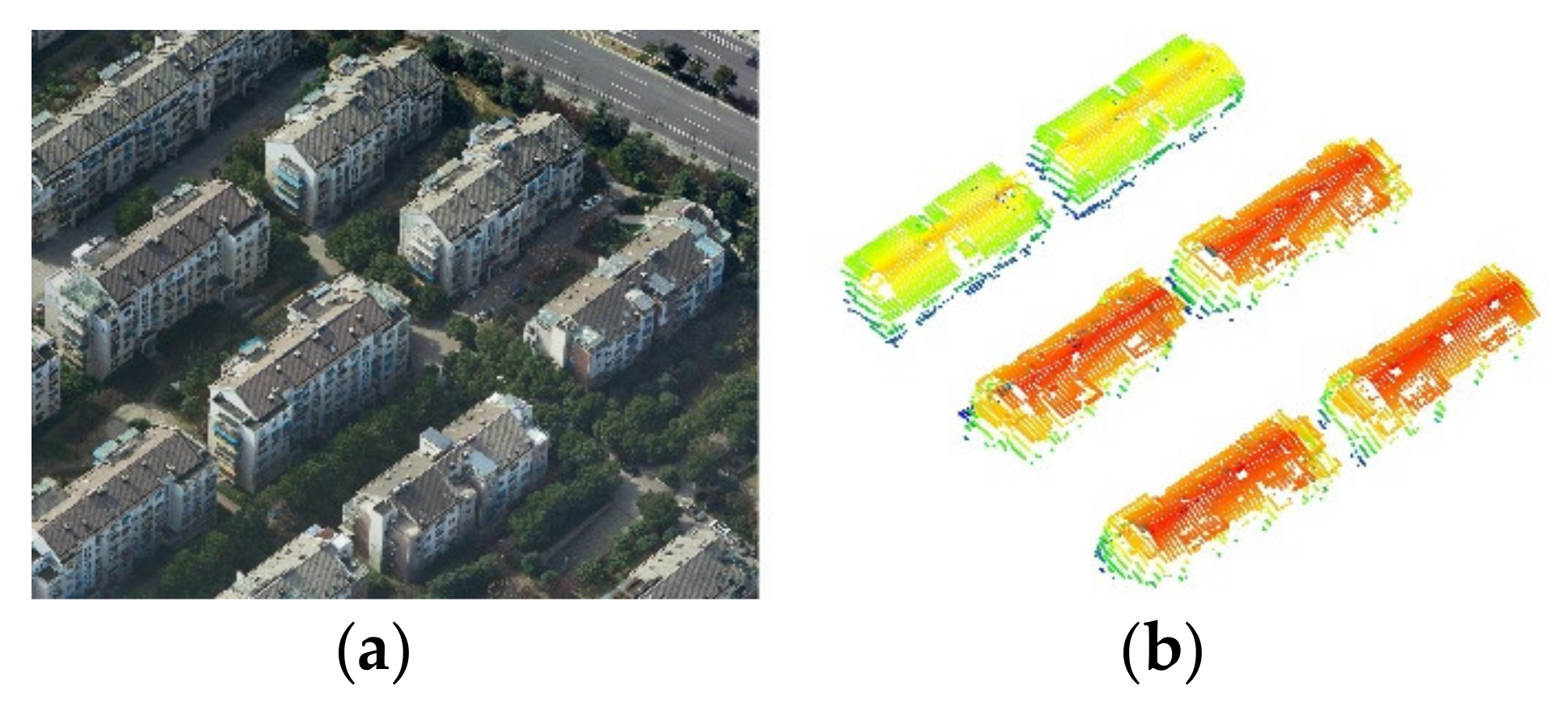
3.1. Datasets Description
3.2. Evaluation Criteria
3.3. Parameter Settings
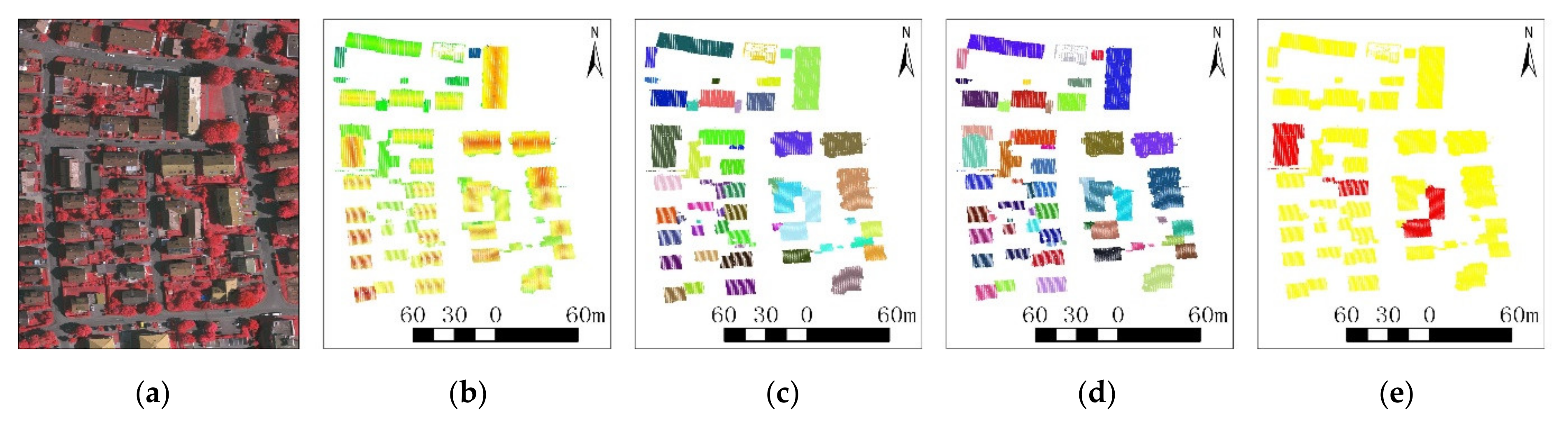
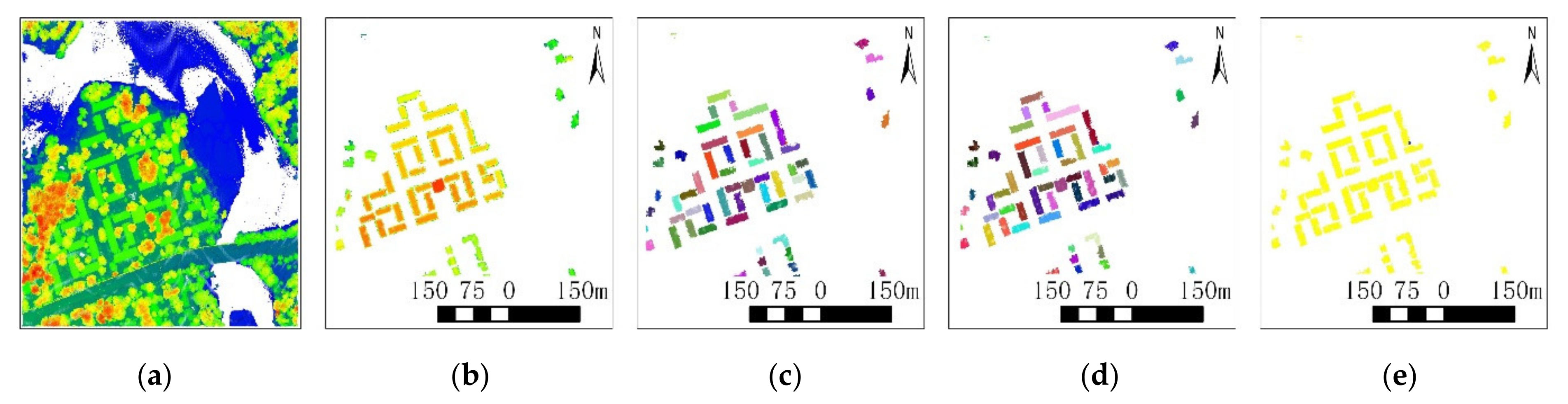
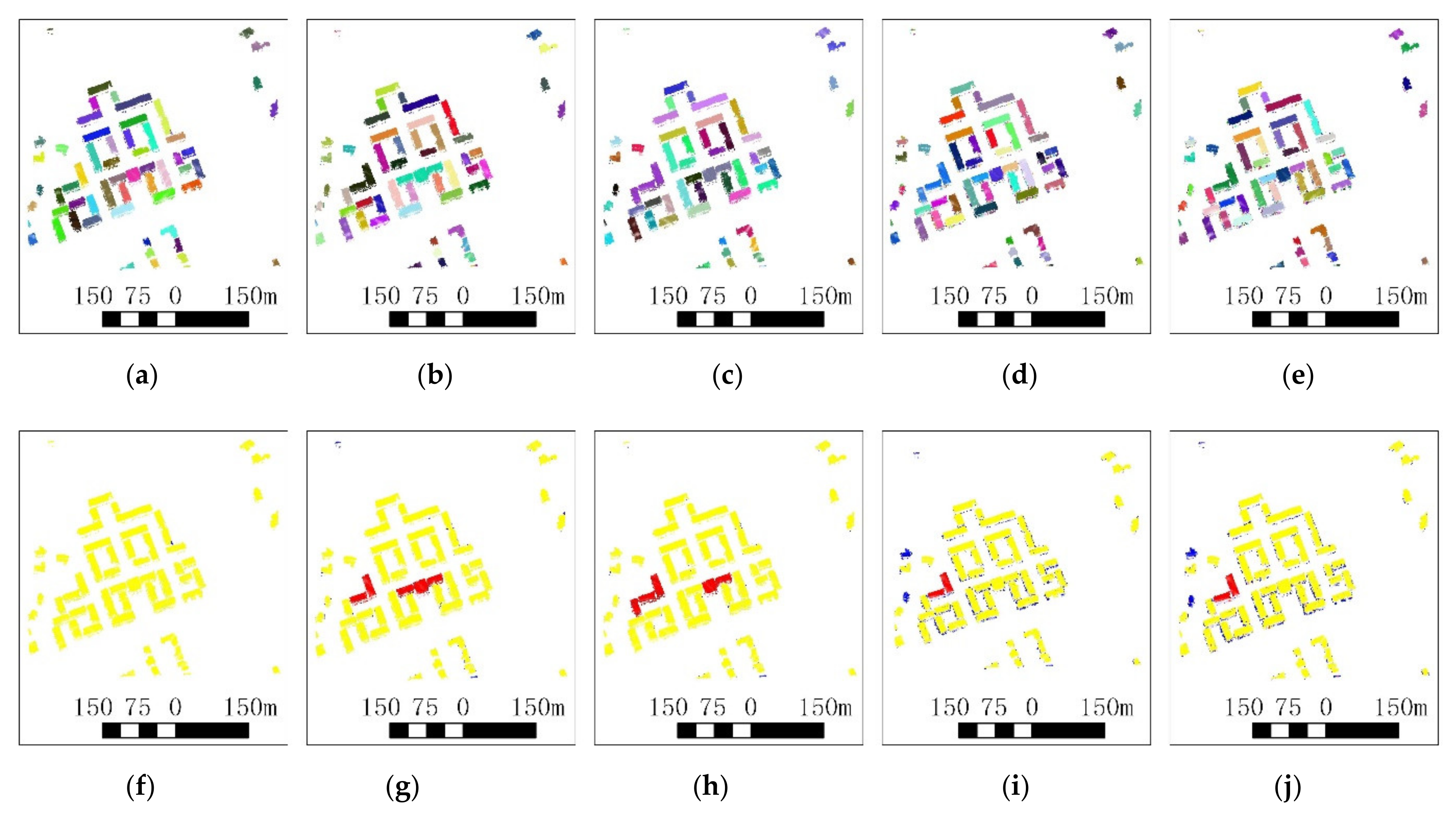
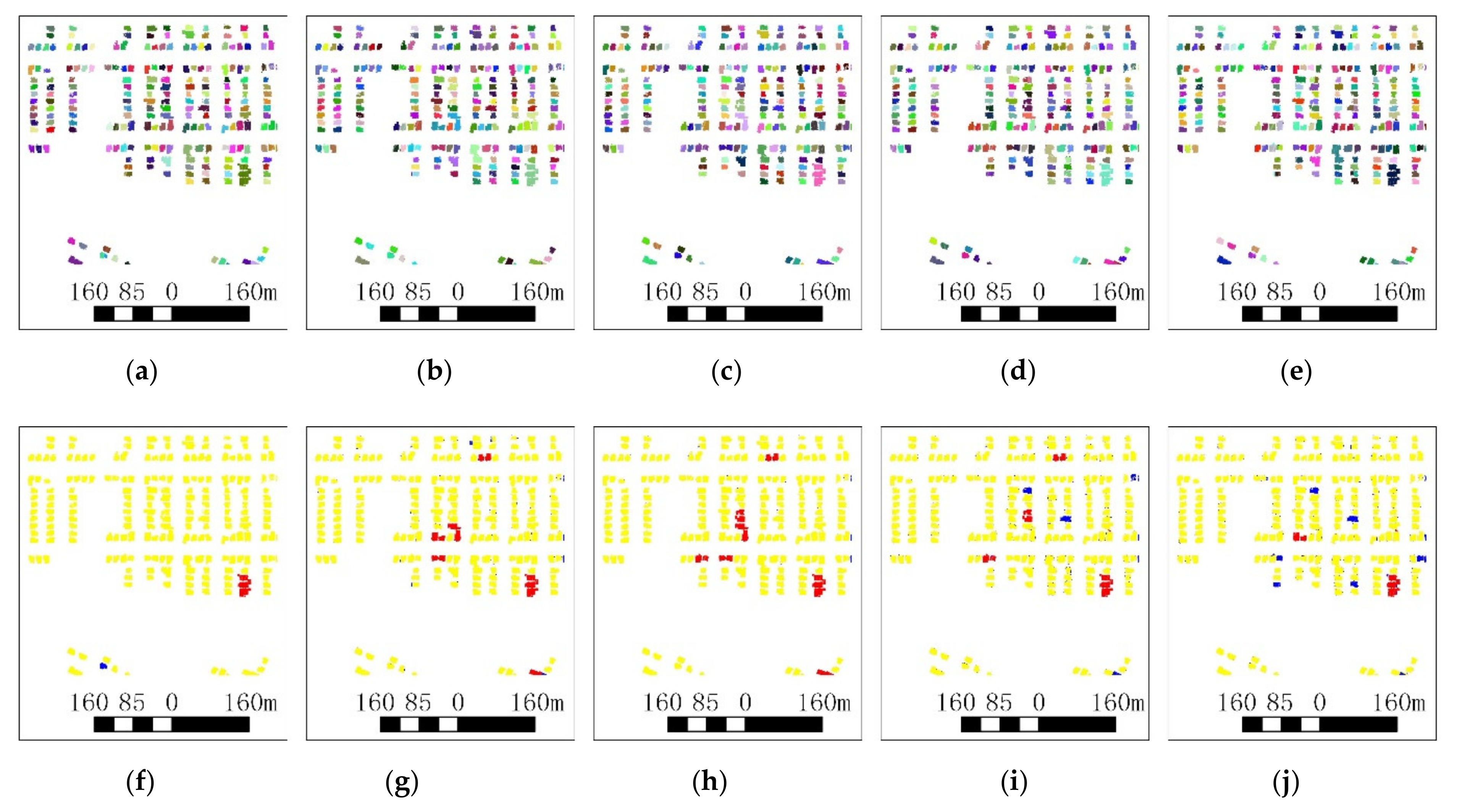
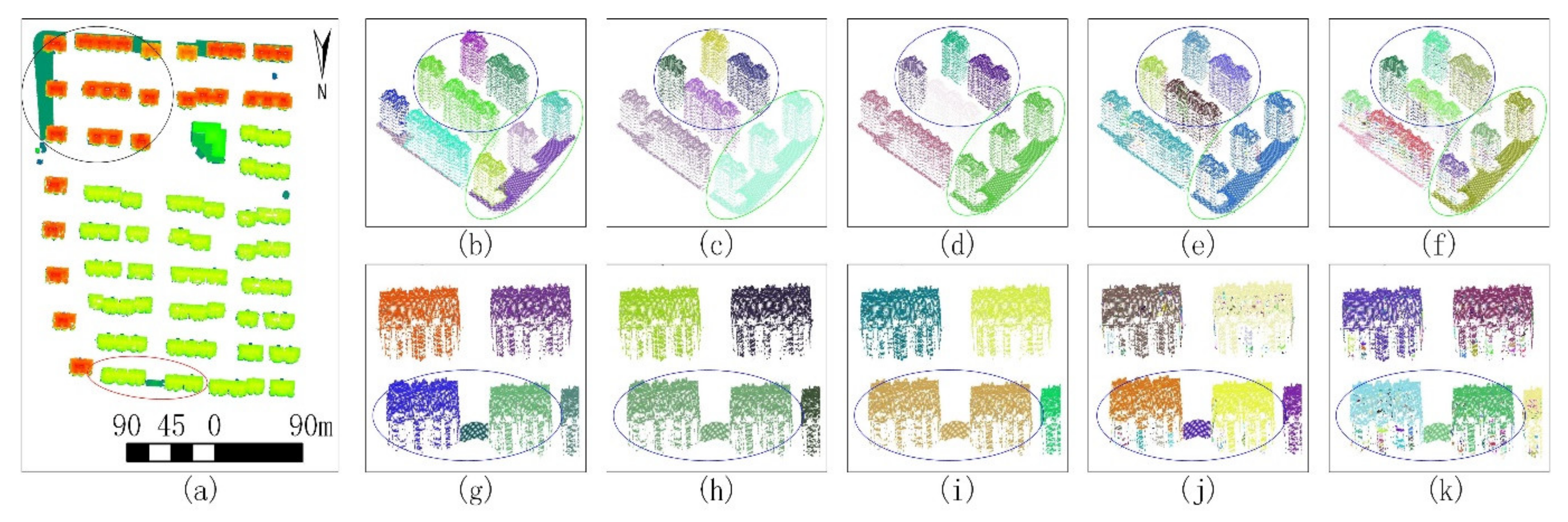
3.4. Experimental Results
3.5. Performance Comparison
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Baltsavias, E.P. A comparison between photogrammetry and laser scanning. ISPRS J. Photogramm. Remote Sens. 1999, 54, 83–94. [Google Scholar] [CrossRef]
- Wehr, A.; Lohr, U. Airborne laser scanning-an introduction and overview. ISPRS J. Photogramm. Remote Sens. 1999, 54, 68–82. [Google Scholar] [CrossRef]
- Zhang, Y.; Shen, X. Direct georeferencing of airborne LiDAR data in national coordinates. ISPRS J. Photogramm. Remote Sens. 2013, 84, 43–51. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, X. Filtering airborne LiDAR data by embedding smoothness-constrained segmentation in progressive TIN densification. ISPRS J. Photogramm. Remote Sens. 2013, 81, 44–59. [Google Scholar] [CrossRef]
- Zhao, X.; Guo, Q.; Su, Y.; Xue, B. Improved progressive TIN densification filtering algorithm for airborne LiDAR data in forested areas. ISPRS J. Photogramm. Remote Sens. 2016, 117, 79–91. [Google Scholar] [CrossRef]
- Kang, X.; Liu, J.; Lin, X. Streaming Progressive TIN Densification Filter for Airborne LiDAR Point Clouds Using Multi-Core Architectures. Remote Sens. 2014, 6, 7212–7232. [Google Scholar] [CrossRef]
- Sithole, G.; Vosselman, G. Experimental comparison of filter algorithms for bare-Earth extraction from airborne laser scanning point clouds. ISPRS J. Photogramm. Remote Sens. 2004, 59, 85–101. [Google Scholar] [CrossRef]
- Hackel, T.; Savinov, N.; Ladicky, L.; Wegner, J.D.; Schindler, K.; Pollefeys, M. Semantic3D.net: A new Large-scale Point Cloud Classification Benchmark. arXiv 2017, arXiv:1704.03847. [Google Scholar] [CrossRef]
- Uy, M.A.; Pham, Q.; Hua, B.; Nguyen, T.; Yeung, S. Revisiting Point Cloud Classification: A New Benchmark Dataset and Classification Model on Real-World Data. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–3 November 2019. [Google Scholar]
- Benshabat, Y.; Lindenbaum, M.; Fischer, A. 3D Point Cloud Classification and Segmentation using 3D Modified Fisher Vector Representation for Convolutional Neural Networks. arXiv 2017, arXiv:1711.08241. [Google Scholar]
- Liu, X.; Zhang, Y.; Ling, X.; Wan, Y.; Li, Q. Topolap: Topology recovery for building reconstruction by deducing the relationships between linear and planar primitives. Remote Sens. 2019, 11, 1372. [Google Scholar] [CrossRef]
- Cao, R.; Zhang, Y.; Liu, X.; Zhao, Z. 3d building roof reconstruction from airborne lidar point clouds: A framework based on a spatial database. Int. J. Geogr. Inf. Sci. 2017, 31, 1359–1380. [Google Scholar] [CrossRef]
- Filip, B.; Jantien, S.; Hugo, L.; Sisi, Z.; Çöltekin, A. Applications of 3d city models: State of the art review. ISPRS Int. J. Geo-Inf. 2015, 4, 2842–2889. [Google Scholar]
- Haala, N.; Kada, M. An update on automatic 3D building reconstruction. ISPRS J. Photogramm. Remote Sens. 2010, 65, 570–580. [Google Scholar] [CrossRef]
- Wang, R.; Peethambaran, J.; Dong, C. LiDAR Point Clouds to 3D Urban Models: A Review. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 606–627. [Google Scholar] [CrossRef]
- Ferraz, A.; Bretar, F.; Jacquemoud, S.; Gonçalves, G.; Pereira, L.; Tomé, M.; Soares, P. 3-D mapping of a multi-layered Mediterranean forest using ALS data. Remote Sens. Environ. 2012, 121, 210–223. [Google Scholar] [CrossRef]
- Dai, W.; Yang, B.; Dong, Z.; Shaker, A. A new method for 3d individual tree extraction using multispectral airborne lidar point clouds. ISPRS J. Photogramm. Remote Sens. 2018, 144, 400–411. [Google Scholar] [CrossRef]
- Yang, B.; Dai, W.; Dong, Z.; Liu, Y. Automatic Forest Mapping at Individual Tree Levels from Terrestrial Laser Scanning Point Clouds with a Hierarchical Minimum Cut Method. Remote Sens. 2016, 8, 372. [Google Scholar] [CrossRef]
- Wang, D. Unsupervised semantic and instance segmentation of forest point clouds. ISPRS J. Photogramm. Remote Sens. 2020, 165, 86–97. [Google Scholar] [CrossRef]
- Liang, X.; Hyyppa, J.; Kaartinen, H.; Lehtomaki, M.; Pyorala, J.; Pfeifer, N.; Wang, Y. International benchmarking of terrestrial laser scanning approaches for forest inventories. ISPRS J. Photogramm. Remote Sens. 2018, 144, 137–179. [Google Scholar] [CrossRef]
- Hafiz, A.M.; Bhat, G.M. A survey on instance segmentation: State of the art. Int. J. Multimed. Inf. Retr. 2020, 9, 171–189. [Google Scholar] [CrossRef]
- Wang, X.; Liu, S.; Shen, X.; Shen, C.; Jia, J. Associatively Segmenting Instances and Semantics in Point Clouds. arXiv 2019, arXiv:1902.09852. [Google Scholar]
- Jia, Z.; Gallagher, A.C.; Saxena, A.; Chen, T. 3D Reasoning from Blocks to Stability. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 905–918. [Google Scholar] [CrossRef]
- Bonde, U.; Badrinarayanan, V.; Cipolla, R. Robust Instance Recognition in Presence of Occlusion and Clutter. Lect. Notes Comput. Sci. 2014, 8690, 520–535. [Google Scholar]
- Wang, T.; He, X.; Barnes, N. Learning Structured Hough Voting for Joint Object Detection and Occlusion Reasoning. In Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013. [Google Scholar]
- Zermas, D.; Izzat, I.; Papanikolopoulos, N. Fast Segmentation of 3D Point Clouds: A Paradigm on LiDAR Data for Autonomous Vehicle Applications. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017. [Google Scholar]
- Bogoslavskyi, I.; Stachniss, C. Efficient Online Segmentation for Sparse 3D Laser Scans. Photogramm. Fernerkund. Geoinf. 2017, 85, 41–52. [Google Scholar] [CrossRef]
- Bogoslavskyi, I.; Stachniss, C. Fast Range Image-Based Segmentation of Sparse 3D Laser Scans for Online Operation. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 163–169. [Google Scholar]
- Korchev, D.; Cheng, S.; Owechko, Y.; Kim, K. On Real-Time LIDAR Data Segmentation and Classification. In Proceedings of the IPCV’13—2013 International Conference on Image Processing, Computer Vision, and Pattern Recognition, Las Vegas, VA, USA, 23–25 July 2013. [Google Scholar]
- Chen, S.; Liu, B.; Feng, C.; Vallespi-Gonzalez, C.; Wellington, C. 3D Point Cloud Processing and Learning for Autonomous Driving. IEEE Signal Process. Mag. 2020, 38, 68–86. [Google Scholar] [CrossRef]
- Kaiming, H.; Georgia, G.; Piotr, D.; Ross, G. Mask r-cnn. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 386–397. [Google Scholar]
- Stein, S.C.; Wrgtter, F.; Schoeler, M.; Papon, J.; Kulvicius, T. Convexity Based Object Partitioning for Robot Applications. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014. [Google Scholar]
- Choy, C.B.; Park, J.; Koltun, V. Fully Convolutional Geometric Features. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–3 November 2019. [Google Scholar]
- Gu, X.; Wang, Y.; Wu, C.; Lee, Y.J.; Wang, P. HPLFlowNet: Hierarchical Permutohedral Lattice FlowNet for Scene Flow Estimation on Large-Scale Point Clouds. arXiv 2017, arXiv:1906.05332. [Google Scholar]
- Liu, X.; Qi, C.R.; Guibas, L.J. FlowNet3D: Learning Scene Flow in 3D Point Clouds. arXiv 2019, arXiv:1806.01411. [Google Scholar]
- Chen, T.; Dai, B.; Wang, R.; Liu, D. Gaussian-Process-Based Real-Time Ground Segmentation for Autonomous Land Vehicles. J. Intell. Robot. Syst. 2014, 76, 563–582. [Google Scholar] [CrossRef]
- Ramiya, A.M.; Nidamanuri, R.R.; Krishnan, R. Segmentation based building detection approach from LiDAR point cloud. Egypt. J. Remote Sens. Space Sci. 2017, 20, 71–77. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, W.; Chen, Y.; Chen, M.; Yan, K. Semantic Decomposition and Reconstruction of Compound Buildings with Symmetric Roofs from LiDAR Data and Aerial Imagery. Remote Sens. 2015, 7, 13945–13974. [Google Scholar] [CrossRef]
- Matei, B.C.; Sawhney, H.S.; Samarasekera, S.; Kim, J.; Kumar, R. Building Segmentation for Densely Built Urban Regions Using Aerial LIDAR Data. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008. [Google Scholar]
- Awrangjeb, M.; Fraser, C.S. Rule-based segmentation of lidar point cloud for automatic extraction of building roof planes. ISPRS Ann. Photogramm. 2013, II-3/W3, 1–6. [Google Scholar] [CrossRef]
- Mohammad, A.; Clive, F. Automatic Segmentation of Raw LIDAR Data for Extraction of Building Roofs. Remote Sens. 2014, 6, 3716–3751. [Google Scholar]
- Sampath, A.; Shan, J. Building Boundary Tracing and Regularization from Airborne Lidar Point Clouds. Photogramm. Eng. Remote Sens. 2007, 73, 805–812. [Google Scholar] [CrossRef]
- Yan, L.; Wei, F. Single Part of Building Extraction from Dense Matching Point Cloud. Chin. J. Lasers 2018, 499, 270–277. [Google Scholar]
- Iglovikov, V.; Seferbekov, S.; Buslaev, A.; Shvets, A. Ternausnetv2: Fully convolutional network for instance segmentation. arXiv 2018, arXiv:1806.00844. [Google Scholar]
- Bertolotto, M.; Anh-Vu, V.; Linh, T.; Laefer, D.F. Octree-based region growing for point cloud segmentation. ISPRS J. Photogramm. Remote Sens. 2015, 104, 88–100. [Google Scholar]
- Ester, M. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996. [Google Scholar]
- Czerniawski, T.; Nahangi, M.; Walbridge, S.; Haas, C. Automated Removal of Planar Clutter from 3D Point Clouds for Improving Industrial Object Recognition. In Proceedings of the International Symposium in Automation and Robotics in Construction, Auburn, AL, USA, 18–21 July 2016. [Google Scholar]
- Czerniawski, T.; Sankaran, B.; Nahangi, M.; Haas, C.; Leite, F. 6D DBSCAN-based segmentation of building point clouds for planar object classification. Autom. Constr. 2018, 88, 44–58. [Google Scholar] [CrossRef]
- Jarvis, R.A.; Patrick, E.A. Clustering Using a Similarity Measure Based on Shared Near Neighbors. IEEE Trans. Comput. 2006, C-22, 1025–1034. [Google Scholar] [CrossRef]
- Ertöz, L.; Steinbach, M.; Kumar, V. Finding Clusters of Different Sizes, Shapes, and Densities in Noisy, High Dimensional Data. In Proceedings of the Third SIAM International Conference on Data Mining, San Francisco, CA, USA, 1–3 May 2003. [Google Scholar]
- Faustino, B.F.; João, M.S.; Moreira, G. kd-SNN: A Metric Data Structure Seconding the Clustering of Spatial Data. In Proceedings of the Computational Science and Its Applications—ICCSA 2014, Guimarães, Portugal, 30 June–3 July 2014. [Google Scholar]
- Delsolneux, A.; Moisan, L.; Morel, J.M. From Gestalt Theory to Image Analysis: A Probabilistic Approach; Springer: New York, NY, USA, 2008. [Google Scholar]
- Freeman, H.; Shapira, R. Determining the minimum-area encasing rectangle for an arbitrary closed curve. Commun. ACM 1975, 18, 409–413. [Google Scholar] [CrossRef]
- Chaudhuri, D.; Samal, A. A simple method for fitting of bounding rectangle to closed regions. Pattern Recognit. 2007, 40, 1981–1989. [Google Scholar] [CrossRef]
- Kwak, E.; Habib, A. Automatic representation and reconstruction of DBM from LiDAR data using Recursive Minimum Bounding Rectangle. J. Photogramm. Remote Sens. 2017, 93, 171–191. [Google Scholar] [CrossRef]
- Cramer, M. The DGPF test on digital aerial camera evaluation—Overview and test design. Photogrammetrie Fernerkundung Geoinf. 2010, 2010, 73–82. [Google Scholar] [CrossRef] [PubMed]
- ISPRS Test Project on Urban Classification and 3D Building Reconstruction. GIM International, 2013. Available online: https://www.isprs.org/news/newsletter/03-Apr-2011/3_ISPRS_test_on_urban_object_detection_and_3D_building_reconstruction_will_be_carried_out.pdf (accessed on 15 March 2021).
- Niemeyer, J.; Rottensteiner, F.; Soergel, U. Contextual classification of lidar data and building object detection in urban areas. ISPRS J. Photogramm. Remote Sens. 2014, 87, 152–165. [Google Scholar] [CrossRef]
- Rottensteiner, F.; Sohn, G.; Jung, J.; Gerke, M.; Breitkopf, U. The ISPRS Benchmark on Urban Object Classification and 3D Building Reconstruction. In Proceedings of the XXII ISPRS Congress, Melbourne, Australia, 25 August–1 September 2012. [Google Scholar]
- Varney, N.; Asari, V.K.; Graehling, Q. DALES: A Large-scale Aerial LiDAR Data Set for Semantic Segmentation. arXiv 2020, arXiv:2004.11985. [Google Scholar]
- Wu, C.; Hu, X.; Happold, M.; Xu, Q.; Neumann, U. Geometry-Aware Instance Segmentation with Disparity Maps. arXiv 2020, arXiv:2006.07802. [Google Scholar]
- Song, W.; Haithcoat, T.L. Development of comprehensive accuracy assessment indexes for building footprint extraction. IEEE Trans. Geoence Remote Sens. 2005, 43, 402–404. [Google Scholar] [CrossRef]
- Foody, G.M. Status of land cover classification accuracy assessment. Remote Sens. Environ. 2002, 80, 185–201. [Google Scholar] [CrossRef]
- Rutzinger, M.; Rottensteiner, F.; Pfeifer, N. A comparison of evaluation techniques for building extraction from airborne laser scanning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2009, 2, 11–20. [Google Scholar] [CrossRef]
- Dong, Z.; Yang, B.; Hu, P.; Scherer, S. An efficient global energy optimization approach for robust 3d plane segmentation of point clouds. ISPRS J. Photogramm. Remote Sens. 2018, 137, 112–133. [Google Scholar] [CrossRef]










| Procedure | Parameter | Descriptor | Value | ||
|---|---|---|---|---|---|
| Ningbo | ISPRS | DALES | |||
| Building point cloud segmentation | The neighbor radius of Ikd-2DSNN algorithm | 1.5 m | 1.5 m | 1.7 m | |
| The ratio of shared neighbor number to neighbor number of Ikd-2DSNN algorithm | 0.5 | 0.5 | 0.5 | ||
| The neighbor radius of Ikd-3DSNN algorithm | 1.5 m | 1.5 m | 1.7 m | ||
| The ratio of shared neighbor number to neighbor number of Ikd-3DSNN algorithm | 0.2 | 0.2 | 0.2 | ||
| The threshold of model consistency evaluation | 0.82 | ||||
| The threshold of the angle between multi-building planes’ normal vector and horizontal direction | 30° | ||||
| Merging of building façade point clouds | The lateral dimensions of the grid | 1.5 m | 1.5 m | 1.7 m | |
| Recognition and merging of roof detail instance | The maximum threshold of building roof detail MBR width and length | 10 m | |||
| The minimum threshold of building MBR width and length | 3 m | ||||
| The maximum difference threshold between the maximum height value of roof detail instance and the height maximum value of the single-building instance with building facade point clouds | 8 m | ||||
| The minimum difference threshold between the maximum height value of roof detail instance and the height maximum value of the single-building instance with building facade point clouds | −4 m | ||||
| Data | Point | Runtime (s) | Completeness (%) | Correctness (%) | Quality (%) | |
|---|---|---|---|---|---|---|
| Dataset 1 | 139,997 | 26.99 | 100.00 | 100.00 | 100.00 | |
| 100.00 | 100.00 | 100.00 | ||||
| Dataset 2 | 676,233 | 577.66 | 98.21 | 98.21 | 96.49 | |
| 94.64 | 98.15 | 92.98 | ||||
| Dataset 3 | 69,834 | 4.94 | 100.00 | 100.00 | 100.00 | |
| 100.00 | 92.31 | 92.31 | ||||
| Dataset 4 | 77,228 | 2.38 | 98.28 | 100.00 | 98.28 | |
| 98.28 | 100.00 | 98.28 | ||||
| Dataset 5 | 45,590 | 0.80 | 99.54 | 100.00 | 99.54 | |
| 99.08 | 99.54 | 98.62 |
| Dataset | UBIS | MV | ES2D | ES3D | LCCP | |
|---|---|---|---|---|---|---|
| Dataset 1 | Completeness (%) | 100.00 | 95.00 | 90.48 | 1.65 | 1.45 |
| Correctness (%) | 100.00 | 100.00 | 100.00 | 100.00 | 94.12 | |
| Quality (%) | 100.00 | 95.00 | 90.48 | 1.56 | 1.22 | |
| Dataset 2 | Completeness (%) | 94.64 | 88.37 | 83.33 | 1.59 | 1.12 |
| Correctness (%) | 98.15 | 86.36 | 88.89 | 84.31 | 75.00 | |
| Quality (%) | 92.98 | 77.55 | 75.47 | 1.58 | 1.12 | |
| Dataset 3 | Completeness (%) | 100.00 | 83.33 | 71.43 | 24.73 | 17.02 |
| Correctness (%) | 92.31 | 80.65 | 78.13 | 90.00 | 90.57 | |
| Quality (%) | 92.31 | 69.44 | 59.52 | 24.06 | 16.72 | |
| Dataset 4 | Completeness (%) | 98.28 | 37.14 | 49.53 | 4.70 | 5.22 |
| Correctness (%) | 100.00 | 94.55 | 96.36 | 89.83 | 89.83 | |
| Quality (%) | 98.28 | 36.36 | 48.62 | 4.67 | 5.19 | |
| Dataset 5 | Completeness (%) | 99.08 | 71.53 | 89.87 | 32.85 | 37.23 |
| Correctness (%) | 99.54 | 97.17 | 96.68 | 97.63 | 98.10 | |
| Quality (%) | 98.62 | 70.07 | 87.18 | 32.59 | 36.96 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Yang, W.; Liu, X.; Wan, Y.; Zhu, X.; Tan, Y. Unsupervised Building Instance Segmentation of Airborne LiDAR Point Clouds for Parallel Reconstruction Analysis. Remote Sens. 2021, 13, 1136. https://doi.org/10.3390/rs13061136
Zhang Y, Yang W, Liu X, Wan Y, Zhu X, Tan Y. Unsupervised Building Instance Segmentation of Airborne LiDAR Point Clouds for Parallel Reconstruction Analysis. Remote Sensing. 2021; 13(6):1136. https://doi.org/10.3390/rs13061136
Chicago/Turabian StyleZhang, Yongjun, Wangshan Yang, Xinyi Liu, Yi Wan, Xianzhang Zhu, and Yuhui Tan. 2021. "Unsupervised Building Instance Segmentation of Airborne LiDAR Point Clouds for Parallel Reconstruction Analysis" Remote Sensing 13, no. 6: 1136. https://doi.org/10.3390/rs13061136
APA StyleZhang, Y., Yang, W., Liu, X., Wan, Y., Zhu, X., & Tan, Y. (2021). Unsupervised Building Instance Segmentation of Airborne LiDAR Point Clouds for Parallel Reconstruction Analysis. Remote Sensing, 13(6), 1136. https://doi.org/10.3390/rs13061136






