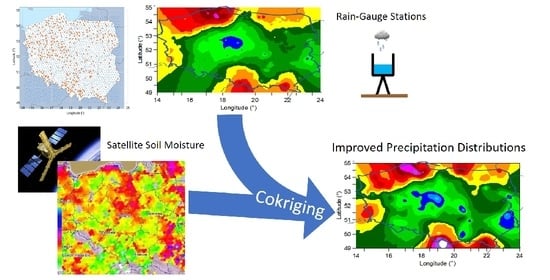
Improvement of Spatial Interpolation of Precipitation Distribution Using Cokriging Incorporating Rain-Gauge and Satellite (SMOS) Soil Moisture Data
Abstract
1. Introduction
2. Study Area and Data Used
3. Methodology
3.1. Semivariograms and Cross-Semivariograms
- −
- spherical model:
- −
- exponential model:
- −
- Gaussian model:
3.2. Interpolation Methods
3.2.1. Inverse Distance Weighting
3.2.2. Ordinary Kriging
3.2.3. Ordinary Cokriging (OCK)
4. Results
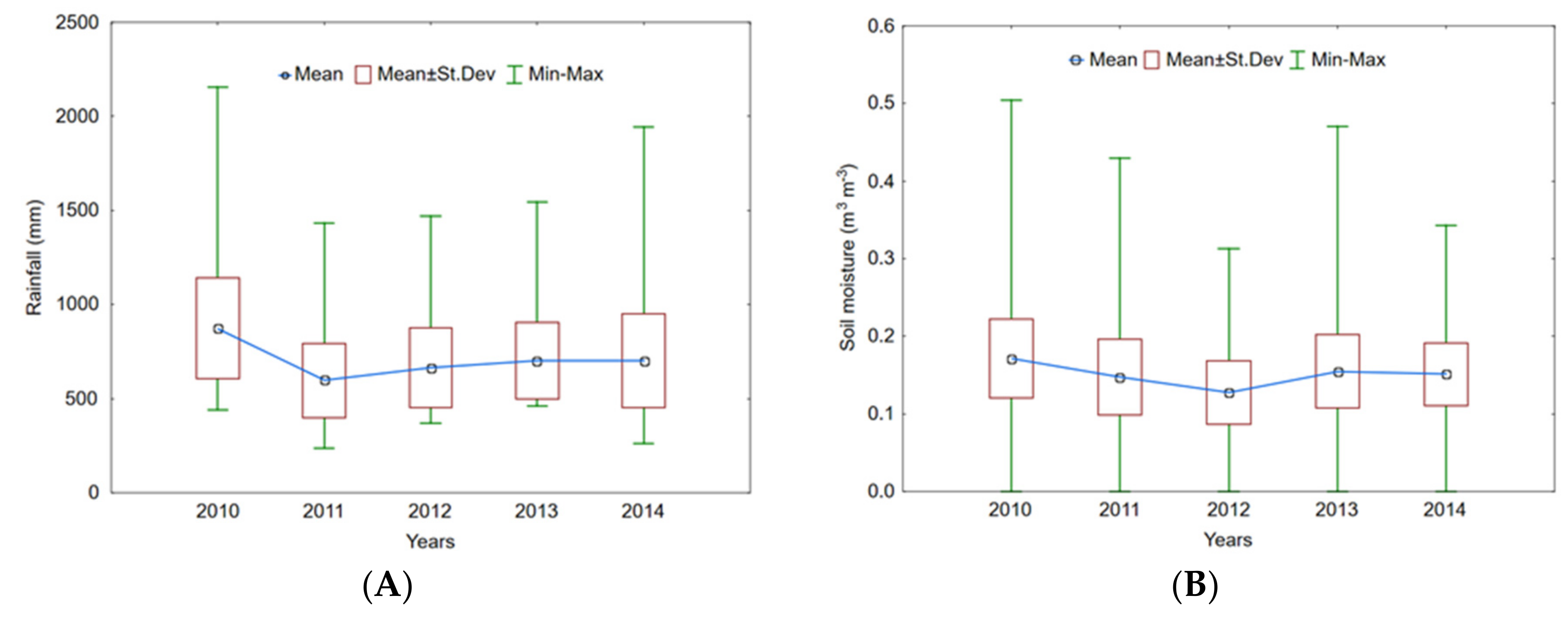
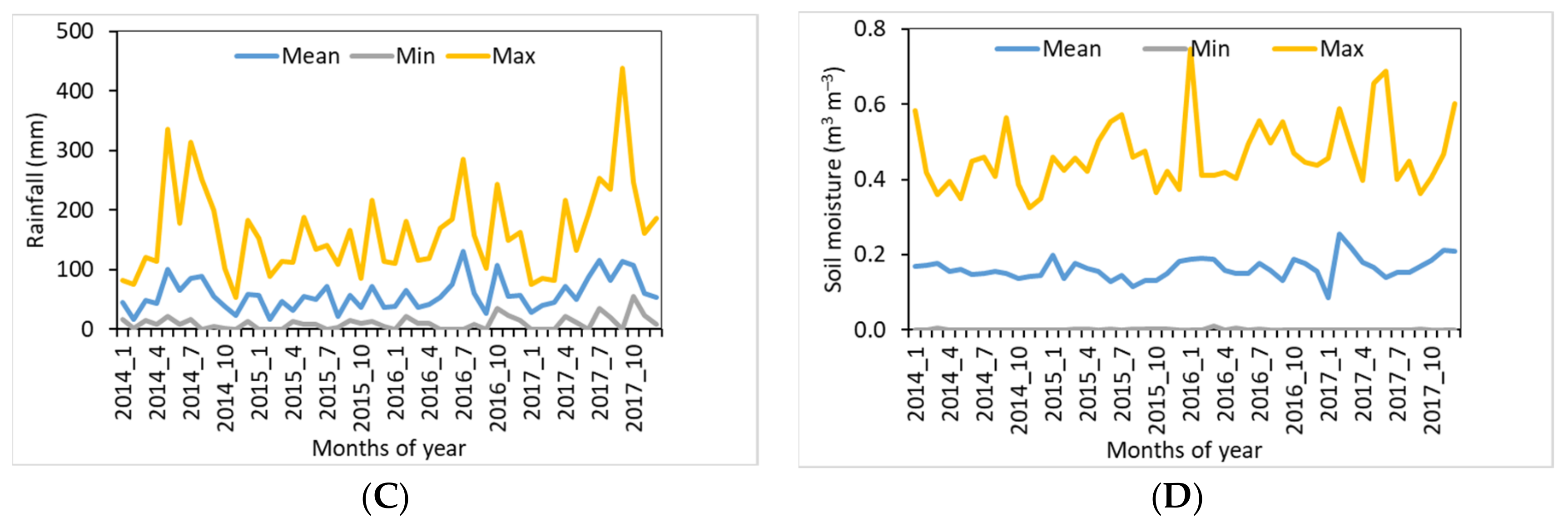
4.1. Statistics of Rain-Gauge Data
4.2. Correlation Analysis
4.3. Semivariogram and Cross-Variogram Models
4.4. Comparison of the Interpolation Methods and Cross-Validation
4.5. Maps of Precipitations
5. Discussion
6. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rivas-Tabares, D.; Tarquis, A.M.; Willaarts, B.; De Miguel, Á. An accurate evaluation of water availability in sub-arid Mediterranean watersheds through SWAT: Cega-Eresma-Adaja. Agric. Water Manag. 2019, 212, 211–225. [Google Scholar] [CrossRef]
- Kalubowila, P.; Lokupitiya, E.; Halwatura, D.; Jayathissa, G. Threshold rainfall ranges for landslide occurrence in Matara district of Sri Lanka and findings on community emergency preparedness. Int. J. Disaster Risk Reduct. 2021, 52, 101944. [Google Scholar] [CrossRef]
- Moral, F.J. Comparison of different geostatistical approaches to map climate variables: Application to precipitation. Int. J. Climatol. 2010, 30, 620–631. [Google Scholar] [CrossRef]
- Delbari, M.; Afrasiab, P.; Jahani, S. Spatial interpolation of monthly and annual rainfall in northeast of Iran. Meteorol. Atmos. Phys. 2013, 122, 103–113. [Google Scholar] [CrossRef]
- Ly, S.; Charles, C.; Degré, A. Different methods for spatial interpolation of rainfall data for operational hydrology and hydrological modeling at watershed scale: A review. Biotechnol. Agron. Soc. Environ. 2013, 17, 392–406. [Google Scholar]
- Wu, H.; Adler, R.F.; Tian, Y.; Huffman, G.J.; Li, H.; Wang, J. Real-time global flood estimation using satellite-based precipitation and a coupled land surface and routing model. Water Resour. Res. 2014, 50, 2693–2717. [Google Scholar] [CrossRef]
- Dao, D.A.; Kim, S.; Kim, T.-W.; Kim, D. Influence of rain gauge density and temporal resolution on the performance of conditional merging method. J. Korean Soc. Hazard Mitig. 2019, 19, 41–51. [Google Scholar] [CrossRef]
- Fernández, J.E. Plant-based methods for irrigation scheduling of woody crops. Horticulturae 2017, 3, 35. [Google Scholar] [CrossRef]
- Fernández, J.E.; Alcon, F.; Diaz-Espejo, A.; Hernandez-Santana, V.; Cuevas, M.V. Water use indicators and economic analysis for on-farm irrigation decision: A case study of a super high density olive tree orchard. Agric. Water Manag. 2020, 233, 106074. [Google Scholar] [CrossRef]
- Rinaldo, A.; Bertuzzo, E.; Mari, L.; Righetto, L.; Blokesch, M.; Gatto, M.; Casagrandi, R.; Murray, M.; Vesenbeckh, S.M.; Rodriguez-Iturbe, I. Reassessment of the 2010–2011 Haiti cholera outbreak and rainfall-driven multiseason projections. Proc. Natl. Acad. Sci. USA 2012, 109, 6602–6607. [Google Scholar] [CrossRef]
- Soane, B.D.; Ball, B.C.; Arvidsson, J.; Basch, G.; Moreno, F.; Roger-Estrade, J. No-till in northern, western and south-western Europe: A review of problems and opportunities for crop production and the environment. Soil Till. Res. 2012, 118, 66–87. [Google Scholar] [CrossRef]
- Carranza, C.; Benninga, H.; van der Velde, R.; van der Ploeg, M. Monitoring agricultural field trafficability using Sentinel-1. Agric. Water Manag. 2019, 224, 105698. [Google Scholar] [CrossRef]
- Morel, J.; Begue, A.; Todoroff, P.; Martine, J.; Lebourgeois, V.; Petit, M. Coupling a sugarcane crop model with the remotely sensed time series of fIPAR to optimise the yield estimation. Eur. J. Agron. 2014, 61, 60–68. [Google Scholar] [CrossRef]
- Thaler, S.; Brocca, L.; Ciabatta, L.; Eitzinger, J.; Hahn, S.; Wagner, W. Effects of different spatial precipitation input data on crop model outputs under a Central European climate. Atmosphere 2018, 9, 290. [Google Scholar] [CrossRef]
- Adhikary, S.K.; Muttil, N.; Yilmaz, A.G. Cokriging for enhanced spatial interpolation of rainfall in two Australian catchments. Hydrol. Process. 2017, 31, 2143–2161. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Al-Yaari, A.; Rodriguez-Fernandez, N.; Parrens, M.; Molero, B.; Leroux, D.; Bircher, S.; Mahmoodi, A.; Mialon, A.; Richaume, P.; et al. Overview of SMOS performance in terms of global soil moisture monitoring after six years in operation. Remote Sens. Environ. 2016, 180, 40–63. [Google Scholar] [CrossRef]
- Lanza, L.G.; Vuerich, E. The WMO field intercomparison of rain intensity gauges. Atmos. Res. 2009, 94, 534–543. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistical approaches for incorporating elevation into the spatial interpolation of rainfall. J. Hydrol. 2000, 228, 113–129. [Google Scholar] [CrossRef]
- Mirás Avalos, J.M.; Paz González, A.; Vidal Vázquez, E.; Sande Fouz, P. Mapping monthly rainfall data in Galicia (NW Spain) using inverse distances and geostatistical methods. Adv. Geosci. 2007, 10, 51–57. [Google Scholar] [CrossRef][Green Version]
- Adhikary, S.K.; Muttil, N.; Yilmaz, A.G. Ordinary kriging and genetic programming for spatial estimation of rainfall in the Middle Yarra River catchment, Australia. Hydrol. Res. 2016, 47, 1182–1197. [Google Scholar] [CrossRef]
- Salleh, N.S.A.; Aziz, M.K.B.M.; Adzhar, N. Optimal design of a rain gauge network models: Review paper. J. Phys. Conf. Ser. 2019, 1366. [Google Scholar]
- Hu, Q.; Li, Z.; Wang, L.; Huang, Y.; Wang, Y.; Li, L. Rainfall Spatial Estimations: A Review from Spatial Interpolation to Multi-Source Data Merging. Water 2019, 11, 579. [Google Scholar] [CrossRef]
- Lu, G.Y.; Wong, D.W. An adaptive inverse-distance weighting spatial interpolation technique. Comput. Geosci. 2008, 34, 1044–1055. [Google Scholar] [CrossRef]
- Chen, F.W.; Liu, C.W. Estimation of the spatial rainfall distribution using inverse distance weighting (IDW) in the middle of Taiwan. Paddy Water Environ. 2012, 10, 209–222. [Google Scholar] [CrossRef]
- Isaaks, E.H.; Srivastava, R.M. Spatial continuity measures for probabilistic and deterministic geostatistics. Math. Geol. 1988, 20, 313–341. [Google Scholar] [CrossRef]
- Zawadzki, J.; Cieszewski, C.J.; Zasada, M.; Lowe, R. Applying geostatistics for investigations of forest ecosystems using remote sensing imagery. Silva Fenn. 2005, 39, 599–617. [Google Scholar] [CrossRef]
- Karahan, G.; Erşahin, S. Geostatistics in characterizing spatial variability of forest ecosystems. Eur. J. Sci. 2018, 6, 9–22. [Google Scholar]
- Liu, S.; Li, Y.; Pauwels, V.R.N.; Walker, J.P. Impact of rain gauge quality control and interpolation on streamflow simulation: An application to the Warwick catchment, Australia. Front Earth Sci. 2018, 5, 114. [Google Scholar] [CrossRef]
- Pellicone, G.; Caloiero, T.; Modica, G.; Guagliardi, I. Application of several spatial interpolation techniques to monthly rainfall data in the Calabria region (southern Italy). Int. J. Climatol. 2018, 9, 3651–3666. [Google Scholar] [CrossRef]
- Chen, T.; Ren, L.; Yuan, F.; Yang, X.; Jiang, S.; Tang, T.; Liu, Y.; Zhao, C.; Zhang, L. Comparison of spatial interpolation schemes for rainfall data and application in hydrological modelling. Water 2017, 9, 342. [Google Scholar] [CrossRef]
- Sadeghi, S.H.; Nouri, H.; Faramarzi, M. Assessing the spatial distribution of rainfall and the effect of altitude in Iran (Hamadan Province). Air Soil Water Res. 2017, 10, 1–7. [Google Scholar] [CrossRef]
- Berndt, C.; Haberlandt, U. Spatial interpolation of climate variables in Northern Germany—Influence of temporal resolution and network density. J. Hydrol. Reg. Stud. 2018, 15, 184–202. [Google Scholar] [CrossRef]
- Ly, S.; Charles, C.; Degré, A. Geostatistical interpolation of daily rainfall at catchment scale: The use of several variogram models in the Ourthe and Ambleve catchments, Belgium. Hydrol. Earth Syst. Sci. 2011, 15, 2259–2274. [Google Scholar] [CrossRef]
- Sideris, I.V.; Gabella, M.; Erdin, R.; Germann, U. Real-time radar-rain-gauge merging using spatio-temporal co-kriging with external drift in the alpine terrain of Switzerland. Q. J. R. Meteor. Soc. 2014, 140, 1097–1111. [Google Scholar] [CrossRef]
- Verdin, A.; Rajagopalan, B.; Kleiber, W.; Funk, C. A Bayesian kriging approach for blending satellite and ground precipitation observations. Water Resour. Res. 2015, 51. [Google Scholar] [CrossRef]
- Kerr, Y.H. Soil moisture from space: Where are we? Hydrogeol. J. 2007, 15, 117–120. [Google Scholar] [CrossRef]
- Wagner, W.; Blöschl, G.; Pampaloni, P.; Calvet, J.C.; Bizzarri, B.; Wigneron, J.P.; Kerr, Y. Operational readiness of microwave remote sensing of soil moisture for hydrologic applications. Hydrol. Res. 2007, 38, 1–20. [Google Scholar] [CrossRef]
- McColl, K.A.; Wang, W.; Peng, B.; Akbar, R.; Short Gianotti, D.J.; Lu, H.; Pan, M.; Entekhabi, D. Global characterization of surface soil moisture dry downs. Geophys. Res. Lett. 2017, 44, 3682–3690. [Google Scholar] [CrossRef]
- McColl, K.A.; Alemohammad, S.H.; Akbar, R.; Konings, A.G.; Yueh, S.; Entekhabi, D. The global distribution and dynamics of surface soil moisture. Nat. Geosci. 2017, 10, 100–104. [Google Scholar] [CrossRef]
- Vivoni, E.R.; Tai, K.; Gochis, D.J. Effects of initial soil moisture on rainfall generation and subsequent hydrologic response during the North American monsoon. J. Hydrometeor. 2009, 10, 644–663. [Google Scholar] [CrossRef]
- Kim, H.; Lakshmi, V. Global dynamics of stored precipitation water in the topsoil layer from satellite and reanalysis data. Water Resour. Res. 2019, 55, 3328–3346. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS mission: New tool for monitoring key elements of the Global Water Cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef]
- Al-Yaari, A.; Wigneron, J.P.; Ducharne, A.; Kerr, Y.H.; Wagner, W.; De Lannoy, G.; Reichle, R.; Al Bitar, A.; Dorigo, W.; Richaume, P.; et al. Global-scale comparison of passive (SMOS) and active (ASCAT) satellite based microwave soil moisture retrievals with soil moisture simulations (MERRA-Land). Remote Sens. Environ. 2014, 152, 614–626. [Google Scholar] [CrossRef]
- Escorihuela, M.J.; Chanzy, A.; Wigneron, J.P.; Kerr, Y.H. Effective soil moisture sampling depth of L-band radiometry: A case study. Remote Sens. Environ. 2010, 114, 995–1001. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Richaume, P.; Wigneron, J.P.; Ferrazzoli, P.; Mahmoodi, A.; Bitar, A.A.; Cabot, F.; Gruhier, C.; Juglea, S.E.; et al. The SMOS soil moisture retrieval algorithm. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1384–1403. [Google Scholar] [CrossRef]
- Escorihuela, M.J.; Merlin, O.; Stefan, V.; Moyano, G.; Eweys, O.A.; Zribi, M.; Kamara, S.; Benahi, A.S.; Ebbe, M.A.B.; Chihrane, J.; et al. SMOS based high resolution soil moisture estimates for desert locust preventive management. Remote Sens. Appl. Soc. Environ. 2018, 11, 140–150. [Google Scholar]
- González-Zamora, Á.; Sánchez, N.; Martínez-Fernández, J.; Wagner, W. Root-zone plant available water estimation using the SMOS-Derived Soil Water Index. Adv. Water Resour. 2016, 96, 339–353. [Google Scholar] [CrossRef]
- Deng, K.A.K.; Lamine, S.; Pavlides, A.; Petropoulos, G.P.; Bao, Y.; Srivastava, P.K.; Guan, Y. Large scale operational soil moisture mapping from passive MW radiometry: SMOS product evaluation in Europe & USA. Int. J. Appl. Earth Obs. Geoinf. 2019, 80, 206–217. [Google Scholar] [CrossRef]
- Usowicz, B.; Marczewski, W.; Usowicz, J.B.; Łukowski, M.I.; Lipiec, J. Comparison of surface soil moisture from SMOS satellite and ground measurements. Int. Agrophys. 2014, 28, 359–369. [Google Scholar] [CrossRef]
- Brocca, L.; Pellarin, T.; Crow, W.D.; Ciabatta, L.; Massari, C.; Ryu, D.; Su, C.H.; Rüdiger, C.; Kerr, Y. Rainfall estimation by inverting SMOS soil moisture estimates: A comparison of different methods over Australia. J. Geophys. Res. Atmos. 2016, 121, 12062–12079. [Google Scholar] [CrossRef]
- Brocca, L.; Filippucci, P.; Hahn, S.; Ciabatta, L.; Massari, C.; Camici, S.; Schüller, L.; Bojkov, B.; Wagner, W. SM2RAIN–ASCAT (2007–2018): Global daily satellite rainfall data from ASCAT soil moisture observations. Earth Syst. Sci. Data 2019, 11, 1583–1601. [Google Scholar] [CrossRef]
- Usowicz, B.; Lukowski, M.; Lipiec, J. The SMOS-Derived Soil Water EXtent and equivalent layer thickness facilitate determination of soil water resources. Sci. Rep. 2020, 10, 18330. [Google Scholar] [CrossRef]
- Xu, J.J.; Shuttleworth, W.J.; Gao, X.; Sorooshian, S.; Small, E.E. Soil moisture-precipitation feedback on the North American monsoon system in the MM5-OSU model. Quart. J. R. Meteor. Soc. 2004, 130, 2873–2890. [Google Scholar] [CrossRef]
- Moon, H.; Guillod, B.P.; Gudmundsson, L.; Seneviratne, S.I. Soil moisture effects on afternoon precipitation occurrence in current climate models. Geophys. Res. Lett. 2019, 46, 1861–1869. [Google Scholar] [CrossRef] [PubMed]
- Hohenegger, C.; Brockhaus, P.; Bretherton, C.S.; Schär, C. The soil moisture–precipitation feedback in simulations with explicit and parameterized convection. J. Climatol. 2009, 22, 5003–5020. [Google Scholar] [CrossRef]
- Hong, S.-Y.; Pan, H.-L. Impact of soil moisture anomalies on seasonal, summertime circulation over North America in a regional climate model. J. Geophys. Res. 2000, 105, 29625–29634. [Google Scholar] [CrossRef]
- Public Data Base IMGW-PIB. Available online: https://danepubliczne.imgw.pl/ (accessed on 15 October 2020).
- Kerr, Y.H.; Waldteufel, P.; Richaume, P.; Wigneron, J.P.; Ferrazzoli, P.; Gurney, R. SMOS Level 2 Processor for Soil Moisture—Algorithm Theoretical Based Document (ATBD); Technic Report SO-TN-ESL-SM-GS-0001; Array Systems Computing Inc.: Toronto, ON, Canada, 2011; Chapter 3.4.4.1; pp. 1–123. [Google Scholar]
- Usowicz, B.; Lipiec, J.; Łukowski, M. Evaluation of soil moisture variability in Poland from SMOS satellite observations. Remote Sens. 2019, 11, 1280. [Google Scholar] [CrossRef]
- Robertson, G.P. GS+: Geostatistics for the Environmental Sciences; Gamma Design Software: Plainwell, MI, USA, 2008. [Google Scholar]
- Nielsen, D.R.; Bouma, J. Soil spatial variability. In Proceedings of the a Workshop of the ISSS and the SSSA, Las Vegas, NV, USA, 30 November–1 December 1984; p. 243. [Google Scholar]
- Cambardella, C.A.; Moorman, T.B.; Parkin, T.B.; Karlen, D.L.; Novak, J.M.; Turco, R.F.; Konopka, A.E. Field-scale variability of soil properties in Central Iowa soils. Soil Sci. Soc. Am. J. 1994, 58, 1501–1511. [Google Scholar] [CrossRef]
- Kwon, M.; Han, D. Assessment of remotely sensed soil moisture products and their quality improvement: A case study in South Korea. J. Hydro Environ. Res. 2019, 24, 14–27. [Google Scholar] [CrossRef]
- Das, N.N.; Entekhabi, D.; Dunbar, R.S.; Njoku, E.G.; Yueh, S.H. Uncertainty estimates in the SMAP combined active–passive downscaled brightness temperature. IEEE Trans. Geosci. Remote Sens. 2016, 54, 640–650. [Google Scholar] [CrossRef]
- Khodayar, S.; Coll, A.; Lopez-Baeza, E. An improved perspective in the spatial representation of soil moisture: Potential added value of SMOS disaggregated 1 km resolution “all weather” product. Hydrol. Earth Syst. Sci. 2019, 23, 255–275. [Google Scholar] [CrossRef]
- Kędzior, M.; Zawadzki, J. SMOS Data as a source of the agricultural drought information: Case study of the Vistula Catchment, Poland. Geoderma 2017, 306, 167–182. [Google Scholar] [CrossRef]
- Wanders, N.; Pan, M.; Wood, E.F. Correction of real-time satellite precipitation with multi-sensor satellite observations of land surface variables. Remote Sens. Environ. 2015, 160, 206–221. [Google Scholar] [CrossRef]
- Koster, R.D.; Dirmeyer, P.A.; Guo, Z.; Bonan, G.; Chan, E.; Cox, P.; Gordon, C.T.; Kanae, S.; Kowalczyk, E.; Lawrence, D.; et al. Regions of strong coupling between soil moisture and precipitation. Science 2004, 305, 1138–1140. [Google Scholar] [CrossRef]
- Ek, M.B.; Holstag, A.A.M. Influence of soil moisture on boundary layer cloud development. J. Hydrometeorol. 2004, 5, 86–99. [Google Scholar] [CrossRef]
- Zheng, X.Y.; Eltahir, E.A.B. A soil moisture–rainfall feedback mechanism. 2. Numerical experiments. Water Resour. Res. 1998, 34, 777–785. [Google Scholar] [CrossRef]
- Vivoni, E.R.; Moreno, H.A.; Mascaro, G.; Rodriguez, J.C.; Watts, C.J.; Garatuza-Payan, J.; Scott, R.L. Observed relation between evapotranspiration and soil moisture in the North American monsoon region. Geophys. Res. Lett. 2008, 35, L22403. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Førland, E.J.; Piniewski, M. Challenges for developing national climate services—Poland and Norway. Climate Serv. 2017, 8, 17–25. [Google Scholar] [CrossRef]
- Usowicz, Ł.B.; Usowicz, B. Spatial variability of soil particle size distribution in Poland. In Proceedings of the 17th World Congress of Soil Science, Bangkok, Thailand, 14–21 August 2002; pp. 1–10. [Google Scholar]
- Walczak, R.; Ostrowski, J.; Witkowska-Walczak, B.; Slawinski, C. Hydrophysical characteristics of Polish arable mineral soils (in Polish). Acta Agrophys. 2002, 79, 1–64. [Google Scholar]
- Bieganowski, A.; Witkowska-Walczak, B.; Gliński, J.; Sokołowska, Z.; Sławiński, C.; Brzezińska, M.; Włodarczyk, T. Database of Polish arable mineral soils: A review. Int. Agrophys. 2013, 27, 335–350. [Google Scholar] [CrossRef]
- Usowicz, B.; Marczewski, W.; Lipiec, J.; Usowicz, J.B.; Sokołowska, Z.; Dąbkowska-Naskręt, H.; Hajnos, M.; Łukowski, M.I. Water in the Soil—Ground and Satellite Measurements in Studies on Climate Change; Foundation for the Development of Agrophysical Sciences, Committee for Agrophysics PAS, Monograph: Lublin, Poland, 2009. (In Polish) [Google Scholar]
- Orlińska-Woźniak, P.; Wilk, P.; Gębala, J. Water availability in reference to water needs in Poland. Meteor. Hydrol. Water Manag. 2013, 1, 45–50. [Google Scholar] [CrossRef][Green Version]
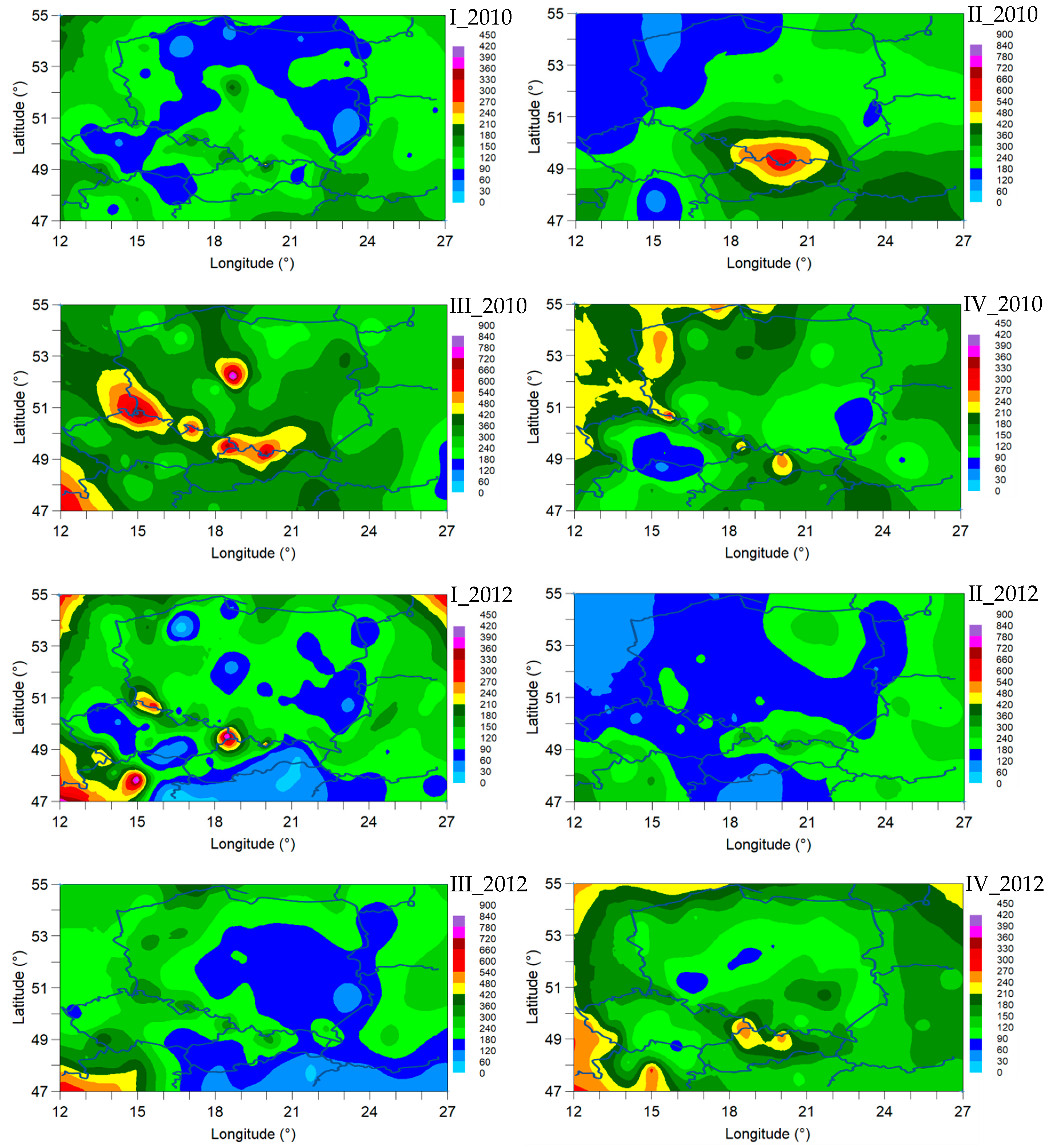
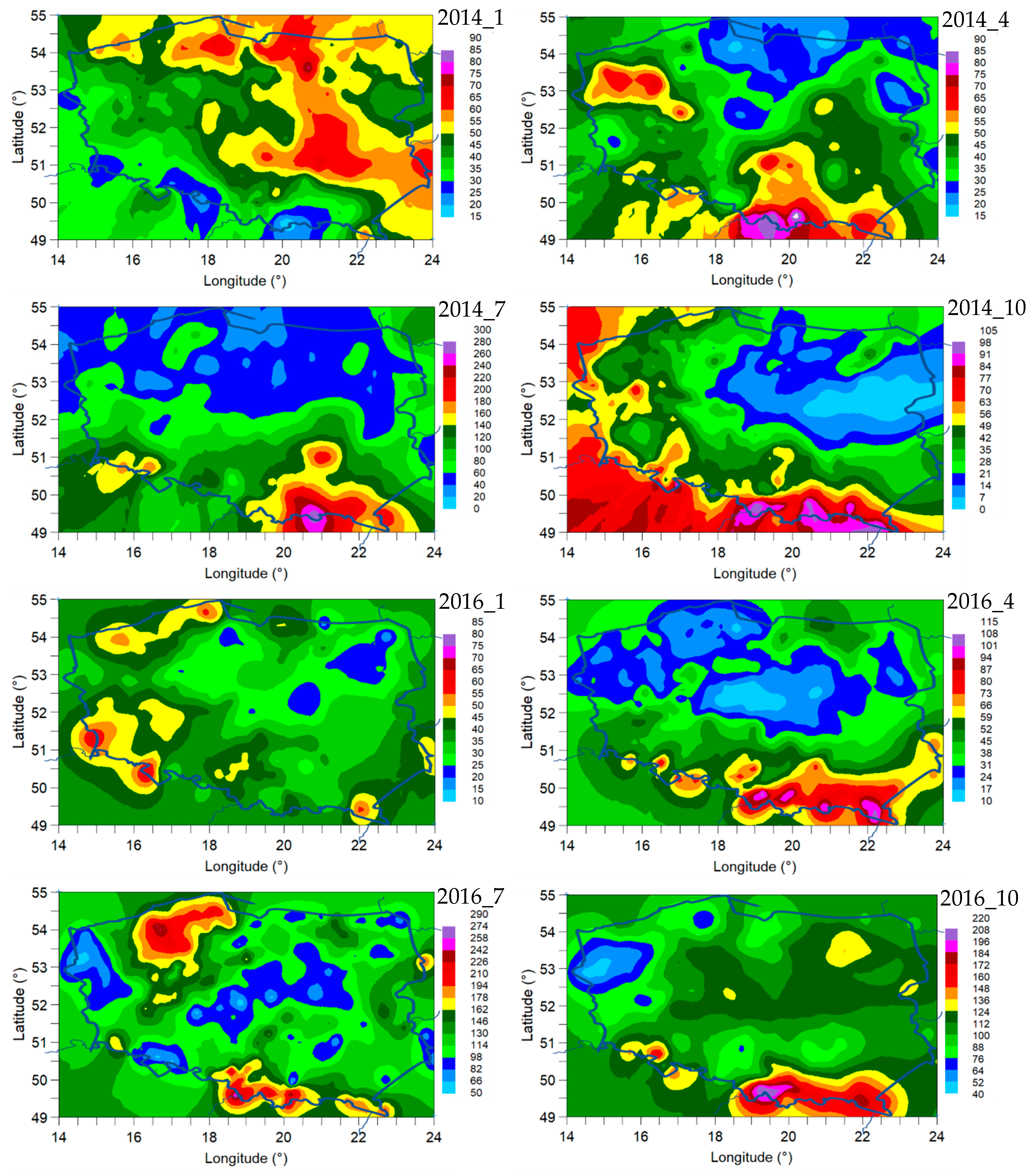
| Quarter of the Year | I 2010 | II 2010 | III 2010 | IV 2010 | I 2011 | II 2011 | III 2011 | IV 2011 | I 2012 | II 2012 | III 2012 | IV 2012 | I 2013 | II 2013 | III 2013 | IV 2013 | I 2014 | II 2014 | III 2014 | IV 2014 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | 115 | 115 | 116 | 116 | 116 | 116 | 113 | 116 | 115 | 116 | 116 | 116 | 114 | 114 | 114 | 114 | 114 | 116 | 116 | 110 |
| Mean | 104.0 | 277.1 | 344.0 | 148.3 | 80.6 | 163.3 | 261.1 | 91.7 | 113.8 | 185.5 | 219.4 | 145.5 | 141.0 | 265.5 | 190.2 | 106.5 | 93.8 | 207.9 | 275.5 | 114.1 |
| SD | 36.3 | 140.2 | 120.6 | 50.6 | 29.7 | 74.9 | 88.3 | 53.2 | 71.1 | 62.5 | 86.4 | 44.1 | 63.4 | 82.6 | 73.6 | 50.2 | 31.7 | 99.1 | 120.5 | 42.7 |
| CV (%) | 34.9 | 50.6 | 35.0 | 34.1 | 36.9 | 45.9 | 33.8 | 58.0 | 62.4 | 33.7 | 39.4 | 30.3 | 45.0 | 31.1 | 38.7 | 47.1 | 33.8 | 47.7 | 43.7 | 37.4 |
| Min | 29.2 | 26.7 | 157 | 49.3 | 30.2 | 46.7 | 94.8 | 23.1 | 11.2 | 69.6 | 53.6 | 69.6 | 48.5 | 129.3 | 37.6 | 27.2 | 31 | 23.8 | 75.5 | 55.4 |
| Max | 247.8 | 898.9 | 894.1 | 343.5 | 241.6 | 530.9 | 608.1 | 315.0 | 444.0 | 444.3 | 519.2 | 290.3 | 425.2 | 625.3 | 402.1 | 309.9 | 255.0 | 673.1 | 792.9 | 279.4 |
| Skewness | 1.302 | 1.523 | 1.998 | 0.847 | 1.947 | 2.045 | 0.900 | 1.900 | 2.312 | 1.166 | 1.034 | 1.071 | 1.535 | 1.163 | 1.042 | 1.477 | 1.165 | 2.081 | 1.360 | 1.523 |
| Kurtosis | 3.179 | 3.777 | 5.415 | 1.309 | 7.355 | 6.048 | 2.125 | 3.851 | 7.525 | 1.983 | 1.287 | 1.309 | 3.305 | 2.500 | 0.915 | 2.626 | 4.930 | 7.626 | 3.315 | 2.636 |
| Transformed rainfall data with a square root | ||||||||||||||||||||
| Mean | 10.1 | 16.2 | 18.3 | 12.0 | 8.8 | 12.5 | 15.9 | 9.3 | 10.3 | 13.4 | 14.5 | 11.9 | 11.6 | 16.1 | 13.6 | 10.1 | 9.6 | 14.1 | 16.2 | 10.5 |
| SD | 1.71 | 4.00 | 2.95 | 2.04 | 1.53 | 2.64 | 2.69 | 2.44 | 2.95 | 2.19 | 2.82 | 1.75 | 2.47 | 2.43 | 2.58 | 2.25 | 1.61 | 3.21 | 3.46 | 1.85 |
| Skewness | 0.524 | 0.526 | 1.327 | 0.282 | 0.985 | 1.178 | 0.239 | 1.239 | 1.008 | 0.679 | 0.455 | 0.653 | 0.888 | 0.633 | 0.465 | 0.853 | 0.218 | 0.621 | 0.575 | 1.020 |
| Kurtosis | 1.578 | 1.236 | 2.904 | 0.368 | 2.820 | 2.464 | 0.660 | 1.544 | 2.563 | 0.518 | 0.362 | 0.433 | 0.932 | 0.768 | 0.561 | 0.771 | 1.619 | 3.179 | 0.850 | 1.146 |
| Correlation coefficients between the quarterly average rainfall and satellite soil moisture (P_SM) in the years 2010–2014. Bold, the correlation coefficients are significant with p < 0.05, n = 76. | |||||||||||||||
| P_SM_I 2010 | P_SM_II 2010 | P_SM_III 2010 | P_SM_IV 2010 | P_SM_I 2011 | P_SM_II 2011 | P_SM_III 2011 | P_SM_IV 2011 | ||||||||
| −0.022 | 0.099 | −0.062 | 0.237 | 0.234 | 0.238 | 0.289 | 0.335 | ||||||||
| P_SM_I 2012 | P_SM_II 2012 | P_SM_III 2012 | P_SM_IV 2012 | P_SM_I 2013 | P_SM_II 2013 | P_SM_III 2013 | P_SM_IV 2013 | ||||||||
| 0.191 | 0.184 | 0.187 | 0.195 | 0.038 | 0.307 | 0.2 | 0.196 | ||||||||
| P_SM_I 2014 | P_SM_II 2014 | P_SM_III 2014 | P_SM_IV 2014 | ||||||||||||
| 0.021 | 0.189 | 0.158 | 0.336 | ||||||||||||
| Correlation coefficients between the monthly average rainfall and satellite soil moisture (P_SM) in the years 2014–2017. Bold, the correlation coefficients are significant with p < 0.05, n = 391. | |||||||||||||||
| Years | P_SM _1 | P_SM _2 | P_SM _3 | P_SM _4 | P_SM _5 | P_SM _6 | P_SM _7 | P_SM _8 | P_SM _9 | P_SM _10 | P_SM _11 | P_SM _12 | |||
| 2014 | 0.208 | −0.028 | −0.199 | −0.186 | −0.333 | −0.090 | −0.150 | −0.063 | −0.003 | 0.072 | −0.206 | 0.131 | |||
| 2015 | −0.087 | −0.342 | 0.095 | 0.049 | 0.008 | 0.171 | 0.141 | −0.118 | 0.309 | −0.029 | 0.053 | 0.362 | |||
| 2016 | −0.147 | −0.260 | −0.007 | 0.088 | 0.037 | 0.309 | 0.296 | 0.459 | 0.160 | −0.155 | 0.454 | 0.316 | |||
| 2017 | 0.360 | −0.012 | 0.200 | 0.054 | 0.025 | 0.210 | 0.255 | 0.376 | 0.203 | 0.429 | 0.271 | 0.441 | |||
| Semivariogram_P | C0/(C0 + C) | Semivariogram_SM | C0/(C0 + C) | Cross-semivariogram_P_SM | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Year | Quarter | Model | C0 | C0 + C | A (°) | Az (°) | Model | C0 | C0 + C | A (°) | Az (°) | Model | C0 | C0 + C | C0/(C0 + C) | A (°) | Az (°) | ||
| 2010 | I | Exp. | 0.641 | 3.11 | 0.206 | 1.50 | 116 | Exp. | 0.00001 | 0.00335 | 0.003 | 1.00 | 105 | Exp. | 0.000 | 1.500 | 0.000 | 4.01 | 33 |
| II | Exp. | 1.263 | 18.24 | 0.069 | 6.47 | 50 | Exp. | 0.00000 | 0.00176 | 0.001 | 1.62 | 58 | Exp. | −0.002 | −0.016 | 0.125 | 3.46 | 12 | |
| III | Exp. | 0.900 | 8.73 | 0.103 | 1.26 | 113 | Exp. | 0.00003 | 0.00168 | 0.017 | 1.54 | 66 | Exp. | 0.000 | −0.016 | 0.000 | 8.11 | 12 | |
| IV | Exp. | 0.540 | 4.16 | 0.130 | 2.00 | 70 | Exp. | 0.00013 | 0.00205 | 0.063 | 1.88 | 116 | Exp. | 0.000 | 0.011 | 0.000 | 5.58 | 63 | |
| 2011 | I | Exp. | 0.327 | 2.39 | 0.137 | 1.29 | 117 | Exp. | 0.00098 | 0.00327 | 0.298 | 2.73 | 97 | Exp. | 0.000 | 0.017 | 0.000 | 4.35 | 107 |
| II | Exp. | 2.680 | 7.29 | 0.367 | 2.82 | 69 | Exp. | 0.00007 | 0.00114 | 0.060 | 1.73 | 124 | Exp. | 0.000 | 0.019 | 0.000 | 3.16 | 115 | |
| III | Exp. | 1.440 | 7.16 | 0.201 | 1.53 | 113 | Exp. | 0.00000 | 0.00131 | 0.002 | 1.70 | 41 | Exp. | 0.004 | 0.022 | 0.179 | 2.08 | 105 | |
| IV | Exp. | 0.100 | 5.48 | 0.018 | 1.49 | 120 | Exp. | 0.00013 | 0.00119 | 0.113 | 2.39 | 58 | Gaus. | 0.005 | 0.040 | 0.122 | 6.20 | 105 | |
| 2012 | I | Exp. | 1.230 | 9.34 | 0.132 | 1.30 | 120 | Exp. | 0.00078 | 0.00371 | 0.209 | 2.03 | 58 | Exp. | 0.000 | 0.039 | 0.003 | 7.05 | 105 |
| II | Exp. | 0.192 | 4.73 | 0.041 | 1.85 | 112 | Exp. | 0.00011 | 0.00108 | 0.106 | 1.63 | 154 | Exp. | 0.001 | 0.024 | 0.045 | 8.98 | 113 | |
| III | Exp. | 1.374 | 8.19 | 0.168 | 5.20 | 26 | Exp. | 0.00091 | 0.00142 | 0.642 | 2.73 | 0 | Exp. | 0.004 | 0.019 | 0.196 | 3.65 | 112 | |
| IV | Exp. | 0.312 | 3.17 | 0.098 | 1.42 | 106 | Exp. | 0.00092 | 0.00135 | 0.684 | 3.85 | 170 | Exp. | 0.000 | −0.002 | 0.000 | 3.69 | 115 | |
| 2013 | I | Exp. | 1.220 | 6.39 | 0.191 | 2.53 | 69 | Exp. | 0.00047 | 0.00290 | 0.163 | 1.81 | 131 | Exp. | 0.000 | −0.025 | 0.000 | 2.30 | 45 |
| II | Exp. | 1.690 | 6.75 | 0.250 | 6.12 | 76 | Exp. | 0.00000 | 0.00222 | 0.000 | 2.10 | 146 | Exp. | 0.000 | 0.008 | 0.013 | 2.67 | 122 | |
| III | Exp. | 2.534 | 7.32 | 0.346 | 3.28 | 105 | Exp. | 0.00057 | 0.00091 | 0.621 | 1.87 | 1 | Exp. | 0.008 | 0.019 | 0.403 | 5.04 | 112 | |
| IV | Exp. | 0.420 | 5.13 | 0.082 | 1.64 | 105 | Exp. | 0.00088 | 0.00154 | 0.570 | 4.08 | 172 | Exp. | 0.002 | 0.011 | 0.152 | 1.58 | 116 | |
| 2014 | I | Exp. | 0.493 | 2.76 | 0.179 | 2.53 | 150 | Exp. | 0.00000 | 0.00127 | 0.001 | 1.49 | 86 | Exp. | 0.000 | −0.006 | 0.000 | 5.88 | 112 |
| II | Exp. | 1.420 | 10.70 | 0.133 | 1.64 | 108 | Exp. | 0.00000 | 0.00095 | 0.001 | 1.59 | 145 | Exp. | 0.000 | 0.012 | 0.000 | 2.91 | 114 | |
| III | Exp. | 2.119 | 12.39 | 0.171 | 5.73 | 108 | Exp. | 0.00078 | 0.00120 | 0.650 | 2.54 | 65 | Exp. | 0.000 | 0.016 | 0.000 | 2.34 | 117 | |
| IV | Exp. | 0.374 | 3.42 | 0.109 | 1.62 | 108 | Exp. | 0.00092 | 0.00184 | 0.498 | 1.73 | 145 | Exp. | 0.000 | 0.017 | 0.000 | 4.79 | 112 | |
| Max | 2.680 | 18.24 | 0.367 | 6.47 | 150 | 0.0010 | 0.0037 | 0.684 | 4.08 | 172.0 | 0.008 | 1.500 | 0.403 | 8.98 | 122 | ||||
| Min | 0.100 | 2.39 | 0.018 | 1.26 | 26 | 0.0000 | 0.0009 | 0.000 | 1.00 | 0.0 | −0.002 | −0.025 | 0.000 | 1.58 | 12 | ||||
| 1 | Exp. | 12.1 | 135.6 | 0.089 | 4.29 | 130 | Exp. | 0.00143 | 0.00340 | 0.421 | 3.46 | 101 | Gaus. | 0.000 | 0.115 | 0.001 | 2.40 | 103 | |
| 4 | Exp. | 101.9 | 308.3 | 0.331 | 4.96 | 93 | Sph. | 0.00097 | 0.00320 | 0.303 | 5.84 | 103 | Gaus. | −0.001 | −0.290 | 0.003 | 4.00 | 68 | |
| 7 | Sph. | 290.0 | 3422.0 | 0.085 | 4.66 | 93 | Sph. | 0.00119 | 0.00311 | 0.382 | 5.23 | 103 | Gaus. | −0.001 | −0.723 | 0.001 | 4.11 | 73 | |
| 10 | Sph. | 1.0 | 626.0 | 0.002 | 5.77 | 110 | Exp. | 0.00087 | 0.00278 | 0.313 | 4.47 | 81 | Gaus. | −0.001 | −0.067 | 0.015 | 3.87 | 73 | |
| 2015 | 1 | Sph. | 29.0 | 434.0 | 0.067 | 2.28 | 86 | Exp. | 0.00160 | 0.00429 | 0.373 | 4.25 | 64 | Gaus. | −0.001 | −0.166 | 0.007 | 4.49 | 100 |
| 4 | Exp. | 86.7 | 173.6 | 0.499 | 3.86 | 86 | Exp. | 0.00049 | 0.00252 | 0.194 | 2.49 | 62 | Gaus. | −0.001 | −0.111 | 0.009 | 4.48 | 87 | |
| 7 | Exp. | 231.5 | 551.9 | 0.419 | 2.67 | 71 | Exp. | 0.00103 | 0.00419 | 0.246 | 4.57 | 69 | Gaus. | 0.001 | 0.284 | 0.004 | 3.94 | 87 | |
| 10 | Exp. | 4.6 | 173.0 | 0.027 | 3.50 | 72 | Exp. | 0.00070 | 0.00273 | 0.256 | 4.77 | 58 | Gaus. | 0.000 | −0.129 | 0.001 | 3.02 | 105 | |
| 2016 | 1 | Exp. | 28.9 | 112.5 | 0.257 | 3.99 | 115 | Sph. | 0.00246 | 0.00863 | 0.285 | 5.46 | 95 | Gaus. | 0.000 | −0.190 | 0.001 | 3.46 | 90 |
| 4 | Exp. | 1.0 | 478.7 | 0.002 | 4.87 | 90 | Exp. | 0.00080 | 0.00224 | 0.357 | 5.16 | 66 | Gaus. | −0.001 | −0.181 | 0.006 | 3.38 | 110 | |
| 7 | Exp. | 145.0 | 2386.0 | 0.061 | 2.97 | 65 | Exp. | 0.00117 | 0.00383 | 0.305 | 4.66 | 74 | Gaus. | 0.000 | 0.359 | 0.000 | 3.61 | 120 | |
| 10 | Exp. | 320.0 | 1095.0 | 0.292 | 4.53 | 73 | Exp. | 0.00090 | 0.00345 | 0.261 | 4.98 | 78 | Gaus. | −0.084 | −1.240 | 0.068 | 4.28 | 120 | |
| 2017 | 1 | Exp. | 0.0 | 210.0 | 0.000 | 3.73 | 77 | Sph. | 0.00127 | 0.00813 | 0.156 | 5.05 | 84 | Gaus. | 0.026 | 0.550 | 0.047 | 4.18 | 120 |
| 4 | Sph. | 1.0 | 1603.0 | 0.001 | 4.35 | 83 | Exp. | 0.00104 | 0.00299 | 0.348 | 4.00 | 106 | Gaus. | −0.001 | −0.512 | 0.002 | 3.32 | 115 | |
| 7 | Exp. | 392.0 | 1592.0 | 0.246 | 4.17 | 60 | Exp. | 0.00090 | 0.00252 | 0.357 | 4.65 | 90 | Gaus. | 0.001 | 0.572 | 0.002 | 3.88 | 115 | |
| 10 | Exp. | 125.0 | 1239.0 | 0.101 | 3.75 | 90 | Exp. | 0.00075 | 0.00389 | 0.193 | 4.62 | 90 | Gaus. | 0.001 | 0.648 | 0.002 | 4.79 | 120 | |
| Max | 392.0 | 3422.0 | 0.499 | 5.77 | 130 | 0.0025 | 0.0086 | 0.421 | 5.84 | 106.0 | 0.026 | 0.648 | 0.068 | 4.79 | 120 | ||||
| Min | 0.0 | 112.5 | 0.000 | 2.28 | 60 | 0.0005 | 0.0022 | 0.156 | 2.49 | 58.0 | −0.084 | −1.240 | 0.000 | 2.40 | 68 | ||||
| IDW | Kriging (OK) | Cokriging (OCK) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Year | Quarter | a | SE | R2 | b | SE Pre. | a | SE | R2 | b | SE Pre. | a | SE | R2 | b | SE Pre. |
| 2010 | I | 0.552 | 0.230 | 0.048 | 47.9 | 35.4 | 0.610 | 0.248 | 0.051 | 42.4 | 36.4 | 1.441 | 0.029 | 0.957 | −43.4 | 7.5 |
| II | 1.062 | 0.082 | 0.599 | −19.7 | 88.7 | 1.011 | 0.072 | 0.634 | −1.3 | 87.8 | 1.066 | 0.009 | 0.992 | −16.7 | 12.7 | |
| III | 0.983 | 0.194 | 0.183 | 2.3 | 108.9 | 1.030 | 0.216 | 0.166 | −14.4 | 110.1 | 1.318 | 0.019 | 0.977 | −108.8 | 18.3 | |
| IV | 0.996 | 0.159 | 0.256 | 6.6 | 43.6 | 1.000 | 0.165 | 0.244 | 7.2 | 44.0 | 1.229 | 0.019 | 0.974 | −31.0 | 8.2 | |
| 2011 | I | 0.651 | 0.302 | 0.039 | 29.6 | 29.3 | 0.734 | 0.339 | 0.040 | 23.7 | 29.3 | 1.428 | 0.019 | 0.980 | −32.6 | 4.2 |
| II | 1.206 | 0.151 | 0.358 | −33.8 | 60.0 | 1.252 | 0.150 | 0.379 | −39.4 | 59.0 | 1.386 | 0.032 | 0.944 | −60.3 | 17.6 | |
| III | 1.393 | 0.209 | 0.285 | −103.9 | 74.6 | 1.517 | 0.258 | 0.237 | −136.8 | 77.1 | 1.371 | 0.020 | 0.978 | −95.7 | 13.1 | |
| IV | 1.129 | 0.195 | 0.227 | −6.6 | 46.7 | 1.140 | 0.217 | 0.195 | −6.3 | 47.7 | 1.216 | 0.012 | 0.989 | −17.5 | 5.6 | |
| 2012 | I | 1.051 | 0.296 | 0.104 | −0.5 | 67.9 | 1.100 | 0.325 | 0.095 | −4.4 | 68.3 | 1.428 | 0.020 | 0.980 | −43.4 | 10.2 |
| II | 1.257 | 0.196 | 0.267 | −44.2 | 53.8 | 1.206 | 0.210 | 0.226 | −33.3 | 55.2 | 1.188 | 0.011 | 0.991 | −33.2 | 6.0 | |
| III | 1.114 | 0.132 | 0.386 | −22.4 | 67.7 | 0.983 | 0.115 | 0.391 | 7.7 | 67.4 | 1.162 | 0.019 | 0.970 | −33.2 | 15.0 | |
| IV | 1.102 | 0.181 | 0.245 | −11.1 | 38.3 | 1.119 | 0.200 | 0.200 | −12.0 | 39.0 | 1.266 | 0.016 | 0.981 | −36.6 | 6.1 | |
| 2013 | I | 1.029 | 0.162 | 0.268 | 1.4 | 54.5 | 1.039 | 0.160 | 0.278 | 1.2 | 54.1 | 1.259 | 0.024 | 0.960 | −33.3 | 12.7 |
| II | 1.226 | 0.155 | 0.357 | −61.4 | 66.2 | 1.119 | 0.133 | 0.387 | −29.6 | 64.7 | 1.241 | 0.024 | 0.960 | −62.3 | 16.6 | |
| III | 1.428 | 0.203 | 0.306 | −73.7 | 61.4 | 1.388 | 0.192 | 0.317 | −64.3 | 60.8 | 1.435 | 0.030 | 0.953 | −76.8 | 16.0 | |
| IV | 1.102 | 0.180 | 0.251 | −6.4 | 43.4 | 1.142 | 0.190 | 0.243 | −9.0 | 43.7 | 1.240 | 0.015 | 0.985 | −23.1 | 6.2 | |
| 2014 | I | 0.755 | 0.165 | 0.157 | 23.5 | 29.1 | 0.796 | 0.161 | 0.179 | 19.9 | 28.7 | 1.260 | 0.024 | 0.960 | −23.3 | 6.3 |
| II | 1.062 | 0.184 | 0.227 | −12.9 | 87.1 | 1.132 | 0.195 | 0.229 | −26.6 | 87.0 | 1.290 | 0.018 | 0.977 | −57.6 | 15.0 | |
| III | 1.099 | 0.092 | 0.557 | −29.7 | 80.2 | 1.016 | 0.082 | 0.574 | −3.8 | 78.6 | 1.129 | 0.020 | 0.965 | −33.6 | 22.5 | |
| IV | 0.927 | 0.927 | 0.127 | 12.2 | 39.9 | 0.928 | 0.246 | 0.117 | 13.0 | 40.1 | 1.306 | 0.018 | 0.981 | −32.4 | 5.9 | |
| Max | 1.428 | 0.927 | 0.599 | 47.9 | 108.9 | 1.517 | 0.339 | 0.634 | 42.4 | 110.1 | 1.441 | 0.032 | 0.992 | −16.7 | 22.5 | |
| Min | 0.552 | 0.082 | 0.039 | −103.9 | 29.1 | 0.610 | 0.072 | 0.040 | −136.8 | 28.7 | 1.066 | 0.009 | 0.944 | −108.8 | 4.2 | |
| 1 | 1.046 | 0.039 | 0.640 | −2.1 | 6.7 | 0.930 | 0.037 | 0.612 | 3.2 | 7.1 | 1.077 | 0.011 | 0.964 | −3.5 | 2.2 | |
| 4 | 1.021 | 0.048 | 0.538 | −0.9 | 11.4 | 1.004 | 0.047 | 0.571 | −0.2 | 10.9 | 1.162 | 0.023 | 0.864 | −6.9 | 6.2 | |
| 7 | 1.013 | 0.036 | 0.665 | −1.45 | 29.5 | 0.970 | 0.034 | 0.675 | 2.3 | 29 | 1.087 | 0.018 | 0.901 | −7.4 | 16.0 | |
| 10 | 1.03 | 0.026 | 0.793 | −1.08 | 9.6 | 0.947 | 0.024 | 0.797 | 1.8 | 9.5 | 1.026 | 0.005 | 0.992 | −1.0 | 1.9 | |
| 2015 | 1 | 1.058 | 0.042 | 0.636 | −3 | 12.1 | 0.927 | 0.038 | 0.619 | 3.8 | 12.4 | 1.088 | 0.014 | 0.941 | −4.9 | 4.9 |
| 4 | 1.129 | 0.054 | 0.534 | −3.6 | 9.0 | 1.086 | 0.049 | 0.559 | −2.5 | 8.7 | 1.222 | 0.028 | 0.824 | −6.8 | 5.5 | |
| 7 | 0.989 | 0.067 | 0.352 | 0.6 | 18.3 | 0.929 | 0.064 | 0.348 | 6.1 | 18.3 | 1.283 | 0.031 | 0.810 | −20.5 | 9.9 | |
| 10 | 1.07 | 0.029 | 0.777 | −2.5 | 6.2 | 1.013 | 0.024 | 0.815 | −0.5 | 5.6 | 1.053 | 0.009 | 0.971 | −1.9 | 2.3 | |
| 2016 | 1 | 1.087 | 0.057 | 0.497 | −2.9 | 7.3 | 1.004 | 0.050 | 0.525 | 0.0 | 7.1 | 1.213 | 0.019 | 0.915 | −7.8 | 2.9 |
| 4 | 1.018 | 0.025 | 0.807 | −0.6 | 9.1 | 0.983 | 0.022 | 0.828 | 0.8 | 8.6 | 1.029 | 0.004 | 0.993 | −1.2 | 1.7 | |
| 7 | 1.034 | 0.043 | 0.595 | −5.7 | 29.3 | 0.939 | 0.039 | 0.589 | 7.5 | 29.5 | 1.103 | 0.009 | 0.974 | −13.6 | 7.5 | |
| 10 | 1.05 | 0.036 | 0.678 | −5.3 | 18.6 | 1.051 | 0.032 | 0.734 | −5.4 | 16.9 | 1.146 | 0.016 | 0.924 | −15.6 | 9.0 | |
| 2017 | 1 | 1.052 | 0.035 | 0.759 | −1.1 | 6.9 | 0.973 | 0.033 | 0.756 | 0.8 | 7.0 | 1.039 | 0.005 | 0.983 | −1.1 | 1.1 |
| 4 | 1.027 | 0.022 | 0.844 | −2.5 | 13.8 | 0.982 | 0.020 | 0.865 | 1.1 | 12.8 | 1.018 | 0.004 | 0.995 | −1.2 | 2.5 | |
| 7 | 1.019 | 0.038 | 0.644 | −2.3 | 23.9 | 0.993 | 0.034 | 0.674 | 0.7 | 22.9 | 1.130 | 0.016 | 0.929 | −15.2 | 10.7 | |
| 10 | 1.09 | 0.041 | 0.645 | −9.1 | 19.5 | 0.996 | 0.035 | 0.672 | 0.7 | 18.7 | 1.101 | 0.010 | 0.967 | −10.8 | 5.9 | |
| Max | 1.129 | 0.067 | 0.844 | 0.6 | 29.5 | 1.086 | 0.064 | 0.865 | 7.5 | 29.5 | 1.283 | 0.031 | 0.995 | −1.0 | 16.0 | |
| Min | 0.989 | 0.022 | 0.352 | −9.1 | 6.2 | 0.927 | 0.020 | 0.348 | −5.4 | 5.6 | 1.018 | 0.004 | 0.810 | −20.5 | 1.1 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Usowicz, B.; Lipiec, J.; Łukowski, M.; Słomiński, J. Improvement of Spatial Interpolation of Precipitation Distribution Using Cokriging Incorporating Rain-Gauge and Satellite (SMOS) Soil Moisture Data. Remote Sens. 2021, 13, 1039. https://doi.org/10.3390/rs13051039
Usowicz B, Lipiec J, Łukowski M, Słomiński J. Improvement of Spatial Interpolation of Precipitation Distribution Using Cokriging Incorporating Rain-Gauge and Satellite (SMOS) Soil Moisture Data. Remote Sensing. 2021; 13(5):1039. https://doi.org/10.3390/rs13051039
Chicago/Turabian StyleUsowicz, Bogusław, Jerzy Lipiec, Mateusz Łukowski, and Jan Słomiński. 2021. "Improvement of Spatial Interpolation of Precipitation Distribution Using Cokriging Incorporating Rain-Gauge and Satellite (SMOS) Soil Moisture Data" Remote Sensing 13, no. 5: 1039. https://doi.org/10.3390/rs13051039
APA StyleUsowicz, B., Lipiec, J., Łukowski, M., & Słomiński, J. (2021). Improvement of Spatial Interpolation of Precipitation Distribution Using Cokriging Incorporating Rain-Gauge and Satellite (SMOS) Soil Moisture Data. Remote Sensing, 13(5), 1039. https://doi.org/10.3390/rs13051039