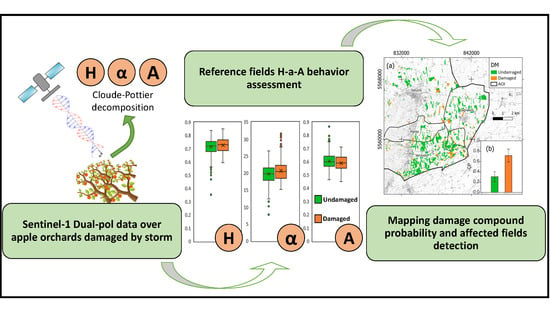
Sentinel-1 Polarimetry to Map Apple Orchard Damage after a Storm
Abstract
1. Introduction
2. Materials and Methods
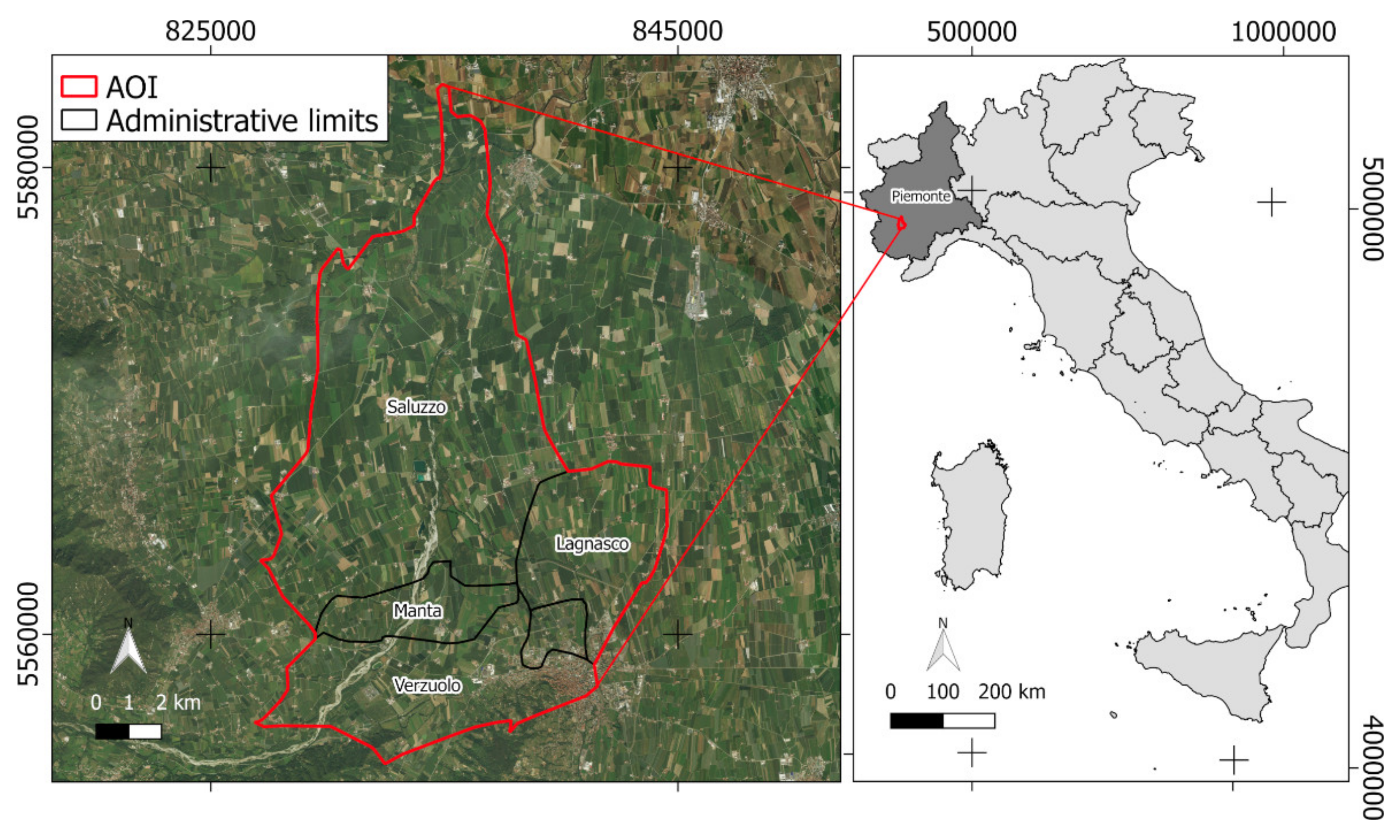
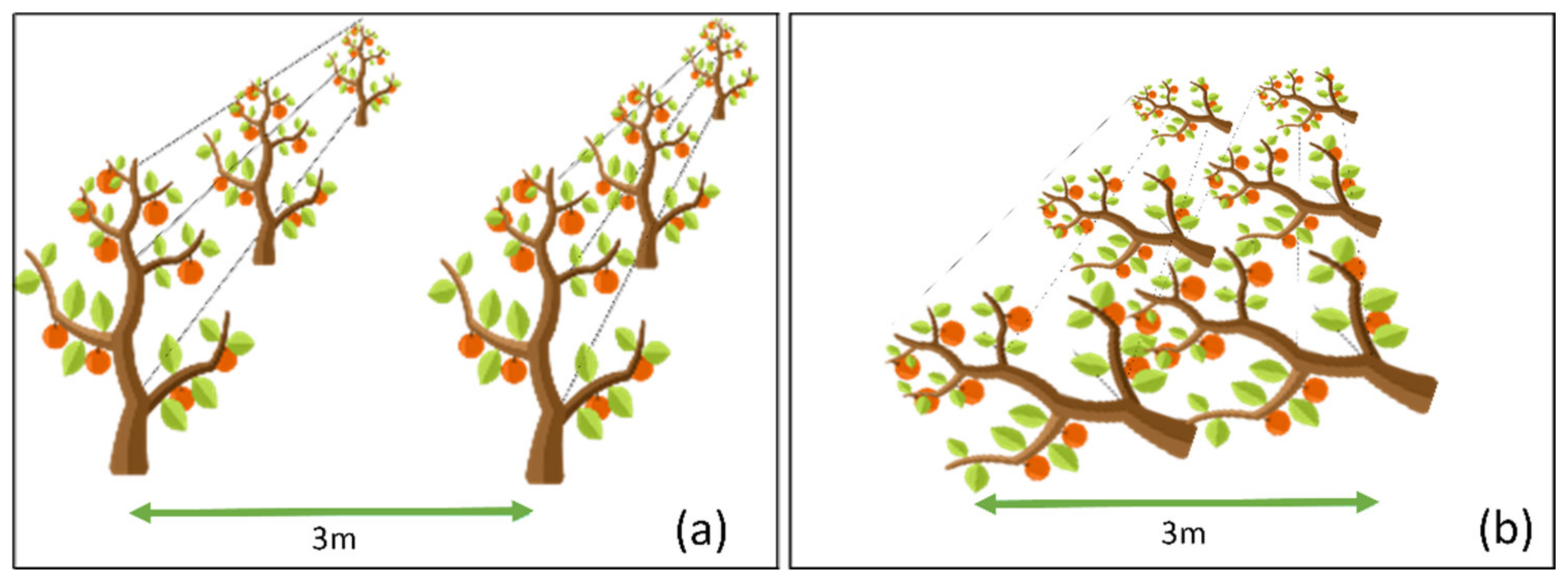
2.1. Study Area
2.2. Data and Data Collection
2.2.1. Sentinel-1 Data
2.2.2. Cadastral Data
2.2.3. Ground Dataset
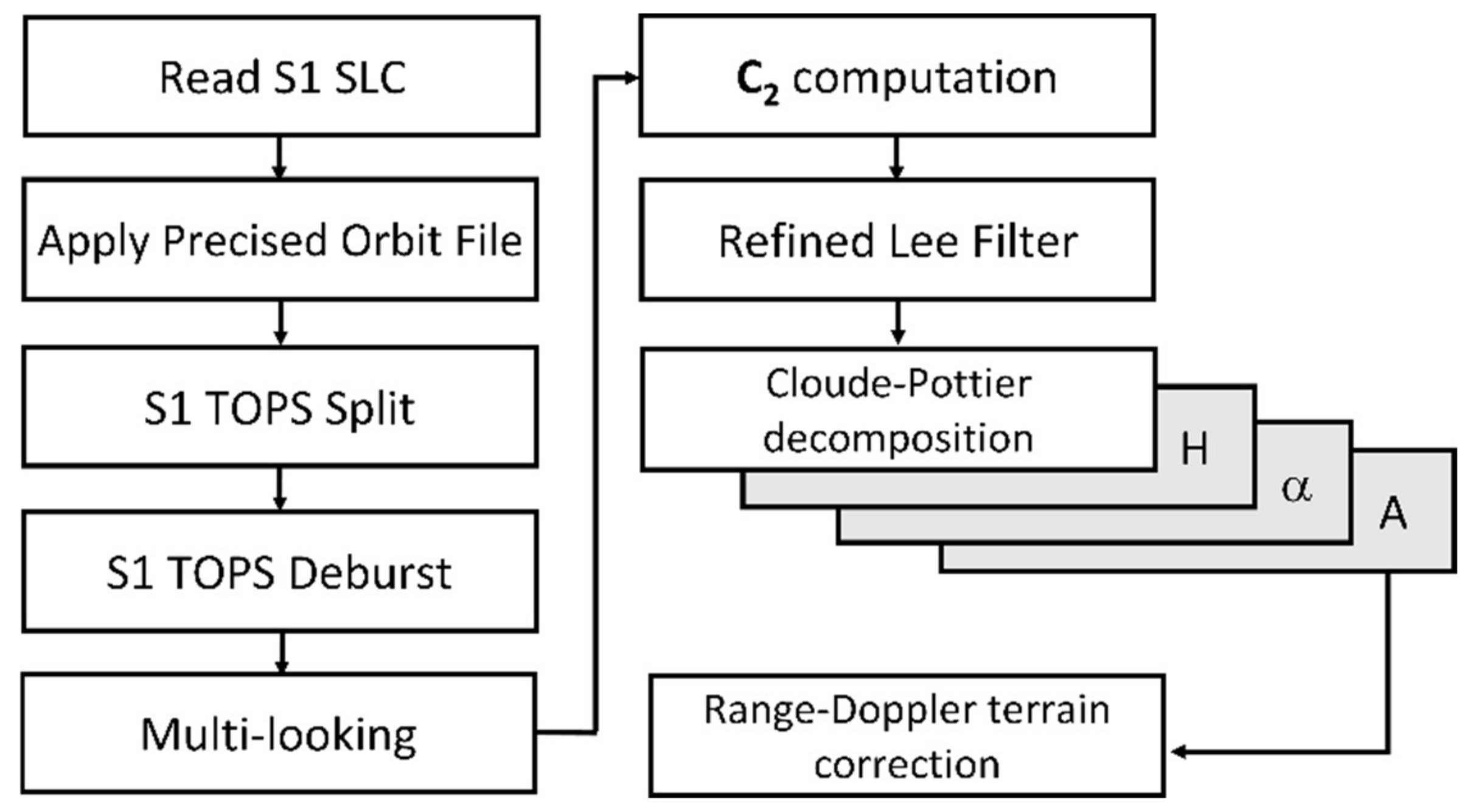
2.3. Data Processing
2.3.1. Polarimetric Decomposition
2.3.2. Testing H-α-A Values after the Storm
2.3.3. Detection of Damaged Orchards
3. Results
3.1. H-α-A Analysis
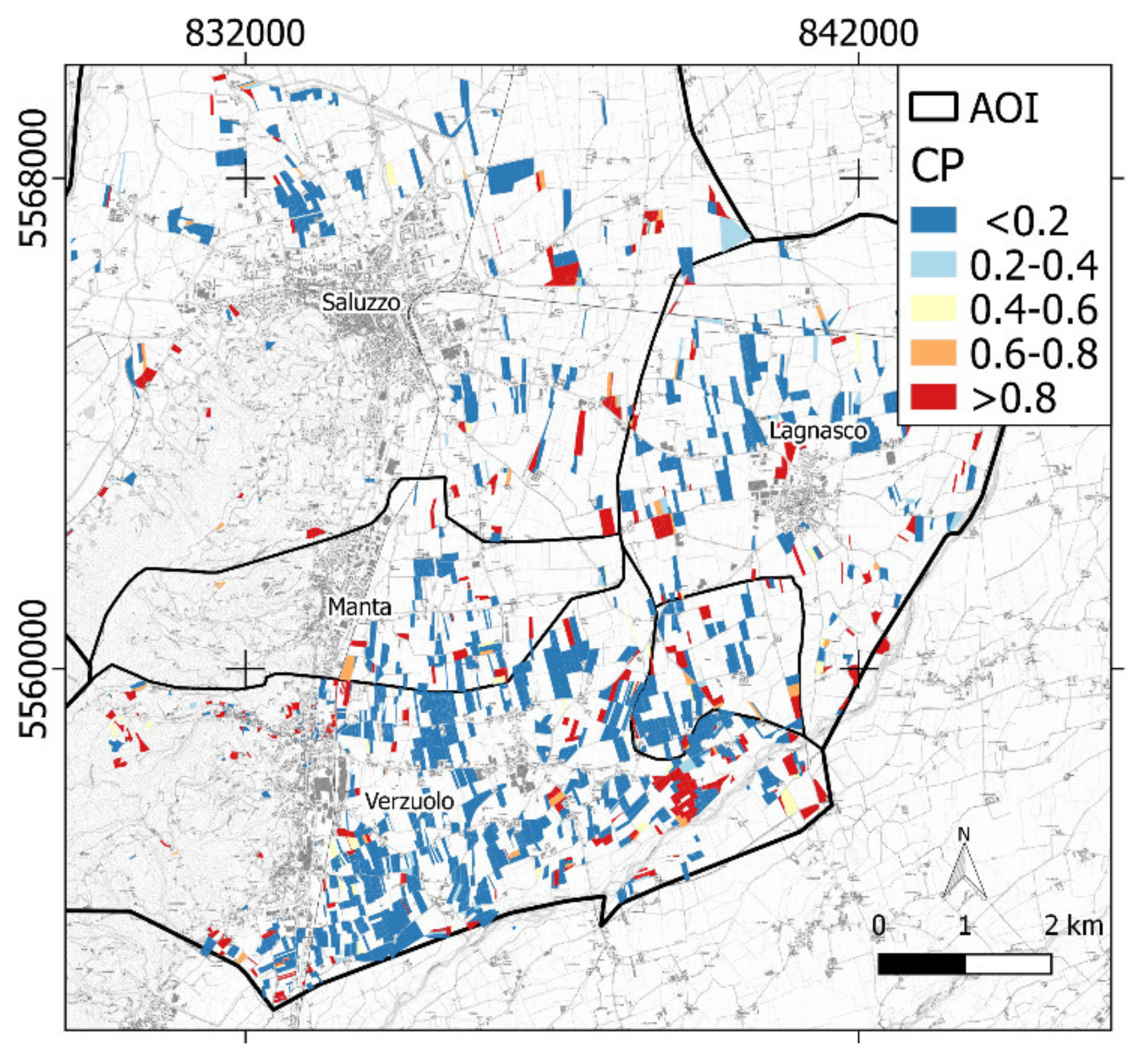
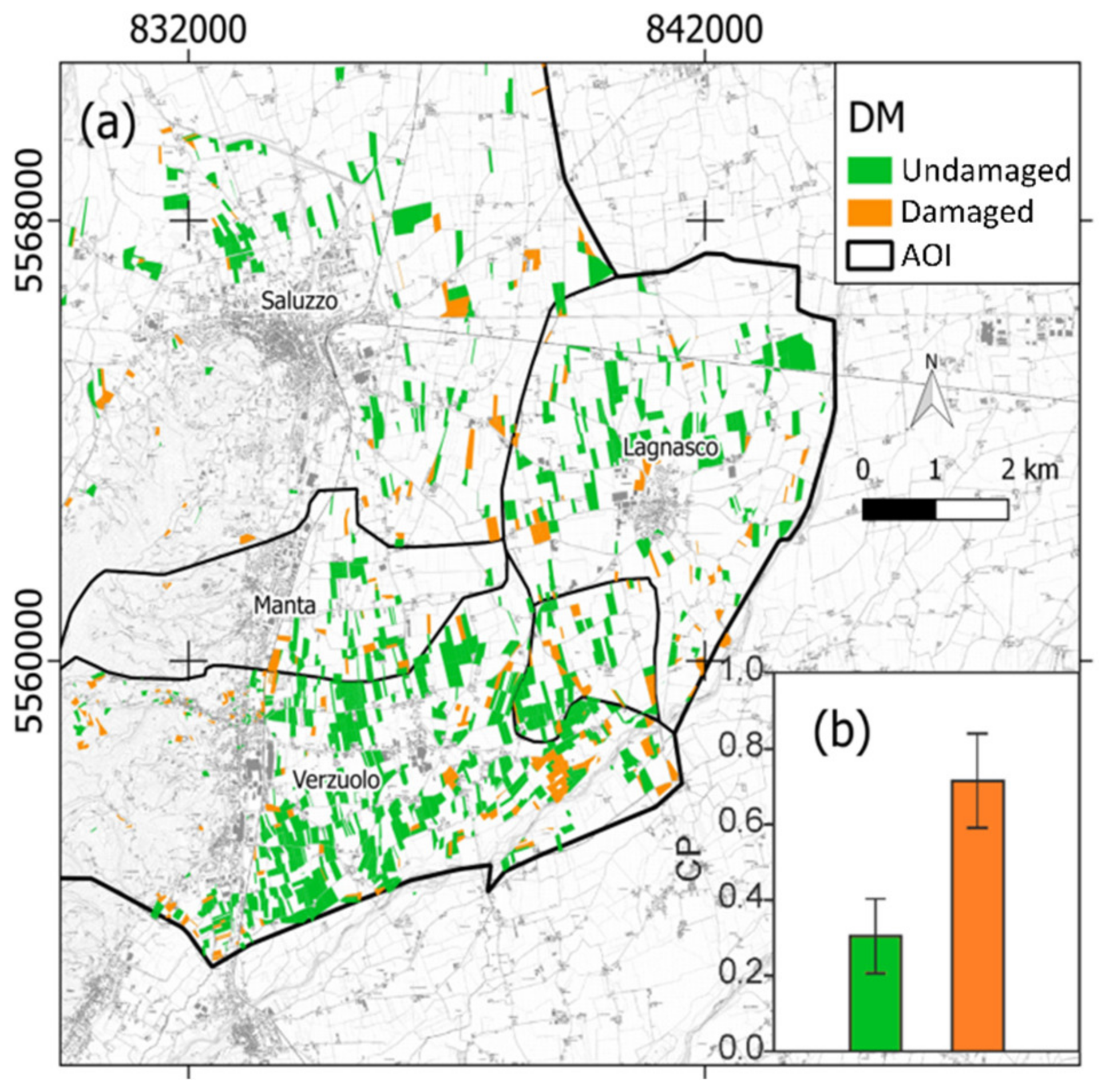
3.2. Damaged Orchards’ Mapping
4. Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hsiang, S.; Kopp, R.; Jina, A.; Rising, J.; Delgado, M.; Mohan, S.; Rasmussen, D.J.; Muir-Wood, R.; Wilson, P.; Oppenheimer, M. Estimating Economic Damage from Climate Change in the United States. Science 2017, 356, 1362–1369. [Google Scholar] [CrossRef]
- Nelson, G.C.; Valin, H.; Sands, R.D.; Havlík, P.; Ahammad, H.; Deryng, D.; Elliott, J.; Fujimori, S.; Hasegawa, T.; Heyhoe, E. Climate Change Effects on Agriculture: Economic Responses to Biophysical Shocks. Proc. Natl. Acad. Sci. USA 2014, 111, 3274–3279. [Google Scholar] [CrossRef]
- Moore, F.C.; Baldos, U.; Hertel, T.; Diaz, D. New Science of Climate Change Impacts on Agriculture Implies Higher Social Cost of Carbon. Nat. Commun. 2017, 8, 1–9. [Google Scholar] [CrossRef]
- FAO The Impact of Natural Hazards and Disasters on Agriculture and Food Security and Nutrition–A Call for Action to Build Resilient Livelihoods. Available online: http://www.fao.org/emergencies/resources/documents/resources-detail/zh/c/280784/ (accessed on 20 December 2020).
- Welbergen, J.A.; Klose, S.M.; Markus, N.; Eby, P. Climate Change and the Effects of Temperature Extremes on Australian Flying-Foxes. Proc. R. Soc. B. Biol. Sci. 2008, 275, 419–425. [Google Scholar] [CrossRef]
- Wang, E.; Bertis, B.L.; Jimmy, R.W.; Yu, Y. Simulation of Hail Effects on Crop Yield Losses for Corn-Belt States in USA. Trans. Chin. Soc. Agric. Eng. 2012, 28, 177–185. [Google Scholar]
- Reighard, G.L.; Parker, M.L.; Krewer, G.W.; Beckman, T.G.; Wood, B.W.; Smith, J.E.; Whiddon, J. Impact of Hurricanes on Peach and Pecan Orchards in the Southeastern United States. HortScience 2001, 36, 250–252. [Google Scholar] [CrossRef]
- Crane, J.; Balerdi, C.; Campbell, R.; Campbell, C.; Goldweber, S. Managing Fruit Orchards to Minimize Hurricane Damage. HortTechnology 1994, 4, 21–27. [Google Scholar] [CrossRef]
- Notarnicola, B.; Tassielli, G.; Renzulli, P.A.; Castellani, V.; Sala, S. Environmental Impacts of Food Consumption in Europe. J. Clean. Prod. 2017, 140, 753–765. [Google Scholar] [CrossRef]
- Bos-Brouwers, H.E.J.; Graf, V.; Aramyan, L.; Oberc, B. Food Redistribution in the EU–Mapping and Analysis of Existing Regulatory and Policy Measures Impacting Food Redistribution from EU Member States. Available online: https://research.wur.nl/en/publications/food-redistribution-in-the-eu-mapping-and-analysis-of-existing-re (accessed on 20 December 2020).
- FAO FAOSTAT. Available online: http://www.fao.org/faostat/en/#home (accessed on 13 November 2020).
- Eccher, T.; Granelli, G. Fruit Quality and Yield of Different Apple Cultivars as Affected by Tree Density. Acta Hortic. 2006, 535–540. [Google Scholar] [CrossRef]
- Childers, N.F.; Morris, J.R.; Sibbett, G.S. Modern Fruit Science: Orchard and Small Fruit Culture; Horticultural Publications: Gainesville, GA, USA, 1995. [Google Scholar]
- Lordan, J.; Gomez, M.; Francescatto, P.; Robinson, T.L. Long-Term Effects of Tree Density and Tree Shape on Apple Orchard Performance, a 20 Year Study–Part 2, Economic Analysis. Sci. Hortic. 2019, 244, 435–444. [Google Scholar] [CrossRef]
- Lauri, P. Apple Tree Architecture and Cultivation-a Tree in a System. In Proceedings of the I International Apple Symposium 1261; ISHS Acta Horticulturae: Yangling, China, 2016; pp. 173–184. [Google Scholar]
- Prabhakar, M.; Gopinath, K.A.; Reddy, A.G.K.; Thirupathi, M.; Rao, C.S. Mapping Hailstorm Damaged Crop Area Using Multispectral Satellite Data. Egypt. J. Remote Sens. Space Sci. 2019, 22, 73–79. [Google Scholar] [CrossRef]
- Botzen, W.J.W.; Bouwer, L.M.; Van den Bergh, J. Climate Change and Hailstorm Damage: Empirical Evidence and Implications for Agriculture and Insurance. Resour. Energy Econ. 2010, 32, 341–362. [Google Scholar] [CrossRef]
- Mandal, D.; Kumar, V.; Ratha, D.; Dey, S.; Bhattacharya, A.; Lopez-Sanchez, J.M.; McNairn, H.; Rao, Y.S. Dual Polarimetric Radar Vegetation Index for Crop Growth Monitoring Using Sentinel-1 SAR Data. Remote Sens. Environ. 2020, 247, 111954. [Google Scholar] [CrossRef]
- De Petris, S.; Berretti, R.; Guiot, E.; Giannetti, F.; Motta, R.; Borgogno-Mondino, E. Detection And Characterization of Forest Harvesting In Piedmont Through Sentinel-2 Imagery: A Methodological Proposal. Ann. Silvic. Res. 2020, 45, 92–98. [Google Scholar] [CrossRef]
- Sarvia, F.; De Petris, S.; Borgogno-Mondino, E. Remotely sensed data to support insurance strategies in agriculture. In Remote Sensing for Agriculture, Ecosystems, and Hydrology XXI; SPIE-Intl. Soc. Opt. Eng.: Strasbourg, France, 2019. [Google Scholar]
- Sarvia, F.; De Petris, S.; Borgogno-Mondino, E. Multi-Scale Remote Sensing to Support Insurance Policies in Agriculture: From Mid-Term to Instantaneous Deductions. GIScience Remote Sens. 2020, 57, 770–784. [Google Scholar] [CrossRef]
- Borgogno-Mondino, E.; Sarvia, F.; Gomarasca, M.A. Supporting Insurance Strategies in Agriculture by Remote Sensing: A Possible Approach at Regional Level. In Proceedings of the Lecture Notes in Computer Science; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2019; pp. 186–199. [Google Scholar]
- Sarvia, F.; De Petris, S.; Borgogno-Mondino, E. A Methodological Proposal to Support Estimation of Damages from Hailstorms Based on Copernicus Sentinel 2 Data Times Series. In Proceedings of the International Conference on Computational Science and Its Applications; Springer: Berlin/Heidelberg, Germany, 2020; pp. 737–751. [Google Scholar]
- Sarvia, F.; Xausa, E.; Petris, S.D.; Cantamessa, G.; Borgogno-Mondino, E. A Possible Role of Copernicus Sentinel-2 Data to Support Common Agricultural Policy Controls in Agriculture. Agronomy 2021, 11, 110. [Google Scholar] [CrossRef]
- Boryan, C.; Yang, Z.; Mueller, R.; Craig, M. Monitoring US Agriculture: The US Department of Agriculture, National Agricultural Statistics Service, Cropland Data Layer Program. Geocarto Int. 2011, 26, 341–358. [Google Scholar] [CrossRef]
- López-Lozano, R.; Duveiller, G.; Seguini, L.; Meroni, M.; García-Condado, S.; Hooker, J.; Leo, O.; Baruth, B. Towards Regional Grain Yield Forecasting with 1 Km-Resolution EO Biophysical Products: Strengths and Limitations at Pan-European Level. Agric. For. Meteorol. 2015, 206, 12–32. [Google Scholar] [CrossRef]
- Chipanshi, A.; Zhang, Y.; Kouadio, L.; Newlands, N.; Davidson, A.; Hill, H.; Warren, R.; Qian, B.; Daneshfar, B.; Bedard, F. Evaluation of the Integrated Canadian Crop Yield Forecaster (ICCYF) Model for in-Season Prediction of Crop Yield across the Canadian Agricultural Landscape. Agric. For. Meteorol. 2015, 206, 137–150. [Google Scholar] [CrossRef]
- de Wit, A.; Duveiller, G.; Defourny, P. Estimating Regional Winter Wheat Yield with WOFOST through the Assimilation of Green Area Index Retrieved from MODIS Observations. Agric. For. Meteorol. 2012, 164, 39–52. [Google Scholar] [CrossRef]
- Doraiswamy, P.C.; Sinclair, T.R.; Hollinger, S.; Akhmedov, B.; Stern, A.; Prueger, J. Application of MODIS Derived Parameters for Regional Crop Yield Assessment. Remote Sens. Environ. 2005, 97, 192–202. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Z.; Tao, F. Improving Regional Winter Wheat Yield Estimation through Assimilation of Phenology and Leaf Area Index from Remote Sensing Data. Eur. J. Agron. 2018, 101, 163–173. [Google Scholar] [CrossRef]
- Patel, N.R.; Bhattacharjee, B.; Mohammed, A.J.; Tanupriya, B.; Saha, S.K. Remote Sensing of Regional Yield Assessment of Wheat in Haryana, India. Int. J. Remote Sens. 2006, 27, 4071–4090. [Google Scholar] [CrossRef]
- Orusa, T.; Orusa, R.; Viani, A.; Carella, E.; Borgogno Mondino, E. Geomatics and EO Data to Support Wildlife Diseases Assessment at Landscape Level: A Pilot Experience to Map Infectious Keratoconjunctivitis in Chamois and Phenological Trends in Aosta Valley (NW Italy). Remote Sens. 2020, 12, 3542. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Microwave Remote Sensing: Active and Passive. Volume 1-Microwave Remote Sensing Fundamentals and Radiometry; Artech House: Norwood, MA, USA, 1981. [Google Scholar]
- Ulaby, F. Radar Response to Vegetation. IEEE Trans. Antennas Propag. 1975, 23, 36–45. [Google Scholar] [CrossRef]
- McNairn, H.; Shang, J. A review of multitemporal synthetic aperture radar (SAR) for crop monitoring. In Multitemporal Remote Sensing; Springer: Berlin, Germany, 2016; pp. 317–340. [Google Scholar]
- Karagiannopoulou, A.; Tsiakos, C.; Tsimiklis, G.; Tsertou, A.; Amditis, A.; Milcinski, G.; Vesel, N.; Protic, D.; Kilibarda, M.; Tsakiridis, N. An integrated service-based solution addressing the modernised common agriculture policy regulations and environmental perspectives. In Proceedings Volume 11528, Remote Sensing for Agriculture, Ecosystems, and Hydrology XXII; International Society for Optics and Photonics: Bellingham, WA, USA, 2020. [Google Scholar]
- Kanjir, U.; DJurić, N.; Veljanovski, T. Sentinel-2 Based Temporal Detection of Agricultural Land Use Anomalies in Support of Common Agricultural Policy Monitoring. ISPRS Int. J. Geo Inf. 2018, 7, 405. [Google Scholar] [CrossRef]
- Lee, J.-S.; Grunes, M.R.; Pottier, E. Quantitative Comparison of Classification Capability: Fully Polarimetric versus Dual and Single-Polarization SAR. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2343–2351. [Google Scholar]
- Ainsworth, T.L.; Kelly, J.P.; Lee, J.-S. Classification Comparisons between Dual-Pol, Compact Polarimetric and Quad-Pol SAR Imagery. ISPRS J. Photogramm. Remote Sens. 2009, 64, 464–471. [Google Scholar] [CrossRef]
- Boerner, W.-M.; Mott, H.; Luneburg, E. Polarimetry in Remote Sensing: Basic and Applied Concepts. In Proceedings of the IGARSS’97, 1997 IEEE International Geoscience and Remote Sensing Symposium Proceedings, Remote Sensing-A Scientific Vision for Sustainable Development Singapore, 3–8 August 1997; Volume 3, pp. 1401–1403. [Google Scholar]
- Cloude, S.R.; Pottier, E. An Entropy Based Classification Scheme for Land Applications of Polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 1997, 35, 68–78. [Google Scholar] [CrossRef]
- Cloude, S.R.; Pottier, E. A Review of Target Decomposition Theorems in Radar Polarimetry. IEEE Trans. Geosci. Remote Sens. 1996, 34, 498–518. [Google Scholar] [CrossRef]
- Nasirzadehdizaji, R.; Balik Sanli, F.; Abdikan, S.; Cakir, Z.; Sekertekin, A.; Ustuner, M. Sensitivity Analysis of Multi-Temporal Sentinel-1 SAR Parameters to Crop Height and Canopy Coverage. Appl. Sci. 2019, 9, 655. [Google Scholar] [CrossRef]
- Betbeder, J.; Fieuzal, R.; Philippets, Y.; Ferro-Famil, L.; Baup, F. Contribution of Multitemporal Polarimetric Synthetic Aperture Radar Data for Monitoring Winter Wheat and Rapeseed Crops. J. Appl. Remote Sens. 2016, 10, 026020. [Google Scholar] [CrossRef]
- Valcarce-Diñeiro, R.; Arias-Pérez, B.; Lopez-Sanchez, J.M.; Sánchez, N. Multi-Temporal Dual-and Quad-Polarimetric Synthetic Aperture Radar Data for Crop-Type Mapping. Remote Sens. 2019, 11, 1518. [Google Scholar] [CrossRef]
- Mercier, A.; Betbeder, J.; Baudry, J.; Le Roux, V.; Spicher, F.; Lacoux, J.; Roger, D.; Hubert-Moy, L. Evaluation of Sentinel-1 & 2 Time Series for Predicting Wheat and Rapeseed Phenological Stages. ISPRS J. Photogramm. Remote Sens. 2020, 163, 231–256. [Google Scholar]
- Qi, Z.; Yeh, A.G.-O.; Li, X. A Crop Phenology Knowledge-Based Approach for Monthly Monitoring of Construction Land Expansion Using Polarimetric Synthetic Aperture Radar Imagery. ISPRS J. Photogramm. Remote Sens. 2017, 133, 1–17. [Google Scholar] [CrossRef]
- Zhao, L.; Yang, J.; Li, P.; Shi, L.; Zhang, L. Characterizing Lodging Damage in Wheat and Canola Using Radarsat-2 Polarimetric SAR Data. Remote Sens. Lett. 2017, 8, 667–675. [Google Scholar] [CrossRef]
- Yang, H.; Chen, E.; Li, Z.; Zhao, C.; Yang, G.; Pignatti, S.; Casa, R.; Zhao, L. Wheat Lodging Monitoring Using Polarimetric Index from RADARSAT-2 Data. Int. J. Appl. Earth Obs. Geoinf. 2015, 34, 157–166. [Google Scholar] [CrossRef]
- Dickinson, C.; Siqueira, P.; Clewley, D.; Lucas, R. Classification of Forest Composition Using Polarimetric Decomposition in Multiple Landscapes. Remote Sens. Environ. 2013, 131, 206–214. [Google Scholar] [CrossRef]
- Trisasongko, B.H. The Use of Polarimetric SAR Data for Forest Disturbance Monitoring. Sens. Imaging 2010, 11, 1–13. [Google Scholar] [CrossRef]
- Le Toan, T.; Beaudoin, A.; Riom, J.; Guyon, D. Relating Forest Biomass to SAR Data. IEEE Trans. Geosci. Remote Sens. 1992, 30, 403–411. [Google Scholar] [CrossRef]
- Ruiz, J.S.; Ordonez, Y.F.; McNairn, H. Corn Monitoring and Crop Yield Using Optical and Microwave Remote Sensing. Geosci. Remote Sens. 2008, 10, 405–420. [Google Scholar]
- Mandal, D.; Kumar, V.; Lopez-Sanchez, J.M.; Bhattacharya, A.; McNairn, H.; Rao, Y.S. Crop Biophysical Parameter Retrieval from Sentinel-1 SAR Data with a Multi-Target Inversion of Water Cloud Model. Int. J. Remote Sens. 2020, 41, 5503–5524. [Google Scholar] [CrossRef]
- Lee, J.-S.; Grunes, M.R.; Ainsworth, T.L.; Du, L.-J.; Schuler, D.L.; Cloude, S.R. Unsupervised Classification Using Polarimetric Decomposition and the Complex Wishart Classifier. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2249–2258. [Google Scholar]
- Freeman, A.; Durden, S.L. A Three-Component Scattering Model for Polarimetric SAR Data. IEEE Trans. Geosci. Remote Sens. 1998, 36, 963–973. [Google Scholar] [CrossRef]
- Ji, K.; Wu, Y. Scattering Mechanism Extraction by a Modified Cloude-Pottier Decomposition for Dual Polarization SAR. Remote Sens. 2015, 7, 7447. [Google Scholar] [CrossRef]
- McNairn, H.; Shang, J.; Jiao, X.; Champagne, C. The Contribution of ALOS PALSAR Multipolarization and Polarimetric Data to Crop Classification. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3981–3992. [Google Scholar] [CrossRef]
- Lopez-Sanchez, J.M.; Cloude, S.R.; Ballester-Berman, J.D. Rice Phenology Monitoring by Means of SAR Polarimetry at X-Band. IEEE Trans. Geosci. Remote Sens. 2011, 50, 2695–2709. [Google Scholar] [CrossRef]
- Ramsey III, E.; Rangoonwala, A.; Suzuoki, Y.; Jones, C.E. Oil Detection in a Coastal Marsh with Polarimetric Synthetic Aperture Radar (SAR). Remote Sens. 2011, 3, 2630. [Google Scholar] [CrossRef]
- Yonezawa, C.; Watanabe, M.; Saito, G. Polarimetric Decomposition Analysis of ALOS PALSAR Observation Data before and after a Landslide Event. Remote Sens. 2012, 4, 2314. [Google Scholar] [CrossRef]
- Cloude, S.R. The Dual Polarisation Entropy/Alpha Decomposition. In Proceedings of the 3rd International Workshop on Science and Applications of SAR Polarimetry and Polarimetric Interferometry, Noordwijk, The Netherlands; 2007; pp. 22–26. [Google Scholar]
- Ghods, S.; Shojaedini, S.V.; Maghsoudi, Y. A Modified H- α Classification Method for Dcp Compact Polarimetric Mode by Reconstructing Quad h and α Parameters from Dual Ones. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2233–2241. [Google Scholar] [CrossRef]
- ISTAT ISTAT Data. Available online: http://dati.istat.it/ (accessed on 13 November 2020).
- Mandal, D.; Vaka, D.S.; Bhogapurapu, N.R.; Vanama, V.S.K.; Kumar, V.; Rao, Y.S.; Bhattacharya, A. Sentinel-1 SLC Preprocessing Workflow for Polarimetric Applications: A Generic Practice for Generating Dual-Pol Covariance Matrix Elements in SNAP S-1 Toolbox. 2019. Available online: https://www.preprints.org/manuscript/201911.0393/v1 (accessed on 9 February 2021).
- Lee, J.-S.; Pottier, E. Polarimetric Radar Imaging: From Basics to Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Shan, Z.; Wang, C.; Zhang, H.; Chen, J. H-Alpha Decomposition and Alternative Parameters for Dual Polarization SAR Data. In Proceedings of the PIERS Proceedings, SuZhou, China, 12–16 September 2011. [Google Scholar]
- Veci, L.; Prats-Iraola, P.; Scheiber, R.; Collard, F.; Fomferra, N.; Engdahl, M. The Sentinel-1 Toolbox. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Quebec City, QC, Canada, 13–18 July 2014; pp. 1–3. [Google Scholar]
- Ainsworth, T.L.; Kelly, J.; Lee, J.-S. Polarimetric Analysis of Dual Polarimetric SAR Imagery. In Proceedings of the 7th European Conference on Synthetic Aperture Radar; VDE, Friedrichshafen, Germany, 2–5 June 2008; 2008; pp. 1–4. [Google Scholar]
- Crabbe, R.A.; Lamb, D.W.; Edwards, C.; Andersson, K.; Schneider, D. A Preliminary Investigation of the Potential of Sentinel-1 Radar to Estimate Pasture Biomass in a Grazed Pasture Landscape. Remote Sens. 2019, 11, 872. [Google Scholar] [CrossRef]
- Chang, J.; Shoshany, M. Radar Polarization and Ecological Pattern Properties across Mediterranean-to-Arid Transition Zone. Remote Sens. Environ. 2017, 200, 368–377. [Google Scholar] [CrossRef]
- Chang, J.G.; Shoshany, M.; Oh, Y. Polarimetric Radar Vegetation Index for Biomass Estimation in Desert Fringe Ecosystems. IEEE Trans. Geosci. Remote Sens. 2018, 56, 7102–7108. [Google Scholar] [CrossRef]
- Cloude, S. Polarisation: Applications in Remote Sensing; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Raney, R.K.; Cahill, J.T.; Patterson, G.W.; Bussey, D.B.J. The M-Chi Decomposition of Hybrid Dual-Polarimetric Radar Data with Application to Lunar Craters. J. Geophys. Res. Planets 2012, 117. [Google Scholar] [CrossRef]
- Borgogno Mondino, E.; Fissore, V.; Lessio, A.; Motta, R. Are the New Gridded DSM/DTMs of the Piemonte Region (Italy) Proper for Forestry? A Fast and Simple Approach for a Posteriori Metric Assessment. iFor. Biogeosci. For. 2016, 9, 901–909. [Google Scholar] [CrossRef]
- Nachar, N. The Mann-Whitney U: A Test for Assessing Whether Two Independent Samples Come from the Same Distribution. Tutor. Quant. Methods Psychol. 2008, 4, 13–20. [Google Scholar] [CrossRef]
- Hollander, M.; Wolfe, D.A.; Chicken, E. Nonparametric Statistical Methods; John Wiley & Sons: Hoboken, NJ, USA, 2013; Volume 751. [Google Scholar]
- R Development Core Team, R. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013. [Google Scholar]
- Conrad, O.; Bechtel, B.; Bock, M.; Dietrich, H.; Fischer, E.; Gerlitz, L.; Wehberg, J.; Wichmann, V.; Böhner, J. System for Automated Geoscientific Analyses (SAGA) v. 2.1. 4. Geosci. Model Dev. Discuss. 2015, 8, 1991–2007. [Google Scholar] [CrossRef]
- Wallis, W.A. Compounding Probabilities from Independent Significance Tests. Econom. J. Econom. Soc. 1942, 10, 229–248. [Google Scholar] [CrossRef]
- Zliobaite, I. On the Relation between Accuracy and Fairness in Binary Classification. arXiv 2015, arXiv:1505.05723. [Google Scholar]
- Akosa, J. Predictive Accuracy: A Misleading Performance Measure for Highly Imbalanced Data. Available online: https://www.semanticscholar.org/paper/Predictive-Accuracy-%3A-A-Misleading-Performance-for-Akosa/8eff162ba887b6ed3091d5b6aa1a89e23342cb5c (accessed on 9 February 2021).
- Guo, X.; Yin, Y.; Dong, C.; Yang, G.; Zhou, G. On the Class Imbalance Problem. In Proceedings of the 2008 Fourth International Conference on Natural Computation; IEEE: Jinan, China, 2008; Volume 4, pp. 192–201. [Google Scholar]

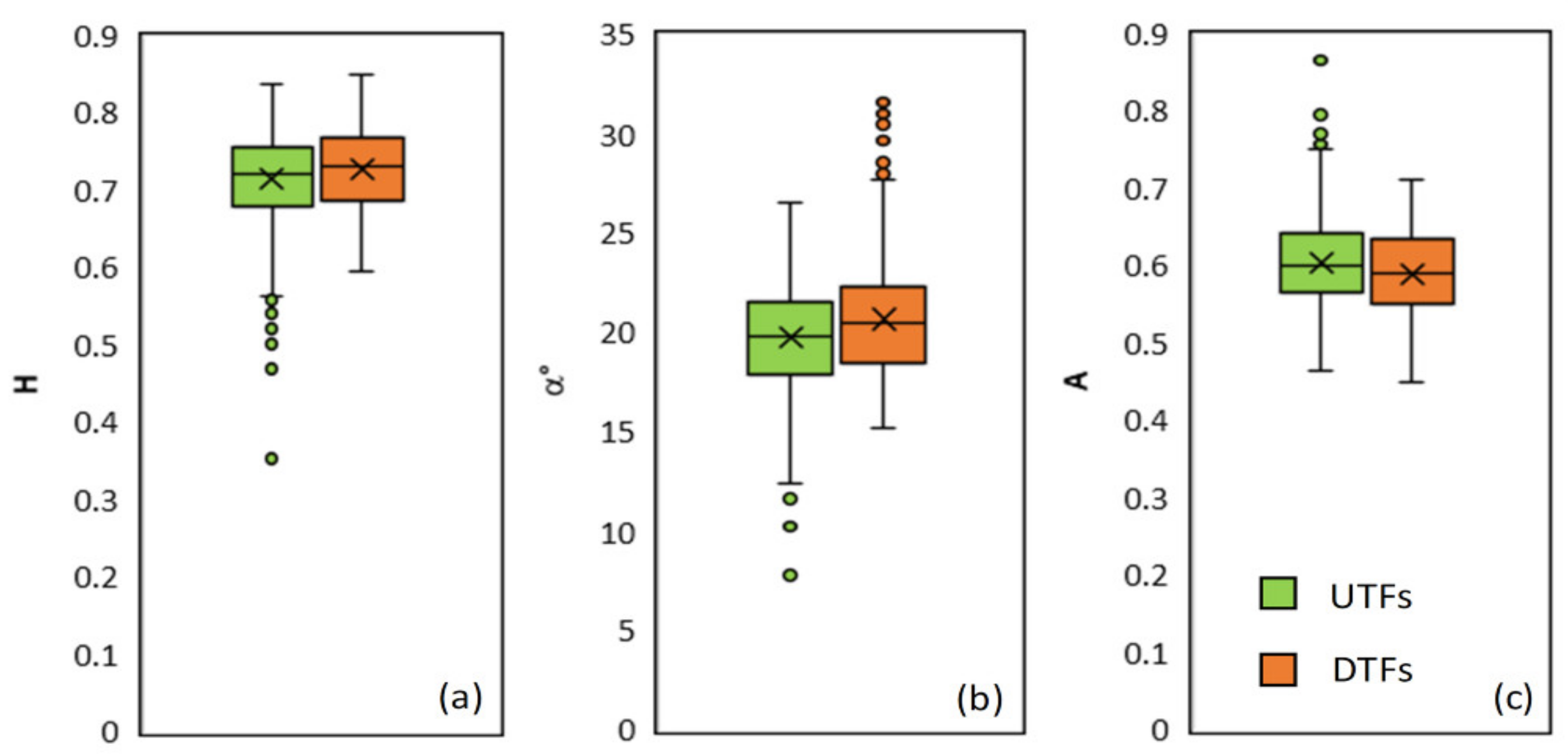
| U | p-Value | |
|---|---|---|
| H | 14,514 | 0.000159 |
| α | 16,604 | 3.83×10−10 |
| A | 8616 | 0.000161 |
| Classification | |||
|---|---|---|---|
| Damaged | Undamaged | ||
| Reference | Damaged | 8 | 2 |
| Undamaged | 6 | 15 | |
| Accuracies | |||
| Measure | Value | Formula | |
| Sensitivity | 0.80 | TPR = TP/ (TP + FN) | |
| Specificity | 0.71 | SPC = TN/ (FP + TN) | |
| Precision | 0.57 | PPV = TP/ (TP + FP) | |
| Negative Predictive Value | 0.88 | NPV = TN/ (TN + FN) | |
| False Positive Rate | 0.28 | FPR = FP/ (FP + TN) | |
| False Discovery Rate | 0.42 | FDR = FP/ (FP + TP) | |
| False Negative Rate | 0.20 | FNR = FN/ (FN + TP) | |
| Overall Accuracy | 0.74 | OA = (TP + TN) / (TP + TN + FP + FN) | |
| F1 Score | 0.66 | F1 = 2TP/ (2TP + FP + FN) | |
| Balanced Accuracy | 0.75 | BA = TPR + TNR/2 | |
| G-Mean | 0.67 | G-mean= sqrt (TPR *PPV) | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Petris, S.; Sarvia, F.; Gullino, M.; Tarantino, E.; Borgogno-Mondino, E. Sentinel-1 Polarimetry to Map Apple Orchard Damage after a Storm. Remote Sens. 2021, 13, 1030. https://doi.org/10.3390/rs13051030
De Petris S, Sarvia F, Gullino M, Tarantino E, Borgogno-Mondino E. Sentinel-1 Polarimetry to Map Apple Orchard Damage after a Storm. Remote Sensing. 2021; 13(5):1030. https://doi.org/10.3390/rs13051030
Chicago/Turabian StyleDe Petris, Samuele, Filippo Sarvia, Michele Gullino, Eufemia Tarantino, and Enrico Borgogno-Mondino. 2021. "Sentinel-1 Polarimetry to Map Apple Orchard Damage after a Storm" Remote Sensing 13, no. 5: 1030. https://doi.org/10.3390/rs13051030
APA StyleDe Petris, S., Sarvia, F., Gullino, M., Tarantino, E., & Borgogno-Mondino, E. (2021). Sentinel-1 Polarimetry to Map Apple Orchard Damage after a Storm. Remote Sensing, 13(5), 1030. https://doi.org/10.3390/rs13051030