A Lidar-Based 3-D Photosynthetically Active Radiation Model Reveals the Spatiotemporal Variations of Forest Sunlit and Shaded Leaves
Abstract
1. Introduction
- (1)
- Develop and validate a lidar-based approach for estimating forest incident direct and diffuse solar radiation from a 3-D perspective;
- (2)
- Identify the sunlit and shaded leaves and map their spatiotemporal distribution patterns;
- (3)
- Investigate the effects of lidar scanning geometry, point density, penumbra effects, and woody materials on the separation of sunlit and shaded leaves.
2. Materials and Methods
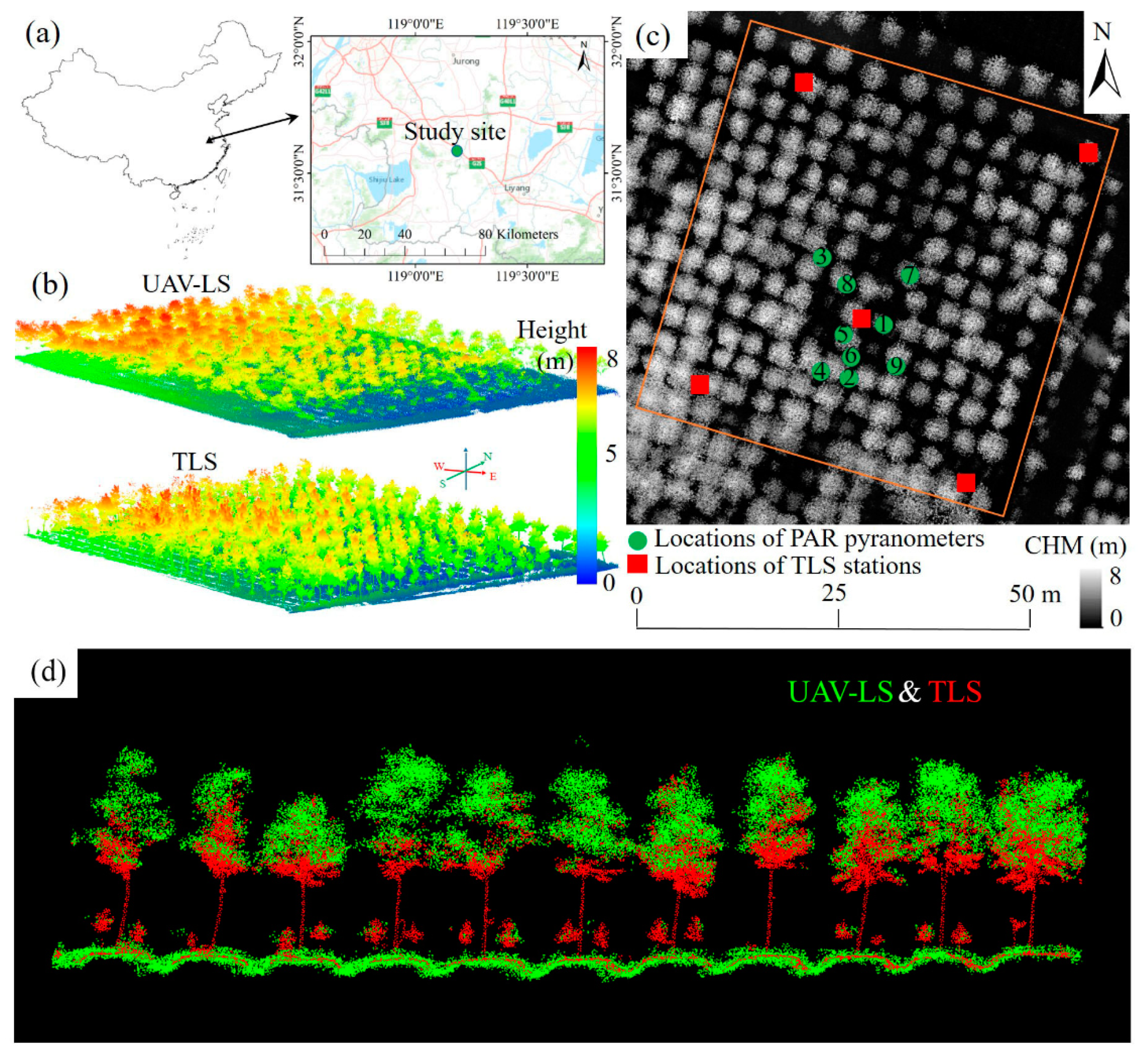
2.1. Study Site
2.2. Datasets
2.2.1. Lidar Data Acquisition and Pre-Processing
- UAV-LS point cloud data
- TLS point cloud data
- Registration of UAV-LS and TLS data
2.2.2. Field-Based Pyranometer Measurements
- BF-5 sunshine sensor data
- Photo quantum sensor data
- TRAC data
2.2.3. Validation Data
- Manually classified forest points
- PAR validation
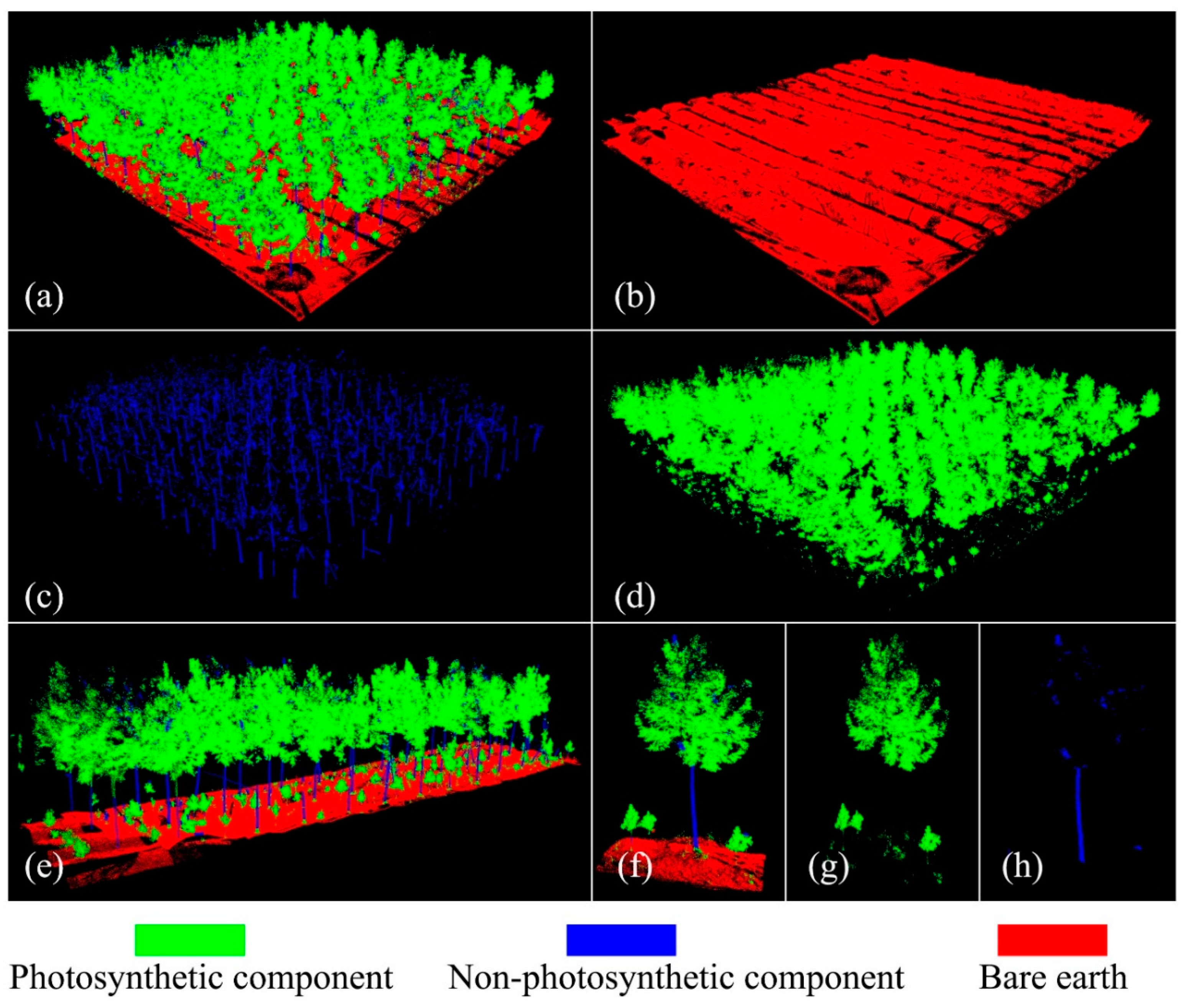
2.3. Separation of Photosynthetic and Non-Photosynthetic Forest Components
2.4. Lidar-Based Forest Sunlit and Shaded Leaves (LFSSL) Identification Algorithm
2.4.1. Lidar-Based Forest 3-D PAR
- Direct PAR component
- Diffuse PAR component
- Scatter PAR component
2.4.2. Forest Penumbra Effects Characterization
2.4.3. Identification of Sunlit and Shaded Leaves
2.5. Sensitivity Analysis
3. Results
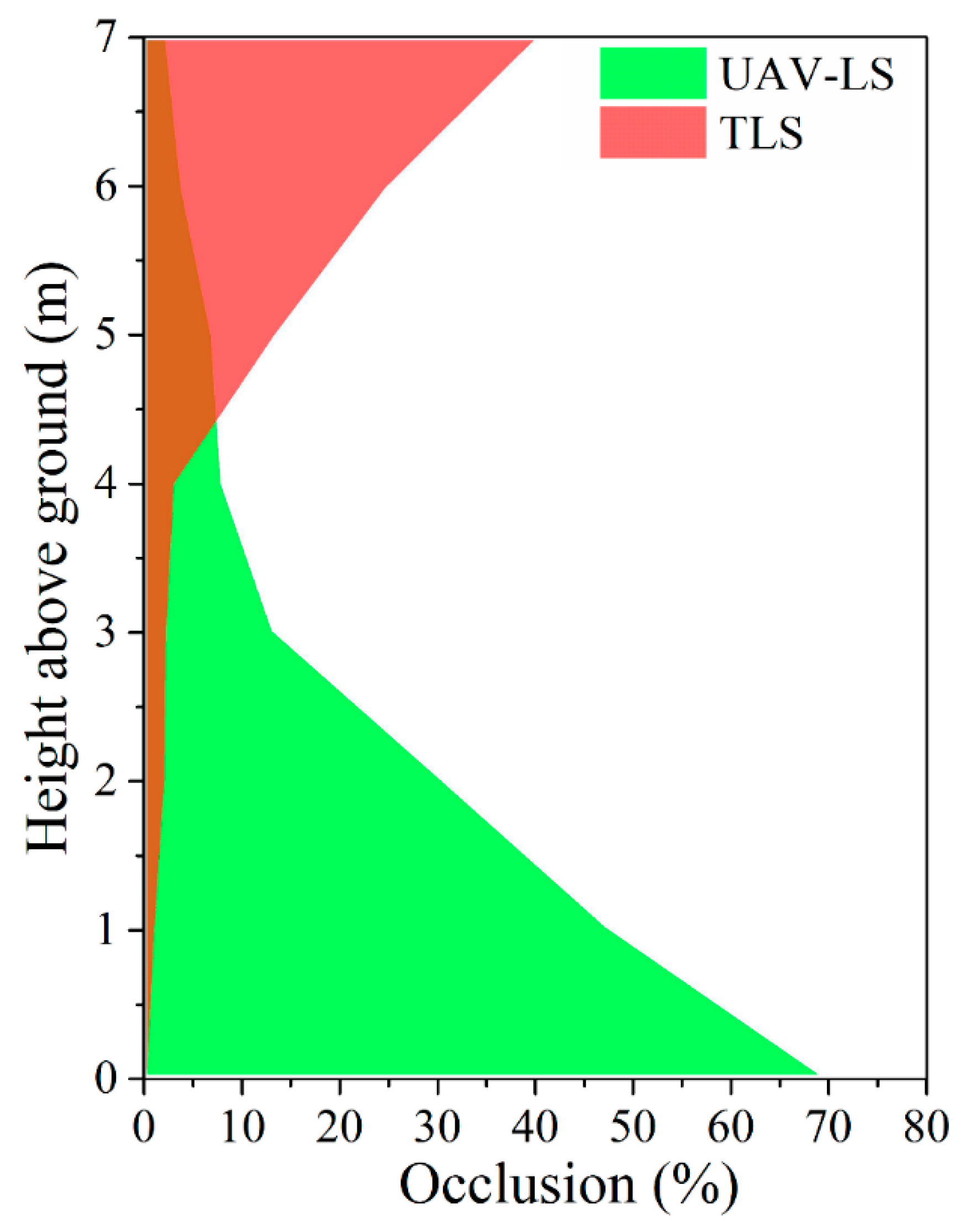
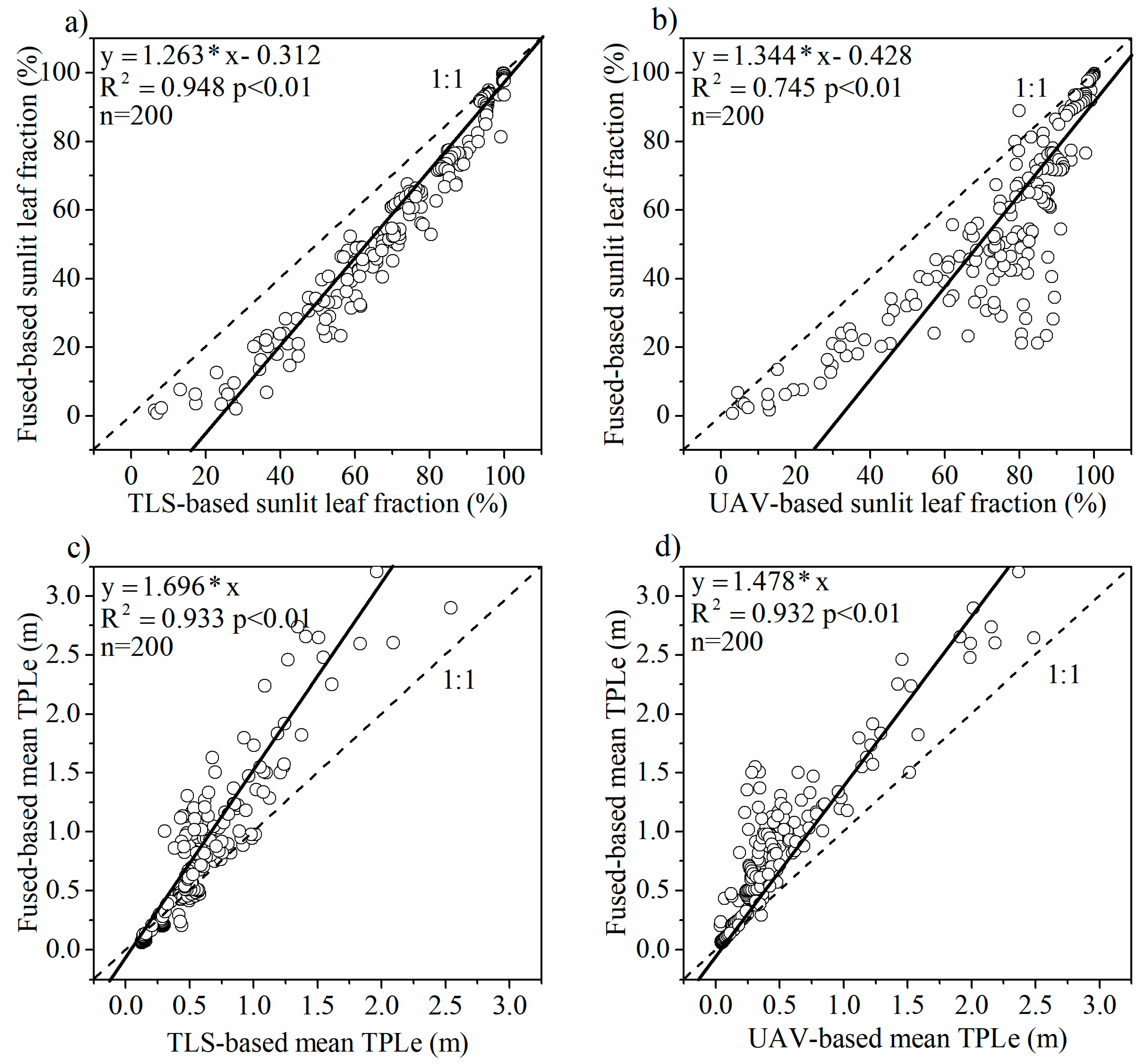
3.1. UAV and TLS Fused Points
3.2. Forest Point Classification
3.3. Sunlit and Shaded Leaves Identification
3.3.1. Spatiotemporal Distributions of PAR
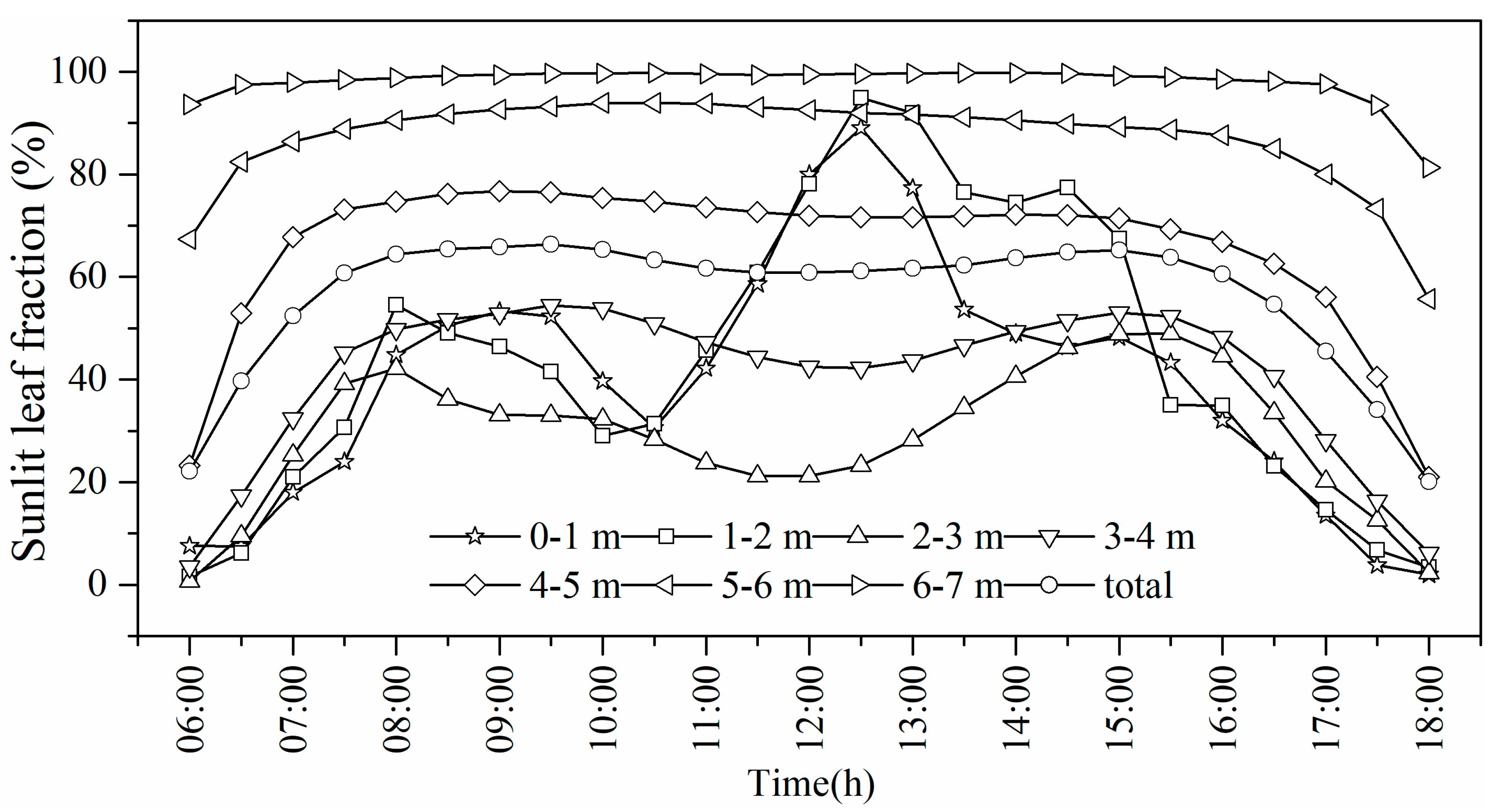
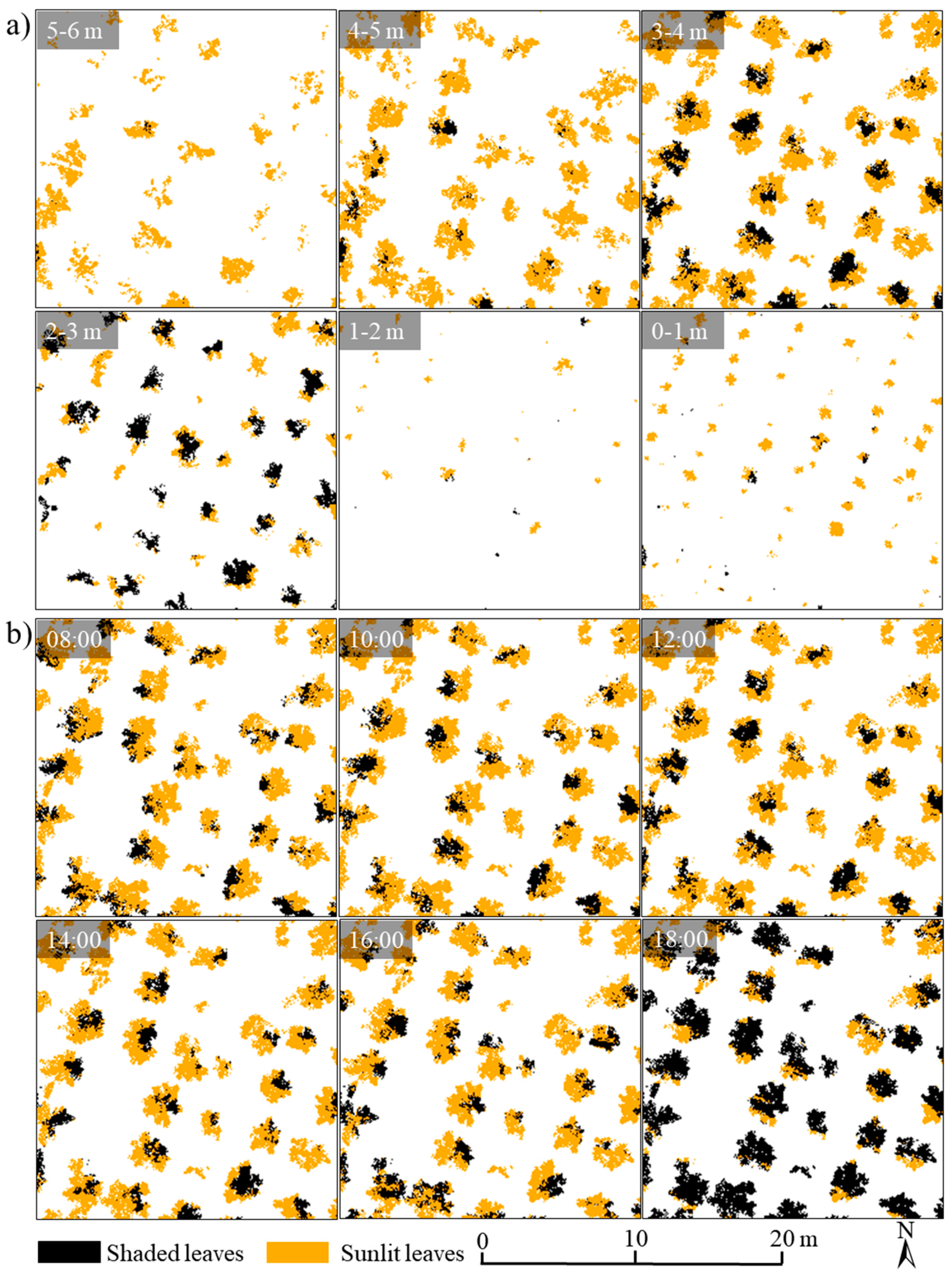
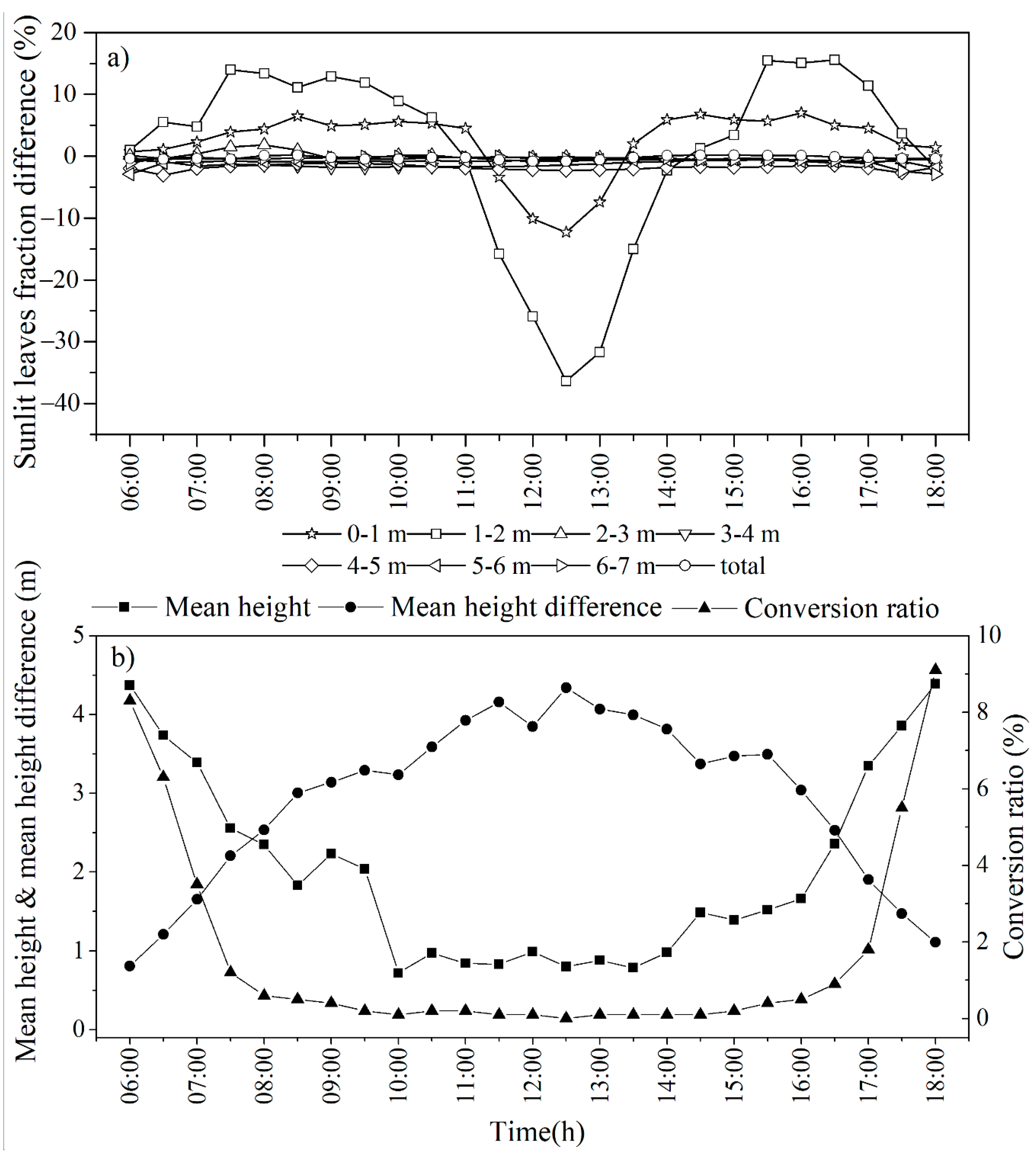
3.3.2. Spatiotemporal Distributions of Sunlit and Shaded Leaves
3.4. Sensitivity Analysis on Sunlit and Shaded Leaves Identification
3.4.1. The Laser Scanning Geometry
3.4.2. The Point Density
3.4.3. Woody Materials
3.4.4. Penumbra Areas
3.4.5. Leaf Movements
4. Discussion
4.1. Effects of Laser Scanning Geometry
4.2. Effects of Point Density
4.3. Effects of Woody Materials
4.4. Effects of Penumbra Areas
4.5. Effects of Leaf Movements
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wilson, J.W. Stand structure and light penetration. III. Sunlit foliage area. J. Appl. Ecol. 1967, 159–165. [Google Scholar] [CrossRef]
- Ellsworth, D.; Reich, P. Canopy structure and vertical patterns of photosynthesis and related leaf traits in a deciduous forest. Oecologia 1993, 96, 169–178. [Google Scholar] [CrossRef]
- Gu, L.; Baldocchi, D.; Verma, S.B.; Black, T.; Vesala, T.; Falge, E.M.; Dowty, P.R. Advantages of diffuse radiation for terrestrial ecosystem productivity. J. Geophys. Res.-Atmos. 2002, 107, ACL 2-1–ACL 2-23. [Google Scholar] [CrossRef]
- Stenberg, P. Penumbra in within-Shoot and between-Shoot Shading in Conifers and Its Significance for Photosynthesis. Ecol. Model. 1995, 77, 215–231. [Google Scholar] [CrossRef]
- Dengel, S.; Grace, J.; MacArthur, A. Transmissivity of solar radiation within a Picea sitchensis stand under various sky conditions. Biogeosci. Discuss. 2015, 12, 3825. [Google Scholar] [CrossRef]
- Denholm, J. The influence of penumbra on canopy photosynthesis I. Theoretical considerations. Agric. Meteorol. 1981, 25, 145–166. [Google Scholar] [CrossRef]
- Zheng, T.; Chen, J.M. Photochemical reflectance ratio for tracking light use efficiency for sunlit leaves in two forest types. ISPRS J. Photogramm. 2017, 123, 47–61. [Google Scholar] [CrossRef]
- Chen, J.M.; Wang, Z.; Zhang, F.; Mo, G. Chlorophyll Fluorescence Is a Better Proxy for Sunlit Leaf Than Total Canopy Photosynthesis//Agu Fall Meeting. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 11–15 December 2015. [Google Scholar]
- Hilker, T.; Coops, N.C.; Schwalm, C.R.; Jassal, R.P.S.; Black, T.A.; Krishnan, P. Effects of mutual shading of tree crowns on prediction of photosynthetic light-use efficiency in a coastal Douglas-fir forest. Tree Physiol. 2008. [Google Scholar] [CrossRef]
- Maguire, A.J.; Eitel, J.U.H.; Griffin, K.L.; Magney, T.S.; Long, R.A.; Vierling, L.A.; Schmiege, S.C.; Jennewein, J.S.; Weygint, W.A.; Boelman, N.T. On the Functional Relationship Between Fluorescence and Photochemical Yields in Complex Evergreen Needleleaf Canopies. Geophys. Res. Lett. 2020, 47. [Google Scholar] [CrossRef]
- Wieneke, S.; Burkart, A.; Cendrero-Mateo, M.P.; Julitta, T.; Rossini, M.; Schickling, A.; Schmidt, M.; Rascher, U. Linking photosynthesis and sun-induced fluorescence at sub-daily to seasonal scales. Remote Sens. Environ. 2018, 219, 247–258. [Google Scholar] [CrossRef]
- Van der Tol, C.; Berry, J.A.; Campbell, P.K.E.; Rascher, U. Models of fluorescence and photosynthesis for interpreting measurements of solar-induced chlorophyll fluorescence. J. Geophys. Res. Biogeosci. 2014, 119, 2312–2327. [Google Scholar] [CrossRef] [PubMed]
- Canham, C.D.; Coates, K.D.; Bartemucci, P.; Quaglia, S. Measurement and modeling of spatially explicit variation in light transmission through interior cedar-hemlock forests of British Columbia. Can. J. For. Res. 1999, 29, 1775–1783. [Google Scholar] [CrossRef]
- Kotchenova, S.Y.; Song, X.; Shabanov, N.V.; Potter, C.S.; Knyazikhin, Y.; Myneni, R.B. Lidar remote sensing for modeling gross primary production of deciduous forests. Remote Sens. Environ. 2004, 92, 158–172. [Google Scholar] [CrossRef]
- Norman, J.M. Simulations of microclimates. In Biometeorology in Integrated Pest Management; Hatfield, J.L., Thomason, I.J., Eds.; Academic Press: Cambridge, MA, USA, 1982. [Google Scholar] [CrossRef]
- Huang, Q.; Qiu, F.; Fan, W.; Liu, Y.; Zhang, Q. Evaluation of Different Methods for Estimating the Fraction of Sunlit Leaves and Its Contribution for Photochemical Reflectance Index Utilization in a Coniferous Forest. Remote Sens. 2019, 11, 1643. [Google Scholar] [CrossRef]
- Wang, Y.P.; Jarvis, P.G. Description and Validation of an Array Model–Maestro. Agric. For. Meteorol. 1990, 51, 257–280. [Google Scholar] [CrossRef]
- Begue, A.; Hanan, N.P.; Prince, S.D. Radiative-Transfer in Shrub Savanna Sites in Niger—Preliminary-Results from Hapex-Sahel.2. Photosynthetically Active Radiation Interception of the Woody Layer. Agric. For. Meteorol. 1994, 69, 247–266. [Google Scholar] [CrossRef]
- Guillen-Climent, M.L.; Zarco-Tejada, P.J.; Berni, J.A.J.; North, P.R.J.; Villalobos, F.J. Mapping radiation interception in row-structured orchards using 3D simulation and high-resolution airborne imagery acquired from a UAV. Precis. Agric. 2012, 13, 473–500. [Google Scholar] [CrossRef]
- Asrar, G.M.; Fuchs, M.; Kanemasu, E.T.; Hatfield, J.L. Estimating Absorbed Photosynthetic Radiation and Leaf Area Index from Spectral Reflectance in Wheat1. Agron. J. 1984, 76, 121A. [Google Scholar] [CrossRef]
- Gallo, K.P.; Daughtry, C.S.T.; Bauer, M.E. Spectral estimation of absorbed photosynthetically active radiation in corn canopies. Remote Sens. Environ. 1985, 17, 221–232. [Google Scholar] [CrossRef]
- Daughtry, C.S.T.; Gallo, K.P.; Goward, S.N.; Prince, S.D.; Kustas, W.P. Spectral Estimates of Absorbed Radiation and Phytomass Production in Corn and Soybean Canopies. Remote Sens. Environ. 1992, 39, 141–152. [Google Scholar] [CrossRef]
- Hanan, N.P.; Prince, S.D.; Begue, A. Estimation of absorbed photosynthetically active radiation and vegetation net production efficiency using satellite data. Agric. For. Meteorol. 1995, 76, 259–276. [Google Scholar] [CrossRef]
- Isabelle, P.-E.; Nadeau, D.F.; Asselin, M.-H.; Harvey, R.; Musselman, K.N.; Rousseau, A.N.; Anctil, F. Solar radiation transmittance of a boreal balsam fir canopy: Spatiotemporal variability and impacts on growing season hydrology. Agric. For. Meteorol. 2018, 263, 1–14. [Google Scholar] [CrossRef]
- Moeser, D.; Roubinek, J.; Schleppi, P.; Morsdorf, F.; Jonas, T. Canopy closure, LAI and radiation transfer from airborne LiDAR synthetic images. Agric. For. Meteorol. 2014, 197, 158–168. [Google Scholar] [CrossRef]
- Musselman, K.N.; Molotch, N.P.; Margulis, S.A.; Kirchner, P.B.; Bales, R.C. Influence of canopy structure and direct beam solar irradiance on snowmelt rates in a mixed conifer forest. Agric. For. Meteorol. 2012, 161, 46–56. [Google Scholar] [CrossRef]
- Fan, W.; Li, J.; Liu, Q. GOST2: The improvement of the canopy reflectance model GOST in separating the sunlit and shaded leaves. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 1423–1431. [Google Scholar] [CrossRef]
- Olpenda, A.S.; Sterenczak, K.; Bedkowski, K. Modeling Solar Radiation in the Forest Using Remote Sensing Data: A Review of Approaches and Opportunities. Remote Sens. 2018, 10, 694. [Google Scholar] [CrossRef]
- Tymen, B.; Vincent, G.; Courtois, E.A.; Heurtebize, J.; Dauzat, J.; Marechaux, I.; Chave, J. Quantifying micro-environmental variation in tropical rainforest understory at landscape scale by combining airborne LiDAR scanning and a sensor network. Ann. For. Sci. 2017, 74. [Google Scholar] [CrossRef]
- Bode, C.A.; Limm, M.P.; Power, M.E.; Finlay, J.C. Subcanopy Solar Radiation model: Predicting solar radiation across a heavily vegetated landscape using LiDAR and GIS solar radiation models. Remote Sens. Environ. 2014, 154, 387–397. [Google Scholar] [CrossRef]
- Alexander, C.; Moeslund, J.E.; Bocher, P.K.; Arge, L.; Svenning, J.C. Airborne laser scanner (LiDAR) proxies for understory light conditions. Remote Sens. Environ. 2013, 134, 152–161. [Google Scholar] [CrossRef]
- Oshio, H.; Asawa, T. Estimating the Solar Transmittance of Urban Trees Using Airborne LiDAR and Radiative Transfer Simulation. IEEE T Geosci. Remote 2016, 54, 5483–5492. [Google Scholar] [CrossRef]
- Musselman, K.N.; Margulis, S.A.; Molotch, N.P. Estimation of solar direct beam transmittance of conifer canopies from airborne LiDAR. Remote Sens. Environ. 2013, 136, 402–415. [Google Scholar] [CrossRef]
- Nyman, P.; Metzen, D.; Hawthorne, S.N.D.; Duff, T.J.; Inbar, A.; Lane, P.N.J.; Sheridan, G.J. Evaluating models of shortwave radiation below Eucalyptus canopies in SE Australia. Agric. For. Meteorol. 2017, 246, 51–63. [Google Scholar] [CrossRef]
- Van der Zande, D.; Stuckens, J.; Verstraeten, W.W.; Mereu, S.; Muys, B.; Coppin, P. 3D modeling of light interception in heterogeneous forest canopies using ground-based LiDAR data. Int. J. Appl. Earth Obs. 2011, 13, 792–800. [Google Scholar] [CrossRef]
- Bittner, S.; Gayler, S.; Biernath, C.; Winkler, J.B.; Seifert, S.; Pretzsch, H.; Priesack, E. Evaluation of a ray-tracing canopy light model based on terrestrial laser scans. Can. J. Remote Sens. 2012, 38, 619–628. [Google Scholar] [CrossRef]
- Cifuentes, R.; Van der Zande, D.; Salas, C.; Tits, L.; Farifteh, J.; Coppin, P. Modeling 3D Canopy Structure and Transmitted PAR Using Terrestrial LiDAR. Can. J. Remote Sens. 2017, 43, 124–139. [Google Scholar] [CrossRef]
- Peng, S.Z.; Zhao, C.Y.; Xu, Z.L. Modeling spatiotemporal patterns of understory light intensity using airborne laser scanner (LiDAR). ISPRS-J. Photogramm. Remote Sens. 2014, 97, 195–203. [Google Scholar] [CrossRef]
- Zheng, G.; Ma, L.; He, W.; Eitel, J.U.; Moskal, L.M.; Zhang, Z. Assessing the contribution of woody materials to forest angular gap fraction and effective leaf area index using terrestrial laser scanning data. IEEE Trans. Geosci. Remote 2015, 54, 1475–1487. [Google Scholar] [CrossRef]
- Verrelst, J.; Schaepman, M.E.; Malenovsky, Z.; Clevers, J.G.P.W. Effects of woody elements on simulated canopy reflectance: Implications for forest chlorophyll content retrieval. Remote Sens. Environ. 2010, 114, 647–656. [Google Scholar] [CrossRef]
- Schneider, F.D.; Kukenbrink, D.; Schaepman, M.E.; Schimel, D.S.; Morsdorf, F. Quantifying 3D structure and occlusion in dense tropical and temperate forests using close-range LiDAR. Agric. For. Meteorol. 2019, 268, 249–257. [Google Scholar] [CrossRef]
- Calders, K.; Adams, J.; Armston, J.; Bartholomeus, H.; Bauwens, S.; Bentley, L.P.; Chave, J.; Danson, F.M.; Demol, M.; Disney, M.; et al. Terrestrial laser scanning in forest ecology: Expanding the horizon. Remote Sens. Environ. 2020, 251, 112102. [Google Scholar] [CrossRef]
- Vaaja, M.T.; Virtanen, J.P.; Kurkela, M.; Lehtola, V.; Hyyppa, J.; Hyyppa, H. The Effect of Wind on Tree Stem Parameter Estimation Using Terrestrial Laser Scanning. ISPRS Ann. Photogramm. Remote 2016, 3, 117–122. [Google Scholar] [CrossRef]
- Zeng, K.; Zheng, G.; Ma, L.; Ju, W.; Pang, Y. Modelling Three-Dimensional Spatiotemporal Distributions of Forest Photosynthetically Active Radiation Using UAV-Based Lidar Data. Remote Sens. 2019, 11, 2806. [Google Scholar] [CrossRef]
- Chen, J.M.; Cihlar, J. Plant canpy gap-size analysis theory for improving optical measurement of leaf-area index. Appl. Opt. 1995, 34, 6211–6222. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.X.; Zheng, G.; Eitel, J.U.H.; Moskal, L.M.; He, W.; Huang, H.B. Improved Salient Feature-Based Approach for Automatically Separating Photosynthetic and Nonphotosynthetic Components Within Terrestrial Lidar Point Cloud Data of Forest Canopies. IEEE Trans. Geosci. Remote Sens. 2016, 54, 679–696. [Google Scholar] [CrossRef]
- Grant, R.H.; Heisler, G.M.; Gao, W. Photosynthetically-active radiation: Sky radiance distributions under clear and overcast conditions. Agric. For. Meteorol. 1996, 82, 267–292. [Google Scholar] [CrossRef]
- Chen, J.M.; Liu, J.; Cihlar, J.; Goulden, M.L. Daily canopy photosynthesis model through temporal and spatial scaling for remote sensing applications. Ecol. Model. 1999, 124, 99–119. [Google Scholar] [CrossRef]
- Liu, J.; Chen, J.M.; Cihlar, J. Mapping evapotranspiration based on remote sensing: An application to Canada’s landmass. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Zheng, G.; Moskal, L.M.; Kim, S.H. Retrieval of Effective Leaf Area Index in Heterogeneous Forests With Terrestrial Laser Scanning. IEEE Trans. Geosci. Remote Sens. 2013, 51, 777–786. [Google Scholar] [CrossRef]
- Chen, J.M.; Cihlar, J. Quantifying the effect of canopy architecture on optical measurement of leaf area index using 2 gap size analysis mehtods. IEEE Trans. Geosci. Remote Sens. 1995, 33, 777–787. [Google Scholar] [CrossRef]
- Miller, E.E.; Norman, J.M. Sunfleck theory for plant canopies: 2. penumbra effect—Intensity distributions along sunfleck segments. Agron. J. 1971, 63, 739–743. [Google Scholar] [CrossRef]
- Celebi, M.E.; Kingravi, H.A.; Vela, P.A. A comparative study of efficient initialization methods for the k-means clustering algorithm. Expert. Syst. Appl. 2013, 40, 200–210. [Google Scholar] [CrossRef]
- Morsdorf, F.; Kukenbrink, D.; Schneider, F.D.; Abegg, M.; Schaepman, M.E. Close-range laser scanning in forests: Towards physically based semantics across scales. Interface Focus 2018, 8. [Google Scholar] [CrossRef]
- Kükenbrink, D.; Schneider, F.D.; Leiterer, R.; Schaepman, M.E.; Morsdorf, F. Quantification of hidden canopy volume of airborne laser scanning data using a voxel traversal algorithm. Remote Sens. Environ. 2017, 194, 424–436. [Google Scholar] [CrossRef]
- Crespo-Peremarch, P.; Fournier, R.; Nguyen, V.-T.; Lier, O.; Ruiz, L. A comparative assessment of the vertical distribution of forest components using full-waveform airborne, discrete airborne and discrete terrestrial laser scanning data. For. Ecol. Manag. 2020, 473, 118268. [Google Scholar] [CrossRef]
- Hilker, T.; Coops, N.C.; Newnham, G.J.; van Leeuwen, M.; Wulder, M.A.; Stewart, J.; Culvenor, D.S. Comparison of Terrestrial and Airborne LiDAR in Describing Stand Structure of a Thinned Lodgepole Pine Forest. J. For. 2012, 110, 97–104. [Google Scholar] [CrossRef]
- Campbell, M.; Dennison, P.; Hudak, A.T.; Parham, L.; Butler, B. Quantifying understory vegetation density using small-footprint airborne lidar. Remote Sens. Environ. 2018, 215, 330–342. [Google Scholar] [CrossRef]
- Luo, S.; Chen, J.; Wang, C.; Xiaohuan, X.; Zeng, H.; Peng, D.; Li, D. Effects of LiDAR point density, sampling size and height threshold on estimation accuracy of crop biophysical parameters. Opt. Express 2016, 24, 11578. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.; Liu, H.; Pang, L.; Fang, L.; Dou, W. DBSCAN-based point cloud extraction for Tomographic synthetic aperture radar (TomoSAR) three-dimensional (3D) building reconstruction. Int. J. Remote Sens. 2021, 42, 2327–2349. [Google Scholar] [CrossRef]
- Kazemi, U.; Boostani, R. FEM-DBSCAN: An Efficient Density-Based Clustering Approach. Iran. J. Sci. Technol.-Trans. Electr. Eng. 2021. [Google Scholar] [CrossRef]
- Michalowska, M.; Rapinski, J. A Review of Tree Species Classification Based on Airborne LiDAR Data and Applied Classifiers. Remote Sens. 2021, 13, 353. [Google Scholar] [CrossRef]
- Zhang, J.; Whiting, M.D.; Zhang, Q. Diurnal pattern in canopy light interception for tree fruit orchard trained to an upright fruiting offshoots (UFO) architecture. Biosyst. Eng. 2015, 129, 1–10. [Google Scholar] [CrossRef]
- Smith, W.; Knapp, A.; Reiners, W. Penumbral Effects on Sunlight Penetration in Plant Communities. Ecology 1989, 70. [Google Scholar] [CrossRef]
- Bakay, L.; Moravcik, L. Quantification of Circadian Movement of Small-Leaved Lime (Tilia cordata Mill.) Saplings With Short Interval Terrestrial Laser Scanning. Front. Plant Sci. 2020, 11, 984. [Google Scholar] [CrossRef] [PubMed]
- Seidel, D.; Fleck, S.; Leuschner, C. Analyzing forest canopies with ground-based laser-scanning: A comparison with hemispherical photography. Agric. For. Meteorol. 2011, 154–155, 1–8. [Google Scholar] [CrossRef]
- Zlinszky, A.; Molnár, B.; Barfod, A. Not All Trees Sleep the Same—High Temporal Resolution Terrestrial Laser Scanning Shows Differences in Nocturnal Plant Movement. Front. Plant Sci. 2017, 8, 1814. [Google Scholar] [CrossRef]
- Jackson, T.; Shenkin, A.; Moore, J.; Bunce, A.; van Emmerik, T.; Kane, B.; Burcham, D.; James, K.; Selker, J.; Calders, K.; et al. An architectural understanding of natural sway frequencies in trees. J. R. Soc. Interface 2019, 16. [Google Scholar] [CrossRef]
- Campos, M.; Litkey, P.; Wang, Y.; Chen, Y.; Hyyti, H.; Hyyppä, J.; Puttonen, E. A Long-Term Terrestrial Laser Scanning Measurement Station to Continuously Monitor Structural and Phenological Dynamics of Boreal Forest Canopy. Front. Plant Sci. 2021, 11. [Google Scholar] [CrossRef]





| Class Type | Total Number of Points | Correctly Classified Number of Points | User’s Accuracy | Producer’s Accuracy |
|---|---|---|---|---|
| Bare earth | 244,549 | 235,794 | 96.42% | 93.56% |
| Photosynthetic component | 1,138,333 | 1,106,004 | 97.16% | 98.92% |
| Non-photosynthetic component | 105,746 | 80,705 | 76.32% | 78.41% |
| Overall | 1,488,628 | 1,422,503 | 95.55% | 95.69% |
| Canopy Layer | NPD = 25 mm | NPD = 45 mm | NPD = 65 mm | NPD = 85 mm | NPD = 100 mm |
|---|---|---|---|---|---|
| 6–7 m | 0.40% | 0.80% | 1.20% | 3.10% | 4.10% |
| 5–6 m | 1.40% | 3.90% | 6.30% | 7.10% | 8.50% |
| 4–5 m | 4.30% | 11.90% | 14.80% | 20.30% | 13.60% |
| 3–4 m | 8.90% | 19.10% | 22.60% | 36.50% | 17.20% |
| 2–3 m | 12.0% | 24.70% | 33.00% | 44.50% | 56.60% |
| 1–2 m | −4.50% | −7.50% | −13.40% | −13.10% | −23.80% |
| 0–1 m | −9.40% | −10.60% | −18.00% | −17.00% | −34.20% |
| total | 4.40% | 11.70% | 17.60% | 19.60% | 23.50% |
| Time | To the North | To the South | To the East | To the West |
|---|---|---|---|---|
| 06:00 | −4.50% | −4.40% | −4.50% | −4.40% |
| 08:00 | −6.30% | −6.20% | −6.50% | −6.00% |
| 10:00 | −1.80% | −1.90% | −2.40% | −1.30% |
| 12:00 | 2.50% | 1.80% | 2.10% | 2.10% |
| 14:00 | −0.70% | −1.00% | −0.30% | −1.40% |
| 16:00 | −7.90% | −7.90% | −7.70% | −8.00% |
| 18:00 | −4.80% | −4.90% | −4.80% | −4.80% |
| Daily | −3.36% | −3.50% | −3.44% | −3.40% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, S.; Zheng, G.; Eitel, J.U.; Zhang, Q. A Lidar-Based 3-D Photosynthetically Active Radiation Model Reveals the Spatiotemporal Variations of Forest Sunlit and Shaded Leaves. Remote Sens. 2021, 13, 1002. https://doi.org/10.3390/rs13051002
Tian S, Zheng G, Eitel JU, Zhang Q. A Lidar-Based 3-D Photosynthetically Active Radiation Model Reveals the Spatiotemporal Variations of Forest Sunlit and Shaded Leaves. Remote Sensing. 2021; 13(5):1002. https://doi.org/10.3390/rs13051002
Chicago/Turabian StyleTian, Shihao, Guang Zheng, Jan U. Eitel, and Qian Zhang. 2021. "A Lidar-Based 3-D Photosynthetically Active Radiation Model Reveals the Spatiotemporal Variations of Forest Sunlit and Shaded Leaves" Remote Sensing 13, no. 5: 1002. https://doi.org/10.3390/rs13051002
APA StyleTian, S., Zheng, G., Eitel, J. U., & Zhang, Q. (2021). A Lidar-Based 3-D Photosynthetically Active Radiation Model Reveals the Spatiotemporal Variations of Forest Sunlit and Shaded Leaves. Remote Sensing, 13(5), 1002. https://doi.org/10.3390/rs13051002






