KVGCN: A KNN Searching and VLAD Combined Graph Convolutional Network for Point Cloud Segmentation
Abstract
1. Introduction
- We propose an edge convolution on the constructed KNN graph to encode the local features. The query point denotes the global position and the edges, namely, the relative positions of the query point and its neighbors, represent the local geometry. By concatenating this information, representative features can be achieved via edge convolution.
- We employ max pooling and average pooling as the symmetric functions, and because VLAD layer is symmetric, the proposed network guarantees invariance to the point order.
- By embedding the VLAD layer in the feature encoding block, we construct an enhanced feature merging encoder which effectively aggregate the local features and the global contextual information. The segmentation in dense region or confusable region improves.
- Experimental results on two datasets show that KVGCN achieves comparable or superior performance compared with state-of-the-art methods.
2. Related Work
2.1. Networks with Preprocessings
2.2. End-to-End Learning Networks
3. Method
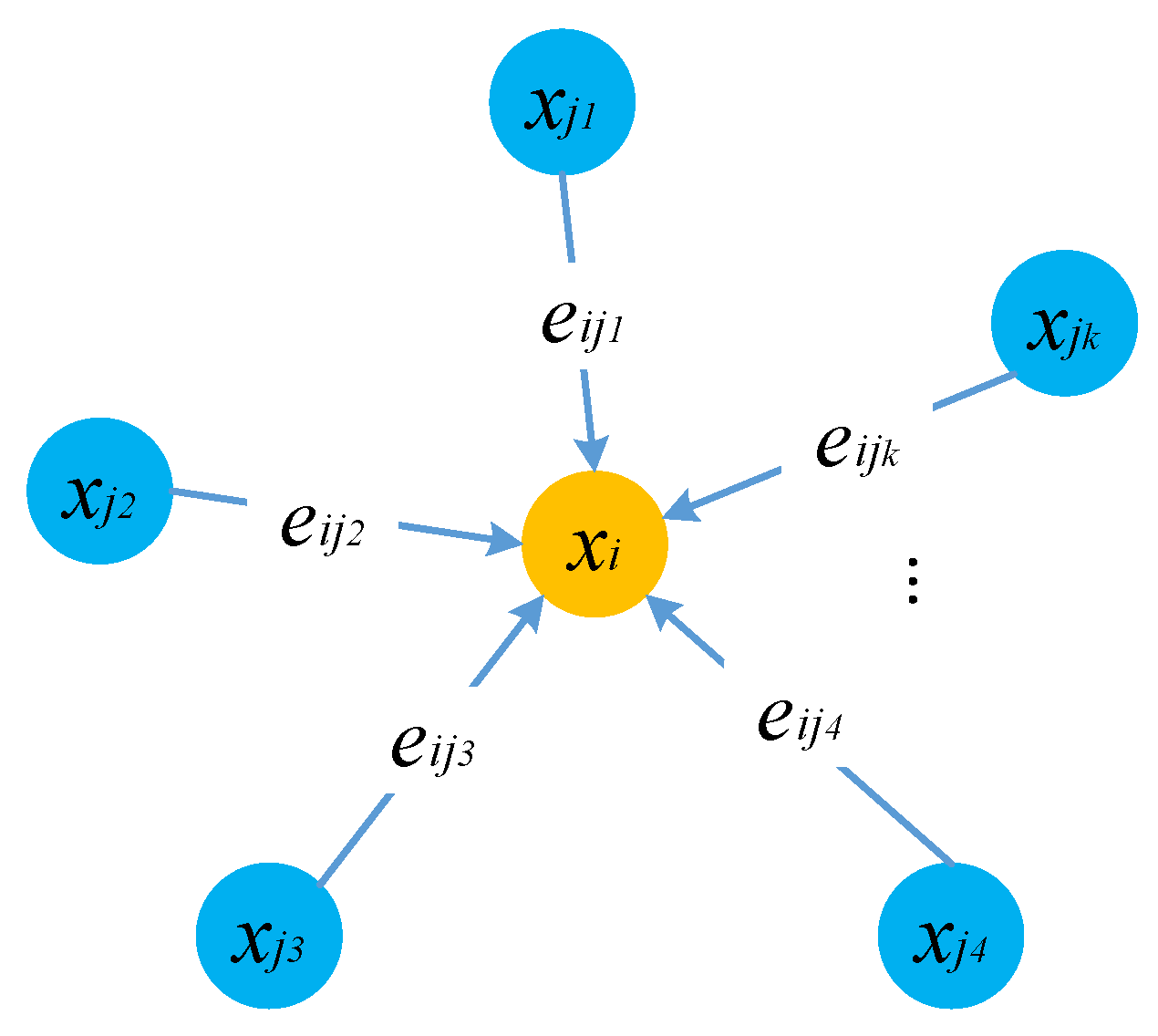
3.1. Knn Graph Convolution
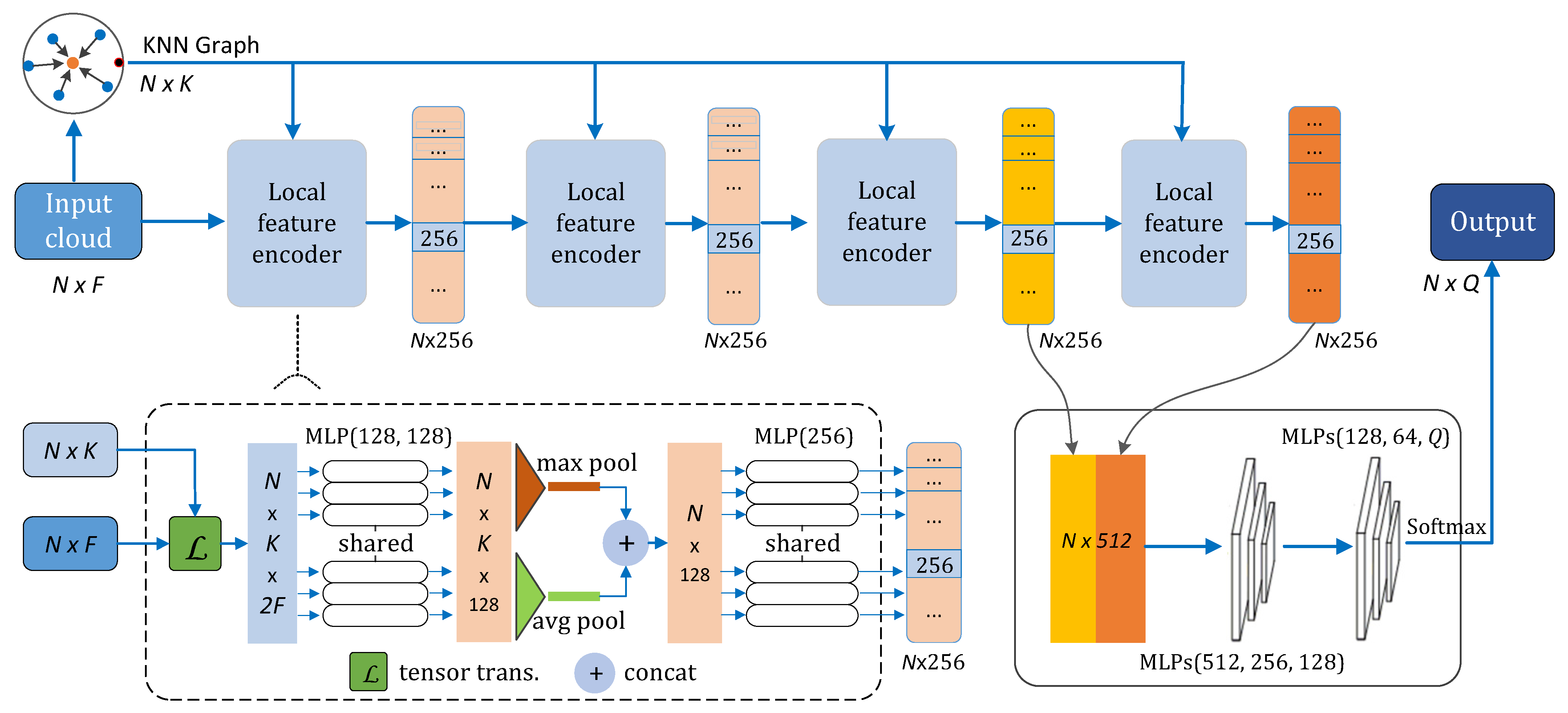
3.2. Kgcn
- -
- First, it searches the K nearest neighbors of each point and constructs the KNN graph ( tensor, N is the number of points) for the input point cloud ( tensor, here F represents the data dimension, usually including coordinates, colors, normals, etc.).
- -
- Afterward, the point cloud and its KNN graph are sent into the local feature encoder which transforms the inputs to a tensor. The local feature encoder block is recursively assembled for four times to expand the perception field, and each block could output different level of feature abstraction.
- -
- Finally, the third-level features and the final features are concatenated in the jump-connection style, followed by two sets of shared MLPs (MLPs and MLPs ) for dimensionality reduction to get the semantic labels. The final output of the network is a matrix, namely, the possibilities of each point belonging to P different categories, which can be further assigned by a softmax function.
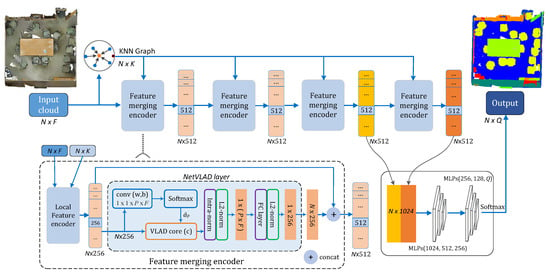
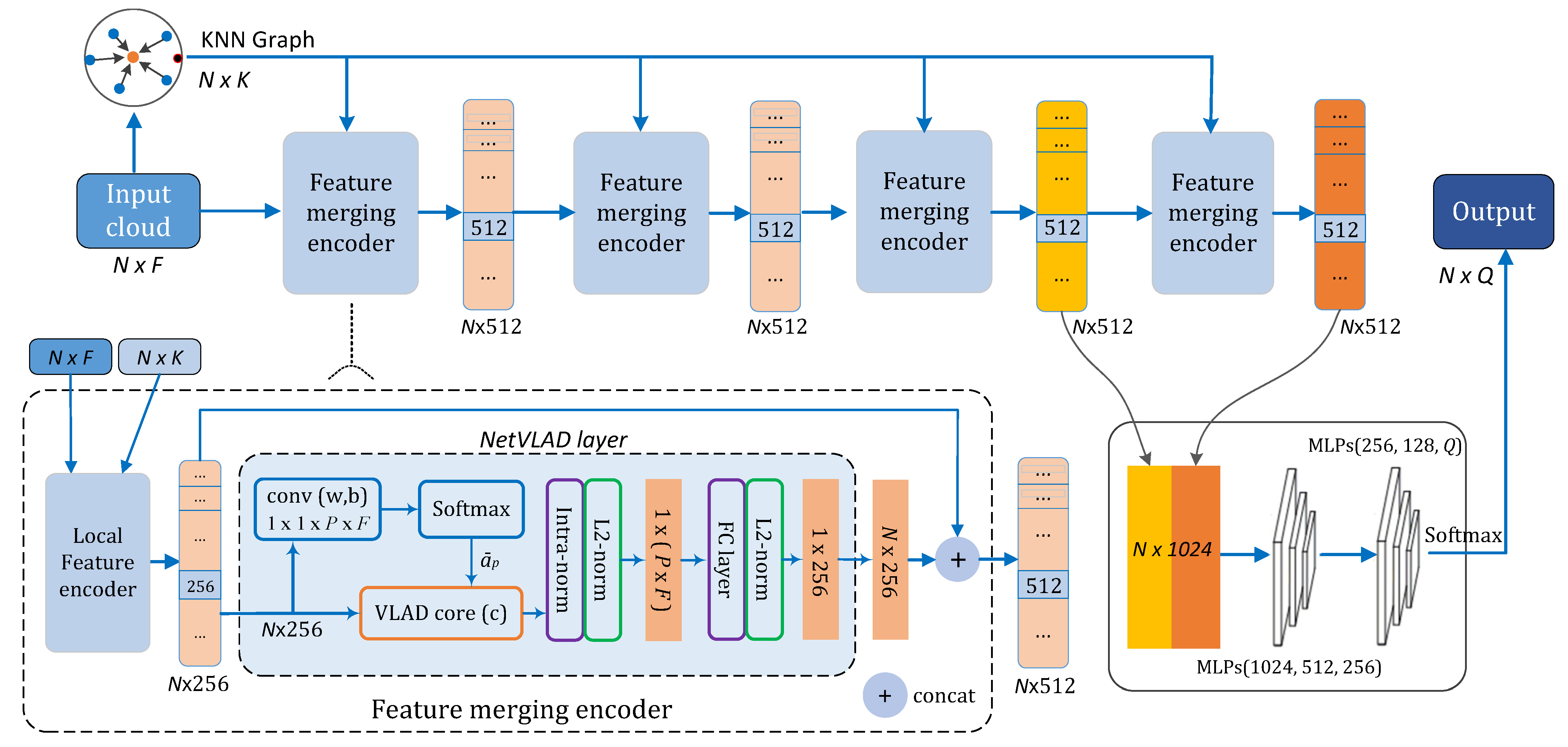
3.3. Kvgcn
3.3.1. Overall Structure
3.3.2. Netvlad Layer
3.4. Permutation Invariance
4. Experimental Results
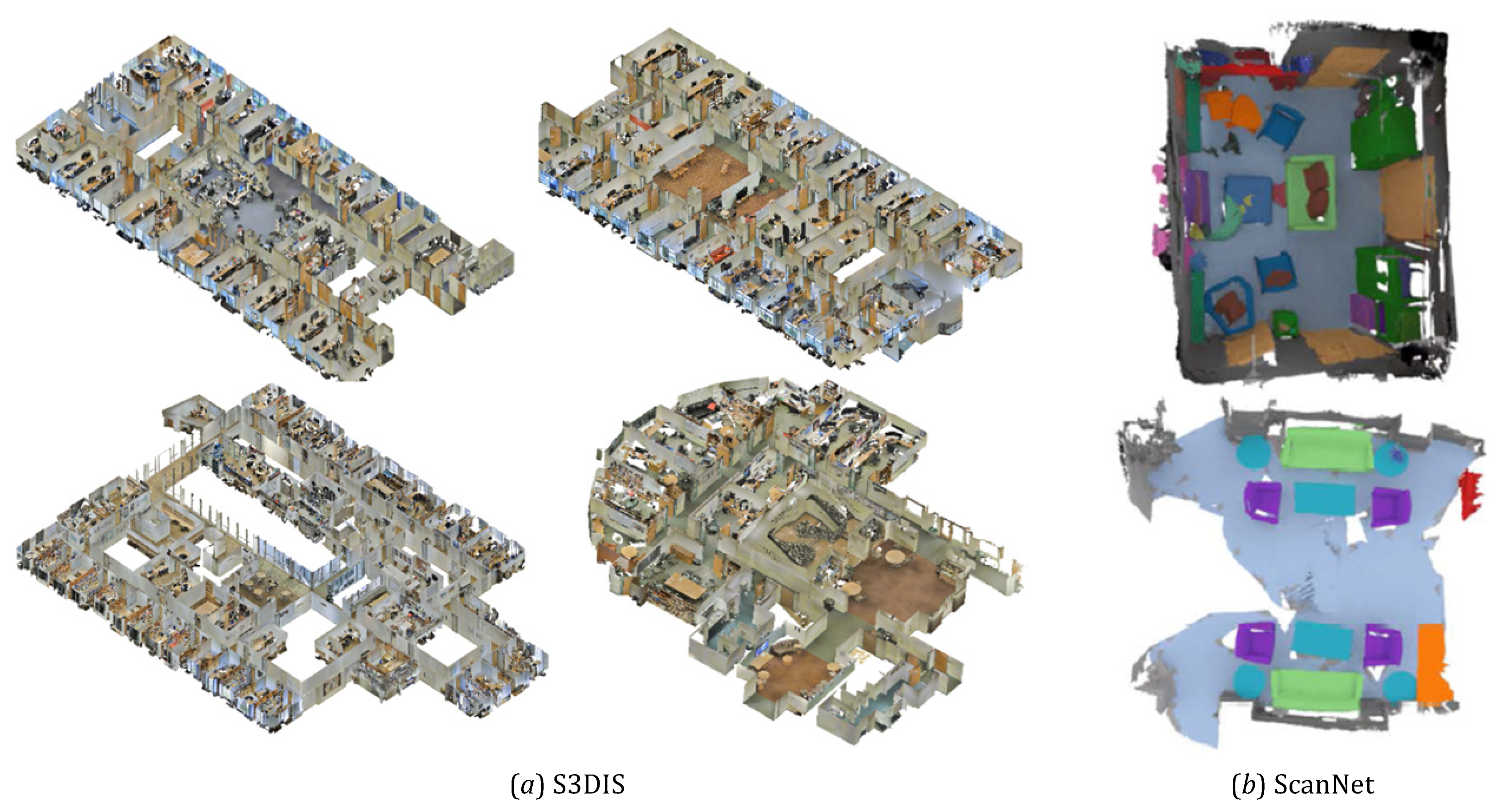
4.1. Datasets
4.2. Experimental Details
4.3. Parameter Evaluations
4.3.1. Parameter K
4.3.2. Parameter D
4.4. Comparison with Other Networks
4.4.1. S3dis Dataset
4.4.2. Scannet Dataset
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| KNN | K-Nearest Neighbors |
| GCN | Graph Convolutional Network |
| MLP | Multi-Layer Perception |
| VLAD | Vector of Locally Aggregated Descriptors |
| KGCN | KNN Grpah Convolutional Network |
| KVGCN | KNN and VLAD combined Graph Convolutional Network |
References
- Armeni, I.; Sener, O.; Zamir, A.R.; Jiang, H.; Brilakis, I.; Fischer, M.; Savarese, S. 3d semantic parsing of large-scale indoor spaces. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1534–1543. [Google Scholar]
- Engelmann, F.; Kontogianni, T.; Hermans, A.; Leibe, B. Exploring spatial context for 3d semantic segmentation of point clouds. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 716–724. [Google Scholar]
- Tchapmi, L.; Choy, C.; Armeni, I.; Gwak, J.; Savarese, S. Segcloud: Semantic segmentation of 3d pointclouds. In Proceedings of the 2017 International Conference on 3D Vision (3DV), Qingdao, China, 10–12 October 2017; pp. 537–547. [Google Scholar]
- Su, H.; Maji, S.; Kalogerakis, E.; Learned-Miller, E. Multi-view convolutional neural networks for 3d shape recognition. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 945–953. [Google Scholar]
- Maturana, D.; Scherer, S. Voxnet: A 3d convolutional neural network for real-time object recognition. In Proceedings of the 2015 IEEE RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 922–928. [Google Scholar]
- Kalogerakis, E.; Averkiou, M.; Maji, S.; Chaudhuri, S. 3D shape segmentation with projective convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 3779–3788. [Google Scholar]
- Le, T.; Bui, G.; Duan, Y. A multi-view recurrent neural network for 3D mesh segmentation. Comput. Graph. 2017, 66, 103–112. [Google Scholar] [CrossRef]
- Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3d shapenets: A deep representation for volumetric shapes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1912–1920. [Google Scholar]
- Qi, C.R.; Su, H.; Niessner, M.; Dai, A.; Yan, M.; Guibas, L.J. Volumetric and Multi-view CNNs for Object Classification on 3D Data. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 5648–5656. [Google Scholar]
- Shi, B.; Bai, S.; Zhou, Z.; Bai, X. Deeppano: Deep panoramic representation for 3-d shape recognition. IEEE Signal Process. Lett. 2015, 22, 2339–2343. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. PointNet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. arXiv 2017, arXiv:1706.02413. [Google Scholar]
- Huang, Q.; Wang, W.; Neumann, U. Recurrent slice networks for 3d segmentation of point clouds. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 2626–2635. [Google Scholar]
- Scarselli, F.; Gori, M.; Tsoi, A.C.; Hagenbuchner, M.; Monfardini, G. The graph neural network model. IEEE Trans. Neural Netw. 2009, 20, 61–80. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.X.; Dai, W.R.; Shen, Y.M.; Xiong, H.K. MSGCNN: Multi-scale Graph Convolutional Neural Network for Point Cloud Segmentation. In Proceedings of the Fifth IEEE International Conference on Multimedia Big Data, Singapore, 11–13 September 2019; pp. 118–127. [Google Scholar]
- Mao, J.G.; Wang, X.G.; Li, H.S. Interpolated Convolutional Networks for 3D Point Cloud Understanding. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 1578–1587. [Google Scholar] [CrossRef]
- Thomas, H.; Qi, C.R.; Deschaud, J.; Marcotegui, B.; Goulette, F.; Guibas, L. KPConv: Flexible and Deformable Convolution for Point Clouds. In Proceedings of the 2019 IEEE CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27–28 October 2019; pp. 6410–6419. [Google Scholar] [CrossRef]
- Li, Y.; Bu, R.; Sun, M.; Wu, W.; Di, X.; Chen, B. PointCNN: Convolution On X-Transformed Points. arXiv 2018, arXiv:1801.07791. [Google Scholar]
- Xie, S.; Liu, S.; Chen, Z.; Tu, Z. Attentional shapecontextnet for point cloud recognition. In Proceedings of the IEEE Conferenceon Computer Vision and Pattern Recognition (CVRP), Salt Lake City, UT, USA, 18–22 June 2018; pp. 4606–4615. [Google Scholar]
- Komarichev, A.; Zhong, Z.C.; Hua, J. A-CNN: Annularly Convolutional Neural Networks on Point Clouds. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVRP), Long Beach, CA, USA, 16–20 June 2019; pp. 7421–7430. [Google Scholar]
- Bello, S.A.; Yu, S.; Wang, C.; Adam, J.M.; Li, J. Review: Deep Learning on 3D Point Clouds. Remote Sens. 2020, 12, 1729. [Google Scholar] [CrossRef]
- Jégou, H.; Douze, M.; Schmid, C.; Pérez, P. Aggregating local descriptors into a compact image representation. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 3304–3311. [Google Scholar] [CrossRef]
- Huang, J.; You, S.Y. Pole-like object detection and classification from urban point clouds. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 3032–3038. [Google Scholar]
- Pang, G.; Neumann, U. Fast and Robust Multi-view 3D Object Recognition in Point Clouds. In Proceedings of the International Conference on 3D Vision, Lyon, France, 19–22 October 2015; pp. 171–179. [Google Scholar]
- Pang, G.; Neumann, U. 3D point cloud object detection with multi-view convolutional neural network. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 585–590. [Google Scholar]
- Qiu, R.Q.; Neumann, U. Exemplar-Based 3D Shape Segmentation in Point Clouds. In Proceedings of the International Conference on 3D Vision, Stanford, CA, USA, 25–28 October 2016; pp. 203–211. [Google Scholar]
- Liu, W.; Wang, Z.; Liu, X.; Zeng, N.; Liu, Y.; Alsaadi, F.E. A survey of deep neural network architectures and their applications. Neurocomputing 2017, 234, 11–26. [Google Scholar] [CrossRef]
- Klokov, R.; Lempitsky, V. Escape from cells: Deep kd-networks for the recognition of 3d point cloud models. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 863–872. [Google Scholar]
- Riegler, G.; Osman, U.A.; Geiger, A. Octnet: Learning deep 3d representations at high resolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 3577–3586. [Google Scholar]
- Liang, Z.D.; Yang, M.; Deng, L.Y.; Wang, C.X.; Wang, B. Hirarchical Depthwise Graph Convolutional Neural Network for 3D Semantic Segmentation of Point Clouds. In Proceedings of the International Conference on Robotics and Automation(ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 8152–8158. [Google Scholar]
- Wang, Y.; Sun, Y.B.; Liu, Z.W.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic Graph CNN for Learning on Point Clouds. ACM Trans. Graph (TOG) 2019, 38, 146. [Google Scholar] [CrossRef]
- Xie, Z.Y.; Chen, J.Z.; Peng, B. Point clouds learning with attention-based graph convolution networks. Neurocomputing 2020, 402, 245–255. [Google Scholar] [CrossRef]
- Landrieu, L.; Simonovsky, M. Large-scale pointcloud semantic segmentation with superpointgraphs. In Proceedings of the IEEE Conferenceon Computer Vision and Pattern Recognition (CVRP), Salt Lake City, UT, USA, 18–23 June 2018; pp. 4558–4567. [Google Scholar]
- Hu, Z.; Zhen, M.; Bai, X.; Fu, H.; Tai, C.L. JSENet: Joint semantic segmentation and edge detection network for 3d point clouds. In Proceedings of the European Conference on Computer Vision (ECCV), Glasgow, UK, 23–28 August 2020. [Google Scholar]
- Mazur, K.; Lempitsky, V. Cloud Transformers. 2020. Available online: https://arxiv.org/pdf/2007.11679v2.pdf (accessed on 2 March 2021).
- Zhao, H.; Jiang, L.; Jia, J.; Torr, P.; Koltun, V. Point Transformer. Available online: https://arxiv.org/pdf/2012.09164v1.pdf (accessed on 2 March 2021).
- Arandjelović, R.; Gronat, P.; Torii, A.; Pajdla, T.; Sivic, J. NetVLAD: CNN Architecture for Weakly Supervised Place Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 1437–1451. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.; Chen, H.; Dou, Q.; Wang, L.; Qin, J.; Heng, P. Scannet: A fast and dense scanning framework for metastatic breast cancer detection from whole-slide images. In Proceedings of the 2018 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, NV, USA, 12–15 March 2018; pp. 539–546. [Google Scholar] [CrossRef]
- Perronnin, F.; Liu, Y.; Sanchez, J.; Poirier, H. Large-scale image retrieval with compressed Fisher vectors. In Proceedings of the 2010 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), San Francisco, CA, USA, 13–18 June 2010; pp. 3384–3391. [Google Scholar] [CrossRef]
- Philbin, J.; Chum, O.; Isard, M.; Sivic, J.; Zisserman, A. Object retrieval with large vocabularies and fast spatial matching. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar] [CrossRef]
- Semantic Segmentation on S3DIS. Available online: https://paperswithcode.com/sota/semantic-segmentation-on-s3dis (accessed on 2 March 2021).




| Metric | K = 5 | K = 10 | K = 15 | K = 20 | K = 25 | K = 30 |
|---|---|---|---|---|---|---|
| mAcc | 52.4 | 59.6 | 62.8 | 63.5 | 63.2 | 60.3 |
| mIoU | 47.7 | 50.6 | 55.2 | 56.3 | 56.4 | 54.7 |
| oAcc | 74.6 | 79.5 | 81.8 | 83.2 | 82.5 | 79.6 |
| Metric | D = 4 | D = 8 | D = 12 | D = 16 | D = 20 | D = 24 |
|---|---|---|---|---|---|---|
| mAcc | 60.9 | 62.1 | 66.7 | 62.9 | 61.7 | 59.8 |
| mIoU | 54.7 | 57.6 | 59.3 | 56.3 | 54.4 | 51.1 |
| oAcc | 74.6 | 75.3 | 85.3 | 80.2 | 79.1 | 78.3 |
| Method | mIoU | oAcc | mAcc |
|---|---|---|---|
| PointNet [11] | 41.1 | 78.5 | 49.0 |
| G+RCU [2] | 49.7 | 81.1 | 66.4 |
| SEGCloud [3] | 48.9 | - | - |
| RSNet [13] | 51.9 | 81.7 | 59.4 |
| A-SCN [19] | 52.7 | 81.6 | - |
| KGCN | 59.0 | 85.8 | 70.9 |
| KVGCN | 60.9 | 87.4 | 72.3 |
| Method | Celling | Floor | Wall | Beam | Column | Window | Door | Chair | Table | Bookcase | Sofa | Board | Clutter |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PointNet [11] | 88.6 | 97.3 | 69.8 | 0.05 | 3.92 | 46.3 | 10.8 | 52.6 | 58.9 | 40.3 | 5.9 | 26.4 | 33.2 |
| G+RCU [2] | 90.3 | 92.1 | 67.9 | 44.7 | 24.2 | 52.3 | 51.2 | 58.1 | 41.9 | 6.9 | 47.4 | 39.0 | 30.0 |
| SEGCloud [3] | 90.1 | 96.1 | 69.9 | 0.0 | 18.4 | 38.4 | 23.1 | 78.6 | 70.4 | 58.4 | 40.9 | 13.0 | 41.1 |
| RSNet [13] | 92.5 | 92.8 | 78.6 | 32.8 | 34.4 | 51.6 | 68.1 | 60.1 | 59.7 | 50.2 | 16.4 | 44.9 | 52.0 |
| SPGraph [33] | 89.9 | 95.1 | 72.0 | 62.8 | 47.1 | 55.3 | 60.0 | 73.5 | 69.2 | 3.2 | 45.9 | 8.7 | 52.9 |
| KGCN | 94.3 | 93.5 | 78.4 | 52.5 | 35.0 | 53.7 | 62.9 | 64.4 | 62.0 | 20.4 | 51.5 | 42.0 | 50.2 |
| KVGCN | 94.5 | 94.1 | 79.5 | 53.4 | 36.3 | 56.8 | 63.2 | 67.5 | 64.3 | 23.6 | 54.3 | 43.1 | 53.2 |
| Method | mIoU | oAcc | mAcc |
|---|---|---|---|
| PointNet [11] | 14.3 | 52.6 | 18.6 |
| PointNet++ [12] | 32.2 | 73.8 | 43.1 |
| RSNet [13] | 37.5 | 75.2 | 46.2 |
| KGCN | 38.7 | 80.7 | 48.3 |
| KVGCN | 40.4 | 82.3 | 49.4 |
| Method | Wall | Floor | Chair | Table | Desk | Bed | Bookshelf | Sofa | Sink | Bathtub |
| PointNet [11] | 68.3 | 86.6 | 35.4 | 31.8 | 1.42 | 19.3 | 2.7 | 30.6 | 0.3 | 0.4 |
| PointNet++ [12] | 72.1 | 88.3 | 60.3 | 44.7 | 10.9 | 48.6 | 49.1 | 49.3 | 28.3 | 40.3 |
| RSNet [13] | 78.4 | 90.5 | 61.3 | 49.9 | 34.4 | 51.5 | 50.3 | 53.3 | 32.4 | 45.6 |
| KGCN | 79.3 | 91.6 | 63.4 | 46.1 | 28.9 | 47.5 | 49.3 | 51.2 | 28.5 | 55.4 |
| KVGCN | 82.4 | 94.3 | 65.1 | 48.3 | 30.5 | 49.1 | 52.1 | 56.3 | 30.3 | 56.3 |
| Method | Toilet | Curtain | Counter | Door | Window | Showercurtain | Refrigerator | Picture | Cabinet | Otherfurniture |
| PointNet [11] | 0 | 0 | 4.3 | 0 | 0 | 0 | 0 | 0 | 3.7 | 0.2 |
| PointNet++ [12] | 29.8 | 31.8 | 19.5 | 25.5 | 3.6 | 1.8 | 17.6 | 0 | 21.7 | 1.8 |
| RSNet [13] | 53.6 | 5.8 | 21.8 | 27.5 | 7.3 | 2.8 | 36.5 | 0.6 | 29.7 | 17.6 |
| KGCN | 56.7 | 22.2 | 23.4 | 33.1 | 10.1 | 5.6 | 35.3 | 1.6 | 26.1 | 18.1 |
| KVGCN | 58.3 | 23.1 | 24.2 | 35.2 | 12.2 | 6.3 | 36.2 | 2.6 | 26.3 | 19.2 |
| Encoders | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
| mAcc | 52.3 | 54.6 | 63.5 | 61.4 | 59.2 |
| mIoU | 47.1 | 50.6 | 56.3 | 53.2 | 51.7 |
| oAcc | 71.2 | 72.3 | 83.2 | 82.1 | 81.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, N.; Yu, H.; Huo, Z.; Liu, J.; Wang, Q.; Xu, Y.; Gao, Y. KVGCN: A KNN Searching and VLAD Combined Graph Convolutional Network for Point Cloud Segmentation. Remote Sens. 2021, 13, 1003. https://doi.org/10.3390/rs13051003
Luo N, Yu H, Huo Z, Liu J, Wang Q, Xu Y, Gao Y. KVGCN: A KNN Searching and VLAD Combined Graph Convolutional Network for Point Cloud Segmentation. Remote Sensing. 2021; 13(5):1003. https://doi.org/10.3390/rs13051003
Chicago/Turabian StyleLuo, Nan, Hongquan Yu, Zhenfeng Huo, Jinhui Liu, Quan Wang, Ying Xu, and Yun Gao. 2021. "KVGCN: A KNN Searching and VLAD Combined Graph Convolutional Network for Point Cloud Segmentation" Remote Sensing 13, no. 5: 1003. https://doi.org/10.3390/rs13051003
APA StyleLuo, N., Yu, H., Huo, Z., Liu, J., Wang, Q., Xu, Y., & Gao, Y. (2021). KVGCN: A KNN Searching and VLAD Combined Graph Convolutional Network for Point Cloud Segmentation. Remote Sensing, 13(5), 1003. https://doi.org/10.3390/rs13051003