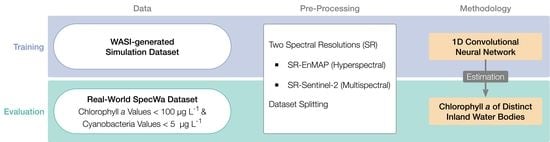
Deep Learning with WASI Simulation Data for Estimating Chlorophyll a Concentration of Inland Water Bodies
Abstract
1. Introduction
1.1. Focus of This Study and Background
1.2. Motivation, Objectives, and Contributions
- the development of a DL approach for estimating chlorophyll a concentrations of different inland water bodies inspired by a 1D CNN architecture;
- a detailed investigation and evaluation of the potential of this approach concerning the generalization aspects on unknown datasets;
- the comparison of the estimation performance of 1D CNN with a commonly applied ANN, RF and BR approach.
2. Data and Methods
2.1. Requirements for DL Approaches
- Number of datapoints: Many datapoints are needed to apply and train the DL models.
- Variety of water parameters: a combination of different water parameters is necessary since the ML models need to link different spectra (spectral input data) with different chlorophyll a values while these spectra are also characterized by signatures of other water parameters (“unmixing”). These occurring water parameters are, for example, CDOM, suspended materials, the consistency of the water bodies’ benthic substrate, and different algae species with different pigments. Besides, atmospherical effects and different radiation conditions during a day or a year are also considered.
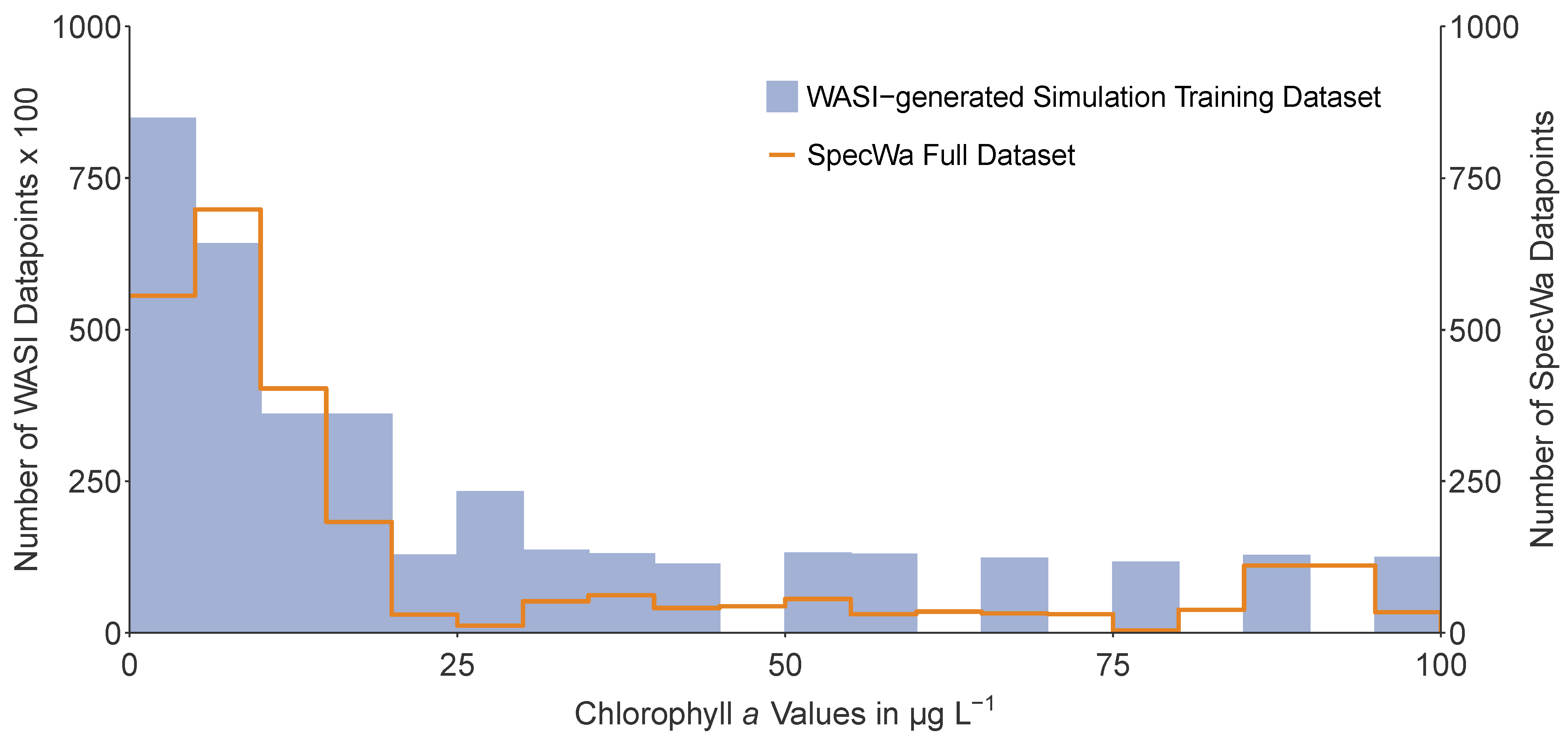
- Value range of the target variable: To avoid dataset shift, the value range of the chlorophyll a values as desired target variable should be similar to the value ranges of many inland water bodies, and especially of the SpecWa dataset’s chlorophyll a values.
- Spectral distribution of the input data: The WASI-simulated spectral input data need to be in a similar distribution as the spectral data of the SpecWa dataset. Besides, as a pre-processing step, the WASI-simulated spectral data have to be scaled to the same spectral resolution as the SpecWa dataset to ensure compatibility.
2.2. Data Characteristics of the SpecWa Dataset
- datapoints with a chlorophyll a concentration lower than 100 μg L−1 are included;
- datapoints with a cyanobacteria concentration lower than 5 μg L−1 are included.
2.3. Fundamentals of the WASI Tool and Simulation of the WASI Data
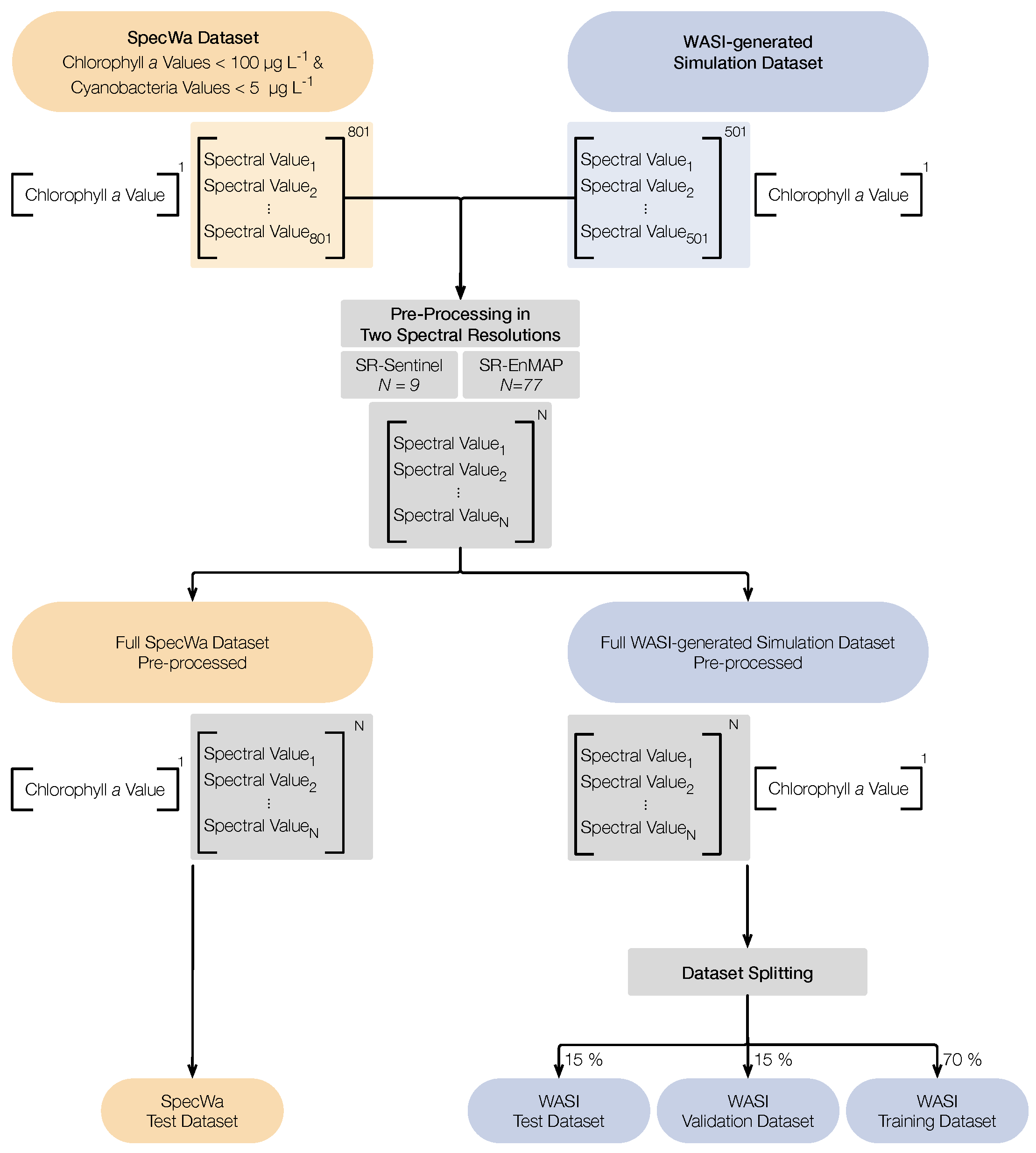
2.4. Data Pre-Processing
2.4.1. Downsampling
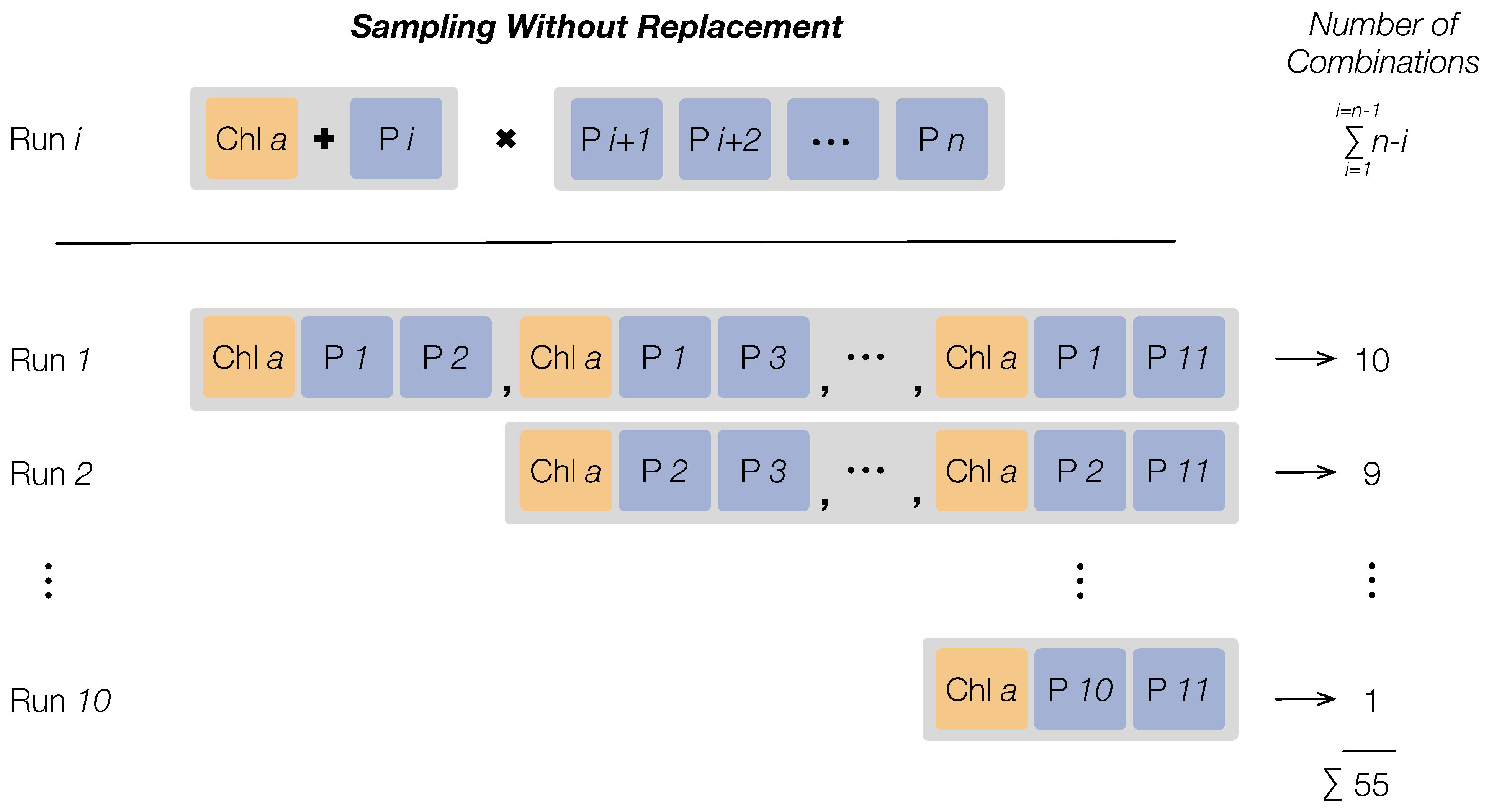
2.4.2. Dataset Splitting in Subsets
2.5. Machine Learning Models
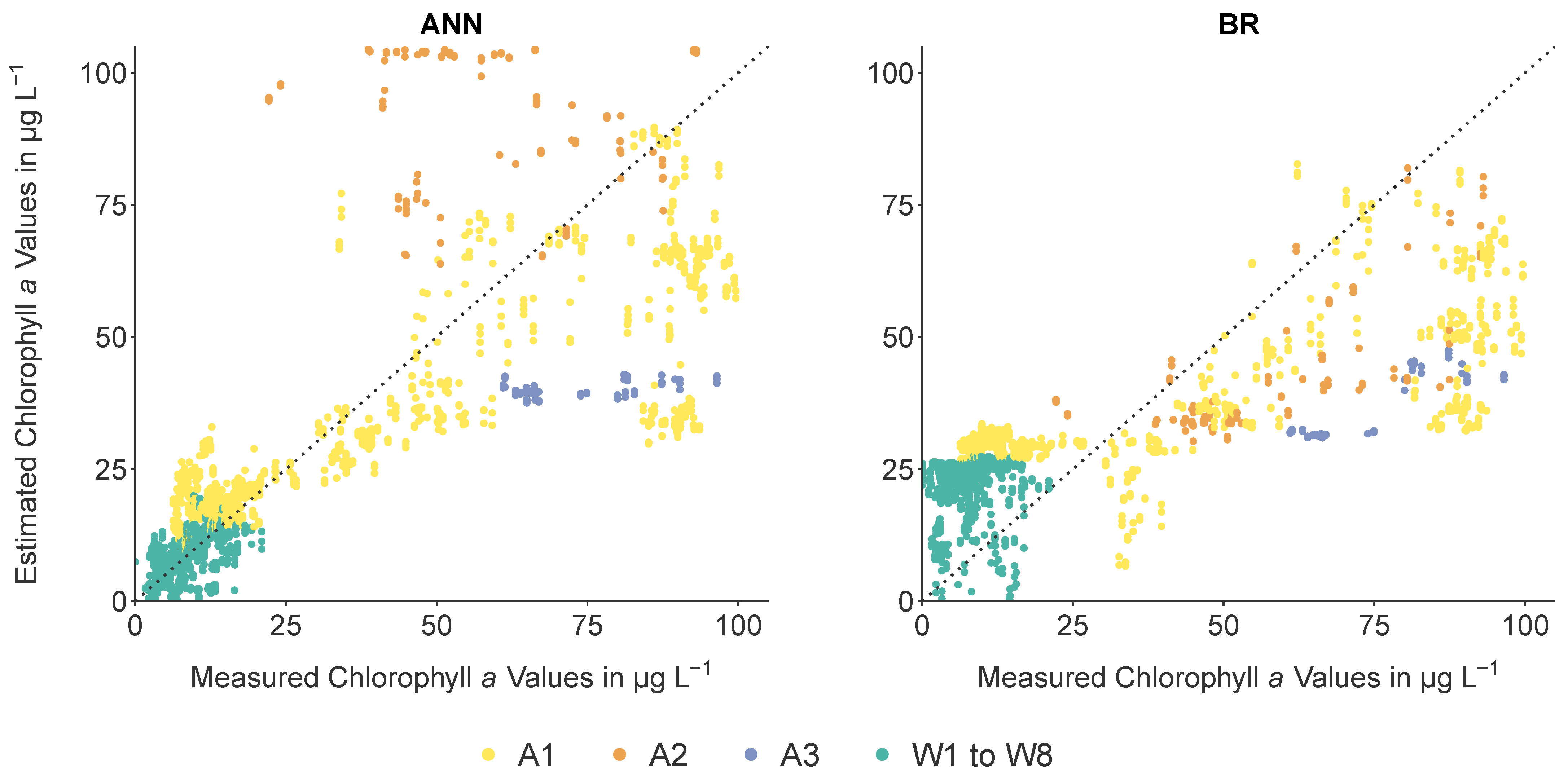
3. Results
4. Discussion
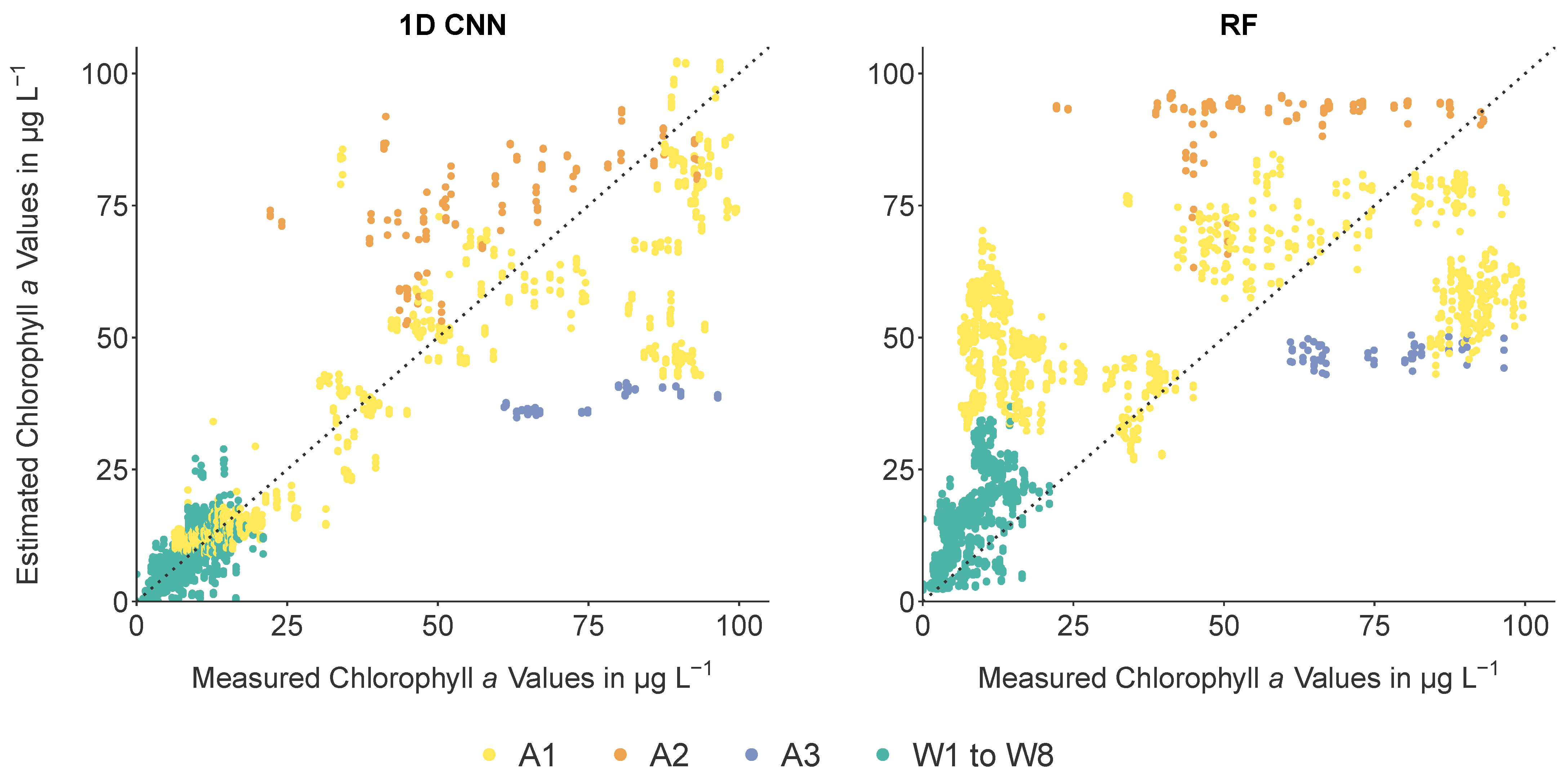
4.1. Estimation Performance Concerning the Two Downsampled Spectral Data and the Different ML Models
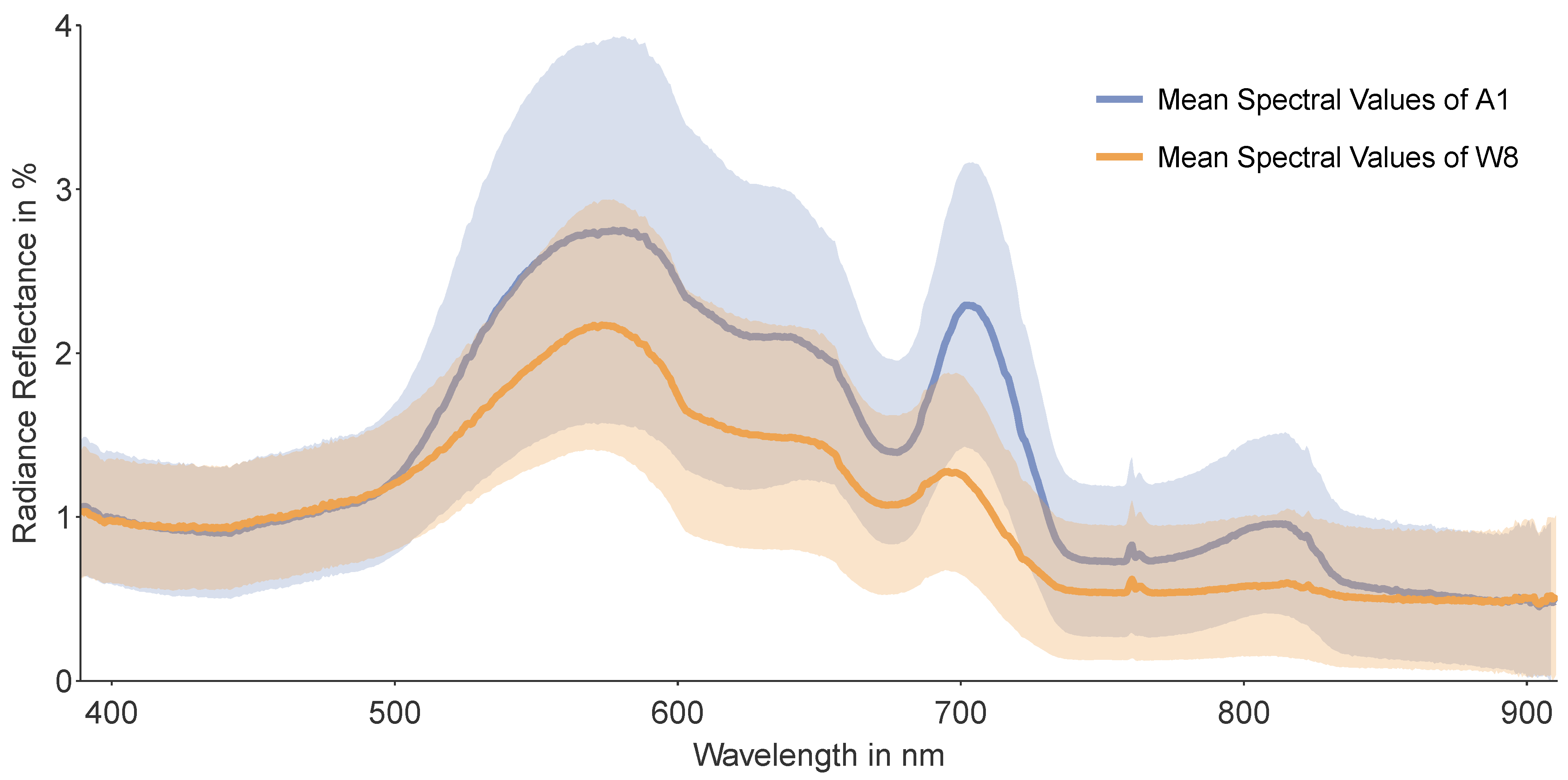
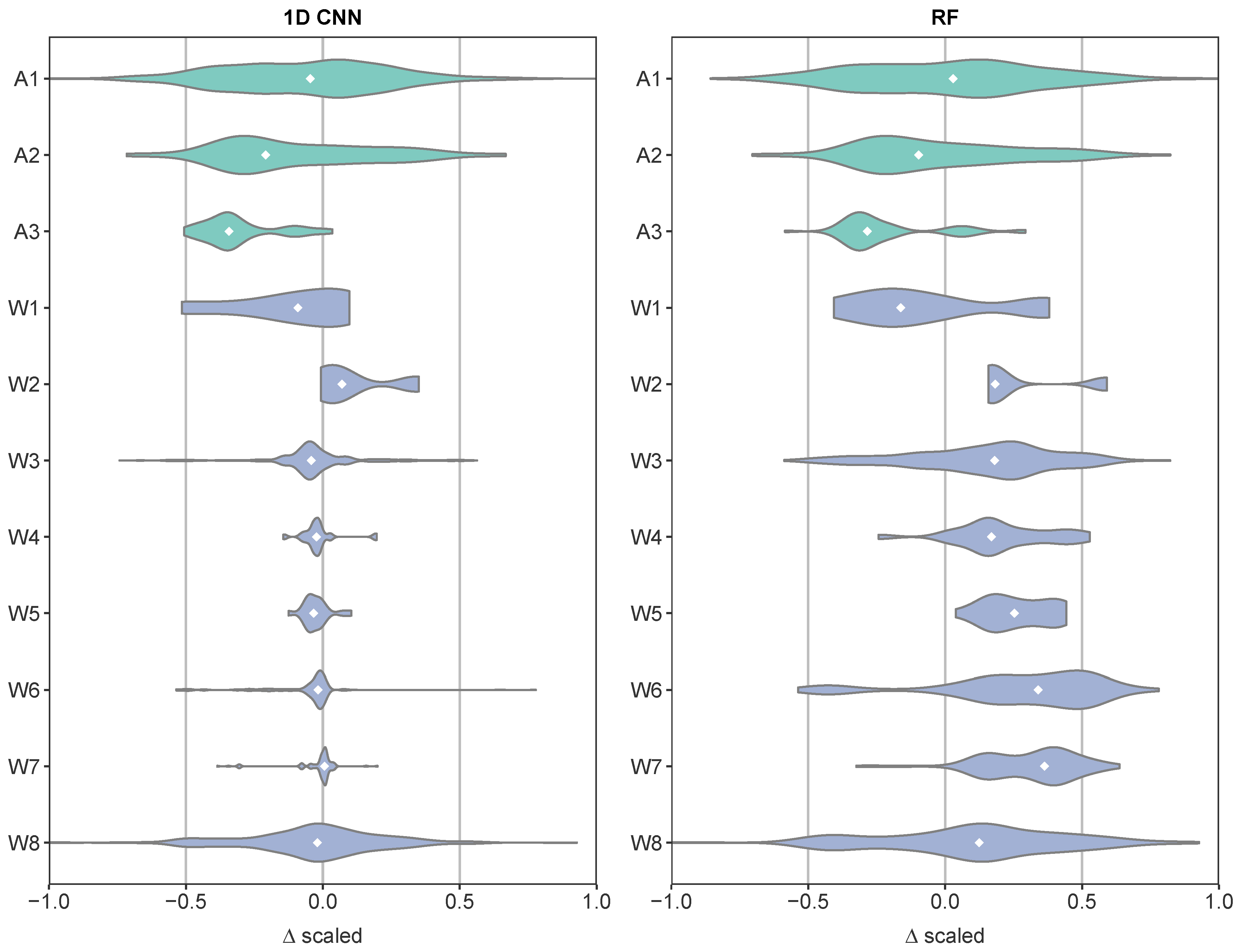
4.2. Estimation Performance Concerning the Individual Water Bodies
- We simulated the WASI-generated dataset with three different benthic substrates: sand, silt, and a macrophyte species. Natural water bodies have additional materials such as gravel, leaves, or other organic materials that are not covered in the WASI tool.
- In different geogenic regions, a diversity of minerals occur, resulting in distinct reflective properties and colors for, e.g., suspended materials.
- Besides, several phytoplankton species exist, while the WASI-generated simulation data consist only of two species.
5. Conclusions and Outlook
- Yes. ML approaches can be trained on a simulation dataset and can estimate the chlorophyll a concentration of real-world water bodies not included in the training process. The best model is the newly adapted and applied 1D CNN. It can handle noise in the data and different illumination conditions caused by the sun- and sky glint.
- However, the ML models must be provided with appropriate information in the input data. This is the main reason why the estimation performances on the finer resolved SR-EnMAP data are significantly better than on the SR-Sentinal data.
- As for the generalization aspect of the ML models, we demonstrate that it is possible, under specific conditions, that models are trained on a distinct dataset as later applied. Since the DL model performs the best estimation, we take a chance to assume it would perform similarly on another dataset covering the same chlorophyll a values. Indeed, we need to consider the water bodies’ composition.
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Parameter | Standard Value | Unit | Description |
|---|---|---|---|
| C[0] | 0 | μg L−1 | Concentration of phytoplankton class 0 |
| C[1] | 0 | μg L−1 | Concentration of phytoplankton class 1 |
| C[2] | 0 | μg L−1 | Concentration of phytoplankton class 2 |
| C[4] | 0 | μg L−1 | Concentration of phytoplankton class 4 |
| fluo | 0 | chlorophyll a fluorescence quantum yield | |
| S | 0.014 | nm −1 | Exponent of CDOM absorption |
| n | −1 | - | Angström exponent of particle scattering |
| T_W | 25 | °C | Water temperature |
| f | 0.033 | - | f-factor of R |
| Q | 5 | Sr−1 | Anisotropie factor of upwelling radiation |
| z | 0 | m | Sensor depth |
| view | 0 | ° | Viewing angle |
| bbs_phy | 0.001 | m2 mg−1 | Specific backscattering coefficient of phytoplankton |
| f_nw | 0 | - | Fraction of non-water area |
| fA[0] | 0 | - | fraction of bottom type #0 (constant) |
| fA[3] | 0 | - | fraction of bottom type #3 (seagrass) |
| fA[4] | 0 | - | fraction of bottom type #4 (mussel) |
| f_dd | 1 | - | Fraction of direct downwelling irradiance |
| f_ds | 1 | - | Fraction of diffuse downwelling irradiance |
| H_oz | 0.38 | cm | Scale height of ozone |
| alpha | 1.3170 | - | Angström exponent of aerosols |
| beta | 0.2606 | - | Turbidity coefficient |
| WV | 2.500 | cm | Scale height of precipitable water in the atmosphere |
| rho_L | 0.02006 | - | Fresnel reflecance of downwelling radiance |
| rho_dd | 0.03325 | - | Reflection factor of Edd |
| rho_ds | 0.0889 | - | Reflection factor of Eds |
| Hyperparameters | CNN + SR-EnMAP | ANN + SP-EnMAP | CNN + SR-Sentinel | ANN + SR-Sentinel |
|---|---|---|---|---|
| Number of epochs | 50 | 50 | 100 | 100 |
| Batch size | 256 | 256 | 256 | 256 |
| Kernel size 1 | 5 | - | 3 | - |
| Kernel size 2 | 4 | - | 2 | - |
| Kernel size 3 | 3 | - | - | - |
| Kernel size 4 | 2 | - | - | - |
| Pooling size | 2 | - | 2 | - |
| Activations | ReLU | ReLU | ReLU | ReLU |
| c1 | 128 | - | 128 | - |
| c2 | 128 | - | 128 | - |
| c3 | 256 | - | - | - |
| c4 | 256 | - | - | - |
| f1 | 200 | 100 | 100 | 100 |
| f2 | 200 | 100 | 100 | 100 |
| Dropout | 0.2 | 0.2 | 0.2 | 0.2 |
| Loss | Mean squared error | |||
| Optimizer | Adam | |||
References
- Matthews, M.W. A current review of empirical procedures of remote sensing in inland and near-coastal transitional waters. Int. J. Remote Sens. 2011, 32, 6855–6899. [Google Scholar] [CrossRef]
- Palmer, S.C.; Kutser, T.; Hunter, P.D. Remote sensing of inland waters: Challenges, progress and future directions. Remote Sens. Environ. 2015, 157, 1–8. [Google Scholar] [CrossRef]
- Schaeffer, B.A.; Schaeffer, K.G.; Keith, D.; Lunetta, R.S.; Conmy, R.; Gould, R.W. Barriers to adopting satellite remote sensing for water quality management. Int. J. Remote Sens. 2013, 34, 7534–7544. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Gurlin, D.; Moses, W.J.; Barrow, T. A bio-optical algorithm for the remote estimation of the chlorophyll- a concentration in case 2 waters. Environ. Res. Lett. 2009, 4, 045003. [Google Scholar] [CrossRef]
- Kallio, K.; Kutser, T.; Hannonen, T.; Koponen, S.; Pulliainen, J.; Vepsäläinen, J.; Pyhälahti, T. Retrieval of water quality from airborne imaging spectrometry of various lake types in different seasons. Sci. Total Environ. 2001, 268, 59–77. [Google Scholar] [CrossRef]
- Giardino, C.; Candiani, G.; Zilioli, E. Detecting chlorophyll-a in Lake Garda using TOA MERIS radiances. Photogramm. Eng. Remote Sens. 2005, 71, 1045–1051. [Google Scholar] [CrossRef]
- Koponen, S.; Attila, J.; Pulliainen, J.; Kallio, K.; Pyhälahti, T.; Lindfors, A.; Rasmus, K.; Hallikainen, M. A case study of airborne and satellite remote sensing of a spring bloom event in the Gulf of Finland. Cont. Shelf Res. 2007, 27, 228–244. [Google Scholar] [CrossRef]
- Gons, H.J.; Rijkeboer, M.; Ruddick, K.G. A chlorophyll-retrieval algorithm for satellite imagery (Medium Resolution Imaging Spectrometer) of inland and coastal waters. J. Plankton Res. 2002, 24, 947–951. [Google Scholar] [CrossRef]
- Kutser, T.; Pierson, D.C.; Kallio, K.Y.; Reinart, A.; Sobek, S. Mapping lake CDOM by satellite remote sensing. Remote Sens. Environ. 2005, 94, 535–540. [Google Scholar] [CrossRef]
- Petus, C.; Chust, G.; Gohin, F.; Doxaran, D.; Froidefond, J.M.; Sagarminaga, Y. Estimating turbidity and total suspended matter in the Adour River plume (South Bay of Biscay) using MODIS 250-m imagery. Cont. Shelf Res. 2010, 30, 379–392. [Google Scholar] [CrossRef]
- Maier, P.M.; Keller, S. Machine learning regression on hyperspectral data to estimate multiple water parameters. In Proceedings of the 2018 9th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Amsterdam, The Netherlands, 23–26 September 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Dekker, A.; Vos, R.; Peters, S. Comparison of remote sensing data, model results and in situ data for total suspended matter (TSM) in the southern Frisian lakes. Sci. Total Environ. 2001, 268, 197–214. [Google Scholar] [CrossRef]
- Doxaran, D.; Froidefond, J.M.; Castaing, P.; Babin, M. Dynamics of the turbidity maximum zone in a macrotidal estuary (the Gironde, France): Observations from field and MODIS satellite data. Estuarine Coast. Shelf Sci. 2009, 81, 321–332. [Google Scholar] [CrossRef]
- Olmanson, L.G.; Bauer, M.E.; Brezonik, P.L. A 20-year Landsat water clarity census of Minnesota’s 10,000 lakes. Remote Sens. Environ. 2008, 112, 4086–4097. [Google Scholar] [CrossRef]
- Ruiz-Verdú, A.; Simis, S.G.; de Hoyos, C.; Gons, H.J.; Peña-Martínez, R. An evaluation of algorithms for the remote sensing of cyanobacterial biomass. Remote Sens. Environ. 2008, 112, 3996–4008. [Google Scholar] [CrossRef]
- Maier, P.M.; Hinz, S.; Keller, S. Estimation of Chlorophyll a, Diatoms and Green Algae Based on Hyperspectral Data with Machine Learning Approaches. In Proceedings of the 38. Wissenschaftlich-Technische Jahrestagung der DGPF und PFGK18 Tagung in München—Publikationen der DGPF, Band 27, 2018, Munchen, Germany, 7–9 May 2018. [Google Scholar]
- Gholizadeh, M.H.; Melesse, A.M.; Reddi, L. A comprehensive review on water quality parameters estimation using remote sensing techniques. Sensors 2016, 16, 1298. [Google Scholar] [CrossRef] [PubMed]
- Toming, K.; Kutser, T.; Laas, A.; Sepp, M.; Paavel, B.; Nõges, T. First experiences in mapping lake water quality parameters with Sentinel-2 MSI imagery. Remote Sens. 2016, 8, 640. [Google Scholar] [CrossRef]
- Ansper, A.; Alikas, K. Retrieval of chlorophyll a from Sentinel-2 MSI data for the European Union water framework directive reporting purposes. Remote Sens. 2019, 11, 64. [Google Scholar] [CrossRef]
- Cazzaniga, I.; Bresciani, M.; Colombo, R.; Della Bella, V.; Padula, R.; Giardino, C. A comparison of Sentinel-3-OLCI and Sentinel-2-MSI-derived Chlorophyll-a maps for two large Italian lakes. Remote Sens. Lett. 2019, 10, 978–987. [Google Scholar] [CrossRef]
- Pahlevan, N.; Smith, B.; Schalles, J.; Binding, C.; Cao, Z.; Ma, R.; Alikas, K.; Kangro, K.; Gurlin, D.; Hà, N.; et al. Seamless retrievals of chlorophyll-a from Sentinel-2 (MSI) and Sentinel-3 (OLCI) in inland and coastal waters: A machine-learning approach. Remote Sens. Environ. 2020, 240, 111604. [Google Scholar] [CrossRef]
- Carlson, R.E. A trophic state index for lakes. Limnol. Oceanogr. 1977, 22, 361–369. [Google Scholar] [CrossRef]
- Hall, R.I.; Leavitt, P.R.; Quinlan, R.; Dixit, A.S.; Smol, J.P. Effects of agriculture, urbanization, and climate on water quality in the northern Great Plains. Limnol. Oceanogr. 1999, 44, 739–756. [Google Scholar] [CrossRef]
- Kovács, J.; Tanos, P.; Várbíró, G.; Anda, A.; Molnár, S.; Hatvani, I.G. The role of annual periodic behavior of water quality parameters in primary production–Chlorophyll-a estimation. Ecol. Indic. 2017, 78, 311–321. [Google Scholar] [CrossRef]
- Gordon, H.R.; Brown, O.B.; Jacobs, M.M. Computed Relationships Between the Inherent and Apparent Optical Properties of a Flat Homogeneous Ocean. Appl. Opt. 1975. [Google Scholar] [CrossRef] [PubMed]
- Dekker, A.G.; Hoogenboom, H.J.; Goddijn, L.M.; Malthus, T. The relation between inherent optical properties and reflectance spectra in turbid inland waters. Remote Sens. Rev. 1997, 15, 59–74. [Google Scholar] [CrossRef]
- Odermatt, D.; Heege, T.; Nieke, J.; Kneubühler, M.; Itten, K. Water Quality Monitoring for Lake Constance with a Physically Based Algorithm for MERIS Data. Sensors 2008, 8, 4582–4599. [Google Scholar] [CrossRef] [PubMed]
- Schiller, H.; Doerffer, R. Neural network for emulation of an inverse model operational derivation of Case II water properties from MERIS data. Int. J. Remote Sens. 1999, 20, 1735–1746. [Google Scholar] [CrossRef]
- Gege, P. The water color simulator WASI: An integrating software tool for analysis and simulation of optical in situ spectra. Comput. Geosci. 2004, 30, 523–532. [Google Scholar] [CrossRef]
- Gege, P.; Dekker, A.G. Spectral and radiometric measurement requirements for inland, coastal and reef waters. Remote Sens. 2020, 12, 2247. [Google Scholar] [CrossRef]
- Moses, W.J.; Gitelson, A.A.; Berdnikov, S.; Povazhnyy, V. Satellite Estimation of Chlorophyll-a Concentration Using the Red and NIR Bands of MERIS—The Azov Sea Case Study. IEEE Geosci. Remote Sens. Lett. 2009, 6, 845–849. [Google Scholar] [CrossRef]
- Neil, C.; Spyrakos, E.; Hunter, P.D.; Tyler, A.N. A global approach for chlorophyll-a retrieval across optically complex inland waters based on optical water types. Remote Sens. Environ. 2019, 229, 159–178. [Google Scholar] [CrossRef]
- Spyrakos, E.; O’Donnell, R.; Hunter, P.D.; Miller, C.; Scott, M.; Simis, S.G.; Neil, C.; Barbosa, C.C.; Binding, C.E.; Bradt, S.; et al. Optical types of inland and coastal waters. Limnol. Oceanogr. 2018, 63, 846–870. [Google Scholar] [CrossRef]
- Mitchell, T.M. Machine Learning; Machine Learning Department Carnegie Mellon University: Pittsburgh, PA, USA, 1997. [Google Scholar]
- Zhang, Y.; Pulliainen, J.; Koponen, S.; Hallikainen, M. Application of an empirical neural network to surface water quality estimation in the Gulf of Finland using combined optical data and microwave data. Remote Sens. Environ. 2002, 81, 327–336. [Google Scholar] [CrossRef]
- González Vilas, L.; Spyrakos, E.; Torres Palenzuela, J.M. Neural network estimation of chlorophyll a from MERIS full resolution data for the coastal waters of Galician rias (NW Spain). Remote Sens. Environ. 2011, 115, 524–535. [Google Scholar] [CrossRef]
- Maier, P.M.; Keller, S. Application of different simulated spectral data and machine learning to estimate the chlorophyll a concentration of several inland waters. In Proceedings of the 2019 10th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS), Amsterdam, The Netherlands, 24–26 September 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Chebud, Y.; Naja, G.M.; Rivero, R.G.; Melesse, A.M. Water quality monitoring using remote sensing and an artificial neural network. Water Air Soil Pollut. 2012, 223, 4875–4887. [Google Scholar] [CrossRef]
- Hafeez, S.; Wong, M.S.; Ho, H.C.; Nazeer, M.; Nichol, J.; Abbas, S.; Tang, D.; Lee, K.H.; Pun, L. Comparison of machine learning algorithms for retrieval of water quality indicators in case-II waters: A case study of Hong Kong. Remote Sens. 2019, 11, 617. [Google Scholar] [CrossRef]
- Syariz, M.A.; Lin, C.H.; Nguyen, M.V.; Jaelani, L.M.; Blanco, A.C. WaterNet: A convolutional neural network for chlorophyll-a concentration retrieval. Remote Sens. 2020, 12, 1966. [Google Scholar] [CrossRef]
- Pu, F.; Ding, C.; Chao, Z.; Yu, Y.; Xu, X. Water-quality classification of inland lakes using landsat8 images by convolutional neural networks. Remote Sens. 2019, 11, 1674. [Google Scholar] [CrossRef]
- Maier, P.; Keller, S. Estimating chlorophyll a concentrations of several inalnd waters with hyperspectral data and machine learning models. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 4. [Google Scholar] [CrossRef]
- Maier, P.M.; Keller, S. SpecWa: Spectral Remote Sensing Data and Chlorophyll a Values of Inland Waters; GFZ Data Services: Potsdam, Germany, 2020. [Google Scholar] [CrossRef]
- Mobley, C.D.; Sundman, L.K. HYDROLIGHT 5 ECOLIGHT 5; Sequoia Scientific Inc: Bellevue, WA, USA, 2008. [Google Scholar]
- Riese, F.M.; Keller, S. Soil Texture Classification with 1D Convolutional Neural Networks based on Hyperspectral Data. ISPRS Ann. Photogramm. Remote Sens. Spatial Inf. Sci. 2019, IV-2/W5, 615–621. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 1, 5–32. [Google Scholar] [CrossRef]
- Keller, S.; Maier, P.M.; Riese, F.M.; Norra, S.; Holbach, A.; Börsig, N.; Wilhelms, A.; Moldaenke, C.; Zaake, A.; Hinz, S. Hyperspectral data and machine learning for estimating CDOM, chlorophyll a, diatoms, green algae and turbidity. Int. J. Environ. Res. Public Health 2018, 15, 1881. [Google Scholar] [CrossRef]
- Guanter, L.; Kaufmann, H.; Segl, K.; Foerster, S.; Rogass, C.; Chabrillat, S.; Kuester, T.; Hollstein, A.; Rossner, G.; Chlebek, C.; et al. The EnMAP spaceborne imaging spectroscopy mission for earth observation. Remote Sens. 2015, 7, 8830–8857. [Google Scholar] [CrossRef]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s optical high-resolution mission for GMES operational services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Keller, S.; Riese, F.M.; Stötzer, J.; Maier, P.M.; Hinz, S. Developing a machine learning framework for estimating soil moisture with VNIR hyperspectral data. ISPRS Ann. Photogramm. Remote Sens. Spatial Inf. Sci. 2018, IV-1, 101–108. [Google Scholar] [CrossRef]
- Riese, F.M.; Keller, S.; Hinz, S. Supervised and Semi-Supervised Self-Organizing Maps for Regression and Classification Focusing on Hyperspectral Data. Remote Sens. 2020, 12, 7. [Google Scholar] [CrossRef]
- Moreno-Torres, J.G.; Raeder, T.; Alaiz-Rodríguez, R.; Chawla, N.V.; Herrera, F. A unifying view on dataset shift in classification. Pattern Recognit. 2012, 45, 521–530. [Google Scholar] [CrossRef]
- Quionero-Candela, J.; Sugiyama, M.; Schwaighofer, A.; Lawrence, N. Dataset Shift in Machine Learning; The MIT Press: Cambridge, MA, USA, 2009. [Google Scholar] [CrossRef]
- Gege, P.; Albert, A. A tool for inverse modeling of spectral measurements in deep and shallow waters. In Remote Sensing of Aquatic Coastal Ecosystem Processes; Springer: Dordrecht, The Netherlands, 2006; pp. 81–109. [Google Scholar] [CrossRef]
- Gege, P.; Grötsch, P. A spectral model for correcting sunglint and skyglint. In Proceedings of the Ocean Optics XXIII, Victoria, Kanada, 23–28 October 2016; pp. 1–10. [Google Scholar]
- Gege, P. WASI5_Manual; Gege: Taipei, Taiwan, 2019. [Google Scholar]
- Beck, R.; Zhan, S.; Liu, H.; Tong, S.; Yang, B.; Xu, M.; Ye, Z.; Huang, Y.; Shu, S.; Wu, Q.; et al. Comparison of satellite reflectance algorithms for estimating chlorophyll-a in a temperate reservoir using coincident hyperspectral aircraft imagery and dense coincident surface observations. Remote Sens. Environ. 2016, 178, 15–30. [Google Scholar] [CrossRef]
- Lehnert, L.W.; Meyer, H.; Obermeier, W.A.; Silva, B.; Regeling, B.; Bendix, J. Hyperspectral data analysis in R: The hsdar package. J. Stat. Softw. 2018, 89. [Google Scholar] [CrossRef]
- Liu, L.; Ji, M.; Buchroithner, M. Transfer learning for soil spectroscopy based on convolutional neural networks and its application in soil clay content mapping using hyperspectral imagery. Sensors 2018, 18, 3169. [Google Scholar] [CrossRef] [PubMed]
- Stevens, A.; Ramirez-Lopez, L.; Stevens, M.A.; Rcpp, L. Package ‘Prospectr’. R Package Version, (2). 2020. Available online: https://www.google.com.hk/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&ved=2ahUKEwi3-_26u-vuAhUIJhoKHWvLDmYQFjAA\egQIAxAC&url=https%3A%2F%2Fcran.r-project.org%2Fweb%2Fpackages%2Fprospectr%2Fprospectr.pdf&usg=AOvVaw3zgdDSp-x6QxrPPFHVyFSV (accessed on 15 February 2021).
- Hu, W.; Huang, Y.; Wei, L.; Zhang, F.; Li, H. Deep convolutional neural networks for hyperspectral image classification. J. Sens. 2015, 2015, 258619. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A.; Bengio, Y. Deep Learning; MIT Press Cambridge: Cambridge, MA, USA, 2016; Volume 1. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Morel, A.; Prieur, L. Analysis of variations in ocean color. Limnol. Oceanogr. 1977, 22, 709–722. [Google Scholar] [CrossRef]
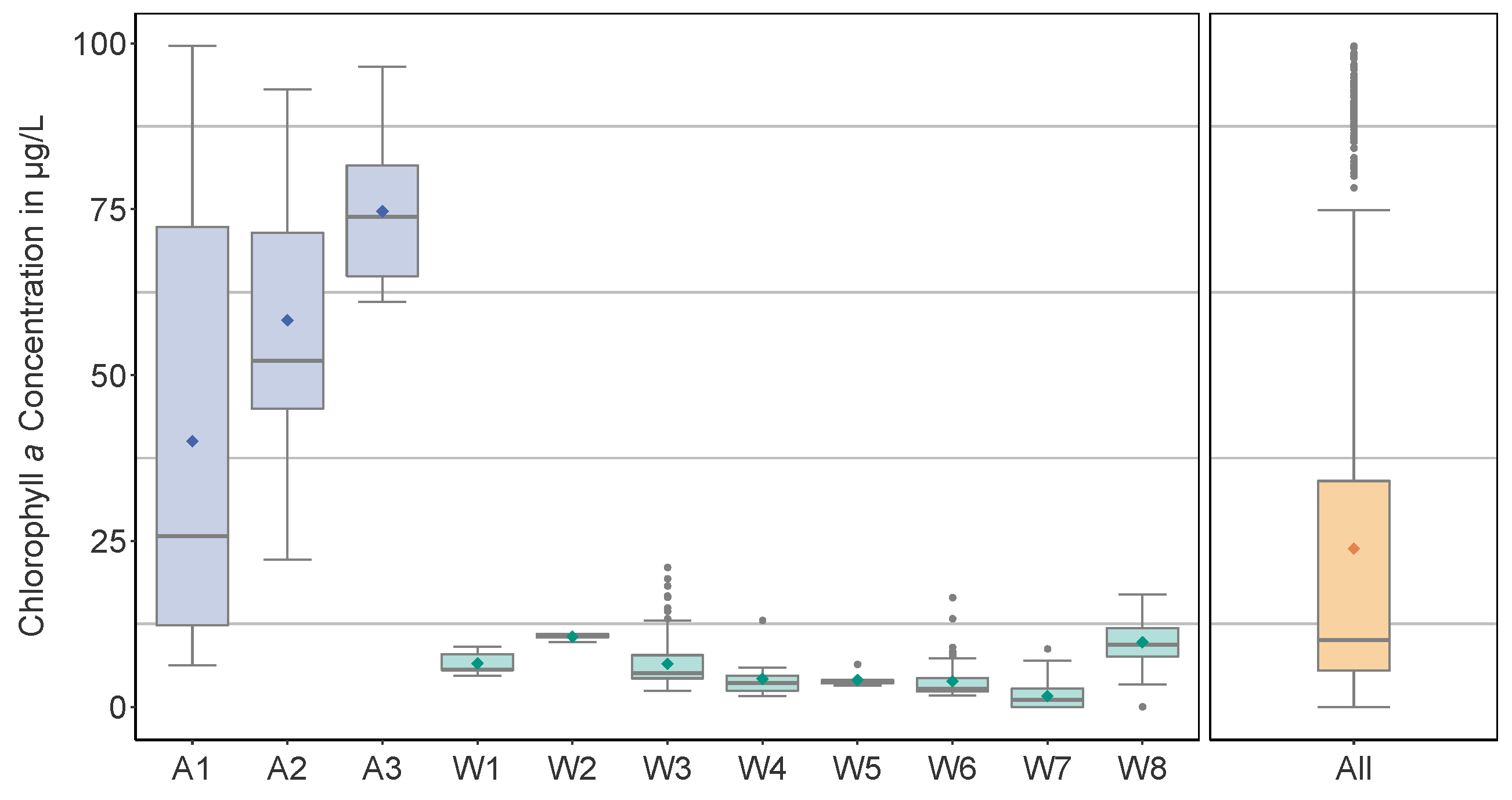



| Water Body | Water ID | Number of Datapoints | Water Depth | Chlorophyll a Range |
|---|---|---|---|---|
| in m | in μg L−1 | |||
| ap castle garden | A1 | 1048 | 1.0 to 2.0 | 16.3 to 99.6 |
| ap KIT | A2 | 116 | 0.5 to 1.0 | 22.2 to 93.0 |
| ap TMB | A3 | 57 | 2.0 to 3.0 | 61.0 to 96.5 |
| old rhine au | W1 | 21 | 2.0 to 3.0 | 4.7 to 9.1 |
| old rhine leopoldshafen | W2 | 8 | 0.5 to 1.0 | 9.8 to 11.0 |
| qp blankenloch | W3 | 494 | 0.5 to 3.0 | 2.4 to 21.0 |
| qp epple | W4 | 42 | 1.0 to 3.0 | 1.6 to 13.0 |
| qp ferma | W5 | 20 | 1.0 to 3.0 | 3.3 to 6.4 |
| qp heide | W6 | 221 | 1.0 to 3.0 | 1.7 to 16.5 |
| qp leopoldshafen | W7 | 105 | 1.5 to 3.0 | 0.0 to 8.7 |
| qp waldstadt | W8 | 485 | 1.5 to 3.0 | 0.0 to 17.0 |
| WASI Parameter | Range | Standard | Steps | Log Scale | Description |
|---|---|---|---|---|---|
| Chlorophyll a | 1 μg L−1 to 100 μg L−1 | - | 30 | yes | concentration of chlorophyll a |
| C | 0.1 mg L−1 to 100 mg L−1 | 1 | 20 | yes | concentration of non-algal particles type I |
| C | 1 mg L−1 to 20 mg L−1 | 0 | 20 | no | concentration of non-algal particles type II |
| C | 0.1 m−1 to 5 m−1 | 0.1 | 20 | no | CDOM concentration |
| zB | 1 m to 5 m | 2 | 10 | no | water depth |
| Sun | 35° to 65° | 50 | 10 | no | sun position |
| FA1 | 0.1 to 5 | 0 | 10 | no | background type sand |
| FA2 | 0.1 to 5 | 0 | 10 | no | background type silt |
| FA5 | 0.1 to 3 | 0 | 10 | no | background type macrophyte |
| g | 0 Sr−1 to 0.5 Sr−1 | 0.02 | 10 | no | fraction of sky radiance due to direct solar radiation |
| g | 0 Sr−1 to 1 Sr−1 | 0.318 | 10 | no | fraction of sky radiance due to molecule scattering |
| g | 0 Sr−1 to 1 Sr−1 | 0.318 | 10 | no | fraction of sky radiance due to aerosol scattering |
| Dataset | % | Number of Datapoints |
|---|---|---|
| Training | 70 | 369,600 |
| Validation | 15 | 79,200 |
| Test | 15 | 79,200 |
| Model | SR-EnMAP | SR-Sentinel | ||||
|---|---|---|---|---|---|---|
| R2 in % | RMSE in μg L−1 | MAE in μg L−1 | R2 in % | RMSE in μg L−1 | MAE in μg L−1 | |
| 1D CNN | 81.9 | 12.4 | 6.7 | 62.4 | 19.3 | 14.6 |
| ANN | 66.6 | 16.6 | 9.3 | 54.8 | 23.4 | 17.1 |
| RF | 51.1 | 22.7 | 17.0 | 51.1 | 20.2 | 14.7 |
| BR | 37.9 | 23.0 | 19.3 | 51.5 | 22.3 | 17.8 |
| Water ID | Model | SR-EnMAP | SR-Sentinel | ||
|---|---|---|---|---|---|
| RMSE in μg L−1 | MAE in μg L−1 | RMSE in μg L−1 | MAE in μg L−1 | ||
| A1 | 1D CNN | 15.4 | 9.1 | 24.0 | 20.9 |
| ANN | 20.4 | 13.8 | 21.8 | 14.1 | |
| RF | 31.2 | 27.7 | 24.7 | 21.1 | |
| BR | 27.8 | 22.0 | 27.3 | 19.7 | |
| A2 | 1D CNN | 22.0 | 18.2 | 33.1 | 27.5 |
| ANN | 40.9 | 34.6 | 56.7 | 53.3 | |
| RF | 37.6 | 33.4 | 37.0 | 32.6 | |
| BR | 20.0 | 17.2 | 16.6 | 13.7 | |
| A3 | 1D CNN | 37.9 | 36.8 | 43.9 | 42.5 |
| ANN | 35.9 | 34.5 | 33.2 | 32.0 | |
| RF | 29.7 | 27.8 | 57.8 | 57.0 | |
| BR | 38.1 | 37.6 | 18.6 | 16.3 | |
| W1 | 1D-CNN | 2.6 | 2.4 | 4.5 | 3.2 |
| ANN | 3.1 | 3.0 | 3.9 | 3.6 | |
| RF | 6.5 | 6.2 | 4.6 | 4.0 | |
| BR | 17.0 | 16.8 | 16.9 | 16.8 | |
| W2 | 1D CNN | 14.2 | 14.1 | 14.9 | 14.9 |
| ANN | 8.4 | 8.3 | 14.6 | 14.5 | |
| RF | 17.5 | 17.4 | 3.6 | 3.3 | |
| BR | 13.9 | 13.9 | 17.7 | 17.7 | |
| W3 | 1D CNN | 3.9 | 3.0 | 7.8 | 6.4 |
| ANN | 4.0 | 3.0 | 4.5 | 3.4 | |
| RF | 7.5 | 6.6 | 6.8 | 6.0 | |
| BR | 17.8 | 16.8 | 17.8 | 16.9 | |
| W4 | 1D CNN | 3.0 | 2.0 | 3.0 | 2.0 |
| ANN | 4.4 | 3.8 | 3.3 | 2.5 | |
| RF | 2.8 | 1.7 | 2.8 | 1.8 | |
| BR | 9.6 | 8.3 | 10.5 | 7.6 | |
| W5 | 1D CNN | 2.0 | 1.4 | 5.5 | 4.0 |
| ANN | 2.3 | 2.1 | 2.3 | 2.0 | |
| RF | 5.1 | 4.4 | 6.3 | 6.0 | |
| BR | 13.8 | 12.3 | 13.8 | 12.5 | |
| W6 | 1D CNN | 2.8 | 1.6 | 2.9 | 2.2 |
| ANN | 3.2 | 2.0 | 2.7 | 1.6 | |
| RF | 3.3 | 2.7 | 6.0 | 5.6 | |
| BR | 20.0 | 17.2 | 21.7 | 17.2 | |
| W7 | 1D CNN | 2.8 | 1.8 | 2.5 | 2.1 |
| ANN | 5.7 | 4.8 | 3.3 | 2.9 | |
| RF | 2.4 | 2.0 | 4.1 | 3.7 | |
| BR | 21.7 | 21.2 | 20.1 | 19.5 | |
| W8 | 1D CNN | 3.9 | 2.9 | 14.3 | 13.2 |
| ANN | 2.9 | 2.3 | 5.9 | 4.8 | |
| RF | 12.3 | 11.2 | 9.8 | 9.1 | |
| BR | 16.6 | 16.2 | 17.2 | 16.9 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maier, P.M.; Keller, S.; Hinz, S. Deep Learning with WASI Simulation Data for Estimating Chlorophyll a Concentration of Inland Water Bodies. Remote Sens. 2021, 13, 718. https://doi.org/10.3390/rs13040718
Maier PM, Keller S, Hinz S. Deep Learning with WASI Simulation Data for Estimating Chlorophyll a Concentration of Inland Water Bodies. Remote Sensing. 2021; 13(4):718. https://doi.org/10.3390/rs13040718
Chicago/Turabian StyleMaier, Philipp M., Sina Keller, and Stefan Hinz. 2021. "Deep Learning with WASI Simulation Data for Estimating Chlorophyll a Concentration of Inland Water Bodies" Remote Sensing 13, no. 4: 718. https://doi.org/10.3390/rs13040718
APA StyleMaier, P. M., Keller, S., & Hinz, S. (2021). Deep Learning with WASI Simulation Data for Estimating Chlorophyll a Concentration of Inland Water Bodies. Remote Sensing, 13(4), 718. https://doi.org/10.3390/rs13040718