Endmember Estimation with Maximum Distance Analysis
Abstract
1. Introduction
2. Literature Review
2.1. Endmember Counting
- The first family includes some kind of criteria information, such as theoretic criteria that are based on minimum description length [26,27], Akaike’s information criterion [28], and Bayesian information criterion [29]. Furthermore, different models have been developed for encoding a negative data log-likelihood term and a penalty term. An accurate estimation of the number of endmembers is expected to be obtained when the model achieves a global optimum. These strategies rely on the empirical configuration of specific mixed models or likelihood functions, and improper configurations will cause estimation errors of the number of endmembers.
- The second family is related to a thresholding scheme, in which a threshold is applied to the eigen-decomposition results from subspace analysis. Eigenvalue thresholding algorithms include principal component analysis (PCA) [30], hyperspectral signal subspace by minimum error (Hysime) [31], and the so-called Harsanyi-Farrand-Chang (HFC) method [32], coupled with its noise-whitened implementation (NWHFC) [33]. The PCA-based approaches aim to characterize a cutoff gap between the eigenvalues that are caused by signals and noise. However, these approaches will provide an incorrect estimation of the number of endmembers if the variation between the two eigenvalues is negligible. The Hysime approach conducts spectrum noise characterization and noise covariance estimation, and it requires high computational complexity. The HFC approach requires a fixed false alarm probability, which affects the estimated number of endmembers.
- The third family includes the geometry-based estimation of the number of endmembers (GENE), which includes the convex hull (GENE-CH) algorithm and affine hull (GENE-AH) algorithm [34]. Both GENE-CH and the GENE-AH utilize data geometry and exploit the fact that all the observed pixel vectors should lie in the convex hull (CH) and affine hull (AH) of the endmember signatures, respectively. Specifically, GENE algorithms operate along with an endmember extraction algorithm (EEA). In this scenario, a maximum hull volume would stop the EEA from extracting the next endmember signature. Therefore, the GENE algorithms depend on the effectiveness of the EEA used, and different endmember extraction algorithms (EEAs) cause different accuracies for counting endmembers.
2.2. Endmember Extraction
- If there is at least one pure pixel for per endmember, then EEAs search for the spectral vectors in the data set that corresponds to the vertices of the data simplex. Typical algorithms that are based on the pure pixel assumption are pixel purity index (PPI) [36], N-FINDR [37,38], and vertex component analysis (VCA) [39], among others. The PPI algorithm projects all of the observed pixels onto randomly generated unit-norm vectors, and it records the number of times (i.e., scores) that the value of each projected pixel has an extreme value (either minimum or maximum projection value). Then, the endmembers are those pixels with the highest scores. The N-FINDR algorithm and its derivatives search for a simplex with the greatest volume over all pixel combinations, and the vertices of the simplex correspond to the endmembers. The VCA algorithm iteratively projects data onto a direction orthogonal to the subspace that is spanned by the endmembers already determined, and the new endmember is the pixel with the extreme value of the projected data. It is worth noting that PPI, N-FINDR, and VCA require the number of endmembers in advances to perform endmember extraction.
- If the pure pixel assumption is not satisfied (this is a more realistic scenario, since HSI data are often dominated by highly mixed pixel [9]), the endmember extraction process is a rather intractable task. The difficulty is that the HSI data set may not contain any endmembers or at least some of them. Some popular algorithms that are implemented under this assumption are the minimum volume constrained nonnegative matrix factorization (MVCNMF) [40], minimum-volume enclosing simplex (MVES) [41], minimum volume simplex analysis (MVSA) [42,43], etc. MVCNMF adopts constrained nonnegative matrix factorization, together with a volume-based constraint, to decompose mixed pixels in multispectral and hyperspectral remote sensing images. MVES finds a simplex containing all of the dimensionally-reduced pixels by minimizing the simplex volume subject to the constraint. MVSA fits a minimum volume simplex to the hyperspectral data, constraining the abundance fractions to belong to the probability simplex. Specifically, MVCNMF, MVES, and MVSA also require the number of endmembers when they implement endmember extraction.
2.3. From the Literature to Our Contributions
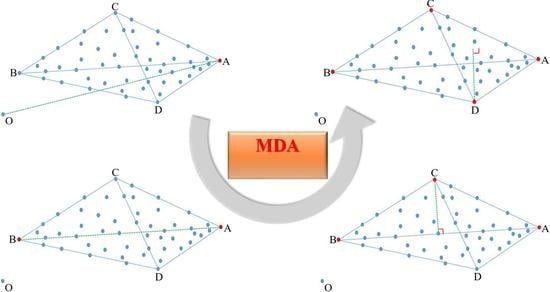
- The major contribution of our work is a novel endmember estimation method, referred to as maximum distance analysis (MDA), which accomplishes the overall endmember estimation task (that normally comprises of two independent steps, i.e., determining the number of endmembers and extracting their endmember signatures). Our newly proposed MDA method sequentially identifies pixel points as endmembers that are farthest from specific pixel point, line, plane, and affine hulls. The sequential endmember extraction terminates when the maximum distance between all the pixel points and the affine hull [41,44] formed by all extracted endmembers is zero. Our proposed MDA method does not require knowing the number of endmembers. It only involves straightforward vector-based computations, keeping its computational complexity very low. Moreover, our proposed MDA method does not use dimension reduction.
- A second major contribution of our work is that the proposed MDA method provides an effective way for generalizing most existing EEAs that require prior knowledge of the number of endmembers into more accurate ones without the requirement. We use the MVSA as a special case to demonstrate the generalization strategy that is based on the MDA. Specifically, MVSA requires the number of endmembers and uses the traditional VCA method as an initialization method for extracting endmembers. Therefore, our proposed MDA framework is not only capable of simultaneously counting and extracting endmembers by itself without any prior knowledge, but it also provides a general framework for developing new endmember extraction schemes that are based on arbitrary existing endmember extraction methods without the pure pixel assumption.
3. Maximum Distance Analysis
3.1. Extracting Endmember Signatures
3.2. Estimating the Number of Endmembers
4. Experiments
4.1. Synthetic Data
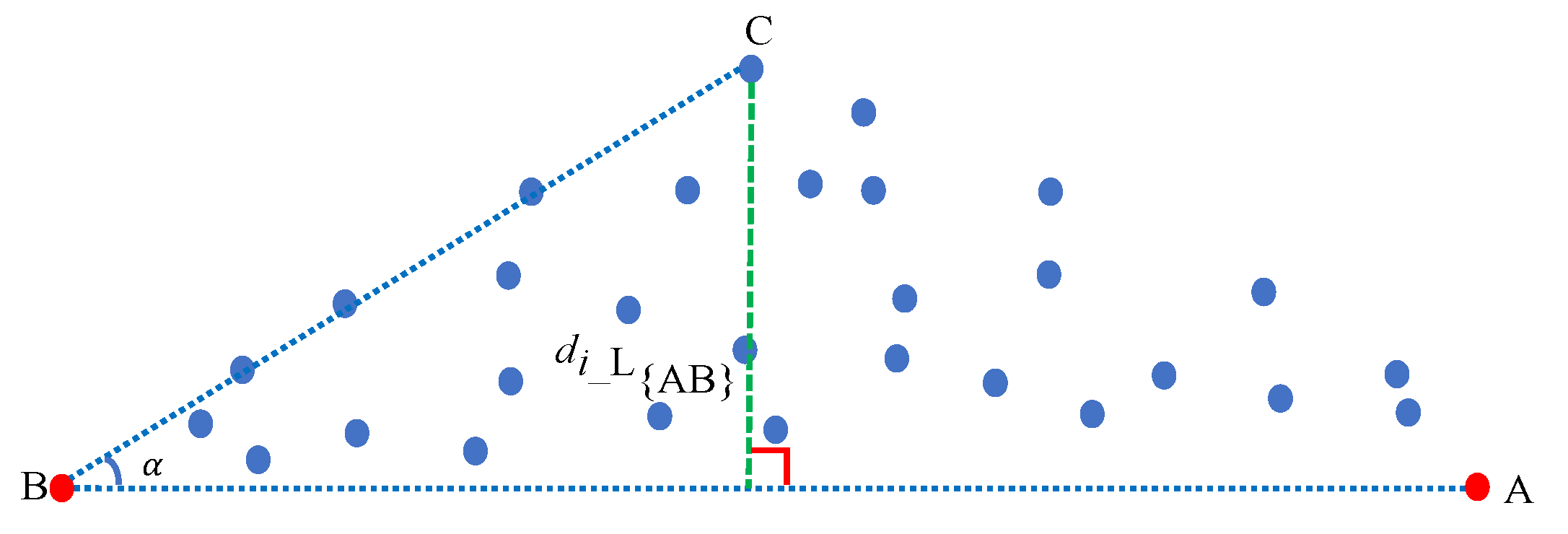
- We calculate the distance between every pixel point and coordinate origin in the pixel space and extract the pixel point with the maximum distance as the first endmember.
- We calculate the distance between every pixel point and the first extracted endmember in the pixel space and extract the pixel point with the maximum distance as the second endmember.
- We calculate the distance between every pixel point and the line defined by the first and second extracted endmembers, extracting the pixel point with the maximum distance as the third endmember.
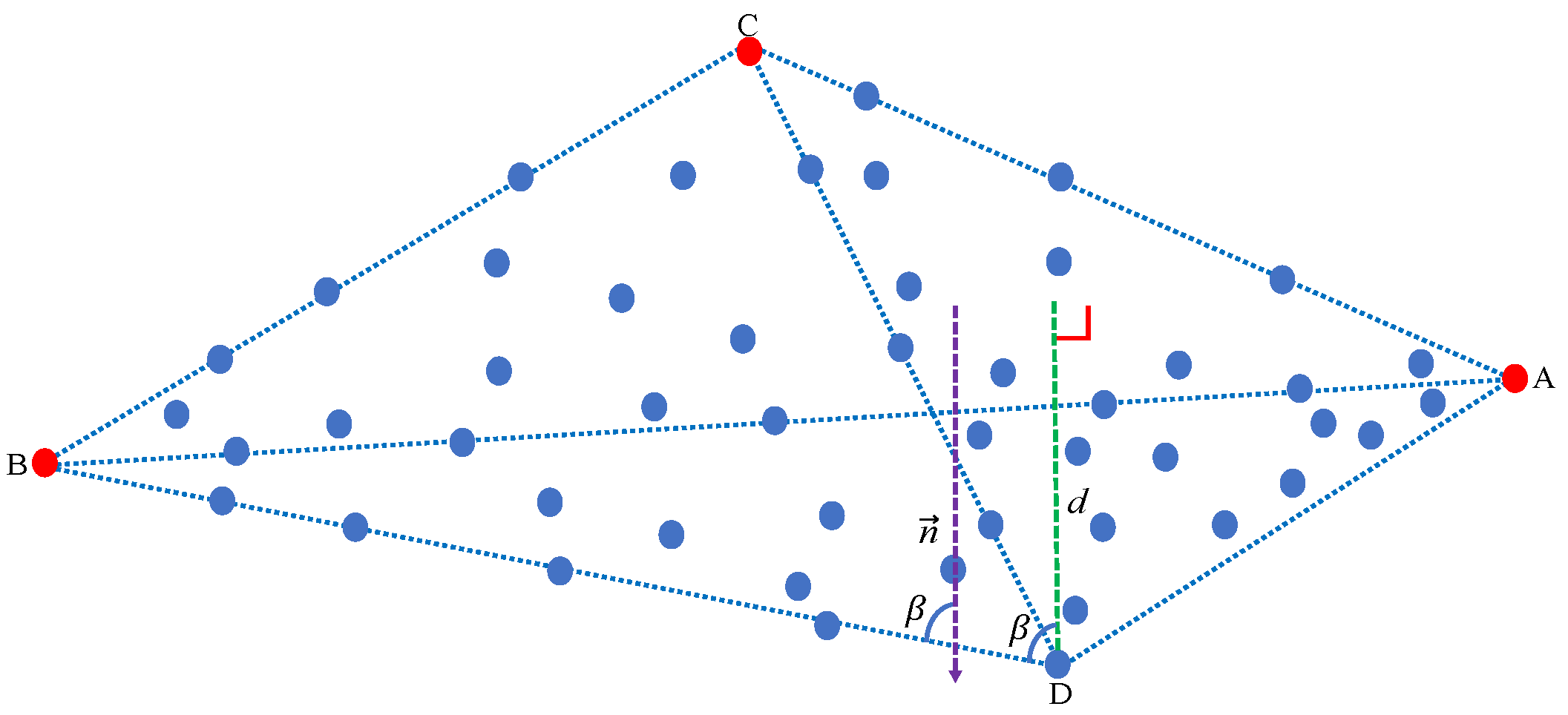
- We calculate the distance between every pixel point and the plane formed by the first, second, and third extracted endmembers, extracting the pixel point with the maximum distance as the fourth endmember.
- We calculate the distance between every pixel point and the affine hull formed by all the previously extracted endmembers, extracting the pixel point with the maximum distance as the next endmember.
- We finish the overall endmember extraction procedure when the maximum distance between all pixel points and the affine hull formed by all the previously extracted endmembers is zero. Simultaneously, we determine the number of endmembers by counting the number of pixel points that have been extracted. In the following, we describe the conducted experiments.
4.1.1. Straightforward MDA Algorithm
4.1.2. MDA for Improving MVSA
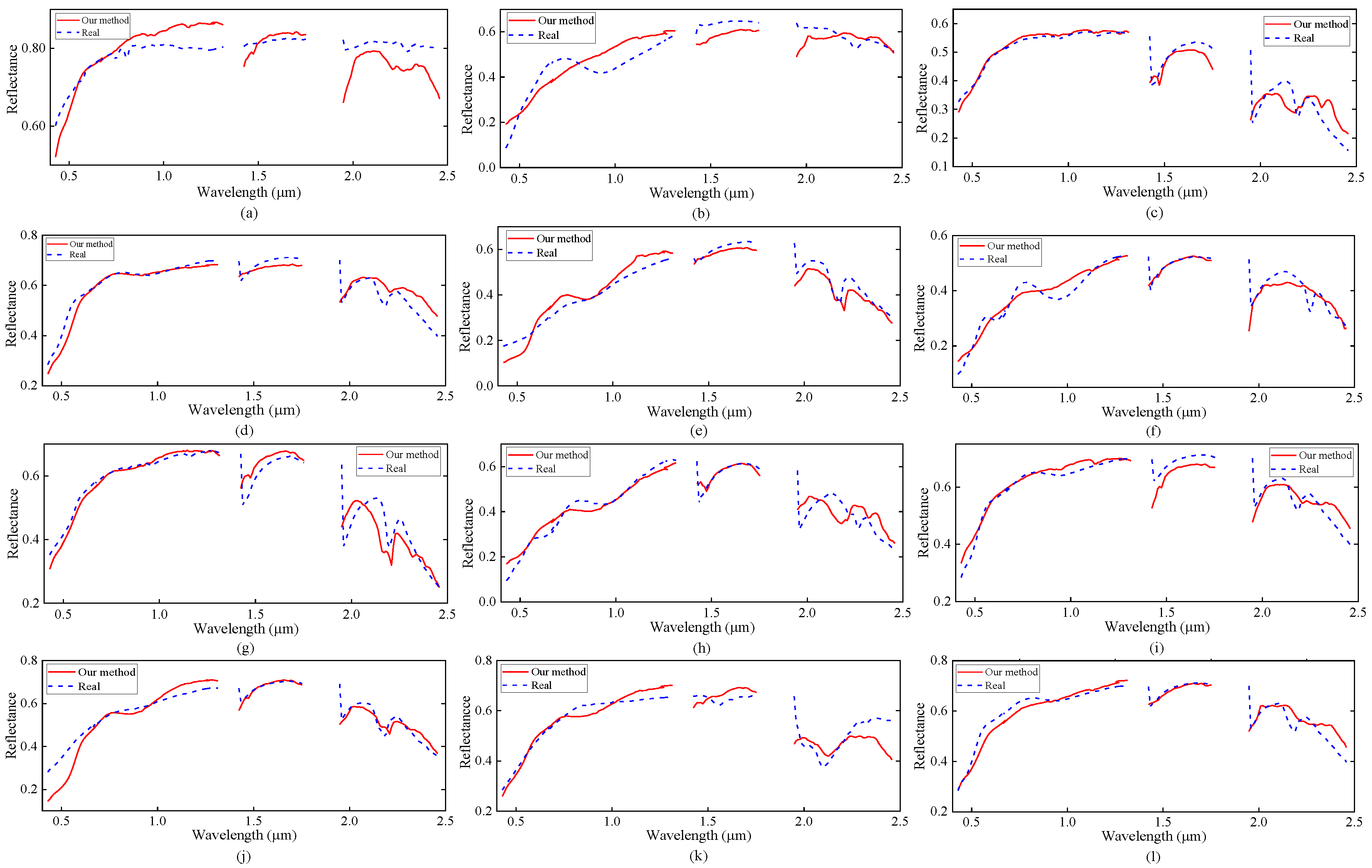
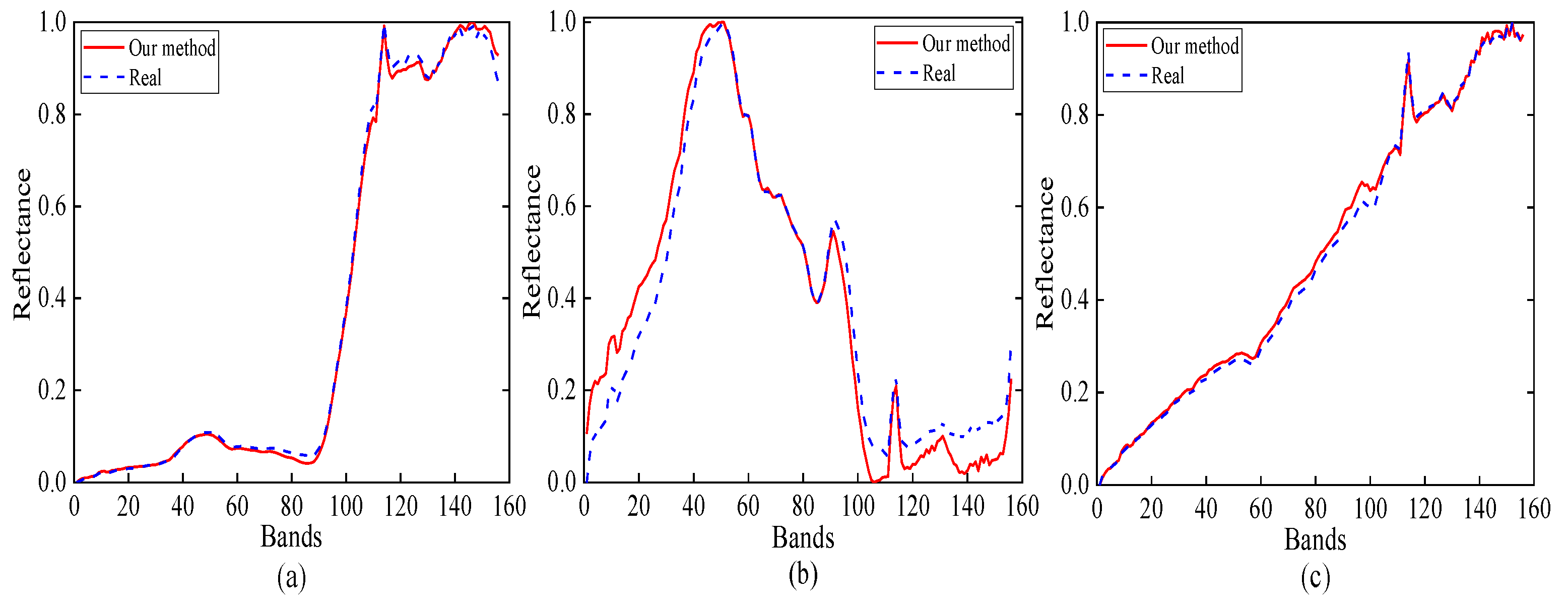
4.2. Real Data
4.2.1. Cuprite Data
4.2.2. Samson Data
5. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Luo, F.; Du, B.; Zhang, L.; Zhang, L.; Tao, D. Feature learning using spatial-spectral hypergraph discriminant analysis for hyperspectral image. IEEE Trans. Cybern. 2018, 49, 2406–2419. [Google Scholar] [CrossRef] [PubMed]
- Vane, G.; Green, R.O.; Chrien, T.G.; Enmark, H.T.; Hansen, E.G.; Porter, W.M. The airborne visible/infrared imaging spectrometer (AVIRIS). Remote Sens. Environ. 1993, 44, 127–143. [Google Scholar] [CrossRef]
- Goetz, A.F.; Vane, G.; Solomon, J.E.; Rock, B.N. Imaging spectrometry for earth remote sensing. Science 1985, 228, 1147–1153. [Google Scholar] [CrossRef]
- Paoletti, M.; Haut, J.; Plaza, J.; Plaza, A. Deep learning classifiers for hyperspectral imaging: A review. ISPRS J. Photogramm. Remote Sens. 2019, 158, 279–317. [Google Scholar] [CrossRef]
- Keshava, N.; Mustard, J.F. Spectral unmixing. IEEE Signal Process. Mag. 2002, 19, 44–57. [Google Scholar] [CrossRef]
- Gao, F.; You, J.; Wang, J.; Sun, J.; Yang, E.; Zhou, H. A novel target detection method for SAR images based on shadow proposal and saliency analysis. Neurocomputing 2017, 267, 220–231. [Google Scholar] [CrossRef]
- Adams, J.B.; Smith, M.O.; Johnson, P.E. Spectral mixture modeling: A new analysis of rock and soil types at the Viking Lander 1 site. J. Geophys. Res. Solid Earth 1986, 91, 8098–8112. [Google Scholar] [CrossRef]
- Chan, T.H.; Ma, W.K.; Ambikapathi, A.; Chi, C.Y. An optimization perspective onwinter’s endmember extraction belief. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 1143–1146. [Google Scholar]
- Bioucas-Dias, J.M.; Plaza, A.; Dobigeon, N.; Parente, M.; Du, Q.; Gader, P.; Chanussot, J. Hyperspectral unmixing overview: Geometrical, statistical, and sparse regression-based approaches. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 354–379. [Google Scholar] [CrossRef]
- Li, J.; Bioucas-Dias, J.M.; Plaza, A.; Liu, L. Robust Collaborative Nonnegative Matrix Factorization for Hyperspectral Unmixing. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6076–6090. [Google Scholar] [CrossRef]
- Tao, X.; Cui, T.; Plaza, A.; Ren, P. Simultaneously Counting and Extracting Endmembers in a Hyperspectral Image Based on Divergent Subsets. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8952–8966. [Google Scholar] [CrossRef]
- Xu, X.; Pan, B.; Chen, Z.; Shi, Z.; Li, T. Simultaneously Multiobjective Sparse Unmixing and Library Pruning for Hyperspectral Imagery. IEEE Trans. Geosci. Remote Sens. 2020. [Google Scholar] [CrossRef]
- Xu, X.; Shi, Z.; Pan, B.; Li, X. A classification-based model for multi-objective hyperspectral sparse unmixing. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9612–9625. [Google Scholar] [CrossRef]
- Geng, X. Study on Hyperspectral Target Detection and Classification. Ph.D. Thesis, Chinese Academy of Sciences, Beijing, China, January 2005. [Google Scholar]
- Wang, R.; Li, H.C.; Pizurica, A.; Li, J.; Plaza, A.; Emery, W.J. Hyperspectral unmixing using double reweighted sparse regression and total variation. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1146–1150. [Google Scholar] [CrossRef]
- Fernandez-Beltran, R.; Plaza, A.; Plaza, J.; Pla, F. Hyperspectral unmixing based on dual-depth sparse probabilistic latent semantic analysis. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6344–6360. [Google Scholar] [CrossRef]
- Delgado, J.; Martín, G.; Plaza, J.; Jiménez, L.I.; Plaza, A. Fast spatial preprocessing for spectral unmixing of hyperspectral data on graphics processing units. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 9, 952–961. [Google Scholar] [CrossRef]
- Zhang, L.; Du, B.; Zhong, Y. Hybrid detectors based on selective endmembers. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2633–2646. [Google Scholar] [CrossRef]
- Kowkabi, F.; Ghassemian, H.; Keshavarz, A. A fast spatial–spectral preprocessing module for hyperspectral endmember extraction. IEEE Geosci. Remote Sens. Lett. 2016, 13, 782–786. [Google Scholar] [CrossRef]
- Kowkabi, F.; Keshavarz, A. Using spectral Geodesic and spatial Euclidean weights of neighbourhood pixels for hyperspectral Endmember Extraction preprocessing. ISPRS J. Photogramm. Remote Sens. 2019, 158, 201–218. [Google Scholar] [CrossRef]
- Zhang, C.; Qin, Q.; Zhang, T.; Sun, Y.; Chen, C. Endmember extraction from hyperspectral image based on discrete firefly algorithm (EE-DFA). ISPRS J. Photogramm. Remote Sens. 2017, 126, 108–119. [Google Scholar] [CrossRef]
- Sun, W.; Yang, G.; Wu, K.; Li, W.; Zhang, D. Pure endmember extraction using robust kernel archetypoid analysis for hyperspectral imagery. ISPRS J. Photogramm. Remote Sens. 2017, 131, 147–159. [Google Scholar] [CrossRef]
- Du, B.; Wei, Q.; Liu, R. An improved quantum-behaved particle swarm optimization for endmember extraction. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6003–6017. [Google Scholar] [CrossRef]
- Tong, L.; Du, B.; Liu, R.; Zhang, L. An improved multiobjective discrete particle swarm optimization for hyperspectral endmember extraction. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7872–7882. [Google Scholar] [CrossRef]
- Lin, C.H.; Chi, C.Y.; Chen, L.; Miller, D.J.; Wang, Y. Detection of sources in non-negative blind source separation by minimum description length criterion. IEEE Trans. Neural Networks Learn. Syst. 2017, 29, 4022–4037. [Google Scholar] [CrossRef]
- Rissanen, J. Modeling by shortest data description. Automatica 1978, 14, 465–471. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Akaike, H. Akaike, H. A new look at the statistical model identification. In Selected Papers of Hirotugu Akaike; Springer: Berlin/Heidelberg, Germany, 1974; pp. 716–723. [Google Scholar]
- Graham, M.W.; Miller, D.J. Unsupervised learning of parsimonious mixtures on large spaces with integrated feature and component selection. IEEE Trans. Signal Process. 2006, 54, 1289–1303. [Google Scholar] [CrossRef]
- Peres-Neto, P.R.; Jackson, D.A.; Somers, K.M. How many principal components? Stopping rules for determining the number of non-trivial axes revisited. Comput. Stat. Data Anal. 2005, 49, 974–997. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Nascimento, J.M. Hyperspectral subspace identification. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2435–2445. [Google Scholar] [CrossRef]
- Chang, C.I.; Du, Q. Estimation of number of spectrally distinct signal sources in hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2004, 42, 608–619. [Google Scholar] [CrossRef]
- Halimi, A.; Honeine, P.; Kharouf, M.; Richard, C.; Tourneret, J.Y. Estimating the intrinsic dimension of hyperspectral images using a noise-whitened eigengap approach. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3811–3821. [Google Scholar] [CrossRef]
- Ambikapathi, A.; Chan, T.H.; Chi, C.Y.; Keizer, K. Hyperspectral data geometry-based estimation of number of endmembers using p-norm-based pure pixel identification algorithm. IEEE Trans. Geosci. Remote Sens. 2012, 51, 2753–2769. [Google Scholar] [CrossRef]
- Parente, M.; Plaza, A. Survey of geometric and statistical unmixing algorithms for hyperspectral images. In Proceedings of the 2010 2nd Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing, Reykjavik, Iceland, 14–16 June 2010; pp. 1–4. [Google Scholar]
- Boardman, J.W.; Kruse, F.A.; Green, R.O. Mapping target signatures via partial unmixing of AVIRIS data. In Proceedings of the Summaries 5th JPL Airborne Earth Science Workshop, Pasadena, CA, USA, 23–26 January 1995; Volume 1, pp. 23–26. [Google Scholar]
- Tao, X.; Cui, T.; Yu, Z.; Ren, P. Locality Preserving Endmember Extraction for Estimating Green Algae Area. In Proceedings of the 2018 OCEANS-MTS/IEEE Kobe Techno-Oceans (OTO), Kobe, Japan, 28–31 May 2018; pp. 1–4. [Google Scholar]
- Tao, X.; Cui, T.; Ren, P. Cofactor-Based Efficient Endmember Extraction for Green Algae Area Estimation. IEEE Geosci. Remote Sens. Lett. 2019, 16, 849–853. [Google Scholar] [CrossRef]
- Nascimento, J.M.; Dias, J.M. Vertex component analysis: A fast algorithm to unmix hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 898–910. [Google Scholar] [CrossRef]
- Miao, L.; Qi, H. Endmember extraction from highly mixed data using minimum volume constrained nonnegative matrix factorization. IEEE Trans. Geosci. Remote Sens. 2007, 45, 765–777. [Google Scholar] [CrossRef]
- Chan, T.H.; Chi, C.Y.; Huang, Y.M.; Ma, W.K. A convex analysis-based minimum-volume enclosing simplex algorithm for hyperspectral unmixing. IEEE Trans. Signal Process. 2009, 57, 4418–4432. [Google Scholar] [CrossRef]
- Li, J.; Bioucas-Dias, J.M. Minimum volume simplex analysis: A fast algorithm to unmix hyperspectral data. In Proceedings of the IGARSS 2008-2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008; Volume 3, p. III–250. [Google Scholar]
- Li, J.; Agathos, A.; Zaharie, D.; Bioucas-Dias, J.M.; Plaza, A.; Li, X. Minimum volume simplex analysis: A fast algorithm for linear hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5067–5082. [Google Scholar]
- Lin, C.H.; Chi, C.Y.; Wang, Y.H.; Chan, T.H. A fast hyperplane-based minimum-volume enclosing simplex algorithm for blind hyperspectral unmixing. IEEE Trans. Signal Process. 2015, 64, 1946–1961. [Google Scholar] [CrossRef]
- Hearst, M.A.; Dumais, S.T.; Osuna, E.; Platt, J.; Scholkopf, B. Support vector machines. IEEE Intell. Syst. Their Appl. 1998, 13, 18–28. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Figueiredo, M.A. Alternating direction algorithms for constrained sparse regression: Application to hyperspectral unmixing. In Proceedings of the 2010 2nd Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing, Reykjavik, Iceland, 14–16 June 2010; pp. 1–4. [Google Scholar]





| VCA | MDA | Hysime | HFC | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SAD | Time | SAD | Time | Time | Time | |||||||
| 5 | 0 | 0 | 0.252 | 0 | 0 | 0.204 | 5 + 0.1066 | 6 + 0 | 5 | 0.161 | 5 | 0.089 |
| 10 | 0 | 0 | 0.246 | 0 | 0 | 0.216 | 10 + 0.0844 | 11 + 0 | 10 | 0.142 | 10 | 0.063 |
| 15 | 0 | 0 | 0.245 | 0 | 0 | 0.233 | 15 + 0.0015 | 16 + 0 | 15 | 0.143 | 15 | 0.064 |
| 20 | 0 | 0 | 0.259 | 0 | 0 | 0.251 | 20 + 0.0020 | 21 + 0 | 19 | 0.157 | 20 | 0.065 |
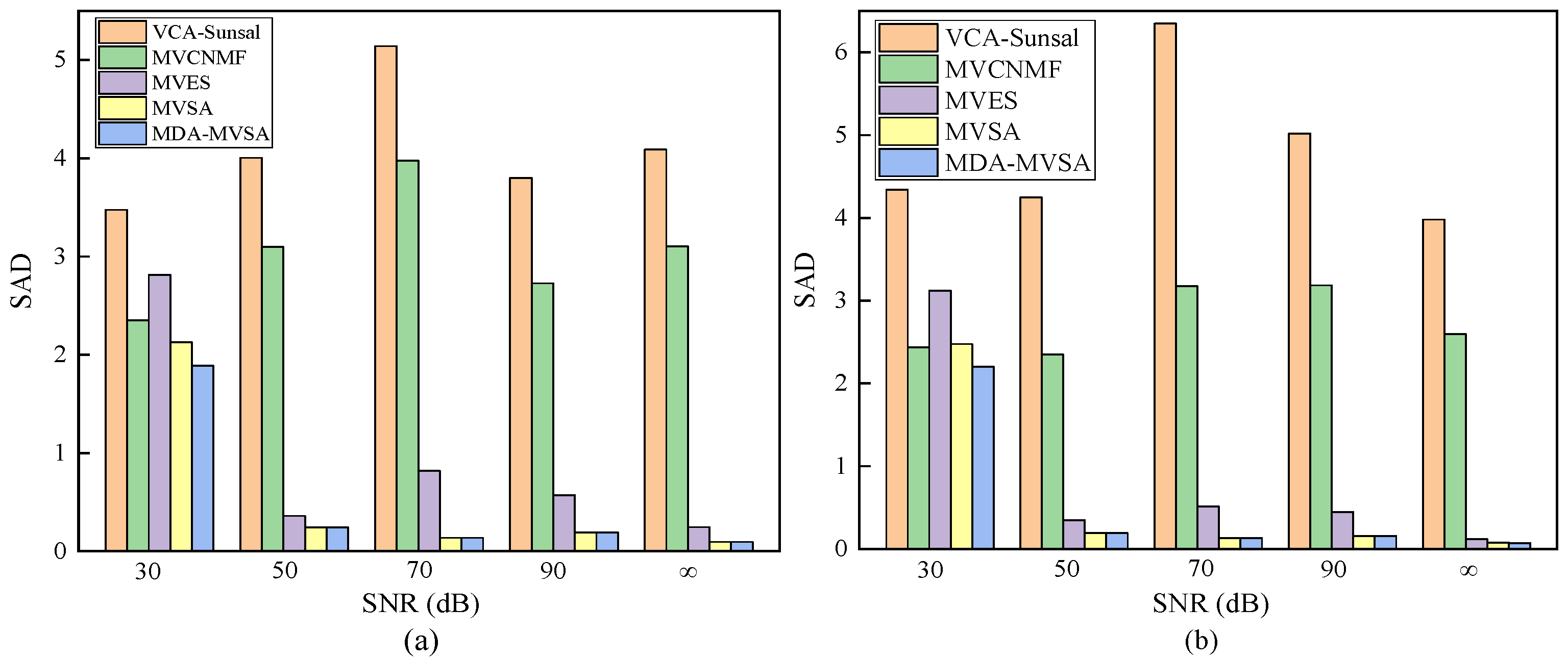
| VCA-Sunsal | MVCNMF | MVES | MVSA | MDA-MVSA | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| dB | Time | Time | Time | Time | Time | |||||||||||||||
| 30 | 0.091 | 0.281 | 0.012 | 0.338 | 0.053 | 0.171 | 0.004 | 10.362 | 0.051 | 0.157 | 0 | 2.409 | 0.054 | 0.127 | 0 | 0.530 | 0.047 | 0.122 | 0 | 0.588 |
| 50 | 0.095 | 0.322 | 0.013 | 0.346 | 0.056 | 0.195 | 0.005 | 9.443 | 0.009 | 0.024 | 0 | 2.562 | 0.005 | 0.016 | 0 | 0.684 | 0.005 | 0.016 | 0 | 0.582 |
| 70 | 0.188 | 0.472 | 0.047 | 0.350 | 0.066 | 0.191 | 0.005 | 9.439 | 0.019 | 0.038 | 0 | 3.385 | 0.002 | 0.006 | 0 | 0.561 | 0.002 | 0.006 | 0 | 0.571 |
| 90 | 0.131 | 0.307 | 0.014 | 0.352 | 0.069 | 0.178 | 0.004 | 10.169 | 0.009 | 0.017 | 0 | 3.865 | 0.002 | 0.005 | 0 | 0.562 | 0.002 | 0.005 | 0 | 0.570 |
| ∞ | 0.186 | 0.555 | 0.040 | 0.346 | 0.055 | 0.164 | 0.003 | 10.448 | 0.004 | 0.009 | 0 | 3.714 | 0.002 | 0.004 | 0 | 0.554 | 0.002 | 0.004 | 0 | 0.569 |
| VCA-Sunsal | MVCNMF | MVES | MVSA | MDA-MVSA | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| dB | Time | Time | Time | Time | Time | |||||||||||||||
| 30 | 0.164 | 0.496 | 0.035 | 0.345 | 0.057 | 0.187 | 0.005 | 10.200 | 0.059 | 0.153 | 0 | 2.427 | 0.056 | 0.142 | 0 | 0.662 | 0.051 | 0.140 | 0 | 0.696 |
| 50 | 0.206 | 0.489 | 0.045 | 0.355 | 0.192 | 0.305 | 0.004 | 10.370 | 0.007 | 0.022 | 0 | 2.528 | 0.003 | 0.011 | 0 | 0.671 | 0.003 | 0.011 | 0 | 0.563 |
| 70 | 0.285 | 0.497 | 0.111 | 0.362 | 0.078 | 0.190 | 0.005 | 9.853 | 0.010 | 0.023 | 0 | 3.006 | 0.003 | 0.005 | 0 | 0.568 | 0.003 | 0.005 | 0 | 0.567 |
| 90 | 0.134 | 0.351 | 0.018 | 0.364 | 0.084 | 0.215 | 0.005 | 10.306 | 0.011 | 0.025 | 0 | 3.461 | 0.003 | 0.005 | 0 | 0.568 | 0.003 | 0.005 | 0 | 0.571 |
| ∞ | 0.109 | 0.409 | 0.017 | 0.335 | 0.057 | 0.180 | 0.002 | 10.299 | 0.002 | 0.009 | 0 | 3.555 | 0.002 | 0.005 | 0 | 0.551 | 0.002 | 0.005 | 0 | 0.678 |
| dB | The Estimated Number of Endmembers + The Maximum Distance | |||
|---|---|---|---|---|
| SD with Pure Pixel Points | SD with Nonpure Pixel Points | |||
| 30 | 5 + 0.094 | 6 + 0.068 | 5 + 0.086 | 6 + 0.06 |
| 50 | 5 + 0.048 | 6 + 0.008 | 5 + 0.021 | 6 + 0.007 |
| 70 | 5 + 0.029 | 6 + 0.001 | 5 + 0.02 | 6 + 0.001 |
| 90 | 5 + 0.014 | 6 + 0 | 5 + 0.017 | 6 + 0 |
| ∞ | 5 + 0.014 | 6 + 0 | 5 + 0.007 | 6 + 0 |
| dB | Synthetic Data with Pure Pixel Points | Synthetic Data with Nonpure Pixel Points | ||||
|---|---|---|---|---|---|---|
| Hysime | HFC | MDA-MVSA | Hysime | HFC | MDA-MVSA | |
| 30 | 5 + 0.13 | 188 + 0.068 | 5 + 0.588 | 5 + 0.133 | 188 + 0.067 | 5 + 0.696 |
| 50 | 5 + 0.128 | 5 + 0.067 | 5 + 0.582 | 5 + 0.127 | 5 + 0.067 | 5 + 0.563 |
| 70 | 5 + 0.13 | 5 + 0.067 | 5 + 0.571 | 5 + 0.126 | 5 + 0.067 | 5 + 0.567 |
| 90 | 5 + 0.132 | 5 + 0.066 | 5 + 0.57 | 5 + 0.126 | 5 + 0.067 | 5 + 0.571 |
| ∞ | 5 + 0.126 | 5 + 0.068 | 5 + 0.569 | 5 + 0.127 | 5 + 0.066 | 5 + 0.678 |
| MVES | MDA-MVSA | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| c | SAD | Time | SAD | Time | + | ||||||||
| 4000 | 5 | 0.0034 | 0.0147 | 0 | 0.1264 | 5.4033 | 0.0005 | 0.0025 | 0 | 0.0286 | 0.7657 | 5 + 0.0206 | 6 + 0.0009 |
| 10 | 0.0046 | 0.0146 | 0 | 0.1981 | 158.3557 | 0.0018 | 0.0067 | 0 | 0.1034 | 1.4707 | 10 + 0.0040 | 11 + 0.0008 | |
| 15 | 0.0335 | 0.0927 | 0 | 4.2413 | 478.3535 | 0.0228 | 0.0755 | 0 | 1.6291 | 2.8269 | 15 + 0.0012 | 16 + 0.0008 | |
| 20 | 0.0152 | 0.0700 | 0 | 0.6945 | 1572.6336 | 0.0072 | 0.0316 | 0 | 0.2972 | 3.9038 | 20 + 0.0017 | 21 + 0.0008 | |
| 8000 | 5 | 0.0032 | 0.0061 | 0 | 0.2002 | 3.2270 | 0.0007 | 0.0014 | 0 | 0.0349 | 1.0759 | 5 + 0.0369 | 6 + 0.0007 |
| 10 | 0.0086 | 0.0267 | 0 | 0.6264 | 365.4279 | 0.0036 | 0.0068 | 0 | 0.0939 | 1.7829 | 10 + 0.0037 | 11 + 0.0006 | |
| 15 | 0.0099 | 0.0286 | 0 | 1.1329 | 1233.9985 | 0.0046 | 0.0124 | 0 | 0.3029 | 4.1594 | 15 + 0.0008 | 16 + 0.0012 | |
| 20 | 0.0300 | 0.0950 | 0 | 18.8659 | 3319.7858 | 0.0155 | 0.0515 | 0 | 0.7091 | 7.1124 | 20 + 0.0012 | 21 + 0.0010 | |
| 12,000 | 5 | 0.0024 | 0.0048 | 0 | 0.0423 | 6.2190 | 0.0004 | 0.0011 | 0 | 0.0257 | 1.4246 | 5 + 0.0023 | 6 + 0.0009 |
| 10 | 0.0047 | 0.0110 | 0 | 0.3527 | 534.3258 | 0.0017 | 0.0051 | 0 | 0.0359 | 9.5453 | 10 + 0.0105 | 11 + 0.0008 | |
| 15 | 0.0314 | 0.0808 | 0 | 1.7409 | 2651.6650 | 0.0222 | 0.0603 | 0 | 1.2631 | 5.9396 | 15 + 0.0012 | 16 + 0.0009 | |
| 20 | 0.0278 | 0.0832 | 0 | 1.6324 | 13,125.5823 | 0.0178 | 0.0458 | 0 | 0.7527 | 11.1843 | 20 + 0.0014 | 21 + 0.0010 | |
| Methods | SAD | Time | ||
|---|---|---|---|---|
| MDA-MVSA | 0.0747 | 0.4919 | 4.4705 | 34.6597 |
| MVCNMF | 0.0927 | 0.5519 | 5.4707 | 1230.8838 |
| Methods | SAD | Time | |||
|---|---|---|---|---|---|
| MDA-MVSA | 0.0833 | 0.2026 | 1.3961 | 4.3788 | 1.1834 |
| MVCNMF | 0.3007 | 0.8321 | 1.5881 | 11.7210 | 23.7691 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, X.; Paoletti, M.E.; Haut, J.M.; Ren, P.; Plaza, J.; Plaza, A. Endmember Estimation with Maximum Distance Analysis. Remote Sens. 2021, 13, 713. https://doi.org/10.3390/rs13040713
Tao X, Paoletti ME, Haut JM, Ren P, Plaza J, Plaza A. Endmember Estimation with Maximum Distance Analysis. Remote Sensing. 2021; 13(4):713. https://doi.org/10.3390/rs13040713
Chicago/Turabian StyleTao, Xuanwen, Mercedes E. Paoletti, Juan M. Haut, Peng Ren, Javier Plaza, and Antonio Plaza. 2021. "Endmember Estimation with Maximum Distance Analysis" Remote Sensing 13, no. 4: 713. https://doi.org/10.3390/rs13040713
APA StyleTao, X., Paoletti, M. E., Haut, J. M., Ren, P., Plaza, J., & Plaza, A. (2021). Endmember Estimation with Maximum Distance Analysis. Remote Sensing, 13(4), 713. https://doi.org/10.3390/rs13040713