Abstract
For decades, satellite altimetry is providing reliable data on the sea level, surface currents, tides, planetary and wind waves and sea ice. We propose a potential enhancement of collecting special data subsets for a better temporal and spatial sampling of dynamics of the Sub-Polar seas. We show that peculiarities of the orbits of the TOPEX/Poseidon and Jasons’ missions generate a regular grid of crossovers which locations are fixed in space and time of the orbit cycles. Two types of these special crossovers are specified: self-crossovers (SC) occurring as intersections of tracks of the same satellite and inter-crossovers (IC) appearing during the phases of interleaved orbits when tracks of two different satellites are crossing. The time delay between two consecutive measurements in the high-latitude sites is less than 2 h for SC and 1 h for IC, thus providing a ground for monitoring large-scale currents (including current direction) and wind waves. The sets of the special crossovers can be regarded as networks of virtual ocean buoys. The Norwegian Sea case study illustrates the value of the special crossovers for the Sub-Polar seas and the feasibility of building the networks of SC and IC in other areas of the World Ocean.
1. Introduction
Satellite altimetry has successfully been developing for ocean studies during the past three decades. It shows numerous applications for the sea level, ocean dynamics, coastal oceanography, planetary waves, ocean tides, wind and wave, ice cover, Earth’s gravity field and climatology research [1,2,3,4,5,6,7,8,9]. The altimetry “adequate sampling… have revolutionized oceanography” by providing data previously impossible to obtain, in the words of the outstanding oceanographer Walter Munk [10]. The TOPEX/Poseidon, “the most successful ocean experiment of all time” [10], together with its follow-on Jason’s missions is operating continuously at the same reference orbits for almost thirty years.
The crossovers, that is, points of intersection of ground tracks of altimeters, play an exclusive role in maintenance of functionality and performance of satellite altimetry. Calibration and validation of measurements, assessment of the measurement corrections, retracking procedure and reconstruction of spatial and temporal fields of the measured physical quantities inevitably refer to the crossovers [3]. For the primary task of satellite altimetry, measurements of the ocean surface, the acceptable delay between two measurements is assumed to be less than 10 days [11]. For wind-wave studies the corresponding spatial mismatch of measurements 50 km and time delay 1 h is recommended (e.g., http://globwave.ifremer.fr/products/globwave-satellite-data/satellite-crossovers, last access on 11 February 2021). The latter implies severe limitations on the number of crossovers and orientation of the altimeter orbits. Generally, such kind of crossovers is possible to find only for different altimetry missions that dictates new difficulties to overcome. We mention only two issues among many others:
- The crossovers of different missions require their careful intercalibration accounting for features of hardware (different types of radars) and data processing methods (including different types of applied corrections).
- Incommensurability of their orbit periods excludes repetitive monitoring of the particular sites because the corresponding crossovers appear to be unique, i.e., are irregularly distributed in space and time.
TOPEX/Poseidon–Jasons’ missions provide special crossover datasets that are free of the above-mentioned difficulties and generate an adequate spatial and temporal sampling of the ocean processes at high latitudes [12]. The distance between ground tracks of these satellites varies from more than 300 km at the Equator to just several kilometers in high latitudes. Time intervals between two consecutive measurements at the same point (self-crossover—self-intersection of the altimeter track) can also be rather short, close to one orbit period (less than two hours). The orbit repetition period of about 10 days provides a series of such cross-over points with time lag of the same period. The locations of these points are fixed, which makes them an essential component of calibration/validation procedures of the altimetry. The orbit inclination of of TOPEX/Poseidon–Jasons’ missions implies the coverage of the major part of the ice-free area of the World Ocean by measurements of these satellites.
Based on the above listed features, we present a special subset of data of High Latitude Crossovers (HLC) with minimal time intervals between consecutive measurements and identify two of their types:
- self-crossovers (SC) when the crossover point is provided by measurements of the same satellite; and
- inter-crossovers (IC) when measurements in a point are made by different altimeters, e.g., by a pair TOPEX/Poseidon/Jason-1, Jason-1/Jason-2 or Jason-2/Jason-3 during phases of interleaved orbits.
Because of these, individual (for SC) and synchronized (for IC) orbits of Jason’s altimeters generate regular in space and periodic in time measurements in a number of special fixed sites. The SC and IC altimeter data with regular space and time sampling can be regarded as virtual stationary sea stations, analog of continuous buoy measurements of the sea level, wind speed and wave height. There are evident analogs in satellite altimetry of rivers when virtual water level gauges are established at locations where satellite ground tracks cross riverbed or river tributary. It makes the topic of the new crossovers quite promising, especially for the Sub-Arctic seas.
The above arguments constitute an idea and the essence of this study: special subsets of altimetry data with improved sampling can provide additional information on ocean dynamics and new opportunities for monitoring the seas.
In Section 2, we describe useful features of the CS and IC of the TOPEX/Poseidon–Jason’s missions.
Section 3 describes geographical distributions of SC and IC in the World Ocean and possible gains of using the data of these special crossovers, especially in the Sub-Arctic seas.
Section 4 presents a case study where advantages and problems of the data subset to be solved are discussed. The paper is finalized by Discussion and Conclusions.
2. The Self- and Inter-Crossovers
2.1. Self-Crossovers: Standard Jason’S Orbits
Figure 1a shows standard tracks of the Jason’s missions in the North Atlantic. The ascending track N165 is given in red as a reference one. The self-crossover (SC) of the orbit occurs at descending track N168 (plus 3 to the ascending track number) near the limiting latitude in a time lag a bit longer that one orbit period (≈112 min). In one more orbit period (plus 5 to the reference track N165), a similar SC occurs at lower latitude. The new crossovers with the fixed ascending track (N165 in our case) continues to appear with every new orbit, thus travelling to the South Pole. The passage of crossovers between poles takes approximately 1 day (about 12 orbit periods) for the fixed reference track (track N165 in our case of Figure 1).
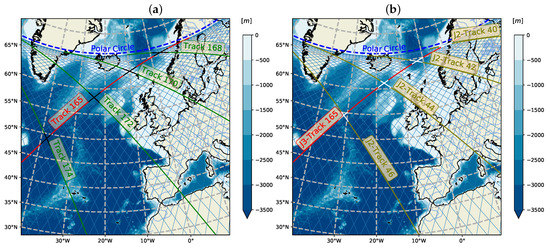
Figure 1.
Crossovers of Jasons’ orbits in the North Atlantic. The ascending track N165 of Jason-3 is given in red, and green trajectories show its descending counterparts generating crossovers within the one-day delay: (a) self-crossovers (SCs) of Jason-3 standard orbits; and (b) inter-crossovers (ICs) of Jason-3 and Jason-2 during the phase of interleaved orbits October 2016–April 2017.
The selected area of the North Atlantic in Figure 1a contains four crossovers of this type (descending tracks are shown in green). Time delay of SC is growing from north to south for the fixed ascending track and from south to north for a fixed descending track. Variation of the ocean conditions between two consecutive measurements in SC, evidently, depends on time delay and on characteristic scales of variability in the particular site. Time delay is minimal in high latitudes where variability of ocean environment can be rather strong. On the other hand, low variability in tropical crossovers can essentially reduce the effect of relatively large time lag of about half-day. In this way, quality of a particular crossover is not easy to assess in advance. This important issue is detailed in the next section. Here, one should emphasize that SCs occur regularly at the same points and time of the satellite cycle (i.e., for fixed pairs of track numbers), thus comprising an abundant data subset.
2.2. Inter-Crossovers: The Jason’s Interleaved Orbits
At the beginning of every new mission (TOPEX/Poseidon—Jason-1; Jason-1–Jason-2; Jason-2–Jason-3) two satellites conform a special configuration of the so-called interleaved orbits when “old” satellite is positioned midway between standard ground tracks and two satellites are placed on opposite sides of the Earth. These phases have been realized during mid-September 2002–October 2005 for the tandem TOPEX/Poseidon–Jason-1, mid-February 2009–March 2012 for Jason-1/2 and mid October 2016–April 2017 for Jason-2/3. Such a configuration of two orbits provides a new family of crossovers we call inter-crossovers (IC). For IC, the shortest time lag between consecutive measurements is about one-half of the orbit period (56 min). It occurs near the latitudes approximately in the Northern and Southern Hemispheres, i.e., a bit closer to the limiting latitudes of the orbits than SCs. As a result, similar ICs with longer time delay (approximately orbit periods) conform a configuration resembling the SC one shown in Figure 1b for the same reference track of Jason-3 N165 and descending tracks of Jason-2 N.
Table 1 presents meridional dependencies of variability of parameters measured by altimeter for the ICs with the fixed ascending track N165 of Jason-3 and Jason-2 tracks N40–62. The corresponding ICs latitudes vary from the most northern to the most southern limit during the one-day period. The estimates are given for all the duration of the phase of interleaved orbits (October 2016–April 2017, totally, 19 cycles). Similar estimates can be made for SCs in Figure 1a.

Table 1.
Variability of the altimetry measurements in ICs during the phase of interleaved orbits of Jason-2/3 (mid October 2016–April 2017). Ascending track N165 of Jason-3 is taken as a reference one, descending track numbers of Jason-2 are shown in the first column. Estimates for last two lines (tracks 60 and 62) are absent because of low data quality.
The most northern IC has a minimal time lag a bit less than 1 h. The delay of the most southern one N62 in Table 1 is about one day (23 h 28 min). Variability of significant wave height and normalized radar cross-section directly measured by altimeters grows in moderate latitudes with the time lag. The standard deviation (STD) of difference of measurements of Jason-2 and Jason-3 in IC with time lag about 9 h (Jason-2 track 48, Line 5) is six times higher than one of minimal time lag for wave height (Column 5), more than three times for normalized radar cross-section (Column 7) and times for altimetry-derived near-surface wind speed (Column 8). The variability is even stronger for extreme values of wave height (Column 6) exceeding one order of magnitude. The variability weakens in tropical and subtropical ICs (Lines 6 and 7) but remains higher than in the Sub-Arctic IC with the minimal time delay.
An additional aspect of this variability is its effect on numerous corrections of altimetry measurements. Some of these corrections are directly linked with the time delay, e.g., tidal corrections. Other corrections, such as Sea State Bias (SSB), are estimated parametrically [13,14,15] as functions of the directly measured values (e.g., and ). One can easily show that all these corrections are minimal for the HLCs with minimal time lags that nudges us to draw special attention to these crossovers located near the Polar Circles. These special crossovers provide an additional information on anomalies of ocean currents and characteristics of wind-driven waves and near-surface winds (altimetric wind speed, e.g., [16]). The angle between the tracks in the SCs and ICs is quite large (about and correspondingly) that can be used for calculation of quasi-instantaneous values of:
- anomalies of geostrophic current velocities and their directions [17,18,19]; and
- wave heights, periods and directions of wind-driven waves [15,20,21].
It should be stressed that an instantaneous assessment of the geostrophic currents governed by balance of the Coriolis force and the sea surface height anomaly (SSHA) gradient is, generally, unattainable in the classic altimetry. Usually, estimates of non-collinear components of the geostrophic velocity vector are widely spaced over time. Interpolation of altimetry data in space and time is used to construct a generalized field of the ocean circulation. It leads to undersampling of relatively fast and small-scale ocean dynamics, especially in the Sub-Polar seas where the Rossby radius of deformation is small. The instantaneous along-track assessment of geostrophic currents with SCs and ICs near the limiting latitudes becomes a worthy solution of the problem.
2.3. Crossover Clusters: Temporal Sampling of SCs and ICs
As mentioned above, inter-mission crossovers are irregularly distributed in space and time due to different periods of satellites. The standard orbits of the TOPEX/Poseidon and Jasons’ missions gives an essential advantage providing fixed periodically spaced sites where crossovers occur each cycle of approximately 10 days. Different types of these crossovers can be grouped into clusters, as shown in Figure 2, for the phase of interleaved orbits of Jason-2/3 (October 2016–April 2017). Further on, we refer to this phase if otherwise stated.
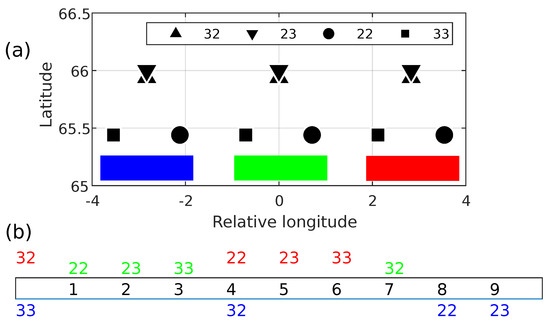
Figure 2.
Crossover clusters with minimal time lags. (a) Relative location of three clusters. Symbols and codes of SCs and ICs are given in legend. Longitude is shown relative to the IC of green cluster (see column 3 of Table 2). (b) Timeline of crossovers in days of cycle (black numbers 1–9) relatively to IC 32 of the central cluster. The color code corresponds to the cluster colors in (a).
We introduce codes for particular crossovers: “22” and “33” mean SCs of Jason-2 and Jason-3, correspondingly. The IC “23” means that Jason-2 passes the crossover before Jason-3, and “IC 32” is used for the opposite case. Each cluster comprises two SCs (circles and squares) and two ICs (triangles) centered relative to the ICs latitude. Table 2 presents key characteristics of the cluster of crossovers with minimal time lags we are mostly interested in. The cluster’s SCs are located at approximately the same latitude about N(S). IC 32 is approximately 30 nautical miles (nmi) to the north (south) close to the latitude and its counterpart IC 23 is nmi more apart to the north (south) at approximately the same longitude. Time delays for SCs 22 and 33 are evidently very close to each other because of equivalence of individual orbit periods of satellites (Column 4 of Table 2). The difference of about 9 min of time lags of ICs is explained by shift of Jason-2 and 3 orbits slightly different than one-half of the orbit period. Taking the track number of Jason-3 of IC 32 as a reference, one can get the track numbers of all elements of the cluster following rules of two last columns of Table 2 (track number more than 254 means a shift on one cycle).

Table 2.
Spacing of crossovers with minimal time lag.
Figure 2 shows location of three clusters (Figure 2a) together with timeline of crossovers in Figure 2b. Codes of crossovers correspond to colors of the clusters. One can see that the group of three clusters provide at least one measurement per day for distance of approximately 212 nmi along latitude. As shown below, many crossovers with minimal time lag are located in ocean straits. Thus, the issue of clustering of SCs and ICs can be useful for assessment water mass transport across these areas.
All the above mentioned predetermines our special attention to the high latitude SCs and ICs with minimal time lags, their geographical distribution and features of dynamics.
3. Geography of High Latitude Crossovers: Issues of Monitoring Sub-Polar Seas
In this section, we discuss the geographic location of SC and IC points with minimal time lags in both hemispheres, which fortunately cross a series of crucially important water bodies (Figure 3):
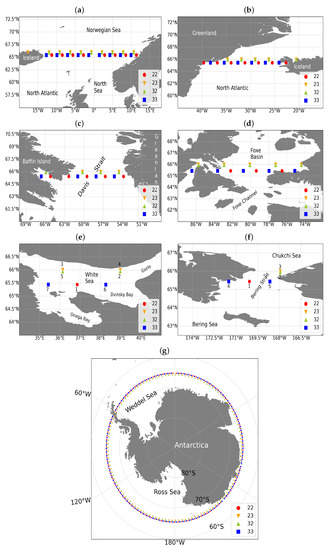
Figure 3.
SCs and ICs of the phase of interleaved orbits of Jason-2/3: (a) the Norwegian Sea; (b) the Denmark Strait; (c) the Davis Strait; (d) the Foxe Basin; (e) the White Sea; (f) the Bering Strait; and (g) the Southern Ocean.
- The Norwegian Sea
- The Denmark Strait
- The Davis Strait
- Foxe Basin north of Hudson Bay in the Canadian Arctic Archipelago
- The White Sea
- The Bering Strait
- The Southern Ocean
Sea ice conditions in the White Sea, Foxe Basin, the Bering Strait and along Antarctica can significantly affect quantity and quality of the altimetry data. Below, we show all these areas in their connection with specific tasks for their studies and monitoring.
3.1. The Norwegian Sea
In the Norwegian Sea, the chain of 18 SCs and 18 ICs forms nine full clusters in the southern part of the sea between Iceland and Norway (Figure 3a). This is an important area where calculations of water mass and heat transfer from the Atlantic Ocean to the Arctic Ocean are made to understand climate change in the Arctic Ocean. Large-scale circulation in the Norwegian Sea and adjacent areas largely determines the climate in the North Atlantic Ocean [22,23,24,25,26,27,28].
The hydrological regime of the Norwegian Sea is determined by the flux of the Atlantic water, transferred by the Norwegian Current (a branch of the North Atlantic Current) through the Faeroe–Shetland Strait. In addition, a small part of the Atlantic water penetrates between Iceland and the Shetland Islands. Besides, freshened water of the Baltic Current comes from the North Sea along the coast of Norway. The total volume of the Atlantic water coming to the Norwegian Sea amounts to about 100,000 km/year, and the water carried out to the Atlantic Ocean is about 40,000 km/year. The maximum inflow of water in the Norwegian Sea is observed in December and January, the minimum being in April and May. The magnitude of interannual fluctuations of the Atlantic water inflow reaches 40,000 km/year [29,30]. The chain of new crossovers crosses the following currents which determines water exchange between the North Atlantic Ocean and the Norwegian Sea (from west to east): (i) the Coastal Iceland branch of the Irminger Current; (ii) the East Icelandic Current, which flows southward around eastern coast of Iceland; (iii) the Norwegian Current; and (iv) the Norwegian Coastal Current (to the south of N it is called the Baltic Current), which flows northward into the Norwegian Sea [29,30].
A possibility of along-track estimates of geostrophic current magnitudes and directions at the high latitude SCs and ICs from instantaneous SSHA provided by altimetry represents a strong advantage in establishing permanent monitoring of fields of currents and calculation of precise water exchange anomalies between sub-basins in this region. Nine clusters provide at least three independent estimates of the current field across the cross-section per day (see Section 2.3 and Figure 2). Thus, currents and water exchange can be monitored with essentially better time resolution that is usually made on the basis of gridded altimetry products for SSHA.
The region is also characterized by intense wind wave variability, especially in the conditions of severe weather which is a characteristic feature of the region. In winter season, wave heights can exceed 20 m, while the duration of “weather windows” (periods with waves less than m) is never more than three days [31]. Wave models reproduce the wave and wind fields in the Norwegian Sea with high accuracy, showing a good correlation with buoy measurements [32,33]. Nevertheless, permanent wave monitoring at the HLCs can further support the analysis of the sea state under ongoing climate change. Being concentrated near the Polar Circle away from stationary buoys, these points can also be used for the additional calibration and validation of wave models.
3.2. The Denmark Strait
In the Denmark Strait, the chain of four full clusters (eight SCs and eight ICs) and five more SCs in the near-shore zone is located between Greenland and Iceland, just southward of the southern border of the Greenland Sea (Figure 3b).
The strait stretches 480 km long and 290 km wide, and it has a sill of 191 m depth at the Greenland–Iceland Rise. Being relatively narrow, it plays an exceptional role in the ocean circulation and water transport in the North Atlantic Ocean. In the Denmark Strait, the East Greenland Current flowing southward meets the northern branch of the Irminger Current (also known as the North Icelandic Irminger Current) flowing around Iceland northward and forms the East Greenland Frontal Zone [29,30]. That is why most hydrographic surveys and theoretical and model studies in this region are focused on the water transport between the Greenland Sea (Iceland Sea) and the North Atlantic Ocean [34,35,36]. Repeated transects across the Denmark Strait based on local SCs and ICs allows one to derive new high accuracy time series of sea level, current velocity, water transport, significant wave height (SWH) and wind speed measurements and compare them with standard oceanographic (CTD, ADCP) and wave data (visual observations, model simulations and buoy measurements).
The Greenland ice sheet essentially conditions the features of storm activity in this area, in particular the phenomena of bora-types in the western part of the section called a “Piteraq”. This is a very strong katabatic wind which rushes down the east coast of Greenland usually in the autumn and winter. Wind speeds typically reach 50–80 m/s (180–288 km/h). On 6 February 1970, the Tasiilaq village located southward of the Denmark Strait was hit by the worst Piteraq ever documented in Greenland with estimated wind speed of 90 m/s (325 km/h) causing severe damage. Since the beginning of 1970, special Piteraq warnings are issued by the Danish Meteorological Institute [37]. Measurements of wind speed at the HLCs in the Denmark Strait can contribute to the understanding the characteristics and impact of the Piteraq on water area and estimate the distance of its impact from the coast.
3.3. The Davis Strait
The chain of three full clusters (six CSs and six ICs) and three more nearshore SCs is located in the narrowest part of the Davis Strait, between the Baffin Island and western coast of Greenland, right in the middle of the strait which stretches from to N where it meets the Labrador Sea (Figure 3c). The width of the strait is between 300 and 1000 km, and its depth varies from 350 to 500 m at the sill in the narrowest part along the Arctic Circle. The Davis Strait separates the Baffin Bay and the Labrador Sea. This area is poorly understood due to a lack of in-situ measurements.
Two currents pass through the strait in different directions. The relatively warm West Greenland Current carries water along the coast of the West Greenland to the north, and the cold Labrador Current is along the eastern coast of the Baffin Land to the south, into the Labrador Sea and further into the Atlantic Ocean. The cold current carries numerous icebergs breaking away from the Greenland Ice Sheet in Melville Bay. Thus, near the eastern coast of the strait, the conditions for navigation are noticeably better; the navigation season in this part of the strait lasts from mid-summer to late autumn, and it was there that fishing and whaling vessels traditionally went north. At this time of the year, the main ports of Greenland are in operation: Paamiut, Nuuk and Sisimiut. In the winter months, more than 50% of the water area is covered with ice, while, in the warm season, more than 90% of the water area is ice-free [38]. More than 90% of the water area of the Davis Strait is used for navigation: from 50 to 70 large-tonnage vessels are constantly in the waters of the strait, and the total number of vessels passing through the strait ranges in different years from 400 to 700. The main types of vessels are fishing, cargo and passenger, including coastal ferries off the Greenland coast, tourist liners and tankers [38,39].
Regular satellite altimetry tracks crossing the Davis Strait allow assessing anomalies of water exchange between the Baffin Bay and the Labrador Sea. During the ice-free period, there is the possibility to establish a permanent monitoring of water exchange through the Davis Strait and of the West Greenland and Labrador currents. These measurements can contribute significantly to the oceanography of this region under climate change.
The non-Jasons’ tracks are almost parallel to the strait axis and, thus, their use for instantaneous assessment of water mass transfer across the strait is questionable. On the contrary, the Jasons’ satellite tracks are close to zonal directions, i.e., they better capture geostrophic currents along the strait axis. The instantaneous currents can be successfully estimated from two intersecting tracks with a short time lag. A similar approach was tested in the Caspian Sea when calculating water exchange between sub-basins from satellite altimetry data [18,19]. Jasons’ HLCs with minimal time lags make such periodic in time along-track estimates at fixed sites more adequate to the problem of monitoring water exchange.
The Arctic warming shows new opportunities for intensification of shipping via the Northwest Passage, which starts from the Davis Strait [39]. The present and future shipping activities (including those related to offshore oil and gas exploration) require better knowledge on wind and wave regime in this area which can be gained from the advantages of satellite altimetry including those related to measurements of wave characteristics at SCs and ICs.
3.4. Foxe Basin
The length of the Foxe Basin in the Canadian Arctic Archipelago is of 600 km with a width of 500 km. The chain of four full clusters (eight SCs and eight ICs), two ICs in the main water body and one SC in the eastern nearshore area covers the basin between the Melville Peninsula on the west and the Baffin Island on the east (Figure 3d), the Frosen Strait and the Roes Welcome Sound. The basin is shallow with depths of 100 m in the northern and central parts and up to 400 m in the southern part, which is connected with the Hudson Bay on the west and Hudson Strait on the east via Foxe Channel. Foxe Basin is rarely ice-free even in summer season, which complicates all types of oceanographic observations. Tidal currents and strong winds keep the ice pack in constant motion and contribute to the formation of numerous polynyas and shore leads, which are found throughout the region, especially in the southern part of the Foxe Basin. Regional warming allows establishing monitoring of wind-wave characteristics and water exchange between Foxe Basin and Hudson Bay during 2–3 months with the help of satellite altimetry and contributing significantly in the unknown oceanography of this area with a unique wildlife.
3.5. The White Sea
In the White Sea, two incomplete clusters (three SCs and four ICs) are located in the middle of the sea (Figure 3e). The crossover events occur on seven different days of each 10-day Jason’s cycle, thus providing a reasonably good temporal coverage of the area. The White Sea has a very complicated shoreline and complex water dynamics conditioned by wind forcing, water exchange with the Barents Sea in its northeastern part, strong tidal motions and river inflows [30,40,41,42,43]. The cyclonic activity over the White Sea is quite intense forming specific wind-wave climate. In winter, the wind-wave regime is determined mostly by the influence of the Icelandic Low. In summer, it is formed under the influence of Arctic invasions of cold air. The storminess activity in the White Sea is relatively low due to its small size (about 250 km km) and winter ice cover.
In general, the White Sea is well studied region covered by visual observations, stationary buoys and weather stations measurements complemented by numerous national research programs, sea expeditions [41] and global and regional wind-wave models [44]. Nevertheless, three SCs and four ICs in the White Sea can be used as an alternative source of valuable data on sea level variability, tides, currents, water exchange with the Barents Sea, wind and wave regime and ice cover [45,46]. Satellite altimetry is already applied to the White Sea in order to study sea level variability, tidal, wind and ice regime [17,18,47,48,49,50,51].
3.6. The Bering Strait
In the Pacific Ocean, three SCs and two ICs fall exactly into the Bering Strait (Figure 3f), which is of great value for the assessment of water exchange between the Pacific and Arctic oceans. The Bering Strait is 90 km wide and 60 m deep and has a cross-section of km. The water transport mainly directed into the Arctic Ocean varies between and Sv in relation to atmospheric condition (local winds and atmospheric pressure). The strait is usually completely frozen over from October to June [30,52]. The first extensive survey of the Northern Bering Sea was probably carried on in the mid-1980s for five years in the scope of the NSF ISHTAR Program [30,53]. The observations were concentrated in the summer months with the objective of determining the main physical, chemical and biological characteristics of the Northern Bering Sea in typical summer situations. The ISHTAR Program included, beside extensive field surveys, the application of a three-dimensional General Circulation Model derived and adapted to the Northern Bering Sea from the three-dimensional model developed at the GeoHydrodynamics and Environmental Research Laboratory (GHER) of the University of Liege, Belgium [30,54,55,56,57]. The objectives of the model were to gain a general understanding of the Northern Bering Sea dynamics in the summer season, including modeling of the currents in the Bering Strait which were compared with measurements at buoys deployed in summer 1985 and 1986.
Now, a regular monitoring of water exchange can be based on the evaluation of the vectors of geostrophic velocity for every Jason cycle (i.e., about 10 days) at five crossovers (Figure 3f). This will provide unique regular information on water exchange between the Bering Sea and Chukchi Sea with a step of 10 days for the past 30 years since the beginning of the TOPEX/Poseidon mission in September 1992. Wind and wave measurements are also of high value taking in mind intensification of shipping activities along the Northern Sea Route with a decline of the Arctic sea ice cover.
3.7. The Southern Ocean
In the Southern Hemisphere, crossovers form a belt ranging between and S near the Antarctic Circle (Figure 3g). The points do not cross the Polar Front (PF) and the Antarctic Circumpolar Current (ACC), but in some places they cross the Southern Boundary (SB) of the ACC and the Antarctic Slope Front (ASF) located over the upper continental slope of Antarctica (for example, close to the Drake Passage from the side of the Pacific Ocean) [30,58,59,60,61,62]. In the ice-free conditions, it would be possible to measure ocean currents, eddies, calculate energy of jets and eddies. Regular measurements of wave heights and periods can fill the gaps in the sea state data in the Southern Ocean caused by a lack of buoys and visual observations, and can also be used to validate wave models. The experiment is complicated by ice conditions, but the regular coverage of the area with crossover points (497 by about 16,000 km) will doubtless be useful for better understanding of the ongoing metocean processes in the coastal zone of Antarctica.
4. High Latitude Crossovers in the Norwegian Sea
In this section, we present an analysis of HLCs in the Norwegian Sea based on open access altimetry data of the portal AVISO (http://www.aviso.altimetry.fr/en/home.html, last access on 11 February 2021). Ocean data reanalysis of Copernicus Marine Service (https://resources.marine.copernicus.eu/, last access on 11 February 2021) was used for comparison of large-scale (geostrophic) currents and wind wave fields retrieved in the crossovers.
4.1. High Latitude Crossovers for Assessment Currents and Wind Waves
Assessment of large-scale current velocities is a key output of the satellite altimetry for ocean studies. Assuming a balance of the Coriolis force and pressure gradient due to the deviation of sea surface from equipotential surface of the Earth gravity field, one has
where is the Coriolis parameter and is the latitude of the site of measurements. The unit vector is tangential to the velocity vector in Equation (1) while its orthogonal counterpart is tangential to the pressure gradient . Thus, and are always orthogonal to each other within the model of geostrophic balance.
Figure 4a provides the well-known scheme of altimetry measurements of currents in a crossover point. Non-parallel tracks (red is ascending as in our previous figures and green is descending) allow the components of the geostrophic current, which are perpendicular to track directions (dashed lines in Figure 4), to be estimated. The linearity of Equation (1) eases estimate of both wind values and associated errors. Local differences in current velocity can be used to estimate changes in water transport. Anomalies of current velocity, derived from the Sea Level Anomaly, can be used for calculation of anomalies of water transport, or they can be transformed into absolute current velocity (and then to absolute water transport) by adding the Mean Dynamic Topography derived from the difference between the mean sea surface and the geoid or from ocean drifters and hydrographic profiles.
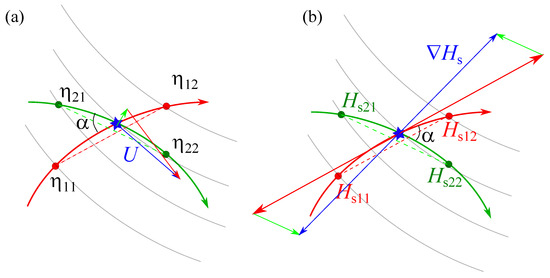
Figure 4.
Setups of altimetry measurements in a crossover point. (a) Measurements of large-scale currents by satellite altimeter. Along-track differences of the sea surface height anomaly and are used to get transversal projection of the current velocity. (b) Measurements of wave steepness. Along-track differences of the significant wave height and are used to estimate along-track components of with “back–forth” ambiguity. Two possible configurations are shown by solid and dash-dotted vectors.
Analogously to the above scheme, the physical model of wave periods from altimetry data [20] is also based on estimates of spatial gradient. The appearance of gradient of is associated with two important features of the model. First, the fetch-limited scenario of wind-wave evolution is considered as the most adequate to the dynamics of wind-driven sea [63,64,65]. This allows the variations of wave height to be related with spectral flux of energy, which is documented by instantaneous sea state parameters: wave height and wave period. Second, these variations of () are hypothesized to be aligned with the direction of wave group velocity (general direction of wave propagation). Thus, the balance equation can be reduced to the one for the spatial derivative of total energy and the energy flux due to nonlinear wave–wave interactions P [66]
Assuming self-similarity of wave evolution [67,68], one can express the energy flux P as function of instantaneous wave height and period. The resulting relationship among , wave period and its along-propagation derivative can be used to construct a method of wave period estimates from altimetry data [20] ( is the unit vector and is the group velocity of the spectral peak component along the direction of wave propagation).
The result of the model can be expressed in a quite compact relationship between wave steepness and the spatial gradient [20,21]
where is dimensionless parameter of the theory of weak turbulence of wind-driven waves [66,69]. Wave steepness is defined in terms of significant wave height and spectral peak period
One should emphasize that the model “forgets” the wave direction when operating with the gradient projection in the left-hand side of (2). Despite this difficulty, the modulo of “full gradient” can be reconstructed as a maximal possible sum of vectors with given projections onto altimeter tracks and the corresponding wave direction can be estimated with the “back–forth” ambiguity. This trouble of inherently nonlinear model (3) for wind waves is in heavy contrast with the scheme of linear conversion of scalar field of sea surface height into vector field of pressure gradient and, then, to the vector of geostrophic current.
Figure 4b shows gradients of for estimates of wave steepness and, then, wave period in the spirit of the similar scheme for geostrophic currents in Figure 4a. Two different configurations for alternative signatures of along-track derivatives are shown by solid and dash-dotted vectors, thus illustrating the problem of ambiguity of assessment of direction of wind waves. This ambiguity can be resolved with a priori information on wind and waves in the area under study.
Figure 4 also shows a possible problem of HLCs when angle between tracks is rather small. Errors of measurements can affect significantly estimates of directions. In the case of wind wave measurements, high nonlinearity of the relationship (3) mitigate the problem when angle between track and wave direction is not too close to . Generally, the single track measurements give rather good approximation [21]. On the contrary, linearity of the geostrophic relationship (1) becomes a problem when estimating currents at low angles in Figure 4a.
In the following section, we discuss features of reconstruction of slowly varying large-scale currents and sea waves as it is documented by reanalysis of the Copernicus Marine Service (https://marine.copernicus.eu/, last access on 11 February 2021) and reconstructed from along-track estimates of the HLC. The Norwegian Sea is a good area for such a study. Here, HLCs form a regular array of nine full clusters and, thus, provide at least three daily measurements in the crossover points.
4.2. Geostrophic Currents in the Area between Iceland and Norway
The GLORYS12V1 product has been used for assessment of large-scale currents. The data are provided at a standard regular grid at (approximatively 8 km) resolution. This eddy resolving reanalysis is based on altimetry data since 1993. We choose the period 17–27 October 2016 covering the whole cycle of Jasons’ altimeters. The absolute values of the current velocity are shown in Figure 5a,b for the first and last (27 October) days of the period under study. The figures reflect the complicated structure of jets in this area described in Section 3.1. At the same time, the fine structure of the currents that visually correlates with directions and locations of Jasons’ tracks look somewhat suspicious. This distrust is confirmed by trivial spectral analysis.
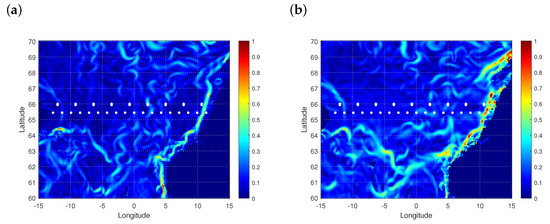
Figure 5.
Geostrophic currents in the Norwegian Sea from the GLORYS12V1 reanalysis. Absolute value of current velocity in m/s for: 17 October (a); and 27 October (b). White circles show crossover sites (for details, see Figure 3a).
Figure 6 and Figure 7 present two cross-sections along latitudes and , i.e., only 30 nmi to the north derived from the GLORYS12V1 reanalysis. The zonal component U and the meridional one V demonstrate general feature of circulation in the area shown in Figure 5. The meridional component of the current V is directed to the North along the main eastern part of the transect between Iceland and Norway in full agreement with distribution of the Coastal Iceland branch of the Irminger Current and the East Icelandic Current, which flow southward around eastern coast of Iceland (see western side of the transect), and the Norwegian Current and the Norwegian Coastal Current, which flow northward into the Norwegian Sea. Several peaks directed northward represent known branches of the Norwegian Current and the Norwegian Coastal Current at coast of Norway.
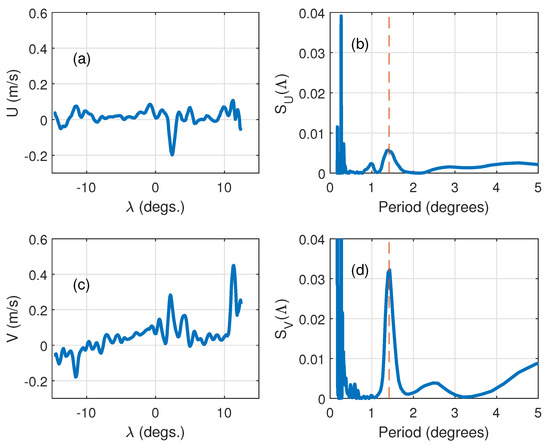
Figure 6.
Transection along latitude N on 17 October 2016: (a,c) the current velocity components; and (b,d) spatial spectral densities of the current components vs. spatial period (degrees).
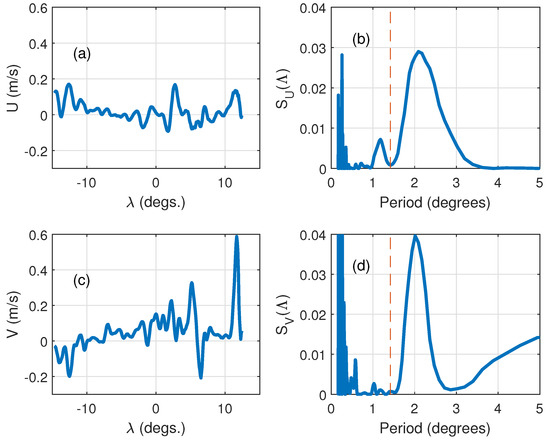
Figure 7.
Same as in Figure 6 at transection along N.
Discrete Fourier decomposition of a current velocity component G as function of longitude is defined as follows ( is the imaginary unit):
Here, Fourier amplitude is calculated for the corresponding spatial nth frequency of the discrete set of longitudes (, in this study)
Longitudes are western and eastern boundaries of the transect in Figure 5. Figure 6b,d and Figure 7b,d show spectral densities of the current components as function of the spatial period . For the latitude , slightly below the limiting one for the Jasons’ missions (Figure 6b,d), the spectral peaks at the period ≈1.42 matches the spacing of Jason’s 254 tracks (). Only 30 nmi (≈55.56 km) to the north, the period of spectral peak becomes 50% longer (≈2). This example clearly shows possible problems of the reanalysis based on the altimetry data near the latitude where an essential fraction of data (Jasons’ data) disappears.
The problem of the current reanalysis is confirmed by comparison with along-track estimates of geostrophic currents for SCs and ICs for the period under study in Figure 8. Both meridional and zonal components show rather strong dispersion. At the same time, the along-track estimate of zonal component of geostrophic current shows remarkably low variations relative to a median value close to zero. On the contrary, the reanalysis predicts rather strong currents in the zonal direction. Both patterns, reanalysis and along-track estimates, do not contradict observations, but the dominance of meridional currents (north-south direction) looks more realistic, in the authors’ opinion.
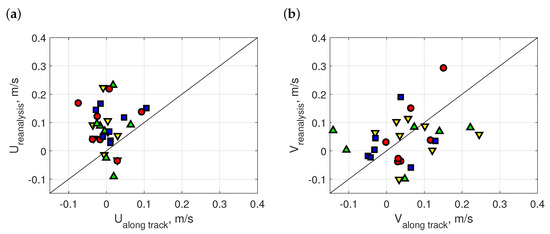
Figure 8.
Scatterplot of current velocity components of the reanalysis vs. along-track estimates of geostrophic currents at ISs and SCs: (a) zonal; and (b) meridional components.
In fact, there is a problem of along-track estimates as long as tracks are close to parallels in high latitudes and, thus, capture meridional currents (cross-track variations of SSHA) better than the reanalysis that smoothes data more or less isotropically.
4.3. Wind Waves. Wave Period Estimates by Altimetry
The short time delay between consecutive measurements in HLC is an essential gain for wind wave studies. In some cases, it allows one to capture periods and directions of wave field that are, generally, unavailable from altimetry data using along-track records.
The reanalysis WAVERYS on a regular grid with a 3 h time step of the Copernicus Marine Service has been used for demonstration features of the HLC data subset for the same time interval 17–27 October 2016. The altimetry data are assimilated by MFWAM (Meteo-France WAve Model) taking into account oceanic currents from the GLORYS12 physical ocean reanalysis.
An essential result is good agreement of two consecutive measurements in the crossovers as illustrated by Figure 9a. Both ICs (triangles) with a delay of about 1 h and SCs (circles and squares) with 2 h delay show dispersion of about 30 cm that is close to the declared accuracy of wave height measurements by altimeters and ocean buoys [70]. As expected, the wave heights measured by altimeters agree perfectly well with the reanalysis (not shown here).
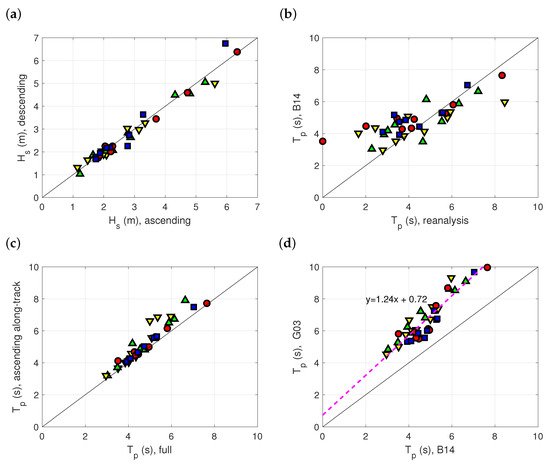
Figure 9.
Scatterplots of wave parameters in HLCs: (a) significant wave heights; (b) wave periods of the model of Badulin [20] vs. reanalysis; (c) single-track vs. “full” periods of Badulin [20]; and (d) periods with the model of Gommenginger et al. [71] ( G03) vs. Badulin [20] ( B14).
Wave periods cannot be measured by altimeters directly but can be recovered within different approaches. The most used empirical parametrical models (e.g., [71,72,73]) postulate dependence of wave period on significant wave height and the normalized radar cross-section (NRCS) . These models are able to provide the accuracy better than 1 s [73]. At the same time, validity of these models can be questionable for high latitudes where buoy measurements are absent and, thus, the models are not properly substantiated. Additionally, these parameterizations are mission dependent: every mission requires its own set of empirical coefficients.
Alternative models of wave periods (e.g., [20,74]) rely upon physical links of wave parameters and, in this way, are less dependent on features of particular altimeter and an instantaneous sea state environment. Figure 9b shows quite good correspondence of the physical model (Equations (3) and (4)) and the WAVERYS reanalysis for the spectral moments , wave period
High deviation of the model from the reanalysis quantities occurs at relatively short periods less than 4 s (wavelength less than approximately 25 m) where the model validity is questionable. In Figure 9b, both track records in the crossovers are used to retrieve the “full” period in accordance with the scheme of Figure 4b. This “full” period does not differ significantly from its approximate counterpart when the full gradient is replaced by the along-track derivative of one of altimeters. We present the ascending track calculations in Figure 9c with less than 15% of the period overestimate.
Results from the comparison between the physical model of Badulin [20] and its empirical counterpart of Gommenginger et al. [71] are reported in Figure 9d and show a remarkable similarity. The excess of the period of the model [71] is essentially higher than one fixed for a one-year period at ocean buoy sites (cf. Figure 2d in [21]). Such difference can be explained by characteristics of altimeters (Envisat in [21] and Jasons in this study) or, as an alternative, by the effect of high latitudes where the empirical model [71] has never been tested.
The apparent correlation of the two period estimates demonstrates, in our opinion, a good potential of the parametric models regardless their quantitative fail. The pronounced linear correlation of two models in Figure 9d signifies correspondence of the parametric representation to the inherent physical feature of self-similarity of evolution of wind-driven waves.
5. Discussion
The HLCs with fixed location and minimal time lags between consecutive measurements can be seen as a network of virtual ocean buoys with enhanced temporal and spatial sampling. Building and exploitation of the network may provide a solid ground for international collaboration in studies of currents, water exchange, wind and wave characteristics in the Sub-Arctic seas and the Southern Ocean.
One can propose a list of particular tasks for the HLC network. The tackling of these tasks will shed light on important problems of ocean dynamics in Sub-Polar seas.
The first set of tasks mentioned above is associated with studies of the areas in Section 3 considering their special features. For greater oceanography purposes, this means getting reliable high-quality data on currents, winds and waves from the remote regions of Sub-Polar seas.
The permanent monitoring of large-scale currents with regular temporal sampling (see Section 4.2) becomes self-evident for the Norwegian Sea and Denmark Strait as vital gates connecting the North Atlantic and Arctic oceans and, thus, essentially determining the climate changes in the Arctic Ocean and the North Atlantic.
Measurements of currents, wind and waves in the Davis Strait and Foxe Basin will significantly enrich our knowledge of sea dynamics in these remote regions with severe weather and ice conditions. We see the HLC network as a decisive add-on and extension of rare sea campaigns and in situ observations in these areas.
The Arctic warming shows new opportunities for intensification of shipping via the Northwest Passage which starts from the Davis Strait. Satellite altimetry monitoring at SCs and ICs will bring valuable knowledge to the future studies, exploitation and nature conservation of these areas.
The White Sea is well supported by a set of meteostations and regular expeditions organized by the Russian Academy of Sciences, Ministry of Natural Resources and Environment of the Russian Federation and universities. This regional sea can be regarded as a testing ground for calibration and validation of satellite altimetry against in-situ measurements in the open sea and near-shore environment.
The Bering Strait plays a key role in water exchange between the Bering Sea and Arctic Ocean. Several SCs and ICs are located right in the Strait and, thus, are of vital importance primarily for regular water exchange measurements through the Strait.
In the Southern Ocean, we have about 400 HLCs which can be regarded as a huge virtual buoy network since the launch of TOPEX/Poseidon in September 1992. This world-around zonal loop allows for tracing seasonal and interannual variability of currents, wind, waves and swells. It is difficult to imagine that such a unique experiment could ever be carried out by traditional in-situ tools.
The second block includes specific problems of altimetry methods. We do not mention these problems in the paper intentionally because of their technical complexity and numerous logistical issues. Here, we restrict the discussion to very few remarks.
Fixed locations of SCs and ICs and rather short time intervals between consecutive measurements provoke a question on control of altimetry measurements and building regional models of numerous altimetry corrections based, firstly, on data of HLCs. White Sea and Foxe Basin with their high tidal activity are the first candidates for developing such an approach.
Interpolation (and, quite often, extrapolation) of altimetry data can lead to suspicious results, as demonstrated in Section 4.2. The instantaneous estimates in HLCs can help to fix possible artifacts due to global data processing.
The final point of the discussion is the value of the TOPEX/Poseidon–Jason program for studies of high-latitude areas of the World Ocean as compared to other altimetry missions. HLCs generated by inclined orbits of the program cover vital sea areas. On the contrary, near-pole orbits of other altimeters (e.g., Envisat, SARAL/AltiKa, Sentinel, etc.) provide an abundant series of HLCs in ice-covered seas above latitudes and continental part of the Antarctica. Further support and development of the Jasons’ missions, especially of their special phases of interleaved orbits, could be a good contribution to studies and exploitation of Sub-Polar seas.
6. Conclusions
In the present paper, we propose new essential add-ons of satellite altimetry related to the peculiarities of the orbits of the TOPEX/Poseidon and Jasons (Jason-1, Jason-2, Jason-3) satellite missions which have not been mentioned before in the scientific literature. The first one is related with the use of the self-crossover (SC) points that occur near the latitude of the Jason’s orbits turn just below the Polar Circles where the satellite intersects its own orbit with one orbit period of 112 min. The second one is related to the inter-crossover points (IC) that occurs as intersection of tracks of interleaved orbits of two subsequent altimetry satellites with the time lag of about 1 h (approximately one half of the orbit period).
The features of self- and inter-crossovers relevant for improving the measurements of sea conditions are listed below:
- Measurements at these crossovers are carried out by the same (in the case of self-crossovers) or similar (in the case of inter-crossovers) radar altimeters with the subsequent use of compatible processing and retracking procedures.
- Points of both types of crossovers are the same within the accuracy of the altimeter tracks. It permits organizing repetitive monitoring of currents, water exchange, wind and wave characteristics at these points with periods of full cycle for the SCs (about 10 days) and half-cycle (about five days) for ICs.
- The short time lag of high latitude crossovers (HLC) less than 2 h for SCs and about 1 h for ICs (see Table 2) reduces the effect of variability of sea environment (sea state) even for such short-scale phenomenon as wind-driven waves.
- Angles between tracks in the intersection points are large enough (about for SCs and for ICs) to get full vector of geostrophic current velocity and wave direction from along-track records. In the conventional satellite altimetry, estimates of current velocity are usually based on interpolated fields of sea surface height anomaly that are associated with essential smoothing of instantaneous fields in time and space. The latter can essentially corrupt the resulting current field.
- The number of these crossovers in the vital ice-free Sub-Polar areas of the World Ocean is large enough to conduct permanent monitoring of key oceanographic parameters for ocean dynamics, marine meteorology and climate research.
- In many regions, the spatial distribution of these crossovers allows the assessment of anomalies of water exchange between the most important sub-basins in the Sub-Arctic seas. It is interesting to apply this methodology to the Southern Ocean where these crossovers do not cross the Antarctic Circumpolar Current (ACC), its branches and its fronts because the chain of these crossovers goes along the ACC and all the crossovers are located between the ACC and the coast of Antarctica.
The Norwegian Sea case study shows important advantages in the application of the new technology for ocean dynamics, sea state and climate studies which was unattainable for conventional satellite altimetry. Our preliminary results show a good correspondence of wave characteristics derived from HLC and reanalysis data. For the first time, zonal and meridional components of currents in the Norwegian Sea were estimated and found consistent with a classical scheme of currents on the transection between Iceland and Norway. The authors encourage the altimetry community to pay more attention to the specific subsets of altimetry data presented in this study as an important add-on to conventional approaches.
We have to note that the precise orbits of Jason satellites are fundamental for altimetry records. Jason satellites as well as other altimetry satellites are equipped with three main instruments for precise orbit determination: (i) the Global Navigation Satellite System (GNSS) or Global Positioning System (GPS) receivers; (ii) Doppler Orbitography and Radiopositioning Integrated by Satellite (DORIS) receiver, and (iii) Satellite Laser Ranging (SLR) or Laser Retroreflector (LRR) retroreflectors.
The main progress in the Low Earth Orbit (LEO) modeling in terms of GNSS orbits is related to employing proper GNSS antenna calibrations and fixed phase GNSS ambiguities [75]. The DORIS receivers now have more channels which allow improvements of the ground network in the DORIS-based Jason orbits [76]. It was shown that the Terrestrial Reference Frame 2014 (TRF2014) SLR/DORIS complement impact on the ITRF2008 orbit is only 1–2 mm RMS radial difference during 1992–2009, and it increases after 2009, up to 5 mm RMS radial difference in 2016. Crossover data show the Deutsche Geodätisches Forschungsinstitut DTRF2014 orbits are the most accurate for the TOPEX and Jason-2 test periods, and those of the Jet Propulsion Laboratory JTRF2014 orbits for the Jason-1 period [76].
Arnold et al. [77] presented a parameter estimation approach to investigate systematic orbit errors and showed that SLR validation of the LEO satellites is not only able to detect radial but also along-track and cross-track offsets. Using the residual-based parameter estimation approach, corrections to the International Laser Ranging Service (ILRS) station coordinates, range biases and timing offsets were derived. As a result, RMS residuals of 5–10 mm were obtained over one-year data in 2016 using observations from a subset of high-performance stations and ambiguity-fixed orbits of four LEO missions [77].
Melachroinos et al. [78] investigated the effect of geocenter motion, which is a non-stationary process that includes secular trends, on Jason-2 orbits and the mean sea level. They found that, for the SLR/DORIS std0905 orbits, currently used by the oceanographic community, only the negligence of the annual term of the geocenter motion correction results in a mm error in the Z-component of the orbit frame, which creates the systematic error in the Mean Sea Level (MSL) of mm mainly due to the uneven distribution of the oceans between the Northern and Southern hemispheres [78].
The recent improvement in the precise orbit determination of Jason orbits includes the improvement of the orbit models, for instance, the improved macromodels such as box-wing models used to properly handle the non-gravitational forces emerging from the solar radiation pressure, albedo and atmospheric drag [79,80,81]
The present study was based on Level 2 altimetry products where recent results of all the techniques, orbit correction and modeling are converted into physical parameters of Sea Surface Height (SSH), Sea Level Anomaly (SLA), Significant Wave Height (SWH), etc. This is why the discussion of the issues related to the modeling of the Jason orbits, including the LEO (Low Earth Orbit) modeling issues of Jason satellites, are beyond the scope of the paper.
Finally, we have to note that the more precise determination of the satellite orbit will not impact the new idea and results presented in the paper because we draw attention to new crossovers which have never been mentioned before whatever the accuracy of the Jason satellites is. The present spatial accuracy of the Jason satellites orbit of about km [70] is fine enough for the application of the presented methodology because the SC and IC will not be shifted significantly in space (or even moved from the sea to the land) from the locations which are ascribed to these crossovers now. Orbit determination with an uncertainty of less than 2 cm in radial direction is supported by the above-mentioned GNSS, GPS and DORIS receivers, as well as by a complementary laser retroreflectors (SLR or LRR) [81]. As shown by numerous publications on the application of satellite altimetry to different oceanography tasks, this accuracy is sufficient to measure sea level variability, ocean currents, wave height, wind speed and other physical parameters. All the above-mentioned improvements and corrections are partially realized in the modern satellite altimetry products, and, in any case, they are much less than the above-mentioned uncertainty.
Our new methodology can also be used with the recent Sentinel-6/Jason-CS (launched on 21 November 2020) mission, which has the same inclination of . For new and future altimetry missions such as Sentinel-3A (launched on 16 February 2016), Sentinel-3B (launched on 25 April 2018), Sentinel-3C and Sentinel-3D, which have an inclination of and an orbital cycle of 27 days ( orbits per day, 385 orbits per cycle), the proposed methodology should be modified because they have very dense satellite track overlaps around the poles. However, for these satellites with near-polar orbits, the SC and IC fall in the ice-covered areas of the Arctic Ocean and on the continental part of Antarctica. Thus, this will not be interesting for the above-mentioned oceanic studies.
Author Contributions
Conceptualization, S.B. and V.G.; methodology, S.B., A.K., V.G. and S.L.; formal analysis, P.S. and S.L.; data curation, P.S. and V.S.; writing—original draft preparation S.B., A.K. and V.G.; writing—review and editing V.G., V.S. and S.L.; and visualization, V.S. and P.S. All authors have read and agreed to the published version of the manuscript.
Funding
Section 1, Section 2 and Section 4 were done within the Russian Foundation for Basic Research project N 19-05-00147 (S.B., V.G., P.S. and V.S.). A.K. (Section 3) was supported in the framework of the P.P. Shirshov Institute of Oceanology RAS state assignment N 0128-2021-0002. The case study was done in the framework of the Russian Foundation for Basic Research project N18-05-80065.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The altimeter data for the investigated region are available from http://www.aviso.altimetry.fr/en/home.html, last access on 11 February 2021 under the open data source. Reanalysis data of Copernicus Marine Service (https://resources.marine.copernicus.eu, last access on 11 February 2021) has been used.
Acknowledgments
Open access data of the portals AVISO (http://www.aviso.altimetry.fr/en/home.html, last access on 11 February 2021) and Copernicus Marine Service (https://resources.marine.copernicus.eu, last access on 11 February 2021) were used in this work. The authors are extremely grateful to three reviewers for their stimulating critics and helpful suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SC | self-crossover(s) |
| IC | inter-crossover(s) |
| STD | Standard deviation |
| HLC | high-latitude crossovers |
| SSHA | sea surface height anomaly |
| PF | Polar Front |
| ACC | Antarctic Circumpolar Current |
| SB | the Southern Boundary |
| ASF | Antarctic Slope Front |
References
- Wunsch, C.; Gaposchkin, E.M. On using satellite altimetry to determine the general circulation of the oceans with application to geoid improvement. Rev. Geophys. 1980, 18, 725–745. [Google Scholar] [CrossRef]
- Wunsch, C.; Stammer, D. Satellite altimetry, the marine geoid, and the oceanic general circulation. Annu. Rev. Earth Planet. Sci. 1998, 26, 219–253. [Google Scholar] [CrossRef]
- Fu, L.; Cazenave, A. Satellite Altimetry and the Earth Sciences: A Handbook of Techniques and Applications; International Geophysics Series; Academic Press: San Diego, CA, USA; San Francisco, CA, USA; New York, NY, USA; Boston, MA, USA; London, UK; Sydney, Australia; Tokyo, Japan, 2001; Volume 69. [Google Scholar]
- Lebedev, S.; Kostianoy, A. Satellite Altimetry of the Caspian Sea; Sea: Moscow, Russia, 2005; 366p. (In Russian) [Google Scholar]
- Vignudelli, S.; Kostianoy, A.G.; Cipollini, P.; Benveniste, J. (Eds.) Coastal Altimetry; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Lebedev, S.A. Satellite altimetry in the Earth Sciences. Sovrem. Probl. Distantsionnogo Zondirovaniya Zemli Kosmosa 2013, 10, 33–49. (In Russian) [Google Scholar]
- Frappart, F.; Andersen, O.; Lebedev, S.; Ramillien, G. (Eds.) Satellite Altimetry for Earth Sciences; MDPI: Basel, Switzerland; Beijing, China; Wuhan, China; Barcelona, Spain; Belgrade, Serbia, 2019; 484p. [Google Scholar] [CrossRef]
- Rosmorduc, V.; Srinivasan, M.; Richardson, A.; Cipollini, P. The first 25 years of altimetry outreach. Adv. Space Res. 2020. [Google Scholar] [CrossRef]
- International Altimetry Team Altimetry for the future: Interdisciplinary recommendations following the “25 Years of Progress in Radar Altimetry” Anniversary. Adv. Space Res. 2021. [CrossRef]
- Munk, W. Lecture 1:40–42:00 p.m., Thursday, 18 April. In Proceedings of the Southwest Regional Meeting, Los Angeles, CA, USA, 18–19 April 2002; The U.S. Commission on Ocean Policy: Los Angeles, CA, USA, 2002. [Google Scholar]
- Ablain, M.; Philipps, S.; Picot, N.; Bronner, E. Jason-2 global statistical assessment and cross-calibration with Jason-1. Mar. Geod. 2010, 33, 162–185. [Google Scholar] [CrossRef]
- Stammer, D.; Cazenave, A. (Eds.) Satellite Altimetry over Oceans and Land Surfaces; CRC Press: Boca Raton, FL, USA, 2017; 643p. [Google Scholar] [CrossRef]
- Gaspar, P.; Ogor, F.; Traon, P.Y.L.; Zanife, O.Z. Estimating the sea state bias of the TOPEX and POSEIDON altimeters from crossover differences. J. Geophys. Res. 1994, 99, 24981–24994. [Google Scholar] [CrossRef]
- Gommenginger, C.; Srokosz, M.; Bellingham, C.; Snaith, H.; Pires, N.; Fernandes, M.J.; Tran, N.; Vandemark, D.; Moreau, T.; Labroue, S. Sea State Bias: 25 Years on. In 25 Years of Progress in Radar Altimetry; CNES: Ponta Delgada, Saő Miguel Island, Azores, Portugal, 2018. [Google Scholar]
- Badulin, S.; Grigorieva, V.; Shabanov, P.; Sharmar, V.; Karpov, I. Sea state bias in altimetry measurements within the theory of similarity for wind-driven seas. Adv. Space Res. 2019. [Google Scholar] [CrossRef]
- Abdalla, S. Ku-band radar altimeter surface wind speed algorithm. In Proceedings of the Envisat Symposium 2007, Montreux, Switzerland, 23–27 April 2007. [Google Scholar]
- Lebedev, S.A. Technique for processing satellite altimetry data for the waters of the White, Barents and Kara seas. Mod. Probl. Remote Sens. Earth Space 2016, 13, 203–223. [Google Scholar]
- Lebedev, S.; Kostianoy, A. Interannual variability of water exchange anomalies between the Northern, Middle and Southern Caspian based on satellite altimetry data. Ecol. Montenegrina 2019, 25, 106–115. [Google Scholar] [CrossRef]
- Lebedev, S.; Kostianoy, A. Investigation of seasonal and interannual variability of water exchange through the Middle Caspian based on satellite altimetry. Sovrem. Probl. Distantsionnogo Zondirovaniya Zemli Kosmosa 2020, 17, 103–109. [Google Scholar] [CrossRef]
- Badulin, S.I. A physical model of sea wave period from altimeter data. J. Geophys. Res. Oceans 2014, 119, 856–869. [Google Scholar] [CrossRef]
- Badulin, S.; Grigorieva, V.; Gavrikov, A.; Geogjaev, V.; Krinitskiy, M.; Markina, M. Wave steepness from satellite altimetry for wave dynamics and climate studies. Russ. J. Earth. Sci. 2018, 18, ES5005. [Google Scholar] [CrossRef]
- Schlesinger, M.E.; Ramankutty, N. An Oscillation in the global climate system of period 65–70 years. Nature 1994, 367, 723–726. [Google Scholar] [CrossRef]
- Kushnir, Y. Interdecadal variations in North Atlantic sea surface temperature and Associated Atmospheric Conditions. J. Clim. 1994, 7, 141–157. [Google Scholar] [CrossRef]
- Delworth, T.L.; Mann, M.E. Observed and simulated multidecadal variability in the Northern Hemisphere. Clim. Dyn. 2020, 16, 661–676. [Google Scholar] [CrossRef]
- Lappo, S.S.; Gulev, S.K.; Dobrolyubov, S.A. Actual Problems of Oceanology; Chapter the North Atlantic and Its Impact on the Climate of Europe; Nauka: Moscow, Russia, 2003; pp. 8–59. [Google Scholar]
- Byshev, V.I. Synoptic and Large-Scale Variability of the Ocean and Atmosphere; Nauka: Moscow, Russia, 2003; 344p. (In Russian) [Google Scholar]
- Sutton, R.T.; Hodson, D.L.R. Atlantic ocean forcing of North American and European summer climate. Science 2005, 309, 115–118. [Google Scholar] [CrossRef] [PubMed]
- Sutton, R.T.; Dong, B. Atlantic Ocean influence on a shift in European climate in the 1990s. Nat. Geosci. 2012, 5, 788–792. [Google Scholar] [CrossRef]
- Rodionov, V.B.; Kostianoy, A.G. Oceanic Fronts of the North-European Basin Seas; GEOS: Moscow, Russia, 1998; 293p. (In Russian) [Google Scholar]
- Kostianoy, A.G.; Nihoul, J.C.J.; Rodionov, V.B. Physical Oceanography of Frontal Zones in the Subarctic Seas; Elsevier Oceanography Series; Elsevier: Amsterdam, The Netherlands, 2004; Volume 71, 316p. [Google Scholar]
- Davidan, I.N.; Lopatukhin, L.I. Towards the Storms; Hydrometeoizdat: Leningrad, Russia, 1982; 136p. (In Russian) [Google Scholar]
- Reistad, M.; Breivik, O.; Haakenstad, H.; Aarnes, O.J.; Furevik, B.R.; Bidlot, J. A high-resolution hindcast of wind and waves for the North Sea, the Norwegian Sea, and the Barents Sea. J. Geophys. Res. 2011, 116, C05019. [Google Scholar] [CrossRef]
- Semedo, A.; Vettor, R.; Breivik, O.; Sterl, A.; Reistad, M.; Lima, D.C.A. The wind sea and swell waves climate in the Nordic seas. Ocean. Dyn. 2014, 65. [Google Scholar] [CrossRef]
- Jonsson, S.; Valdimarsson, H. A new path for the Denmark Strait overflow water from the Iceland Sea to Denmark Strait. Geophys. Res. Lett. 2004, 31, L03305. [Google Scholar] [CrossRef]
- Pickart, R.S.; Spall, M.A.; Torres, D.J.; Vage, K.; Valdimarsson, H.; Nobre, C.; Moore, G.W.K.; Jonsson, S.; Mastropole, D. The North Icelandic Jet and its relationship to the North Icelandic Irminger Current. J. Mar. Res. 2017, 75, 605–639. [Google Scholar] [CrossRef]
- Semper, S.; Vage, K.; Pickart, R.; Valdimarsson, H.; Torres, D.J.; Jonsson, S. The emergence of the North Icelandic Jet and its evolution from Northeast Iceland to Denmark Strait. J. Phys. Oceanogr. 2019, 49, 2499–2521. [Google Scholar] [CrossRef]
- Cappelen, J.; Jorgensen, B.V.; Laursen, E.V.; Stannius, L.S.; Thomsen, R.S. The Observed Climate of Greenland, 1958–1999—With Climatological Standard Normals 1961–1990; Danish Meteorological Institute: Copenhagen, Denmark, 2001; 152p. [Google Scholar]
- Silber, G.K.; Adams, J.D. Vessel operations in the Arctic, 2015–2017. Front. Mar. Sci. 2019, 6. [Google Scholar] [CrossRef]
- Christensen, T.; Lasserre, F.; Dawson, J.; Guy, E.; Pelletier, J.F. Adaptation Actions for a Changing Arctic: Perspectives from the Baffin Bay/Davis Strait Region; Oslo: Arctic Monitoring and Assessment Programme (AMAP); Chapter Shipping; AMAP: Oslo, Norway, 2018; pp. 243–259. [Google Scholar]
- Filatov, N.; Pozdnyakov, D.; Johannessen, O.M.; Pettersson, L.H.; Bobylev, L.P. White Sea. Its Marine Environment and Ecosystem Dynamics Influenced by Global Change; Springer-Praxis: Chichester, UK, 2005; 463p. [Google Scholar]
- Lisitzin, A.P.; Shevchenko, V.P.; Gordeev, V.V.; Kravchishina, M.D.; Pantyulin, A.N.; Kosobokova, K. (Eds.) The White Sea System; Water column and the atmosphere, cryosphere, river runoff and biosphere interacting with it; Nauchny Mir: Moscow, Russia, 2012; Volume 2, 782p. (In Russian) [Google Scholar]
- Lisitzin, A.P.; Gordeev, V.V. (Eds.) Biogeochemistry of the Atmosphere, Ice and Water of the White Sea. The White Sea Environment. Part I; Springer Nature Switzerland AG: Cham, Switzerland, 2018; 327p. [Google Scholar]
- Lisitzin, A.P.; Demina, L.L. (Eds.) Sedimentation Processes in the White Sea. The White Sea Environment. Part II; Springer Nature Switzerland AG: Cham, Switzerland, 2018; 311p. [Google Scholar] [CrossRef]
- Lopatukhin, L.I.; Bukhanovsky, A.V.; Chernysheva, E.S. Reference Data on Wind-Wave Regime in the Bering and White Seas; Russian Maritime Register of Shipping: St.-Petersburg, Russia, 2010; 566p. (In Russian) [Google Scholar]
- Badulin, S.I.; Grigorieva, V.G.; Shabanov, P.A.; Sharmar, V.D.; Karpov, I.; Lebedev, S.A.; Kostianoy, A. Case study of wind-driven waves in the White Sea during the tandem phase of Jason-2 and Jason-3 missions. In Proceedings of the Coastal Altimetry Workshop 12, Frascati, Italy, 4–7 February 2020. [Google Scholar]
- Badulin, S.I.; Grigorieva, V.G.; Shabanov, P.A.; Sharmar, V.D.; Lebedev, S.A.; Kostianoy, A.G. Altimeter crossovers for monitoring waves and currents in the White Sea. In Proceedings of the Waves in Shallow Water Environment, Bergen, Norway, 10–14 May 2020. [Google Scholar]
- Lebedev, S.A.; Zilberstein, O.I.; Popov, S.K.; Tikhonova, O.V. Satellite Altimetry for Geodesy, Geophysics and Oceanography; iag symposia, chapter analysis of Temporal Sea Level Variation in the Barents and the White Seas from Altimetry, Tide Gauges and Hydrodynamic Simulation; Hwang, C., Shum, C.K., Li, J.C., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 126, pp. 243–249. [Google Scholar] [CrossRef]
- Lebedev, S.A.; Kostianoy, A.G.; Ginzburg, A.I.; Medvedev, D.P.; Sheremet, N.A.; Shauro, S.N. The ALTICORE Project: The Barents and White seas. In Proceedings of the International Conference Electronic Geophysical Year: State of the Art and Results, Pereslavl-Zalessky, Russia, 3–6 June 2009; p. 49. [Google Scholar] [CrossRef]
- Lebedev, S.A.; Kostianoy, A.G.; Ginzburg, A.I.; Medvedev, D.P.; Sheremet, N.A.; Shauro, S.N. Satellite Altimetry Applications in the Barents and White Seas; Chapter Coastal Altimetry; Vignudelli, S., Kostianoy, A.G., Cipollini, P., Benveniste, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 389–415. [Google Scholar] [CrossRef]
- Lebedev, S.A.; Bogoutdinov, S.R.; Nekhoroshev, S.A.; Kravchenko, P.N. Identification of the Baltic and White Seas ice cover based on satellite altimetry and radiometry. In Proceedings of the IEEE/OES Baltic International Symposium (BALTIC), Klaipeda, Lithuania, 12–15 June 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Lebedev, S.A.; Kostianoy, A.G. Seasonal and interannual sea level and ice fraction variability in the Barents and White seas based on remote sensing data. In Proceedings of the PORSEC, Guangzhou, China, 2–6 December 2008; p. 34. [Google Scholar]
- Coachman, L.; Aagaard, K.; Tripp, R.B. Bering Strait: The Regional Physical Oceanography; University of Washington Press: Seattle, WA, USA, 1975; 172p. [Google Scholar]
- Walsh, J.J.; McRoy, C.P.; Coachman, L.K.; Goering, J.J.; Nihoul, J.C.J.; Whitledge, T.E.; Blackburn, T.; Parker, P.L.; Wirick, C.D.; Shuert, P.G.; et al. Carbon and nitrogen cycling within the Bering/Chukchi Sea: source regions for organic matter affecting AOU demands of the Arctic Ocean. Progr. Ocean. 1989, 22, 277–359. [Google Scholar] [CrossRef]
- Nihoul, J.C.J. Marine Interfaces Ecohydrodynamics; Chapter Aspects of the Northern Bering Sea Ecohydrodynamics; Elsevier: Amsterdam, The Netherlands, 1986; pp. 385–399. [Google Scholar]
- Nihoul, J.C.J. Application of Mathematical Modelling to the Marine Environment; E. Riga Publ.: Liege, Belgium, 1976; 69p. [Google Scholar]
- Nihoul, J.C.J.; Adam, P.; Brasseur, P.; Deleersnijder, E.; Djenidi, S.; Haus, J. Three-dimensional general circulation model of the northern Bering Sea’s summer ecohydrodynamics. Cont. Shelf Res. 1993, 13, 509–542. [Google Scholar] [CrossRef]
- Nihoul, J.C.J.; Adam, P.; Brasseur, P. Data assimilation. Tools for Modelling the Ocean in a Global Change Perspective; NATO ASI Series 19; Chapter Mathematical Visualisation of the Northern Bering Sea’s summer Ecohydrodynamics; Springer: Berlin/Heidelberg, Germany, 1994; pp. 107–134. [Google Scholar]
- Sokolov, S.; Rintoul, S.R. Structure of Southern Ocean fronts at 140∘E. J. Mar. Sys. 2002, 37, 151–184. [Google Scholar] [CrossRef]
- Sokolov, S.; Rintoul, S.R. Circumpolar structure and distribution of the Antarctic Circumpolar Current fronts: 2. Variability and relationship to sea surface height. J. Geophys. Res. 2009, 114, C11019. [Google Scholar] [CrossRef]
- Ginzburg, A.I.; Kostianoy, A.G.; Frankignoulle, M.; Delille, B. Investigations of fronts in the southern part of the Indian Ocean by satellite temperature data. Issled. Zemli Kosmosa 2002, 5, 39–49. (In Russian) [Google Scholar]
- Kostianoy, A.G.; Ginzburg, A.I.; Lebedev, S.A.; Frankignoulle, M.; Delille, B. Fronts and mesoscale variability in the Southern Indian Ocean as inferred from altimetric data of TOPEX/POSEIDON and ERS-2. Oceanology 2003, 43, 632–642. [Google Scholar]
- Koshlyakov, M.N.; Tarakanov, R.Y.; Savchenko, D.S. Energy interaction of the jets and eddies of Antarctic Circumpolar Current in the near-surface layer of the Southern Ocean. J. Oceanol. Res. 2019, 47, 39–57. [Google Scholar] [CrossRef]
- Zavadsky, A.; Shemer, L. Water waves excited by near-impulsive wind forcing. J. Fluid Mech. 2017, 828, 459–495. [Google Scholar] [CrossRef]
- Shemer, L. On Evolution of young wind waves in time and space. Atmosphere 2019, 10, 562. [Google Scholar] [CrossRef]
- Shemer, L.; Singh, S.K.; Chernyshova, A. Spatial evolution of young wind waves: numerical modelling verified by experiments. J. Fluid Mech. 2020, 901. [Google Scholar] [CrossRef]
- Badulin, S.I.; Babanin, A.V.; Resio, D.; Zakharov, V. Weakly turbulent laws of wind-wave growth. J. Fluid Mech. 2007, 591, 339–378. [Google Scholar] [CrossRef]
- Badulin, S.I.; Pushkarev, A.N.; Resio, D.; Zakharov, V.E. Self-similarity of wind-driven seas. Nonl. Proc. Geophys. 2005, 12, 891–946. [Google Scholar] [CrossRef]
- Zakharov, V.E.; Badulin, S.I.; Hwang, P.A.; Caulliez, G. Universality of Sea Wave Growth and Its Physical Roots. J. Fluid Mech. 2015, 708, 503–535. [Google Scholar] [CrossRef]
- Gagnaire-Renou, E.; Benoit, M.; Badulin, S.I. On weakly turbulent scaling of wind sea in simulations of fetch-limited growth. J. Fluid Mech. 2011, 669, 178–213. [Google Scholar] [CrossRef]
- Dumont, J.P.; Rosmorduc, V.; Picot, N.; Bronner, E.; Desai, S.; Bonekamp, H.; Figa, J.; Lillibridge, J.; Scharroo, R. OSTM/Jason-2 Products Handbook, 8th ed.; CNES: SALP-MU-M-OP-15815-CN, EUMETSAT: EUM/OPS-JAS/MAN/08/0041, JPL: OSTM-29-1237, NOAA/NESDIS: Polar Series/OSTM J400; 2011. Available online: https://www.ospo.noaa.gov/Products/documents/J2_handbook_v1-8_no_rev.pdf (accessed on 1 January 2021).
- Gommenginger, C.P.; Srokosz, M.A.; Challenor, P.G.; Cotton, P.D. Measuring ocean wave period with satellite altimeters: A simple empirical model. Geophys. Res. Lett. 2003, 30, 2150. [Google Scholar] [CrossRef]
- Quilfen, Y.; Chapron, B.; Serre, M. Calibration/validation of an altimeter wave period model and application to TOPEX/Poseidon and Jason-1 altimeters. Mar. Geod. 2004, 27, 535–549. [Google Scholar] [CrossRef]
- Mackay, E.B.L.; Retzler, C.H.; Challenor, P.G.; Gommenginger, C.P. A parametric model for ocean wave period from Ku-band altimeter data. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Hwang, P.A.; Teague, W.J.; Jacobs, G.A.; Wang, D.W. A statistical comparison of wind speed, wave height and wave period derived from satellite altimeters and ocean buoys in the Gulf of Mexico region. J. Geophys. Res. 1998, 103, 10451–10468. [Google Scholar] [CrossRef]
- Montenbruck, O.; Hackel, S.; Jäggi, A. Precise orbit determination of the Sentinel-3A altimetry satellite using ambiguity-fixed GPS carrier phase observations. J. Geod. 2017. [Google Scholar] [CrossRef]
- Zelensky, N.P.; Lemoine, F.G.; Beckley, B.D.; Chinn, D.S.; Pavlis, D.E. Impact of ITRS 2014 realizations on altimeter satellite precise orbit determination. Adv. Space Res. 2018, 61, 45–73. [Google Scholar] [CrossRef]
- Arnold, D.; Montenbruck, O.; Hackel, S.; Sośnica, K. Satellite laser ranging to low Earth orbiters: orbit and network validation. J. Geod. 2018. [Google Scholar] [CrossRef]
- Melachroinos, S.; Lemoine, F.; Zelensky, N.; Rowlands, D.; Luthcke, S.; Bordyugov, O. The effect of geocenter motion on Jason-2 orbits and the mean sea level. Adv. Space Res. 2013, 51, 1323–1334. [Google Scholar] [CrossRef]
- Montenbruck, O.; Gill, E. Satellite Orbits: Models, Methods and Applications; Springer: Heidelberg, Germany, 2000; Volume 1. [Google Scholar] [CrossRef]
- Montenbruck, O.; Steigenberger, P.; Hugentobler, U. Enhanced solar radiation pressure modeling for Galileo satellites. J. Geod. 2015, 89, 283–297. [Google Scholar] [CrossRef]
- Montenbruck, O.; Steigenberger, P.; Darugna, F. Semi-analytical solar radiation pressure modeling for QZS-1 orbit-normal and yaw-steering attitude. Adv. Space Res. 2017, 59, 2088–2100. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).