1. Introduction
Insect migration is a natural phenomenon occurring seasonally [
1], but many migratory insects are agricultural pests and bring major crop production loss every year. Fortunately, entomological radars have been developed into one of the most effective tools for monitoring insect migration, making early warning systems possible to prevent pest outbreaks in time [
2,
3]. Effective target detection methods are essential to extract accurate motion parameters from radar returns for insect migration analysis. Valuable information can then be provided for biological insect research, including flight orientation, velocity, and species identification [
4,
5,
6,
7].
Unlike targets such as unmanned aerial vehicles or large birds, insects are much smaller and often fly hundreds of meters above the ground with complex trajectories [
8], which can be considered as typically weak and maneuvering targets. Thus, advanced radar detection and tracking methods are needed for motion parameter estimation of small insects. In modern radar signal processing, long-time integration can effectively improve the output signal-to-noise ratio (SNR) of targets by accumulating the energy of targets in radar returns, and it is usually divided into incoherent integration and coherent integration. However, the across range unit (ARU) effect caused by target range-walk and across Doppler unit (ADU) effect caused by target maneuverability may easily occur in the long observation time. Both of the long-time integration methods need to correct the ARU effect, and coherent integration has to solve the Doppler frequency dispersion problem brought by the ADU effect in addition.
Incoherent integration methods, including Hough transform (HT) and dynamic programming-based methods [
9,
10], are widely used to detect linear motion targets with constant speed because they do not require strict coherence of radar returns and the system. However, compared with coherent integration, the lack of phase information significantly decreases the integration gain and would make it completely invalid when the SNR is under a certain threshold [
11]. Thus, incoherent integration methods are less effective in the application for weak target detection under a low SNR environment.
Long-time coherent integration can get better integration gain by the use of both amplitude and phase information. However, the traditional coherent method, moving target detection (MTD) [
12], would be invalid in long-time integration because it cannot effectively focus the energy of targets scattered in several range units. Keystone transform (KT) is a typical method introduced to achieve long-time coherent integration [
13,
14]. It removes the linear range migration via rescaling the time axis for each frequency. Second-order KT [
15] is proposed to correct the range curvature brought by acceleration motion, and generalized KT and generalized de-chirp process (GKTGDP) [
16] are proposed to detect the targets with higher-order motion. However, all the KT-based methods need to correct Doppler ambiguity by repetitive KT processing, which brings a heavy computational burden that increases with the search number of ambiguous integers in its application.
Radon–Fourier transform (RFT) [
17,
18,
19] has been proposed to deal with the ARU and ADU effects. It compensates for range migration and phase fluctuation together by jointly searching in the range-velocity domain. For maneuvering targets with higher-order motion, generalized Radon–Fourier transform (GRFT) [
20] was proposed to improve the detection performance by parameter match in higher-dimensional space. However, with the increase of motion order, the unacceptable computational cost of ergodic search would make GRFT hard to be applied in practical signal processing. Essentially, GRFT converts a long-time coherent integration into an optimal parametric motion model match problem, and its fast implementation can be realized by heuristic optimization algorithms [
21,
22,
23]. Particle swarm optimization (PSO) [
24] is an effective population-based heuristic optimization widely used in many fields to solve scientific and engineering problems. It uses the personal best and global best information to cooperatively evolve into the optimal solution and could be applied in GRFT detection to significantly reduce the computational cost. However, the blind-speed sidelobes (BSSL) in GRFT search space would mislead the particles into local convergence. In [
21], the relationship between the BSSL and target’s main lobe was used to address the local convergence to BSSL, called BSSL learning-based PSO (BPSO). However, BPSO-based GRFT suffers significant detection performance loss and is only validated in single target simulation, which is not suitable for insect multi-target detection in the real-time radar data processing. Thus, a new fast implementation method is needed to obtain the insect trajectories.
This paper introduces a novel multimodal optimization to solve this problem. Multimodal optimization can obtain multiple optimal results within a single run. In addition, many population-based evolutionary algorithms can be used to achieve multimodal optimization, such as PSO, differential evolution (DE) [
25], quasi-affine transformation evolutionary (QUATRE) [
26], and cat swarm optimization (CSO) [
27]. These methods have advantages over classical optimization techniques in maintaining a population of possible solutions during the iterations. In many practical applications, niching methods are widely used as diversity-preserving mechanisms in population-based heuristics to solve multimodal optimization problems. The typical niching method divides the population into several species in terms of a prespecified niche radius, and the individuals will be identified as the same species if their distances from the species seed are within the radius [
28]. This radius parameter directly impacts the optimization performance and should be decided by the prior knowledge of optima distribution, which is usually unknown, especially in insect target detection. Thus, a novel niching method without radius is proposed in this paper to distinguish unevenly distributed insect targets. Species reset strategy and boundary constraint strategy are further proposed to improve the multi-target detection performance of multimodal optimization.
The remainder of this paper is organized as follows. In
Section 2, GRFT and multimodal optimization problems are discussed based on the radar return signal model in insect multi-target detection. The proposed niching method and improvements are described in detail. In
Section 3, the simulation results analyses are given, and the proposed method is compared with traditional methods to validate its effectiveness in the signal processing of real data acquired from Ku-band entomological radar. Conclusions and future work are presented in
Section 4.
2. Methodology
2.1. Signal Model
Suppose the transmitted linear frequency modulated (LFM) signal is
where
is fast-time,
is the pulse duration,
is the frequency modulation rate of LFM,
is the signal bandwidth,
is the carrier frequency, and
represents the rectangular function.
In the observation of insect targets, the received signal after the pulse compression can be expressed as
where
is the slow-time when the
th pulse is received,
is pulse repetition interval, and
is the total number of pulses to be integrated.
is the number of insect targets observed by radar. The signal amplitude of the
th target is
and its time delay
directly depends on the time-varying slant range
of the target, which can be expressed as
where
is light speed. The movement of insects contains high motion components caused by maneuvering flight. Therefore, the range
can be denoted as higher-order polynomial
where
is the highest motion order,
is the
-th order motion parameter of the
th target, generally,
represents the initial range,
represents velocity,
represents acceleration, etc.
From (2) and (3), it is obvious that the peak location of the th target in different pulses varies with . In long-time coherent integration, even a slowly moving target may come across several range units, called the across range unit (ARU) effect. Across Doppler unit (ADU) effect will occur if the time-varying Doppler, which is caused by acceleration and higher motion parameters, exceeds the Doppler frequency resolution. Both ARU and ADU effects could decrease the integration gain of traditional methods and lead to weak maneuvering targets in radar detection being missed.
2.2. Optimization Problem for GRFT
GRFT can effectively overcome the coupling ARU and ADU effects. Because the target motion determines its range migration and phase fluctuation simultaneously, GRFT can correct range migration and compensate high-order motion at the same time by matching with the motion parameters of real targets in the search space.
Define a search parameter set
in a
-dimensional motion parameter search space, and GRFT of the received signal
can be expressed as
where
represents the time delay according to search parameters as
From (5), it can be found that integration peak will be obtained in the GRFT plane if is exactly the same as the th target’s real parameter set . Thus, the ergodic search is usually used to find integration peaks in the GRFT search space and realize detection and motion estimation of different targets. However, no matter how many targets exist, it has to search each parameter set in the whole space, whose cost is usually unacceptable in addressing real-world problems. Fast implementation is needed to apply this effective detection method to insect multi-target detection problems.
As is described above, GRFT achieves target detection via motion parameters matching, which can be converted into a parameter set optimization problem. For single target detection, the optimization problem can be expressed as
Equation (5) can be used as an objective function in optimization to search the fittest parameter sets as the target detection results. Thus, the fast implementation of GRFT detection and motion estimation can be achieved by heuristic optimization methods.
However, there exists phase ambiguity in the phase compensation of GRFT because different parameter sets may compensate for phase fluctuation of the same target. Once the integration paths of these sets of parameters overlap with the real target path, integration peaks will occur at the ambiguity interval of the real target in the GRFT plane, which will seriously interfere with the parameter set matching and optimization.
In the case of insect target detection, acceleration and other higher-order motion parameters are limited to a small range in which phase ambiguity will not happen. Therefore, only the phase ambiguity in low dimensional motion parameters such as velocity, called the BSSL problem in GRFT, is discussed as follows.
The phase after velocity compensation in the search for the
th target is
It is obvious only if
and the phase fluctuation can be compensated. The parameter ambiguity interval is exactly blind speed
, and ambiguity integer
, where
is velocity search range.
In practice, integration paths of the real target and its BSSL intersect in several pulses due to discrete pulse sampling and finite range resolution. The overlapped pulse number is
where
is the range resolution, and
is the wavelength. These overlapped pulses may generate sidelobes at ambiguity intervals after coherent integration. The primary lobe-to-sidelobe ratio (PSLR) can be calculated as
Equation (11) shows the relation of BSSL and the main lobe. The peak value of BSSL is smaller than the main lobe and decrease with the growth of while the location of BSSL deviating away from the main lobe. Thus, BSSL can be suppressed according to this relation, and the search performance can be further improved with the help of BSSL to find the main lobe.
2.3. Fast GRFT Based on Multimodal Optimization
2.3.1. Multimodal Optimization Problems in Insect Multi-Target Detection
Multimodal optimization is proposed to locate multiple optimal or sub-optimal solutions, which is exactly consistent with the purpose of locating multiple targets in insect detection [
29]. Unlike common optimization problems, specific mechanisms known as niching methods are needed in multimodal optimization to keep the population diversity and prevent individuals from converging to a single global optimum. Niches are divisions of search space according to solution distribution, and the population can be separated to search for different solutions in each niche.
According to whether utilizing speciation, niching methods are mainly classified into two categories [
30]. Non-speciation-based niching methods are primally aimed at preserving population diversity at the individual level. In contrast, speciation-based niching methods divide the population into several species to search for different targets at the species level, which are more appropriate for locating several insect targets under a noise background.
Niching methods can be used in many population-based heuristics to solve multimodal optimization problems, and PSO is a popular choice because its properties are well fitted to induce niching behaviors. PSO is a stochastic population-based optimization algorithm inspired by the bird flocking behavior and has been widely applied in many real-world situations. In PSO, the optimization problem is usually described as a fitness function to evaluate the quality of solutions represented by particle positions in a
-dimensional search space. Each individual records their personal best position
found so far, and shares this information in the population to cooperatively converge to the global best position
. The velocity
and position
of the
th particle in the
th generation are updated as follows:
where
is inertia weight generally used to balance the global and local search performance, higher
drives particles to explore in the whole search space, and lower
is beneficial to the local exploitation.
are learning factors set between [0, 2] that represent the weights of
and
.
are uniformly distributed random numbers within [0, 1] used to achieve the random particle walk in the search space.
In the typical PSO algorithm, particles only converge to the global best, which is not suitable for multi-target detection in a single run. In order to keep multiple optimal solutions during the iterations, it is necessary to maintain particles scattered in the search space and make them converge to different optimal solutions simultaneously. These two contradictory behaviors are consistent with two inherent parts of PSO—(1) current positions as explorers and (2) personal best positions as convergence center. Current particles can explore better solutions based on the memory and help to evolve into optimal solutions.
This property can be used to induce niching behavior. If an appropriate topology is introduced to limit the communication between particles and distract the attention of particles from the global best, the individuals will converge to different optima in their own neighborhood. In speciation-based niching methods, the population can be divided into several species according to the neighborhood defined by the topology. Each species respectively evolves to cover different niches and eventually finds different optimal solutions in each niche.
Therefore, the GRFT multi-target detection can be converted into a multimodal optimization problem, which can be solved by a PSO algorithm with speciation-based niching methods. The GRFT plane can be seen as a multimodal function landscape, the target motion parameters can be seen as different particle positions in the search space, and the targets in the radar detection can be seen as the multiple solutions. We can use multimodal optimization to search optimal solutions and detect the targets in radar signal processing.
However, compared with the general multimodal optimization problems, the following challenges exist in the applications of insect multi-target detection:
Motion parameters of insect individuals are unevenly distributed and dynamically changing during the flight. The traditional niching method with a fixed radius cannot effectively distinguish each target;
Signal amplitude and reflection characteristics of different targets and insect species differ a lot. Thus, most particles may gather at the strong target positions with high fitness, which leads to weak targets missing;
In radar target detection, particles may easily get trapped in local peaks caused by noise interference, and it would lead to poor detection performance.
To solve these problems, this paper proposes three improvements: species divide strategy, overlapped species reset strategy, and boundary constraint strategy. In addition, the improved multimodal optimization is introduced into GRFT for insect multi-target detection, named BSSL-learning-based multimodal optimization (BMMO). The details are provided as follows.
2.3.2. Improved Multimodal Optimization Method Based on PSO
Traditional multimodal optimization with a fixed niche radius is no longer suitable for locating unevenly distributed insect targets. Motivated by the idea that chooses the nearest individuals within a certain distance to form a species, the radius is substitute by a fixed species size to divide the population in the proposed BMMO. In order to solve the species gathering problem, the species overlapping on the same target is proposed to be reset, which could balance the global search resources and increase the detection probability of weak targets. Moreover, the boundary constraint strategy is improved to enhance the searchability by increasing the search utilization of particles. Finally, the procedure of the proposed method is presented.
A. Species Divide Strategy
In multimodal optimization, niche radius is used to decide particle neighbors and divide the whole population into several species. Particles only communicate with the neighborhood best
in their own species, use
to substitute for
in Equation (12), the new velocity update equation can be obtained as
where
records the index of the neighborhood best for the
th particle.
This method is susceptible to the predefined niche radius and solution distribution in the search space. If the radius is too small, interactions within each species will be less effective with the size decreasing, and particles are more likely to get trapped in the local optimum rather than evolve into the optima. On the contrary, if the radius is larger than the shortest distance between solutions, which happens in the detection of unevenly distributed targets, several desirable solutions will be covered by a single species, and only the best solution will be located. Furthermore, the large species size means that lots of searching resources are wasted on the same solution, and the evolution abilities of other species are reduced.
Target distribution is often priorly unknown or hard to predict, especially in insect detection. The fixed niche radius is proposed to divide different species based on particle clustering. Similarly, fixed species size can be used to divide the population substituting for the niche radius, and the details are presented in Algorithm 1. Once the fittest personal best position is chosen as a species seed, a new species is formed by nearest particles of the seed. Repeating this process divides the remaining particles until the whole population has been speciated.
Species number and species size are introduced to divide the population in the proposed method. Compared with the niche radius, the new division parameters are much easier to determine. Uneven insect distribution will not bring a severe decrease in detection performance as long as the parameters are large enough to cover predicted target numbers, which can be estimated by the insect density of the radar detection area. In practical radar detection, the detection threshold
and insect biological features can help remove the redundant solutions known as false alarms, and is determined by a preset false alarm probability and average noise power. Moreover, fixed species size could avoid the situation that most particles gather in the same species and ensure that each species has equal opportunity to converge to the target.
| Algorithm 1Species divide |
| 1: Initialize: Regard all the personal best p as a pool P, set seed index i=1; |
| 2: while P ≠ ∅ do |
| 3: Find the fittest particles’ index id in P; |
| 4: Set i-th seed: si = id; |
| 5: Calculate the Euclidean distances between psi and all the other particles in P; |
| 6: Extract Nss nearest particles’ index q; |
| 7: Set neighborhood best index: nq = si; |
| 8: Remove pq from P; |
| 9: i = i + 1; |
| 10: end white |
B. Species Reset Strategy
Insect targets have diverse sizes, weights, and radar reflection characteristics. Their signal energy intensity and integration results differ from each other. Particles tend to evolve towards the highest fitness position, which means most particles may gather around the targets with better integration result, and the detection probability of weak targets would be decreased due to finite particle resource. In order to avoid the waste of search abilities, a species reset strategy is proposed to increase searching resource utilization, and details are presented in Algorithm 2. If two species seeds are very close to each other or constitute the first BSSL relationship, they will be considered as located on the same target. All the particles in the species with less fitted seed are judged as doing inefficient searching behavior. Their position, velocity, and personal best memory are randomly reset so that they can be reused to search other targets.
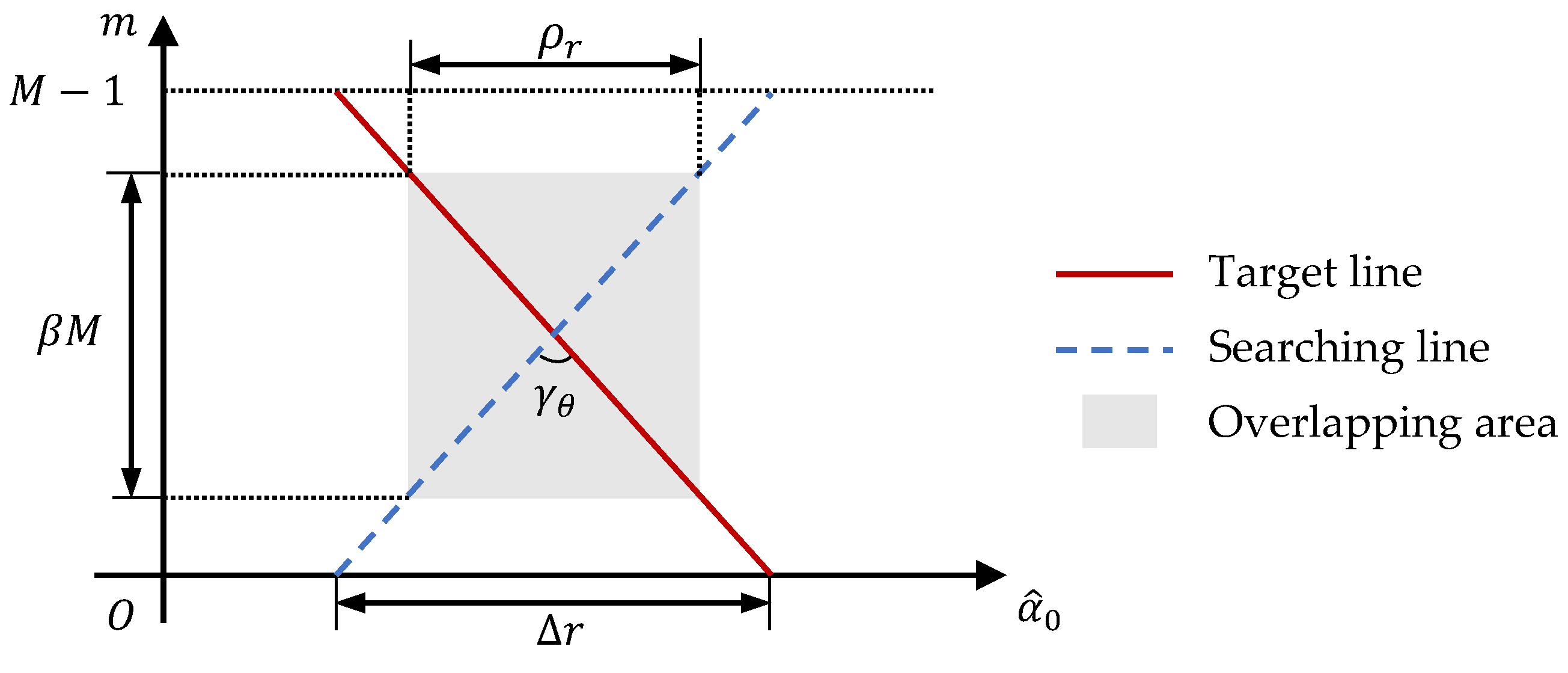
Due to discrete pulse sampling and finite range resolution, several pulses overlapped when the range-walk line of the target intersects the searching line with another parameter set, as shown in
Figure 1. Different from BSSL, part of the target energy is incoherently integrated into this situation, which generates sidelobes near the main lobe in the GRFT plane. The sidelobes may be higher than normal noise peaks and mislead particles.
In the proposed method, two seeds will be considered as searching for the same target if their overlapped pulse number exceeds the threshold
, where
is a reset factor. Because it is complex to count the overlapped pulses, this condition can be evaluated by whether the angle between the average velocities is smaller than
when the distance between the start ranges
is within
, where
and
can be calculated as
and
is the range resolution. The average velocity of the parameter set
is
The angle between
and
is
The BSSL problem has been discussed in
Section 2.2. If the position difference of two seeds is within
, one of the seeds will be considered as falling into the supporting area of the first BSSL, where
and
, and
is a small value to control the reset scale.
| Algorithm 2Species reset |
| 1: Initialize: Regard all the seed as a pool S; |
| 2: for each in S do |
| 3: for each in S do |
| 4: Calculate and |
| 5: if |
| 6: if then id = i; |
| 7: else id = j; |
| 8: Find indexes q ← nq == Sid; |
| 9: Reset xq, vq, pq; |
| 10: Remove from S; |
| 11: end if |
| 12: end for |
| 13: end for |
C. Boundary Constraint Strategy
A Boundary constraint strategy is proposed to improve the detection performance.
During the population evolution, particles often fly out of the search space. In traditional methods, once a particle hits the search boundary in any dimension, its position is set to the boundary in that dimension. However, the reset particles would stay around the boundary for a period of invalid searching due to the space truncation at the search boundary. Therefore, in order to increase search efficiency, the particle position is proposed to be randomly reset in the dimension exceeding the boundary. Its personal best is reserved to make sure that the targets near the boundary can still be found.
Moreover, the limit of particle speed could avoid a search efficiency decrease caused by excessively random walks in the search space. According to the scale of the search space, the speed limit
can be calculated as
where
is a scale factor, and
and
represent the upper and lower boundaries of the search space, respectively. Maximum speed limit
can control the global search ability and prevent the step size from being too large, which could make the update equation useless especially in the early iterations. In order to get better optimization performance in different optimization problems, Monte Carlo tests can be used to determine the appropriate value of
. The particle speed
should be limited to
and reset to the boundary in the dimension exceeding the limit.
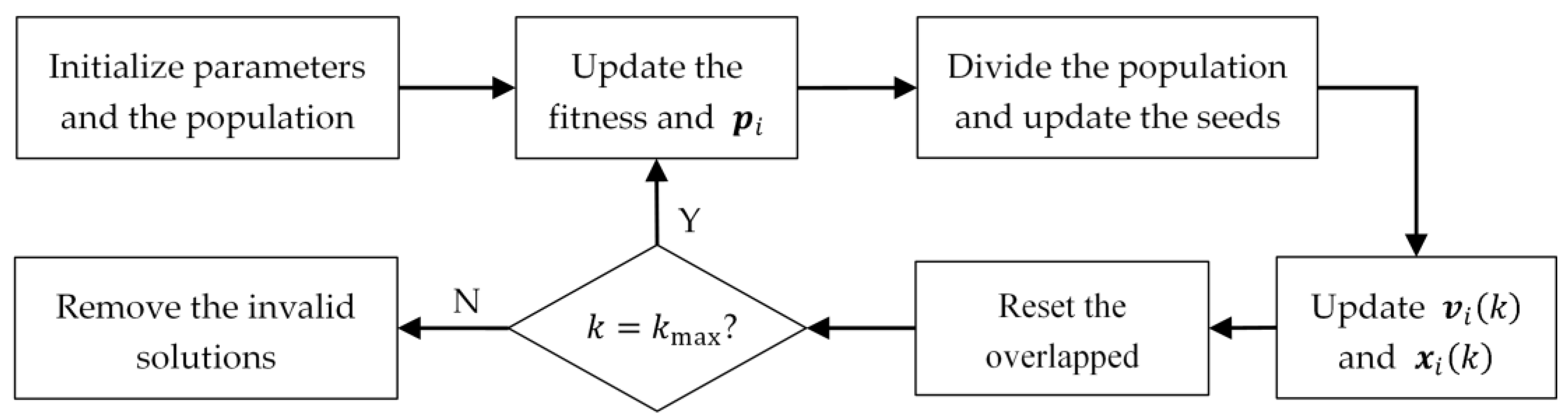
D. Procedure of BMMO
The procedure of the proposed BMMO algorithm can be described in
Figure 2.
Initialize algorithm parameters, including the motion order which also means the dimension of the search space, position boundary , species number and species size according to strategy A, the maximum iteration , reset factors and , speed limit factor , and according to Equation (19);
Initialize the population by randomly generating within the search space as the initial position and within the speed limit as the initial velocity, where ;
Calculate the GRFT result as the fitness value of each particle according to Equation (5).
and update the
as follows:
Divide the population according to strategy A;
Update the
th seed according to the relation between the BSSL and the main lobe;
where
, the blind speed integer
, and
,
. The seeds could jump out to the real target location when stuck in BSSL peaks because BSSL is smaller than the main lobe, as proved in [
22];
Update the velocity by Equation (14) and limit it within the range of . Then, update position by Equation (13) and reset it according to strategy C;
Reset the overlapped species according to strategy B;
Repeat steps 2–7 until ;
Remove the invalid solutions according to strategy A.
3. Simulation and Experimental Results
In this section, the detection performance and computational cost of the proposed BMMO-based GRFT method are analyzed based on simulation results, and the BMMO is compared with the original GRFT method and other optimization methods. The effectiveness of the BMMO is validated by processing real observation data acquired from a Ku-band entomological radar, and the proposed method is compared with traditional methods in the detection performance and track quality.
3.1. Simulation Analysis
Simulation analysis consists of detection performance and computational costs. The detection probability and motion parameter estimation accuracy are analyzed in the detection performance comparison of different methods. The single-target detection case is also provided to validate the performance improvement compared with the original BPSO methods. Subsequently, the computational costs of different methods are provided, and the relationships between parameters and time cost are also analyzed.
Radar simulation parameters are listed in
Table 1. In the following simulation, the targets are assumed to move in a constant acceleration motion model, and they are uniformly and randomly generated in the target motion parameter space between (−250 m, −5m/s, −3m/s
2) and (250 m, 5 m/s, 3 m/s
2), the search space boundary is set as
(−400 m, −10 m/s, −5 m/s
2) and
(400 m, 10 m/s, 5m/s
2) for both GRFT and optimization methods. The SNR after pulse compression is set between −5 dB and 15 dB to test the performance of the proposed method under different optimization problem complexity, and white Gaussian noise is added to the simulation data.
3.1.1. Detection Performance
A. Single-Target Case
The detection results for the single-target case are provided to validate the effectiveness of the proposed boundary constraint strategy and learning factor improvement. Average results of 5000 Monte Carlo trials are provided to ensure the reliability of tests, where 500 groups of independent data are simulated for different targets under each SNR environment, and 10 independent runs are taken for each group of data.
The following methods are tested in this simulation:
For the BPSO-based methods given above, set the population size
= 60 and maximum iteration times
= 3000. The results exceeding the fixed detection threshold determined by the false alarm rate
are considered as valid detections.
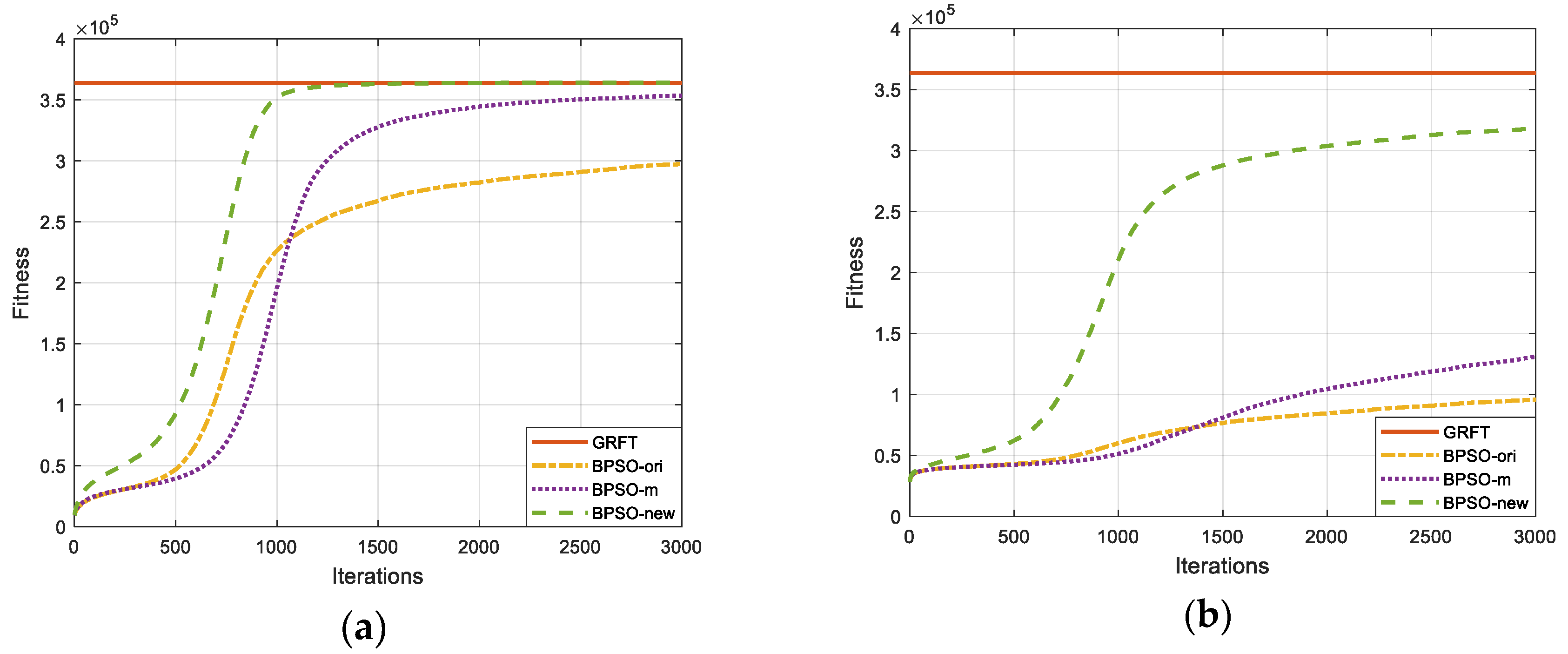
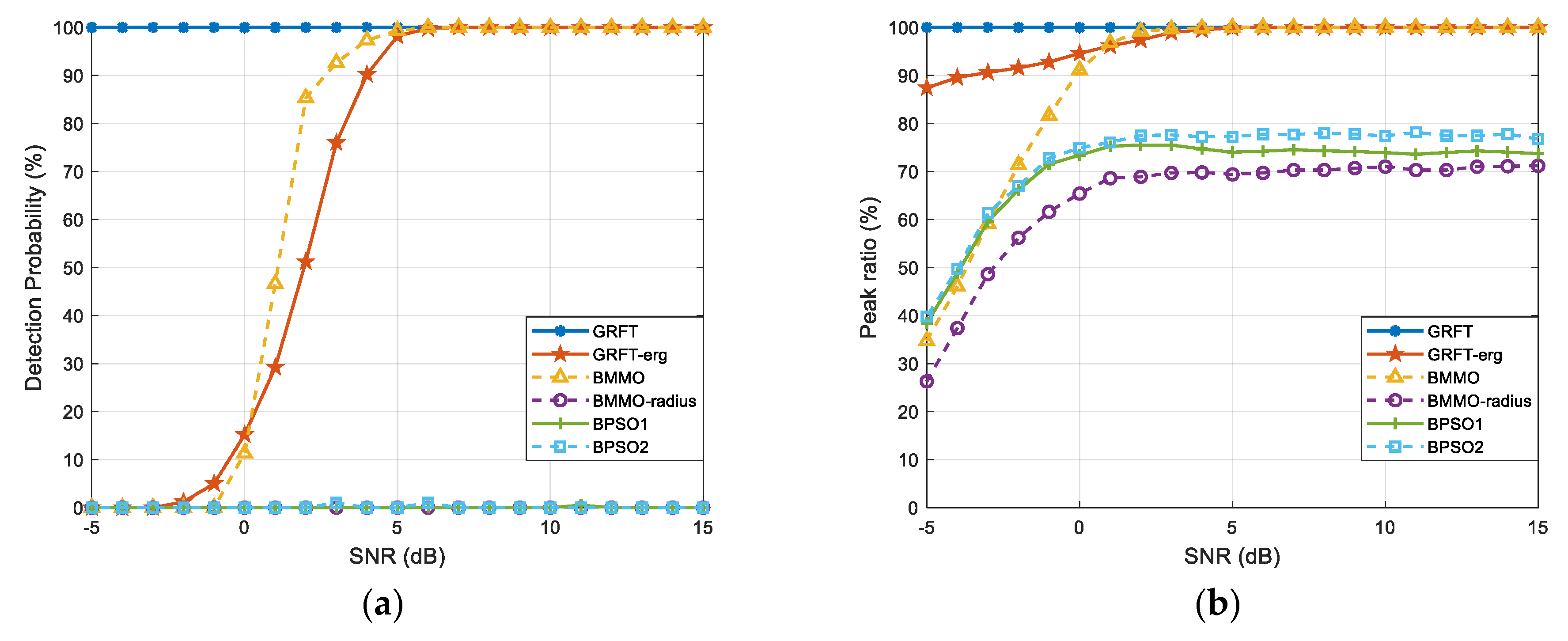
Figure 3 presents the detection probability of the five detectors under different SNR.
It is shown that the probability of the proposed method is much better than the original BPSO method under the same SNR, although it still suffers apparent loss compared with traditional GRFT. Required SNR of BPSO-new is at least 6 dB lower than that of BPSO-ori to achieve the same detection probability. The curve of BPSO-m demonstrates that the improvements of learning factors and boundary constraint strategy both benefit the performance to a different extent.
The converge process of different BPSO-based GRFT methods under 15 dB and 5 dB SNR are shown in
Figure 4. It can be seen that the increase of noise intensity in the low SNR environment has a severe impact on the convergence, which means the optimization problems become more complex and difficult. The convergence speed is much faster in a higher SNR environment, and more iteration times are needed to converge to the optimum under a low SNR environment. As shown in
Figure 4b, the fitness of BPSO-new is much closer to the optimal fitness while the other BPSO-based methods have almost lost the searchability. Comparing the results of BPSO-m and BPSO-ori, the weight increase of the personal best slows down the convergence of BPSO-m, but it improves the performance significantly. It may not be a good choice to use the weight factors that lead to fast convergence.
B. Multiple-Target Case
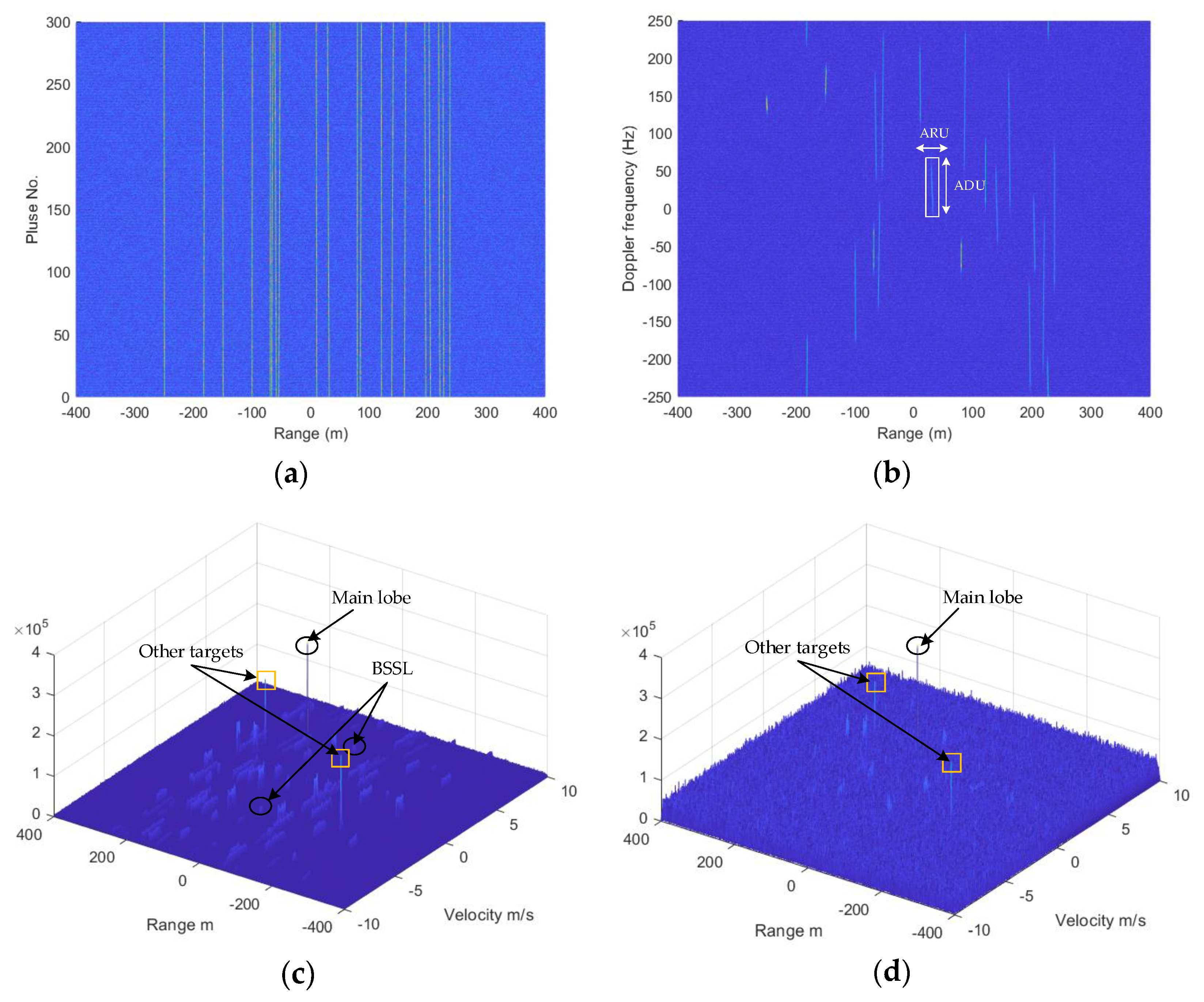
In order to test the multi-target detection performance of different methods, 20 different targets are simulated in the same radar detection scene, as displayed in
Figure 5. The average detection results of 500 Monte Carlo trials are analyzed in the following.
Figure 5a shows that the simulated targets are unevenly distributed along with the range. In
Figure 5b, both ARU and ADU effects occur in the MTD result, which indicates that MTD is not suitable for insect target detection. If the target has higher maneuverability, its energy will distribute in more range units and Doppler units. Because each input series of MTD filter bank is within one range unit, their energy cannot be well focused and the output SNR would also be decreased significantly.
Figure 5c,d displays the complex optimization space of multiple target simulation. BSSL can be seen beside the main lobes in
Figure 5c, which were submerged by noise when SNR = 0 dB in
Figure 5d. Unlike most of the benchmark test functions used in the performance evaluation of niching methods, whose landscapes are consisted of continuous peaks and valleys, the target impulse is hard to be discovered by particles in the GRFT plane, and it may be interfered with by the noise peaks and other targets. Therefore, it is hard for particles to come across these spiculate target peaks during the optimization for radar target detection.
As a comparison, two unimodal optimization methods are given based on the BPSO-new described above. They achieve multi-target detection by archiving the position as soon as it was detected until all the targets are found with the detection loop. Two different archiving mechanisms are proposed as follows:
BPSO1: archiving by reducing the fitness weight of the detected targets. Fitness function can be rewritten as Equation (23),
is fitness weight determined by its distance to all the positions that have already been detected and can be calculated by (24). The closer the particle to any of the detected positions, the smaller
is. Factor
is inversely proportional to the archiving scope around the archived targets and
=1000 in this simulation;
BPSO2: archiving by deleting the pulse compression data along the searching lines of detected targets, and their adjacent range units should also be deleted. needs to be big enough to reduce the impact of residual target energy on the subsequent search, but nearby targets may be affected at the same time. We chose to delete the range bins within 1 m around the target; thus = 9 in this simulation.
The following are two multimodal detection methods based on BPSO-new:
Because the detection situation of multi-target is much more complicated than the single optimum search problem, we expand the maximum iterations to = 6000 in multimodal methods BMMO-radius and BMMO, its population size = = 1000. Set = 3000 and = 200 in unimodal methods BPSO1 and BPSO2, which are the same as the parameters in single target simulation, and run 40 detection loops.
In multi-target detection, it is hard to evaluate whether the search results hit the true targets by the fixed threshold. Therefore, the detection threshold
is firstly set according to the probability of false alarm
to remove the invalid solutions. The solution can then be considered a successful detection if its position difference is within (1 m, 0.1 m/s, 0.1 m/s
2), and the fitness difference is within 1% compared with the true targets. The detection performance is measured in terms of two criteria—(1) detection probability, which is the percentage of run times that all the simulated targets are successfully found, and (2) peak ratio, which is the ratio of the average detected target number in each run to the simulated target number.
Figure 6 shows the performance results of different methods.
It can be seen in
Figure 6a that the detection probability of BMMO is very close to GRFT-erg and even better under the 1 dB to 5 dB SNR environment. They both have apparent performance loss compared with GRFT when the SNR is lower than 5 dB, whereas all the other three methods failed to find all targets under any SNR.
Figure 6b shows that the peak ratio of the proposed BMMO is close to GRFT-erg when SNR is higher than 0 dB, and it maintains better detection probability than the other three methods when SNR is higher than −3 dB. Two unimodal methods, BPSO1 and BPSO2, have similar performance, and the BMMO-radius has the worst performance among all the methods. It is apparent that the species divided by fixed niche radius cannot identify the concentrated targets shown in
Figure 5a, and only the fittest one of them can be discovered as the solution.
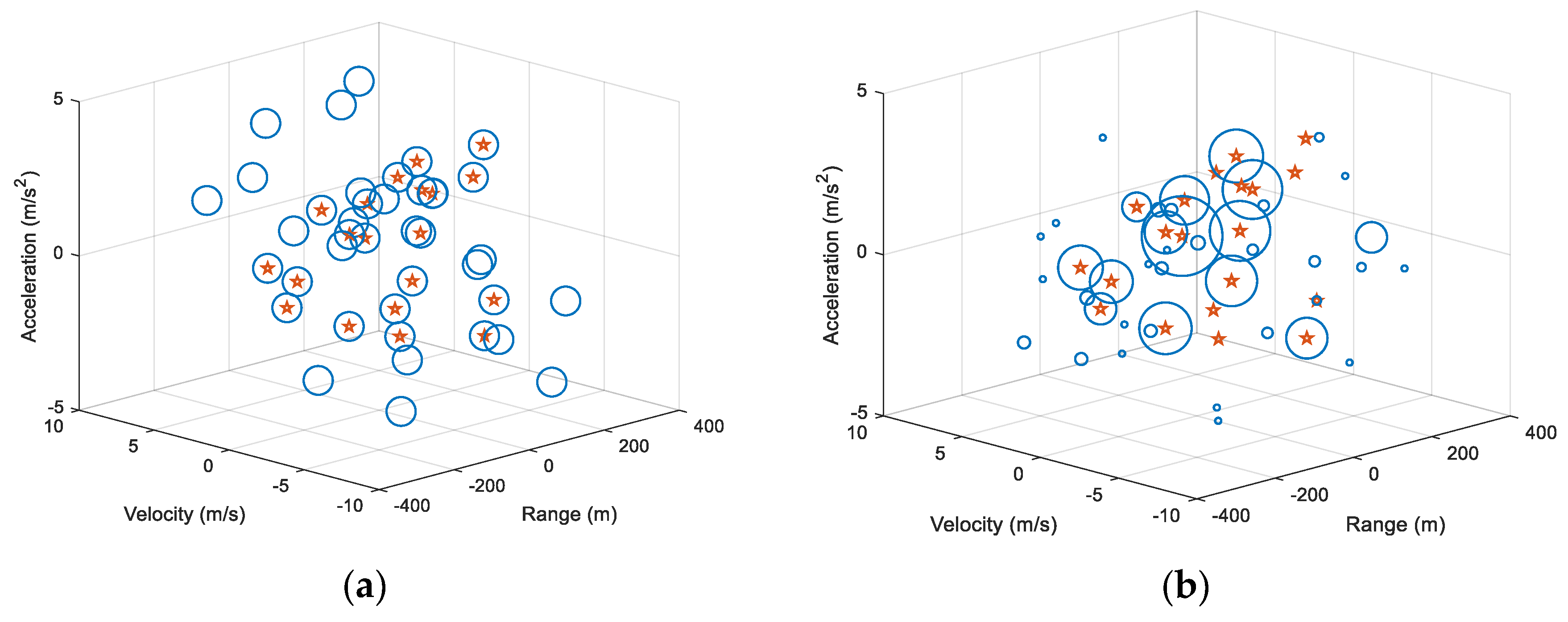
Figure 7 illustrates the comparison of speciation results between BMMO and BMMO-radius. Red pentagrams represent the simulated targets, and the searched solutions are marked as the center of blue circles, where circle size is proportional to the number of particles involved in each species. In
Figure 7a, species are distributed more evenly in the search space to adequately cover each solution compared with the species shown in
Figure 7b. It means all the solutions scattered at different positions in the search space have equal discovery possibilities in the BMMO method. In traditional niching methods, it can be seen that most of the particles gather in a few species. The unbalanced particle resource leads to poor optimization performance and decreases the detection probability of unevenly distributed targets.
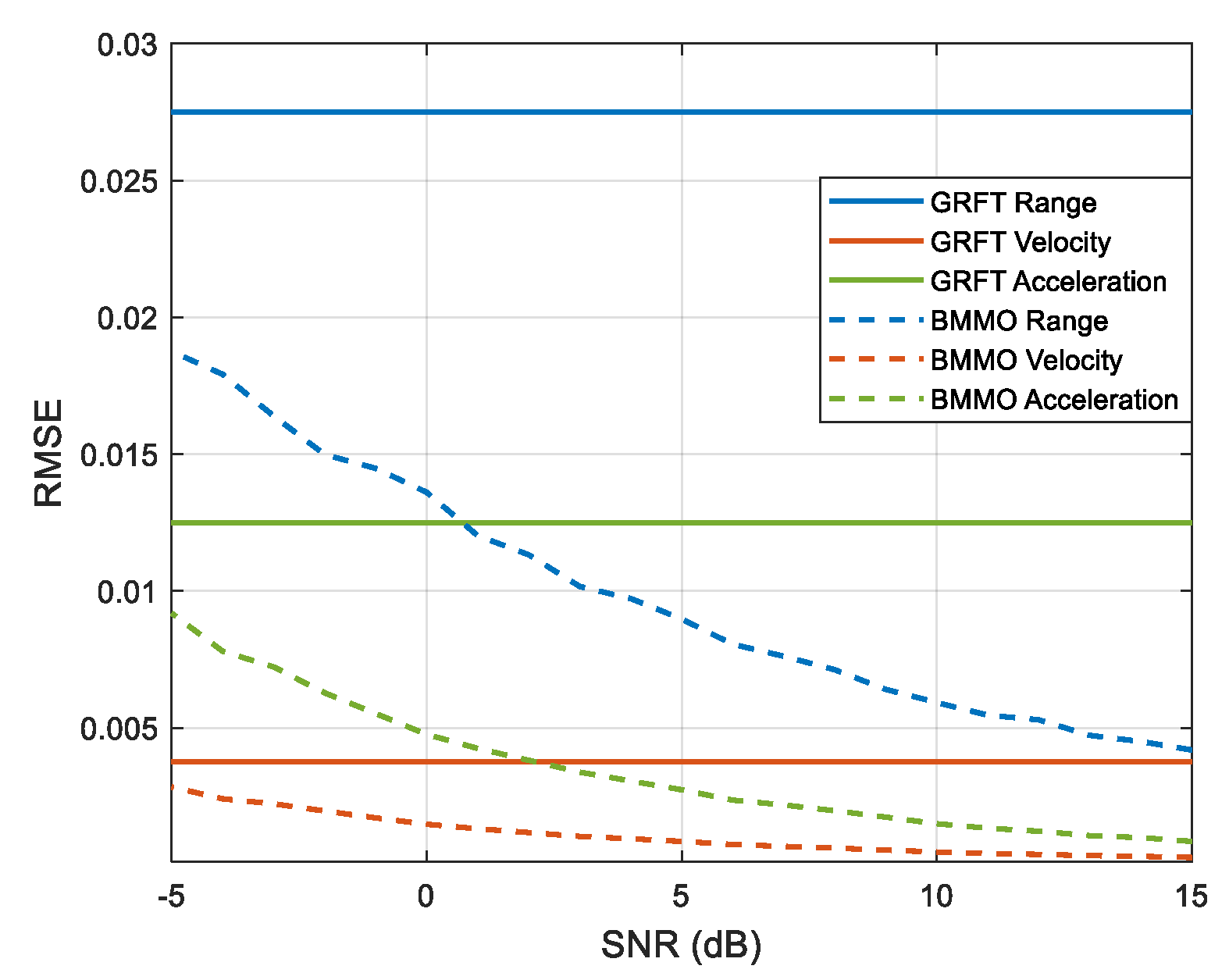
Furthermore,
Figure 8 gives the root mean square error (RMSE) of motion parameter estimation in different motion orders, marked with different lines. The horizontal solid lines represent the RMSE of GRFT-erg calculated as a quarter of their search interval. The dotted lines represent the RMSE of the search results that hitting the true targets in BMMO. It can be seen that the RMSE of BMMO gets worse with the SNR decreasing but performs better than that of GRFT-erg because particles search the motion parameters in a continuous space rather than the discrete space in the GRFT-erg method.
3.1.2. Computational Cost
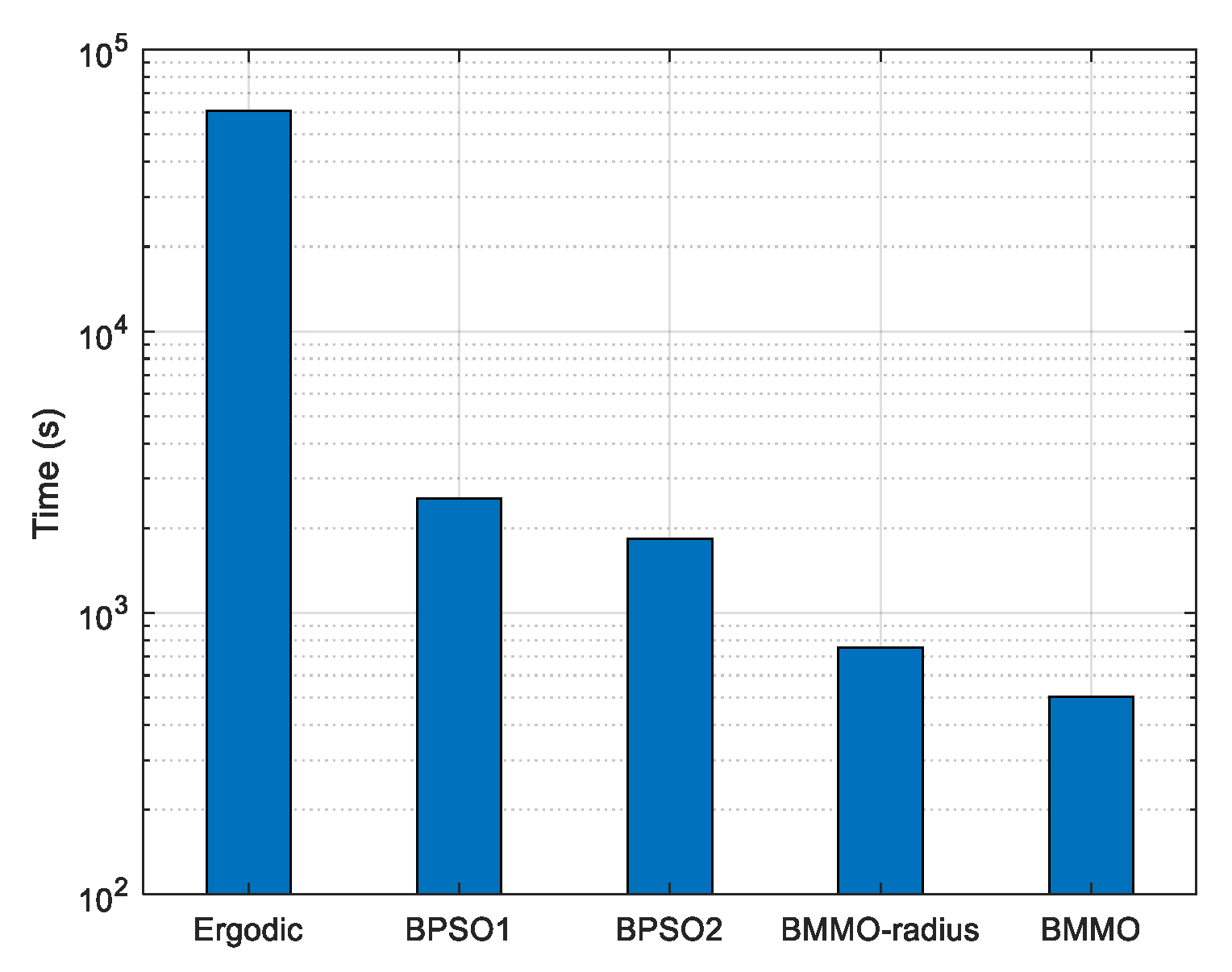
In this subsection, we analyze the computational costs of the traditional ergodic-search GRFT and four multi-target detection methods mentioned above, as shown in
Figure 9. The computational burden of ergodic-search GRFT is evaluated according to the total ergodic search times and average single search cost of 10,000 runs. In addition, the time costs of other methods are the average results tested in the multi-target detection.
It is obvious that the computational cost of ergodic-search GRFT is much higher than all the other methods and is about 100 times higher than that of BMMO. Time costs of unimodal search methods are higher than those of multimodal methods due to the repeated detection used to search for multiple targets. In the BMMO-radius method, many inefficient small species contain only a few particles because of the radius limitation and still need extra time to deal with, as shown in
Figure 7b. According to the detection performance given in
Figure 6 and the computational costs in
Figure 9, it can be concluded that BMMO could achieve better detection performance with less computational cost than the other three multi-target detection methods based on optimization.
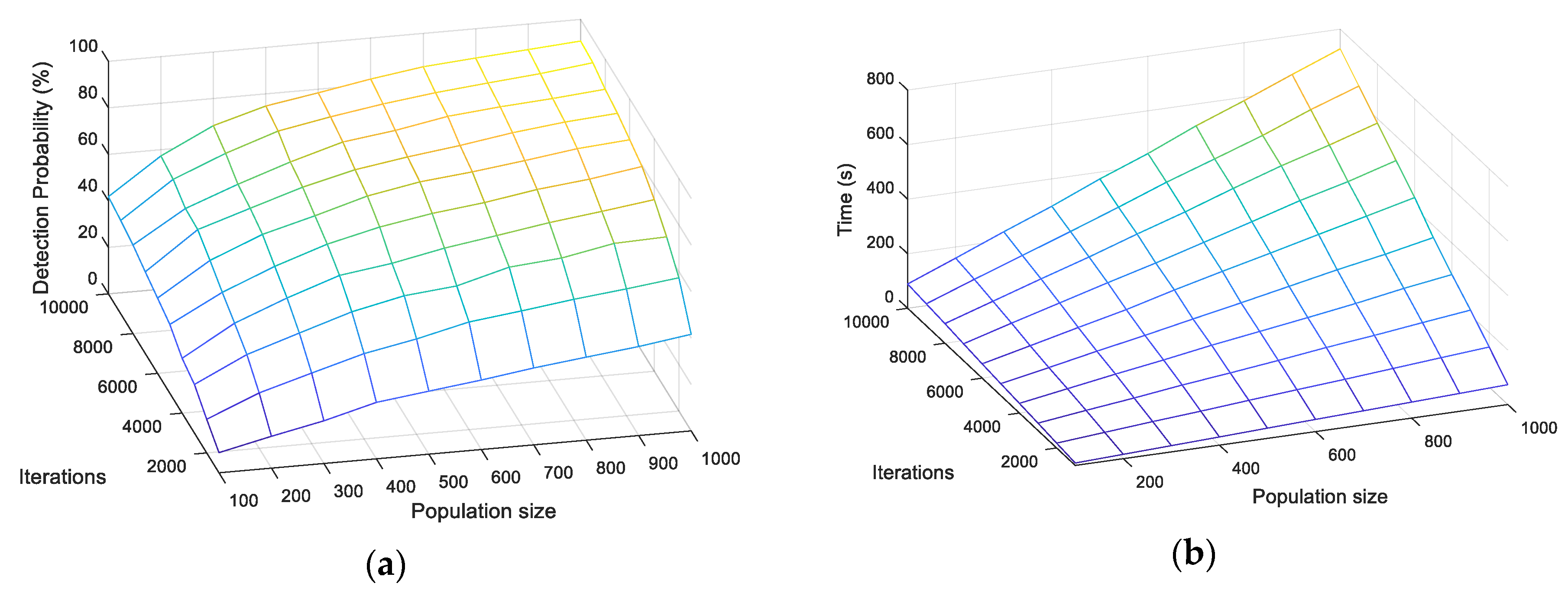
Furthermore, the performance of BPSO-based methods is directly influenced by the maximum iterations and population size. The BPSO-new is tested in single target simulation to present their relations when SNR = 0 dB. As shown in
Figure 10, the increase of two parameters could effectively improve the detection probability while the computational cost also proportionally increases. It is worth noticing that the detection probability of BPSO-new reaches 90%, higher than GRFT-erg, when
= 10,000 and
= 1000. It indicates the potential of BPSO to achieve better performance than GRFT-erg in a shorter time. It is suggested to choose appropriate parameters to achieve the desired performance as short as the time consumed.
3.2. Experimental Validations
In this section, the detection results of the proposed method and traditional methods are compared in the processing of the real insect observation data. The data were collected by the vertical-looking radar as shown in
Figure 11 in Yunnan Province on the night of 27 September 2018, and there are 1500 radar return pulses in each 3 s observation cycle. The radar data processing parameters are presented in
Table 1.
In the traditional pulse Doppler (PD) signal processing, short-time coherent integration and constant false alarm rate detection (CFAR) are carried out for every 20 pulses, which is named as PD-CFAR method. The targets below the CFAR threshold would be considered a false alarm and be eliminated. New detected results would be associated with the nearest existing tracks according to the time and range threshold. In this experiment, the false alarm rate is set as
, the tracks maintained more than 0.4 s would be reserved in each observation cycle. In the proposed BMMO method, the detection duration is set as 0.6 s corresponding to 300 pulses for long-time coherent integration. CFAR
is also used in the GRFT plane to reduce false alarms. Five groups of detection results would be associated to form target tracks during each cycle, and the tracks that longer than 1.2 s would be reserved. We set
(0 m, −10 m/s, −5 m/s
2),
(960 m, 10 m/s, 5 m/s
2), and other parameters are the same as the multi-target simulation in
Section 3.1.1.
In order to verify the detection validity of BMMO, the pulse compression (PC) and MTD images are presented as a comparison. Typical results are shown in
Figure 12. Each column represents a group of results detected by PC, MTD, PD-CFAR, and BMMO, where PD-CFAR results are represented by the blue lines and BMMO are represented by the red lines in the third row. It can be seen from the PC images that the radar returns of insect targets are too weak to be observed due to the long observation distance and the low radar cross-section of insects. It also shows apparent amplitude fluctuations between weak and strong targets. The targets, which can be clearly found in the MTD images, are marked as reference. The box marks the targets detected by both methods, the circle marks the ones only detected by BMMO, and the triangle marks the ones detected by traditional methods but missed by BMMO.
Comparing the red and blue lines in the third row, it can be seen that most of the target tracks obtained by PD-CFAR are covered and extended by the proposed method, which proves that BMMO performs better in real insect detection. Note the results (d) and (e), where the continuous trajectories obtained by BMMO were cut into different target tracks by PD-CFAR. It demonstrates that BMMO can effectively reduce the cases that a single target is incorrectly identified as multiple targets, and improve the track association continuity and target recognition accuracy, especially for the targets with apparent amplitude fluctuations in radar returns.
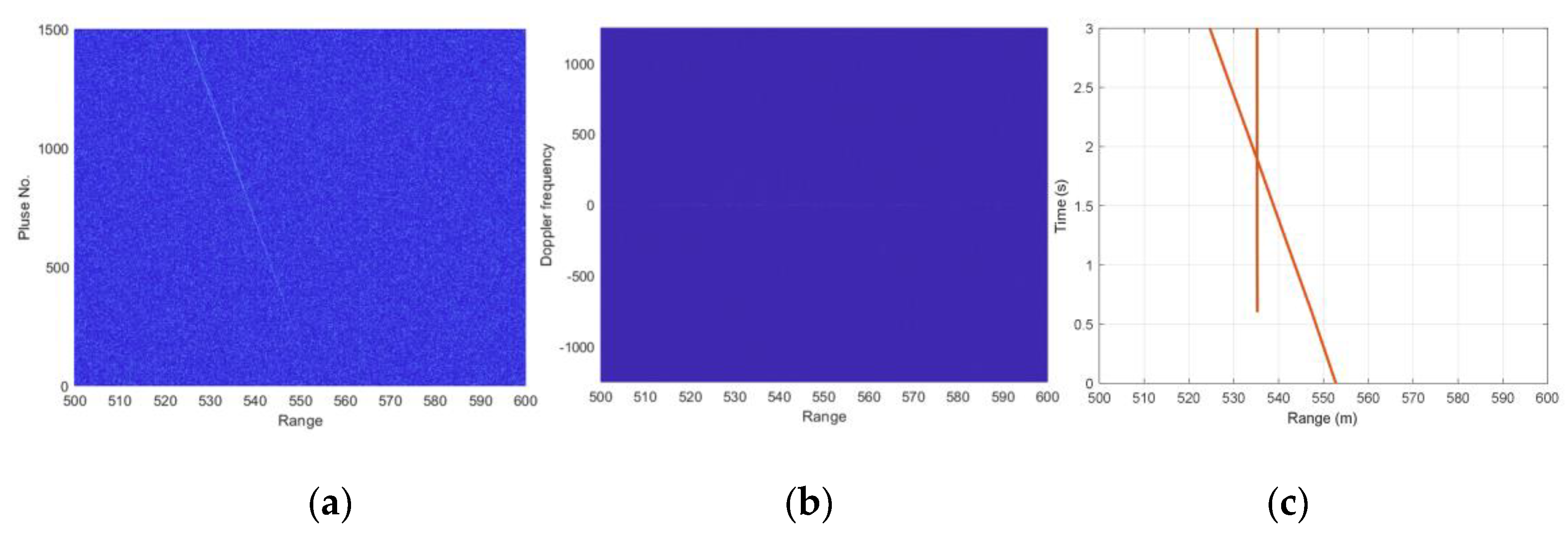
In each group of results, BMMO obtains more targets than PD-CFAR, and most of the targets only obtained by BMMO can be considered as true targets according to the PC and MTD images. Both weak and strong targets can be detected simultaneously by BMMO in the same observation, which validates the effectiveness of the species reset strategy. It should pay attention to the target around 550 m flying towards the radar with relatively high speed in the PC image of result (c), as shown in zoomed-in
Figure 13. Both MTD and PD-CFAR cannot focus the target energy distributed among different range units due to the ARU effect, but BMMO successfully obtains the trajectory shown in the PC result.
BMMO missed the short track marked by the triangle in the result (e). It is probably because that 0.6 s detection segments exactly cut this track into different integration duration, and the integrated peak is too small in each part to be easily submerged by noise. Thus, the PD-CFAR with short time integration is more suitable for these instantaneous targets. With regard to insect detection, further biological analysis of targets is hoped, which requires long stable tracks. Therefore, the miss detection of the instantaneous target has little impact on insect target detection.
4. Discussion
As typically weak maneuvering targets, insects cannot be effectively detected by traditional long-time integration methods due to the ARU and ADU effects in the observation of entomological radar. GRFT can overcome these two effects, but the expensive computational cost is a critical problem in its application. Thus, we use heuristic optimization to reduce unnecessary GRFT computation and multimodal optimization to detect multiple insect targets in a single run. In this paper, a novel niching method and several strategies are proposed to achieve the fast insect multi-target GRFT detection.
In the single target detection case, the boundary constraint strategy and modified learning factors bring significant performance improvements. Both the reduction of the global best weight in the velocity update equation and the velocity limit preventing the excessive random walk-in search space help particles explore better solutions scattered in the whole search space and get out of the local optimum traps in the noise background. The position reset for the particles flying out of the boundary benefits the performance by improving the utilization of the limited search resources.
The multiple-target simulation shows that the proposed species divide strategy with limited species size rather than niche radius can successfully distinguish unevenly distributed insects, and the unified species size makes each species have an equal probability of evolving into an optimal solution. It indicates that a predefined niche radius is not suitable for insect multi-target detection and the other optimization problems with unevenly distributed optima. With the help of the species reset strategy, overlapped species can be reallocated to locate the weak targets that have less possibility to be discovered, which makes BMMO more efficient than the other BPSO-based methods. Regarding the unimodal optimization methods with archiving mechanisms, no matter the weight reduction or the data deletion of the searched targets, archiving methods would inevitably change the original information included in radar returns. Once the detected result is a false target exactly near the true target, this error archived result would severely affect the subsequent detection process. Their little fluctuated peak ratios between 0 dB and 15 dB in
Figure 6b demonstrate that this truly happened in each run.
Moreover, compared with the original GRFT method, the apparent detection probability decrease of GRFT-erg indicates that quantization error introduced by ergodic searching at fixed intervals would result in a performance loss, which is inversely proportional to the interval length and sharpens with the SNR decrease. In addition, the quantization error of GRFT-erg also results in worse motion parameter estimation accuracy compared to the BMMO method.
The computational cost of BMMO is less than the other methods in the multi-target detection. In BMMO-based GRFT, stochastic searching and cooperative evaluation effectively avoid most of the unnecessary GRFT computational cost at the price of the performance loss below 0 dB SNR. It should be cautiously considered whether it is worth trading off such expensive time costs for the significant performance advantage under the extremely low SNR environment. Moreover, the detection performance of GRFT-erg is closely related to the search interval, and the smaller the interval means the better performance and the exponential increase of the computational cost. In multi-target detection, BMMO may be a balanced choice to achieve relatively good performance with acceptable computational costs.
In the signal processing of the real observation data, the proposed method is superior to the traditional methods in the detected target amount. Benefited by higher detection probability, it can also obtain longer and more continuous tracks for the same targets detected by PD-CFAR. In the comparison of different methods, traditional methods would miss some targets influenced by the range-walk caused by the ARU effect and the Doppler frequency dispersion caused by the ADU effect. BMMO-based GRFT effectively addresses these problems with the range migration correction and phase fluctuation compensation during the long-time integration.
Sometimes, it is hard to identify whether it is a true target, false alarms, or the clutters depending on the PC and MTD results. Generally speaking, the confidence of long tracks is much higher, and short tracks are more likely to be false alarms caused by incorrect association. Moreover, the target features could assist in distinguishing the desired targets from all the detected targets. For example, biological information such as body mass and wing-beat frequency estimation can be used for insect recognition [
33,
34].
Moreover, if the target is over maneuvering within the integration time, the constant acceleration motion model would be inefficient and then a higher-order motion model is needed. It should be noted that BMMO is essentially a stochastic optimization used in the fast GRFT searching process, which would miss targets at a certain probability related to the performance under different SNR environments. According to the results in
Section 3.1.1, the targets under relatively high SNR usually will not be missed in terms of the simulation and real data detection results.
In future work, new niching methods and their combination with other optimization algorithms are needed to improve the detection performance under the low SNR environment. The time consumption of BMMO can be further reduced by parallel computing, which is significant to the real-time signal processing in radar observation for insect migration.