An Improved Algorithm Robust to Illumination Variations for Reconstructing Point Cloud Models from Images
Abstract
1. Introduction
2. Related Work
2.1. Single Image-Based Methods
2.2. Two Images-Based Methods
2.3. Image Sequence-Based Methods
2.3.1. Reconstruction Based on Depth Mapping
2.3.2. Reconstruction Based on Feature Propagation
2.3.3. Patch-Based Reconstruction
2.4. Deep-Learning-Based Reconstruction
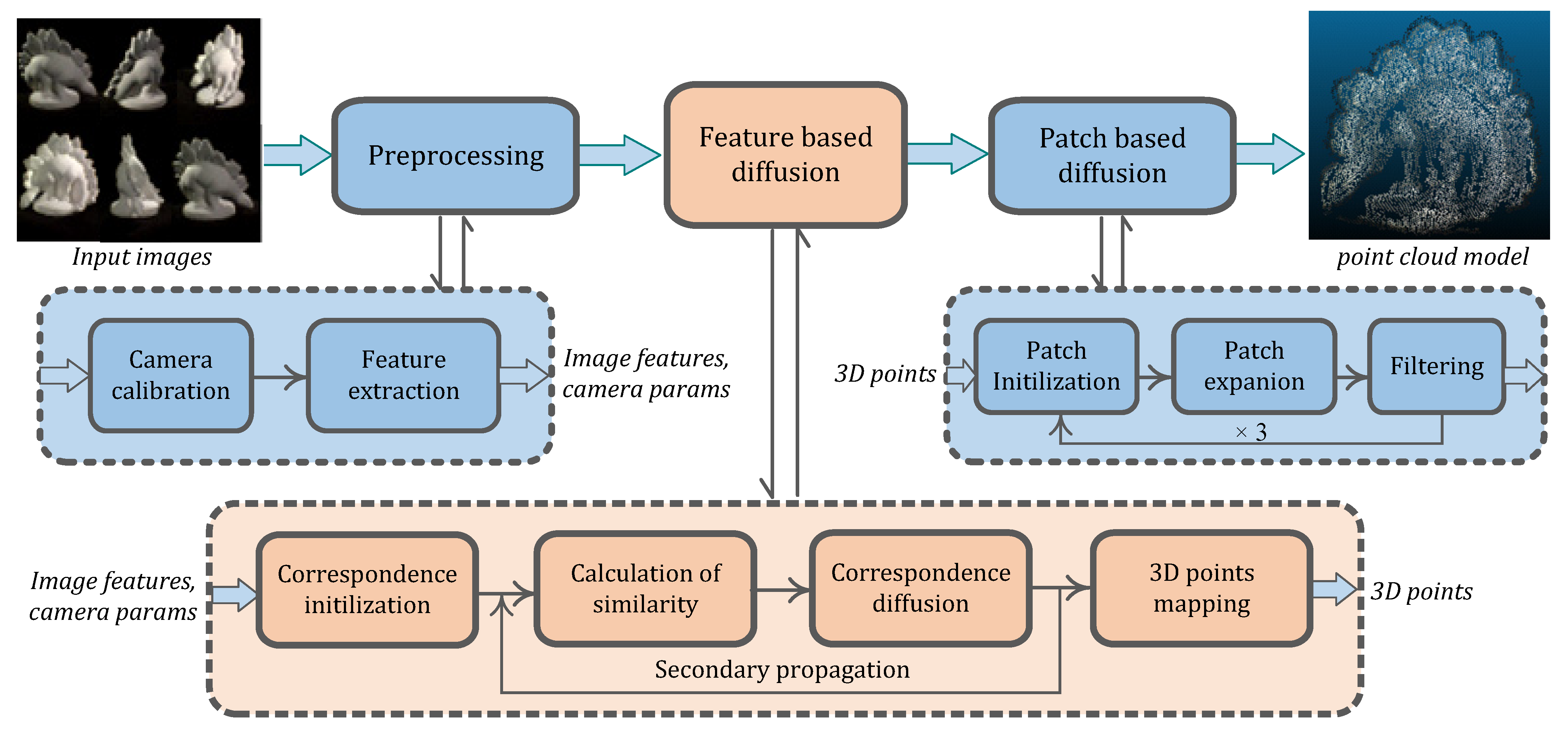
3. Framework of 3D Reconstruction
- Preprocessing. The seed-and-expand dense reconstruction scheme takes sparse seed feature matches as input and propagates them to the neighborhoods, and then restores the 3D points by stereo mapping using calibrated camera parameters. This step calibrates the input images to yield camera parameters and extract features for subsequent feature matching and diffusion. It is the preparation stage of the whole algorithm.
- Feature diffusion. Initializes seed matches from extracted features employing image pruning and epipolar constraints. Then, it propagates them to the neighborhoods by the similarity metric of each potential match, combining the constraints of disparity gradient and confidence measure as filtering criteria. Afterwards, it elects the eligible ones and retrieves 3D points by triangulation principle. This stage generates comparative dense points for the following patch diffusion in 3D space.
- Patch based dense diffusion. 3D patch is firstly defined at each retrieved point. As similar in the feature diffusion stage, seed patches are pruned by the appearance consistency (the proposed similarity metric) and geometry consistency, and then expanded within the grid neighborhoods to gain dense patches. At last, the expanded patches are filtered. This stage is recursively proceeded in multiple rounds, and the final 3D point cloud is obtained from retained patches.
4. Preprocessing
4.1. Camera Parameter Estimation
4.2. Feature Extraction
5. Feature Diffusion
5.1. Correspondence Initialization
5.2. Calculation of Similarity
5.3. Correspondence Diffusion
- -
- Matches with are not only selected as candidates for restoring 3D points, but also pushed into the seed queue for diffusion.
- -
- Matches with are only reserved as candidates for 3D points restoring.
- -
- Matches with are treated as false correspondences and deleted from the set.
5.3.1. Diffusing
5.3.2. Secondary Diffusing
5.4. 3D Points Restoring
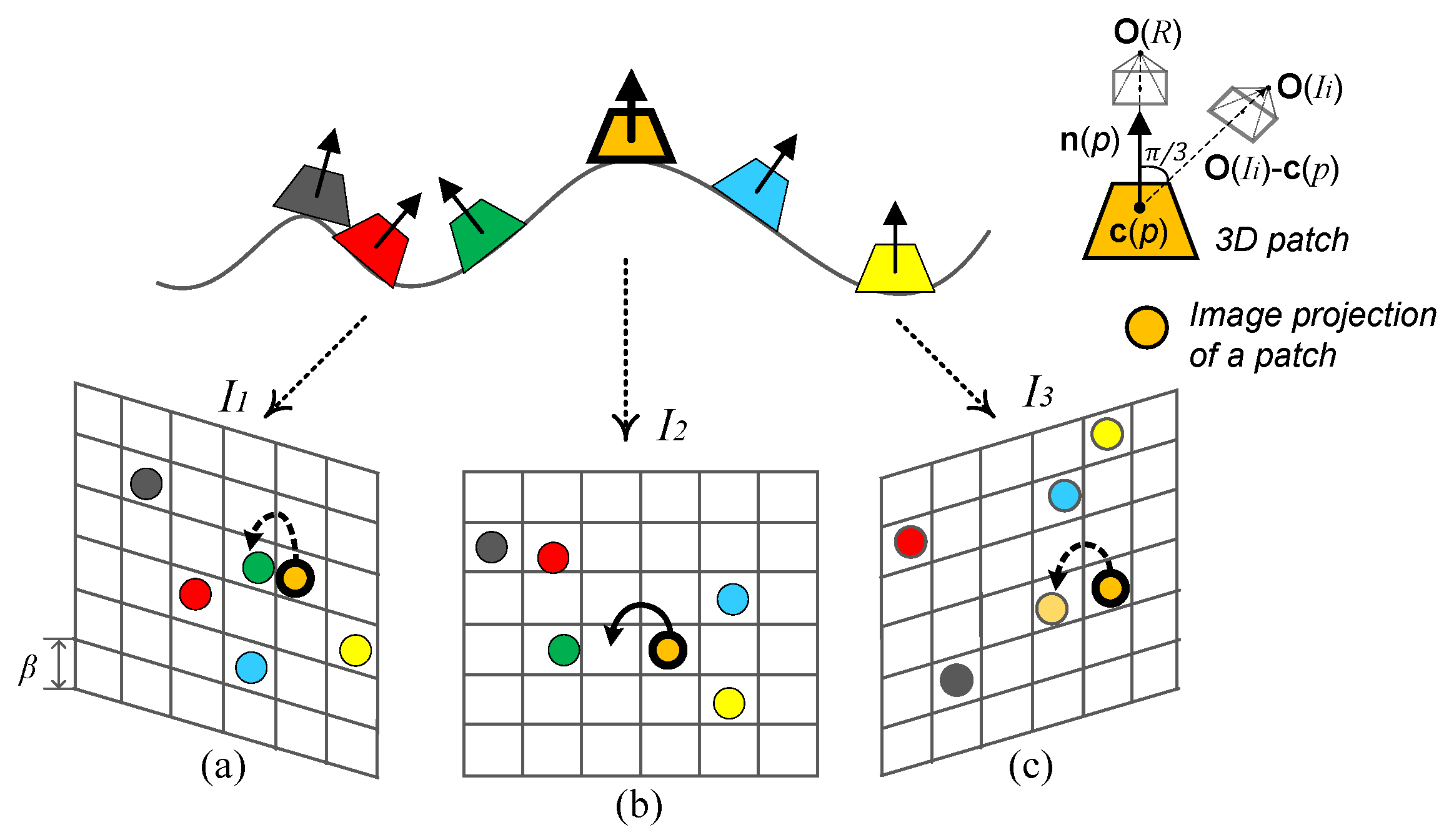
6. Patch-Based Dense Diffusion
6.1. Patch Initialization
6.2. Patch Expansion
- -
- Generate a new patch by copying p, then optimize its center and normal by maximizing the similarity score;
- -
- Gather the visible images (). If , then push to .
6.3. Patch Filtering
7. Experimental Evaluation
7.1. Reconstruction Results of the Proposed Method
7.2. Evaluation of the Proposed Metric
7.2.1. Textureless Scenarios
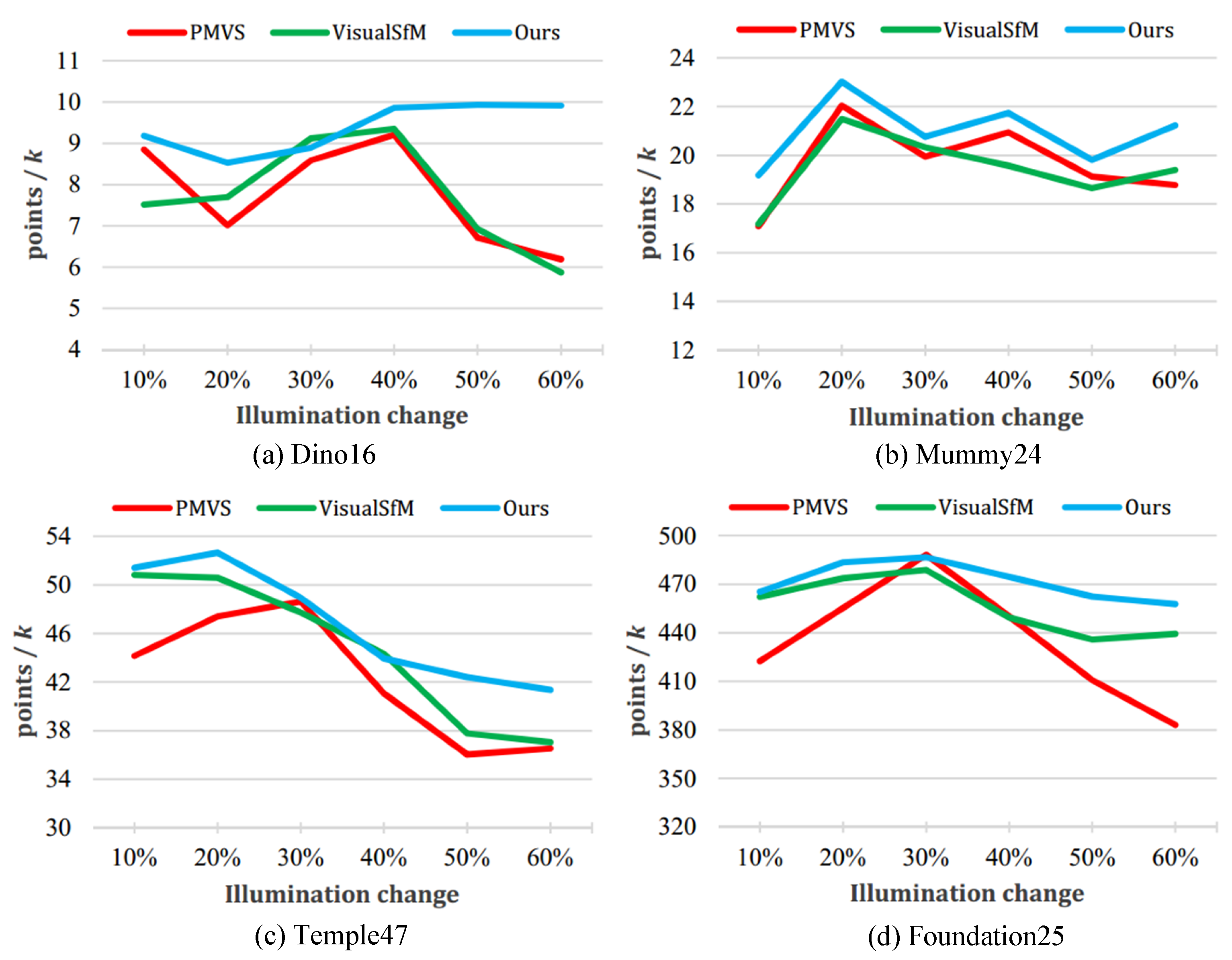
7.2.2. Differences in Illumination
7.3. Quantitative Evaluations
7.3.1. Completeness and Accuracy
7.3.2. Parameters
7.4. Discussion
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Huang, F.; Yang, H.; Tan, X.; Peng, S.; Tao, J.; Peng, S. Fast Reconstruction of 3D Point Cloud Model Using Visual SLAM on Embedded UAV Development Platform. Remote Sens. 2020, 12, 3308. [Google Scholar] [CrossRef]
- Hu, S.R.; Li, Z.Y.; Wang, S.H.; Ai, M.Y.; Hu, Q.W. A Texture Selection Approach for Cultural Artifact 3D Reconstruction Considering Both Geometry and Radiation Quality. Remote Sens. 2020, 12, 2521. [Google Scholar] [CrossRef]
- McCulloch, J.; Green, R. Conductor Reconstruction for Dynamic Line Rating Using Vehicle-Mounted LiDAR. Remote Sens. 2020, 12, 3718. [Google Scholar] [CrossRef]
- Snavely, N.; Seitz, S.M.; Szeliski, R. Modeling the World from Internet Photo Collections. Int. J. Comput. Vis. 2008, 80, 189–210. [Google Scholar] [CrossRef]
- Furukawa, Y.; Curless, B.; Seitz, S.M.; Szeliski, R. Towards Internet-scale multi-view stereo. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 1434–1441. [Google Scholar]
- Yang, Y.; Liang, Q.; Niu, L.; Zhang, Q. Belief propagation stereo matching algorithm using ground control points. In Proceedings of the SPIE—The International Society for Optical Engineering, San Diego, CA, USA, 17–21 August 2014; Volume 9069, pp. 90690W-1–90690W-7. [Google Scholar]
- Furukawa, Y. Multi-View Stereo: A Tutorial. Found. Trends Comput. Graph. Vis. 2015, 9, 1–148. [Google Scholar] [CrossRef]
- Wu, C. VisualSFM: A Visual Structure From Motion System 2012. [Online]. Available online: http://homes.cs.washington.edu/~ccwu/vsfm (accessed on 31 July 2019).
- Wu, P.; Liu, Y.; Ye, M.; Li, J.; Du, S. Fast and Adaptive 3D Reconstruction With Extensively High Completeness. IEEE Trans. Multimed. 2017, 19, 266–278. [Google Scholar] [CrossRef]
- Schonberger, J.L.; Radenovic, F.; Chum, O.; Frahm, J.M. From single image query to detailed 3D reconstruction. In Proceedings of the Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 5126–5134. [Google Scholar]
- Huang, Q.; Wang, H.; Koltun, V. Single-view reconstruction via joint analysis of image and shape collections. ACM Trans. Graph. 2015, 34, 87. [Google Scholar] [CrossRef]
- Yan, F.; Gong, M.; Cohen-Or, D.; Deussen, O.; Chen, B. Flower reconstruction from a single photo. Comput. Graph. Forum 2014, 33, 439–447. [Google Scholar] [CrossRef]
- Chai, M.L.; Luo, L.J.; Sunkavalli, K.; Carr, N.; Hadap, S.; Zhou, K. High-quality hair modeling from a single portrait photo. ACM Trans. Graph. 2015, 34, 204. [Google Scholar] [CrossRef]
- Eigen, D.; Puhrsch, C.; Fergus, R. Depth map prediction from a single image using a multi-scale deep network. In Proceedings of the International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 2366–2374. [Google Scholar]
- Li, F.; Sekkati, H.; Deglint, J.; Scharfenberger, C.; Lamm, M.; Clausi, D.; Zelek, J.; Wong, A. Simultaneous Projector-Camera Self-Calibration for Three-Dimensional Reconstruction and Projection Mapping. IEEE Trans. Comput. Imaging 2017, 3, 74–83. [Google Scholar] [CrossRef]
- Fraser, C.S. Automatic Camera Calibration in Close Range Photogrammetry. Photogramm. Eng. Remote. Sens. 2013, 79, 381–388. [Google Scholar] [CrossRef]
- Li, Y.; Wang, S.; Tian, Q.; Ding, X. A survey of recent advances in visual feature detection. Neurocomputing 2015, 149, 736–751. [Google Scholar] [CrossRef]
- Dehais, J.; Anthimopoulos, M.; Shevchik, S.; Mougiakakou, S. Two-View 3D Reconstruction for Food Volume Estimation. IEEE Trans. Multimed. 2017, 19, 1090–1099. [Google Scholar] [CrossRef]
- Seitz, S.M.; Curless, B.; Diebel, J.; Scharstein, D.; Szeliski, R. A Comparison and Evaluation of Multi-View Stereo Reconstruction Algorithms. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, New York, NY, USA, 17–22 June 2006; pp. 519–528. [Google Scholar]
- Alexiadis, D.S.; Zarpalas, D.; Daras, P. Real-Time, Full 3D Reconstruction of Moving Foreground Objects From Multiple Consumer Depth Cameras. IEEE Trans. Multimed. 2013, 15, 339–358. [Google Scholar] [CrossRef]
- Bradley, D.; Boubekeur, T.; Heidrich, W. Accurate multi-view reconstruction using robust binocular stereo and surface meshing. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Liu, Y.; Cao, X.; Dai, Q.; Xu, W. Continuous depth estimation for multi-view stereo. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 2121–2128. [Google Scholar]
- Li, Z.; Wang, K.; Meng, D.; Xu, C. Multi-view stereo via depth map fusion: A coordinate decent optimization method. Neurocomputing 2016, 178, 46–61. [Google Scholar] [CrossRef]
- Gargallo, P.; Sturm, P. Bayesian 3D Modeling from Images Using Multiple Depth Maps. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2005), San Diego, CA, USA, 20–25 June 2005; Volume 2, pp. 885–891. [Google Scholar]
- Fan, H.; Kong, D.; Li, J. Reconstruction of high-resolution Depth Map using Sparse Linear Model. In Proceedings of the International Conference on Intelligent Systems Research and Mechatronics Engineering, Zhengzhou, China, 11–13 April 2015; pp. 283–292. [Google Scholar]
- Lasang, P.; Shen, S.M.; Kumwilaisak, W. Combining high resolution color and depth images for dense 3D reconstruction. In Proceedings of the IEEE Fourth International Conference on Consumer Electronics—Berlin, Berlin, Germany, 7–10 September 2014; pp. 331–334. [Google Scholar]
- Lhuillier, M.; Quan, L. Match propagation for image-based modeling and rendering. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 1140–1146. [Google Scholar] [CrossRef]
- Habbecke, M.; Kobbelt, L. A Surface-Growing Approach to Multi-View Stereo Reconstruction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, CVPR ’07, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar]
- Zhang, Z.; Shan, Y. A Progressive Scheme for Stereo Matching. In Revised Papers from Second European Workshop on 3D Structure from Multiple Images of Large-Scale Environments; Springer: Berlin/Heidelberg, Germany, 2000; pp. 68–85. [Google Scholar]
- Cech, J.; Sara, R. Efficient Sampling of Disparity Space for Fast In addition, Accurate Matching. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, CVPR ’07, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar]
- Goesele, M.; Snavely, N.; Curless, B.; Hoppe, H.; Seitz, S.M. Multi-View Stereo for Community Photo Collections. In Proceedings of the IEEE International Conference on Computer Vision, Rio de Janeiro, Brazil, 14–21 October 2007; pp. 1–8. [Google Scholar]
- Snavely, N.; Seitz, S.M.; Szeliski, R. Photo Tourism: Exploring Photo Collections in 3D. In ACM SIGGRAPH; ACM: New York, NY, USA, 2006; pp. 835–846. [Google Scholar]
- Furukawa, Y.; Ponce, J. Accurate, Dense, and Robust Multi-View Stereopsis. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1362–1376. [Google Scholar] [CrossRef] [PubMed]
- Tanskanen, P.; Kolev, K.; Meier, L.; Camposeco, F.; Saurer, O.; Pollefeys, M. Live Metric 3D Reconstruction on Mobile Phones. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 65–72. [Google Scholar]
- Snavely, N. Bundler: Structure from Motion (SfM) for Unordered Image Collections. July 2010. [Online]. Available online: http://phototour.cs.washington.edu/bundler (accessed on 20 June 2019).
- Han, X.; Laga, H.; Bennamoun, M. Image-based 3D Object Reconstruction: State-of-the-Art and Trends in the Deep Learning Era. IEEE Trans. Pattern Anal. Mach. Intell. (Early Access) 2019. [Google Scholar] [CrossRef] [PubMed]
- Park, J.J.; Florence, P.; Straub, J.; Newcombe, R.; Lovegrove, S. DeepSDF: Learning Continuous Signed Distance Functions for Shape Representation. In Proceedings of the IEEE CVPR, Long Beach, CA, USA, 15–20 June 2019; pp. 165–174. [Google Scholar]
- Riegler, G.; Ulusoy, A.O.; Geiger, A. OctNet: Learning deep 3D representations at high resolutions. In Proceedings of the IEEE CVPR, Honolulu, HI, USA, 21–26 July 2017; Volume 3. [Google Scholar]
- Nie, Y.Y.; Han, X.G.; Guo, S.H.; Zheng, Y.; Chang, J.; Zhang, J.J. Total3DUnderstanding: Joint Layout, Object Pose and Mesh Reconstruction for Indoor Scenes from a Single Image. In Proceedings of the CVPR, Seattle, WA, USA, 14–19 June 2020. [Google Scholar]
- Pontes, J.K.; Kong, C.; Sridharan, S.; Lucey, S.; Eriksson, A.; Fookes, C. Image2Mesh: A Learning Framework for Single Image 3D Reconstruction. In Asian Conference on Computer Vision; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Li, K.; Pham, T.; Zhan, H.; Reid, I. Efficient dense point cloud object reconstruction using deformation vector fields. In Proceedings of the ECCV, Munich, Germany, 8–14 September 2018; pp. 497–513. [Google Scholar]
- Wang, J.; Sun, B.; Lu, Y. MVPNet: Multi-View Point Re-gression Networks for 3D Object Reconstruction from A Single Image. Proc. AAAI Conf. Artif. Intell. 2018, 33, 8949–8956. [Google Scholar] [CrossRef]
- Mandikal, P.; Murthy, N.; Agarwal, M.; Babu, R.V. 3D-LMNet: Latent Embedding Matching for Accurate and Diverse 3D Point Cloud Reconstruction from a Single Image. In Proceedings of the BMVC, Newcastle, UK, 3–6 September 2018; pp. 662–674. [Google Scholar]
- Jiang, L.; Shi, S.; Qi, X.; Jia, J. GAL: Geometric Adversarial Loss for Single-View 3D-Object Reconstruction. In Proceedings of the ECCV, Munich, Germany, 8–14 September 2018. [Google Scholar]
- Insafutdinov, E.; Dosovitskiy, A. Unsupervised learning of shape and pose with differentiable point clouds. In Proceedings of the NIPS, Montreal, QC, Canada, 3–8 December 2018; pp. 2802–2812. [Google Scholar]
- Fan, H.; Su, H.; Guibas, L. A point set generation network for 3D object reconstruction from a single image. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, CVPR ’17, Honolulu, HI, USA, 21–26 July 2017; Volume 38. [Google Scholar]
- Tatarchenko, M.; Dosovitskiy, A.; Brox, T. Multi-view 3D models from single images with a convolutional network. In Proceedings of the ECCV, Amsterdam, The Netherlands, 11–14 October 2016; pp. 322–337. [Google Scholar]
- Lin, C.H.; Kong, C.; Lucey, S. Learning Efficient Point Cloud Generation for Dense 3D Object Reconstruction. In Proceedings of the AAAI, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Triggs, B.; Mclauchlan, P.F.; Hartley, R.I.; Fitzgibbon, A.W. Bundle Adjustment—A Modern Synthesis. In Proceedings of the ICCV ’99 Proceedings of the International Workshop on Vision Algorithms: Theory and Practice, Corfu, Greece, 21–22 September 1999; pp. 298–372.
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Robot Vision Group, National Laboratory of Pattern Recognition Institute of Automation, Chinese Academy of Sciences. [Online]. Available online: http://vision.ia.ac.cn/data/ (accessed on 15 December 2020).
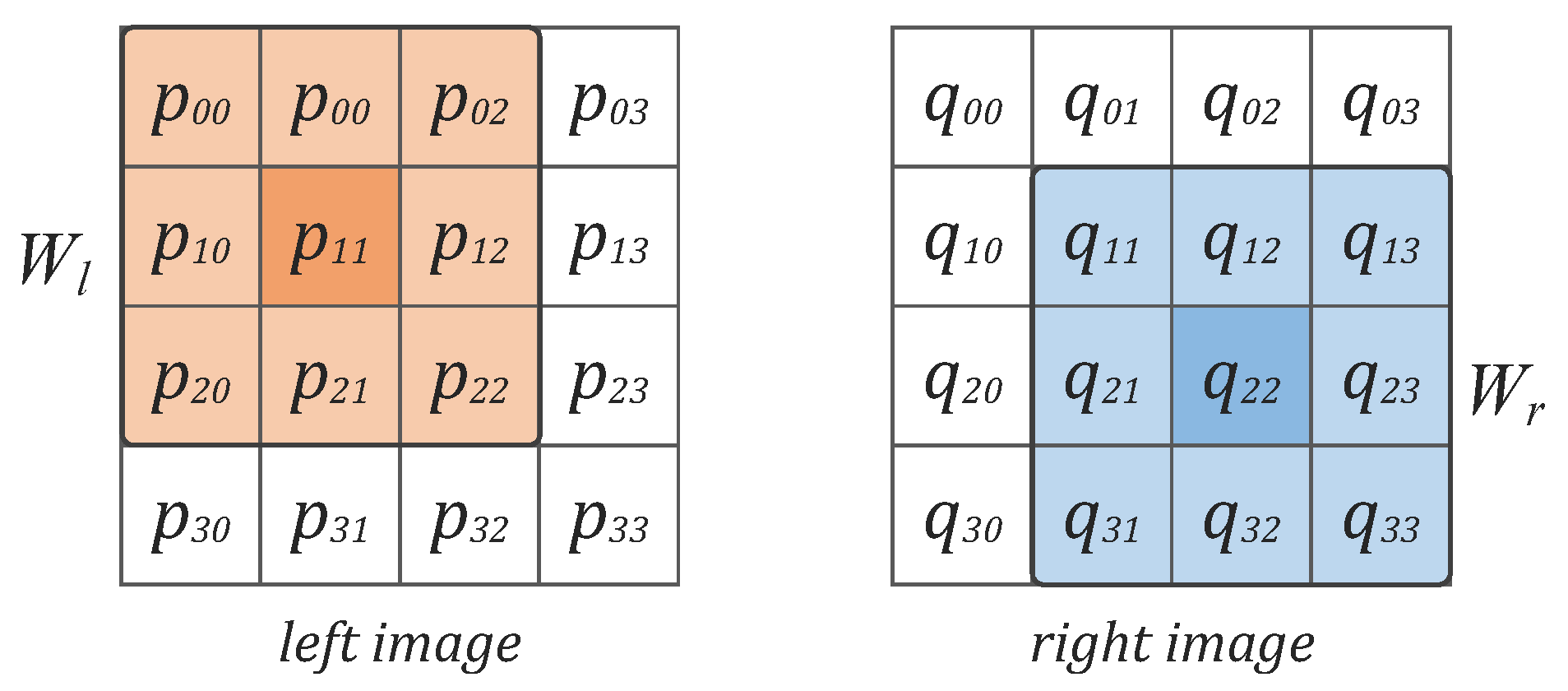






| Image Sequences | Retrieved Points | |||
|---|---|---|---|---|
| Name | No. | Resolution | Feature Diffusion | Patch Diffusion |
| Dino16 | 16 | 640 × 480 | 7329 | 8834 |
| Dino48 | 48 | 640 × 480 | 6369 | 9694 |
| Dino363 | 363 | 640 × 480 | 21,679 | 33,869 |
| Temple16 | 16 | 480 × 640 | 5936 | 8458 |
| Temple47 | 26 | 480 × 640 | 15,106 | 20720 |
| Mummy24 | 24 | 1600 × 1100 | 36,384 | 48,272 |
| Fountain25 | 25 | 3072 × 2048 | 355,330 | 463,935 |
| Stone39 | 39 | 3024 × 4032 | 469,342 | 624,971 |
| Sculpture58 | 58 | 2592 × 1728 | 600,217 | 997,770 |
| Statue70 | 70 | 1920 × 1080 | 50,972 | 75,688 |
| Image Sequences | Retrieved Points | Time (s) | ||||||
|---|---|---|---|---|---|---|---|---|
| Name | No. | Resolution | PMVS | VisualSfM | Ours | PMVS | VisualSfM | Ours |
| Dino16 | 16 | 640 × 480 | 8138 | 9036 | 8834 | 6 | 5 | 6 |
| Dino48 | 48 | 640 × 480 | 9484 | 9528 | 9694 | 8 | 9 | 11 |
| Dino363 | 363 | 640 × 480 | 32,030 | 34,462 | 33,869 | 51 | 63 | 60 |
| Temple16 | 16 | 480 × 640 | 6997 | 7868 | 8458 | 5 | 7 | 6 |
| Temple47 | 26 | 480 × 640 | 17,735 | 17,773 | 20,720 | 19 | 20 | 23 |
| Mummy24 | 24 | 1600 × 1100 | 40,348 | 45,548 | 48,272 | 26 | 36 | 31 |
| Fountain25 | 25 | 3072 × 2048 | 447,552 | 455,511 | 463,935 | 323 | 418 | 310 |
| Stone39 | 39 | 3024 × 4032 | 618,829 | 562,521 | 624,971 | 756 | 890 | 786 |
| Sculpture58 | 58 | 2592 × 1728 | 1,018,650 | 924,024 | 997,770 | 780 | 912 | 810 |
| Statue70 | 70 | 1920 × 1080 | 61,311 | 67,825 | 75,688 | 87 | 101 | 97 |
| Qinghuamen | Shengkelou | Shengkelou | |||||||
|---|---|---|---|---|---|---|---|---|---|
| (68 Images, 4368 × 2912) | (102 Images, 4368 × 2912) | (51 Images, 4368 × 2912) | |||||||
| Method | Points | Comp. | Acc. | Points | Comp. | Acc. | Points | Comp. | Acc. |
| Ours | 1,283,729 | 96.3% | 0.001346 | 2,446,138 | 97.2% | 0.004367 | 1,592,848 | 96.2% | 0.004732 |
| PMVS | 1,270,131 | 96.1% | 0.001379 | 2,382,383 | 97.0% | 0.005221 | 1,592,127 | 95.6% | 0.005696 |
| VisualSfM | 1,237,815 | 96.0% | 0.001327 | 2,226,646 | 96.8% | 0.004387 | 1,535,094 | 94.9% | 0.004706 |
| Parameter Setting | Qinghuamen | Shengkelou | Shengkelou | |||
|---|---|---|---|---|---|---|
| (68 Images) | (102 Images) | (51 Images) | ||||
| Comp. | Acc. | Comp. | Acc. | Comp. | Acc. | |
| = 0.3, = 0.8, = 0.6, = 0.7, = 1.0, = 2.25 | 96.0% | 0.001419 | 97.1% | 0.004916 | 96.1% | 0.004759 |
| = 0.5, = 0.8, = 0.6, = 0.7, = 1.0, = 2.25 | 96.3% | 0.001346 | 97.2% | 0.004367 | 96.1% | 0.004732 |
| = 0.5, = 0.7, = 0.5, = 0.6, = 1.0, = 2.25 | 96.4% | 0.001442 | 96.9% | 0.005034 | 96.2% | 0.004914 |
| = 0.5, = 0.9, = 0.7, = 0.8, = 1.0, = 2.25 | 95.4% | 0.001389 | 96.4% | 0.004947 | 95.3% | 0.004753 |
| = 0.5, = 0.8, = 0.6, = 0.7, = 0.5, = 2.25 | 96.1% | 0.001394 | 96.9% | 0.004257 | 95.9% | 0.004907 |
| = 0.5, = 0.8, = 0.6, = 0.7, = 1.0, = 1.5 | 96.1% | 0.001380 | 96.2% | 0.003959 | 95.6% | 0.004824 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, N.; Huang, L.; Wang, Q.; Liu, G. An Improved Algorithm Robust to Illumination Variations for Reconstructing Point Cloud Models from Images. Remote Sens. 2021, 13, 567. https://doi.org/10.3390/rs13040567
Luo N, Huang L, Wang Q, Liu G. An Improved Algorithm Robust to Illumination Variations for Reconstructing Point Cloud Models from Images. Remote Sensing. 2021; 13(4):567. https://doi.org/10.3390/rs13040567
Chicago/Turabian StyleLuo, Nan, Ling Huang, Quan Wang, and Gang Liu. 2021. "An Improved Algorithm Robust to Illumination Variations for Reconstructing Point Cloud Models from Images" Remote Sensing 13, no. 4: 567. https://doi.org/10.3390/rs13040567
APA StyleLuo, N., Huang, L., Wang, Q., & Liu, G. (2021). An Improved Algorithm Robust to Illumination Variations for Reconstructing Point Cloud Models from Images. Remote Sensing, 13(4), 567. https://doi.org/10.3390/rs13040567








