Deep Learning Forecasts of Soil Moisture: Convolutional Neural Network and Gated Recurrent Unit Models Coupled with Satellite-Derived MODIS, Observations and Synoptic-Scale Climate Index Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Theoretical Frameworks
2.1.1. Convolutional Neural Network
2.1.2. Gated Recurrent Unit Network
2.1.3. Hybrid CNN–GRU. Neural Network
2.1.4. Complete Ensemble Empirical Mode Decomposition with Adaptive Noise (CEEMDAN)
- Step 1: The decomposition of p-realizations of using EMD to develop their first intrinsic approach, as explained according to the equation:
- Step 2: Putting k = 1, the 1st residue is computed following Equation (7).
- Step 3: Putting k = 2, the 2nd residual is obtained as:
- Step 4: Setting k = 2… K calculates the kth residue as:
- Step 5: Now we decompose the realisations until their first model of EMD is reached; here, the (k + 1) is:
- Step 6: Now the k value is incremented, and steps 4–6 are repeated. Consequently, the final residue is achieved:
2.1.5. Feature Selection: Neighbourhood Component Analysis
3. Study Area and Data
3.1. Study Area and Description of Predictive Model Development Dataset
3.1.1. MODIS Satellite Dataset
3.1.2. Scientific Information for Landowners (SILO) Dataset
3.1.3. Climate Indices
3.2. Predictive Model Development
3.2.1. Feature Selection
3.2.2. Hybrid Deep Learning Algorithm Implementation
3.2.3. Predictive Model Evaluation
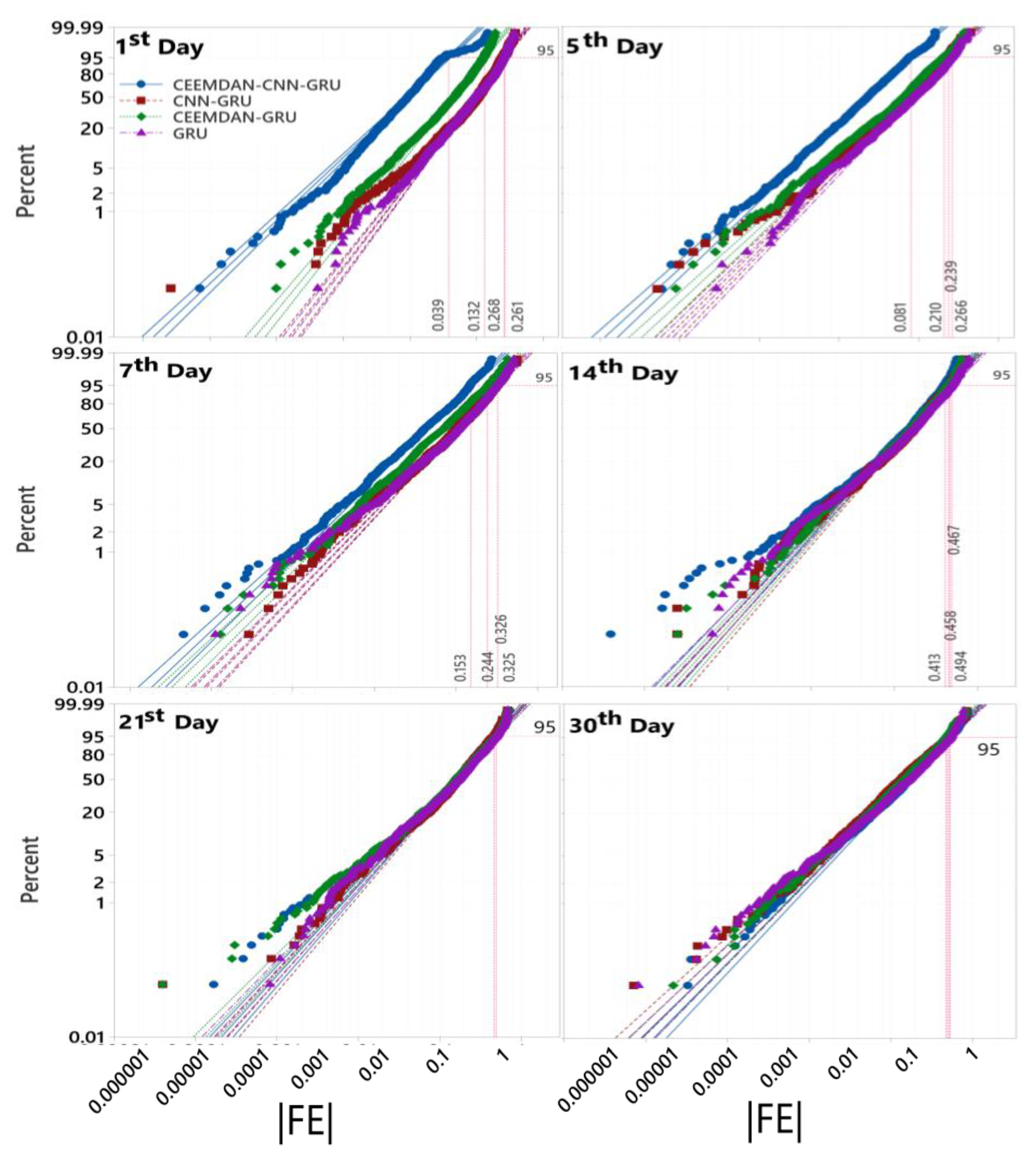
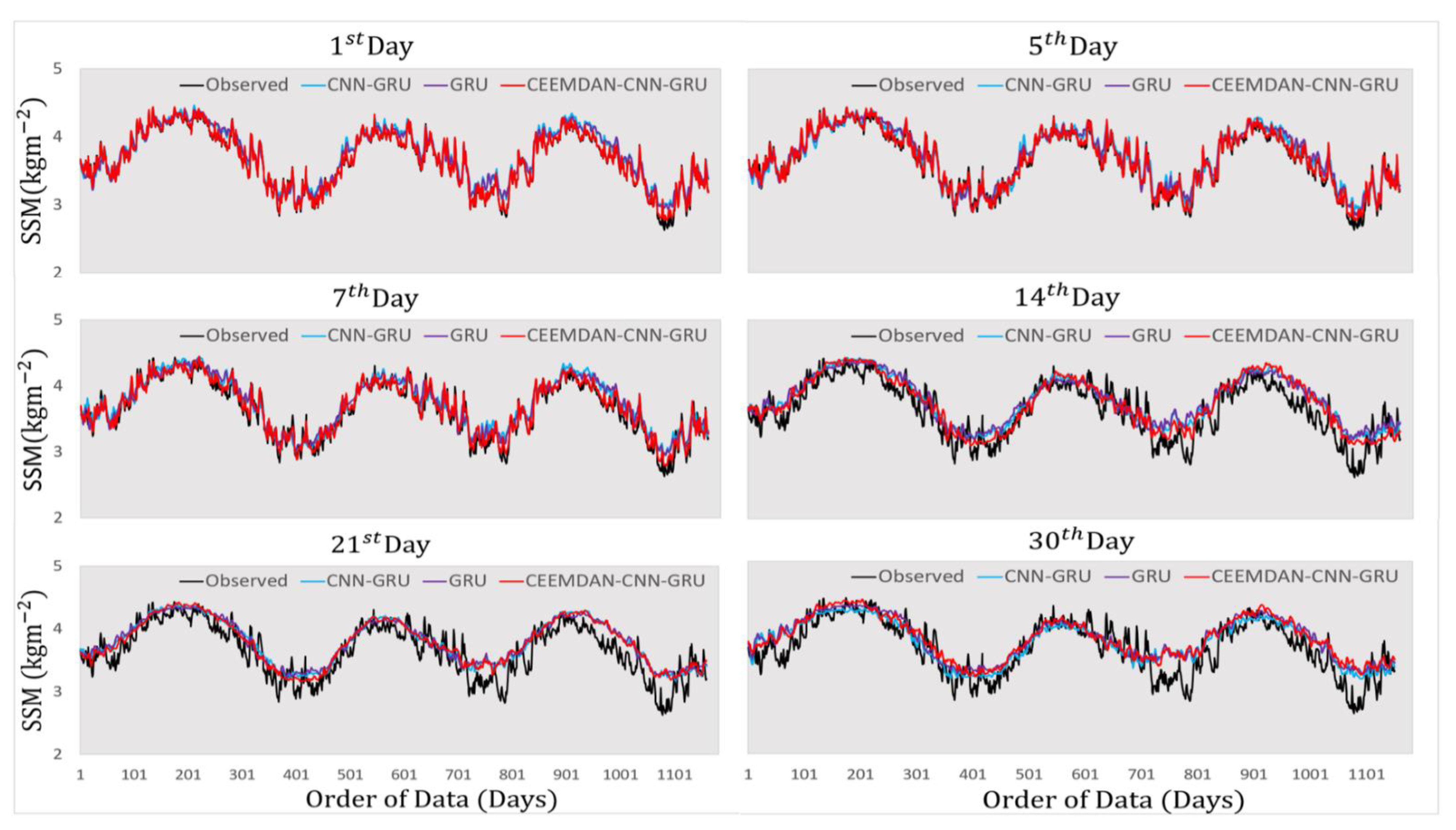
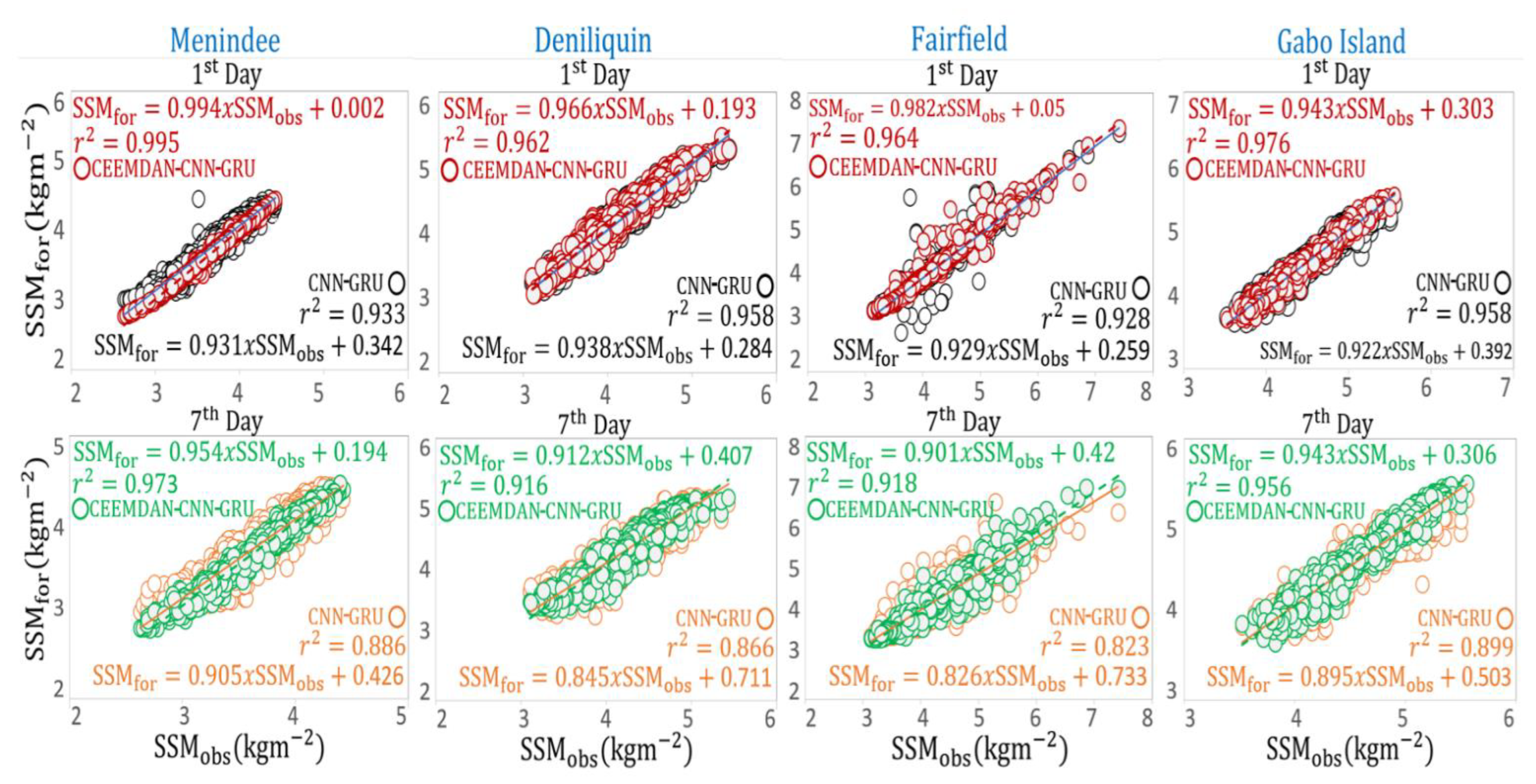
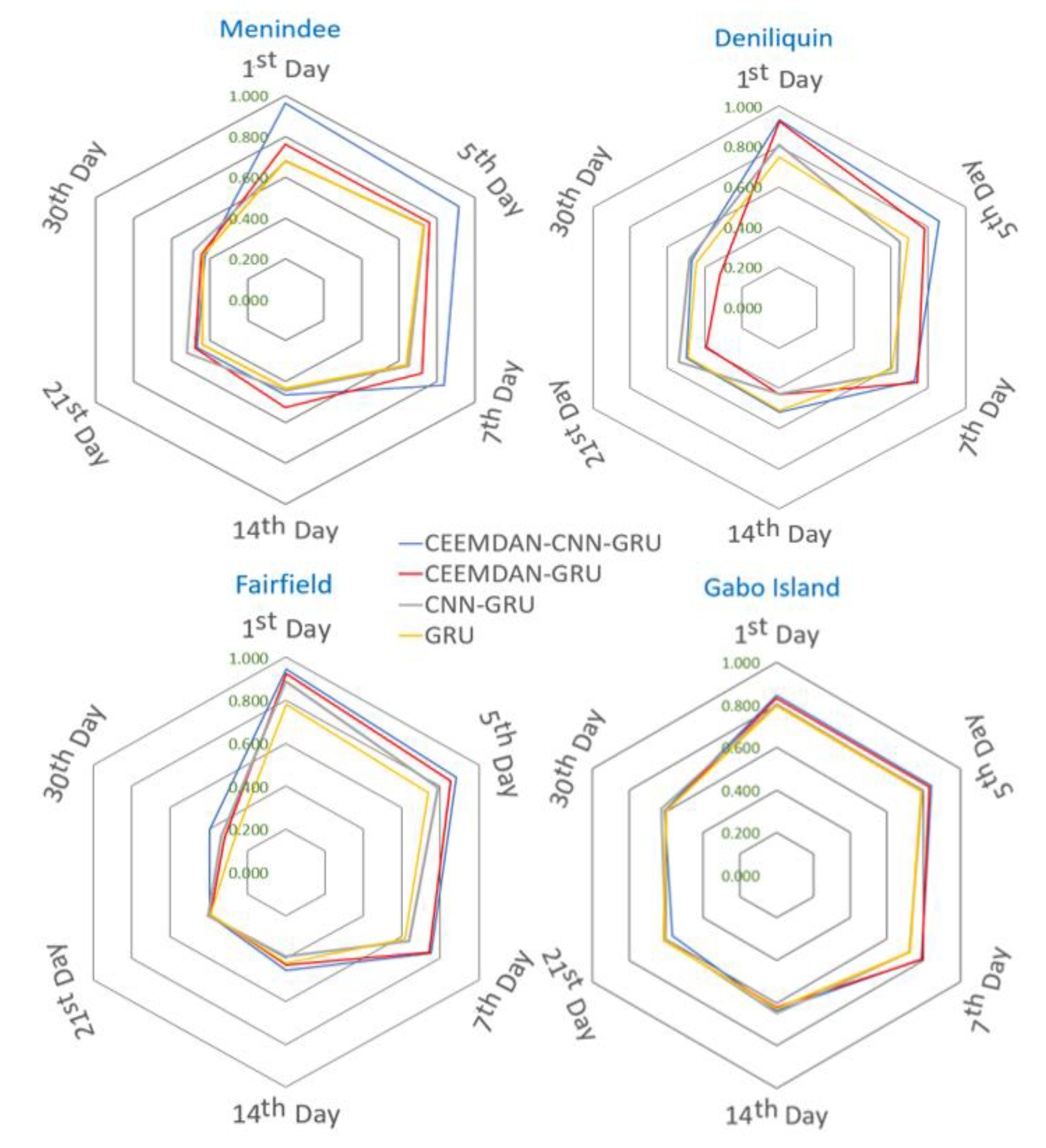
4. Results
5. Discussions
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Van Loon, A.F.; Laaha, G. Hydrological drought severity explained by climate and catchment characteristics. J. Hydrol. 2015, 526, 3–14. [Google Scholar] [CrossRef]
- Brocca, L.; Melone, F.; Moramarco, T.; Morbidelli, R. Spatial—temporal variability of soil moisture and its estimation across scales. Water Resour. Res. 2010, 46, W02516. [Google Scholar] [CrossRef]
- Brocca, L.; Ciabatta, L.; Massari, C.; Camici, S.; Tarpanelli, A. Soil Moisture for Hydrological Applications: Open Questions and New Opportunities. Water 2017, 9, 140. [Google Scholar] [CrossRef]
- Chang, X.; Zhao, W.; Zeng, F. Crop evapotranspiration-based irrigation management during the growing season in the arid region of northwestern China. Environ. Monit. Assess. 2015, 187, 699. [Google Scholar] [CrossRef]
- Gill, M.K.; Asefa, T.; Kemblowski, M.W.; McKee, M. Soil moisture prediction using support vector machines 1. JAWRA J. Am. Water Resour. Assoc. 2006, 42, 1033–1046. [Google Scholar] [CrossRef]
- Akbari Asanjan, A.; Yang, T.; Hsu, K.; Sorooshian, S.; Lin, J.; Peng, Q. Short-Term Precipitation Forecast Based on the PERSIANN System and LSTM Recurrent Neural Networks. J. Geophys. Res. Atmos. 2018, 123. [Google Scholar] [CrossRef]
- Tripathi, S.; Srinivas, V.V.; Nanjundiah, R.S. Downscaling of precipitation for climate change scenarios: A support vector machine approach. J. Hydrol. 2006, 330, 621–640. [Google Scholar] [CrossRef]
- Yang, L.; Feng, Q.; Yin, Z.; Wen, X.; Deo, R.C.; Si, J.; Li, C. Application of multivariate recursive nesting bias correction, multiscale wavelet entropy and AI-based models to improve future precipitation projection in upstream of the Heihe River, Northwest China. Theor. Appl. Climatol. 2018, 137, 323–339. [Google Scholar] [CrossRef]
- Nguyen-Huy, T.; Deo, R.C.; An-Vo, D.-A.; Mushtaq, S.; Khan, S. Copula-statistical precipitation forecasting model in Australia’s agro-ecological zones. Agric. Water Manag. 2017, 191, 153–172. [Google Scholar] [CrossRef]
- Deo, R.C.; Şahin, M. Application of the extreme learning machine algorithm for the prediction of monthly Effective Drought Index in eastern Australia. Atmos. Res. 2015, 153, 512–525. [Google Scholar] [CrossRef]
- Prasad, R.; Deo, R.C.; Li, Y.; Maraseni, T. Input selection and performance optimisation of ANN-based streamflow forecasts in the drought-prone Murray Darling Basin region using IIS and MODWT algorithm. Atmos. Res. 2017, 197, 42–63. [Google Scholar] [CrossRef]
- Ahmed, A.M.; Shah, S.M.A. Application of artificial neural networks to predict peak flow of Surma River in Sylhet Zone of Bangladesh. Int. J. Water 2017, 11, 363–375. [Google Scholar] [CrossRef]
- Hu, C.; Wu, Q.; Li, H.; Jian, S.; Li, N.; Lou, Z. Deep Learning with a Long Short-Term Memory Networks Approach for Rainfall-Runoff Simulation. Water 2018, 10, 1543. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–runoff modelling using Long Short-Term Memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef]
- Arto, I.; Garcia-Muros, X.; Cazcarro, I.; Gonzalez-Eguino, M.; Markandya, A.; Hazra, S. The socioeconomic future of deltas in a changing environment. Sci. Total Environ. 2019, 648, 1284–1296. [Google Scholar] [CrossRef] [PubMed]
- Le, H.; Lee, J. Application of Long Short-Term Memory (LSTM) Neural Network for Flood Forecasting. Water 2019, 11, 1387. [Google Scholar] [CrossRef]
- Ahmed, A.M.; Deo, R.C.; Ghahramani, A.; Raj, N.; Feng, Q.; Yin, Z.; Yang, L. LSTM integrated with Boruta-random forest optimiser for soil moisture estimation under RCP4. 5 and RCP8. 5 global warming scenarios. Stoch. Environ. Res. Risk Assess. 2021, 1–31. [Google Scholar] [CrossRef]
- Gedefaw, M.; Hao, W.; Denghua, Y.; Girma, A. Variable selection methods for water demand forecasting in Ethiopia: Case study Gondar town. Cogent Environ. Sci. 2018, 4, 1537067. [Google Scholar] [CrossRef]
- Mouatadid, S.; Adamowski, J. Using extreme learning machines for short-term urban water demand forecasting. Urban Water J. 2017, 14, 630–638. [Google Scholar] [CrossRef]
- Ahmed, A.A.M. Prediction of dissolved oxygen in Surma River by biochemical oxygen demand and chemical oxygen demand using the artificial neural networks (ANNs). J. King Saud Univ. Eng. Sci. 2017, 29, 151–158. [Google Scholar] [CrossRef]
- Ahmed, A.A.M.; Shah, S.M.A. Application of adaptive neuro-fuzzy inference system (ANFIS) to estimate the biochemical oxygen demand (BOD) of Surma River. J. King Saud Univ. Eng. Sci. 2017, 29, 237–243. [Google Scholar] [CrossRef]
- Huang, C.; Li, L.; Ren, S.; Zhou, Z. Research of soil moisture content forecast model based on genetic algorithm BP neural network. In Proceedings of the International Conference on Computer and Computing Technologies in Agriculture, Nanchang, China, 22–25 October 2010; pp. 309–316. [Google Scholar]
- Prasad, R.; Deo, R.C.; Li, Y.; Maraseni, T. Soil moisture forecasting by a hybrid machine learning technique: ELM integrated with ensemble empirical mode decomposition. Geoderma 2018, 330, 136–161. [Google Scholar] [CrossRef]
- 24. Ghimire, S.; Deo, R.C.; Raj, N.; Mi, J. Deep Learning Neural Networks Trained with MODIS Satellite-Derived Predictors for Long-Term Global Solar Radiation Prediction. Energies 2019, 12, 2407. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, Y.; Zhang, X.; Ye, M.; Yang, J. Developing a Long Short-Term Memory (LSTM) based model for predicting water table depth in agricultural areas. J. Hydrol. 2018, 561, 918–929. [Google Scholar] [CrossRef]
- Le, X.-H.; Ho, H.V.; Lee, G. Application of gated recurrent unit (GRU) network for forecasting river water levels affected by tides. In Proceedings of the International Conference on Asian and Pacific Coasts, Hanoi, Vietnam, 25–28 September 2019; pp. 673–680. [Google Scholar]
- Gao, S.; Huang, Y.; Zhang, S.; Han, J.; Wang, G.; Zhang, M.; Lin, Q. Short-term runoff prediction with GRU and LSTM networks without requiring time step optimisation during sample generation. J. Hydrol. 2020, 589, 125188. [Google Scholar] [CrossRef]
- Ghimire, S.; Deo, R.C.; Raj, N.; Mi, J. Deep solar radiation forecasting with convolutional neural network and long short-term memory network algorithms. Appl. Energy 2019, 253, 113541. [Google Scholar] [CrossRef]
- Deo, R.C.; Sahin, M. An extreme learning machine model for the simulation of monthly mean streamflow water level in eastern Queensland. Environ. Monit. Assess. 2016, 188, 90. [Google Scholar] [CrossRef] [PubMed]
- Nourani, V.; Komasi, M.; Mano, A. A multivariate ANN-wavelet approach for rainfall–runoff modeling. Water. Resour. Manag. 2009, 23, 2877–2894. [Google Scholar] [CrossRef]
- Nourani, V.; Baghanam, A.H.; Adamowski, J.; Kisi, O. Applications of hybrid wavelet–Artificial Intelligence models in hydrology: A review. J. Hydrol. 2014, 514, 358–377. [Google Scholar] [CrossRef]
- Deo, R.C.; Wen, X.; Qi, F. A wavelet-coupled support vector machine model for forecasting global incident solar radiation using limited meteorological dataset. Appl. Energy 2016, 168, 568–593. [Google Scholar] [CrossRef]
- Cornish, C.R.; Bretherton, C.S.; Percival, D.B. Maximal overlap wavelet statistical analysis with application to atmospheric turbulence. Bound.-Layer Meteorol. 2006, 119, 339–374. [Google Scholar] [CrossRef]
- Rathinasamy, M.; Khosa, R.; Adamowski, J.; Ch, S.; Partheepan, G.; Anand, J.; Narsimlu, B. Wavelet-based multiscale performance analysis: An approach to assess and improve hydrological models. Water Resour. Res. 2014, 50, 9721–9737. [Google Scholar] [CrossRef]
- Di, C.; Yang, X.; Wang, X. A four-stage hybrid model for hydrological time series forecasting. PLoS ONE 2014, 9, e104663. [Google Scholar] [CrossRef] [PubMed]
- Prasad, R.; Deo, R.C.; Li, Y.; Maraseni, T. Weekly soil moisture forecasting with multivariate sequential, ensemble empirical mode decomposition and Boruta-random forest hybridiser algorithm approach. Catena 2019, 177, 149–166. [Google Scholar] [CrossRef]
- Seo, Y.; Kim, S. Hydrological Forecasting Using Hybrid Data-Driven Approach. Am. J. Appl. Sci. 2016, 13, 891–899. [Google Scholar] [CrossRef]
- Beltrán-Castro, J.; Valencia-Aguirre, J.; Orozco-Alzate, M.; Castellanos-Domínguez, G.; Travieso-González, C.M. Rainfall forecasting based on ensemble empirical mode decomposition and neural networks. In Proceedings of the International Work-Conference on Artificial Neural Networks, Tenerife, Spain, 12–14 June 2013; pp. 471–480. [Google Scholar]
- Jiao, G.; Guo, T.; Ding, Y. A new hybrid forecasting approach applied to hydrological data: A case study on precipitation in Northwestern China. Water 2016, 8, 367. [Google Scholar] [CrossRef]
- Ouyang, Q.; Lu, W.; Xin, X.; Zhang, Y.; Cheng, W.; Yu, T. Monthly rainfall forecasting using EEMD-SVR based on phase-space reconstruction. Water Resour. Manag. 2016, 30, 2311–2325. [Google Scholar] [CrossRef]
- Ali, M.; Deo, R.C.; Maraseni, T.; Downs, N.J. Improving SPI-derived drought forecasts incorporating synoptic-scale climate indices in multi-phase multivariate empirical mode decomposition model hybridized with simulated annealing and kernel ridge regression algorithms. J. Hydrol. 2019, 576, 164–184. [Google Scholar] [CrossRef]
- Adarsh, S.; Sanah, S.; Murshida, K.; Nooramol, P. Scale dependent prediction of reference evapotranspiration based on Multi-Variate Empirical mode decomposition. Ain Shams Eng. J. 2018, 9, 1839–1848. [Google Scholar] [CrossRef]
- Hu, W.; Si, B.C. Soil water prediction based on its scale-specific control using multivariate empirical mode decomposition. Geoderma 2013, 193, 180–188. [Google Scholar] [CrossRef]
- Schepen, A.; Wang, Q.J.; Robertson, D. Evidence for Using Lagged Climate Indices to Forecast Australian Seasonal Rainfall. J. Clim. 2012, 25, 1230–1246. [Google Scholar] [CrossRef]
- Yuan, C.; Yamagata, T. Impacts of IOD, ENSO and ENSO Modoki on the Australian winter wheat yields in recent decades. Sci. Rep. 2015, 5, 1–8. [Google Scholar] [CrossRef]
- Risbey, J.S.; Pook, M.J.; McIntosh, P.C.; Wheeler, M.C.; Hendon, H.H. On the remote drivers of rainfall variability in Australia. Mon. Weather Rev. 2009, 137, 3233–3253. [Google Scholar] [CrossRef]
- Royce, F.S.; Fraisse, C.W.; Baigorria, G.A. ENSO classification indices and summer crop yields in the Southeastern USA. Agric. For. Meteorol. 2011, 151, 817–826. [Google Scholar] [CrossRef]
- Shuai, J.; Zhang, Z.; Sun, D.-Z.; Tao, F.; Shi, P. ENSO, climate variability and crop yields in China. Clim. Res. 2013, 58, 133–148. [Google Scholar] [CrossRef]
- Rashid, M.M.; Sharma, A.; Johnson, F. Multi-model drought predictions using temporally aggregated climate indicators. J. Hydrol. 2020, 581. [Google Scholar] [CrossRef]
- Nikolopoulos, E.I.; Anagnostou, E.N.; Borga, M. Using high-resolution satellite rainfall products to simulate a major flash flood event in northern Italy. J. Hydrometeorol. 2013, 14, 171–185. [Google Scholar] [CrossRef]
- Nikolopoulos, E.I.; Anagnostou, E.N.; Hossain, F.; Gebremichael, M.; Borga, M. Understanding the scale relationships of uncertainty propagation of satellite rainfall through a distributed hydrologic model. J. Hydrometeorol. 2010, 11, 520–532. [Google Scholar] [CrossRef]
- Yong, B.; Hong, Y.; Ren, L.L.; Gourley, J.J.; Huffman, G.J.; Chen, X.; Wang, W.; Khan, S.I. Assessment of evolving TRMM-based multisatellite real-time precipitation estimation methods and their impacts on hydrologic prediction in a high latitude basin. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Ghimire, S.; Deo, R.C.; Downs, N.J.; Raj, N. Self-adaptive differential evolutionary extreme learning machines for long-term solar radiation prediction with remotely-sensed MODIS satellite and Reanalysis atmospheric products in solar-rich cities. Remote Sens. Environ. 2018, 212, 176–198. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436. [Google Scholar] [CrossRef] [PubMed]
- Oehmcke, S.; Zielinski, O.; Kramer, O. Input quality aware convolutional LSTM networks for virtual marine sensors. Neurocomputing 2018, 275, 2603–2615. [Google Scholar] [CrossRef]
- Nunez, J.C.; Cabido, R.; Pantrigo, J.J.; Montemayor, A.S.; Velez, J.F. Convolutional neural networks and long short-term memory for skeleton-based human activity and hand gesture recognition. Pattern Recognit. 2018, 76, 80–94. [Google Scholar] [CrossRef]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE international conference on acoustics, speech and signal processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar]
- Prasad, R.; Deo, R.C.; Li, Y.; Maraseni, T. Ensemble committee-based data intelligent approach for generating soil moisture forecasts with multivariate hydro-meteorological predictors. Soil Tillage Res. 2018, 181, 63–81. [Google Scholar] [CrossRef]
- Wen, X.; Feng, Q.; Deo, R.C.; Wu, M.; Yin, Z.; Yang, L.; Singh, V.P. Two-phase extreme learning machines integrated with the complete ensemble empirical mode decomposition with adaptive noise algorithm for multi-scale runoff prediction problems. J. Hydrol. 2019, 570, 167–184. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E.; Chen, X. The multi-dimensional ensemble empirical mode decomposition method. Adv. Adapt. Data Anal. 2009, 1, 339–372. [Google Scholar] [CrossRef]
- Bowden, G.J.; Dandy, G.C.; Maier, H.R. Input determination for neural network models in water resources applications. Part 1—background and methodology. J. Hydrol. 2005, 301, 75–92. [Google Scholar] [CrossRef]
- Maier, H.R.; Jain, A.; Dandy, G.C.; Sudheer, K.P. Methods used for the development of neural networks for the prediction of water resource variables in river systems: Current status and future directions. Environ. Model. Softw. 2010, 25, 891–909. [Google Scholar] [CrossRef]
- Yang, W.; Wang, K.; Zuo, W. Neighborhood Component Feature Selection for High-Dimensional Data. JCP 2012, 7, 161–168. [Google Scholar] [CrossRef]
- Murray–Darling Basin Authority. Guide to the Proposed Basin Plan; Murray–Darling Basin Auth.: Canberra, Australia, 2010. [Google Scholar]
- Australian Bureau of Statistics. Household Use of Information Technology; Australia Bureau of Statistics: Canberra, Australia, 2010.
- Hijmans, R.J.; Cameron, S.E.; Parra, J.L.; Jones, P.G.; Jarvis, A. Very high resolution interpolated climate surfaces for global land areas. Int. J. Climatol. J. R. Meteorol. Soc. 2005, 25, 1965–1978. [Google Scholar] [CrossRef]
- ASRIS. The Australian Soil Resource Information System; Department of Agricuture, Fisheries and Forestry: Canberra, Australia, 2014. Available online: https://www.asris.csiro.au/ (accessed on 12 December 2020).
- BOM. Bureau of Meteorology. 2020. Available online: http://www.bom.gov.au/ (accessed on 31 December 2020).
- Deo, R.C.; Sahin, M. Forecasting long-term global solar radiation with an ANN algorithm coupled with satellite-derived (MODIS) land surface temperature (LST) for regional locations in Queensland. Renew. Sustain. Energy Rev. 2017, 72, 828–848. [Google Scholar] [CrossRef]
- Deo, R.C.; Şahin, M.; Adamowski, J.F.; Mi, J. Universally deployable extreme learning machines integrated with remotely sensed MODIS satellite predictors over Australia to forecast global solar radiation: A new approach. Renew. Sustain. Energy Rev. 2019, 104, 235–261. [Google Scholar] [CrossRef]
- Deo, R.C.; Syktus, J.I.; McAlpine, C.A.; Lawrence, P.J.; McGowan, H.A.; Phinn, S.R. Impact of historical land cover change on daily indices of climate extremes including droughts in eastern Australia. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Nguyen-Huy, T.; Deo, R.C.; Mushtaq, S.; An-Vo, D.-A.; Khan, S. Modeling the joint influence of multiple synoptic-scale, climate mode indices on Australian wheat yield using a vine copula-based approach. Eur. J. Agron. 2018, 98, 65–81. [Google Scholar] [CrossRef]
- Berrick, S.W.; Leptoukh, G.; Farley, J.D.; Rui, H. Giovanni: A web service workflow-based data visualization and analysis system. IEEE Trans. Geosci. Remote Sens. 2008, 47, 106–113. [Google Scholar] [CrossRef]
- Chen, C.; Jiang, H.; Zhang, Y.; Wang, Y. Investigating spatial and temporal characteristics of harmful Algal Bloom areas in the East China Sea using a fast and flexible method. In Proceedings of the 2010 18th International Conference on Geoinformatics, Beijing, China, 18–20 June 2010; pp. 1–4. [Google Scholar]
- Morshed, A.; Aryal, J.; Dutta, R. Environmental spatio-temporal ontology for the Linked open data cloud. In Proceedings of the 2013 12th IEEE International Conference on Trust, Security and Privacy in Computing and Communications, Melbourne, VIC, Australia, 16–18 July 2013; pp. 1907–1912. [Google Scholar]
- Trouet, V.; Van Oldenborgh, G.J. KNMI Climate Explorer: A web-based research tool for high-resolution paleoclimatology. Tree-Ring Res. 2013, 69, 3–13. [Google Scholar] [CrossRef]
- Adnan, M.; Rehman, N.; Sheikh, M.; Khan, A.; Mir, K.; Khan, M. Influence of natural forcing phenomena on precipitation of Pakistan. Pak. J. Meteorol. 2016, 12, 23–35. [Google Scholar]
- Philander, S.G.H. El Nino southern oscillation phenomena. Nature 1983, 302, 295–301. [Google Scholar] [CrossRef]
- Chiew, F.H.; Piechota, T.C.; Dracup, J.A.; McMahon, T.A. El Nino/Southern Oscillation and Australian rainfall, streamflow and drought: Links and potential for forecasting. J. Hydrol. 1998, 204, 138–149. [Google Scholar] [CrossRef]
- Madden, R.A.; Julian, P.R. Detection of a 40–50 day oscillation in the zonal wind in the tropical Pacific. J. Atmos. Sci. 1971, 28, 702–708. [Google Scholar] [CrossRef]
- Henley, B.J.; Gergis, J.; Karoly, D.J.; Power, S.; Kennedy, J.; Folland, C.K. A tripole index for the interdecadal Pacific oscillation. Clim. Dyn. 2015, 45, 3077–3090. [Google Scholar] [CrossRef]
- Troup, A. The ‘southern oscillation’. Q. J. R. Meteorol. Soc. 1965, 91, 490–506. [Google Scholar] [CrossRef]
- Ketkar, N. Introduction to keras. In Deep Learning with Python; Springer: Berlin/Heidelberg, Germany, 2017; pp. 97–111. [Google Scholar]
- Brownlee, J. Deep Learning with Python: Develop Deep Learning Models on Theano and TensorFlow Using Keras; Machine Learning Mastery: Vermont, VIC, Australia, 2016. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M. Tensorflow: A system for large-scale machine learning. In Proceedings of the 12th {USENIX} Symposium on Operating Systems Design and Implementation ({OSDI} 16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Jayalakshmi, T.; Santhakumaran, A. Statistical normalization and back propagation for classification. Int. J. Comput. Theory Eng. 2011, 3, 1793–8201. [Google Scholar]
- Maier, H.R.; Dandy, G.C. Neural networks for the prediction and forecasting of water resources variables: A review of modelling issues and applications. Environ. Model. Softw. 2000, 15, 101–124. [Google Scholar] [CrossRef]
- Deo, R.C.; Downs, N.; Parisi, A.V.; Adamowski, J.F.; Quilty, J.M. Very short-term reactive forecasting of the solar ultraviolet index using an extreme learning machine integrated with the solar zenith angle. Environ. Res. 2017, 155, 141–166. [Google Scholar] [CrossRef]
- Arhami, M.; Kamali, N.; Rajabi, M.M. Predicting hourly air pollutant levels using artificial neural networks coupled with uncertainty analysis by Monte Carlo simulations. Environ. Sci. Pollut. Res. 2013, 20, 4777–4789. [Google Scholar] [CrossRef]
- Jekabsons, G. ARESLab: Adaptive Regression Splines Toolbox for Matlab/Octave. 2011. Available online: http://www.cs.rtu.lv/jekabsons (accessed on 18 January 2021).
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Willmott, C.J.; Robeson, S.M.; Matsuura, K. A refined index of model performance. Int. J. Climatol. 2012, 32, 2088–2094. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. A refined index of model performance: A rejoinder. Int. J. Climatol. 2013, 33, 1053–1056. [Google Scholar] [CrossRef]
- Yin, Z.; Feng, Q.; Wen, X.; Deo, R.C.; Yang, L.; Si, J.; He, Z. Design and evaluation of SVR, MARS and M5Tree models for 1, 2 and 3-day lead time forecasting of river flow data in a semiarid mountainous catchment. Stoch. Environ. Res. Risk Assess. 2018, 32, 2457–2476. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe Jr, G.J. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Friedman, J.H. Estimating Functions of Mixed Ordinal and Categorical Variables Using Adaptive Splines; Stanford University CA Lab for Computational Statistics: Stanford, CA, USA, 1991. [Google Scholar]
- Ghimire, S.; Deo, R.C.; Downs, N.J.; Raj, N. Global solar radiation prediction by ANN integrated with European Centre for medium range weather forecast fields in solar rich cities of Queensland Australia. J. Clean. Prod. 2019, 216, 288–310. [Google Scholar] [CrossRef]
- Cai, Y.; Zheng, W.; Zhang, X.; Zhangzhong, L.; Xue, X. Research on soil moisture prediction model based on deep learning. PLoS ONE 2019, 14, e0214508. [Google Scholar] [CrossRef]

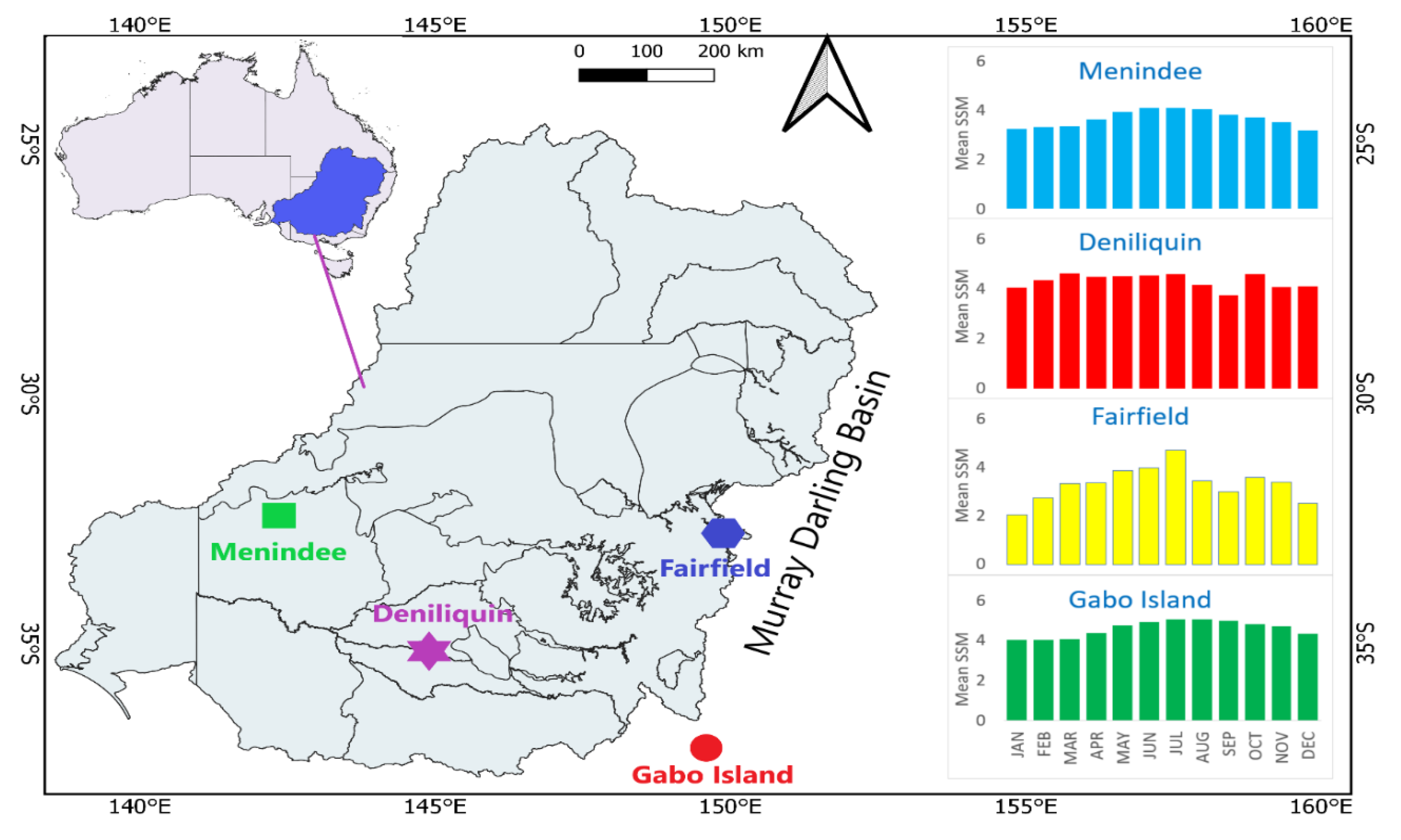
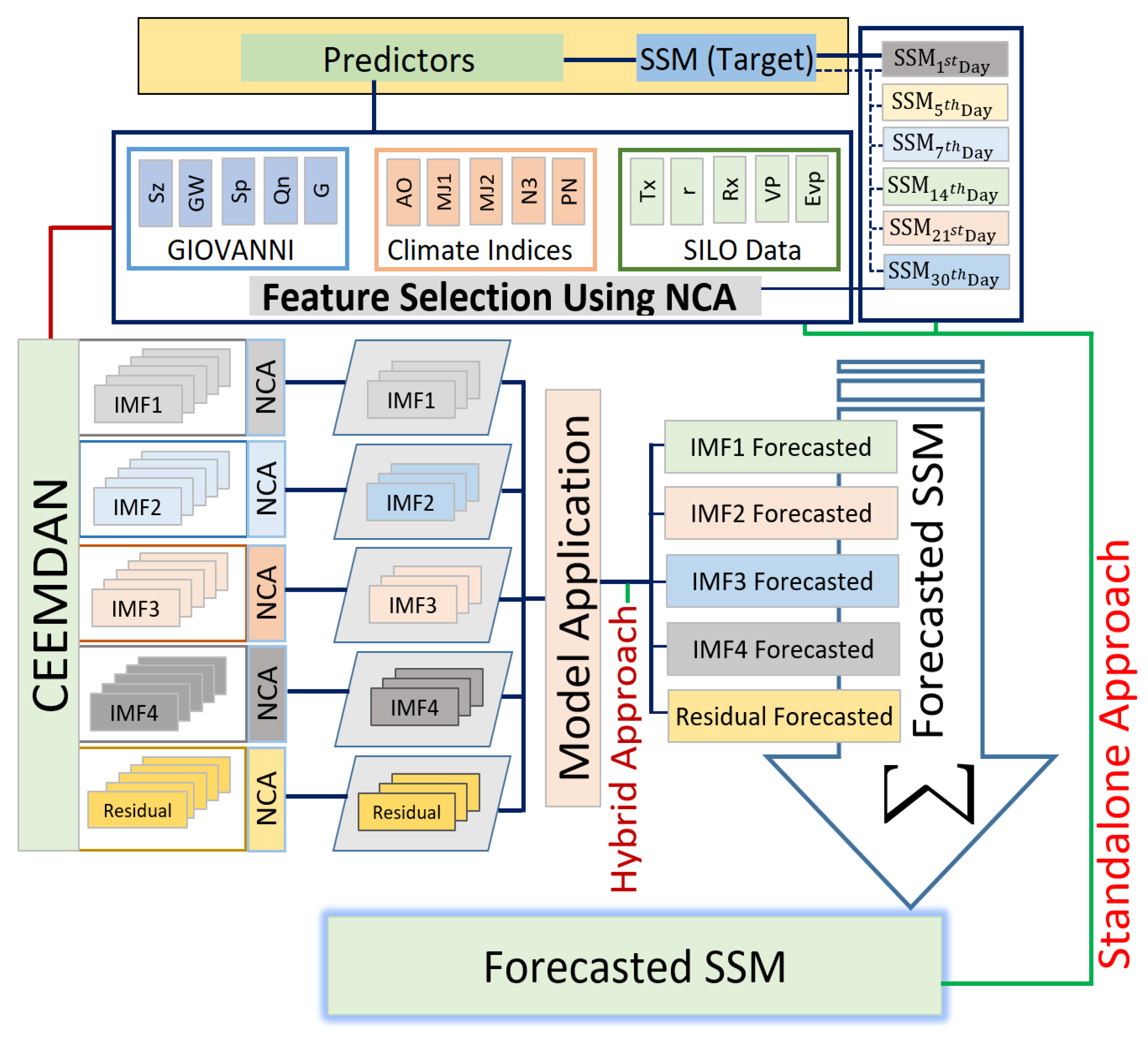
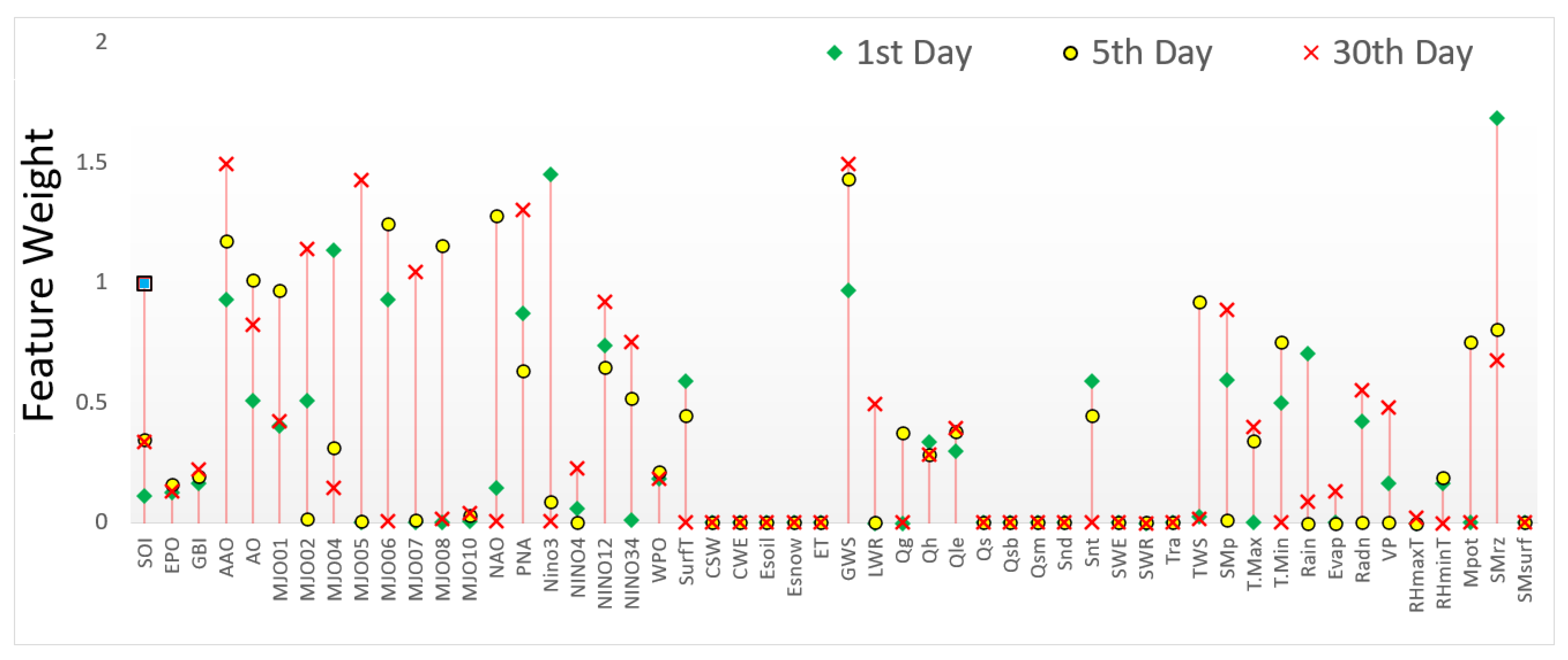
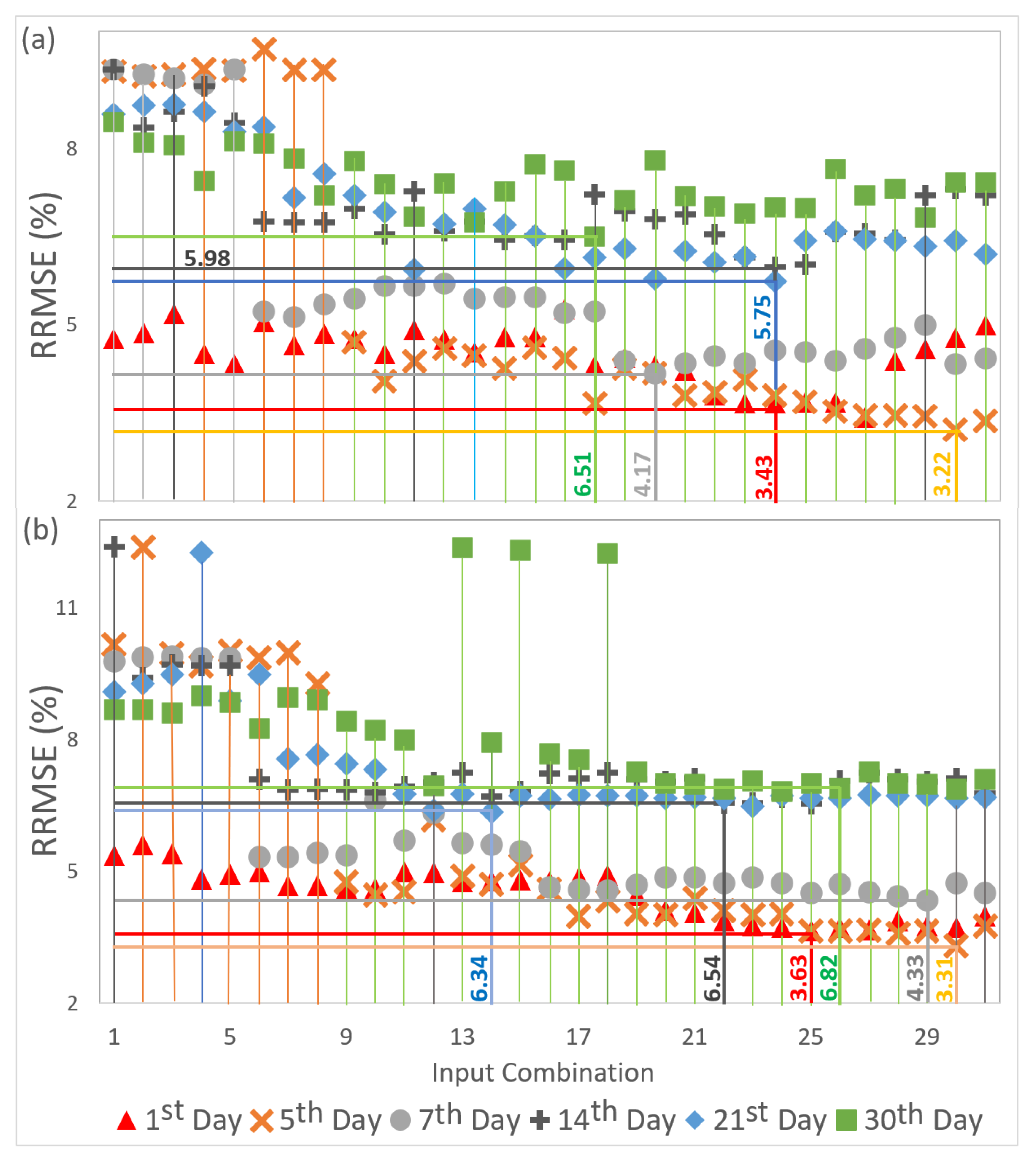
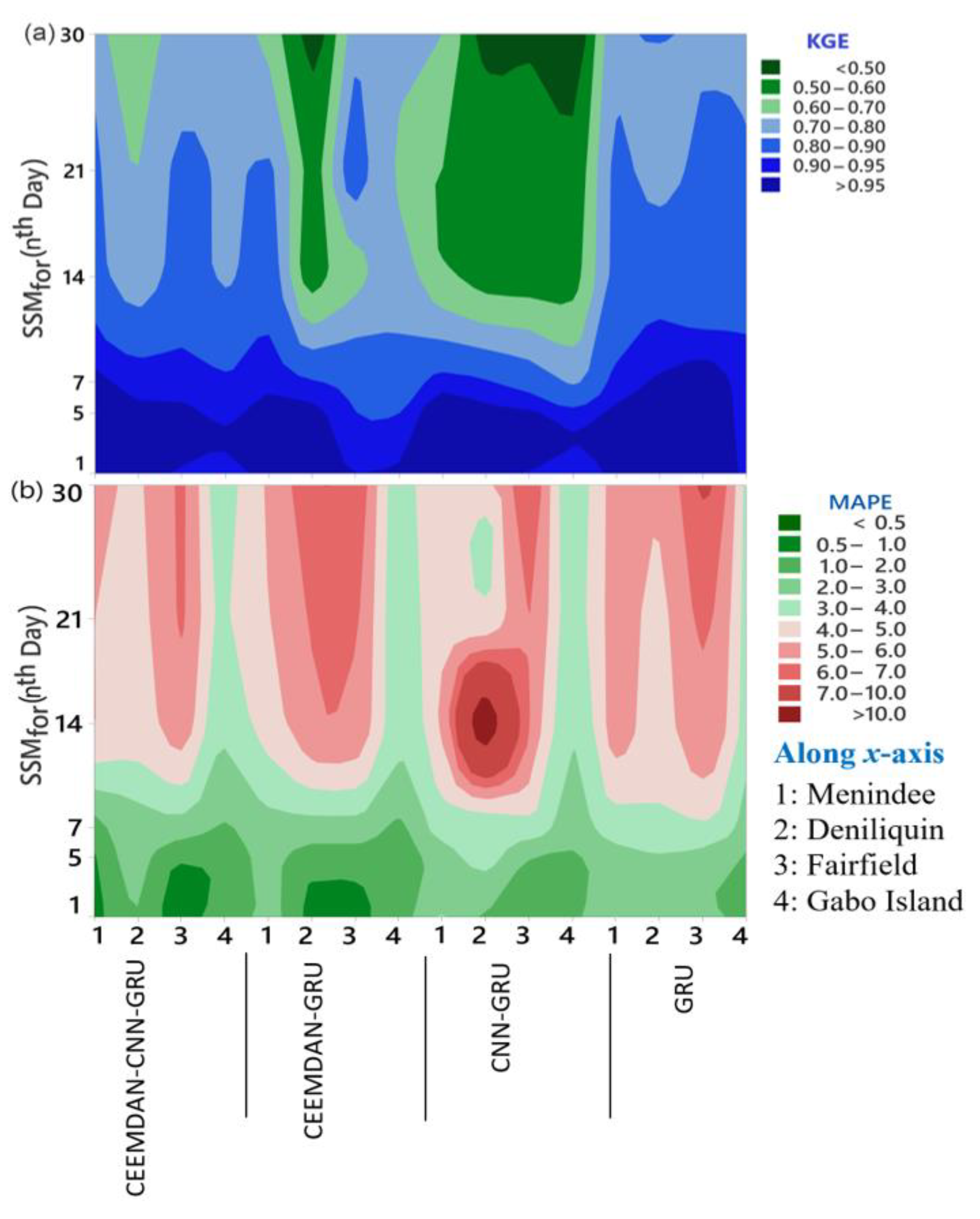
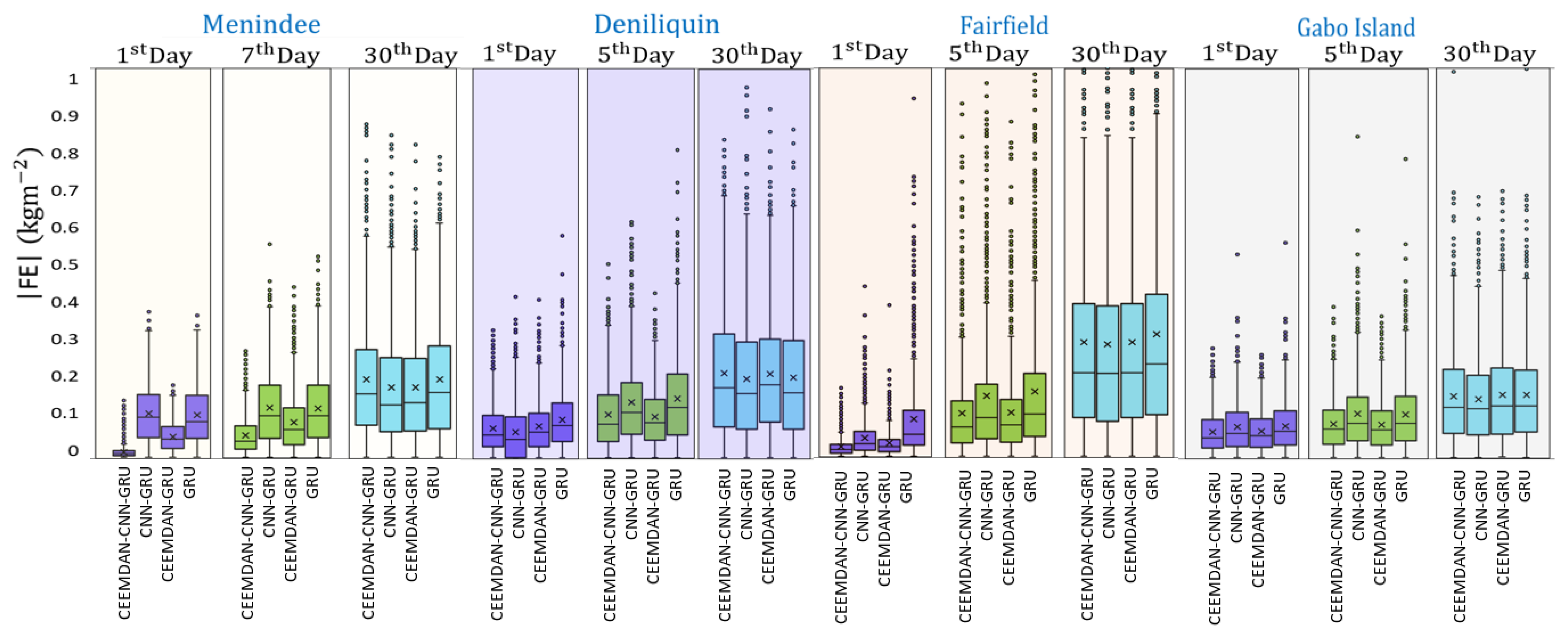
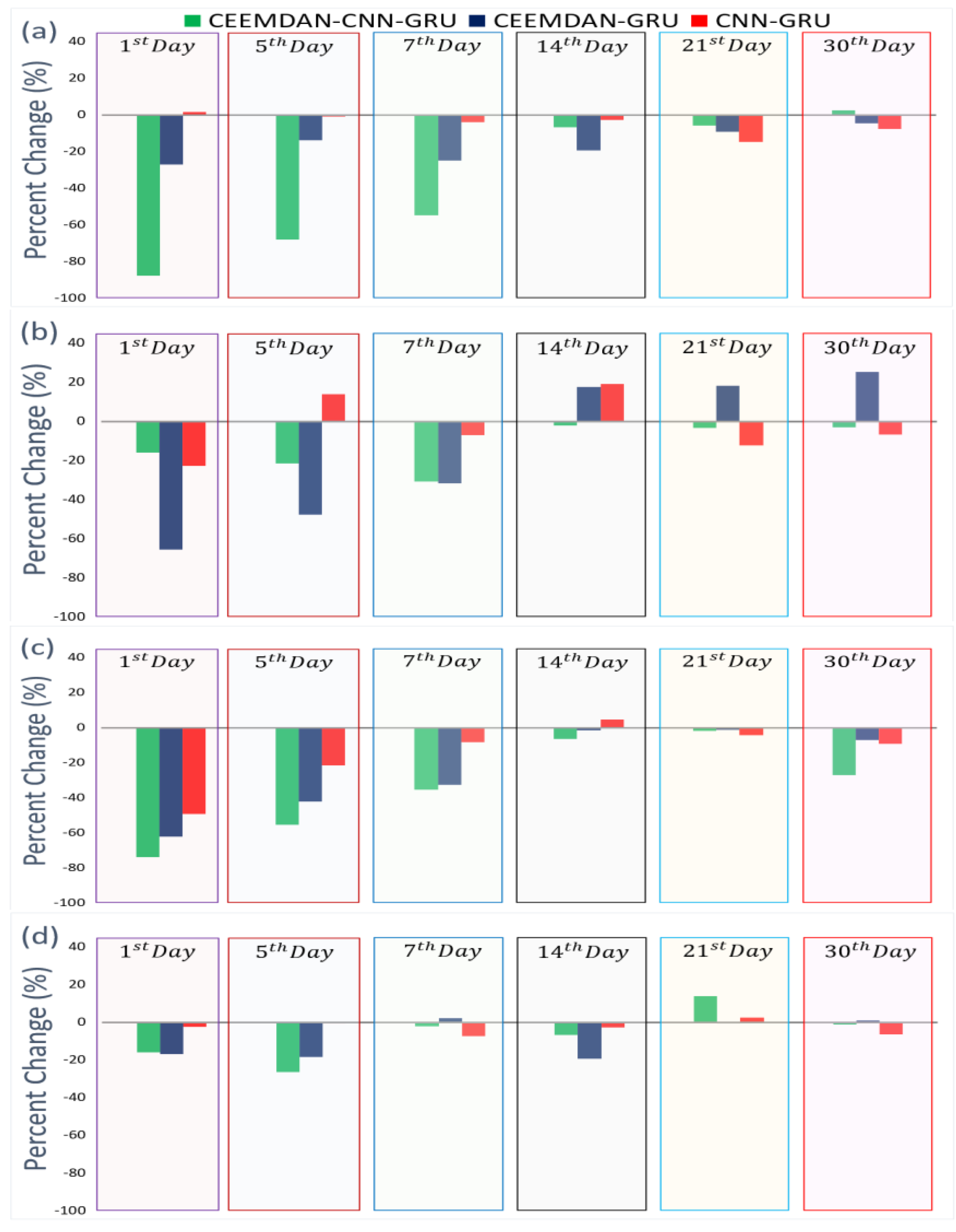
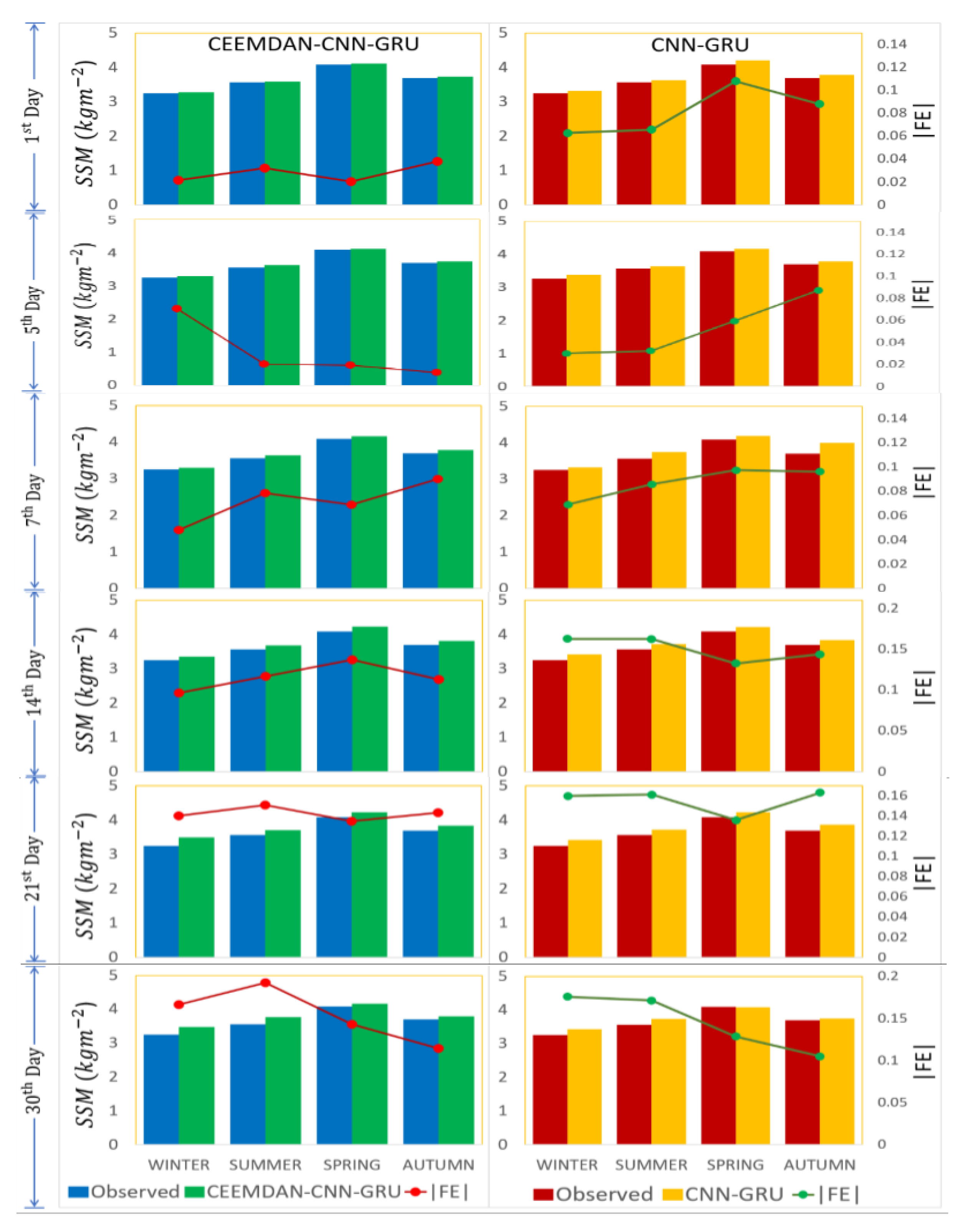
| Station Name | BOM Station ID | SILO Position (MODIS Grid Area) | Major Climate Class [68] | Soil Type [69] | Elevation [70] |
|---|---|---|---|---|---|
| Menindee | 047019 | 32.39°S, 142.42°E (142.5°E, 32.5°S, 142.25°E, 32.25°S) | Desert | Calcarosol | 61 |
| Deniliquin | 074128 | 35.53°S, 144.97° (145°E, 35.25°S, 144.75°E, 35°S) | Savannah | Calcarosol | 94 |
| Fairfield | 066137 | 33.92°S, 150.98°E (149.75°E, 37.75°S, 150.0°E, 37.5°S) | Savannah | Vertosol | 15 |
| Gabo Island | 084016 | 37.57°S, 149.92°E (150°E, 37.75°S, 149.75°E, 37.5°S) | Sub-Tropical | Sodosol | 15 |
| GLDAS 2.0: Modis Satellite Data from Giovanni Repository | |||
|---|---|---|---|
| Predictor Variable | Notation | Description | Units |
| SurT | St | Average Surface Skin temperature | K |
| CSW | CW | Plant canopy surface water | Kg m−2 |
| CWE | CE | Canopy water evaporation | kg m−2 s−1 |
| Esoil | Es | Direct Evaporation from Bare Soil | kg m−2 s−1 |
| ET | ET | Evapotranspiration | kg m−2 s−1 |
| Esnow | Es | Snow Evaporation | kg m−2 s−1 |
| GWS | GW | Groundwater storage | mm |
| LWR. | LW | Net longwave radiation flux | W m−2 |
| Qg | Qg | Ground heat flux | W m−2 |
| Qh | Qh | Sensible heat net flux | W m−2 |
| Qle | Qle | Latent heat net flux | W m−2 |
| Qs | Qs | Storm surface runoff | Kg m−2 s−1 |
| Qsb | Qb | Baseflow-groundwater runoff | Kg m−2 s−1 |
| Qsm | Qm | Snow-melt | Kg m−2 s−1 |
| Snd | Sn | Snow depth | m |
| Snt | Snt | Snow Surface temperature | m |
| SMp | Sp | Profile Soil moisture | Kg m−2 |
| SMrz | Sz | Root Zone Soil moisture | Kg m−2 |
| SSM | SSM | Surface Soil moisture | Kg m−2 |
| SWE | SW | Snow depth water equivalent | Kg m−2 |
| SWR | SR | Net short-wave radiation flux | W m−2 |
| Tra | Tr | Transpiration | Kg m−2 s−1 |
| TWS | TW | Terrestrial water storage | mm |
| SILO (Ground-Based Observations) | |||
| T.Max | Tx | Maximum Temperature | °C |
| T.Min | Tn | Minimum Temperature | °C |
| Rain | r | Rainfall | mm |
| Evap | Ep | Evaporation | mm |
| Radn | Rd | Radiation | MJ m−2 |
| VP | VP | Vapour Pressure | hPa |
| RHmaxT | Rx | Relative Humidity at Temperature T.Max | % |
| RHminT | Rn | Relative Humidity at Temperature T.Min | % |
| Mpot | Mp | Morton potential evapotranspiration overland | mm |
| SYNOPTIC-SCALE (Climate Mode Indices) | |||
| Nino3.0 | N3 | Average SSTA over 150°–90°W and 5°N–5°S | NONE |
| Nino3.4 | N34 | Average SSTA over 170°E–120°W and 5°N–5°S | |
| Nino4.0 | N4 | Average SSTA over 160°E–150°W and 5°N–5°S | |
| Nino1+2 | N12 | Average SSTA over 90°W–80°W and 0°–10°S | |
| AO | A | Arctic Oscillation | |
| AAO | AO | Antarctic Oscillation | |
| MJO1 | MJ1 | Madden Julian Oscillation-1 | |
| MJO2 | MJ2 | Madden Julian Oscillation-2 | |
| MJO4 | MJ4 | Madden Julian Oscillation-4 | |
| MJO5 | MJ5 | Madden Julian Oscillation-5 | |
| MJO6 | MJ6 | Madden Julian Oscillation-6 | |
| MJO7 | MJ7 | Madden Julian Oscillation-7 | |
| MJO8 | MJ8 | Madden Julian Oscillation-8 | |
| MJO10 | MJ10 | Madden Julian Oscillation-10 | |
| EPO | EP | East Pacific Oscillation | |
| GBI | G | Greenland Blocking Index (GBI) | |
| WPO | WP | Western Pacific Oscillation (WPO.) | |
| PNA | PN | Pacific North American Index | |
| NAO | N | North Atlantic Oscillation | |
| SAM | SM | Southern Annular Mode index | |
| SOI | SOI | Southern Oscillation Index, as per Troup [84] | |
| (a) Tested Range of Model Hyper-Parameters | ||
| Model | Model Hyper-parameter Names | Search Space for Optimal Hyper-Parameters |
| CNN-GRU | Filter 1 | (70, 80, 100, 150) |
| Filter 2 | (70, 80, 100,150) | |
| Filter 3 | (70, 80, 100, 150) | |
| GRU Cell Units | (40, 50, 70, 80, 100, 150) | |
| Epochs | (500, 800, 1000) | |
| Activation function | (ReLU) | |
| Optimiser | (Adam, SGD) | |
| Batch Size | (5, 10, 20, 50, 100) | |
| GRU | GRU Cell 1 | (70, 80, 100, 110) |
| GRU Cell 2 | (70, 80, 100,150, 200, 210) | |
| Epochs | (500, 800, 1000) | |
| Activation function | (ReLU) | |
| Optimiser | (Adam, SGD) | |
| Batch Size | (5, 10, 20, 50, 100) | |
| (b) Optimally Selected Hyper-Parameters | ||
| CNN-GRU | Convolution Layer 1 (C1) | 80 |
| C1-Activation function | ReLU | |
| C1-Pooling Size | 1 | |
| Convolution Layer 2 (C2) | 70 | |
| C2-Activation function | ReLU | |
| C2-Pooling Size | 1 | |
| Convolution Layer 3 (C3) | 80 | |
| C3-Activation function | ReLU | |
| C3-Pooling Size | 1 | |
| GRU Layer 1 (L1) | 200 | |
| L1-Activation function | ReLU | |
| GRU Layer 2 (L2) | 60 | |
| L2-Activation function | ReLU | |
| Drop-out rate | 0.2 | |
| Optimiser | Adam | |
| Padding | Same | |
| Batch Size | 5 | |
| Epochs | 400 | |
| GRU | GRU Cell 1 (G1) | 110 |
| G1-Activation function | ReLU | |
| GRU Cell 2 (G2) | 250 | |
| G2-Activation function | ReLU | |
| Epochs | 300 | |
| Optimiser | SGD | |
| Drop-out rate | 0.2 | |
| Batch Size | 15 | |
| Epochs | 1000 | |
| Soil Moisture Forecasting Horizon, nth Day Lead Time | ||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1st Day | 5th Day | 7th Day | 14th Day | 21st Day | 30th Day | |||||||||||||||||||||||||
| r | NSE | RMSE | MAE | APB | r | NSE | RMSE | MAE | APB | r | NSE | RMSE | MAE | APB | r | NSE | RMSE | MAE | APB | r | NSE | RMSE | MAE | APB | r | NSE | RMSE | MAE | APB | |
| Study Station 1: Menindee | ||||||||||||||||||||||||||||||
| CEEMDAN-CNN-GRU | 0.996 | 0.995 | 0.021 | 0.013 | 0.359 | 0.993 | 0.991 | 0.040 | 0.030 | 0.823 | 0.985 | 0.967 | 0.075 | 0.057 | 1.559 | 0.906 | 0.896 | 0.226 | 0.185 | 5.079 | 0.895 | 0.787 | 0.230 | 0.186 | 5.098 | 0.869 | 0.714 | 0.255 | 0.201 | 5.493 |
| CNN-GRU | 0.967 | 0.892 | 0.135 | 0.112 | 3.061 | 0.966 | 0.918 | 0.117 | 0.094 | 2.569 | 0.945 | 0.861 | 0.152 | 0.121 | 3.330 | 0.892 | 0.770 | 0.235 | 0.193 | 5.285 | 0.899 | 0.788 | 0.210 | 0.168 | 4.594 | 0.851 | 0.765 | 0.238 | 0.181 | 4.945 |
| CEEMDAN-GRU | 0.976 | 0.937 | 0.116 | 0.094 | 2.234 | 0.970 | 0.933 | 0.120 | 0.095 | 2.265 | 0.957 | 0.909 | 0.140 | 0.110 | 2.613 | 0.882 | 0.738 | 0.237 | 0.186 | 4.424 | 0.864 | 0.781 | 0.262 | 0.206 | 4.918 | 0.866 | 0.742 | 0.275 | 0.217 | 5.163 |
| GRU | 0.962 | 0.893 | 0.134 | 0.110 | 3.020 | 0.962 | 0.933 | 0.121 | 0.094 | 2.589 | 0.940 | 0.851 | 0.158 | 0.126 | 3.452 | 0.882 | 0.745 | 0.244 | 0.197 | 5.390 | 0.887 | 0.748 | 0.243 | 0.196 | 5.360 | 0.863 | 0.726 | 0.251 | 0.197 | 5.386 |
| Study Station 2: Deniliquin | ||||||||||||||||||||||||||||||
| CEEMDAN-CNN-GRU | 0.990 | 0.899 | 0.048 | 0.034 | 0.778 | 0.989 | 0.975 | 0.091 | 0.065 | 1.489 | 0.959 | 0.917 | 0.165 | 0.113 | 2.611 | 0.801 | 0.607 | 0.355 | 0.247 | 5.716 | 0.768 | 0.573 | 0.374 | 0.266 | 6.130 | 0.703 | 0.465 | 0.415 | 0.295 | 6.807 |
| CNN-GRU | 0.979 | 0.955 | 0.098 | 0.075 | 1.799 | 0.945 | 0.866 | 0.169 | 0.137 | 3.270 | 0.929 | 0.846 | 0.181 | 0.143 | 3.405 | 0.866 | 0.624 | 0.283 | 0.224 | 5.333 | 0.873 | 0.749 | 0.231 | 0.181 | 4.298 | 0.848 | 0.687 | 0.258 | 0.202 | 4.806 |
| CEEMDAN-GRU | 0.987 | 0.958 | 0.106 | 0.081 | 1.930 | 0.968 | 0.929 | 0.123 | 0.096 | 2.279 | 0.969 | 0.920 | 0.131 | 0.106 | 2.524 | 0.872 | 0.730 | 0.240 | 0.189 | 4.505 | 0.859 | 0.712 | 0.249 | 0.197 | 4.701 | 0.869 | 0.671 | 0.264 | 0.207 | 4.926 |
| GRU | 0.967 | 0.927 | 0.125 | 0.099 | 2.350 | 0.947 | 0.889 | 0.154 | 0.121 | 2.874 | 0.918 | 0.822 | 0.195 | 0.153 | 3.655 | 0.867 | 0.722 | 0.244 | 0.191 | 4.560 | 0.868 | 0.695 | 0.256 | 0.201 | 4.787 | 0.850 | 0.659 | 0.269 | 0.217 | 5.152 |
| Study Station 3: Fairfield | ||||||||||||||||||||||||||||||
| CEEMDAN-CNN-GRU | 0.975 | 0.976 | 0.035 | 0.024 | 0.554 | 0.972 | 0.975 | 0.069 | 0.052 | 1.189 | 0.959 | 0.920 | 0.162 | 0.110 | 2.524 | 0.842 | 0.628 | 0.349 | 0.238 | 5.493 | 0.762 | 0.573 | 0.374 | 0.264 | 6.088 | 0.746 | 0.523 | 0.374 | 0.261 | 6.078 |
| CNN-GRU | 0.945 | 0.935 | 0.061 | 0.048 | 1.099 | 0.962 | 0.943 | 0.135 | 0.091 | 2.107 | 0.907 | 0.821 | 0.240 | 0.156 | 3.612 | 0.764 | 0.560 | 0.376 | 0.264 | 6.109 | 0.759 | 0.554 | 0.379 | 0.259 | 5.988 | 0.708 | 0.477 | 0.410 | 0.289 | 6.671 |
| CEEMDAN-GRU | 0.947 | 0.943 | 0.048 | 0.034 | 0.778 | 0.939 | 0.935 | 0.091 | 0.065 | 1.489 | 0.929 | 0.917 | 0.165 | 0.113 | 2.611 | 0.801 | 0.607 | 0.355 | 0.247 | 5.716 | 0.768 | 0.573 | 0.374 | 0.266 | 6.130 | 0.703 | 0.465 | 0.415 | 0.295 | 6.807 |
| GRU | 0.925 | 0.919 | 0.153 | 0.096 | 2.205 | 0.913 | 0.905 | 0.177 | 0.115 | 2.659 | 0.904 | 0.809 | 0.250 | 0.168 | 3.864 | 0.778 | 0.585 | 0.369 | 0.254 | 5.850 | 0.775 | 0.568 | 0.376 | 0.267 | 6.165 | 0.666 | 0.411 | 0.435 | 0.314 | 7.267 |
| Study Station 4: Gabo Island | ||||||||||||||||||||||||||||||
| CEEMDAN-CNN- GRU | 0.988 | 0.966 | 0.085 | 0.067 | 1.455 | 0.987 | 0.971 | 0.079 | 0.062 | 1.346 | 0.978 | 0.944 | 0.109 | 0.086 | 1.887 | 0.931 | 0.899 | 0.188 | 0.147 | 3.206 | 0.909 | 0.764 | 0.224 | 0.175 | 3.829 | 0.913 | 0.807 | 0.202 | 0.158 | 3.456 |
| CNN-GRU | 0.979 | 0.951 | 0.101 | 0.078 | 1.707 | 0.973 | 0.944 | 0.109 | 0.084 | 1.826 | 0.948 | 0.897 | 0.147 | 0.113 | 2.457 | 0.921 | 0.843 | 0.182 | 0.141 | 3.087 | 0.911 | 0.803 | 0.204 | 0.160 | 3.493 | 0.879 | 0.862 | 0.193 | 0.151 | 3.284 |
| CEEMDAN-GRU | 0.986 | 0.966 | 0.085 | 0.067 | 1.472 | 0.983 | 0.964 | 0.087 | 0.069 | 1.508 | 0.974 | 0.945 | 0.107 | 0.085 | 1.844 | 0.924 | 0.821 | 0.194 | 0.153 | 3.340 | 0.913 | 0.814 | 0.198 | 0.156 | 3.394 | 0.912 | 0.798 | 0.206 | 0.161 | 3.520 |
| GRU | 0.977 | 0.950 | 0.102 | 0.081 | 1.773 | 0.970 | 0.940 | 0.113 | 0.086 | 1.868 | 0.951 | 0.902 | 0.144 | 0.111 | 2.423 | 0.919 | 0.825 | 0.192 | 0.150 | 3.283 | 0.912 | 0.813 | 0.199 | 0.156 | 3.411 | 0.815 | 0.743 | 0.203 | 0.160 | 3.499 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, A.A.M.; Deo, R.C.; Raj, N.; Ghahramani, A.; Feng, Q.; Yin, Z.; Yang, L. Deep Learning Forecasts of Soil Moisture: Convolutional Neural Network and Gated Recurrent Unit Models Coupled with Satellite-Derived MODIS, Observations and Synoptic-Scale Climate Index Data. Remote Sens. 2021, 13, 554. https://doi.org/10.3390/rs13040554
Ahmed AAM, Deo RC, Raj N, Ghahramani A, Feng Q, Yin Z, Yang L. Deep Learning Forecasts of Soil Moisture: Convolutional Neural Network and Gated Recurrent Unit Models Coupled with Satellite-Derived MODIS, Observations and Synoptic-Scale Climate Index Data. Remote Sensing. 2021; 13(4):554. https://doi.org/10.3390/rs13040554
Chicago/Turabian StyleAhmed, A. A. Masrur, Ravinesh C Deo, Nawin Raj, Afshin Ghahramani, Qi Feng, Zhenliang Yin, and Linshan Yang. 2021. "Deep Learning Forecasts of Soil Moisture: Convolutional Neural Network and Gated Recurrent Unit Models Coupled with Satellite-Derived MODIS, Observations and Synoptic-Scale Climate Index Data" Remote Sensing 13, no. 4: 554. https://doi.org/10.3390/rs13040554
APA StyleAhmed, A. A. M., Deo, R. C., Raj, N., Ghahramani, A., Feng, Q., Yin, Z., & Yang, L. (2021). Deep Learning Forecasts of Soil Moisture: Convolutional Neural Network and Gated Recurrent Unit Models Coupled with Satellite-Derived MODIS, Observations and Synoptic-Scale Climate Index Data. Remote Sensing, 13(4), 554. https://doi.org/10.3390/rs13040554













