1. Introduction
Synthetic Aperture Radar (SAR) uses electromagnetic waves to characterize target geometrical structures and dielectric properties. When the incident wave interacts with the object, the polarization state of the reradiated wave is changed. Target information is recorded in the scattered wave, and the scattering process is a function of the incident and scattered fields. Radar measurement is polarization dependent [
1]. For the single-polarization transmit and single-polarization receive case, which corresponds to a single-pol system, target backscatter is characterized by a single scattering coefficient. For the single-polarization transmit and orthogonal-polarization simultaneous receive case, which corresponds to the dual-pol system, backscatter is characterized by a complex scattering vector. If we alternatively transmit orthogonal polarizations and use orthogonal polarizations to simultaneously receive backscatter, we get the scattering matrix, and this corresponds to the full-pol (FP) system. Compared to the full-pol system, the dual-pol system has advantages on imaging swath, power consumption, system complexity, and data volume [
2,
3], but meanwhile it cannot complete characterize the backscattering natures of scatterers. In recent years, the dual-pol system is discussed in two cases, i.e., the conventional dual-pol imaging mode (HH/HV or VH/VV) and the hybrid dual-pol imaging mode (i.e., the transmitted wave is not H or V polarized, generally known as compact polarimetry). Some studies have shown that the compact polarimetric (CP) mode performs better than the conventional dual-pol modes, in applications such as land use and land cover classification [
4], ship and oil-spill detection [
5,
6], etc. Currently, the Indian RISAT-1 (2012), Japan JAXA ALOS-2/PALSAR (2014), SAOCOM-1A (2018), and the RADARSAT Constellation Mission (RCM-3/4/5, 2019) have the capability of providing CP images.
Compact polarimetry allows choices of the transmitted wave polarization state. The monochromatic electromagnetic wave is represented by a complex vector. In this vector space, there are actually numerous possibilities of transmitted polarizations. The commonly considered CP modes are the linear π/4 mode, which transmits a linear polarization oriented at 45°, and the circular mode, which transmits a left or right circular polarization. It should be noted that although the scattering vector is associated with a particular receiving coordinate, the backscattered information of the scattered wave has no relation with the orthogonal receivers, because the receiving polarization bases possess the unitary transformation [
1]. Thus, in this study we only discuss the H/V polarization receiving configuration. In order to extract more information from the CP data and utilize the many well-developed quad-pol algorithms, Souyris et al. (2005) [
7] were the first to propose an algorithm to reconstruct the pseudo quad-pol imagery from the π/4 mode.
Several studies can be found in the current publications concentrating on reconstructing (or estimating) the 3 × 3 quad-pol covariance matrix from the 2 × 2 linear π/4 or circular CP covariance matrix. These algorithms are discussed on three aspects: (1) the symmetric scattering assumption [
7], (2) the reconstruction model [
7,
8,
9,
10,
11,
12,
13], and (3) the solving approach [
14]. Reflection symmetry [
15,
16,
17] is a generally used approach for scatterers to give a prior assumption about zero correlations of co-polarized and cross-polarized terms. By assuming reflection symmetry, three simplified equations are formed via the CP observables. Then, there is only one more equation needed to implement the estimation, which is the reconstruction model. Reconstruction models had a general form (see Equation (4) in [
14]), and different models have different model parameter
.
is determined either by theoretical assumptions [
7,
12] or by scenario-based empirical tests [
9,
10,
11]. The cross-pol term is the only variable to be solved. In previous studies, the solution is obtained via an iterative approach [
7,
8,
9,
10,
11,
12,
13]. However, the iterative approach often overestimates the cross-pol intensity. In [
14], we proposed a least squares (LS)-based method to approximate the solution and obtained promising results based on the linear π/4 mode.
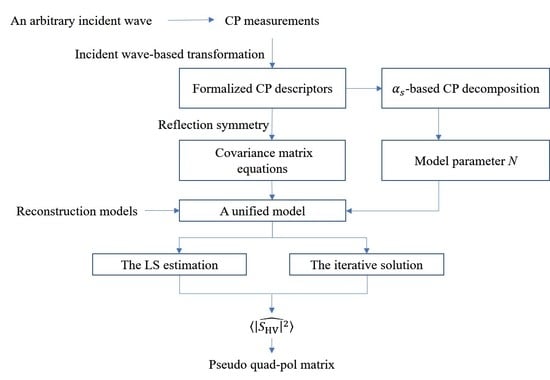
The current reconstruction methods were developed for either the linear π/4 or circular CP mode, with specific reconstruction procedures. This is because CP measurements are transmitting polarization dependent. When the transmit wave varies, CP channels capture different combinations of the scattering coefficients, leading to different equation forms of the co-polarization coherence. In the open literature, there is no study about estimating quad-pol scattering coefficients from the general CP mode, which refers to the hybrid dual-pol mode with an arbitrary transmit ellipse wave. In this study, we deal with the reconstruction problem from the general CP mode. First, the CP formalism method [
18] is exploited to formulate the system of non-linear equations for the quad-pol unknowns. The formalism is a linear operator, using the transmit wave parameters to map the scattering vector to another vector which has a fixed reference point in the radar measurement space for all CP modes. Second, the LS method is extended to the general CP mode to refine the cross-pol term. Results in [
14] showed that the LS method greatly improved the reconstruction accuracy, especially for the estimation of the co-polarized phase difference (CPD). The LS method needs a constant
-model to construct the objective. In [
14], we developed the symmetric scattering type
-based CP decomposition method for the linear π/4 mode, with the purpose to give a priori estimate of
for the decomposition-based reconstruction model. Then, we extended the
-based decomposition to the general CP case [
19]. It should be noticed that the
-based CP decomposition if without the descriptor standardization step will have different formulas for the π/4 [
14] and the circular [
20] modes. In this study, the general
-based decomposition are used to provide an approximation for
.
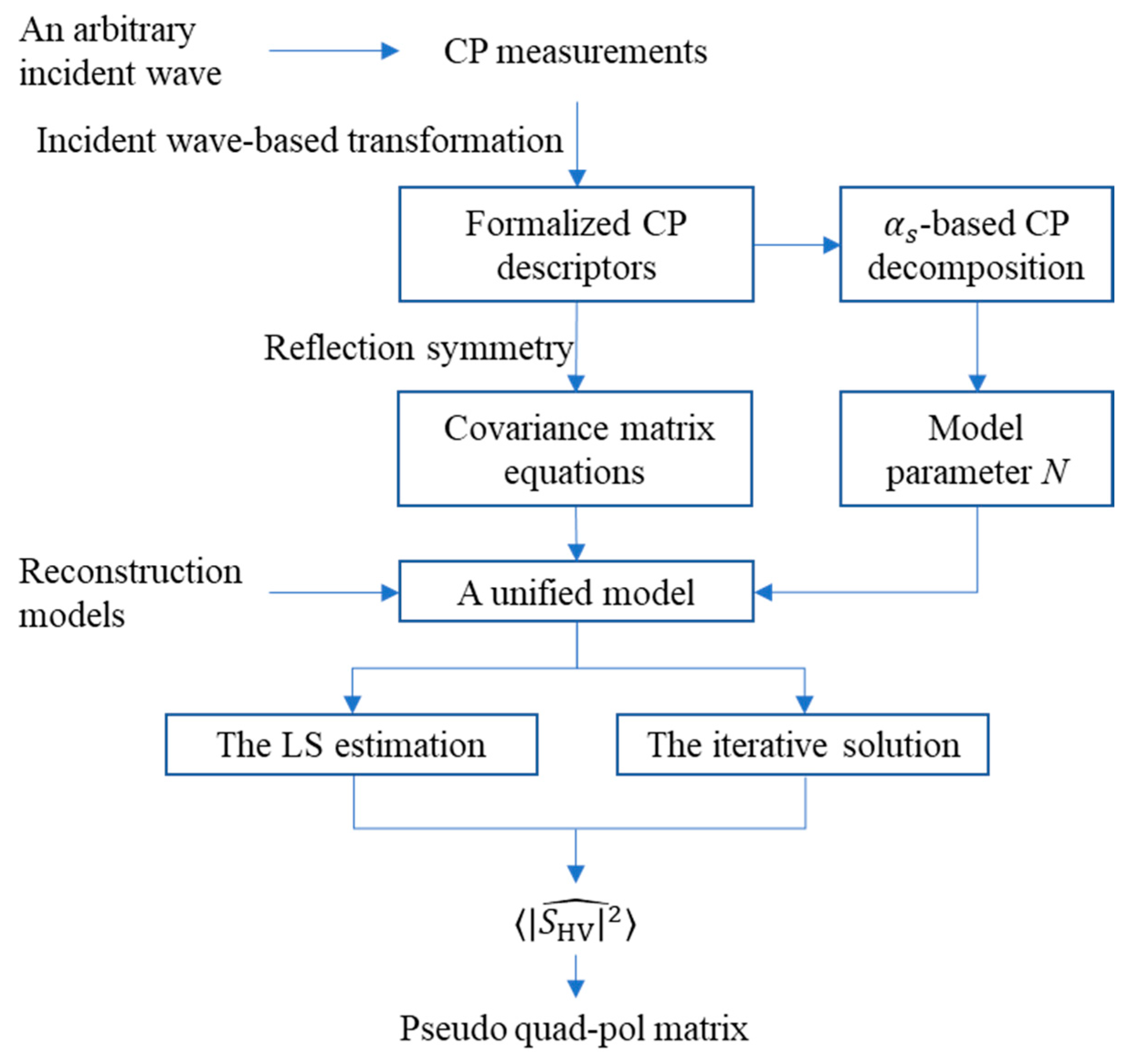
An overview of the current related techniques is presented. The current iteration-based techniques, which were developed for either the circular or the linear CP modes, are also extended for the general CP mode. The contents of this study are summarized in
Figure 1. In
Section 2, we introduce the test data used for illustration. In
Section 3, the formalism of the general CP descriptors in terms of the covariance matrix is introduced. In
Section 4, we first summarize the reconstruction models, and then based on the formalized CP covariance matrix the iterative solving approach is extended for the general CP SAR images. In
Section 5, the LS model function is proposed, and the approximation to the model parameter
is also given. In
Section 6, multiple polarimetric data sets are used to show the reconstruction performances of both the iterative and the LS methods, as well as the abilities of different CP modes for revealing the quad-pol information. Finally, the paper is summarized in
Section 7.
3. Formalism of the CP Descriptors
In this section, we will briefly introduce the formalized scattering vector and covariance matrix [
18].
A general form of the electromagnetic field is represented by a transverse ellipse which is described by two parameters, i.e., the ellipse orientation angle
and the ellipticity angle
[
1], as follows.
where
. The CP system measures a projection of the complex scattering matrix
onto a transmitted wave. Then for an arbitrary transmit wave
, the received backscattered wave
is
For an arbitrary
, the received compact (or traditional dual) polarimetric signal is totally dependent on
and
. For the commonly considered linear π/4, left circular, right circular, horizontal and vertical transmitted waves, the values of
are
,
,
,
and
, respectively. Note that the circular polarization is not affected by wave orientation angles, and thus
.
in (2) is received in the linear-polarization orthogonal basis and can be easily transformed to the circular polarization basis through a unitary transformation [
1,
6,
21]. The dual-polarization measurement is independent of the elliptical basis of radar receivers, and thus we only discuss the linear H/V-polarization received CP data. We notice that
contains
and
contains
when none of
and
is 0. Then, the scattering vector (2) can be formulated as
where
is the diagonal matrix of a vector, and
are the wave component ratios.
and
are the formalized elements for
to characterize the scattered wave. This formalism is only for the general compact polarimetric mode. It is not applicable to the conventional dual polarizations, i.e., the
or
measurements.
From the defined scattering vector
, the second order product, named as the CP covariance matrix following that in full polarimetry, is constructed for the partially polarized backscattered waves, as follows.
where
H denotes matrix conjugate transpose, and
denotes ensemble average.
is the basis in this study to analyze the general CP matrix for the multi-polarization reconstruction.
The formalized scattering vector in (3) and the corresponding CP covariance matrix defined in (4) provide a unified method representing CP data. For a monostatic polarimetric SAR and reciprocal scatterers, the scattering matrix is symmetric, i.e.,
. In this case, expansion of
in terms of the scattering coefficients of the medium is given in (5). If scattering reflection symmetry is further assumed for the CP covariance matrix, which means the components involving products of co-polarized and cross-polarized terms are much smaller than the others and thus negligible,
only contains the co-polarized and cross-polarized terms, as shown in (6). When the transmit wave is linearly polarized, e.g., in the linear
π/4 mode,
has the same form as the wave covariance matrix [
7,
8,
12] except that the matrix power is doubled. When the transmit wave is circularly polarized,
has a different form from the wave covariance matrix as that shown in (4) in [
8]. This formalism provides a unified description for the backscattered wave, which facilitates the analysis of CP imagery. Under this formalism, the system of non-linear equations for the reconstruction is easily formulated as a function of the transmit wave, which will be discussed in
Section 4 and
Section 5.
6. Experiments
The LS-based methods are applied to the single-look complex data, and the estimation is performed within a 7 × 7 square window. The iterative methods are applied to the multi-look data where a 7 × 7 sliding window is used for speckle reduction. is set to 1 for the symmetric scattering type-based decomposition.
The pseudo quad-pol imagery reconstruction can be implemented via the combination of the reconstruction models and the LS-based or the iteration-based solving approach. The reconstruction model can be with either constant
, which is a pre-defined parameter, or variable
, which is updated during the iteration procedure. In
Section 4.1, we formulated the reconstruction model and presented both the empirical and theoretical model parameters in
Table 1. The empirical model is closely related to the observation scenarios and can only be applied to areas with a single terrain type, so we do not include the empirical model in the experiments. The Nord et al. variable
model needs initial values for the iterative approach and is sensitive to the initialization [
9], which cannot be embedded in the LS estimator. Thus, we only consider two reconstruction models, i.e., the
model [
7] and the decomposition-based model [
12]. These two models can be combined with both the LS estimator and the iterative approach. For the iterative approach, different updating strategies can be applied to the model parameter
, either constant or variable with different initial values. Hence, from the explanation above, we consider 6 reconstruction algorithms, that is, the LS estimators with Souyris’s and Yin’ model parameters, the iterative approaches with constant Souyris’s and Yin’ model parameters, and the iterative approaches with Yin’s model in which
is variable and initialized with
as well as initialized by the CP
- based decomposition method. The above algorithms are denoted in turn as LSN4, LSND, IterNC4, IterNCD, IterNV4, and IterNVD, respectively.
Experiments are conducted on the following aspects: (1) performances of the iterative and LS-based methods, (2) reconstruction accuracies of the reconstruction models, (3) reconstruction accuracies under different CP modes, and (4) comparison of the performances of CP data, pseudo quad-pol data, and FP data for multi-temporal agriculture field classification. Three CP modes, i.e., the linear π/4 mode (), an elliptical mode (), and the left circular mode (), are used for demonstration. For these CP modes, the transmit waves are balanced in amplitude, i.e., , so the variable-N algorithm is applicable. The linear π/4 and circular modes are commonly considered imaging configurations. They are included so as to get comparable results with those found in the open literature.
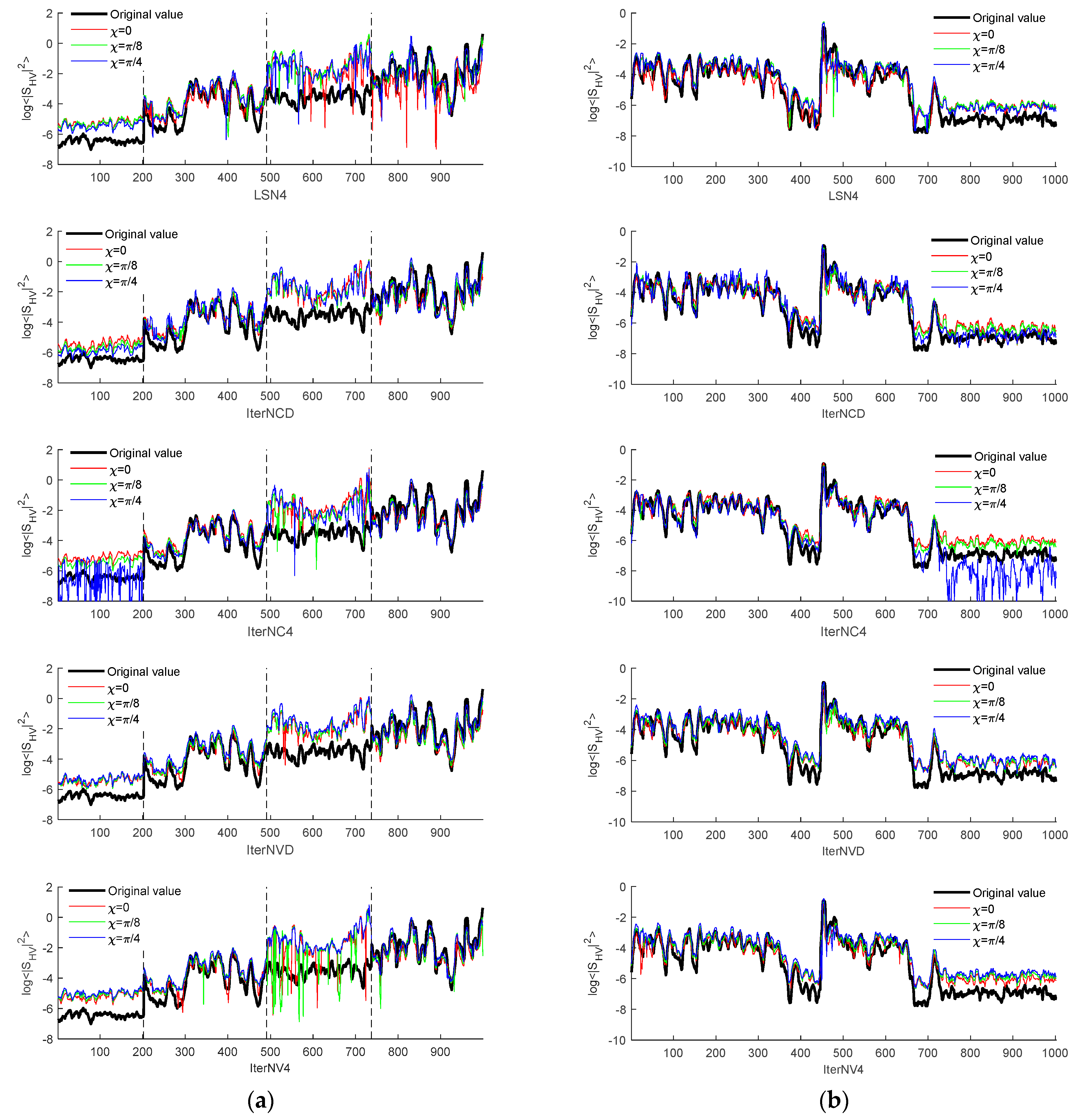
Reconstructed results for the line segments in
Figure 2 are given in
Figure 5. It shows that in general the results from the decomposition-based model is better than those from the
model, no matter which solving approaches is used. For the variable
methods, we again verify that the initialization affects the reconstructed results, especially for the circular CP mode, as can be observed from the last two rows in
Figure 5. Initial values given by the
-based decomposition generates better results than the initial guess with
. For the iterative methods with constant
, it shows that the
model under the circular mode does not performs well for the ocean surface, as can be observed in the IterNC4 plots that the blue profiles for the ocean surface has larger variations. Results show that the iterative method with constant-
estimated by the
-based decomposition outperforms the other methods under the circular mode for the ocean surface. Compared to the iterative methods, the LS estimator is superior for reconstruction of the urban area data when combined with the decomposition-based model. In the LS-based method, the linear CP mode gives lower estimates for the cross-pol term as compared with the elliptical and circular CP modes for land areas. From
Figure 5, it shows that the constant
iterative method is not suitable for ocean surface reconstruction, especially in the circularly polarized mode. Comparatively, the constant-
N method with
N estimated from the
-based decomposition (IterNCD) has the best reconstruction accuracy for ocean surface under the circular mode. While for land areas, the LS-based method LSND has the best result. However, for the urban area without obvious rotation, all methods tend to overestimate the cross-pol term. Further, results in
Figure 5 also show that the decomposition-based model fit the urban areas better in both iterative and LS-based solving approaches, which is because the typical reflection asymmetry model, i.e., the helix scattering models, also satisfies the decomposition-based reconstruction model. However, the reflection asymmetric models do not agree with the
N = 4 model.
Evaluation in terms of root mean square errors (RMSE) and percentages of the pixels that deviate from the real values by 5% of the total range are given in
Table 2.
directly affects the reconstruction performances and CPD is associated with the identification of scattering mechanisms. RMSE is calculated for both
and CPD, and the pixel percentage of deviation is calculated for CPD. In
Table 2, for each assessment index, the first two methods that are with best estimation results are highlighted. Reconstruction are performed under the aforementioned 3 CP modes for the test data sets. In total, each method is quantified 27 times. Results show that for the LSND, LSN4, IterNCD, IterNC4, IterNVD, and IterNV4 methods, the frequencies that those methods perform best are 21/27, 1/27, 10/27, 8/27, 13/27, and 2/27, respectively. The LS estimator with the decomposition-based model can provide the best overall results, and the variable-
method initialized by parameters from the
-based decomposition is in the second position.
In the LSND method, for the linear π/4 mode, the elliptical model with , and the circular mode, on average 0.98%, 0.6% and 0% pixels, respectively, cannot find minimums in the solution constraint. With the LSN4 method, for the 3 CP modes, 1.17%, 1.14%, and 1.83% pixels cannot find minimums within the constraint. This indicates that the decomposition-based model is more accurate to fit the CP data under different modes.
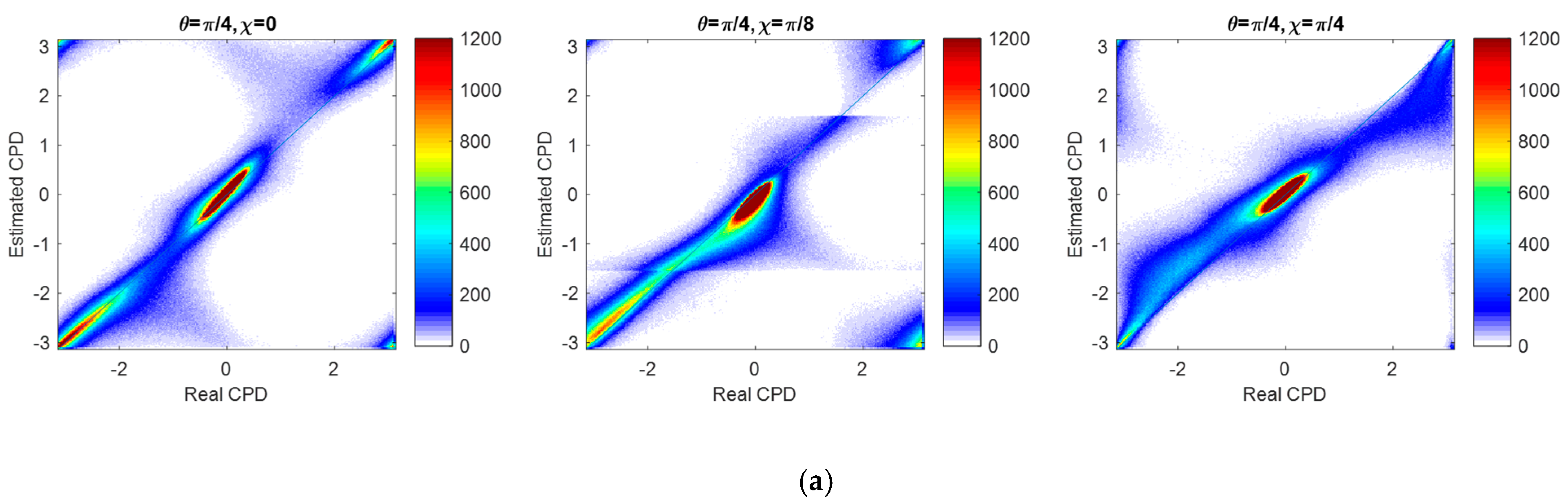
The reconstructed accuracy of CPD is another important factor to evaluate the reconstruction performance. On average, the LSND method performs best in phase reconstruction. By using the L-band ALOS-2/PALSAR data for illustration, CPDs estimated by LSND for the three CP modes are shown in
Figure 6a. It shows that under the linear π/4 mode, most pixels distribute along the diagonal line, indicating a superior reconstruction result. The reconstructed
is evaluated in
Figure 6b in terms of the relative error. Similar analysis results can be found in [
14] (see
Figure 5 and
Figure 6) for the C-band RADARSAT-2 data over the same test site for the Linear CP mode.
Figure 6b shows that for the urban area without obvious rotation, the linear π/4 mode has smaller relative errors compared to the other two modes, but still the relative error of city areas is larger than those of ocean surface and forested areas. For the rotated urban area, the linear π/4 mode has the larger relative errors and in contrast the circular mode performs best. Since for this test set, the rotated urban area and the forested areas are characterized by a similar cross-pol and co-pol ratio, i.e., ratio between the cross-pol intensity and the sum of co-pol intensities, it is expected that the circular mode would also perform better for the forested areas. Relative errors of the reconstructed
for the areas outlined in
Figure 2c are listed in
Table 3. The quantitative result is consistent with the explanation for the results shown in
Figure 6b.
Results in
Figure 5 and
Figure 6b, and
Table 3 show that a same method performs differently for different terrain types when the CP mode varies. Since from
Table 2, it is shown that apart from the LSND method, the IterNCD and IterNVD methods have relatively better overall reconstruction accuracies, in
Table 4 we further show the relative errors of
for those methods. In combination with the profiles in
Figure 5, it confirms that the IterNCD method is favorable for the circular mode to reconstruct the scattering coefficient of ocean surface. The combination use of the linear CP mode and the LSND method is better than any other combinations of the CP modes and the reconstruction algorithms for the urban areas which do not possess obvious rotation angles. For the forested and tilted urban areas, reconstruction results obtained from the circular mode are better, especially when LSND is used.
Table 2 shows that for all methods, the deviation percentage which evaluates the agreement of reconstructed and real CPDs is smallest in the linear π/4 mode. In combination with the scatter plots in
Figure 6a, we found that the π/4 mode outperforms the other two CP modes in the reconstruction of the phase term. RMSE of CPD is larger for the π/4 mode is due to the period of 2π radians phase. When the real CPD is close to ±π, a small perturbation on the estimated
will lead to dramatic changes of ±2π in the estimated CPD (e.g., from −π to π or from π to −π), as can be observed in
Figure 6a that in the π/4 mode a certain amount of pixels lies in the corners of (−π, π) and (π, −π). This results in larger RMSEs. For the other two test sets in
Figure 2, distributions of the CPD estimated by LSND under the 3 CP modes are quite similar to those in
Figure 6a. The omitted terms in (5) by assuming reflection symmetry has different impacts on CPD when the CP mode varies. In
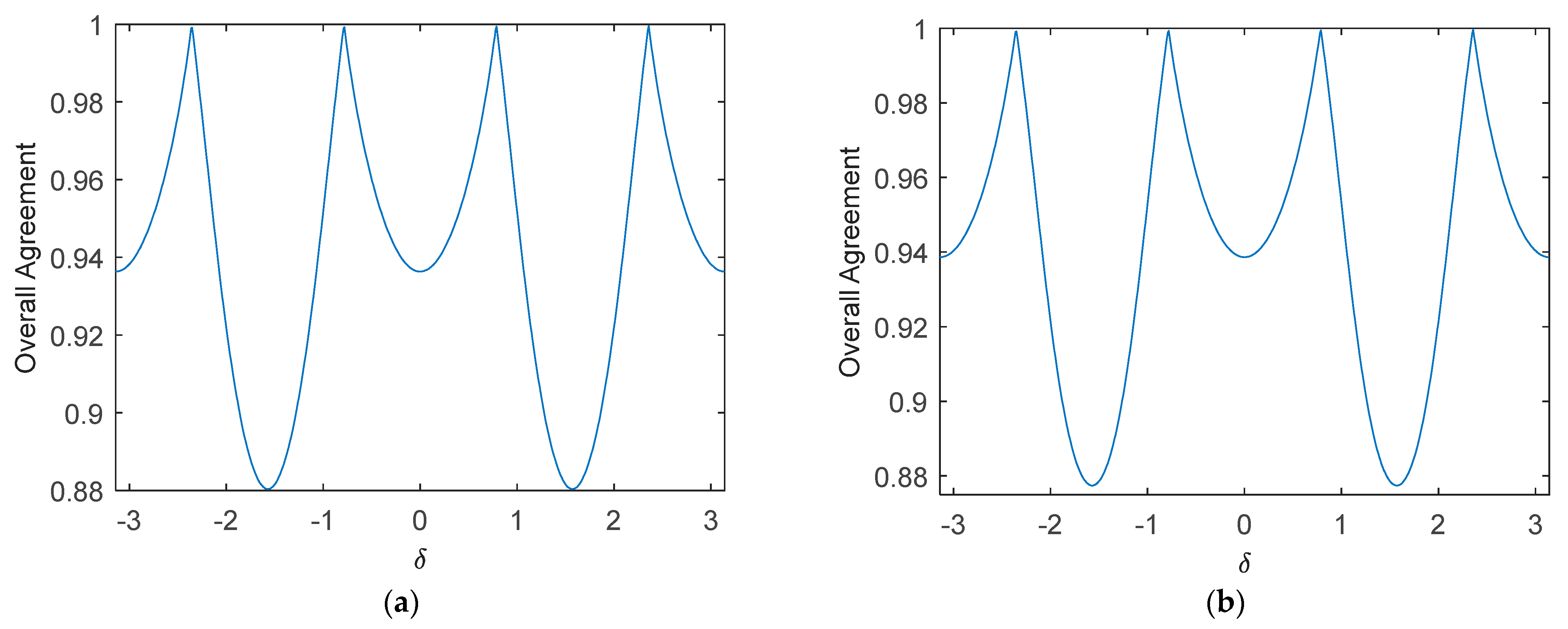
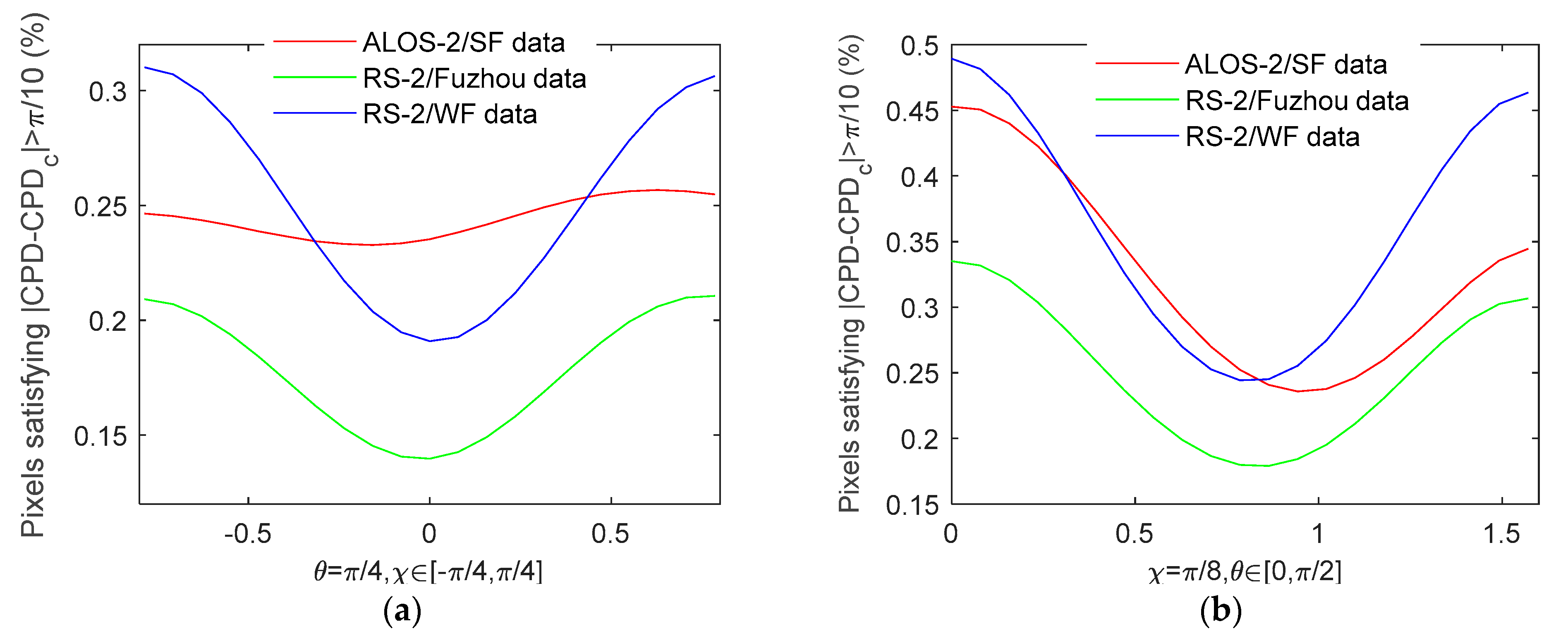
Figure 7, assuming that
is perfectly reconstructed, we show variation of the deviation percentages of the reconstructed CPD with the varying CP modes. It shows that for all test data sets, when the transmit wave channel amplitude is balanced, the estimated CPD is least affected by the assumption of reflection symmetry in the linear mode. The case that the channel amplitudes of the transmit wave are imbalanced is also tested. We found that the more the CP mode is linearly polarized, the closer the reconstructed CPD is to the real value. This implies that if applications are based on the pseudo quad-pol images and the algorithms applied subsequently are CPD-based, results obtained from the linear π/4 mode may be expected to be closer to that of the FP mode. For example, if CPD is used to discriminate surface and double-bounce scattering such as in the application of Freeman-Durden’s decomposition, the overall agreements in |CPD|>π/2 between the FP data (ALOS-2/PALSAR SF data) and the pseudo-FP data reconstructed by LSND are 88.75% and 84.72%, respectively, for the linear π/4 and circular modes, and by IterNVD the agreements are 89.35% and 81.34%, respectively.
Another application is carried out for example, which is the crop type classification by using the RS-2 Wallerfing data. The iterative Wishart classifier [
23] is used to perform the classification, with 5% pixels randomly selected as the training samples based on ground data. For each data set, same training samples are used for all the subsequent experimental implementation. Although several studies [
3,
4,
24] have been conducted on the comparison of the performances of CP, pseudo quad-pol, and FP data for terrain type classification, there is rare study giving a clear illustration on the variation of the overall classification accuracies under different circumstances. In
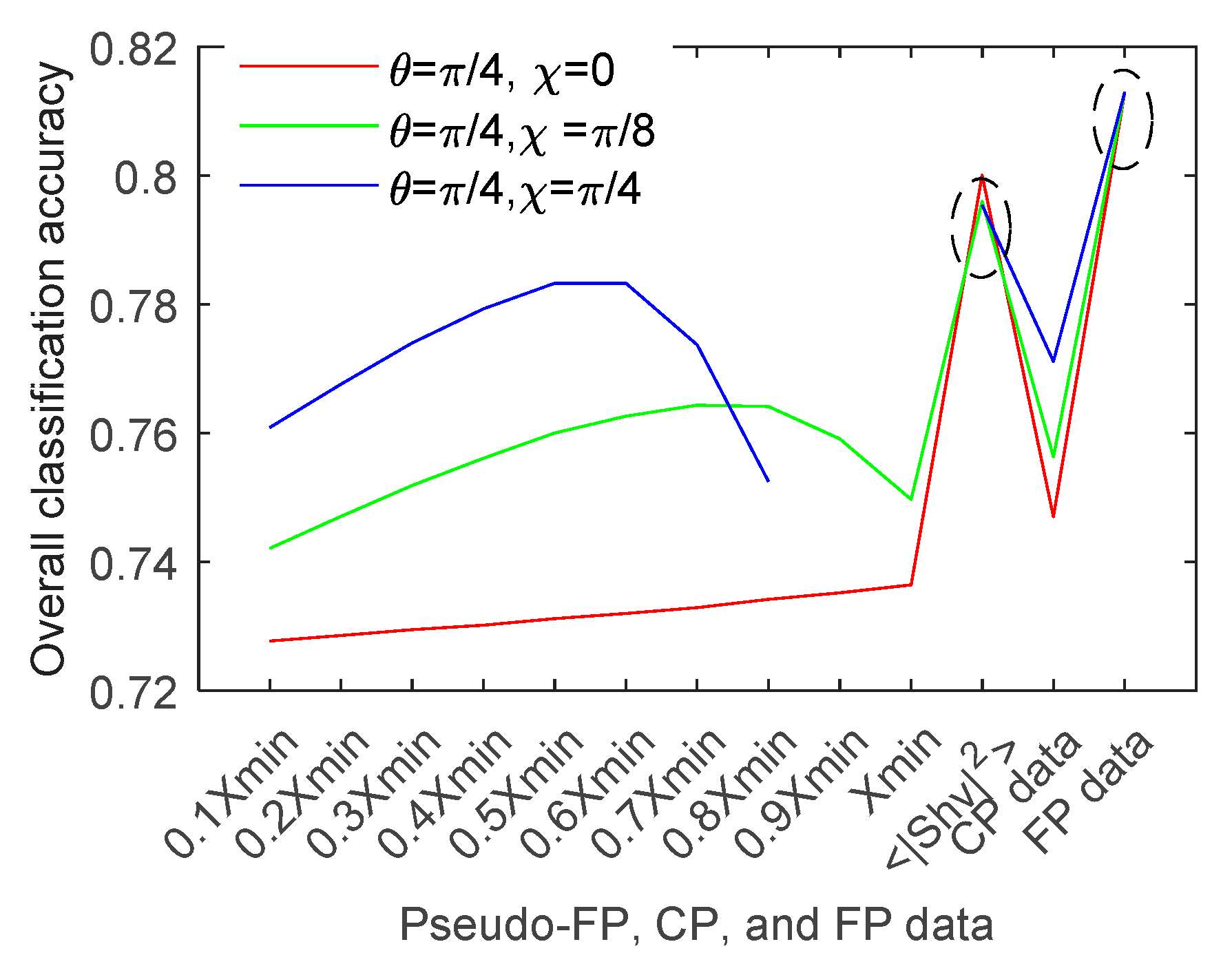
Figure 8, by using the Wallerfing data acquired by RADARSAT-2 on May 28, 2014, we tested the classification performances of the reconstructed data, the original 2 × 2 CP covariance matrix data, and the original 3 × 3 FP covariance matrix data. The reconstructed
is assumed to be
with
, where
is the upper bound for the cross-pol term in estimation. By this means, the pseudo FP data is accordingly reconstructed. It shows that compared to the original CP data, the reconstructed data with the accurately estimated
greatly improve the classification accuracy, especially for the linear CP mode, in which case the classification accuracy is improved by 5.3%. For the circular mode, when the estimated
is too large, the classification accuracy will deteriorate dramatically. In
Figure 8, we did not give the classification rates in the cases of
and
for the circular mode, because in both cases the term
of the reconstructed coherency matrix is close to 0 or even negative for a certain amount of pixels, for instance, 15% pixels in the
case and 23% in the
case. However, if the estimation is accurate,
Figure 8 shows that in general the circular mode is better for agriculture field classification.
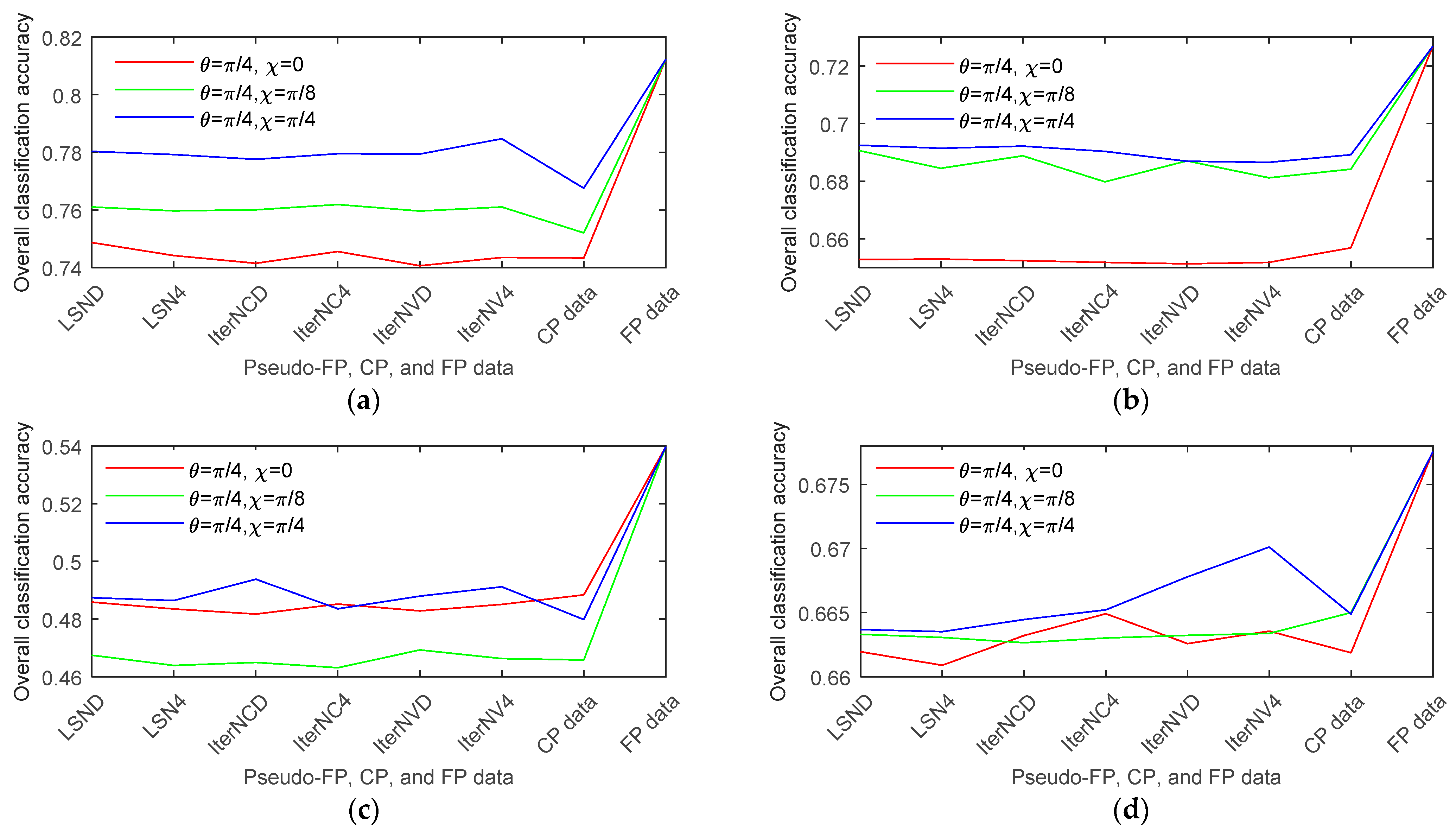
Next we consider the performances of the pseudo quad-pol data sets reconstructed via the test methods for multi-phase crop classification. The overall classification accuracies of the 6 methods, and those of the original CP as well as the FP data are shown in
Figure 9. We observe that the circular mode performs best, which is in accordance with the analysis in
Figure 8. However, for the multi-phase data sets, due to different phenology periods and disturbance of environmental changes, the best method evaluated in terms of overall classification accuracy varies. However, in general, data reconstructed by the iterative approach with the decomposition-based model provides comparatively better and stable classification accuracies if the Wishart classifier is applied. It also shows that classification carried out on the reconstructed data is better than that on the original CP data.