Evaluation of Pre-Earthquake Anomalies of Borehole Strain Network by Using Receiver Operating Characteristic Curve
Abstract
1. Introduction
2. Data and Observations
2.1. Borehole Strain Observations
2.2. Studied Earthquakes
2.3. Tectonic Settings in Brief
3. Data Analysis
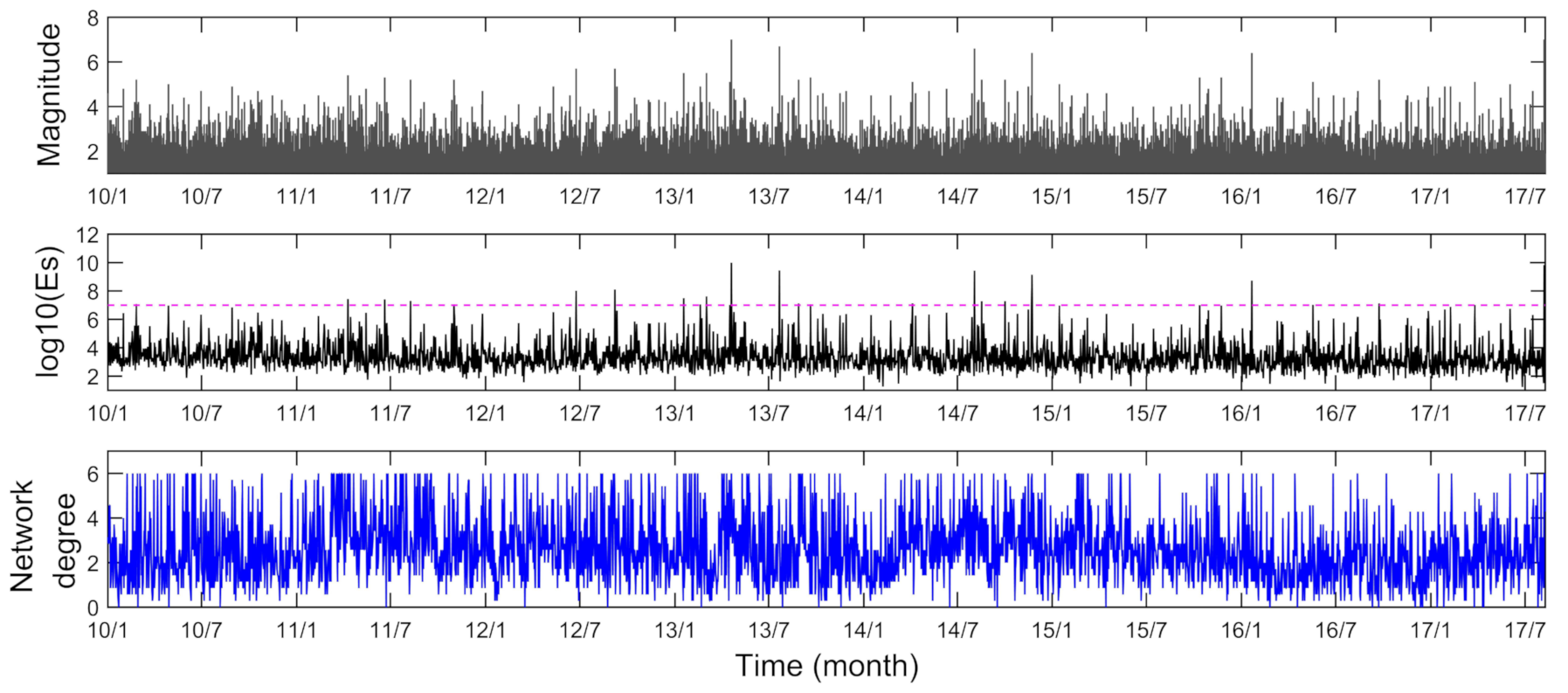
3.1. Extracting Network Anomalies of Borehole Strain
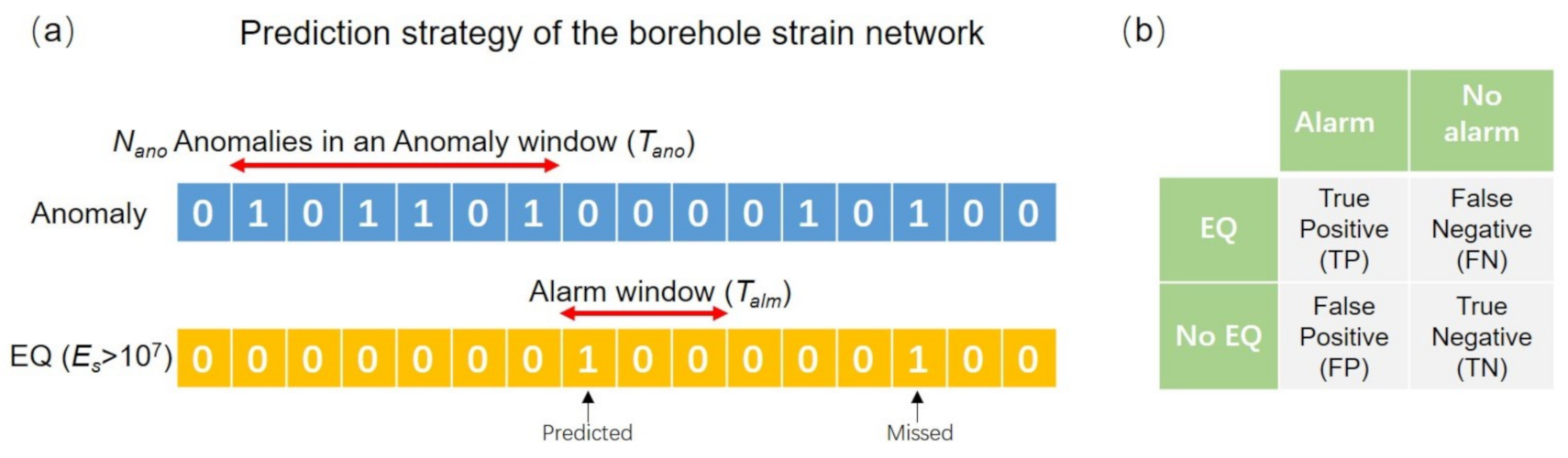
3.2. Evaluation of Strain Network Anomalies and Earthquake Occurrence
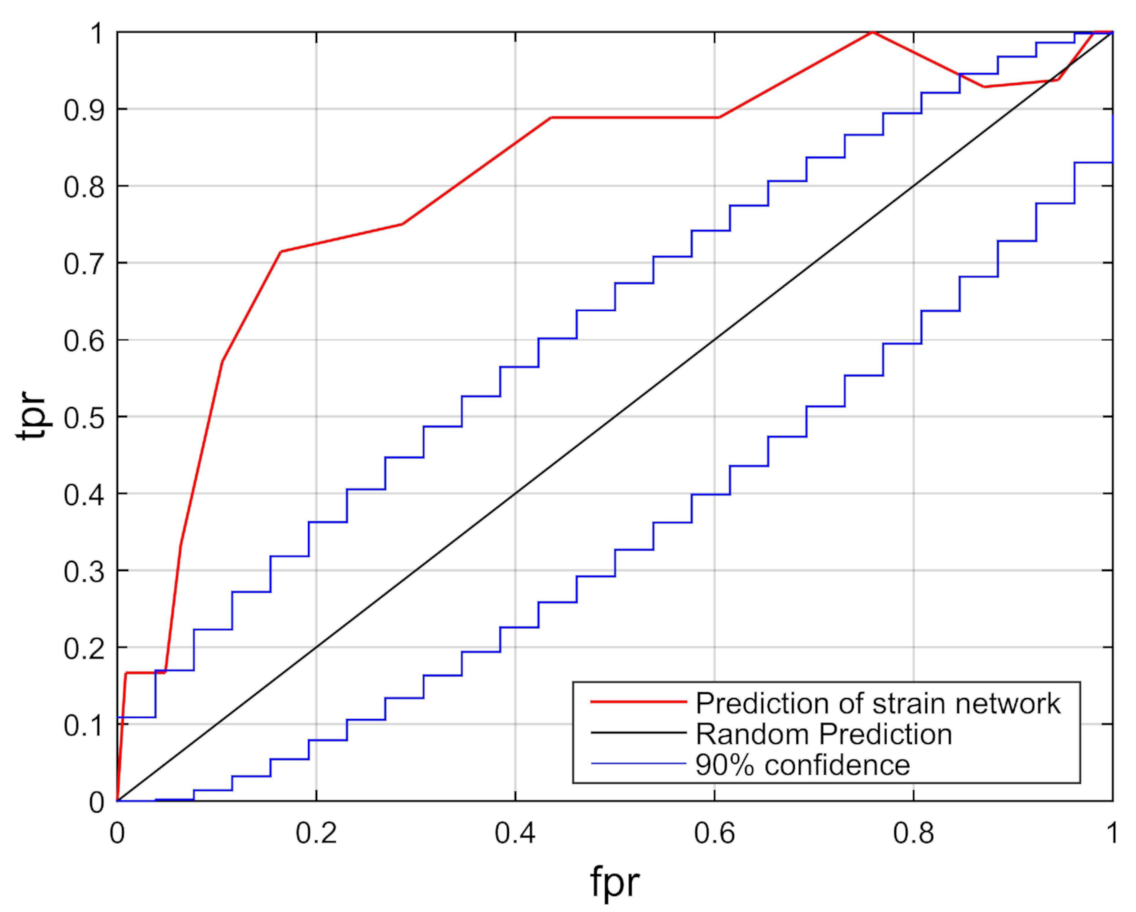
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Noda, H.; Nakatani, M.; Hori, T. Large nucleation before large earthquakes is sometimes skipped due to cascade-up-Implications from a rate and state simulation of faults with hierarchical asperities. J. Geophys. Res. Solid Earth 2013, 118, 2924–2952. [Google Scholar] [CrossRef]
- Wu, W.; Su, X.; Meng, G.; Li, C. Crustal deformation prior to the 2017 Jiuzhaigou, northeastern Tibetan Plateau (China), Ms 7.0 earthquake derived from GPS observations. Remote Sens. 2018, 10, 2028. [Google Scholar] [CrossRef]
- Li, S.; Tao, T.; Gao, F.; Qu, X.; Zhu, Y.; Huang, J.; Wang, Q. Interseismic Coupling beneath the Sikkim–Bhutan Himalaya Constrained by GPS Measurements and Its Implication for Strain Segmentation and Seismic Activity. Remote Sens. 2020, 12, 2202. [Google Scholar] [CrossRef]
- Johnston, M.; Borcherdt, R.; Linde, A.; Gladwin, M. Continuous borehole strain and pore pressure in the near field of the 28 September 2004 M 6.0 Parkfield, California, earthquake: Implications for nucleation, fault response, earthquake prediction, and tremor. Bull. Seismol. Soc. Am. 2006, 96, S56–S72. [Google Scholar] [CrossRef]
- Santis, A.D.; Balasis, G.; Pavon-Carrasco, F.J.; Cianchini, G.; Mandea, M. Potential earthquake precursory pattern from space: The 2015 Nepal event as seen by magnetic Swarm satellites. Earth Planet. Sci. Lett. 2017, 461, 119–126. [Google Scholar] [CrossRef]
- Qiu, Z.H.; Zhang, B.H.; Chi, S.L.; Tang, L.; Song, M. Abnormal strain changes observed at Guza before the Wenchuan earthquake. Sci. China Earth Sci. 2011, 54, 233–240. [Google Scholar] [CrossRef]
- Zhang, L.; Cao, D.; Zhang, J. Strain Observation Affected by Groundwater-Level Change in Seismic Precursor Monitoring. Pure Appl. Geophys. 2017, 174, 981–996. [Google Scholar] [CrossRef]
- Kong, X.; Li, N.; Lin, L.; Xiong, P.; Qi, J. Relationship of Stress changes and anomalies in OLR data of the Wenchuan and Lushan earthquakes. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2966–2976. [Google Scholar] [CrossRef]
- Chi, C.; Zhu, K.; Yu, Z.; Fan, M.; Li, K.; Sun, H. Detecting Earthquake-Related Borehole Strain Data Anomalies With Variational Mode Decomposition and Principal Component Analysis: A Case Study of the Wenchuan Earthquake. IEEE Access 2019, 7, 157997–158006. [Google Scholar] [CrossRef]
- Parsons, T.; Ji, C.; Kirby, E. Stress changes from the 2008 Wenchuan earthquake and increased hazard in the Sichuan basin. Nature 2008, 454, 509–510. [Google Scholar] [CrossRef]
- Lai, G.; Ge, H.; Xue, L.; Brodsky, E.E.; Huang, F.; Wang, W. Tidal response variation and recovery following the Wenchuan earthquake from water level data of multiple wells in the nearfield. Tectonophysics 2014, 619, 115–122. [Google Scholar] [CrossRef]
- Kato, A.; Obara, K.; Igarashi, T.; Tsuruoka, H.; Nakagawa, S.; Hirata, N. Propagation of slow slip leading up to the 2011 Mw 9.0 Tohoku-Oki earthquake. Science 2012, 335, 705–708. [Google Scholar] [CrossRef]
- Skordas, E.; Sarlis, N. On the anomalous changes of seismicity and geomagnetic field prior to the 2011 Mw 9.0 Tohoku earthquake. J. Asian Earth Sci. 2014, 80, 161–164. [Google Scholar] [CrossRef]
- Meng, G.; Su, X.; Wu, W.; Nikolay, S.; Takahashi, H.; Ohzono, M.; Gerasimenko, M. Crustal Deformation of Northeastern China Following the 2011 Mw 9.0 Tohoku, Japan Earthquake Estimated from GPS Observations: Strain Heterogeneity and Seismicity. Remote Sens. 2019, 11, 3029. [Google Scholar] [CrossRef]
- Sturkell, E.; Ágústsson, K.; Linde, A.T.; Sacks, S.I.; Einarsson, P.; Sigmundsson, F.; Geirsson, H.; Pedersen, R.; LaFemina, P.C.; Ólafsson, H. New insights into volcanic activity from strain and other deformation data for the Hekla 2000 eruption. J. Volcanol. Geotherm. Res. 2013, 256, 78–86. [Google Scholar] [CrossRef]
- Sacks, I.S.; Linde, A.T.; Suyehiro, S.; Snoke, J.A. Slow earthquakes and stress redistribution. Nature 1978, 275, 599. [Google Scholar] [CrossRef]
- Sacks, I.S.; Linde, A.T.; Snoke, J.A.; Suyehiro, S. A Slow Earthquake Sequence Following the Izu-Oshima Earthquake of 1978. In Earthquake Prediction; American Geophysical Union (AGU): Washington, DC, USA, 2013; pp. 617–628. [Google Scholar] [CrossRef]
- Johnston, M.; Linde, A.; Agnew, D. Continuous borehole strain in the San Andreas fault zone before, during, and after the 28 June 1992, Mw 7.3 Landers, California, earthquake. Bull. Seismol. Soc. Am. 1994, 84, 799–805. [Google Scholar]
- Linde, A.T.; Johnston, M.J.S.; Gladwin, M.T.; Bilham, R.G.; Gwyther, R.L. A slow earthquake sequence on the San Andreas fault. Nature 1996, 383, 65–68. [Google Scholar] [CrossRef]
- Qi, L.; Jing, Z. Application of S transform in analysis of strain changes before and after Wenchuan earthquake. J. Geod. Geodyn. 2011, 31, 6–9. (In Chinese) [Google Scholar] [CrossRef]
- Qiu, Z.H.; Tang, L.; Zhang, B.; Guo, Y. In situ calibration of and algorithm for strain monitoring using Four-gauge borehole strainmeters (FGBS). J. Geophys. Res. Solid Earth 2013, 118, 1609–1618. [Google Scholar] [CrossRef]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Mandrekar, J.N. Receiver Operating Characteristic Curve in Diagnostic Test Assessment. J. Thorac. Oncol. 2010, 5, 1315–1316. [Google Scholar] [CrossRef]
- Molchan, G.M. Structure of optimal strategies in earthquake prediction. Tectonophysics 1991, 193, 267–276. [Google Scholar] [CrossRef]
- Molchan, G.; Kagan, Y. Earthquake prediction and its optimization. J. Geophys. Res. Solid Earth 1992, 97, 4823–4838. [Google Scholar] [CrossRef]
- Sarlis, N.V.; Christopoulos, S.R.G. Visualization of the significance of Receiver Operating Characteristics based on confidence ellipses. Comput. Phys. Commun. 2014, 185, 1172–1176. [Google Scholar] [CrossRef]
- Wang, T.; Zhuang, J.; Kato, T.; Bebbington, M. Assessing the potential improvement in short-term earthquake forecasts from incorporation of GPS data. Geophys. Res. Lett. 2013, 40, 2631–2635. [Google Scholar] [CrossRef]
- Han, P.; Hattori, K.; Zhuang, J.; Chen, C.H.; Liu, J.Y.; Yoshida, S. Evaluation of ULF seismo-magnetic phenomena in Kakioka, Japan by using Molchan’s error diagram. Geophys. J. Int. 2016, ggw404. [Google Scholar] [CrossRef]
- Sarlis, N.V.; Skordas, E.S.; Christopoulos, S.R.; Varotsos, P. Statistical significance of minimum of the order parameter fluctuations of seismicity before major earthquakes in Japan. Pure Appl. Geophys. 2016, 173, 165–172. [Google Scholar] [CrossRef]
- Kapplerab, K.N.; Schneidera, D.D.; MacLeana, L.S.; Bleiera, T.; Lemona, J.J. An algorithmic framework for investigating the temporal relationship of magnetic field pulses and earthquakes applied to California. Comput. Geosci. 2019, 133, 104317. [Google Scholar] [CrossRef]
- Sarlis, N.V.; Skordas, E.S.; Christopoulos, S.R.G.; Varotsos, P.A. Natural Time Analysis: The Area under the Receiver Operating Characteristic Curve of the Order Parameter Fluctuations Minima Preceding Major Earthquakes. Entropy 2020, 22, 583. [Google Scholar] [CrossRef]
- Marzocchi, W.; Melini, D. On the earthquake predictability of fault interaction models. Geophys. Res. Lett. 2014, 41, 8294–8300. [Google Scholar] [CrossRef]
- Papadopoulos, G.A.; Agalos, A.; Minadakis, G.; Triantafyllou, I.; Krassakis, P. Short-Term Foreshocks as Key Information for Mainshock Timing and Rupture: The Mw6.8 25 October 2018 Zakynthos Earthquake, Hellenic Subduction Zone. Sensors 2020, 20, 5681. [Google Scholar] [CrossRef]
- Hattori, K.; Serita, A.; Yoshino, C.; Hayakawa, M.; Isezaki, N. Singular spectral analysis and principal component analysis for signal discrimination of ULF geomagnetic data associated with 2000 Izu Island Earthquake Swarm. Phys. Chem. Earth Parts A/B/C 2006, 31, 281–291. [Google Scholar] [CrossRef]
- Reasenberg, P. Second-order moment of central California seismicity, 1969–1982. J. Geophys. Res. Solid Earth 1985, 90, 5479–5495. [Google Scholar] [CrossRef]
- Wiemer, S. A software package to analyze seismicity: ZMAP. Seismol. Res. Lett. 2001, 72, 373–382. [Google Scholar] [CrossRef]
- Sisheng, L.; Zhu, Z. Characteristics of the seismic source stress field in the intersection region of Xianshuihe, Longmenshan and Anninghe faults. ACTA Seismol. Sin. 2000, 22, 457–464. (In Chinese) [Google Scholar]
- Xuan, S.; Shen, C.; Li, H.; Hao, H. Characteristics of subsurface density variations before the 4.20 Lushan M S7.0 earthquake in the Longmenshan area: Inversion results. Earthq. Sci. 2015, 28, 49–57. (In Chinese) [Google Scholar] [CrossRef]
- Yi, G.; Wen, X.; Xu, X. Study on Recurrence Behaviors of Strong Earthquakes for Several Entireties of Active Fault Zones in Sichuan-Yunnan Region. Earthq. Res. China 2002, 18, 267–276. (In Chinese) [Google Scholar]
- Zhang, P. Earthquake disaster prevention and reduction in China. Seismol. Geol. 2008, 30, 577–583. (In Chinese) [Google Scholar]
- Zhang, X.; Jiang, F.; Cui, D.; Zhang, X.; Li, R. Analysis of strain accumulation and influence of great earthquake observed by GPS in Sichuan and its adjacent areas. J. Geod. Geodyn. 2011, 31, 9–13. (In Chinese) [Google Scholar]
- Wang, W.; Zhang, P.; Zheng, D.; Pang, J. Late Cenozoic tectonic deformation of the Haiyuan fault zone in the northeastern margin of the Tibetan Plateau. Earth Sci. Front. 2014, 21, 266–274. (In Chinese) [Google Scholar]
- Abe, S.; Suzuki, N. Small-world structure of earthquake network. Phys. A Stat. Mech. Its Appl. 2004, 337, 357–362. [Google Scholar] [CrossRef]
- Min, L.; Xiao-Wei, Z.; Tian-Lun, C. A Modified Earthquake Model of Self-Organized Criticality on Small World Networks. Commun. Theor. Phys. 2004, 41, 557. [Google Scholar] [CrossRef]
- Jiménez, A.; Tiampo, K.F.; Posadas, A.M. Small world in a seismic network: The California case. Nonlinear Process. Geophys. 2008, 15, 389–395. [Google Scholar] [CrossRef]
- Baiesi, M.; Paczuski, M. Scale-free networks of earthquakes and aftershocks. Phys. Rev. E 2004, 69, 066106. [Google Scholar] [CrossRef]
- Pastén, D.; Torres, F.; Toledo, B.; Muñoz, V.; Rogan, J.; Valdivia, J.A. Time-Based Network Analysis Before and After the M_w 8.3 Illapel Earthquake 2015 Chile. Pure Appl. Geophys. 2016, 173, 2267–2275. [Google Scholar] [CrossRef]
- Abe, S.; Suzuki, N. Main shocks and evolution of complex earthquake networks. Braz. J. Phys. 2009, 39, 428–430. [Google Scholar] [CrossRef]
- Chorozoglou, D.; Kugiumtzis, D.; Papadimitriou, E. Application of complex network theory to the recent foreshock sequences of Methoni (2008) and Kefalonia (2014) in Greece. Acta Geophys. 2017, 65, 543–553. [Google Scholar] [CrossRef]
- Yu, Z.; Hattori, K.; Zhu, K.; Chi, C.; Fan, M.; He, X. Detecting Earthquake-Related Anomalies of a Borehole Strain Network Based on Multi-Channel Singular Spectrum Analysis. Entropy 2020, 22, 1086. [Google Scholar] [CrossRef]
- Han, P.; Zhuang, J.; Hattori, K.; Chen, C.H.; Febriani, F.; Chen, H.; Yoshino, C.; Yoshida, S. Assessing the Potential Earthquake Precursory Information in ULF Magnetic Data Recorded in Kanto, Japan during 2000–2010: Distance and Magnitude Dependences. Entropy 2020, 22, 859. [Google Scholar] [CrossRef]
- Lalkhen, A.G.; McCluskey, A. Clinical tests: Sensitivity and specificity. Contin. Educ. Anaesth. Crit. Care Pain 2008, 8, 221–223. [Google Scholar] [CrossRef]
- Zechar, J.D.; Jordan, T.H. Testing alarm-based earthquake predictions. Geophys. J. Int. 2008, 172, 715–724. [Google Scholar] [CrossRef]
- Han, P.; Hattori, K.; Hirokawa, M.; Zhuang, J.; Chen, C.H.; Febriani, F.; Yamaguchi, H.; Yoshino, C.; Liu, J.Y.; Yoshida, S. Statistical analysis of ULF seismomagnetic phenomena at Kakioka, Japan, during 2001–2010. J. Geophys. Res. Space Phys. 2014, 119, 4998–5011. [Google Scholar] [CrossRef]
- Hocke, K. Oscillations of global mean TEC. J. Geophys. Res. Phys. 2008, 113, 4302. [Google Scholar] [CrossRef]
- Kon, S.; Nishihashi, M.; Hattori, K. Ionospheric anomalies possibly associated with M >= 6 earthquakes in Japan during 1998–2011: Case studies and statistical study. J. Asian Earth Sci. 2011, 41, 410–420. [Google Scholar] [CrossRef]
- Hattori, K.; Han, P.; Yoshino, C.; Febriani, F.; Yamaguchi, H.; Chen, C.H. Investigation of ULF Seismo-Magnetic Phenomena in Kanto, Japan During 2000–2010: Case Studies and Statistical Studies. Surv. Geophys. 2013, 34, 293–316. [Google Scholar] [CrossRef]
- Němec, F.; Santolík, O.; Parrot, M.; Berthelier, J.J. Spacecraft observations of electromagnetic perturbations connected with seismic activity. Geophys. Res. Lett. 2008, 35, 544–548. [Google Scholar] [CrossRef]
- Huang, Q. Direction speciality of fault network and its self-organization evolution. Crustal Deform. Earthq. 1994, 14, 24–28. (In Chinese) [Google Scholar]
- Akopian, S.T. Open dissipative seismic systeMs and ensembles of strong earthquakes: Energy balance and entropy funnels. Geophys. J. Int. 2015, 201, 1618–1641. [Google Scholar] [CrossRef]
- Zhu, K.; Yu, Z.; Chi, C.; Fan, M.; Li, K. Negentropy anomaly analysis of the borehole strain associated with the Ms 8.0 Wenchuan earthquake. Nonlinear Process. Geophys. 2019, 26, 371–380. [Google Scholar] [CrossRef]
- Chen, C.H.; Su, X.; Cheng, K.C.; Meng, G.; Wen, S.; Han, P. Seismo-deformation anomalies associated with the M6. 1 Ludian earthquake on August 3, 2014. Remote Sens. 2020, 12, 1067. [Google Scholar] [CrossRef]
- Sarlis, N.; Skordas, E.; Lazaridou, M.; Varotsos, P. Investigation of seismicity after the initiation of a seismic electric signal activity until the main shock. Proc. Jpn. Acad. Ser. B 2008, 84, 331–343. [Google Scholar] [CrossRef] [PubMed]
- Sarlis, N.V.; Skordas, E.S.; Varotsos, P.A.; Nagao, T.; Kamogawa, M.; Tanaka, H.; Uyeda, S. Minimum of the order parameter fluctuations of seismicity before major earthquakes in Japan. Proc. Natl. Acad. Sci. USA 2013, 110, 13734–13738. [Google Scholar] [CrossRef] [PubMed]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Identifying the occurrence time of an impending major earthquake: A review. Earthq. Sci. 2017, 30, 209–218. [Google Scholar] [CrossRef]
- Christopoulos, S.R.G.; Skordas, E.S.; Sarlis, N.V. On the Statistical Significance of the Variability Minima of the Order Parameter of Seismicity by Means of Event Coincidence Analysis. Appl. Sci. 2020, 10, 662. [Google Scholar] [CrossRef]
- Xu, K.; Gan, W.; Wu, J. Pre-seismic deformation detected from regional GNSS observation network: A case study of the 2013 Lushan, eastern Tibetan Plateau (China), Ms7.0 earthquake. J. Asian Earth Sci. 2019, 180, 103859. [Google Scholar] [CrossRef]
- Scholz, C.H.; Sykes, L.R.; Aggarwal, Y.P. Earthquake prediction: A physical basis. Science 1973, 181, 803–810. [Google Scholar] [CrossRef]
- Qi, L.; Tan, K.; Zhao, B.; Zhang, C.; Lu, X.; Wang, D.; Yu, J. Slip rate change of East Kunlun fault and its stress effect on 2017 Jiuzhaigou earthquak. Chin. J. Geophys. 2019, 62, 912–922. [Google Scholar] [CrossRef]
- Mao, Z.; Chen, C.H.; Zhang, S.; Yisimayili, A.; Yu, H.; Yu, C.; Liu, J.Y. Locating Seismo-Conductivity Anomaly before the 2017 Mw 6.5 Jiuzhaigou Earthquake in China Using Far Magnetic Stations. Remote Sens. 2020, 12, 1777. [Google Scholar] [CrossRef]
- Chi, S.; Jing, Z.; Yi, C. Failure of self-consistent strain data before Wenchuan, Ludian and Kangding earthquakes and its relation with earthquake nucleation. Recent Dev. World Seismol. 2014, 12, 3–13. [Google Scholar] [CrossRef]
- Zhang, X.; Bai, Z.; Liu, X. Discussion on the Mechanism of Short-term Anomalies for Cross-fault Short-leveling before the 2016 Menyuan Ms6.4 Earthquake. J. Seismol. Res. 2020, 43, 644–650. (In Chinese) [Google Scholar]
- Chen, C.H.; Yeh, T.K.; Wen, S.; Meng, G.; Han, P.; Tang, C.C.; Liu, J.Y.; Wang, C.H. Unique Pre-Earthquake Deformation Patterns in the Spatial Domains from GPS in Taiwan. Remote Sens. 2020, 12, 366. [Google Scholar] [CrossRef]
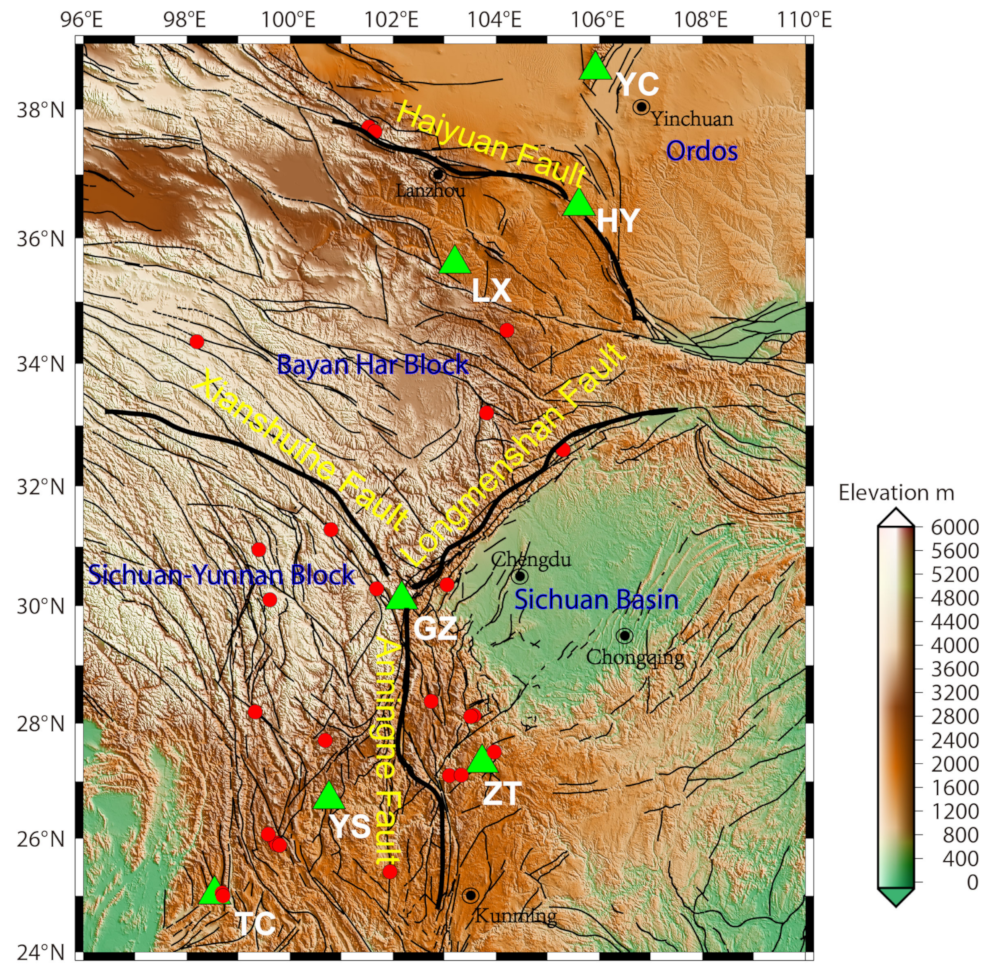

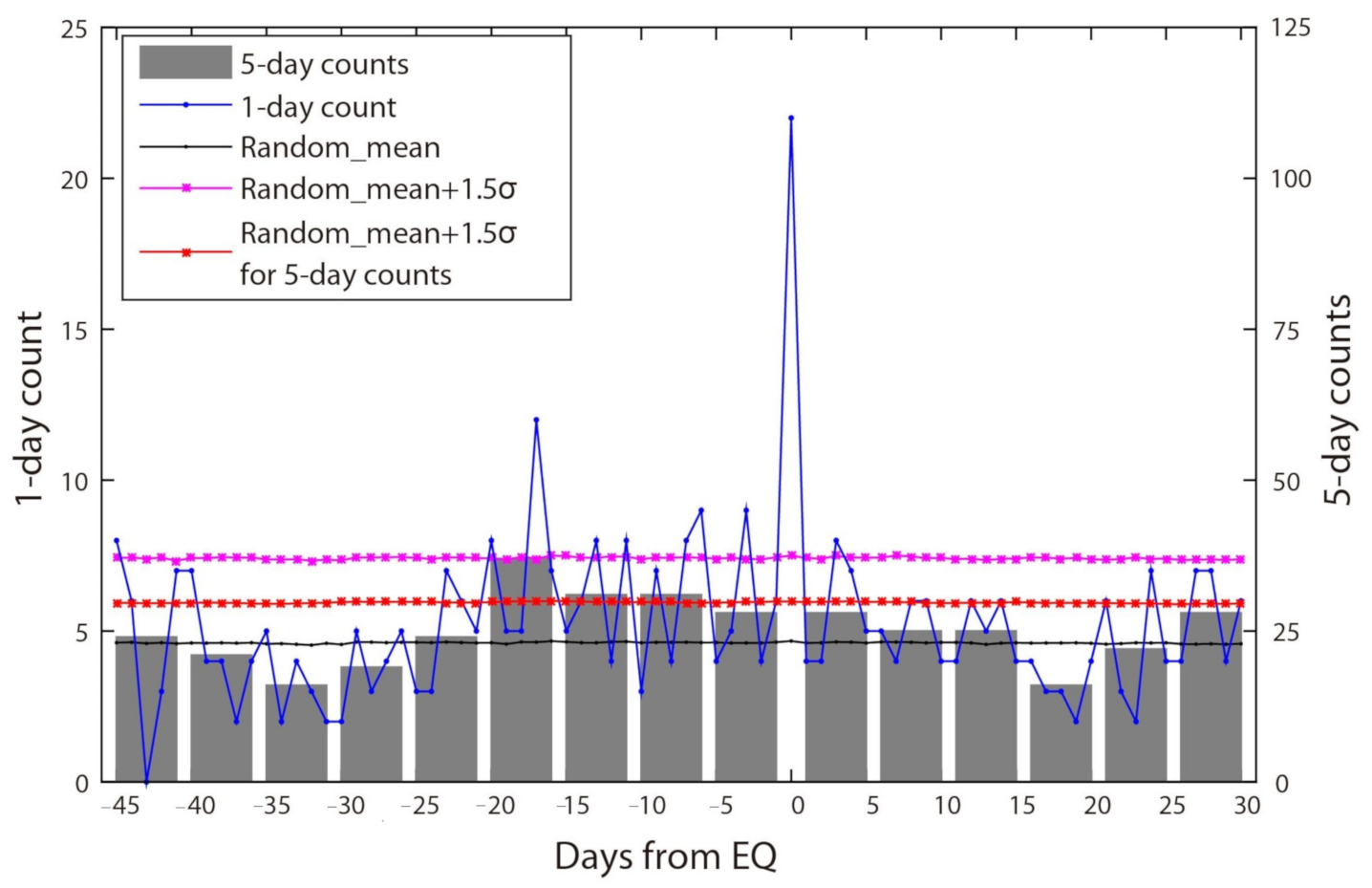
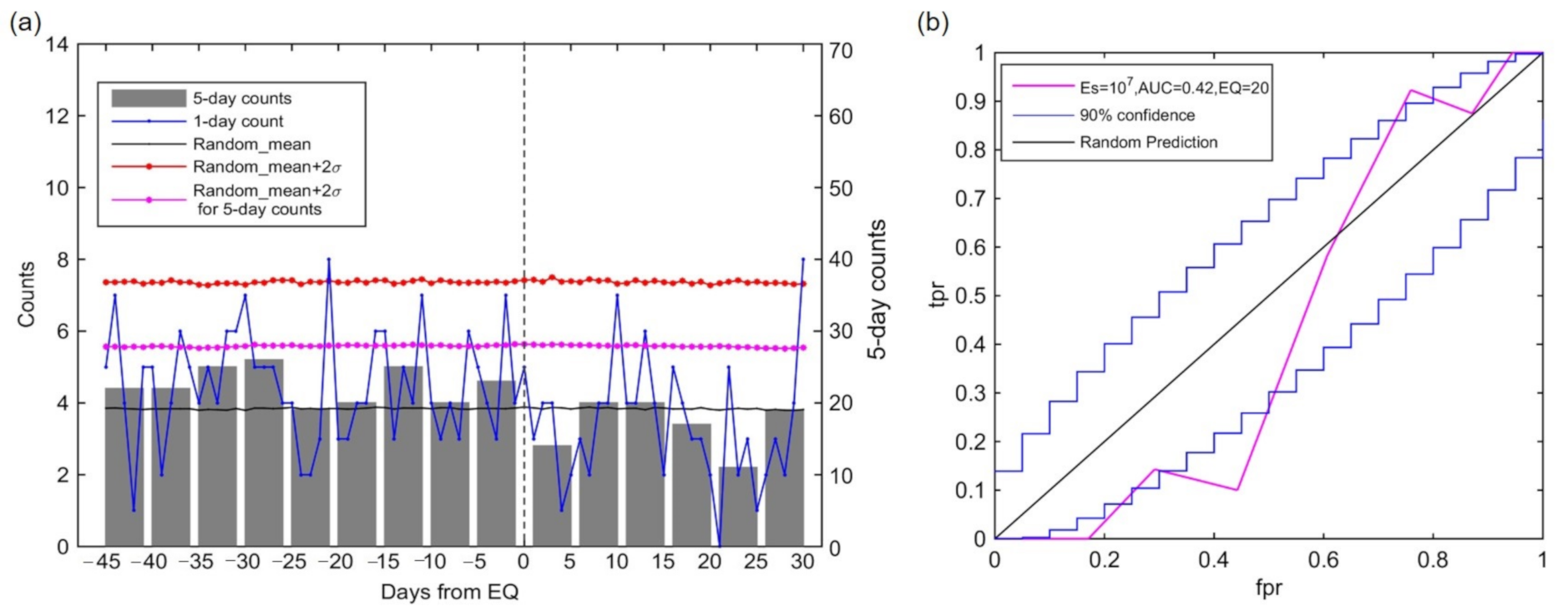

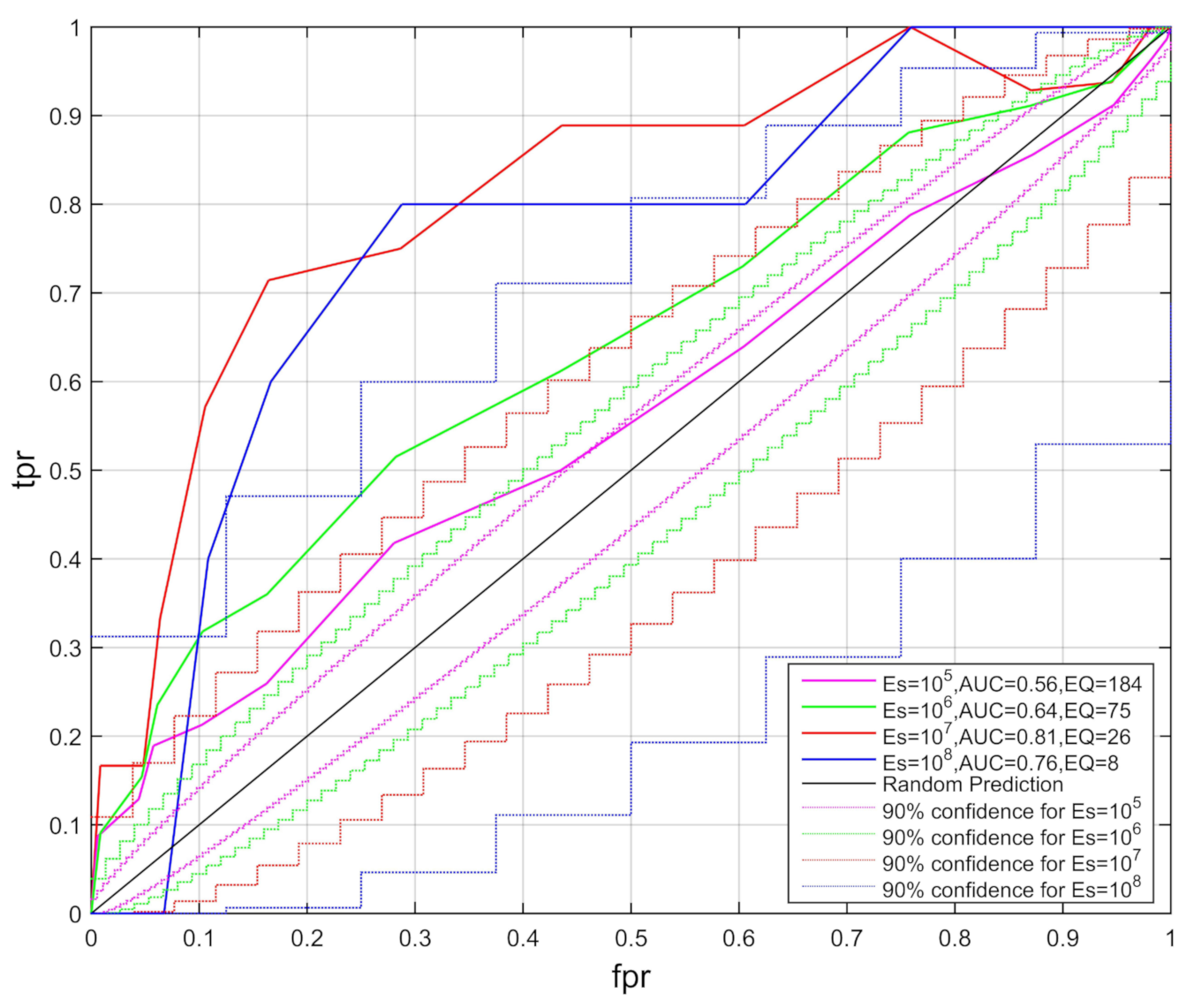

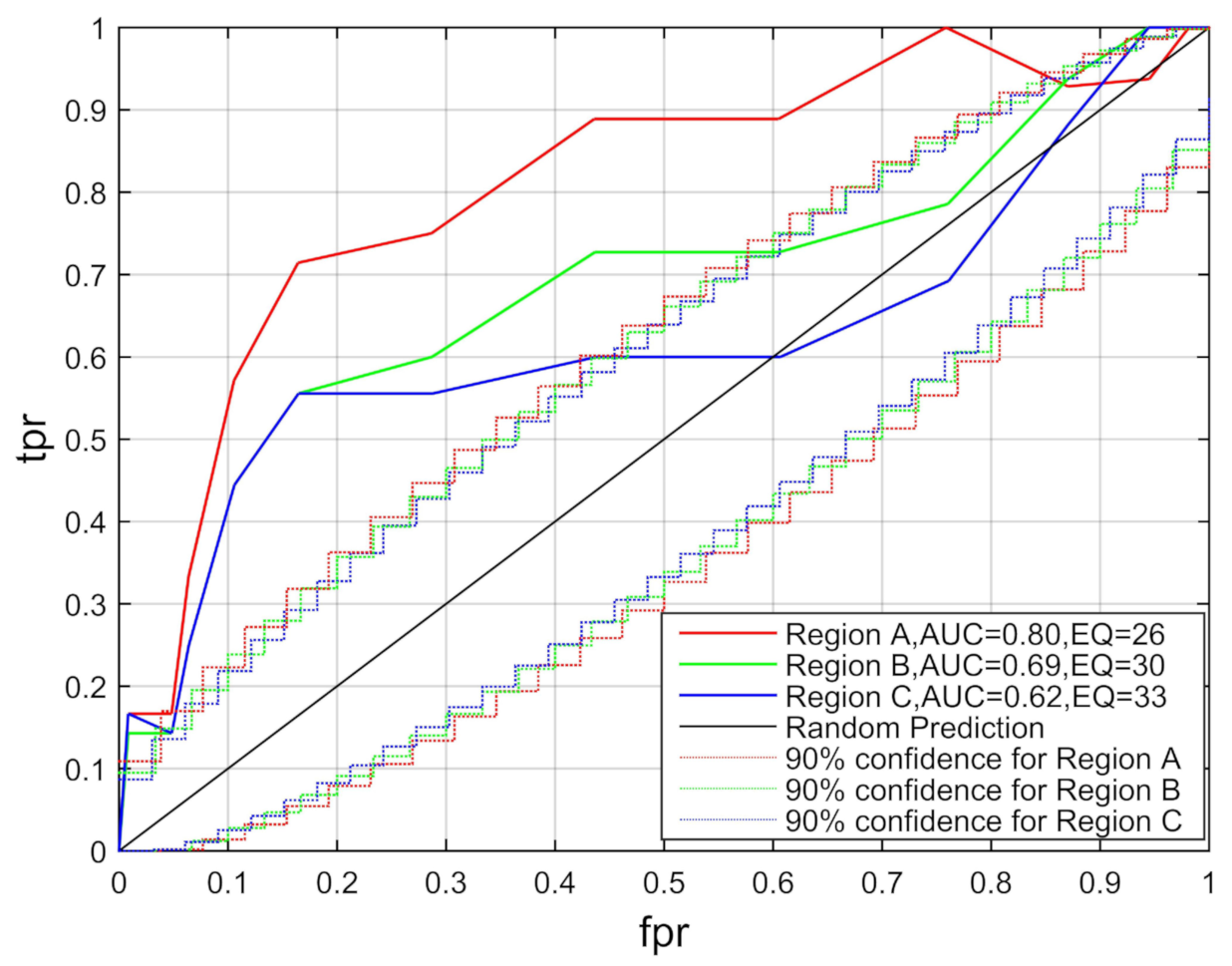
| Station Name | Locations | Depth (m) |
|---|---|---|
| YC | 38.61°N, 105.61°E | 50.00 |
| HY | 36.51°N, 105.93°E | 60.37 |
| LX | 35.60°N, 103.20°E | 44.70 |
| GZ | 30.11°N, 102.17°E | 41.00 |
| ZT | 27.32°N, 103.73°E | 45.00 |
| YS | 26.69°N, 100.76°E | 43.00 |
| TC | 25.02°N, 98.54°E | 45.00 |
| No. | Date | Locations | Depth (km) | Magnitude () | Es (lg) | Type of Fault |
|---|---|---|---|---|---|---|
| 1 | 25 February 2010 | 25.42°N, 101.94°E | 20 | 5.2 | 7.1 | right-lateral strike-slip |
| 2 | 10 April 2011 | 31.28°N, 100.80°E | 10 | 5.4 | 7.4 | left-lateral strike-slip |
| 3 | 20 June 2011 | 25.05°N, 98.69°E | 10 | 5.3 | 7.4 | |
| 4 | 9 August 2011 | 25.00°N, 98.70°E | 11 | 5.2 | 7.3 | |
| 5 | 1 November 2011 | 32.60°N, 105.30°E | 6 | 5.2 | 7.1 | reverse |
| 6 | 24 June 2012 | 27.71°N, 100.69°E | 11 | 5.7 | 8.0 | normal |
| 7 | 7 September 2012 | 27.51°N, 103.97°E | 14 | 5.7 | 8.3 | strike-slip |
| 8 | 18 January 2013 | 30.95°N, 99.40°E | 15 | 5.5 | 7.4 | left-lateral strike-slip |
| 9 | 19 February 2013 | 27.10°N, 103.10°E | 10 | 4.9 | 7.1 | |
| 10 | 3 March 2013 | 25.93°N, 99.72°E | 9 | 5.5 | 7.6 | normal |
| 11 | 17 April 2013 | 25.90°N, 99.75°E | 10 | 5.1 | 7.0 | |
| 12 | 20 April 2013 | 30.30°N, 102.90°E | 17 | 7.0 | 10.0 | reverse |
| 13 | 22 July 2013 | 34.54°N, 104.21°E | 15 | 6.7 | 9.4 | reverse |
| 14 | 31 August 2013 | 28.15°N, 99.35°E | 10 | 5.9 | 8.2 | normal |
| 15 | 20 September 2013 | 37.73°N, 101.53°E | 15 | 5.3 | 7.1 | |
| 16 | 5 April 2014 | 28.14°N, 103.57°E | 13 | 5.1 | 7.1 | |
| 17 | 3 August 2014 | 27.11°N, 103.33°E | 10 | 6.6 | 9.4 | left-lateral strike-slip |
| 18 | 17 August 2014 | 28.12°N, 103.51°E | 7 | 5.2 | 7.3 | |
| 19 | 1 October 2014 | 28.38°N, 102.74°E | 10 | 5.2 | 7.3 | |
| 20 | 22 November 2014 | 30.29°N, 101.68°E | 20 | 6.4 | 9.1 | strike-slip |
| 21 | 12 October 2015 | 34.36°N, 98.20°E | 10 | 5.3 | 7.0 | |
| 22 | 21 January 2016 | 37.66°N, 101.65°E | 10 | 6.4 | 8.7 | reverse |
| 23 | 18 May 2016 | 26.08°N, 99.58°E | 17 | 5.1 | 7.1 | |
| 24 | 23 September 2016 | 30.11°N, 99.61°E | 16 | 5.2 | 7.4 | |
| 25 | 27 March 2017 | 25.89°N, 99.80°E | 12 | 5.1 | 7.2 | |
| 26 | 8 August 2017 | 33.20°N, 103.82°E | 10 | 7.0 | 9.8 | left-lateral strike-slip |
| The date refers to UTC+8 time. is the largest magnitude on one day. | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Z.; Hattori, K.; Zhu, K.; Fan, M.; Marchetti, D.; He, X.; Chi, C. Evaluation of Pre-Earthquake Anomalies of Borehole Strain Network by Using Receiver Operating Characteristic Curve. Remote Sens. 2021, 13, 515. https://doi.org/10.3390/rs13030515
Yu Z, Hattori K, Zhu K, Fan M, Marchetti D, He X, Chi C. Evaluation of Pre-Earthquake Anomalies of Borehole Strain Network by Using Receiver Operating Characteristic Curve. Remote Sensing. 2021; 13(3):515. https://doi.org/10.3390/rs13030515
Chicago/Turabian StyleYu, Zining, Katsumi Hattori, Kaiguang Zhu, Mengxuan Fan, Dedalo Marchetti, Xiaodan He, and Chengquan Chi. 2021. "Evaluation of Pre-Earthquake Anomalies of Borehole Strain Network by Using Receiver Operating Characteristic Curve" Remote Sensing 13, no. 3: 515. https://doi.org/10.3390/rs13030515
APA StyleYu, Z., Hattori, K., Zhu, K., Fan, M., Marchetti, D., He, X., & Chi, C. (2021). Evaluation of Pre-Earthquake Anomalies of Borehole Strain Network by Using Receiver Operating Characteristic Curve. Remote Sensing, 13(3), 515. https://doi.org/10.3390/rs13030515









