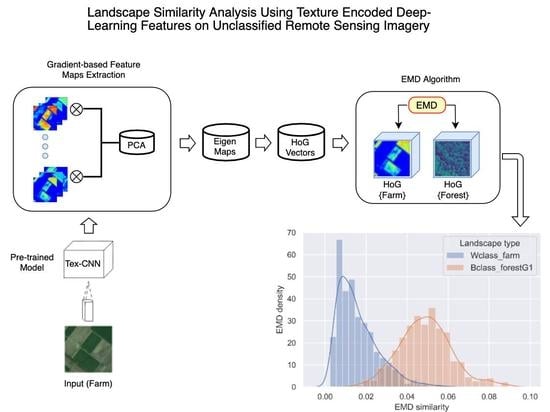
Landscape Similarity Analysis Using Texture Encoded Deep-Learning Features on Unclassified Remote Sensing Imagery
Abstract
1. Introduction
2. Related Work
2.1. Representing Patterns in CNN Feature Maps
2.2. CNN-Feature-Based Image Retrieval
3. Materials and Methods
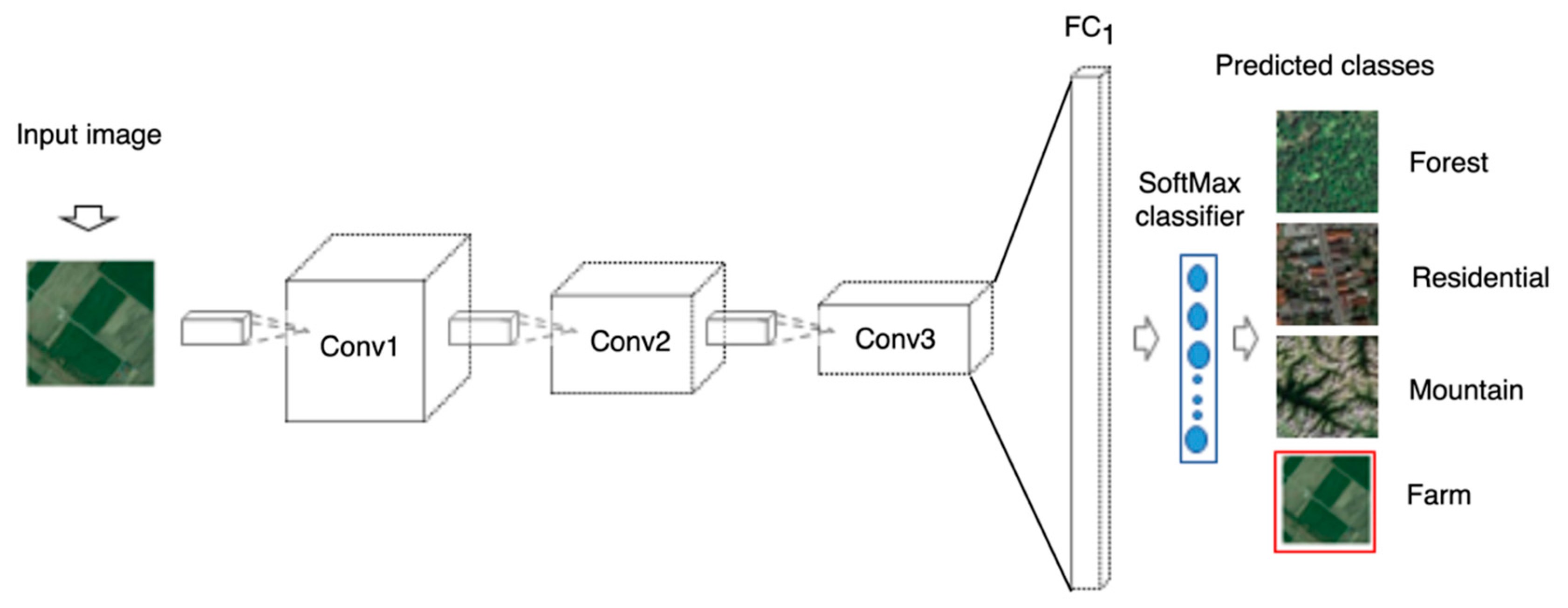
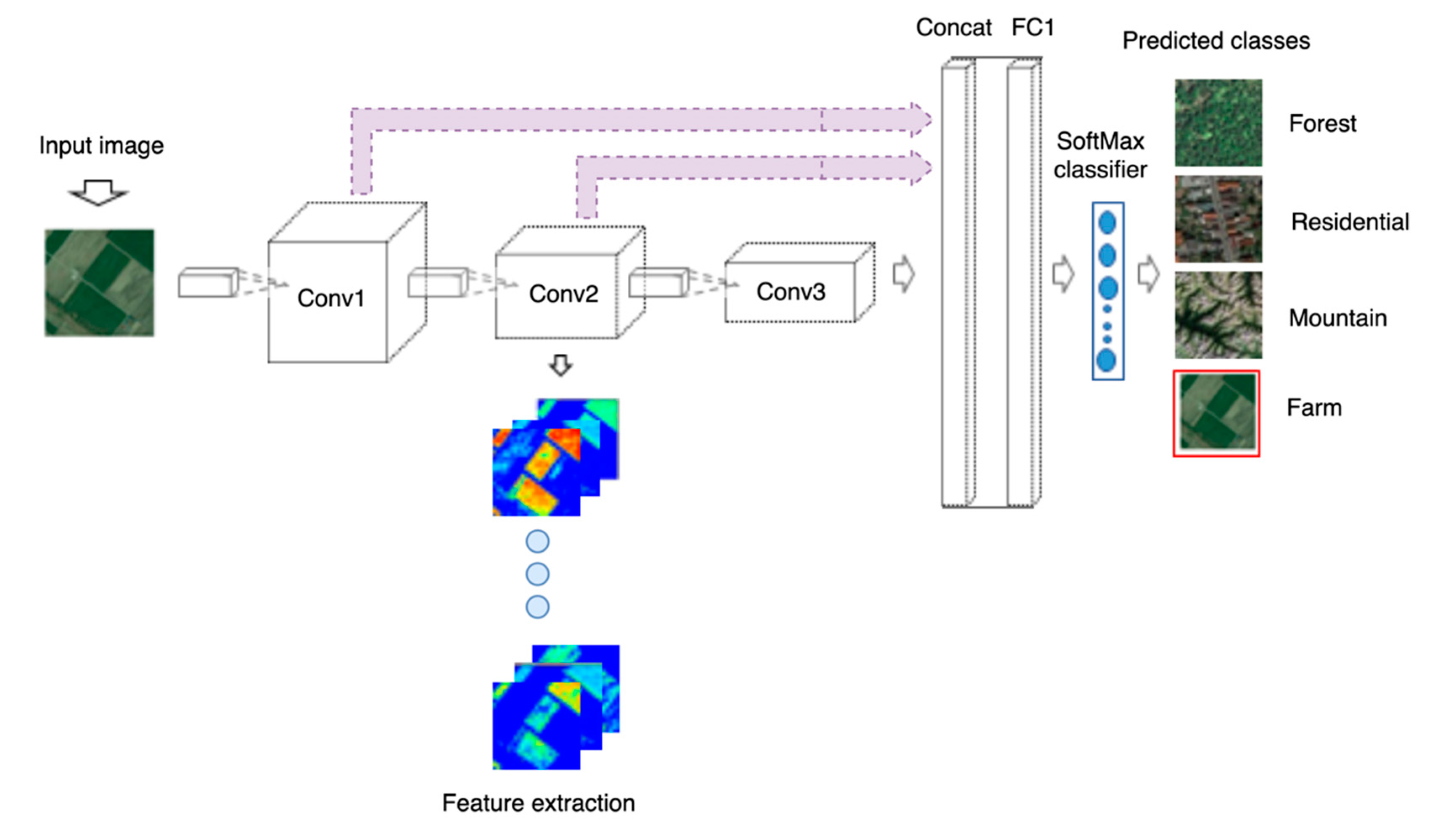
3.1. Models’ Architecture
3.2. Model Parameterization and Training
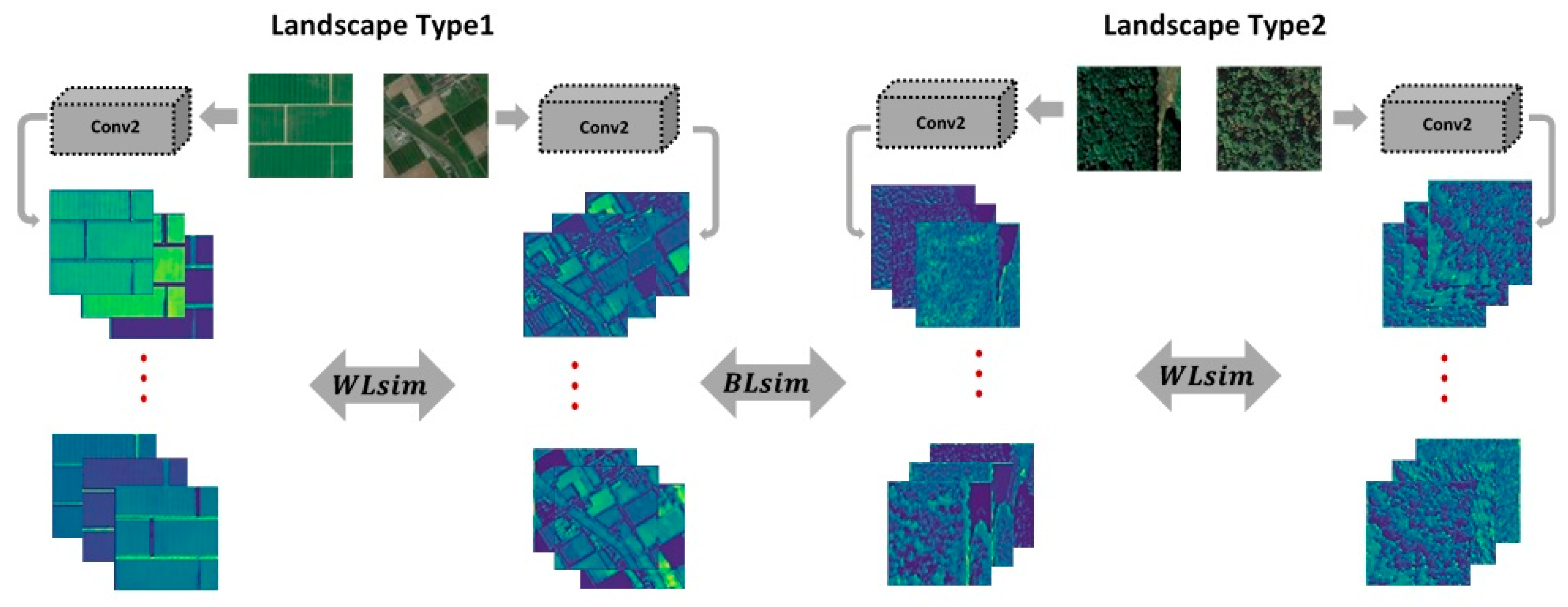
3.3. Application Context: Landscape Comparison
3.4. Data Augmentation
3.5. Activation/Feature Maps Derivation
3.6. Extracting HoG Vector from Feature Maps
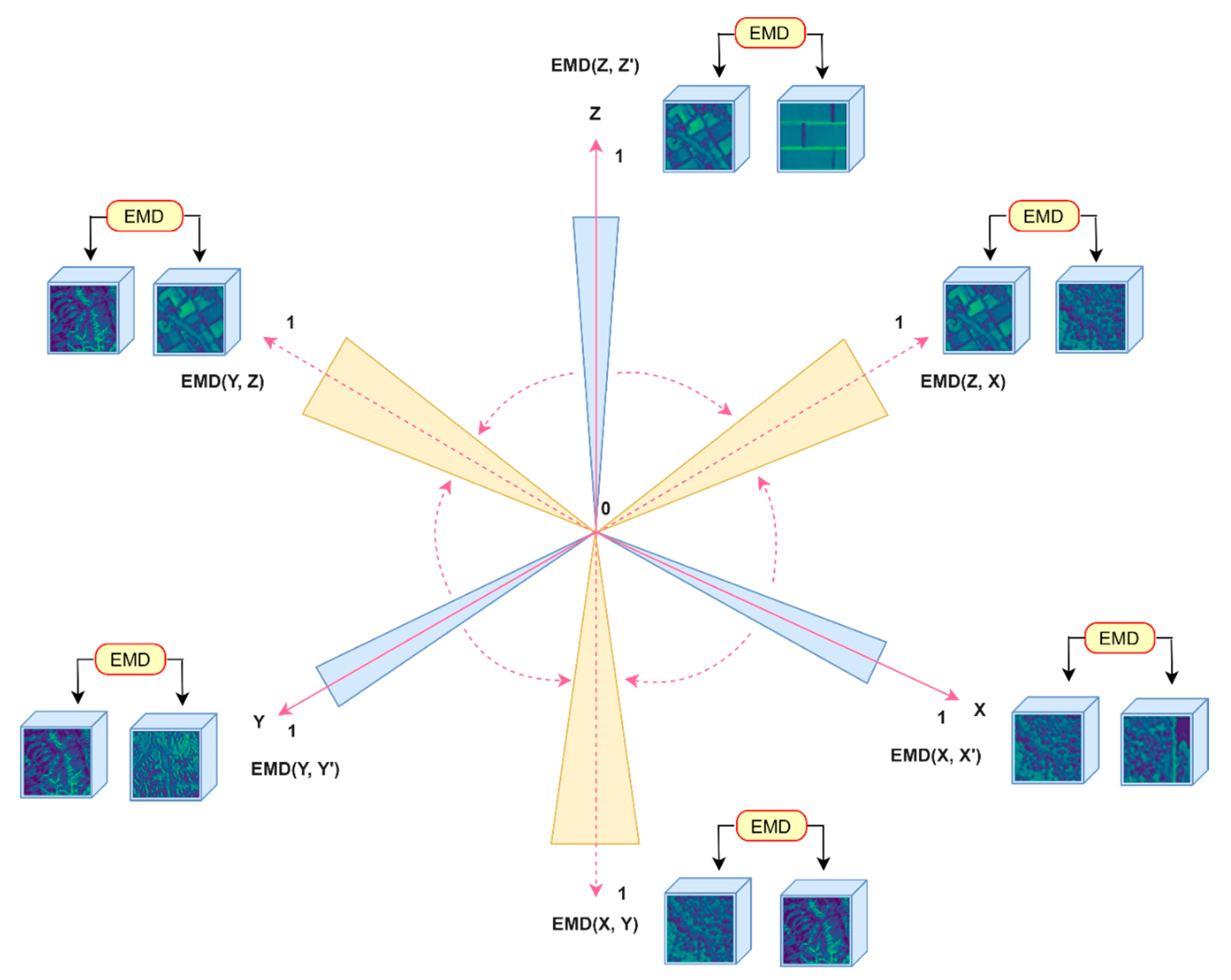
3.7. Formulating the Feature Map Comparison Metric
4. Experimental Results
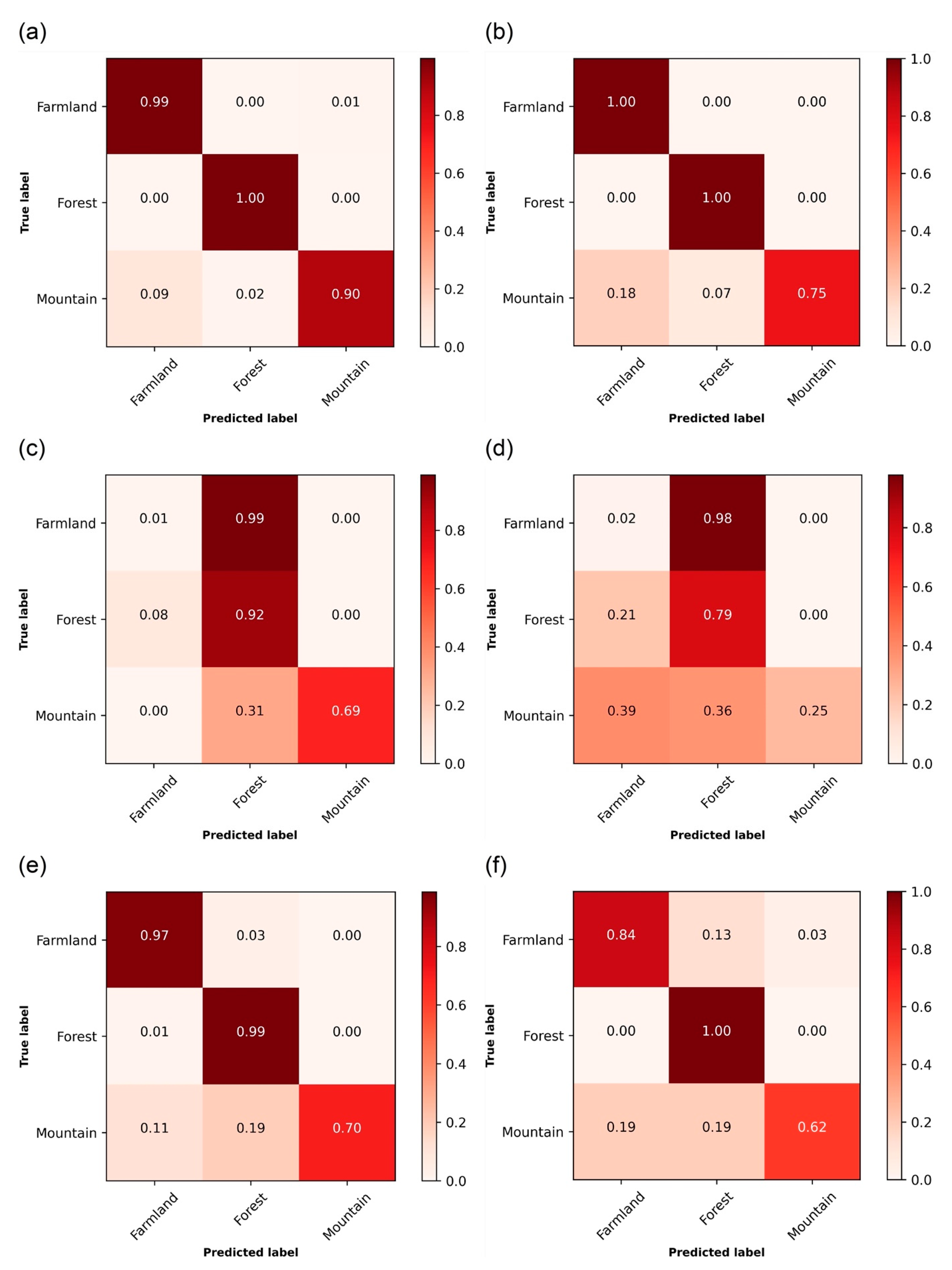
4.1. Landscape Type Prediction Models
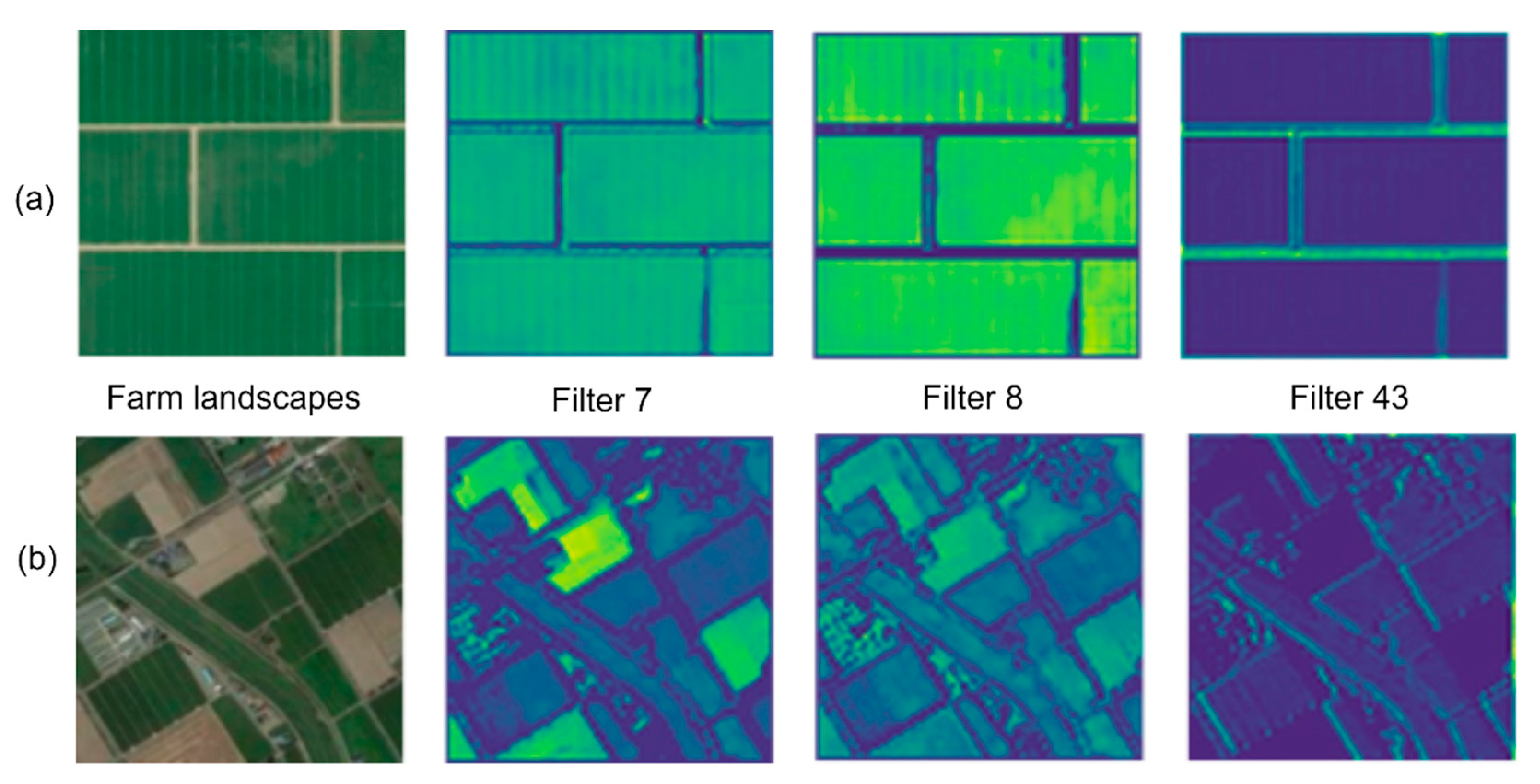
4.2. Exploring CNN Layer Features Suitability for Landscape Comparison
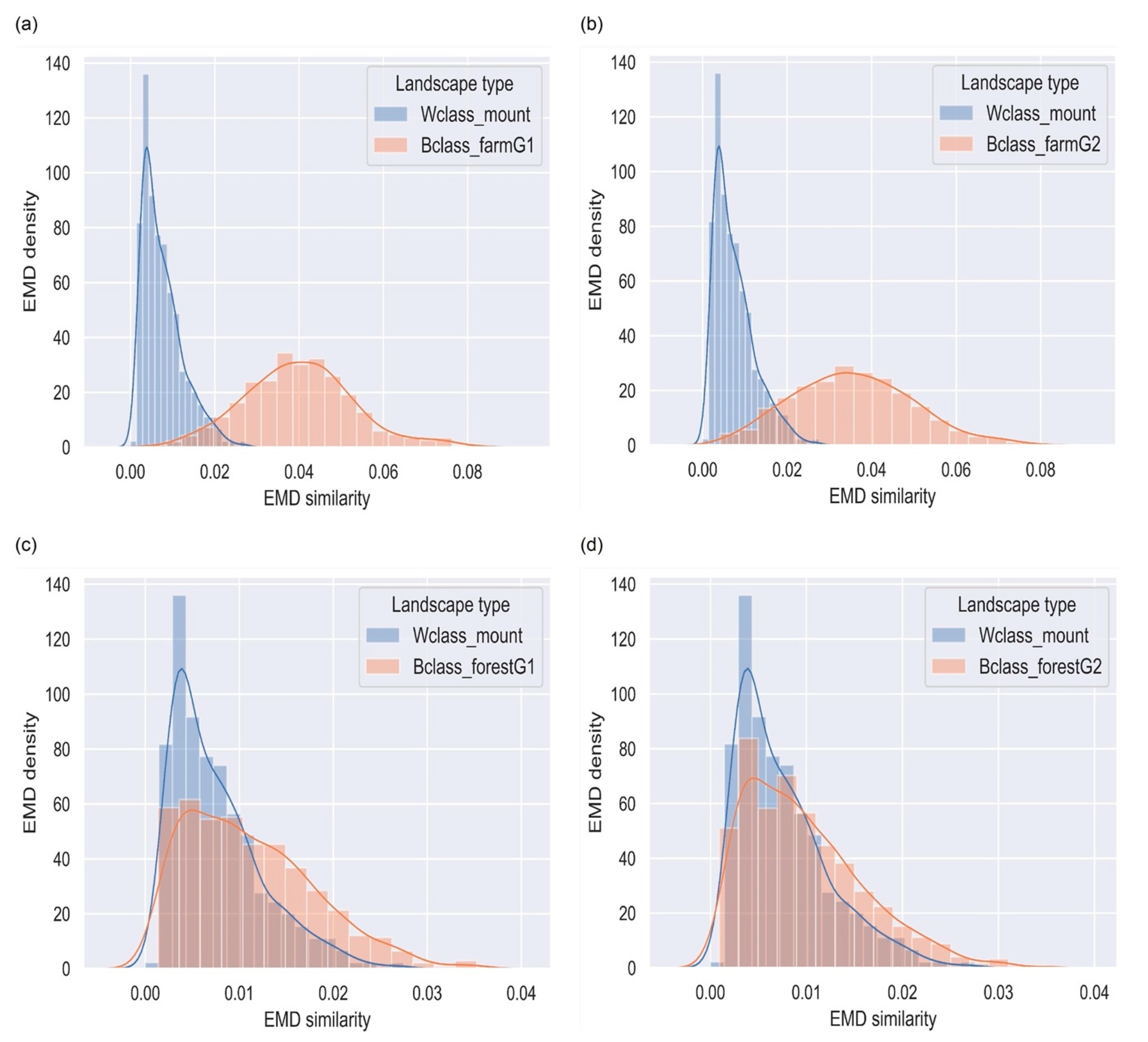
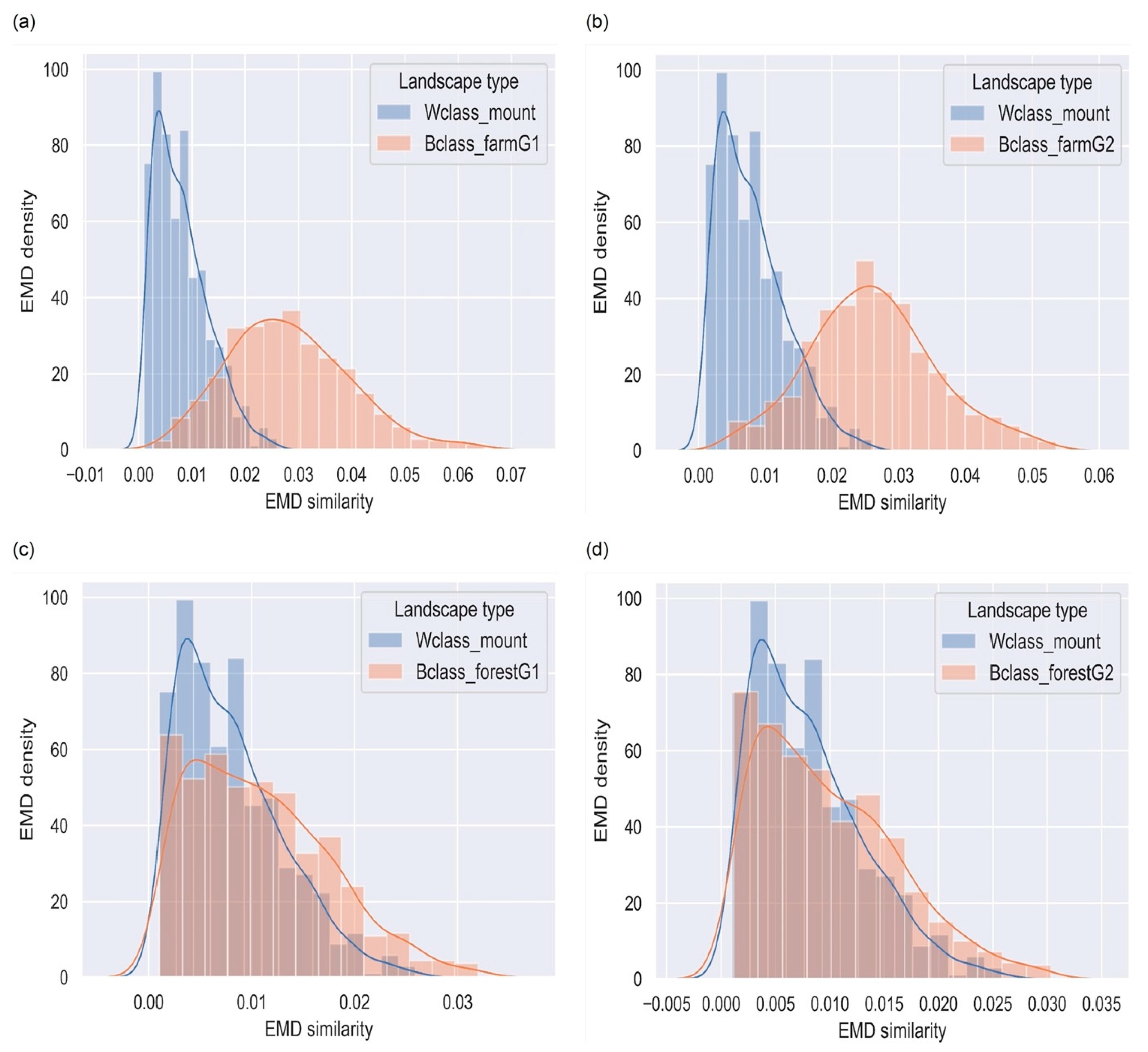
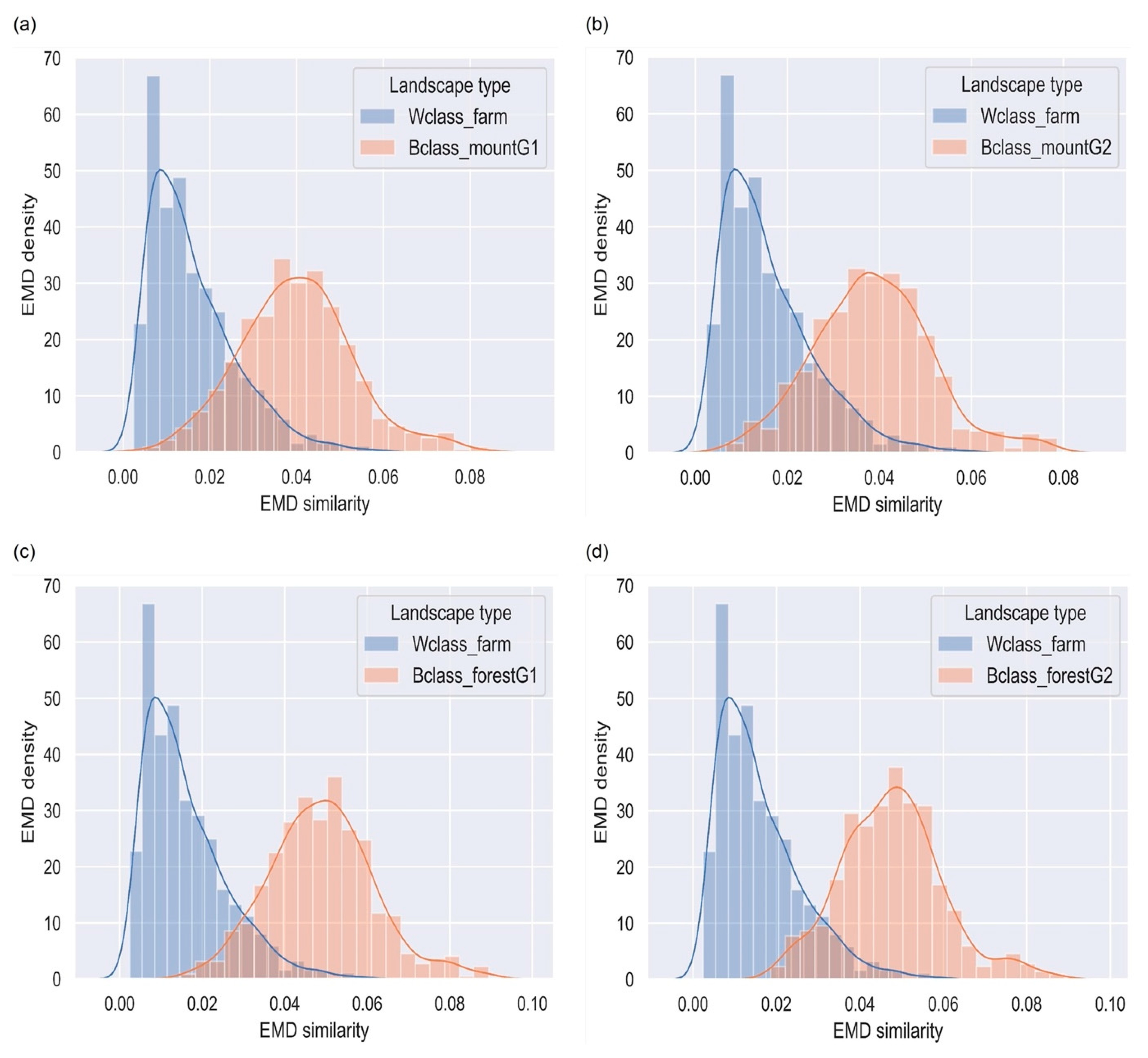
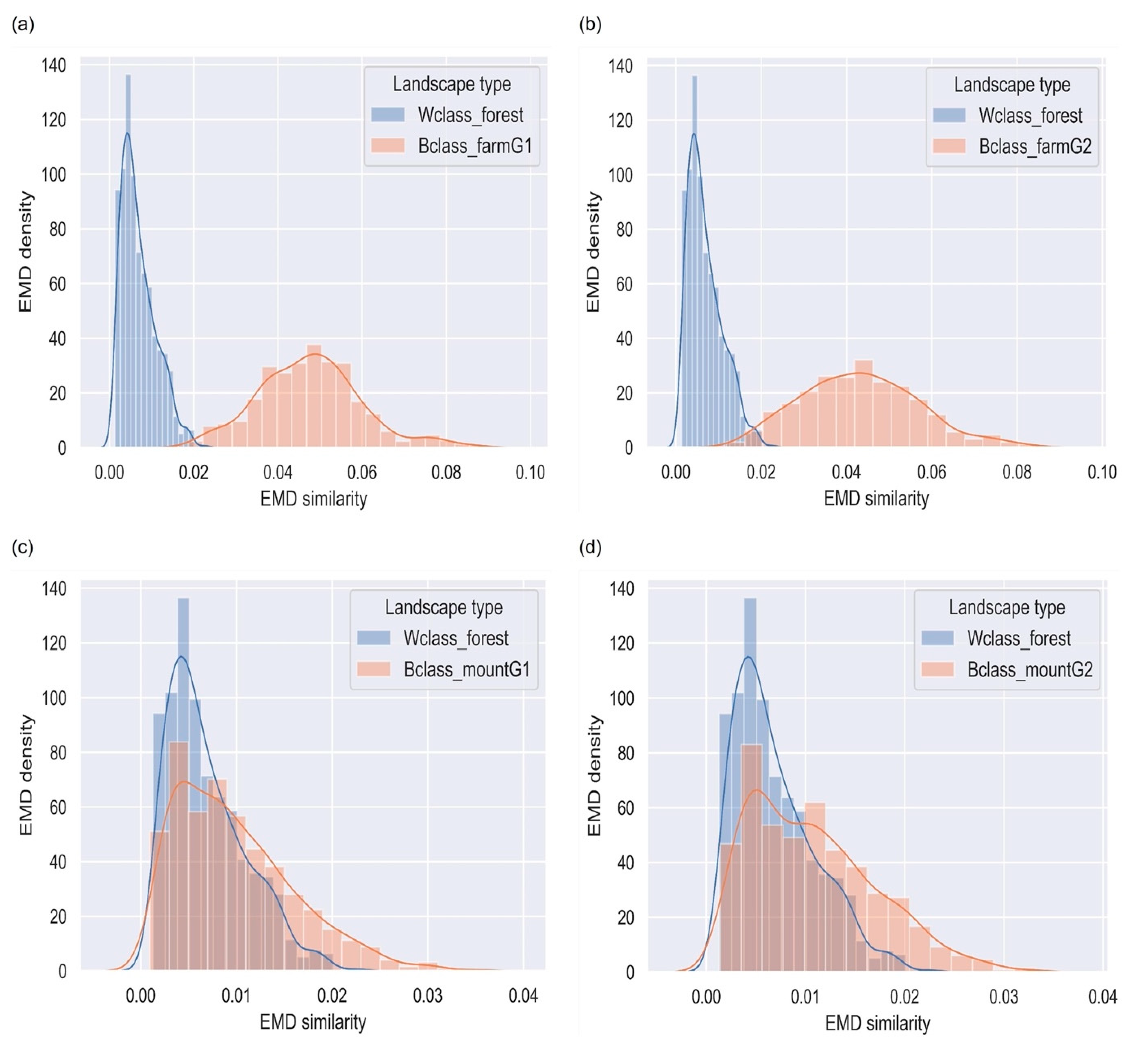
4.3. Mountainous Terrains
4.4. Farm Landscapes
4.5. Forested Landscapes
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dandois, J.P.; Ellis, E.C. High spatial resolution three-dimensional mapping of vegetation spectral dynamics using computer vision. Remote Sens. Environ. 2013, 136, 259–276. [Google Scholar] [CrossRef]
- Miller, H.J.; Goodchild, M.F. Data-driven geography. GeoJournal 2014, 80, 449–461. [Google Scholar] [CrossRef]
- Townshend, J.R.; Masek, J.G.; Huang, C.; Vermote, E.F.; Gao, F.; Channan, S.; Sexton, J.O.; Feng, M.; Narasimhan, R.; Kim, D.; et al. Global characterization and monitoring of forest cover using Landsat data: Opportunities and challenges. Int. J. Digit. Earth 2012, 5, 373–397. [Google Scholar] [CrossRef]
- Wulder, M.A.; Coops, N.C.; Roy, D.P.; White, J.C.; Hermosilla, T. Land cover 2.0. Int. J. Remote Sens. 2018, 39, 4254–4284. [Google Scholar] [CrossRef]
- Comber, A.; Wulder, M.A. Considering spatiotemporal processes in big data analysis: Insights from remote sensing of land cover and land use. Trans. GIS 2019, 23, 879–891. [Google Scholar] [CrossRef]
- Peng, F.; Wang, L.; Zou, S.; Luo, J.; Gong, S.; Li, X. Content-based search of earth observation data archives using open-access multitemporal land cover and terrain products. Int. J. Appl. Earth Obs. Geoinf. 2019, 81, 13–26. [Google Scholar] [CrossRef]
- Long, J.; Robertson, C. Comparing spatial patterns. Geogr. Compass 2018, 12, e12356. [Google Scholar] [CrossRef]
- Li, Z.; White, J.; Wulder, M.A.; Hermosilla, T.; Davidson, A.M.; Comber, A. Land cover harmonization using Latent Dirichlet Allocation. Int. J. Geogr. Inf. Sci. 2021, 35, 348–374. [Google Scholar] [CrossRef]
- Turner, M.G. Landscape Ecology: The Effect of Pattern on Process. Annu. Rev. Ecol. Syst. 1989, 20, 171–197. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N. Prabhat Deep learning and process understanding for data-driven Earth system science. Nat. Cell Biol. 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Tracewski, L.; Bastin, L.; Fonte, C.C. Repurposing a deep learning network to filter and classify volunteered photographs for land cover and land use characterization. Geo-Spatial Inf. Sci. 2017, 20, 252–268. [Google Scholar] [CrossRef]
- Grinblat, G.L.; Uzal, L.C.; Larese, M.G.; Granitto, P.M. Deep learning for plant identification using vein morphological patterns. Comput. Electron. Agric. 2016, 127, 418–424. [Google Scholar] [CrossRef]
- Jasiewicz, J.; Netzel, P.; Stepinski, T.F. Landscape similarity, retrieval, and machine mapping of physiographic units. Geomorphology 2014, 221, 104–112. [Google Scholar] [CrossRef]
- Buscombe, D.; Ritchie, A.C. Landscape Classification with Deep Neural Networks. Geosciences 2018, 8, 244. [Google Scholar] [CrossRef]
- Janowicz, K.; Gao, S.; McKenzie, G.; Hu, Y.; Bhaduri, B.L. GeoAI: Spatially explicit artificial intelligence techniques for geographic knowledge discovery and beyond. Int. J. Geogr. Inf. Sci. 2019, 34, 625–636. [Google Scholar] [CrossRef]
- Cimpoi, M.; Maji, S.; Kokkinos, I.; Vedaldi, A. Deep Filter Banks for Texture Recognition, Description, and Segmentation. Int. J. Comput. Vis. 2016, 118, 65–94. [Google Scholar] [CrossRef]
- Gong, Y.; Wang, L.; Guo, R.; Lazebnik, S. Multi-scale orderless pooling of deep convolutional activation features. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; Springer: Berlin/Heidelberg, Germany, 2014; pp. 392–407. [Google Scholar]
- Mahendran, A.; Vedaldi, A. Understanding deep image representations by inverting them. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 5188–5196. [Google Scholar]
- Qi, X.; Li, C.-G.; Zhao, G.; Hong, X.; Pietikäinen, M. Dynamic texture and scene classification by transferring deep image features. Neurocomputing 2016, 171, 1230–1241. [Google Scholar] [CrossRef]
- Li, H.; Ellis, J.G.; Zhang, L.; Chang, S.F. PatternNet: Visual pattern mining with deep neural network. In Proceedings of the 2018 ACM on International Conference on Multimedia Retrieval, Yokohama, Japan, 11–14 June 2018; pp. 291–299. [Google Scholar]
- Lettry, L.; Perdoch, M.; Vanhoey, K.; Van Gool, L. Repeated Pattern Detection Using CNN Activations. In Proceedings of the 2017 IEEE Winter Conference on Applications of Computer Vision (WACV), Santa Rosa, CA, USA, 24–31 March 2017; pp. 47–55. [Google Scholar]
- Kalantar, B.; Ueda, N.; Al-Najjar, H.A.; Halin, A.A. Assessment of convolutional neural network architectures for earth-quake-induced building damage detection based on pre-and post-event orthophoto images. Remote Sens. 2020, 12, 3529. [Google Scholar] [CrossRef]
- Flores, C.F.; Gonzalez-Garcia, A.; van de Weijer, J.; Raducanu, B. Saliency for fine-grained object recognition in domains with scarce training data. Pattern Recognit. 2019, 94, 62–73. [Google Scholar] [CrossRef]
- Ghorbanzadeh, O.; Blaschke, T.; Gholamnia, K.; Meena, S.R.; Tiede, D.; Aryal, J. Evaluation of Different Machine Learning Methods and Deep-Learning Convolutional Neural Networks for Landslide Detection. Remote. Sens. 2019, 11, 196. [Google Scholar] [CrossRef]
- Liu, Y.; Zhong, Y.; Fei, F.; Zhu, Q.; Qin, Q. Scene Classification Based on a Deep Random-Scale Stretched Convolutional Neural Network. Remote. Sens. 2018, 10, 444. [Google Scholar] [CrossRef]
- Gong, X.; Xie, Z.; Liu, Y.; Shi, X.; Zheng, Z. Deep Salient Feature Based Anti-Noise Transfer Network for Scene Classification of Remote Sensing Imagery. Remote. Sens. 2018, 10, 410. [Google Scholar] [CrossRef]
- Zhu, Q.; Zhong, Y.; Liu, Y.; Zhang, L.; Li, D. A Deep-Local-Global Feature Fusion Framework for High Spatial Resolution Imagery Scene Classification. Remote. Sens. 2018, 10, 568. [Google Scholar] [CrossRef]
- Zhuang, S.; Wang, P.; Jiang, B.; Wang, G.; Wang, C. A Single Shot Framework with Multi-Scale Feature Fusion for Geospatial Object Detection. Remote. Sens. 2019, 11, 594. [Google Scholar] [CrossRef]
- Petrovska, B.; Zdravevski, E.; Lameski, P.; Corizzo, R.; Štajduhar, I.; Lerga, J. Deep Learning for Feature Extraction in Remote Sensing: A Case-Study of Aerial Scene Classification. Sensors 2020, 20, 3906. [Google Scholar] [CrossRef]
- Ye, L.; Wang, L.; Sun, Y.; Zhao, L.; Wei, Y. Parallel multi-stage features fusion of deep convolutional neural networks for aerial scene classification. Remote. Sens. Lett. 2018, 9, 294–303. [Google Scholar] [CrossRef]
- Kang, M.; Ji, K.; Leng, X.; Lin, Z. Contextual Region-Based Convolutional Neural Network with Multilayer Fusion for SAR Ship Detection. Remote. Sens. 2017, 9, 860. [Google Scholar] [CrossRef]
- Fu, G.; Liu, C.; Zhou, R.; Sun, T.; Zhang, Q. Classification for high resolution remote sensing imagery using a fully con-volutional network. Remote Sens. 2017, 9, 498. [Google Scholar] [CrossRef]
- Gao, Q.; Lim, S.; Jia, X. Hyperspectral Image Classification Using Convolutional Neural Networks and Multiple Feature Learning. Remote. Sens. 2018, 10, 299. [Google Scholar] [CrossRef]
- Huang, H.; Xu, K. Combing Triple-Part Features of Convolutional Neural Networks for Scene Classification in Remote Sensing. Remote. Sens. 2019, 11, 1687. [Google Scholar] [CrossRef]
- Zeng, D.; Chen, S.; Chen, B.; Li, S. Improving remote sensing scene classification by integrating global-context and lo-cal-object features. Remote Sens. 2018, 10, 734. [Google Scholar] [CrossRef]
- Gahegan, M. Fourth paradigm GIScience? Prospects for automated discovery and explanation from data. Int. J. Geogr. Inf. Sci. 2020, 34, 1–21. [Google Scholar] [CrossRef]
- Simonyan, K.; Vedaldi, A.; Zisserman, A. Deep Inside Convolutional Networks: Visualising Image Classification Models and Saliency Maps. arXiv 2013, arXiv:1312.6034. [Google Scholar]
- Zeiler, M.D.; Fergus, R. Visualizing and understanding convolutional networks. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Zhou, B.; Khosla, A.; Lapedriza, A.; Oliva, A.; Torralba, A. Learning Deep Features for Discriminative Localization. In CVPR 2016, Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; IEEE: New York, NY, USA, 2016; pp. 2921–2929. [Google Scholar]
- Springenberg, J.T.; Dosovitskiy, A.; Brox, T.; Riedmiller, M. Striving for simplicity: The all convolutional net. arXiv 2014, arXiv:1412.6806. [Google Scholar]
- Zagoruyko, S.; Komodakis, N. Paying more attention to attention: Improving the performance of convolutional neural networks via attention transfer. In Proceedings of the 5th International Conference on Learning Representations, Toulon, France, 24–26 April 2017; pp. 1–13. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-CAM: Visual Explanations from Deep Networks via Gradient-Based Localization. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar]
- Omeiza, D.; Speakman, S.; Cintas, C.; Weldermariam, K. Smooth Grad-CAM++: An Enhanced Inference Level Visualization Technique for Deep Convolutional Neural Network Models. arXiv 2019, arXiv:1908.01224. [Google Scholar]
- Zhang, H.; Zhang, T.; Pedrycz, W.; Zhao, C.; Miao, D. Improved adaptive image retrieval with the use of shadowed sets. Pattern Recognit. 2019, 90, 390–403. [Google Scholar] [CrossRef]
- Chen, J.; Zhou, Z.; Pan, Z.; Yang, C.-N. Instance Retrieval Using Region of Interest Based CNN Features. J. New Media 2019, 1, 87–99. [Google Scholar] [CrossRef]
- Shi, X.; Qian, X. Exploring spatial and channel contribution for object based image retrieval. Knowl.-Based Syst. 2019, 186, 104955. [Google Scholar] [CrossRef]
- Ustyuzhaninov, I.; Brendel, W.; Gatys, L.A.; Bethge, M. Texture Synthesis Using Shallow Convolutional Networks with Random Filters. arXiv 2016, arXiv:1606.00021. [Google Scholar]
- Gatys, L.A.; Ecker, A.S.; Bethge, M. Texture and art with deep neural networks. Curr. Opin. Neurobiol. 2017, 46, 178–186. [Google Scholar] [CrossRef]
- Girdhar, R.; Ramanan, D. Attentional pooling for action recognition. Adv. Neural. Inf. Process. Syst. 2017, 34–45. [Google Scholar]
- Cao, J.; Liu, L.; Wang, P.; Huang, Z.; Shen, C.; Shen, H.T. Where to Focus: Query Adaptive Matching for Instance Retrieval Using Convolutional Feature Maps. arXiv 2016, arXiv:1606.06811. [Google Scholar]
- El Amin, A.M.; Liu, Q.; Wang, Y. Convolutional neural network features based change detection in satellite images. In First International Workshop on Pattern Recognition; SPIE: Tokyo, Japan, 2016; Volume 10011, p. 100110W. [Google Scholar] [CrossRef]
- Albert, A.; Kaur, J.; Gonzalez, M.C. Using Convolutional Networks and Satellite Imagery to Identify Patterns in Urban Environments at a Large Scale. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 1357–1366. [Google Scholar]
- Yandex, A.B.; Lempitsky, V.S. Aggregating Local Deep Features for Image Retrieval. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 1269–1277. [Google Scholar]
- Wang, A.; Wang, Y.; Chen, Y. Hyperspectral image classification based on convolutional neural network and random forest. Remote Sens. Lett. 2019, 10, 1086–1094. [Google Scholar] [CrossRef]
- Unar, S.; Wang, X.; Wang, C.; Wang, Y. A decisive content based image retrieval approach for feature fusion in visual and textual images. Knowl. Based Syst. 2019, 179, 8–20. [Google Scholar] [CrossRef]
- Gu, Y.; Wang, Y.; Li, Y. A Survey on Deep Learning-Driven Remote Sensing Image Scene Understanding: Scene Classification, Scene Retrieval and Scene-Guided Object Detection. Appl. Sci. 2019, 9, 2110. [Google Scholar] [CrossRef]
- Liu, L.; Shen, C.; Hengel, A.V.D. The treasure beneath convolutional layers: Cross-convolutional-layer pooling for image classification. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 4749–4757. [Google Scholar]
- Lim, L.A.; Keles, H.Y. Learning multi-scale features for foreground segmentation. Pattern Anal. Appl. 2019, 23, 1369–1380. [Google Scholar] [CrossRef]
- Andrearczyk, V.; Whelan, P.F. Using filter banks in Convolutional Neural Networks for texture classification. Pattern Recognit. Lett. 2016, 84, 63–69. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. In Proceedings of the International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Nogueira, K.; Penatti, O.A.B.; Dos Santos, J.A. Towards better exploiting convolutional neural networks for remote sensing scene classification. Pattern Recognit. 2017, 61, 539–556. [Google Scholar] [CrossRef]
- Hinton, G.E.; Srivastava, N.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R.R. Improving neural networks by preventing co-adaptation of feature detectors. arXiv 2012, arXiv:1207.0580. [Google Scholar]
- Kingma, D.P.; Ba, J.L. Adam: A method for stochastic optimization. arXiv 2015, arXiv:1412.6980. [Google Scholar]
- Liu, Y.; Cao, G.; Sun, Q.; Siegel, M. Hyperspectral classification via deep networks and superpixel segmentation. Int. J. Remote Sens. 2015, 36, 3459–3482. [Google Scholar] [CrossRef]
- Xia, G.; Hu, J.; Hu, F.; Shi, B. AID: A Benchmark Dataset for Performance Evaluation of Aerial Scene Classification. IEEE Trans. Geosci. Remote Sens. 2016, 55, 3965–3981. [Google Scholar] [CrossRef]
- Yang, B.; Yan, J.; Lei, Z.; Li, S.Z. Convolutional channel features. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 82–90. [Google Scholar] [CrossRef]
- Xie, X.; Han, X.; Liao, Q.; Shi, G. Visualization and Pruning of SSD with the base network VGG16. In Proceedings of the 2017 International Conference on Compilers, Architectures and Synthesis for Embedded Systems Companion, Seoul, Korea, 15–20 October 2017; pp. 90–94. [Google Scholar] [CrossRef]
- Luo, J.-H.; Zhang, H.; Zhou, H.-Y.; Xie, C.-W.; Wu, J.; Lin, W. ThiNet: Pruning CNN Filters for a Thinner Net. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 41, 2525–2538. [Google Scholar] [CrossRef]
- Déniz, O.; Bueno, G.; Salido, J.; De La Torre, F. Face recognition using Histograms of Oriented Gradients. Pattern Recognit. Lett. 2011, 32, 1598–1603. [Google Scholar] [CrossRef]
- Truong, Q.B.; Kiet, N.T.T.; Dinh, T.Q.; Hiep, H.X. Plant species identification from leaf patterns using histogram of oriented gradients feature space and convolution neural networks. J. Inf. Telecommun. 2020, 4, 140–150. [Google Scholar] [CrossRef]
- Rubner, Y.; Tomasi, C.; Guibas, L.J. The Earth Mover’s Distance as a Metric for Image Retrieval. Int. J. Comput. Vis. 2000, 40, 99–121. [Google Scholar] [CrossRef]
- Anwer, R.M.; Khan, F.S.; Van De Weijer, J.; Molinier, M.; Laaksonen, J. Binary patterns encoded convolutional neural networks for texture recognition and remote sensing scene classification. ISPRS J. Photogramm. Remote. Sens. 2018, 138, 74–85. [Google Scholar] [CrossRef]
- Yu, Y.; Liu, F. Aerial Scene Classification via Multilevel Fusion Based on Deep Convolutional Neural Networks. IEEE Geosci. Remote. Sens. Lett. 2018, 15, 287–291. [Google Scholar] [CrossRef]
- Xu, K.; Huang, H.; Li, Y.; Shi, G. Multilayer Feature Fusion Network for Scene Classification in Remote Sensing. IEEE Geosci. Remote. Sens. Lett. 2020, 17, 1894–1898. [Google Scholar] [CrossRef]
- Basu, S.; Mukhopadhyay, S.; Karki, M.; DiBiano, R.; Ganguly, S.; Nemani, R.R.; Gayaka, S. Deep neural networks for texture classification—A theoretical analysis. Neural Netw. 2018, 97, 173–182. [Google Scholar] [CrossRef]
- Murabito, F.; Spampinato, C.; Palazzo, S.; Giordano, D.; Pogorelov, K.; Riegler, M. Top-down saliency detection driven by visual classification. Comput. Vis. Image Underst. 2018, 172, 67–76. [Google Scholar] [CrossRef]
- Coops, N.C.; Wulder, M.A. Breaking the Habit(at). Trends Ecol. Evol. 2019, 34, 585–587. [Google Scholar] [CrossRef] [PubMed]
- Song, F.; Yang, Z.; Gao, X.; Dan, T.; Yang, Y.; Zhao, W.; Yu, R. Multi-Scale Feature Based Land Cover Change Detection in Mountainous Terrain Using Multi-Temporal and Multi-Sensor Remote Sensing Images. IEEE Access 2018, 6, 77494–77508. [Google Scholar] [CrossRef]
- Amirshahi, S.A.; Pedersen, M.; Yu, S.X. Image quality assessment by comparing CNN features between images. Electron. Imaging. 2017, 12, 42–51. [Google Scholar] [CrossRef]
- Liu, Y.; Han, Z.; Chen, C.; Ding, L.; Liu, Y. Eagle-Eyed Multitask CNNs for Aerial Image Retrieval and Scene Classification. IEEE Trans. Geosci. Remote. Sens. 2020, 58, 6699–6721. [Google Scholar] [CrossRef]
- Liu, Y.; Zhong, Y.; Qin, Q. Scene Classification Based on Multiscale Convolutional Neural Network. IEEE Trans. Geosci. Remote. Sens. 2018, 56, 7109–7121. [Google Scholar] [CrossRef]
- Ahmad, K.T.; Ummesafi, S.; Iqbal, A. Content based image retrieval using image features information fusion. Inf. Fusion 2019, 51, 76–99. [Google Scholar] [CrossRef]
- Rui, T.; Zou, J.; Zhou, Y.; Fei, J.; Yang, C. Convolutional neural network feature maps selection based on LDA. Multimed. Tools Appl. 2017, 77, 10635–10649. [Google Scholar] [CrossRef]




| Layer Name | Convolution | Max-Pooling | Activation | Drop-Out |
|---|---|---|---|---|
| Conv-1 | 7 × 7 × 32 | 2 × 2 | ReLU | 25% |
| Conv-2 | 7 × 7 × 64 | 2 × 2 | ReLU | 25% |
| Conv-3 | 7 × 7 × 128 | 2 × 2 | ReLU | 25% |
| FC1 | No | No | SoftMax | 50% |
| Data Source | Attribute | How Data Is Utilized | No. of Images |
|---|---|---|---|
| AID | Aerial imagery, pixel resolution vary between 0.5 and 8 m | Training and testing models, and building similarity distributions | 9000 images used training (75%) and validation (25%). 900 images used for testing (e.g., deriving confusion matrix) |
| Sentinel data | Open-source satellite data; 10 m pixel resolution | Visualizing feature maps in medium resolution imagery Demonstrate potential application in Sentinel dataset | 600 images used for testing and computing confusion matrix. Image tiles are extracted from sentinel scenes at different spatial locations |
| Methods | Farmland (%) | Mountain (%) | Forest (%) | OA (%) |
|---|---|---|---|---|
| TEX-Net-LF [72] | 95.5 | 99.9 | 95.75 | 92.96 |
| Fine-Tuned SVM [73] | 97.0 | 99.0 | 98.0 | 95.36 |
| PMS [29] | 98.0 | 99.0 | 99.0 | 95.56 |
| CTFCNN [34] | 99.0 | 100 | 99.0 | 94.91 |
| GCFs + LOFs [35] | 94.0 | 99.0 | 99.0 | 96.85 |
| MF2Net [74] | 97.0 | 91.0 | 94.0 | 95.93 |
| Classical CNN | 100 | 75.0 | 100 | 91.67 |
| Tex-CNN | 99.0 | 90.0 | 100 | 96.33 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malik, K.; Robertson, C. Landscape Similarity Analysis Using Texture Encoded Deep-Learning Features on Unclassified Remote Sensing Imagery. Remote Sens. 2021, 13, 492. https://doi.org/10.3390/rs13030492
Malik K, Robertson C. Landscape Similarity Analysis Using Texture Encoded Deep-Learning Features on Unclassified Remote Sensing Imagery. Remote Sensing. 2021; 13(3):492. https://doi.org/10.3390/rs13030492
Chicago/Turabian StyleMalik, Karim, and Colin Robertson. 2021. "Landscape Similarity Analysis Using Texture Encoded Deep-Learning Features on Unclassified Remote Sensing Imagery" Remote Sensing 13, no. 3: 492. https://doi.org/10.3390/rs13030492
APA StyleMalik, K., & Robertson, C. (2021). Landscape Similarity Analysis Using Texture Encoded Deep-Learning Features on Unclassified Remote Sensing Imagery. Remote Sensing, 13(3), 492. https://doi.org/10.3390/rs13030492