Abstract
Determining the correct height of mountain peaks is vital for tourism, but it is also important as a reference point for devices equipped with GPS (Global Positioning System), e.g., watches or car navigation systems. The peak altitude data are part of geographic and geodetic information. As more modern technologies and equipment become available, their precisions should increase. However, verification of peak heights is usually only conducted for the highest, well-known mountains—lower peaks or mountain passes are rarely verified. Therefore, this study focuses on an investigation of 12 altitude points on a section of the longest and most famous touristic trail in Poland (the Main Beskid Trail), located in the Orava–Żywiec Beskids Mts (Mountains). The aim of this research is to measure and verify the heights of the 12 selected mountain peaks, in addition to evaluating the chosen methods based on the quality of the obtained data and determining their suitability and opportunities for use in further research. Measurements were obtained at the most specific height points—on the 12 highest points of the summits. This study compares two modern measurement techniques: the global navigation satellite system (GNSS) and light detection and ranging (LiDAR). The obtained results were later compared with those widely used on the internet and in printed materials (period covered: 1884–2015). This analysis demonstrates that lesser-known objects are rarely the subject of remeasurement and significant altitude errors may occur, primarily because the heights originated from a source in the past when modern methods were not available. Our findings indicate that the heights of the peaks presented in cartographic materials are inaccurate. The assumed heights should be corrected by direct measurements using modern techniques.
1. Introduction
Mountain peaks (and their altitudes) have always been of interest to researchers as the subject poses as a challenge for those who have attempted to measure and standardise them in the past [1,2,3,4]. Measurement methods and techniques have changed and developed over the years [5,6], leading to more accurate measurements [7] and, consequently, more accurate determination of peak altitudes. New data on the peak altitudes have emerged, primarily due to the development of several modern geodetic height determination methods, such as the global navigation satellite system (GNSS) and light detection and ranging (LiDAR). GNSSs have developed significantly in recent years [8,9,10]. Currently, apart from the signals of the GPS (Global Positioning System), Galileo, Beidou, and GLONASS systems, the signals of the Japanese quasi-zenith satellite system (QZSS) and the Indian regional navigation satellite system (IRNSS/NavIC) are also available [11,12]. The GNSS has been used to determine the precise altitudes of many globally recognised peaks, such as Mount Everest [13,14,15,16], Mont Blanc [17], Aconcagua [18], Kilimanjaro [19], and Bolivar [20]. It has been approved as the most effective tool for calculating the heights of mountains where it is inappropriate to perform traditional geometric levelling [20,21]. In comparison with earlier measurements obtained from trigonometric triangulations using theodolites [22,23], GNSS measurements, in general, differ by a few metres or more [20]. In addition to providing a high degree of accuracy and reliability, the instruments are also compact and light, and researchers can carry them to the peak of a mountain to determine its ellipsoidal height [24]. During the past 20 years, remeasurement of several of the most famous mountains in the Alps and Himalayas [25,26,27] has been conducted. For example, the altitude of Mont Blanc is measured every two years as it varies continuously due to wind intensity, precipitation, and the footsteps of mountaineers [28]. However, as [21] highlighted, there is a lack of research for the lesser-known peaks, which are rarely visited and, consequently, are not so interesting from a tourism point of view. Therefore, it represents a certain potential and innovation in this research.
Conversely, airborne LiDAR has recently become the preferred method for the acquisition of digital elevation data in a wide range of applications, as it ensures accuracy to within 10 cm [29], and the capturing of data is fast and relatively easy [30]. However, this technique can be susceptible to distortions due to resolution, weather conditions, or plant cover, therefore, when determining peak heights, results based solely on LiDAR or derived digital elevation model (DEM) data, are not sufficient. It is necessary to understand the nature of the vegetation, buildings, or residue from human activities at the summit, and this cannot be achieved without verification. Automatic transfer of peak heights from LiDAR or derived DEM data can also be affected by random errors that the statistical apparatus cannot detect [21]. Therefore, in addition to the use of LiDAR data, verification by another method is required.
In the past, several authors have shown that GNSS levelling, i.e., the combination of GNSS height determination and geoid models, is an economic technique for determining physical heights [31,32,33,34,35,36,37]. However, the method itself is limited in two aspects: the accuracy of the ellipsoid height determination and the accuracy of the geoid model. Featherstone and Stewart [38] were the first to raise the question of the accuracy of data obtained in GNSS height determination. Ellipsoid heights can be determined with several GNSS methods, namely relative static or kinematic GNSS processing, and the widely used method of precise point positioning (PPP), which was proposed by [39] and further upgraded by several authors [40,41,42,43,44]. Higgins [45] highlighted the existence of possibilities and limitations in GPS height determination. The first issue involves the quality of GNSS height determination (which is solved by different measurement and processing approaches) and the second challenge involves the quality of the determination of the geoid model.
A quality geoid model is an important component of GNSS levelling. Several authors have claimed that by using GNSS levelling, a height determination accuracy of 1 cm can be achieved [46,47,48]. However, additional studies have shown that it is almost impossible to achieve such an accurate geoid model in mountainous regions [36,49]. The Earth’s external gravitational field and is functionals (in addition to the geoid heights of interest and the gravitational anomalies and potential) can be determined using global gravity models (GGMs). As a result of several satellite gravity missions, there are several models available, namely EGM-96 (EGM = Earth Gravitational Model), EGM2008, EIGEN-51C (EIGEN = European Improved Gravity model of the Earth by New techniques), EIGEN-6C, EIGEN-6S, GGM03C, GGM03S and GOCO02S (GOCO = Gravity Observation Combination). The use of GGMs is not a priority where regional models are available, however, where more effective models are not available, GNSS levelling depends on such data [50,51]. The accuracy of the models should be validated for the area of interest, similar to studies that have already been conducted [52,53,54,55]. For geoids, it is most effective to use regional, national, or local geoid models, which are of better quality and can achieve an accuracy of a few centimetres [56], especially when measurements are based on geoid elevation [57]. Therefore, to obtain new insight into mountain peak altitudes, this study compared two modern techniques: GNSS and LiDAR. The results obtained were later compared with those used in maps, atlases and books.
As mentioned above, verification of peak heights is generally only conducted for the highest, well-known mountains; lower peaks or mountain passes are rarely verified. However, if the errors in accuracy can amount to several dozen metres, and even the highest peaks can be determined incorrectly [4,21], it is useful to assess the situation for less outstanding peaks. Thus, the aim of this research was to measure and verify the heights of the 12 selected mountain peaks (located on one mountain trail) to evaluate the selected methods based on the quality of the data obtained, and to determine suitability of those methods in further research. Of particular interest was the accuracy of the two techniques, especially LiDAR, for which it was assumed that the resolution or the potential vegetation, buildings or residue from human activities that covered the mountain peaks would be a limiting factor. Moreover, the authors focused on a mountain range, which consists of a single well-known summit (Babia Góra Mountain) and is a frequent destination for tourists, as it is the highest peak in Poland outside the Tatra Mountains and the other summits are not well known.
2. Background on Altitude Measurements in the Mountains
2.1. Historical Methods
Historically, three methods were applied, namely the geodetic method, the barometric method and the boiling point method (thermometric method). The geodetic method was most likely used by the ancient Greeks, while the barometric and thermometric methods were used in the 17th and 18th centuries, respectively. All three of these methods are still used nowadays. As described by Cajori [6], the ancient mountain summit method was based on the geodetic, Thales-based method, which measured similar right-angled triangles. Two triangulation methods are mentioned; however, there is a lack of detail for these methods. The first method was based on the inaccessible distance measurement and the second (in which the height was measured) was based on the fact that the distance to the observer and the mountain face was known. There were five possible instruments with which the ancient Greeks could have measured the height of mountains: the dioptra, the quadrant, the ancient astrolabe, the ancient cross-staff, and the gnomon. Cajori reported that of all the instruments, Heron’s dioptra or a similar instrument was the most suitable for measuring angles to determine the height. Although levelling was used long before the dioptra, it was not suitable for determining most mountain peaks, although it was already possible in ancient times to achieve a high degree of accuracy in determining relative heights. The principal disadvantage of this method was that it was necessary to reach the summit to determine the height of a mountain.
Research conducted from the 16th century onwards revealed that the right-angled triangle solution was not so straightforward and that it should be improved by taking into account the radius of curvature of the Earth. In the 17th century, it was also recognised that atmospheric refraction should be taken into account in calculations. Snell calculated the peak altitudes of Tenerife and Aetna, considering the atmospheric refraction and his estimate of the Earth’s radius of curvature. Snell and Picard resented a more scientific approach to the issue and concluded that improved tools and the impact on the measurements should be used when calculating the altitudes of mountain peaks. In 1883, in California, levelling was used to determine the altitude of Mount Diablo [6]; however, most peaks were measured by the geodetic method or by setting up triangulation networks.
The barometric method was first used by Sinclair from 1661 to 1666 to determine mountain heights in Scotland. From measurements obtained by von Guericke, it was ascertained that the method was complex, primarily due to the construction of the barometer and the potential for the instrument to be damaged during transport. The first person to calculate peak heights from barometric measurements was Johann Jakob Scheuchzer in the years from 1705 to 1707. An improvement in the construction of the barometer in the 19th century led to most peak heights being determined barometrically [6].
2.2. GNSS and Its Accuracy
GNSS (previously GPS) in combination with a high-quality quasi-geoid model revolutionised altitude determination. The method is based on a simple transformation of geometrically defined ellipsoidal heights into physical heights in relation to mean sea level, and was proposed by Heiskanen and Moritz as early as 1967 [58]. Regardless of the method used to determine the height above the ellipsoid, the principal factors limiting the quality of GNSS height determination are the station and atmosphere-dependent factors (usually the troposphere) that influence satellite observations. These factors are critical, especially in the vertical direction. A combination of satellite geometry that correlates with atmospheric and station-dependent factors results in a weaker height estimate. For example, the tropospheric effect causes approximately 3 cm of a height difference in bases of approximately 50 km wide [59]. Several novel concepts based on atmospheric parameters obtained from the numerical weather prediction (NWP) model have allowed for an improvement of the tropospheric effect and the ellipsoidal height can now be determined with enhanced accuracy of 1–2 cm [59]. It is also possible to estimate the troposphere via processing [60,61,62], with station-dependent factors, such as multipath and antenna phase centre issues being the remaining limiting factors in determining the ellipsoid height.
GNSS also plays an important role in LiDAR and stereophotogrammetry as it is used for precise geo-localisation. Through the combined use of GNSS and an integrated inertial measurement unit (IMU), any point from the point cloud can be geo-referenced. Recent advances in unmanned aerial systems include GNSS real-time kinematic (RTK) for direct geo-referencing, which is based on an on-board GNSS receiver [63].
2.3. LiDAR Measurements
LiDAR is a remote sensing technology that measures the topography of the Earth’s surface [64,65]. It works on the same principle as radar, as it transmits short laser pulses to the observed objects and receives the light scattered and reflected by the objects [66]. The distance between the antenna and the backscattering surface is determined by the timing of the transmission of laser light pulses and the reception of the backscattered light at the antenna [30,67,68]. LiDAR can be used on space, air, and ground-based platforms [64,69]. An airborne system consists of a laser scanner, a ranging unit, controls, monitoring, and recording units and a position and orientation system. The laser scanner unit consists of a pulse generator (wavelength in the range of 0.5 µm to 1.6 µm) and a receiver to receive the pulses reflected by the target objects [64,65,69]. The distance between the LiDAR sensor and the target object is calculated by multiplying the speed of light by half the time it takes for the light to travel from the sensor to the target and back [66]. The position and orientation system is also referred to as differential global positioning system (DGPS) and generates an accurate position (longitude, latitude, and altitude) and contains an IMU that generates accurate orientation information (roll, pitch, and heading) [64,65]. These data are then combined with the slant distance and information on atmospheric conditions, hardware characteristics, and other relevant parameters to generate an XYZ coordinate triplet of a point on the ground. The output measurements of LiDAR are, therefore, three-dimensional points that provide a dense digital terrain model (DTM) [70]. These points are initially represented by latitude, longitude, and ellipsoidal height, based on the WGS84 (World Geodetic System 1984) reference ellipsoid. The elevation can be converted from an ellipsoidal height to an orthometric height with the transformation of the coordinate system to a national or regional one. The transformation is based on a national or regional height data [64,65,69]. LiDAR data can be used in a range of applications, for example, in geography, geology, and archaeology. It is useful in flood analysis [71,72,73], in the estimation of tree heights [74,75,76], and in determining land cover [77,78]. LiDAR data are also extremely useful in geomorphology [79] for examining volcanic landforms [80], pre-planning mountain rescues [81], or responding quickly to natural disasters, such as landslides or hurricanes.
2.4. Other Methods for Height Determination
In addition to GNSS and LiDAR, there are several other techniques used to measure the height of mountains. First, there is the precise levelling technique, which has been the most accurate and reliable technique for height determination for more than a century. It differs from the satellite-based techniques as it measures the geopotential differences relative to the geoid, whereas the satellite-based techniques measure distances from the reference ellipsoid [82]. Although there have been several improvements to levelling instruments, with the modern version (motorised levelling) improving the speed of the measurement process by 40–200%, the process itself is slow, laborious, and expensive [83]. To measure an area of several km2 with the precise levelling technique is time-consuming and expensive. In contrast to precise levelling, satellite-borne synthetic aperture radar (SAR) images cover a much larger area, offer good spatial coverage and, in suitable conditions, millimetre-level deformation rates [84].
Interferometric synthetic aperture radar (InSAR) is a remote sensing technique that uses two or more SAR images to generate maps of surface deformation or digital elevation, using differences in the phase of the waves returning to the satellite or aircraft [85,86,87]. SAR interferometry measures the relative height of a surface with the difference in phase between two SAR images taken from different locations with precision in the centimetre and even millimetre range [88]. The heights are relative within the SAR interferometry image prior to the calibration of the absolute phase constant using additional information, such as the ground control point of a known location and elevation. Although InSAR can measure relative height changes precisely, the absolute heights are less accurate (accuracy between 1.0 and 1.5 m for high-resolution data and between 2.0 and 2.5 m for standard resolution data) [89].
Digital elevation models (DEMs) are also important sources for various geospatial applications requiring height information, more precisely digital terrain models (DTMs), which are free of buildings and vegetation. In addition to laser scanning data, elevation data in the form of DEMs can also be generated by stereophotogrammetry from aerial photographs, stereo satellite images, and radar interferometry. DEMs generated from different data sources differ in resolution and final accuracy. A detailed review of recent studies that focused on the differentiation of DEMs from satellite images by data source, date, generation method, and accuracy or metric was conducted by [90]. In this study, digital surface models (DSMs) with 30 m resolution were improved (the Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER), the Shuttle Radar Topography Mission (SRTM) and the Advanced Land Observing Satellite (ALOS)) based on DSMs with a resolution of 3 m and 1 m obtained from tri-stereo images from the SPOT-6 (SPOT = Satellite Probatoire d’Observation de la Terre lub Satellite Pour l’Observation de la Terre) and Pleiades high-resolution 1A satellites. Although they improved the high-resolution DSMs, the vertical accuracy remained within several metres. A combination of 30 cm high-resolution satellite images and advances in photogrammetry facilitates levels of detail in three-dimensional (3D) models that could previously only be obtained using airborne sensors [91]. An additional, more accurate method for collecting terrain data is through the use of unmanned aerial systems (UAS), although they are generally limited to a smaller coverage area. UAS are equipped with consumer-quality imaging sensors that allow for cost-effective and automated production of point clouds. The geometrically calibrated camera makes it easy to obtain heights of the surveyed area. Unmanned aerial vehicles (UAVs) have been used for geological mapping; Piras et al. [92] demonstrated the possibility of using high-resolution data to create a slope map provided that the ground dynamics observed in the field can be identified and evaluated.
2.5. Reference System and the Geoid Model Issue
Nowadays, geoid modelling based on gravity anomalies is one of the most common methods used to obtain basic data. However, the quality of the local geoid model depends on several factors, such as the number of terrestrial gravity points, the gravity density, the accuracy of gravity, the number and density of GNSS or levelling points, the accuracy of GNSS point determination, and the resolution of the digital elevation model (DEM), or digital terrain model (DTM). Considering these factors, the quality of geoid models varies depending on the assumptions used in the calculations. In Reference [49], an extensive study compared sixteen different national geoid models. The results demonstrated that the national geoid models are based on different computation methods, including GRAVSOFT (from the University of Copenhagen, Denmark), the compute-remove-restore method (from [93], KTH GEOLAB (based on a least-squares modification of the Stokes formula with an additive correction from the Royal Institute of Technology), KTH [94], and Precise GEOID computation software (SHGEO, based on the Stokes–Helmert method from the University of New Brunswick, Canada [95].
In practice, altitudes are presented as above sea level, which, depending on the country, are based on the ellipsoidal height (, Figure 1), and either the orthometric (geoid) or normal (quasi-geoid) height system. The distance between the surface of the earth and the geoid or quasi-geoid surface is the orthometric or normal height, which is the difference between the ellipsoidal height (e.g., from a GNSS measurement) and the undulation or anomaly .
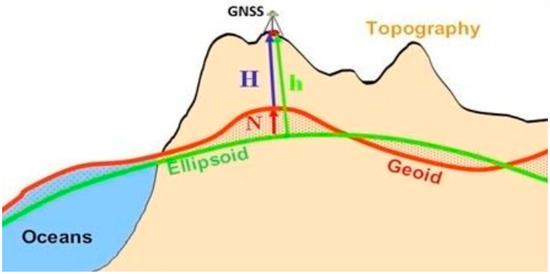
Figure 1.
The relationship between the orthometric height, ellipsoidal height, and geoid height [96].
Such geoid or quasi-geoid models are calculated (by fitting) into national geodetic height datum, which differ from country-to-country, and must, therefore, be used with caution at the global level. Poland has a normal altitude system based on a quasi-geoid. Poland has two normal vertical frames based on a quasi-geoid: one with zero point in Amsterdam (PL-EVRF2007-NH), and the second in Kronstadt (PL-KRON86-NH) [97]. The differences among these data change irregularly, from 12 cm to 20 cm, depending on the area [98]. Thus, for the remainder of the text, the authors will refer to the normal height system only, and its practical realization—the PL-KRON86-NH.
3. Materials and Methods
3.1. Study Area
The Orava Beskids Mountains (or Orava–Żywiec Beskids Mts, Polish: Beskid Żywiecko–Orawski) are the highest in the Polish section of the Outer Carpathians [99,100]. The Polish–Slovak border divides this region into two administrative sections (Figure 2). This mountain range is composed of a Magura flysch unit—a typical fault-folded structure of the Outer Carpathians [101]. At the Slovak–Polish border, the mountains are divided by several saddles, into relatively massive separate groups. In the Polish territory, these groups belong to the Orava–Żywiec Beskids [99].
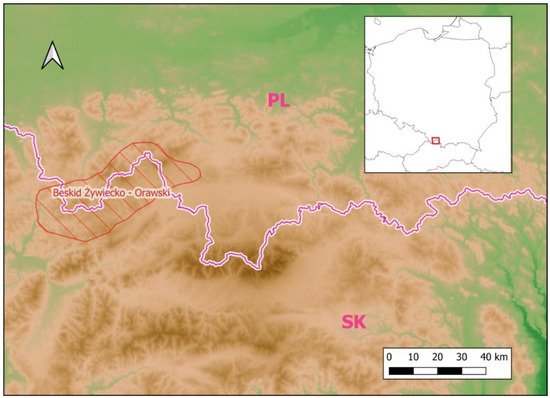
Figure 2.
Location of the study area.
The geological structure of the mountain range is relatively monotonous. The geological structure is part of the Cretaceous and Palaeogene of the Outer Carpathians with Magura sandstone predominant over clay shales [102]. The type of relief is classified as a medium-altitude mountain [103]. The mountain range is divided into multiple separate sandstone massifs, between which are deep valleys and saddles. Most of the summit heights range between 1200 and 1400 m; only the two largest peaks (Babia Góra and Pilsko) are higher. The valley bottoms are approximately 600 to 700 m, so the relative heights are between 600 and 800 m. The relief is fluvial landslide modelled. On the northern slopes of the largest peak, Babia Góra, only semi-permanent firn patches (nivation) took part in modelling during the Pleistocene [104]. The top of Babia Góra and part of its northern slope are covered by sandstone blocks [105]. Similar to other flysch Carpathian mountains, the slopes of the entire Orava Beskids range of mountains are intensively modelled by landslides [106]. This can be seen on the website of Poland’s landslide counteracting system (SOPO, in Polish) [107].
The climate conditions of this mountain range are relatively cold and humid. The average rainfall is approximately 1400 mm per year. The number of days with snow cover is between 90 (in the lowest valleys) and 120 (in the highest ridges) [108]. Climatic factors have significantly contributed to the height of the soil zonality in this mountain range. Cambisols developed to a height of approximately 1300 m above sea level, followed by podzols and lithosols to a height of approximately 1600 m.
Most of the survey area was situated in the forest montane belt. Potential forests in the lower montane belt should be beech dominant (mostly Dentario glandulosae-Fagetum). Both potential and actual forests in the higher montane belt are spruce dominant (mostly Plagiothecio-Piceetum). Improper forest management in the past has resulted in spruce being the predominant species present in the area nowadays.
In this study, the authors measured 12 peaks located in the Orava–Żywiec Beskids Mts (Figure 3).
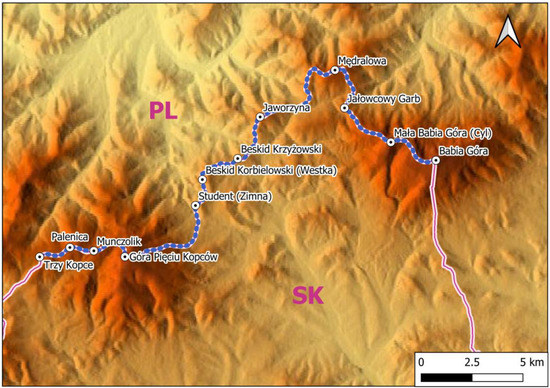
Figure 3.
Summits where altitudes were measured.
The highest parts of the Babia Góra and Pilsko massifs reach the cold mountain belt with dwarf pine scrubs and sub-alpine meadows. The main ridge (and the national border) is the primary European watershed between the Baltic and Black Seas. Most of the Orava–Żywiec Beskids Mts are protected by different conservation statuses, as protected landscape areas, landscape parks, or national reserves. Its highest parts, including Babiogórski National Park, belong to the UNESCO (United Nations Educational, Scientific and Cultural Organization) World Network of Biosphere Reserves.
The focus of this research was the main ridge of the Orava–Żywiec Beskids Mts., which is also part of the main ridge of the Carpathian Mountains. Measurements were taken at the most specific height-points—the 12 highest points of the summits. The profile began at the top of Babia Góra Mountain (the highest point of the profile) and ended at the summit of Trzy Kopce. The lowest point of the profile was Przełęcz Glinne (Glinne Pass), but the lowest measurement point was Beskid Krzyżowski (Figure 4).
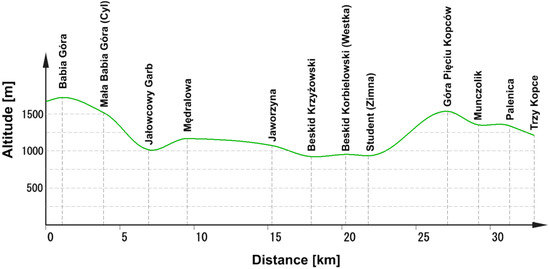
Figure 4.
Terrain profile of the measured peaks.
Most of the profile followed the red touristic trail, which is the longest and most famous touristic trail in Poland (The Kazimierz Sosnkowski Main Beskid Trail).
3.2. Methods
Examining historical sources of altitude data requires source criticism methods. A source criticism is an interdisciplinary study of how information sources are evaluated for given tasks, and it was employed in this study. As a reference for altitude information evaluation, we analysed data used by authors of other studies. Overall, in relation to a given purpose (altitude data), a given information source may be valid, reliable, or relevant. The authors of this study chose the most reliable and common sources, such as scientific books, guidebooks, cartographic materials, and maps. Furthermore, the altitude data of old maps were analysed.
Each summit was measured using a Leica Viva GS-16 Smart antenna GNSS receiver in real-time kinematic (RTK) or static mode, both using GPS signals. For the kinematic mode, three independent 30 s sessions based on ASG-EUPOS (Aktywna Sieć Geodezyjna—Positioning System) corrections were conducted. In the case of a lack of a precise RTK solution, a 1 h session was conducted. Part of the highest points was located in a large forest, so the heights were transferred by geometrical levelling from a point with good sky view conditions. The most accurate national quasi-geoid model, known as pl-geoid-2011, was used for both modes [109]. The above assumptions allowed for height determination with an accuracy level of 5–10 cm.
The point cloud from airborne laser scanning was acquired from the Central Documentation Centre of Geodesy and Cartography, from a dataset prepared under the IT system of the country guard (ISOK) project (http://www.isok.gov.pl/en/). The DEM was created from a LiDAR point cloud with a density of 4 pts/m2 (Table 1) and verified by an independent body [110]. LiDAR-based DEM has a resolution of 1 m.

Table 1.
Parameters of the airborne laser scanning IT system of the country guard (ISOK) project [110].
The methodology of the present study was based on the identification of the source of the terrain altitude data, which are widely available and have the greatest accuracy. Commonly available models, such as the SRTM, are not fully accurate. This model was created using the radar technique, has a low accuracy when determining height, and contains a small number of points. In 2020, in Poland, free access was granted to DTM measurement data obtained using LiDAR technology. Therefore, these data were used for comparative analysis with GNSS post-survey data. Measurement data from aerial laser scanning of the terrain surface were used in the analysis of the height of mountain peaks. The data were provided by the head office of Geodesy and Cartography (GUGiK) and were delivered in the form of point clouds saved in *.las format files. Data of this type were created during the survey of the area using airborne laser scanning (ALS) technology as part of the ISOK project. Depending on the category of land development, the scanning was performed with the assumption of different measurement parameters. The research area was classified as a Standard I type of development. In this standard, the area of the land was scanned with a density of 4 points per 1 m2 or greater. Research has shown that the data provided by GUGiK contain a greater number of points per square metre [111]. Unfortunately, the points are unevenly distributed over the surface of the ground. The accuracy of the height measurement (mean error) of the ALS point cloud after alignment (on flat surfaces) should be mh ≤ 0.15 m. Certain randomness of the location of the measurement points in the field causes an unfavourable phenomenon, which is the lack of a measurement point at the very top of the mountain. However, the high point density ensures that the measurement result is representative.
However, in order to identify the highest point on the six peaks, an RTK measurement was performed and the highest point was identified based on this (Table A1 in Appendix A, column 25: Method). On the remaining six peaks (Mała Babia Góra (Cyl); Jałowcowy Garb; Mędralowa; Jaworzyna; Góra Pięciu Kopców; Trzy Kopce), the search for the highest point was performed by means of levelling, just like the points measured with static mode. A levelling rod was placed in various places and readings were taken (the measurement was taken from one position of the leveller). In this way, the highest point was found. We are aware that this method is not ideal, but taking into account the difficult terrain, we believe that it was the only possible (and available) way to identify the highest point taken for the measurement.
Columns 27 (GNSS accuracy) and 28 (altitude accuracy) of Table A1 contain information about the achieved accuracy of GNSS positioning and altitude determination, respectively. The achieved altitude accuracy based on the GNSS positioning (column 27) is based on the RTK/static reports. Altitude accuracy is calculated according to error propagation based on the:
- Quasi-geoid model error, which, according to the pl-geoid-2011 model [109], was adopted as the maximum—10 cm—due to measuring in mountaineering areas. This was the same for all peaks.
- Errors of determining the highest point, levelling, and centric error—2 cm. This was the same for all peaks.
- GNSS positioning error (Table A1, column 27: GNSS accuracy), which was based on the RTK/static post-processing reports, and altitude error in the range from 1.3 cm to 4.6 cm.
4. Results and Discussion
A literature review was conducted based on 20 sources (Table 2) that included maps, books, guidebooks (item numbers VI–XII) and the internet (numbers I–V); it also included the sources of these data and the years of creation, which covered the period from 1884 to 2015.

Table 2.
List of sources used in the literature review.
The results of the review of data used by authors of other studies on peak heights are presented in Table A1. The altitudes obtained from the literature review were compared with the results from the LiDAR data and direct GNSS measurements (Figure 5). However, as demonstrated in previous studies, the GNSS is the most reliable and accurate technique [7,21].
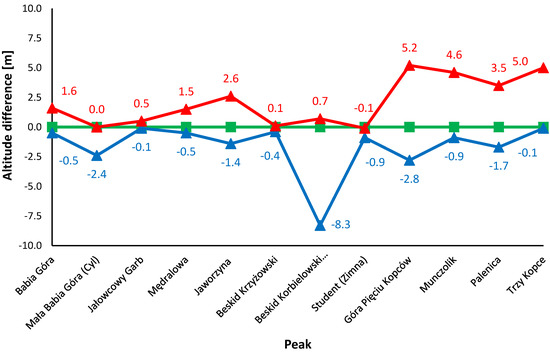
Figure 5.
The maximum (red) and minimum (blue) differences of each peak heights (m) taken from archived data, compared to the GNSS measurements (“zero” level, green).
Figure 5 shows the maximum and minimum difference of peak heights taken from archived data, compared to the GNSS measurements (“zero” level). Most often, extrema come from the source no. VI—the Third Military Survey (1875–1884). This source has data for nine peaks; five of them are significantly different (more than 1 m) from GNSS measurements—for Beskid Korbielowski (Westka) Mt., the difference has the highest value (–8.3 m). One value has a difference at the level of 0.9 m, two others—of about 0.5. It is rather surprising that the data for Mała Babia Góra do not differ from GNSS measurements. The values for Munczolik (+4.6 m), Palenica (+3.5 m) and Trzy Kopce (+5.0 m higher then GNSS) peaks were probably not verified during the updating survey (Table 2, no. VII) in 1920–1934 and they may also be found in touristic maps (Table 2, no. II, no. XII, no. XIII, no. XVII, no. XVIII, and no. XX). The height of Palenica was updated in source no. XIX (–1.5 m), but others have the same incorrect values. On the other hand, data sources no. V and no. XV (topographic maps from the 1990s) have the best-fitted values to GNSS with the average difference about 0.5–0.6 m.
Such a wide range of different values of peak heights is a result of:
- -
- The uncertain position of the “peak” and simultaneous difficulty in measuring an orthometric/normal height not directly, but, e.g., by stereoscopic photogrammetry, which has been a popular method in Poland since the 1950s;
- -
- The presence of vegetation and therefore photogrammetric identification errors (height differences between the DSM and DTM), especially for small-scale maps and photos;
- -
- Different survey techniques and equipment used;
- -
- Different height systems and vertical data used from 1875;
- -
- Systematic errors.
The influence of such factors cannot be estimated for each source. The lack of metadata—especially for sources I, II, and VIII—make accurate analysis impossible. The Third Military Survey (source VI) was performed using orthometric heights that referenced Trieste sea level [112], which indicates values of about +0.5 compared to Kronstadt sea level. The updated measurements in the 1920s–1930s (source VII) were referred to as “Normal Null”—Amsterdam sea level [113] (+0.1–0.2 m). For source VIII, sea level is unknown. Other sources probably reference different variants of Kronstadt sea level (+0.0–0.1 m). The aforementioned factors allow us to claim that the differences in heights of up to 1 m, compared to GNSS, are caused by these factors. Source XV has data for Munczolik, Palenica, and Trzy Kopce peaks, with an average difference of about 0.6 m. This means that the incorrect heights have existed in tourism for over 100 years.
The inconsistency in the topographic maps presented above has resulted in differences in touristic and popular sources. These height differences in tourist maps—both printed and online—are quite common. Among the 12 summits analysed in this study, only half had the same heights as presented in the sources that were examined. Moreover, the authors of this study focused on the number of appearances of summit height in each source (last row in Table A1) and the number of appearances of each summit in the sources (column 24: no. of sources, in Table A1).
The highest summit subject to research was Babia Góra Mountain, which differed over a range of two metres (between 1723 and 1725 m). The same range was noted on adjacent Mała Babia Gora Mountain and Medralowa Mountain, while Jałowcowy Garb Mountain and Student Mountain had the same height in each source. This suggests that all of the sources were based on one height measurement only.
The largest differences were noted for Beskid Korbielowski Mountain (9 m, 14 sources), Góra Pięciu Kopców Mountain (8 m, three sources), and Munczolik Mountain (5.5 m, 11 sources). The editors of tourist maps use topographic maps as base data for their publications, so the misinformation is generally at the same level as on topographic maps.
The authors noted that the altitude data received from professional GNSS devices tended to differ from data used in maps, guidebooks, and scientific books. It was also noted that many tourist maps and guidebook publishers use altitude data that were established using outdated technology. Furthermore, in general, the data received from GNSS and LiDAR were similar. First, differences between heights obtained using LiDAR and GNSS were less than 20 cm. The only exception was Babia Gora Mountain (40 cm); however, this may have been caused by the rocky nature of the peak. An RTK receiver was placed at the top of the rock peak while LiDAR data were smoothed out, thus, the height obtained from LiDAR was different by 40 cm. Such high compatibility of the results from both modern methods confirmed their accuracy rounded to 1 m. However, in comparison with existing sources, the heights obtained from the GNSS measurement were assumed more reliable.
Differences between GNSS measurements were used to determine which of the sources were invalid and could not be treated as a reference. The biggest differences proved existence of such incorrect height summits. For Jaworzyna Mountain, some of the sources showed a height of 1050 m, which was incorrect (proved by GNSS measurement). The GNSS receiver indicated a height of 1047.4 m; therefore, according to the authors, this is the correct height that should be used. In the case of the Beskid Korbielowski Mountain, the correct height was 954.3 m (from GNSS measurement), thus, the values of 946 m and 948 m indicated in three sources were incorrect. Góra Pięciu Kopców Mountain only appeared in four sources, two of them showed an incorrect height (1542 m) which was almost 5 m higher compared to the GNSS measurement. For Munczolik Mountain, Palenica Mountain, and Trzy Kopce Mountain, a comparison of existing sources with GNSS results showed that some had heights almost 5 m higher for each mountain. This was mostly because their heights originated from a single source in the past and have not been measured more frequently (including the use of modern measuring techniques) than other, more well-known objects.
Accurate peak heights are important not only for tourism (e.g., the selection of ascents, how hiking trails are operated), but are also elements of the growing trust in geodetic research and science as a whole. For this reason, even fragmentary, local, or regional measurements are important. In addition, altitude data marked on maps or located on trails are often used as reference points for devices equipped with GPS (such as watches); an incorrect reference will result in subsequent reading errors. Therefore, it should be emphasised that several of the mountain peak heights presented in the literature are out of date. Moreover, this topic is not raised on a larger scale in global literature. To our knowledge, this is the first study of its type; hence, our research is innovative and brings new knowledge. It is our opinion that similar research should be conducted on a larger scale. This would encourage a discussion on the remeasurement of lesser-known peaks that are seldom visited by tourists. This is a major challenge facing scientists today.
5. Conclusions
In the present study, the heights of 12 selected mountain peaks were verified. The research focused on the main ridge of the Orava–Żywiec Beskids Mts (Poland), which is part of the principal ridge of the Carpathian Mountains. To obtain new insight into mountain peak altitudes, this study compared two modern height determination techniques: GNSS and LiDAR. The results were later compared with those used in maps, atlases, and books. This analysis was conducted to demonstrate that lesser known objects (mountain peaks) are rarely the subject of research. Therefore, there may be errors in the heights, which are presented in the literature and cartographic materials.
This study highlighted that the measurement differences between the two methods (GNSS and LiDAR) were generally only 20 cm (40 cm in the case of Babia Góra). Such small deviations indicate that LiDAR and GNSS are currently the most accurate techniques and should be used for this type of research. Conversely, the slight difference observed between the results demonstrates the advantage of LiDAR over GNSS, which is much more time-consuming. Overall, differences between the most precise GNSS measurements and the other results allowed for the determination of which sources were invalid and could not be treated as the reference. As the measurements obtained via GNSS were more accurate, it should be the principal method used when examining the height of main peaks.
Our findings may prove to be helpful in identifying differences in peak heights found in the literature versus peak heights obtained via direct measurement.
Author Contributions
K.M. 25%, M.A. 20%, J.M. 15%, T.L. 10%, M.P. 5%, T.N. 5%, P.K. 5%, A.K. 5%, Ł.B. 5%, P.P.-P. 5%. Conceptualization, K.M., M.A., J.M., T.L., M.P., T.N., P.K., A.K., Ł.B., and P.P.-P.; methodology, K.M., M.A., J.M., T.L., M.P., T.N., P.K., A.K., Ł.B., and P.P.-P.; software, K.M., M.A., J.M., T.L., M.P., T.N., P.K., A.K., Ł.B., and P.P.-P.; validation, K.M., M.A., J.M., T.L., M.P., T.N., P.K., A.K., Ł.B., and P.P.-P.; formal analysis, K.M., M.A., J.M., T.L., M.P., T.N., P.K., A.K., Ł.B., and P.P.-P.; investigation, K.M., M.A., J.M., T.L., M.P., T.N., P.K., A.K., Ł.B., and P.P.-P.; resources, K.M., M.A., J.M., T.L., M.P., T.N., P.K., A.K., Ł.B., and P.P.-P.; data curation, K.M., M.A., J.M., T.L., M.P., T.N., P.K., A.K., Ł.B., and P.P.-P.; writing—original draft preparation, K.M., M.A., J.M., T.L., M.P., T.N., P.K., A.K., Ł.B., and P.P.-P.; writing—review and editing, K.M., M.A., J.M., T.L., M.P., T.N., P.K., A.K., Ł.B., and P.P.-P.; visualization, K.M., M.A., J.M., T.L., M.P., T.N., P.K., A.K., Ł.B., and P.P.-P.; supervision, K.M., M.A., J.M., T.L., M.P., T.N., P.K., A.K., Ł.B., and P.P.-P.; project administration, K.M., M.A., J.M., T.L., M.P., T.N., P.K., A.K., Ł.B., and P.P.-P.; funding acquisition, K.M., M.A., J.M., T.L., M.P., T.N., P.K., A.K., Ł.B., and P.P.-P. All authors have read and agreed to the published version of the manuscript.
Funding
This paper was produced under scientific activity and cooperation with the Pedagogical University of Cracow (Krakow, Poland), the University of Warsaw (Warsaw, Poland), the AGH University of Science and Technology (Krakow, Poland), the Technical University in Zvolen (Zvolen, Slovakia), the University of Primorska (Koper, Slovenia), the University of Agriculture in Krakow (Krakow, Poland), the Lublin University of Technology (Lublin, Poland), and the University of Ljubljana (Ljubljana, Slovenia). This research was funded by the AGH University of Science and Technology under grant number 16.16.150.545.
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
List of the altitudes of each summit (in metres) with data sources, global navigation satellite system (GNSS) and light detection and ranging (LiDAR).
Table A1.
List of the altitudes of each summit (in metres) with data sources, global navigation satellite system (GNSS) and light detection and ranging (LiDAR).
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| No | Source (Table 2) | I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII | XIII | XIV | XV | XVI | XVII | XVIII | XIV | XX | Max | No of Sources | Method * | GNSS | GNSS Accuracy ** | Altitude Accuracy *** | LiDAR | |
| Summit | |||||||||||||||||||||||||||||
| 1 | Babia Góra | 1725 | 1723 | 1724 | 1725 | 1725 | 1724 | 1724 | 1725 | 1724.8 | 1725 | 1725 | 1722.9 | 1722.9 | 1725 | 1724.6 | 1724.6 | 1725 | 1725 | 2.1 | 18 | R | 1723.4 | 0.030 | 0.11 | 1723.0 | |||
| 2 | Mała Babia Góra (Cyl) | 1517 | 1515 | 1517 | 1515 | 1517 | 1517 | 1517 | 1517 | 1514.6 | 1517 | 1517 | 1514.8 | 1514.8 | 1515 | 1515 | 1515 | 1517 | 1517 | 2.4 | 18 | S | 1517.0 | 0.018 | 0.10 | 1516.9 | |||
| 3 | Jałowcowy Garb | 1017 | 1017 | 1017 | 1017 | 1017 | 1017 | 0.0 | 6 | S | 1016.5 | 0.046 | 0.11 | 1016.4 | |||||||||||||||
| 4 | Mędralowa | 1169 | 1169 | 1169 | 1168 | 1169 | 1169 | 1169 | 1170 | 1168.1 | 1170 | 1170 | 1168.5 | 1168.5 | 1169 | 1169 | 1169 | 1169 | 1169 | 2.0 | 18 | S | 1168.5 | 0.041 | 0.11 | 1168.4 | |||
| 5 | Jaworzyna | 1047 | 1047 | 1050 | 1047 | 1047 | 1050 | 1050 | 1050 | 1046.5 | 1050 | 1050 | 1046 | 1046 | 1047.3 | 1047.3 | 1047 | 1047 | 1047 | 1047 | 1047 | 4.0 | 20 | S | 1047.4 | 0.029 | 0.11 | 1047.3 | |
| 6 | Beskid Krzyżowski | 923 | 923 | 923 | 923 | 923 | 923.4 | 923 | 923 | 923.4 | 923.4 | 923 | 923 | 923 | 923 | 923 | 0.4 | 15 | R | 923.4 | 0.027 | 0.11 | 923.5 | ||||||
| 7 | Beskid Korbielowski (Westka) | 955 | 954 | 954 | 954 | 946 | 946 | 948 | 954.5 | 954 | 954 | 954 | 955 | 955 | 954 | 955 | 9.0 | 15 | R | 954.3 | 0.015 | 0.10 | 954.1 | ||||||
| 8 | Student (Zimna) | 935 | 935 | 935 | 935 | 935 | 935 | 935 | 935 | 935 | 935 | 935 | 935 | 0.0 | 12 | R | 935.9 | 0.020 | 0.10 | 935.8 | |||||||||
| 9 | Góra Pięciu Kopców | 1534 | 1534 | 1542 | 1542 | 8.0 | 4 | S | 1536.8 | 0.013 | 0.10 | 1536.9 | |||||||||||||||||
| 10 | Munczolik | 1356 | 1356 | 1356 | 1356 | 1350.5 | 1356 | 1356 | 1350.8 | 1356 | 1356 | 1356 | 1356 | 5.5 | 12 | R | 1351.4 | 0.022 | 0.10 | 1351.5 | |||||||||
| 11 | Palenica | 1343 | 1338 | 1343 | 1339 | 1343 | 1343 | 1338.8 | 1343 | 1343 | 1337.8 | 1339.1 | 1343 | 1343 | 1343 | 1338 | 1343 | 5.2 | 16 | R | 1339.5 | 0.019 | 0.10 | 1339.4 | |||||
| 12 | Trzy Kopce | 1216 | 1216 | 1216 | 1216 | 1216 | 1211.4 | 1216 | 1216 | 1213.4 | 1211.7 | 1216 | 1216 | 1216 | 1216 | 4.6 | 14 | S | 1211.0 | 0.032 | 0.11 | 1210.9 | |||||||
| No of summits | 12 | 12 | 7 | 6 | 7 | 9 | 9 | 7 | 9 | 4 | 4 | 7 | 7 | 7 | 8 | 7 | 11 | 12 | 11 | 12 | |||||||||
* Method of the measurement: (R)TK, (S)tatic. ** Based on the RTK or static post-processing reports, both based on the fixed ambiguities solutions only. *** Altitude accuracy—calculated according to the propagation of the error, including quasi geoid error, GNSS accuracy and centre/levelling error.
References
- Podobnikar, T. Detecting Mountain Peaks and Delineating Their Shapes Using Digital Elevation Models, Remote Sensing and Geographic Information Systems Using Autometric Methodological Procedures. Remote Sens. 2012, 4, 784–809. [Google Scholar] [CrossRef]
- Buscaini, G.; Labande, F.; Brandt, M. The 4000ers of the Alps—Official UIAA List. UIAA Bull. 1994, 9–16. Available online: http://www.hikr.org/files/40196.pdf (accessed on 14 January 2021).
- Munro, H. Tables Giving All the Scottish Mountains Exceeding 3000 Feet in Height. Scott. Mt. Club J. 1891, 1, 279–281. [Google Scholar]
- Apollo, M.; Mostowska, J.; Maciuk, K.; Wengel, Y.; Jones, T.E.; Cheer, J.M. Peak-Bagging and Cartographic Misrepresentations: A Call to Correction. Curr. Issues Tour. 2020, 1–6. [Google Scholar] [CrossRef]
- Bilham, R. Height Measurements Mt Everest. Available online: http://dos.gov.np/everest/downloads/Roger_Bilham.pdf (accessed on 15 November 2020).
- Cajori, F. History of Determinations of the Heights of Mountains. Isis 1929, 12, 482–514. [Google Scholar] [CrossRef]
- Kudrys, J.; Buśko, M.; Kozioł, K.; Maciuk, K. Determination of the Normal Height of Chornohora Summits by a Precise Modern Measurement Techniques. Maejo Int. J. Sci. Technol. 2020, 14, 156–165. [Google Scholar]
- Langley, R.B. Innovation: GLONASS—Past, Present and Future. GPS World. Available online: https://www.gpsworld.com/innovation-glonass-past-present-and-future/ (accessed on 21 November 2020).
- Benedicto, J. Directions 2020: Galileo Moves Ahead. GPS World. Available online: https://www.gpsworld.com/directions-2020-galileo-moves-ahead/ (accessed on 1 December 2020).
- Barnes, D. GPS Status and Modernization Plans. In Proceedings of the Munich Satellite Navigation Summit 2019, Munich, Germany, 25–27 March 2019. [Google Scholar]
- Hein, G.W. Status, Perspectives and Trends of Satellite Navigation. Satell. Navig. 2020, 1, 22. [Google Scholar] [CrossRef]
- Zrinjski, M.; Matika, K.; Barković, Đ. Razvoj i Modernizacija GNSS-a. Geod. List 2019, 73, 45–65. [Google Scholar]
- Ward, M. The Height of Mount Everest. Alp. J. 1995, 100, 30–33. [Google Scholar] [CrossRef]
- Junyong, C.; Yanping, Z.; Janli, Y.; Chunxi, G.; Peng, Z. Height Determination of Qomolangma Feng (MT. Everest) in 2005. Surv. Rev. 2010, 42, 122–131. [Google Scholar] [CrossRef]
- De Graaff-Hunter, J. De Various Determinations over a Century of the Height of Mount Everest. Geogr. J. 1955, 121, 21. [Google Scholar] [CrossRef]
- Poretti, G. Is Mt. Everest Higher Than 100 Years Ago. In The Seventy Great Mysteries of the Natural World; Thames & Hudson: London, UK, 2008; pp. 68–70. [Google Scholar]
- De Beer, G. The History of the Altimetry of Mont Blanc. Ann. Sci. 1956, 12, 3–29. [Google Scholar] [CrossRef]
- Poretti, G.G. America’s highest peak now measures 6962 metres! Report. Mag. Leica Geosystems. 1999, 47, 28–29. [Google Scholar]
- Saburi, J.; Angelakis, N.; Jaeger, R.; Illner, M.; Jackson, P.; Pugh, K.T. Height Measurement of Kilimanjaro. Surv. Rev. 2000, 35, 552–562. [Google Scholar] [CrossRef]
- Pérez, O.J.; Hoyer, M.; Hernández, J.; Rodríguez, C.; Márques, V.; Sué, N.; Velandia, J.; Fernandes, J.; Deiros, D. GPS Height Measurement of Peak Bolivar, Venezuela. Surv. Rev. 2006, 38, 697–702. [Google Scholar] [CrossRef]
- Kozioł, K.; Maciuk, K. New Heights of the Highest Peaks of Polish Mountain ranges. Remote Sens. 2020, 12, 1446. [Google Scholar] [CrossRef]
- Gulatee, B.L. Heights of Himalayan Snow Peaks. J. Meteorol. Geophys. 1952, 17, 165–172. [Google Scholar]
- Pugh, K.T. Height Determination of Kilimanjaro. Emp. Surv. Rev. 1954, 91, 194–206. [Google Scholar] [CrossRef]
- Poretti, G.; Mandler, R.; Lipizer, M. The Height of Mountains. Boll. Geofis. Teor. Appl. 2006, 47, 557–575. [Google Scholar]
- Poretti, G. Quanto è Alto il Monte Everest? Tessere, G., Ed.; CUEN Napoli: Napoli, Italy, 1995. [Google Scholar]
- Poretti, G. Geophysical, Geological and Geographycal features of the Himalayas. In Ecovision World Monograph Series; Schweizerbart Science Publishers: Sttutgart, Germany, 1998; pp. 19–34. [Google Scholar]
- Poretti, G.; Lohmar, F.J.; Puruckherr, R.; Marchesini, C.; Beinat, A.; Eckardt, M.; Marchesini, A. Geodetic Measurements in the Himalayas and New Determination of the Height of Mount K2. Boll. Geofis. Teor. Appl. 2000, 41, 219–231. [Google Scholar]
- Rondeau, M.C. Scanning the Top of Europe 2020. Available online: https://leica-geosystems.com/case-studies/surveying-and-engineering/scanning-the-top-of-europe (accessed on 15 November 2020).
- Yamagishi, H.; Bhandary, N.P. (Eds.) GIS Landslide; Springer: Tokyo, Japan, 2017; ISBN 978-4-431-54390-9. [Google Scholar]
- Liu, X. Accuracy Assessment of Lidar Elevation Data Using Survey Marks. Surv. Rev. 2011, 43, 80–93. [Google Scholar] [CrossRef]
- Featherstone, W.E.; Kirby, J.F.; Kearsley, A.H.W.; Gilliland, J.R.; Johnston, G.M.; Steed, J.; Forsberg, R.; Sideris, M.G. The AUSGeoid98 Geoid Model of Australia: Data Treatment, Computations and Comparisons with GPS-Levelling Data. J. Geod. 2001, 75, 313–330. [Google Scholar] [CrossRef]
- Kenyeres, A. GPS/Leveling; Springer: Cham, Switzeraland, 1994. [Google Scholar] [CrossRef]
- Fotopoulos, G. UCGE Reports an Analysis on the Optimal Combination of Geoid, Orthometric and Ellipsoidal Height Data. 2003. Available online: https://www.ucalgary.ca/engo_webdocs/MGS/03.20185.GFotopoulos.pdf (accessed on 15 November 2020).
- Meyer, T.H.; Roman, D.R.; Zilkoski, D.B. What Does Height Really Mean? Part IV: GPS Orthometric Heighting; American Association for Geodetic Surveying: Gaithersburg, MD, USA, 2006. [Google Scholar]
- Hirt, C.; Wübbena, G. Mutual Validation of GNSS Height Measurements and High-Precision Geometric-Astronomical Levelling. GPS Solut. 2011, 15, 149–159. [Google Scholar] [CrossRef]
- Erenoglu, R.C.; Yucel, M.A.; Pirti, A.; Sanli, D.U. On the Performance of GNSS Levelling over Steep Slopes. Bol. Ciências Geodésicas 2012, 18, 645–660. [Google Scholar] [CrossRef]
- Erol, B.; Erol, S. GNSS in Practical Determination of Regional Heights. Glob. Navig. Satell. Syst. Signal Theory Appl. 2012. [Google Scholar] [CrossRef]
- Featherstone, W.E.; Stewart, M.P. Possible Evidence for Distortions in the Australian Height Datum in Western Australia. Aust. J. Geod. Photogramm. Surv. 1998, 68, 1–11. [Google Scholar]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Kouba, J.A.N.; Heroux, P. Precise Point Positioning Using IGS Orbit and Clock Products. GPS Solut. 2001, 5, 12–28. [Google Scholar] [CrossRef]
- Gao, Y.; Chen, K. Performance Analysis of Precise Point Positioning Using Rea-Time Orbit and Clock Products. J. Glob. Position. Syst. 2004, 3, 95–100. [Google Scholar] [CrossRef]
- Leandro, R.F.; Santos, M.; Langley, R.B. Analyzing GNSS Data in Precise Point Positioning Software Analyzing GNSS Data in Precise Point Positioning Software. GPS Solut. 2011. [Google Scholar] [CrossRef]
- Li, X.; Ge, M.; Dai, X.; Ren, X.; Fritsche, M.; Wickert, J.; Schuh, H. Accuracy and Reliability of Multi-GNSS Real-Time Precise Positioning: GPS, GLONASS, BeiDou, and Galileo. J. Geod. 2015, 89, 607–635. [Google Scholar] [CrossRef]
- Sterle, O.; Stopar, B.; Pavlovčič Prešeren, P. Single-Frequency Precise Point Positioning: An Analytical Approach. J. Geod. 2015, 89. [Google Scholar] [CrossRef]
- Higgins, M.B. Heighting with GPS: Possibilities and Limitations. Comm. 5 Int. Fed. Surv. 1999, 1–10. Available online: https://www.semanticscholar.org/paper/HEIGHTING-WITH-GPS-%3A-POSSIBILITIES-AND-LIMITATIONS-Higgins/8b6f8a55603742d5a17e2735f4322be6311ef341 (accessed on 14 January 2021).
- Wu, J.; Yiu, F.-G. Local Height Determination Using GPS-Monitored Atmospheric Path Delays. J. Surv. Eng. 2001, 127, 1–11. [Google Scholar] [CrossRef]
- Wu, J.; Lin, S.-G. Leveling by GPS Relative Positioning with Carrier Phases. J. Surv. Eng. 1996, 122, 145–157. [Google Scholar] [CrossRef]
- Featherstone, W.E.E.; Dentith, M.C.C.; Kirby, J.F.F. Strategies for the Accurate Determination of Orthometric Heights from GPS. Surv. Rev. 1998, 34, 278–296. [Google Scholar] [CrossRef]
- Jamal, S.; Arif, T.; Hassan, A.; Anom, W.; Aris, W.; Shen, W.; Faiz, M. Geodesy and Geodynamics Influencing Factors on the Accuracy of Local Geoid Model. Geod. Geodyn. 2019, 10. [Google Scholar] [CrossRef]
- Gruber, T. Evaluation of the EGM2008 Gravity Field by Means of GPS-Levelling and Sea Surface Topography Solutions. Newtons Bull 2009, 4, 3–17. [Google Scholar]
- Mouratidis, A.; Ampatzidis, D. European Digital Elevation Model Validation against Extensive Global Navigation Satellite Systems Data and Comparison with SRTM DEM and ASTER GDEM in Central Macedonia (Greece). ISPRS Int. J. Geo Inf. 2019, 8, 108. [Google Scholar] [CrossRef]
- Featherstone, W.E. Improvement to Long-Wavelength Australian Gravity Anomalies Expected from the CHAMP, GRACE and GOCE Dedicated Satellite Gravimetry Missions. Explor. Geophys. 2003, 34, 69–76. [Google Scholar] [CrossRef]
- Bilker, M. Evaluation of the New Global Gravity Field Models from CHAMP and GRACE with GPS-Levelling Data in Fennoscandia. In Proceedings of the XXII Geofysiikan Päivät, Helsinki, Finland, 19–20 May 2005; pp. 21–26. [Google Scholar]
- Kotsakis, C.; Katsambalos, K. Quality Analysis of Global Geopotential Models at 1542 GPS/Levelling Benchmarks over the Hellenic Mainland. Surv. Rev. 2010, 42, 327–344. [Google Scholar] [CrossRef]
- Gad, M.A.; Odalović, O.R. Evaluation the Performance of Recently Global Geopotential Models GGMs Over Egypt. Int. J. Sci. Eng. Res. 2017, 8, 936. [Google Scholar] [CrossRef]
- Erol, B.; Celik, R.N. Precise Local Geoid Determination to Make GPS Technique More Effective in Practical Applications of Geodesy. In Proceedings of the FIG Working Week 2004, Athens, Greece, 22–27 May 2004; pp. 1–13. [Google Scholar]
- Banasik, P.; Bujakowski, K. The Use of Quasigeoid in Leveling Through Terrain Obstacles. Rep. Geod. Geoinformatics 2018, 104, 57–64. [Google Scholar] [CrossRef]
- Heiskanen, W.A.; Moritz, H. Physical Geodesy; Springer: Wien, Austria, 1967. [Google Scholar]
- Yilmaz, S.A. Improvement of Elipsoidal Heights with Athmospherical Data Calculated from GNSS Data Improvement of Elipsoidal Heights with Athmospherical Data Calculated from GNSS Data. 2011. Available online: https://www.fig.net/resources/proceedings/fig_proceedings/fig2011/papers/ts08i/ts08i_yilmaz_5203.pdf (accessed on 22 November 2020).
- Schu, T. Impact of Systematic Errors on Precise Long-Baseline Kinematic GPS Positioning. GPS Solut. 2006, 108–125. [Google Scholar] [CrossRef]
- Mousa, A.E.-K.; Aboualy, N.; Sharaf, M.; Zahra, H.; Darrag, M. Tropospheric Wet Delay Estimation Using GNSS: Case Study of a Permanent Network in Egypt. NRIAG J. Astron. Geophys. 2016, 5, 76–86. [Google Scholar] [CrossRef]
- Dach, R.; Lutz, S.; Walser, P.; Fridez, P. Bernese GNSS Software Version 5.2; Astronomical Institute, University of Bern: Bern, Switzerland, 2015; Volume 47, ISBN 1879621142. [Google Scholar]
- Ekaso, D.; Nex, F.; Kerle, N.; Nex, F.; Kerle, N. Geo-Spatial Information Science Accuracy Assessment of Real-Time Kinematics (RTK) Measurements on Unmanned Aerial Vehicles (UAV) for Direct Geo-Referencing. Geo Spat. Inf. Sci. 2020, 23, 165–181. [Google Scholar] [CrossRef]
- Oštir, K. Daljinsko Zaznavanje; Inštitut za Antropološke in Prostorske Študije ZRC SAZU: Ljubljana, Slovenia, 2006. [Google Scholar]
- Dong, P.; Chen, Q. LiDAR Remote Sensing and Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Fujii, T.; Fukushi, T. Lidar: Introduction. In Laser Remote Sensing; CRC Press: Boca Raton, FL, USA, 2005; ISBN 9780824742560. [Google Scholar]
- Kovačič, B.; Supej, B. Najsodobnejša Tehnologija Lidar za Zajem Terestičnih Podatkov. Gradb. Rev. Gradnjo Sanacije Gradb. Mater. 2007, 10, 41–43. [Google Scholar]
- Gao, J. Towards Accurate Determination of Surface Height Using Modern Geoinformatic Methods: Possibilities and Limitations. Prog. Phys. Geogr. 2007, 31, 591–605. [Google Scholar] [CrossRef]
- Wehr, A.; Lohr, U. Airborne Laser Scanning—An Introduction and Overview. ISPRS J. Photogramm. Remote Sens. 1999, 54, 68–82. [Google Scholar] [CrossRef]
- Belcher, T. Leica ALS40 and ADS40 Systems Dominate LIDAR and Digital Airborne Data Acquisition. Report. Mag. Leica Geosystems 2002, 47, 14–15. [Google Scholar]
- Webster, T.L.; Forbes, D.L.; Dickie, S.; Shreenan, R. Using Topographic Lidar to Map Flood Risk from Storm-Surge Events for Charlottetown, Prince Edward Island, Canada. Can. J. Remote Sens. 2004, 30, 64–76. [Google Scholar] [CrossRef]
- Gomes Pereira, L.M.; Wicherson, R.J. Suitability of Laser Data for Deriving Geographical Information. A Case Study in the Context of Management of Fluvial Zones. ISPRS J. Photogramm. Remote Sens. 1999, 54, 105–114. [Google Scholar] [CrossRef]
- Jones, J.L. Mapping a Flood...Before It Happens. Available online: https://pubs.usgs.gov/fs/2004/3060/ (accessed on 15 November 2020).
- Means, J.E.; Acker, S.A.; Fitt, B.J.; Renslow, M.; Emerson, L.; Hendrix, C.J. Predicting Forest Stand Characteristics with Airborne Scanning Lidar. Photogramm. Eng. Remote Sens. 2000, 66, 1367–1371. [Google Scholar]
- Andersen, H.E.; McGaughey, R.J.; Reutebuch, S.E. Estimating Forest Canopy Fuel Parameters Using LIDAR Data. Remote Sens. Environ. 2005, 94, 441–449. [Google Scholar] [CrossRef]
- Hollaus, M.; Wagner, W.; Eberhöfer, C.; Karel, W. Accuracy of Large-Scale Canopy Heights Derived from LiDAR Data under Operational Constraints in a Complex Alpine Environment. ISPRS J. Photogramm. Remote Sens. 2006, 60, 323–338. [Google Scholar] [CrossRef]
- Viñas, O.; Ruiz, A.; Xandri, R.; Palà, V.; Arbiol, R. Combined Use of LiDAR and QuickBird Data for the Generation of Land Use Maps. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2006, 36. [Google Scholar]
- Ho, H.Y.; Hsiao, K.H.; Yang, M.S.; Liu, J.K. Landuse Classification Using Aerial Photographs and LiDAR Data. In Proceedings of the ACRS 2008 29th Asian Conference on Remote Sensing, Colombo, Sri Lanka, 10–14 November 2008; Volume 3, pp. 1741–1746. [Google Scholar]
- Engelkemeir, R.M.; Khan, S.D. Lidar Mapping of Faults in Houston, Texas, USA. Geosphere 2008, 4, 170–182. [Google Scholar] [CrossRef]
- Ridgway, J.R.; Minster, J.B.; Williams, N.; Bufton, J.L.; Krabill, W.B. Airborne Laser Altimeter Survey of Long Valley, California. Geophys. J. Int. 1997, 131, 267–280. [Google Scholar] [CrossRef]
- Kroh, P. Identification of Landing Sites for Rescue Helicopters in Mountains with Use of Geographic Information Systems. J. Mt. Sci. 2020, 17, 261–270. [Google Scholar] [CrossRef]
- Saari, T.; Poutanen, M.; Saaranen, V.; Kaartinen, H.; Kukko, A.; Lahtinen, S. Height Determination Techniques for the Next National Height System of Finland—A Case Study. Geod. Cartogr. 2015, 41, 145–155. [Google Scholar] [CrossRef]
- Becker, J.-M. History and Evolution of Height Determination Techniques Especially in Sweden. In Proceedings of the Geodesy and Surveying in the Future—The Importance of Heights, Gavle, Sweden, 15–17 March 1999; pp. 43–57. [Google Scholar]
- Karila, K.; Karjalainen, M.; Hyyppä, J.; Koskinen, J.; Saaranen, V.; Rouhiainen, P. A Comparison of Precise Leveling and Persistent Scatterer SAR Interferometry for Building Subsidence Rate Measurement. ISPRS Int. J. Geo Inf. 2013, 2, 797–816. [Google Scholar] [CrossRef]
- Burgmann, R.; Rosen, P.A.; Fielding, E.J. Synthetic Aperture Radar Interferometry to Measure Earth’s Surface Topography and Its Deformation. Annu. Rev. Earth Planet. Sci. 2000, 28, 169–209. [Google Scholar] [CrossRef]
- Hanssen, R.F. Radar Interferometry, Data Interpretation and Error Analysis; Springer: Dordrecht, The Netherlands, 2002. [Google Scholar]
- Yongjun, Z.; Zemin, W. Analyses and Solutions of Errors on GPS/GLONASS Positioning. Geo Spat. Inf. Sci. 2002, 5, 6–12. [Google Scholar] [CrossRef]
- Bamler, R.; Hartl, P. Synthetic Aperture Radar Interferometry. Inverse Probl. 1998, 14. [Google Scholar] [CrossRef]
- SkyGeo InSAR Technical Background 2020. Available online: https://skygeo.com/insar-technical-background/ (accessed on 15 November 2020).
- Alganci, U. Accuracy Assessment of Different Digital Surface Models. ISPRS Int. J. Geo Inf. 2018, 7, 114. [Google Scholar] [CrossRef]
- Bates, P.D.; Lane, S.N.; Ferguson, R.I. Computational Fluid Dynamics: Applications in Environmental Hydraulics; John Wiley & Sons: Chichester, UK, 2005; ISBN 0470843594. [Google Scholar]
- Piras, M.; Taddia, G.; Forno, M.G.; Gattiglio, M.; Aicardi, I.; Dabove, P.; Russo, S.L.; Lingua, A. Detailed Geological Mapping in Mountain Areas Using an Unmanned Aerial Vehicle: Application to the Rodoretto Valley, NW Italian Alps. Geomat. Nat. Hazards Risk 2017, 8, 137–149. [Google Scholar] [CrossRef]
- Forsberg, R.; Tscherning, C. An Overview Manual for the GRAVSOFT Geodetic Gravity Field Modelling Programs; DTU Space: Kongens Lyngby, Denmark, 2008; pp. 1–59. [Google Scholar]
- Sjöberg, L.E. A Solution to the Downward Continuation Effect on the Geoid Determined by Stokes’ Formula. J. Geod. 2003, 77, 94–100. [Google Scholar] [CrossRef]
- Tenzer, R.; Jának, J. Stokes-Helmert’s Scheme for Precise Geoid Determination. Rev. Cartogr. 2002, 74–75, 135. [Google Scholar]
- Ssengendo, R. A Height Datum for Uganda Based on a Gravimetric Quasigeoid Model and GNSS/Levelling. Ph.D. Thesis, KTH, School of Architecture and the Built Environment (ABE), Urban Planning and Environment, Geodesy and Satellite Positioning, Stockholm, Sweden, 2015. [Google Scholar]
- Borowski, L.; Banasik, P. The Conversion of Heights of the Benchmarks of the Detailed Vertical Reference Network into the PL-EVRF2007-NH frame. Rep. Geod. Geoinform. 2020, 109, 1–7. [Google Scholar] [CrossRef]
- Borowski, Ł.; Lal, A.; Nepelski, K. Analiza Osiadania Wybranych Typów Znaków Osnowy Geodezyjnej. Bud. Archit. 2017, 16, 135–142. [Google Scholar] [CrossRef]
- Balon, J.; Jodłowski, M. Regionalizacja Fizycznogeograficzna Karpat Zachodnich—Studium Metodologiczne. In Struktura Środowiska Przyrodniczego a Fizjonomia Krajobrazu; Instytut Geografii i Gospodarki Przestrzennej UJ: Krakow, Poland, 2014; pp. 85–106. ISBN 978-83-64089-02-2. [Google Scholar]
- Solon, J.; Borzyszkowski, J.; Bidłasik, M.; Richling, A.; Badora, K.; Balon, J.; Brzezińska-Wójcik, T.; Chabudziński, Ł.; Dobrowolski, R.; Grzegorczyk, I.; et al. Physico-Geographical Mesoregions of Poland: Verification and Adjustment of Boundaries on the Basis of Contemporary Spatial Data. Geogr. Pol. 2018, 91, 143–170. [Google Scholar] [CrossRef]
- Mazúr, E.; Činčura, J.; Kvitkovič, J. Geomorfológia. Atlas SSR, SAV, SÚGK; Bratislava, Slovakia, 1980. [Google Scholar]
- Štúra, 8. Štátny Geologický Ústav Dionýza Geologická Mapa Slovenska M 1:50 000. Available online: http://apl.geology.sk/gm50js (accessed on 15 November 2020).
- Izmaiłow, B.; Kaszowski, L.; Krzemień, K.; Święchowicz, J. Rzeźba. In Karpaty Polskie; Warszyńska, J., Ed.; Uniwersytet Jagielloński: Kraków, Poland, 1995; pp. 23–30. [Google Scholar]
- Rączkowska, Z.; Łajczak, A.; Margielewski, W.; Święchowicz, J. Recent Landform Evolution in the Polish Carpathians. In Recent Landform Evolution; Springer: Dordrecht, The Netherlands, 2012; pp. 47–101. [Google Scholar]
- Midriak, R. Morfogenéza Povrchu Vysokých Pohorí; VEDA: Bratislava, Slovakia, 1983. [Google Scholar]
- Marciniec, P.; Granoszewski, W.; Zimnal, Z. Osuwisko na Stokach Magury Witowskiej (Podhale). Przegląd Geol. 2019, 67, 405–413. [Google Scholar] [CrossRef]
- Państwowy Instytut Geologiczny—Państwowy Instytut Badawczy. Wyszukiwanie i Przeglądanie Informacji o Zagrożeniach Ruchami Masowymi. Available online: http://geoportal.pgi.gov.pl/portal/page/portal/SOPO/Wyszukaj3 (accessed on 1 December 2020).
- Obrębska-Starklowa, B. Differentiation of Topoclimatic Conditions in a Carpathian Foreland Valley Based on Multiannual Observations. Zesz. Nauk. Uniw. Jagiellońskiego. Pr. Geogr. 1995, 101, 1–120. [Google Scholar]
- Kadaj, R. Algorytm Opracowania Modelu PL-geoid-2011. In Proceedings of the Realizacja Osnów Geodezyjnych a Problemy Geodynamiki, Grybów, Poland, 25–27 September 2012; p. 26. [Google Scholar]
- Wężyk, P. Podręcznik dla Uczestników Szkoleń z Wykorzystania Produktów LiDAR. 2014. Available online: http://www.gugik.gov.pl/__data/assets/pdf_file/0019/23752/PODRECZNIK_ISOK_wyd.2.pdf (accessed on 15 November 2020).
- GUGiK Numeryczny Model Terenu. Available online: http://www.gugik.gov.pl/pzgik/zamow-dane/numeryczny-model-terenu (accessed on 14 October 2020).
- Raicich, F. A Study of Early Trieste Sea Level Data (1875–1914). J. Coast. Res. 2007, 23, 1067–1073. [Google Scholar] [CrossRef]
- Zbiorowa, P. Niwelacja Precyzyjna, 2nd ed.; Baran, W., Ed.; Polskie Przedsiębiorstwo Wydawnictw Kartograficznych: Warszawa/Wrocław, Poland, 1993; ISBN 83-7000-082-7. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).