GNSS Receiver-Related Pseudorange Biases: Characteristics and Effects on Wide-Lane Ambiguity Resolution

Abstract

Satellite chip shape distortions lead to signal tracking errors in pseudorange measurements, which are related to the receiver manufacturers, called receiver-related pseudorange biases. Such biases will lead to adverse effects for differential code bias (DCB) and satellite clock estimation, single point positioning (SPP) and precise point positioning (PPP) applications with pseudoranges. In order to assess the characteristics of receiver-related pseudorange biases for global positioning system (GPS), Galileo navigation satellite system (Galileo) and BeiDou navigation satellite system (BDS), seven short baselines from the Multi-GNSS experiment (MGEX) network are tested. The results demonstrate that there are significant inconsistences of pseudorange biases according to satellites, frequencies, receiver and antenna types. For the baselines using the same receivers of TRIMBLE, pseudorange biases are within ±0.2 ns with the same antennas, while they increase to ±0.6 ns with the different antennas. As for baselines with mixed receiver types, pseudorange biases can reach up to 2.5 ns. Among GPS/Galileo/BDS, Galileo shows the smallest pseudorange biases, and the obvious inconsistences of pseudorange biases are observed between BDS-2 and BDS-3, and Galileo in-orbit validation (IOV) satellites and full operational configuration (FOC) satellites. In order to validate receiver-related pseudorange biases, we carry out relative positioning experiments using short baselines. The results show that the RMS values of position errors are reduced 12.6% and 11.4% in horizontal and vertical components with biases correction. The impacts of receiver-related pseudorange biases on wide-lane (WL) ambiguity are also discussed. The results indicate that the percentage of the fractional parts within ±0.1 cycles have an obvious increase with the pseudorange biases correction, and RMS values of the fractional parts are reduced 28.9% and 67.6% for GPS and BDS, respectively.

1. Introduction

With the development of global navigation satellite systems (GNSS), navigation and positioning applications are evolving from single system to multifrequency and multisystem [1]. Global positioning system (GPS), global navigation satellite system (GLONASS), Galileo and BeiDou navigation satellite system (BDS) are fully operational and aiming to offer a continuous, more flexible and precise positioning service [2,3,4,5]. Multi-GNSS provides a larger number of satellites, which can reduce position dilution of precision (PDOP) values, and improve real-time precise point positioning (PPP) accuracy, reliability and availability [6]. It also provides triple-frequency signals, improving the performance of ambiguity resolution especially for medium and long baselines [7,8]. In addition to navigation and positioning applications, multifrequency signals also benefit to ray tracing the neutral atmosphere and the ionosphere [9]. Moreover, different types of satellite orbits offer more ways for earth rotation monitoring and global reference framework establishment [10].

According to previous research, there are multiple bias items in GNSS pseudorange observations. One of the bias items is usually attributed to frequency-dependent hardware group delays, which are quite stable, called differential code bias (DCB). This code bias includes two parts, the satellite-dependent and receiver-dependent [10,11]. Receiver-dependent DCB can be lumped into receiver clock offset, thus most of the existing studies focus on the satellite-dependent DCB, which can be estimated using methods involving ionospheric models [12,13]. At present, studies in this field are quite mature. Multi-GNSS DCB products can be downloaded from International GNSS Service (IGS) data centers, and it is applied to precise positioning and timing applications as a correction. For single point positioning (SPP) based on pseudorange observation and broadcast ephemeris, the satellite-dependent code bias can also be corrected using time group delay (TGD) parameters provided by various GNSS, which can be derived from IGS DCB products [14], but this is limited to code-division multiple access (CDMA) systems [15]. Moreover, studies have shown that there are elevation-dependent systematic code-carrier divergences on BDS-2 signal, called BDS satellite-induced code biases, which are likely attributed to the spacecraft internal multipath [16,17,18]. This code bias is proved to vary with satellite frequencies (B1, B2 and B3) and satellite types (medium earth orbit (MEO)/inclined geostationary orbit (IGSO) and geostationary orbit (GEO)). Corresponding correction models are proposed for IGSO/MEO satellites and GEO satellites by Wanninger and Beer [19] and Lou et al. [20]. When code-carrier biases are corrected, it improves wide-lane (WL) ambiguity resolution success rate [20], the accuracy of single-frequency PPP [19] and the accuracy of precise orbit estimation [21,22].

Except for the code biases caused by hardware group delays, recently research indicate that satellite chip shape distortions also lead to code biases in pseudorange observations, which differ from satellite to satellite. It is also reported that these distortions cause the tracking errors of the receivers, which are related to the receiver’s front-end and correlator [23,24,25,26,27,28]. Furthermore, it is found that when the receiver is set a tight correlator spacing to mitigate multipath errors, it will cause the increase of root mean square (RMS) of pseudorange biases [25]. It can be concluded that this receiver-related pseudorange biases cannot be rigorously split into satellite-dependent and receiver-dependent, but depend on the satellite and receiver pair. That is to say, these biases cannot be eliminated according to double difference (DD) operation, which will affect a number of GNSS applications especially when the mixed receivers are used. For example, Hauschild et al. found that there are inconsistencies in satellite DCB and clock offsets estimated by different receiver types and satellite systems, and the positioning errors of GPS-only SPP have shown a small increase when clock product is inconsistent with a user receiver [29]. Hauschild et al. [25] estimated receiver-related pseudorange biases for GPS, GLONASS, Galileo and BDS-2. The results prove that the largest inconsistence of pseudorange biases between satellites are found in GLONASS frequency-division multiple access (FDMA) signals, followed by GPS and BDS signals, and then Galileo signals. Zheng et al. [30] analyzed the characteristics of BDS-2 triple-frequency receiver-related pseudorange biases by different receiver types. Their results show that the largest difference between two different receiver types could reach up to 2.0 ns. When these receiver-related pseudorange biases are corrected, it greatly improves the accuracy of single-frequency SPP, and reduces the convergence time of single-frequency and dual-frequency PPP [30]. Moreover, satellite clock offsets estimated by mixed receiver types are more consistent with those estimated by the same receiver types [31].

At present, most research about GNSS receiver-related pseudorange biases focus on their applications in DCB, clock offsets estimation and positioning. The effects on WL ambiguity resolution need further studies. Moreover, the constellation of BDS-3 has been completed on 31 July 2020, and there is no relevant research on the characteristics of receiver-related pseudorange biases for BDS-3. In this contribution, we use the DD observation model to calculate the DD receiver-related pseudorange biases for GPS, Galileo, BDS-2 and BDS-3. On this basis, the characteristics and stabilities of pseudorange biases are concretely analyzed. Then, we discuss the effects of GNSS pseudorange biases on WL ambiguity resolution. Finally, some conclusions and prospects are given.

2. Methodology

In this section, we first proposed the observation model to estimate the DD receiver-related pseudorange biases, and the process strategy is explained. Then, the details of IGS stations applied in the experiment are listed, including station name, receiver model, antenna type and signals.

2.1. Observation Model

In GNSS data processing, raw pseudorange observation is defined as follows [30],

$$P_{r,f}^s={\rho }_r^s+c·d{t}_r-c·d{t}^s+{\alpha }^s·T^s+{\beta }_f·I^s+B_{r,f}-B_f^s+Bia{s}_{r,f}^s+{\epsilon }_{r,f}^s$$

(1)

where $P_{r,f}^s$ is pseudorange observation from satellite s to receiver r on frequency f (f = 1,2,3…); ${\rho }_r^s$ is geometric distance with Earth rotation correction; c is the speed of light in vacuum; $d{t}_r$ and $d{t}^s$ are receiver clock offset and satellite clock offset, respectively; $T^s$ is the zenith tropospheric delay, which can be converted to slant delay using the mapping function ${\alpha }^s$; $I^s$ denotes ionospheric delay with the frequency-dependent factor ${\beta }_f$; $B_{r,f}$ and $B_f^s$ are receiver-dependent and satellite-dependent pseudorange hardware delay, respectively; $Bia{s}_{r,f}^s$ represents receiver-related pseudorange biases on frequency f and ${\epsilon }_{r,f}^s$ is the measure for noise and multipath errors.

Differential positioning techniques are widely applied in GNSS data processing. According to double difference between two satellites (p, q) and two receivers (i, j), satellite clock offset, receiver clock offset and hardware delay can be eliminated [32]. For the zero baselines and short baselines with the distance less than 100 m, the DD ionospheric delay and tropospheric delay can be ignored [33]. From Equation (1), the DD GNSS receiver-related pseudorange biases becomes:

$$∆\nabla Bia{s}_{ij,f}^{pq}=∆\nabla P_{ij,f}^{pq}-∆\nabla {\rho }_{ij}^{pq}-∆\nabla {\epsilon }_{ij,f}^{pq}$$

(2)

where ∆∇ represents the DD operation, $∆\nabla Bia{s}_{ij,f}^{pq}$ is the DD GNSS receiver-related pseudorange biases, $∆\nabla P_{ij,f}^{pq}$ is the DD pseudorange observation, $∆\nabla {\rho }_{ij}^{pq}$ is the DD geometric distance and $∆\nabla {\epsilon }_{ij,f}^{pq}$ is the DD measure noise and multipath errors.

In order to reduce measure noise and multipath errors, the satellite elevation cutoff angle is set to 30° [6], and the length of the common tracking arc for two satellites is set to more than 20 min. The DD geometric distance $∆\nabla {\rho }_{ij}^{pq}$ can be removed by the precise station coordinates from IGS and orbits from broadcast ephemeris.

We refer to Tang et al., one reference satellite is selected for each satellite system [34]. In the following experiment, we set the reference satellite as G01, E02 and C11 for GPS, Galileo and BDS, respectively. It should be noted: If satellite $S_1$ is commonly visible with the reference satellite A, its receiver-related pseudorange biases can be estimated directly using Equation (2). If satellite $S_2$ is not common visible with the reference satellite, but satellite $S_1$ and $S_2$ can be tracked by the baseline at the same time, we also can figure out pseudorange biases of satellite $S_2$ using the following equation:

$$∆\nabla Bia{s}_{ij,f}^{A{S}_2}=∆\nabla Bia{s}_{ij,f}^{A{S}_1}+∆\nabla Bia{s}_{ij,f}^{S_1{S}_2}$$

(3)

2.2. Data Collection

With the rapid development of Multi-GNSS, there are large IGS stations that can track multifrequency and multisystem signals [10]. In order to analyze the characteristics of GNSS receiver-related pseudorange biases, we selected thirteen IGS stations to form seven short baselines (ZIM2_ZIM3, ZIM2_ZIMM, KOKB_KOKV, USN7_USN8, GODS_GODN, MAR6_MAR7 and KIR0_KIR8). These stations are equipped with different types of receivers and antennas, and the details are listed in

Table 1. Overview of stations. The signals listed in the table are limited to those used in the experiments, and the definition of signals corresponds to RINEX 3.03.

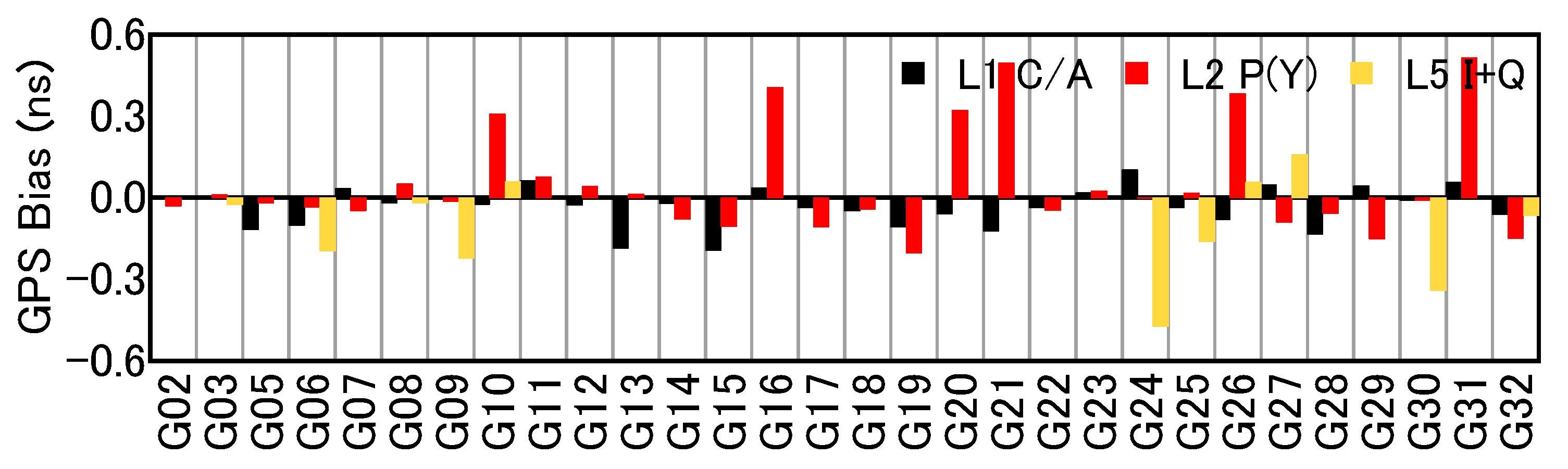
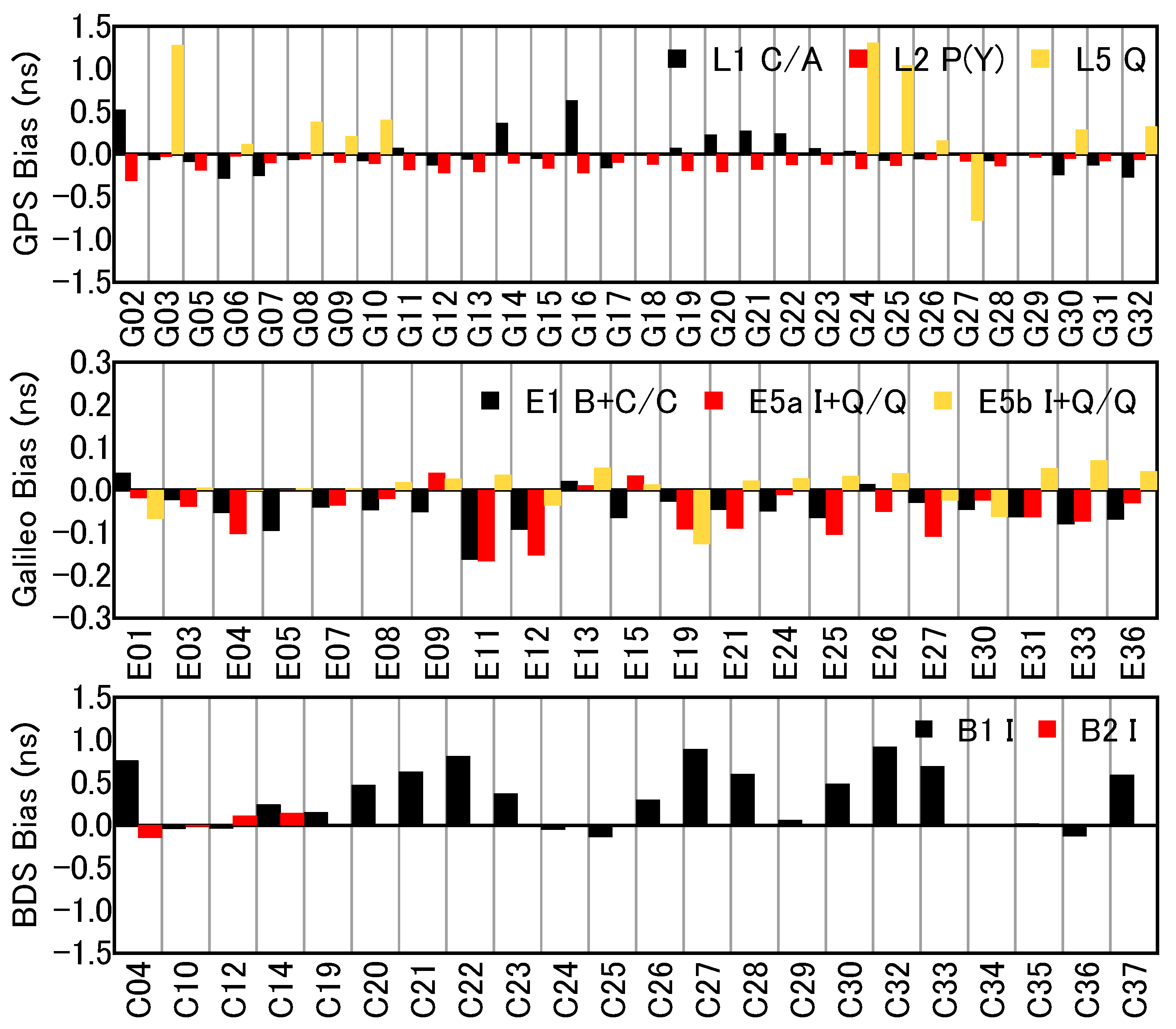
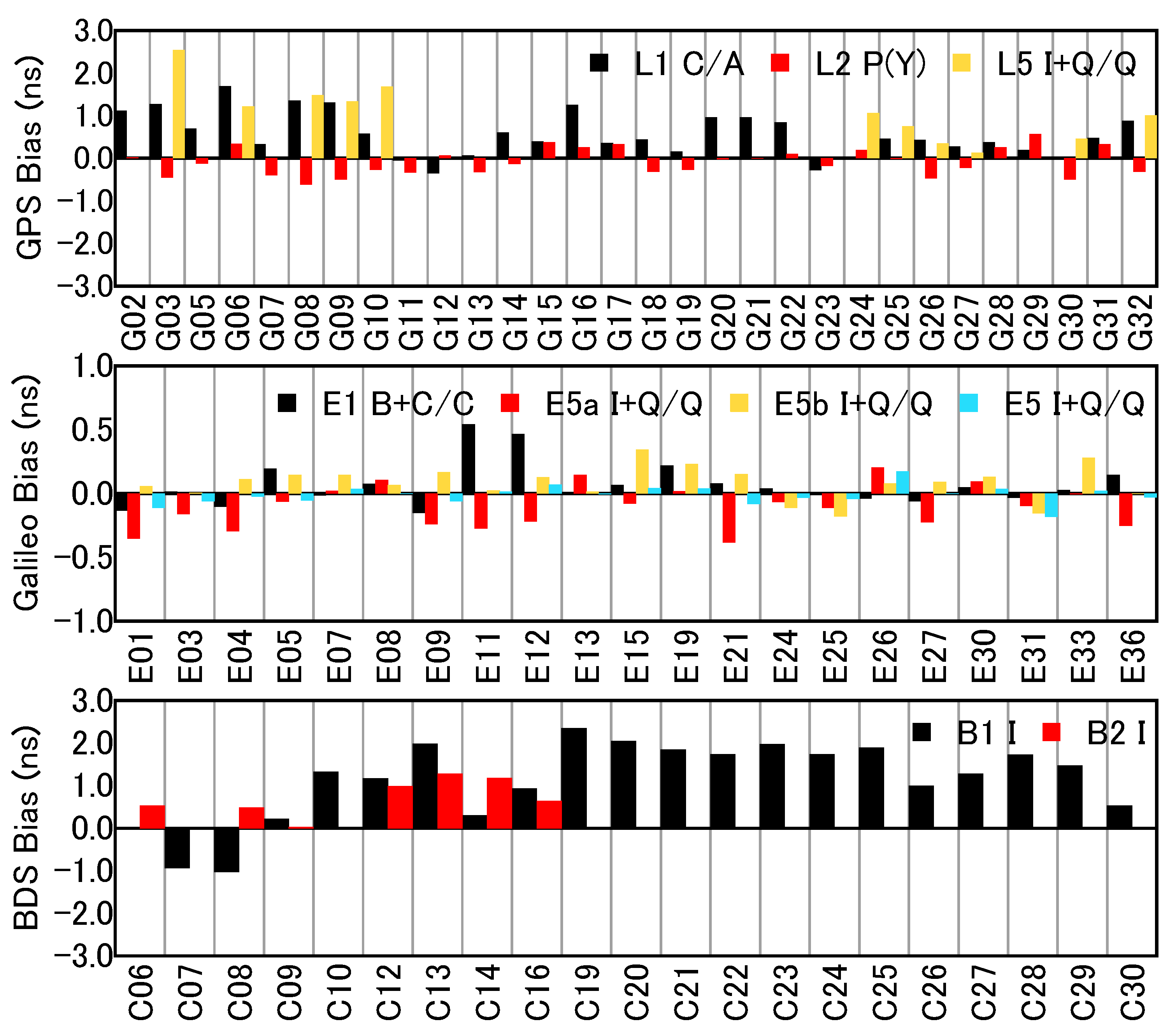
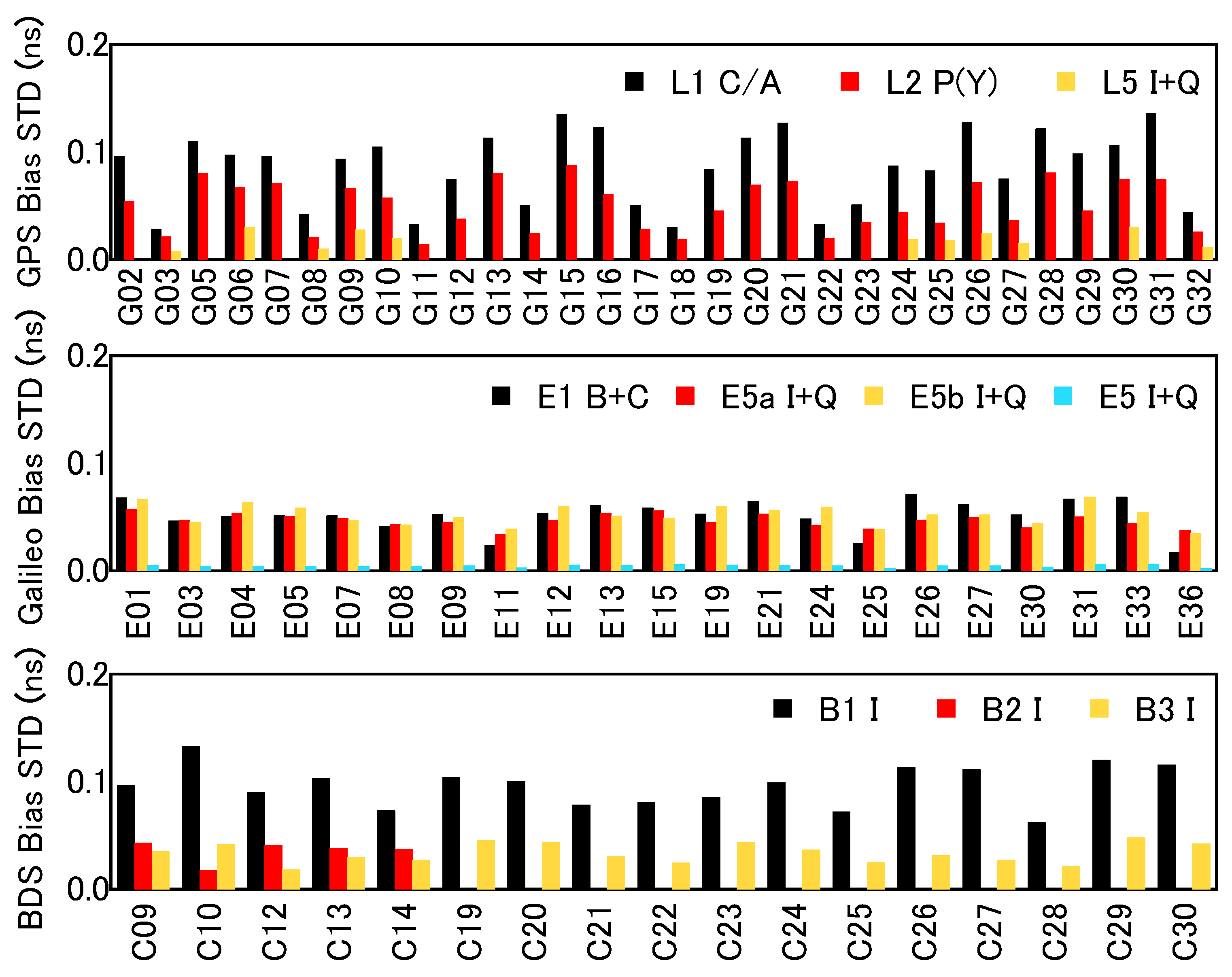
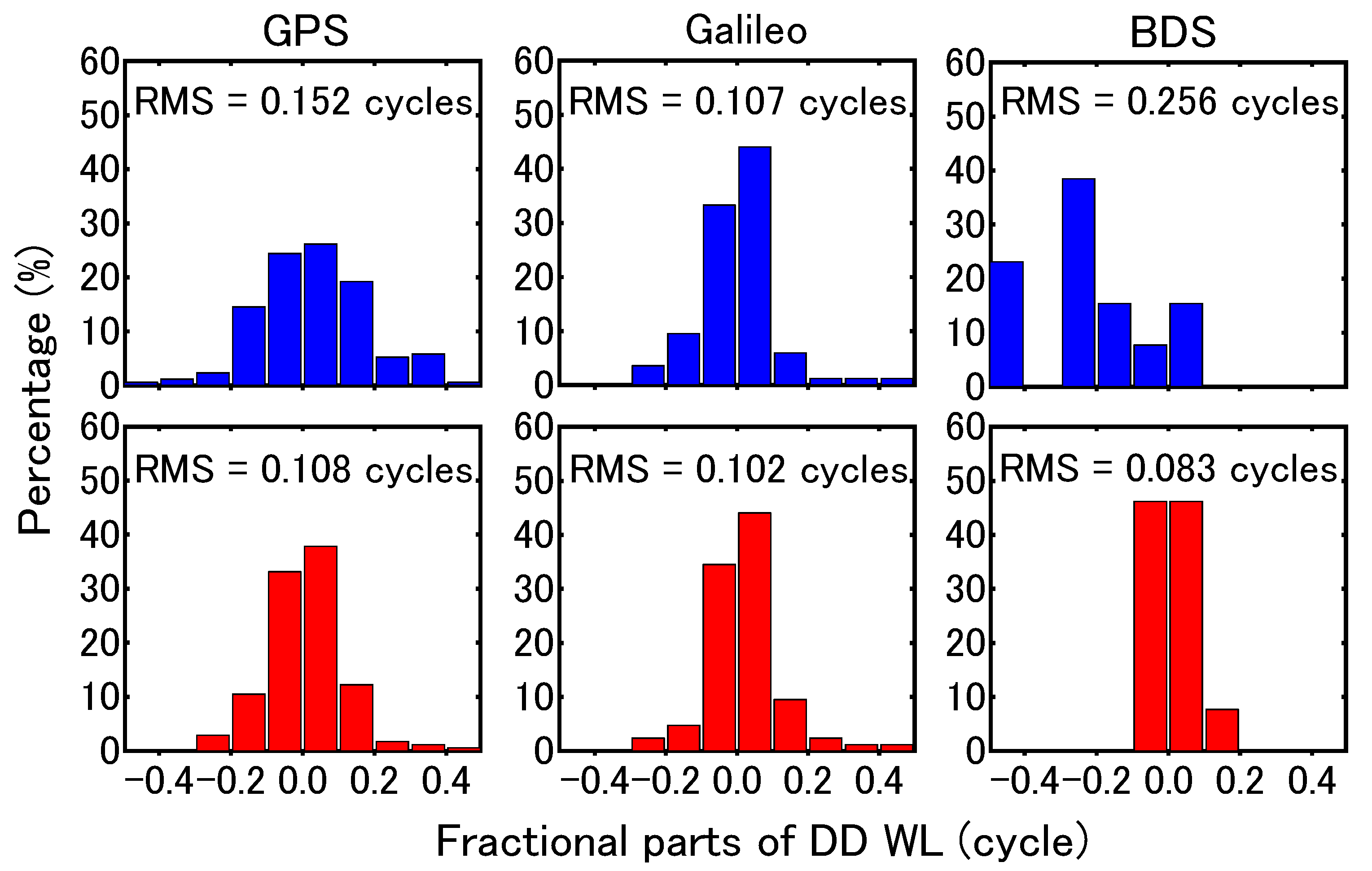
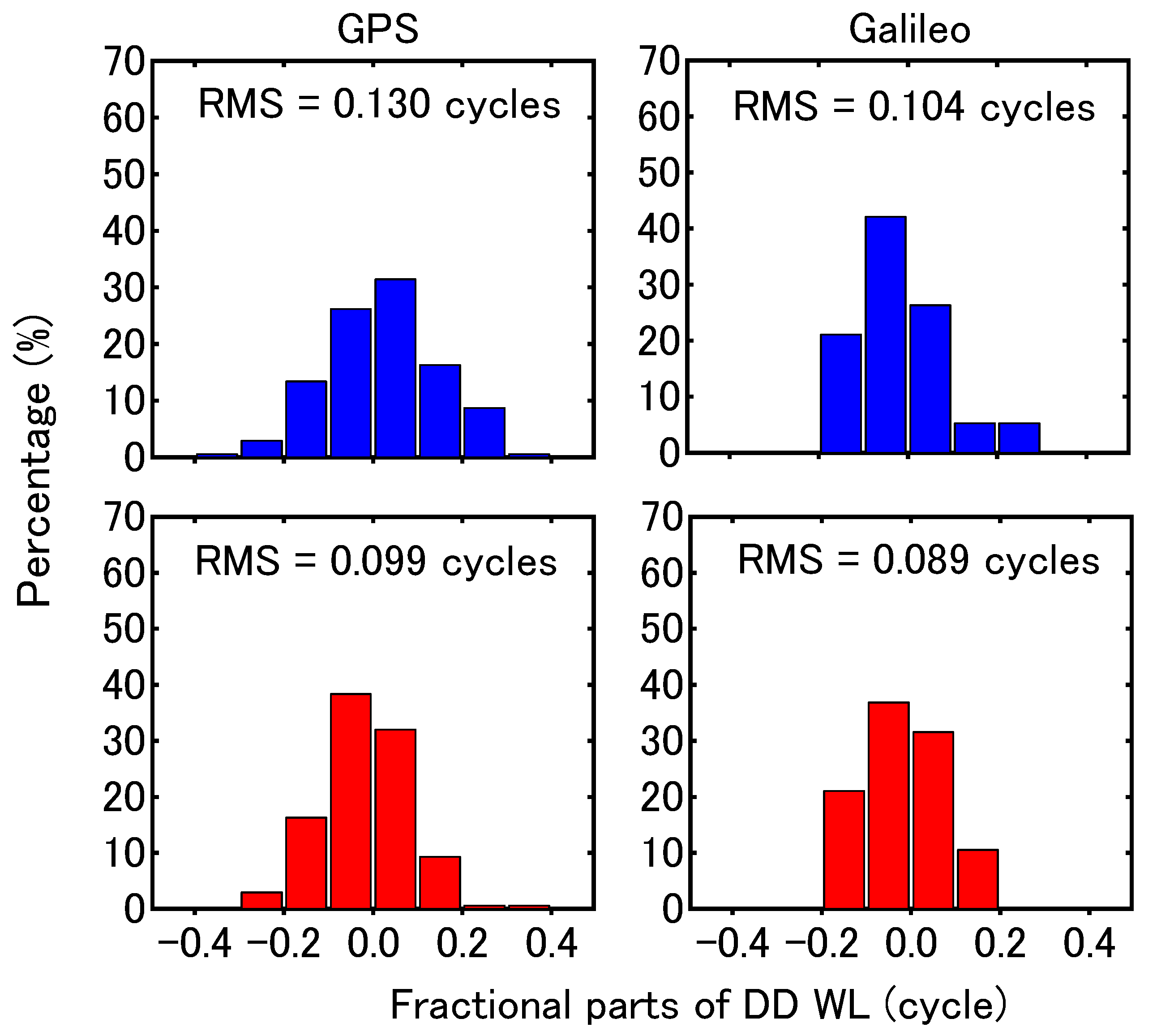
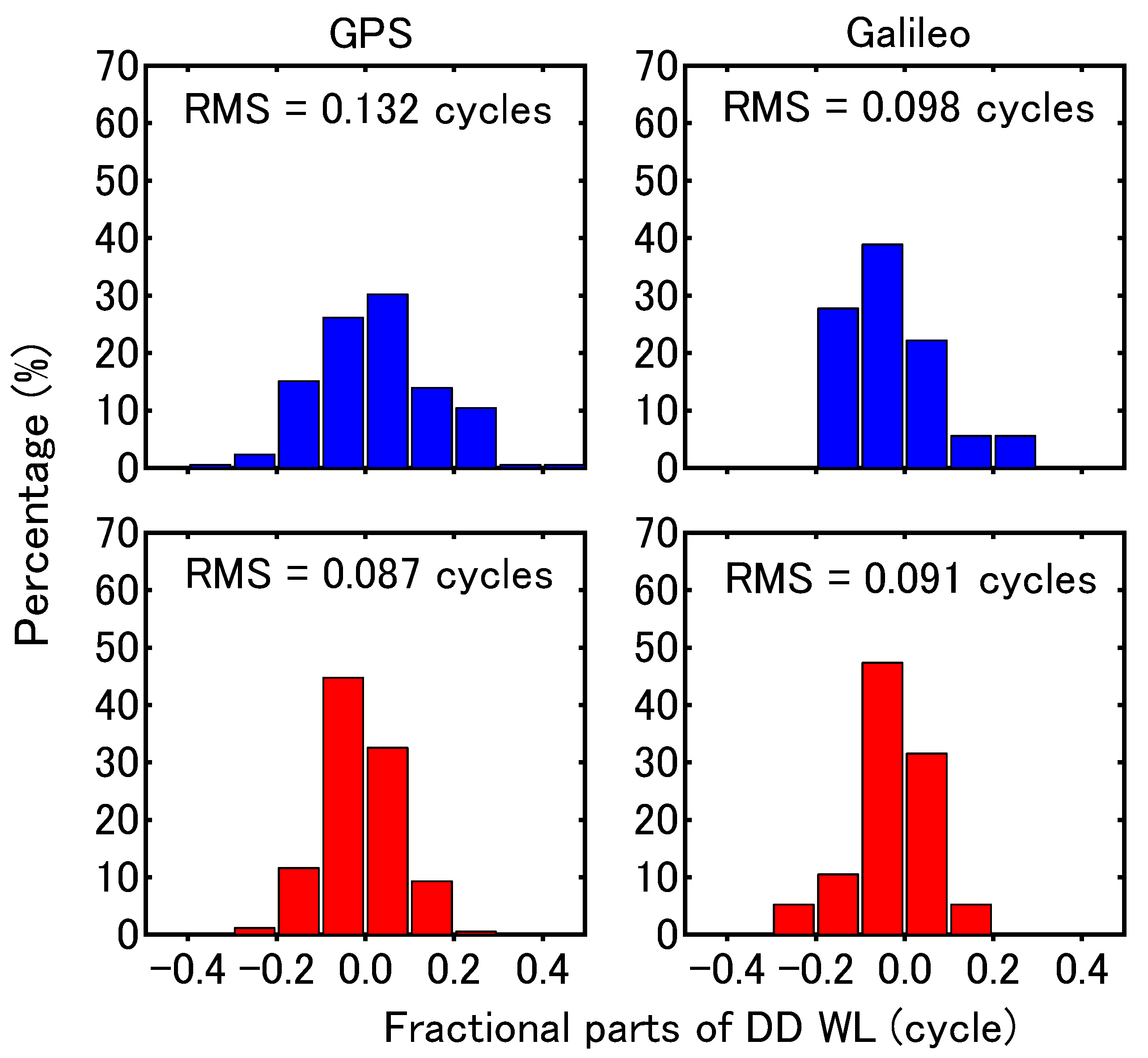
Station	Length	Receiver Model	Antenna Type	Signal
ZIM3	(0 m)	TRIMBLE NETR9	TRM59800.00	G: L1 C/A; L2 P(Y); L5 I + Q E: E1 B + C; E5a I + Q; E5b I + Q; E5 I + Q C: B1 I; B2 I; B3 I
ZIM2		TRIMBLE NETR9	TRM59800.00	G: L1 C/A; L2 P(Y); L5 I + Q E: E1 B + C; E5a I + Q; E5b I + Q; E5 I + Q C: B1 I; B2 I; B3 I
ZIMM		TRIMBLE NETR9	TRM29659.00	G: L1 C/A; L2 P(Y); L5 I + Q
USN7	(0.65 m)	SEPT POLARX5TR	TPSCR.G5	G: L1 C/A; L2 P(Y); L5 Q E: E1 C; E5a Q; E5b Q; E5 Q; E6 C C: B1 I; B2 I; B3 I
USN8		SEPT POLARX5TR	TPSCR.G5	G: L1 C/A; L2 P(Y); L5 Q E: E1 C; E5a Q; E5b Q; E5 Q; E6 C C: B1 I; B2 I; B3 I
GODS	(76.02 m)	JAVAD TRE_3 DELTA	TPSCR.G3	G: L1 C/A; L2 P(Y); L5 I + Q E: E1 B + C; E5a I + Q; E5b I + Q; E5 I + Q; E6 B + C C: B1 I; B2 I; B3 I
GODN		JAVAD TRE_3 DELTA	TPSCR.G3	G: L1 C/A; L2 P(Y); L5 I + Q E: E1 B + C; E5a I + Q; E5b I + Q; E5 I + Q; E6 B + C C: B1 I; B2 I; B3 I
KOKB	(0 m)	SEPT POLARX5TR	ASH701945G_M	G: L1 C/A; L2 P(Y); L5 Q E: E1 C; E5a Q; E5b Q C: B1 I; B2 I
KOKV		JAVAD TRE_G3TH DELTA	ASH701945G_M	G: L1 C/A; L2 P(Y); L5 Q E: E1 B + C; E5a I + Q; E5b I + Q C: B1 I; B2 I
MAR6	(10.96 m)	SEPT POLARX5	AOAD/M_T	G: L1 C/A; L2 P(Y); L5 Q E: E1 C; E5a Q; E5b Q; E5 Q C: B1 I; B2 I
MAR7		TRIMBLE NETR9	LEIAR25.R3	G: L1 C/A; L2 P(Y); L5 I + Q E: E1 B + C; E5a I + Q; E5b I + Q; E5 I + Q C: B1 I; B2 I
KIR0	(4.26 m)	SEPT POLARX5	JNSCR_C146-22-1	G: L1 C/A; L2 P(Y); L5 Q E: E1 C; E5a Q; E5b Q; E5 Q C: B1 I; B2 I; B3 I
KIR8		TRIMBLE NETR9	LEIAR25.R3	G: L1 C/A; L2 P(Y); L5 I + Q E: E1 B + C; E5a I + Q; E5b I + Q; E5 I + Q C: B1 I; B2 I; B3 I

. In addition, the observations from the day of year (DOY) 101 to 160, 2019 with the sampling intervals of 30 s are used in the experiments, which can be downloaded from Crustal Dynamics Data Information System (CDDIS) (ftp://cddis.gsfc.nasa.gov/).

3. Results

Previous studies have shown that the receiver-related pseudorange biases are related to the receiver’s front-end and correlator, which varies with the receiver types [24,25]. Thus, we divided all the baselines into two groups. One group is the baselines equipped with the same receiver types (ZIM2_ZIM3, ZIM2_ZIMM, USN7_USN8 and GODS_GODN), and the other group is the baselines equipped with mixed receiver types (KOKB_KOKV, MAR6_MAR7 and KIR0_KIR8). In the following, the characteristics of receiver-related pseudorange biases for two groups of baselines were analyzed, respectively. It should be pointed out that, pseudorange biases cannot be estimated in several cases: the satellite is not tracked by the station during the day, or the observation on a certain frequency has not been received. Moreover, two satellites whose elevation angle was below 30° or the common tracking arc was less than 20 min.

3.1. Baselines with the Same Receiver Types

Take zero baseline ZIM2_ZIM3 as an example, which was equipped with TRIMBLE receivers, the results of estimated receiver-related pseudorange biases are depicted in Figure 1. It is obvious that there were inconsistences of pseudorange biases between different satellites on each frequency. For GPS, biases were less than ±0.1 ns on frequencies L2 and L5, and close to −0.15 ns on L1. For Galileo satellites, receiver-related pseudorange biases were within ±0.1 ns on each frequency. As for BDS, we could see that there were significant inconsistences between BDS-2 and BDS-3 satellites. The receiver-related pseudorange biases did not exceed ±0.05 ns on triple-frequency for BDS-2 (satellite C09, C10, C12, C13 and C14). For BDS-3, pseudorange biases increased to −0.15 ns on B3 frequency (satellite C19, C20 and C24), and even up to −0.2 ns on B1 frequency (satellite C25). This notable inconsistence may be caused by system biases between BDS-2 and BDS-3.

We also estimated receiver-related pseudorange biases of baselines USN7_USN8 and GODS_GODN. These two baselines were equipped with SEPTENTRIO and JAVAD receivers, respectively. For each system and frequency, satellites with the largest pseudorange biases were selected as representatives and their results are listed in

Table 2. Receiver-related pseudorange biases of baselines USN7_USN8 and GODS_GODN for GPS, Galileo and BDS (unit: ns).

	USN7_USN8 (SEPTENTRIO)					GODS_GODN (JAVAD)
	L1 C/A	L2 P(Y)	L5 Q	-	-	L1 C/A	L2 P(Y)	L5 I + Q	-	-
	E1 C	E5a Q	E5b Q	E5 Q	E6 C	E1 B + C	E5a I + Q	E5b I + Q	E5 I + Q	E6 B + C
	B1 I	B2 I	B3 I	-	-	B1 I	B2 I	B3 I	-	-
G06	−0.079	−0.011	0.170	-	-	−0.097	0.143	−0.173	-	-
G12	0.201	0.006	-	-	-	−0.318	−0.043	-	-	-
G13	0.242	0.023	-			−0.049	−0.045
G24	0.006	−0.022	−0.114	-	-	0.104	0.426	−0.011	-	-
E04	−0.066	−0.066	−0.008	0.004	−0.061	0.214	0.221	0.072	−0.282	0.031
E05	−0.021	−0.132	0.042	0.004	−0.025	0.052	0.055	−0.033	−0.109	−0.002
E13	0.090	0.038	−0.010	0.002	−0.074	−0.041	−0.042	−0.039	0.064	0.088
E14	−0.016	−0.065	0.071	0.021	−0.094	-	-	-	-	-
E21	0.119	0.018	−0.064	0.005	−0.048	−0.005	−0.039	−0.026	0.005	0.027
E24	0.080	−0.073	0.020	0.002	−0.003	0.214	0.079	0.145	−0.108	−0.033
C14	0.045	0.032	−0.062	-	-	−0.016	−0.020	0.015
C19	0.056	-	-	-	-	0.572	0.067	−0.136
C33	0.008	-	0.105	-	-	0.278	−0.167	−0.053	-	-
C36	0.132	-	-	-	-	0.502	0.246	−0.182
C37	0.078	-	-	-	-	0.105	−0.117	−0.183	-	-

The bold data represents the maximum of pseudorange biases on each frequency for SEPTENTRIO and JAVAD receivers.

. We could also see the inconsistences of pseudorange biases between satellites on each frequency, which were similar to the results of TRIMBLE receivers. However, compared to TRIMBLE receivers, significant increases of pseudorange biases could be observed. For GPS frequency L1, receiver-related pseudorange biases more than 0.2 ns for SEPTENTRIO receiver (satellite G13) and −0.3 ns for JAVAD receiver (satellite G12). For GPS frequency L2, pseudorange biases exceed 0.4 ns for the JAVAD receiver (satellite G24). Similarly, the increase appeared on frequency L5 (satellite G06).

For Galileo, pseudorange biases had a slight increase on each frequency for SEPTENTRIO receiver. As for JAVAD, the maximum of pseudorange biases was around ±0.2 ns on frequencies E1 and E5a, and were near to −0.3 ns on frequency E5 (satellite E04). For BDS, the inconsistence of receiver-related pseudorange biases between BDS-2 and BDS-3 satellites were very significant for the JAVAD receiver. The largest inconsistence more than 0.5 ns on frequency B1 (satellite C14 and C19). These results show that the inconsistence of receiver-related pseudorange biases between different receiver types could not be neglected.

Receiver-related pseudorange biases of baseline ZIM2_ZIMM are depicted in Figure 2. This baseline is equipped with TRIMBLE receivers and only GPS signals can be received. From Figure 2, pseudorange biases can reach up to 0.5 ns on GPS frequency L2 (satellite G21 and G31) and are close to −0.5 ns on GPS frequency L5 (satellite G24). There is a significant increase compared to baseline ZIM2_ZIM3. From Table 1, we can see that the antenna type of station ZIM2 and ZIM3 are both TRM59800.00, while the antenna type of station ZIMM is TRM29659.00. Previous research suggests that different antenna models using different low noise amplifiers [25], which likely lead to the inconsistence of DD receiver-related pseudorange biases estimated by the same antenna types and mixed antenna types.

3.2. Baselines with Mixed Receiver Types

In this section, we analyzed the characteristics of receiver-related pseudorange biases for baselines with mixed receiver types. Taking two baselines KOKB_KOKV and MAR6_MAR7 as an example, the results are depicted in Figure 3 and Figure 4, respectively.

From Figure 3, we could also see that pseudorange biases differ from satellite to satellite. Moreover, compared to the baselines with the same receiver types, pseudorange biases had an obvious increase. For GPS, pseudorange biases were within ±0.5 ns on frequencies L1 and L2 and were the largest on frequency L5, which was close to 1.5 ns (satellite G03 and G24). For Galileo, pseudorange biases within 0.2 ns were smaller than those of GPS and BDS. It is interesting to note, on frequencies E1 and E5a, two in-orbit validation (IOV) satellites E11 and E12 significantly exhibited the larger pseudorange biases, compared to the full operational configuration (FOC) satellites. For BDS, receiver-related pseudorange biases less than ±0.25 ns on frequency B2, and which was close to 1.0 ns on frequency B1.

From Figure 4, we could see that receiver-related pseudorange biases of baseline MAR6_MAR7 were approximately twice for those of baseline KOKB_KOKV. For GPS, pseudorange biases were larger than 1.0 ns on frequency L1 (satellite G03, G06, G08 and G09) and even up to 2.5 ns on frequency L5 (satellite G03). For Galileo, pseudorange biases were close to ±0.5 ns. Additionally, the inconsistence between IOV satellites (E11 and E12) and FOC satellites could also be observed on frequency E1. For BDS, receiver-related pseudorange biases reached up to 1.0 ns on frequency B2 and were close to 2.0 ns on frequency B1.

3.3. Pseudorange Biases Stabilities

In this section, we assessed the stabilities of receiver-related pseudorange biases during the period of DOY 101–160, 2019. Taking baseline ZIM2_ZIM3 as an example, the standard deviations (STDs) of pseudorange biases over a span of 60 days were calculated and shown in Figure 5. For GPS frequency L2 and L5, we could see that the STDs of pseudorange biases were less than 0.1 ns for all the satellites. On frequency L1, the largest STD was close to 0.15 ns, which was also quite small compared with the precision of pseudorange observations. Galileo shows the smallest STDs among three systems, which was around 0.05 ns. Moreover, we could see that the STDs were quite consistent between different Galileo satellites. As for BDS, the STDs were within 0.15 ns on frequency B1 and were within 0.05 ns on frequency B2 and B3. We could tell that receiver-related pseudorange biases were quite stable for GPS/Galileo/BDS.

3.4. Impacts on Short Baseline Solutions

In this section, combined GPS/Galileo/BDS DD relative positioning using a short baseline was carried out to validate GNSS receiver-related pseudorange biases. In the following experiment, GPS L1, Galileo E1 and BDS B1 frequencies were applied. The observation and broadcast ephemeris on DOY 101, 2019 were provided by CDDIS. Two receivers and two satellites constitute DD observations. Taking short baseline MAR6_MAR7 as an example, Figure 6 displays the time series of positioning errors and RMS with and without receiver-related pseudorange biases correction. It shows that when pseudorange biases corrections were employed, the RMS values were reduced to 0.549 m, 0.305 m and 1.201 m in northward, eastward and upward components, with the reduction of 6.0%, 11.1% and 11.4%, respectively. From the results, it is clear that receiver-related pseudorange biases correction can improve the accuracy of short baseline solutions.

4. Discussion

GNSS pseudorange measurements play an important role in several precise positioning techniques at the centimeter level. As is well known, WL ambiguity is widely applied to ionosphere-free ambiguity resolution [35]. In the following part, we discussed the effects of receiver-related pseudorange biases on WL ambiguity resolution. Firstly, we present the estimation model of DD WL ambiguity with receiver-related pseudorange biases correction. Then, the corresponding results were analyzed.

The Melbourne–Wübbena (MW) linear combination of dual-frequency code and carrier phase measurements was originally proposed by Hatch (1982) and serves for fixing the WL ambiguity [36,37], which can be expressed as follows,

$$M{W}_r^s=\frac{f_1{L}_{r,1}^s-f_2{L}_{r,2}^s}{f_1-f_2}-\frac{f_1{P}_{r,1}^s+f_2{P}_{r,2}^s}{f_1+f_2}={\lambda }_{WL}{N}_{r,WL}^s+B_{r,MW}-B_{MW}^s+D_{r,MW}^s$$

(4)

with

$$D_{r,MW}^s=-\frac{f_{1}Bia{s}_{r,f_1}^s+f_{2}Bia{s}_{r,f_2}^s}{f_1+f_2}$$

(5)

where $M{W}_r^s$ is MW combination, ${\lambda }_{WL}$ is the WL wavelength, $N_{r,WL}^s$ is the WL integer ambiguity and $B_{r,MW}$ and $B_{MW}^S$ are WL hardware delay for receiver and satellite, which can be eliminated by the DD between two satellites and two receivers. $D_{r,MW}^s$ represents the effect of pseudorange biases on MW combination.

According to Equation (4), the DD MW combination between two satellites (p, q) and two receivers (i, j) can be obtained as follows:

$$∆\nabla MW=\frac{f_1∆\nabla L_1-f_2∆\nabla L_2}{f_1-f_2}-\frac{f_1∆\nabla P_1+f_2∆\nabla P_2}{f_1+f_2}={\lambda }_{WL}∆\nabla N_{WL}+∆\nabla D_{MW}$$

(6)

with

$$∆\nabla D_{MW}=(D_{i,MW}^p-D_{j,MW}^p)-\left(D_{i,MW}^q-D_{j,MW}^q\right)=-\frac{f_1∆\nabla Bia{s}_{ij,f_1}^{pq}+f_2∆\nabla Bia{s}_{ij,f_2}^{pq}}{f_1+f_2}$$

(7)

where $∆\nabla MW$ is the DD MW combination and $∆\nabla L_1$ and $∆\nabla L_2$ and $∆\nabla P_1$ and $∆\nabla P_2$ are the DD carrier phase and pseudorange measurements on frequency $f_1$ and $f_2$, respectively. $\mathsf{\Delta }\nabla N_{WL}$ represents the DD WL integer ambiguity and $∆\nabla D_{MW}$ is the effect of DD pseudorange biases on MW combination.

From Equations (6) and (7), we can see that receiver-related pseudorange biases cannot be eliminated according to DD operation, which will spoil the integer nature of DD WL ambiguity. Therefore, it is necessary to analyze the effects of pseudorange biases. In the following experiments, GPS L1 and L5, Galileo E1 and E5a, BDS B1 and B2 frequencies were used to calculate DD WL ambiguity with and without the receiver-related pseudorange biases correction for all the common tracked satellite pairs.

Taking baseline MAR6_MAR7 as an example, we plotted the histogram distribution of the fractional parts of DD WL ambiguities for three systems in Figure 7, and the corresponding RMS values were also given. It is clear that the application of receiver-related pseudorange biases correction made the RMS values of the fractional parts reduce to 28.9%, 4.67% and 67.6% for GPS, Galileo and BDS, respectively, which is benefit to WL ambiguity resolution. The maximum improvement was shown in BDS, followed by GPS, and finally was Galileo, which was consistent with the result that pseudorange biases for BDS were the largest, and those for Galileo was the smallest.

As is well known, long baselines are widely used for satellite orbit determination. In the following, we analyzed the impacts of receiver-related pseudorange biases on WL ambiguities for long baselines. Two long baselines were selected: MAR6_ZIM2 and KIR0_ZIM2, whose lengths were 1649.27 km and 2449.34 km, respectively. The histogram distribution of the fractional parts of DD WL ambiguities for two baselines is shown in Figure 8 and Figure 9, respectively. We could see that receiver-related pseudorange biases correction significantly increased the percentage of the fractional parts within ±0.1 cycles for GPS, and RMS values of the fractional parts were reduced 23.8% for baseline MAR6_ZIM2, and 34.1% for baseline KIR0_ZIM2. For Galileo, the RMS values had slight decreases after correction due to the small magnitude of pseudorange biases, which was approximately around 10%.

5. Conclusions

Receiver-related pseudorange biases were caused by satellite chip shape distortions and differed from satellite to satellite. These biases were also related to the receiver’s front-end and correlator. In this contribution, detailed research of GNSS receiver-related pseudorange biases were presented using short baselines. The results indicate that there were significant inconsistences of receiver-related pseudorange biases according to the satellites, frequencies, receiver and antenna types. For the baselines with mixed receiver types, pseudorange biases could reach up to 2.5 ns. In addition, receiver-related pseudorange biases were also related to receiver antenna type. For the baseline with mixed receiver antennas, pseudorange biases had a significant increase compared to those of the baselines with the same receiver antennas. Among GPS/Galileo/BDS, the smallest receiver-related pseudorange biases were found for Galileo. It is worth noting that IOV satellites show larger pseudorange biases compared to FOC satellites. As for BDS, there were significant inconsistences of receiver-related pseudorange biases between BDS-2 and BDS-3 satellites, which reached up to about 1.0 ns. Moreover, the time series of receiver-related pseudorange biases proved that receiver-related pseudorange biases were stable over a long time. The best stabilities of pseudorange biases were found for Galileo, followed by GPS and BDS.

In order to validate receiver-related pseudorange biases, combined GPS, Galileo and BDS DD relative positioning using short baseline was carried out. When pseudorange biases were corrected, the accuracy of positioning was improved by 12.6% and 11.4% in horizontal and vertical components, respectively. Then, we investigated the impacts of receiver-related pseudorange biases on the WL ambiguity. The results show that, for the baselines with mixed receiver types, the percentage of the fractional parts within ±0.1 cycles increased when the receiver-related pseudorange biases were corrected. The RMS values reduced to 28.9%, 4.67% and 67.6% for GPS, Galileo and BDS, respectively. Additionally, for long baselines, it reduced to 34.1% and 14.4% for GPS and Galileo.

The research results proved that receiver-related pseudorange biases had significant contributions on short baseline solutions and WL ambiguity resolutions. In the future, GNSS receiver-related pseudorange biases may be calibrated for a single receiver, and then these biases can be provided to users as a precise product. Moreover, the results reveal that there may be receiver-related pseudorange system biases between BDS-2 and BDS-3, which should be considered in the data processing.