Inversion of Terrain Slope and Roughness with Satellite Laser Altimeter Full-Waveform Data Assisted by Shuttle Radar Topographic Mission
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Collections
2.2.1. ICESat/GLAS Data
2.2.2. SRTM Data
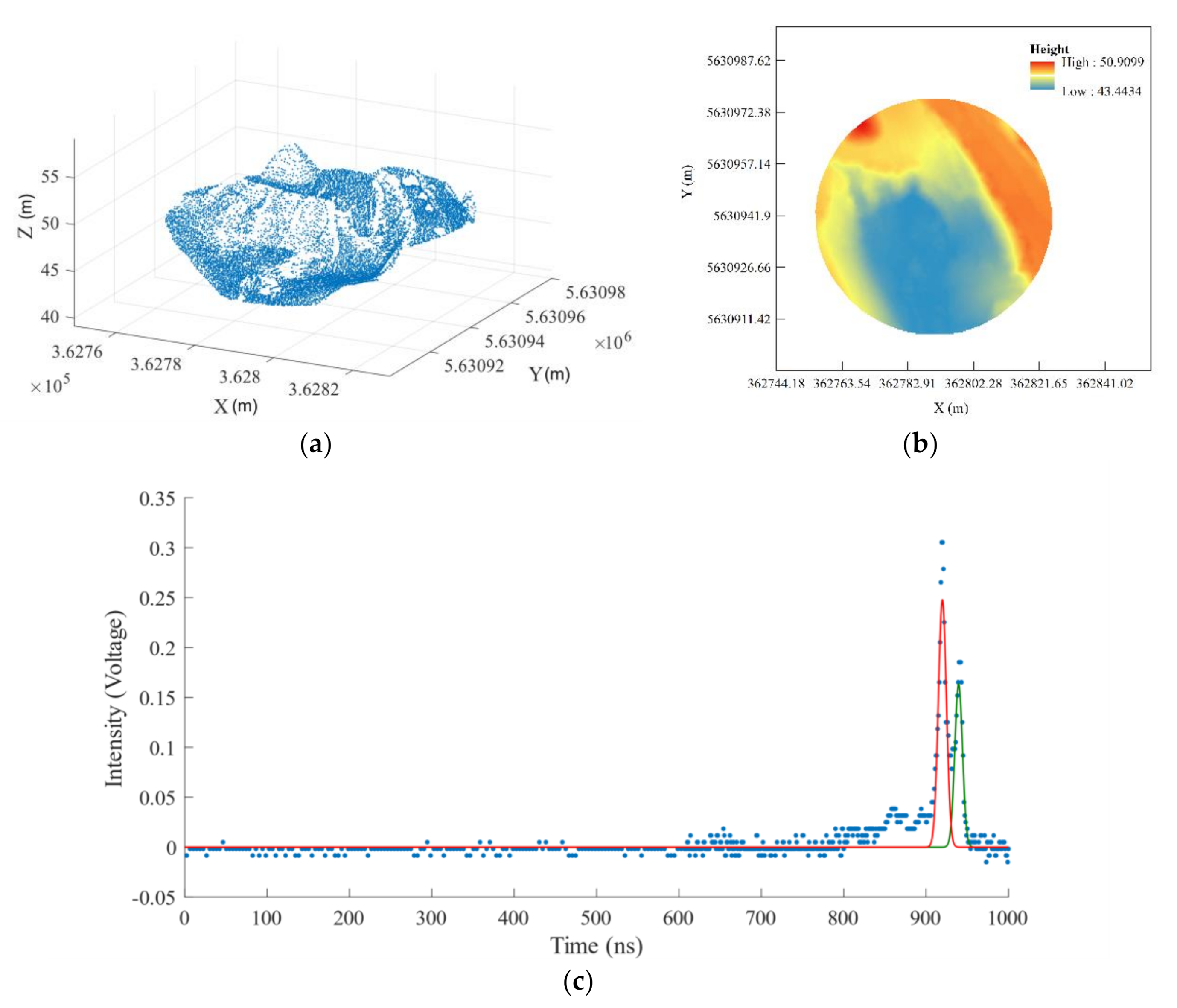
2.2.3. Airborne Lidar Data
2.2.4. National Land Cover Database (NCLD)
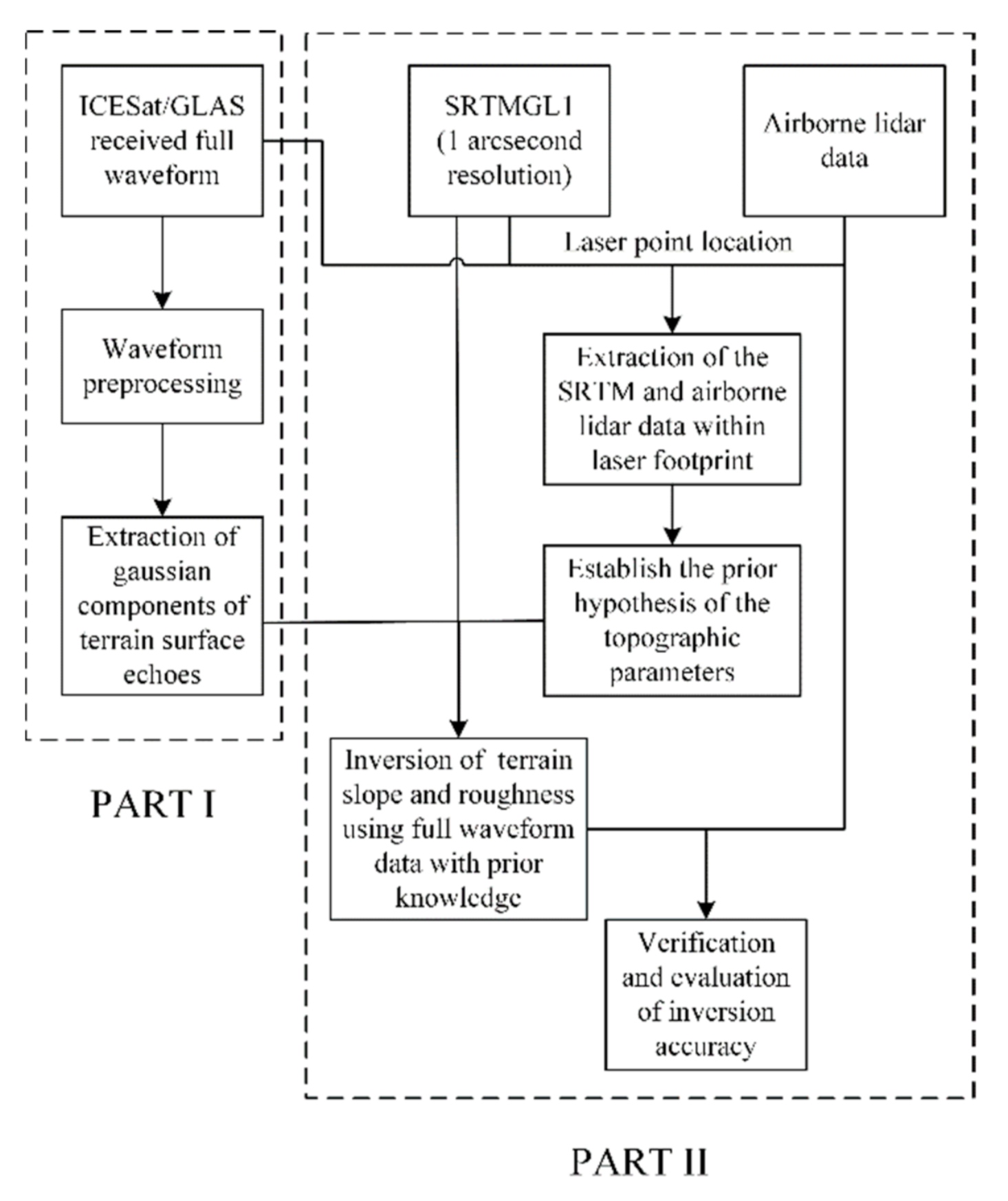
2.3. Methodology
2.3.1. ICESat/GLAS Data Processing
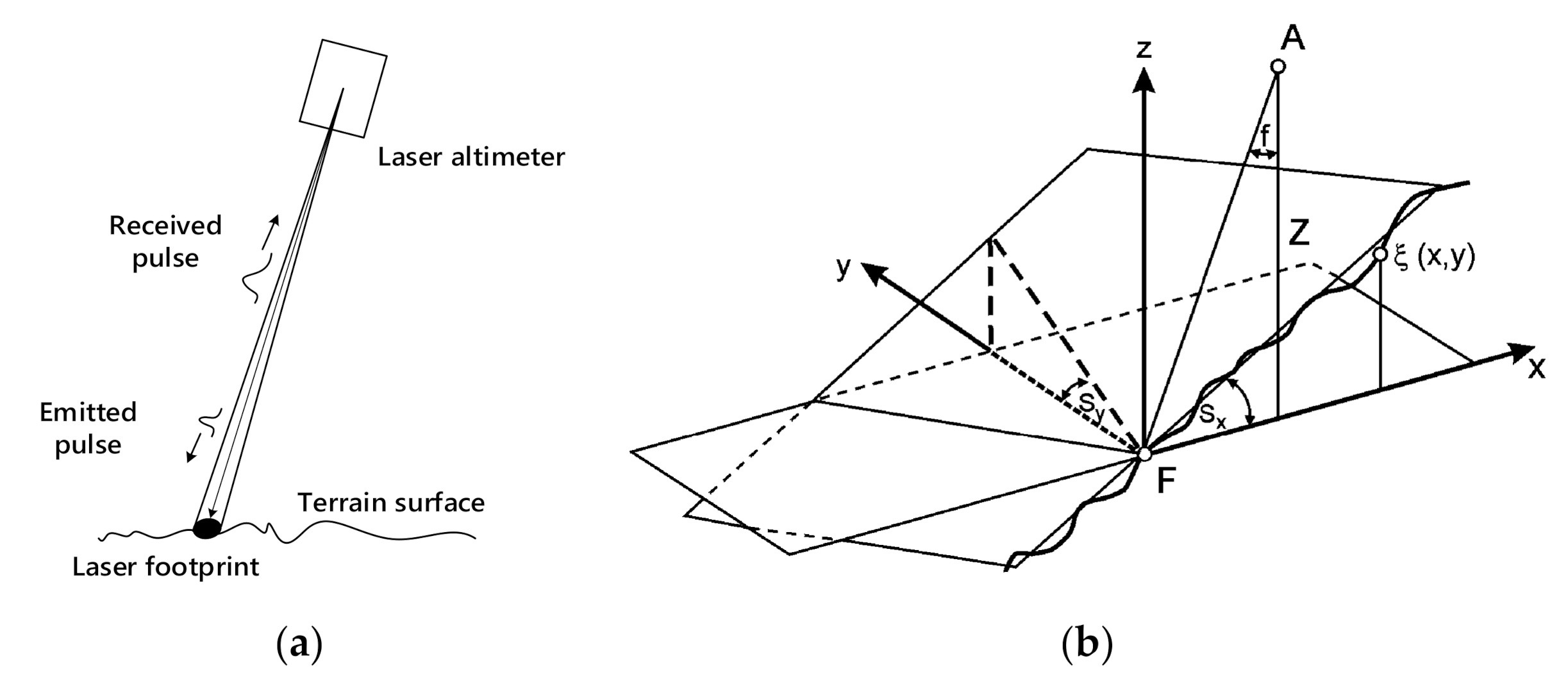
2.3.2. Theoretical Model of Pulse Signal of Land Echo
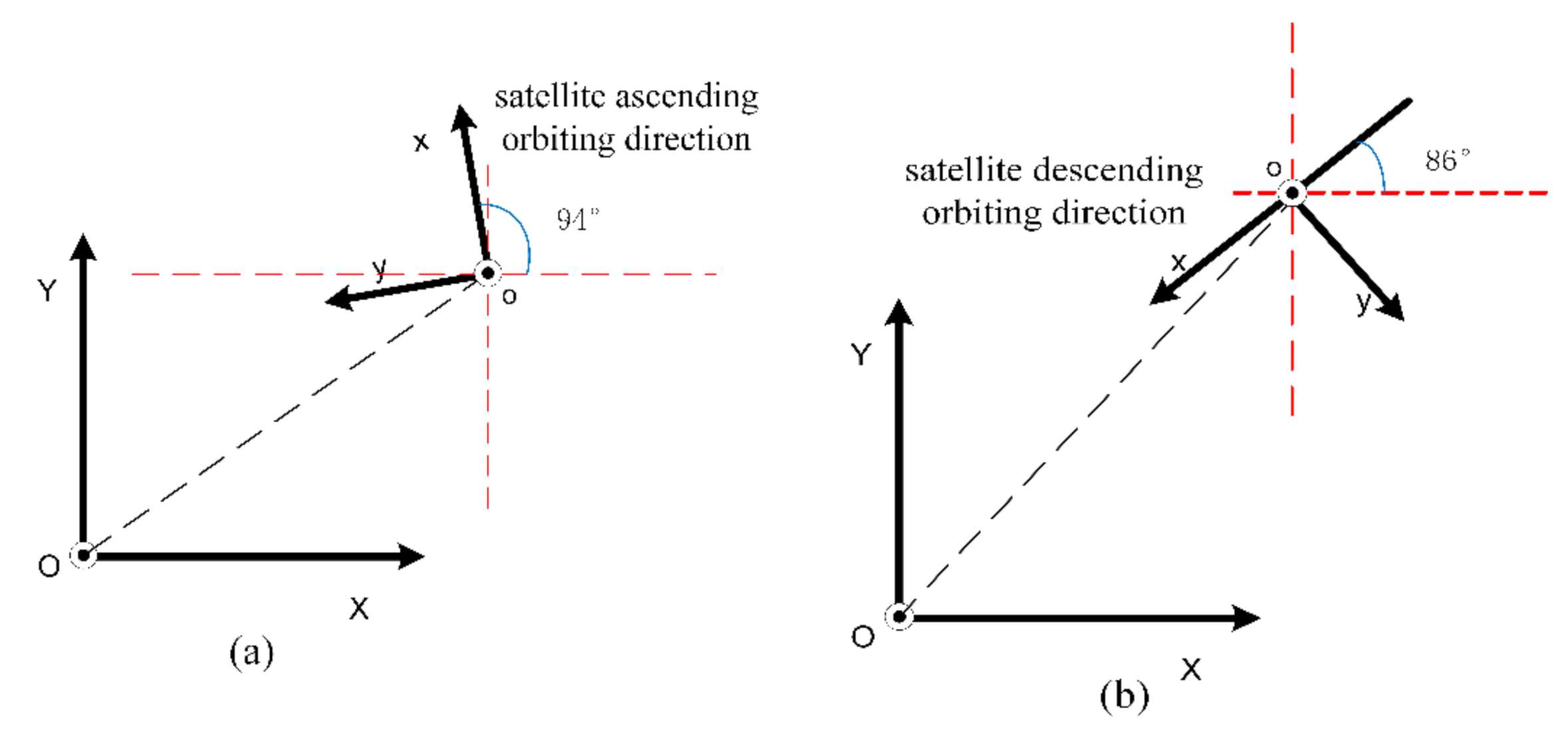
2.3.3. Prior Hypothesis of Terrain Slope and Roughness
2.3.4. Proposed Method for Inversion of Terrain Slope and Roughness
- ① (a) and (b) in Figure 7, if , then and ;
- ② (c) and (d) in Figure 7, if and , then find the slope in inversion data sequence (1) with minimum distance to , assuming to be , then and ;
- ③ (e) and (f) in Figure 7, if , then and .
3. Results
3.1. ICESat/GLAS Full-Waveform Data Selection for Inversion
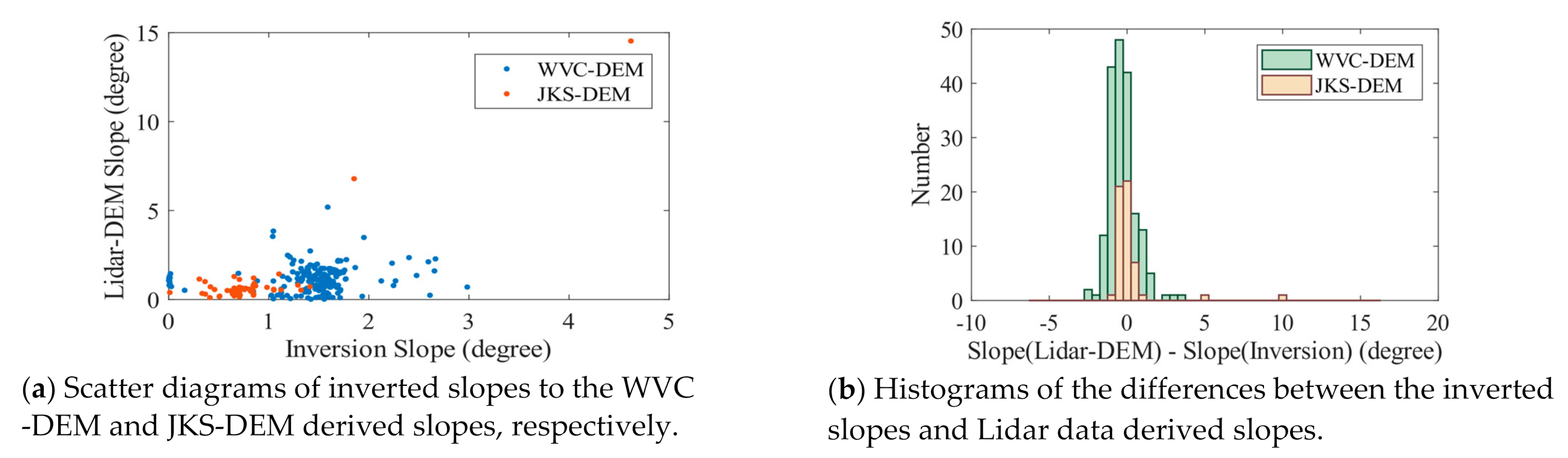
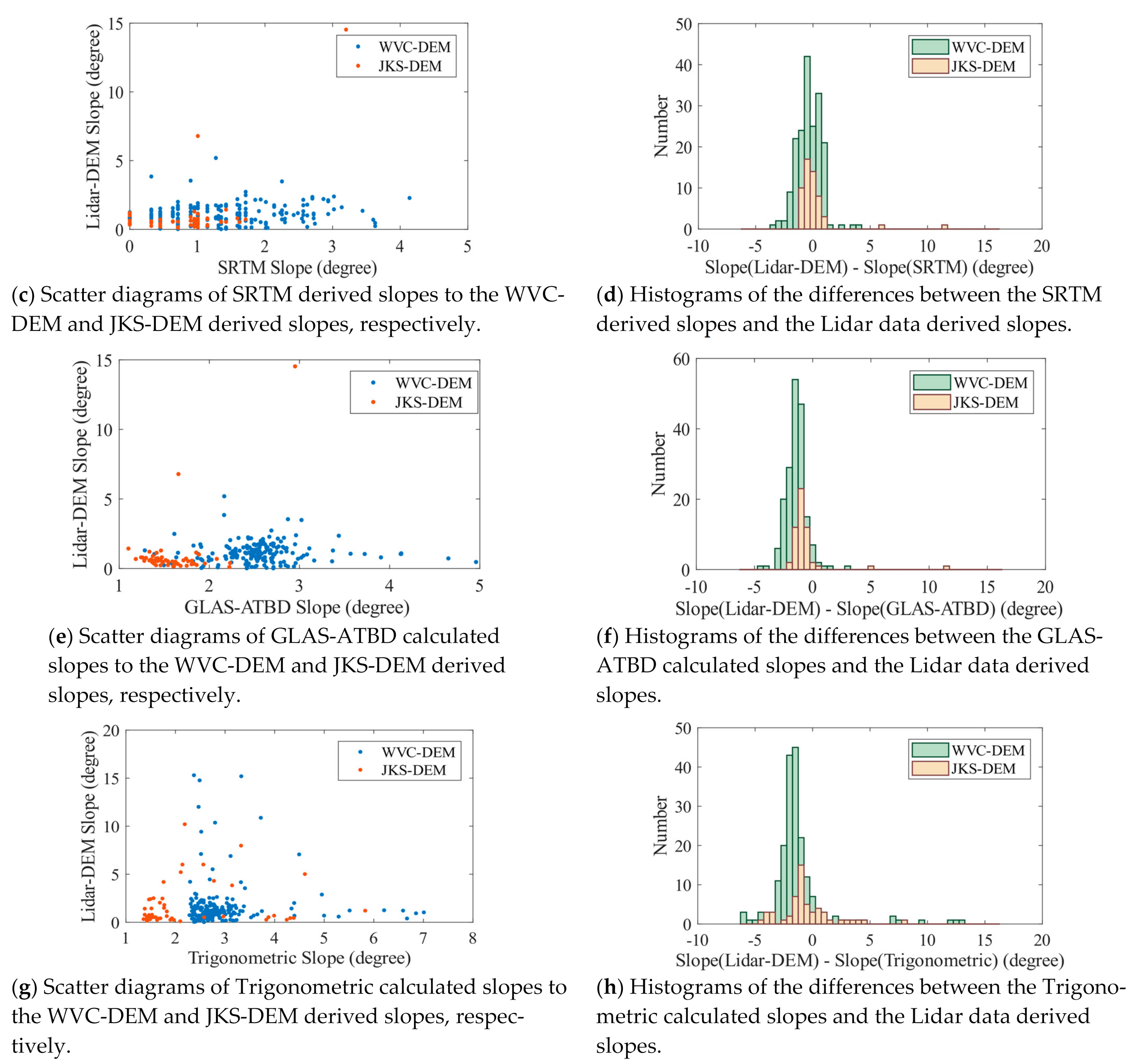
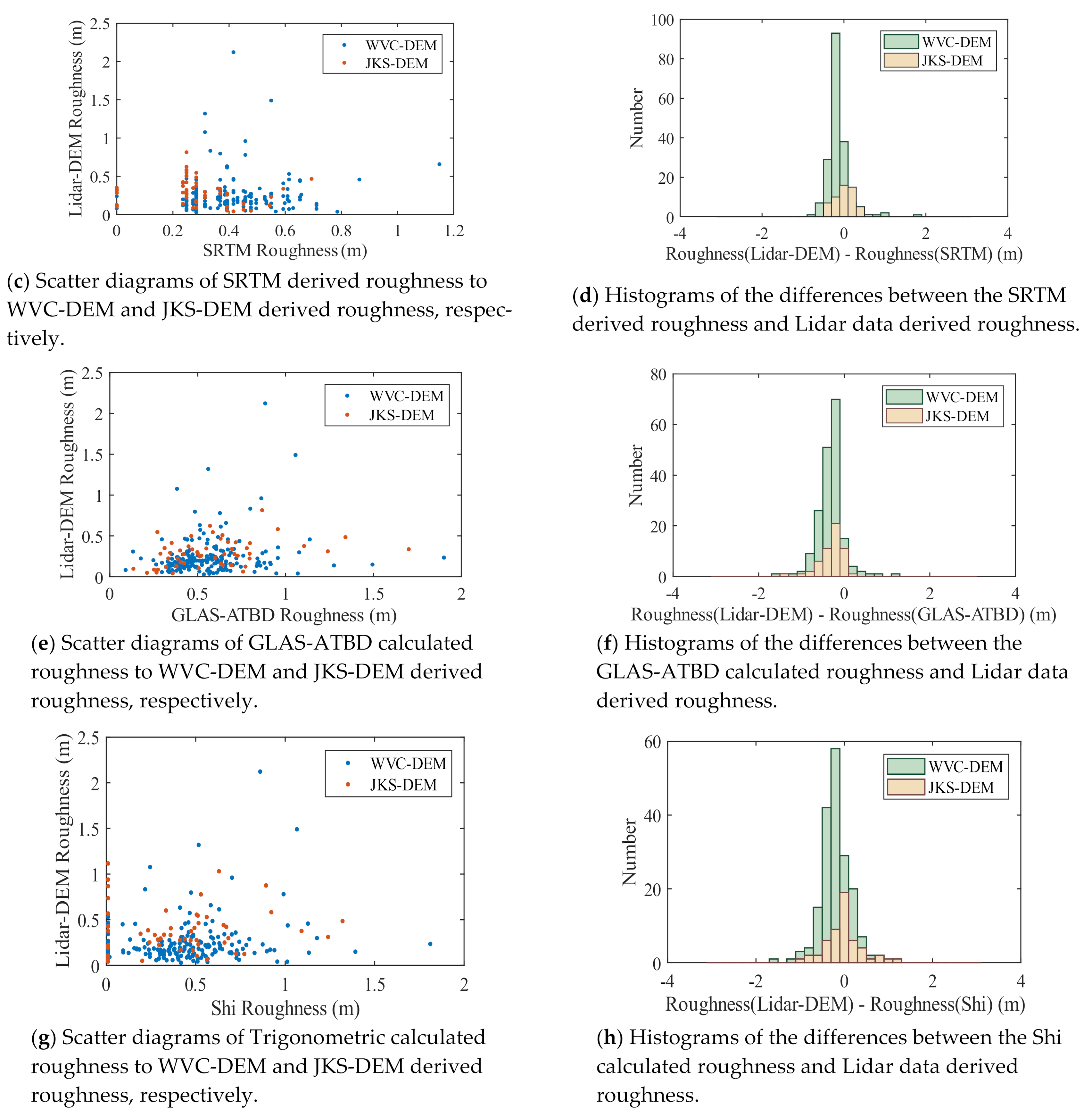
3.2. Inversion Results and Evaluation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Thomas, N.; Spohn, T.; Barriot, J.-P.; Benz, W.; Beutler, G.; Christensen, U.; Dehant, V.; Fallnich, C.; Giardini, D.; Groussin, O. The BepiColombo Laser Altimeter (BELA): Concept and baseline design. Planet. Space Sci. 2007, 55, 1398–1413. [Google Scholar] [CrossRef]
- Smith, D.E.; Zuber, M.T.; Jackson, G.B.; Cavanaugh, J.F.; Neumann, G.A.; Riris, H.; Sun, X.; Zellar, R.S.; Coltharp, C.; Connelly, J. The lunar orbiter laser altimeter investigation on the lunar reconnaissance orbiter mission. Space Sci. Rev. 2010, 150, 209–241. [Google Scholar] [CrossRef]
- Smith, D.E.; Zuber, M.T.; Frey, H.V.; Garvin, J.B.; Head, J.W.; Muhleman, D.O.; Pettengill, G.H.; Phillips, R.J.; Solomon, S.C.; Zwally, H.J. Mars Orbiter Laser Altimeter: Experiment summary after the first year of global mapping of Mars. J. Geophys. Res. Planets 2001, 106, 23689–23722. [Google Scholar] [CrossRef]
- Abshire, J.B.; Sun, X.; Riris, H.; Sirota, J.M.; McGarry, J.F.; Palm, S.; Yi, D.; Liiva, P. Geoscience laser altimeter system (GLAS) on the ICESat mission: On-orbit measurement performance. Geophys. Res. Lett. 2005, 32, 1–4. [Google Scholar] [CrossRef]
- Flood, M. Laser altimetry: From science to commercial lidar mapping. Photogramm. Eng. Remote Sens. 2001, 67, 1209–1217. [Google Scholar]
- Hilbert, C.; Schmullius, C. Influence of surface topography on ICESat/GLAS forest height estimation and waveform shape. Remote Sens. 2012, 4, 2210–2235. [Google Scholar] [CrossRef]
- Mallet, C.; Bretar, F. Full-waveform topographic lidar: State-of-the-art. ISPRS J. Photogramm. Remote Sens. 2009, 64, 1–16. [Google Scholar] [CrossRef]
- Zwally, H.J.; Schutz, B.; Abdalati, W.; Abshire, J.; Bentley, C.; Brenner, A.; Bufton, J.; Dezio, J.; Hancock, D.; Harding, D. ICESat’s laser measurements of polar ice, atmosphere, ocean, and land. J. Geodyn. 2002, 34, 405–445. [Google Scholar] [CrossRef]
- Schutz, B.E.; Zwally, H.; Shuman, C.; Hancock, D.; DiMarzio, J. Overview of the ICESat mission. Geophys. Res. Lett. 2005, 32, L21S01. [Google Scholar] [CrossRef]
- Dubayah, R.; Blair, J.B.; Goetz, S.; Fatoyinbo, L.; Hansen, M.; Healey, S.; Hofton, M.; Hurtt, G.; Kellner, J.; Luthcke, S.; et al. The Global Ecosystem Dynamics Investigation: High-resolution laser ranging of the Earth’s forests and topography. Sci. Remote Sens. 2020, 1, 100002. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, S.; Bao, H.; Zhao, X. Characteristics and influencing factors of rainfall-induced landslide and debris flow hazards in Shaanxi Province, China. Nat. Hazards Earth Syst. Sci. 2019, 19, 93–105. [Google Scholar] [CrossRef]
- Smith, M.W.; Quincey, D.J.; Dixon, T.; Bingham, R.G.; Carrivick, J.L.; Irvine-Fynn, T.D.; Rippin, D.M. Aerodynamic roughness of glacial ice surfaces derived from high-resolution topographic data. J. Geophys. Res. Earth Surf. 2016, 121, 748–766. [Google Scholar] [CrossRef]
- Li, B.; Yue, Z.; Zhang, J.; Fu, X.; Ling, Z.; Chen, S.; Chen, J.; Yao, P.J.E.; Science, S. High-resolution terrain analysis for lander safety landing and rover path planning based on Lunar Reconnaissance Orbiter Narrow Angle Camera images: A case study of China’s Chang’e-4 probe. Earth Space Sci. 2019, 6, 398–410. [Google Scholar] [CrossRef]
- Dong, L.; Tang, S.; Min, M.; Veroustraete, F. Estimation of Forest Canopy Height in Hilly Areas Using Lidar Waveform Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1559–1571. [Google Scholar] [CrossRef]
- Gardner, C.S. Ranging performance of satellite laser altimeters. IEEE Trans. Geosci. Remote Sens. 1992, 30, 1061–1072. [Google Scholar] [CrossRef]
- Urban, T.J.; Schutz, B.E.; Neuenschwander, A.L. A Survey of ICESat Coastal Altimetry Applications: Continental Coast, Open Ocean Island, and Inland River. Terr. Atmos. Ocean. Sci. 2008, 19, 1–19. [Google Scholar] [CrossRef]
- Shean, D.E.; Alexandrov, O.; Moratto, Z.M.; Smith, B.E.; Joughin, I.R.; Porter, C.; Morin, P. An automated, open-source pipeline for mass production of digital elevation models (DEMs) from very-high-resolution commercial stereo satellite imagery. ISPRS J. Photogramm. Remote Sens. 2016, 116, 101–117. [Google Scholar] [CrossRef]
- Cheng, C.; Huang, G.; Wen, H.; Zhang, J.; Zhang, L.; Zuo, Z. Method for Extracting Elevation Control Point with Assistance of Satellite Laser Altimetry Data. U.S. Patent 16/702,503, 2 April 2020. [Google Scholar]
- Harding, D.J.; Bufton, J.L.; Frawley, J.J. Satellite laser altimetry of terrestrial topography: Vertical accuracy as a function of surface slope, roughness, and cloud cover. IEEE Trans. Geosci. Remote Sens. 1994, 32, 329–339. [Google Scholar] [CrossRef]
- Gardner, C. Target signatures for laser altimeters: An analysis. Appl. Opt. 1982, 21, 448–453. [Google Scholar] [CrossRef]
- NASA Shuttle Radar Topography Mission Global 1 arc Second; LP DAAC: Sioux Falls, SD, USA, 2013. [CrossRef]
- Brenner, A.C.; Zwally, H.J.; Bentley, C.R.; Csathó, B.M.; Harding, D.J.; Hofton, M.A.; Minster, J.-B. Derivation of Range and Range Distributions From Laser Pulse Waveform Analysis for Surface Elevations, Roughness, Slope, and Vegetation Heights. GLAS Algorithm Theoretical Basis Document V5.0. 2011, pp. 1–125. Available online: http://www.csr.utexas.edu/glas/pdf/Atbd_20031224.Pdf (accessed on 1 August 2020).
- Yi, D.; Zwally, H.J.; Sun, X. ICESat measurement of Greenland ice sheet surface slope and roughness. Ann. Glaciol. 2005, 42, 83–89. [Google Scholar] [CrossRef]
- Nie, S.; Wang, C.; Dong, P.; Li, G.; Xi, X.; Wang, P.; Yang, X. A novel model for terrain slope estimation using ICESat/GLAS waveform data. IEEE Trans. Geosci. Remote Sens. 2017, 56, 217–227. [Google Scholar]
- Xie, H.; Tang, H.; Du, W.; Tong, X. A Comparison of Surface Slopes Extracted from ICESat Waveform Data and High Resolution DEM. In Proceedings of EPJ Web of Conferences; EDP Sciences: Les Ulis, France, 2020; p. 01001. [Google Scholar]
- Li, X.; Xu, L.; Tian, X.; Kong, D. Terrain slope estimation within footprint from ICESat/GLAS waveform: Model and method. J. Appl. Remote Sens. 2012, 6, 063534. [Google Scholar]
- Grigsby, S.; Abdalati, W.; Colgan, L.; Rajaram, H. Sub-footprint Surface Extraction & Classification of ICESat Laser Waveforms in Southwest Greenland. Remote Sens. Environ. 2021. under review. [Google Scholar]
- Shi, J.; Menenti, M.; Lindenbergh, R. Parameterization of surface roughness based on ICESat/GLAS full waveforms: A case study on the Tibetan Plateau. J. Hydrometeorol. 2013, 14, 1278–1292. [Google Scholar] [CrossRef]
- Jiancheng, L.; Chunbo, F.; Chu, Y.; Shengkai, Z. Using ICESAT altimeter data to determine the Antarctic ice sheet elevation model. Geomat. Inf. Sci. Wuhan Univ. 2008, 33, 226–228. [Google Scholar]
- Zwally, H.J.; Schutz, R.; Bentley, C.R.; Bufton, J.L.; Thomas, H.; Jean-Bernard, M.; James, S.; Thomas, R. GLAS/ICESat L1A Global Altimetry Data (HDF5); Version 33; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2013. [Google Scholar] [CrossRef]
- Zwally, H.J.; Schutz, R.; John, D.; Hancock, D. GLAS/ICESat L1B Global Waveform-based Range Corrections Data (HDF5); Version 34; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2014. [Google Scholar] [CrossRef]
- Zwally, H.J.; Schutz, R.; Hancock, D.; John, D. GLAS/ICESat L2 Global Land Surface Altimetry Data (HDF5); Version 34; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2014. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L. The shuttle radar topography mission. Rev. Geophys. 2007, 45, 1–33. [Google Scholar] [CrossRef]
- Lemoine, F.G.; Kenyon, S.C.; Factor, J.K.; Trimmer, R.G.; Pavlis, N.K.; Chinn, D.S.; Cox, C.M.; Klosko, S.M.; Luthcke, S.B.; Torrence, M.H. The Development of the Joint NASA GSFC and NIMA Geopotential Model EGM96; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 1998. [Google Scholar]
- Land NRW. Digitales Geländemodell mittlerer Punktabstand 1m-dl-de/by-2-0. 2019; Available online: http://www.govdata.de/dl-de/by-2-0 and https://www.opengeodata.nrw.de/produkte/geobasis/dgm/dgm1/; (accessed on 9 August 2020). [Google Scholar]
- Caffier, A.; Elsner, C.; Rath, C.; Robens, F.; Seidel, J.; Will, K. Offene Geobasisdaten für NRW. Zeitschrift für Geodäsie Geoinformation und Landmanagement 2017, 142, 133–145. [Google Scholar]
- Federal Agency for Cartography and Geodesy. Quasigeoid of the Federal Republic of Germany—GCG2016; Federal Agency for Cartography and Geodesy: Frankfurt, Germany, 2017; Available online: https://upd.geodatenzentrum.de/docpdf/quasigeoid_eng.pdf (accessed on 10 August 2020).
- State of Utah and Partners. Regional Utah High-Resolution Lidar Data 2015–2017; OpenTopography Facility: La Jolla, CA, USA, 2019. [Google Scholar]
- TCDWY. Teton Conservation District, Wyoming Lidar; OpenTopography Facility: La Jolla, CA, USA, 2008. [Google Scholar]
- Yang, L.; Jin, S.; Danielson, P.; Homer, C.; Gass, L.; Bender, S.M.; Case, A.; Costello, C.; Dewitz, J.; Fry, J.; et al. A new generation of the United States National Land Cover Database: Requirements, research priorities, design, and implementation strategies. ISPRS J. Photogramm. Remote Sens. 2018, 146, 108–123. [Google Scholar] [CrossRef]
- Wagner, W.; Ullrich, A.; Ducic, V.; Melzer, T.; Studnicka, N. Gaussian decomposition and calibration of a novel small-footprint full-waveform digitising airborne laser scanner. ISPRS J. Photogramm. Remote Sens. 2006, 60, 100–112. [Google Scholar] [CrossRef]
- Hartley, H.O. The modified Gauss-Newton method for the fitting of non-linear regression functions by least squares. Technometrics 1961, 3, 269–280. [Google Scholar] [CrossRef]
- Duong, V.; Lindenbergh, R.; Pfeifer, N.; Vosselman, G. Single and two epoch analysis of ICESat full waveform data over forested areas. Int. J. Remote Sens. 2008, 29, 1453–1473. [Google Scholar] [CrossRef]
- Chen, Q. Assessment of terrain elevation derived from satellite laser altimetry over mountainous forest areas using airborne lidar data. ISPRS J. Photogramm. Remote Sens. 2010, 65, 111–122. [Google Scholar] [CrossRef]
- Neuenschwander, A.L.; Magruder, L.A.; Tyler, M. Landcover classification of small-footprint, full-waveform lidar data. J. Appl. Remote Sens. 2009, 3, 033544. [Google Scholar] [CrossRef]
- Bhushan, B. Surface roughness analysis and measurement techniques. In Modern Tribology Handbook, Two Volume Set; CRC Press: Boca Raton, FL, USA, 2000; pp. 79–150. [Google Scholar]
- DeGarmo, E.P.; Black, J.T.; Kohser, R.A.; Klamecki, B.E. Materials and Process in Manufacturing; Prentice Hall: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
- Shepard, M.K.; Campbell, B.A.; Bulmer, M.H.; Farr, T.G.; Gaddis, L.R.; Plaut, J.J. The roughness of natural terrain: A planetary and remote sensing perspective. J. Geophys. Res. Planets 2001, 106, 32777–32795. [Google Scholar] [CrossRef]
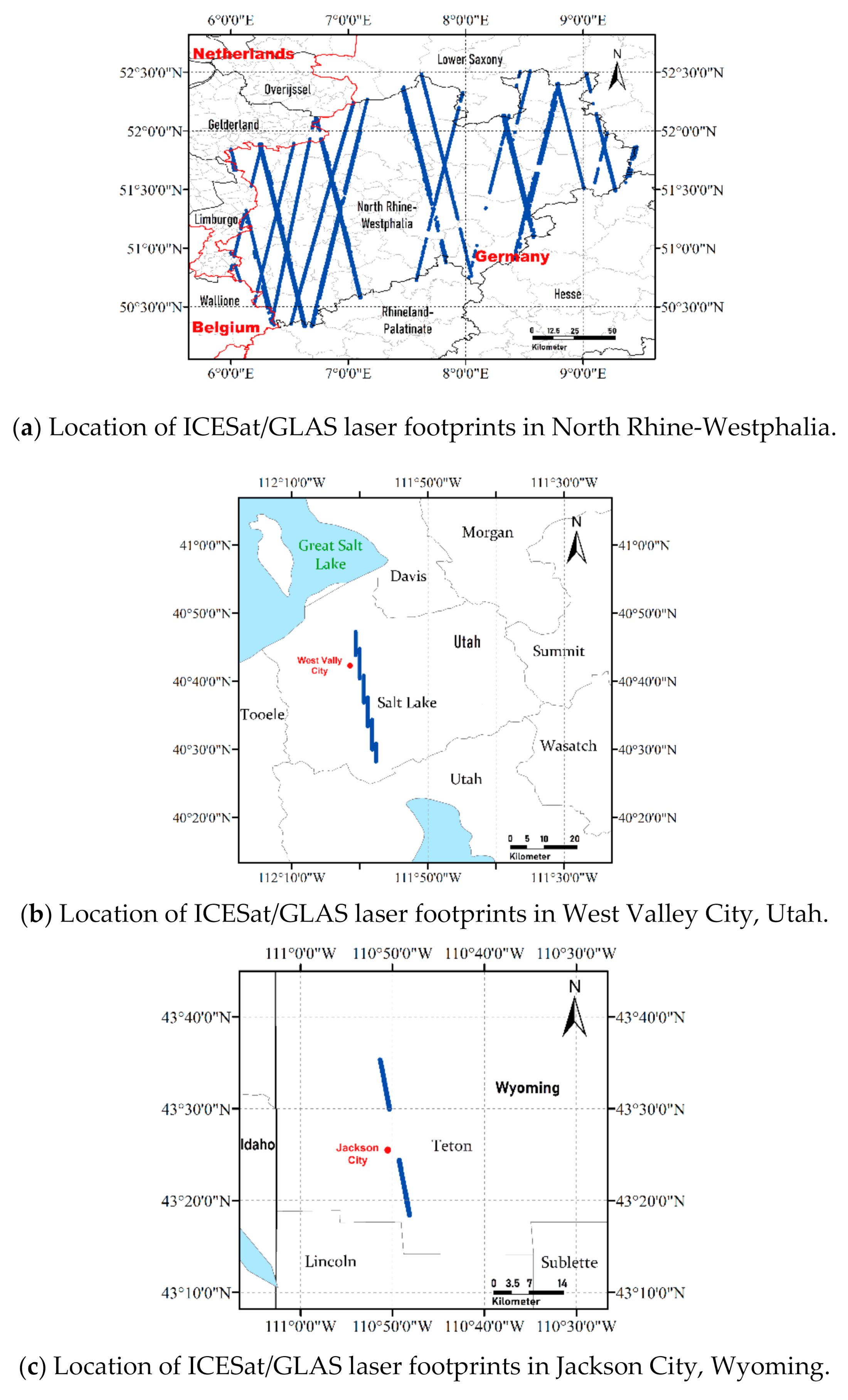




| Slope Difference (°) | Number | Proportion (Difference within ± 1°) |
|---|---|---|
| Slope (WVC-DEM)—Slope (Inversion) | 185 | 76.20% |
| Slope (WVC-DEM)—Slope (SRTM) | 185 | 66.40% |
| Slope (WVC-DEM)—Slope (GLAS-ATBD) | 185 | 27.00% |
| Slope (WVC-DEM)—Slope (Trigonometric) | 185 | 17.80% |
| Slope (JKS-DEM)—Slope (Inversion) | 54 | 96.30% |
| Slope (JKS-DEM)—Slope (SRTM) | 54 | 88.80% |
| Slope (JKS-DEM)—Slope (GLAS-ATBD) | 54 | 46.30% |
| Slope (JKS-DEM)—Slope (Trigonometric) | 54 | 38.90% |
| Slope (Lidar-DEM) *—Slope (Inversion) | 239 | 80.70% |
| Slope (Lidar-DEM)—Slope (SRTM) | 239 | 71.50% |
| Slope (Lidar-DEM)—Slope (GLAS-ATBD) | 239 | 31.30% |
| Slope (Lidar-DEM)—Slope (Trigonometric) | 239 | 22.60% |
| Roughness Difference (meter) | Number | Proportion (Difference within ± 0.4 m) |
|---|---|---|
| Roughness (WVC-DEM)—Roughness (Inversion) | 185 | 86.50% |
| Roughness (WVC-DEM)—Roughness (SRTM) | 185 | 85.40% |
| Roughness (WVC-DEM)—Roughness (GLAS-ATBD) | 185 | 68.60% |
| Roughness (WVC-DEM)—Roughness (Shi) | 185 | 73.50% |
| Roughness (JKS-DEM)—Roughness (Inversion) | 54 | 96.30% |
| Roughness (JKS-DEM)—Roughness (SRTM) | 54 | 94.40% |
| Roughness (JKS-DEM)—Roughness (GLAS-ATBD) | 54 | 72.20% |
| Roughness (JKS-DEM)—Roughness (Shi) | 54 | 70.30% |
| Roughness (Lidar-DEM)—Roughness (Inversion) | 239 | 88.70% |
| Roughness (Lidar-DEM)—Roughness (SRTM) | 239 | 87.40% |
| Roughness (Lidar-DEM)—Roughness (GLAS-ATBD) | 239 | 69.40% |
| Roughness (Lidar-DEM)—Roughness (Shi) | 239 | 72.80% |
| Calculated Slope (°) | Slope True-Value (°) | MAE (°) | RMSE (°) |
|---|---|---|---|
| Inversion slope | WVC-DEM slope | 0.694 | 0.835 |
| SRTM slope | WVC-DEM slope | 0.862 | 1.051 |
| GLAS-ATBD slope | WVC-DEM slope | 1.472 | 0.874 |
| Trigonometric slope | WVC-DEM slope | 2.144 | 2.604 |
| Inversion slope | JKS-DEM slope | 0.575 | 1.561 |
| SRTM slope | JKS-DEM slope | 0.769 | 1.831 |
| GLAS-ATBD slope | JKS-DEM slope | 1.268 | 1.939 |
| Trigonometric slope | JKS-DEM slope | 1.732 | 2.245 |
| Inversion slope | Lidar-DEM slope | 0.667 | 1.054 |
| SRTM slope | Lidar-DEM slope | 0.841 | 1.279 |
| GLAS-ATBD slope | Lidar-DEM slope | 1.426 | 1.237 |
| Trigonometric slope | Lidar-DEM slope | 2.051 | 2.538 |
| Calculated Roughness (m) | Roughness True-Value (m) | MAE (m) | RMSE (m) |
|---|---|---|---|
| Inversion roughness | WVC-DEM roughness | 0.175 | 0.268 |
| SRTM roughness | WVC-DEM roughness | 0.237 | 0.275 |
| GLAS-ATBD roughness | WVC-DEM roughness | 0.358 | 0.303 |
| Shi Roughness | WVC-DEM roughness | 0.311 | 0.351 |
| Inversion roughness | JKS-DEM roughness | 0.154 | 0.182 |
| SRTM roughness | JKS-DEM roughness | 0.194 | 0.235 |
| GLAS-ATBD roughness | JKS-DEM roughness | 0.31 | 0.28 |
| Shi roughness | JKS-DEM roughness | 0.292 | 0.407 |
| Inversion roughness | Lidar-DEM roughness | 0.171 | 0.25 |
| SRTM roughness | Lidar-DEM roughness | 0.228 | 0.274 |
| GLAS-ATBD roughness | Lidar-DEM roughness | 0.347 | 0.298 |
| Shi roughness | Lidar-DEM roughness | 0.307 | 0.37 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zuo, Z.; Tang, X.; Li, G.; Ma, Y.; Zhang, W.; Li, S. Inversion of Terrain Slope and Roughness with Satellite Laser Altimeter Full-Waveform Data Assisted by Shuttle Radar Topographic Mission. Remote Sens. 2021, 13, 424. https://doi.org/10.3390/rs13030424
Zuo Z, Tang X, Li G, Ma Y, Zhang W, Li S. Inversion of Terrain Slope and Roughness with Satellite Laser Altimeter Full-Waveform Data Assisted by Shuttle Radar Topographic Mission. Remote Sensing. 2021; 13(3):424. https://doi.org/10.3390/rs13030424
Chicago/Turabian StyleZuo, Zhiqiang, Xinming Tang, Guoyuan Li, Yue Ma, Wenhao Zhang, and Song Li. 2021. "Inversion of Terrain Slope and Roughness with Satellite Laser Altimeter Full-Waveform Data Assisted by Shuttle Radar Topographic Mission" Remote Sensing 13, no. 3: 424. https://doi.org/10.3390/rs13030424
APA StyleZuo, Z., Tang, X., Li, G., Ma, Y., Zhang, W., & Li, S. (2021). Inversion of Terrain Slope and Roughness with Satellite Laser Altimeter Full-Waveform Data Assisted by Shuttle Radar Topographic Mission. Remote Sensing, 13(3), 424. https://doi.org/10.3390/rs13030424










