Crop Height Estimation of Corn from Multi-Year RADARSAT-2 Polarimetric Observables Using Machine Learning
Abstract
1. Introduction
2. Materials and Methods
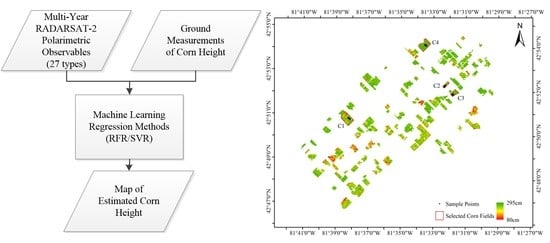
2.1. Study Site and Dataset
2.2. Polarimetric Observables
2.3. Machine Learning Method Used in This Study
2.3.1. Support Vector Regression (SVR)
2.3.2. Random Forest Regression (RFR)
2.3.3. Experimental Design
3. Results.
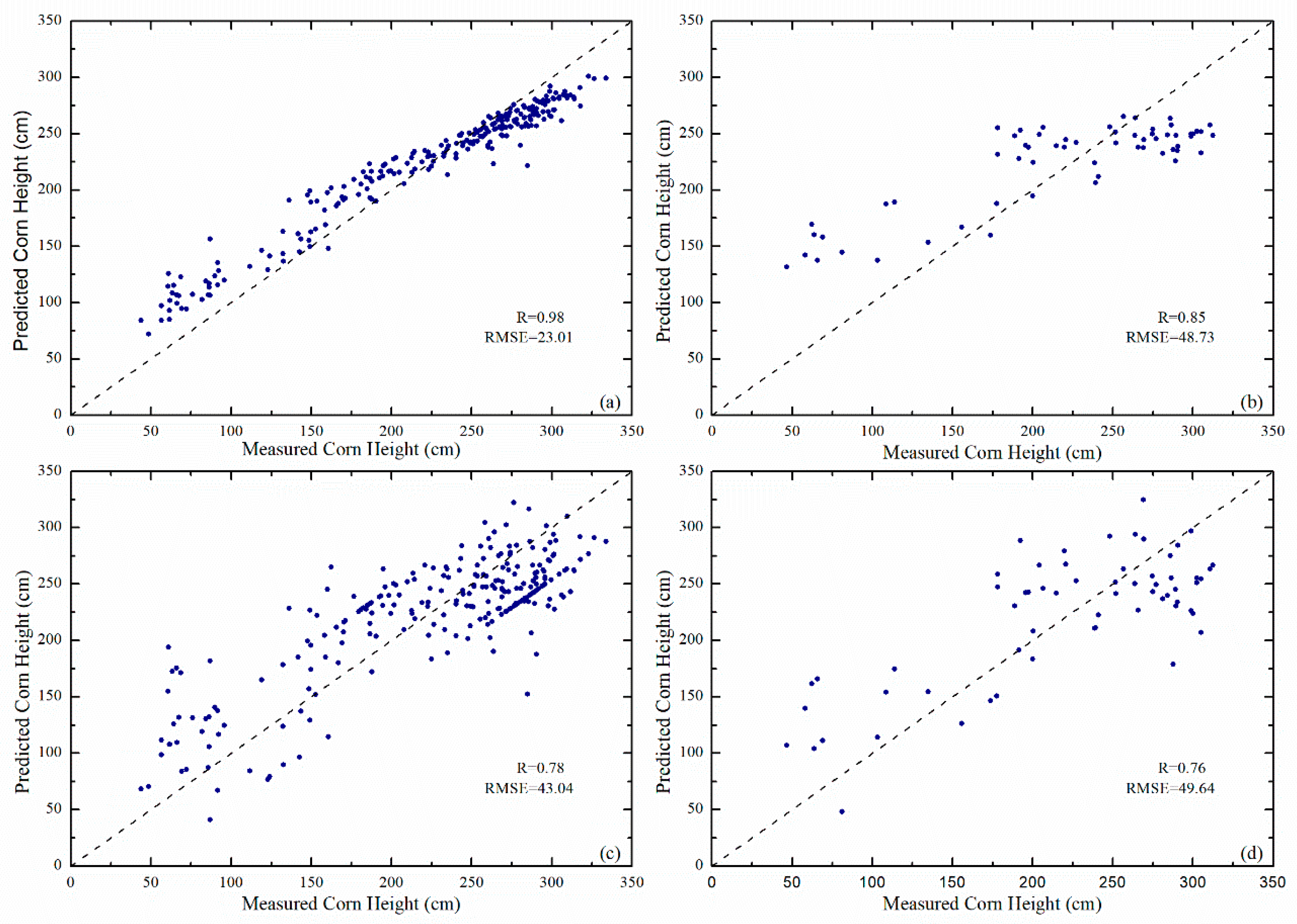
3.1. Comparison between SVR and RFR
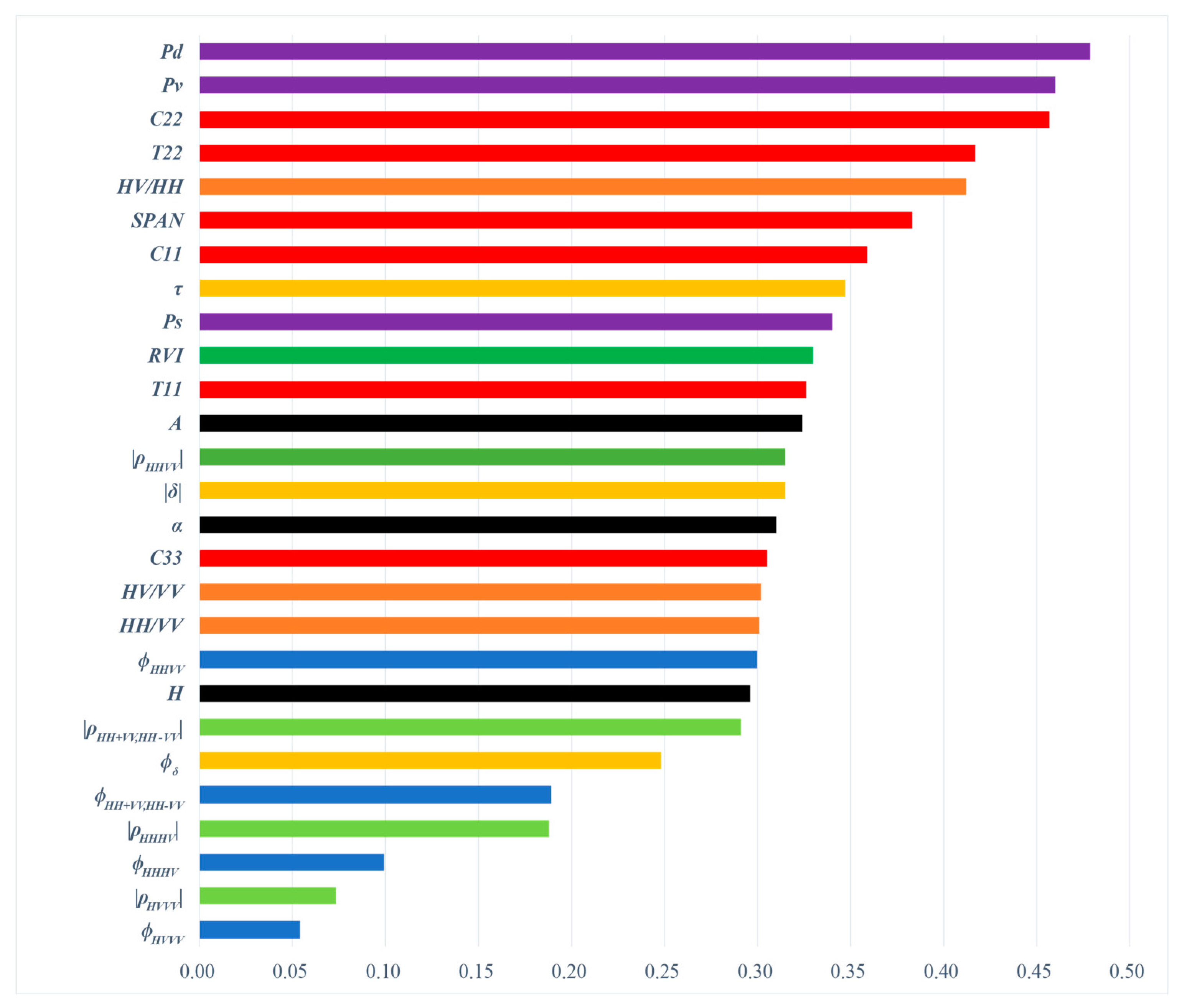
3.2. Normalized Variable Importance of RFR
4. Discussion
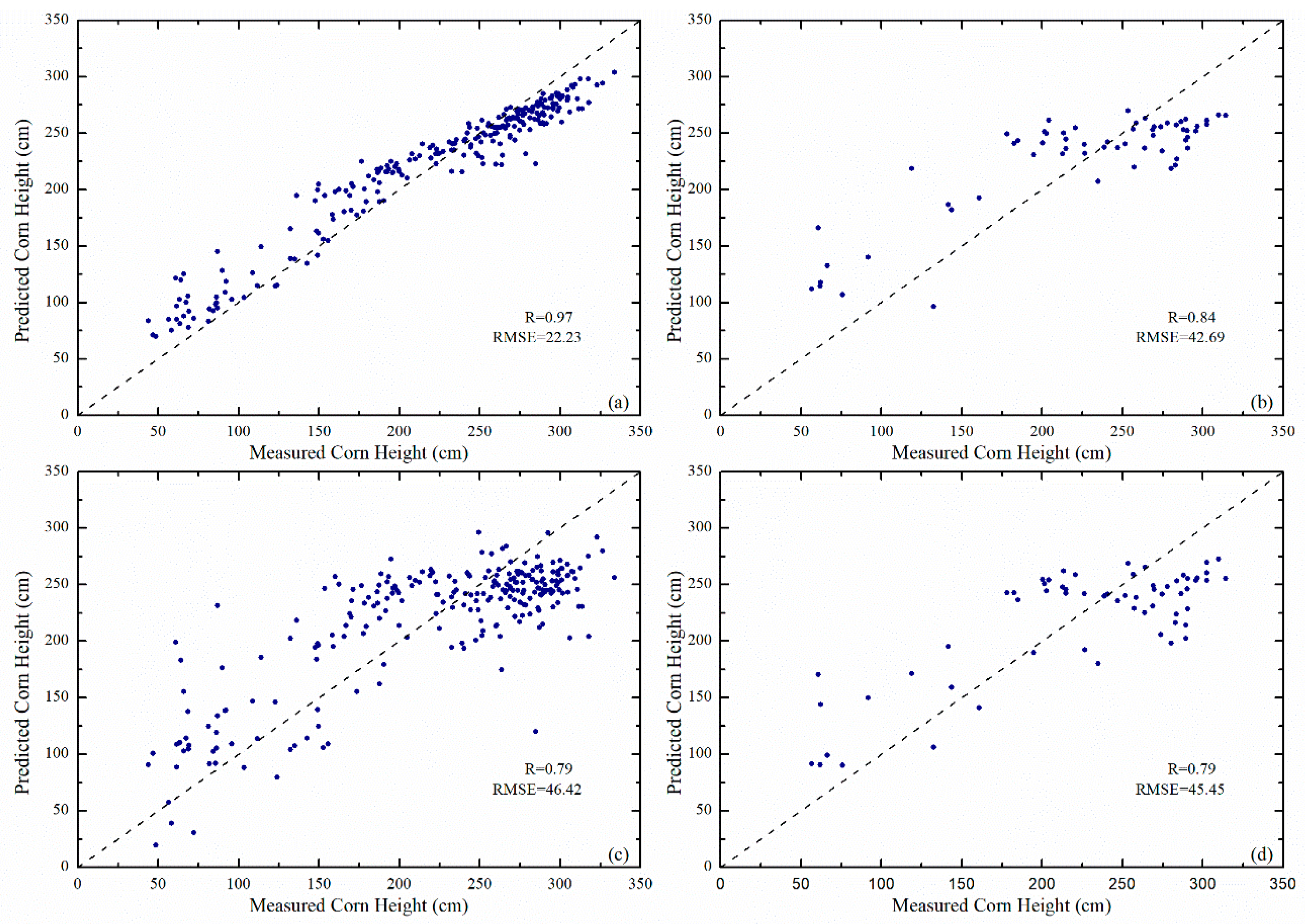
4.1. Tests with Fewer Polarimetric Observables
4.2. Tests with All Images Including Very Short Corn Height
4.3. Limitations and Future Research
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Erten, E.; Lopez-Sanchez, J.M.; Yuzugullu, O.; Hajnsek, I. Retrieval of agricultural crop height from space: A comparison of SAR techniques. Remote Sens. Environ. 2016, 187, 130–144. [Google Scholar] [CrossRef]
- Lopez-Sanchez, J.M.; Ballester-Berman, J.D. Potentials of polarimetric SAR interferometry for agriculture monitoring. Radio Sci. 2009, 44, 1–20. [Google Scholar] [CrossRef]
- Lopez-Sanchez, J.M.; Vicente-Guijalba, F.; Erten, E.; Campos-Taberner, M.; Garcia-Haro, F.J. Retrieval of vegetation height in rice fields using polarimetric SAR interferometry with TanDEM-X data. Remote Sens. Environ. 2017, 192, 30–44. [Google Scholar] [CrossRef]
- Yuzugullu, O.; Erten, E.; Hajnsek, I. Assessment of Paddy Rice Height: Sequential Inversion of Coherent and Incoherent Models. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3001–3013. [Google Scholar] [CrossRef]
- Karam, M.; Amar, F.; Fung, A.K.; Mougin, E.; Lopes, A.; Le Vine, D.M.; Beaudoin, A. A microwave polarimetric scattering model for forest canopies based on vector radiative transfer theory. Remote Sens. Environ. 1995, 53, 16–30. [Google Scholar] [CrossRef]
- Karam, M.; Fung, A.; Lang, R.; Chauhan, N. A microwave scattering model for layered vegetation. IEEE Trans. Geosci. Remote Sens. 1992, 30, 767–784. [Google Scholar] [CrossRef]
- Karam, M.; Fung, A.; Antar, Y. Electromagnetic wave scattering from some vegetation samples. IEEE Trans. Geosci. Remote Sens. 1988, 26, 799–808. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, K.-S.; Xu, P.; Li, Z.-L. Modeling and Characteristics of Microwave Backscattering From Rice Canopy over Growth Stages. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6757–6770. [Google Scholar] [CrossRef]
- Toure, A.; Thomson, K.; Edwards, G.; Brown, R.; Brisco, B. Adaptation of the MIMICS backscattering model to the agricultural context-wheat and canola at L and C bands. IEEE Trans. Geosci. Remote Sens. 1994, 32, 47–61. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Sarabandi, K.; McDonald, K.; Whitt, M.; Dobson, M.C. Michigan microwave canopy scattering model. Int. J. Remote Sens. 1990, 11, 1223–1253. [Google Scholar] [CrossRef]
- Ni, W.; Sun, G.; Ranson, K.J.; Zhang, Z.; He, Y.; Huang, W.; Guo, Z. Model-Based Analysis of the Influence of Forest Structures on the Scattering Phase Center at L-Band. IEEE Trans. Geosci. Remote Sens. 2013, 52, 3937–3946. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, X.; Su, S.; Wang, C. Retrieving canopy height and density of paddy rice from Radarsat-2 images with a canopy scattering model. Int. J. Appl. Earth Obs. Geoinf. 2014, 28, 170–180. [Google Scholar] [CrossRef]
- Yuzugullu, O.; Marelli, S.; Erten, E.; Sudret, B.; Hajnsek, I. Determining Rice Growth Stage with X-Band SAR: A Metamodel Based Inversion. Remote Sens. 2017, 9, 460. [Google Scholar] [CrossRef]
- Yuzugullu, O.; Erten, E.; Hajnsek, I. Estimation of Rice Crop Height from X- and C-Band PolSAR by Metamodel-Based Optimization. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 10, 194–204. [Google Scholar] [CrossRef]
- Attema, E.P.W.; Ulaby, F.T. Vegetation modeled as a water cloud. Radio Sci. 1978, 13, 357–364. [Google Scholar] [CrossRef]
- Yang, Z.; Li, K.; Shao, Y.; Brisco, B.; Liu, L. Estimation of Paddy Rice Variables with a Modified Water Cloud Model and Improved Polarimetric Decomposition Using Multi-Temporal RADARSAT-2 Images. Remote Sens. 2016, 8, 878. [Google Scholar] [CrossRef]
- Homayouni, S.; McNairn, H.; Hosseini, M.; Jiao, X.; Powers, J. Quad and compact multitemporal C-band PolSAR observations for crop characterization and monitoring. Int. J. Appl. Earth Obs. Geoinf. 2019, 74, 78–87. [Google Scholar] [CrossRef]
- Mandal, D.; Kumar, V.; McNairn, H.; Bhattacharya, A.; Rao, Y. Joint estimation of Plant Area Index (PAI) and wet biomass in wheat and soybean from C-band polarimetric SAR data. Int. J. Appl. Earth Obs. Geoinf. 2019, 79, 24–34. [Google Scholar] [CrossRef]
- Baghdadi, N.; El Hajj, M.; Zribi, M.; Bousbih, S. Calibration of the Water Cloud Model at C-Band for Winter Crop Fields and Grasslands. Remote Sens. 2017, 9, 969. [Google Scholar] [CrossRef]
- Bamler, R.; Hartl, P. Synthetic aperture radar interferometry. Inverse Probl. 1998, 14, R1–R54. [Google Scholar] [CrossRef]
- Fu, H.; Zhu, J.; Wang, C.; Zhao, R.; Xie, Q. Underlying Topography Estimation Over Forest Areas Using Single-Baseline InSAR Data. IEEE Trans. Geosci. Remote Sens. 2018, 57, 2876–2888. [Google Scholar] [CrossRef]
- Fu, H.; Wang, C.; Zhu, J.; Xie, Q.; Zhang, B. Estimation of Pine Forest Height and Underlying DEM Using Multi-Baseline P-Band PolInSAR Data. Remote Sens. 2016, 8, 820. [Google Scholar] [CrossRef]
- Liao, Z.; He, B.; Van Dijk, A.I.; Bai, X.; Quan, X. The impacts of spatial baseline on forest canopy height model and digital terrain model retrieval using P-band PolInSAR data. Remote Sens. Environ. 2018, 210, 403–421. [Google Scholar] [CrossRef]
- Fu, H.; Zhu, J.; Wang, C.; Li, Z. Underlying topography extraction over forest areas from multi-baseline PolInSAR data. J. Geod. 2018, 92, 727–741. [Google Scholar] [CrossRef]
- Peng, X.; Li, X.; Wang, C.; Fu, H.; Du, Y. A Maximum Likelihood Based Nonparametric Iterative Adaptive Method of Synthetic Aperture Radar Tomography and Its Application for Estimating Underlying Topography and Forest Height. Sensors 2018, 18, 2459. [Google Scholar] [CrossRef]
- Papathanassiou, K.; Cloude, S. Single-baseline polarimetric SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2352–2363. [Google Scholar] [CrossRef]
- Cloude, S.R.; Papathanassiou, K.P. Polarimetric SAR interferometry. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1551–1565. [Google Scholar] [CrossRef]
- Xie, Q.; Zhu, J.; Wang, C.; Fu, H.; Lopez-Sanchez, J.M.; Ballester-Berman, J.D. A Modified Dual-Baseline PolInSAR Method for Forest Height Estimation. Remote Sens. 2017, 9, 819. [Google Scholar] [CrossRef]
- Fu, H.; Wang, C.; Zhu, J.; Xie, Q.; Zhao, R. Inversion of vegetation height from PolInSAR using complex least squares adjustment method. Sci. China Earth Sci. 2015, 58, 1018–1031. [Google Scholar] [CrossRef]
- Garestier, F.; Dubois-Fernandez, P.C.; Papathanassiou, K.P. Pine Forest Height Inversion Using Single-Pass X-Band PolInSAR Data. IEEE Trans. Geosci. Remote Sens. 2007, 46, 59–68. [Google Scholar] [CrossRef]
- Garestier, F.; Dubois-Fernandez, P.; Champion, I. Forest Height Inversion Using High-Resolution P-Band Pol-InSAR Data. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3544–3559. [Google Scholar] [CrossRef]
- Hajnsek, I.; Kugler, F.; Lee, S.-K.; Papathanassiou, K.P. Tropical-Forest-Parameter Estimation by Means of Pol-InSAR: The INDREX-II Campaign. IEEE Trans. Geosci. Remote Sens. 2009, 47, 481–493. [Google Scholar] [CrossRef]
- Garestier, F.; Dubois-Fernandez, P.; Champion, I.; Le Toan, T. Pine forest investigation using high resolution P-band Pol-InSAR data. Remote Sens. Environ. 2011, 115, 2897–2905. [Google Scholar] [CrossRef]
- Kugler, F.; Schulze, D.; Hajnsek, I.; Pretzsch, H.; Papathanassiou, K.P. TanDEM-X Pol-InSAR Performance for Forest Height Estimation. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6404–6422. [Google Scholar] [CrossRef]
- Praks, J.; Kugler, F.; Papathanassiou, K.P.; Hajnsek, I.; Hallikainen, M. Height Estimation of Boreal Forest: Interferometric Model-Based Inversion at L- and X-Band versus HUTSCAT Profiling Scatterometer. IEEE Geosci. Remote Sens. Lett. 2007, 4, 466–470. [Google Scholar] [CrossRef]
- Neumann, M.; Ferro-Famil, L.; Reigber, A. Estimation of Forest Structure, Ground, and Canopy Layer Characteristics from Multibaseline Polarimetric Interferometric SAR Data. IEEE Trans. Geosci. Remote Sens. 2009, 48, 1086–1104. [Google Scholar] [CrossRef]
- Zhang, B.; Fu, H.; Zhu, J.; Peng, X.; Xie, Q.; Lin, D.; Liu, Z. A Multibaseline PolInSAR Forest Height Inversion Model Based on Fourier-Legendre Polynomials. IEEE Geosci. Remote Sens. Lett. 2020, 1–5. [Google Scholar] [CrossRef]
- Xie, Y.; Fu, H.; Zhu, J.; Wang, C.; Xie, Q. A LiDAR-Aided Multibaseline PolInSAR Method for Forest Height Estimation: With Emphasis on Dual-Baseline Selection. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1807–1811. [Google Scholar] [CrossRef]
- Kumar, S.; Govil, H.; Srivastava, P.K.; Thakur, P.K.; Kushwaha, S.P.S. Spaceborne Multifrequency PolInSAR-Based Inversion Modelling for Forest Height Retrieval. Remote Sens. 2020, 12, 4042. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, C.; Zhang, H.; Tang, Y.; Liu, X. Analysis of Permafrost Region Coherence Variation in the Qinghai–Tibet Plateau with a High-Resolution TerraSAR-X Image. Remote Sens. 2018, 10, 298. [Google Scholar] [CrossRef]
- Sagues, L.; Lopez-Sanchez, J.M.; Fortuny, J.; Fabregas, X.; Broquetas, A.; Sieber, A. Indoor experiments on polarimetric SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2000, 38, 671–684. [Google Scholar] [CrossRef]
- Ballester-Berman, J.; Lopez-Sanchez, J.M.; Fortuny-Guasch, J. Retrieval of biophysical parameters of agricultural crops using polarimetric SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2005, 43, 683–694. [Google Scholar] [CrossRef]
- Lopez-Sanchez, J.M.; Hajnsek, I.; Ballester-Berman, J.D. First Demonstration of Agriculture Height Retrieval with PolInSAR Airborne Data. IEEE Geosci. Remote Sens. Lett. 2012, 9, 242–246. [Google Scholar] [CrossRef]
- Pichierri, M.; Hajnsek, I.; Papathanassiou, K.P. A Multibaseline Pol-InSAR Inversion Scheme for Crop Parameter Estimation at Different Frequencies. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4952–4970. [Google Scholar] [CrossRef][Green Version]
- Nasirzadehdizaji, R.; Balik Sanli, F.; Abdikan, S.; Cakir, Z.; Sekertekin, A.; Ustuner, M. Sensitivity Analysis of Multi-Temporal Sentinel-1 SAR Parameters to Crop Height and Canopy Coverage. Appl. Sci. 2019, 9, 655. [Google Scholar] [CrossRef]
- Jiao, X.; McNairn, H.; Shang, J.; Pattey, E.; Liu, J.; Champagne, C. The sensitivity of RADARSAT-2 polarimetric SAR data to corn and soybean leaf area index. Can. J. Remote Sens. 2011, 37, 69–81. [Google Scholar] [CrossRef]
- Erten, E.; Taskin, G.; Lopez-Sanchez, J.M. Selection of PolSAR Observables for Crop Biophysical Variable Estimation with Global Sensitivity Analysis. IEEE Geosci. Remote Sens. Lett. 2019, 16, 766–770. [Google Scholar] [CrossRef]
- Liao, C.; Wang, J.; Shang, J.; Huang, X.; Liu, J.; Huffman, T. Sensitivity study of Radarsat-2 polarimetric SAR to crop height and fractional vegetation cover of corn and wheat. Int. J. Remote Sens. 2017, 39, 1475–1490. [Google Scholar] [CrossRef]
- Sarti, M.; Migliaccio, M.; Nunziata, F.; Mascolo, L.; Brugnoli, E. On the sensitivity of polarimetric SAR measurements to vegetation cover: The Coiba National Park, Panama. Int. J. Remote Sens. 2017, 38, 6755–6768. [Google Scholar] [CrossRef]
- Hosseini, M.; McNairn, H.; Merzouki, A.; Pacheco, A. Estimation of Leaf Area Index (LAI) in corn and soybeans using multi-polarization C- and L-band radar data. Remote Sens. Environ. 2015, 170, 77–89. [Google Scholar] [CrossRef]
- Wiseman, G.; McNairn, H.; Homayouni, S.; Shang, J. RADARSAT-2 Polarimetric SAR Response to Crop Biomass for Agricultural Production Monitoring. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4461–4471. [Google Scholar] [CrossRef]
- Reisi-Gahrouei, O.; Homayouni, S.; McNairn, H.; Hosseini, M.; Safari, A. Crop biomass estimation using multi regression analysis and neural networks from multitemporal L-band polarimetric synthetic aperture radar data. Int. J. Remote Sens. 2019, 40, 6822–6840. [Google Scholar] [CrossRef]
- Mandal, D.; Kumar, V.; Lopez-Sanchez, J.M.; Bhattacharya, A.; McNairn, H.; Rao, Y.S. Crop biophysical parameter retrieval from Sentinel-1 SAR data with a multi-target inversion of Water Cloud Model. Int. J. Remote Sens. 2020, 41, 5503–5524. [Google Scholar] [CrossRef]
- Mandal, D.; Hosseini, M.; McNairn, H.; Kumar, V.; Bhattacharya, A.; Rao, Y.; Mitchell, S.; Robertson, L.D.; Davidson, A.; Dabrowska-Zielinska, K. An investigation of inversion methodologies to retrieve the leaf area index of corn from C-band SAR data. Int. J. Appl. Earth Obs. Geoinf. 2019, 82, 101893. [Google Scholar] [CrossRef]
- Fieuzal, R.; Baup, F. Estimation of leaf area index and crop height of sunflowers using multi-temporal optical and SAR satellite data. Int. J. Remote Sens. 2016, 37, 2780–2809. [Google Scholar] [CrossRef]
- Yang, H.; Chen, E.; Li, Z.; Yang, G.; Xu, X.; Yuan, L.; Feng, Q.; Zhao, L. Capability of multi-temporal Radarsat-2 data in monitoring canola crop and its plant height. In Proceedings of the 2014 the Third International Conference on Agro-Geoinformatics, Beijing, China, 11–14 August 2014; pp. 1–5. [Google Scholar]
- Canisius, F.; Shang, J.; Liu, J.; Huang, X.; Ma, B.; Jiao, X.; Geng, X.; Kovacs, J.M.; Walters, D. Tracking crop phenological development using multi-temporal polarimetric Radarsat-2 data. Remote Sens. Environ. 2018, 210, 508–518. [Google Scholar] [CrossRef]
- El Hajj, M.; Baghdadi, N.; Bazzi, H.; Zribi, M. Penetration Analysis of SAR Signals in the C and L Bands for Wheat, Maize, and Grasslands. Remote Sens. 2018, 11, 31. [Google Scholar] [CrossRef]
- Ballester-Berman, J.D.; Lopez-Sanchez, J.M.; Fortuny-Guasch, J. Retrieval of height and topography of corn fields by polarimetric SAR interferometry. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, IGARSS’04, Anchorage, AK, USA, 20–24 September 2004; Volume 2, pp. 1228–1231. [Google Scholar]
- Liu, C.; Shang, J.; Vachon, P.W.; McNairn, H. Multiyear Crop Monitoring Using Polarimetric RADARSAT-2 Data. IEEE Trans. Geosci. Remote Sens. 2012, 51, 2227–2240. [Google Scholar] [CrossRef]
- Cloude, S.R. Polarisation: Applications in Remote Sensing Polarisation; Oxford University Press: New York, NY, USA, 2010; ISBN 978-0-19-956973-1. [Google Scholar]
- Lee, J.; Pottier, E. Polarimetric Radar Imaging: From Basics to Applications; CRC Press: Boca Raton, FL, USA, 2009; ISBN 142005497X. [Google Scholar]
- Vicente-Guijalba, F.; Martinez-Marin, T.; Lopez-Sanchez, J.M. Dynamical Approach for Real-Time Monitoring of Agricultural Crops. IEEE Trans. Geosci. Remote Sens. 2014, 53, 3278–3293. [Google Scholar] [CrossRef]
- Huapeng, L.; Zhang, C.; Zhang, S.; Atkinson, P.M. Full year crop monitoring and separability assessment with fully-polarimetric L-band UAVSAR: A case study in the Sacramento Valley, California. Int. J. Appl. Earth Obs. Geoinf. 2019, 74, 45–56. [Google Scholar] [CrossRef]
- Lopez-Sanchez, J.M.; Ballester-Berman, J.D.; Hajnsek, I. First Results of Rice Monitoring Practices in Spain by Means of Time Series of TerraSAR-X Dual-Pol Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 4, 412–422. [Google Scholar] [CrossRef]
- Lopez-Sanchez, J.M.; Cloude, S.R.; Ballester-Berman, J.D. Rice Phenology Monitoring by Means of SAR Polarimetry at X-Band. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2695–2709. [Google Scholar] [CrossRef]
- Lopez-Sanchez, J.M.; Vicente-Guijalba, F.; Ballester-Berman, J.D.; Cloude, S.R. Influence of Incidence Angle on the Coherent Copolar Polarimetric Response of Rice at X-Band. IEEE Geosci. Remote Sens. Lett. 2014, 12, 249–253. [Google Scholar] [CrossRef]
- Cloude, S.; Pottier, E. An entropy based classification scheme for land applications of polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 1997, 35, 68–78. [Google Scholar] [CrossRef]
- Neumann, M.; Ferro-Famil, L.; Jager, M.; Reigber, A.; Pottier, E. A polarimetric vegetation model to retrieve particle and orientation distribution characteristics. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009; Volume 4, p. IV-145. [Google Scholar]
- Neumann, M.; Saatchi, S.S.; Ulander, L.M.H.; Fransson, J.E.S. Assessing Performance of L- and P-Band Polarimetric Interferometric SAR Data in Estimating Boreal Forest Above-Ground Biomass. IEEE Trans. Geosci. Remote Sens. 2012, 50, 714–726. [Google Scholar] [CrossRef]
- Xie, Q.; Zhu, J.; Lopez-Sanchez, J.M.; Wang, C.; Fu, H. A Modified General Polarimetric Model-Based Decomposition Method with the Simplified Neumann Volume Scattering Model. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1229–1233. [Google Scholar] [CrossRef]
- Xie, Q.; Wang, J.; Liao, C.; Shang, J.; Lopez-Sanchez, J.M.; Fu, H.; Liu, X. On the Use of Neumann Decomposition for Crop Classification Using Multi-Temporal RADARSAT-2 Polarimetric SAR Data. Remote Sens. 2019, 11, 776. [Google Scholar] [CrossRef]
- Kim, Y.; Van Zyl, J. Comparison of forest parameter estimation techniques using SAR data. In Proceedings of the IGARSS 2001, Scanning the Present and Resolving the Future, IEEE 2001 International Geoscience and Remote Sensing Symposium (Cat. No.01CH37217), Sydney, NSW, Australia, 9–13 July 2001; Volume 3, pp. 1395–1397. [Google Scholar]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.-S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep Learning in Remote Sensing: A Comprehensive Review and List of Resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Du, B. Deep Learning for Remote Sensing Data: A Technical Tutorial on the State of the Art. IEEE Geosci. Remote Sens. Mag. 2016, 4, 22–40. [Google Scholar] [CrossRef]
- Tuia, D.; Verrelst, J.; Alonso, L.; Perez-Cruz, F.; Camps-Valls, G. Multioutput Support Vector Regression for Remote Sensing Biophysical Parameter Estimation. IEEE Geosci. Remote Sens. Lett. 2011, 8, 804–808. [Google Scholar] [CrossRef]
- Karimi, Y.; Prasher, S.O.; Madani, A.; Kim, S. Application of support vector machine technology for the estimation of crop biophysical parameters using aerial hyperspectral observations. Can. Biosyst. Eng. 2008, 50, 713–720. [Google Scholar]
- Siegmann, B.; Jarmer, T. Comparison of different regression models and validation techniques for the assessment of wheat leaf area index from hyperspectral data. Int. J. Remote Sens. 2015, 36, 4519–4534. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Waske, B.; Van Der Linden, S.; Oldenburg, C.; Jakimow, B.; Rabe, A.; Hostert, P. Imager—A user-oriented implementation for remote sensing image analysis with Random Forests. Environ. Model. Softw. 2012, 35, 192–193. [Google Scholar] [CrossRef]
- Austin, P.C.; Tu, J.V. Bootstrap Methods for Developing Predictive Models. Am. Stat. 2004, 58, 131–137. [Google Scholar] [CrossRef]



| Date | Mode | Incidence | Resolution | Orbit | Fieldwork Date | Number of Corn Sample Points | Average Corn Height (cm) | Study Site |
|---|---|---|---|---|---|---|---|---|
| 23 May 2013 | FQ9W | 27.2 ~ 30.5 | 5.1 × 4.7 | Ascending | 24 May 2013 | 4 | 5.75 | Stratford |
| 2 June 2013 | FQ19W | 37.7 ~ 40.4 | 4.7 × 4.7 | Ascending | 4 June 2013 | 16 | 10.06 | |
| 16 June 2013 | FQ9W | 27.2 ~ 30.5 | 5.1 × 4.7 | Ascending | 16 June 2013 | 17 | 25.13 | |
| 26 June 2013 | FQ19W | 37.7 ~ 40.4 | 4.7 × 4.7 | Ascending | 24 June 2013/ 25 June 2013 | 17 | 59.87 | |
| 10 July 2013 | FQ9W | 27.2 ~ 30.5 | 5.1 × 4.7 | Ascending | 10 July 2013 | 17 | 142.29 | |
| 20 July 2013 | FQ19W | 37.7 ~ 40.4 | 4.7 × 4.7 | Ascending | 21 July 2013 | 11 | 214.35 | |
| 3 August 2013 | FQ9W | 27.2 ~ 30.5 | 5.1 × 4.7 | Ascending | 3 August 2013 | 13 | 254.84 | |
| 13 August 2013 | FQ19W | 37.7 ~ 40.4 | 4.7 × 4.7 | Ascending | 13 August 2013/ 14 August 2013 | 17 | 260.78 | |
| 23 June 2015 | FQ10W | 28.4 ~ 31.6 | 5.5 × 4.7 | Ascending | 23 June 2015 | 25 | 88.44 | London |
| 10 August 2015 | FQ10W | 28.4 ~ 31.6 | 5.5 × 4.7 | Ascending | 11 August 2015 | 6 | 266.61 | |
| 3 September 2015 | FQ10W | 28.4 ~ 31.6 | 5.5 × 4.7 | Ascending | 3 September 2015 | 6 | 265.61 | |
| 13 September 2015 | FQ20W | 38.6 ~ 41.3 | 5.1 × 4.7 | Ascending | 13 September 2015 | 6 | 276.72 | |
| 1 July 2018 | FQ10W | 28.4 ~ 31.6 | 5.5 × 4.7 | Ascending | 4 July 2018 | 24 | 182.07 | |
| 25 July 2018 | FQ10W | 28.4 ~ 31.6 | 5.5 × 4.7 | Ascending | 25 July 2018 | 32 | 252.76 | |
| 1 August 2018 | FQ5W | 22.5 ~ 26.0 | 5.0 × 4.7 | Ascending | 2 August 2018 | 32 | 275.22 | |
| 18 August 2018 | FQ10W | 28.4 ~ 31.6 | 5.5 × 4.7 | Ascending | 18 August 2018 | 32 | 267.77 | |
| 25 August 2018 | FQ5W | 22.5 ~ 26.0 | 5.0 × 4.7 | Ascending | 25 August 2018 | 8 | 214.99 | |
| 1 September 2018 | FQ1W | 17.2 ~ 21.2 | 4.8 × 4.7 | Ascending | 1 September 2018 | 32 | 267.04 | |
| 15 September 2018 | FQ9W | 27.3 ~ 30.5 | 5.1 × 4.7 | Descending | 11 September 2018 | 32 | 267.22 |
| Polarimetric Observable | Description |
|---|---|
| C11, C22, C33, | Backscattering coefficients in the linear polarization channels |
| T11, T22 | Backscattering coefficients in the Pauli polarization channels |
| SPAN | Total backscattering power |
| |ρHHVV|, |ρHVVV|, |ρHHHV|, |ρHH+VV,HH−VV| | Correlation between polarimetric channels |
| ϕHHVV, ϕHVVV, ϕHHHV, ϕHH+VV,HH−VV | Phase difference between polarimetric channels |
| HH/VV, HV/HH, HV/VV | Backscattering ratios |
| Ps, Pd, Pv | Scattering Power from different scattering mechanisms derived from Freeman-Durden decomposition |
| H, A, α | Entropy, anisotropy, alpha angle from Cloude-Pottier decomposition |
| |δ|, ϕδ, τ | Magnitude and phase of the particle scattering anisotropy, the degree of orientation randomness derived from Neumann decomposition |
| RVI | Radar Vegetation Index |
| Scenario | Model Calibration | Model Validation | ||||||
|---|---|---|---|---|---|---|---|---|
| SVR | RFR | SVR | RFR | |||||
| RMSE (cm) | R | RMSE (cm) | R | RMSE (cm) | R | RMSE (cm) | R | |
| 1 | 42.05 | 0.84 | 22.15 | 0.98 | 56.61 | 0.64 | 52.81 | 0.74 |
| 2 | 43.04 | 0.82 | 23.01 | 0.98 | 49.64 | 0.76 | 48.73 | 0.85 |
| 3 | 51.14 | 0.75 | 22.65 | 0.98 | 51.35 | 0.75 | 49.27 | 0.82 |
| 4 | 43.10 | 0.82 | 22.53 | 0.98 | 49.62 | 0.76 | 49.83 | 0.82 |
| 5 | 41.27 | 0.84 | 21.95 | 0.98 | 58.49 | 0.64 | 51.73 | 0.78 |
| 6 | 41.28 | 0.84 | 21.98 | 0.98 | 58.49 | 0.64 | 51.82 | 0.78 |
| 7 | 50.37 | 0.75 | 22.19 | 0.98 | 54.17 | 0.75 | 50.93 | 0.80 |
| 8 | 42.59 | 0.83 | 22.35 | 0.98 | 48.92 | 0.81 | 51.10 | 0.80 |
| 9 | 43.08 | 0.82 | 22.28 | 0.98 | 49.63 | 0.76 | 48.82 | 0.84 |
| 10 | 43.30 | 0.82 | 22.51 | 0.98 | 49.56 | 0.76 | 48.99 | 0.84 |
| Average | 44.12 | 0.81 | 22.36 | 0.98 | 54.69 | 0.73 | 50.40 | 0.81 |
| Scenario | Model Calibration | Model Validation | ||||||
|---|---|---|---|---|---|---|---|---|
| SVR | RFR | SVR | RFR | |||||
| RMSE (cm) | R | RMSE (cm) | R | RMSE (cm) | R | RMSE (cm) | R | |
| 1 | 46.42 | 0.79 | 22.33 | 0.97 | 45.45 | 0.79 | 42.69 | 0.84 |
| 2 | 49.14 | 0.76 | 22.69 | 0.97 | 48.04 | 0.78 | 47.81 | 0.79 |
| 3 | 45.84 | 0.79 | 21.91 | 0.97 | 50.75 | 0.74 | 48.07 | 0.78 |
| 4 | 45.73 | 0.79 | 22.04 | 0.97 | 46.20 | 0.80 | 48.12 | 0.79 |
| 5 | 45.34 | 0.81 | 21.53 | 0.97 | 53.89 | 0.72 | 50.68 | 0.74 |
| 6 | 48.69 | 0.77 | 21.28 | 0.97 | 51.57 | 0.73 | 51.29 | 0.73 |
| 7 | 45.81 | 0.80 | 22.42 | 0.97 | 45.38 | 0.81 | 46.14 | 0.82 |
| 8 | 45.82 | 0.80 | 22.44 | 0.97 | 45.38 | 0.81 | 47.07 | 0.81 |
| 9 | 45.71 | 0.79 | 22.31 | 0.97 | 46.14 | 0.80 | 47.72 | 0.79 |
| 10 | 45.74 | 0.79 | 22.36 | 0.97 | 46.22 | 0.80 | 48.01 | 0.79 |
| Average | 46.42 | 0.79 | 22.13 | 0.97 | 47.90 | 0.78 | 47.76 | 0.79 |
| Scenario | Model Validation | |||||||
|---|---|---|---|---|---|---|---|---|
| SVR (Height < 150 cm) | SVR (Height > 150 cm) | RFR (Height < 150 cm) | RFR (Height > 150 cm) | |||||
| RMSE (cm) | R | RMSE (cm) | R | RMSE (cm) | R | RMSE (cm) | R | |
| 1 | 53.91 | 0.52 | 43.41 | 0.27 | 62.02 | 0.51 | 37.23 | 0.40 |
| 2 | 59.61 | 0.16 | 45.16 | 0.32 | 49.19 | 0.64 | 47.51 | 0.26 |
| 3 | 44.46 | 0.80 | 52.01 | 0.10 | 48.47 | 0.92 | 47.98 | 0.10 |
| 4 | 51.75 | 0.34 | 44.91 | 0.35 | 50.71 | 0.58 | 47.55 | 0.26 |
| 5 | 55.13 | 0.76 | 53.49 | 0.31 | 68.37 | 0.72 | 43.55 | 0.30 |
| 6 | 60.29 | 0.67 | 48.46 | 0.35 | 66.06 | 0.71 | 45.58 | 0.26 |
| 7 | 59.99 | 0.37 | 41.99 | 0.47 | 64.46 | 0.48 | 41.71 | 0.41 |
| 8 | 59.99 | 0.37 | 41.99 | 0.47 | 64.59 | 0.49 | 42.89 | 0.38 |
| 9 | 51.76 | 0.34 | 44.84 | 0.35 | 49.00 | 0.60 | 47.44 | 0.28 |
| 10 | 51.75 | 0.34 | 44.94 | 0.35 | 51.06 | 0.63 | 47.33 | 0.28 |
| Average | 54.86 | 0.47 | 46.12 | 0.33 | 57.39 | 0.63 | 44.88 | 0.29 |
| Field Name | Corn Height (cm) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| C1 | Measured | 274.83 | 251.5 | 295.17 | 286.83 | 290.67 | 285.5 | 235.75 | 271.41 |
| Estimated | 252.55 | 228.26 | 283.05 | 275.69 | 279.13 | 274.72 | 244.21 | 263.61 | |
| C2 | Measured | 273.92 | 301 | 371.58 | 260.42 | 241.08 | 283.17 | 298.75 | 283.92 |
| Estimated | 255.66 | 259.90 | 255.99 | 255.32 | 244.74 | 273.18 | 282.48 | 227.11 | |
| C3 | Measured | 255.75 | 251.67 | 219.83 | 248.08 | 162.5 | 220.67 | 253.5 | 204.33 |
| Estimated | 258.35 | 261.41 | 228 | 232.20 | 199.91 | 254.53 | 248.51 | 261.60 | |
| C4 | Measured | 276.25 | 288.50 | 290.75 | 288.08 | 296.58 | 298.92 | 306 | 284.25 |
| Estimated | 270.46 | 280.46 | 246.22 | 252.87 | 255.87 | 284.98 | 268.49 | 262.39 | |
| RMSE (cm) | 32.61 | ||||||||
| R | 0.59 | ||||||||
| Scenario | Model Calibration | Model Validation | ||||||
|---|---|---|---|---|---|---|---|---|
| SVR | RFR | SVR | RFR | |||||
| RMSE (cm) | R | RMSE (cm) | R | RMSE (cm) | R | RMSE (cm) | R | |
| 1 | 48.63 | 0.87 | 22.38 | 0.99 | 58.81 | 0.80 | 54.41 | 0.84 |
| 2 | 48.53 | 0.86 | 22.63 | 0.99 | 58.75 | 0.82 | 55.62 | 0.86 |
| 3 | 50.05 | 0.86 | 22.22 | 0.99 | 59.87 | 0.75 | 54.56 | 0.83 |
| 4 | 50.45 | 0.87 | 22.78 | 0.99 | 54.37 | 0.76 | 52.98 | 0.78 |
| 5 | 49.09 | 0.87 | 22.20 | 0.99 | 55.16 | 0.79 | 54.73 | 0.84 |
| 6 | 48.27 | 0.87 | 22.18 | 0.99 | 57.64 | 0.83 | 57.62 | 0.84 |
| 7 | 49.13 | 0.86 | 23.05 | 0.99 | 53.44 | 0.85 | 53.15 | 0.88 |
| 8 | 49.95 | 0.86 | 22.43 | 0.99 | 54.86 | 0.76 | 50.65 | 0.82 |
| 9 | 48.51 | 0.87 | 22.14 | 0.99 | 56.53 | 0.81 | 55.59 | 0.82 |
| 10 | 49.23 | 0.86 | 22.47 | 0.99 | 58.05 | 0.78 | 56.20 | 0.83 |
| Average | 49.18 | 0.87 | 22.45 | 0.99 | 56.75 | 0.80 | 54.55 | 0.83 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Q.; Wang, J.; Lopez-Sanchez, J.M.; Peng, X.; Liao, C.; Shang, J.; Zhu, J.; Fu, H.; Ballester-Berman, J.D. Crop Height Estimation of Corn from Multi-Year RADARSAT-2 Polarimetric Observables Using Machine Learning. Remote Sens. 2021, 13, 392. https://doi.org/10.3390/rs13030392
Xie Q, Wang J, Lopez-Sanchez JM, Peng X, Liao C, Shang J, Zhu J, Fu H, Ballester-Berman JD. Crop Height Estimation of Corn from Multi-Year RADARSAT-2 Polarimetric Observables Using Machine Learning. Remote Sensing. 2021; 13(3):392. https://doi.org/10.3390/rs13030392
Chicago/Turabian StyleXie, Qinghua, Jinfei Wang, Juan M. Lopez-Sanchez, Xing Peng, Chunhua Liao, Jiali Shang, Jianjun Zhu, Haiqiang Fu, and J. David Ballester-Berman. 2021. "Crop Height Estimation of Corn from Multi-Year RADARSAT-2 Polarimetric Observables Using Machine Learning" Remote Sensing 13, no. 3: 392. https://doi.org/10.3390/rs13030392
APA StyleXie, Q., Wang, J., Lopez-Sanchez, J. M., Peng, X., Liao, C., Shang, J., Zhu, J., Fu, H., & Ballester-Berman, J. D. (2021). Crop Height Estimation of Corn from Multi-Year RADARSAT-2 Polarimetric Observables Using Machine Learning. Remote Sensing, 13(3), 392. https://doi.org/10.3390/rs13030392