Automatic Image-Based Event Detection for Large-N Seismic Arrays Using a Convolutional Neural Network
Abstract
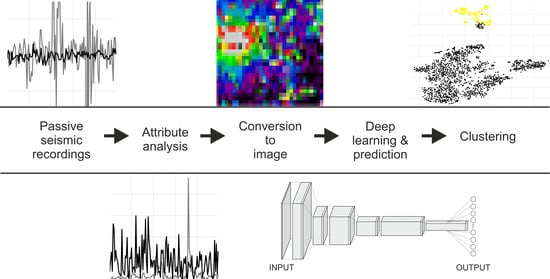
1. Introduction
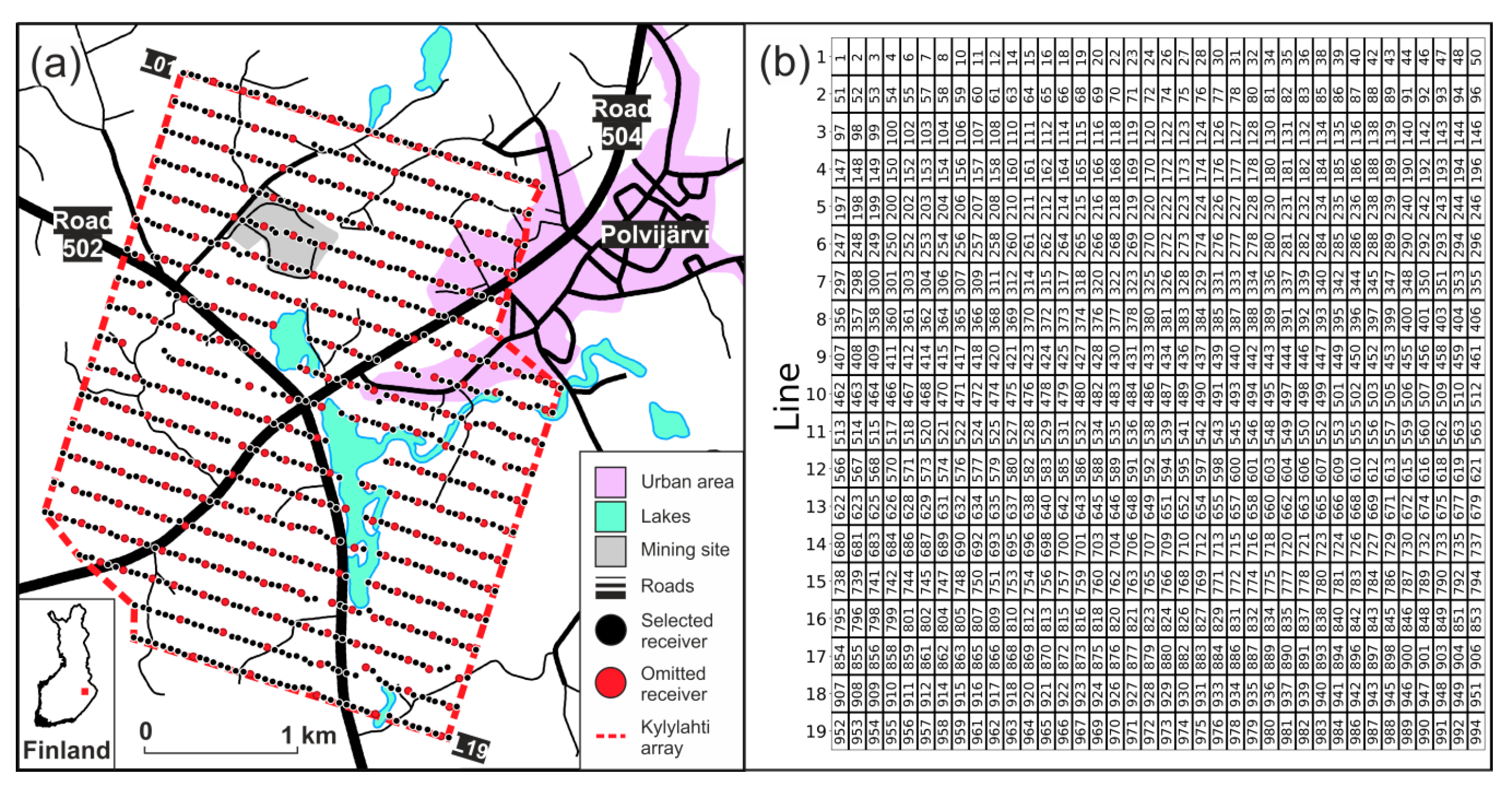
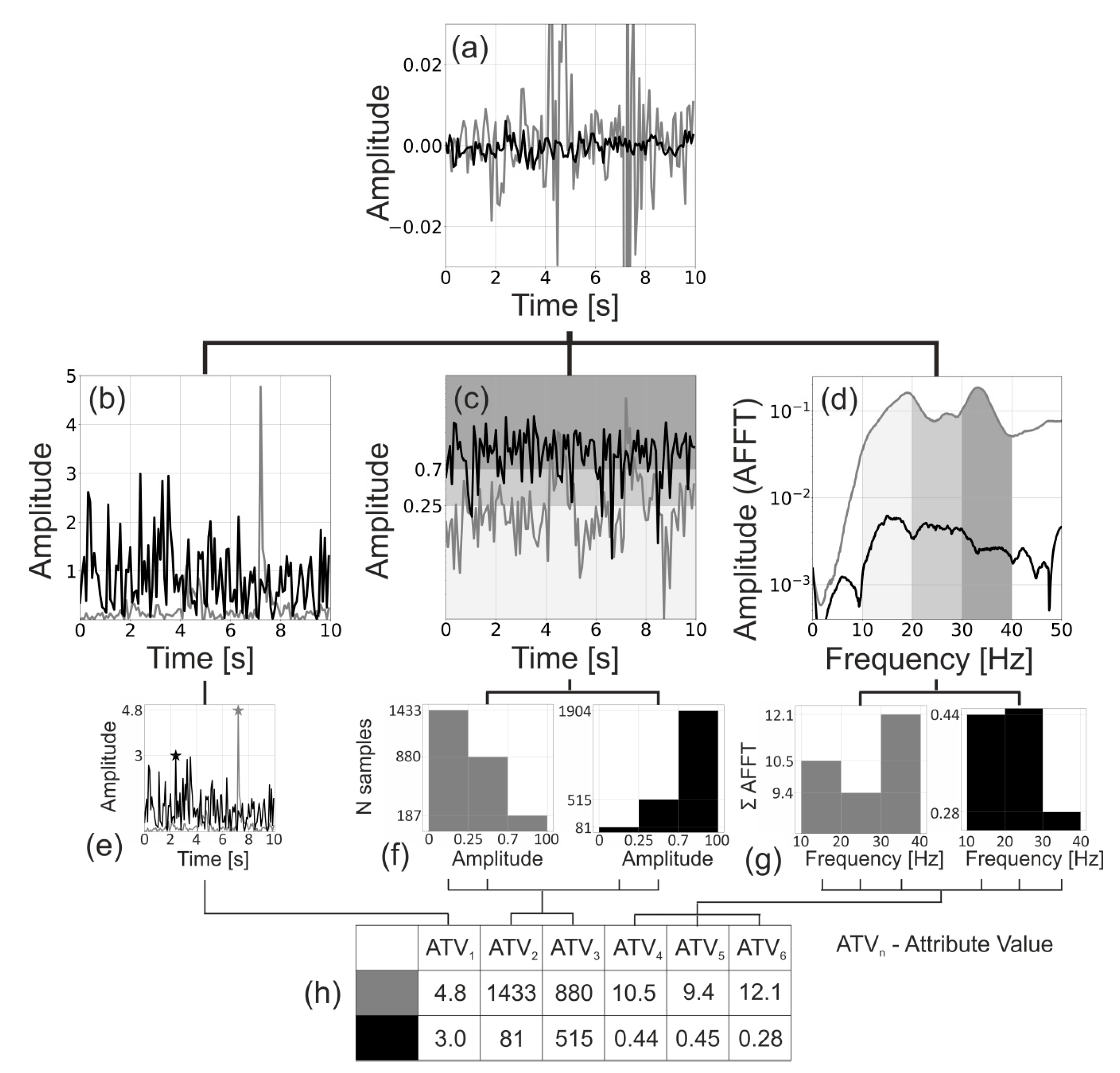
2. Dataset and Attribute Maps
3. Deep Supervised Learning
3.1. Training Dataset
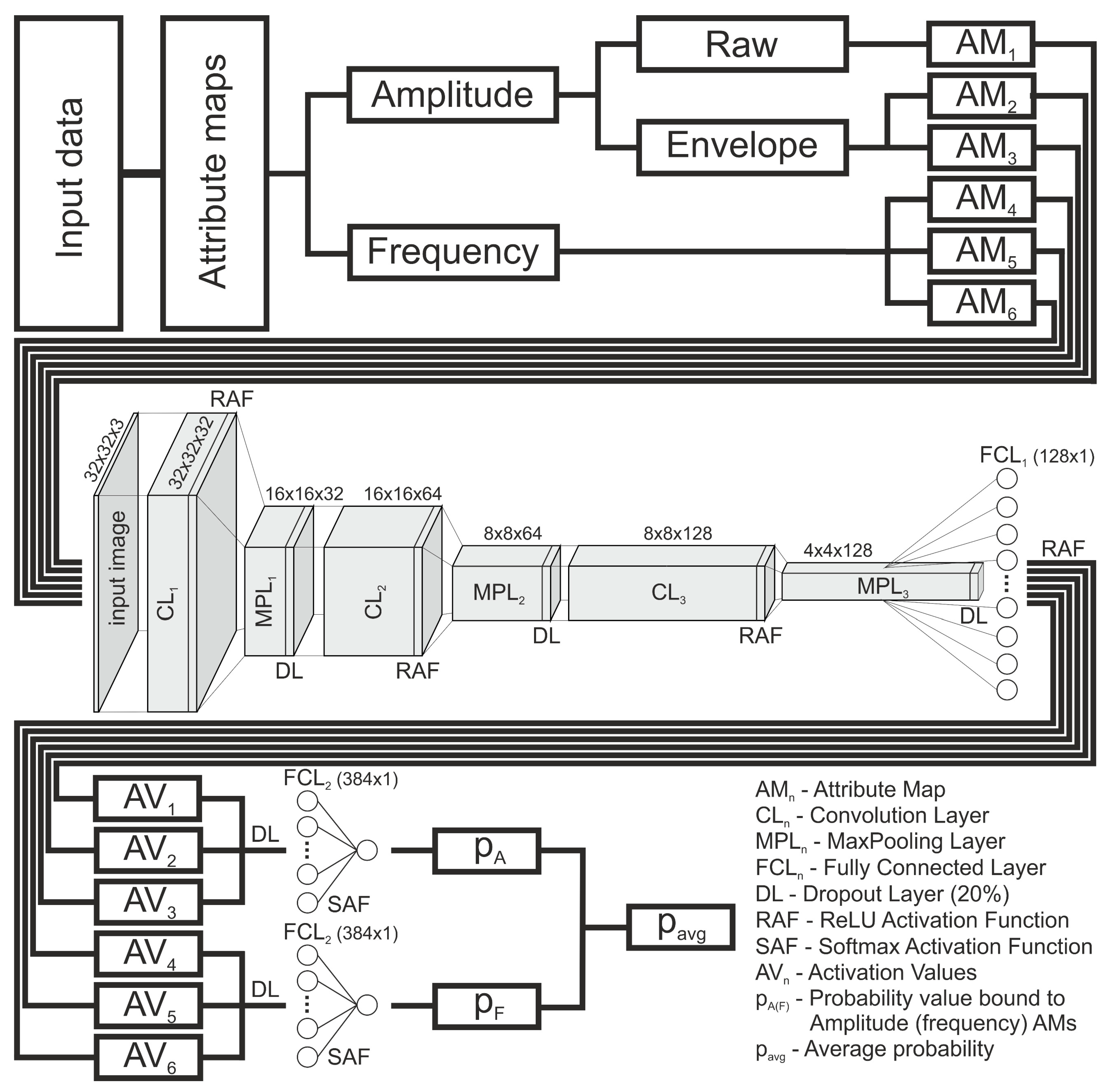
3.2. CNN Architecture
3.3. Building a Prediction Pipeline
4. Results
4.1. Metrics
4.2. Prediction
4.3. Deep Embedded Clustering
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AM | Attribute Map |
| ANSI | Ambient Noise Seismic Interferometry |
| ATV | Attribute Value |
| AUC-PR | Area Under Curve—Precision-Recall |
| AV | Activation Value |
| AW | Air Wave |
| CCF | Cross-Correlation Functions |
| CNN | Convolutional Neural Network |
| CL | Convolution Layer |
| CPU | Central Processing Unit |
| CV | Cross-Validation |
| DAS | Distributed Acoustic Sensing |
| DL | Dropout Layer |
| EGF | Empirical Green’s Function |
| FCL | Fully Connected Layer |
| FN | False Negative |
| FP | False Positive |
| MEMS | Micro-Electromechanical System |
| ML | Machine Learning |
| MPL | MaxPooling Layer |
| PR | Precision-Recall |
| RAF | ReLU Activation Function |
| ReLU | Rectified Linear Unit |
| RGB | Red-Green-Black |
| RMS | Root-Mean-Square |
| ROC | Receiver Operator Characteristic |
| SAF | Softmax Activation Function |
| SGD | Stochastic Gradient Descent |
| SI | Seismic Interferometry |
| SNR | Signal-to-Noise Ratio |
| SVM | Support Vector Machine |
| SW | Surface Wave |
| TN | True Negative |
| TP | True Positive |
| t-SNE | t-Distributed Stochastic Neighbor Embedding |
| VGG | Visual Geometry Group |
| XGBoost | eXtreme Gradient Boosted Tree |
References
- Draganov, D.; Ruigrok, E. Passive seismic interferometry for subsurface imaging. In Encyclopedia of Earthquake Engineering; Beer, M., Patelli, E., Kougioumtzoglou, I., Au, I.S.-K., Eds.; Springer: New York, NY, USA, 2015; pp. 1–13. [Google Scholar] [CrossRef]
- Campillo, M. Phase and correlation of ‘random’ seismic fields and the reconstruction of the Green function. Pure Appl. Geophys. 2006, 163, 475–502. [Google Scholar] [CrossRef]
- Sánchez-Sesma, F.J.; Pérez-Ruiz, J.A.; Luzón, F.; Campillo, M.; Rodríguez-Castellanos, A. Diffuse fields in dynamic elasticity. Wave Motion 2008, 45, 641–654. [Google Scholar] [CrossRef]
- Wapenaar, K.; Van Der Neut, J.; Ruigrok, E.; Draganov, D.; Hunziker, J.; Slob, E.; Snieder, R. Seismic interferometry by crosscorrelation and by multidimensional deconvolution: A systematic comparison. Geophys. J. Int. 2011, 185, 1335–1364. [Google Scholar] [CrossRef]
- Draganov, D.; Campman, X.; Thorbecke, J.; Verdel, A.; Wapenaar, K. Reflection images from ambient seismic noise. Geophysics 2009, 74, 63–67. [Google Scholar] [CrossRef]
- Ruigrok, E.; Wapenaar, K. Global-phase seismic interferometry unveils P-wave reflectivity below the Himalayas and Tibet. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Panea, I.; Draganov, D.; Almagro Vidal, C.; Mocanu, V. Retrieval of reflections from ambient noise recorded in Mizil area, Romania. Geophysics 2014, 79, Q31–Q42. [Google Scholar] [CrossRef]
- Cheraghi, S.; Craven, J.A.; Bellefleur, G. Feasibility of virtual source reflection seismology using interferometry for mineral exploration: A test study in the Lalor Lake volcanogenic massive sulphide mining area, Manitoba, Canada. Geophys. Prospect. 2015, 63, 833–848. [Google Scholar] [CrossRef]
- Quiros, D.A.; Brown, L.D.; Kim, D. Seismic interferometry of railroad induced ground motions: Body and surface wave imaging. Geophys. J. Int. 2016, 205, 301–313. [Google Scholar] [CrossRef]
- Roots, E.; Calvert, A.J.; Craven, J. Interferometric seismic imaging around the active Lalor mine in the Flin Flon greenstone belt, Canada. Tectonophysics 2017, 718, 92–104. [Google Scholar] [CrossRef]
- Dantas, O.A.B.; do Nascimento, A.F.; Schimmel, M. Retrieval of Body-Wave Reflections Using Ambient Noise Interferometry Using a Small-Scale Experiment. Pure Appl. Geophys. 2018, 175, 2009–2022. [Google Scholar] [CrossRef]
- Qian, R.; Liu, L. Imaging the active faults with ambient noise passive seismics and its application to characterize the Huangzhuang-Gaoliying fault in Beijing Area, northern China. Eng. Geol. 2020, 105520. [Google Scholar] [CrossRef]
- Cheraghi, S.; White, D.J.; Draganov, D.; Bellefleur, G.; Craven, J.A.; Roberts, B. Passive seismic reflection interferometry: A case study from the Aquistore CO2 storage site, Saskatchewan, Canada. Geophysics 2017, 82, B79–B93. [Google Scholar] [CrossRef]
- Cao, H.; Askari, R. Comparison of seismic interferometry techniques for the retrieval of seismic body waves in CO2 sequestration monitoring. J. Geophys. Eng. 2019, 16, 1094–1115. [Google Scholar] [CrossRef]
- Wapenaar, K.; Draganov, D.; Snieder, R.; Campman, X.; Verdel, A. Tutorial on seismic interferometry: Part 1—Basic principles and applications. Geophysics 2010, 75, 75A195–75A209. [Google Scholar] [CrossRef]
- Mulargia, F. The seismic noise wavefield is not diffuse. J. Acoust. Soc. Am. 2012, 131, 2853–2858. [Google Scholar] [CrossRef] [PubMed]
- Draganov, D.; Campman, X.; Thorbecke, J.W.; Verdel, A.; Wapenaar, K. Seismic exploration-scale velocities and structure from ambient seismic noise (>1 Hz). J. Geophys. Res. Solid Earth 2013, 118, 4345–4360. [Google Scholar] [CrossRef]
- Laine, J.; Mougenot, D. A high-sensitivity MEMS-based accelerometer. Lead. Edge 2014, 33, 1234–1242. [Google Scholar] [CrossRef]
- Martin, E. Passive Imaging and Characterization of the Subsurface with Distributed Acoustic Sensing. Ph.D. Dissertation, Stanford University, Stanford, CA, USA, June 2018. [Google Scholar]
- Hansen, S.M.; Schmandt, B. Automated detection and location of microseismicity at Mount St. Helens with a large-N geophone array. Geophys. Res. Lett. 2015, 42, 7390–7397. [Google Scholar] [CrossRef]
- Karplus, M.; Schmandt, B. Preface to the Focus Section on Geophone Array Seismology. Seismol. Res. Lett. 2018, 89, 1597–1600. [Google Scholar] [CrossRef]
- Chamarczuk, M.; Malinowski, M.; Nishitsuji, Y.; Thorbecke, J.; Koivisto, E.; Heinonen, S.; Juurela, S.; Mężyk, M.; Draganov, D. Automatic 3D illumination-diagnosis method for large-N arrays: Robust data scanner and machine-learning feature provider. Geophysics 2019, 84, 1–48. [Google Scholar] [CrossRef]
- Huot, F.; Martin, E.R.; Biondi, B. Automated ambient-noise processing applied to fiber-optic seismic acquisition (DAS). In SEG Technical Program Expanded Abstracts; Society of Exploration Geophysicists: Tusla, OK, USA, 2018. [Google Scholar] [CrossRef]
- Dumont, V.; Tribaldos, V.R.; Ajo-Franklin, J.; Wu, K. Deep Learning for Surface Wave Identification in Distributed Acoustic Sensing Data. arXiv 2020, arXiv:2010.10352. [Google Scholar]
- Jakkampudi, S.; Shen, J.; Li, W.; Dev, A.; Zhu, T.; Martin, E.R. Footstep detection in urban seismic data with a convolutional neural network. Lead. Edge 2020, 39, 654–660. [Google Scholar] [CrossRef]
- Perol, T.; Gharbi, M.; Denolle, M. Convolutional neural network for earthquake detection and location. Sci. Adv. 2018, 4, e1700578. [Google Scholar] [CrossRef] [PubMed]
- Ross, Z.E.; Meier, M.-A.; Hauksson, E. P Wave Arrival Picking and First-Motion Polarity Determination With Deep Learning. J. Geophys. Res. Solid Earth 2018, 123, 5120–5129. [Google Scholar] [CrossRef]
- Ross, Z.E.; Meier, M.; Hauksson, E.; Heaton, T.H. Generalized Seismic Phase Detection with Deep Learning. Bull. Seismol. Soc. Am. 2018, 108, 2894–2901. [Google Scholar] [CrossRef]
- Zhu, W.; Beroza, G.C. PhaseNet: A Deep-Neural-Network-Based Seismic Arrival Time Picking Method. Geophys. J. Int. 2018, 216, 261–273. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Zhu, W.; Sheng, Y.; Beroza, G.C. CRED: A Deep Residual Network of Convolutional and Recurrent Units for Earthquake Signal Detection. Sci. Rep. 2019, 9, 10267. [Google Scholar] [CrossRef]
- Ramin, M.H.D.; Honn, K.; Ryan, V.; Brindley, S. Seismic Event and Phase Detection Using Time–Frequency Representation and Convolutional Neural Networks. Seismol. Res. Lett. 2019, 90, 481–490. [Google Scholar] [CrossRef]
- Wang, J.; Xiao, Z.; Liu, C.; Zhao, D.; Yao, Z. Deep Learning for Picking Seismic Arrival Times. J. Geophys. Res. Solid Earth 2019, 124, 6612–6624. [Google Scholar] [CrossRef]
- Zhu, L.; Peng, Z.; McClellan, J.; Li, C.; Yao, D.; Li, Z.; Fang, L. Deep learning for seismic phase detection and picking in the aftershock zone of 2008 M7.9 Wenchuan Earthquake. Phys. Earth Planet. Int. 2019, S0031920118301407. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Ellsworth, W.L.; Zhu, W.; Chuang, L.Y.; Beroza, G.C. Earthquake transformer—an attentive deep-learning model for simultaneous earthquake detection and phase picking. Nat. Commun. 2020, 11, 3952. [Google Scholar] [CrossRef] [PubMed]
- Seydoux, L.; Balestriero, R.; Poli, P.; de Hoop, M.; Campillo, M.; Baraniuk, R. Clustering earthquake signals and background noises in continuous seismic data with unsupervised deep learning. Nat. Commun. 2020, 11, 3972. [Google Scholar] [CrossRef] [PubMed]
- Schimmel, M.; Stutzmann, E.; Gallart, J. Using instantaneous phase coherence for signal extraction from ambient noise data at a local to a global scale. Geophys. J. Int. 2010, 184, 494–506. [Google Scholar] [CrossRef]
- Groos, J.C.; Bussat, S.; Ritter, J.R.R. Performance of different processing schemes in seismic noise cross-correlations. Geophys. J. Int. 2011, 188, 498–512. [Google Scholar] [CrossRef]
- Vidal, C.A.; Draganov, D.; van der Neut, J.; Drijkoningen, G.; Wapenaar, K. Retrieval of reflections from ambient noise using illumination diagnosis. Geophys. J. Int. 2014, 198, 1572–1584. [Google Scholar] [CrossRef]
- Zhou, C.; Xi, C.; Pang, J.; Liu, Y. Ambient noise data selection based on the asymmetry of cross-correlation functions for near surface applications. J. Appl. Geophys. 2018, 159, 803–813. [Google Scholar] [CrossRef]
- Li, Z.; Peng, Z.; Hollis, D.; Zhu, L.; McClellan, J. High-resolution seismic event detection using local similarity for Large-N arrays. Sci. Rep. 2018, 8, 1646. [Google Scholar] [CrossRef]
- Olivier, G.; Brenguier, F.; Campillo, M.; Lynch, R.; Roux, P. Body-wave reconstruction from ambient seismic noise correlations in an underground mine. Geophysics 2015, 80, KS11–KS25. [Google Scholar] [CrossRef]
- Nakata, N.; Chang, J.P.; Lawrence, J.F.; Boué, P. Body wave extraction and tomography at Long Beach, California, with ambient-noise interferometry. J. Geophys. Res. Solid Earth 2015, 120, 1159–1173. [Google Scholar] [CrossRef]
- Pang, J.; Cheng, F.; Shen, C.; Dai, T.; Ning, L.; Zhang, K. Automatic passive data selection in time domain for imaging near-surface surface waves. J. Appl. Geophys. 2019, 162, 108–117. [Google Scholar] [CrossRef]
- Afonin, N.; Kozlovskaya, E.; Nevalainen, J.; Narkilahti, J. Improving quality of empirical Greens functions, obtained by crosscorrelation of high-frequency ambient seismic noise. Solid Earth 2019, 10, 1621–1634. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Japkowicz, N.; Stephen, S. The class imbalance problem: A systematic study. Intell. Data Anal. 2002, 6, 429–449. [Google Scholar] [CrossRef]
- Buda, M.; Maki, A.; Mazurowski, M.A. A systematic study of the class imbalance problem in convolutional neural networks. Neural Netw. 2018, 106, 249–259. [Google Scholar] [CrossRef] [PubMed]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going Deeper with Convolutions. arXiv 2014, arXiv:1409.4842. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.-J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Miami, FL, USA, 25 June 2009. [Google Scholar] [CrossRef]
- Gu, J.; Wang, Z.; Kuen, J.; Ma, L.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.; Wang, G.; Cai, J.; et al. Recent advances in convolutional neural networks. Pattern Recognit. 2008, 77, 354–377. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.I.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learning Res. 2014, 15, 1929–1958. [Google Scholar] [CrossRef]
- Chollet, F. et al. Keras. 2015. Available online: http://keras.io (accessed on 10 December 2020).
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. arXiv 2015, arXiv:1603.04467. Available online: http://www.tensorflow.org (accessed on 10 December 2020).
- Sokolova, M.; Japkowicz, N.; Szpakowicz, S. Beyond Accuracy, F-Score and ROC: A Family of Discriminant Measures for Performance Evaluation. In Proceedings of the AI 2006: Advances in Artificial Intelligence, Hobart, Australia, 4–8 December 2006; pp. 1015–1021. [Google Scholar] [CrossRef]
- Davis, J.; Goadrich, M. The relationship between Precision-Recall and ROC curves. In Proceedings of the 23rd International Conference on Machine Learning—ICML ’06, Pittsburgh, PA, USA, 25–29 June 2006. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. Assoc. Comput. Mach. 2016, 785–794. [Google Scholar] [CrossRef]
- Zhang, L.; Zhan, C. Machine Learning in Rock Facies Classification: An Application of XGBoost. In Proceedings of the International Geophysical Conference, Qingdao, China, 17–20 April 2017. [Google Scholar] [CrossRef]
- Mężyk, M.; Malinowski, M. Multi-pattern algorithm for first-break picking employing an open-source machine learning libraries. J. Appl. Geophys. 2019, 170, 103848. [Google Scholar] [CrossRef]
- Zhang, X.; Nguyen, H.; Bui, X.-N.; Tran, Q.-H.; Nguyen, D.-A.; Bui, D.T.; Moayedi, H. Novel Soft Computing Model for Predicting Blast-Induced Ground Vibration in Open-Pit Mines Based on Particle Swarm Optimization and XGBoost. Nat. Res. Res. 2019, 29, 711–721. [Google Scholar] [CrossRef]
- Ren, C.X.; Peltier, A.; Ferrazzini, V.; Rouet-Leduc, B.; Johnson, P.A.; Brenguier, F. Machine Learning Reveals the Seismic Signature of Eruptive Behavior at Piton de la Fournaise Volcano. Geophys. Res. Lett. 2020. [Google Scholar] [CrossRef] [PubMed]
- Timofeev, A.V.; Groznov, D.I. Classification of Seismoacoustic Emission Sources in Fiber Optic Systems for Monitoring Extended Objects. Optoelectronics. Instrum. Data Process. 2020, 56, 50–60. [Google Scholar] [CrossRef]
- Zeiler, M.D.; Fergus, R. Visualizing and Understanding Convolutional Networks. In Lecture Notes in Computer Science; Springer: New York, NY, USA, 2014; pp. 818–833. [Google Scholar] [CrossRef]
- van der Maaten, L.; Hinton, G. Visualizing Data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Linderman, G.C.; Steinerberger, S. Clustering with t-SNE, Provably. SIAM J. Math. Data Sci. 2019, 1, 313–332. [Google Scholar] [CrossRef]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Cai, J.; Luo, J.; Wang, S.; Yang, S. Feature selection in machine learning: A new perspective. Neurocomputing 2018, 300, 70–79. [Google Scholar] [CrossRef]

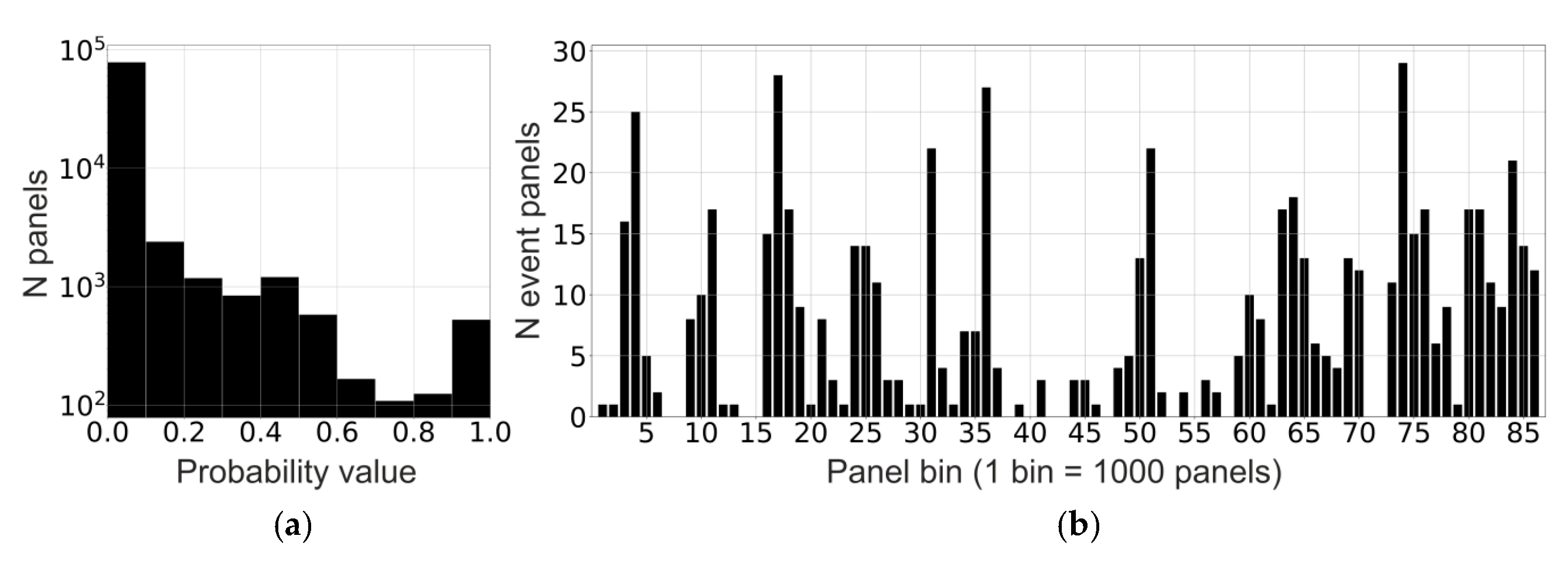
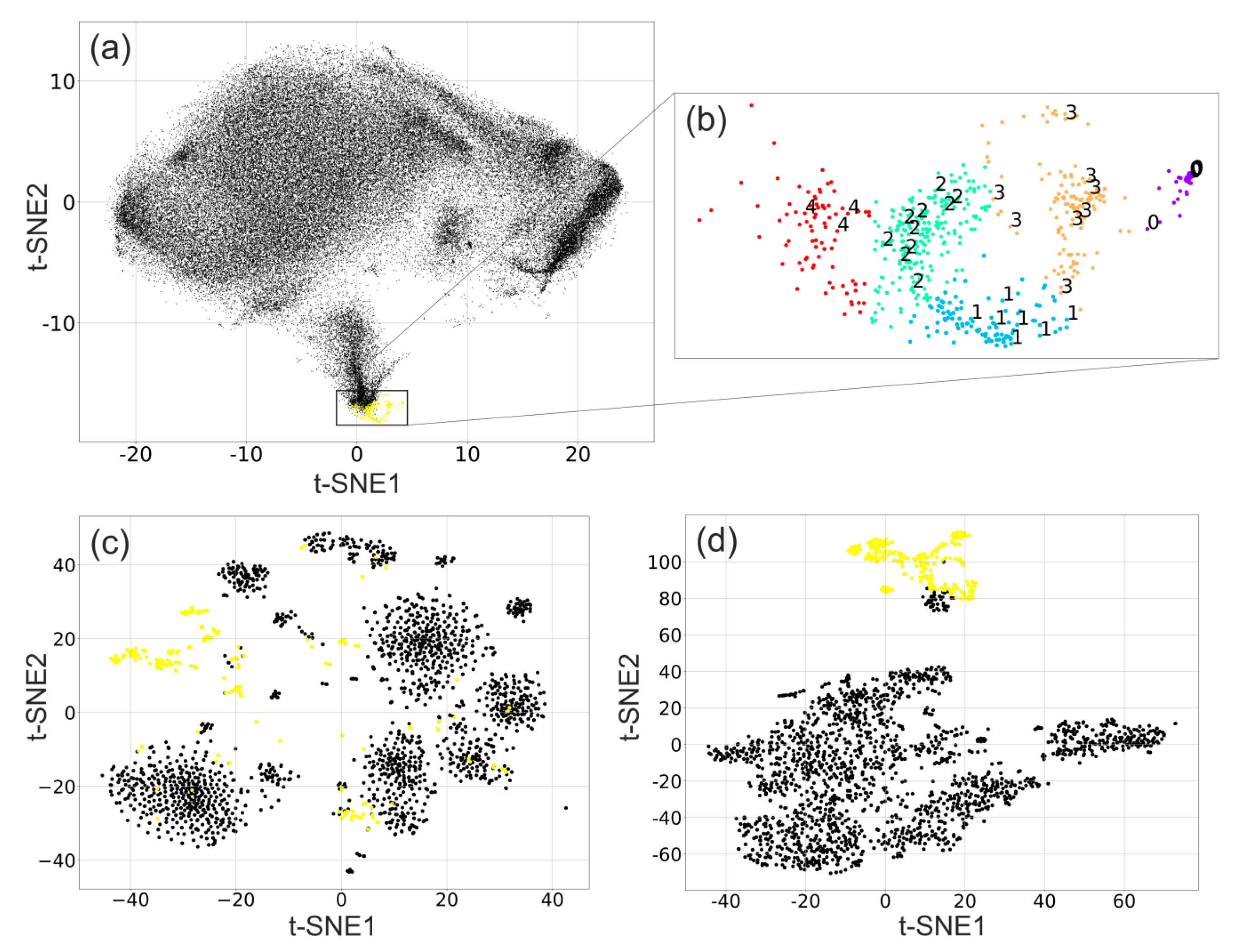
| Parameter | Value/Type |
|---|---|
| Input image size | 32 × 32 px × 3 channels (RGB) |
| Number of epochs | 200 |
| Batch size | 16 |
| Kernel initializer | He uniform |
| Activation function | ReLU |
| Classification function | Softmax |
| Loss function | Categorical cross-entropy |
| Dropout rate | 0.2 |
| Optimizer | SGD |
| Learning rate | 0.001 |
| Momentum | 0.9 |
| Predicted Class | ||
|---|---|---|
| Actual Class | True Negative (TN) | False Positive (FP) |
| False Negative (FN) | True Positive (TP) | |
| Amplitude-Based CNN | Frequency-Based CNN | Ensemble-Based CNN | Ensemble-Based XGBoost | |
|---|---|---|---|---|
| F1 | 0.890 | 0.894 | 0.963 | 0.849 |
| AUC-PR | 0.961 | 0.964 | 0.997 | 0.939 |
| Ensemble-Based CNN | Ensemble-Based XGBoost | ||
|---|---|---|---|
| TN = 1653 | FP = 16 | TN = 1657 | FP = 12 |
| FN = 2 | TP = 229 | FN = 51 | TP = 180 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mężyk, M.; Chamarczuk, M.; Malinowski, M. Automatic Image-Based Event Detection for Large-N Seismic Arrays Using a Convolutional Neural Network. Remote Sens. 2021, 13, 389. https://doi.org/10.3390/rs13030389
Mężyk M, Chamarczuk M, Malinowski M. Automatic Image-Based Event Detection for Large-N Seismic Arrays Using a Convolutional Neural Network. Remote Sensing. 2021; 13(3):389. https://doi.org/10.3390/rs13030389
Chicago/Turabian StyleMężyk, Miłosz, Michał Chamarczuk, and Michał Malinowski. 2021. "Automatic Image-Based Event Detection for Large-N Seismic Arrays Using a Convolutional Neural Network" Remote Sensing 13, no. 3: 389. https://doi.org/10.3390/rs13030389
APA StyleMężyk, M., Chamarczuk, M., & Malinowski, M. (2021). Automatic Image-Based Event Detection for Large-N Seismic Arrays Using a Convolutional Neural Network. Remote Sensing, 13(3), 389. https://doi.org/10.3390/rs13030389