Abstract
An airgun source in a water reservoir has been developed in the past decade as a green active source that had been proven effective to derive short-term subsurface structural changes. However, seasonal water level fluctuation in the reservoir affects the airgun signal, and thus whether the airgun signals can be used to derive robust seasonal variation in subsurface structure remains unclear. We use the airgun data observed in the Binchuan basin to estimate the seasonal variation of seismic travel time and compare the results with those derived from ambient noise data in the same frequency band. Our main observation is that seasonal change from airgun is negatively correlated to the variation of dominant frequency and water table fluctuation in the reservoir. One possible explanation is that water table fluctuation in the reservoir affects the dominant frequency of the airgun signal and causes significant phase shift. We also compute the travel time changes in P-wave from the empirical Green’s function after deconvolving the waveforms from a reference station that is 50 m from the airgun source. The dominant frequency after deconvolution still shows seasonal variation and correlates inversely to the travel time changes, suggesting that deconvolution cannot completely eliminate the source effect on travel time changes. We also use ambient noise cross-correlation to retrieve coda waves and then derive travel time changes in monthly stacked cross-correlations relative to a yearly average cross-correlation. We observe that seismic travel time increases to its local maximum in the end of August. The travel time changes lag behind the precipitation for about one month. We apply a poroelastic physical model to explain seismic travel time changes and find that a combined effect from precipitation and evaporation might induce the seasonal changes as shown in the ambient noise data. However, the pattern of travel time changes from the airgun differs from that from ambient noise, reflecting the strong effects of airgun source property changes. Therefore, we should be cautious to derive long-term subsurface structural variation from the airgun source and put more attention on stabilizing the dominant frequency of each excitation in the future experiments.
1. Introduction
Extensive field observations and lab experiments [1,2,3,4,5] have suggested that slowly evolving, low-amplitudes phases usually appear before the onset of natural hazards such as earthquakes, landslides, and volcanic eruptions. A better understanding of the related crustal deformation and responsible mechanisms of these phases are critical for effective early warnings of such hazards. Crust deforms under the loading of tectonic and climatological forces. In order to precisely measure the deformation from tectonic loading, we need to remove deformation related to climatological forces. Seismic velocity changes are usually used as a proxy to quantitatively understand crustal deformation. Temporal changes in seismic velocity can reflect fault zone co-seismic damage and post-seismic healing [6,7,8], volcanic eruption [6,9], groundwater level changes [10,11,12], temperature and atmospheric pressure variations [13,14,15,16,17,18], and solid earth and oceanic tidal deformation [17,19,20,21]. Thus, high temporal resolution monitoring and high precision measurements of seismic velocity changes are necessary.
Seismic velocity changes have been estimated through measuring travel time or phase difference from active sources including explosion [21,22,23,24,25], electronic hammer [26], airguns [18,27,28], repeating earthquakes [29,30,31,32,33,34], and dephasing of ambient noise cross-correlations (CCs) [6,35]. Among these methods, temporal changes in ambient noise amplitude and heterogeneous distribution of noise sources [12,17] may introduce a bias to the measurements of seismic velocity changes. The uncertainties in locations of repeating earthquakes might cause concern to the reliability of the measurements of seismic velocity changes. Explosions are not environmentally friendly and thus are not possible to operate in a populated region. In contrast, a large volume airgun array with stable signal excitation has been suggested as a better method to monitor seismic velocity changes [36].
Since 2011, a permanent seismic source [36,37,38] has been deployed in a water reservoir called Dayindian in Binchuan, Yunnan, China, to image velocity structure [39,40] and monitor seismic velocity changes [8,41,42,43,44]. It has been in routine operation since September 2012. The source is composed of four 2000 in3 LongLife airguns manufactured by Bolt Co., which can ignite sufficient seismic signal penetrating down to a depth of 10–20 km and propagating further to tens of kilometers away [36,38]. The four airguns were towed 2 m below the four corners of a 7 m × 7 m steel frame hanging under a tower crane [37]. The source causes negligible effects to the wildlife and local communities in terms of ground shaking and noise pollution [37].
We target the Binchuan region because it is located at the eastern margin of the collision zone between the Indian and Eurasia plates, accumulating strong shear strain [45], accommodating millions of people, and experiencing many devastating earthquakes. The largest one was the M7.75 Yongsheng earthquake which occurred on the Chenghai fault in 1515 [46,47]. This region has recorded numerous earthquakes, including eight events with magnitude greater than 7, and 70 with magnitudes greater than 6 [48].
Since the deployment of the airgun array, [18] used one-week hourly-shooting signals to observe diurnal and semidiurnal P- and S-wave velocity changes. They proposed that the thermal strains from air temperature changes are the primary cause. The reservoir water level did not fluctuate significantly during the one-week period. However, we must consider the effect of water level fluctuation when investigating seasonal changes in seismic velocity, as it may change a few meters from winter to summer. The authors of [49] observed that the dominant frequency of airgun data correlates to the changes in water level in the reservoir, which may potentially affect measurements of travel time changes. In this study, we use airgun data in the frequency ranges of 2–6 Hz to compute variation of the dominant frequency and amplitude, derive seasonal changes in seismic velocity, and explore how water level fluctuation of the reservoir affects seismic velocity changes through investigating the correlation between seismic velocity changes and variations of the dominant frequency and amplitude. We also use ambient noise in the same frequency range to obtain seasonal changes in seismic velocity for coda waves and compare them with velocity changes for body waves.
2. Airgun Data
The Binchuan airgun array shot a few tests in 2011 and began to operate routinely after September 2012. On average, a few shots were made every day (Figure S1), accumulating hundreds to thousands of excitations per year. From June to August, the water level in the Dayindian reservoir is too low to excite airgun shot because of irrigation for farming (Figure S1). However, in 2016, water level fluctuation in the reservoir did not affect the airgun operation and the average number of daily excitations is also higher than that in other years. We therefore use the airgun data in 2016 to investigate the seasonal variation of seismic arrival time of P- and S-waves.
2.1. Source Characteristics
Forty portable three-component short-period stations have been deployed since the operation of the airgun source, and we selected 14 stations with clear body wave arrivals to compute travel time change (Figure 1). Each station is equipped with a Güralp 40 T sensor (a flat response from 0.5–100 Hz) and a RefTek 130 data logger. We convert daily data from MiniSEED to sac and merge them if there is more than one segment in a day. We then extract all airgun signals from the original dataset, starting from the shooting time to 20 s after that.
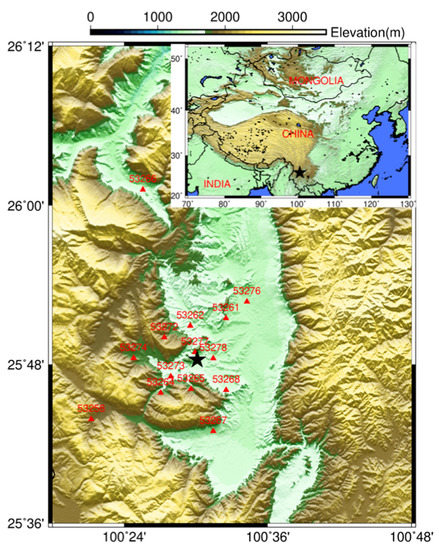
Figure 1.
Short-period stations (red triangle) installed during the airgun source excitation experiment. Red text above the triangle denotes the station name. The black stars mark the location of the airgun array.
We first inspect the waveform recorded at the nearest station CKT, which is ~50 m from the airgun source. A near-field airgun wavelet is composed of primary pulse and bubble pulse (Figure 2). Primary pulse is generated by high-pressure gas releasing into the water and is usually in high energy with a wide bandwidth, e.g., 7 to 30 Hz (Figure 2). It was mostly used in shallow oil and gas exploration. In comparison, bubble pulse is generated by the oscillation of bubbles after high-pressure gas was released into the water. It is in a relatively low-frequency band from 2 to 6 Hz [36,38], so it was often used in deep seismic exploration (Figure 2).
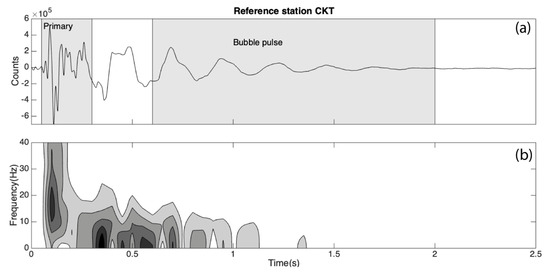
Figure 2.
Original near-field waveform (a) recorded by a reference station CKT. The signal from 0 to 0.3 s is the primary pulse (gray area marked as primary). The signal from 0.6 to 2 s is bubble pulse. (b) The spectrogram of the waveform in (A). The primary pulse is in high energy and in a wide bandwidth, e.g., 7–30 Hz. The bubble pulse is in a relatively low frequency bandwidth, 2–6 Hz.
We compute power spectral density of the bubble pulse and define the frequency with the maximum power spectral density as the dominant frequency. We observe that the dominant frequency of the bubble pulse decreases in the summer at the reference station (Figure 3a) and others (Figure 3b,c and Figure S2), similar to the reports in [49]. In fact, the towing depth of the airgun array decreases in summer when water in the reservoir was used for farming. An experimental study from [50] also indicates that the dominant frequency decreases when the towing depth of the airgun array decreases. Such variation in frequency content is quite common. For instance, at a global scale, seasonal or multi-decadal variation of storm activities have been reported to cause long-term variation in noise frequency content [51,52]. It has been suggested that temporal variation of frequency content can cause apparent seismic velocity change [53]. In addition to the dominant frequency, we also observe that the maximum amplitude in the bubble pulse window decreases in the summer, which is similar to the reports in [50].
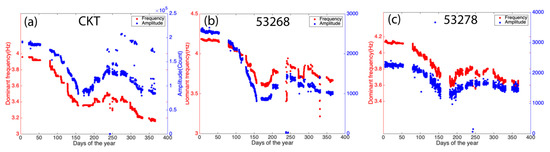
Figure 3.
Seasonal variation of the dominant frequency (red) and P-wave signal amplitude (blue) for the reference station (a) and other receivers (b,c). They decrease in the summer and correlate to each other.
2.2. Airgun Data Quality
We interpolate the airgun signals to 0.001 s/sample and bandpass all waveforms with a 2–6 Hz filter, the dominant frequency band of the bubble pulse [38]. With the single shot data, we can observe clear P-wave and S-wave arrivals up to 30 km with apparent velocities of 5.5 km/s and 2.8 km/s, respectively (Figure 4), consistent with previous observations [38].
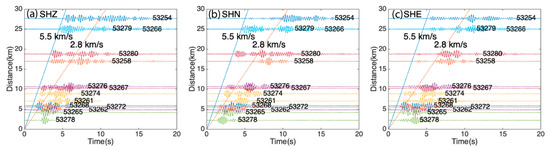
Figure 4.
Airgun signals within 30 km from the excitation site. We observe P-wave arrivals and S-wave arrivals with apparent P- and S-wave velocities of 5.5 km/s and 2.8 km/s, respectively. Text near the tail of each signal denotes the station name.
When inspecting the waveforms throughout the entire year, we observe strong clock drifts in the reference station CKT and other receivers, approximately from day 230 in 2016 (Figure 5a,c and Figure S3). Because the differential times are nearly the same among all stations (Figure S4), it is mostly attributed to the timing log system of the airgun array. In additional to that, sensors in the 53273 and 53277 also have timing problem. To fix the clock drift, we determine P-wave arrival time at each station through a polarization analysis introduced by [54]. For a three-component airgun waveform in the passband of 2–30 Hz at station 53278 (Figure 6a), we first convert each component to an analytic signal.
in which , , and are vertical, east-west and north-south components. represents Hilbert transform. is . We then define a 0.02 s moving window and a 0.01 s moving step and compute the covariance matrix between windowed three-components , , and as:
where the asterisks represent complex conjugation. We compute three eigenvalues , , and from the covariance matrix and calculate the rectilinearity R [55,56] through:
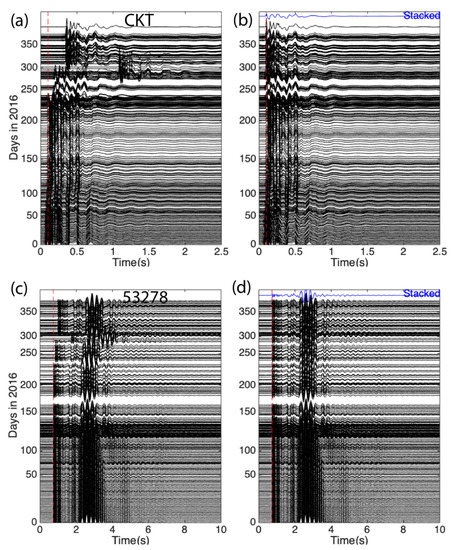
Figure 5.
Waveform cross section of vertical components at the reference station, CKT (a), and one receiver 53278 (c). Waveforms are aligned with the original time of each shot (b,d). Strong clock drifts in the reference station and receivers start around days 230.
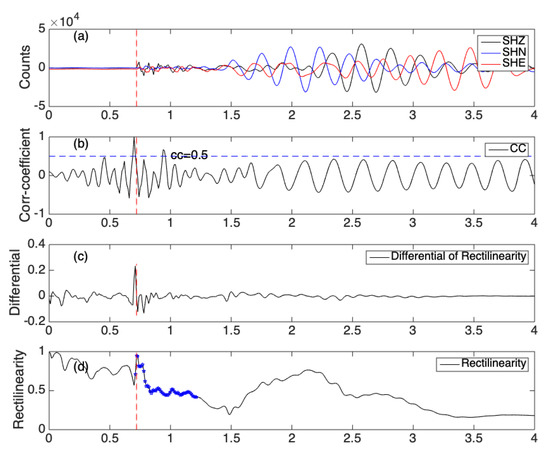
Figure 6.
Computation of the rectilinearity of one shot at the station 53278. (a) Three components of one airgun shot. (b) Correlation coefficient between a P-wave template and the vertical SHZ component. (c) Maximum value of differential of rectilinearity constrains the rough arrival time of P-wave. (d) Rectilinearity of the vertical component. The rectilinearity of P-wave is close to 1.
It has a value of 1 when the signal is linearly polarized and a value of 0 when it is unpolarized.
Due to interference of noise in the airgun signals, we cannot directly determine the P-wave arrival time from the maximum of rectilinearity in different moving windows. We first select a P-wave template and compute moving window correlation coefficient between the template and each raw vertical waveform. We then select points with correlation coefficient greater than 50% of the maximum value (Figure 6b). Among these points, we determine an arrival time with the maximum differential rectilinearity (Figure 6c). From the arrival time to 0.5 s after it, we finally determine the P-wave arrival time from the maximum value of the rectilinearity (Figure 6d).
As subtle subsurface changes cannot be reflected by direct P wave arrival changes, we then align P-wave arrivals through correcting travel time difference from the first shot. The airgun waveforms are significantly improved after clock drift correction (Figure 5b,d). We still observe that S-wave coda at 3–6 s (Figure 5d) varies in amplitude and duration, which is attributed to the effect of changing airgun array.
We then stack all the waveform at each station for the entire year as the reference waveform (Figure 5b,d), and derive differential time by a modified moving-window cross-spectrum method that will be introduced in the following section. We cannot use the entire time-series to compute delay time between one single shot and the reference because of the changes in the airgun array. We thus investigate how delay time changes for the time-series between P-wave initial arrival and S-coda wave, which is 0.7–3 s in Figure 5d.
3. A Modified Moving-Window Cross-Spectrum method
We follow the method of Moving-Window Cross-Spectral (MWCS) [30,57] to compute the phase shift between stacked reference and current airgun signals. For a reference and a current airgun signal at station CKT with the center time at 0.5 s and window length of 0.6 s (Figure 7a), two segments are mean-adjusted and cosine-tapered before transforming into the spectral domain. The cross-spectrum, , between the two segments is constructed as:
where and are Fourier-transformed representations of the windowed reference and current signals. denotes complex conjugation. is the interested frequency range. We can represent the cross-spectrum, , as:
where represents frequency-dependent phase shift of a current signal relative to the reference one. represents a constant phase shift.
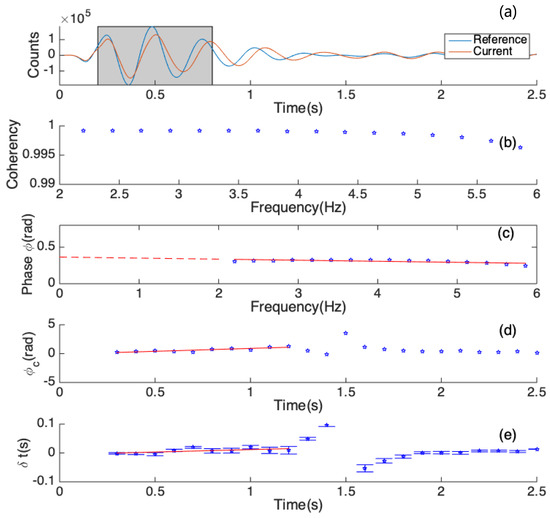
Figure 7.
Procedures of the moving-window-cross-spectrum to compute the delay time. (a) Airgun segments center at 0.5 s with length of 0.6 s from the reference and a current airgun signal of station CKT in the passband of 2 to 6 Hz. The gray area marks the selected segments. (b) The cross-coherency between two selected signals. (c) Phase change over the interested frequency range. The slope determines the delay time, and the intercept constrains a constant phase shift. We can estimate a delay time from the frequency-dependent phase shift . We can also compute a frequency-independent phase shift from the intercept of the linear regression. (d) The constant phase shift over different moving window. Steps in (a–c) estimate one point centering at 0.5 s. Looping through different moving window, we can estimate constant phase shift in different travel time . (e) Similar to (d) but for delay time.
To quantify the reliability of the estimations of phase shift, and , we compute the cross-coherence (Figure 7b) between their energy densities as:
where the overlines represent 5-point smoothing.
The values of and can be derived from the unwrapped phase of the cross-spectrum (Figure 7c). The frequency-dependent phase shift between the reference and the current airgun signals is linearly proportional to frequency so that the cross-spectrum can also be represented as:
where the time delay is estimated from the slope of a weighted linear regression of phase in frequency of interest. We estimate a constant phase shift from the intercept of the linear regression. The slope (Figure 7c) is estimated as:
where is number of samples within the frequency range. The weight function for linear regression at the sample in the frequency of interest is:
The associated error for the slope is:
in which is the squared misfit of the data to the modelled phase shift.
All the above steps are used to compute one data point at the time 0.5 s in Figure 7d,e. If we obtain delay-time and constant phase shift estimations for all moving windows, we can further estimate how they vary with the travel time. For each measurement with window centered at second,
where b corresponds to the relative time change . The estimation for b is:
where and The error of the slope is
4. Results
4.1. δt/t Derived Directly from Corrected Airgun Waveforms
A critical point in the MWCS analysis is the selection of the length of the moving window. The window length needs to be short to satisfy a constant time shift and to obtain a relative high temporal resolution. On the other hand, the window length needs to be long enough to ensure an accurate measurement, as well as avoid cycle skipping. Thus, the tradeoff between the temporal resolution and the accuracy of seismic velocity measurements can help to constrain the window length. Previous studies [17,58,59] suggested that the window length needs to be equal or larger than the longest period of interest, which is 0.5 s in this study. We computed of P-wave at station 53278 (Figure S5) using different lengths (i.e., 0.5, 0.6, 0.7, 0.8 s) of moving windows and found that the estimation of is more stable when the moving window is longer than 0.5 s. We thus use a moving window of 0.6 s to compute the differential time for all stations.
The other important parameter in linear regression of delay time over moving window is the window of P-wave arrivals (Figure S6). Rather than selecting the begin and end time of P-wave from the raw airgun signal, we handpick them from the diagram of delay time verse travel time. We first visually inspect and determine the rough arrival time of P-waves. We then select the begin and end time of P-wave based on the linearity of delay time in different moving windows.
Because the arrivals of S-wave are not as obvious as those of P-waves (Figure 4), we only investigate how the arrival time of P- and P-coda wave changes. We observe that fluctuates between −5% to 5% for all stations (Figure 8) The error bars represent standard deviation of in one day. For measurements of P-wave arrivals on uncorrected waveforms, we observe strong uncertainties after the day 220 (Figure S7). After clock drift correction, measurements show smoother seasonal change. Considering the uncertainty of correction imposed through this procedure, we conclude that measurements are more reliable for days before 220 than after. Although scattering varies at different stations, nearly all of them show an abrupt increase near days 150 and decrease around days 220 (Figure 8). For closer stations from the source, such as 53277 and 53278, measurements on signals shot within the same day are constrained in a narrow range. For farther stations, such as 53276, 53264 and 53258, measurements have relatively large uncertainty. We can barely observe clear P-wave arrivals for stations farther than 20 km except the station 53266, in which we observe clear travel time changes.
Figure 8.
Seismic travel time change for all stations. The with error bar increases from −5% in the winter to 5% in the summer. The error bars represent standard deviation of in one day.
4.2. δt/t Derived after Deconvolution of the CKT Waveform
Deconvolution has usually been used to remove the source effect of the airgun. For instance, [18] and [28] deconvolve a receiver station from a reference station to retrieve the empirical Green’s function, based on which they measure the relative time delay to compute diurnal and semidiurnal seismic velocity change in the Binchuan basin. However, when the airgun excitation conditions change significantly, including the towing depth and firing pressure, the deconvolution cannot eliminate the source effect [43]. To investigate whether deconvolution can eliminate the source effect, we apply a frequency-domain water level deconvolution method [18,60] to construct empirical Green’s functions and measure seismic velocity changes in P-wave.
in which and are Fourier spectrum of the receiver and source signals, respectively. We treat the recording at the reference station CKT as the source signal. The asterisk represents the complex conjugation. ranges from 0.01% to 1%, depending on the signal-to-noise ratio. We use a same value 0.01% as of [18] because of high-quality of our datasets. We finally invert frequency-domain Green’s function to time-domain time-series through inverse Fourier transform. If deconvolution can completely remove source effect, we should observe constant dominant frequency within one-year cycles, and seasonal change should be in the same magnitude with these values measured from ambient noise, which is usually less than 1%. After deconvolution, we observe that the dominant frequency of P-wave in these empirical Green’s functions correlates inversely to the delay time change (Figure 9). The dominant frequency still shows seasonal variation, which causes obvious phase shift and affects the differential time calculation. Thus, deconvolution cannot eliminate the source effect on computation of differential time.
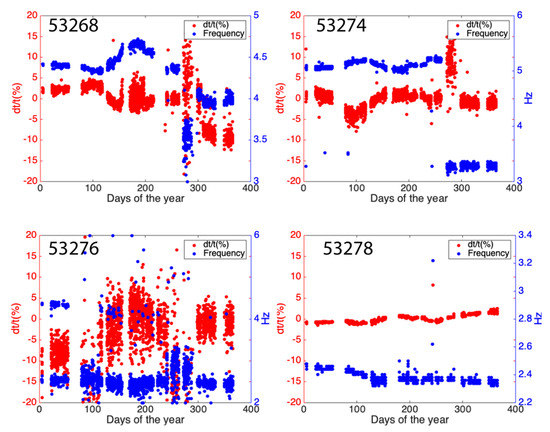
Figure 9.
P-wave seismic travel time change from empirical Green’s functions. After the deconvolution, we observe that the dominant frequency of P-wave in these empirical Green’s functions varies and correlate inversely to the delay time change.
To investigate the effect of deconvolution, we also compare of P-wave in original airgun waveforms and the empirical Green’s functions (Figure 10). We do not correct airgun data through procedures described above before retrieving of the empirical Green’s function. If all receivers and the reference station share exactly same clock drift, the deconvolution will eliminate the clock drift effect. If not, we might observe large uncertainties of measurements on Green’s functions. For station 53268, we observe that from airgun signals correlates inversely to that from the empirical Green’s functions. For other stations, they are positively correlated to each other. For the stations 53268 and 53274, we observe large uncertainty of at day 280 from the Green’s functions, which may reflect different clock drifts in these stations from the reference station CKT.
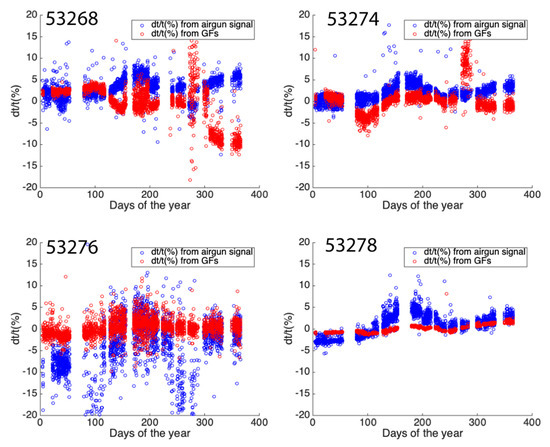
Figure 10.
Comparison of before and after the deconvolution.
5. Discussion
5.1. The Magnitude of Change from Airgun
Almost 5% travel time change in P-wave from airgun measurement is huge compared to ~0.2% S-wave velocity decrease after the 2004 Parkfield earthquake [7] and ~0.4% increase due to thermoelastic strain increase in the San Jacinto fault area [17]. However, it is in the same magnitude with observations from [61] who observed an abrupt 4% co-seismic velocity decrease for P wave after the Wenchuan mainshock. The reason why travel time change for P-wave is a lot larger than that for S-wave is still not well known. Before attempting to elucidate possible mechanisms for such discrepancy, we first need to inspect that our obtained reflects subsurface variation or not.
Seismic travel time changes computed from ambient noise cross-correlation is a typical method to monitor the magnitude and trend of property change in the shallow crust. In the following section, we use ambient noise cross-correlation to compute seasonal change in seismic coda wave and compare its magnitude and trend with these from airgun data. If the magnitude and trend of seismic travel time changes from airgun are similar to these from ambient noise, we may suggest that the seismic travel time changes in P-wave from airgun are related to crustal property change. Otherwise, they are related to the source.
5.2. δt/t from Ambient Noise
If seismic travel time change is due to shallow crust property change, we should observe similar trend of travel time change for P-wave from airgun and S-wave from ambient noise. To verify the travel time changes derived from the airgun source, we compute seismic travel time changes from ambient noise for coda waves in the passband of 2–6 Hz for 91 pairs of stations with the interstation distance less than 30 km (Figure 11 and Figure S6). We first scan MiniSEED data into MSNoise [62], downsample to 20 Hz, remove earthquakes and airgun signals by the root-mean-square (RMS) temporal normalization, and reduce the effect of heterogeneous distributions by spectral whitening. We then compute daily CCs and construct a monthly CC through stacking and averaging CCs in the past one month before the selected date. We stack and average CCs in the entire year to construct a reference CC. We finally compute the delay time between monthly CCs and the reference CC with a moving window of 3 s and a step of 1 s. We do not follow a similar monthly stacking procedure in the previous airgun computation because of high similarity of waveforms of airgun. If similar procedure is followed in the computation of travel time changes for airgun data, the final seasonal variation will be smoother, but the magnitude and trend will not change significantly. We define the starting time of the coda window as one time of interstation distance and specify the width of the window as 30 s.
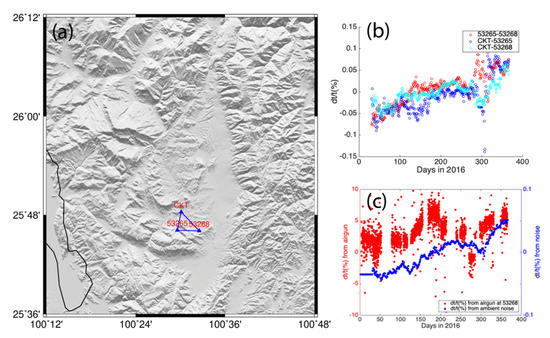
Figure 11.
dt/t(%) measurements (b) from ambient noise among CKT, 53265 and 53268 (a) and dt/t(%) measurements from airgun at the station 53268 (c).
We compare the trave time changes in three pairs among station CKT, 53265 and 53268 (Figure 11a,b). Similar travel time changes among all station pairs reflect the robustness of derived from ambient noise. Indeed, 29 out of 91 station pairs show similar magnitude of , from −0.1% to 0.1% (Figure S8b). Station pairs with seasonal changes in seismic travel time distribute in a broad region, up to 30 km from the reservoir (Figure S8a).
5.3. Possible Mechanism of from Ambient Noise
Travel time changes from ambient noise are usually related to environmental parameters changes, such as precipitation or water table fluctuation, temperature, and air pressure. To explore the correlation between the travel time changes and each environmental parameter (Figure 12), we requested such environmental data from one meteorological station in Lijiang, 150 km from the airgun source, from China Meteorological Data Service Center (http://data.cma.cn, accessed on 8 May 2021). We also compared the travel time changes to the water table fluctuation in the reservoir (Figure 12a).
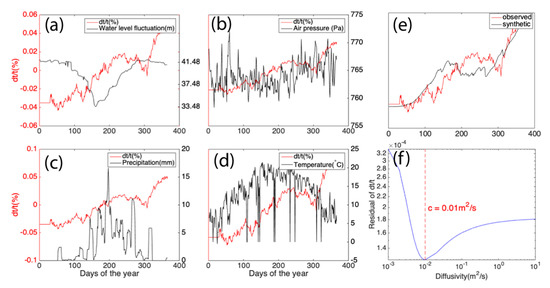
Figure 12.
Investigation of mechanism for seasonal changes in seismic travel time from ambient noise. Seismic travel time changes do not obviously correlate to the water table fluctuation of the reservoir (a), local precipitation (c), air pressure (b), and temperature (d). (e) Seismic travel time changes modeled from a poroelastic physical model match with the observed ones. (f) The optimal diffusivity is 0.01 m2/s for a minimum residual between synthetic and observed seismic velocity changes.
We first observe that air pressure increases and correlates to the travel time change in the long-term trend (Figure 12b), which is opposite to [15], showing that seismic velocity increased with air pressure. Temperature increases in the summer and usually causes seismic velocity increase with a time lag of months [17]. However, we do not observe clear short-term and long-term correlation between the temperature and travel time changes (Figure 12d). Precipitation affects travel time changes through water mass loading or pore pressure changes. Water mass loading affects the travel time instantaneously, but the pore pressure causes travel time change with months of time lag. We compute a 10-day moving average value for the precipitation (Figure 12c). We observe that major precipitation (Figure 12c) occurs at day 200 in the summer. Seismic travel time changes increase to a local maximum at day 230 and lag behind the maximum precipitation for about one month, which is similar to the observation in [12].
To investigate if the pore pressure affects seismic velocity change, we use a poroelastic model to estimate seasonal variation of seismic travel time in 2016. The authors of [63] proposed a solution for the one-dimension fully coupled diffusion equation, which was used for understanding seismic travel time changes [12,59,64]. Assuming water diffuses in the vertical direction with constant hydraulic diffusivity, we can compute the pore pressure changes at kilometer depth from the surface on day as:
in which is the number of time increments from the day of the rainfall to the time ; is the ground water load changes () at the sampled instant . We compute by using precipitation subtracting evaporation in 2016 (Figure S9). is set to 1 day in second. is the complementary error function. is the hydraulic diffusivity. The depth is set to 500 m, which is the maximum depth sensitivity of surface waves in the frequency ranges of 2–6 Hz. A mathematical transfer function from [12,59,64] to compute a synthetic seismic travel time change:
where is synthetic seismic travel time change; is the average over observed seismic travel time change. We find the optimal diffusivity value of (Figure 12f) through minimizing the residual :
where is number of days. Overall, the synthetic seismic travel time change correlates to the observed one (Figure 12e). The climatological data are from a Lijiang station, around 150 km from the study region. The discrepancy between synthetic results and the observed ones might be due to the uncertainty of the climatological data.
We also investigated the effect of noise amplitude change on seismic travel time measurements. To compute the noise amplitude of ambient noise in the passband of 2–6 Hz, we remove airgun signals from the original dataset and calculate root-mean-square amplitude of the noise (Figure S10). We observed that ambient noise amplitude increases in the summer when the water level in the reservoir decreases. The increasing noise amplitude in the summer might be related to active anthropogenic activities. We do not observe an obvious correlation between seismic travel time changes and variation of noise amplitude, so we conclude that changes in noise amplitude introduce negligible effects on velocity changes.
We finally propose that pore pressure change from a combined effect of precipitation and evaporation causes seismic travel time changes in coda waves in the ambient noise cross-correlations.
5.4. Difference of from Ambient Noise and Airgun
Changes of 5% in travel time from airgun are a lot larger than 0.1% changes from ambient noise.
Changing of noise source property and shallow crustal structures are two major factors causing such change. A change of 0.1% seismic travel time may better reflect structural change in shallow crust than that from airguns. First, [12,17] proposed that changes in ambient noise source property cause a bias on travel time measurements, but the effect is negligible. Second, when measuring seismic travel time change for coda wave from ambient noise, we usually use a longer time window to include all possible scattered waves and multiple reflections, which better sample the crustal structure than direct P-wave arrivals. We need to understand the property change in the airgun source before investigating the correlation between and subsurface structural change.
5.5. Mechanism of Change from Airgun
To understand the effect of the change in source property on travel time measurements, we compare seasonal change in travel time to the dominant frequency (Figure 13). We observe that is inversely correlated to the dominant frequency of P-wave and water level fluctuation in the reservoir. One possible explanation is that water table fluctuation in the reservoir causes signal frequency content change so that we can observe phase shift. The authors of [65] observed that signal amplitude changes are positively correlated to significant travel time delay, which is opposite to our observation. Since the change in source property cause significant effect on deriving seasonal change in seismic travel time, we should put more attention on stabilizing dominant frequency of airgun signals in further experiments.
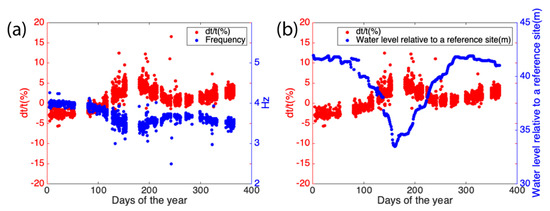
Figure 13.
at the station 53278 is inversely correlated to the dominant frequency of P-wave from airgun (a) and the water table fluctuation (b).
6. Conclusions
We computed seismic travel time changes in the Binchuan basin and adjacent area, estimated seasonal change in the dominant frequency and signal amplitude, and determined how they correlate with the water level changes in the reservoir. The airgun signals exhibit 5.5 km/s and 2.8 km/s in apparent P- and S-wave velocities, respectively. Because S-wave is strongly interfered from multiple reflections and reverberations, we thus only investigated how seismic velocity of P-wave changes. We observed that the correlates to the variation of dominant frequency and water table fluctuation in the reservoir. One possible explanation is that water table fluctuation affects the dominant frequency of airgun signals so that we can measure obvious phase shift. We also investigated seismic travel time changes in P-wave in the empirical Green’s function and found that the correlates inversely to the frequency change.
We computed 91 pairs of ambient noise cross-correlation to derive how seismic travel time changes in the passband of 2–6 Hz. We observed that the travel time changes increase to its local maximum in the end of August, but the variation of seismic velocity does not correlate with the changes in the water table in the reservoir. The seismic velocity changes lag behind the precipitation for about one month. We applied a poroelastic physical model to explain seismic travel time changes and found that a combined effect from precipitation and evaporation matches the observations. The optimal diffusivity to explain seismic travel time changes is 0.01 m2/s. Changes in ambient noise amplitude introduce negligible effects on seismic travel time changes.
Supplementary Materials
The supplementary materials are available online at https://www.mdpi.com/article/10.3390/rs13122421/s1. Figure S1: Airgun excitation time from 2011 to 2020 (Up) and the number of average daily excitation (Down). From June to August, the water level in the reservoir is too low so it is not suitable for the airgun to operate. Data is more complete in 2016 than other. The number of average daily excitation is 7 times/day in 2016, Figure S2: Continued, Figure S3: Different Airgun shots in 2016 at different stations. We observe strong clock drifts, Figure S4: Delay time of P-wave arrivals relative to the time in the first day of 2016, Figure S5: Seismic travel time change for station 53278 using different moving windows. We observe that the estimation of seismic travel time change is more stable when the length of the window is longer than 0.5 s, Figure S6: Determination of window for P-wave arrivals. We inspect the waveform to get a rough estimate of the begin and end time of P-wave arrivals. We then handpick the exact arrival time of P-wave based on the linearity of data points in the diagram of delay time verse travel time in different days, Figure S7: measurements on P-wave arrivals at four stations with or without clock drift correction, Figure S8: (a) Station pairs with similar seasonal changes of seismic travel time distribute in a broad region, at most 30 km from the reservoir. (b) 29 out of 91 station pairs show similar seismic travel time change . Figure S9: Precipitation substracts evaporation. Figure S10: Ambient noise amplitude increases in the summer when the water level in the reservoir decreases. The increasing noise amplitude in the summer might be related to active anthropogenic activities.
Author Contributions
Conceptualization, C.L. and H.Y.; methodology, C.L. and H.Y.; software, C.L.; validation, C.L., H.Y., B.W. and J.Y.; formal analysis, C.L. and H.Y.; investigation, C.L., H.Y., B.W. and J.Y.; resources, H.Y., B.W. and J.Y.; data curation, H.Y., B.W. and J.Y.; writing—original draft preparation, C.L.; writing—review and editing, C.L. and H.Y.; supervision, H.Y.; project administration, H.Y.; funding acquisition, H.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the National Key R&D Program of China (2018YFC1503400), China Earthquake Science Experiment Project, CEA (grants no. 2018CSES0102, 2019CSES0107), HKSAR Research Grant Council GRF Grant 14305617, CUHK Direct Grant from Faculty of Science, National Natural Scientific Foundation of China (41790462), and Chen Yong Academician Workstation of Yunnan Province in China (2014IC007).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Waveform data used in this study are available from Data Management Centre of China Seismic Experimental Site (http://www.cses.ac.cn, accessed on 8 May 2021). The climatological data is available from China Meteorological Data Service Center (http://data.cma.cn, accessed on 8 May 2021).
Acknowledgments
We thank Junhao Song for help prepare the dataset and appreciate two anonymous reviewers for constructive suggestions and comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Whitcomb, J.H.; Garmany, J.D.; Anderson, D.L. Earthquake prediction: Variation of seismic velocities before the San Francisco earthquake. Science 1973, 180, 632–635. [Google Scholar] [CrossRef] [PubMed]
- Rikitake, T. Earthquake precursors. Bull. Seismol. Soc. Am. 1975, 65, 1133–1162. [Google Scholar]
- Campillo, M.; Paul, A. Long-range correlations in the diffuse seismic coda. Science 2003, 299, 547–549. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cicerone, R.D.; Ebel, J.E.; Britton, J. A systematic compilation of earthquake precursors. Tectonophysics 2009, 476, 371–396. [Google Scholar]
- Moro, M.; Saroli, M.; Stramondo, S.; Bignami, C.; Albano, M.; Falcucci, E.; Wegmüller, U. New insights into earthquake precursors from InSAR. Sci. Rep. 2017, 7, 1–11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brenguier, F.; Shapiro, N.M.; Campillo, M.; Ferrazzini, V.; Duputel, Z.; Coutant, O.; Nercessian, A. Towards forecasting volcanic eruptions using seismic noise. Nat. Geosci. 2008, 1, 126. [Google Scholar] [CrossRef] [Green Version]
- Wu, C.; Delorey, A.; Brenguier, F.; Hadziioannou, C.; Daub, E.G.; Johnson, P. Constraining depth range of s wave velocity decrease after large earthquakes near Parkfield, California. Geophys. Res. Lett. 2016, 43, 6129–6136. [Google Scholar] [CrossRef]
- Yang, H.; Duan, Y.; Song, J.; Wang, W.; Yang, W.; Tian, X.; Wang, B. Illuminating high-resolution crustal fault zones using multi-scale dense arrays and airgun source. Earthq. Res. Adv. 2021. [Google Scholar] [CrossRef]
- Duputel, Z.; Ferrazzini, V.; Brenguier, F.; Shapiro, N.; Campillo, M.; Nercessian, A. Real time monitoring of relative velocity changes using ambient seismic noise at the Piton de la Fournaise volcano (La Réunion) from January 2006 to June 2007. J. Volcanol. Geotherm. Res. 2009, 184, 164–173. [Google Scholar] [CrossRef]
- Lecocq, T.; Longuevergne, L.; Pedersen, H.A.; Brenguier, F.; Stammler, K. Monitoring ground water storage at mesoscale using seismic noise: 30 years of continuous observation and thermo-elastic and hydrological modeling. Sci. Rep. 2017, 7, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Clements, T.; Denolle, M.A. Tracking groundwater levels using the ambient seismic field. Geophys. Res. Lett. 2018, 45, 6459–6465. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Aslam, K.; Daub, E. Seismic velocity changes caused by water table fluctuation in the New Madrid seismic zone and Mississippi embayment. J. Geophys. Res. Solid Earth 2020, 125. [Google Scholar] [CrossRef]
- Silver, P.G.; Daley, T.M.; Niu, F.; Majer, E.L. Active source monitoring of cross-well seismic travel time for stress-induced changes. Bull. Seismol. Soc. Am. 2007, 97, 281–293. [Google Scholar] [CrossRef]
- Sens-Schönfelder, C.; Larose, E. Temporal changes in the lunar soil from correlation of diffuse vibrations. Phys. Rev. E 2008, 78, 045601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Niu, F.; Silver, P.G.; Daley, T.M.; Cheng, X.; Majer, E.L. Preseismic velocity changes observed from active source monitoring at the Parkfield SAFOD drill site. Nature 2008, 454, 204. [Google Scholar] [CrossRef] [PubMed]
- Meier, U.; Shapiro, N.M.; Brenguier, F. Detecting seasonal variations in seismic velocities within Los Angeles basin from correlations of ambient seismic noise. Geophys. J. Int. 2010, 181, 985–996. [Google Scholar] [CrossRef] [Green Version]
- Hillers, G.; Retailleau, L.; Campillo, M.; Inbal, A.; Ampuero, J.-P.; Nishimura, T. In situ observations of velocity changes in response to tidal deformation from analysis of the high-frequency ambient wavefield. J. Geophys. Res. Solid Earth 2015, 120, 210–225. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Yang, W.; Wang, W.; Yang, J.; Li, X.; Ye, B. Diurnal and semidiurnal P-and S-wave velocity changes measured using an airgun source. J. Geophys. Res. Solid Earth 2020, 125. [Google Scholar] [CrossRef]
- De Fazio, T.L.; Aki, K.; Alba, J. Solid earth tide and observed change in the in situ seismic velocity. J. Geophys. Res. 1973, 78, 1319–1322. [Google Scholar] [CrossRef]
- Yamamura, K.; Sano, O.; Utada, H.; Takei, Y.; Nakao, S.; Fukao, Y. Long-term observation of in situ seismic velocity and attenuation. J. Geophys. Res. 2003, 108, 2317. [Google Scholar] [CrossRef]
- Mao, S.; Campillo, M.; van der Hilst, R.D.; Brenguier, F.; Stehly, L.; Hillers, G. High temporal resolution monitoring of small variations in crustal strain by dense seismic arrays. Geophys. Res. Lett. 2019, 46, 128–137. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.-G.; Chen, P.; Cochran, E.S.; Vidale, J.E.; Burdette, T. Seismic evidence for rock damage and healing on the San Andreas fault associated with the 2004 M 6.0 Parkfield earthquake. Bull. Seismol. Soc. Am. 2006, 96, S349–S363. [Google Scholar] [CrossRef]
- Li, Y.-G.; Vidale, J.E.; Aki, K.; Xu, F.; Burdette, T. Evidence of shallow fault zone strengthening after the 1992 M7. 5 Landers, California, earthquake. Science 1998, 279, 217–219. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.-G.; Vidale, J.E.; Day, S.M.; Oglesby, D.D.; Cochran, E. Postseismic fault healing on the rupture zone of the 1999 M 7.1 Hector Mine, California, earthquake. Bull. Seismol. Soc. Am. 2003, 93, 854–869. [Google Scholar] [CrossRef]
- Nishimura, T.; Uchida, N.; Sato, H.; Ohtake, M.; Tanaka, S.; Hamaguchi, H. Temporal changes of the crustal structure associated with the M6.1 earthquake on September 3, 1998, and the volcanic activity of Mount Iwate, Japan. Geophys. Res. Lett. 2000, 27, 269–272. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Zhu, P.; Chen, Y.; Niu, F.; Wang, B. Continuous subsurface velocity measurement with coda wave interferometry. J. Geophys. Res. Solid Earth 2008, 113. [Google Scholar] [CrossRef] [Green Version]
- Wegler, U.; Lühr, B.-G.; Snieder, R.; Ratdomopurbo, A. Increase of shear wave velocity before the 1998 eruption of Merapi volcano (Indonesia). Geophys. Res. Lett. 2006, 33, L09303. [Google Scholar] [CrossRef] [Green Version]
- Yang, W.; Wang, B.; Yuan, S.; Ge, H. Temporal variation of seismic-wave velocity associated with groundwater level observed by a downhole airgun near the Xiaojiang fault zone. Seismol. Res. Lett. 2018, 89, 1014–1022. [Google Scholar] [CrossRef]
- Peng, Z.; Ben-Zion, Y. Temporal changes of shallow seismic velocity around the Karadere-Düzce branch of the north Anatolian fault and strong ground motion. Pure Appl. Geophys. 2006, 163, 567–600. [Google Scholar] [CrossRef]
- Poupinet, G.; Ellsworth, W.L.; Frechet, J. Monitoring velocity variations in the crust using earthquake doublets: An application to the Calaveras Fault, California. J. Geophys. Res. 1984, 89, 5719–5731. [Google Scholar] [CrossRef] [Green Version]
- Rubinstein, J.L.; Beroza, G.C. Evidence for widespread nonlinear strong ground motion in the Mw 6.9 Loma Prieta earthquake. Bull. Seismol. Soc. Am. 2004, 94, 1595–1608. [Google Scholar] [CrossRef]
- Rubinstein, J.L.; Beroza, G.C. Nonlinear strong ground motion in the ML 5.4 Chittenden earthquake: Evidence that preexisting damage increases susceptibility to further damage. Geophys. Res. Lett. 2004, 31, L23614. [Google Scholar] [CrossRef]
- Rubinstein, J.L.; Uchida, N.; Beroza, G.C. Seismic velocity reductions caused by the 2003 Tokachi-Oki earthquake. J. Geophys. Res. 2007, 112, B05315. [Google Scholar] [CrossRef] [Green Version]
- Schaff, D.P.; Beroza, G.C. Coseismic and postseismic velocity changes measured by repeating earthquakes. J. Geophys. Res. 2004, 109, B10302. [Google Scholar] [CrossRef]
- Sens-Schönfelder, C.; Wegler, U. Passive image interferometry and seasonal variations of seismic velocities at Merapi Volcano, Indonesia. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, B.; Yao, H. Seismic airgun exploration of continental crust structures. Sci. China Earth Sci. 2017, 60, 1739–1751. [Google Scholar] [CrossRef]
- Wang, B.; Ge, H.; Yang, W.; Wang, W.; Wang, B.; Wu, G.; Su, Y. Transmitting seismic station monitors fault zone at depth. Eos Trans. Am. Geophys. Union 2012, 93, 49–50. [Google Scholar] [CrossRef]
- Wang, B.; Tian, X.; Zhang, Y.; Li, Y.; Yang, W.; Zhang, B.; Li, X. Seismic signature of an untuned large-volume airgun array fired in a water reservoir. Seismol. Res. Lett. 2018, 89, 983–991. [Google Scholar] [CrossRef]
- Yang, H.; Duan, Y.; Song, J.; Jiang, X.; Tian, X.; Yang, W.; Yang, J. Fine Structure of the Chenghai Fault Zone, Yunnan, China, Constrained from Teleseismic Travel Time and Ambient Noise Tomography. J. Geophys. Res. Solid Earth 2020, 125, e2020JB019565. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, B.; Lin, G.; Wang, W.; Yang, W.; Wu, Z. Upper crustal velocity structure of Binchuan, Yunan revealed by dense array local seismic tomography. Chin. J. Geophys. 2020, 63, 3292–3306. (In Chinese) [Google Scholar] [CrossRef]
- Liu, Z.; Su, Y.; Wang, B.; Wang, B.; Yang, J.; Li, X. Study on analysis method of travel time variations of seismic wave of active source in Binchuan. J. Seismol. Res. 2015, 38, 591–597. (In Chinese) [Google Scholar]
- Chen, J.; Ye, B.; Gao, Q.; Wang, J.; Li, X.; Yang, J. Study on travel time variation of the wave from large volume air-gun source before and after 2016 Yunlong Ms 5.0 earthquake. J. Seismol. Res. 2017, 40, 550–557. (In Chinese) [Google Scholar]
- Zhou, Q.; Chen, J. Influence of different triggering conditions of airgun source on travel time changes. J. Seismol. Res. 2018, 41, 264–272. [Google Scholar]
- Xiang, Y.; Yang, R.; Wang, B.; Zhou, Y.; Lu, Y.; Wu, H.; Junwei, Q.I.; Peng, J. Study on the Influence of Airgun Excitation Conditions on Airgun Signals and Travel Time Variation Measurements. Earthq. Res. China 2019, 33, 336–353. [Google Scholar] [CrossRef]
- Wang, M.; Shen, Z.K. Present-day crustal deformation of continental China derived from GPS and its tectonic implications. J. Geophys. Res. Solid Earth 2020, 125, e2019JB018774. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Q.; Guo, S.; Xiang, H. Principle and method of delineation of potential seismic sources in northeastern Yunnan province. Seismol. Geol. 2004, 26, 761–771. [Google Scholar]
- Wang, B.; Wu, G.; Su, Y.; Wang, B.; Ge, H.; Jin, M. Site construction of the Binchuan transmitting seismic stations and preliminary observational data. J. Seismol. Res. 2015, 38, 1–6. [Google Scholar]
- Huang, X.; Wu, Z.; Li, J.; Nima, C.; Liu, Y.; Huang, X.; Zhang, D. Tectonic geomorphology and Quaternary tectonic activity in the northwest Yunnan rift zone. Geol. Bull. China 2014, 3, 578–593. [Google Scholar]
- Luan, Y.; Yang, H.; Wang, B. Large volume air-gun waveform data processing (I): Binchuan, Yunnan. Earthq. Res. China 2016, 32, 305–318. [Google Scholar]
- Xia, J.; Jin, X.; Cai, H.; Xu, J. The time-frequency characteristic of a large volume airgun source wavelet and its influencing factors. Earthq. Res. China 2016, 30, 364–379. [Google Scholar]
- McNamara, D.E.; Buland, R.P. Ambient noise levels in the continental United States. Bull. Seismol. Soc. Am. 2004, 94, 1517–1527. [Google Scholar] [CrossRef]
- Aster, R.C.; McNamara, D.E.; Bromirski, P.D. Multidecadal climate-induced variability in microseisms. Seismol. Res. Lett. 2008, 79, 194–202. [Google Scholar] [CrossRef]
- Zhan, Z.; Tsai, V.C.; Clayton, R.W. Spurious velocity changes caused by temporal variations in ambient noise frequency content. Geophys. J. Int. 2013, 194, 1574–1581. [Google Scholar] [CrossRef] [Green Version]
- Vidale, J.E. Complex polarization analysis of particle motion. Bull. Seismol. Soc. Am. 1986, 76, 1393–1405. [Google Scholar]
- Samson, J.C.; Olson, J.V. Some comments on the descriptions of the polarization states of waves. Geophys. J. Int. 1980, 61, 115–129. [Google Scholar] [CrossRef] [Green Version]
- Bataille, K.; Chiu, J.M. Polarization analysis of high-frequency, three-component seismic data. Bull. Seismol. Soc. Am. 1991, 81, 622–642. [Google Scholar]
- Clarke, D.; Zaccarelli, L.; Shapiro, N.M.; Brenguier, F. Assessment of resolution and accuracy of the Moving Window Cross Spectral technique for monitoring crustal temporal variations using ambient seismic noise. Geophys. J. Int. 2011, 186, 867–882. [Google Scholar] [CrossRef]
- Mordret, A.; Mikesell, T.D.; Harig, C.; Lipovsky, B.P.; Prieto, G.A. Monitoring southwest Greenland’s ice sheet melt with ambient seismic noise. Sci. Adv. 2016, 2, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.-Y.; Brenguier, F.; Campillo, M.; Lecointre, A.; Takeda, T.; Aoki, Y. Seasonal crustal seismic velocity changes throughout Japan. J. Geophys. Res. Solid Earth 2017, 122, 7987–8002. [Google Scholar] [CrossRef]
- Langston, C.A. Structure under Mount Rainier, Washington, inferred from teleseismic body waves. J. Geophys. Res. Solid Earth 1979, 84, 4749–4762. [Google Scholar] [CrossRef] [Green Version]
- Pei, S.; Niu, F.; Ben-Zion, Y.; Sun, Q.; Liu, Y.; Xue, X. Recovery due to earthquakes on the Longmenshan fault. Nat. Geosci. 2019, 12, 387–392. [Google Scholar] [CrossRef]
- Lecocq, T.; Caudron, C.; Brenguier, F. MSNoise, a python package for monitoring seismic velocity changes using ambient seismic noise. Seismol. Res. Lett. 2014, 85, 715–726. [Google Scholar] [CrossRef] [Green Version]
- Talwani, P.; Chen, L.; Gahalaut, K. Seismogenic permeability, ks. J. Geophys. Res. Solid Earth 2007, 112, B07309. [Google Scholar] [CrossRef]
- Rivet, D.; Brenguier, F.; Cappa, F. Improved detection of preeruptive seismic velocity drops at the Piton de la Fournaise volcano. Geophys. Res. Lett. 2015, 42, 6332–6339. [Google Scholar] [CrossRef] [Green Version]
- Yu, W.; Yang, X.; Yu, J.; Sun, D. Temporal variations of surface wave amplitude in the data collected from Hutubi, Xinjiang airgun experiment. J. Seismol. Res. 2021, 44, 23–33. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).