Exploring the Potential of Statistical Modeling to Retrieve the Cloud Base Height from Geostationary Satellites: Applications to the ABI Sensor on Board of the GOES-R Satellite Series
Abstract
1. Introduction
2. Materials and Methods
2.1. Observational Datasets
2.2. Machine Learning Model
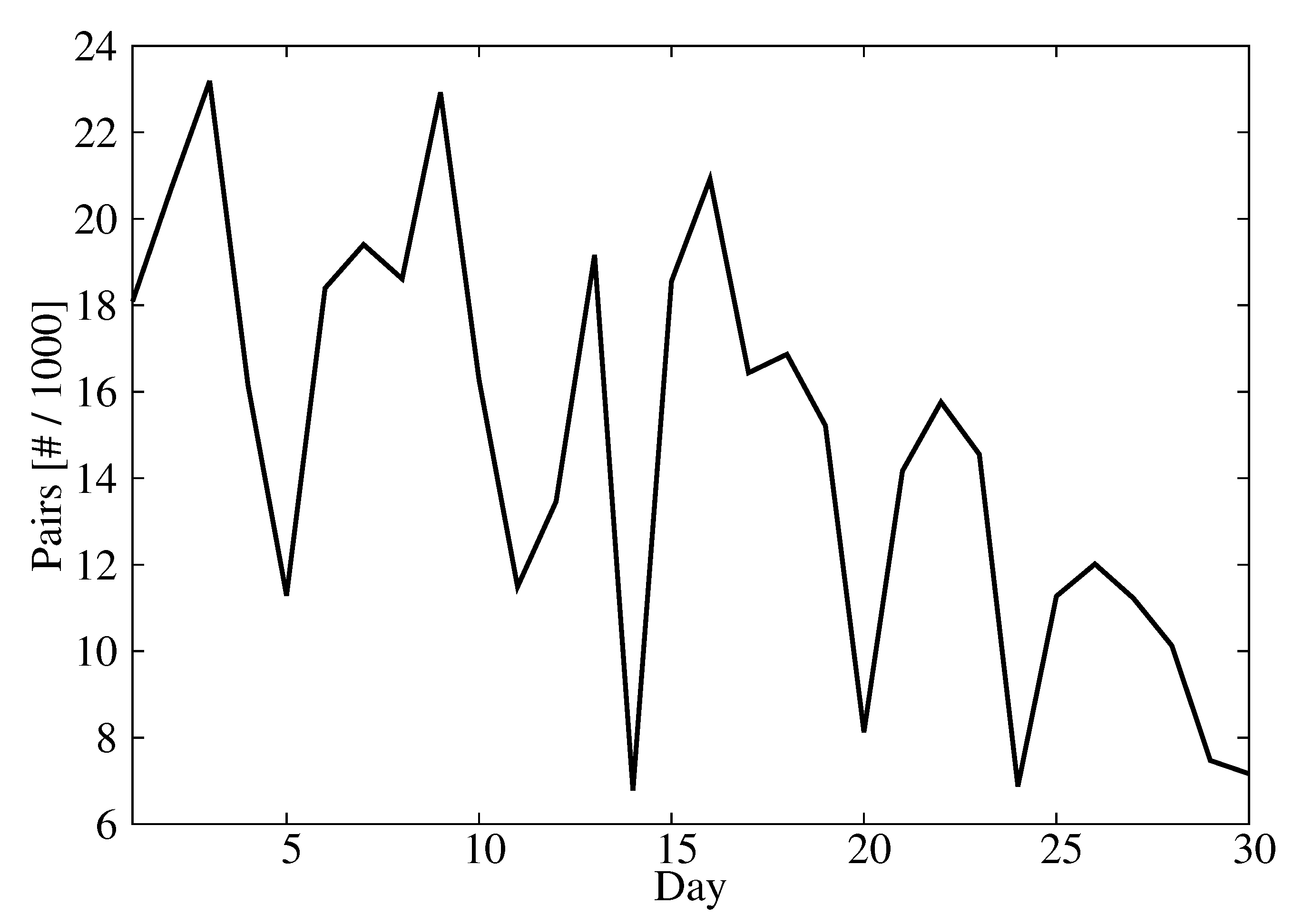
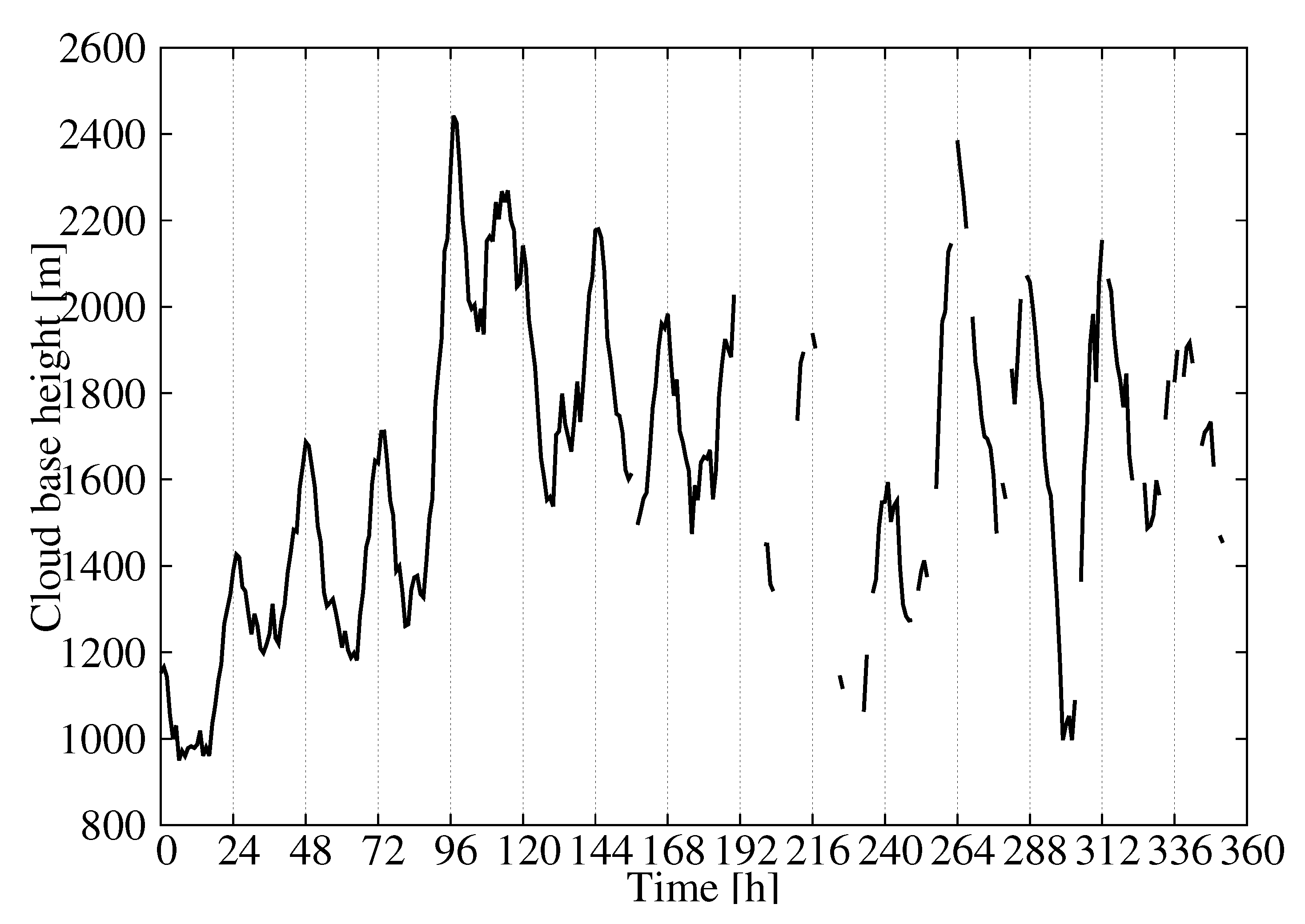
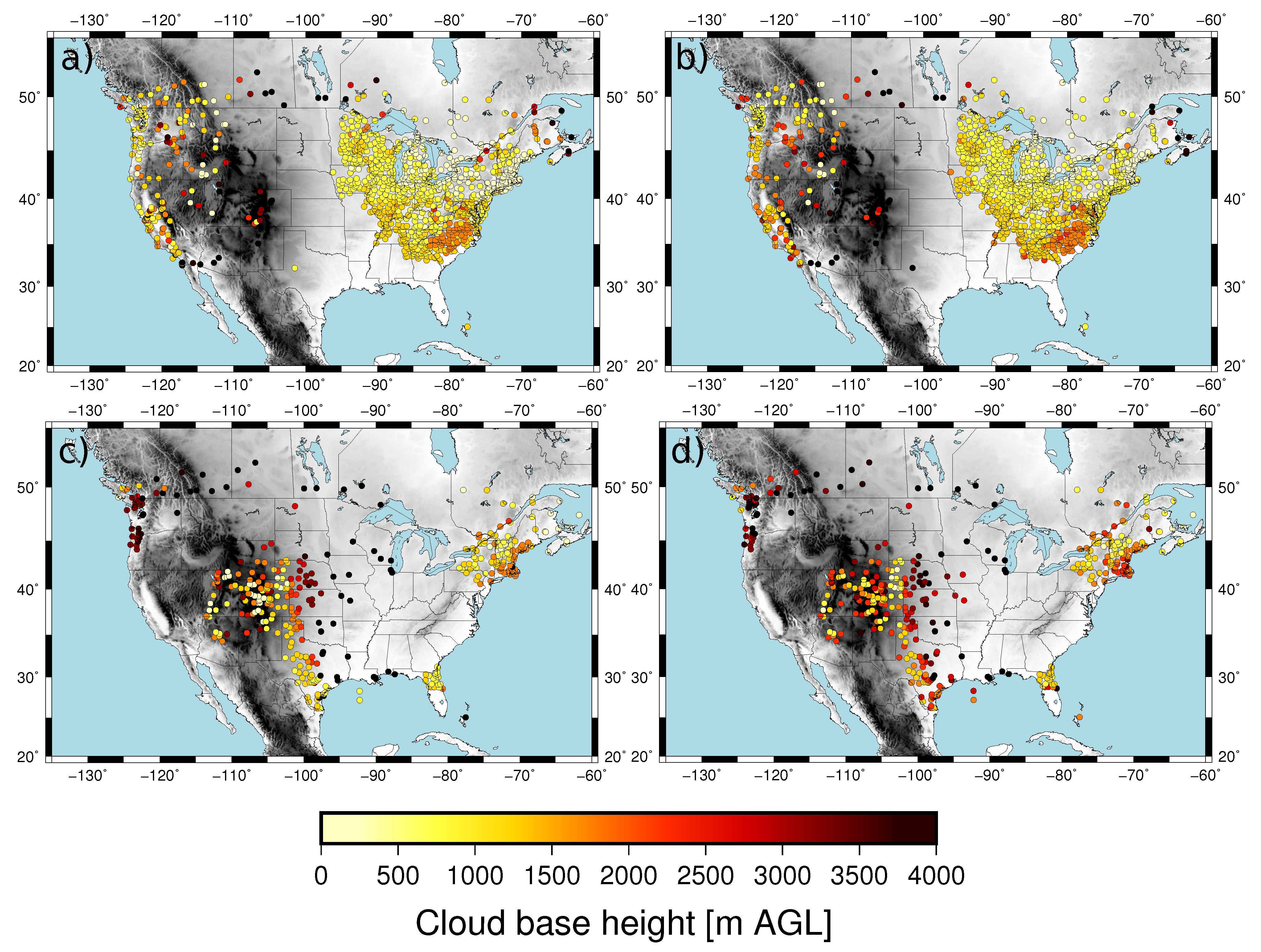
3. Results
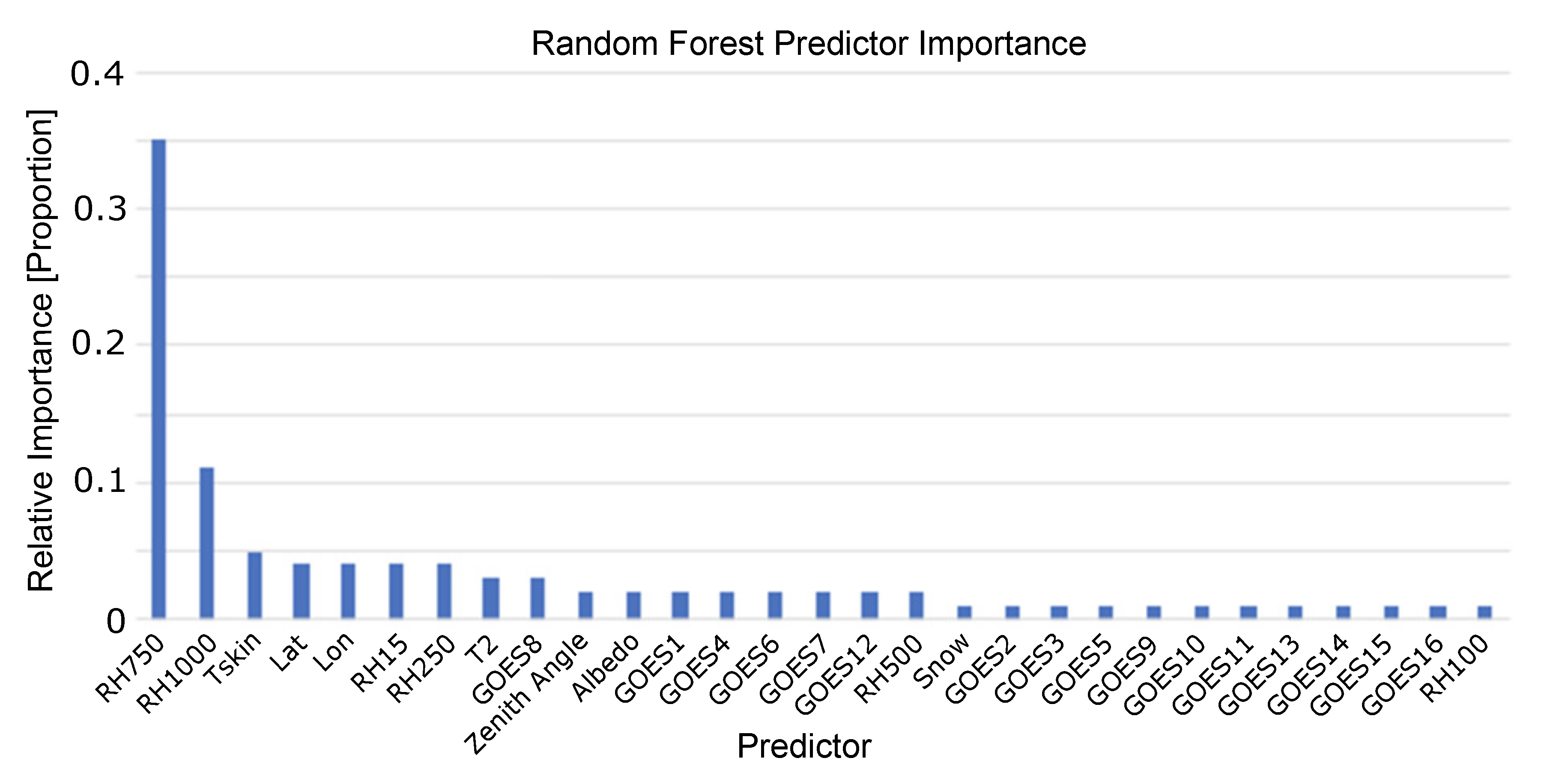
3.1. Model Calibration
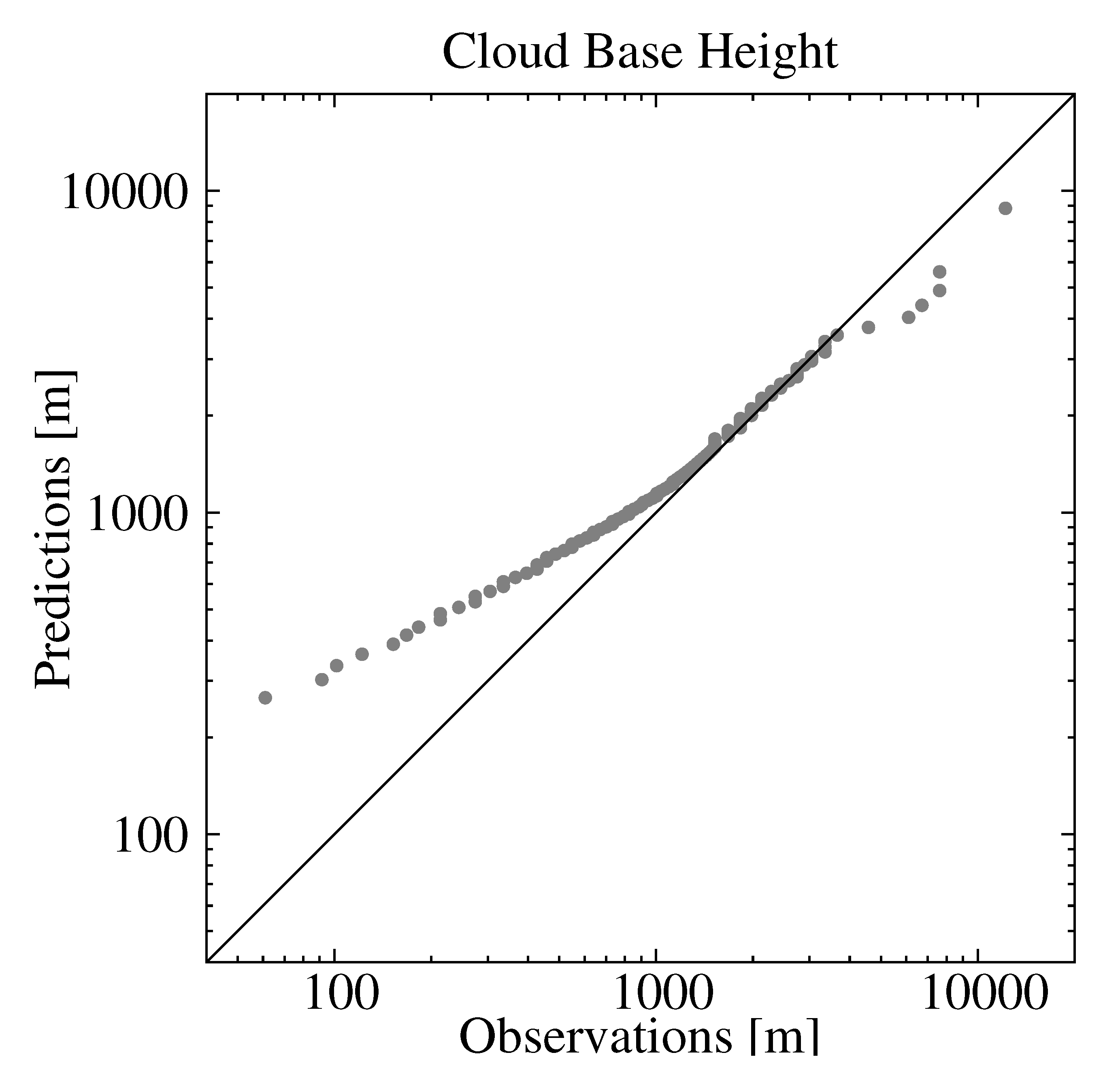
3.2. Model Performance
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ellrod, G.P.; Gultepe, I. Inferring low cloud base heights at night for aviation using satellite infrared and surface temperature data. Pure Appl. Geophys. 2007, 164, 1193–1205. [Google Scholar] [CrossRef]
- Jiménez, P.A.; Hacker, J.P.; Dudhia, J.; Haupt, S.E.; Ruiz-Arias, J.A.; Gueymard, C.A.; Thompson, G.; Eidhammer, T.; Deng, A. WRF-Solar: Description and clear sky assessment of an augmented NWP model for solar power prediction. Bull. Am. Met. Soc. 2016, 97, 1249–1264. [Google Scholar] [CrossRef]
- Ryu, Y.H.; Hodzic, A.; Barre, J.; Descombes, G.; Minnis, P. Quantifying errors in surface ozone predictions associated with clouds over the CONUS: A WRF-Chem modeling study using satellite cloud retrievals. Atm. Chem. Phys. 2018, 18, 7509–7525. [Google Scholar] [CrossRef]
- Schmit, T.J.; Gunshor, M.M.; Menzel, W.P.; Gurka, J.J.; Li, J.; Bachmeier, A.S. Introducing the next-generation advanced baseline imager on GOES-R. Bull. Am. Met. Soc. 2005, 86, 1079–1096. [Google Scholar] [CrossRef]
- Noh, Y.J.; Forsythe, J.; Miller, S.; Seaman, C.; Li, Y.; Heidinger, A.; Lindsey, D.; Rogers, M.; Partain, P. Cloud-base height estimation from VIIRS. Part II: A statistical algorithm based on A-Train satellite data. J. Atmos. Ocean. Technol. 2017, 34, 585–598. [Google Scholar] [CrossRef]
- Feijt, A.; van Lammeren, A. Ground based satellite observations of cloud fields in The Netherlands. Mon. Wea. Rev. 1996, 124, 1914–1923. [Google Scholar]
- Forsythe, J.; Haar, T.V.; Reinke, D. Cloud-base height estimates using a combination of meteorological satellite imagery and surface reports. J. Appl. Meteor. 2000, 39, 2236–2347. [Google Scholar] [CrossRef]
- Barker, H.; Jerg, M.; Wehr, T.; Kato, S.; Donovan, D.; Hogan, R. A 3D cloud-construction algorithm for the EarthCARE satellite mission. Quarter. J. R. Met. Soc. 2011, 137, 1042–1058. [Google Scholar] [CrossRef]
- Sun, X.; Li, J.; Barker, H.; Zhang, R.; Zhou, Y.; Liu, L. Satellite-based estimation of cloud-base heights using constrained spectral radiance matching. Quarter. J. R. Met. Soc. 2016, 142, 224–232. [Google Scholar] [CrossRef]
- Miller, S.; Forsythe, J.; Partain, P.; Haynes, J.; Bankert, R.; Sengupta, M.; Mitrescu, C.; Hawkins, J.; Haar, T.V. Estimating three-dimensional cloud structure via statistically blended satellite observations. J. Appl. Meteor. Climatol. 2014, 53, 437–455. [Google Scholar] [CrossRef]
- Liang, Y.; Sun, X.; Miller, S.D.; Li, H.; Zhou, Y.; Zhang, R.; Li, S. Cloud base height estimation from ISCCP cloud-type classification applied to A-Train data. Adv. Meteorol. 2017, 2017, 3231719. [Google Scholar] [CrossRef]
- Minnis, P.; Coakley, J.A., Jr.; King, M.; Garber, D.; Heck, P.; Mayor, S.; Young, D.; Arduini, R. Cloud Optical Property Retrieval (Subsystem 4.3), in Clouds and the Earth’s Radiant Energy System (CERES) Algorithm Theoretical Basis Document, Volume III: Cloud Analyses and Radiance Inversions (Subsystem 4). In Technical Report NASA RP 1376; NASA, Langley Res. Cent.: Hampton, VA, USA, 1995. [Google Scholar]
- Chakrapani, V.; Doelling, D.; Rapp, A.D.; Minnis, P. Cloud thickness estimation from GOES-8 satellite data over the ARM-SGP site. In Proceedings of the Twelfth ARM Science Team Meeting Proceedings, St. Petersburg, FL, USA, 8–12 April 2002; pp. 1–7. [Google Scholar]
- Hutchison, K. The retrieval of cloud base heights from MODIS and three-dimensional cloud fields from NASA’s EOS Aqua mission. Int. J. Remote Sens. 2002, 23, 5249–5265. [Google Scholar] [CrossRef]
- Hutchison, K.; Wong, E.; Ou, C. Cloud base heights retrieved during night-time conditions with MODIS data. Int. J. Remote Sens. 2006, 27, 2847–2862. [Google Scholar] [CrossRef]
- Baker, N. Joint Polar Satellite System (JPSS) VIIRS cloud base height algorithm theoretical basis document (ATBD). In Technical Report JPSS Ground Project Code 474-00045, NASA Goddard; Space Flight Center: Greenbelt, MD, USA, 2011. [Google Scholar]
- Seaman, C.; Noh, Y.J.; Miller, S.; Heidinger, A.; Lindsey, D. Cloud-base height estimations from VIIRS. Part I: Operational algorithm validation against CloudSat. J. Atmos. Ocean. Technol. 2017, 34, 567–583. [Google Scholar] [CrossRef]
- Benjamin, S.; Weygandt, S.; Brown, J.; Hu, M.; Alexander, C.; Smirnova, T.; Olson, J.; James, E.; Dowell, D.; Grell, G.; et al. A North American hourly assimilation and model forecast cycle: The Rapid Refresh. Mon. Weather Rev. 2016, 144, 1669–1694. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, L.; Guo, J.; Feng, J.; Cao, L.; Wang, Y.; Zhou, Q.; Li, L.; Xu, B.L.H.; Liu, L.; et al. Climatology of cloud-base height from long-term radiosonde measurements in China. Adv. Atmos. Sci. 2018, 35, 158–168. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, Q.; Lv, S.; Jia, S.; Tao, F.; Chen, D.; Guo, J. Elucidating cloud vertical structures based on three-year Ka-band cloud radar observations from Beijing, China. Atmos. Res. 2019, 222, 88–99. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhang, Y.; Li, B.; Li, L.; Feng, J.; Jia, S.; Lv, S.; Tao, F.; Guo, J. Cloud-base and cloud-top heights determined from a ground-based cloud radar in Beijing, China. Atmos. Environ. 2019, 201, 381–390. [Google Scholar] [CrossRef]
- An, N.; Wang, K.; Zhou, C.; Pinker, R.T. Observed variability of cloud frequency and cloud-base height within 3600 m above the surface over the Contiguous United States. J. Clim. 2017, 30, 3725–3742. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.; Huang, X.Y.; Wang, W.; Powers, J.G. A description of the advanced research WRF version 3. In Technical Report TN-475+STR; NCAR: Boulder, CO, USA, 2008. [Google Scholar]
- Beiman, L. Random Forest. Mach. Learn. 2011, 45, 5–32. [Google Scholar] [CrossRef]
- Witten, I.; Frank, E. Data Mining: Practical Machine Learning Tools and Techniques; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2005. [Google Scholar]
- McCandless, T.C.; Haupt, S.E. The super-turbine wind power conversion paradox: Using machine learning to reduce errors caused by Jensen’s inequality. Wind Energy Sci. 2019, 4, 343–353. [Google Scholar] [CrossRef]
- McCandless, T.C.; Jiménez, P.A. Examining the potential of a random forest derived cloud mask from GOES-R satellites to improve solar irradiance forecasting. Energies 2020, 13, 1671. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Wagner, T.; Kleiss, J. Error characteristics of ceilometer-based observations of cloud amount. J. Atmos. Ocean. Technol. 2016, 33, 1557–1567. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiménez, P.A.; McCandless, T. Exploring the Potential of Statistical Modeling to Retrieve the Cloud Base Height from Geostationary Satellites: Applications to the ABI Sensor on Board of the GOES-R Satellite Series. Remote Sens. 2021, 13, 375. https://doi.org/10.3390/rs13030375
Jiménez PA, McCandless T. Exploring the Potential of Statistical Modeling to Retrieve the Cloud Base Height from Geostationary Satellites: Applications to the ABI Sensor on Board of the GOES-R Satellite Series. Remote Sensing. 2021; 13(3):375. https://doi.org/10.3390/rs13030375
Chicago/Turabian StyleJiménez, Pedro A., and Tyler McCandless. 2021. "Exploring the Potential of Statistical Modeling to Retrieve the Cloud Base Height from Geostationary Satellites: Applications to the ABI Sensor on Board of the GOES-R Satellite Series" Remote Sensing 13, no. 3: 375. https://doi.org/10.3390/rs13030375
APA StyleJiménez, P. A., & McCandless, T. (2021). Exploring the Potential of Statistical Modeling to Retrieve the Cloud Base Height from Geostationary Satellites: Applications to the ABI Sensor on Board of the GOES-R Satellite Series. Remote Sensing, 13(3), 375. https://doi.org/10.3390/rs13030375






