The Role of Weather Radar in Rainfall Estimation and Its Application in Meteorological and Hydrological Modelling—A Review
Abstract
1. Introduction
2. The Importance of Rainfall Input for Hydrological Modelling
2.1. Spatial and Temporal Resolution of Weather Radar and Rain Gauge Data
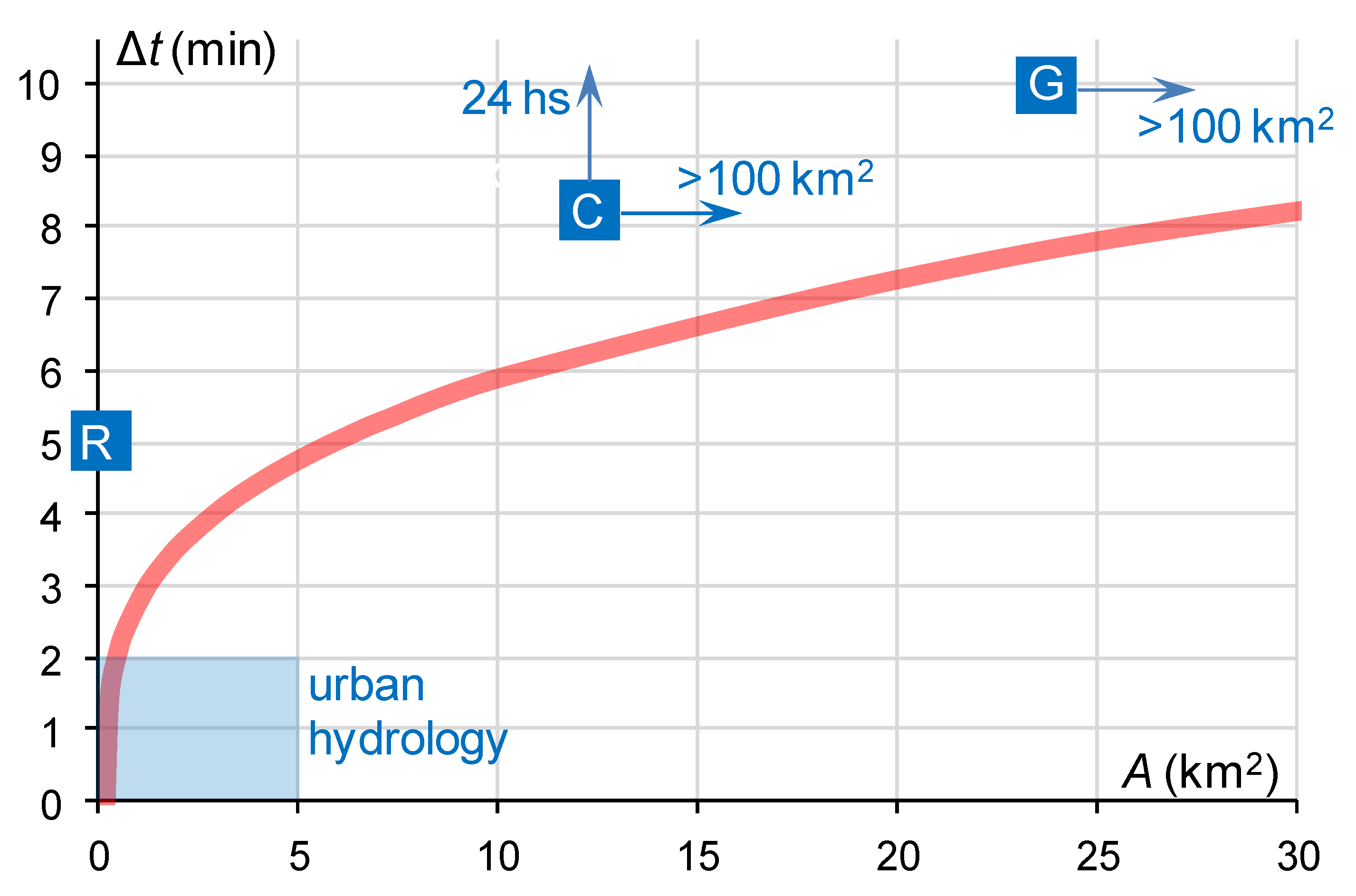
2.2. Needs of Urban Hydrology in Terms of Resolution of Precipitation Data
3. High-Resolution Techniques for Precipitation Measurement and Estimation
3.1. Rain Gauge Networks
3.2. Weather Radar Networks
3.2.1. Introduction
- S-band (2.7–2.9 GHz) is well suited for detecting heavy rain at very long ranges (up to 300 km), as it is least affected by attenuation. However, quantitative precipitation estimation observations are reliable up to ranges of about 200 km, as a larger beam width brings limitations. Data corrections are most robust and easiest to implement for S-band weather radars; however, they are also the most expensive.
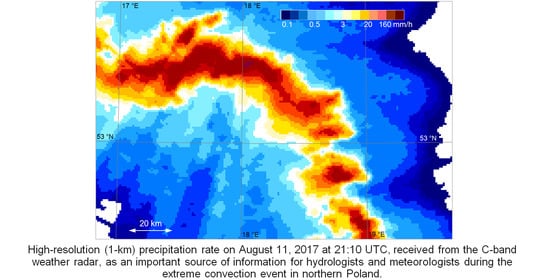
- C-band (5.6–5.65 GHz) represents a compromise between range and reliability of reflectivity measurements and cost. A C-band weather radar can provide rain detection up to a range of 200 km, but it is less expensive than an S-band radar. Attenuation of the received signal is significantly stronger than in case of an S-band radar. Thus, the attenuation limits the QPE to ranges of about 100–150 km.
- X-band (9.3–9.5 GHz) weather radars are more sensitive to hydrometeors than S- or C-band weather radars when measuring up to a range of 50 km. Attenuation of the signal by rain is strongest in the case of X-band radars (compared to S- and C-band radars) and strongly limits the QPE. Accurate QPE is usually possible up to ranges of about 30 km. On the other hand, X-band weather radars are the least expensive.
3.2.2. Sources of Errors in Weather Radar Data
3.2.3. Dual-Polarization Weather Radars
3.2.4. Radar-Based Precipitation Estimates
3.2.5. Machine Learning for Radar-Based Precipitation Estimates
3.2.6. Weather Radar Composites
3.3. Multi-Source Precipitation Estimation
4. Techniques for High-Resolution Nowcasting
4.1. Extrapolation Methods
4.1.1. Motion Field
4.1.2. Quantitative Precipitation Forecast
4.1.3. Probabilistic and Ensemble Forecasts
4.2. Blending Methods
4.3. Artificial Intelligence-Based Methods
4.4. Conceptual Models
5. Using Radar Data in NWP Modeling: Radar Data Assimilation
5.1. Methods of Assimilation of Radar Reflectivity Data into a NWP
5.1.1. Latent Heat Nudging (LHN)
5.1.2. Water Vapor Correction Method
5.1.3. Inverse Modelling Technique
5.2. Assimilation of Doppler Radial Velocity into a NWP
6. Using Radar Rainfall Data in Flash Flood Modeling
6.1. Flash Flood Modelling Approaches Using Radar Data
6.2. Uncertainty in Radar Estimates for Hydrological Modeling
6.3. Radar Spatial Resolution and Catchment Scale
6.4. Usefulness of Blending Data and Ancillary Data
6.5. Post-Event Flash Flood Analyses
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Marshall, J.S.; Langille, R.C.; Palmer, W.M.K. Measurement of Rainfall by Radar. J. Meteor. 1947, 4, 186–192. [Google Scholar] [CrossRef]
- Wilk, K.E.; Kessler, E. Quantitative Radar Measurements of Precipitation. In Meteorological Observations and Instrumentation; Teweles, S., Giraytys, J., Eds.; American Meteorological Society: Boston, MA, USA, 1970; pp. 315–329. ISBN 978-1-935704-35-5. [Google Scholar]
- Wilson, J.W.; Brandes, E.A. Radar Measurement of Rainfall—A Summary. Bull. Amer. Meteor. Soc. 1979, 60, 1048–1060. [Google Scholar] [CrossRef]
- Zawadzki, I. Factors Affecting the Precision of Radar Measurements of Rain. In Proceedings of the 22nd Conference on Radar Meteorology, Boston, MA, USA, 1 January 1984; pp. 251–256. [Google Scholar]
- Joss, J.; Waldvogel, A.; Collier, C.G. Precipitation Measurement and Hydrology. In Radar in Meteorology: Battan Memorial and 40th Anniversary Radar Meteorology Conference; Atlas, D., Ed.; American Meteorological Society: Boston, MA, USA, 1990; pp. 577–606. ISBN 978-1-935704-15-7. [Google Scholar]
- Krajewski, W.F.; Smith, J.A. Radar Hydrology: Rainfall Estimation. Adv. Water Resour. 2002, 25, 1387–1394. [Google Scholar] [CrossRef]
- Collier, C.G. Applications of Weather Radar Systems: A Guide to Uses of Radar Data in Meteorology and Hydrology, 2nd ed.; John Wiley & Sons: Chichester, UK; New York, NY, USA, 1996; ISBN 978-0-471-96013-3. [Google Scholar]
- Zappa, M.; Beven, K.J.; Bruen, M.; Cofiño, A.S.; Kok, K.; Martin, E.; Nurmi, P.; Orfila, B.; Roulin, E.; Schröter, K.; et al. Propagation of Uncertainty from Observing Systems and NWP into Hydrological Models: COST-731 Working Group 2. Atmos. Sci. Lett. 2010, 11, 83–91. [Google Scholar] [CrossRef]
- Zhang, Y.; Xie, S.; Klein, S.A.; Marchand, R.; Kollias, P.; Clothiaux, E.E.; Lin, W.; Johnson, K.; Swales, D.; Bodas-Salcedo, A.; et al. The ARM cloud radar simulator for global climate models: Bridging field data and climate models. Bull. Am. Meteorol. Soc. 2018, 99, 21–26. [Google Scholar] [CrossRef]
- Joss, J. Operational Use of Radar for Precipitation Measurements in Switzerland; Vdf Hochschulverl. an der ETH Zürich: Zürich, Switherlands, 1998; ISBN 978-3-7281-2501-9. [Google Scholar]
- Savina, M.; Schäppi, B.; Molnar, P.; Burlando, P.; Sevruk, B. Comparison of a Tipping-Bucket and Electronic Weighing Precipitation Gage for Snowfall. Atmos. Res. 2012, 103, 45–51. [Google Scholar] [CrossRef]
- Gires, A.; Tchiguirinskaia, I.; Schertzer, D.; Schellart, A.; Berne, A.; Lovejoy, S. Influence of Small Scale Rainfall Variability on Standard Comparison Tools between Radar and Rain Gauge Data. Atmos. Res. 2014, 138, 125–138. [Google Scholar] [CrossRef]
- Song, Y.; Han, D.; Rico-Ramirez, M.A. High Temporal Resolution Rainfall Information Retrieval from Tipping-Bucket Rain Gauge Measurements. Procedia Eng. 2016, 154, 1193–1200. [Google Scholar] [CrossRef][Green Version]
- De Vos, L.; Leijnse, H.; Overeem, A.; Uijlenhoet, R. The Potential of Urban Rainfall Monitoring with Crowdsourced Automatic Weather Stations in Amsterdam. Hydrol. Earth Syst. Sci. 2017, 21, 765–777. [Google Scholar] [CrossRef]
- Berne, A.; Delrieu, G.; Creutin, J.; Obled, C. Temporal and Spatial Resolution of Rainfall Measurements Required for Urban Hydrology. J. Hydrol. 2004, 299, 166–179. [Google Scholar] [CrossRef]
- Emmanuel, I.; Andrieu, H.; Leblois, E.; Flahaut, B. Temporal and Spatial Variability of Rainfall at the Urban Hydrological Scale. J. Hydrol. 2012, 430–431, 162–172. [Google Scholar] [CrossRef]
- Ochoa-Rodriguez, S.; Wang, L.-P.; Gires, A.; Pina, R.D.; Reinoso-Rondinel, R.; Bruni, G.; Ichiba, A.; Gaitan, S.; Cristiano, E.; van Assel, J.; et al. Impact of Spatial and Temporal Resolution of Rainfall Inputs on Urban Hydrodynamic Modelling Outputs: A Multi-Catchment Investigation. J. Hydrol. 2015, 531, 389–407. [Google Scholar] [CrossRef]
- Thorndahl, S.; Einfalt, T.; Willems, P.; Nielsen, J.E.; ten Veldhuis, M.-C.; Arnbjerg-Nielsen, K.; Rasmussen, M.R.; Molnar, P. Weather Radar Rainfall Data in Urban Hydrology. Hydrol. Earth Syst. Sci. 2017, 21, 1359–1380. [Google Scholar] [CrossRef]
- Yoon, J.; Joo, J.; Yoo, C.; Hwang, S.; Lim, S. On Quality of Radar Rainfall with Respect to Temporal and Spatial Resolution for Application to Urban Areas. Meteorol. Appl. 2017, 24, 19–30. [Google Scholar] [CrossRef]
- Michaelides, S.; Levizzani, V.; Anagnostou, E.; Bauer, P.; Kasparis, T.; Lane, J.E. Precipitation: Measurement, Remote Sensing, Climatology and Modeling. Atmos. Res. 2009, 94, 512–533. [Google Scholar] [CrossRef]
- Michelson, D.B. Systematic Correction of Precipitation Gauge Observations Using Analyzed Meteorological Variables. J. Hydrol. 2004, 290, 161–177. [Google Scholar] [CrossRef]
- Martinaitis, S.M.; Cocks, S.B.; Qi, Y.; Kaney, B.T.; Zhang, J.; Howard, K. Understanding Winter Precipitation Impacts on Automated Gauge Observations within a Real-Time System. J. Hydrometeor. 2015, 16, 2345–2363. [Google Scholar] [CrossRef]
- WMO. Guide to the Global Observing System, 3rd ed.; World Meteorological Organization: Geneva, Switherlands, 2007. [Google Scholar]
- Otop, I.; Szturc, J.; Ośródka, K.; Djaków, P. Automatic Quality Control of Telemetric Rain Gauge Data for Operational Applications at IMGW-PIB. ITM Web Conf. 2018, 23, 00028. [Google Scholar] [CrossRef][Green Version]
- Jurczyk, A.; Szturc, J.; Otop, I.; Ośródka, K.; Struzik, P. Quality-Based Combination of Multi-Source Precipitation Data. Remote Sens. 2020, 12, 1709. [Google Scholar] [CrossRef]
- Ahrens, B. Distance in Spatial Interpolation of Daily Rain Gauge Data. Hydrol. Earth Syst. Sci. 2006, 10, 197–208. [Google Scholar] [CrossRef]
- Han, D.; Bray, M. Automated Thiessen Polygon Generation. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Berndt, C.; Rabiei, E.; Haberlandt, U. Geostatistical Merging of Rain Gauge and Radar Data for High Temporal Resolutions and Various Station Density Scenarios. J. Hydrol. 2014, 508, 88–101. [Google Scholar] [CrossRef]
- Sideris, I.V.; Gabella, M.; Erdin, R.; Germann, U. Real-Time Radar–Rain-Gauge Merging Using Spatio-Temporal Co-Kriging with External Drift in the Alpine Terrain of Switzerland. Q. J. R. Meteorol. Soc. 2014, 140, 1097–1111. [Google Scholar] [CrossRef]
- Orellana-Alvear, J.; Célleri, R.; Rollenbeck, R.; Bendix, J. Analysis of Rain Types and Their Z–R Relationships at Different Locations in the High Andes of Southern Ecuador. J. Appl. Meteor. Clim. 2017, 56, 3065–3080. [Google Scholar] [CrossRef]
- Neuper, M.; Ehret, U. Quantitative Precipitation Estimation with Weather Radar Using a Data- and Information-Based Approach. Hydrol. Earth Syst. Sci. 2019, 23, 3711–3733. [Google Scholar] [CrossRef]
- Meischner, P. (Ed.) Weather Radar: Principles and Advanced Applications; Physics of Earth and Space Environments; Springer: Berlin/Heidelberg, Germany, 2004; ISBN 978-3-540-00328-1. [Google Scholar]
- Michelson, D.B.; Einfalt, T.; Holleman, I.; Gjertsen, U.; Friedrich, K.; Haase, G.; Lindskog, M.; Jurczyk, A. COST Action 717: Weather Radar Data Quality in Europe–Quality Control and Characterization: Review; EUR-OP: Luxembourg, 2005; ISBN 92-898-0018-6. [Google Scholar]
- Villarini, G.; Krajewski, W.F. Review of the Different Sources of Uncertainty in Single Polarization Radar-Based Estimates of Rainfall. Surv. Geophys. 2010, 31, 107–129. [Google Scholar] [CrossRef]
- Ośródka, K.; Szturc, J.; Jurczyk, A. Chain of Data Quality Algorithms for 3-D Single-Polarization Radar Reflectivity (RADVOL-QC System). Meteorol. Appl. 2014, 21, 256–270. [Google Scholar] [CrossRef]
- Gekat, F.; Meischner, P.; Friedrich, K.; Hagen, M.; Koistinen, J.; Michelson, D.B.; Huuskonen, A. The State of Weather Radar Operations, Networks and Products. In Weather Radar: Principles and Advanced Applications; Springer: Berlin/Heidelberg, Germany, 2004; pp. 1–51. [Google Scholar]
- Krajewski, W.F.; Vignal, B.; Seo, B.-C.; Villarini, G. Statistical Model of the Range-Dependent Error in Radar-Rainfall Estimates Due to the Vertical Profile of Reflectivity. J. Hydrol. 2011, 402, 306–316. [Google Scholar] [CrossRef]
- Sebastianelli, S.; Russo, F.; Napolitano, F.; Baldini, L. On Precipitation Measurements Collected by a Weather Radar and a Rain Gauge Network. Nat. Hazards Earth Syst. Sci. 2013, 13, 605–623. [Google Scholar] [CrossRef]
- Angulo, I.; Grande, O.; Jenn, D.; Guerra, D.; de la Vega, D. Estimating Reflectivity Values from Wind Turbines for Analyzing the Potential Impact on Weather Radar Services. Atmos. Meas. Tech. 2015, 8, 2183–2193. [Google Scholar] [CrossRef]
- Norin, L. A Quantitative Analysis of the Impact of Wind Turbines on Operational Doppler Weather Radar Data. Atmos. Meas. Tech. 2015, 8, 593–609. [Google Scholar] [CrossRef]
- Seo, B.-C.; Krajewski, W.F.; Mishra, K.V. Using the New Dual-Polarimetric Capability of WSR-88D to Eliminate Anomalous Propagation and Wind Turbine Effects in Radar-Rainfall. Atmos. Res. 2015, 153, 296–309. [Google Scholar] [CrossRef]
- Saltikoff, E.; Cho, J.Y.N.; Tristant, P.; Huuskonen, A.; Allmon, L.; Cook, R.; Becker, E.; Joe, P. The Threat to Weather Radars by Wireless Technology. Am. Meteorol. Soc. 2016, 97, 1159–1167. [Google Scholar] [CrossRef]
- Gauthreaux, S.; Diehl, R. Discrimination of Biological Scatterers in Polarimetric Weather Radar Data: Opportunities and Challenges. Remote Sens. 2020, 12, 545. [Google Scholar] [CrossRef]
- Bech, J.; Gjertsen, U.; Haase, G. Modelling Weather Radar Beam Propagation and Topographical Blockage at Northern High Latitudes. Q. J. R. Meteorol. Soc. 2007, 133, 1191–1204. [Google Scholar] [CrossRef]
- McRoberts, D.B.; Nielsen-Gammon, J.W. Detecting Beam Blockage in Radar-Based Precipitation Estimates. J. Atmos. Ocean. Technol. 2017, 34, 1407–1422. [Google Scholar] [CrossRef]
- Gu, J.-Y.; Ryzhkov, A.; Zhang, P.; Neilley, P.; Knight, M.; Wolf, B.; Lee, D.-I. Polarimetric Attenuation Correction in Heavy Rain at C Band. J. Appl. Meteor. Clim. 2011, 50, 39–58. [Google Scholar] [CrossRef]
- Bebbington, D.; Rae, S.; Bech, J.; Codina, B.; Picanyol, M. Modelling of Weather Radar Echoes from Anomalous Propagation Using a Hybrid Parabolic Equation Method and NWP Model Data. Nat. Hazards Earth Syst. Sci. 2007, 7, 391–398. [Google Scholar] [CrossRef]
- Lee, H.; Kim, S. Ensemble Classification for Anomalous Propagation Echo Detection with Clustering-Based Subset-Selection Method. Atmosphere 2017, 8, 11. [Google Scholar] [CrossRef]
- Einfalt, T.; Szturc, J.; Ośródka, K. The Quality Index for Radar Precipitation Data: A Tower of Babel? Atmos. Sci. Lett. 2010, 11, 139–144. [Google Scholar] [CrossRef]
- Huuskonen, A.; Saltikoff, E.; Holleman, I. The Operational Weather Radar Network in Europe. Bull. Am. Meteor. Soc. 2014, 95, 897–907. [Google Scholar] [CrossRef]
- Saltikoff, E.; Haase, G.; Delobbe, L.; Gaussiat, N.; Martet, M.; Idziorek, D.; Leijnse, H.; Novák, P.; Lukach, M.; Stephan, K. OPERA the Radar Project. Atmosphere 2019, 10, 320. [Google Scholar] [CrossRef]
- Michelson, D.; Henja, A.; Ernes, S.; Haase, G.; Koistinen, J.; Ośródka, K.; Peltonen, T.; Szewczykowski, M.; Szturc, J. BALTRAD Advanced Weather Radar Networking. J. Open Res. Softw. 2018, 6, 12. [Google Scholar] [CrossRef]
- Bringi, V.N.; Chandrasekar, V. Polarimetric Doppler Weather Radar: Principles and Applications; Cambridge University Press: Cambridge, UK, 2001; ISBN 978-0-521-62384-1. [Google Scholar]
- Montopoli, M.; Roberto, N.; Adirosi, E.; Gorgucci, E.; Baldini, L. Investigation of Weather Radar Quantitative Precipitation Estimation Methodologies in Complex Orography. Atmosphere 2017, 8, 34. [Google Scholar] [CrossRef]
- Simpson, M.J.; Fox, N.I. Dual-Polarized Quantitative Precipitation Estimation as a Function of Range. Hydrol. Earth Syst. Sci. 2018, 22, 3375–3389. [Google Scholar] [CrossRef]
- Voormansik, T.; Cremonini, R.; Post, P.; Moisseev, D. Use of Dual-Polarization Weather Radar Quantitative Precipitation Estimation for Climatology. Hydrol. Earth Syst. Sci. Discuss. 2020, 1–14. [Google Scholar] [CrossRef]
- Gjertsen, U.; Šálek, M.; Michelson, D.B. COST Action 717: Use of Radar Observation in Hydrological and NWP Models: Gauge-Adjustement of Radar-Based Precipitation Estimates: Review; COST Action 717; EUR-OP: Luxembourg, 2004; ISBN 978-92-898-0000-6. [Google Scholar]
- Bruen, M.; O’Loughlin, F. Towards a Nonlinear Radar-Gauge Adjustment of Radar via a Piece-Wise Method. Meteorol. Appl. 2014, 21, 675–683. [Google Scholar] [CrossRef]
- Berg, P.; Norin, L.; Olsson, J. Creation of a High Resolution Precipitation Data Set by Merging Gridded Gauge Data and Radar Observations for Sweden. J. Hydrol. 2016, 541, 6–13. [Google Scholar] [CrossRef]
- Goudenhoofdt, E.; Delobbe, L. Evaluation of Radar-Gauge Merging Methods for Quantitative Precipitation Estimates. Hydrol. Earth Syst. Sci. 2009, 13, 195–203. [Google Scholar] [CrossRef]
- Alqudah, A.; Chandrasekar, V.; Le, M. Investigating Rainfall Estimation from Radar Measurements Using Neural Networks. Nat. Hazards Earth Syst. Sci. 2013, 13, 535–544. [Google Scholar] [CrossRef]
- Orellana-Alvear, J.; Célleri, R.; Rollenbeck, R.; Bendix, J. Optimization of X-Band Radar Rainfall Retrieval in the Southern Andes of Ecuador Using a Random Forest Model. Remote Sens. 2019, 11, 1632. [Google Scholar] [CrossRef]
- Fornasiero, A.; Alberoni, P.P.; Amorati, R.; Marsigli, C. Improving the Radar Data Mosaicking Procedure by Means of a Quality Descriptor. In Proceedings of the ERAD, Barcelona, Spain, 18–22 September 2006; pp. 378–381. [Google Scholar]
- Jurczyk, A.; Szturc, J.; Ośródka, K. Quality-Based Compositing of Weather Radar Derived Precipitation. Meteorol. Appl. 2020, 27, e1812. [Google Scholar] [CrossRef]
- Ebert, E.E.; Janowiak, J.E.; Kidd, C. Comparison of Near-Real-Time Precipitation Estimates from Satellite Observations and Numerical Models. Bull. Amer. Meteor. Soc. 2007, 88, 47–64. [Google Scholar] [CrossRef]
- Chumchean, S.; Seed, A.; Sharma, A. Correcting of Real-Time Radar Rainfall Bias Using a Kalman Filtering Approach. J. Hydrol. 2006, 317, 123–137. [Google Scholar] [CrossRef]
- Velasco-Forero, C.A.; Sempere-Torres, D.; Cassiraga, E.F.; Jaime Gómez-Hernández, J. A Non-Parametric Automatic Blending Methodology to Estimate Rainfall Fields from Rain Gauge and Radar Data. Adv. Water Resour. 2009, 32, 986–1002. [Google Scholar] [CrossRef]
- Pereira Filho, A.J.; Crawford, K.C.; Hartzell, C.L. Improving WSR-88D Hourly Rainfall Estimates. Weather Forecast. 1998, 13, 1016–1028. [Google Scholar] [CrossRef]
- Pereira Filho, A.J. Integrating Gauge, Radar and Satellite Rainfall. In Proceedings of the 2nd International Precipitation Working Group Workshop, Monterey, CA, USA, 25–28 October 2004. [Google Scholar]
- Šálek, M.; Novák, P.; Seo, D.-J. Operational Application of Combined Radar and Raingauges Precipitation Estimation at the CHMI. In Proceedings of the ERAD, Copernicus GmbH, Visby, Island of Gotland, Sweden, 6–10 September 2004; pp. 16–20. [Google Scholar]
- Rosenfeld, D.; Wolff, D.B.; Amitai, E. The Window Probability Matching Method for Rainfall Measurements with Radar. J. Appl. Meteor. 1994, 33, 682–693. [Google Scholar] [CrossRef][Green Version]
- Sun, X.; Mein, R.G.; Keenan, T.D.; Elliott, J.F. Flood Estimation Using Radar and Raingauge Data. J. Hydrol. 2000, 239, 4–18. [Google Scholar] [CrossRef]
- Piman, T.; Babel, M.S.; Das Gupta, A.; Weesakul, S. Development of a Window Correlation Matching Method for Improved Radar Rainfall Estimation. Hydrol. Earth Syst. Sci. 2007, 11, 1361–1372. [Google Scholar] [CrossRef]
- Krajewski, W.F. Cokriging Radar-Rainfall and Rain Gage Data. J. Geophys. Res. Atmos. 1987, 92, 9571–9580. [Google Scholar] [CrossRef]
- Seo, D.-J. Real-Time Estimation of Rainfall Fields Using Radar Rainfall and Rain Gage Data. J. Hydrol. 1998, 208, 37–52. [Google Scholar] [CrossRef]
- Haberlandt, U. Geostatistical Interpolation of Hourly Precipitation from Rain Gauges and Radar for a Large-Scale Extreme Rainfall Event. J. Hydrol. 2007, 332, 144–157. [Google Scholar] [CrossRef]
- Delrieu, G.; Wijbrans, A.; Boudevillain, B.; Faure, D.; Bonnifait, L.; Kirstetter, P.-E. Geostatistical Radar–Raingauge Merging: A Novel Method for the Quantification of Rain Estimation Accuracy. Adv. Water Resour. 2014, 71, 110–124. [Google Scholar] [CrossRef]
- Sinclair, S.; Pegram, G. Combining Radar and Rain Gauge Rainfall Estimates Using Conditional Merging. Atmos. Sci. Lett. 2005, 6, 19–22. [Google Scholar] [CrossRef]
- Ehret, U.; Götzinger, J.; Bárdossy, A.; Pegram, G.G.S. Radar-based Flood Forecasting in Small Catchments, Exemplified by the Goldersbach Catchment, Germany. Int. J. River Basin Manag. 2008, 6, 323–329. [Google Scholar] [CrossRef]
- Todini, E. A Bayesian Technique for Conditioning Radar Precipitation Estimates to Rain-Gauge Measurements. Hydrol. Earth Syst. Sci. 2001, 5, 187–199. [Google Scholar] [CrossRef]
- Seo, D.-J.; Breidenbach, J.P. Real-Time Correction of Spatially Nonuniform Bias in Radar Rainfall Data Using Rain Gauge Measurements. J. Hydrometeor. 2002, 3, 93–111. [Google Scholar] [CrossRef]
- Sivasubramaniam, K.; Sharma, A.; Alfredsen, K. Merging Radar and Gauge Information within a Dynamical Model Combination Framework for Precipitation Estimation in Cold Climates. Environ. Model. Softw. 2019, 119, 99–110. [Google Scholar] [CrossRef]
- McKee, J. Evaluation of Gauge-Radar Merging Methods for Quantitative Precipitation Estimation in Hydrology: A Case Study in the Upper Thames River Basin. Electronic Thesis, University of Western Ontario, London, UK, 2015; p. 151. [Google Scholar]
- Saltikoff, E.; Friedrich, K.; Soderholm, J.; Lengfeld, K.; Nelson, B.; Becker, A.; Hollmann, R.; Urban, B.; Heistermann, M.; Tassone, C. An Overview of Using Weather Radar for Climatological Studies: Successes, Challenges, and Potential. Bull. Am. Meteor. Soc. 2019, 100, 1739–1752. [Google Scholar] [CrossRef]
- Chappell, A.; Renzullo, L.J.; Raupach, T.H.; Haylock, M. Evaluating Geostatistical Methods of Blending Satellite and Gauge Data to Estimate near Real-Time Daily Rainfall for Australia. J. Hydrol. 2013, 493, 105–114. [Google Scholar] [CrossRef]
- Todini, E.; Mazzetti, C. A Bayesian Multisensor Combination Approach to Rainfall Estimate. In Proceedings of the 2nd International Symposium on Communications, Control and Signal Processing, Marrakech, Morocco, 13–15 March 2006; p. 5. [Google Scholar]
- Brandes, E.A. Optimizing Rainfall Estimates with the Aid of Radar. J. Appl. Meteor. 1975, 14, 1339–1345. [Google Scholar] [CrossRef]
- Pierce, C.E.; Ebert, E.; Seed, A.W.; Sleigh, M.; Collier, C.G.; Fox, N.I.; Donaldson, N.; Wilson, J.W.; Roberts, R.; Mueller, C.K. The Nowcasting of Precipitation during Sydney 2000: An Appraisal of the QPF Algorithms. Weather Forecast. 2004, 19, 7–21. [Google Scholar] [CrossRef]
- Wilson, J.W.; Feng, Y.; Chen, M.; Roberts, R.D. Nowcasting Challenges during the Beijing Olympics: Successes, Failures, and Implications for Future Nowcasting Systems. Weather Forecast. 2010, 25, 1691–1714. [Google Scholar] [CrossRef]
- Lucas, B.D.; Kanade, T. An Iterative Image Registration Technique with an Application to Stereo Vision. In Proceedings of the 7th international joint conference on Artificial intelligence, San Francisco, CA, USA, 24 August 1981; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1981; Volume 2, pp. 674–679. [Google Scholar]
- Germann, U.; Zawadzki, I. Scale-Dependence of the Predictability of Precipitation from Continental Radar Images. Part I: Description of the Methodology. Mon. Weather Rev. 2002, 130, 2859–2873. [Google Scholar] [CrossRef]
- Bouguet, J.-Y. Pyramidal Implementation of the Lucas Kanade Feature Tracker. Intel Corporation, Microprocessor Research Labs. 2000. Available online: http://robots.stanford.edu/cs223b04/algo_tracking.pdf (accessed on 20 January 2021).
- Ruzanski, E.; Chandrasekar, V.; Wang, Y. The CASA Nowcasting System. J. Atmos. Ocean. Technol. 2011, 28, 640–655. [Google Scholar] [CrossRef]
- Rinehart, R.E.; Garvey, E.T. Three-Dimensional Storm Motion Detection by Conventional Weather Radar. Nature 1978, 273, 287–289. [Google Scholar] [CrossRef]
- Li, L.; Schmid, W.; Joss, J. Nowcasting of Motion and Growth of Precipitation with Radar over a Complex Orography. J. Appl. Meteor. 1995, 34, 1286–1300. [Google Scholar] [CrossRef]
- Johnson, J.T.; MacKeen, P.L.; Witt, A.; Mitchell, E.D.W.; Stumpf, G.J.; Eilts, M.D.; Thomas, K.W. The Storm Cell Identification and Tracking Algorithm: An Enhanced WSR-88D Algorithm. Weather Forecast. 1998, 13, 263–276. [Google Scholar] [CrossRef]
- Dixon, M.; Wiener, G. TITAN: Thunderstorm Identification, Tracking, Analysis, and Nowcasting—A Radar-Based Methodology. J. Atmos. Ocean. Technol. 1993, 10, 785–797. [Google Scholar] [CrossRef]
- Novák, P. The Czech Hydrometeorological Institute’s Severe Storm Nowcasting System. Atmos. Res. 2007, 83, 450–457. [Google Scholar] [CrossRef]
- Reyniers, M. Quantitative Precipitation Forecasts Based on Radar Observations: Principles, Algorithms and Operational Systems; Institut Royal Météorologique de Belgique: Brussel, Belgium, 2008. [Google Scholar]
- Haiden, T.; Kann, A.; Wittmann, C.; Pistotnik, G.; Bica, B.; Gruber, C. The Integrated Nowcasting through Comprehensive Analysis (INCA) System and Its Validation over the Eastern Alpine Region. Weather Forecast. 2011, 26, 166–183. [Google Scholar] [CrossRef]
- Sokol, Z.; Pesice, P. Nowcasting of Precipitation—Advective Statistical Forecast Model (SAM) for the Czech Republic. Atmos. Res. 2012, 103, 70–79. [Google Scholar] [CrossRef]
- Sokol, Z.; Zacharov, P. Nowcasting of Precipitation by an NWP Model Using Assimilation of Extrapolated Radar Reflectivity. Q. J. R. Meteorol. Soc. 2012, 138, 1072–1082. [Google Scholar] [CrossRef]
- Foresti, L.; Panziera, L.; Mandapaka, P.V.; Germann, U.; Seed, A. Retrieval of Analogue Radar Images for Ensemble Nowcasting of Orographic Rainfall. Meteorol. Appl. 2015, 22, 141–155. [Google Scholar] [CrossRef]
- Bližňák, V.; Sokol, Z.; Zacharov, P. Nowcasting of Deep Convective Clouds and Heavy Precipitation: Comparison Study between NWP Model Simulation and Extrapolation. Atmos. Res. 2017, 184, 24–34. [Google Scholar] [CrossRef]
- Mejsnar, J.; Sokol, Z.; Minářová, J. Limits of Precipitation Nowcasting by Extrapolation of Radar Reflectivity for Warm Season in Central Europe. Atmos. Res. 2018, 213, 288–301. [Google Scholar] [CrossRef]
- Germann, U.; Zawadzki, I. Scale Dependence of the Predictability of Precipitation from Continental Radar Images. Part II: Probability Forecasts. J. Appl. Meteor. 2004, 43, 74–89. [Google Scholar] [CrossRef]
- Seed, A.W. A Dynamic and Spatial Scaling Approach to Advection Forecasting. J. Appl. Meteor. 2003, 42, 381–388. [Google Scholar] [CrossRef]
- Foresti, L.; Reyniers, M.; Seed, A.; Delobbe, L. Development and Verification of a Real-Time Stochastic Precipitation Nowcasting System for Urban Hydrology in Belgium. Hydrol. Earth Syst. Sci. 2016, 20, 505–527. [Google Scholar] [CrossRef]
- Schmid, W.; Mecklenburg, S.; Joss, J. Short-Term Risk Forecasts of Severe Weather. Phys. Chem. Earth Part B 2000, 25, 1335–1338. [Google Scholar] [CrossRef]
- Kitzmiller, D.H. One-Hour Forecasts of Radar-Estimated Rainfall by an Extrapolative-Statistical Method; TDL Office Note 96-1; U.S. Department of Commerce: Washington, DC, USA; National Weather Service: Silver Spring, MD, USA; NOAA: Washington, DC, USA, 1996. [Google Scholar]
- Pop, L.; Sokol, Z.; Minářová, J. Nowcasting of the Probability of Accumulated Precipitation Based on the Radar Echo Extrapolation. Atmos. Res. 2019, 216, 1–10. [Google Scholar] [CrossRef]
- Bowler, N.E.; Pierce, C.E.; Seed, A.W. STEPS: A Probabilistic Precipitation Forecasting Scheme Which Merges an Extrapolation Nowcast with Downscaled NWP. Q. J. R. Meteorol. Soc. 2007, 132, 2127–2155. [Google Scholar] [CrossRef]
- Atencia, A.; Zawadzki, I. A Comparison of Two Techniques for Generating Nowcasting Ensembles. Part I: Lagrangian Ensemble Technique. Mon. Weather Rev. 2014, 142, 4036–4052. [Google Scholar] [CrossRef]
- Berenguer, M.; Sempere-Torres, D.; Pegram, G.G.S. SBMcast—An Ensemble Nowcasting Technique to Assess the Uncertainty in Rainfall Forecasts by Lagrangian Extrapolation. J. Hydrol. 2011, 404, 226–240. [Google Scholar] [CrossRef]
- Pegram, G.; Clothier, A. Downscaling Rainfields in Space and Time, Using the String of Beads Model in Time Series Mode. Hydrol. Earth Syst. Sci. 2001, 5. [Google Scholar] [CrossRef]
- Panziera, L.; Germann, U.; Gabella, M.; Mandapaka, P.V. NORA–Nowcasting of Orographic Rainfall by Means of Analogues. Q. J. R. Meteorol. Soc. 2011, 137, 2106–2123. [Google Scholar] [CrossRef]
- Atencia, A.; Zawadzki, I. A Comparison of Two Techniques for Generating Nowcasting Ensembles. Part II: Analogs Selection and Comparison of Techniques. Mon. Wea. Rev. 2015, 143, 2890–2908. [Google Scholar] [CrossRef]
- Pulkkinen, S.; Nerini, D.; Pérez Hortal, A.A.; Velasco-Forero, C.; Seed, A.; Germann, U.; Foresti, L. Pysteps: An Open-Source Python Library for Probabilistic Precipitation Nowcasting (v1.0). Geosci. Model Dev. 2019, 12, 4185–4219. [Google Scholar] [CrossRef]
- Sokol, Z.; Mejsnar, J.; Pop, L.; Bližňák, V. Probabilistic Precipitation Nowcasting Based on an Extrapolation of Radar Reflectivity and an Ensemble Approach. Atmos. Res. 2017, 194, 245–257. [Google Scholar] [CrossRef]
- Huynh, H.T.; Lai, V.S.; Soumaré, I. Stochastic Simulation and Applications in Finance with MATLAB Programs; Wiley Finance; John Wiley & Sons: Chichester, UK; Hoboken, NJ, USA, 2008; ISBN 978-0-470-72538-2. [Google Scholar]
- Kotsuki, S.; Kurosawa, K.; Otsuka, S.; Terasaki, K.; Miyoshi, T. Global Precipitation Forecasts by Merging Extrapolation-Based Nowcast and Numerical Weather Prediction with Locally Optimized Weights. Weather Forecast. 2019, 34, 701–714. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: Cambridge, MA, USA, 2011; ISBN 978-0-12-385022-5. [Google Scholar]
- Lin, C.; Vasić, S.; Kilambi, A.; Turner, B.; Zawadzki, I. Precipitation Forecast Skill of Numerical Weather Prediction Models and Radar Nowcasts. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Golding, B.W. Nimrod: A System for Generating Automated Very Short Range Forecasts. Meteorol. Appl. 1998, 5, 1–16. [Google Scholar] [CrossRef]
- Mai, X.; Zhong, H.; Li, L. Using SVM to Provide Precipitation Nowcasting Based on Radar Data. In Proceedings of the Advances in Natural Computation, Fuzzy Systems and Knowledge Discovery; Liu, Y., Wang, L., Zhao, L., Yu, Z., Eds.; Springer International Publishing: Cham, Switherlands, 2020; pp. 349–356. [Google Scholar]
- He, J.; Chen, K.; Chen, J.; Xu, W.; Tang, L.; Liu, J. A Multi Time Scales SVM Method for Local Short Term Rainfall Prediction. Meteorology 2017, 43, 402–412. [Google Scholar] [CrossRef]
- Liu, Y.; Lipo, W.; Zhao, L.; Yu, Z. Advances in Natural Computation, Fuzzy Systems and Knowledge Discovery: Volume 2; Advances in Intelligent Systems and Computing; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; ISBN 978-3-030-32590-9. [Google Scholar]
- Huang, D.-S.; Bevilacqua, V.; Premaratne, P.; Gupta, P. Intelligent Computing Theories and Application. In Proceedings of the 14th International Conference, ICIC 2018, Wuhan, China, 15–18 August 2018; Springer: Berlin/Heidelberg, Germany, 2018. ISBN 978-3-319-95930-6. [Google Scholar]
- Samsi, S.; Mattioli, C.J.; Veillette, M.S. Distributed Deep Learning for Precipitation Nowcasting. In Proceedings of the HPEC 2019 The IEEE High Performance Extreme Computing Conference, Boston, MA, USA, 17 May–1 June 2019. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.-Y.; Wong, W.; WOO, W. Convolutional LSTM Network: A Machine Learning Approach for Precipitation Nowcasting. In Advances in Neural Information Processing Systems 28; Cortes, C., Lawrence, N.D., Lee, D.D., Sugiyama, M., Garnett, R., Eds.; Curran Associates Inc.: Red Hook, NY, USA, 2015; pp. 802–810. [Google Scholar]
- Ahijevych, D.; Pinto, J.O.; Williams, J.K.; Steiner, M. Probabilistic Forecasts of Mesoscale Convective System Initiation Using the Random Forest Data Mining Technique. Weather Forecast. 2016, 31, 581–599. [Google Scholar] [CrossRef]
- Pierce, C.E.; Hardaker, P.J.; Collier, C.G.; Haggett, C.M. GANDOLF: A System for Generating Automated Nowcasts of Convective Precipitation. Meteorol. Appl. 2000, 7, 341–360. [Google Scholar] [CrossRef]
- Roberts, R.D.; Burgess, D.; Meister, M. Developing Tools for Nowcasting Storm Severity. Weather Forecast. 2006, 21, 540–558. [Google Scholar] [CrossRef]
- Liu, X.; Zhou, K.; Lan, Y.; Mao, X.; Trapp, R.J. On the Construction Principle of Conceptual Models for Severe Convective Weather Forecasting Operations in China. Weather Forecast. 2020, 35, 299–308. [Google Scholar] [CrossRef]
- Ba, M.; Xin, L.; Crockett, J.; Smith, S.B. Evaluation of NCAR’s AutoNowCaster for Operational Application within the National Weather Service. Weather Forecast. 2017, 32, 1477–1490. [Google Scholar] [CrossRef]
- Mueller, C.; Saxen, T.; Roberts, R.; Wilson, J.; Betancourt, T.; Dettling, S.; Oien, N.; Yee, J. NCAR Auto-Nowcast System. Weather Forecast. 2003, 18, 545–561. [Google Scholar] [CrossRef]
- Ducrocq, V.; Lapore, J.-P.; Redelsperger, J.-L.; Orain, F. Initialization of a Fine-Scale Model for Convective-System Prediction: A Case Study. Q. J. R. Meteorol. Soc. 2000, 126, 3041–3065. [Google Scholar] [CrossRef]
- Zhang, F.; Snyder, C.; Sun, J. Impacts of Initial Estimate and Observation Availability on Convective-Scale Data Assimilation with an Ensemble Kalman Filter. Mon. Weather Rev. 2004, 132, 1238–1253. [Google Scholar] [CrossRef]
- Gustafsson, N.; Janjić, T.; Schraff, C.; Leuenberger, D.; Weissmann, M.; Reich, H.; Brousseau, P.; Montmerle, T.; Wattrelot, E.; Bučánek, A.; et al. Survey of Data Assimilation Methods for Convective-Scale Numerical Weather Prediction at Operational Centres. Q. J. R. Meteorol. Soc. 2018, 144, 1218–1256. [Google Scholar] [CrossRef]
- Holton, J.R. An Introduction to Dynamic Meteorology, 2nd ed.; Academic Press: New York, NY, USA, 1992; ISBN 978-0-12-354360-8. [Google Scholar]
- Leuenberger, D.; Rossa, A. Revisiting the Latent Heat Nudging Scheme for the Rainfall Assimilation of a Simulated Convective Storm. Meteorol. Atmos. Phys. 2007, 98, 195–215. [Google Scholar] [CrossRef]
- Stephan, K.; Klink, S.; Schraff, C. Assimilation of Radar-Derived Rain Rates into the Convective-Scale Model COSMO-DE at DWD. Q. J. R. Meteorol. Soc. 2008, 134, 1315–1326. [Google Scholar] [CrossRef]
- Jones, C.D.; Macpherson, B. A Latent Heat Nudging Scheme for the Assimilation of Precipitation Data into an Operational Mesoscale Model. Meteorol. Appl. 1997, 4, 269–277. [Google Scholar] [CrossRef]
- Falkovich, A.; Kalnay, E.; Lord, S.; Mathur, M.B. A New Method of Observed Rainfall Assimilation in Forecast Models. J. Appl. Meteor. 2000, 39, 1282–1298. [Google Scholar] [CrossRef]
- Sokol, Z.; Rezacova, D. Assimilation of the Radar-Derived Water Vapour Mixing Ratio into the LM COSMO Model with a High Horizontal Resolution. Atmos. Res. 2009, 92, 331–342. [Google Scholar] [CrossRef]
- Sokol, Z. Effects of an Assimilation of Radar and Satellite Data on a Very-Short Range Forecast of Heavy Convective Rainfalls. Atmos. Res. 2009, 93, 188–206. [Google Scholar] [CrossRef]
- Barker, D.M.; Huang, W.; Guo, Y.-R.; Bourgeois, A.J.; Xiao, Q.N. A Three-Dimensional Variational Data Assimilation System for MM5: Implementation and Initial Results. Mon. Weather Rev. 2004, 132, 897–914. [Google Scholar] [CrossRef]
- Lewis, J.M.; Derber, J.C. The Use of Adjoint Equations to Solve a Variational Adjustment Problem with Advective Constraints. Tellus A Dyn. Meteorol. Oceanogr. 1985, 37, 309–322. [Google Scholar] [CrossRef]
- Huang, X.-Y.; Xiao, Q.; Barker, D.M.; Zhang, X.; Michalakes, J.; Huang, W.; Henderson, T.; Bray, J.; Chen, Y.; Ma, Z.; et al. Four-Dimensional Variational Data Assimilation for WRF: Formulation and Preliminary Results. Mon. Weather Rev. 2009, 137, 299–314. [Google Scholar] [CrossRef]
- Evensen, G. Sequential Data Assimilation with a Nonlinear Quasi-Geostrophic Model Using Monte Carlo Methods to Forecast Error Statistics. J. Geophys. Res. Ocean. 1994, 99, 10143–10162. [Google Scholar] [CrossRef]
- Gustafsson, N.; Bojarova, J.; Vignes, O. A Hybrid Variational Ensemble Data Assimilation for the HIgh Resolution Limited Area Model (HIRLAM). Nonlin. Process. Geophys. 2014, 21, 303–323. [Google Scholar] [CrossRef]
- Johnson, A.; Wang, X.; Carley, J.R.; Wicker, L.J.; Karstens, C. A Comparison of Multiscale GSI-Based EnKF and 3DVar Data Assimilation Using Radar and Conventional Observations for Midlatitude Convective-Scale Precipitation Forecasts. Mon. Weather Rev. 2015, 143, 3087–3108. [Google Scholar] [CrossRef]
- Gao, S.; Min, J. Comparison of 3DVar and EnSRF Data Assimilation Using Radar Observations for the Analysis and Prediction of an MCS. Adv. Meteorol. 2018, 2018, 1–18. [Google Scholar] [CrossRef]
- Mazzarella, V.; Maiello, I.; Capozzi, V.; Budillon, G.; Ferretti, R. Comparison between 3D-Var and 4D-Var Data Assimilation Methods for the Simulation of a Heavy Rainfall Case in Central Italy. Adv. Sci. Res. 2017, 14, 271–278. [Google Scholar] [CrossRef]
- Gao, J.; Stensrud, D.J. Assimilation of Reflectivity Data in a Convective-Scale, Cycled 3DVAR Framework with Hydrometeor Classification. J. Atmos. Sci. 2012, 69, 1054–1065. [Google Scholar] [CrossRef]
- Dowell, D.C.; Wicker, L.J.; Snyder, C. Ensemble Kalman Filter Assimilation of Radar Observations of the 8 May 2003 Oklahoma City Supercell: Influences of Reflectivity Observations on Storm-Scale Analyses. Mon. Weather Rev. 2011, 139, 272–294. [Google Scholar] [CrossRef]
- Snook, N.; Xue, M.; Jung, Y. Analysis of a Tornadic Mesoscale Convective Vortex Based on Ensemble Kalman Filter Assimilation of CASA X-Band and WSR-88D Radar Data. Mon. Weather Rev. 2011, 139, 3446–3468. [Google Scholar] [CrossRef]
- Yussouf, N.; Stensrud, D.J. Comparison of Single-Parameter and Multiparameter Ensembles for Assimilation of Radar Observations Using the Ensemble Kalman Filter. Mon. Weather Rev. 2012, 140, 562–586. [Google Scholar] [CrossRef]
- Sun, J.; Crook, N.A. Dynamical and Microphysical Retrieval from Doppler Radar Observations Using a Cloud Model and Its Adjoint. Part I: Model Development and Simulated Data Experiments. J. Atmos. Sci. 1997, 54, 1642–1661. [Google Scholar] [CrossRef]
- Caya, A.; Sun, J.; Snyder, C. A Comparison between the 4DVAR and the Ensemble Kalman Filter Techniques for Radar Data Assimilation. Mon. Weather Rev. 2005, 133, 3081–3094. [Google Scholar] [CrossRef]
- Chandrasekar, V.; Lim, S.; Bharadwaj, N.; Li, W.; McLaughlin, D.; Bringi, V.N.; Gorgucci, E. Principles of Networked Weather Radar Operation at Attenuating Frequencies. In Proceedings of the ERAD, Visby, Island of Gotland, Sweeden, 6–10 September 2004; pp. 109–114. [Google Scholar]
- Wang, Y.; Wang, X. Direct Assimilation of Radar Reflectivity without Tangent Linear and Adjoint of the Nonlinear Observation Operator in the GSI-Based EnVar System: Methodology and Experiment with the 8 May 2003 Oklahoma City Tornadic Supercell. Mon. Weather Rev. 2017, 145, 1447–1471. [Google Scholar] [CrossRef]
- Duda, J.D.; Wang, X.; Wang, Y.; Carley, J.R. Comparing the Assimilation of Radar Reflectivity Using the Direct GSI-Based Ensemble–Variational (EnVar) and Indirect Cloud Analysis Methods in Convection-Allowing Forecasts over the Continental United States. Mon. Weather Rev. 2019, 147, 1655–1678. [Google Scholar] [CrossRef]
- James, C.; Houze, R.A. A Real-Time Four-Dimensional Doppler Dealiasing Scheme. J. Atmos. Ocean. Technol. 2001, 18, 1674–1683. [Google Scholar] [CrossRef]
- Xu, Q.; Nai, K.; Liu, S.; Karstens, C.; Smith, T.; Zhao, Q. Improved Doppler Velocity Dealiasing for Radar Data Assimilation and Storm-Scale Vortex Detection. Adv. Meteorol. 2013, 2013, 1–10. [Google Scholar] [CrossRef]
- He, G.; Sun, J.; Ying, Z.; Zhang, L. A Radar Radial Velocity Dealiasing Algorithm for Radar Data Assimilation and Its Evaluation with Observations from Multiple Radar Networks. Remote Sens. 2019, 11, 2457. [Google Scholar] [CrossRef]
- Kato, R.; Shimizu, S.; Shimose, K.; Iwanami, K. Storm, Flood and Landslide Research Division, National Research Institute for Earth Science and Disaster Resilience (NIED) 3-1 Tennodai, Tsukuba, Ibaraki 305-0006, Japan Very Short Time Range Forecasting Using CReSS-3DVAR for a Meso-γ-Scale, Localized, Extremely Heavy Rainfall Event: Comparison with an Extrapolation-Based Nowcast. J. Disaster Res. 2017, 12, 967–979. [Google Scholar] [CrossRef]
- Zhang, L.; Tian, X.; Zhang, H. Application of Multigrid NLS-4DVar in Radar Radial Velocity Data Assimilation with WRF-ARW. Atmos. Ocean. Sci. Lett. 2019, 12, 409–416. [Google Scholar] [CrossRef]
- Zhang, B.; Tian, X.; Sun, J.; Chen, F.; Zhang, Y.; Zhang, L.; Fu, S. PODEn4DVar-Based Radar Data Assimilation Scheme: Formulation and Preliminary Results from Real-Data Experiments with Advanced Research WRF (ARW). Tellus A Dyn. Meteorol. Oceanogr. 2015, 67, 26045. [Google Scholar] [CrossRef]
- Snyder, C.; Zhang, F. Assimilation of Simulated Doppler Radar Observations with an Ensemble Kalman Filter. Mon. Weather Rev. 2003, 131, 1663–1677. [Google Scholar] [CrossRef]
- Chen, Y.; Snyder, C. Assimilating Vortex Position with an Ensemble Kalman Filter. Mon. Weather Rev. 2007, 135, 1828–1845. [Google Scholar] [CrossRef]
- Zeng, Y.; Janjić, T.; de Lozar, A.; Welzbacher, C.A.; Blahak, U.; Seifert, A. Assimilating Radar Radial Wind and Reflectivity Data in an Idealized Setup of the COSMO-KENDA System. Atmos. Res. 2021, 249, 105282. [Google Scholar] [CrossRef]
- Seo, D.-J.; Habib, E.; Andrieu, H.; Morin, E. Hydrologic Applications of Weather Radar. J. Hydrol. 2015, 531, 231–233. [Google Scholar] [CrossRef]
- Berne, A.; Krajewski, W.F. Radar for Hydrology: Unfulfilled Promise or Unrecognized Potential? Adv. Water Resour. 2013, 51, 357–366. [Google Scholar] [CrossRef]
- Loumagne, C.; Normand, M.; Riffard, M.; Weisse, A.; Quesney, A.; Hégarat-Mascle, S.L.; Alem, F. Integration of Remote Sensing Data into Hydrological Models for Reservoir Management. Hydrol. Sci. J. 2001, 46, 89–102. [Google Scholar] [CrossRef]
- Loritz, R.; Hrachowitz, M.; Neuper, M.; Zehe, E. The Role and Value of Distributed Precipitation Data for Hydrological Models. Hydrol. Earth Syst. Sci. 2020, 25, 147–167. [Google Scholar] [CrossRef]
- Li, Y.; Grimaldi, S.; Walker, J.P.; Pauwels, V.R.N. Application of Remote Sensing Data to Constrain Operational Rainfall-Driven Flood Forecasting: A Review. Remote Sens. 2016, 8, 456. [Google Scholar] [CrossRef]
- Ridler, M.-E.; Madsen, H.; Stisen, S.; Bircher, S.; Fensholt, R. Assimilation of SMOS-Derived Soil Moisture in a Fully Integrated Hydrological and Soil-Vegetation-Atmosphere Transfer Model in Western Denmark. Water Resour. Res. 2014, 50, 8962–8981. [Google Scholar] [CrossRef]
- Gabriele, S.; Chiaravalloti, F.; Procopio, A. Radar–Rain-Gauge Rainfall Estimation for Hydrological Applications in Small Catchments. In Proceedings of the Advances in Geosciences, Fargau-Pratjau, Germany, 12 July 2017; Volume 44, pp. 61–66. [Google Scholar]
- Delrieu, G.; Braud, I.; Berne, A.; Borga, M.; Boudevillain, B.; Fabry, F.; Freer, J.; Gaume, E.; Nakakita, E.; Seed, A.; et al. Weather Radar and Hydrology. Adv. Water Resour. 2009, 32, 969–974. [Google Scholar] [CrossRef]
- Mosavi, A.; Ozturk, P.; Chau, K. Flood Prediction Using Machine Learning Models: Literature Review. Water 2018, 10, 1536. [Google Scholar] [CrossRef]
- Dinu, C.; Drobot, R.; Pricop, C.; Blidaru, T.V. Genetic Programming Technique Applied for Flash-Flood Modelling Using Radar Rainfall Estimates. Math. Model. Civ. Eng. 2017, 13, 27–38. [Google Scholar] [CrossRef][Green Version]
- Orellana-Alvear, J.; Célleri, R.; Rollenbeck, R.; Muñoz, P.; Contreras, P.; Bendix, J. Assessment of Native Radar Reflectivity and Radar Rainfall Estimates for Discharge Forecasting in Mountain Catchments with a Random Forest Model. Remote Sens. 2020, 12, 1986. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–Runoff Modelling Using Long Short-Term Memory (LSTM) Networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef]
- Xiang, Z.; Demir, I. Distributed Long-Term Hourly Streamflow Predictions Using Deep Learning—A Case Study for State of Iowa. Environ. Model. Softw. 2020, 131, 104761. [Google Scholar] [CrossRef]
- Smith, P.J.; Panziera, L.; Beven, K.J. Forecasting Flash Floods Using Data-Based Mechanistic Models and NORA Radar Rainfall Forecasts. Hydrol. Sci. J. 2014, 59, 1403–1417. [Google Scholar] [CrossRef]
- Borga, M. Accuracy of Radar Rainfall Estimates for Streamflow Simulation. J. Hydrol. 2002, 267, 26–39. [Google Scholar] [CrossRef]
- Seo, B.-C.; Krajewski, W.F.; Quintero, F.; ElSaadani, M.; Goska, R.; Cunha, L.K.; Dolan, B.; Wolff, D.B.; Smith, J.A.; Rutledge, S.A.; et al. Comprehensive Evaluation of the IFloodS Radar Rainfall Products for Hydrologic Applications. J. Hydrometeor. 2018, 19, 1793–1813. [Google Scholar] [CrossRef]
- Cecinati, F.; Rico-Ramirez, M.A.; Heuvelink, G.B.M.; Han, D. Representing Radar Rainfall Uncertainty with Ensembles Based on a Time-Variant Geostatistical Error Modelling Approach. J. Hydrol. 2017, 548, 391–405. [Google Scholar] [CrossRef]
- Dai, Q.; Han, D.; Zhuo, L.; Huang, J.; Islam, T.; Srivastava, P.K. Impact of Complexity of Radar Rainfall Uncertainty Model on Flow Simulation. Atmos. Res. 2015, 161–162, 93–101. [Google Scholar] [CrossRef]
- Beven, K.; Binley, A. The Future of Distributed Models: Model Calibration and Uncertainty Prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Poméon, T.; Wagner, N.; Furusho, C.; Kollet, S.; Reinoso-Rondinel, R. Performance of a PDE-Based Hydrologic Model in a Flash Flood Modeling Framework in Sparsely-Gauged Catchments. Water 2020, 12, 2157. [Google Scholar] [CrossRef]
- Seo, B.-C.; Cunha, L.K.; Krajewski, W.F. Uncertainty in Radar-Rainfall Composite and Its Impact on Hydrologic Prediction for the Eastern Iowa Flood of 2008. Water Resour. Res. 2013, 49, 2747–2764. [Google Scholar] [CrossRef]
- Paz, I.; Tchiguirinskaia, I.; Schertzer, D. Rain Gauge Networks’ Limitations and the Implications to Hydrological Modelling Highlighted with a X-Band Radar. J. Hydrol. 2020, 583, 124615. [Google Scholar] [CrossRef]
- Zhu, D.H.; Peng, D.Z.; Cluckie, I.D. Statistical Analysis of Error Propagation from Radar Rainfall to Hydrological Models. Hydrol. Earth Syst. Sci. Discuss. 2012, 9, 10277–10302. [Google Scholar] [CrossRef]
- Sikorska, A.E.; Seibert, J. Value of Different Precipitation Data for Flood Prediction in an Alpine Catchment: A Bayesian Approach. J. Hydrol. 2018, 556, 961–971. [Google Scholar] [CrossRef]
- Shakti, P.C.; Tsuyoshi, N.; Ryohei, M. The Role of the Spatial Distribution of Radar Rainfall on Hydrological Modeling for an Urbanized River Basin in Japan. Water 2019, 11, 1703. [Google Scholar] [CrossRef]
- Paz, I.; Willinger, B.; Gires, A.; Alves de Souza, B.; Monier, L.; Cardinal, H.; Tisserand, B.; Tchiguirinskaia, I.; Schertzer, D. Small-Scale Rainfall Variability Impacts Analyzed by Fully-Distributed Model Using C-Band and X-Band Radar Data. Water 2019, 11, 1273. [Google Scholar] [CrossRef]
- Anagnostou, M.N.; Nikolopoulos, E.I.; Kalogiros, J.; Anagnostou, E.N.; Marra, F.; Mair, E.; Bertoldi, G.; Tappeiner, U.; Borga, M. Advancing Precipitation Estimation and Streamflow Simulations in Complex Terrain with X-Band Dual-Polarization Radar Observations. Remote Sens. 2018, 10, 1258. [Google Scholar] [CrossRef]
- Cristiano, E.; ten Veldhuis, M.-C.; van de Giesen, N. Spatial and Temporal Variability of Rainfall and Their Effects on Hydrological Response in Urban Areas—A Review. Hydrol. Earth Syst. Sci. 2017, 21, 3859–3878. [Google Scholar] [CrossRef]
- Cristiano, E.; Veldhuis, M.; Wright, D.B.; Smith, J.A.; van de Giesen, N. The Influence of Rainfall and Catchment Critical Scales on Urban Hydrological Response Sensitivity. Water Resour. Res. 2019, 55, 3375–3390. [Google Scholar] [CrossRef]
- Lobligeois, F.; Andréassian, V.; Perrin, C.; Tabary, P.; Loumagne, C. When Does Higher Spatial Resolution Rainfall Information Improve Streamflow Simulation? An Evaluation Using 3620 Flood Events. Hydrol. Earth Syst. Sci. 2014, 18, 575–594. [Google Scholar] [CrossRef]
- Ochoa-Rodriguez, S.; Wang, L.-P.; Willems, P.; Onof, C. A Review of Radar-Rain Gauge Data Merging Methods and Their Potential for Urban Hydrological Applications. Water Resour. Res. 2019, 55, 6356–6391. [Google Scholar] [CrossRef]
- McKee, J.L.; Binns, A.D. A Review of Gauge–Radar Merging Methods for Quantitative Precipitation Estimation in Hydrology. Can. Water Resour. J./Rev. Can. Des Ressour. Hydr. 2016, 41, 186–203. [Google Scholar] [CrossRef]
- Jadidoleslam, N.; Mantilla, R.; Krajewski, W.F.; Goska, R. Investigating the Role of Antecedent SMAP Satellite Soil Moisture, Radar Rainfall and MODIS Vegetation on Runoff Production in an Agricultural Region. J. Hydrol. 2019, 579, 124210. [Google Scholar] [CrossRef]
- Heuvelink, D.; Berenguer, M.; Brauer, C.C.; Uijlenhoet, R. Hydrological Application of Radar Rainfall Nowcasting in The Netherlands. Environ. Int. 2020, 136, 105431. [Google Scholar] [CrossRef]
- Yu, W.; Nakakita, E.; Kim, S.; Yamaguchi, K. Improvement of Rainfall and Flood Forecasts by Blending Ensemble NWP Rainfall with Radar Prediction Considering Orographic Rainfall. J. Hydrol. 2015, 531, 494–507. [Google Scholar] [CrossRef]
- Alfieri, L.; Berenguer, M.; Knechtl, V.; Liechti, K.; Sempere-Torres, D.; Zappa, M. Flash Flood Forecasting Based on Rainfall Thresholds. In Handbook of Hydrometeorological Ensemble Forecasting; Duan, Q., Pappenberger, F., Thielen, J., Wood, A., Cloke, H.L., Schaake, J.C., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 1–38. ISBN 978-3-642-40457-3. [Google Scholar]
- Bouilloud, L.; Delrieu, G.; Boudevillain, B.; Kirstetter, P.-E. Radar Rainfall Estimation in the Context of Post-Event Analysis of Flash-Flood Events. J. Hydrol. 2010, 394, 17–27. [Google Scholar] [CrossRef]
- Marchi, L.; Borga, M.; Preciso, E.; Gaume, E. Characterisation of Selected Extreme Flash Floods in Europe and Implications for Flood Risk Management. J. Hydrol. 2010, 394, 118–133. [Google Scholar] [CrossRef]
- Bronstert, A.; Agarwal, A.; Boessenkool, B.; Crisologo, I.; Fischer, M.; Heistermann, M.; Köhn-Reich, L.; López-Tarazón, J.A.; Moran, T.; Ozturk, U.; et al. Forensic Hydro-Meteorological Analysis of an Extreme Flash Flood: The 2016-05-29 Event in Braunsbach, SW Germany. Sci. Total Environ. 2018, 630, 977–991. [Google Scholar] [CrossRef] [PubMed]
- Borga, M.; Comiti, F.; Ruin, I.; Marra, F. Forensic Analysis of Flash Flood Response. Wires Water 2019, 6, e1338. [Google Scholar] [CrossRef]
- Borga, M.; Gaume, E.; Creutin, J.D.; Marchi, L. Surveying Flash Floods: Gauging the Ungauged Extremes. Hydrol. Process. 2008, 22, 3883–3885. [Google Scholar] [CrossRef]
- Javelle, P.; Demargne, J.; Defrance, D.; Pansu, J.; Arnaud, P. Evaluating Flash-Flood Warnings at Ungauged Locations Using Post-Event Surveys: A Case Study with the AIGA Warning System. Hydrol. Sci. J. 2014, 59, 1390–1402. [Google Scholar] [CrossRef]
- Borga, M.; Stoffel, M.; Marchi, L.; Marra, F.; Jakob, M. Hydrogeomorphic Response to Extreme Rainfall in Headwater Systems: Flash Floods and Debris Flows. J. Hydrol. 2014, 518, 194–205. [Google Scholar] [CrossRef]

| Measurement Technique | Spatial Resolution | Temporal Resolution | The Most Important Properties for Combination |
|---|---|---|---|
| Recording rain gauge network | Point measurements interpolated spatially | 1 min–1 h | Measurements considered of relatively high quality at gauge locations. |
| Weather radar network | 0.5–2.0 km | 5–15 min | Numerous measurement errors. Good high-resolution reproduction of spatial distribution of precipitation field. |
| Meteorological satellite Meteosat or GOES (VIS and IR channels) | About 4–6 km (depending on latitude) | 5–15 min | Low spatial resolution and approximate measurements. Good reproduction of location of clouds and convective phenomena. High data availability. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sokol, Z.; Szturc, J.; Orellana-Alvear, J.; Popová, J.; Jurczyk, A.; Célleri, R. The Role of Weather Radar in Rainfall Estimation and Its Application in Meteorological and Hydrological Modelling—A Review. Remote Sens. 2021, 13, 351. https://doi.org/10.3390/rs13030351
Sokol Z, Szturc J, Orellana-Alvear J, Popová J, Jurczyk A, Célleri R. The Role of Weather Radar in Rainfall Estimation and Its Application in Meteorological and Hydrological Modelling—A Review. Remote Sensing. 2021; 13(3):351. https://doi.org/10.3390/rs13030351
Chicago/Turabian StyleSokol, Zbyněk, Jan Szturc, Johanna Orellana-Alvear, Jana Popová, Anna Jurczyk, and Rolando Célleri. 2021. "The Role of Weather Radar in Rainfall Estimation and Its Application in Meteorological and Hydrological Modelling—A Review" Remote Sensing 13, no. 3: 351. https://doi.org/10.3390/rs13030351
APA StyleSokol, Z., Szturc, J., Orellana-Alvear, J., Popová, J., Jurczyk, A., & Célleri, R. (2021). The Role of Weather Radar in Rainfall Estimation and Its Application in Meteorological and Hydrological Modelling—A Review. Remote Sensing, 13(3), 351. https://doi.org/10.3390/rs13030351