Abstract
In the past few years, demands on flash flood forecasting have grown. The Flash Flood Indicator (FFI) is a system used at the Czech Hydrometeorological Institute for the evaluation of the risk of possible occurrence of flash floods over the whole Czech Republic. The FFI calculation is based on the current soil saturation, the physical-geographical characteristics of every considered area, and radar-based quantitative precipitation estimates (QPEs) and forecasts (QPFs). For higher reliability of the flash flood risk assessment, calculations of QPEs and QPFs are crucial, particularly when very high intensities of rainfall are reached or expected. QPEs and QPFs entering the FFI computations are the products of the Czech Weather Radar Network. The QPF is based on the COTREC extrapolation method. The radar-rain gauge-combining method MERGE2 is used to improve radar-only QPEs and QPFs. It generates a combined radar-rain gauge QPE based on the kriging with an external drift algorithm, and, also, an adjustment coefficient applicable to radar-only QPEs and QPFs. The adjustment coefficient is applied in situations when corresponding rain gauge measurements are not yet available. A new adjustment coefficient scheme was developed and tested to improve the performance of adjusted radar QPEs and QPFs in the FFI.
1. Introduction
The Czech Hydrometeorological Institute (CHMI) is the national weather service of the Czech Republic and, as such, it operates the Czech Weather Radar Network (CZRAD) [1,2]. Calculation of radar-based quantitative precipitation estimates (QPEs) started at the CHMI in 1996, shortly after establishing the CZRAD that covered the whole area of the Czech Republic and its neighborhood by digital radar measurements. Even though the first QPEs were calculated from non-optimized maximum reflectivity products without any subsequent corrections, their usefulness was proven. However, the need for further improvements was also clearly stated [3,4]. Therefore, several improvements were implemented in the following years. The maximum reflectivity product was replaced by the more appropriate PseudoCAPPI 2 km product (radar reflectivity from 2 km above sea level (ASL) or the closest level if data from 2 km ASL are not available), which mainly improved the overestimation of radar QPEs close to the radars [5,6]. Since only a very limited amount of rain gauge data was available on-line in the 1990s, the vertical profile of reflectivity (VPR) correction and statistical corrections based on off-line rain gauge data were developed [5,6] to correct the most significant problems connected with radar-only QPEs, that is, the underestimation of radar-only QPEs at bigger distances from the radar and in mountainous areas. As the number of digital on-line rain gauge measurements was increasing at the end of the 1990s, a new, more effective method of radar QPE correction was developed. The new method, named MERGE, that combines radar and on-line rain gauge data was introduced into the CHMI operation in 2003 [7]. The MERGE method was continuously developed, and a significant update was introduced in 2009 [8,9]. In 2014, it was completely rewritten, but its principal philosophy remained the same. The last version, which is called MERGE2, has been used until today [10,11]. MERGE2 generates a combined radar-rain gauge QPE (called MERGE) based on kriging with external drift, and, also, an adjustment coefficient applicable to radar-only QPEs in situations when corresponding rain gauge measurements are not yet available.
Radar-based quantitative precipitation forecasts (QPFs) are calculated from extrapolated PseudoCAPPI 2 km products using the COTREC motion field. Operational calculation of the COTREC motion field started at the CHMI in 2003 [1]. Radar QPFs up to 3 h based on the COTREC extrapolation has been operationally calculated since 2007 [12]. The MERGE2 adjustment coefficient is applied to radar-only QPFs to improve the quality of the forecasts.
Radar-based QPEs and QPFs are used by a wide range of users and applications. Hydrological modeling and warnings belong to a very important part of flood forecasting services. In most cases, radar-based QPEs and QPFs are used by rainfall-runoff hydrological models for operative discharge prediction in catchments of a typical area of about thousands of square kilometers [13]. These models are not oriented on flash flood prediction; however, use of radar-based QPEs and QPFs for flash flood prediction was also evaluated [14,15]. Radar-based QPEs and QPFs are used also by the Flash Flood Indicator (FFI) application [16] that has been running operationally for several years at the CHMI. The FFI evaluates the risk of a possible occurrence of flash floods in defined areas of an average size of several square kilometers over the whole Czech Republic. For higher reliability of the flash flood risk assessment, calculations of QPEs and QPFs are crucial, particularly when very high intensities of rainfall are reached or expected. Because of its focus on flash flood nowcasting, the FFI has more pressing needs for timely inputs, which partially excludes the MERGE product that is available with a bigger time delay after the end of measurements. Instead, the adjustment coefficient applied to radar-only QPEs and QPFs is used. It turned out that in intense convective and convective-stratiform situations with the highest flash flood risk, the adjustment coefficient deficiencies are enhanced, which requires special care and corrections in order to obtain the best and most reliable results.
The purpose of this paper is to describe radar-based QPE and QPF computation and its utilization for flash flood nowcasting at the CHMI. The paper introduces the radar-based QPE based on a new local bias adjustment scheme and shows its statistical evaluation, as well as its performance as an FFI input.
2. Materials and Methods
2.1. Radar-Only QPE
The radar-only QPE is based on the PseudoCAPPI 2 km radar product [17,18], which was identified to be optimal for rainfall estimates over the territory of the Czech Republic [6]. It is close enough to the ground to be representative of the rainfall at the ground, but on the other hand, far enough not to be significantly influenced, such as by the ground clutters or orography attenuation.
The composite of PseudoCAPPI 2 km is based primarily on data from two CZRAD radars (radar Brdy-Praha and radar Skalky) covering the whole area of the Czech Republic and its neighborhood, see Figure 1. If data from any CZRAD radar are not available (in case of radar failure or maintenance), then exchanged data from neighboring German or Slovak radars are used to fill the gap. In 2015, the CHMI replaced both radars with new state-of-the-art C-band polarimetric Doppler weather radars Vaisala WRM 200 [2]. These new radars are much more effective than the previous radars when it comes to the removal of non-meteorological echoes (mainly RLAN/WIFI interferences, wind farms, etc.) from corrected radar reflectivity volume data. The new polarimetric radars also enabled correction of attenuation of the radar signal in intense precipitation. Horizontal resolution of the PseudoCAPPI 2 km composites is 1 × 1 km.
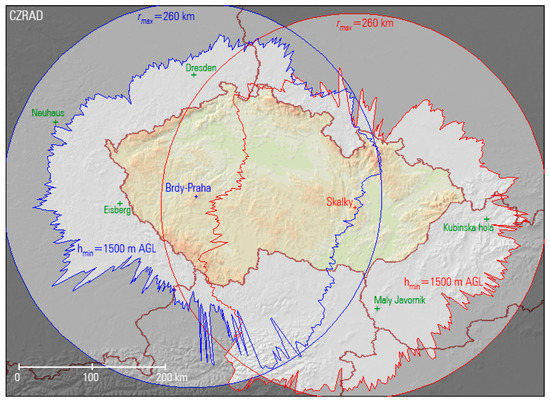
Figure 1.
The Czech Weather Radar Network—locations of radars (crosses), maximum coverage of radars (circles) and coverage for precipitation estimation according to the recommendations of the project COST 73 (the lowest usable beam 1500 m above ground level) [19,20]. Locations of the gap-filling German and Slovak radars (i.e., used in case of unavailability of Czech radars) are depicted by a green color.
Originally, compositing of PseudoCAPPI 2 km used the maximum reflectivity approach, that is, the highest reflectivity value from all available radars was used in each grid point. This approach is very useful to correct problems of attenuation of radar echoes by close intense precipitation, if the attenuated area is in the reach of another non-attenuated radar [21]. However, the attenuation by intense precipitation became less significant after upgrading the CZRAD when polarimetric correction of precipitation attenuation was introduced. On the other hand, another aspect of this compositing approach, which sometimes caused problems, became more important. It was the detection of overhanging precipitation (e.g., storm anvils) at the bigger distances from the radar. Specific issues posed the lowest radar beam that was significantly higher than 2 km ASL. Therefore, since 2020, the composition method of the PseudoCAPPI 2 km products has been changed. Currently, the quality-based compositing approach is used; the highest reflectivity value from all radars measured within ±200 m from 2 km ASL is used in each grid point. If no radar measurement is available at this level in a given grid point, then the radar measurement from the altitude closest to 2 km ASL is used, regardless of its value. An example of the comparison of the old and new PseudoCAPPI 2 km composite approaches is shown in Figure 2. Part of the higher-altitude storm anvil can be seen in the old PseudoCAPPI 2 km composite that has been reduced in the new type of composite.
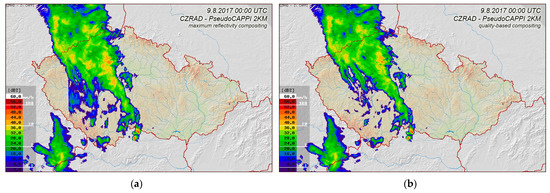
Figure 2.
Difference between the old maximum reflectivity compositing (a) and the new quality-based compositing (b) of the PseudoCAPPI 2 km product. The difference is most apparent in the middle-left part of the composites.
The Marshall–Palmer Z-R relationship [22] is used for conversion of the radar reflectivity into the rainfall rate. Although the Z-R relationship coefficients may take on a large number of values depending on the precipitation type and geographical location, the relationship in the form
is predominantly used over the European continent, and is also used at the CHMI. In this equation, Z is the radar reflectivity factor in [mm6 m–3] and R is the rainfall rate in [mm h–1]. In addition, two thresholds are applied to the converted rainfall rate values:
- For Z < 7 dBZ, R = 0 mm h–1; threshold condition is used to eliminate weak non-precipitation echoes,
- For Z ≥ 55 dBZ, R = 99.85 mm h–1; threshold condition is applied to reduce rainfall rate overestimation caused by the occurrence of hails in cores of convective storms.
These thresholds were derived on the basis of independent internal analysis [6], however, they are similar to the thresholds used in other meteorological services [18,23].
Converted rainfall rate fields are, in the next step, integrated for given time periods to get the radar-only QPE. The CZRAD radar measurements are updated every 5 min, which should be fine in most cases to get the realistic smooth areal rainfall estimate. Problems may occur in the case of fast-moving precipitation clouds when we can see periodic changes in rainfall along their path (‘stroboscopic’ effect). To eliminate this effect, the PseudoCAPPI 2 km products are interpolated into fields with a 1 min time-step using the COTREC motion field [1] before the accumulation. Figure 3 shows that the interpolation into 1 min time-steps is sufficient to effectively suppress the ‘stroboscopic’ effect. In operation, rainfall accumulations (radar-only QPEs) are calculated every 5 min for different time intervals (15 min, 1 h, 3 h, 6 h, 12 h, 24 h, 72 h).
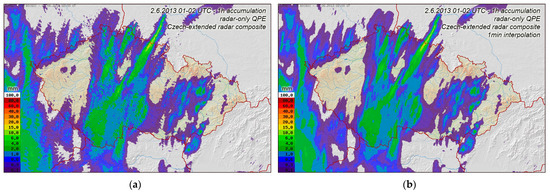
Figure 3.
An example of the comparison of 1 h radar-only QPEs calculated from the non-interpolated (a) and interpolated (b) PseudoCAPPI 2 km composites. A ‘stroboscopic’ effect is apparent in the QPE using the non-interpolated PseudoCAPPI 2 km composites.
2.2. MERGE2—Combined Radar-Rain Gauge QPE
Every 10 min, as the new rain gauge measurements are available, the advanced radar-rain gauge combining method MERGE2 (see [10,11]) is run operationally to improve the radar-only QPE. The method generates the combined radar-rain gauge QPE, called the MERGE product (or simply MERGE), and, also, an adjustment coefficient applicable to the radar-only QPE or the radar-only extrapolation QPF. The MERGE2 method was developed as a universal tool for all types of precipitation, and it was not targeted at any specific hydrological model or application. All the calculations are based on the 1 h rainfall sums.
The input data of the MERGE2 method are 1 h radar-only QPEs, described in the previous section, and rain gauge measurements. Automatic rain gauges that report 10 min precipitation sums are used. Measurements from the CHMI rain gauges, as well as from the rain gauges of partner organizations (e.g., river basin authorities) are collected in the CLIDATA database operated by the CHMI. The rain gauge data for the MERGE2 calculation are downloaded from the CLIDATA database. Downloaded 10 min precipitation totals are summed into 1 h totals. Currently, about 500 rain gauges, covering the area of the Czech Republic of 78,870 km2, are available in the CLIDATA database, typically in 10–20 min after the end of their measurement. Since radar-only QPEs are available within approximately two minutes after the end of the radar measurement, the timeliness of rain gauge data is governing the timeliness of the MERGE products. MERGE is computed in the 24th min and again in the 99th min after the end of the measurement. Such a time delay can also be problematic when used in subsequent applications that need as recent inputs as possible because of the fast development of convective storms, to name an example.
Only very limited quality-checking may be done during the automatic import of the rain gauge data into the database and during the MERGE2 preprocessing stage. For instance, it is possible to identify unreasonably high values caused by improper data coding or corrupted data transfer, but, on the other hand, it is problematic to detect underestimation caused, such as that by clogged rain gauges or by wind drift. Rain gauge quality checks in the MERGE2 method differ. The checks are stricter for the calculation of the adjustment coefficient because this coefficient should be robust and conservative. The checks for the MERGE product calculation are less strict; the reason is to avoid elimination of possibly real high precipitation totals that could be important for identification of dangerous flood-causing rain. MERGE2 also utilizes a user-defined grey list and a black list, prepared by operational hydrologists. The rain gauges in the black list are not used for any computations. The rain gauges in the grey list are not used in the calculation of the adjustment coefficient, but they may be used in the MERGE2 computation if they registered a significant precipitation total and there is no other reliable station with the same or higher precipitation in the vicinity. These rain gauges in the gray list are typically stations that underestimate precipitation because of unsuitable location or insufficient maintenance. To improve the identification of problematic rain gauges, manual checking must be incorporated. Manual checks and flagging of rain gauge data in the CLIDATA database are performed regularly but, typically, on a daily basis. Therefore, the advantage of the checked rain gauge data is observable in most cases only in the MERGE2 recalculations that are done daily at 8:30 UTC for 1 h rainfalls from 7 UTC of the previous day until 6 UTC of the current day.
The adjustment coefficient in the current operational version of the MERGE2 method is called Mean Field Bias (MFB). It is a robust conservative scalar coefficient computed as a ratio between the sums of 1 h rainfalls measured by rain gauges over the territory of the Czech Republic and the sums of corresponding 1 h radar-only QPEs (i.e., the best match from the area of 3 × 3 grid points surrounding the gauge). Both current and older rain gauge measurements are used for the MFB calculation. The time window used for the summation is dynamic (between 3 h and 3 days), depending on available rainfall measurements. The summation process is finished when a sufficiently big sum of rain gauge measurements (currently 100 mm) is obtained. The weights of the older rainfall measurements decrease exponentially.
The MERGE product is calculated using kriging with external drift (KED), where the rain gauge measurements are interpolated and the radar field is used as the external drift field. KED is one of the best available geostatistical methods for the calculation of combined radar-rain gauge QPEs (see [24,25]), and is also used in other countries. The primary MERGE products are moving 1 h QPEs, and their calculation is updated every 10 min. The MERGE2 method also generates QPEs for longer time intervals (e.g., 3 h, 6 h, 12 h, 24 h, 72 h). These sums are calculated as sums of the primary 1 h MERGE2 products.
Adjusted radar QPEs, that is, the radar-only QPEs multiplied by the adjustment coefficient, significantly improve the radar-only QPEs, but they are typically worse than the MERGE QPEs [10,11]. The reason why the adjustment coefficient is calculated is that the adjusted radar QPE is used instead of the MERGE QPE in cases when performing KED is numerically impossible or the result would be problematic (too low correlation between radar and rain gauge values or not enough non-zero rain gauge measurements). The second reason is that the adjustment coefficient can be applied also to the radar-only QPEs or QPFs when rain gauge measurements are not yet available to calculate MERGE (rain gauge measurements are available for the MERGE calculation process approx. 20 min after the end of the measurement). An example of this is the provision of radar QPEs for the FFI. The FFI needs these data as early as possible. Delays related to the MERGE product availability are not acceptable. That is why the last available adjustment coefficient is used to adjust the radar-only QPEs and QPFs. These products, on the other hand, are available with the delay of 1 or 2 min after the end of the measurement.
2.3. Radar-Based QPF
To calculate radar-based QPFs, the latest PseudoCAPPI 2 km composite is first extrapolated into future times using the COTREC motion field. The COTREC method operationally performed at the CHMI [1] is based on the well-known technique described, for example, by [26,27]. The PseudoCAPPI 2 km composite is extrapolated up to 3 h with a 5 min time step. The next steps are the same as in the case of the radar-only QPE, that is, the same Z-R relationship is used to convert radar reflectivity into rain rates and then the converted rain rate fields are integrated into rainfall for specific time intervals. Most hydrological applications use 1 h QPF sums [12]; four 15 min QPF sums for the first forecasted hour are calculated for use by the FFI. As the last step, the adjustment coefficient is applied to the radar-only QPF to improve the quality of the forecast.
2.4. Flash Flood Indicator
The FFI was developed while working on the project under the supervision of the Ministry of the Environment from 2007 to 2011 [28]. It deals with the calculation of the flash flood risk resulting from torrential rainfall events. The approach highlights the requirement of a more accurate prediction of torrential rainfall along with its location to improve the accuracy of flash flood forecasting. Nowadays, one may take advantage of the fact that it is possible to identify areas where the occurrence of intense rainfall, due to physical-geographical characteristics, may lead to saturated soil conditions, resulting in an increased probability of flash flood formation. Adjusted radar QPEs and QPFs are utilized to calculate the current flash flood risk over the forecast lead time. For this purpose, it is possible to use established and simple methods of rainfall-runoff modelling, such as the Soil Conservation Service Curve Number (SCS-CN) method [29,30] and the unit hydrograph technique [31], and to use the data on antecedent soil moisture together with the physical-geographical and soil characteristics of the watershed. FFI’s main outputs are the current soil moisture conditions, the potential risk precipitation of a given duration, and the real-time estimation of the flash flood risk within a given territory. The FFI has been operating since 2010 at the Central Forecasting Office of the CHMI. It was in experimental operation only until 2016. Recalibration of its parameters was carried out, and since 2017, the calculations of the FFI have been left intact. Its results obtained in 2017–2019 were evaluated in detail [32], and since 2020, the FFI has been one of the important parts of the forecasting system at the CHMI.
The system consists of the following main components:
- Calculation of the current soil moisture conditions over an area in a daily step based on the water balance of rainfall, runoff and actual evapotranspiration;
- Calculation of the potential risk rainfall with the durations of 1, 3, and 6 h, which may cause significant surface runoff;
- An estimate of the general flash flood risk based on the 15 min adjusted radar QPE and QPF and defined runoff thresholds. The general flash flood risk is computed as a combination of the local flooding risk for grids with a cell size of 9 km2 and the flash flood risk by using the schematic of hydrologically connected river basins and reaches.
The FFI procedures are operated in the following ways:
- Run in a daily time step;
- Run in a shorter time step (by configuration).
In the daily step, the output is produced in the following GIS layers:
- Actual data on the soil moisture conditions of the area (represented by CN values), derived from the daily time step of the water balance of the daily rainfall (24 h MERGE QPE), runoff and evapotranspiration, where the main output, is the so-called soil saturation indicator;
- Potential risk amounts of rainfall of a given duration (of 1, 3, and 6 h) for grids with a cell size of 9 km2.
The shorter, user-defined, step starts by a comprehensive procedure ensuring the import of the adjusted radar QPE and QPF and the calculation of runoff response of the corresponding individual catchments through a network of hydrologically connected elements of the river basin and river reaches. For each individual catchment, the level of the flash flood risk is computed.
After the completion of the above procedure, the calculation of the level of the local flooding risk in the grids with a cell size of 9 km2 starts.
The original intention of the FFI was to calculate the potential risk rainfall for the hydrological catchments. As these catchments differ considerably in size, due to the different physical-geographical characteristics (e.g., the lengths of the valleys), this leads to some inhomogeneity in estimating the flash flood risk. To avoid this, the calculation was designed in a way that largely removed the influence of the catchment size, namely by employing a grid with a fixed, experimentally derived cell size. These grid cells in the calculations thus act as hypothetical ‘catchment areas’ with a uniform area of 9 km2. The total number of cells, which cover the Czech territory, is 8717.
There are 6916 catchments in the FFI with an area from several tens of thousands of square meters to 30 km2 (in average 9 km2), which are hydrologically connected. The total number of hydrological gauging stations with a catchment area of 120 km2 (maximum reasonable catchment size in the FFI) or less is roughly 300, which covers a small part with respect to all catchments involved.
For each individual grid cell and catchment, the physical-geographical characteristics are calculated as average values over each given location having its specific slope, altitude, SCS-CN value, 100-year 1-day rainfall, 100-year 1-day runoff, and so forth. The length of the ‘valley’ of grid cells is uniformly set to 3000 m. The Extremity Index IE100 [33] and the 100-year specific runoff q100i are determined from the above-mentioned characteristics for each individual grid cell and catchment.
As the main result, the risk level of local flooding and flash flood risk are determined for each municipality with extended powers (MEP). There are 205 MEPs in the Czech Republic with clearly defined responsibilities in the flood management.
Flash flood risk and local flooding risk levels are based on threshold ratios (r1, r2 and r3) between the computed maximum specific runoff qmaxi and the theoretical 100-year specific runoff q100i. The ratios were estimated experimentally and are constant all over the Czech Republic. Their values may be changed based on operational experience.
The levels of the flash flood and local flooding risks are determined as follows:
- Level 1—low to medium risk (yellow color), where qmaxi ≥ r1 · q100i;
- Level 2—high risk (orange color), where qmaxi ≥ r2 · q100i;
- Level 3—very high risk (red color), where qmaxi ≥ r3 · q100i.
In the case of flash floods, these levels could be interpreted as follows:
- Level 1—high rise of water level, flow stays in the river bed, the general public should be informed about the situation;
- Level 2—flow gets out of the river bed locally, mainly not significant damages, the general public should pay increased attention, try to protect its property;
- Level 3—flow gets out of the river bed in many places, significant damages of property, possible loss of life, the general public should be prepared for evacuation.
The description of the levels for local flooding is quite similar, but the risk is primarily focused on the places that are not near-permanent watercourses. Flash flood, unlike local flooding, can also occur in places that have not been directly affected by torrential rainfall.
A more detailed description of the FFI is available in [16]. Figure 4 depicts an example of the FFI output as displayed through a web map application [34]. Outputs from the FFI are also available at the CHMI Flood Forecasting Service’s web page [35].
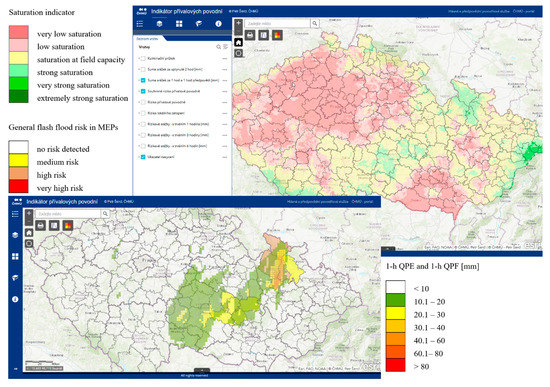
Figure 4.
The outputs from the web map application ‘Flash Flood Indicator’, running on the ArcGIS Online platform. It depicts the soil saturation indicator (top right panel), 1 h QPE + 1 h QPF ≥ 10 mm/2 h and the actual general flash flood risk in MEPs (bottom left panel).
2.5. Performance of Radar-Based QPEs and QPFs in the FFI
The FFI uses 24 h MERGE QPE for soil moisture conditions. Unfortunately, until today, the short-term calculations of MERGE could not be utilized in the FFI for the calculation of the flash flood risk. The shortest calculated 1 h MERGE sums are too long for this task and an approx. 25 min delay of MERGE availability is also a limiting factor. For this reason, instead, the 15 min sums of adjusted radar QPEs together with adjusted radar QPFs are used for the flash flood risk calculation.
The new polarimetric weather radars installed in 2015 enabled much more effective filtering of such non-meteorological echoes compared to the previous non-polarimetric radars. They also enabled the correction of radar signal attenuation in strong precipitation, which, together with improved radar calibration, led to a decrease in bias of the radar-only QPEs. As shown in Figure 5a, on average, the radar-only QPEs are currently not biased, which means that the radars are correctly calibrated and that the coefficients of the Marshall–Palmer equation are chosen correctly as well. Nevertheless, the over- and underestimation of radar-only QPEs may be quite significant in specific cases, which should be corrected using the adjustment coefficient or the MERGE product. The variability of the radar-only QPE over- and underestimation is caused by the natural variability of drop size distribution in the precipitation clouds, but also by the variability of other factors, such as evaporation of precipitation in the lower parts of the atmosphere and orographic enhancement of precipitation.
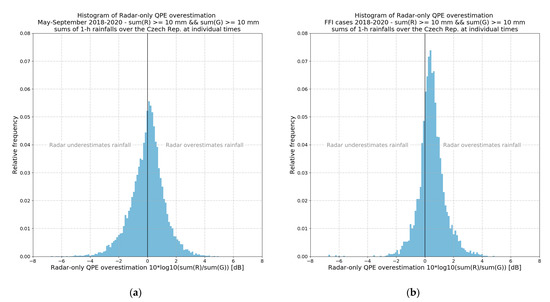
Figure 5.
Distribution of radar-only QPEs vs. rain gauge under- or over-estimation. Comparison is based on 1 h rainfalls over the Czech Republic. Distribution calculated at individual times with a 10 min step during May–September 2018–2020 (a) and during selected significant FFI cases from 2018–2020 (b). Distributions are calculated only from pairs where areal sums of rain gauge measurements over the Czech Republic are ≥10.0 mm.
While the performance of the MERGE product in the FFI is satisfying (only optimization of the manual check of rain gauges is discussed), adjusted radar QPEs tend to overestimate the precipitation significant for the FFI, which consequently leads to FFI false alarms. To analyze the problem in more detail, the cases with the flash flood occurrence or flash flood risk signalized by the FFI were identified in all the periods May–September of 2018–2020. Every case is represented by the 24 h interval from 06:00 to 06:00 UTC. These cases were further called the ‘FFI cases’. The FFI cases were defined by the following criteria:
- 24 h rainfall have reached or exceeded 10 mm in at least 10 rain gauges during the particular rain event;
- Precipitation was exclusively convective;
- Events with stratiform precipitation, even orographically amplified, were not considered;
- The FFI has detected the flash flood risk or local flooding risk, or there has been direct evidence of a flash flood occurrence.
The measured 24 h rainfall and corresponding radar QPE values at rain gauge locations derived from the grid with the 1 km2 cell size were paired together and evaluated. Evaluation showed that, during the FFI cases, the adjusted radar QPE, on average, overestimated significant rain gauge measurements by about 10%, as summarized in Table 1. It was further shown that, in the FFI cases, radar-only QPEs also, on average, overestimated rain gauge measurements, as depicted in Figure 5b. During the FFI cases, the overestimation of radar-only QPEs was higher than that of adjusted radar QPEs. Thus, the adjustment coefficient seemingly corrects the radar-only estimates, but not enough.

Table 1.
Performance of the MFB-adjusted radar QPE for rainfalls ≥ 10 mm/24 h during the FFI cases in 2018–2020.
Insufficient correction of the MFB adjustment coefficient might be caused by two reasons:
- Conservativeness and robustness of the scalar adjustment coefficient averaged over the whole Czech Republic and the time window;
- Assignment of the corresponding radar-only QPE to the rain gauge measurements for the adjustment coefficient.
The spatial and temporal variability of precipitation and its physical parameters lead to the variability of the radar-rain gauges ratio. In some cases, the ratio between the radar and the rain gauge measurements may vary in different parts of the Czech Republic. A spatially variable adjustment coefficient should work better in such situations, and it was already used in the past. However, such an adjustment coefficient, calculated by kriging interpolation of ratios at individual rain gauges, did not yield good results when applied to the extrapolated radar-only QPFs. The problem with the spatially variable adjustment coefficient lies in different physical nature of the effects that cause the radar rainfall under- or overestimation; some are stationary over time (e.g., orography shielding, partial bright-band detection, evaporation of precipitation in dry low levels of the atmosphere), and some are moving with the precipitation clouds (e.g., specific drop-size distribution in clouds). When the adjustment coefficient is applied to the radar QPE or QPF from some future time (operationally, it is used for QPFs up to 3 h ahead), it is not possible to determine the measure of various effects influencing the different parts of the domain and, thus, it is not clear how the adjustment coefficient should be applied (whether it should be stationary, or moved with the radar motion field).
There is also an issue with the big temporal variability of the radar-rain gauge ratio. The use of a variable time window for the calculation of the adjustment coefficient is intentional in order to smooth this big variability, which, otherwise, could cause overcorrections mainly in the cases when the coefficient is applied to the extrapolation forecasts. On the other hand, the adjustment coefficient may need some time to accommodate to the temporal changes of the radar-rain gauge ratio.
The variability of the radar-rain gauge ratio and the corresponding MFB adjustment coefficient is graphically demonstrated in Figure 6. It illustrates the changes of ratios of radar-only QPEs to corresponding rain gauge measurements at individual locations during the period of several days (selected FFI cases) (Figure 6a) and several hours (Figure 6b). The scattered values reveal that the ratios at individual stations are very variable in a given time. The comparison of MFB values and corresponding ratios of areal sums from actual time shows differences caused by the temporal smoothing of the MFB coefficient. This especially happens in situations with the presence of convective clouds or mixed convective/stratiform regions, which are usually situations that are interesting for the FFI application.
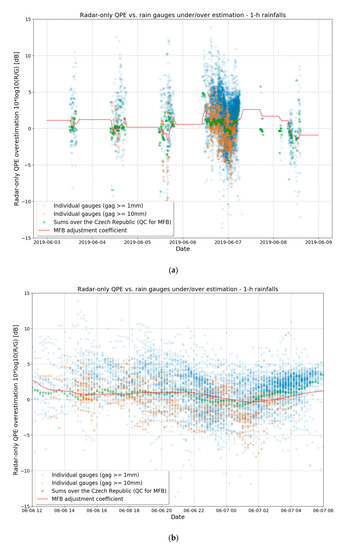
Figure 6.
An example of the radar under- or over-estimation variability over 6 days from 3 June 2019 to 9 June 2019 (a) and a detailed view of variability over the 18 h period from 6 June 2019 12:00 UTC to 7 June 2019 06:00 UTC (b). Figures depict one of the episodes with intense rainfall significant for the FFI. Intense rainfalls with FFI response were identified on 4 June 2019, 5 June 2019, and 6–7 June 2019.
As mentioned above, the second possible reason for the insufficient MFB correction involves the way of assignment of the corresponding radar-rain gauge pairs. The assignment of the corresponding radar-only QPE to the rain gauge measurements for the MFB calculation is done as the best match from the area of 3 × 3 grid points around the rain gauge location (grid point resolution is 1 × 1 km). The reason for that has been an attempt on the correction for the wind drift of the rain particles between the level of radar measurement (2 km ASL) and the ground. Operational experience, however, showed that this approach does not work well.
2.6. New Local Bias Adjustment Scheme
The above-mentioned problems lead to the development of a new adjustment scheme, specifically for the utilization in the FFI. The new spatially variable adjustment scheme is called local bias (LB), and it is quite different from the old kriging-based adjustment scheme calculated in the older version of the MERGE2 method (between 2009 and 2013).
As a first step of the LB calculation, a slightly modified MFBmod adjustment coefficient is computed. The differences from the previous MFB calculation are:
- Radar-only QPE at the rain gauge location (instead of the best match from the area of 3 × 3 grid points surrounding the rain gauge) is used to pair the radar-only QPE and the rain gauge measurements;
- Minimum time window from which MFBmod is calculated is 2 h (instead of 3 h);
- Default MFBmod value is 0.9 (instead of 1.0 formerly used for MFB). The change of the default value is based on the results shown in Figure 5b. The default MFBmod value is used at the beginning of the precipitation event when it is not possible to accumulate enough precipitation.
In the next step, a spatially variable field of LB is calculated. Because of bad experiences with too high variability of the LB field in the older version of the MERGE2 method based on the kriging interpolation of the bias at individual rain gauges, now, a more conservative approach has been used. Eleven virtual stations evenly distributed over the territory of the Czech Republic were defined, see Figure 7. The MFBmod coefficients are calculated within the 75 km circular surroundings of each virtual station using the same modified MFBmod method as for the whole domain in the previous step. Only the radar-rain gauge pairs used for whole-domain MFBmod are used. If the sum of the rain gauge measurements in the surrounding area of a given virtual station is less than 10 mm, the MFBmod coefficient calculated for the whole domain in the previous step is used for this virtual station. After the computation of the bias for all virtual stations, a spatial interpolation is performed using the linear radial basis function (RBF) [36,37]. In addition to the eleven virtual stations on the territory of the Czech Republic, nine other virtual stations are defined outside the Czech Republic to improve the result of the linear RBF interpolation. The bias from the closest virtual station located on the territory of the Czech Republic is assigned to each virtual station outside the Czech Republic. An example of the LB adjustment field calculation result is shown in Figure 8.
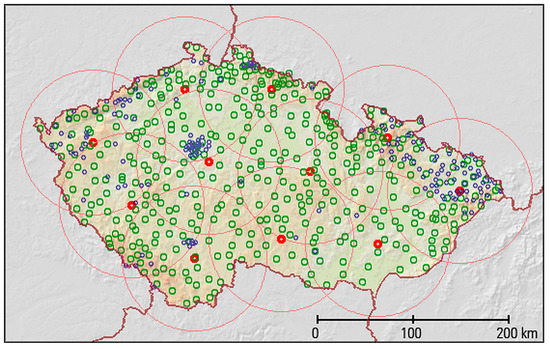
Figure 7.
Locations of 11 virtual stations used for the computation of LB field are depicted by red circles. Circles of 75 km around each virtual station represent the surroundings from which the bias is computed for the given virtual station. Locations of the CHMI rain gauges are depicted by green circles. Locations of rain gauges of partner organizations are depicted by smaller blue circles.
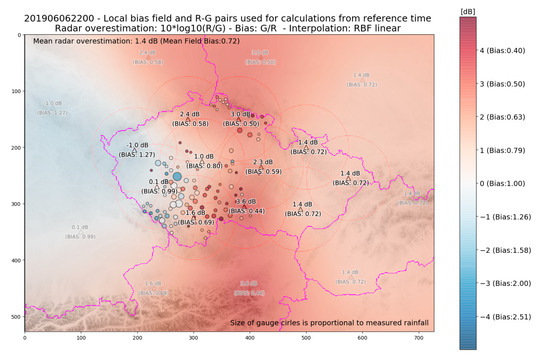
Figure 8.
An example of the LB adjustment field calculation result. The value of bias is written near the location of each virtual station represented by a triangle. The underlying field filling out the whole domain is the visualization of the LB adjustment field obtained using the linear RBF interpolation technique. The nine virtual stations added outside the territory of the Czech Republic ensure that too low or too high values are not present in LB in peripheral areas. Circles represent the real rain gauges; the size of the circle grows with the increasing precipitation sum measured at the rain gauge. The color of the circle corresponds with the radar-rain gauge bias at the grid point where the rain gauge is located.
3. Results
3.1. Statistical Evaluation of the New LB Adjustment Scheme
To compare the MFB and LB adjustment schemes and to evaluate possible benefits of LB over MFB, several analyses were done. Figure 9 shows cumulative distributions of the bias of radar-based QPEs for precipitation levels higher or equal to 1 mm (Figure 9a) and to 10 mm (Figure 9b). Distributions are computed for 24 h rainfalls from all FFI cases. For both rainfall thresholds, the results are similar. As expected, the radar-only QPE gives the worst results in this comparison. MFB performs better, and LB gives the best results from these three types of the QPE. The bias of LB-adjusted QPEs for rainfalls higher than or equal to 10 mm is almost perfectly balanced; however, in the case of the lower threshold, it is apparent that even LB-adjusted QPEs still overestimate the rain gauge measurements more often than underestimation, although to a lesser extent than other radar-based QPEs.
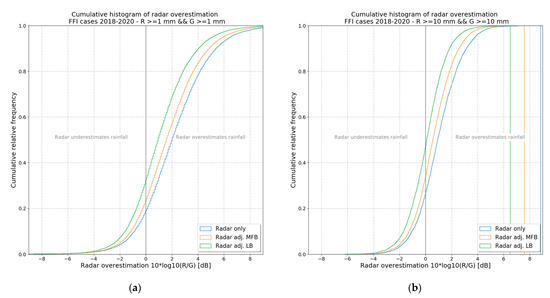
Figure 9.
Cumulative distribution of the bias of individual radar-based QPEs (radar-only QPE, radar QPE adjusted using the MFB coefficient and radar QPE adjusted using the LB field). Distributions were calculated for radar-rain gauge pairs where both the 1 h measured rainfall (rain gauge) and the 1 h radar-based QPE is higher or equal to 1 mm (a) and higher or equal to 10 mm (b). Pairs of 24 h rainfalls from selected significant FFI cases from 2018–2020 were used.
Critical Success Index (CSI), False Alarm Rate (FAR) and Probability of Detection (POD), as explained in [38], were used as other performance measures for the evaluation of the QPE quality for various rainfall thresholds. The performance was evaluated for seven different threshold values of 24 h rainfalls: 1, 5, 10, 20, 30, 40, and 50 mm.
Since CSI, FAR, and POD are not independent, they are usually presented using a well-known performance diagram [38]. Figure 10 shows the performance diagram of radar-based QPEs for selected significant FFI cases from 2018–2020. The diagram uses the success ratio (1-FAR) on the x-axis and POD on the y-axis. The curves correspond to contours of the CSI values with the step of 0.1. The straight lines beginning at 0 correspond to the BIAS quantity which is computed as BIAS = POD/(1 − FAR).
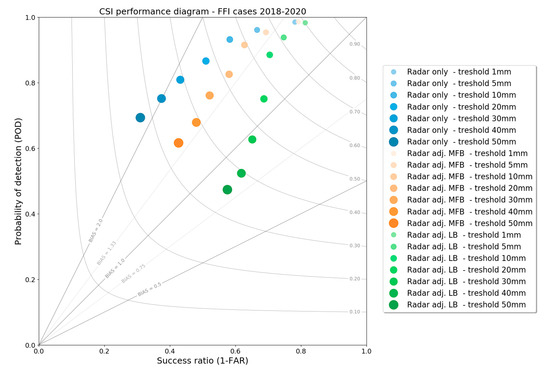
Figure 10.
Performance diagram of radar-based QPEs (radar-only QPE, radar QPE adjusted using the MFB coefficient and radar QPE adjusted using the LB field) for selected significant FFI cases from 2018–2020.
BIAS, in this case, represents the frequency of the under- and over-estimation of radar QPEs of a given threshold. It is not equal to the mean ratio between the radar QPE and the measured rainfall sum obtained from rain gauges. Ideally, BIAS should be equal to 1, which means that the overestimation and underestimation occur in the same number of cases (i.e., the QPE does not tend to overestimate or underestimate).
In Figure 10, it can be seen that the radar-only QPE and the MFB-adjusted QPE generally tend to overestimate in comparison to the rain gauge measurements for all tested rainfall thresholds. LB-adjusted QPEs also more often overestimate the rain gauge measurements for the lower rainfall thresholds, but for the thresholds equal to 30 mm and higher, the underestimation slightly prevails. The overestimation gets worse for the radar-only QPE with the rising threshold, while the MFB-adjusted radar QPE keeps the overestimation similar for all thresholds, slightly above BIAS = 1.33. BIAS of the LB-adjusted QPE is improving with the increasing thresholds up to 30 mm, but gets worse for the 40 and 50 mm thresholds. The MFB-adjusted radar QPE surpasses the radar-only QPE for all thresholds not only in terms of BIAS, but also in terms of the general performance measured by CSI. More importantly, the LB-adjusted radar QPE surpasses the radar-only QPE and the MFB-adjusted radar QPE for all thresholds.
As mentioned above, the BIAS quantity in the performance diagram does not correspond to the mean ratio between the radar-based QPE and the measured rainfall at rain gauges. Determination of the mean ratio for a specific rainfall sum or interval can be quite tricky because of the problem with proper thresholding of radar-rain gauge pairs. To get a better overview, Figure 11 shows the scatter plot of rainfall sums measured at rain gauges vs. radar-based QPEs for selected significant FFI cases from 2018–2020. For a better description of the dense data, solid lines are drawn over the scatter plot, representing the density contours, while the dotted lines show the sixth-order polynomial regression fits. The BIAS lines in this plot represent the mean ratio between the radar-based QPE and the measured rainfall sums at rain gauges. It is apparent that the majority of the pairs lies below approx. 30 mm. The number of pairs decreases with increasing rainfall, and it is very low above approx. 50 mm, which decreases the representativeness for a statistical evaluation. The overestimation of radar QPEs is obvious for rainfall sums below 50 mm. It is evident that in the rainfall range with the majority of measurements, the overestimation of the MFB-adjusted radar QPE is smaller than for the radar-only QPE, and the LB-adjusted radar QPE outperforms both of them. The radar-rain gauge ratio is the highest for the low rainfall sums, and it decreases with growing rainfall sums.
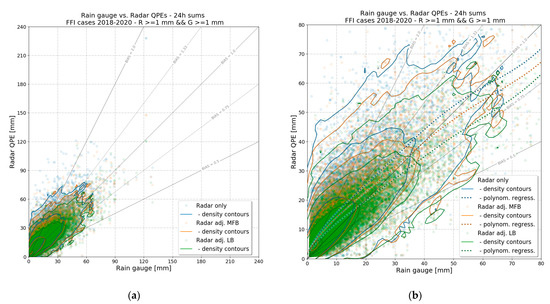
Figure 11.
Scatter plots of rainfall sums measured at rain gauges vs. radar-based QPEs for selected significant FFI cases from 2018–2020. An overview plot (a) shows all radar-rain gauge pairs with rainfall above or equal 1 mm, a detailed plot (b) shows only the <1 mm; 80 mm> rainfall interval with the majority of pairs. Solid lines represent the density contours Dotted lines show the sixth-order polynomial regression fits.
3.2. Case Studies of the Adjusted Radar QPE Performance as an FFI Input
During the FFI performance assessment period, there were several rainfall events particularly in 2020 when false alarms were provably detected, but there were also events with flash floods that were not adequately captured by the FFI. Some events were not part of the FFI cases because they were caused by stratiform precipitation.
For that reason, a total number of four days with significant convective and stratiform precipitation were selected to compare the results of the risk calculation based on the original MFB-adjusted QPE and the new LB-adjusted QPE. In all cases, there were flash flood risks, and in three cases local flooding risks were generated.
On 19 June 2020 and 4 August 2020, with the occurrence of sustained stratiform precipitation, the overestimation of the QPE and strong soil saturation generated many false alarms. The purpose of comparing the MFB and LB methods was to determine whether there would be a significant reduction in these alarms if the new LB method was used.
On the contrary, on 18 June 2020, when there were both sustained stratiform rainfall and later convective rainfall, there was an underestimation of the QPE in certain parts of the territory and an adequate failure to capture the FFI flood events. Therefore, the purpose of comparing the MFB and LB methods was also to determine whether the application of the new LB method would result in regional differences of the adjustment coefficients so that the flood events would be better captured by the FFI system.
Finally, yet importantly, on 13 June 2020, exclusively convective rainfall occurred, and local flash floods were observed. MFB-adjusted QPEs were overestimated. In this case, the purpose of the comparison was to detect the differences in the number of alarms generated.
The results of the comparison are summarized in Table 2 and Table 3. There are no significant changes in the risk detection on 13 June 2020. In the precipitation episodes on 19 June 2020 and 4 August 2020, the number of computed risks, in fact false alarms, drops very significantly with use of the LB-adjusted QPE. On the other hand, on 18 July 2020, more risks are detected using the LB-adjusted QPE. In all four cases, the improvement, when compared to reality, is evident.

Table 2.
Risk of local flooding in grid cells of size 3 × 3 km with 2 h rainfall ≥ 10 mm.

Table 3.
Flash flood risk in catchments.
It appears from the initial calculations that the new LB-adjusted QPE will enable significant refinement of the FFI output, compared to the measured precipitation totals, and, thus, may prevent the generation of false alarms in certain situations. In particular, this should apply to the situations with stratiform precipitation characterized by significant bright-band, where, moreover, the territory may be highly saturated from previous precipitation events. Another (side) effect is the acceleration of calculation when estimating the flash flood risk, as the number of catchments involved in the calculation will be significantly smaller in cases where precipitation is less overestimated (e.g., 4 August 2020; Table 3).
Furthermore, the new LB-adjusted QPE can help significantly in situations with both stratiform and convective precipitation, where the adjustment coefficient changes very significantly regionally (e.g., 18 June 2020).
4. Discussion
Evaluation of the MFB-adjusted radar QPE within the FFI system showed that it does not yield optimal results, especially in intense convective and convective-stratiform situations when the flash flood risk is the highest. In reaction to the need for better reflecting the large spatial variability of radar-rain gauge ratios, a new LB adjustment scheme was designed to improve the radar-only QPE. The LB field is not computed for each individual rain gauge, because based on its large spatial variability, it yields much worse results when applied to the QPF. Instead, a more conservative approach was used to produce a smoother LB adjustment field. Another advantage of the smoother LB field is its bigger resistance to erroneous measurements. Although quality checks are applied to both radar and rain gauge measurements, not all errors can be eliminated.
The most important change brought to the adjustment coefficient computation lies in the way of assignment of the radar grid value to the rain gauge from the best match of 3 × 3 grid points surrounding the rain gauge to the grid point representing the exact location of the rain gauge. The best match assignment was originally introduced to mitigate the time and place inaccuracies. The place inaccuracies occurred due to wind-drifting hydrometeors. The time inaccuracy or the lack of representativeness of the radar measurements was, at least partially, solved by the interpolation of radar reflectivity composites into 1 min time steps. This procedure was introduced after the set-up of the MFB, but the best match assignment was maintained to correct the place inaccuracies. However, after the comparison of the MFB with the MFBmod/LB adjustment, it turns out that its drawbacks are bigger that its advantages. When looking at the scatter plots in Figure 11, it can be seen that the LB-adjusted QPE is less biased and its density contours define a smaller area, which means that the LB adjustment is able, to some extent, decrease the variability of the radar-rain gauge ratio in individual measurements.
Identified improvements of the new approach to the radar-rain gauge assignment led to a change of the assignment also in the operational calculation of the MFB in April 2021. The calculation of the MFB adjustment coefficient will remain operational for applications outside the FFI.
Evaluation of the adjustment methods in the FFI faces difficulties regarding the determination of ‘reality’. It is possible to check the readings from the measurements of hydrological stations in the affected catchments (but only a small portion of them is observed), from the interventions of the rescue system at a given time in the affected location, or only from the available pictures and videos taken mostly by amateur observers or random witnesses of the flood event. If torrential rainfall occurs in an uninhabited area, where there is also no hydrological observation, the evaluation of the success of the FFI application procedures is even more difficult. Thus, the uncertainty in the evaluation is likely to remain. Currently, however, procedures are set to capture all very significant flash floods. In case of less significant flash floods, a certain number of undetected flash floods is anticipated.
Evaluation of the MFB and LB adjustment methods in the FFI based on four selected cases suggests that the LB adjustment method will lead to a reduction in the number of false alarms, not only in case of convective rainfall, but also in situations with heavy stratiform rainfall and strong soil saturation. The LB adjustment improved the FFI outputs also in case of the underestimation of the MFB-adjusted QPE.
Another quality improvement of the radar QPE input into the FFI is supposed to be achieved by using the 1 h MERGE product interpolated into suitable shorter sums (currently 15 min sums, probably 10 min sums in the future). To do that, the interpolation of the 1 h MERGE product must be implemented first. These interpolated MERGE products should be even more precise than the LB adjustment fields, but they will not be available for approx. the last half an hour and for the 1 h extrapolation forecasts. For this time interval, the new LB adjustment will be used also in the future.
The MERGE product interpolation method is currently being developed. It is expected to be available for the next convective season 2022. However, use of the interpolated MERGE products in the FFI may require the FFI recalibration and the setting of new flash flood and local flooding thresholds.
5. Conclusions
Identified deficiency of the MFB adjustment scheme for use in the FFI caused the development of a new LB adjustment scheme based on a smoothed conservatively variable field of radar-rain gauge biases.
Evaluation of the comparison of individual radar-based QPEs showed that the LB adjustment coefficient is clearly an improvement over the MFB adjustment coefficient. Results show that LB is less biased for various thresholds of rainfall. At the same time, the results suggested that LB reduces the variability of the radar-rain gauge ratio in individual time intervals.
The LB adjustment superiority was also clearly confirmed directly in the FFI on four selected cases of both convective and stratiform rainfall types.
Future development will focus on use of the MERGE products interpolated into shorter sums in place of the adjusted radar QPEs for the times when rain gauge measurements are available.
Author Contributions
Conceptualization, P.N., H.K., M.P. and P.Š.; methodology, P.N.; software, P.N.; validation, P.N., H.K., M.P., V.S. and P.Š.; investigation, M.P., P.Š. and V.S.; writing—original draft preparation, P.N., H.K., M.P. and P.Š.; writing—review and editing, P.N., H.K., M.P., P.Š.,V.S. and O.L.; visualization, P.N. and V.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the Ministry of the interior of the Czech Republic (project no. VI20192021166, “Hydrometeorological Risks in the Czech Republic—Changes in Risks and Improvements in their Predictions”) in frame of the Czech Republic’s Security Research Programme 2015–2022.
Acknowledgments
The authors wish to thank the colleagues in the CHMI responsible for operation and maintenance of the measurement networks (mainly weather radars and rain gauges), without whom the data necessary for this research would not be available.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ASL | Above sea level |
| CAPPI | Constant Altitude Plan Position Indicator |
| CHMI | Czech Hydrometeorological Institute |
| COTREC | Continuity of TREC vectors |
| CZRAD | Czech Weather Radar Network |
| dBZ | Logarithmic unit of radar reflectivity |
| FFI | Flash Flood Indicator |
| LB | Local Bias |
| MAX | Maximum Reflectivity |
| MEP | Municipality with Extended Powers |
| MFB | Mean Field Bias |
| QPE | Quantitative precipitation estimate |
| QPF | Quantitative precipitation forecast |
| SCS-CN | Soil Conservation Service Curve Number |
| VPR | Vertical profile of reflectivity |
| Z-R | conversion from radar reflectivity factor Z to precipitation intensity R |
References
- Novák, P. The Czech hydrometeorological institute’s severe storm nowcasting system. Atmos. Res. 2007, 83, 450–457. [Google Scholar] [CrossRef]
- Novák, P.; Kyznarová, H. Upgrade of the CZRAD meteorological radar network in 2015. Meteorol. Bull. 2016, 69, 137–144. [Google Scholar]
- Šálek, M.; Kráčmar, J. Precipitation estimates by meteorological radar Skalky. Meteorol. Bull. 1997, 50, 99–109. [Google Scholar]
- Šálek, M.; Kráčmar, J.; Novák, P.; Setvák, M. Application of remote sensing methods during the July 1997 floods in the Czech Republic. Meteorol. Bull. 1997, 50, 177–178. [Google Scholar]
- Kráčmar, J.; Joss, J.; Novák, P.; Havránek, P.; Šálek, M. First steps towards quantitative usage of data from weather radar network. In Proceedings of the Final Seminar of COST-75: Advanced Weather Radar Systems, Locarno, Switzerland, 23–27 March 1998; European Commission: Luxembourg, 1999; pp. 91–101, ISBN 9282849074. [Google Scholar]
- Novák, P.; Kráčmar, J. Vertical reflectivity profiles in the Czech Weather Radar Network. In Preprint of Proceedings of 30th International Conference on Radar Meteorology, Munich, Germany, 19–24 July 2001; [CD-ROM, P15.3.]; American Meteorological Society: Boston, MA, USA, 2001. [Google Scholar]
- Šálek, M.; Novák, P.; Seo, D.J. Operational application of combined radar and raingauges precipitation estimation at the CHMI. In Proceedings of the 3rd European Conference on Radar in Meteorology and Hydrology (ERAD 2004), ERAD Publication Series, Visby, Sweden, 6–10 September 2004; Copernicus GmbH: Göttingen, Germany, 2004; Volume 2, pp. 16–20. [Google Scholar]
- Šálek, M. Operational application of the precipitation estimate by radar and raingauges using local bias correction and regression kriging. In Proceedings of the 6th European Conference on Radar in Meteorology and Hydrology (ERAD 2010), Sibiu, Romania, 6–10 September 2010; National Meteorological Administration of Romania: Sibiu, Romania, 2010; pp. 39–43. [Google Scholar]
- Šálek, M. Merging of Weather Radar and Rain Gauge Measurements for Precipitation Estimation. Ph.D. Thesis, Brno University of Technology, Brno, Czech Republic, 2011. [Google Scholar]
- Novák, P.; Kyznarová, H. Progress in operational quantitative precipitation estimation in the Czech Republic. In Proceedings of the 8th European Conference on Radar in Meteorology and Hydrology (ERAD 2014), Garmisch-Partenkirchen, Germany, 1–5 September 2014. QPE.P06. [Google Scholar]
- Novák, P.; Kyznarová, H. MERGE2—the upgraded system of quantitative precipitation estimates operated at the Czech Hydrometeorological Institute. Meteorol. Bull. 2016, 69, 137–144. [Google Scholar]
- Novák, P.; Březková, L.; Frolík, P. Quantitative precipitation forecast using radar echo extrapolation. Atmos. Res. 2009, 93, 328–334. [Google Scholar] [CrossRef]
- Šálek, M.; Březková, L. Utilization of radar-based precipitation estimate in hydrological models in the Czech Republic. In Proceedings of the 3rd European Conference on Radar in Meteorology and Hydrology (ERAD 2004), ERAD Publication Series, Visby, Sweden, 6–10 September 2004; Copernicus GmbH: Göttingen, Germany, 2004; Volume 2, pp. 516–521. [Google Scholar]
- Šálek, M.; Březková, L.; Novák, P. The use of radar in hydrological modelling in the Czech Republic—Case studies of flash floods. Nat. Hazards Earth Syst. Sci. 2006, 6, 229–236. [Google Scholar] [CrossRef]
- Březková, L.; Novák, P.; Šálek, M.; Kyznarová, H.; Jonov, M.; Frolík, P.; Sokol, Z. The operational use of nowcasting methods in hydrological forecasting at the Czech Hydrometeorological Institute. In Weather Radar and Hydrology, Proceedings of the International Symposium, Exeter, UK, 18–21 April 2011; IAHS: Wallingford, UK, 2012; Volume 351, pp. 490–495. ISBN 9781907161261. [Google Scholar]
- Šercl, P. Flash Flood Indicator. Possibilities of prediction of flash floods in the conditions of the Czech Republic. In Transactions of the CHMI; CHMI: Prague, Czech Republic, 2015; Volume 60, pp. 10–28. ISBN 9788087577271. [Google Scholar]
- Šálek, M.; Cheze, J.-L.; Handwerker, J.; Delobbe, L.; Uijlenhoet, R. Radar Techniques for Identifying Precipitation Type and Estimating Quantity of Precipitation; Document of COST Action 717; Office for Official Publications of the European Communities: Luxembourg, 2004; p. 51. ISBN 9289800046. [Google Scholar]
- Overeem, A.; Holleman, I.; Buishand, A. Derivation of a 10-year radar-based climatology and rainfall. J. Appl. Meteorol. Climatol. 2009, 48, 1448–1463. [Google Scholar] [CrossRef]
- Newsome, D.H. Weather radar networking. In Final Report of COST 73 Project; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1992; pp. 41–50. [Google Scholar]
- Kráčmar, J. Radar horizons and the occurrence of ground clutters for weather radar network of the Czech Republic. Meteorol. Bull. 1994, 47, 163–171. [Google Scholar]
- Jurczyk, A.; Szturc, J.; Ośródka, K. Quality-based compositing of weather radar derived precipitation. Meteorol. Appl. 2020, 27, e1812. [Google Scholar] [CrossRef] [Green Version]
- Marshall, J.S.; Palmer, W. McK. The distribution of rain drops with size. J. Meteor. 1948, 5, 165–166. [Google Scholar] [CrossRef]
- Fulton, R.A.; Breidenbach, J.P.; Seo, D.-J.; Miller, D.A.; O’Bannon, T. The WSR-88D rainfall algorithm. Weather Forecast. 1998, 13, 377–395. [Google Scholar] [CrossRef]
- Goudenhoofdt, E.; Delobbe, L. Evaluation of radar-gauge merging methods for quantitative precipitation estimates. Hydrol. Earth Syst. Sci. 2009, 13, 195–203. [Google Scholar] [CrossRef] [Green Version]
- Keller, D. Evaluation and comparison of radar-rain gauge combination methods. In Scientific Report MeteoSwiss; MeteoSwiss: Zürich, Switzerland, 2013; Volume 94. [Google Scholar]
- Li, L.; Schmid, W.; Joss, J. Nowcasting of motion and growth of precipitation with radar over a complex orography. J. Appl. Meteorol. 1995, 34, 1286–1300. [Google Scholar] [CrossRef] [Green Version]
- Zgonc, A.; Rakovec, J. Time extrapolation of radar echo patterns. In Proceedings of the Final Seminar of COST-75: Advanced Weather Radar Systems, Locarno, Switzerland, 23–27 March 1998; European Commission: Luxembourg, 1999; pp. 229–238, ISBN 9282849074. [Google Scholar]
- Šercl, P. The robust method for an estimate of runoff caused by torrential rainfall and proposal of a warning system. In Proceedings of the Early Warning for Flash Floods Workshop, Prague, Czech Republic, 1–2 November 2010; CHMI: Prague, Czech Republic, 2011; pp. 76–81, ISBN 9788086690919. [Google Scholar]
- Mishra, S.K.; Singh, V.P. Soil Conservation Service Curve Number (SCS-CN) Methodology; Springer: Basel, Switzerland, 2003; p. 216. ISBN 9781402011320. [Google Scholar] [CrossRef]
- Janeček, M. Using the CN runoff curve number method to design anti-erosion measures. In Soil Protection against Erosion; Dům Techniky České Budějovice: České Budějovice, Czech Republic, 1998; pp. 1–35. ISBN 9788002012313. [Google Scholar]
- US Army Corps of Engineer. Engineering and Design: Flood-Runoff Analysis (Engineer Manual 1110-2-1417); Military Bookshop: Washington, DC, USA, 1994; p. 228. ISBN 978-1780397474. [Google Scholar]
- Borovička, P. Preventing of Security Hazards Caused by Extreme Meteorological Phenomena—Their Specification and Innovation of Forecasting and Warning Systems with Regards to Climate Change; Final Report on Project VH20172020017; Ministry of the Interior of the Czech Republic: Prague, Czech Republic, 2020; p. 76.
- Šercl, P. Impact of physio-geographical factors on theoretical design flood wave characteristics. In Transactions of the CHMI; CHMI: Prague, Czech Republic, 2009; Volume 54, ISBN 9788086690629. [Google Scholar]
- Flash Flood Indicator in Web Mapping Application. Available online: https://1url.cz/vKEoE (accessed on 2 July 2021).
- CHMI’s Flood Forecasting Service. Available online: https://hydro.chmi.cz/hpps/main_rain.php?mt=ffg (accessed on 2 July 2021).
- ArcGIS Pro Help/RBF (Radial Basis Functions)/How Radial Basis Functions Work. Available online: https://pro.arcgis.com/en/pro-app/latest/help/analysis/geostatistical-analyst/how-radial-basis-functions-work.htm (accessed on 2 July 2021).
- SciPy API Reference—Scipy.interpolate.Rbf. Available online: https://docs.scipy.org/doc/scipy/reference/generated/scipy.interpolate.Rbf.html (accessed on 2 July 2021).
- Roebber, P.J. Visualizing multiple measures of forecast quality. Wea. Forecast. 2009, 24, 601–608. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).