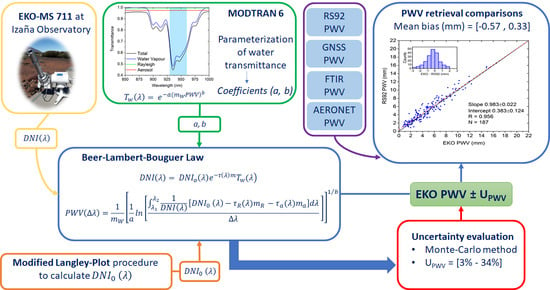
Water Vapor Retrievals from Spectral Direct Irradiance Measured with an EKO MS-711 Spectroradiometer—Intercomparison with Other Techniques
Abstract
1. Introduction
2. Site Description
3. Materials and Methods
3.1. EKO MS-711 Spectroradiometer
3.2. Ancillary Instrumentation
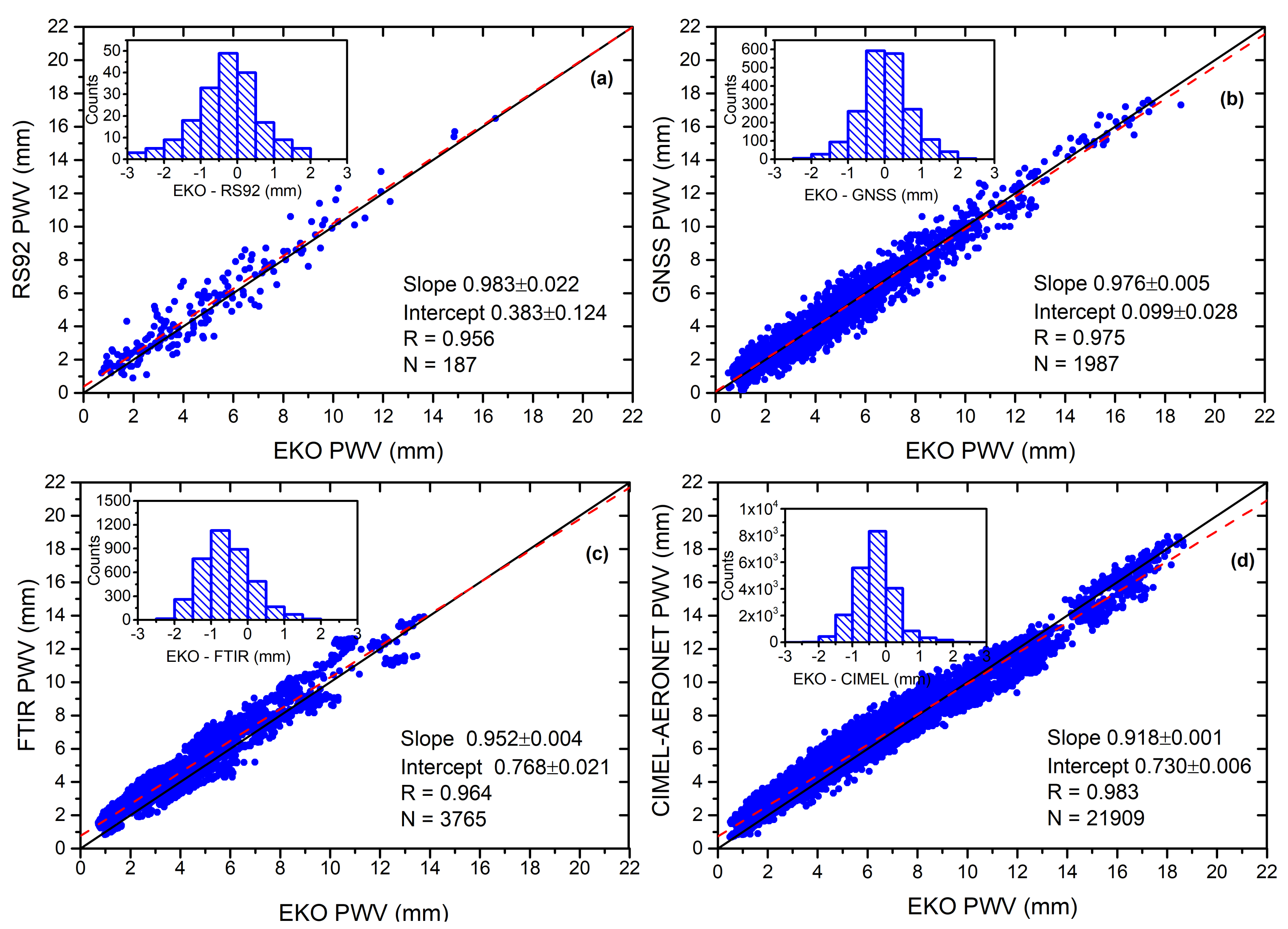
- Meteorological Radiosonde (RS92)Since June 2005, meteorological radiosondes are routinely launched twice daily, at ∼ 11:15 and ∼ 23:15 UTC at the Güimar station (28.32°N, 16.38°W, 105 m a.s.l.) situated at the coastline, approximately 15 km to the southeast of IZO at Tenerife island. This station is part of the Global Climate Observing System (GCOS)–Upper-Air Network (GUAN) (WMO GRUAN station #60018). Since 2008 the Vaisala RS-92 radiosondes corresponding to 12 UTC (hereafter, RS92) have been used.The PWV content in the atmosphere column is determined from the measured vertical profiles of temperature, relative humidity and atmospheric pressure acquired with the meteorological radiosondes [6]. The obtained PWV values have been post-corrected for radiation dependence (daytime radiosondes) and temperature following et al. [41]. The precision is 5% for total column water vapor in the lower and middle troposphere, increasing to between 10% and 20% in the upper troposphere for very dry conditions [6,25].
- Global Navigation Satellite System (GNSS)Using GNSS receivers, it is possible to determine the PWV content due to the delay of the signal caused by water vapor molecules [8,42]. The principle of the PWV retrieval lies in the decomposition of the indicated signal delay received from the GNSS receivers in components such as the ionosphere, the clock, the geometric and the neutral atmosphere’s delays. Ref. [8] developed the technique to evaluate the atmospheric delay caused by refractivity effects, which occurs mainly in the troposphere, and split it into two components, the zenith hydrostatic delay (ZHD) and the zenith wet delay (ZWD). The ZHD is caused by dry air plus the non-dipole contribution of water vapor and can be accurately modelled from the surface pressure, altitude and latitude [8]. The PWV is calculated from the ZWD by the knowledge of a weighted mean temperature of the atmosphere, as defined in [8].In this work, PWV retrievals from a Leica GRX 1200GG pro GPS/GLONASS receiver, installed at IZO since 2008, have been used. This receiver belongs to the Spanish National Geographic Institute (IGN), and forms part of the Network of European Meteorological Services (EUMETNET) GPS water vapor program (EGVAP) [43]. The GNSS PWV retrievals came from precise orbits and are available every hour (GNSS-P; [41]). Their expected precision is of 20% for PWV < 3.5 mm and about 10% above this value [25].
- CIMEL Sun PhotometerSince 2003, IZO has formed part of AERONET that is a federation of ground-based remote sensing aerosol networks [20]. The reference instrument of AERONET is the CIMEL Electronique CE318-T multiband sun photometer [44] that performs measurements of spectral sun and moon irradiance and sky radiances, at 340, 380, 440, 500, 675, 870 and 1020 nm with a FOV of 1.3[45]. An additional channel centered at 940 nm (with a FWHM of 10 nm) is used to retrieve PWV, following the procedure described in [21], with an uncertainty of 10%. Ref. [25] found that the uncertainty for this instrument depends on humidity conditions, with 7% for humid conditions and 25% for very dry conditions (PWV ≤ 2 mm). In this work, we use AERONET Version 3.0 Level 1.5 data (http://aeronet.gsfc.nasa.gov, last access: 10 December 2020).
- FTIRWithin the IZO’s atmospheric research activities, the FTIR solar measurements started in 1999 in the framework of a collaboration between the AEMET and the KIT (Karlsruhe Institute of Technology) [46], contributing to NDACC and TCCON networks since 1999 and 2007, respectively.In this work, the FTIR PWV data retrieved within the TCCON activities are used [47]. These data are derived with the 2014 version of the GGG processing software [26] by analyzing direct solar absorption spectra measured between 4500 and 6500 cm (corresponding to wavelengths between 1500 and 2200 nm) at a spectral resolution of 0.02 cm. The latter represents a resolution power / at 5000 cm of about 2.5 × 10 [25]. The aperture diameter is limited to 0.5 mm, leading to a narrow spectrometer’s FOV angle of only 0.07°. Several scans are co-added to increase the signal-to-noise ratio and, thus, the sampling frequency of TCCON FTIR PWV data is about 2 min at IZO. Using collocated meteorological radiosoundings at globally distributed TCCON sites, a scale factor of 1.0180 ± 0.0040 has been determined for the TCCON FTIR water vapor columnar products (XHO) [26].Recently, at IZO, Ref. [35] further studies corroborated these results, obtaining a mean bias of −0.006 mm (−1.3%) when comparing TCCON FTIR PWV values to those obtained from meteorological radiosondes launched on Tenerife island and processed according to the GRUAN scheme (http://www.gruan.org, last access: 28 November 2020). The Almansa’s study also found a relative difference of +3.4% respect to collocated CIMEL-AERONET data (FTIR-CIMEL). Further details of the FTIR program at IZO are given [25,37,46].
4. PWV Retrieval Method
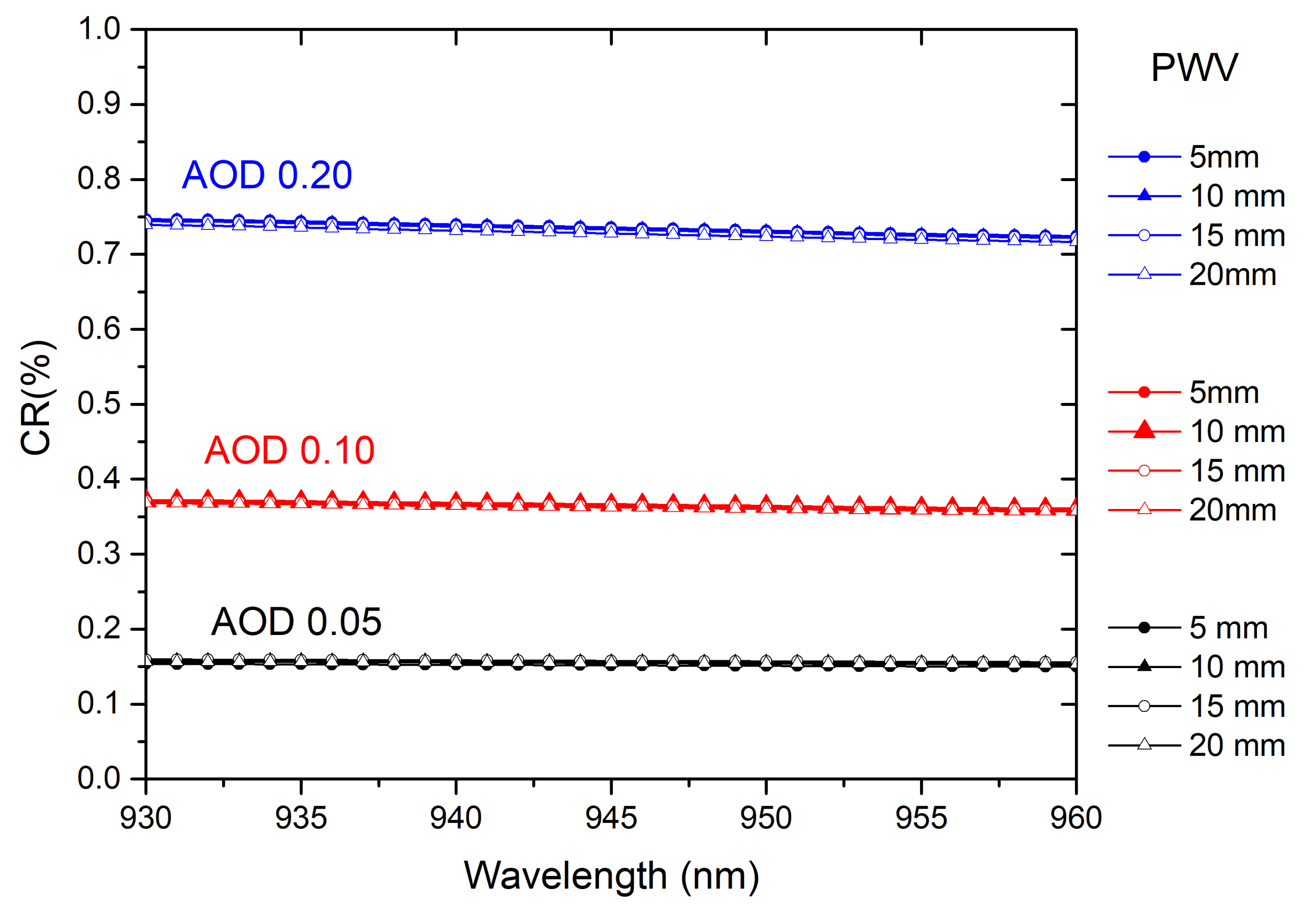
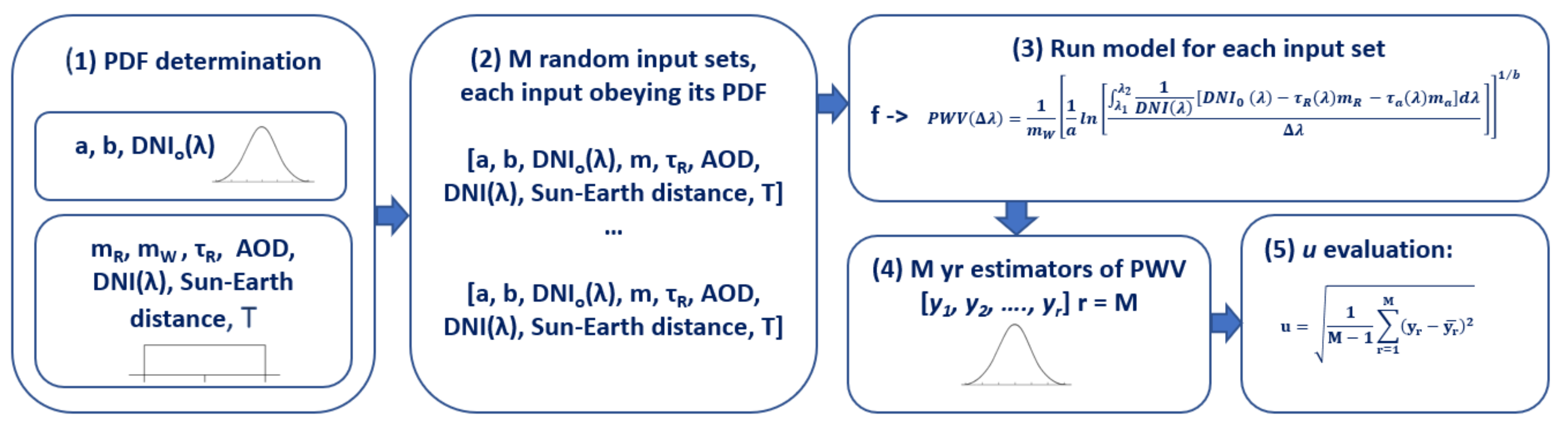
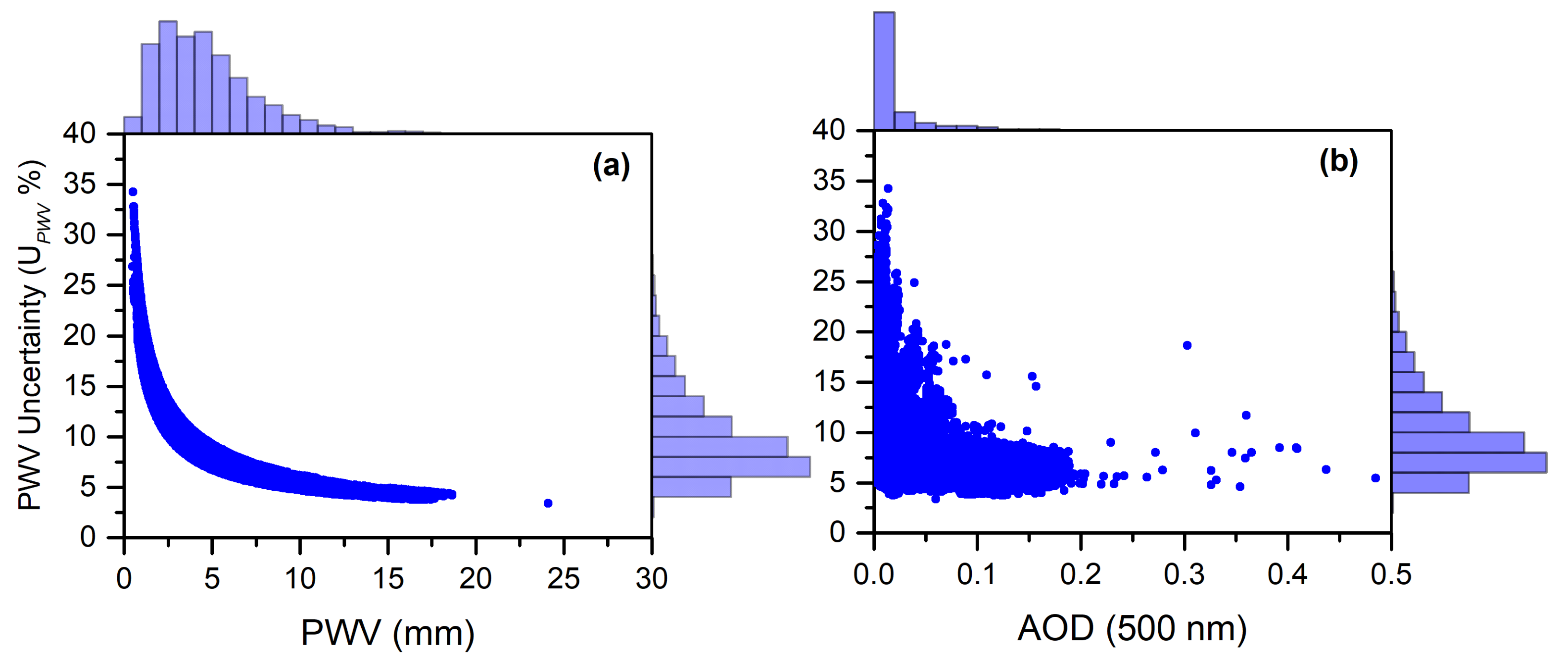
5. PWV Uncertainty Analysis
6. Results: Comparison to PWV Observations
7. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IPCC. The Physical Science Basis; Intergovernmental Panel on Climate Change: Genève, Switzerland, 2013. [Google Scholar]
- Bojinski, S.; Verstraete, M.; Peterson, T.C.; Richter, C.; Simmons, A.; Zemp, M. The concept of essential climate variables in support of climate research, applications, and policy. Bull. Am. Meteorol. Soc. 2014, 95, 1431–1443. [Google Scholar] [CrossRef]
- Cubasch, U.; Wuebbles, D.; Chen, D.; Facchini, M.C.; Frame, D.; Mahowald, N.; Winther, J.G. Introduction. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Hartmann, D.L.; Tank, A.M.K.; Rusticucci, M.; Alexander, L.V.; Brönnimann, S.; Charabi, Y.A.R.; Dentener, F.J.; Dlugokencky, E.J.; Easterling, D.R.; Kaplan, A.; et al. Observations: atmosphere and surface. In Climate Change 2013 the Physical Science Basis: Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Trenberth, K.E.; Stepaniak, D.P. The flow of energy through the earth’s climate system. Q. J. R. Meteorol. Soc. 2004, 130, 2677–2701. [Google Scholar] [CrossRef]
- Miloshevich, L.M.; Vömel, H.; Whiteman, D.N.; Leblanc, T. Accuracy assessment and correction of Vaisala RS92 radiosonde water vapor measurements. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Güldner, J. A model-based approach to adjust microwave observations for operational applications: Results of a campaign at Munich Airport in winter 2011/2012. Atmos. Meas. Tech. 2013, 6, 2879–2891. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS meteorology: Remote sensing of atmospheric water vapor using the global positioning system. J. Geophys. Res. Atmos. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Volz, F.E. Economical Multispectral Sun Photometer for Measurements of Aerosol Extinction from 0.44 µm to 1.6 µm and Precipitable Water. Appl. Opt. 1974, 13, 1732–1733. [Google Scholar] [CrossRef]
- Bruegge, C.J.; Conel, J.E.; Green, R.O.; Margolis, J.S.; Holm, R.G.; Toon, G. Water vapor column abundance retrievals during FIFE. J. Geophys. Res. Atmos. 1992, 97, 18759–18768. [Google Scholar] [CrossRef]
- Michalsky, J.J.; Liljegren, J.C.; Harrison, L.C. A comparison of Sun photometer derivations of total column water vapor and ozone to standard measures of same at the Southern Great Plains Atmospheric Radiation Measurement site. J. Geophys. Res. Atmos. 1995, 100, 25995–26003. [Google Scholar] [CrossRef]
- Halthore, R.N.; Schwartz, S.E.; Michalsky, J.J.; Anderson, G.P.; Ferrare, R.A.; Holben, B.N.; Ten Brink, H.M. Comparison of model estimated and measured direct-normal solar irradiance. J. Geophys. Res. Atmos. 1997, 102, 29991–30002. [Google Scholar] [CrossRef]
- Ingold, T.; Schmid, B.; Mätzler, C.; Demoulin, P.; Kämpfer, N. Modeled and empirical approaches for retrieving columnar water vapor from solar transmittance measurements in the 0.72, 0.82, and 0.94 μ absorption bands. J. Geophys. Res. Atmos. 2000, 105, 24327–24343. [Google Scholar] [CrossRef]
- Schmid, B.; Michalsky, J.; Slater, D.; Barnard, J.; Halthore, R.; Liljegren, J.; Holben, B.; Eck, T.; Livingston, J.; Philip, B.R.; et al. Comparison of columnar water-vapor measurements from solar transmittance methods. Appl. Opt. 2001, 40, 1886–1896. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Li, X.; Gu, X. Estimation of water vapor amount over Beijing from sun photometer measurements. J. Remote Sens. 2006, 10, 749. [Google Scholar]
- Haiou, Z.; Youfei, Z.; Ziying, C.; Chao, P. Retrieval of Atmospheric Column Water Vapor Content over Zhengzhou with Sun-Photometer. Available online: https://kns.cnki.net/kcms/detail/detail.aspx?dbcode=CJFD&dbname=CJFD2009&filename=QXKJ200905014&v=%25mmd2B7DBZDjW1N2icVGIHYL6gzYNnYsdUFVptFZjcCzESKFxG%25mmd2BCi%25mmd2FFnMpe4WcDWl0oto (accessed on 19 January 2021).
- Che, H.; Gui, K.; Chen, Q.; Zheng, Y.; Yu, J.; Sun, T.; Zhang, X.; Shi, G. Calibration of the 936 nm water-vapor channel for the China aerosol remote sensing NETwork (CARSNET) and the effect of the retrieval water-vapor on aerosol optical property over Beijing, China. Atmos. Pollut. Res. 2016, 7, 743–753. [Google Scholar] [CrossRef]
- Campanelli, M.; Mascitelli, A.; Sanò, P.; Diémoz, H.; Estellés, V.; Federico, S.; Iannarelli, A.M.; Fratarcangeli, F.; Mazzoni, A.; Realini, E.; et al. Precipitable water vapour content from ESR/SKYNET sun–sky radiometers: validation against GNSS/GPS and AERONET over three different sites in Europe. Atmos. Meas. Tech. 2018, 11, 81–94. [Google Scholar] [CrossRef]
- WMO. Environmental Pollution Monitoring and Reasearch Programme; GAW Report No. 43; WMO: Geneve, Switzerland, 1986. [Google Scholar]
- Holben, B.; Eck, T.; Slutsker, I.; Tanré, D.; Buis, J.; Setzer, A.; Vermote, E.; Reagan, J.; Kaufman, Y.; Nakajima, T.; et al. AERONET—A Federated Instrument Network and Data Archive for Aerosol Characterization. Remote Sens. Environ. 1998, 66, 1–16. [Google Scholar] [CrossRef]
- Smirnov, A.; Holben, B.; Lyapustin, A.; Slutsker, I.; Eck, T. AERONET processing algorithms refinement. In AERONET Workshop; El Arenosillo: Mazagón, Spain, 2004; pp. 10–14. [Google Scholar]
- Wehrli, C. Calibrations of filter radiometers for determination of atmospheric optical depth. Metrologia 2000, 37, 419. [Google Scholar] [CrossRef]
- Campanelli, M.; Estelles, V.; Smyth, T.; Tomasi, C.; Martìnez-Lozano, M.; Claxton, B.; Muller, P.; Pappalardo, G.; Pietruczuk, A.; Shanklin, J.; et al. Monitoring of Eyjafjallajökull volcanic aerosol by the new European Skynet Radiometers (ESR) network. Atmos. Environ. 2012, 48, 33–45. [Google Scholar] [CrossRef]
- Campanelli, M.; Nakajima, T.; Khatri, P.; Takamura, T.; Uchiyama, A.; Estelles, V.; Liberti, G.L.; Malvestuto, V. Retrieval of characteristic parameters for water vapour transmittance in the development of ground-based sun–sky radiometric measurements of columnar water vapour. Atmos. Meas. Tech. 2014, 7, 1075–1087. [Google Scholar] [CrossRef]
- Schneider, M.; Romero, P.M.; Hase, F.; Blumenstock, T.; Cuevas, E.; Ramos, R. Continuous quality assessment of atmospheric water vapour measurement techniques: FTIR, Cimel, MFRSR, GPS, and Vaisala RS92. Atmos. Meas. Tech. 2010, 3, 323–338. [Google Scholar] [CrossRef]
- Wunch, D.; Toon, G.C.; Blavier, J.F.L.; Washenfelder, R.A.; Notholt, J.; Connor, B.J.; Griffith, D.W.T.; Sherlock, V.; Wennberg, P.O. The total carbon column observing network. Philos. Trans. R. Soc. Ser. A Math. Phys. Eng. Sci. 2011, 369, 2087–2112. [Google Scholar] [CrossRef]
- Schneider, M.; Barthlott, S.; Hase, F.; González, Y.; Yoshimura, K.; García, O.E.; Sepúlveda, E.; Gomez-Pelaez, A.; Gisi, M.; Kohlhepp, R.; et al. Ground-based remote sensing of tropospheric water vapour isotopologues within the project MUSICA. Atmos. Meas. Tech. 2012, 5, 3007–3027. [Google Scholar] [CrossRef]
- Cachorro, V.; De Frutos, A.; Casanova, J. Determination of total vertical water vapor in the atmosphere. Atmos. Res. 1986, 20, 67–74. [Google Scholar] [CrossRef]
- Cachorro, V.E.; Utrillas, P.; Vergaz, R.; Durán, P.; de Frutos, A.M.; Martinez-Lozano, J.A. Determination of the atmospheric-water-vapor content in the 940-nm absorption band by use of moderate spectral-resolution measurements of direct solar irradiance. Appl. Opt. 1998, 37, 4678–4689. [Google Scholar] [CrossRef] [PubMed]
- Raptis, P.I.; Kazadzis, S.; Gröbner, J.; Kouremeti, N.; Doppler, L.; Becker, R.; Helmis, C. Water vapour retrieval using the Precision Solar Spectroradiometer. Atmos. Meas. Tech. 2018, 11, 1143–1157. [Google Scholar] [CrossRef]
- Fowle, F. The spectroscopic determination of aqueous vapor. Astrophys. J. 1912, 35, 149. [Google Scholar] [CrossRef]
- Fowle, F. The determination of aqueous vapor above Mount Wilson. Astrophys. J. 1913, 37, 359. [Google Scholar] [CrossRef]
- Schmid, B.; Thorne, K.; Demoulin, P.; Peter, R.; Mätzler, C.; Sekler, J. Comparison of modeled and empirical approaches for retrieving columnar water vapor from solar transmittance measurements in the 0.94-µm region. J. Geophys. Res. Atmos. 1996, 101, 9345–9358. [Google Scholar] [CrossRef]
- Barreto, A.; Cuevas, E.; Damiri, B.; Romero, P.M.; Almansa, F. Column water vapor determination in night period with a lunar photometer prototype. Atmos. Meas. Tech. 2013, 6, 2159–2167. [Google Scholar] [CrossRef]
- Almansa, A.F.; Cuevas, E.; Barreto, A.; Torres, B.; García, O.E.; Delia García, R.; Velasco-Merino, C.; Cachorro, V.E.; Berjón, A.; Mallorquín, M.; et al. Column Integrated Water Vapor and Aerosol Load Characterization with the New ZEN-R52 Radiometer. Remote Sens. 2020, 12, 1424. [Google Scholar] [CrossRef]
- WMO. Commission for Instruments and Methods of Observation, Sixteenth Session WMO; No.1138; Secretariat of the World Meteorological Organization: Saint Petersburg, Russia, 2014. [Google Scholar]
- Cuevas, E.; Milford, C.; Bustos, J.J.; García, O.E.; García, R.D.; Gómez-Peláez, A.J.; Guirado-Fuentes, C.; Marrero, C.; Prats, N.; Ramos, R.; et al. Izaña Atmospheric Research Center Activity Report 2017–2018. Technical Report WMO/GAW No. 247, World Meteorological Organization & Izaña Atmospheric Resear Center (AEMET). 2019. Available online: https://izana.aemet.es/wp-content/docs/Izana_Report_2017_2018.pdf (accessed on 19 January 2021).
- Egli, L.; Gröbner, J.; Hülsen, G.; Bachmann, L.; Blumthaler, M.; Dubard, J.; Khazova, M.; Kift, R.; Hoogendijk, K.; Serrano, A.; et al. Quality assessment of solar UV irradiance measured with array spectroradiometers. Atmos. Meas. Tech. 2016, 9, 1553–1567. [Google Scholar] [CrossRef]
- Pavanello, D.; Galleano, R.; Zaaiman, W.; Ankit, M.; Kouremeti, N.; Gröbner, J.; Hoogendijk, K.; Po, M.; Lisbona, E.; Alius, W.; et al. Results of the IX International Spectroradiometer Intercomparison and impact on precise measurements of new photovoltaic technologies. Prog. Photovolt. Res. Appl. 2020, 29, 109–123. [Google Scholar] [CrossRef]
- García-Cabrera, R.D.; Cuevas-Agulló, E.; Barreto, A.; Cachorro, V.E.; Pó, M.; Ramos, R.; Hoogendijk, K. Aerosol retrievals from the EKO MS-711 spectral direct irradiance measurements and corrections of the circumsolar radiation. Atmos. Meas. Tech. 2020, 13, 2601–2621. [Google Scholar] [CrossRef]
- Romero Campos, P.M.; Marrero de la Santa Cruz, C.L.; Alonso-Pérez, S.; Cuevas Agulló, E.; Afonso Gómez, S.; Ortiz de Galisteo, J.P. Una climatología del agua precipitable en la región subtropical sobre la isla de Tenerife basada en datos de radiosondeos; Nota Técnica Digital N° 6; Agencia Estatal de Meteorología: Madrid, Spain; Available online: http://www.aemet.es/documentos/es/conocermas/publicaciones/NT6-Tenerife.pdf (accessed on 19 January 2021).
- Yuan, L.L.; Anthes, R.A.; Ware, R.H.; Rocken, C.; Bonner, W.D.; Bevis, M.G.; Businger, S. Sensing climate change using the global positioning system. J. Geophys. Res. Atmos. 1993, 98, 14925–14937. [Google Scholar] [CrossRef]
- Romero Campos, P.M.; Agulló, C.; Ramón, R.; de Vargas, M.V.P.; Schneider, M. Programa de vapor de agua en columna del Centro de Investigación Atmosférica de Izaña: Análisis e Intercomparación de diferentes Técnicas de Medida; Nota Técnica Digital N° 1; NIPO 784-09-009-9; Agencia Estatal de Meteorología: Madrid, Spain, 2009; pp. 1–67. Available online: http://www.aemet.es/es/conocermas/recursos_en_linea/publicaciones_y_estudios/publicaciones/detalles/Programa_de_vapor_de_agua (accessed on 19 January 2021).
- Barreto, A.; Cuevas, E.; Granados-Muñoz, M.J.; Alados-Arboledas, L.; Romero, P.M.; Gröbner, J.; Kouremeti, N.; Almansa, A.F.; Stone, T.; Toledano, C.; et al. The new sun-sky-lunar Cimel CE318-T multiband photometer a comprehensive performance evaluation. Atmos. Meas. Tech. 2016, 9, 631–654. [Google Scholar] [CrossRef]
- Torres, B.; Toledano, C.; Berjón, A.; Fuertes, D.; Molina, V.; Gonzalez, R.; Canini, M.; Cachorro, V.E.; Goloub, P.; Podvin, T.; et al. Measurements on pointing error and field of view of Cimel-318 Sun photometers in the scope of AERONET. Atmos. Meas. Tech. 2013, 6, 2207–2220. [Google Scholar] [CrossRef]
- Schneider, M.; Blumenstock, T.; Chipperfield, M.P.; Hase, F.; Kouker, W.; Reddmann, T.; Ruhnke, R.; Cuevas, E.; Fischer, H. Subtropical trace gas profiles determined by ground-based FTIR spectroscopy at Izaña (28.5deg; N, 16.3deg; W): Five-year record, error analysis, and comparison with 3-D CTMs. Atmos. Chem. Phys. 2005, 5, 153–167. [Google Scholar] [CrossRef]
- Blumenstock, T.; Hase, F.; Schneider, M.; García, O.; Sepúlveda, E. TCCON data from Izana. In TCCON Data from Izana (ES), Release GGG2014.R1 (Version R1) [Data Set]; CaltechDATA: Pasadena, CA, USA, 2017. [Google Scholar] [CrossRef]
- Thomason, L.; Herman, B.M.; Schotland, R.M.; Reagan, J.A. Extraterrestrial solar flux measurement limitations due to a Beer’s law assumption and uncertainty in local time. Appl. Opt. 1982, 21, 1191–1195. [Google Scholar] [CrossRef]
- Hansen, J.E.; Travis, L.D. Light scattering in planetary atmospheres. Space Sci. Rev. 1974, 16, 527–610. [Google Scholar] [CrossRef]
- Kasten, F.; Young, A.T. Revised optical air mass tables and approximation formula. Appl. Opt. 1989, 28, 4735–4738. [Google Scholar] [CrossRef]
- Kasten, F. A new table and approximation formula for the relative optical air mass. Arch. Meteor. Geophy. B 1966, 14, 206–223. [Google Scholar] [CrossRef]
- Halthore, R.N.; Markham, B.L.; Deering, D.W. Atmospheric Correction and Calibration During Kurex-91. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS ’92), Houston, TX, USA, 26–29 May 1992; Volume 2, pp. 1278–1280. [Google Scholar] [CrossRef]
- Berk, A.; Hawes, F. Validation of MODTRAN® 6 and its line-by-line algorithm. J. Quant. Spectrosc. Radiat. Transf. 2017, 203, 542–556. [Google Scholar] [CrossRef]
- Anderson, G.P.; Clough, S.A.; Kneizys, F.; Chetwynd, J.H.; Shettle, E.P. AFGL atmospheric constituent profiles (0.120 km). In Technical Report; Air Force Geophysics Lab Hanscom AFB MA: Lexington, MA, USA, 1986. [Google Scholar]
- Ångström, A. Techniques of determinig the turbidity of the atmosphere. Tellus 1961, 13, 214–223. [Google Scholar] [CrossRef]
- Mayer, B.; Kylling, A. Technical note: The libRadtran software package for radiative transfer calculations—Description and examples of use. Atmos. Chem. Phys. 2005, 5, 1855–1877. [Google Scholar] [CrossRef]
- Emde, C.; Buras-Schnell, R.; Kylling, A.; Mayer, B.; Gasteiger, J.; Hamann, U.; Kylling, J.; Richter, B.; Pause, C.; Dowling, T.; et al. The libRadtran software package for radiative transfer calculations (version 2.0. 1). Geosci. Model Dev. 2016, 9, 1647–1672. [Google Scholar] [CrossRef]
- Bipm, I.; Ifcc, I.; Iso, I.; Iupap, O. Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement, JCGM 100: 2008 GUM 1995 with Minor Corrections. Available online: https://ncc.nesdis.noaa.gov/documents/documentation/JCGM_100_2008_E.pdf (accessed on 19 January 2021).
- Jcgm, Y. Evaluation of Measurement Data—Supplement 1 to the “Guide to the Expression of Uncertainty in Measurement”—Propagation of Distributions Using a Monte Carlo Method; Organisation for Standardization: Geneva, Switzerland, 2008. [Google Scholar]
- Metrology, J.C. Evaluation of Measurement Data—An Introduction to the “Guide to the Expression of Uncertainty in Measurement” and Related Documents (JCGM 104: 2009); Organisation for Standardization: Geneva, Switzerland, 2009. [Google Scholar]
- Bipm, I.; Ifcc, I.; Iso, I.; Iupap, O. Evaluation of measurement data—Supplement 2 to the ‘Guide to the expression of uncertainty in measurement’—Extension to any number of output quantities. JCGM 2011, 102, 2011. [Google Scholar]
- Fröhlich, C.; Shaw, G.E. New determination of Rayleigh scattering in the terrestrial atmosphere. Appl. Opt. 1980, 19, 1773–1775. [Google Scholar] [CrossRef]
- Spencer, R.P.; Lange, R.C.; Treves, S. Use of 135mBa and 131Ba as bone-scanning agents. J. Nucl. Med. 1971, 12, 216–221. [Google Scholar]
- Stephens, M.A. EDF statistics for goodness of fit and some comparisons. J. Am. Stat. Assoc. 1974, 69, 730–737. [Google Scholar] [CrossRef]
- Rodriguez-Franco, J.J.; Cuevas, E. Characteristics of the subtropical tropopause region based on long-term highly resolved sonde records over Tenerife. J. Geophys. Res. Atmos. 2013, 118, 10754–10769. [Google Scholar] [CrossRef]
- Andrey, J.; Cuevas, E.; MC, P.; Alonso-Pérez, S.; Redondas, A.; Gil-Ojeda, M. Quantification of ozone reductions within the Saharan air layer through a 13-year climatologic analysis of ozone profiles. Atmos. Environ. 2014, 84, 28–34. [Google Scholar] [CrossRef]
- García, R.D.; Barreto, A.; Cuevas, E.; Gröbner, J.; García, O.E.; Gómez-Peláez, A.; Romero-Campos, P.M.; Redondas, A.; Cachorro, V.E.; Ramos, R. Comparison of observed and modeled cloud-free longwave downward radiation (2010–2016) at the high mountain BSRN Izaña station. Geosci. Model Dev. 2018, 11, 2139–2152. [Google Scholar] [CrossRef]



| Parameter | Uncertainty | Reference | |
|---|---|---|---|
| a | 0.00168 | MCM | Gaussian |
| b | 0.00485 | MCM | Gaussian |
| ; | 0.065% | [50] | Rectangular |
| 0.7% | [62] | Rectangular | |
| (AOD) | 0.02 | [40] | Rectangular |
| 3.8% | Calibration Certificate EKO MS-711 | Rectangular | |
| 4.1% | MCM | Gaussian | |
| Sun-Earth distance | 0.0001 | [63] | Rectangular |
| Transmittance (MODTRAN) | 0.005 | [53] | Rectangular |
| N | R | RMSE (mm) | MB (mm) | STD (mm) | ||
|---|---|---|---|---|---|---|
| (%) | (%) | (%) | ||||
| RS92/EKO | 187 | 0.956 | 0.94 | −0.30 | 0.89 | |
| (18.5%) | (−4.7%) | (25.3%) | ||||
| All data | GNSS/EKO | 1987 | 0.975 | 0.68 | 0.02 | 0.68 |
| (14.1%) | (3.3%) | (26.7%) | ||||
| FTIR/EKO | 3765 | 0.964 | 0.88 | −0.57 | 0.68 | |
| (18.6%) | (14.5%) | (17.3%) | ||||
| CIMEL-AERONET/EKO | 21,909 | 0.983 | 0.67 | 0.33 | 0.59 | |
| (12.8%) | (9.5%) | (13.6%) | ||||
| RS92/EKO | 118 | 0.796 | 0.90 | −0.32 | 0.85 | |
| (27.6%) | (6.5%) | (29.8%) | ||||
| EKO PWV ≤ 5 mm | GNSS/EKO | 1230 | 0.884 | 0.60 | −0.02 | 0.60 |
| (20.0%) | (4.0%) | (32.6%) | ||||
| FTIR/EKO | 2692 | 0.883 | 0.82 | −0.61 | 0.55 | |
| (23.4%) | (−18.3%) | (17.5%) | ||||
| CIMEL-AERONET/EKO | 13,155 | 0.937 | 0.64 | 0.47 | 0.44 | |
| (18.7%) | (14.6%) | (13.8%) | ||||
| RS92/EKO | 69 | 0.932 | 1.00 | −0.26 | 0.97 | |
| (12.2%) | (−1.6%) | (14.2%) | ||||
| EKO PWV > 5 mm | GNSS/EKO | 757 | 0.956 | 0.79 | 0.08 | 0.79 |
| (10.2%) | (2.2%) | (12.1%) | ||||
| FTIR/EKO | 1073 | 0.919 | 1.02 | −0.45 | 0.91 | |
| (13.0%) | (−4.9%) | (12.3%) | ||||
| CIMEL-AERONET/EKO | 8754 | 0.966 | 0.71 | 0.11 | 0.71 | |
| (8.9%) | (1.9%) | (8.8%) |
| Station | Referencia | Period | Instruments | Results PWV Differences | |
|---|---|---|---|---|---|
| (mm) | (%) | ||||
| Izaña (Spain) | FTIR/CIMEL-AERONET | – | −25.4 ± 12.7 | ||
| [25] | 2005–2009 | FTIR/GNSS | – | −5.36 ± 19.5 | |
| FTIR/RS92 | – | −3.33 ± 15.5 | |||
| [34] | July–August 2011 | Lunar CIMEL/GNSS | 1.8 | – | |
| Lunar CIMEL/RS92 | 2.5 | – | |||
| [35] | August 2017–June 2018 | FTIR/ZEN-R52 | – | 9.1 | |
| CIMEL-AERONET/ZEN-R52 | – | 17.1 | |||
| Bern (Switzerland) | [33] | 1992–1993 | Sunphotometer/RS92 | 1.9 | 13 |
| USA and Canada | [12] | July 1993; April 1994 | Sunphotometer/RS92 | – | 10 |
| September 1994 | Sunphotometer/MWR | – | 5 | ||
| Rome (Italy) | 1.35 | 6 | |||
| Aosta (Italy) | [18] | 2011, 2012 and 2014 | Sun-Sky radiometers/GNSS | 1.97 | 13 |
| Valencia (Spain) | Sun-Sky radiometers/CIMEL-AERONET | 1.28 | 8 | ||
| Lindenberg (Germany) | PSR/CIMEL-AERONET | 1.10 | 0.7 | ||
| [30] | May 2014–April 2016 | PSR/GNSS | 0.50 | 0.40 | |
| PSR/RS92 | 0.40 | 0.50 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
García, R.D.; Cuevas, E.; Cachorro, V.E.; García, O.E.; Barreto, Á.; Almansa, A.F.; Romero-Campos, P.M.; Ramos, R.; Pó, M.; Hoogendijk, K.; et al. Water Vapor Retrievals from Spectral Direct Irradiance Measured with an EKO MS-711 Spectroradiometer—Intercomparison with Other Techniques. Remote Sens. 2021, 13, 350. https://doi.org/10.3390/rs13030350
García RD, Cuevas E, Cachorro VE, García OE, Barreto Á, Almansa AF, Romero-Campos PM, Ramos R, Pó M, Hoogendijk K, et al. Water Vapor Retrievals from Spectral Direct Irradiance Measured with an EKO MS-711 Spectroradiometer—Intercomparison with Other Techniques. Remote Sensing. 2021; 13(3):350. https://doi.org/10.3390/rs13030350
Chicago/Turabian StyleGarcía, Rosa Delia, Emilio Cuevas, Victoria Eugenia Cachorro, Omaira E. García, África Barreto, A. Fernando Almansa, Pedro M. Romero-Campos, Ramón Ramos, Mário Pó, Kees Hoogendijk, and et al. 2021. "Water Vapor Retrievals from Spectral Direct Irradiance Measured with an EKO MS-711 Spectroradiometer—Intercomparison with Other Techniques" Remote Sensing 13, no. 3: 350. https://doi.org/10.3390/rs13030350
APA StyleGarcía, R. D., Cuevas, E., Cachorro, V. E., García, O. E., Barreto, Á., Almansa, A. F., Romero-Campos, P. M., Ramos, R., Pó, M., Hoogendijk, K., & Gross, J. (2021). Water Vapor Retrievals from Spectral Direct Irradiance Measured with an EKO MS-711 Spectroradiometer—Intercomparison with Other Techniques. Remote Sensing, 13(3), 350. https://doi.org/10.3390/rs13030350