Abstract
The availability of free and high temporal resolution satellite data and advanced SAR techniques allows us to analyze ground displacement cost-effectively. Our aim was to properly define subsidence and uplift areas to delineate a geothermal field and perform time-series analysis to identify temporal trends. A Persistent Scatterer Interferometry (PSI) algorithm was used to estimate vertical displacement in the Brady geothermal field located in Nevada by analyzing 70 Sentinel-1A Synthetic-Aperture Radar (SAR) images, between January 2017 and December 2019. To classify zones affected by displacement, an unsupervised Self-Organizing Map (SOM) algorithm was applied to classify points based on their behavior in time, and those clusters were used to determine subsidence, uplift, and stable regions automatically. Finally, time-series analysis was applied to the clustered data to understand the inflection dates. The maximum subsidence is –19 mm/yr with an average value of –6 mm/yr within the geothermal field. The maximum uplift is 14 mm/yr with an average value of 4 mm/yr within the geothermal field. The uplift occurred on the NE of the field, where the injection wells are located. On the other hand, subsidence is concentrated on the SW of the field where the production wells are located. The coupling of the PSInSAR and the SOM algorithms was shown to be effective in analyzing the direction and pattern of the displacements observed in the field.
1. Introduction
Geothermal operations including injection and production can create displacements on the geothermal fields [1]. Surface displacement caused by geothermal operations affects the construction of facilities, such as buildings, pipelines, and other infrastructure [2], and can be monitored through several methods [3,4,5]. Availability of radar, laser, satellite, and unmanned aerial vehicle (UAV) images and also recent technological developments in Remote Sensing (RS), Geographic Information system (GIS), and radar imaging, tools, and techniques have demonstrated reliable, accurate, cost-effective, and high-performance displacement analysis opportunities for various purposes. Moreover, the development of artificial intelligence (AI) and machine learning (ML) algorithms provide strong analysis tools that can be applied to the analysis of the displacements to investigate the patterns. Besides, Sentinel 1, Radarsat, ERS SAR provide reliable Interferometric Synthetic Aperture Radar (InSAR), high spatial resolution data with short revisit times. The type of data (e.g., radar, laser, optic), radiometric resolution (e.g., 8-bit, 16-bit), and spatial resolution (e.g., 1 cm, 10 m) are coupled with new and promising algorithms such as SqueeSAR [6], SBAS [5,7], and PSInSAR [8], which provide meaningful information for a wide variety of research fields, like analyses of landslides [9,10,11], displacement monitoring [12,13], natural hazard and risk mitigation [14], deformation and time-series analysis [15], deformation caused by earthquakes [16] and volcanic activity monitoring [17], monitoring the surface impacts of groundwater pumping [18], mining subsidence monitoring [19,20], observing subsidence in reclaimed coastal land [21], and water level changes [22].
Geoscientists have been using SAR data and its specific components (e.g., amplitude or phase) to analyze and monitor slow-motion displacement caused by various field operations [15,23,24]. In geothermal energy production, injection, and production of water from the wells cause slow-motion displacements in a geothermal field. Several studies have used slow-motion displacement analysis to monitor various geothermal sites like Brady, Nevada-USA [25], Landau-Germany [26], Euhanean-Italy [27], Marangin Jambi-Indonesia [27], Cerro Prieto and Heber-USA [28], Coso-USA [3], and Acoculco-Mexico [11]. The spatial distribution, magnitude, and rate variations of displacement in the field depend on the structural geology, geothermal operations, and seismic activities in the fields. Most studies focus on the displacement between two-time steps, but there is a limited number of studies [2,7,25] that perform temporal and sequential displacement monitoring in geothermal sites.
Although these techniques and tools have been applied to geothermal sites in the last decade, there are not many complementary studies on geothermal fields that monitor displacements caused by the geothermal operations for shorter time periods using PSInSAR, which is relatively new and provides highly accurate results. The previous studies [25,29] on the same geothermal field had been investigated the displacements using various types of data (e.g., TerraSAR-X, ERS-2, Envisat, ALOS) with various InSAR analysis techniques (e.g., GIPhT, Geospatial Inversion) for a longer period of time (e.g., 2004 to 2018). All these studies have been only concentrated on monitoring the number of displacements caused by geothermal operations. On the other hand, the nature of geothermal operations causes a specific pattern of subsidence and uplift. The subsidence in a geothermal field stems from the interaction of various complex geological and production-related factors. Among these various factors, three of them can be considered as the leading factors [25,28,30]. As [25] stated, the first reason is the thermal cooling of the reservoir due to water injection via wells and recycling of the cooler brings back into the subsurface. The second reason is the compaction of the sedimentary layers as the pore pressure decreases and the formations desaturate. The third reason is the disturbance of the equilibrium between the fluids and reactive minerals due to dissolved minerals via reinjected water, which cause a mass loss due to hydrothermal alteration. While geothermal fields experience slow rates of subsidence, some amount of uplift is also observed due to the disturbed equilibrium via production and injection. The areas of uplift and subsidence together have the potential to provide insights into the dynamics of the operations and factors influencing the dynamics. Therefore, analyzing spatial and temporal patterns of the subsidence and uplift for a geothermal field has the potential to produce more knowledge about the characteristics of the slow-motion displacements and the factors causing them.
In this paper, we present a novel approach for analyzing the spatiotemporal pattern of subsidence and uplift for a geothermal field using the PSInSAR [31] and ML for a short time interval (from February 2017 to December 2019). Since the displacement is accepted as slow-motion [32] by looking at previous research [25] on the same site, time-series analysis for a short time period is an important tool to extract temporal anomalies on the field caused by geothermal operations. We demonstrated the implementation of the methodology for the Brady’s Hot Spring Geothermal field as it is one of the most widely studied geothermal fields in the literature. We used the self-organizing map (SOM) as an ML approach to obtain spatiotemporal clustering of the displacements. The time-series and pattern analyses have been applied in a multitude of fields in economics, finance, environmental sciences, and others [33]. The SOM approach provides successful results when the data are evenly spaced with some degree of noise [34]. The PSI analysis results in sparse displacement predictions [1,6,7,10,35,36,37,38,39,40,41] with better accuracy. Using SOM allows one to identify patterns of subsidence and uplift from sparse PSInSAR results, which has not been performed before to the authors’ knowledge. We compared the PSInSAR analysis results, with previous research for validation. In order to understand production dynamics in the study area we further conducted an analysis on the time series data for the subsidence and uplift clusters obtained from SOM results. These analyses provide an in-depth understanding of the relation between displacement behavior and geothermal operations, which have the potential to investigate the dynamic nature of the geothermal operations.
In the remaining part of the paper, the study area and the data are explained in Section 2. The methodology and algorithms are described in Section 3. In Section 4, we summarize and discuss the results of PSInSAR, SOM Clustering, and Time-Series Analysis in more detail, and we examine the results of earlier studies for comparison and validation. Finally, in our conclusion, we elaborate on the analysis results and describe directions for future research.
2. The Study Area and the Data
In this study, we used Sentinel-1 Synthetic Aperture Radar Interferometric Wide Swath (SAR-IW) data, which can be downloaded from https://scihub.copernicus.eu. The study covers Brady’s Hot Springs Geothermal Area in Churchill County, Nevada, a geothermal field containing a plant that has been operational since 1992 [25]. Previous research on the site [25] has identified the displacement on the site as slow-motion [32] confirming the suitability of PSInSAR for the site.
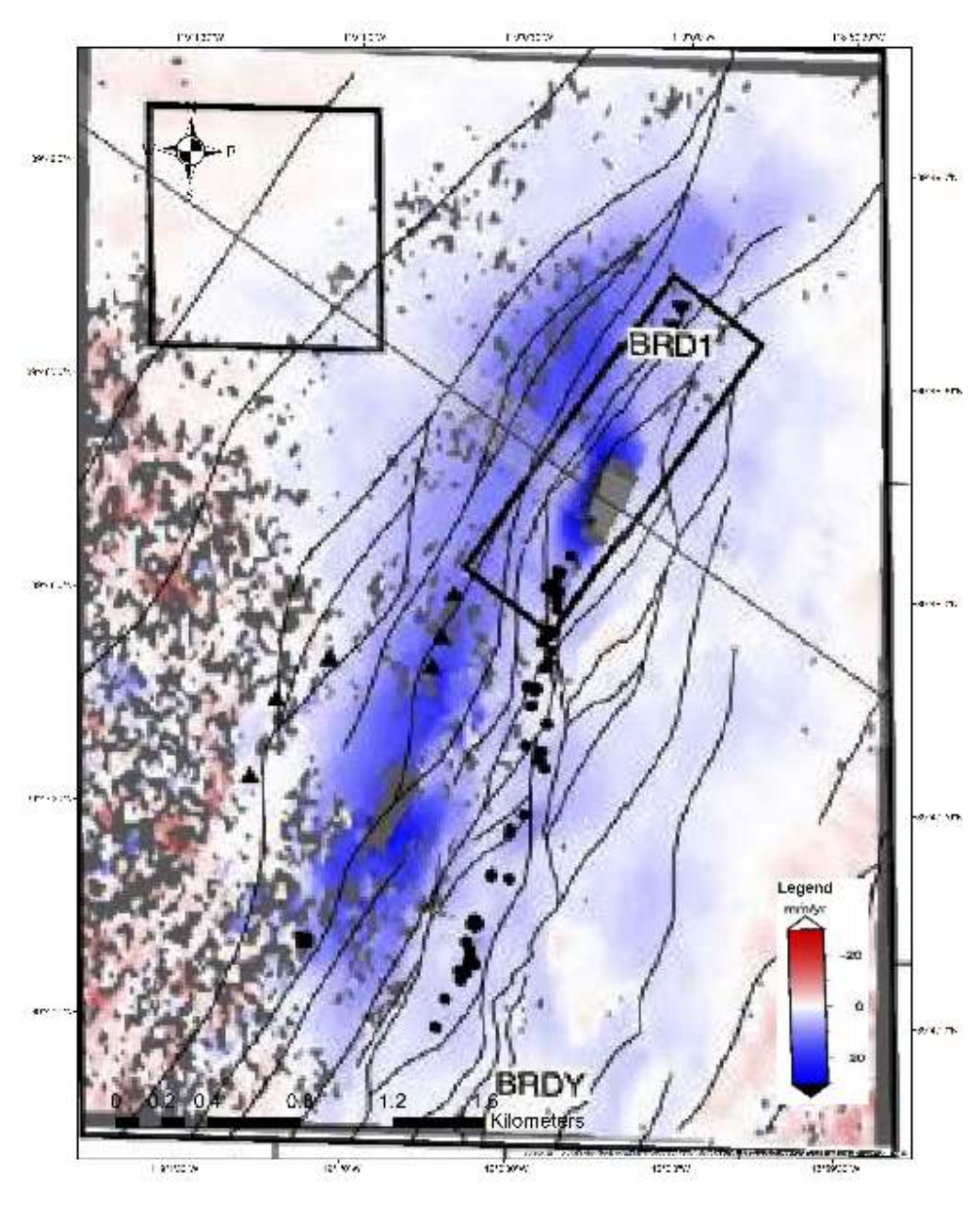
The study area of the Brady’s Hot Spring Geothermal field is located 80 km east-northeast of Reno, Nevada. Figure 1 illustrates the location of various wells (injection and production), distribution of faults, build-up areas, and roads.
Figure 1.
Brady’s hot spring geothermal study area.
The Brady geothermal Hot Spring has been functional since 1992 and there are three injection and six production wells active on the field (Figure 1). In addition, there are human-made structures and buildings in the Area of Interest (AOI), and buildings can provide good persistent scatterers for the analysis. The predominant fault direction (Figure 1) is north-northeast (NNE), which is commonly observed in geothermal fields [31]. In the literature, a correlation was found between subsidence and geothermal operations at Brady’s Hot Spring Geothermal field [25]. Some other researchers also stated that deformation may occur due to thermal effects and/or pore pressure changes in this geothermal field [25,28,30].
In this study, we limited our dataset to Sentinel 1A as the Sentinel-1A products are available with a revisit cycle of 12 days for this satellite, which allowed us to construct time series data for a short time period. We downloaded 72 SAR images (Orbit track 144, descending from February 2017 to December 2019), for PSInSAR analysis. The orbital file, atmospheric data, and Digital Elevation Model (DEM) were also downloaded to complete the data processing. Table 1 shows the summary of SAR data, which were used for the PSInSAR analysis.

Table 1.
Dataset used for PSInSAR analysis.
In this study, the analysis was conducted using a Single Look Complex (SLC) Interferometric Wide (IW) C-band of Sentinel-1A images. Displacement analysis was performed specifically in the VV polarization due to having a higher number of backscattered Persistent Scatterers (PSs) in VV than HH polarization [39]. Since the phase contribution of the SAR is more suitable for slow-motion displacement [42], phase values have been used for displacement calculation and error corrections. In data processing, we identified two images with some anomalies and hence excluded them. The final set of images used for PSInSAR was 70.
Once we obtained PSInSAR results we constructed a time series of displacements. We wanted to include enough data to monitor for at least two years, to make sure we had a sense of annual trends, and to obtain monitoring at regular and frequent intervals. The Sentinel data for the area are available for earlier years; however, the number of images per year is significantly low. For this reason, we did not consider the previous years in the analyses. Moreover, the SOM analysis for the time series data requires data with the same frequency. Therefore, the final set of images we used reduced to 59 spanning from the period of 22 December 2017 to 24 December 2019, where the displacement results were available with a 12-day frequency.
3. The Proposed Methodology
The proposed methodology consists of three main steps. Step I is the analysis of displacements using PSInSAR. Step II is the analysis of spatiotemporal patterns with respect to subsidence and uplift using SOM. Step III is the temporal analysis of displacements using the time-series obtained from SOM to obtain finer patterns in time. The following subsections explain each step in more detail with their implementation of the case study.
3.1. Step I—Analysis of Displacements Using PSInSAR
Synthetic Aperture Radar is a microwave imaging system penetrating clouds and water, providing day and night imaging capabilities. Backscattered microwave signals from the ground, rocks, buildings, and vegetation carries amplitude and phase information. Rapid Motion Tracking (RMT) algorithms use amplitude values for rapid landslides or fast-moving areas [43]. Differential Synthetic Aperture Radar Interferometry (DInSAR) uses two different radar images for the same field to form interferometric pairs that show the displacement information [8]. On the other hand, Persistent Scatterer Interferometry (PSI) methods like SqueeSAR, SBAS [3,6,7], and PSInSAR [8] are a specific class of DInSAR, used for extremely slow (< 16 mm/yr) or very slow displacements (between 16 mm/yr ≤ and < 1.6 m/yr) [41,44]. Additionally, PSInSAR gives good results on non-vegetated [42,44], and bare fields [41]. In addition, PSI with PSs from large coherent targets measures the displacement more accurately than those with many small Distributed Scatterers (DSs). Brady is a field in a deserted area with slow movement and, as such, the PSInSAR approach was selected for displacement analysis in this study.
PSI can help remove atmospheric errors, which require a higher number of images to provide reliable, precise, and accurate results than simpler algorithms in the DInSAR family (which only compares two images). The higher number of interferograms increases the reliability of the estimated deformation scatter points [44]. The studies in the literature suggest that the algorithm requires at least 15 images [45] to 20 images [46] for better accuracy. The SARPROZ software was used to analyze the displacements with the PSInSAR method [47]. The method of PSInSAR can be divided into five [31] steps. Figure 2 shows the flowchart of the PSInSAR analysis.
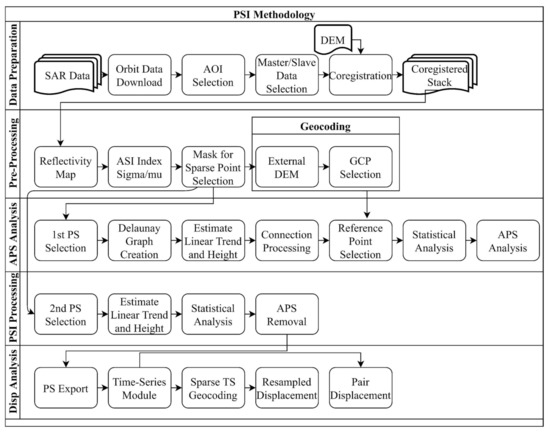
Figure 2.
The flowchart of PSInSAR analysis.
In the data preparation step (Figure 2), once the images, orbit data, and DEM are downloaded, the images were Co-registered using the selected master/slave pairs, and a Co-registered stack is obtained. In Preprocessing, a reflectivity map was constructed which is the first meaningful result that could be evaluated, and then the Amplitude Stability Index (ASI) index is obtained. The parameter of the ASI is critical and is recommended to be higher than 0.75 [31,40]. Hence, we used the recommended parameter of 0.75 for the ASI index, which cause a sparse final PSI result as expected [46]. After masking the sparse points, a geocoded map was obtained using GCPs and the DEM (Figure 2). GCPs are the reference points in PSI analysis. The SARPROZ software automatically downloads the SRTM data as DEM. It is also possible to incorporate a user-defined DEM. We used SRTM in our analyses. In Atmospheric Phase Screening (APS) Analysis, the first step is to find stable PSs. After GCP selection, we performed statistical analysis to make sure the PSs were normally distributed and accumulated on the zero axes. The Delaunay Graph creates a reference network by connecting the PSs. In general, the atmospheric phase is not expected to show significant linear trends. Therefore, we subtracted height to refine the baselines to have a linear trend. Then we estimated the parameter that connects the graph in Connection Processing. Figure 3 shows the histograms of the cumulative displacement, integrated cumulative displacement, and integrated residual height histograms, which should have zero mean for the identification of stable points. As can be seen from the graph illustrated in Figure 3, the majority of points accumulate at or around zero, indicating that the selected points are suitable for further analysis.
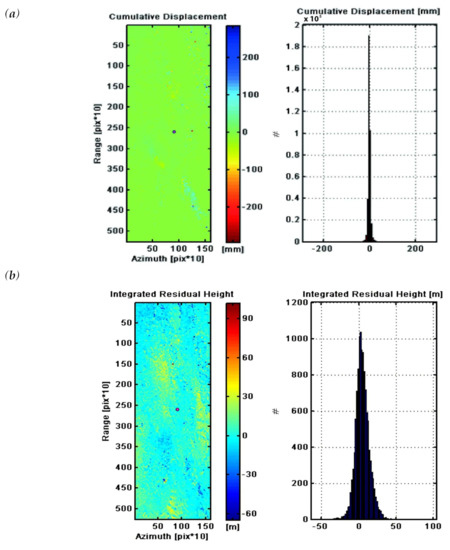
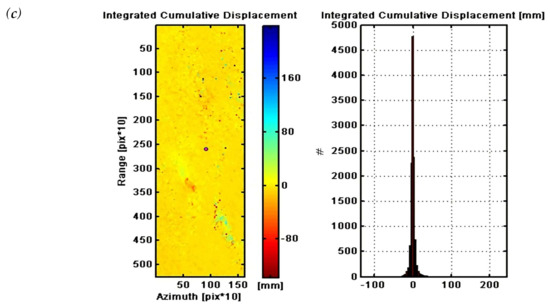
Figure 3.
Displacement histograms and maps after Atmospheric Phase Screening (APS) removal. (a) Cumulative displacement, (b) Integrated residual height, (c) Integrated cumulative displacement (Single Red Point: Selected GCP).
Figure 4 shows the PSI Processing that includes the Linear Trend and Height Estimation and APS Removal. Similar to the APS Analysis step, a threshold was needed to have a denser PSs analysis result. Then, the height was subtracted, and the APS was removed. We found that 13,048 (out of 13,517) points have a coherence value higher than 0.75 (Figure 4). In the final stage of the PSI analysis (Figure 2), 13,048 PSs were geocoded and exported for visualization. We exported maps as point scatters and resampled them to obtain cumulative and pair displacements.
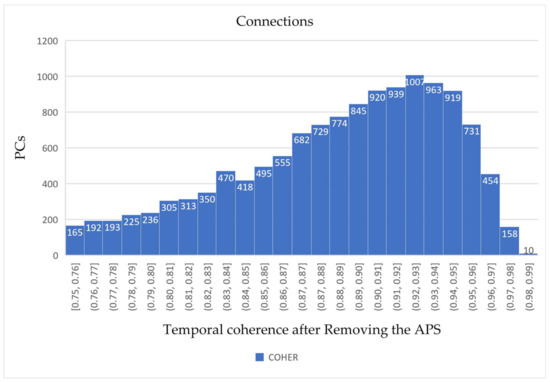
Figure 4.
PSs coherence values after the APS removal.
In the final step, we visualized the displacement values. SARPROZ provides Line of Sight displacement, that is, there is no breakdown of vertical and horizontal displacements. In the case of Brady, the horizontal displacement is assumed to be zero due to no/limited seismic or other major geological activity. Moreover, the previous studies conducted in the area did not also report significant horizontal displacements. Hence, we have assumed LOS and vertical displacement to be equivalent.
3.2. Step II—Analysis of Spatiotemporal Patterns Using Self-Organizing Map (SOM)
This step is for the identification and analysis of displacement patterns in time and space. The SOM is an unsupervised machine learning algorithm introduced by Teuvo Kohenen in 1982 [48]. The main purpose of the SOM is to classify high-dimensional inputs into spatially related two-dimensional maps. The SOM has spatial smoothness constraints on analysis; otherwise, the SOM algorithm is similar to a K-means clustering [49]. There are mainly three types of segmentation methods applied to the clustering of pixels in an image: supervised, semi-supervised, and unsupervised. Some unsupervised methods, like Iterative Self-Organizing Map Data (ISODATA) and Stochastic Expectation Maximization (SEM), depend on parameters, and they are susceptible to noise [49]. The SOM clustering algorithm is robust in eliminating the disadvantages of supervised methods and does not require the effort of manual or semiautomatic labeling operations. This algorithm is an Artificial Neural Network, ANN, algorithm [50], which has been used in many engineering tasks including clustering, dimensionality reduction, classification, sampling, vector quantization, and data mining [48] and for various image processing research [51]. It has also been used recently for pattern recognition by geoscience researchers [52], including satellite image segmentation [53]. There are several advantages of using SOM for segmentation: unsupervised learning [54], preserving topological relationships [55], translating high dimensional input into two-dimensional output map [56], and visualization [55]. The SOM algorithm is a suitable tool for our purposes given its ability to handle multidimensional data (as in our time series) while delineating small linear features [55]. The SOM has neurons for each data point in each dimension. The output layer is a two-dimensional map array of neurons. The output neurons are connected to input neurons by weight vectors. The initial weight is started with random estimation and the learning phase is to update the weights while learning [55].
The flowchart of the SOM algorithm, as applied in our framework, is summarized in Figure 5. The SOM analysis for the time series displacement data requires data with the same frequency. Therefore, the final set of images we used reduced to 59 spanning from the period of 22 December 2017 to 24 December 2019, where the displacement results were available with a 12-day frequency. We developed codes in R with the CRAN kohonen package for the application of the SOM algorithm to our dataset and selected a 3 × 3 SOM map, with a square grid and planar map (nontoroidal). The 3 × 3 SOM map results in nine clusters that can provide an efficient separation between subsidence, uplift, and no-displacement points. It is to be noted that we tried 4 × 4, 5 × 5, 6 × 6, and 7 × 7 SOM maps and analyzed the results. As an example, a 7 × 7 SOM map showed a large variety in trends and geographical dispersion, at the cost of fewer points classified in each cluster. We found that the 3 × 3 SOM map was enough to segregate the data to an adequate level of granularity and the 3x3 SOM map provides a good separability between subsidence, uplift, and no-displacement points.
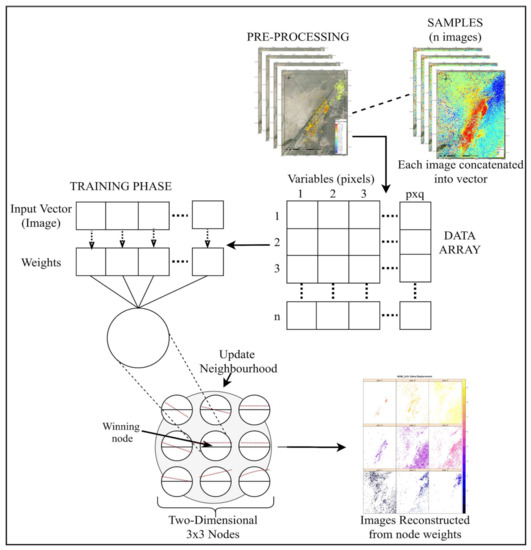
Figure 5.
The SOM algorithm, as used in our framework.
In Figure 5, the input layer (Table 2) is a feature vector composed of an image stack indicating displacement in our case. It includes normalized X, Y, and displacement values for different dates, and 2 years of data for SOM and time-series analysis for a total of 61 columns of data and 13,048 rows corresponding to displacement results for that number of points with coherence over 0.75.

Table 2.
Input layer for SOM analysis.
The SOM segments the values and creates several clusters that show trends in time for similarly behaved points. Once SOM results are mapped in space, the spatial pattern of the displacements with their temporal behavior can be visualized. The segments are a two-dimensional representation of the clusters on a map.
3.3. Step III—Temporal Analysis of Displacements Using the Time-Series from SOM
As the last step, we analyzed the clustered PSInSAR time-series data obtained from SOM to identify dates that exhibit significant change, called inflection points in the field. This analysis forms the basis of an in-depth understanding of the relation between the time of activity in the geothermal site and the displacements. It was stated that gradual thermal cooling of the reservoir, sediment compaction because of decreasing pore pressure and desaturation, and transportation of the dissolved salt flow are three reasons for subsidence [25]. The effect of these processes can be monitored in time through deformation, and the changes in the acceleration of the displacement can show the pattern of factors playing a role in the subsidence and uplift behavior in time. An inflection is a point where a function changes from concave to convex, or vice versa [57]. This coincides with a change in the direction of the acceleration, which relates to changes in the factors influencing the patterns of displacements in the geothermal field. Mathematically, this corresponds to the second derivative of the function associated with the deformation and, experimentally, in the difference of the differences between the displacement points:
The acceleration is given by the second derivative of the displacement in Equation (1).
where s is the pixel elevation, and t is time.
In addition, the inflection dates of this new function would show the moments in time where the influencing factors changed directions (from uplift to subsidence or vice versa).
The accuracy of the measurements must also be considered when analyzing the PSInSAR displacement result in the SOM algorithm. In addition, grouping samples in clusters or smoothing the curves in time can reduce the error. From previous studies, we know that high-quality PSInSAR measurements can achieve millimeter accuracy, but some of the variations between displacements are submillimeter; and this could result in noisy inputs during the displacement analysis. Therefore, before taking the derivative of the data (Table 3), we applied a three-date moving average (3-dma) on displacement data to make it smooth as shown in Equation (2).
where the displacement values are and n = 3 (we used three-date for smoothing values).

Table 3.
Input and output layers for time series analysis (for a single point).
4. Results and Discussion
4.1. Step I—The PSInSAR Analysis
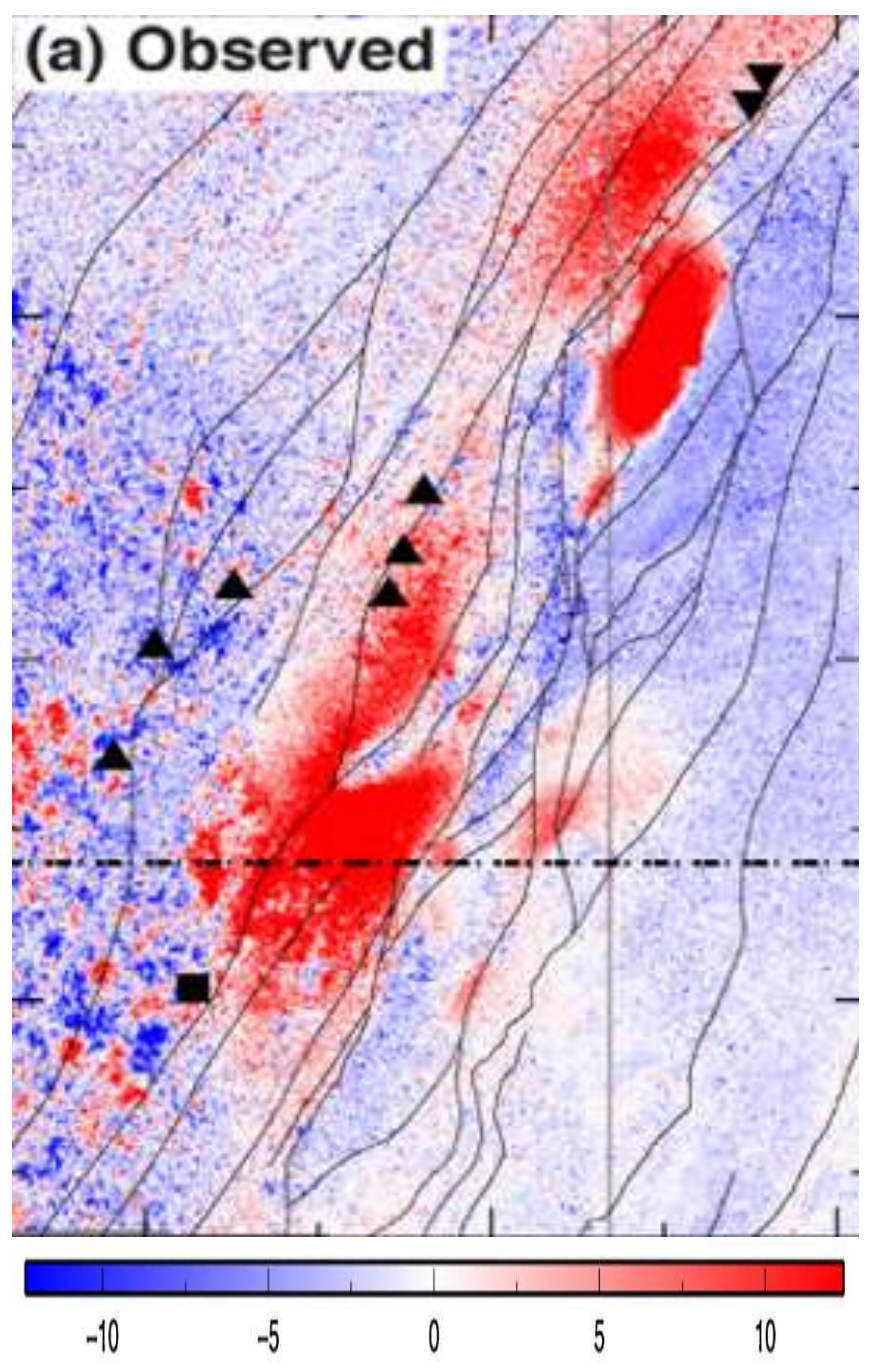
The results of the PSInSAR analysis are given in Figure 6. The highest subsidence detected in this analysis is −21 mm/yr whereas the highest uplift detected is 14 mm/yr. The average displacement of the field in AOI is 0 ± 2 mm/yr. In the map (Figure 6), hot colors (e.g., yellow to red) indicate subsidence, and cold colors (e.g., light blue to dark blue) indicate uplift.
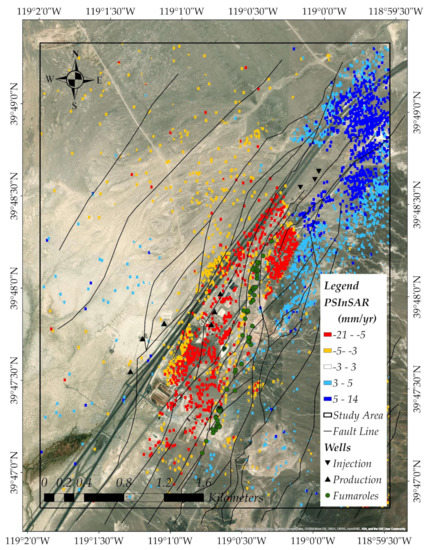
Figure 6.
The PSI analysis of Brady’s field with 70 images (± 3 mm/yr displacement values are not shown as accepted as stable).
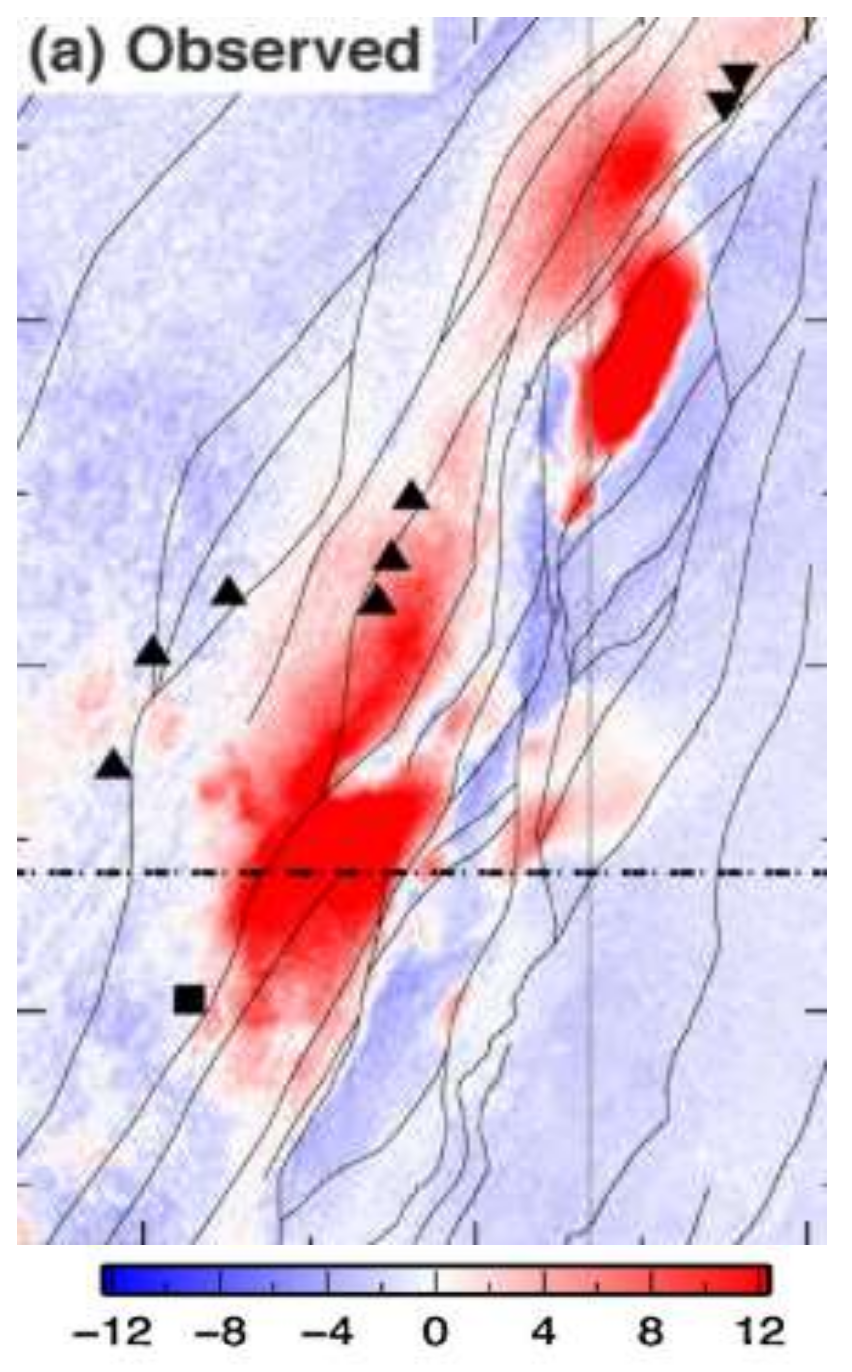
The displacement direction and magnitude in the map show patterns in the field from the PSInSAR analysis. However, to determine the pattern of velocity variation and to evaluate them concerning site-specific activity, it is better to first cluster them to improve the reliability of the analysis. Figure 7 shows the same results after applying Universal Kriging (UK) to the data, thus creating a smooth surface that shows more clearly the areas with large displacement.
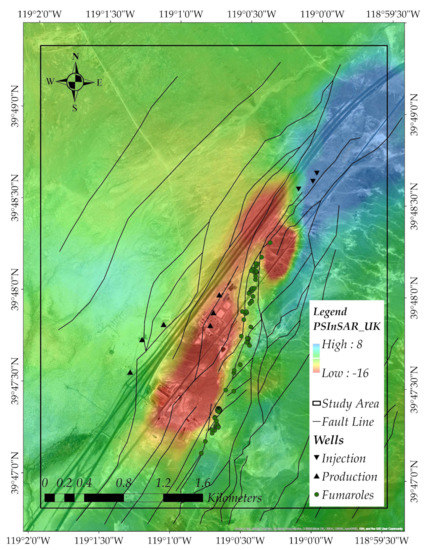
Figure 7.
The universal kriging applied to PSI displacement analysis result (PSInSAR_UK: PSInSAR_Universal Kriging).
The result of the PSInSAR with 70 images shows that subsided areas in the geothermal field overlap with production wells (black upright triangles) which are located on SW of the field, while the uplift areas overlap with the injection wells (black upside-down triangles) which are located NE of the field. Additionally, the faults in the region are oriented in the NE and SW direction [58], which also contribute to the evaluated subsidence and uplift trends.
As stated earlier the pore pressure changes and thermal contraction are possible two mechanisms that may cause displacement in the geothermal sites [29]. Both mechanisms have the potential to occur in the Brady Geothermal field as hot fluids are extracted at SW of the field and cooled in the heat exchanger at the power plant and then injected NE of the field. The first mechanism which decreases pore pressure causes subsidence on the other hand second mechanism which decreases the temperature causes the uplift [29]. Figure 7 shows that the uplift occurred on the NE of the field, where injection wells are located, whereas subsidence is concentrated on the SW of the field where the production wells are located.
4.2. Step II—The SOM Analysis
The 3×3 SOM map yielded the clusters indicated in Figure 8. When the data points in the clusters were mapped in the AOI (Figure 8), the spatial pattern of each SOM cluster can be visualized. These are related to the deformation behavior in time for each cluster.
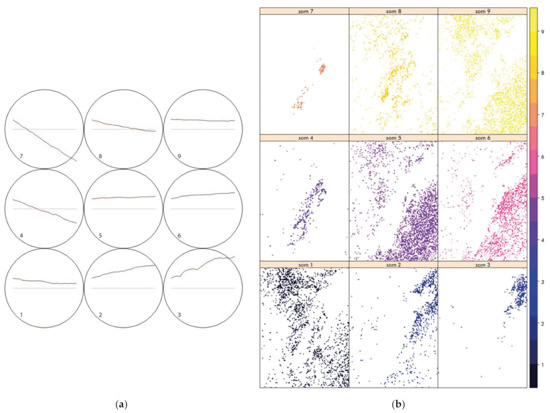
Figure 8.
The SOM result and maps, (a) SOM Results in 3 × 3, (b) SOM Analysis Maps 3x3.
Clusters 2, 3, and 6 show uplift patterns in time (of those, 2 and 3 are steep uplift patterns), while clusters 4, 7, and 8 show subsidence (of those, 4 and 7 are steep subsidence patterns) in Figure 8. The rest of the clusters shown in Figure 8b are mostly stable (no/very small deformation). Figure 8b shows the maps with the locations of the pixels for each cluster shown in Figure 8a.
In Figure 9, subsidence clusters (4 and 7) are shown with yellow-red, whereas uplift clusters (2 and 3) are shown with light-dark blue; and stable clusters (1, 5, 6, 8, and 9) are not shown. As can be seen from Figure 6 and Figure 9, the subsided area has almost the same pattern. By using the SOM, subsets that present similar behavior in time is classified automatically, which allowed us to identify stable, subsided, and uplifted zones in time. The range of displacement is from −21 mm/year to 14 mm/year. Table 4 illustrates statistics for areas experiencing subsidence (clusters 4 and 7) and uplift (clusters 2 and 3). When we investigated the subsidence and uplift clusters, we found that 3 % of the pixels are classified incorrectly. This means that there are pixels classified as subsidence with positive displacement values (between 0.0016 and 2 mm/year) and there are pixels classified as uplift with negative displacement values (between −0.00064 and −1 mm/year). We excluded these pixels as an outlier in the post-processing of SOM results. For the subsidence clusters, the average displacement is −6 mm/year. Conversely, uplift points have an average displacement of 4 mm/year across all the samples in the considered study period.

Figure 9.
The SOM analysis in 9 clusters (Up: Uplift, Down: Subsidence).

Table 4.
Statistics about stable, subsidence, and uplift clusters.
Table 5 shows the comparison of the earlier studies and PSInSAR analysis results from this study. Visual assessment of the images in Table 5 indicates a similar pattern and direction of the displacement. The pattern and direction of the analysis overlap in all analyses from 2011 to 2019, as shown in Table 5. It also shows that the range of all analyses is closer to each other, especially when using similar time frames and methods. Table 5c and Table 5d compare average displacement values. Since Table 5c gives statistics specifically for the geothermal field shown in purple color (Table 5c), we have given the statistics specifically for the same cluster shown in hot colors (Table 5d - yellow to red). In addition to statistics in Table 5, it was stated that the subsidence rate between 2004 and 2014 was 10 mm/yr [25]. Besides, subsidence was observed at −13.5 ± 2.9 mm/yr by using GPS data and −9.9 ± 3.3 mm/yr by using InSAR data analysis [29]. One of the recent studies in the same field observed by InSAR results at rates as high as ∼25 mm/year [3]. In our study, we found the range being between −21 mm/yr and 14 mm/yr which is consistent with the previous studies. The average displacement is −6.4 ± 2.2 mm/yr which is again consistent with the previous studies.

Table 5.
Comparison of the previous studies with our analysis result (Imgs: Images – Stdv: Standard Deviation – Ave: Average – Ref: Reference).
4.3. Step III—Temporal Analysis of Displacements
To explore in more detail the dynamics in the geothermal field, we analyzed the time-series data obtained from SOM. For this purpose, we first calculated the second derivative of the displacement, and then we identified the inflection dates associated with the variations in displacement by tagging the moments when acceleration changes its direction. This analysis serves for establishing correlations between the displacements and operational activities in the geothermal field. Based on previous studies, we know that a PSInSAR analysis can achieve submillimeter accuracy for a location, under good conditions, and we use the differentials of the clusters to calculate the variations in acceleration. Consequently, additional sources of error are introduced. To mitigate this, we established an experimental threshold of 0.25 mm/(period2) to reduce noise caused by smaller changes in acceleration, we accept those points as inflection dates. Additionally, it is expected that points around subsidence would present uplift as opposing forces exist at the same time in close regions. That is, when there is acceleration in one direction in a cluster, an opposite cluster should accelerate in the opposite direction.
Figure 10 compares the inflection dates of cluster 3 (uplift) and cluster 7 (subsidence). To make the relationships more visible, we stacked the acceleration values in between inflection dates for each cluster. If there is an inflection on specific dates, it is expected that uplift and subsidence clusters should appear on opposite sides, and the delta value should be equal to two.
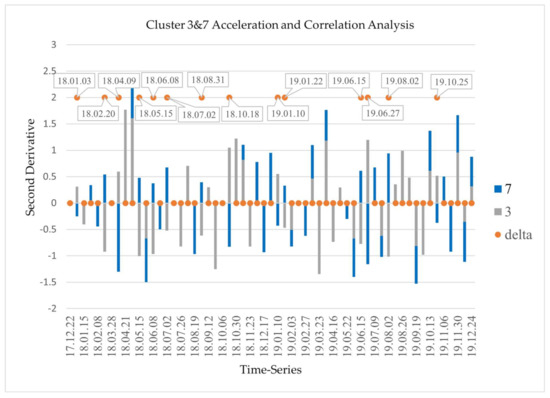
Figure 10.
Inflection dates using uplift (cluster 3) and subsidence (cluster 7) (7: cluster 7; 3: cluster 3; delta: difference in sign of cluster 3 and cluster 7).
The time-series analysis indicates the inflection dates in Table 6. It shows that January and June have a higher frequency of inflections in 2019.

Table 6.
The inflection dates.
To verify that there are inflections in cluster 3 and cluster 7 and the methodology that we applied is correct for finding inflection dates, we applied the same selection logic on the stable clusters such as cluster 5 and cluster 6. If there are zero or a small number of inflection dates, it means that these two selected clusters are stable. As shown in Figure 11, there are no inflection dates between cluster 5 and cluster 6 that prove the stable points have no opposite acceleration in time. The time-series analysis between cluster 5 and cluster 6 verify the process of finding inflection dates by using this methodology.
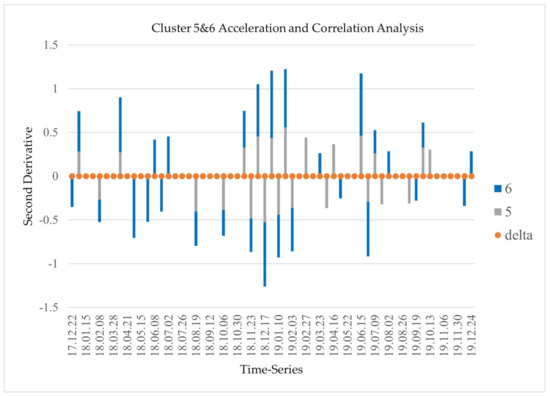
Figure 11.
Inflection dates using stable (cluster 5) and stable (cluster 6).
5. Conclusions
This study introduced a methodology for the identification of spatiotemporal displacement patterns for monitoring geothermal sites, which have usually slow-movement profiles. The successful application of the methodology to the Brady’s Hot Spring Geothermal field, which is one of the highly studied geothermal sites in the literature, proves that the proposed methodology serves for monitoring such a slow-moving geothermal site in a short time period as opposed to previous studies with longer time periods. After the application of the PSInSAR analysis, we applied an unsupervised SOM algorithm for clustering uplift, subsidence, and stable areas in the geothermal field. We used time-series analysis to find the inflection dates that may indicate the dynamics of the geothermal operations. The coupling of the PSInSAR and the SOM algorithms was shown to be effective in analyzing the direction and pattern of the displacements observed in the field. In PSInSAR analysis, the range of the displacement is between −21 and 14 mm/yr and the average displacement with standard deviation is 0 ± 2 mm/yr for the entire AOI. In the subsidence cluster, we found that the minimum subsidence is −19 mm/yr with an average displacement of −6 mm/yr. On the other hand, in the uplift cluster, we found that the maximum uplift is 14 mm/yr with an average displacement of 4 mm/yr.
Several inflection dates have been extracted from the time-series analysis. In order to decide inflection dates, we analyzed the displacement direction in different two clusters such as uplift and subsidence. These dates have the potential to show the dynamics of the operations which cause a significant change in the displacement patterns in the field. It needs some field and detailed research that we address for future studies.
The expected subsidence field and its direction should be similar for every year if there is no extraordinary situation like a landslide, natural hazard, production change in the site. The former studies on the same site in different years and with different algorithms prove that the pattern of the subsidence is similar. The findings in this study can highlight in-depth monitoring of displacements in other geothermal sites and establishing and understanding the relationship between the dynamics of geothermal operations and subsidence and uplift patterns. Such an in-depth analysis has the potential to identify the contribution of factors causing subsidence and uplift patterns when surface and subsurface datasets are analyzed with ML algorithms. The authors plan to study these relations in the future.
Author Contributions
For research articles with several authors, a short paragraph specifying their individual contributions must be provided. The following statements should be used “Conceptualization, H.S.D. and M.C., J.M.; methodology, M.C. and J.M.; validation, M.C., H.S.D. and J.M.; formal analysis, M.C. and J.M.; investigation, M.C. and J.M.; resources, M.C., J.M. and H.S.; data curation, M.C., J.M.; writing—original draft and, H.S.D. and M.C., J.M.; writing—review and editing, H.S.D. and M.C., J.M., G.J. and H.S.; visualization, M.C. and J.M.; supervision, M.C. and J.M., and H.S.D.; project administration, J.M., and H.S.D.; funding acquisition, J.M., and H.S.D. and H.S. All authors have read and agreed to the published version of the manuscript.”, please turn to the CRediT taxonomy for the term explanation. Authorship must be limited to those who have contributed substantially to the work reported.
Funding
This research was funded by U.S. Department of Energy, grant number DE- EE0008760.
Data Availability Statement
Data available openly from https://scihub.copernicus.eu.
Acknowledgments
We thank the US Department of Energy DOE-EERE—Geothermal Technologies Program for funding this work within the project DE- EE0008760 entitled “Detection of Potential Geothermal Exploration Sites from Hyperspectral Images via Deep Learning”. We also thank Dr. Daniele Perissin for providing SARPROZ software for free to conduct the work presented in the paper. We are grateful to Dr. Curtis W. Chen and Dr. Howard A. Zebker for providing Snaphu for free to researchers. We appreciate the European Space Agency (ESA) for making Synthetic Aperture Radar data from the Sentinel satellite missions available to this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Békési, E.; Fokker, P.A.; Martins, J.E.; Limberger, J.; Bonté, D.; Van Wees, J.-D. Production-Induced Subsidence at the Los Humeros Geothermal Field Inferred from PS-InSAR. Geofluids 2019, 2019, 1–12. [Google Scholar] [CrossRef]
- Wang, W.; Diessl, J.; Bruno, M.S. Surface deformation study for a geothermal operation field. Adv. Geosci. 2018, 45, 243–249. [Google Scholar] [CrossRef][Green Version]
- Reinisch, E.C.; Ali, S.T.; Cardiff, M.; Kaven, J.O.; Feigl, K.L. Geodetic Measurements and Numerical Models of Deformation at Coso Geothermal Field, California, USA, 2004–2016. Remote Sens. 2020, 12, 225. [Google Scholar] [CrossRef]
- Manunta, M.; De Luca, C.; Zinno, I.; Casu, F.; Manzo, M.; Bonano, M.; Fusco, A.; Pepe, A.; Onorato, G.; Berardino, P.; et al. The Parallel SBAS Approach for Sentinel-1 Interferometric Wide Swath Deformation Time-Series Generation: Algorithm Description and Products Quality Assessment. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6259–6281. [Google Scholar] [CrossRef]
- Kabeyi, M.J. Geothermal Electricity Generation, Challenges, Opportunities and Recommendations. Int. J. Adv. Sci. Res. Eng. 2019, 5, 53–95. [Google Scholar] [CrossRef]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A New Algorithm for Processing Interferometric Data-Stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3460–3470. [Google Scholar] [CrossRef]
- Lubitz, C.; Motagh, M.; Kaufmann, C. Ground Surface Response to Geothermal Drilling and the Following Counteractions in Staufen im Breisgau (Germany) Investigated by TerraSAR-X Time Series Analysis and Geophysical Modeling. Remote Sens. 2014, 6, 10571–10592. [Google Scholar] [CrossRef]
- Crosetto, M.; Monserrat, O.; Cuevas-González, M.; Devanthéry, N.; Crippa, B. Persistent Scatterer Interferometry: A review. ISPRS J. Photogramm. Remote Sens. 2016, 115, 78–89. [Google Scholar] [CrossRef]
- Cavur, M.; Camalan, M.; Ketizmen, H.; Agitoglu, S. Monitoring of Mine Landslide and Deformation Using Sentinel-1 Sar Data. In Proceedings of the IMCET 2019 26th International Mining Congress and Exhibition of Turkey 2019, Antalya, Turkey, 2019; Benzer, H., Aydogan, N., Karadeniz, M., Altun, O., Dundar, H., Gulsun Kilic, M., Kundak, E., Yilmazkaya, E., Eds.; Baski: Antalya, Turkey, 2019; pp. 509–517. [Google Scholar]
- Bardi, F.; Raspini, F.; Ciampalini, A.; Kristensen, L.; Rouyet, L.; Lauknes, T.R.; Frauenfelder, R.; Casagli, N. Space-Borne and Ground-Based InSAR Data Integration: The Åknes Test Site. Remote Sens. 2016, 8, 237. [Google Scholar] [CrossRef]
- Cigna, F.; Tapete, D.; Hugo, G.-M.V.; Muñiz-Jauregui, J.A.; García-Hernández, O.H.; Jiménez-Haro, A. Wide-Area InSAR Survey of Surface Deformation in Urban Areas and Geothermal Fields in the Eastern Trans-Mexican Volcanic Belt, Mexico. Remote Sens. 2019, 11, 2341. [Google Scholar] [CrossRef]
- Komac, M.; Holley, R.; Mahapatra, P.S.; Van Der Marel, H.; Bavec, M. Coupling of GPS/GNSS and radar interferometric data for a 3D surface displacement monitoring of landslides. Landslides 2014, 12, 241–257. [Google Scholar] [CrossRef]
- Carlà, T.; Raspini, F.; Intrieri, E.; Casagli, N. A simple method to help determine landslide susceptibility from spaceborne InSAR data: The Montescaglioso case study. Environ. Earth Sci. 2016, 75, 75. [Google Scholar] [CrossRef]
- Lu, P.; Catani, F.; Tofani, V.; Casagli, N. Quantitative hazard and risk assessment for slow-moving landslides from Persistent Scatterer Interferometry. Landslides 2013, 11, 685–696. [Google Scholar] [CrossRef]
- Tomás, R.; Li, Z.; Lopez-Sanchez, J.M.; Liu, P.; Singleton, A. Using wavelet tools to analyse seasonal variations from InSAR time-series data: A case study of the Huangtupo landslide. Landslides 2015, 13, 437–450. [Google Scholar] [CrossRef]
- Massonnet, D.; Rabaute, T. Radar interferometry: Limits and potential. IEEE Trans. Geosci. Remote Sens. 1993, 31, 455–464. [Google Scholar] [CrossRef]
- Jónsson, S.; Zebker, H.; Cervelli, P.F.; Segall, P.; Garbeil, H.; Rowland, S.; Mouginis-Mark, P. A shallow-dipping dike fed the 1995 flank eruption at Fernandina Volcano, Galápagos, observed by satellite radar interferometry. Geophys. Res. Lett. 1999, 26, 1077–1080. [Google Scholar] [CrossRef]
- Brandt, J.T.; Sneed, M.; Danskin, W.R. Detection and measurement of land subsidence and uplift using interferometric synthetic aperture radar, San Diego, California, USA, 2016–2018. Proc. Int. Assoc. Hydrol. Sci. 2020, 382, 45–49. [Google Scholar] [CrossRef]
- Carnec, C.; Delacourt, C. Three years of mining subsidence monitored by SAR interferometry, near Gardanne, France. J. Appl. Geophys. 2000, 43, 43–54. [Google Scholar] [CrossRef]
- Crosetto, M.; Monserrat, O.; Barra, A.; Crippa, B. Deformation Measurement Using Sentinel-1a/b Imagery. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42. [Google Scholar] [CrossRef]
- Kim, S.; Lee, C.; Song, K.; Min, K.D.; Won, J. Application of L-band differential SAR interferometry to subsidence rate estimation in reclaimed coastal land. Int. J. Remote Sens. 2005, 26, 1363–1381. [Google Scholar] [CrossRef]
- Alsdorf, D.E.; Melack, J.M.; Dunne, T.; Mertes, L.A.K.; Hess, L.L.; Smith, L.C. Interferometric radar measurements of water level changes on the Amazon flood plain. Nat. Cell Biol. 2000, 404, 174–177. [Google Scholar] [CrossRef] [PubMed]
- Colesanti, C.; Wasowski, J. Investigating landslides with space-borne Synthetic Aperture Radar (SAR) interferometry. Eng. Geol. 2006, 88, 173–199. [Google Scholar] [CrossRef]
- López-Davalillo, J.C.G.; Herrera, G.; Notti, D.; Strozzi, T.; Fernández, M.I.; Álvarez, D. InSAR analysis of ALOS PALSAR images for the assessment of very slow landslides: The Tena Valley case study. Landslides 2014, 11, 225–246. [Google Scholar] [CrossRef]
- Ali, S.; Akerley, J.; Baluyut, E.; Cardiff, M.; Davatzes, N.; Feigl, K.; Foxall, W.; Fratta, D.; Mellors, R.; Spielman, P.; et al. Time-series analysis of surface deformation at Brady Hot Springs geothermal field (Nevada) using interferometric synthetic aperture radar. Geothermics 2016, 61, 114–120. [Google Scholar] [CrossRef]
- Heimlich, C.; Gourmelen, N.; Masson, F.; Schmittbuhl, J.; Kim, S.-W.; Azzola, J. Uplift around the geothermal power plant of Landau (Germany) as observed by InSAR monitoring. Geotherm. Energy 2015, 3, 2. [Google Scholar] [CrossRef]
- Strozzi, T.; Tosi, L.; Carbognin, L.; Wegmüller, U.; Galgaro, A. Monitoring Land Subsidence in the Euganean Geothermal Basin with Differential SAR Interferometry. Eur. Sp. Agency Spec. Publ. ESA SP 2000, 167–176. [Google Scholar]
- Sandwell, D.T.; Mellors, R.J.; Tong, X.; Wei, M.; Wessel, P. Open radar interferometry software for mapping surface Deformation. EOS 2011, 92, 234. [Google Scholar] [CrossRef]
- Reinisch, E.C.; Cardiff, M.; Feigl, K.L. Characterizing volumetric strain at Brady Hot Springs, Nevada, USA using geodetic data, numerical models and prior information. Geophys. J. Int. 2018, 215, 1501–1513. [Google Scholar] [CrossRef]
- Barbour, A.J.; Evans, E.L.; Hickman, S.H.; Eneva, M. Subsidence rates at the southern Salton Sea consistent with reservoir depletion. J. Geophys. Res. Solid Earth 2016, 121, 5308–5327. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Raspini, F.; Ciampalini, A.; Del Conte, S.; Lombardi, L.; Nocentini, M.; Gigli, G.; Ferretti, A.; Casagli, N. Exploitation of Amplitude and Phase of Satellite SAR Images for Landslide Mapping: The Case of Montescaglioso (South Italy). Remote Sens. 2015, 7, 14576–14596. [Google Scholar] [CrossRef]
- Izakian, H.; Pedrycz, W.; Jamal, I. Fuzzy clustering of time series data using dynamic time warping distance. Eng. Appl. Artif. Intell. 2015, 39, 235–244. [Google Scholar] [CrossRef]
- Bao, F.; Lobo, V.; Painho, M.; Bacao, F. Applications of Different Self-Organizing Map Variants to Geographical Information Science Problems. Self-Organising Maps 2008, 21–44. [Google Scholar] [CrossRef]
- Lollino, G.; Manconi, A.; Guzzetti, F.; Culshaw, M.; Bobrowsky, P.; Luino, F. Engineering geology for society and territory—Volume 5: Urban geology, sustainable planning and landscape exploitation. Eng. Geol. Soc. Territ. Vol. 5 Urban Geol. Sustain. Plan. Landsc. Exploit. 2015, 5, 1–1400. [Google Scholar] [CrossRef]
- Jia, H.L.; Yu, B.; Zhang, R.; Sang, M.Z. Land Subsidence Detection by PSInSARTM Based on TerraSAR-X Images. Adv. Mater. Res. 2011, 301–303, 641–645. [Google Scholar] [CrossRef]
- Tiwari, R.; Malik, K.; Arora, M. Urban Subsidence Detection Using the Sentinel-1 Multi-Temporal InSAR Data. In Proceedings of the 38th Asian Conference on Remote Sensing (ACRS 2017): Space Applications: Touching Human Lives, New Delhi, India, 27 October 2017; Asian Association on Remote Sensing (AARS); Volume 4, pp. 2410–2414. [Google Scholar]
- Lazecky, M.; Comut, F.C.; Qin, Y.; Perissin, D. Sentinel-1 Interferometry System in the High-Performance Computing Environment. Lect. Notes Geoinf. Cartogr. 2016, 131–139. [Google Scholar] [CrossRef]
- Vaka, D.S.; Sharma, S.; Rao, Y.S. Comparison of HH and VV Polarizations for Deformation Estimation using Persistent Scatterer Interferometry; 2017. [Google Scholar]
- Aslan, G.; Foumelis, M.; Raucoules, D.; De Michele, M.; Bernardie, S.; Çakir, Z. Landslide Mapping and Monitoring Using Persistent Scatterer Interferometry (PSI) Technique in the French Alps. Remote Sens. 2020, 12, 1305. [Google Scholar] [CrossRef]
- Oštir, K.; Komac, M. PSInSAR and DInSAR methodology comparison and their applicability in the field of surface deformations—A case of NW Slovenia. Geologija 2007, 50, 77–96. [Google Scholar] [CrossRef]
- Landslides: Investigation and Mitigation; Turner, A.K., Schuster, R.L., Eds.; Transportation Research Board: Washington, DC, USA, 1996; ISBN 9780309062084. [Google Scholar]
- Strozzi, T.; Luckman, A.; Murray, T.; Wegmuller, U.; Werner, C.L. Glacier motion estimation using SAR offset-tracking procedures. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2384–2391. [Google Scholar] [CrossRef]
- Hooper, A.; Segall, P.; Zebker, H. Persistent scatterer interferometric synthetic aperture radar for crustal deformation analysis, with application to Volcán Alcedo, Galápagos. J. Geophys. Res. Space Phys. 2007, 112, 1–21. [Google Scholar] [CrossRef]
- Hanssen, R.F. Radar Interferometry: Data Interpretation and Error Analysis; Remote Sensing and Digital Image Processing; Springer Netherlands, 2001; ISBN 978-0-7923-6945-5. [Google Scholar]
- Fárová, K.; Jelének, J.; Kopacková-Strnadová, V.; Kycl, P. Comparing DInSAR and PSI Techniques Employed to Sentinel-1 Data to Monitor Highway Stability: A Case Study of a Massive Dobkovičky Landslide, Czech Republic. Remote Sens. 2019, 11, 2670. [Google Scholar] [CrossRef]
- Perissin, D.; Wang, Z.; Prati, C.; Rocca, F. Terrain Monitoring in China Via PS-QPS InSAR: Tibet and the Three Gorges Dam. Eur. Sp. Agency Spec. Publ. ESA SP 2013, 704, 2–6. [Google Scholar]
- Kohonen, T. Self-organized formation of topologically correct feature maps. Biol. Cybern. 1982, 43, 59–69. [Google Scholar] [CrossRef]
- Wehrens, R.; Buydens, L.M.; Fraley, C.; Raftery, A.E. Model-Based Clustering for Image Segmentation and Large Datasets via Sampling. J. Classif. 2004, 21, 231–253. [Google Scholar] [CrossRef]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef]
- Filippi, A.M.; Houser, C.; Dobreva, I.; Cairns, D.M.; Kim, D. Unsupervised Fuzzy ARTMAP Classification of Hyperspectral Hyperion Data for Savanna and Agriculture Discrimination in the Brazilian Cerrado. GIScience Remote Sens. 2009, 46, 1–23. [Google Scholar] [CrossRef]
- Dramsch, J.S. 70 years of machine learning in geoscience in review. Adv. Geophys. 2020, 61, 1–55. [Google Scholar] [CrossRef]
- Awad, M. Segmentation of Satellite Images Using Self-Organizing Maps. Self-Organizing Maps 2010. [Google Scholar] [CrossRef]
- Arias, S.; Gómez, H.; Prieto, F.; Botón, M.; Ramos, R. Satellite Image Classification by Self-Organized Maps on GRID Computing Infrastructures. In Proceedings of the second EELA-2 Conference, Choroni, Venezuela; 2009; pp. 1–11. [Google Scholar]
- Foroutan, M.; Zimbelman, J. Semi-automatic mapping of linear-trending bedforms using ‘Self-Organizing Maps’ algorithm. Geomorphology 2017, 293, 156–166. [Google Scholar] [CrossRef]
- Körting, T.S.; Fonseca, L.M.G.; Câmara, G. A Geographical Approach to Self-Organizing Maps Algorithm Applied to Image Segmentation. In Proceedings of the Advanced Concepts for Intelligent Vision Systems; Blanc-Talon, J., Kleihorst, R., Philips, W., Popescu, D., Scheunders, P., Eds.; Springer: Berlin, Heidelberg, Germany, 2011; Volume 6915 LNCS, pp. 162–170. [Google Scholar] [CrossRef]
- Phillips, F.; Hwang, G.G.; Limprayoon, P. Inflection points and industry change: Was Andy Grove right after all? J. Technol. Manag. Grow. Econ. 2016, 7, 7–26. [Google Scholar] [CrossRef][Green Version]
- Andrianaivo, L.; Ramasiarinoro, V.J. Relations between Drainage Pattern and Fracture Trend in the Itasy Geothermal Prospect, Central Madagascar. Madamines 2011, 2, 22–39. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).