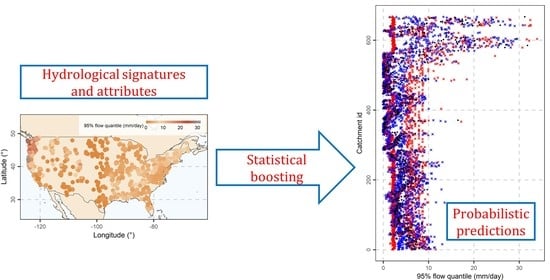
Explanation and Probabilistic Prediction of Hydrological Signatures with Statistical Boosting Algorithms
Abstract
1. Introduction
2. Data and Methods
2.1. Data
2.2. Boosting Algorithms
| Algorithm 1 Formulation of the gradient boosting algorithm, adapted from [29,30,42,43]. |
| Step 1: Initialize f0 with a constant. |
| Step 2: For m = 1 to M: a. Compute the negative gradient gm(xi) of the loss function L at fm–1(xi), i = 1, …, n. b. Fit a new base learner function hm(x) to {(xi, gm(xi))}, i = 1, …, n. c. Update the function estimate fm(x) ← fm–1(x) + ρ hm(x). |
| Step 3: Predict fM(x). |
2.3. Base Learners
2.4. Metrics
2.5. Summary of Methods
3. Results
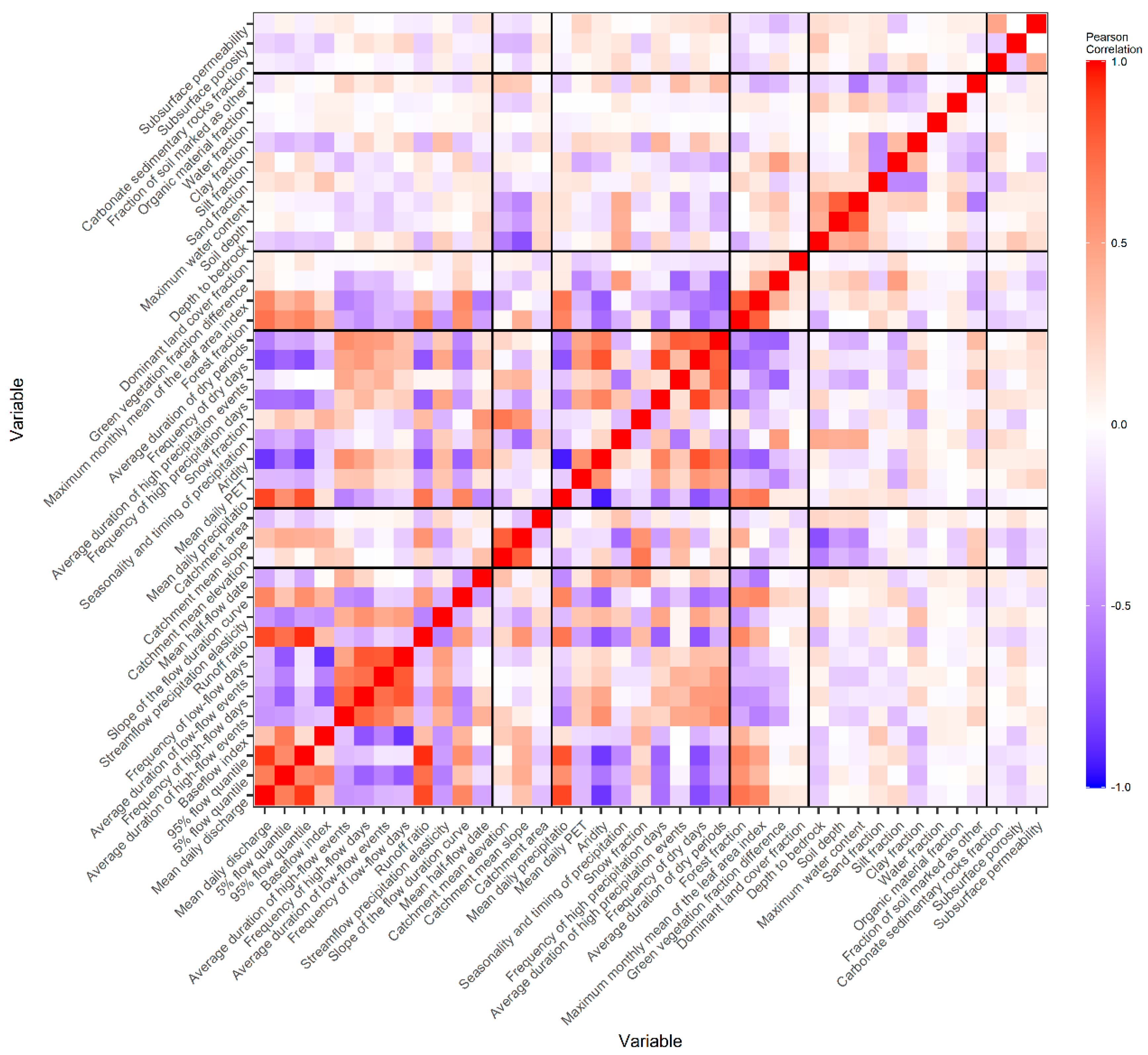
3.1. Exploratory Analysis
3.2. Streamflow Signatures
3.3. Signatures of Duration and Frequency of Extreme Events
3.4. Remaining Signatures
3.5. Assesment and Importance of Predictor Variables
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Type of Variables | Value as Is (Untransformed) | Transformed Using Log | Transformed Using Square Root |
|---|---|---|---|
| Attribute | Attribute | Attribute | |
| Signature | Baseflow index | Mean daily discharge | 5% flow quantile |
| Runoff ratio | 95% flow quantile | ||
| Streamflow precipitation elasticity | Average duration of high-flow events | ||
| Slope of the flow duration curve | Frequency of high-flow days | ||
| Mean half-flow date | Average duration of low-flow events | ||
| Frequency of low-flow days | |||
| Topographic | Catchment mean elevation | ||
| Catchment mean slope | |||
| Catchment area | |||
| Climatic | Seasonality and timing of precipitation | Mean daily precipitation | |
| Snow fraction | Mean daily PET | ||
| Frequency of high precipitation events | Aridity | ||
| Average duration of high precipitation events | Frequency of dry days | ||
| Average duration of dry periods | |||
| Land cover | Forest fraction | ||
| Maximum monthly mean of the leaf area index | |||
| Green vegetation fraction difference | |||
| Dominant land cover fraction | |||
| Soil | Depth to bedrock | ||
| Soil depth | |||
| Maximum water content | |||
| Sand fraction | |||
| Silt fraction | |||
| Clay fraction | |||
| Water fraction | |||
| Organic material fraction | |||
| Fraction of soil marked as other | |||
| Geology | Carbonate sedimentary rock fraction | ||
| Subsurface porosity | |||
| Subsurface permeability |
| Attribute | Description |
|---|---|
| Mean daily discharge | Mean daily discharge (mm/day) |
| 5% flow quantile | 5% flow quantile (low flow, mm/day) |
| 95% flow quantile | 95% flow quantile (high flow, mm/day) |
| Baseflow index | Ratio of mean daily baseflow to mean daily discharge, hydrograph separation using Landson et al. (2013) digital filter |
| Average duration of high-flow events | Number of consecutive days >9 times the median daily flow (days) |
| Frequency of high-flow days | Frequency of high-flow days (>9 times the median daily flow) (days/year) |
| Average duration of low-flow events | Number of consecutive days <0.2 times the mean daily flow (days) |
| Frequency of low-flow events | Frequency of low-flow days (<0.2 times the mean daily flow (days/year) |
| Runoff ratio | Ratio of mean daily discharge to mean daily precipitation |
| Streamflow precipitation elasticity | Streamflow precipitation elasticity (sensitivity of streamflow to changes in precipitation at the annual time scale) |
| Slope of the flow duration curve | Slope of the flow duration curve (between the log-transformed 33rd and 66th streamflow percentiles) |
| Mean half-flow date | Date on which the cumulative discharge since October first reaches half of the annual discharge (day of year) |
| Attribute | Description |
|---|---|
| Catchment mean elevation | Catchment mean elevation (m) |
| Catchment mean slope | Catchment mean slope (m km–1) |
| Catchment area | Catchment area (GAGESII estimate) (km2) |
| Attribute | Description |
|---|---|
| Mean daily precipitation | Mean daily precipitation (mm day–1) |
| Mean daily PET | Mean daily PET, estimated by N15 using Priestley–Taylor formulation calibrated for each catchment (mm day–1) |
| Aridity | Aridity (PET/P, ratio of mean PET, estimated by N15 using Priestley–Taylor formulation calibrated for each catchment, to mean precipitation) |
| Seasonality and timing of precipitation | Seasonality and timing of precipitation (estimated using sine curves to represent the annual temperature and precipitation cycles; positive (negative) values indicate that precipitation peaks in summer (winter); values close to 0 indicate uniform precipitation throughout the year) |
| Snow fraction | Fraction of precipitation falling as snow (i.e., on days colder than 0 °C) |
| Frequency of high precipitation events | Frequency of high precipitation days (≥5 times mean daily precipitation) (days year–1) |
| Average duration of high precipitation events | Average duration of high precipitation events (number of consecutive days ≥5 times mean daily precipitation) (days) |
| Frequency of dry days | Frequency of dry days (<1 mm day–1) (days year–1) |
| Average duration of dry events | Average duration of dry periods (number of consecutive days < 1 mm day–1) (days) |
| Attribute | Description |
|---|---|
| Forest fraction | Forest fraction |
| Maximum monthly mean of the leaf area index | Maximum monthly mean of the leaf area index (based on 12 monthly means) |
| Green vegetation fraction difference | Difference between the maximum and minimum monthly mean of the green vegetation fraction (based on 12 monthly means) |
| Dominant land cover fraction | Fraction of the catchment area associated with the dominant land cover |
| Attribute | Description |
|---|---|
| Depth to bedrock | Depth to bedrock (maximum 50 m) (m) |
| Soil depth | Soil depth (maximum 1.5 m; layers marked as water and bedrock were excluded) (m) |
| Maximum water content | Maximum water content (combination of porosity and soil_depth_statsgo; layers marked as water, bedrock, and “other” were excluded) (m) |
| Sand fraction | Sand fraction (of the soil material smaller than 2 mm; layers marked as organic material, water, bedrock, and “other” were excluded) (%) |
| Silt fraction | Silt fraction (of the soil material smaller than 2 mm; layers marked as organic material, water, bedrock, and “other” were excluded) (%) |
| Clay fraction | Clay fraction (of the soil material smaller than 2 mm; layers marked as organic material, water, bedrock, and “other” were excluded) (%) |
| Water fraction | Fraction of the top 1.5 m marked as water (class 14) (%) |
| Organic material fraction | Fraction of soil_depth_statsgo marked as organic material (class 13) (%) |
| Fraction of soil marked as other | Fraction of soil_depth_statsgo marked as “other” (class 16) (%) |
| Attribute | Description |
|---|---|
| Carbonate sedimentary rocks fraction | Fraction of the catchment area characterized as “carbonate sedimentary rocks” |
| Subsurface porosity | Subsurface porosity |
| Subsurface permeability | Subsurface permeability (log10) (m2) |
Appendix B



Appendix C
References
- McMillan, H. Linking hydrologic signatures to hydrologic processes: A review. Hydrol. Process. 2020, 34, 1393–1409. [Google Scholar] [CrossRef]
- McMillan, H.; Westerberg, I.; Branger, F. Five guidelines for selecting hydrological signatures. Hydrol. Process. 2017, 31, 4757–4761. [Google Scholar] [CrossRef]
- Gupta, H.V.; Wagener, T.; Liu, Y. Reconciling theory with observations: Elements of a diagnostic approach to model evaluation. Hydrol. Process. 2008, 22, 3802–3813. [Google Scholar] [CrossRef]
- Shafii, M.; Tolson, B.A. Optimizing hydrological consistency by incorporating hydrological signatures into model calibration objectives. Water Resour. Res. 2015, 51, 3796–3814. [Google Scholar] [CrossRef]
- Papacharalampous, G.; Tyralis, H.; Papalexiou, S.M.; Langousis, A.; Khatami, S.; Volpi, E.; Grimaldi, S. Global-scale massive feature extraction from monthly hydroclimatic time series: Statistical characterizations, spatial patterns and hydrological similarity. Sci. Total Environ. 2021, 767, 144612. [Google Scholar] [CrossRef]
- Blöschl, G.; Sivapalan, M.; Wagener, T.; Viglione, A.; Savenije, H. Runoff Prediction in Ungauged Basins; Cambridge University Press: New York, NY, USA, 2013; ISBN 978-1-107-02818-0. [Google Scholar]
- Hrachowitz, M.; Savenije, H.H.G.; Blöschl, G.; McDonnell, J.J.; Sivapalan, M.; Pomeroy, J.W.; Arheimer, B.; Blume, T.; Clark, M.P.; Ehret, U.; et al. A decade of Predictions in Ungauged Basins (PUB)—A review. Hydrol. Sci. J. 2013, 58, 1198–1255. [Google Scholar] [CrossRef]
- Singh, R.; Archfield, S.A.; Wagener, T. Identifying dominant controls on hydrologic parameter transfer from gauged to ungauged catchments—A comparative hydrology approach. J. Hydrol. 2014, 517, 985–996. [Google Scholar] [CrossRef]
- Viglione, A.; Parajka, J.; Rogger, M.; Salinas, J.L.; Laaha, G.; Sivapalan, M.; Blöschl, G. Comparative assessment of predictions in ungauged basins—Part 3: Runoff signatures in Austria. Hydrol. Earth Syst. Sci. 2013, 17, 2263–2279. [Google Scholar] [CrossRef]
- Blöschl, G.; Bierkens, M.F.P.; Chambel, A.; Cudennec, C.; Destouni, G.; Fiori, A.; Kirchner, J.W.; McDonnell, J.J.; Savenije, H.H.G.; Sivapalan, M.; et al. Twenty-three Unsolved Problems in Hydrology (UPH)—A community perspective. Hydrol. Sci. J. 2019, 64, 1141–1158. [Google Scholar] [CrossRef]
- Bourgin, F.; Andréassian, V.; Perrin, C.; Oudin, L. Transferring global uncertainty estimates from gauged to ungauged catchments. Hydrol. Earth Syst. Sci. 2015, 19, 2535–2546. [Google Scholar] [CrossRef]
- Wagener, T.; Montanari, A. Convergence of approaches toward reducing uncertainty in predictions in ungauged basins. Water Resour. Res. 2011, 47, W06301. [Google Scholar] [CrossRef]
- Westerberg, I.K.; McMillan, H.K. Uncertainty in hydrological signatures. Hydrol. Earth Syst. Sci. 2015, 19, 3951–3968. [Google Scholar] [CrossRef]
- Westerberg, I.K.; Wagener, T.; Coxon, G.; McMillan, H.K.; Castellarin, A.; Montanari, A.; Freer, J. Uncertainty in hydrological signatures for gauged and ungauged catchments. Water Resour. Res. 2016, 52, 1847–1865. [Google Scholar] [CrossRef]
- Beck, H.E.; de Roo, A.; van Dijk, A.I.J.M. Global maps of streamflow characteristics based on observations from several thousand catchments. J. Hydrometeorol. 2015, 16, 1478–1501. [Google Scholar] [CrossRef]
- Addor, N.; Nearing, G.; Prieto, C.; Newman, A.J.; Le Vine, N.; Clark, M.P. A ranking of hydrological signatures based on their predictability in space. Water Resour. Res. 2018, 54, 8792–8812. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G.; Tantanee, S. How to explain and predict the shape parameter of the generalized extreme value distribution of streamflow extremes using a big dataset. J. Hydrol. 2019, 574, 628–645. [Google Scholar] [CrossRef]
- Zhang, Y.; Chiew, F.H.S.; Li, M.; Post, D. Predicting runoff signatures using regression and hydrological modeling approaches. Water Resour. Res. 2018, 54, 7859–7878. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Meinshausen, N. Quantile regression forests. J. Mach. Learn. Res. 2006, 7, 983–999. [Google Scholar]
- Efron, B.; Hastie, T. Computer Age Statistical Inference; Cambridge University Press: New York, NY, USA, 2016; ISBN 9781107149892. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Abrahart, R.J.; Anctil, F.; Coulibaly, P.; Dawson, C.W.; Mount, N.J.; See, L.M.; Shamseldin, A.Y.; Solomatine, D.P.; Toth, E.; Wilby, R.L. Two decades of anarchy? Emerging themes and outstanding challenges for neural network river forecasting. Prog. Phys. Geogr. Earth Environ. 2012, 36, 480–513. [Google Scholar] [CrossRef]
- Dawson, C.W.; Wilby, R.L. Hydrological modelling using artificial neural networks. Prog. Phys. Geogr. Earth Environ. 2001, 25, 80–108. [Google Scholar] [CrossRef]
- Solomatine, D.P.; Ostfeld, A. Data-driven modelling: Some past experiences and new approaches. J. Hydroinform. 2008, 10, 3–22. [Google Scholar] [CrossRef]
- Maier, H.R.; Jain, A.; Dandy, G.C.; Sudheer, K.P. Methods used for the development of neural networks for the prediction of water resource variables in river systems: Current status and future directions. Environ. Model. Softw. 2010, 25, 891–909. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G.; Langousis, A. A brief review of random forests for water scientists and practitioners and their recent history in water resources. Water 2019, 11, 910. [Google Scholar] [CrossRef]
- Bühlmann, P.; Hothorn, T. Boosting algorithms: Regularization, prediction and model fitting. Stat. Sci. 2007, 22, 477–505. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G. Boosting algorithms in energy research: A systematic review. arXiv 2020, arXiv:2004.07049v1. [Google Scholar]
- Addor, N.; Newman, A.J.; Mizukami, N.; Clark, M.P. The CAMELS data set: Catchment attributes and meteorology for large-sample studies. Hydrol. Earth Syst. Sci. 2017, 21, 5293–5313. [Google Scholar] [CrossRef]
- Newman, A.J.; Mizukami, N.; Clark, M.P.; Wood, A.W.; Nijssen, B.; Nearing, G. Benchmarking of a physically based hydrologic model. J. Hydrometeorol. 2017, 18, 2215–2225. [Google Scholar] [CrossRef]
- Addor, N.; Newman, A.J.; Mizukami, N.; Clark, M.P. Catchment Attributes for Large-Sample Studies; UCAR/NCAR: Boulder, CO, USA, 2017. [Google Scholar] [CrossRef]
- Newman, A.J.; Sampson, K.; Clark, M.P.; Bock, A.; Viger, R.J.; Blodgett, D. A Large-Sample Watershed-Scale Hydrometeorological Dataset for the Contiguous USA; UCAR/NCAR: Boulder, CO, USA, 2014. [Google Scholar] [CrossRef]
- Newman, A.J.; Clark, M.P.; Sampson, K.; Wood, A.; Hay, L.E.; Bock, A.; Viger, R.J.; Blodgett, D.; Brekke, L.; Arnold, J.R.; et al. Development of a large-sample watershed-scale hydrometeorological data set for the contiguous USA: Data set characteristics and assessment of regional variability in hydrologic model performance. Hydrol. Earth Syst. Sci. 2015, 19, 209–223. [Google Scholar] [CrossRef]
- Thornton, P.E.; Thornton, M.M.; Mayer, B.W.; Wilhelmi, N.; Wei, Y.; Devarakonda, R.; Cook, R.B. Daymet: Daily Surface Weather Data on a 1-km Grid for North America, Version 2; ORNL DAAC: Oak Ridge, TN, USA, 2014. [Google Scholar] [CrossRef]
- Miller, D.A.; White, R.A. A conterminous United States multilayer soil characteristics dataset for regional climate and hydrology modeling. Earth Interact. 1998, 2, 1–26. [Google Scholar] [CrossRef]
- Pelletier, J.D.; Broxton, P.D.; Hazenberg, P.; Zeng, X.; Troch, P.A.; Niu, G.-Y.; Williams, Z.; Brunke, M.A.; Gochis, D. A gridded global data set of soil, intact regolith, and sedimentary deposit thicknesses for regional and global land surface modeling. J. Adv. Modeling Earth Syst. 2016, 8, 41–65. [Google Scholar] [CrossRef]
- Gleeson, T.; Moosdorf, N.; Hartmann, J.; Beek, L.P.H. A glimpse beneath earth’s surface: GLobal HYdrogeology MaPS (GLHYMPS) of permeability and porosity. Geophys. Res. Lett. 2014, 41, 3891–3898. [Google Scholar] [CrossRef]
- Hartmann, J.; Moosdorf, N. The new global lithological map database GLiM: A representation of rock properties at the Earth surface. Geochem. Geophys. Geosyst. 2012, 13, Q12004. [Google Scholar] [CrossRef]
- Friedman, J.H.; Hastie, T.; Tibshirani, R. Additive logistic regression: A statistical view of boosting. Ann. Stat. 2000, 28, 337–407. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Natekin, A.; Knoll, A. Gradient boosting machines, a tutorial. Front. Neurorobot. 2013, 7, 21. [Google Scholar] [CrossRef] [PubMed]
- Mayr, A.; Hofner, B. Boosting for statistical modelling: A non-technical introduction. Stat. Model. 2018, 18, 365–384. [Google Scholar] [CrossRef]
- Bühlmann, P.; Yu, B. Boosting. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 69–74. [Google Scholar] [CrossRef]
- Mayr, A.; Binder, H.; Gefeller, O.; Schmid, M. The evolution of boosting algorithms. Methods Inf. Med. 2014, 53, 419–427. [Google Scholar] [CrossRef]
- Mayr, A.; Binder, H.; Gefeller, O.; Schmid, M. Extending statistical boosting. Methods Inf. Med. 2014, 53, 428–435. [Google Scholar] [CrossRef]
- Bühlmann, P. Boosting methods: Why they can be useful for high-dimensional data. In Proceedings of the 3rd International Workshop on Distributed Statistical Computing (DSC 2003), Vienna, Austria, 20–22 March 2003. [Google Scholar]
- Bühlmann, P. Boosting for high-dimensional linear models. Ann. Stat. 2006, 34, 559–583. [Google Scholar] [CrossRef]
- Hothorn, T.; Bühlmann, P. Model-based boosting in high dimensions. Bioinformatics 2006, 22, 2828–2829. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Bühlmann, P.; Yu, B. Boosting with the L2 loss. J. Am. Stat. Assoc. 2003, 98, 324–339. [Google Scholar] [CrossRef]
- Hofner, B.; Mayr, A.; Robinzonov, N.; Schmid, M. Model-based boosting in R: A hands-on tutorial using the R package mboost. Comput. Stat. 2014, 29, 1–35. [Google Scholar] [CrossRef]
- Hothorn, T.; Bühlmann, P.; Kneib, T.; Schmid, M.; Hofner, B. Model-based boosting 2.0. J. Mach. Learn. Res. 2010, 11, 2109–2113. [Google Scholar]
- Schapire, R.E. The strength of weak learnability. Mach. Learn. 1990, 5, 197–227. [Google Scholar] [CrossRef]
- Koenker, R.W.; Machado, J.A.F. Goodness of fit and related inference processes for quantile regression. J. Am. Stat. Assoc. 1999, 94, 1296–1310. [Google Scholar] [CrossRef]
- Gneiting, T.; Raftery, A.E. Strictly proper scoring rules, prediction, and estimation. J. Am. Stat. Assoc. 2007, 102, 359–378. [Google Scholar] [CrossRef]
- Koenker, R.W.; Bassett, G., Jr. Regression quantiles. Econometrica 1978, 46, 33–50. [Google Scholar] [CrossRef]
- Koenker, R.W. Quantile regression: 40 years on. Annu. Rev. Econ. 2017, 9, 155–176. [Google Scholar] [CrossRef]
- Dunsmore, I.R. A Bayesian approach to calibration. J. R. Stat. Society. Ser. B (Methodol.) 1968, 30, 396–405. [Google Scholar] [CrossRef]
- Winkler, R.L. A decision-theoretic approach to interval estimation. J. Am. Stat. Assoc. 1972, 67, 187–191. [Google Scholar] [CrossRef]
- Papacharalampous, G.; Tyralis, H.; Langousis, A.; Jayawardena, A.W.; Sivakumar, B.; Mamassis, N.; Montanari, A.; Koutsoyiannis, D. Probabilistic hydrological post-processing at scale: Why and how to apply machine-learning quantile regression algorithms. Water 2019, 11, 2126. [Google Scholar] [CrossRef]
- Breiman, L. Statistical modeling: The two cultures. Stat. Sci. 2001, 16, 199–231. [Google Scholar] [CrossRef]
- Shmueli, G. To explain or to predict? Stat. Sci. 2010, 25, 289–310. [Google Scholar] [CrossRef]
- Wolpert, D.H. The lack of a priori distinctions between learning algorithms. Neural Comput. 1996, 8, 1341–1390. [Google Scholar] [CrossRef]
- Papacharalampous, G.; Tyralis, H. Hydrological time series forecasting using simple combinations: Big data testing and investigations on one-year ahead river flow predictability. J. Hydrol. 2020, 590, 125205. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G.; Langousis, A. Super ensemble learning for daily streamflow forecasting: Large-scale demonstration and comparison with multiple machine learning algorithms. Neural Comput. Appl. 2020. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G.; Burnetas, A.; Langousis, A. Hydrological post-processing using stacked generalization of quantile regression algorithms: Large-scale application over CONUS. J. Hydrol. 2019, 577, 123957. [Google Scholar] [CrossRef]
- Papacharalampous, G.; Tyralis, H.; Koutsoyiannis, D.; Montanari, A. Quantification of predictive uncertainty in hydrological modelling by harnessing the wisdom of the crowd: A large-sample experiment at monthly timescale. Adv. Water Resour. 2020, 136, 103470. [Google Scholar] [CrossRef]
- Boulesteix, A.L.; Binder, H.; Abrahamowicz, M.; Sauerbrei, W. For the Simulation Panel of the STRATOS Initiative. On the necessity and design of studies comparing statistical methods. Biom. J. 2018, 60, 216–218. [Google Scholar] [CrossRef] [PubMed]
- Papacharalampous, G.; Tyralis, H.; Koutsoyiannis, D. Univariate time series forecasting of temperature and precipitation with a focus on machine learning algorithms: A multiple-case study from Greece. Water Resour. Manag. 2018, 32, 5207–5239. [Google Scholar] [CrossRef]
- Papacharalampous, G.; Tyralis, H.; Koutsoyiannis, D. Comparison of stochastic and machine learning methods for multi-step ahead forecasting of hydrological processes. Stoch. Environ. Res. Risk Assess. 2019, 33, 481–514. [Google Scholar] [CrossRef]
- Biau, G.; Scornet, E. A random forest guided tour. Test 2016, 25, 197–227. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020; Available online: https://www.R-project.org/ (accessed on 13 December 2020).
- Dowle, M.; Srinivasan, A. Data.Table: Extension of ‘Data.Frame’. R Package Version 1.13. 2020. Available online: https://CRAN.R-project.org/package=data.table (accessed on 13 December 2020).
- Warnes, G.R.; Bolker, B.; Gorjanc, G.; Grothendieck, G.; Korosec, A.; Lumley, T.; MacQueen, D.; Magnusson, A.; Rogers, J. Gdata: Various R Programming Tools for Data Manipulation. R Package Version 2.18.0. 2017. Available online: https://CRAN.R-project.org/package=gdata (accessed on 13 December 2020).
- Wickham, H. reshape2: Flexibly Reshape Data: A Reboot of the Reshape Package. R Package Version 1.4.4. 2020. Available online: https://CRAN.R-project.org/package=reshape2 (accessed on 13 December 2020).
- Wickham, H. Reshaping data with the reshape package. J. Stat. Softw. 2007, 21, 1–20. [Google Scholar] [CrossRef]
- Wickham, H. stringr: Simple, Consistent Wrappers for Common String Operations. R Package Version 1.4.0. 2019. Available online: https://CRAN.R-project.org/package=stringr (accessed on 13 December 2020).
- Kuhn, M. caret: Classification and Regression Training. R Package Version 6.0-86. 2020. Available online: https://CRAN.R-project.org/package=caret (accessed on 13 December 2020).
- Hothorn, T.; Bühlmann, P.; Kneib, T.; Schmid, M.; Hofner, B. mboost: Model-Based Boosting. R Package Version 2.9-3. 2020. Available online: https://CRAN.R-project.org/package=mboost (accessed on 13 December 2020).
- Wickham, H. ggplot2; Springer: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Wickham, H.; Chang, W.; Henry, L.; Pedersen, T.L.; Takahashi, K.; Wilke, C.; Woo, K.; Yutani, H.; Dunnington, D. ggplot2: Create Elegant Data Visualisations Using the Grammar of Graphics. R package Version 3.3.2. 2020. Available online: https://CRAN.R-project.org/package=ggplot2 (accessed on 13 December 2020).
- Ram, K.; Wickham, H. wesanderson: A Wes Anderson Palette Generator. R Package Version 0.3.6. 2018. Available online: https://CRAN.R-project.org/package=wesanderson (accessed on 13 December 2020).
- Wickham, H.; Hester, J.; Chang, W. devtools: Tools to Make Developing R Packages Easier. R Package Version 2.3.1. 2020. Available online: https://CRAN.R-project.org/package=devtools (accessed on 13 December 2020).
- Xie, Y. knitr: A comprehensive tool for reproducible research in R. In Implementing Reproducible Computational Research; Stodden, V., Leisch, F., Peng, R.D., Eds.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2014. [Google Scholar]
- Xie, Y. Dynamic Documents with R and Knitr, 2nd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2015. [Google Scholar]
- Xie, Y. knitr: A General-Purpose Package for Dynamic Report Generation in R. R Package Version 1.29. 2020. Available online: https://CRAN.R-project.org/package=knitr (accessed on 13 December 2020).
- Allaire, J.J.; Xie, Y.; McPherson, J.; Luraschi, J.; Ushey, K.; Atkins, A.; Wickham, H.; Cheng, J.; Chang, W.; Iannone, R. rmarkdown: Dynamic Documents for R. R Package Version 2.3. 2020. Available online: https://CRAN.R-project.org/package=rmarkdown (accessed on 13 December 2020).
- Xie, Y.; Allaire, J.J.; Grolemund, G. R Markdown, 1st ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2018; ISBN 9781138359338. [Google Scholar]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tyralis, H.; Papacharalampous, G.; Langousis, A.; Papalexiou, S.M. Explanation and Probabilistic Prediction of Hydrological Signatures with Statistical Boosting Algorithms. Remote Sens. 2021, 13, 333. https://doi.org/10.3390/rs13030333
Tyralis H, Papacharalampous G, Langousis A, Papalexiou SM. Explanation and Probabilistic Prediction of Hydrological Signatures with Statistical Boosting Algorithms. Remote Sensing. 2021; 13(3):333. https://doi.org/10.3390/rs13030333
Chicago/Turabian StyleTyralis, Hristos, Georgia Papacharalampous, Andreas Langousis, and Simon Michael Papalexiou. 2021. "Explanation and Probabilistic Prediction of Hydrological Signatures with Statistical Boosting Algorithms" Remote Sensing 13, no. 3: 333. https://doi.org/10.3390/rs13030333
APA StyleTyralis, H., Papacharalampous, G., Langousis, A., & Papalexiou, S. M. (2021). Explanation and Probabilistic Prediction of Hydrological Signatures with Statistical Boosting Algorithms. Remote Sensing, 13(3), 333. https://doi.org/10.3390/rs13030333