Land Surface Temperature Retrieval from Fengyun-3D Medium Resolution Spectral Imager II (FY-3D MERSI-II) Data with the Improved Two-Factor Split-Window Algorithm
Abstract
:1. Introduction
2. Materials and Study Area
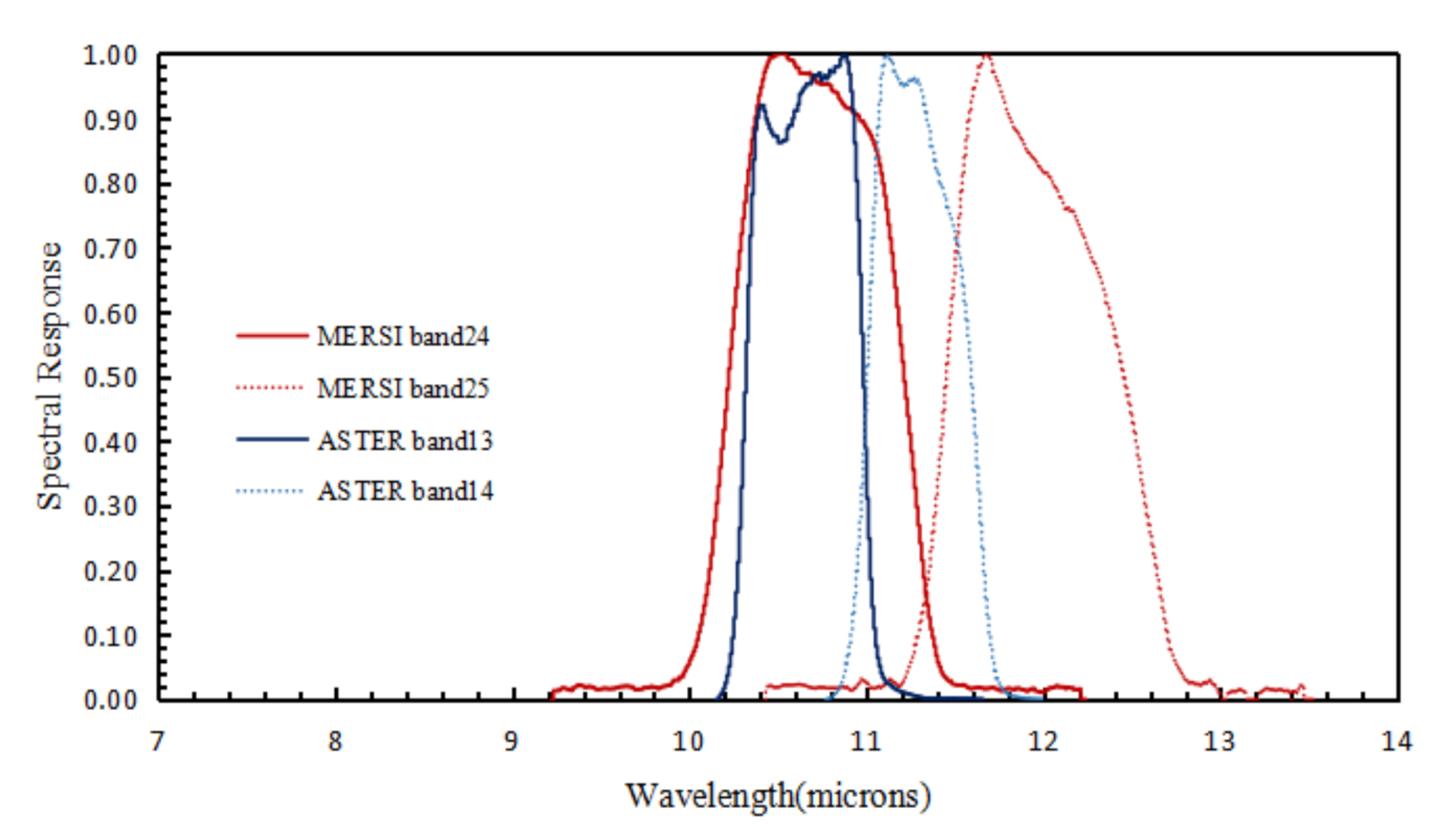
2.1. The FY-3D MERSI-II Data
2.2. The TIGR Profile Database
2.3. The ASTER GED Dataset
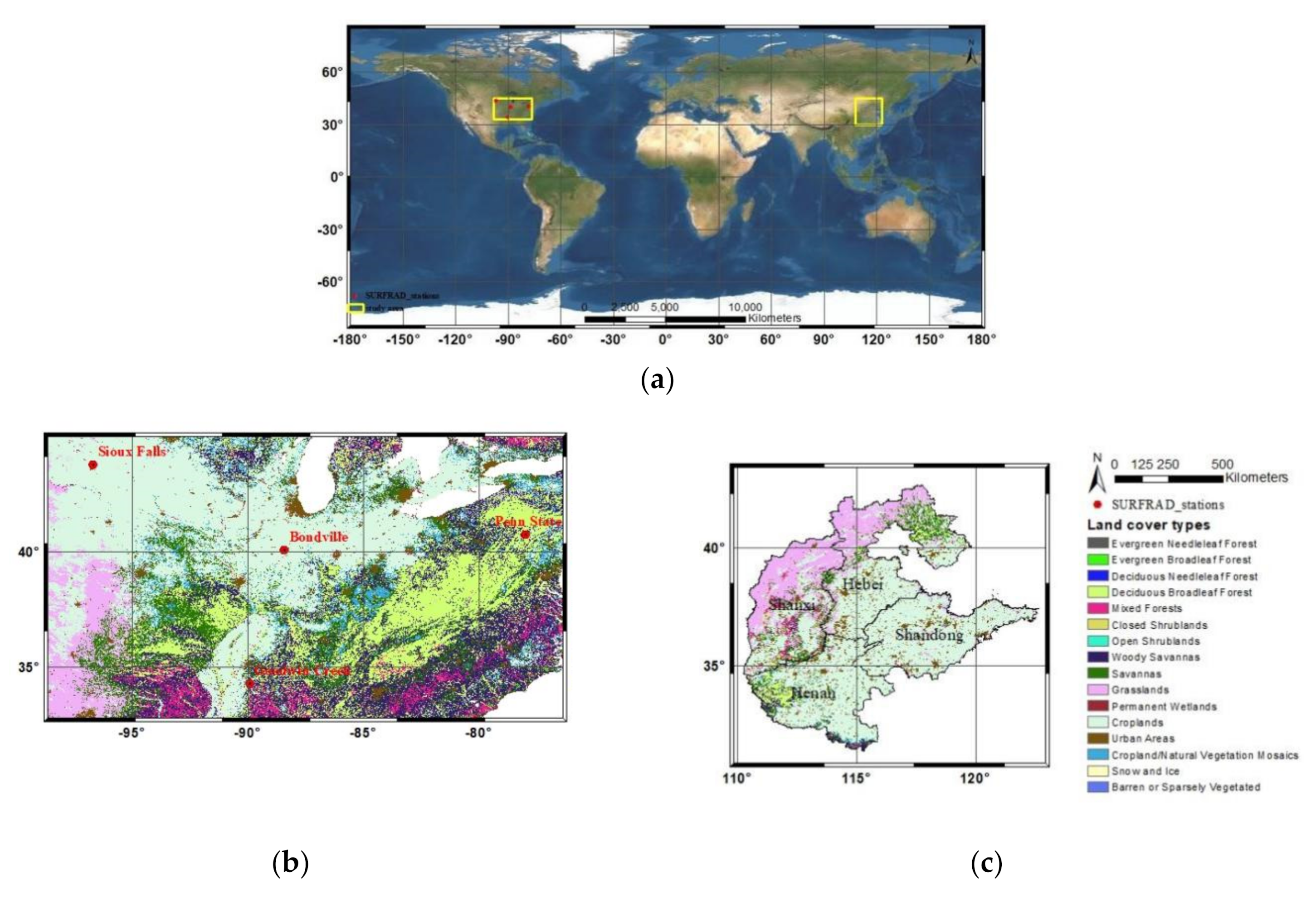
2.4. The SURFRAD Measurements
2.5. The Study Areas for Validation
3. Methodology
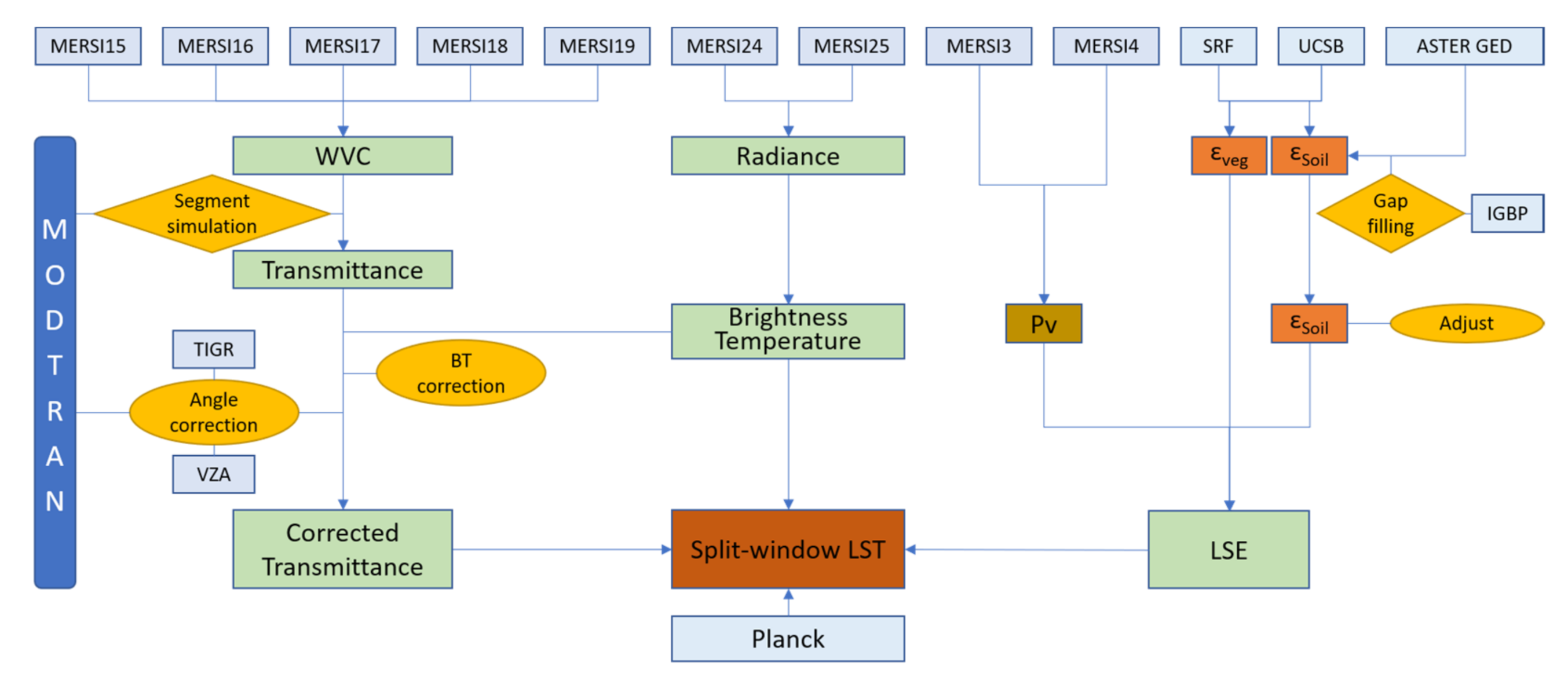
3.1. The Scheme for LST Retrieval
3.2. TFSWA for LST Retrieval
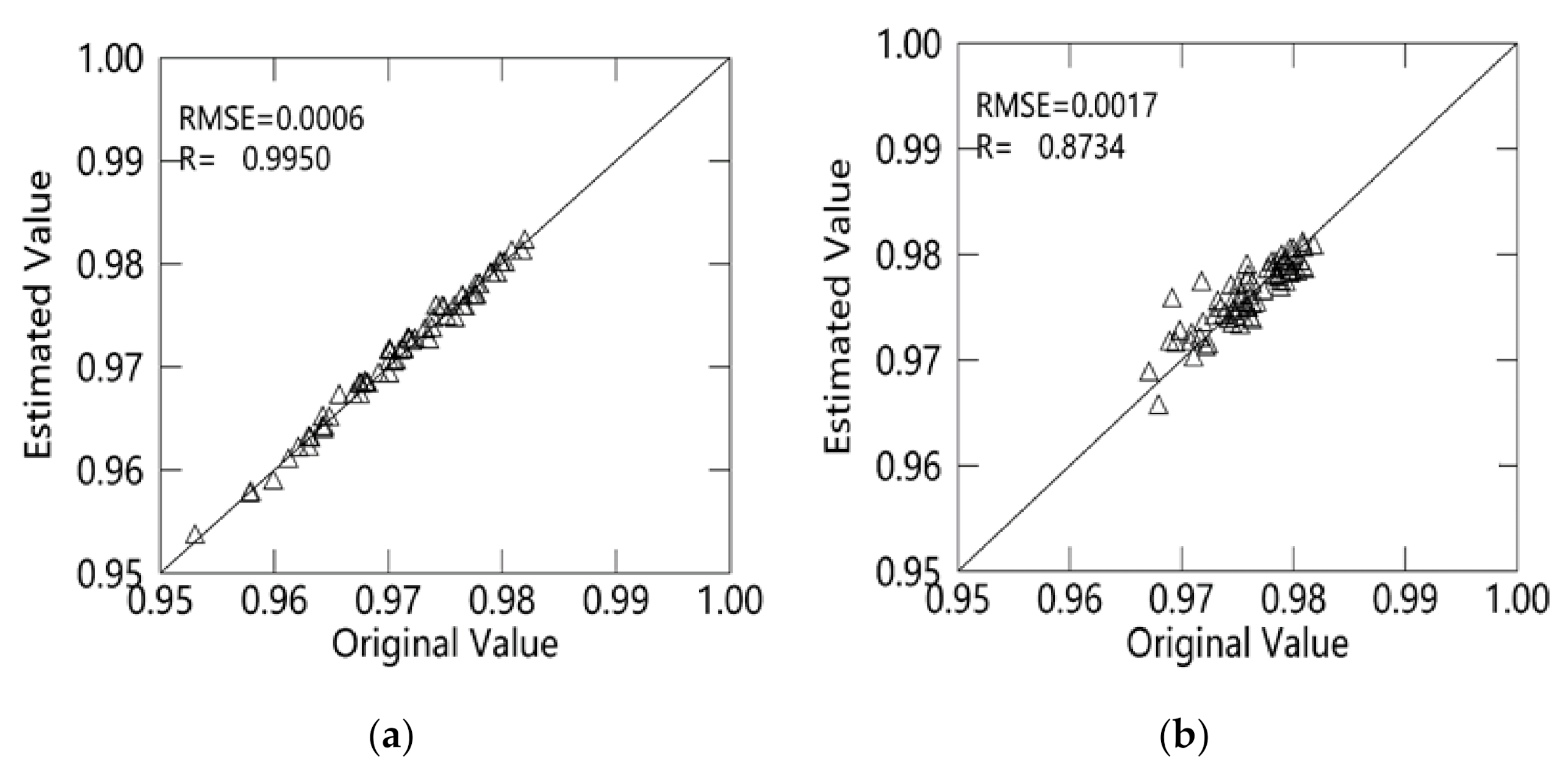
3.3. Estimation of AWVC
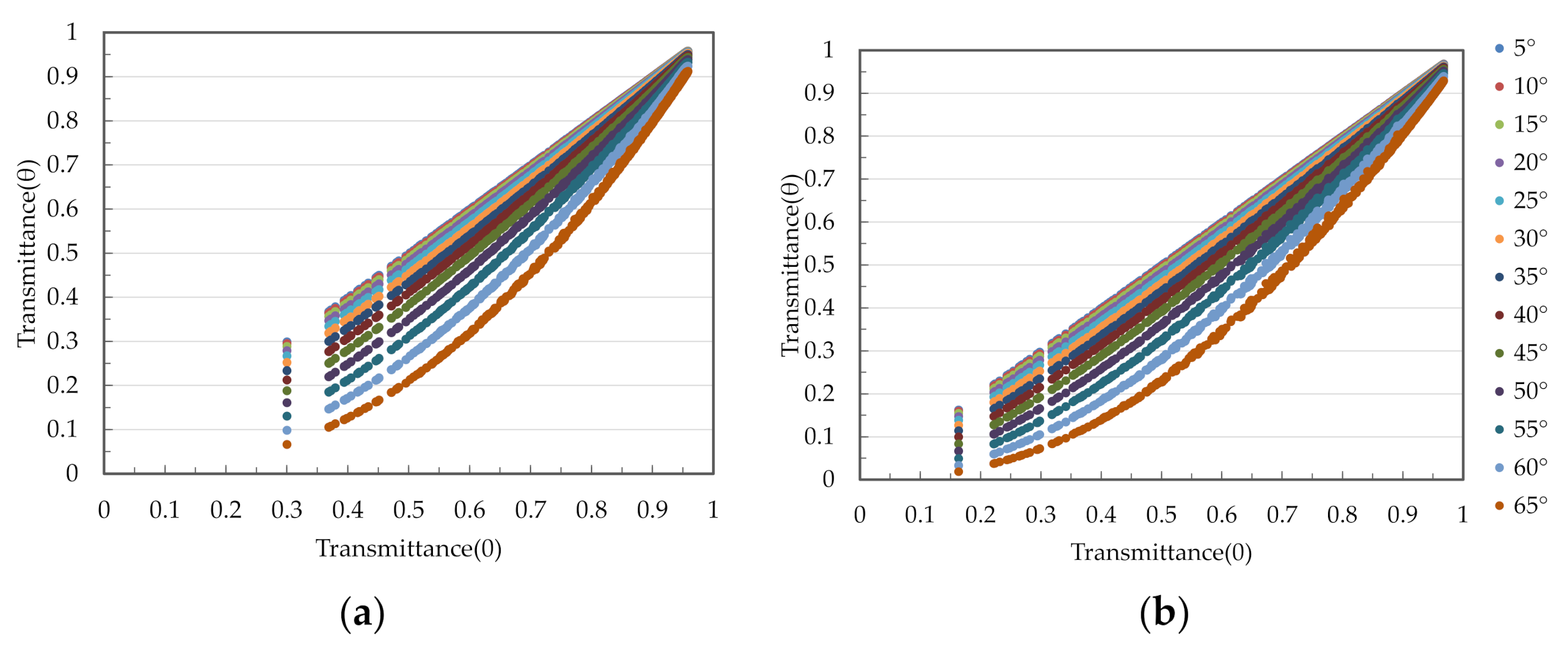
3.4. Estimation of AT
3.5. Estimation of LSE
3.5.1. Estimation of Soil Emissivity from ASTER GED Product
3.5.2. Gap Filling of ASTER Soil Emissivity
3.5.3. Adjustment of ASTER Soil Emissivity to FY-3D MERSI-II TIR Bands
3.5.4. Calculation of the LSE for FY-3D MERSI-II
3.6. Validation of the Improved TFSWA
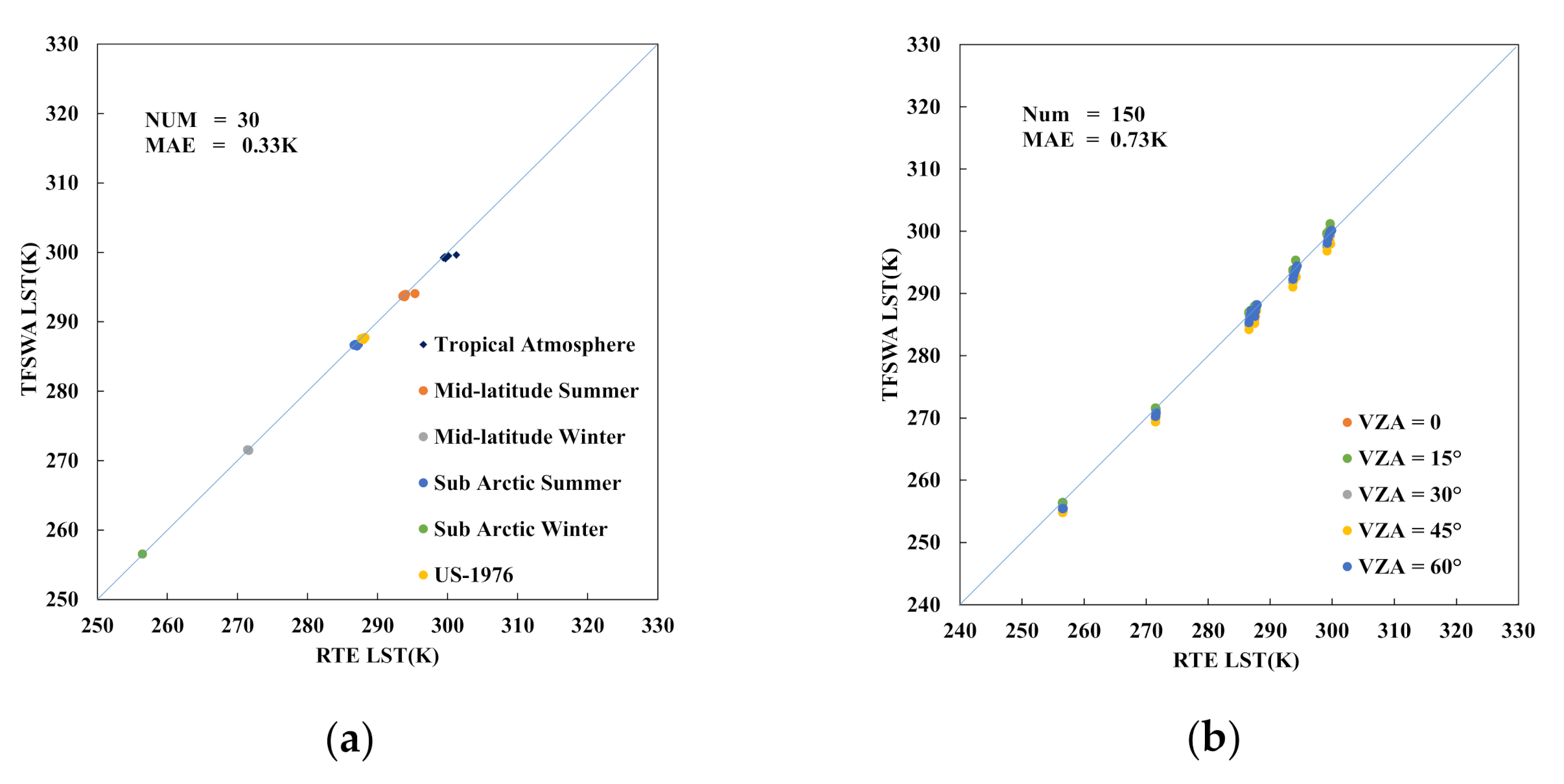
3.6.1. Validation with Atmospheric Radiation Transfer Simulation
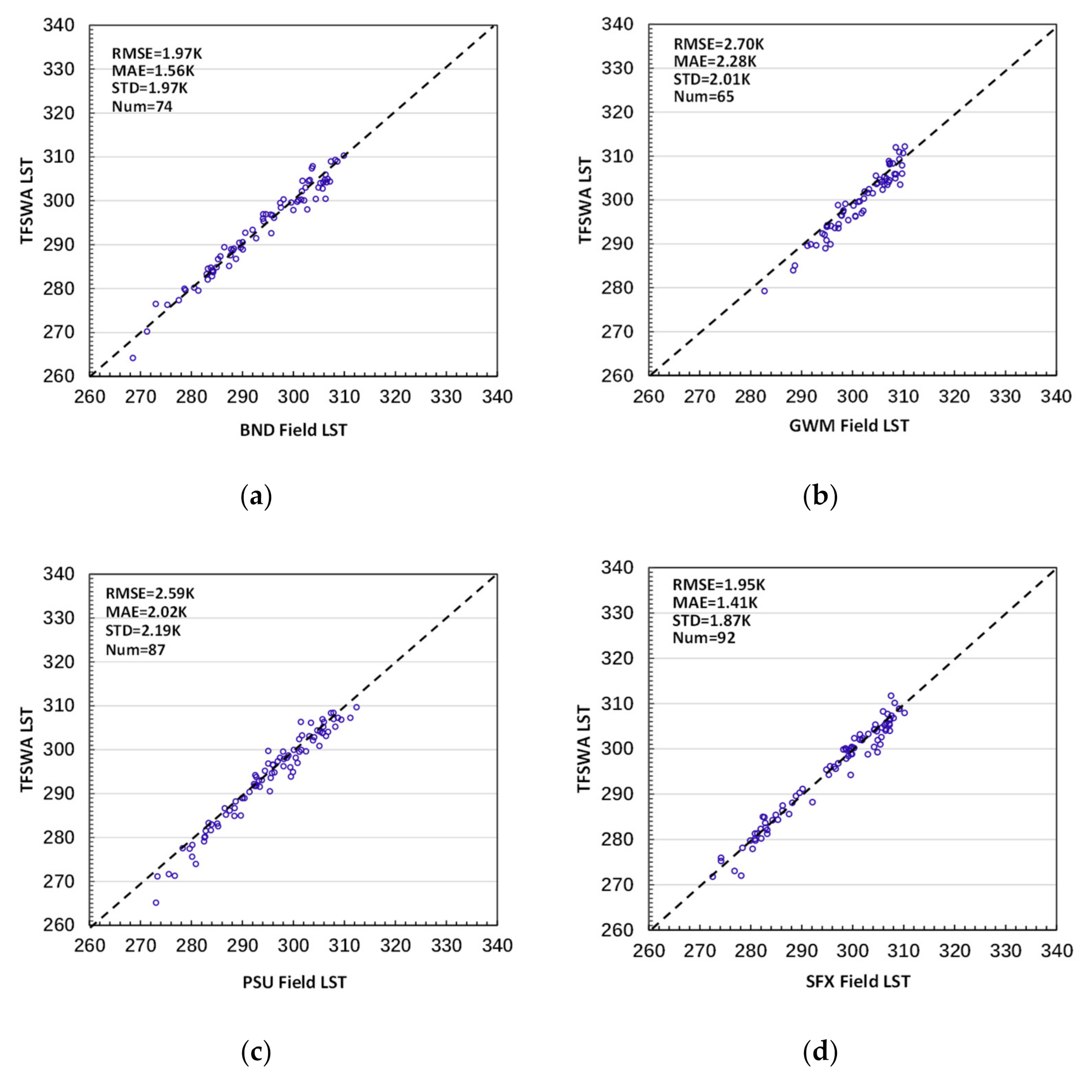
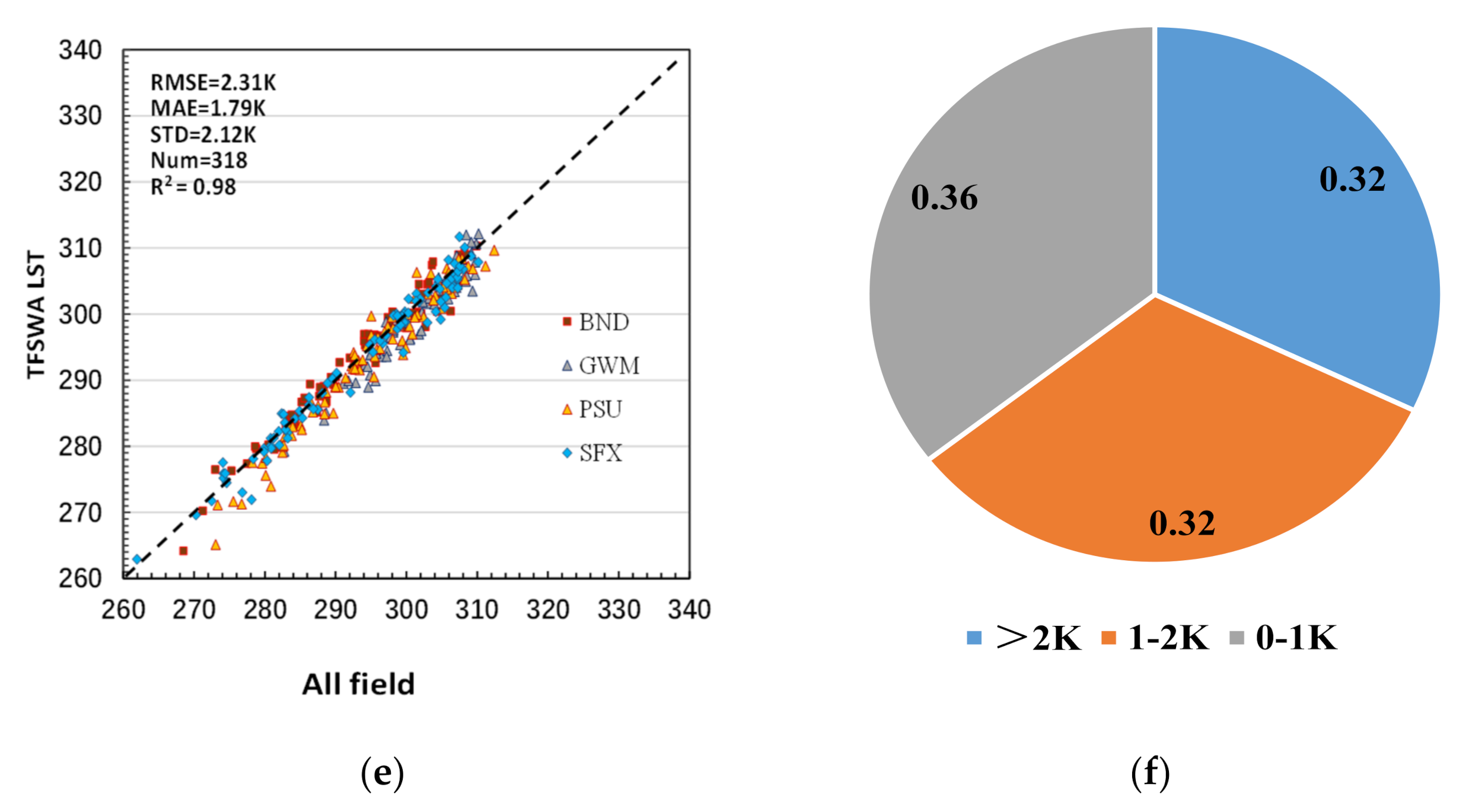
3.6.2. Validation with Field Measurements
3.6.3. Cross-Validation with MODIS LST Products
4. Results and Analysis
4.1. Results from Validation with Atmospheric Radiation Transfer Simulation
4.2. Results from Validation with Field Measurements
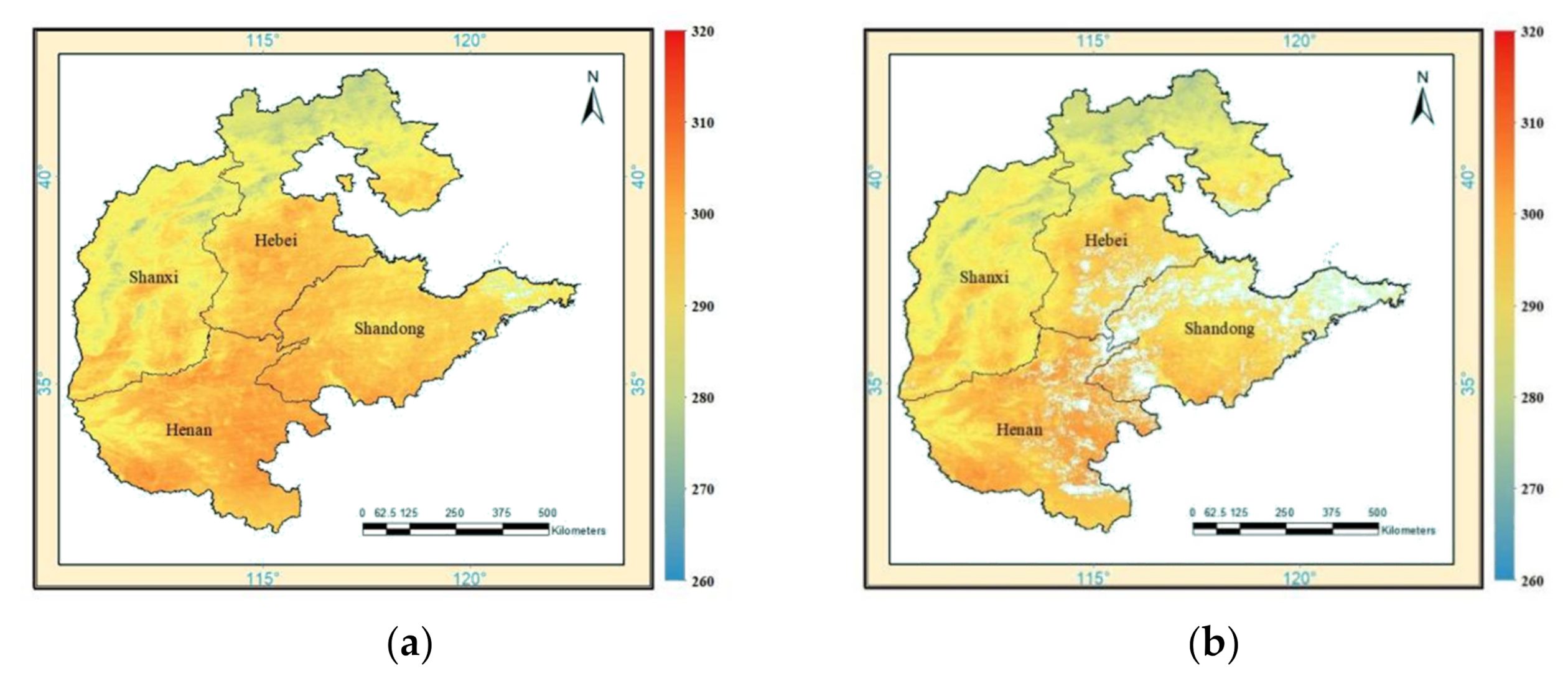
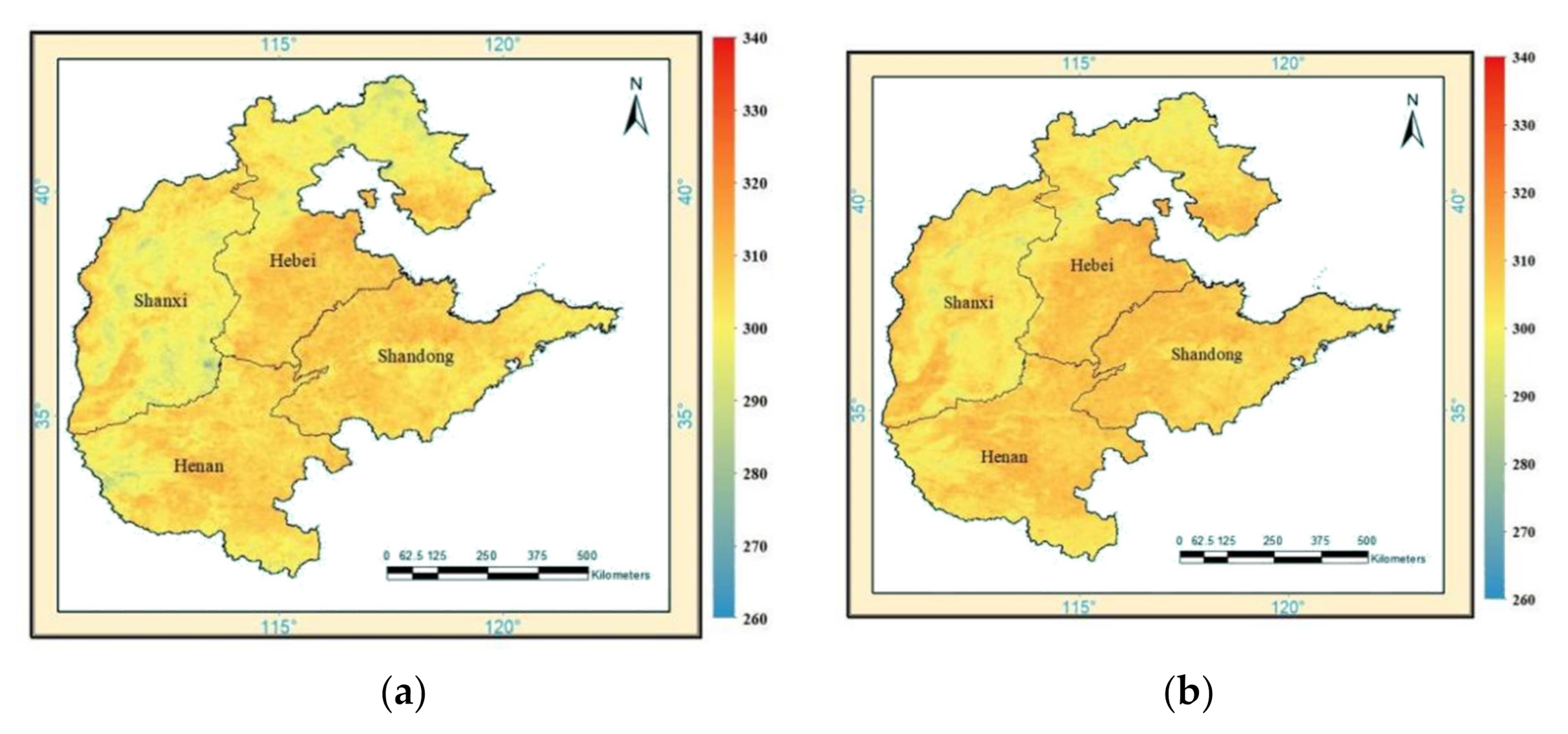
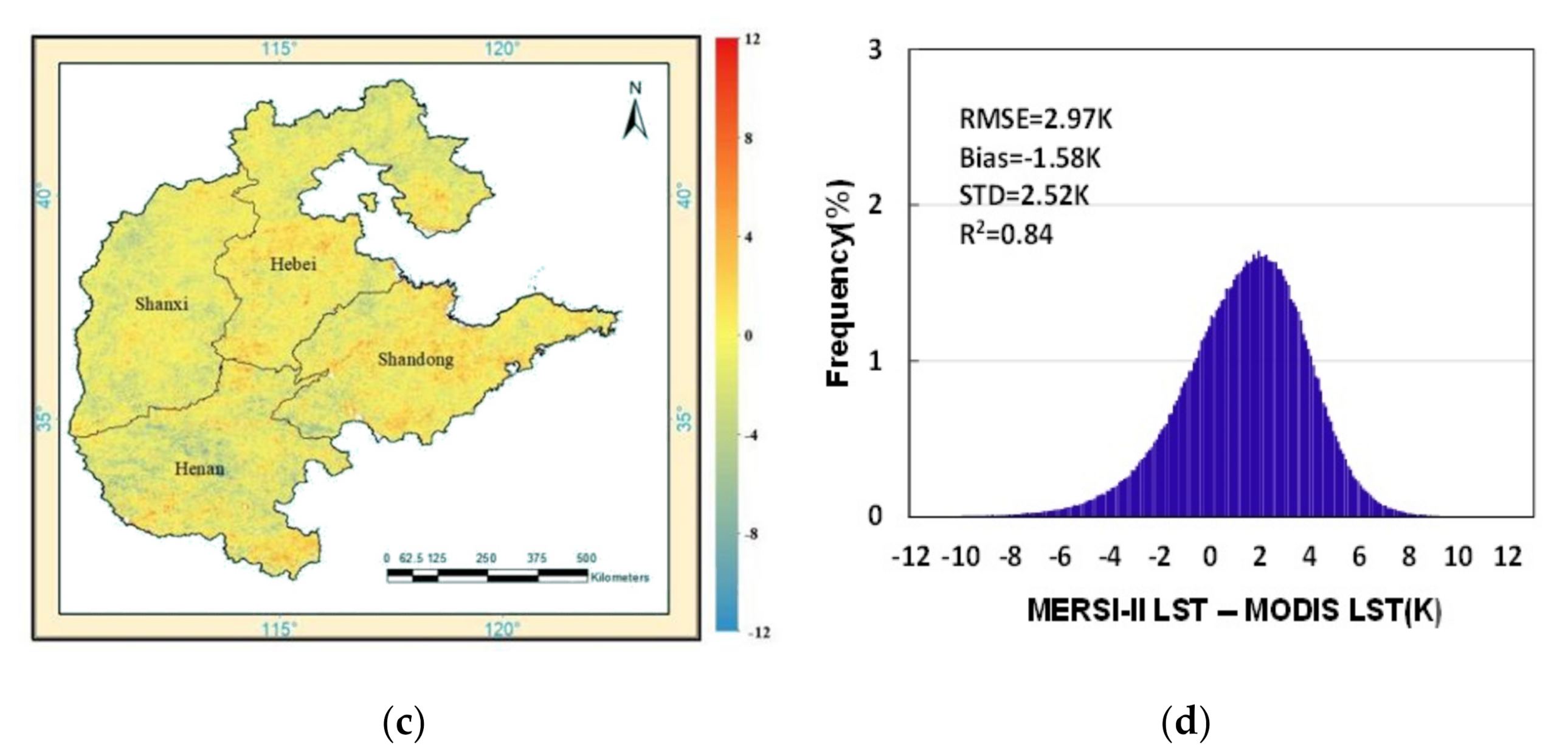
4.3. Cross-Validation on Daily and Monthly Average Images
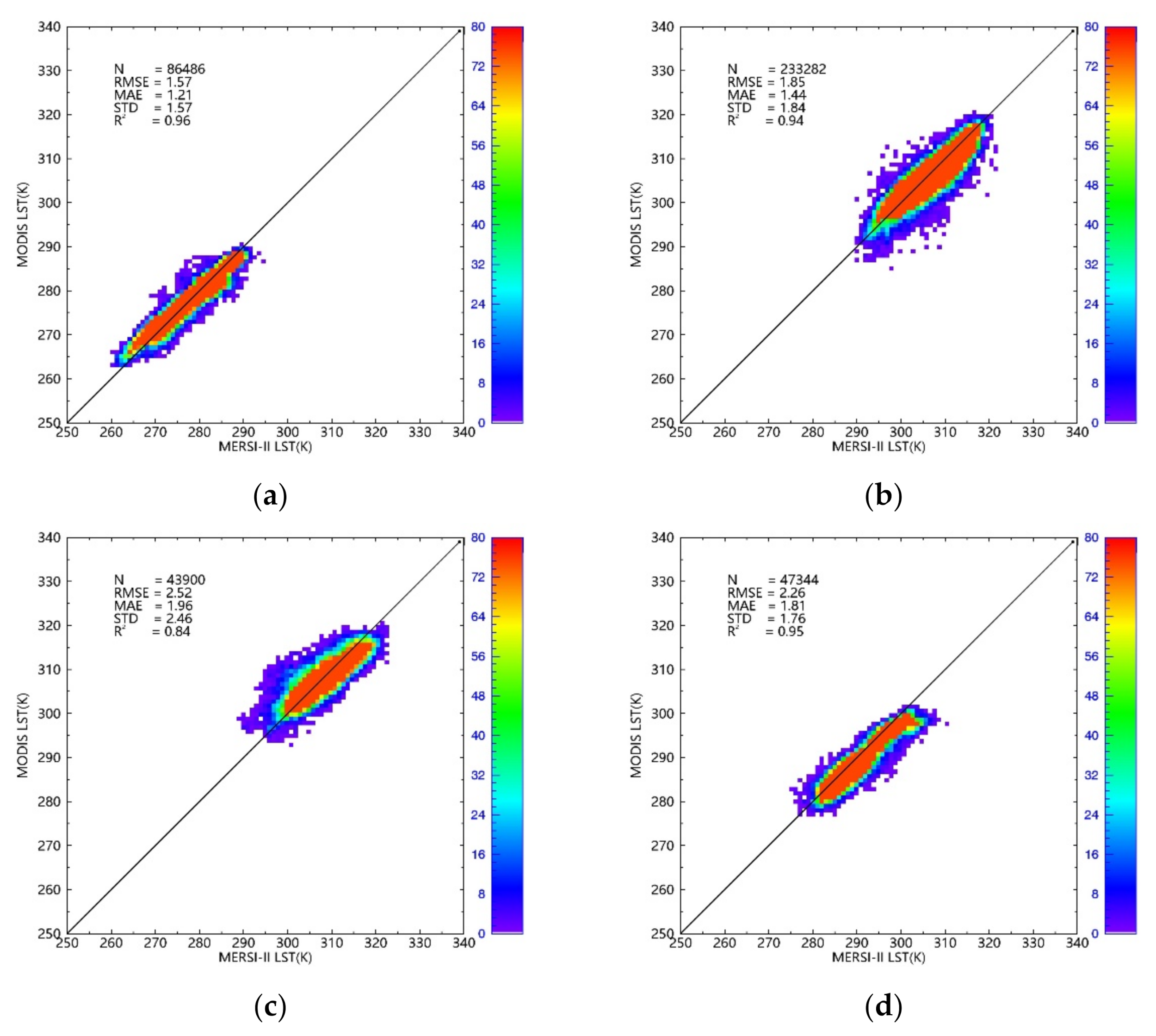
4.4. Cross-Validation over Different Land Surface Types
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ma, X.; Jin, J.; Zhu, L.; Liu, J. Evaluating and improving simulations of diurnal variation in land surface temperature with the Community Land Model for the Tibetan Plateau. PeerJ 2021, 9, e11040. [Google Scholar] [CrossRef]
- Fan, X.; Tang, B.-H.; Wu, H.; Yan, G.; Li, Z.-L. Daytime Land Surface Temperature Extraction from MODIS Thermal Infrared Data under Cirrus Clouds. Sensors 2015, 15, 9942–9961. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qin, Z.; Berliner, P.; Karnieli, A. Ground temperature measurement and emissivity determination to understand the thermal anomaly and its significance on the development of an arid environmental ecosystem in the sand dunes across the Israel–Egypt border. J. Arid Environ. 2005, 60, 27–52. [Google Scholar] [CrossRef]
- Qin, Z.; Karnieli, A.; Berliner, P. Remote sensing analysis of the land surface temperature anomaly in the sand-dune region across the Israel-Egypt border. Int. J. Remote Sens. 2002, 23, 3991–4018. [Google Scholar] [CrossRef]
- Leng, P.; Song, X.; Duan, S.-B.; Li, Z.-L. A practical algorithm for estimating surface soil moisture using combined optical and thermal infrared data. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 338–348. [Google Scholar] [CrossRef]
- Anderson, M.C.; Hain, C.R.; Wardlow, B.; Pimstein, A.; Mecikalski, J.R.; Kustas, W.P. Evaluation of Drought Indices Based on Thermal Remote Sensing of Evapotranspiration over the Continental United States. J. Clim. 2011, 24, 2025–2044. [Google Scholar] [CrossRef]
- Eleftheriou, D.; Kiachidis, K.; Kalmintzis, G.; Kalea, A.; Bantasis, C.; Koumadoraki, P.; Spathara, M.E.; Tsolaki, A.; Tzampazidou, M.I.; Gemitzi, A. Determination of annual and seasonal daytime and nighttime trends of MODIS LST over Greece—climate change implications. Sci. Total Environ. 2018, 616–617, 937–947. [Google Scholar] [CrossRef]
- Zhang, F.; Kung, H.; Johnson, V.C.; LaGrone, B.I.; Wang, J. Change Detection of Land Surface Temperature (LST) and some Related Parameters Using Landsat Image: A Case Study of the Ebinur Lake Watershed, Xinjiang, China. Wetlands 2017, 38, 65–80. [Google Scholar] [CrossRef]
- Hao, Z.; Yuan, X.; Xia, Y.; Hao, F.; Singh, V.P. An Overview of Drought Monitoring and Prediction Systems at Regional and Global Scales. Bull. Am. Meteorol. Soc. 2017, 98, 1879–1896. [Google Scholar] [CrossRef]
- Duan, S.-B.; Li, Z.-L.; Wang, C.; Zhang, S.; Tang, B.-H.; Leng, P.; Gao, M.-F. Land-surface temperature retrieval from Landsat 8 single-channel thermal infrared data in combination with NCEP reanalysis data and ASTER GED product. Int. J. Remote Sens. 2018, 40, 1763–1778. [Google Scholar] [CrossRef]
- Jiménez-Muñoz, J.C.; Cristóbal, J.; Sobrino, J.A.; Soria, G.; Ninyerola, M.; Pons, X. Revision of the Single-Channel Algorithm for Land Surface Temperature Retrieval from Landsat Thermal-Infrared Data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 339–349. [Google Scholar] [CrossRef]
- Tang, B.-H.; Shao, K.; Li, Z.-L.; Wu, H.; Nerry, F.; Zhou, G. Estimation and Validation of Land Surface Temperatures from Chinese Second-Generation Polar-Orbit FY-3A VIRR Data. Remote Sens. 2015, 7, 3250–3273. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.-L.; Tang, B.-H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef] [Green Version]
- Dash, P.; Göttsche, F.-M.; Olesen, F.-S.; Fischer, H. Land surface temperature and emissivity estimation from passive sensor data: Theory and practice-current trends. Int. J. Remote Sens. 2002, 23, 2563–2594. [Google Scholar] [CrossRef]
- Prata, A.J.; Caselles, V.; Coll, C.; Sobrino, J.A.; Ottle, C. Thermal remote sensing of land surface temperature from satellites: Current status and future prospects. Remote Sens. Rev. 1995, 12, 175–224. [Google Scholar] [CrossRef]
- Jiménez-Muñoz, J.C.; Sobrino, J.A. A generalized single-channel method for retrieving land surface temperature from remote sensing data. J. Geophys. Res. Space Phys. 2003, 108. [Google Scholar] [CrossRef] [Green Version]
- Cristóbal, J.; Jiménez-Muñoz, J.C.; Sobrino, J.A.; Ninyerola, M.; Pons, X. Improvements in land surface temperature retrieval from the Landsat series thermal band using water vapor and air temperature. J. Geophys. Res. Space Phys. 2009, 114. [Google Scholar] [CrossRef]
- Qin, Z.; Karnieli, A.; Berliner, P. A mono-window algorithm for retrieving land surface temperature from Landsat TM data and its application to the Israel-Egypt border region. Int. J. Remote Sens. 2001, 22, 3719–3746. [Google Scholar] [CrossRef]
- Coll, C.; Caselles, V. A split-window algorithm for land surface temperature from advanced very high resolution radiometer data: Validation and algorithm comparison. J. Geophys. Res. Space Phys. 1997, 102, 16697–16713. [Google Scholar] [CrossRef]
- Becker, F.; Li, Z.-L. Towards a local split window method over land surfaces. Int. J. Remote Sens. 1990, 11, 369–393. [Google Scholar] [CrossRef]
- Wan, Z.-M.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Trans. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar] [CrossRef] [Green Version]
- Qin, Z.; Dall’Olmo, G.; Karnieli, A.; Berliner, P. Derivation of split window algorithm and its sensitivity analysis for retrieving land surface temperature from NOAA-advanced very high resolution radiometer data. J. Geophys. Res. Space Phys. 2001, 106, 22655–22670. [Google Scholar] [CrossRef]
- Gillespie, A.; Rokugawa, S.; Matsunaga, T.; Cothern, J.; Hook, S.; Kahle, A. A temperature and emissivity separation algorithm for Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) images. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1113–1126. [Google Scholar] [CrossRef]
- Hulley, G.C.; Hook, S.J. Generating Consistent Land Surface Temperature and Emissivity Products Between ASTER and MODIS Data for Earth Science Research. IEEE Trans. Geosci. Remote Sens. 2010, 49, 1304–1315. [Google Scholar] [CrossRef]
- Islam, T.; Hulley, G.C.; Malakar, N.K.; Radocinski, R.G.; Guillevic, P.C.; Hook, S.J. A Physics-Based Algorithm for the Simultaneous Retrieval of Land Surface Temperature and Emissivity from VIIRS Thermal Infrared Data. IEEE Trans. Geosci. Remote Sens. 2016, 55, 563–576. [Google Scholar] [CrossRef]
- Tang, B.; Bi, Y.; Li, Z.-L.; Xia, J. Generalized Split-Window Algorithm for Estimate of Land Surface Temperature from Chinese Geostationary FengYun Meteorological Satellite (FY-2C) Data. Sensors 2008, 8, 933–951. [Google Scholar] [CrossRef] [Green Version]
- Song, X.; Wang, Y.; Tang, B.; Leng, P.; Chuan, S.; Peng, J.; Loew, A. Estimation of Land Surface Temperature Using FengYun-2E (FY-2E) Data: A Case Study of the Source Area of the Yellow River. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3744–3751. [Google Scholar] [CrossRef]
- Hu, Y.; Zhong, L.; Ma, Y.; Zou, M.; Xu, K.; Huang, Z.; Feng, L. Estimation of the Land Surface Temperature over the Tibetan Plateau by Using Chinese FY-2C Geostationary Satellite Data. Sensors 2018, 18, 376. [Google Scholar] [CrossRef] [Green Version]
- Jiang, J.; Liu, Q.; Li, H.; Huang, H. Split-window method for land surface temperature estimation from FY-3A/VIRR data. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 305–308. [Google Scholar]
- Jiang, G.-M.; Zhou, W.; Liu, R. Development of Split-Window Algorithm for Land Surface Temperature Estimation From the VIRR/FY-3A Measurements. IEEE Geosci. Remote Sens. Lett. 2013, 10, 952–956. [Google Scholar] [CrossRef]
- Wang, L.J.; Zuo, H.C.; Ren, P.C.; Qiang, B. Land surface temperature retrieval from MODIS and VIRR data in northwest China. IOP Conf. Ser. Earth Environ. Sci. 2014, 17, 12154. [Google Scholar] [CrossRef] [Green Version]
- Jiang, J.; Li, H.; Liu, Q.; Wang, H.; Du, Y.; Cao, B.; Zhong, B.; Wu, S. Evaluation of Land Surface Temperature Retrieval from FY-3B/VIRR Data in an Arid Area of Northwestern China. Remote Sens. 2015, 7, 7080–7104. [Google Scholar] [CrossRef] [Green Version]
- Gao, C.; Zhao, Y.; Li, C.; Ma, L.; Wang, N.; Qian, Y.; Ren, L. An Investigation of a Novel Cross-Calibration Method of FY-3C/VIRR against NPP/VIIRS in the Dunhuang Test Site. Remote Sens. 2016, 8, 77. [Google Scholar] [CrossRef] [Green Version]
- Gao, C.; Qiu, S.; Zhao, E.-Y.; Li, C.; Tang, L.-L.; Ma, L.-L.; Jiang, X.; Qian, Y.; Zhao, Y.; Wang, N.; et al. Land Surface Temperature Retrieval From FY-3C/VIRR Data and Its Cross-Validation with Terra/MODIS. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4944–4953. [Google Scholar] [CrossRef]
- Meng, X.; Cheng, J.; Liang, S. Estimating Land Surface Temperature from Feng Yun-3C/MERSI Data Using a New Land Surface Emissivity Scheme. Remote Sens. 2017, 9, 1247. [Google Scholar] [CrossRef] [Green Version]
- Gao, C.; Qiu, S.; Li, C.; Tang, L.; Ma, L.; Qian, Y.; Zhao, Y.; Ren, L. Evaluation of land surface temperature by comparing FY-3C/VIRR with Terra/MODIS and MSG/SEVIRI data. Int. J. Remote Sens. 2018, 40, 1779–1792. [Google Scholar] [CrossRef]
- Wang, H.; Mao, K.; Mu, F.; Shi, J.; Yang, J.; Li, Z.; Qin, Z. A Split Window Algorithm for Retrieving Land Surface Temperature from FY-3D MERSI-2 Data. Remote Sens. 2019, 11, 2083. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Duan, S.-B.; Wei, Z.; Li, Z.L. Derivation of new split window algorithm for retrieving land surface temperature from FY-3/VIRR data. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 878–881. [Google Scholar]
- Valor, E. Mapping land surface emissivity from NDVI: Application to European, African, and South American areas. Remote Sens. Environ. 1996, 57, 167–184. [Google Scholar] [CrossRef]
- Carlson, T.N.; Ripley, D.A. On the relation between NDVI, fractional vegetation cover, and leaf area index. Remote Sens. Environ. 1997, 62, 241–252. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Caselles, V.; Becker, F. Significance of the remotely sensed thermal infrared measurements obtained over a citrus orchard. ISPRS J. Photogramm. Remote Sens. 1990, 44, 343–354. [Google Scholar] [CrossRef]
- Guillevic, P.C.; Biard, J.C.; Hulley, G.C.; Privette, J.; Hook, S.J.; Olioso, A.; Göttsche, F.M.; Radocinski, R.; Román, M.O.; Yu, Y.; et al. Validation of Land Surface Temperature products derived from the Visible Infrared Imaging Radiometer Suite (VIIRS) using ground-based and heritage satellite measurements. Remote Sens. Environ. 2014, 154, 19–37. [Google Scholar] [CrossRef]
- Hulley, G.C.; Hook, S.J.; Abbott, E.; Malakar, N.; Islam, T.; Abrams, M. The ASTER Global Emissivity Dataset ( ASTER GED ): Mapping Earth’s emissivity at 100 meter spatial scale. Geophys. Res. Lett. 2015, 42, 7966–7976. [Google Scholar] [CrossRef]
- Meng, X.; Li, H.; Du, Y.; Liu, Q.; Zhu, J.; Sun, L. Retrieving land surface temperature from Landsat 8 TIRS data using RTTOV and ASTER GED. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 4302–4305. [Google Scholar] [CrossRef]
- Meng, X.; Li, H.; Du, Y.; Cao, B.; Liu, Q.; Sun, L.; Zhu, J. Estimating land surface emissivity from ASTER GED products. J. Remote Sens. 2016, 20, 382–396. [Google Scholar] [CrossRef]
- Wang, C.; Duan, S.-B.; Zhang, X.; Wu, H.; Gao, M.-F.; Leng, P. An alternative split-window algorithm for retrieving land surface temperature from Visible Infrared Imaging Radiometer Suite data. Int. J. Remote Sens. 2018, 40, 1640–1654. [Google Scholar] [CrossRef]
- Zhang, S.; Duan, S.-B.; Li, Z.-L.; Huang, C.; Wu, H.; Han, X.-J.; Leng, P.; Gao, M. Improvement of Split-Window Algorithm for Land Surface Temperature Retrieval from Sentinel-3A SLSTR Data Over Barren Surfaces Using ASTER GED Product. Remote Sens. 2019, 11, 3025. [Google Scholar] [CrossRef] [Green Version]
- Chedin, A.; Scott, N.A.; Wahiche, C.; Moulinier, P. The improved initialization inversion method: A high resolution physical meth-od for temperature retrievals from satellites of the Tiros-N series. J. Clim. Appl. Meteorol. 1985, 24, 128–143. [Google Scholar] [CrossRef] [Green Version]
- Achard, V. Trois Problemes Cles de L’analyze 3D de la Structure Thermodinamique de L’atmosphere par Satellite: Mesure du Contenuen Ozone: Classification des Masses D’air; Modelization Hyper Rapide du Ransfert Radiative. Ph.D. Thesis, LMD, Ecole Polytechnique, Palaiseau, France, 1991. [Google Scholar]
- Chevallier, F.; Chédin, A.; Cheruy, F.; Morcrette, J.-J. TIGR-like atmospheric-profile databases for accurate radiative-flux computation. Q. J. R. Meteorol. Soc. 2000, 126, 777–785. [Google Scholar] [CrossRef]
- Tonooka, H. An atmospheric correction algorithm for thermal infrared multispectral data over land-a water-vapor scaling method. IEEE Trans. Geosci. Remote Sens. 2001, 39, 682–692. [Google Scholar] [CrossRef]
- Tonooka, H. Accurate atmospheric correction of ASTER thermal infrared imagery using the WVS method. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2778–2792. [Google Scholar] [CrossRef]
- Parmesan, C.; Root, T.L.; Willig, M.R. Impacts of extreme weather and climate on terrestrial biota. Bull. Am. Meteorol. Soc. 2000, 81, 443–450. [Google Scholar] [CrossRef] [Green Version]
- Sekertekin, A. Validation of Physical Radiative Transfer Equation-Based Land Surface Temperature Using Landsat 8 Satellite Imagery and SURFRAD in-situ Measurements. J. Atmos. Sol.-Terr. Phys. 2019, 196, 105161. [Google Scholar] [CrossRef]
- Li, S.; Yu, Y.; Sun, D.; Tarpley, D.; Zhan, X.; Chiu, L. Evaluation of 10 year AQUA/MODIS land surface temperature with SURFRAD observations. Int. J. Remote Sens. 2014, 35, 830–856. [Google Scholar] [CrossRef]
- Wang, W.; Liang, S.; Meyers, T. Validating MODIS land surface temperature products using long-term nighttime ground measurements. Remote Sens. Environ. 2008, 112, 623–635. [Google Scholar] [CrossRef]
- Cheng, J.; Liang, S.; Yao, Y.; Zhang, X. Estimating the Optimal Broadband Emissivity Spectral Range for Calculating Surface Longwave Net Radiation. IEEE Geosci. Remote Sens. Lett. 2012, 10, 401–405. [Google Scholar] [CrossRef]
- Wang, K.; Liang, S. Evaluation of ASTER and MODIS land surface temperature and emissivity products using long-term surface longwave radiation observations at SURFRAD sites. Remote Sens. Environ. 2009, 113, 1556–1565. [Google Scholar] [CrossRef]
- Gao, B.-C.; Kaufman, Y.J. Water vapor retrievals using Moderate Resolution Imaging Spectroradiometer (MODIS) near-infrared channels. J. Geophys. Res. Space Phys. 2003, 108. [Google Scholar] [CrossRef]
- Kaufman, Y.; Gao, B.-C. Remote sensing of water vapor in the near IR from EOS/MODIS. IEEE Trans. Geosci. Remote Sens. 1992, 30, 871–884. [Google Scholar] [CrossRef]
- Caselles, E.; Valor, E.; Abad, F.; Caselles, V. Automatic classification-based generation of thermal infrared land surface emissivity maps using AATSR data over Europe. Remote Sens. Environ. 2012, 124, 321–333. [Google Scholar] [CrossRef] [Green Version]
- Baldridge, A.M.; Hook, S.J.; Grove, C.I.; Rivera, G. The ASTER spectral library version 2.0. Remote Sens. Environ. 2009, 113, 711–715. [Google Scholar] [CrossRef]
- Snyder, W. Thermal Infrared (3–14 μm) bidirectional reflectance measurements of sands and soils. Remote Sens. Environ. 1997, 60, 101–109. [Google Scholar] [CrossRef]
- Gutman, G.; Ignatov, A. The derivation of the green vegetation fraction from NOAA/AVHRR data for use in numerical weather prediction models. Int. J. Remote Sens. 1998, 19, 1533–1543. [Google Scholar] [CrossRef]
- Masiello, G.; Serio, C.; Venafra, S.; Poutier, L.; Göttsche, F.-M. SEVIRI Hyper-Fast Forward Model with Application to Emissivity Retrieval. Sensors 2019, 19, 1532. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Masiello, G.; Serio, C.; Venafra, S.; Liuzzi, G.; Göttsche, F.; Trigo, I.F.; Watts, P. Kalman filter physical retrieval of surface emissivity and temperature from SEVIRI infrared channels: A validation and intercomparison study. Atmos. Meas. Tech. 2015, 8, 2981–2997. [Google Scholar] [CrossRef] [Green Version]
- Frey, C.M.; Kuenzer, C.; Dech, S. Quantitative comparison of the operational NOAA-AVHRR LST product of DLR and the MODIS LST product V005. Int. J. Remote Sens. 2012, 33, 7165–7183. [Google Scholar] [CrossRef]
- Ermida, S.; Trigo, I.; DaCamara, C.C.; Göttsche, F.M.; Olesen, F.S.; Hulley, G. Validation of remotely sensed surface temperature over an oak woodland landscape—The problem of viewing and illumination geometries. Remote Sens. Environ. 2014, 148, 16–27. [Google Scholar] [CrossRef]
- Qian, Y.-G.; Li, Z.-L.; Nerry, F. Evaluation of land surface temperature and emissivities retrieved from MSG/SEVIRI data with MODIS land surface temperature and emissivity products. Int. J. Remote Sens. 2012, 34, 3140–3152. [Google Scholar] [CrossRef]
- Duan, S. Methodology Development for Retrieval of All-Weather Land Surface Temperature at High Spatial Resolution. Ph.D. Thesis, Chinese Academy of Agricultural Sciences, Beijing, China, 2016. [Google Scholar]
- Hewison, T.; Wu, X.; Yu, F.; Tahara, Y.; Hu, X.; Kim, D.; Koenig, M. GSICS Inter-Calibration of Infrared Channels of Geostationary Imagers Using Metop/IASI. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1160–1170. [Google Scholar] [CrossRef]
- Trigo, I.; Monteiro, I.T.; Olesen, F.; Kabsch, E. An assessment of remotely sensed land surface temperature. J. Geophys. Res. Space Phys. 2008, 113, D17. [Google Scholar] [CrossRef]


| Used Bands No. | Wavelength (μm) | Bandwidth (nm) | Spatial Resolution (m) | Typical Radiation Value (Ltyp W·m−2·μm−1·r−1/Ttyp K) | Signal Noise Ratio/NE∆T (K) | Dynamic Range (Maximum Reflectance ρ /Temperature K) | Usage |
|---|---|---|---|---|---|---|---|
| 3 | 0.650 | 50 | 250 | 22 | 100 | 90% | NDVI & Pv |
| 4 | 0.865 | 50 | 250 | 25 | 100 | 90% | |
| 15 | 0.865 | 20 | 1000 | 17.8 | 500 | 30% | Water vapor content |
| 16 | 0.905 | 20 | 1000 | 22.2 | 200 | 100% | |
| 17 | 0.936 | 20 | 1000 | 20 | 100 | 100% | |
| 18 | 0.940 | 50 | 1000 | 15.0 | 200 | 100% | |
| 19 | 1.030 | 20 | 1000 | 5.4 | 100 | 100% | |
| 24 | 10.8 | 1000 | 250 | 300 K | 0.4 K | 180–330 K | LST |
| 25 | 12.0 | 1000 | 250 | 300 K | 0.4 K | 180–330 K |
| Parameters | a1i | a2i | a3i | b1i | b2i | b3i | c1i | c2i | c3i | R2 |
|---|---|---|---|---|---|---|---|---|---|---|
| τ24(θ) | 0.09893 | 0.73013 | −0.00507 | −0.29205 | −0.48184 | 1.00956 | 0.19071 | −0.24264 | −0.00453 | 1 |
| τ25(θ) | 0.03184 | 0.65283 | −0.00399 | −0.17258 | −0.44020 | 1.00790 | 0.13800 | −0.21343 | −0.00393 | 0.9999 |
| IGBP Class | Land Surface Type | Soil Type | Band13 | Band14 | ||
|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | |||
| 1, 2, 3, 4, 5, | Forest | Alfisol, Spodosol | 0.968 | 0.004 | 0.969 | 0.003 |
| 6, 7 | Shrubland | Aridisol | 0.970 | 0.008 | 0.970 | 0.006 |
| 8, 9, 10 | Grassland | Aridisol | 0.970 | 0.008 | 0.970 | 0.006 |
| 16 | Tundra | Aridisol | 0.970 | 0.008 | 0.970 | 0.006 |
| 11 | Wetland | Water Body, Grass | 0.992 | 0.004 | 0.990 | 0.004 |
| 12 | Cropland | Mollisol | 0.973 | 0.003 | 0.973 | 0.003 |
| 13 | Impervious Surface | Asphalt, Concrete | 0.954 | 0.016 | 0.953 | 0.013 |
| 14 | Bareland | Rock, Sand, Aridisol, Inceptisol | 0.956 | 0.030 | 0.963 | 0.024 |
| 15 | Snow/Ice | Ice, Snow | 0.993 | 0.003 | 0.984 | 0.009 |
| 0 | Water | Water | 0.993 | 0.002 | 0.991 | 0.004 |
| 255 | Unclassified | Mean | 0.972 | 0.006 | 0.972 | 0.005 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, W.; Qin, Z.; Fan, J.; Zhao, C.; Huang, Q.; Cao, K.; Abbasi, B. Land Surface Temperature Retrieval from Fengyun-3D Medium Resolution Spectral Imager II (FY-3D MERSI-II) Data with the Improved Two-Factor Split-Window Algorithm. Remote Sens. 2021, 13, 5072. https://doi.org/10.3390/rs13245072
Du W, Qin Z, Fan J, Zhao C, Huang Q, Cao K, Abbasi B. Land Surface Temperature Retrieval from Fengyun-3D Medium Resolution Spectral Imager II (FY-3D MERSI-II) Data with the Improved Two-Factor Split-Window Algorithm. Remote Sensing. 2021; 13(24):5072. https://doi.org/10.3390/rs13245072
Chicago/Turabian StyleDu, Wenhui, Zhihao Qin, Jinlong Fan, Chunliang Zhao, Qiuyan Huang, Kun Cao, and Bilawal Abbasi. 2021. "Land Surface Temperature Retrieval from Fengyun-3D Medium Resolution Spectral Imager II (FY-3D MERSI-II) Data with the Improved Two-Factor Split-Window Algorithm" Remote Sensing 13, no. 24: 5072. https://doi.org/10.3390/rs13245072
APA StyleDu, W., Qin, Z., Fan, J., Zhao, C., Huang, Q., Cao, K., & Abbasi, B. (2021). Land Surface Temperature Retrieval from Fengyun-3D Medium Resolution Spectral Imager II (FY-3D MERSI-II) Data with the Improved Two-Factor Split-Window Algorithm. Remote Sensing, 13(24), 5072. https://doi.org/10.3390/rs13245072








