Assessing the Effects of Time Interpolation of NDVI Composites on Phenology Trend Estimation
Abstract
:1. Introduction
2. Data and Methods
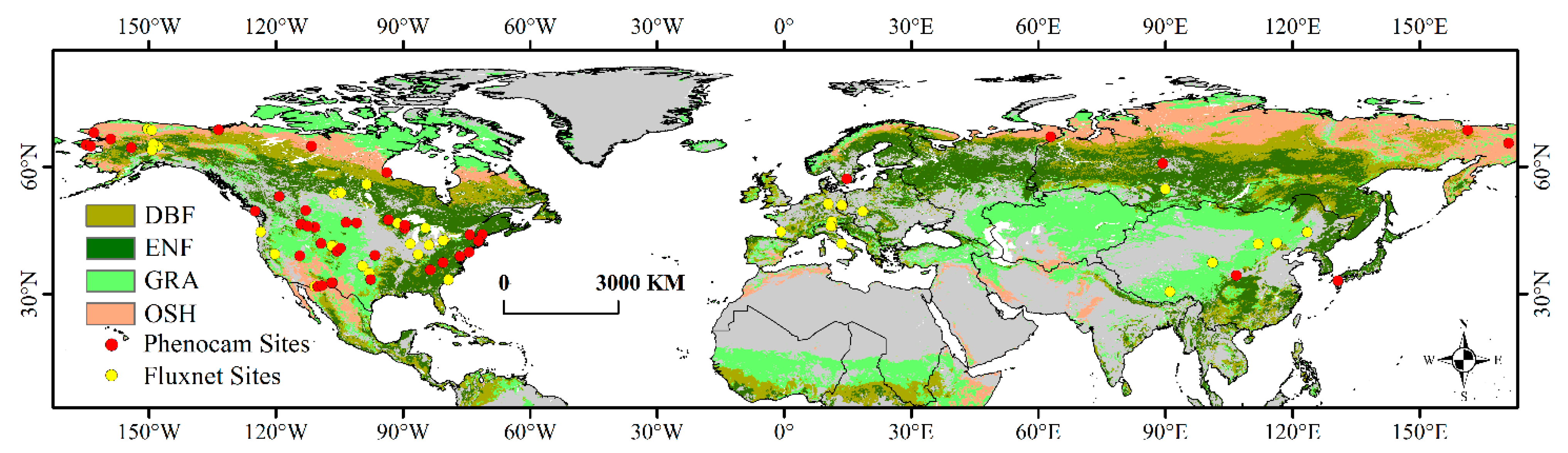
2.1. Study Area and Sites
2.2. Data and Pre-Processing
- (1)
- Calculating daily NDVI during 2001–2019
- (2)
- Constructing single-year daily NDVI data
- (3)
- Denoising single-year daily NDVI data
- (4)
- Constructing single-year composite NDVI data
2.3. Methods
2.3.1. Time Interpolation
2.3.2. Phenology Extraction
2.3.3. Phenology Trend Estimation
2.3.4. Statistical Analysis
3. Results
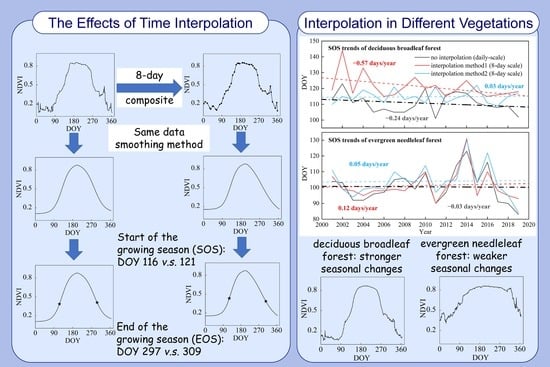
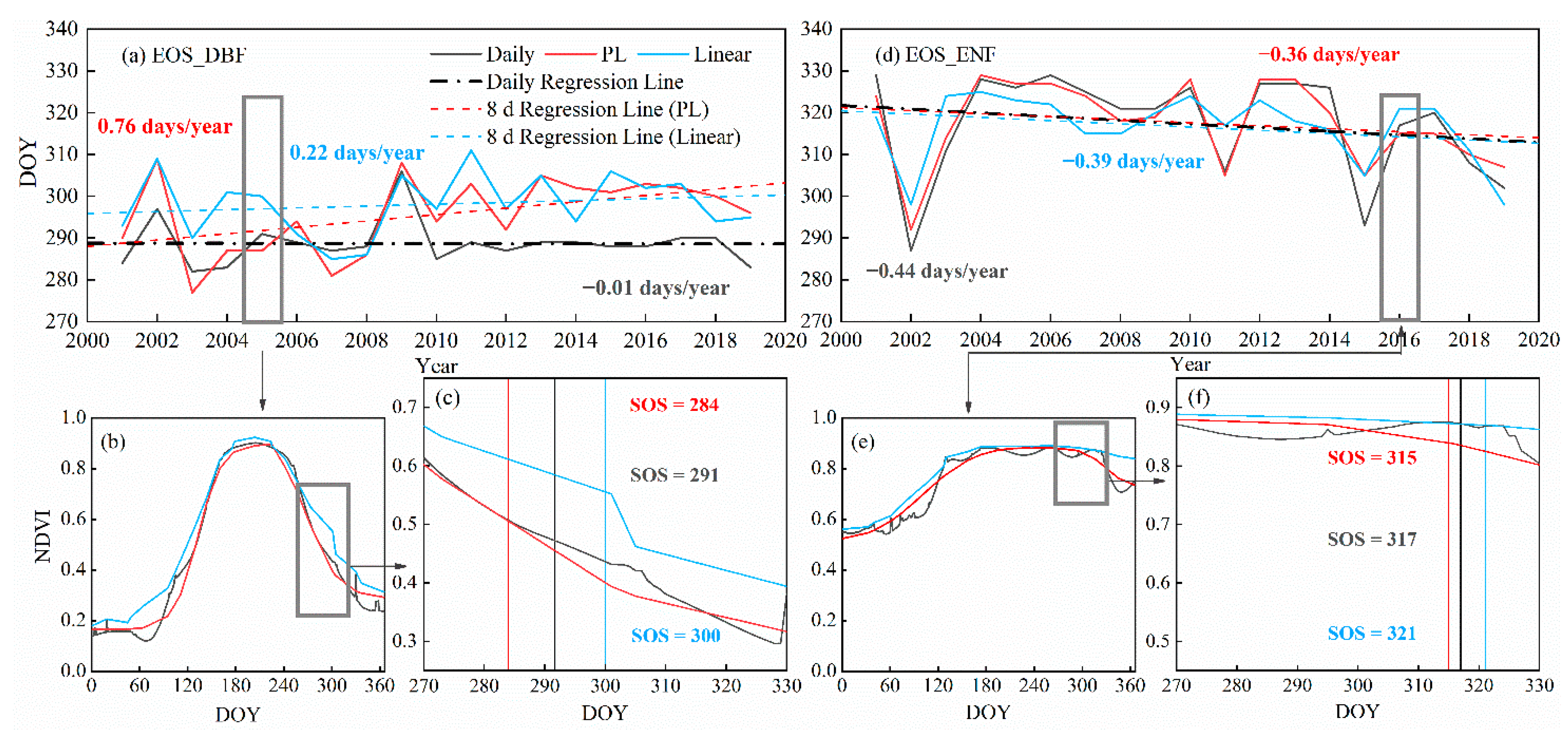
3.1. Comparisons between Trends from Daily NDVI Data and NDVI Composites Based on Different Time Interpolation Methods
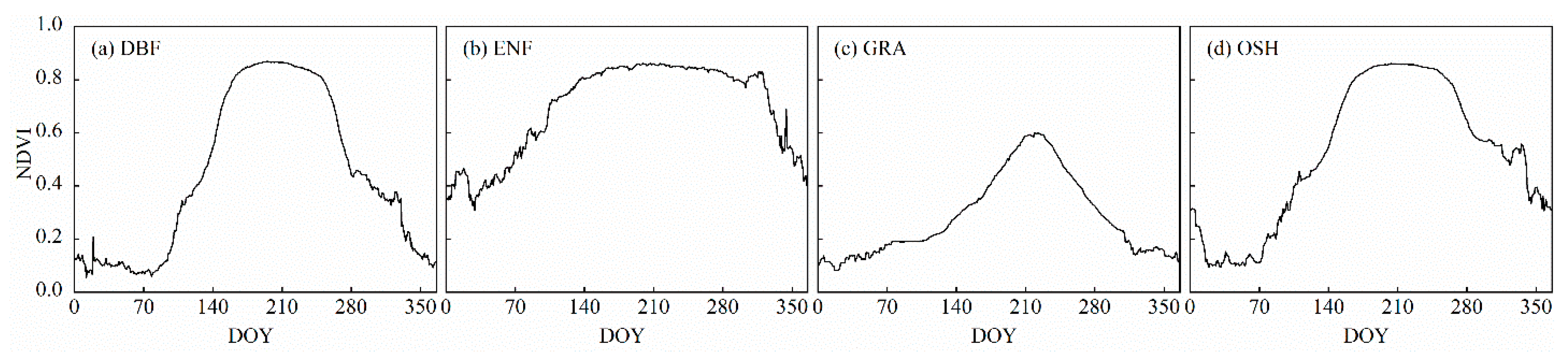
3.2. Comparisons between Trends from Daily NDVI Data and NDVI Composites among Different Vegetation Types
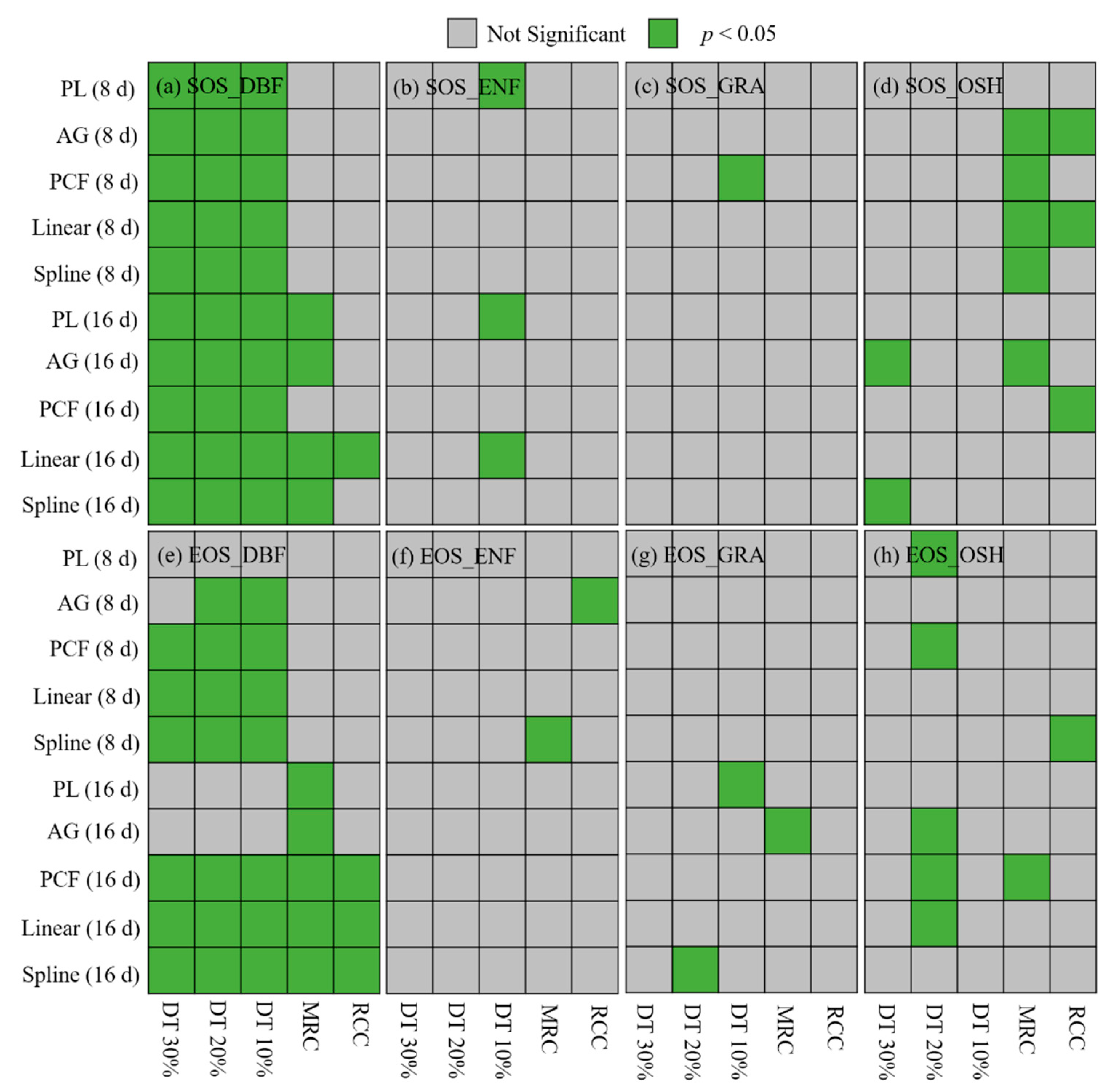
3.3. Comparisons between Trends from Daily NDVI Data and NDVI Composites Based on Different Combinations of Time Interpolation Methods and Phenology Extraction Methods
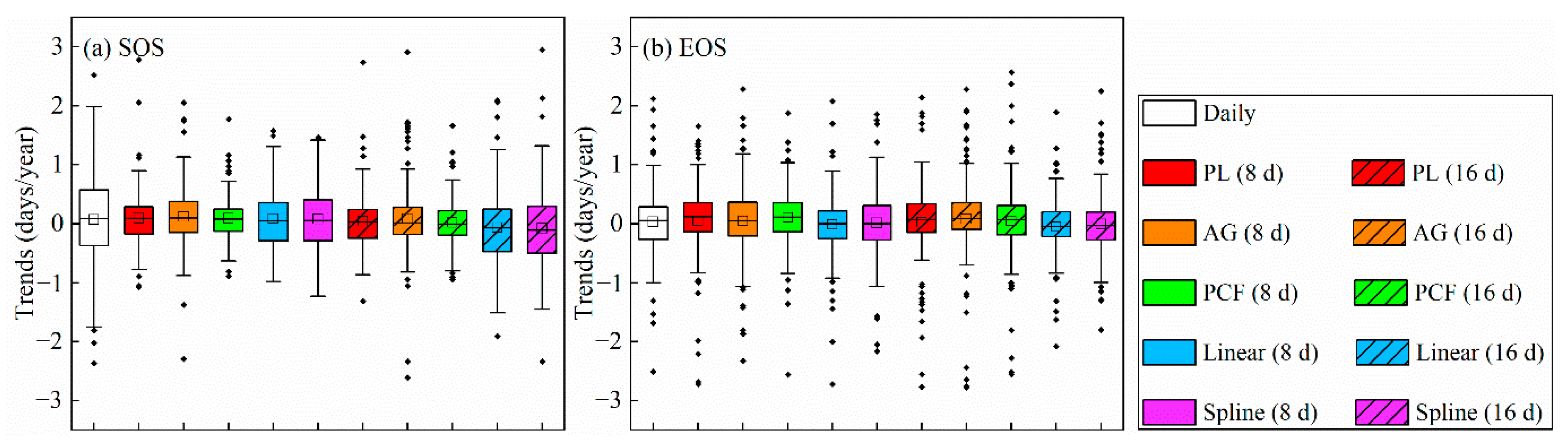
3.4. Comparisons between Trends from the 8-Day and the 16-Day NDVI Composite Data
4. Discussion
4.1. Effects of Time Interpolation on Trend Estimation among Different Interpolation Methods
4.2. Effects of Time Interpolation on Trend Estimation among Different Vegetation Types
4.3. Effects of Time Interpolation on Trend Estimation among Different Combinations of Time Interpolation Methods and Phenology Extraction Methods
4.4. Effects of Time Interpolation on Trend Estimation among Data with Different Temporal Resolutions
4.5. Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- White, M.A.; Thornton, P.E.; Running, S.W. A continental phenology model for monitoring vegetation responses to interannual climatic variability. Glob. Biogeochem. Cycle 1997, 11, 217–234. [Google Scholar] [CrossRef]
- Richardson, A.D.; Bailey, A.S.; Denny, E.G.; Martin, C.W.; O'Keefe, J. Phenology of a northern hardwood forest canopy. Glob. Chang. Biol. 2006, 12, 1174–1188. [Google Scholar] [CrossRef] [Green Version]
- Fu, Y.S.H.; Piao, S.L.; Op de Beeck, M.; Cong, N.; Zhao, H.F.; Zhang, Y.; Menzel, A.; Janssens, I.A. Recent spring phenology shifts in western Central Europe based on multiscale observations. Glob. Ecol. Biogeogr. 2014, 23, 1255–1263. [Google Scholar] [CrossRef]
- Yang, X.Q.; Wu, J.P.; Chen, X.Z.; Ciais, P.; Maignan, F.; Yuan, W.P.; Piao, S.L.; Yang, S.; Gong, F.X.; Su, Y.X.; et al. A comprehensive framework for seasonal controls of leaf abscission and productivity in evergreen broadleaved tropical and subtropical forests. Innovation 2021, 2, 1–7. [Google Scholar] [CrossRef]
- Piao, S.L.; Ciais, P.; Friedlingstein, P.; Peylin, P.; Reichstein, M.; Luyssaert, S.; Margolis, H.; Fang, J.Y.; Barr, A.; Chen, A.P.; et al. Net carbon dioxide losses of northern ecosystems in response to autumn warming. Nature 2008, 451, 49–52. [Google Scholar] [CrossRef]
- Peñuelas, J.; Rutishauser, T.; Filella, I. Phenology Feedbacks on Climate Change. Science 2009, 324, 887–888. [Google Scholar] [CrossRef] [Green Version]
- Dragoni, D.; Schmid, H.P.; Wayson, C.A.; Potter, H.; Grimmond, C.S.B.; Randolph, J.C. Evidence of increased net ecosystem productivity associated with a longer vegetated season in a deciduous forest in south-central Indiana, USA. Glob. Chang. Biol. 2011, 17, 886–897. [Google Scholar] [CrossRef]
- Zhu, Y.X.; Zhang, Y.J.; Zu, J.X.; Wang, Z.P.; Huang, K.; Cong, N.; Tang, Z. Effects of data temporal resolution on phenology extractions from the alpine grasslands of the Tibetan Plateau. Ecol. Indic. 2019, 104, 365–377. [Google Scholar] [CrossRef]
- Gu, F.X. Parameterization of Leaf Phenology for the Terrestrial Ecosystem Models. Prog. Geogr. 2006, 25, 68–75. [Google Scholar]
- Walther, G.R.; Post, E.; Convey, P.; Menzel, A.; Parmesan, C.; Beebee, T.J.C.; Fromentin, J.M.; Hoegh-Guldberg, O.; Bairlein, F. Ecological responses to recent climate change. Nature 2002, 416, 389–395. [Google Scholar] [CrossRef]
- Justice, C.O.; Townshend, J.R.G.; Holben, B.N.; Tucker, C.J. Analysis of the Phenology of Global Vegetation Using Meteorological Satellite Data. Int. J. Remote Sens. 1985, 6, 1271–1318. [Google Scholar] [CrossRef]
- Myneni, R.B.; Keeling, C.D.; Tucker, C.J.; Asrar, G.; Nemani, R.R. Increased plant growth in the northern high latitudes from 1981 to 1991. Nature 1997, 386, 698–702. [Google Scholar] [CrossRef]
- White, M.A.; Hoffman, F.; Hargrove, W.W.; Nemani, R.R. A global framework for monitoring phenological responses to climate change. Geophys. Res. Lett. 2005, 32, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.Y.; Friedl, M.A.; Schaaf, C.B. Global vegetation phenology from Moderate Resolution Imaging Spectroradiometer (MODIS): Evaluation of global patterns and comparison with in situ measurements. J. Geophys. Res. 2006, 111, 1–14. [Google Scholar] [CrossRef]
- Zhu, W.Q.; Tian, H.Q.; Xu, X.F.; Pan, Y.Z.; Chen, G.S.; Lin, W.P. Extension of the growing season due to delayed autumn over mid and high latitudes in North America during 1982–2006. Glob. Ecol. Biogeogr. 2012, 21, 260–271. [Google Scholar] [CrossRef]
- Yang, Y.T.; Guan, H.D.; Shen, M.G.; Liang, W.; Jiang, L. Changes in autumn vegetation dormancy onset date and the climate controls across temperate ecosystems in China from 1982 to 2010. Glob. Chang. Biol. 2015, 21, 652–665. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Liu, L.L.; Liu, Y.; Jayavelu, S.; Wang, J.M.; Moon, M.; Henebry, G.M.; Friedl, M.A.; Schaaf, C.B. Generation and evaluation of the VIIRS land surface phenology product. Remote Sens. Environ. 2018, 216, 212–229. [Google Scholar] [CrossRef]
- Peng, D.L.; Wang, Y.; Xian, G.; Huete, A.R.; Huang, W.J.; Shen, M.G.; Wang, F.M.; Yu, L.; Liu, L.Y.; Xie, Q.Y.; et al. Investigation of land surface phenology detections in shrublands using multiple scale satellite data. Remote Sens. Environ. 2021, 252, 112133. [Google Scholar] [CrossRef]
- Wu, W.; Sun, Y.; Xiao, K.; Xin, Q.C. Development of a global annual land surface phenology dataset for 1982–2018 from the AVHRR data by implementing multiple phenology retrieving methods. Int. J. Appl. Earth Obs. Geoinf. 2021, 103, 102487. [Google Scholar] [CrossRef]
- White, M.A.; de Beurs, K.M.; Didan, K.; Inouye, D.W.; Richardson, A.D.; Jensen, O.P.; O’Keefe, J.; Zhang, G.; Nemani, R.R.; van Leeuwen, W.J.D.; et al. Intercomparison, interpretation, and assessment of spring phenology in North America estimated from remote sensing for 1982–2006. Glob. Chang. Biol. 2009, 15, 2335–2359. [Google Scholar] [CrossRef]
- Hill, M.J.; Roman, M.O.; Schaaf, C.B.; Hutley, L.; Brannstrom, C.; Etter, A.; Hanan, N.P. Characterizing vegetation cover in global savannas with an annual foliage clumping index derived from the MODIS BRDF product. Remote Sens. Environ. 2011, 115, 2008–2024. [Google Scholar] [CrossRef]
- Wang, Y.T.; Hou, X.Y.; Wang, M.J.; Wu, L.; Ying, L.L.; Feng, Y.Y. Topographic controls on vegetation index in a hilly landscape: A case study in the Jiaodong Peninsula, eastern China. Environ. Earth Sci. 2013, 70, 625–634. [Google Scholar] [CrossRef]
- Soudani, K.; Hmimina, G.; Delpierre, N.; Pontailler, J.Y.; Aubinet, M.; Bonal, D.; Caquet, B.; de Grandcourt, A.; Burban, B.; Flechard, C.; et al. Ground-based Network of NDVI measurements for tracking temporal dynamics of canopy structure and vegetation phenology in different biomes. Remote Sens. Environ. 2012, 123, 234–245. [Google Scholar] [CrossRef]
- Hartfield, K.A.; Marsh, S.E.; Kirk, C.D.; Carriere, Y. Contemporary and historical classification of crop types in Arizona. Int. J. Remote Sens. 2013, 34, 6024–6036. [Google Scholar] [CrossRef]
- Hmimina, G.; Dufrene, E.; Pontailler, J.Y.; Delpierre, N.; Aubinet, M.; Caquet, B.; de Grandcourt, A.; Burban, B.; Flechard, C.; Granier, A.; et al. Evaluation of the potential of MODIS satellite data to predict vegetation phenology in different biomes: An investigation using ground-based NDVI measurements. Remote Sens. Environ. 2013, 132, 145–158. [Google Scholar] [CrossRef]
- Ding, C.; Liu, X.N.; Huang, F.; Li, Y.; Zou, X.Y. Onset of drying and dormancy in relation to water dynamics of semi-arid grasslands from MODIS NDWI. Agric. For. Meteorol. 2017, 234, 22–30. [Google Scholar] [CrossRef]
- Testa, S.; Soudani, K.; Boschetti, L.; Mondino, E.B. MODIS-derived EVI, NDVI and WDRVI time series to estimate phenological metrics in French deciduous forests. Int. J. Appl. Earth Obs. Geoinf. 2018, 64, 132–144. [Google Scholar] [CrossRef]
- Huang, K.; Zhang, Y.J.; Tagesson, T.; Brandt, M.; Wang, L.H.; Chen, N.; Zu, J.X.; Jin, H.X.; Cai, Z.Z.; Tong, X.W.; et al. The confounding effect of snow cover on assessing spring phenology from space: A new look at trends on the Tibetan Plateau. Sci. Total Environ. 2021, 756, 144011. [Google Scholar] [CrossRef]
- Fan, D.Q.; Zhao, X.S.; Zhu, W.Q.; Zheng, Z.T. Review of influencing factors of accuracy of plant phenology monitoring based on remote sensing data. Prog. Geogr. 2016, 35, 304–319. [Google Scholar]
- Brown, M.E.; Pinzon, J.E.; Didan, K.; Morisette, J.T.; Tucker, C.J. Evaluation of the consistency of long-term NDVI time series derived from AVHRR, SPOT-Vegetation, SeaWiFS, MODIS, and Landsat ETM+ sensors. IEEE Trans. Geosci. Electron. 2006, 44, 1787–1793. [Google Scholar] [CrossRef]
- Garrity, S.R.; Bohrer, G.; Maurer, K.D.; Mueller, K.L.; Vogel, C.S.; Curtis, P.S. A comparison of multiple phenology data sources for estimating seasonal transitions in deciduous forest carbon exchange. Agric. For. Meteorol. 2011, 151, 1741–1752. [Google Scholar] [CrossRef]
- Zhang, G.L.; Zhang, Y.J.; Dong, J.W.; Xiao, X.M. Green-up dates in the Tibetan Plateau have continuously advanced from 1982 to 2011. Proc. Natl. Acad. Sci. USA 2013, 110, 4309–4314. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shen, M.G.; Zhang, G.X.; Cong, N.; Wang, S.P.; Kong, W.D.; Piao, S.L. Increasing altitudinal gradient of spring vegetation phenology during the last decade on the Qinghai-Tibetan Plateau. Agric. For. Meteorol. 2014, 189, 71–80. [Google Scholar] [CrossRef]
- Donnelly, A.; Liu, L.L.; Zhang, X.Y.; Wingler, A. Autumn leaf phenology: Discrepancies between in situ observations and satellite data at urban and rural sites. Int. J. Remote Sens. 2018, 39, 8129–8150. [Google Scholar] [CrossRef]
- Donnelly, A.; Yu, R.; Liu, L.L. Comparing in situ spring phenology and satellite-derived start of season at rural and urban sites in Ireland. Int. J. Remote Sens. 2021, 42, 7821–7841. [Google Scholar] [CrossRef]
- Peng, D.L.; Zhang, X.Y.; Wu, C.Y.; Huang, W.J.; Gonsamo, A.; Huete, A.R.; Didan, K.; Tan, B.; Liu, X.J.; Zhang, B. Intercomparison and evaluation of spring phenology products using National Phenology Network and AmeriFlux observations in the contiguous United States. Agric. For. Meteorol. 2017, 242, 33–46. [Google Scholar] [CrossRef] [Green Version]
- Zeng, H.Q.; Jia, G.S.; Forbes, B.C. Shifts in Arctic phenology in response to climate and anthropogenic factors as detected from multiple satellite time series. Environ. Res. 2013, 8, 035036. [Google Scholar] [CrossRef]
- Zeng, H.Q.; Jia, G.S.; Epstein, H. Recent changes in phenology over the northern high latitudes detected from multi-satellite data. Res. Lett. 2011, 6, 045508. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Liu, H.Y.; Huang, N.; Bi, J.; Ma, X.L.; Ma, Z.Y.; Shangguan, Z.J.; Zhao, H.F.; Feng, Q.S.; Liang, T.G.; et al. Satellite-derived NDVI underestimates the advancement of alpine vegetation growth over the past three decades. Ecology 2021, 102, e03518. [Google Scholar] [CrossRef] [PubMed]
- Beurs, K.M.d.; Henebry, G.M. Spatio-temporal statistical methods for modeling land surface phenology. In Phenological Research; Hudson, I., Keatley, M., Eds.; Springer: Dordrecht, The Netherlands, 2010; pp. 177–208. [Google Scholar]
- White, K.; Pontius, J.; Schaberg, P. Remote sensing of spring phenology in northeastern forests: A comparison of methods, field metrics and sources of uncertainty. Remote Sens. Environ. 2014, 148, 97–107. [Google Scholar] [CrossRef]
- Cong, N.; Shen, M.G.; Piao, S.L. Spatial variations in responses of vegetation autumn phenology to climate change on the Tibetan Plateau. J. Plant Ecol. 2017, 10, 744–752. [Google Scholar] [CrossRef] [Green Version]
- Shen, R.Q.; Lu, H.B.; Yuan, W.P.; Chen, X.Z.; He, B. Regional evaluation of satellite-based methods for identifying end of vegetation growing season. Remote Sens. Ecol. Conserv. 2021, 175, 88–98. [Google Scholar] [CrossRef]
- Holben, B.N. Characteristics of Maximum-Value Composite Images from Temporal Avhrr Data. Int. J. Remote Sens. 1986, 7, 1417–1434. [Google Scholar] [CrossRef]
- Viovy, N.; Arino, O.; Belward, A.S. The best index slope extraction (BISE)-a method for reducing noise in NDVI yime-series. Int. J. Remote Sens. 1992, 13, 1585–1590. [Google Scholar] [CrossRef]
- Taddei, R. Maximum value interpolated (MVI): A maximum value composite method improvement in vegetation index profiles analysis. Int. J. Remote Sens. 1997, 18, 2365–2370. [Google Scholar] [CrossRef]
- Ma, M.G.; Veroustraete, F. Reconstructing pathfinder AVHRR land NDVI time-series data for the Northwest of China. Adv. Space Res. 2006, 37, 835–840. [Google Scholar] [CrossRef]
- Julien, Y.; Sobrino, J.A. Comparison of cloud-reconstruction methods for time series of composite NDVI data. Remote Sens. Environ. 2010, 114, 618–625. [Google Scholar] [CrossRef]
- Fan, X.W.; Liu, Y.B.; Wu, G.P.; Zhao, X.S. Compositing the minimum NDVI for daily water surface mapping. Remote Sens. 2020, 12, 700. [Google Scholar] [CrossRef] [Green Version]
- Piao, S.L.; Fang, J.Y.; Zhou, L.M.; Ciais, P.; Zhu, B. Variations in satellite-derived phenology in China’s temperate vegetation. Glob. Chang. Biol. 2006, 12, 672–685. [Google Scholar] [CrossRef]
- Liu, Q.; Fu, Y.S.H.; Zeng, Z.Z.; Huang, M.T.; Li, X.R.; Piao, S.L. Temperature, precipitation, and insolation effects on autumn vegetation phenology in temperate China. Glob. Chang. Biol. 2016, 22, 644–655. [Google Scholar] [CrossRef] [PubMed]
- Jeong, S.J.; Ho, C.H.; Gim, H.J.; Brown, M.E. Phenology shifts at start vs. end of growing season in temperate vegetation over the Northern Hemisphere for the period 1982–2008. Glob. Chang. Biol. 2011, 17, 2385–2399. [Google Scholar] [CrossRef]
- Liang, L.A.; Schwartz, M.D.; Fei, S.L. Validating satellite phenology through intensive ground observation and landscape scaling in a mixed seasonal forest. Remote Sens. Environ. 2011, 115, 143–157. [Google Scholar] [CrossRef]
- Meijering, E. A chronology of interpolation: From ancient astronomy to modern signal and image processing. Proc. IEEE 2002, 90, 319–342. [Google Scholar] [CrossRef] [Green Version]
- Wolberg, G.; Alfy, I. Monotonic cubic spline interpolation. Comput. Graph. Int. 1999, 188–195. [Google Scholar]
- Jönsson, P.; Eklundh, L. Seasonality extraction by function fitting to time-series of satellite sensor data. IEEE Trans. Geosci. Remote Sensing. 2002, 40, 1824–1832. [Google Scholar] [CrossRef]
- Beck, P.S.A.; Atzberger, C.; Hogda, K.A.; Johansen, B.; Skidmore, A.K. Improved monitoring of vegetation dynamics at very high latitudes: A new method using MODIS NDVI. Remote Sens. Environ. 2006, 100, 321–334. [Google Scholar] [CrossRef]
- Chen, J.; Jönsson, P.; Tamura, M.; Gu, Z.H.; Matsushita, B.; Eklundh, L. A simple method for reconstructing a high-quality NDVI time-series data set based on the Savitzky-Golay filter. Remote Sens. Environ. 2004, 91, 332–344. [Google Scholar] [CrossRef]
- Cong, N.; Piao, S.L.; Chen, A.P.; Wang, X.H.; Lin, X.; Chen, S.P.; Han, S.J.; Zhou, G.S.; Zhang, X.P. Spring vegetation green-up date in China inferred from SPOT NDVI data: A multiple model analysis. Agric. For. Meteorol. 2012, 165, 104–113. [Google Scholar] [CrossRef]
- Kross, A.; Fernandes, R.; Seaquist, J.; Beaubien, E. The effect of the temporal resolution of NDVI data on season onset dates and trends across Canadian broadleaf forests. Remote Sens. Environ. 2011, 115, 1564–1575. [Google Scholar] [CrossRef]
- Slayback, D.A.; Pinzon, J.E.; Los, S.O.; Tucker, C.J. Northern hemisphere photosynthetic trends 1982-99. Glob. Chang. Biol. 2003, 9, 1–15. [Google Scholar] [CrossRef]
- Klosterman, S.T.; Hufkens, K.; Gray, J.M.; Melaas, E.; Sonnentag, O.; Lavine, I.; Mitchell, L.; Norman, R.; Friedl, M.A.; Richardson, A.D. Evaluating remote sensing of deciduous forest phenology at multiple spatial scales using PhenoCam imagery. Biogeoences. 2014, 11, 4305–4320. [Google Scholar] [CrossRef] [Green Version]
- Zhou, L.; Kaufmann, R.K.; Tian, Y.; Myneni, R.B.; Tucker, C.J. Relation between interannual variations in satellite measures of northern forest greenness and climate between 1982 and 1999. J. Geophys. Res. 2003, 108, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Ding, M.J.; Zhang, Y.L.; Sun, X.M.; Liu, L.S.; Wang, Z.F.; Bai, W.Q. Spatiotemporal variation in alpine grassland phenology in the Qinghai-Tibetan Plateau from 1999 to 2009. Chin. Sci. Bull. 2013, 58, 396–405. [Google Scholar] [CrossRef] [Green Version]
- Zu, J.X.; Zhang, Y.J.; Huang, K.; Liu, Y.J.; Chen, N.; Cong, N. Biological and climate factors co-regulated spatial-temporal dynamics of vegetation autumn phenology on the Tibetan Plateau. Int. J. Appl. Earth Obs. Geoinf. 2018, 69, 198–205. [Google Scholar] [CrossRef]
- Kwak, S.G.; Kim, J.H. Central limit theorem: The cornerstone of modern statistics. Korean J. Anesthesiol. 2017, 70, 144–156. [Google Scholar] [CrossRef] [PubMed]
- Bradley, B.A.; Jacob, R.W.; Hermance, J.F.; Mustard, J.F. A curve fitting procedure to derive inter-annual phenologies from time series of noisy satellite NDVI data. Remote Sens. Environ. 2007, 106, 137–145. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Hird, J.N.; McDermid, G.J. Noise reduction of NDVI time series: An empirical comparison of selected techniques. Remote Sens. Environ. 2009, 113, 248–258. [Google Scholar] [CrossRef]
- Chen, Y.; Cao, R.Y.; Chen, J.; Liu, L.C.; Matsushita, B. A practical approach to reconstruct high-quality Landsat NDVI time-series data by gap filling and the Savitzky-Golay filter. ISPRS-J. Photogramm. Remote Sens. 2021, 180, 174–190. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Friedl, M.A.; Schaaf, C.B.; Strahler, A.H.; Hodges, J.C.F.; Gao, F.; Reed, B.C.; Huete, A. Monitoring vegetation phenology using MODIS. Remote Sens. Environ. 2003, 84, 471–475. [Google Scholar] [CrossRef]
- Heumann, B.W.; Seaquist, J.W.; Eklundh, L.; Jönsson, P. AVHRR derived phenological change in the Sahel and Soudan, Africa, 1982–2005. Remote Sens. Environ. 2007, 108, 385–392. [Google Scholar] [CrossRef]
- Yu, H.Y.; Luedeling, E.; Xu, J.C. Winter and spring warming result in delayed spring phenology on the Tibetan Plateau. Proc. Natl. Acad. Sci. USA 2010, 107, 22151–22156. [Google Scholar] [CrossRef] [Green Version]
- Schaber, J.; Badeck, F.W. Evaluation of methods for the combination of phenological time series and outlier detection. Tree Physiol. 2002, 22, 973–982. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, X.X.; Cui, Y.P.; Liu, S.J.; Li, N.; Fu, Y.M. Evaluation of the accuracy of phenology extraction methods for natural vegetation based on remote sensing. Chin. J. Ecol. 2019, 38, 1589–1599. [Google Scholar]
- Li, N.; Zhan, P.; Pan, Y.Z.; Zhu, X.F.; Li, M.Y.; Zhang, D.J. Comparison of Remote Sensing Time-Series Smoothing Methods for Grassland Spring Phenology Extraction on the Qinghai-Tibetan Plateau. Remote Sens. 2020, 12, 3383. [Google Scholar] [CrossRef]
- Menzel, A.; Sparks, T.H.; Estrella, N.; Koch, E.; Aasa, A.; Ahas, R.; Alm-Kubler, K.; Bissolli, P.; Braslavska, O.; Briede, A.; et al. European phenological response to climate change matches the warming pattern. Glob. Chang. Biol. 2006, 12, 1969–1976. [Google Scholar] [CrossRef]
- Steltzer, H.; Post, E. Seasons and Life Cycles. Science 2009, 324, 886–887. [Google Scholar] [CrossRef]
- Jin, H.X.; Jonsson, A.M.; Olsson, C.; Lindstrom, J.; Jonsson, P.; Eklundh, L. New satellite-based estimates show significant trends in spring phenology and complex sensitivities to temperature and precipitation at northern European latitudes. Int. J. Biometeorol. 2019, 63, 763–775. [Google Scholar] [CrossRef] [Green Version]
- Li, H.B.; Wang, C.Z.; Zhang, L.J.; Li, X.X.; Zang, S.Y. Satellite monitoring of boreal forest phenology and its climatic responses in Eurasia. Int. J. Remote Sens. 2017, 38, 5446–5463. [Google Scholar] [CrossRef]



| Method | Equation | Parameter |
|---|---|---|
| Savitzky-Golay filter | Y* is the resultant NDVI value; Y is the original NDVI value; j is the running index of the original ordinate data; m is the half-width of the smoothing window (filter); Ci is the coefficient for the ith NDVI value of the filter; N is the amount of convoluting integers; the half-width of the smoothing window is set to 1/4 of the year length (90 days); the smoothing polynomial degree is set to 4 [58]. | |
| Maximum value composite | ynew is the resultant NDVI value; yn is the original NDVI value; n is the days for compositing. |
| Method | Equation | Parameter |
|---|---|---|
| Piecewise logistic function fitting (PL) | y(t) is the resultant NDVI value at time t; t is the Julian days; a and b are fitting parameters; c is the amplitude of the NDVI curve; d is the minimum NDVI value [71]. | |
| Asymmetric Gaussian function fitting (AG) | y(t) is the resultant NDVI value at time t; g(t) is the original NDVI value; wNDVI and mNDVI are the minimum and maximum NDVI value of the fitting part; a1 is the position of the maximum or minimum value with respect to time t; a2 (a4) and a3 (a5) are the width and flatness of the right (left) half of the function [56]. | |
| Polynomial curve fitting (PCF) | y(t) is the resultant NDVI value at time t; t is the Julian days; α0-αn are fitting parameters; n is the degree of smoothing polynomial; the smoothing polynomial degree is set to 6 [50]. | |
| Linear interpolation (Linear) | y(t) is the resultant NDVI value at time t; t0 and t1 are the nearest day of year (DOY) of the missing value; y0 and y1 are the nearest NDVI of the missing value; t is the DOY of the interpolating point between t0 and t1. | |
| Cubic spline interpolation (Spline) | yi(t) is the resultant NDVI value at time t in the ith period; t is the interpolating point between ti and ti+1; a-d are function parameters decided by the DOY and NDVI matrix calculation results in the ith period and the (I + 1) th period. |
| Method | Equation | Parameter |
|---|---|---|
| Dynamic threshold (DT) | NDVI(t) is the original NDVI value at time t; NDVImax is the maximum value of the entire curve; NDVImin is the minimum value of the left/right curve (divided by the maximum NDVI); thd is the output ratio, ranging from 0–1 [56]. | |
| Maximum rate of change (MRC) | NDVI(t) is the original NDVI value at time t; NDVI (t+1) is the original NDVI value at time t+1; NDVIratio(t) is the NDVI ratio at time t [50]. | |
| Change rate of curvature (RCC) | NDVI(t) is the rate of change of curve at time t; y(t)′ and y(t)″ are the first and the second derivative of curve at time t [71]. |
| Number | Temporal Resolution | Time Interpolation Methods | Phenology Extraction Methods |
|---|---|---|---|
| (1) | 1 d vs. 8 d, 1 d vs. 16 d | PL, AG, PCF, Linear, Spline | Mean of DT, MRC, and RCC |
| (2) | 1 d vs. 8 d, 1 d vs. 16 d | PL, AG, PCF, Linear, Spline | DT, MRC, RCC |
| (3) | 8 d vs. 16 d | PL, AG, PCF, Linear, Spline | Mean of DT, MRC, and RCC |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Zhu, W.; Xie, Z.; Zhan, P.; Huang, X.; Sun, L.; Duan, Z. Assessing the Effects of Time Interpolation of NDVI Composites on Phenology Trend Estimation. Remote Sens. 2021, 13, 5018. https://doi.org/10.3390/rs13245018
Li X, Zhu W, Xie Z, Zhan P, Huang X, Sun L, Duan Z. Assessing the Effects of Time Interpolation of NDVI Composites on Phenology Trend Estimation. Remote Sensing. 2021; 13(24):5018. https://doi.org/10.3390/rs13245018
Chicago/Turabian StyleLi, Xueying, Wenquan Zhu, Zhiying Xie, Pei Zhan, Xin Huang, Lixin Sun, and Zheng Duan. 2021. "Assessing the Effects of Time Interpolation of NDVI Composites on Phenology Trend Estimation" Remote Sensing 13, no. 24: 5018. https://doi.org/10.3390/rs13245018
APA StyleLi, X., Zhu, W., Xie, Z., Zhan, P., Huang, X., Sun, L., & Duan, Z. (2021). Assessing the Effects of Time Interpolation of NDVI Composites on Phenology Trend Estimation. Remote Sensing, 13(24), 5018. https://doi.org/10.3390/rs13245018