Abstract
In recent years, technology advancement has led to an enormous increase in the amount of satellite data. The availability of huge datasets of remote sensing measurements to be processed, and the increasing need for near-real-time data analysis for operational uses, has fostered the development of fast, efficient-retrieval algorithms. Deep learning techniques were recently applied to satellite data for retrievals of target quantities. Forward models (FM) are a fundamental part of retrieval code development and mission design, as well. Despite this, the application of deep learning techniques to radiative transfer simulations is still underexplored. The DeepLIM project, described in this work, aimed at testing the feasibility of the application of deep learning techniques at the design of the retrieval chain of an upcoming satellite mission. The Land Surface Temperature Mission (LSTM) is a candidate for Sentinel 9 and has, as the main target, the need, for the agricultural community, to improve sustainable productivity. To do this, the mission will carry a thermal infrared sensor to retrieve land-surface temperature and evapotranspiration rate. The LSTM land-surface temperature retrieval chain is used as a benchmark to test the deep learning performances when applied to Earth observation studies. Starting from aircraft campaign data and state-of-the-art FM simulations with the DART model, deep learning techniques are used to generate new spectral features. Their statistical behavior is compared to the original technique to test the generation performances. Then, the high spectral resolution simulations are convolved with LSTM spectral response functions to obtain the radiance in the LSTM spectral channels. Simulated observations are analyzed using two state-of-the-art retrieval codes and deep learning-based algorithms. The performances of deep learning algorithms show promising results for both the production of simulated spectra and target parameters retrievals, one of the main advances being the reduction in computational costs.
1. Introduction
Simulation of instrumental satellite observations is a crucial step in satellite mission developments. The radiance that reaches the sensor can be simulated by radiative transfer models (RTMs). RTMs are used in the prelaunch phase to study the feasibility of a mission, to assess its requirements and its target sensitivity, and, finally, to develop the target retrieval chain. Several forward models (FMs) have been developed during the past decades to model sensor observations in different spectral ranges, accounting for different physical processes (e.g., thermal or solar radiation contribution, molecular or particle scattering, line mixing, etc.). Focusing on the thermal infrared (TIR) spectral region, the main contribution comes from thermal emissions of Earth’s surface and atmosphere. In this region, gases act as emitters/absorbers but do not contribute to scattering due to their dimensions with respect to TIR wavelengths, so that scattering contribution is mainly due to dust/volcanic aerosols and cloud particles. The accurate modeling of atmosphere TIR scattering requires computationally expensive FMs. Some fast models were developed to overcome this issue (e.g., Radiative Transfer for TOVS (RTTOV, [1]), σ-IASI, [2]) and are mainly based on parameterization of heavy computation line-by-line (LBL) FM. Due to the inclusion, at different levels, of FM simulations into retrieval codes developments, to the exponentially increasing availability of satellite data, and the need for near-real-time (NRT) data analysis, the development of computationally fast FM and inversion models is becoming an urgent need.
In recent years, there has been a growing interest in deep learning algorithms to solve this issue, and the development of these tools is rapidly advancing. Recently, deep learning algorithms have been applied to different fields of Earth observations. Applications are found for terrestrial vegetation monitoring [3], satellite images analysis for land classifications, cultural heritage preservation, soil erosion [4], and floods [5].
While all these applications refer to the processing of satellite images (characterized by high spatial resolution and low spectral resolution), at the moment, none of these works explores the possibility of applying the techniques to spectrally resolved measurements. In addition, these applications mainly involve the retrieval part of the process, while the forward one is left to full-physics state-of-the-art techniques. Innovative deep learning techniques, known as generative adversarial nets (GANs [6]), can be used to explore this part of the process.
GANs are neural networks to be trained with an unsupervised approach. They are composed of two sub-models: the generator that is trained to generate new examples, and the discriminator that is trained to classify the examples as real (coming from the original domain) or false (generated by the neural net). The two models are trained together in a zero-sum, known as a contradictory game, until the discriminator model classifies the examples created by the generator as true, which means that the generating model is generating plausible examples. GANs are very versatile and suitable for multiple domains. Auto encoders (AEs) are a particular type of artificial neural network (ANN) model. Those structures are capable of automatic encoding of the data provided as input [7]. This encoding represents a continuous latent space which conserves the characteristics of data provided during training, however with lower dimensionality. That is why AEs are commonly used for image compression [8], data reduction [7], or for semantic segmentation [9]. Moreover, the exploitation of the latent space exploration constitutes an additional class of generative models, alternative to GANs, known as variational autoencoders (VAEs) [10].
In this context, the DeepLIM ESA project aims at demonstrating the applicability of deep learning algorithms to both high-resolution spectra generation (in support of full-physics FMs) and retrieval algorithms, for the possible future application in satellite mission end-to-end simulators. As an example, in this work, we simulate the Land Surface Temperature Mission (LSTM, candidate to Sentinel 9, [11]) retrieval chain. The LSTM will carry a high-spatial–temporal-resolution thermal infrared sensor to provide observations of land-surface temperature and evapotranspiration rate. The mission responds to priority requirements of the agricultural user community for improving sustainable agricultural productivity at field scale in a world of increasing water scarcity and variability [12].
In this work, we use the deep learning algorithms to generate the reliable spectral signature in the infrared without time-expensive computing RTM, and build a NN retrieval code. The performances of this code are compared to those of state-of-the-art codes. The paper, which describes the main outcomes of the DeepLIM project, is structured as follows: Section 2 briefly describes the original spectral datasets and presents the full-physics and deep learning-based methods and algorithms developed during this work for dataset augmentation and land-surface temperature (LST) retrieval. Results are given in Section 3. Finally, discussion is reported in Section 4 and concluding remarks are given in Section 5.
2. Materials and Methods
Starting from provided datasets of high-resolution spectra in the TIR, produced with state-of-the-art FM and obtained from aircraft campaign data, we generate new spectral features using deep learning algorithms. The original and generated spectra are then convolved with LSTM spectral response functions (SRFs) for the five channels at 8.6, 8.9, 9.2, 11, and 12 µm, and noise is added. The used SRFs are preliminary simulations of the LSTM response that does not include modeling the final instrument behavior. These five channels for top of the atmosphere (TOA) and bottom of the atmosphere (BOA) brightness temperatures (BTs) are then used to study the LSTM LST retrieval chain with both full-physics state-of-the-art and deep learning newly developed inversion models.
2.1. Used Datasets
The starting point for the generation of the satellite BTs are radiances produced with a full-physics FM and data measured during an aircraft campaign. Using data from two different sources and produced in a completely different way allows for a better inspection of the potential of deep learning techniques for data generation under different underlying conditions.
These two datasets have higher spectral resolution with respect to the satellite channels. Therefore, before processing, they are convolved with the LSTM SRF. The availability of spectrally resolved radiances allows evaluating of the impact of different SRF if needed. After convolution, a noise level, considered as representative for the LSTM instrument (from ESA project “Assessment of the potential use of the high-resolution Thermal Infra-Red (TIR) band: ESA ITT AO/1-8733/16/NL/AF/eg”, see also the LSTM Mission Requirement Document (MRD) [13]), is added to the obtained channel BTs.
The two following sections describe the original dataset of simulated radiances (then named as “DART dataset”) and one of the aircraft measurements (then named as “TASI dataset”).
2.1.1. DART Dataset
The Discrete Anisotropic Radiative Transfer (DART [14], https://dart.omp.eu, accessed on 2 December 2021) model is one of the most comprehensive physically-based 3D models simulating the Earth–atmosphere radiation interaction from visible to thermal infrared wavelengths. In the frame of the ESA project “Assessment of the potential use of the high-resolution Thermal Infra-Red (TIR) band: ESA ITT AO/1-8733/16/NL/AF/eg”, the DART model has been used to simulate the BOA and TOA spectral radiance (1200 bands from 7 to 13 µm, with 0.005 µm spectral resolution) of agricultural, tree plantation, and urban landscapes. For that, DART created three-dimensional (3D) mock-ups of these landscapes and simulated their BOA and TOA radiance for a large number of experimental configurations, as indicated below. Here, we mainly concentrate on two agricultural scenarios.
- Maizefields: the DART maize mock-ups are simulated using parameters that vary around those measured in the maize fields of Barrax (Spain) during the Sentinel-3 experimental campaign carried out by ESA (project SEN3EXP: https://earth.esa.int/eogateway/campaigns/sen3exp, accessed on 2 December 2021) in June–July 2009. Each mock-up is made of the spatial distribution of clones of a single 3D maize plant at a specific growth stage in terms of height and number of leaves, with some variability (e.g., small random azimuthal rotation of the plant). Three standard growth stages are considered according to the Biologische Bundesanstalt, Bundessortenamt, and CHemical industry (BBCH) scale (https://www.openagrar.de/receive/openagrar_mods_00042351, accessed on 2 December 2021). Each maize plant is duplicated along rows with specific distances between plants and rows and is also rotated so that its leaf mean azimuthal direction is perpendicular to the rows. The density of plants combined with the leaf area of each 3D maize plant gives the leaf area density per ground surface (i.e., leaf area index: LAI). Three-row orientations (0, 45, 90) were simulated to consider the influence of sun rays on the distribution of shadows, and consequently on the spatial distribution of leaf and ground thermodynamic temperature. In all, we have 4,082,400 BOA and TOA maize spectra of 1200 bands: 28 viewing directions, five sun directions, three-leaf emissivity spectra, three ground emissivity spectra, three LAI values, three-row orientations, three ranges of leaf thermodynamic temperature (291 K to 315 K), three ranges of ground thermodynamic temperature (283 K to 323 K), two extreme profiles of atmosphere temperature, two extreme aerosol optical depths, and five atmosphere water vapor contents (from 0.9 g/cm to 6 g/cm).
- Wheatfields: they were simulated with the same configurations as the maize fields, apart from the fact that the row effects were not directly simulated. Indeed, DART created wheat 3D mock-ups by importing wheat fields simulated with the “Plantgen-ADEL” model for 500, 700, and 900 degree days ([15,16,17,18]). In all, we have 1,360,800 BOA and TOA wheat spectra of 1200 bands.
A selection of DART spectra from these two scenes is used for data augmentation.
2.1.2. TASI Dataset
The TASI dataset is made of aircraft measurements acquired during the SurfSense 2018 Grosseto campaign in July 2018 in support of LSTM studies [19]. The Thermal Airborne Spectrographic Imager (TASI-600), a push broom hyperspectral thermal sensor [20], measures the radiance between 8 and 11.5 µm with 0.1 µm spectral resolution in 32 spectral bands at metric spatial resolution. The instrument was onboard a Cessna 208B Grand Caravan aircraft.
The dataset is composed of radiances measured by the instrument, the BOA, and the corresponding retrieved land surface emissivity (LSE) and LST from the processing. TASI LSE and LST retrievals are calculated through the application of the Temperature Emissivity Separation (TES) algorithm (https://olc.czechglobe.cz/en/processing/tasi-data-processing/, accessed on 2 December 2021). The LST-derived fields range from 298 K to about 350 K. As it is, the TASI dataset cannot directly be used for satellite data generation since the radiance is acquired at about 3 km aircraft flight altitude instead of TOA, and, also, the full spectral range required by LSTM is not covered. For this reason, we preprocess these data through a full-physics FM to produce data compliant with the DART format at TOA. The description of this procedure is given in Section 2.2.1.
2.2. Datasets and Algorithms
In this section, we describe all the software and the datasets we develop and the methods we use for assessing the quality of the outputs of deep learning algorithms.
2.2.1. Data Preparation: TASI-to-DART: Algorithm Description, Data Selection
TOA signatures are needed by deep learning techniques to create a link between TASI and simulated satellite data for the generation of new signatures. The DART dataset can be used as it is for this task. As said, the TASI dataset needs to be preprocessed.
Thus, we simulate DART-like signatures using a full-physics FM and the TASI dataset. We use the LBL broadband (BB) FM that has been used for the Along-Track Scanning Radiometer simulations ATSR, [21,22,23]. Due to the computing costs of those simulations, we use the BB FM to simulate only a few scenes of the TASI dataset. We use the data of 18 July 2018. During this day, the TASI instrument acquired the data from 11:50 a.m. to 3:24 p.m. (local time) over the Grosseto area [24] at a flight altitude of about 3 km.
The input data, required by the BB FM, are the atmospheric composition and the surface characterization. These inputs should be as close as possible to the real TASI measurement scenario to correctly simulate the Grosseto conditions on 18 July 2018. In particular:
- 1.
- Atmospheric composition: We used European Centre for Medium-range Weather Forecasts (ECMWF) daily profiles of altitude, temperature, pressure, ozone (O), and water vapor volume mixing ratios at 12:00 a.m. All other gases are taken from the IG2 database [25] for mid-latitude in July.
- 2.
- Surface characterization: Emissivity is obtained from TASI LSE retrieval. TASI measurements and LSE retrievals cover up to 11.5 µm. To produce emissivity values up to 13 µm, we extend the value of emissivity at 11.5 µm as we notice that this approximation is valid in most cases. LST is also taken from TASI retrieval. The surface is treated as Lambertian.
We simulate about 800 spectra for three satellite viewing angles, 0, 30, and 50, selecting scenes that preserve, as much as possible, the emissivity and the LST variability observed by TASI during the flight. We perform pencil beam simulations as the field-of-view (FOV) effects are not relevant for the purposes of this work. This dataset is named here as “TASI-to-DART”. Radiance at 3 km is also simulated and compared to the original TASI radiance at the instrument to check the reliability of simulated conditions. BB takes about 30 min to simulate one DART-like feature (TOA, BOA, downward-looking radiance simulated at the same time) at high spectral resolution. Those spectra are then convolved to obtain the spectral resolution of the DART dataset.
An example of the simulated spectra after the spectral convolution at DART resolution is reported in Figure 7b.
2.2.2. Data Augmentation
Once we produce the TASI-to-DART dataset, the datasets generated with full-physics models are ready for data augmentation. We developed two algorithms for this task: the GANDART for the augmentation of the DART dataset and the TASI2DART for the augmentation of the TASI-to-DART dataset. GANDART is based on GANs, while the TASI2DART is an autoencoder. Both GANs and AEs are generative models, meaning that they can learn a given data distribution and use it to generate new samples. The key difference is how they do it: autoencoders learn the data distribution of inputs and map this distribution into latent space, and starting from this space can generate samples; to wrap up the operational principle, AE compresses data in a lower space dimension. GANs use two cooperative neural networks, the generator and the discriminator. Instead of having data as input, the generator samples randomly, in the latent space, morph random noise into fake samples. The discriminator evaluates the “distance” between the generated outputs and some real samples to distinguish between real and fake ones.
We used these two different approaches for data augmentation due to the different sizes of original datasets: the DART dataset, containing more than 50,000 data, is suitable for GANs applications, while for the TASI-to-DART, containing about 1000 data, AE is preferable:
- 1.
- GANDART (GANs DART):The dataset used for training the GANDART is obtained by preprocessing the original DART dataset, cutting the spectra between 8 and 13 µm (900 points instead of 1200 spectral points as in the original dataset) and reshaping from 1D to 2D. The outputs are stacked in three layers for each sample composed of BOA radiance, TOA radiance, and down-looking irradiance. Then, a final scaling between −1 and 1 is performed. GANs are generally superior to AE for data generation. However, they are particularly hard to work with, as they require a lot of data and tuning. Moreover, GANs suffer from a lot of failure modes, and training them is challenging.The GAN developed for the generation of DART signatures adopts a model called Progressive Growing of GANs (PGGANs) [26].PGGANs is an innovative architecture in which the network is progressively trained to grow the dimension of the input. Hence, PGGANs introduce a new effective training approach. The neural network architecture does not change (parameters are the same) and there are no modifications with respect to the vanilla GANs model [6].The generative model starts the training at very low resolution (usually 4 × 4) and keeps improving at a fixed number of iterations (600 k following the original implementation). The resolution is doubled with a fixed schedule. We scale the resolution results in a transition period where the new convolutional layer is added to the network progressively, using a shortcut, similar to that in architectures such as residual networks [27].The advantages of this approach are mainly the reduced training time due to the progressive structure of the network and the sample accuracy. We adopt this architecture to both allow the fast generation of synthetic signatures without requiring long simulation runs and increase the number of samples to train on the deep learning-based inversion model. The algorithm takes about 0.57 s to generate one signature.The GANDART generator is able to create new samples (without a simulation required) to be used for training the deep learning-based inversion model or for directly performing a retrieval. The obtained training set has a 2D dimension (30 × 30 × 3) ready to be fed to the PGGANs model. A postprocessor reshapes the output of the generated samples, obtaining a 1-dimensional output of (900 × 3, respectively BOA, TOA, and downward irradiance at BOA).The updated version of PGGANs was initially implemented by [26] with StyleGAN. The proposed model introduced major improvements with respect to the original PGGANs. It maintained the progressive technology, reducing the training time. However, a series of changes are made:
- (a)
- Introduction of a controllable and discrete latent space. The input vector is firstly mapped into a multilayer fully connected neural network, avoiding inconsistencies in replicating the original data distribution.
- (b)
- Gaussian noise is introduced to each convolutional layer, making it controllable during both training and inference phases. Stochasticity due to Gaussian noise-induced learning, fine-grained details, increasing accuracy of generated samples.
- (c)
- Custom CUDA-optimized operations to perform on GPU, reducing the computation time and optimizing the batch size.
The training process is the one presented in the original paper with progressive growth of the resolution of the input samples according to Figure 1b of [28]. Preliminarily, the training phase of StyleGAN took almost 3 h using four Nvidia Tesla V100 GPUs. The maize scenario was used for an initial test phase where the maximum mean square error (MSE) obtained was of the order of 0.1%. An example of generated TOA and BOA radiances for the wheat case is reported in Figure 5. Finally, 1024 GANDART spectra are generated with StyleGAN. Although StyleGAN is the final choice, during the work, different techniques were tested to find the most suitable one. Table A1 in Appendix A reports all the tested techniques and the considerations that motivate our choice. - 2.
- TASI to DART AutoEncoder (TASI2DART):The dataset used to train the TASI2DART model for data augmentation is the TASI-to-DART (Section 2.2.1). As said, due to the size of the original dataset, the AE is preferable in this case for data generation. As for the DART dataset, the first step is to cut the spectra between 8 and 13 µm (900 spectral points). Then, the 900 spectral points are upsampled to 1024 to perform a reshape to 64 × 64 required to leverage the two-dimensional convolutions of the AE used and to perform transfer learning on the pretrained EfficientNet B1 used for the feature extraction. A common 70/30 split is used for cross-validating the metrics of the AE. As output for the training phase, there are 600 couples for the training and 250 couples for the cross-validation. For the preprocessing of the dataset, standardization is performed (mean equal to zero, standard deviation equal to one). This additional task avoids inconsistency during the training phase. Moreover, standardization ensures a proper activation of the neurons within the neural network. The AE is composed of three main components [29]:
- the encoder, which extracts significant characteristics of the original dataset to the space of representations or latent space. This AE uses as encoder an EfficientNet B1 for feature extraction [30]. The objective of the network is neural network scaling, increasing the accuracy [30]. Defined as compound model scaling, it is a grid-search method for efficiently retrieving the number of parameters of a neural network considering three main neural network variables (Figure 2 of [30]):
- -
- the width (w, number of channels for each hidden layer).
- -
- the resolution (r, the input resolution of the network).
- -
- the depth (d, number of hidden layers).
The objective of the scaling is to maximize the accuracy of the ImageNet classification dataset [31]. - Latent space: Inside the latent space resides all the high-level characteristics of the original dataset;
- A decoder: Re-expands the latent space to the target two-dimensional target.
The decoder uses learnable upsampling operators called transposed convolution layers (sometimes called deconvolution [32]). Because they are trainable layers, optimization methods include backpropagation [33] through stochastic gradient descent. The model takes as input the previously described dataset, reshaped (64 × 64 × 1). For the train/evaluation phase, MSE, root mean squared error (RMSE), and mean absolute error (MAE) are adopted as metrics for checking the consistency of the model. The results obtained in the preliminary training are realistic for the TOA signature and aligned with the requirements of MSE < 0.04 K, 1/9 of the foreseen LSTM radiometric accuracy (Table 1). An example of generated spectra is given in Figure 7a. Finally, 198 TASI2DART spectra are generated. The algorithm takes about 0.42 s to generate one signature. In this case, different deep learning techniques were also tested in order to find the most suitable one (see Table A1 in Appendix A).

Table 1.
TASI2DART performance assessment in terms of MAE, MSE, and RMSE for training and validation datasets.
2.2.3. Data Verification
The characteristics of generated samples are compared with the characteristics of the original signatures to assess the generation performances. We develop a tool to perform statistical analysis, to define the characteristics of the current dataset.
The analysis is divided into two parts:
- Descriptive data analysis, which uses tools to summarize and has measurements of properties such as tendency and dispersion of data (mean, median).
- Exploratory data analysis (EDA), which summarizes the main characteristics with visual methods to perform initial investigations on data to check assumptions and discover patterns and anomalies.
For this analysis, the signatures (original and newly generated) are analyzed, dividing the whole spectral range into three intervals with common behavior (from 8–9.35 µm, 9.35–10 µm, 10–13 µm). Distribution plots and box plots are used for data verifications.
2.2.4. Retrieval Algorithms
To assess the feasibility of using deep learning techniques in support of satellite mission’s retrieval chains development, it is important to test to what extent the generated spectra can be used for this scope (e.g., in end-to-end simulators).
As an example, we focus on LST retrievals from five TIR channels used by satellite missions. In the past decades, several inversion models algorithms have been developed to obtain the LST, due to the importance of this variable for climate studies. Among them, we can find the generalized split-window (GSW) technique and the temperature emissivity separation (TES) algorithm for the retrieval of both LST and LSE. Nevertheless, neural networks algorithms can be used as well. As one of the objectives of the DeepLIM project is to compare the performances of deep learning codes with respect to state-of-the-art ones for retrieval applications, in this work we used two state-of-the-art and one deep learning-based retrieval algorithms:
- 1.
- TES algorithm:The TES algorithm is one of the state-of-the-art algorithms used for the retrieval of LST and LSE from aircraft and satellite missions. One of the main advantages of this algorithm is the capability to simultaneously retrieve LSE and LST. The algorithm is composed of three modules: (1) the normalized emissivity module (NEM), (2) the ratio module, and (3) the maximum–minimum difference module (MMD). The MMD module links the minimum value of the emissivity to the emissivity spectral contrast calculated as maximum-minimum emissivity. This relation depends on the instrument’s channels and the emissivity database used for the calculations. The MMD module is, then, critical for the correct determination of retrieved values. A complete description of the TES algorithm is beyond our scope and can be found in [34].The inputs of the TES algorithm are the BOA and the downward atmospheric irradiance at BOA, while the outputs are LSE in the instrument’s channels and LST.Generally, the TES inputs are obtained from TOA through the use of a RTM model. In our case, both the DART dataset and the TASI-to-DART dataset and the augmented ones already provide these two quantities; thus, they will be directly used (i.e., the TOA information is not used).As a first step, the signatures of BOA and downward irradiance are converted into BTs and convolved with SRFs for the five TIR channels.The second step is the addition of noise to the channel BTs. As we use BOA as TES input, we need to add the corresponding noise contribution to BOA instead of TOA, and this has an impact on the way the noise is added. The noise contribution that is transferred from TOA to BOA is given by the TOA noise contribution divided by the atmospheric transmissivity.As stated, the MMD module is critical for LSE and LST determination. Generally, MMD relation can be calculated through the use of emissivity laboratory spectra convolved with SRF. However, the scope of this work is to assess the performances of NN with respect to state-of-the-art codes. Thus, the auxiliary information used by the codes should be the same. For this reason, instead of using laboratory emissivity spectra for the calculation of TES MMD relation, we prefer to use the emissivity spectra contained in the DART and TASI-to-DART datasets. This means that the TES method does not use additional information not used by NN. This ensures that the differences in retrieved products are only due to the used methods and not to auxiliary information.
- 2.
- GSW algorithm:The GSW algorithm exploits the relation between LST and the BTs at 11 and 12 µm [35]. No emissivity retrieval is performed. The relation that links LST and BTs at 11 and 12 µm is given by seven retrieval coefficients. It is obtained through the use of a RTM and depends on water vapor and satellite viewing angle. As, in this case, the algorithm exploits the TOA BTs, the noise is added directly onto TOA radiances. We use the same noise scenario adopted for the TES algorithm. In this work, the seven retrieval coefficients are obtained using a part of the simulations performed for the dataset creation (e.g., part of the TASI-to-DART dataset). The mean emissivity value and emissivity contrast required by GSW are calculated as the mean and contrast value of the TASI LSE retrievals used for the coefficient calculations. To obtain the seven retrieval coefficients, we use a least-square regression model. This type of algorithm is used, e.g., for trend calculations (e.g., [36]). The output of this model is shown in Figure 1a. Here, the observed LST values of the TASI training dataset are reported as red triangles as a function of the case number. The black line is the result of the least square fit obtained with the calculated retrieval coefficients. As can be noticed, we obtain a generally good agreement between simulations and observations, highlighting that the retrieved coefficients well reproduce LST–BTs relation.
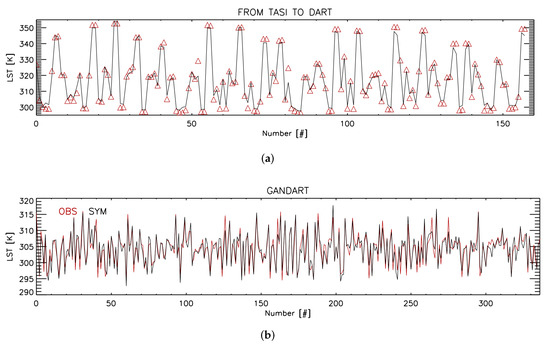 Figure 1. (a) Reduced least-square fit of LST retrieved from TASI-to-DART for GSW coefficients calculated using a part of the from-TASI-to-DART dataset. (b) Reduced least-square fit of LST retrieved from TASI for GSW coefficients calculation using GANDART features. Observations in red, simulations in black.
Figure 1. (a) Reduced least-square fit of LST retrieved from TASI-to-DART for GSW coefficients calculated using a part of the from-TASI-to-DART dataset. (b) Reduced least-square fit of LST retrieved from TASI for GSW coefficients calculation using GANDART features. Observations in red, simulations in black. - 3.
- Deep learning inversion model (DLIM):Deep learning techniques can be an alternative to state-of-the-art methods to perform satellite retrievals.Even if in this work we focused on LST retrievals, for completeness, the developed deep learning model, called the deep learning inversion model (DLIM), is conceived to also retrieve the LSE fields. The model has two branches: one dedicated to LST retrieval (feed-forward NN) and the other one for LSE retrieval (autoencoder) as reported in Figure 2. This happens because the values range of LST and LSE are different: LST falls in the range of hundreds of kelvins, while LSE is in a range between 0.7–1.0.
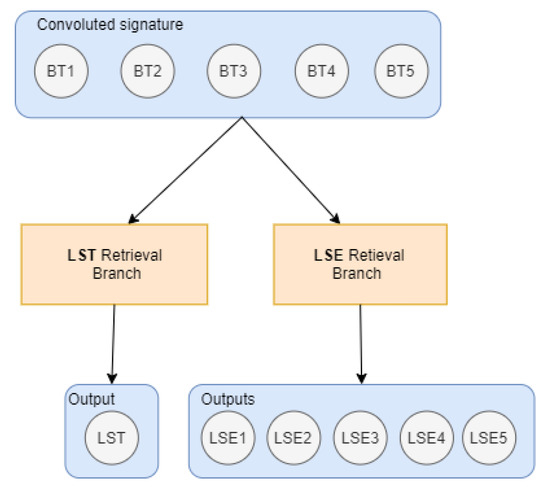 Figure 2. NN structure.Regarding the LST retrieval branch, a feed-forward neural network is selected because the problem perfectly corresponds to a regression problem. The LST branch is made of one dense layer with six neurons and one output layer with one neuron to compute the LST value.NN is trained using stochastic gradient descent and requires a loss (or cost) function when designing and configuring the model. As a loss function, the MAE for the five values of LSE and the MSE for the LST value is used. As the last step, the dataset is split into 70% training and 30% test with a validation split of 30%. For the train/evaluation phase, MAE is adopted as a metric for checking the consistency of the model. The optimizer is an Adam Optimizer [37] and the training epochs (cycles of NN training) are set to 2000 with early stopping callbacks based on validation loss (Figure 3). The list of different techniques tested to obtain the final results are reported in Table A1 in Appendix A.
Figure 2. NN structure.Regarding the LST retrieval branch, a feed-forward neural network is selected because the problem perfectly corresponds to a regression problem. The LST branch is made of one dense layer with six neurons and one output layer with one neuron to compute the LST value.NN is trained using stochastic gradient descent and requires a loss (or cost) function when designing and configuring the model. As a loss function, the MAE for the five values of LSE and the MSE for the LST value is used. As the last step, the dataset is split into 70% training and 30% test with a validation split of 30%. For the train/evaluation phase, MAE is adopted as a metric for checking the consistency of the model. The optimizer is an Adam Optimizer [37] and the training epochs (cycles of NN training) are set to 2000 with early stopping callbacks based on validation loss (Figure 3). The list of different techniques tested to obtain the final results are reported in Table A1 in Appendix A. Figure 3. Loss function.
Figure 3. Loss function.
3. Results
The tools described in Section 2 are all used to assess the potential of deep learning techniques when applied to Earth’s observation science.
Starting from the two original datasets of spectral signature in the range from 7 to 13 µm, the two deep learning generators are used: GANDART is used to generate 1024 new signatures starting from the DART dataset, while TASI2DART autoencoder is used to generate 198 signatures from the TASI-to-DART dataset. The quality and the reliability of the generated signatures are tested against the original ones. These data are then used to retrieve LST, applying state-of-the-art and deep learning algorithms. Results are reported in this section.
3.1. Assessment of Augmented Dataset vs. Original
Two types of plots are used to assess the performances of the augmented dataset: distribution plots and box plots.
The distribution plot is useful to check the linearity of all variables displaying the distribution and range of a set of numeric values plotted against a dimension. In Figure 4b, the distribution plot of the DART TOA signatures is reported, while in Figure 4a the distribution of the GANDART TOA signatures is reported.
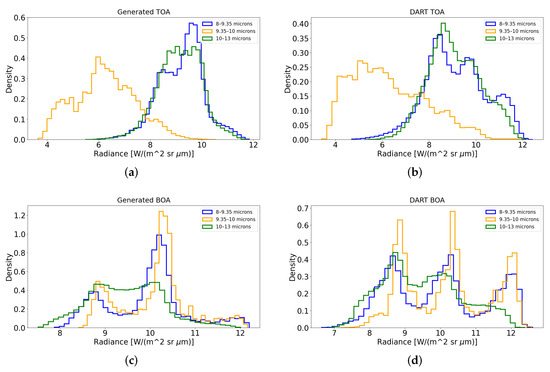
Figure 4.
(a) Generated TOA radiance distribution. (b) DART TOA radiance distribution. (c) Generated BOA radiance distribution. (d) DART BOA radiance distribution.
It is evident that the distribution of the generated data reflects that of the original data. This is an expected result thanks to the nature of the GANs architectures which, in the latent space, preserve the statistical characteristics of training data.
Similar considerations can be made on the distribution for synthetic BOA signatures, as reported in Figure 4c,d.
Box plot is a method for graphically depicting groups of numerical data through their quartiles. Each box plot has these components: Boxes: the main body of box plot showing the quartiles and the median’s confidence intervals (in green). The box represents 50% of overall values or values within 0.6745 sigma. Medians: horizontal lines at the median of each box (in black). Whiskers: vertical lines extending the most extreme outlier data points (in orange). Whiskers represent 99.3% of overall values or values within 2.698 sigma. Outliers: points representing data that extend beyond the whiskers (in red), coming out when there is a difference between the mean and the median values. The attention is focused particularly on discovering and highlighting the outliers and their associated values (Figure 5). It is relevant to note that the mean values of the synthetic signatures present remarkably similar values compared to the original dataset (Table 2), even if some outliers are created by the generative model. However, these outliers are mainly concentrated in the region between 9.35 and 10 µm, where O absorption is present (this spectral region is not covered by LSTM channels) and are only a few cases, as shown by the similar values of the means for original and generated data in this region. In addition, the outliers are not too different from the other values.
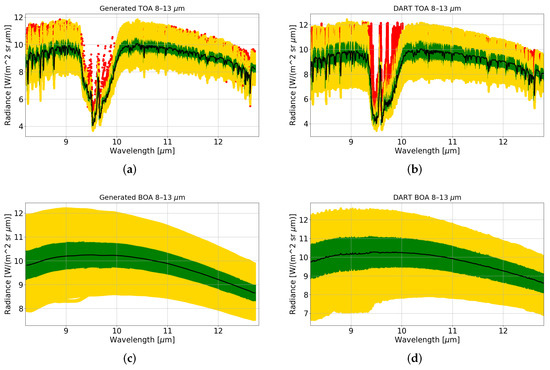
Figure 5.
(a) Generated TOA radiance box plot. (b) DART TOA radiance box plot. (c) Generated BOA radiance box plot. (d) DART BOA radiance box plot. The black line defines the median value for each box. Green represents the maximum and minimum values for the Q1 and Q3 (sigma within 0.6745 or 50% of the overall values). Yellow values represent the maximum and minimum values for the most extreme values (sigma within 2.698 or 99.3% of the overall values). Red crosses show the outliers that appear when there is a difference between the mean and the median values.

Table 2.
TOA and BOA mean values for the considered spectral regions. The mean and standard deviations values are reported both for the DART and GANDART datasets. The DART dataset is composed of 32,541 spectra, while GANDART of 1024.
Concerning the BOA signatures analysis (Figure 5c,d), the box plots have a less-complex structure because the spectral variability is greatly reduced (if compared with TOA signatures) due to the absence of atmospheric absorption. For each window of analysis, the mean values of the synthetic signatures are matching the original data (Table 2). No outliers are generated. It is important to notice that the ratio between BOA and TOA radiances (last two columns of Table 2) is consistent between DART and GANDART datasets. This is a critical aspect that reflects the fact that the generation process preserves the physics at the basis of TOA and BOA radiances behavior. This allows using generated spectra for surface properties retrievals. The same analysis is performed over the TASI-to-DART and TASI2DART datasets. The results are reported in Figure 6 and Figure 7 and in Table 3. As can be seen from average BOA values in the selected regions, TASI-to-DART (and thus TASI2DART) data have higher radiance values with respect to DART (and thus GANDART) data. This is mainly due to higher ground temperatures in the used datasets, and thus in LST (see Figure 1).
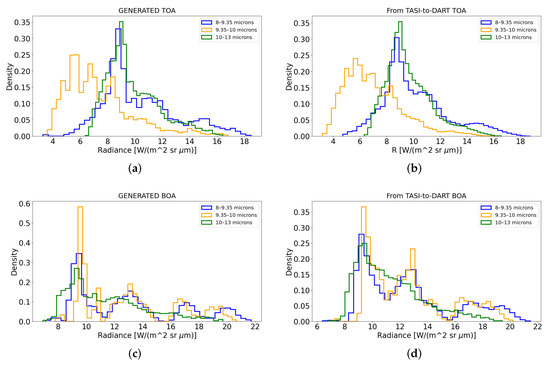
Figure 6.
(a) TASI2DART-generated TOA radiance distribution. (b) TASI-to-DART TOA radiance distribution. (c) TASI2DART-generated BOA radiance distribution. (d) TASI-to-DART BOA radiance distribution.
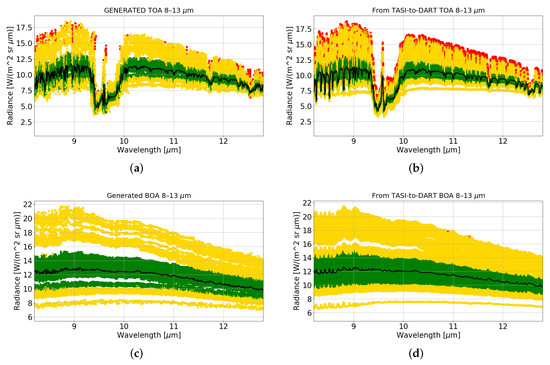
Figure 7.
(a) TASI2DART-generated TOA radiance box plot. (b) TASI-to-DART TOA radiance box plot. (c) TASI2DART-generated BOA radiance box plot. (d) TASI-to-DART BOA radiance box plot. See Figure 5 for legend.

Table 3.
TOA and BOA mean values for the considered spectral regions. In the TASI-to-D. column are the values for the TASI-to-DART dataset, in the TASI2DART column are the mean values and standard deviations for the generated signatures. The TASI-to-DART dataset is composed of about 800 spectra, while TASI2DART of 198.
3.2. Assessment of TIR Retrievals
The augmented datasets, when statistically analyzed, reproduce the radiance characteristics of the original ones. Thus, these spectra can be used for studying retrievals applications. If the generation procedure is completely correct, the physical processes at the basis of spectra generation should be preserved and the retrieval results should be in line with the ones from original data (e.g., no unphysical values are found). Furthermore, we use the two state-of-the-art and the NN algorithms to also assess the deep learning approaches performances on inversion models.
Testing the Deep Learning Forward/Reverse Techniques
The comparison of DLIM and TES retrieval algorithms is meaningful if the algorithms share a common set of background conditions. For this reason, the emissivity values used for the DLIM training are used for the MMD coefficients calculations for TES. In addition, the SRF functions convolution and the noise values added to each channel BT is consistent between the two algorithms.
We aim at testing not only the feasibility but also the limits of deep learning techniques applied to Earth observations. For this reason, we perform a challenging test.
The DLIM model is trained using 1000 signatures generated with GANDART (no original DART signature included). The associated LSE and LST are retrieved applying the TES algorithm with MMD parameters calculated from the previous exercise. Then, DLIM is applied to TASI2DART (augmented dataset only, no original signature included) and the results are compared with the ones from the TES algorithm applied over the same dataset. This test is challenging for two reasons:
- 1.
- The use of generated signatures only: Both the training and the test datasets belong to the augmented dataset. No signatures from physically-based FM are included here. In case of instability in data generation, unphysical results can be found.
- 2.
- The differences in training and test dataset: The NN is trained using signatures generated from DART. The GANDART spectra preserve the features of the original dataset (e.g., wheat emissivity and LST from about 295 K to about 320 K). The TASI2DART dataset, used as a test dataset, is generated from TASI data acquired over different vegetation (e.g., maize, rice) and ground surfaces with temperatures up to 350 K. Then, the training dataset does not fully cover the scenarios of the test dataset (e.g., high LST values, certain type of vegetation) and the NN tends to extrapolate the results.
For this test, the TES algorithm uses the BOA and irradiance values from the TASI2DART dataset. This means that no error due to atmospheric correction, which is the main source of error for the TES algorithm, is present here. At the end of this section, we report the impact of a nonperfect atmospheric correction on TES. To check the performances of the DLIM, we perform an initial test analyzing the 24 GANDART signatures not used in the DLIM training dataset and compare the performances with TES (MMD coefficients computed over the same DLIM training dataset) (Figure 8a).
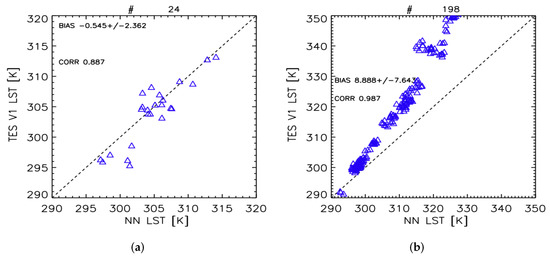
Figure 8.
(a) LST retrieved with TES algorithm vs. LST from DLIM over 24 signatures (#24) of GANDART dataset not used for training. (b) LST retrieved with TES algorithm vs. LST from NN over the 198 signatures of the TASI2DART dataset (#198).
As can be noticed, DLIM produced realistic LST. This is a nonobvious result due to the considerations made at point 1). In addition, retrieved LST (bias 0.5 ± 2.4 K, correlation 0.887) has good performances. This confirms the validity of both the GANDART-generated features and of the developed DLIM algorithm.
Finally, we apply the DLIM and TES to the TASI2DART dataset. Results are reported in Figure 8b. It is worth noticing that, even if under really challenging conditions, physically meaningful values are obtained. However, large deviations are observed in DLIM LST retrievals, even if the correlation of the results is significantly high (0.987). The DLIM results present a slope different from 1 when compared to TES, with NN maximum retrieved LST of about 330 K. This result is not unexpected. As stated before, the NN is trained over a dataset generated from DART spectra with a maximum LST of about 320 K. For this reason, the DLIM is not able to obtain higher temperatures and the retrieved values have a slope that deviates from 1 when compared to TES.
This challenging exercise has an overall positive outcome: no unphysical results are obtained from the augmented dataset, and the retrieved LST are not scattered or randomly distributed. The DLIM results are biased by the fact that the training dataset is very different from the test one, but this is intrinsically related to NN nature.
However, the NN is not the only method affected by this issue. As done for DLIM, the seven retrieval coefficients for the GSW algorithm are computed from the GANDART training dataset. In Figure 1b, we show the analogous of Figure 1a for the first 300 elements of the GANDART training dataset. The coefficients correctly reproduce the LST behavior. The maximum LST is about 315 K, versus the 350 K of Figure 1a, where the original TASI-to-DART dataset is used for the calculation of the coefficients.
We test the GSW algorithm and the calculated coefficients over the 24 remaining GANDART signatures (Figure 9a) in comparison with TES results. Results are comparable to the ones obtained by the NN (Figure 8a) and do not show particular biases.
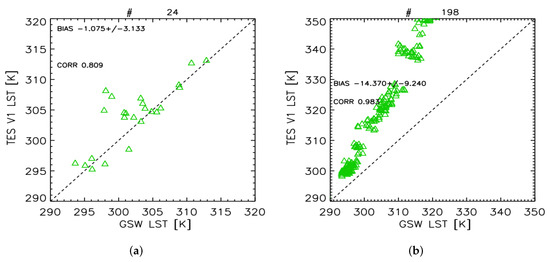
Figure 9.
(a) LST retrieved with GSW vs. TES on 24 GANDART signatures (#24). (b) LST retrieved with GSW vs. TES over 198 TASI2DART signatures (#198).
Finally, we apply the GSW to the 198 TASI2DART signatures and compare them with TES results (Figure 9b). GSW and DLIM results have similar behavior with respect to TES, due to differences between training and test dataset. In addition, in this case, no unphysical LST values are retrieved, once again proving the reliability of generated signatures. As said for DLIM, GSW deviations from TES are due to the a-priori information used to produce retrieval coefficients.
GSW and DLIM behave similarly, with DLIM producing slightly better results when compared to TES. Both methods are really sensitive to the a-priori information used (training dataset for NN and data for coefficients calculations for GSW).
As stated at the beginning of this section, the TES algorithm, used as a benchmark, is initialized with the correct atmospheric correction. To evaluate the impact of a less-than-perfect (and more realistic) correction on TOA BTs to obtain BOA, we use the transmissivity obtained from the DART dataset. Downward irradiance at BOA is taken from DART as well. The impact of this can be evaluated from Figure 10, where we report the results obtained with TES with correct (from TASI2DART) and DART atmospheric corrections. As can be seen, even if the TES with DART correction retrieves lower values at high LST, the agreement with benchmark TES is quite good (bias 1.67 ± 3 K, correlation 0.993), highlighting a lower dependence of TES on a-priori information with respect to GSW and NN algorithms.
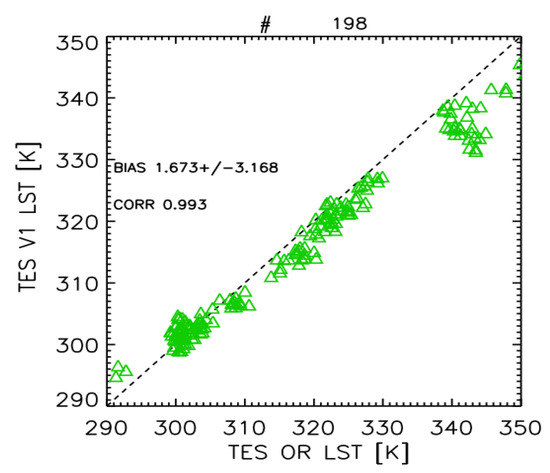
Figure 10.
LST retrieved with TES with DART atmospheric correction vs. TES on TASI2DART dataset.
Finally, we test the validity of our assumption on the bias given by differences in training and test dataset characteristics when using the NN approach: We use as a training dataset both original DART signatures from the maize dataset and GANDART maize-generated signatures. Then, we used a test dataset of 1000 wheat GANDART signatures. In this case, the training and tests datasets have similar characteristics. Results of DLIM and TES retrievals are given in Figure 11.
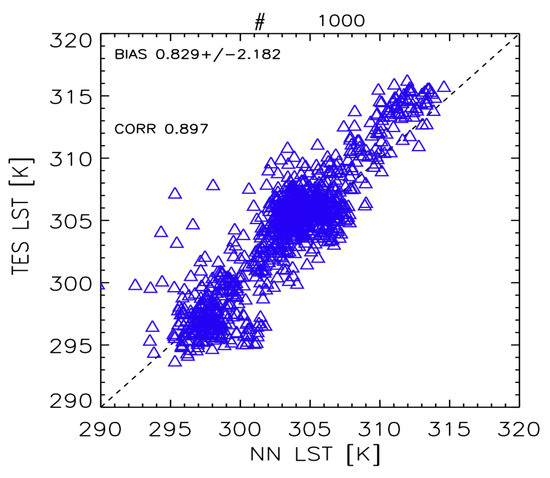
Figure 11.
LST retrieved with TES algorithm vs. LST from DLIM over 1000 wheat signatures.
The overall LST bias is 0.8 ± 2.2 K, and the correlation reaches 0.897. This bias is consistent with biases from state-of-the-art algorithms and is consistent with the requirements for the majority of LST applications (<1–2 K, [38]). This test shows that the generated spectra are reliable since they do not produce unphysical values and they preserve the information of the original dataset. Furthermore, it demonstrates that the DLIM performances are comparable to the ones of the state-of-the-art algorithm.
4. Discussion
This work aims at evaluating the feasibility of using deep learning-based techniques to fully support the next-generation satellite’s retrieval chain. As an example, an application to TIR satellite (LSTM, candiate for Sentinel 9), LST retrievals, is considered. Starting from original spectral datasets from FMs and campaigns data, deep learning techniques are used to augment these datasets. The overall quality of the augmented dataset is evaluated using a statistical tool developed for the comparison of the generated and the original dataset. The results show comparable statistical distribution between the two datasets, hinting at the capability of the generative models to correctly learn the distribution from the training dataset. In this sense, these results pose a high focus on the quality of the training data, which is a fundamental aspect of every deep learning model development.
Generated data are used to retrieve LST with full-physics state-of-the-art and NN inversion algorithms. An indirect evaluation of the quality of the generated dataset can also be obtained from the retrieval performances. When we apply the state-of-the-art TES and GSW algorithms as well as NN code to generated features, realistic LST values are retrieved. This is also true in the case of extremely challenging retrieval conditions. This is a nonobvious result that highlights that deep-learning-generated features can preserve the information of the physical processes behind the TOA spectral behavior.
When the a-priori conditions used for retrieval coefficients or training dataset determination are close to the observed scenarios, the retrieved products are competitive, in terms of bias with physically-based simulated data, thus demonstrating the quality of the deep-learning-generated spectra at high spectral resolution. Regarding the retrieval accuracy, the retrieval results obtained on generated signatures have a quality that is comparable to the ones achieved from previous retrieval studies. LST retrieved using TES and NN are similar, in values and behavior, to the ones obtained from the original DART dataset. This result highlights the consistency between generated and original datasets and the subsequent usability of generated data for retrieval study applications.
A final consideration should be added. During this work, we found that retrieval performances of different methods (TES, GSW, NN) depend, to a different extent, on the used a-priori information. In particular, the NN method is particularly sensitive to the used training dataset. Indeed, if the training dataset is too different from the test one, bias is found. This is not surprising and is intrinsically related to the NN method. However, NN is not the only method that is affected by prior knowledge. Something very similar occurs for GSW. The TES method is the one that is less affected by a-priori information. This outcome should be considered when evaluating retrieval performances.
5. Conclusions
The use of deep learning techniques for Earth observation studies can be extended to a variety of other remote sensing datasets. As stated, the development of end-to-end simulators is a crucial point in satellite missions development. They play a central role in verifying before launch that science requirements will be met by the chosen instrument design, in evaluating the resulting calibration uncertainties, and in ensuring that the instrument data processing will work in a time- and memory-efficient manner. In this frame, FMs are necessary tools to both support the satellite mission concept design and then, at different levels depending on the used technique, to retrieve atmospheric and surface physical variables from the measurements.
Up to now, some fast codes (e.g., based on parameterization of LBL models) were developed (e.g., RTTOV). GANs and AE can be a more elastic and lower-computing-cost solution. Even if for this work LST is retrieved from five spectral channels, the simulations are performed at higher spectral resolution. As demonstrated during this work, the deep learning algorithms can reproduce the spectral behavior of the original spectra (e.g., O band behavior). In the light of these considerations, the developed models are very promising for applications to end-to-end simulations of upcoming missions (e.g., the LSTM mission, candiate for Sentinel 9 and used for this study, or the Far-Infrared-Outgoing Radiation Understanding and Monitoring (FORUM) mission ([39,40]) selected as Earth Explorer 9 that will measure in far-infrared and TIR spectral regions) or for the applications to already existing missions (e.g., Infrared Atmospheric Sounding Interferometer (IASI, [41])) that are characterized by spectrally resolved measurements.
Author Contributions
Conceptualization, E.C., E.P., A.D.R., I.B., M.V. and L.F.; Data curation, E.C., E.P., I.B., M.V., J.-P.G.-E. and L.F.; DART data, J.-P.G.-E.; Formal analysis, E.C., E.P., A.D.R., I.B., M.V. and L.F.; Investigation, H.T.; Methodology, E.C., E.P., A.D.R., I.B., M.V. and L.F.; Project administration, L.F.; Resources, H.T.; Software, E.C., E.P., A.D.R., I.B., M.V., H.T. and L.F.; Writing—original draft, E.C., E.P., A.D.R., I.B., M.V., J.-P.G.-E. and L.F. All authors have read and agreed to the published version of the manuscript.
Funding
Airborne acquisition, data analysis, and DART simulations were financed by the European Space Agency (ESA) in the frame of the FLEXSense campaign (ESA Contract No. 4000125402/18/NL/NA) and the SurfSense campaign (ESA contract No. 4000125840/18/NL/LF), and the LSTM project (ESA contract No.: AO/1-8733/16/NL/AF/eg) and the “Assessment of the potential use of high-resolution TIR bands” project (ESA contract No.: 4000120368/17/NL/AF/hh). TASI data acquisition and processing is based on use of Large Research Infrastructure CzeCOS supported by the Ministry of Education, Youth and Sports of CR within the CzeCOS program, grant number LM2018123. The DeepLIM project was founded with ESA contract Nr. 4000128370/19/NL/AS.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Restrictions apply to the availability of the data produced in the frame of the DeepLIM project. These data are available from the authors with the permission of ESA. DART data are the property of ESA.TASI data of the SurfSense 2018 campaign are available from ESA.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AE | AutoEncoders |
| ANN | Artificial Neural Network |
| ATSR | Along Track Scanning Radiometer simulations |
| BB | Broad Band |
| BBCH | Biologische Bundesanstalt, Bundessortenamt and CHemical industry |
| BOA | Bottom of the Atmosphere |
| BT | Brightness Temperature |
| DART | Discrete Anisotropic Radiative Transfer |
| DLIM | Deep Learning Inversion model |
| EDA | Exploratory Data Analysys |
| ECMWF | European Centre for Medium-range Weather Forecasts |
| ESA | European Space Agency |
| FM | Forward Model |
| FORUM | Far-Infrared-Outgoing Radiation Understanding and Monitoring |
| FOV | Field of View |
| GANs | Generative Adversarial Nets |
| GSW | Generalized Split Window |
| IASI | Infrared Atmospheric Sounding Interferometer |
| LAI | Leaf Area Index |
| LBL | Line-by-line |
| LSE | Land Surface Emissivity |
| LST | Land Surface Temperature |
| LSTM | Land Surface Temperature Mission |
| MAE | Mean Absolute Error |
| MMD | Maximum-Minimum Difference module |
| MRD | Mission Requirement Document |
| MSE | Mean Square Error |
| NEM | Normalized Emissivity Module |
| NN | Neural Network |
| NRT | Near Real Time |
| PGGANs | Progressive Growing of GANs |
| RMSE | Root Mean Square Error |
| RTM | Radiative Transfer Model |
| RTTOV | Radiative Transfer for TOVS |
| SRF | Spectral Response Function |
| TASI | Thermal Airborne Spectrographic Imager |
| TES | Temperature Emissivity Separation |
| TIR | Thermal Infra-Red |
| TOA | Top of the Atmosphere |
| VAE | Variational Autoencoder |
Appendix A

Table A1.
Different deep learning techniques tested during the project for each developed tool.
Table A1.
Different deep learning techniques tested during the project for each developed tool.
| Technology | Comments |
|---|---|
| GANDART | |
| Fully Connected GANs | First technology evaluated during the activity. |
| Results are too noisy to be consistent. | |
| The technology was dropped in favor of other models. | |
| Fully Convolutional GANs | This technology has been tried after the fully connected GANs, |
| it had reduced noise but still highly unreliable signature | |
| generation due to the unstructured latent space. | |
| ACGANs | Technology demonstrator for conditional generation. |
| Reliable and promising first results, | |
| however, the variability of the generated samples was too low. | |
| PGGANs | Very high quality for sample generation. |
| However, some artifacts are generated that disturb | |
| the retrieval process. | |
| Moreover, the unconditionality of the network | |
| reduce the potential for future uses. | |
| StyleGAN2 | Improved sample generation accuracy with respect to PGGANs. |
| Structured latent space generation. | |
| The results were produced using this technology. | |
| The exploration of the latent space needs to be refined. | |
| TASI2DART | |
| UNet + Custom | First technology demonstrator for the TASI to DART |
| generation process. | |
| Noisy results partially solved using a fully connected network. | |
| UNet + ENet | Technology improvement with respect to the previous model. |
| Completely solved the issue of noisy generated data, | |
| without the use of a fully connected network. | |
| Lightweight and fast to train model has been used. | |
| The results were produced using this technology. | |
| DLIM | |
| Convolutional Neural Network | First technology considered for inversion modeling. |
| At this stage of the project, the model input was the full signatures | |
| and not the convolved features. The technology was dropped | |
| when the input was changed to only the 5 convolved features. | |
| Deep Fully Connected | No particular problems with this technology, |
| but not outstanding results either. The technology was dropped | |
| in favor of a more promising technology (Autoencoders). | |
| Deep Autoencoders | Final technology selected for DLIM. Able to map data |
| distribution in a latent space useful to retrieve the outputs. |
References
- Eyre, J.R. A fast radiative transfer model for satellite sounding systems. In ECMWF Research Department Technical Memo; ECMWF: Reading, UK, 1991; Volume 176. [Google Scholar]
- Amato, U.; Masiello, G.; Serio, C.; Viggiano, M. The σ-IASI code for the calculation of infrared atmospheric radiance and its derivatives. Environ. Model. Softw. 2002, 17, 651–667. [Google Scholar] [CrossRef]
- Berger, K.; Rivera Caicedo, J.P.; Martino, L.; Wocher, M.; Hank, T.; Verrelst, J. A Survey of Active Learning for Quantifying Vegetation Traits from Terrestrial Earth Observation Data. Remote Sens. 2021, 13, 287. [Google Scholar] [CrossRef]
- Samarin, M.; Zweifel, L.; Roth, V.; Alewell, C. Identifying Soil Erosion Processes in Alpine Grasslands on Aerial Imagery with a U-Net Convolutional Neural Network. Remote Sens. 2020, 12, 4149. [Google Scholar] [CrossRef]
- Nemni, E.; Bullock, J.; Belabbes, S.; Bromley, L. Fully Convolutional Neural Network for Rapid Flood Segmentation in Synthetic Aperture Radar Imagery. Remote Sens. 2020, 12, 2532. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. Available online: https://arxiv.org/abs/1406.2661 (accessed on 24 November 2021).
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the Dimensionality of Data with Neural Networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Theis, L.; Shi, W.; Cunningham, A.; Huszár, F. Lossy Image Compression with Compressive Autoencoders. Available online: https://arxiv.org/abs/1703.00395 (accessed on 25 November 2021).
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. Available online: https://arxiv.org/abs/1505.04597 (accessed on 25 November 2021).
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. Available online: https://arxiv.org/abs/1312.6114 (accessed on 25 November 2021).
- Koetz, B.; Bastiaanssen, W.; Berger, M.; Defourney, P.; Bello, U.D.; Drusch, M.; Drinkwater, M.; Duca, R.; Fernandez, V.; Ghent, D.; et al. High Spatio-Temporal Resolution Land Surface Temperature Mission—A Copernicus Candidate Mission in Support of Agricultural Monitoring. In Proceedings of the IGARSS 2018–2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 8160–8162. [Google Scholar] [CrossRef]
- Plans for a New Wave of European Sentinel Satellites, ESA. 2020. Available online: https://futureearth.org/wp-content/uploads/2020/01/issuebrief_04_03.pdf (accessed on 25 August 2021).
- ESA Earth and Mission Science Division. Copernicus High Spatio-Temporal Resolution Land Surface Temperature Mission: Mission Requirements Document. Issue Date 14/05/2021 Ref ESA-EOPSM-HSTR-MRD-3276. Available online: https://esamultimedia.esa.int/docs/EarthObservation/Copernicus_LSTM_MRD_v3.0_Issued_20210514.pdf (accessed on 24 November 2021).
- Gastellu–Etchegorry, J.P.; Lauret, N.; Yin, T.G.; Landier, L.; Kallel, A.; Malenovsky, Z.; Al Bitar, A.; Aval, J.; Benhmida, S.; Qi, J.B.; et al. DART: Recent advances in remote sensing data modeling with atmosphere, polarization, and chlorophyll fluorescence. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2640–2649. [Google Scholar] [CrossRef]
- Fournier, C.; Andrieu, B.; Ljutovac, S.; Saint-Jean, S. ADEL-wheat: A 3D architectural model of wheat development. In Plant Growth Modeling and Applications; Hu, B.-G., Jaeger, M., Eds.; Tsinghua University Press: Beijing, China, 2003; pp. 54–63. [Google Scholar]
- Abichou, M.; Fournier, C.; Dornbusch, T.; Chambon, C.; Baccar, R.; Bertheloot, J.; Vidal, T.; Robert, C.; David, G.; Andrieu, B. Re-parametrisation of Adel-wheat allows reducing the experimental effort to simulate the 3D development of winter wheat. Risto Sievänen and Eero Nikinmaa and Christophe Godin and Anna Lintunen and Pekka Nygren. In Proceedings of the 7th International Conference on Functional-Structural Plant Models, Saariselka, Finland, 9–14 June 2013; pp. 304–306. [Google Scholar]
- Abichou, M. Modélisation de L’architecture 4D du blé: Identification des Patterns Dans la Morphologie, la Sénescence et le Positionnement Spatial des Organes Dans une Large Gamme de Situations de Croissance. PhD University Paris-Saclay, AgroParisTech. 2016. Available online: https://www.researchgate.net/profile/Abichou_Mariem (accessed on 2 December 2021).
- Abichou, M.; Fournier, C.; Dornbusch, T.; Chambon, C.; Solan, B.d.; Gouache, D.; Andrieu, B. Parameterising wheat leaf and tiller dynamics for faithful reconstruction of wheat plants by structural plant models. Field Crop. Res. 2018, 218, 213–230. [Google Scholar] [CrossRef]
- Rascher, U.; Sobrino, J.A.; Skokovic, D.; Hanus, J.; Siegmann, B. SurfSense Technical Assistance for Airborne and Ground Measurements during the High Spatio-Temporal Resolution Land Surface Temperature Experiment Final Report. Unpublished work. 2019. [Google Scholar]
- ITRES TASI Instrument Manual; Document ID: 360025-03; ITRES Research Limited: Calgary, AB, Canada, 2008.
- Delderfield, J.; Llewellyn-Jones, D.T.; Bernard, R.; de Javel, Y.; Williamson, E.J.; Mason, I.; Pick, D.R.; Barton, I.J. The Along Track Scanning Radiometer (ATSR) for ERS-1. Proc. SPIE 1986, 589, 114–120. [Google Scholar]
- Casadio, S.; Castelli, E.; Papandrea, E.; Dinelli, B.M.; Pisacane, G.; Bojkov, B. Total column water vapour from along track scanning radiometer series using thermal infrared dual view ocean cloud free measurements: The Advanced Infra-Red Water Vapour Estimator (AIRWAVE) algorithm. Remote Sens. Environ. 2016, 172, 1–14. [Google Scholar] [CrossRef]
- Castelli, E.; Papandrea, E.; Di Roma, A.; Dinelli, B.M.; Casadio, S.; Bojkov, B. The Advanced Infra-RedWAter Vapour Estimator (AIRWAVE) version 2: Algorithm evolution, dataset description and performance improvements. Atmos. Meas. Tech. 2019, 12, 371–388. [Google Scholar] [CrossRef] [Green Version]
- Silvestro, P.C.; Casa, R.; Hanus, J.; Koetz, B.; Rascher, U.; Schuettemeyer, D.; Siegmann, B.; Skokovic, D.; Sobrino, J.; Tudoroiu, M. Synergistic Use of Multispectral Data and Crop Growth Modelling for Spatial and Temporal Evapotranspiration Estimations. Remote Sens. 2021, 13, 2138. [Google Scholar] [CrossRef]
- Remedios, J.J.; Leigh, R.J.; Waterfall, A.M.; Moore, D.P.; Sembhi, H.; Parkes, I.; Greenhough, J.; Chipperfield, M.P.; Hauglustaine, D. MIPAS reference atmospheres and comparisons to V4.61/V4.62 MIPAS level 2 geophysical data sets. Atmos. Chem. Phys. Discuss. 2007, 7, 9973–10017. [Google Scholar]
- Karras, T.; Aila, T.; Laine, S.; Lehtinen, J. Progressive Growing of Gans for Improved Quality, Stability, Variation. Available online: https://arxiv.org/abs/1710.10196 (accessed on 24 November 2021).
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. Available online: https://arxiv.org/abs/1512.03385 (accessed on 24 November 2021).
- Karras, T.; Laine, S.; Timo, A. A Style-Based Generator Architecture for Generative Adversarial Networks. Available online: https://arxiv.org/abs/1812.04948 (accessed on 24 November 2021).
- Ballard, D.H. Modular Learning in Neural Networks. In Proceedings of the Sixth National Conference on Artificial Intelligence (AAAI-87), Seattle, WA, USA, 13–17 July 1987; AAAI Press: Palo Alto, CA, USA, 1987; Volume 1, pp. 279–284. Available online: https://www.aaai.org/Papers/AAAI/1987/AAAI87-050.pdf (accessed on 22 September 2020).
- Tan, M.; Le, Q.V. Efficient Net: Rethinking Model Scaling for Convolutional Neural Networks. In Proceedings of the 36th International Conference on Machine Learning, PMLR 97:6105-6114, Long Beach, CA, USA, 9–15 June 2019; Available online: https://arxiv.org/pdf/1905.11946.pdf (accessed on 31 May 2019).
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Li, F.-F. Image Net: A Large-Scale Hierarchical Image Database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar] [CrossRef] [Green Version]
- Zeiler, M.D.; Krishnaan, D.; Taylor, G.W.; Fergus, G. Deconvolutional networks. In Proceedings of the CVPR, IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Gillespie, A.R.; Rokugawa, S.; Hook, S.J.; Matsunaga, T.; Kahle, A.B. ASTER ATBD, Temperature/Emissivity Separation Algorithm Theoretical Basis Document, Version 2.4, Prepared under NASA Contract NAS5-31372. 22 March 1999. Available online: https://unit.aist.go.jp/igg/rs-rg/ASTERSciWeb_AIST/en/documnts/pdf/2b0304.pdf (accessed on 2 December 2021).
- Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Trans. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar]
- Castelli, E.; Papandrea, E.; Valeri, M.; Greco, F.P.; Ventrucci, M.; Casadio, S.; Dinelli, B.M. ITCZ trend analysis via Geodesic P-spline smoothing of the AIRWAVE TCWV and cloud frequency datasets. Atmos. Res. 2018, 214, 228–238. [Google Scholar] [CrossRef] [Green Version]
- Diederik, P.K.; Adam, J.B. A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference for Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Sobrino, J.A.; Del Frate, F.; Drusch, M.; Jimenez-Munoz, J.C.; Manunta, P.; Regan, A. Review of thermal infrared applications and requirements for future high-resolution sensors. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2963–2972. [Google Scholar] [CrossRef]
- Forum. Available online: https://www.forum-ee9.eu (accessed on 27 August 2021).
- Palchetti, L.; Brindley, H.; Bantges, R.; Buehler, S.A.; Camy-Peyret, C.; Carli, B.; Cortesi, U.; Del Bianco, S.; Di Natale, G.; Dinelli, B.M.; et al. FORUM: Unique far-infrared satellite observations to better understand how Earth radiates energy to space. Bull. Am. Meteor. Soc. 2020, 101, E2030–E2046. [Google Scholar] [CrossRef]
- IASI. Available online: https://www.eumetsat.int/iasi (accessed on 27 August 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).