Abstract
The TH-2 satellite system, including the TH-2A and TH-2B, is the first distributed interferometric synthetic aperture radar (InSAR) satellite system in China. During the in-orbit operation, the TH-2A satellite should perform three maneuvers per day to keep the formation flying geometry. We estimate those maneuvers in the precise orbit determination (POD) by the GPS and BDS2 measurements on board, respectively. The residuals of the POD show that the effects caused by orbital maneuvers can be well eliminated for both the GPS and BDS2 data. The precision of the BDS2-based POD is better than 8.0 cm in the three-dimensional direction (3D) compared with the orbit derived from the GPS observations. Such a precision level of the satellite orbit satisfies the InSAR mission requirement of the TH-2. In addition, the relative error of velocity changes is employed to evaluate the maneuver estimations by the POD using the regional navigation system of BDS2. The results show that the relative error of velocity changes between the GPS- and BDS2-based POD is less than 7.0%, which indicates that the maneuver performance extracted from the regional BDS2 data is as good as that extracted from the global GPS data. In the GNSS fused processing, we found that the independent receiver clock offsets should be taken into account, since the time tag corrections for the GPS and BDS2 observations collected on the TH-2 spaceborne receivers were different. The precision of the GPS and BDS2 (GC) combined single point positioning (SPP) can be improved by 12–14% compared with the GPS-only solution when the position dilution of precision (PDOP) of GPS exceeds three. The overlap comparisons of the GC combined orbits show that the internal orbit precision of the TH-2 satellites is better than 0.7 cm. However, the improvement of the GC combined POD result is only 3–4% with respect to the GPS-only solution, which is limited to the precision of the precise orbit and clock products of BDS2 at the present stage.
1. Introduction
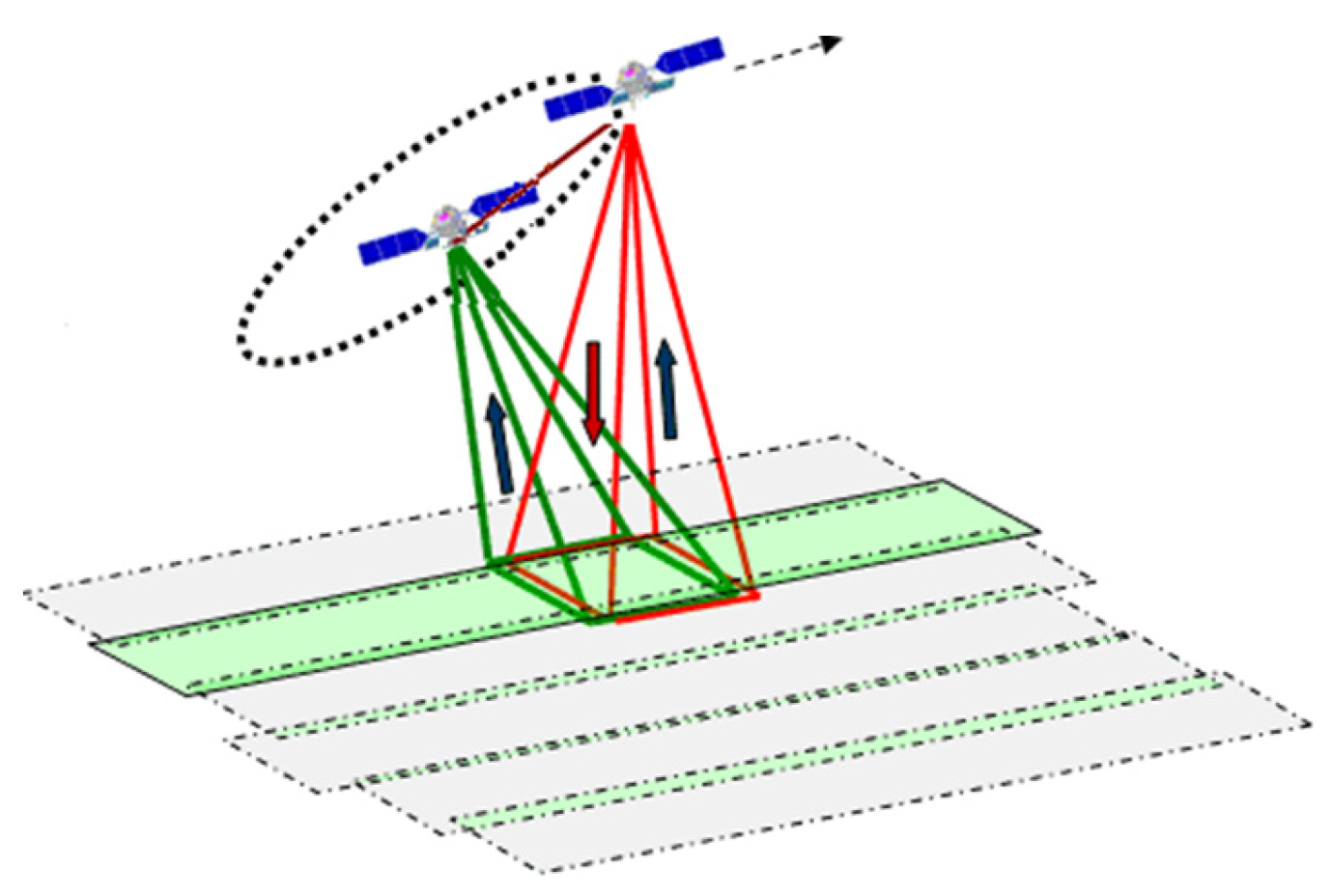
The TH-2 satellite system, which is the first distributed interferometric synthetic aperture radar (InSAR) formation system in China, was sent into space by the Long March-4B launch vehicle on 30 April 2019 [1,2,3]. This formation consists of two almost identical satellites, the TH-2A and TH-2B, which both fly in sun-synchronous orbits (527 km altitude, 97.45° inclination) with a relative distance of 700 m in 2019, as shown in Figure 1. To accomplish the missions of topographic mapping, deformation detection, scientific research, etc., the orbit and baseline accuracy requirements of the TH-2 are 1 m and 8 mm, respectively.
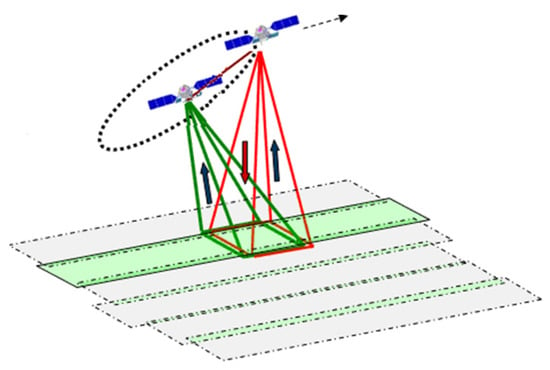
Figure 1.
Schematic view of TH-2A and TH-2B in operation.
The precise orbit determination (POD) of the TH-2 satellites using spaceborne Global Navigation Satellite System (GNSS) observations is a prerequisite for the successful implementation of the InSAR mission. As a crucial navigation system for positioning and timing, the potential of GPS in the POD processing for low Earth orbits (LEOs) was noted early in its development. The initial accuracy of the GPS-based POD results was only dozens of meters [4]. Currently, with the increasing accuracy of force models and tracking systems, the precision of the GPS-based orbits for LEOs such as GRACE [5], SWARM [6], TerraSAR-X and TanDEM-X [7] can be better than 5 cm [8]. The spaceborne GNSS receiver on the TH-2 satellite is able to track both the GPS and the BDS signals, which provides an alternative measurement for the POD. The second and third generation BDSs (the BDS2 and BDS3, respectively) were completed in 2012 and 2020. With the completion of the BDS, and the increasing number of LEOs with BDS receivers, many researchers have investigated the contribution of the BDS to LEO orbit determination. For example, Li et.al. [9] demonstrated that the orbit error of the BDS2-based POD is smaller than 10 cm for the FengYun-3C. Xiong et.al. [10] analyzed the real-time orbit determination of the FengYun-3C and concluded that the precision of the GPS and BDS2 (GC) combined solutions is better than that of the GPS-only. The research on the Fengyun-3D [11] and the China Seismo-Electromagnetic Satellite (CSES) [12] proves that the inclusion of BDS2 can improve the consistency of the POD solutions of LEOs. Therefore, the orbit determination of LEOs based on multi-GNSS data is promising in scientific research and commercial tasks.
The inter-system bias (ISB) is an important parameter in multi-GNSS processing. Generally, there are two strategies to handle ISB. One is to estimate the independent receiver clock offsets for each GNSS [13], and the other is to introduce one constant ISB for the interval of processing [14]. Since the ISB is receiver-dependent [15], it is necessary to consider the characteristics of the receiver during multi-GNSS processing. The ISB is usually estimated as a constant for spaceborne receivers, e.g., the instruments on the Fengyun-3C, Fengyun-3D [16], and CSES [12]. However, the spaceborne receiver of the TH-2 satellite can provide three positioning modes, namely GPS-only, BDS2-only, as well as GC combined. Due to the difference of the time tag corrections for each positioning mode, the ISB processing strategy still needs to be further studied for the GC combined POD of the TH-2 satellites.
In addition, the TH-2A satellite should perform three maneuvers per day due to the requirement of formation keeping. It is necessary to handle the maneuvers properly to avoid the precision degradation of the orbits around the thrust execution periods. There are several maneuver estimation approaches to improve the orbit quality during the maneuvering periods, including instantaneous velocity pulses [17], constant thrust model [18], and piecewise linear and continuous accelerations [19], etc. By using these methods to estimate the maneuvers, centimeter-level precision orbits of the LEOs with maneuvers can be obtained based on global GPS data [20,21]. However, the maneuver estimation based on the spaceborne BDS2 data still needs to be assessed due to the unbalanced distribution of the BDS2 satellites.
In this study, we analyze the orbit precision and the maneuver estimation results based on dual-frequency GPS and BDS2 observations from the TH-2. First, we introduce the spaceborne receiver on the TH-2 and assess its tracking ability, as well as its data quality. Next, the maneuver estimation by the POD using the spaceborne GPS and BDS2 observations is assessed. Furthermore, we analyze the performance of the GPS, BDS2, and GC combined POD of the TH-2. Finally, the conclusions are presented.
2. TH-2 Spaceborne GNSS Data Assessment
2.1. Spaceborne Receiver Feature
For orbit determination, the TH-2A and TH-2B are mounted with identical GNSS receivers that can track the GPS L1 and L2 and the BDS2 B1 and B3 signals simultaneously. All of the GPS satellites, and part of the BDS2 satellites from C01 to C14, can be observed. Besides the GNSS receiver, a rubidium atomic clock is installed on each satellite to provide timing and frequency for the receiver. GPS signals are used to generate the results of in-orbit positioning, clock offsets, and clock drifts, while the GC combined and the BDS2 positioning solutions are chosen as backups. For the time calibration, the time tags and pseudorange offsets of the raw observations are corrected by the combination of the clock offsets and clock drifts. It is noteworthy that the corrections of the receiver to GPS are generated from the last GPS or GC combined positioning results. However, the corrections to BDS2 are obtained from the last GC combined or BDS2 positioning results. Moreover, when the radar is in operation, the receiver suspends the time calibration to guarantee the time synchronization of the InSAR system.
2.2. Tracking Ability of GNSS Satellites
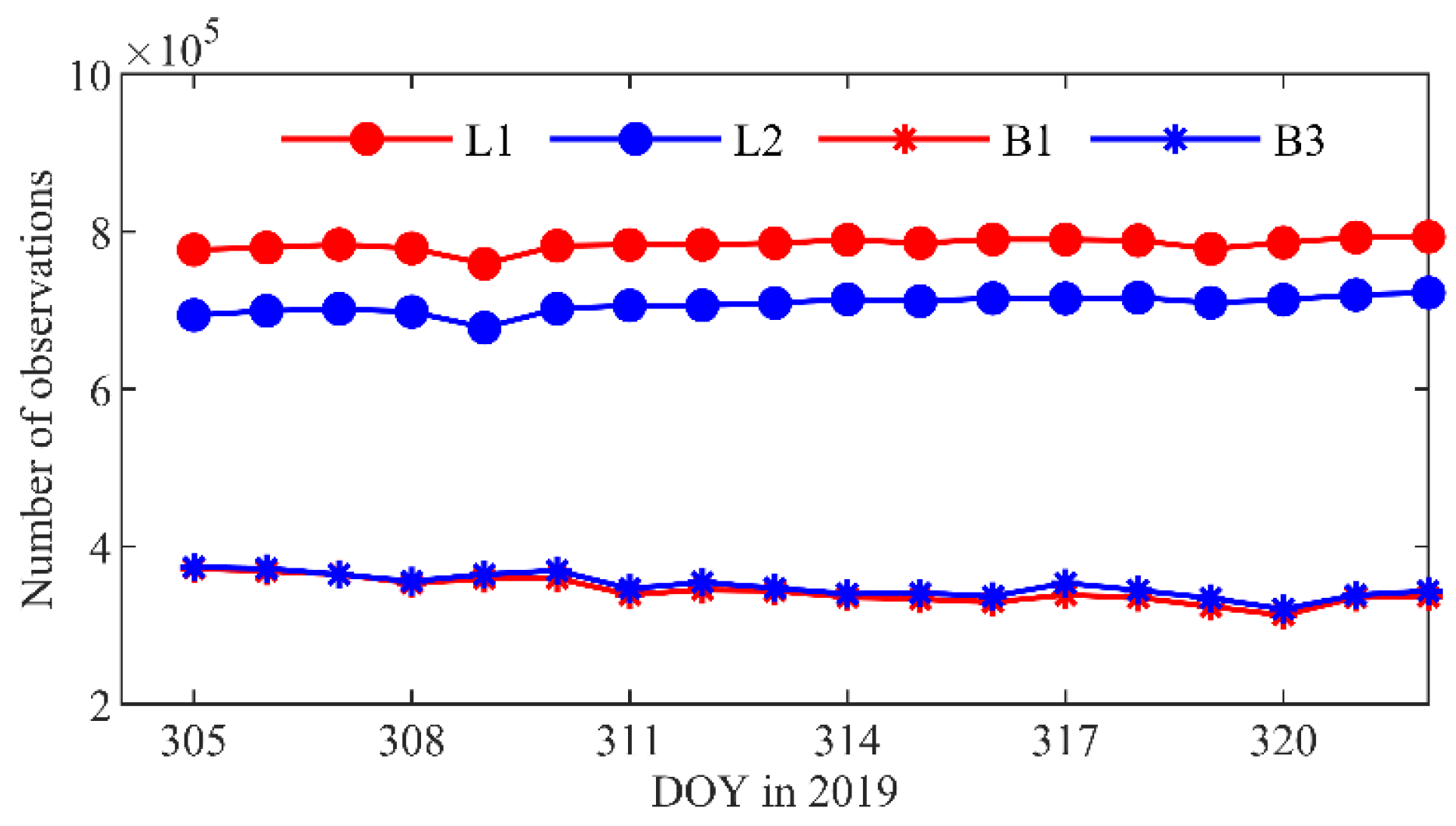
The GPS and BDS2 observations from the TH-2A and TH-2B during day of year (DOY) 305–322 in 2019, with a sampling interval of 1s, are used. Since the receivers on the two satellites are of the same type, the observation tracking performance of the TH-2A is similar to that of the TH-2B. Figure 2 shows the daily number of GPS and BDS2 observations from the TH-2A. For the GPS, owing to the semi-codeless tracking method of the receiver for the L2 frequency [22,23], the number of GPS L2 observations is about 9.7% less than that of the L1. For the BDS2, there is no obvious discrepancy in the tracking performance between the BDS2 B1 and B3 frequencies. The stable tracking abilities provide good support for the orbit determination.
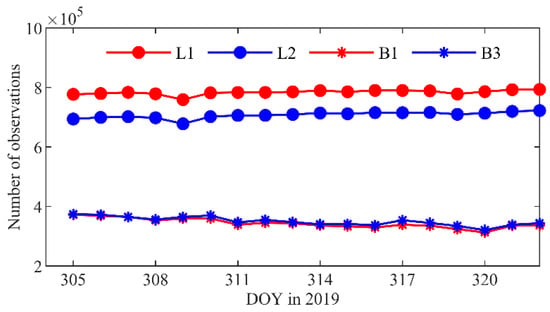
Figure 2.
Daily numbers of GPS and BDS2 observations for TH-2A.
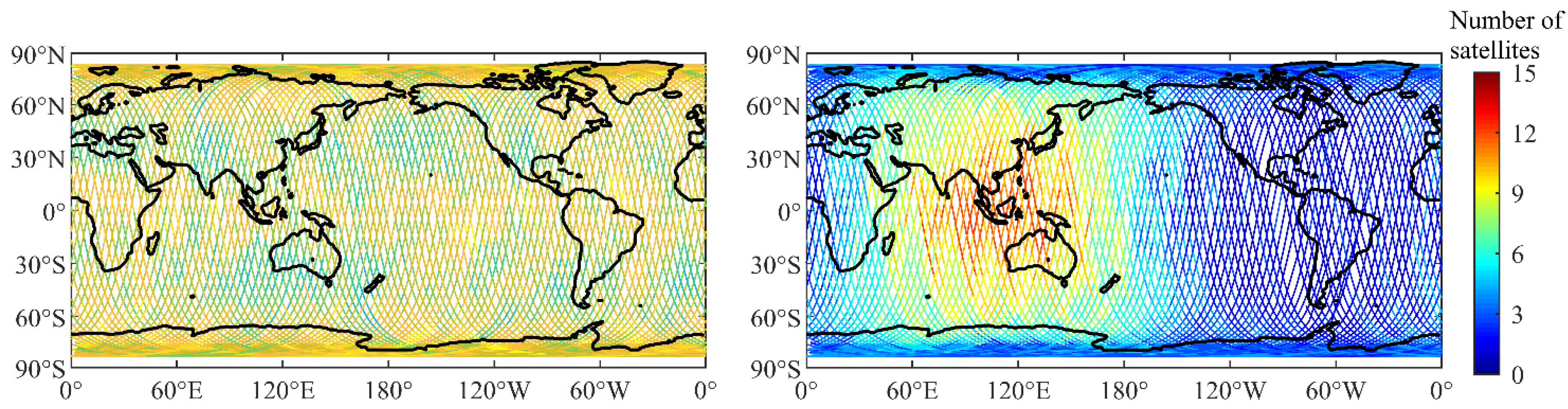
In November 2019, GPS consisted of 32 medium Earth orbit satellites (MEOs), while BDS2 included five geostationary Earth orbit satellites (GEOs), seven inclined geostationary orbit satellites (IGSOs), and three MEOs. Their differences in observation geometry can be reflected by the position dilution of precision (PDOP). When the cutoff elevation angle is set to 5°, the percentage of the epochs with the PDOP of GPS below six is about 99% along the trajectories of the TH-2A and TH-2B, whereas the corresponding percentage for BDS2 is about 60%, which means a weaker observation geometry compared with that of GPS. In addition, as GPS is a global constellation, there is no significant difference in the number of observed satellites in different areas, which is about 7–10, as shown in Figure 3. On the contrary, since the distribution of BDS2 is unbalanced, and most satellites provide service in the Asia-Pacific region from 55°S to 55°N, and 55°E to 180°E [24], the number of BDS2 satellites varies from region to region. The number of BDS2 satellites observed in the Asia-Pacific region is about 8.8, while the number in the Western Hemisphere is only 0–2.
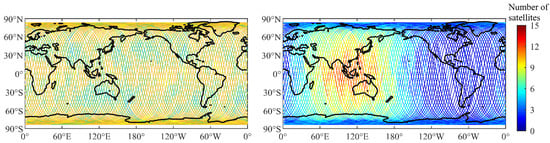
Figure 3.
Average number of GPS (left panel) and BDS2 (right panel) satellites observed along TH-2A orbits from DOY 305 to 310 in 2019.
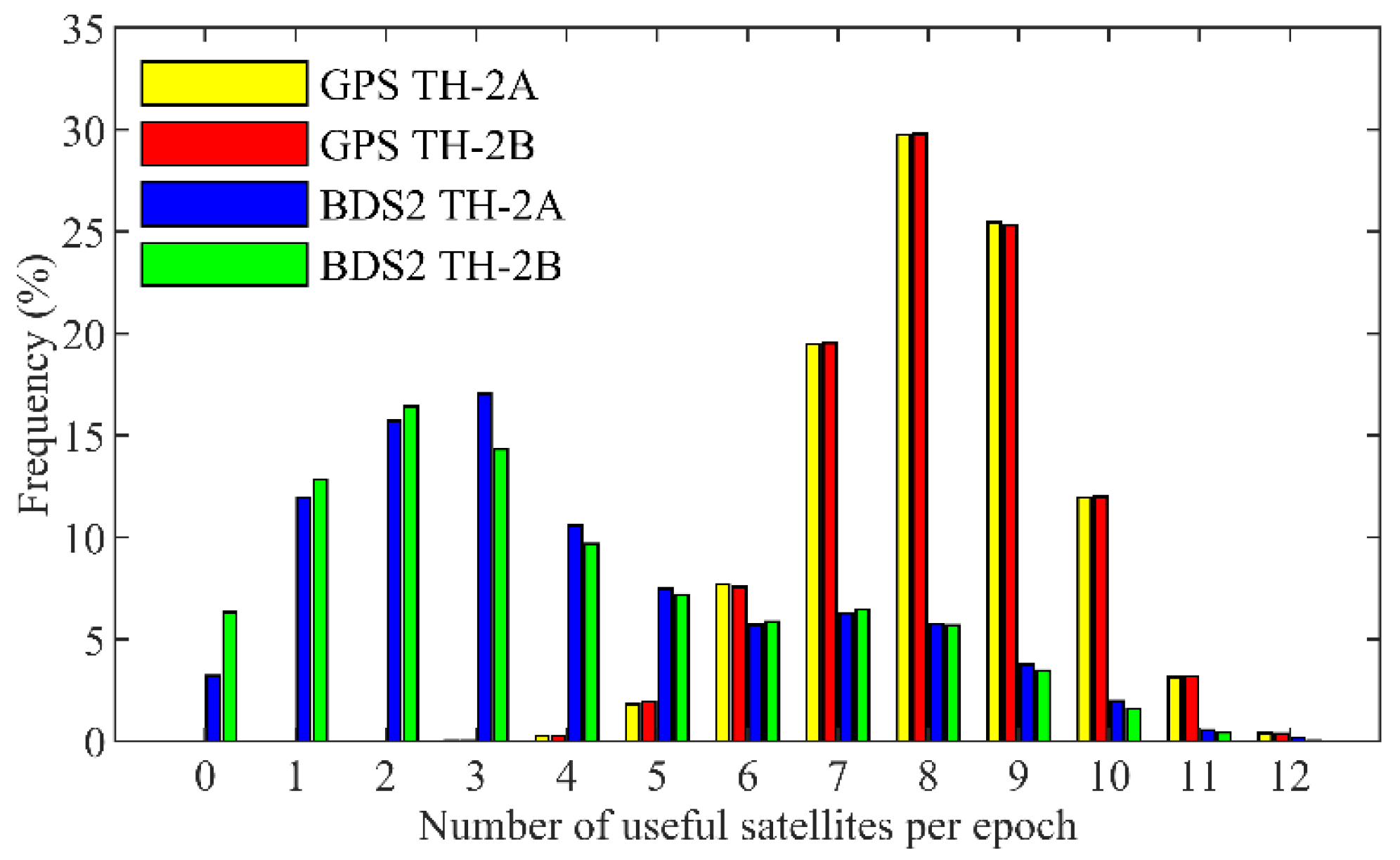
Since the ionospheric-free combination of the pseudorange and carrier phase is chosen as the basic measurement in the POD, we define an available satellite with observations from two frequencies that can be tracked simultaneously. As shown in Figure 4, there are about 99.98% of epochs with at least four available GPS satellites. The average number of available satellites per epoch is approximately 8.2. For the BDS2, it can be found that there is a 3–6% probability with no observation in an epoch, with about 50% of epochs with at least four available satellites. The average number of available BDS2 satellites is significantly smaller than that of GPS, which is about 3.5 per epoch.
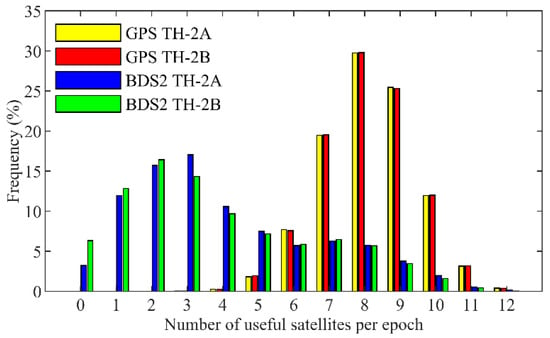
Figure 4.
Statistics of the average number of available GPS and BDS2 satellites per epoch for TH-2A and TH-2B.
2.3. Quality of GNSS Observations
2.3.1. Carrier-to-Noise Ratio
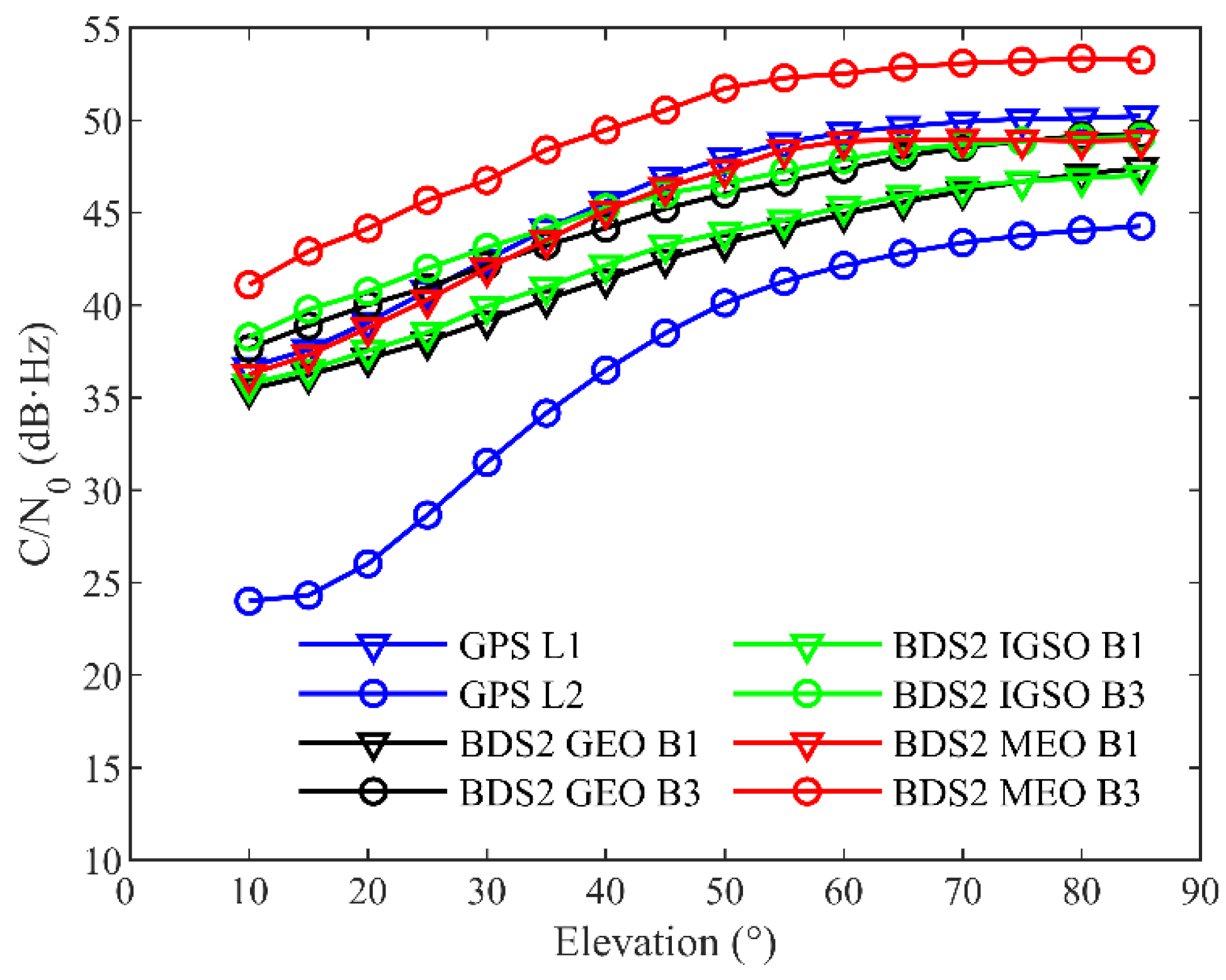
The signal strength can be measured by the carrier-to-noise ratio (C/N0), which shows the ratio of the carrier signal power to the noise power in a 1 Hz bandwidth [25]. Figure 5 indicates that the average C/N0 values of all signals increase as the elevation angle increases. For the GPS, the C/N0 values of the L1 frequency are larger than those of the L2 at all elevations, which is attributed to the differences in their tracking method. For the BDS2, the B3 frequency has about 2–4 dB∙Hz larger C/N0 values than the B1. In addition, it can be noted that the C/N0 values for the MEOs are slightly larger than for the GEOs and IGSOs, which may be due to the higher free-space loss of the GEOs and IGSOs than for the MEOs.
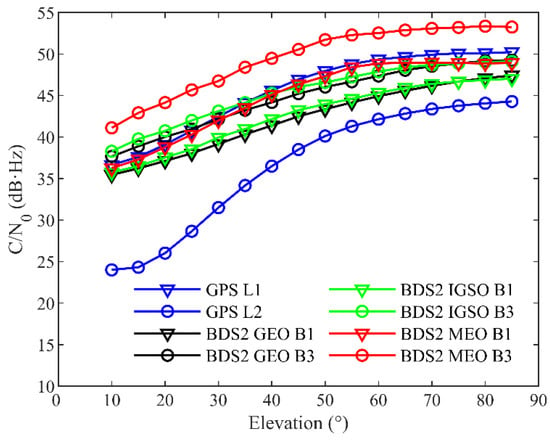
Figure 5.
Average C/N0 values of signals from TH-2A as a function of the elevation angle.
2.3.2. Pseudorange Multipath Combination
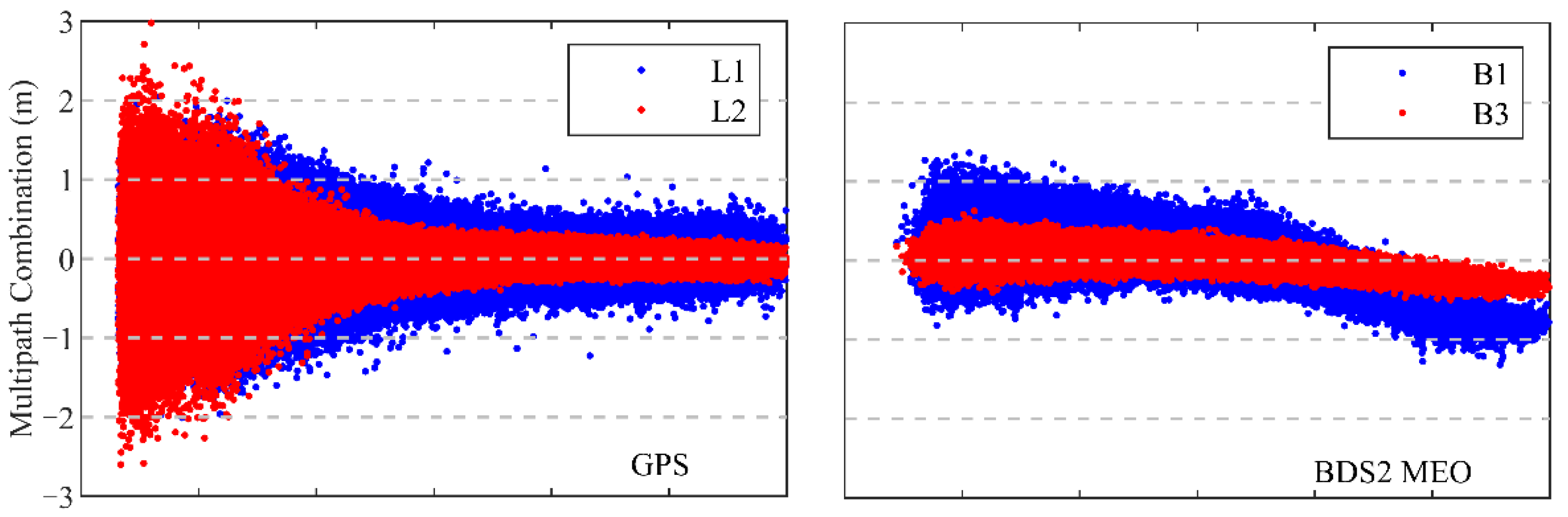
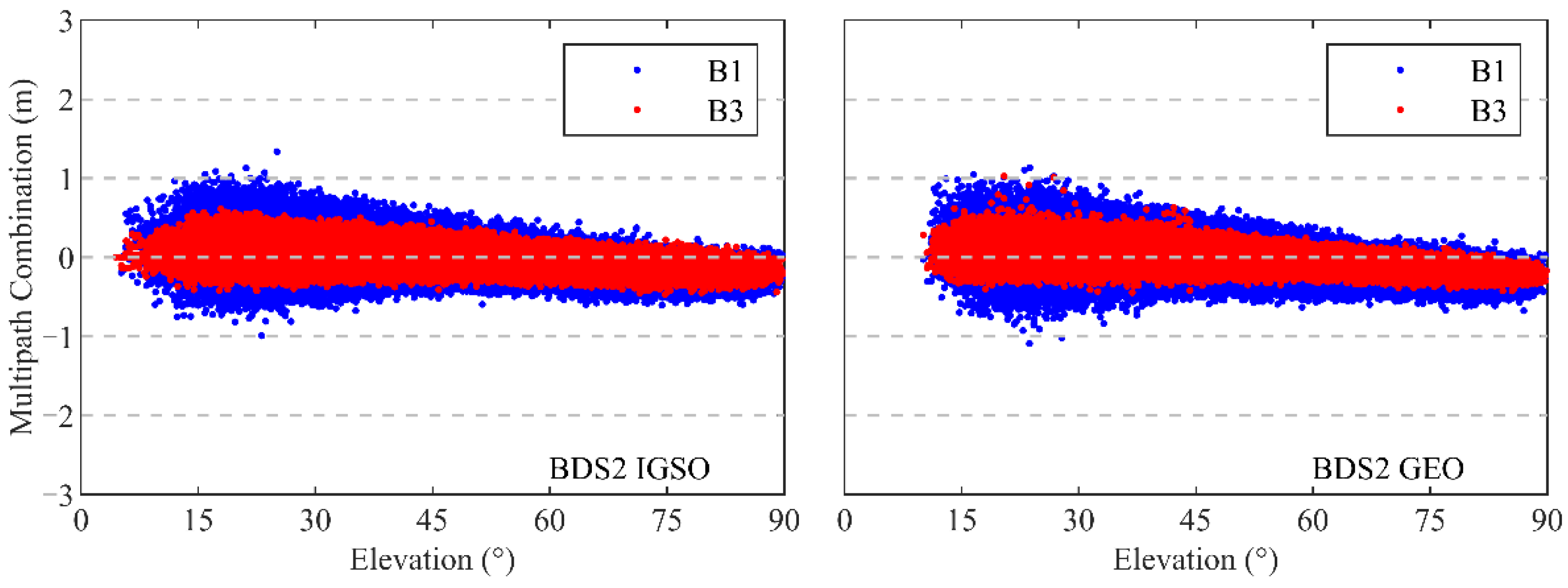
The pseudorange multipath combination (MPC) [26] is an important index to assess the quality of the pseudorange observations. Figure 6 shows the MPCs against the elevation angle of all signals for GPS and BDS2 from the TH-2A. As seen in the figure, the MPCs of the GPS L1 and L2 frequencies are within 3 m, while the MPCs of the BDS2 B1 and B3 are within 1 m in most cases. However, the elevation-dependent systematic bias can be noticed in the pseudorange observations of the BDS2 GEOs, IGSOs, and MEOs, which may be due to the satellite design [27,28]. The MPCs characteristic for the GEOs are close to that for the IGSOs. The systematic variations of the B1 frequency for the BDS2 MEOs are more obvious than those of the other signals, which exceed 1 m close to the zenith. To avoid the precision degradation of the pseudorange caused by systematic biases, an elevation-dependent piecewise linear model, as proposed by Wanninger [27], is applied to compensate for such bias in the BDS2 observations. The RMS of the MPCs for the BDS2 B1 and B3 frequencies are 0.20 and 0.13 m after the correction of the pseudorange observations, while the GPS L1 and L2 frequencies are 0.29 and 0.24 m. The results show that the pseudorange observations for BDS2 achieve a better quality than those for GPS.
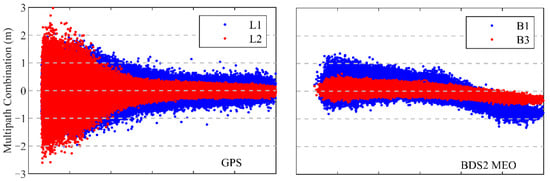
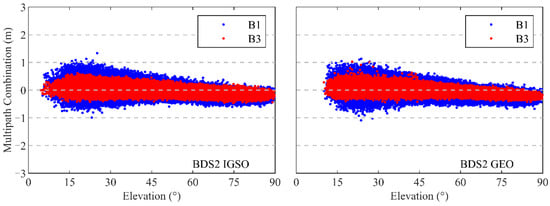
Figure 6.
Multipath combinations of GPS and BDS2 pseudorange observations from TH-2A as a function of the elevation angle.
2.3.3. Noise Level of Carrier Phase
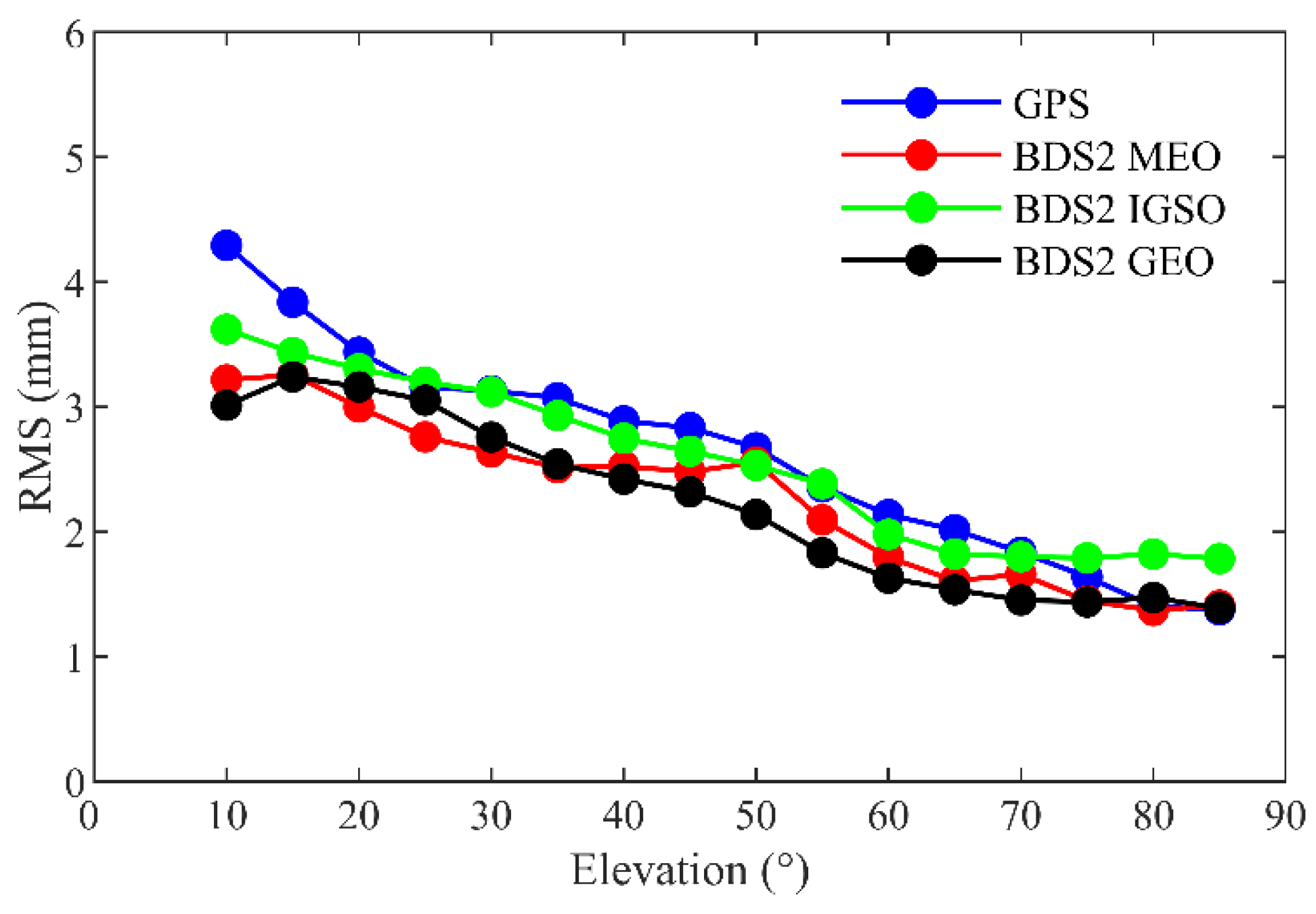
In the POD processing, the weight of carrier phase is greater than that of the pseudorange. Therefore, its quality is important for the POD accuracy of LEOs. The geometry-free combination [29] is adopted to assess the noise level of the carrier phase observations: , where and are the carrier phase measurements from two frequencies. This combination only contains ionospheric delays, initial ambiguities, and noises from the two frequencies. Furthermore, the ionospheric delays and ambiguities are eliminated by a three-order sliding polynomial, and the remaining residuals are considered as the noises of the carrier phase observations. The average RMS of the noises for the GPS is 3.1 mm, while those for the BDS2 MEOs, IGSOs, and GEOs are 2.5, 2.9, and 2.5 mm, respectively. Figure 7 shows the noise levels for the GPS, and BDS2 decrease as the elevation angle increases. The RMS of the noises are smaller than 5 mm, which indicates the good quality of the carrier phase observations.
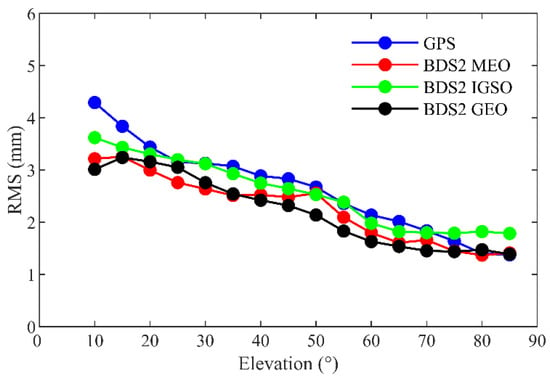
Figure 7.
Noise levels of GPS and BDS2 carrier phase observations from TH-2A as a function of the elevation angle.
3. POD Strategy
Table 1 shows the overview of the observation and dynamic models used in the POD of the TH-2. The GPS, BDS2, and GC combined POD are implemented by the reduced-dynamic orbit determination approach [30] and the experiments are carried out in the National University of Defense Technology orbit determination toolkit (NUDTTK) software [21,31]. The position and velocity of the LEOs are integrated by an 11th-order Adams–Cowell method [32,33] with a 10 s step-size:
where is the initial epoch and denotes the accelerations of the gravitational and nongravitational perturbations acting on the satellites. During the test periods, the TH-2A performed three maneuvers per day in the along-track direction, whose durations vary from 1 to 5 s. In the POD processing, maneuver accelerations are considered as constants over the predefined thrust durations and estimated together with the initial state vector, receiver clock offsets, ambiguities, as well as dynamical relations by the batch least-square estimator. The velocity change for each maneuver can be obtained by , where Δt is the thrust duration. Since irregular thruster operation times may cause the intervals of the Adam–Cowell integrator to not match with the maneuver durations, we adopt an eighth order single-step Runge–Kutta method [34] with a 0.001 s step-size to increase the integration accuracy in the vicinities of the maneuvers. Specific mathematic formulas can be found in the strategy of the NUDTTK [21]. Since the impact of the receiver phase center variation (PCV) is non-negligible in the POD processing [6], we generate the PCV maps by the residual method [35] based on in-flight data and apply them in the GPS, BDS2, as well as GC combined POD. With respect to the GC combined processing, due to the fact that the current precision of the orbit and clock products for BDS2 is weaker than GPS [36,37], the weights of the GPS and BDS2 observations are set to 1 and 0.5, respectively. Meanwhile, the independent epoch-wise receiver clock offsets are introduced for each system because the time tag corrections for the GPS measurements are different than those for the BDS2. Detailed explanations are illustrated in Section 4.3.

Table 1.
Processing strategy for the POD of TH-2.
4. Maneuver Assessment and POD Results
4.1. Maneuver Assessment by POD
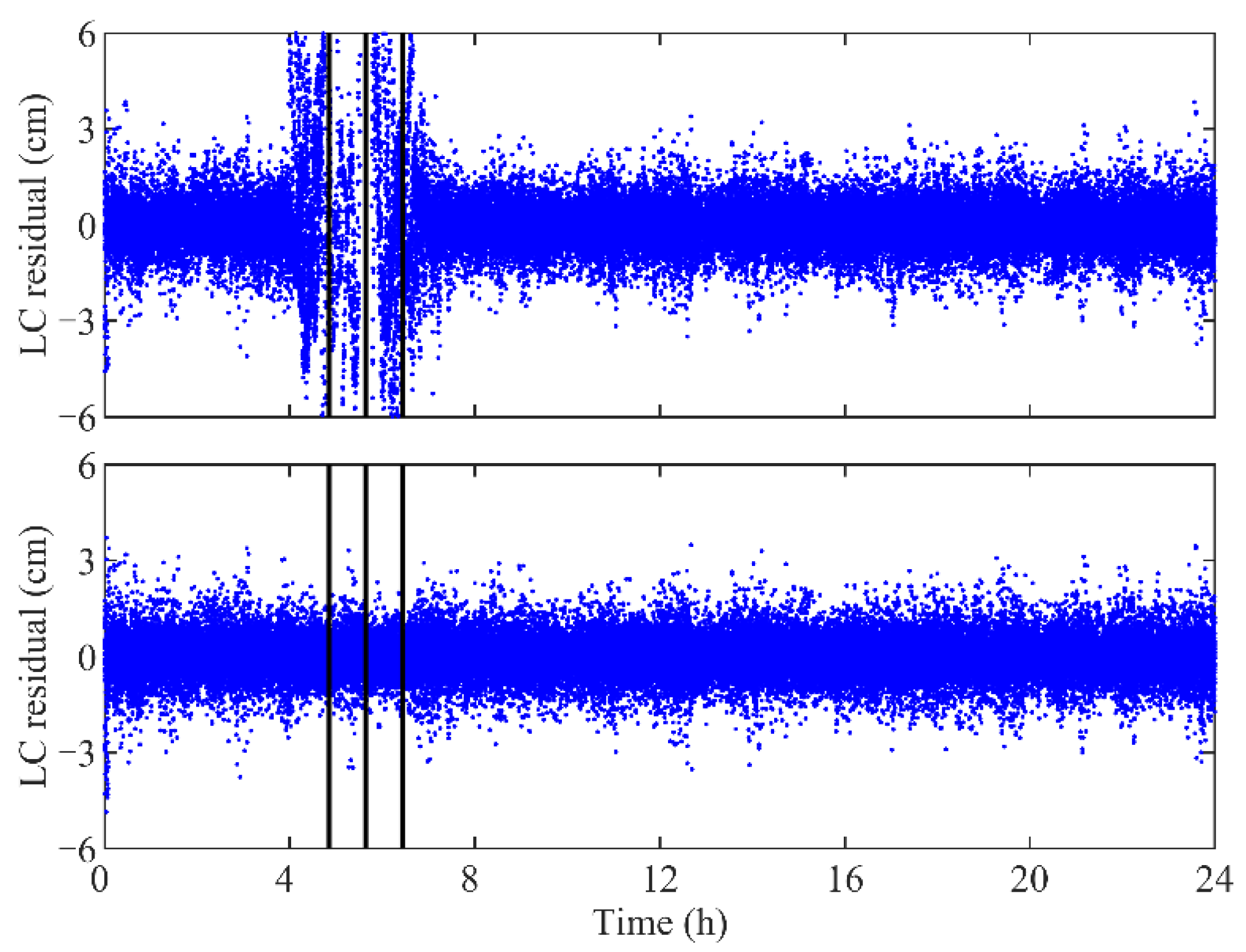
Without proper maneuver handling, the quality of the POD results will degrade around the thrust execution times. Therefore, the performance of the maneuver handling is important for the orbit precision of the satellites. Here, we adopt the residuals of the POD to reflect the influence of thrusts to the orbit accuracy. It may be noted that the ionosphere-free carrier phase linear combination (LC) residuals of the GPS-based POD for the TH-2A without the maneuver estimation are larger than those with the maneuver estimation around the thrust execution periods, as shown in Figure 8.
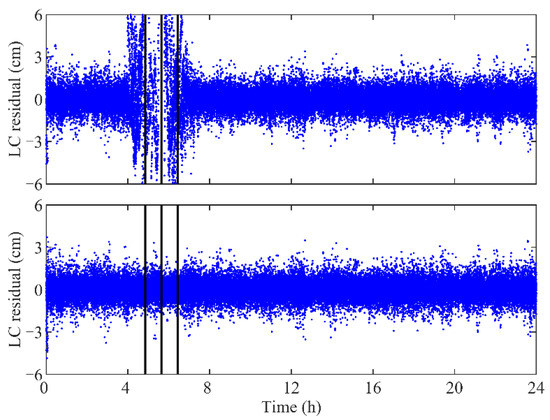
Figure 8.
LC residuals of GPS-based POD for TH-2A without maneuver estimation (top panel) and those with maneuver estimation (bottom panel) on DOY 314, 2019. The vertical bars denote the centers of the thrust execution periods. Residuals beyond ±6 cm are not shown in the top panel.
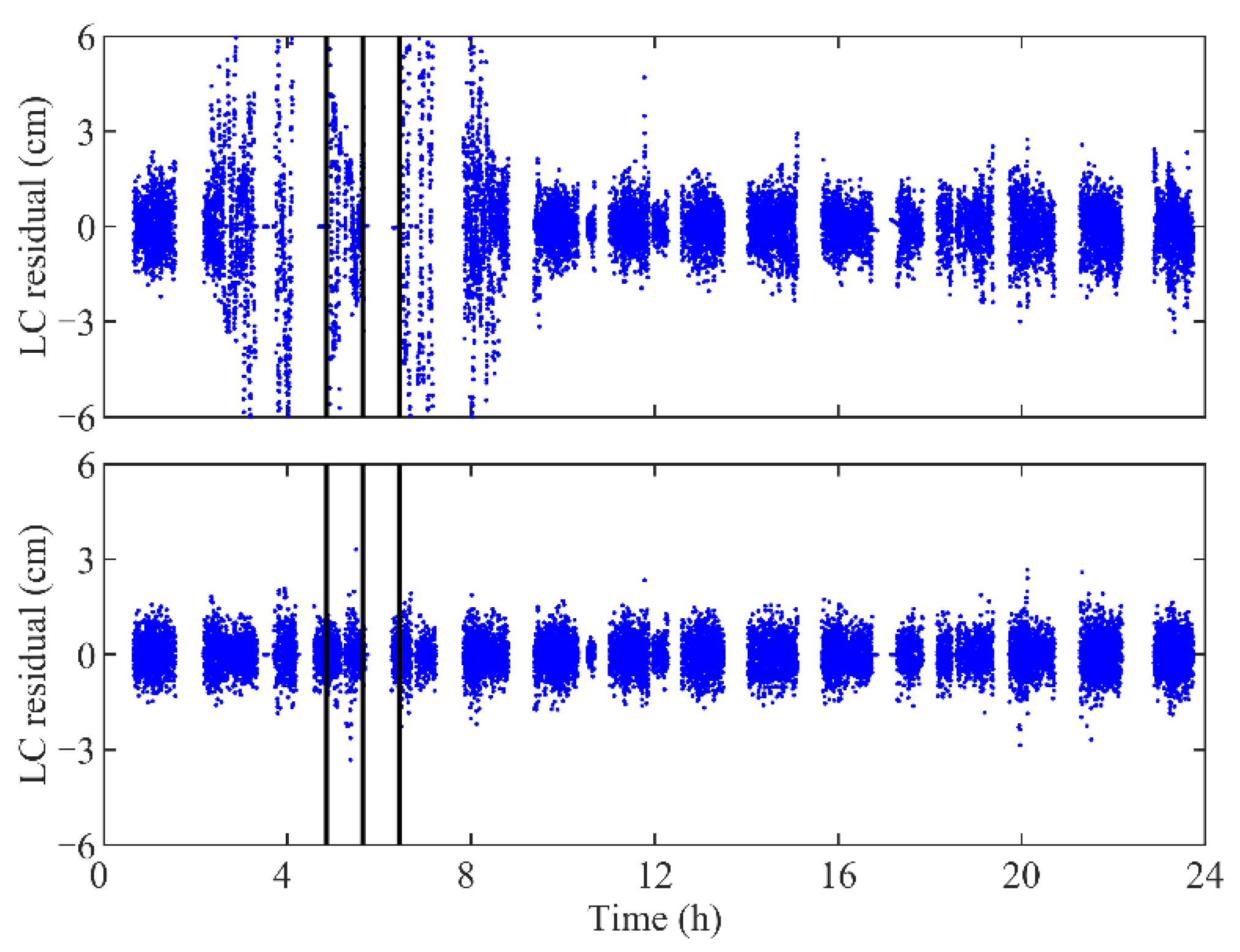
Since the inclusion of the observations from the BDS2 GEOs have a negative influence on the POD precision of LEOs [47,48], only the observations from the MEOs and IGSOs are used in the BDS2-based POD. Since the number of available BDS2 observations is smaller than the GPS, the minimum number of available navigation satellites per epoch is set to two instead of three in the BDS2-based POD. Figure 9 shows the LC residuals of the BDS2-based POD for the TH-2A with and without maneuver estimation. Periodic gaps can be noticed in the BDS2 LC residuals because there is only zero to one available satellite at these epochs. If there is no maneuver handling, the LC residuals during the thrust execution periods are apparently larger than those at other epochs. On the contrary, the significant fluctuations of the residuals around the maneuver thrusts are removed when the maneuver handling is taken into account.
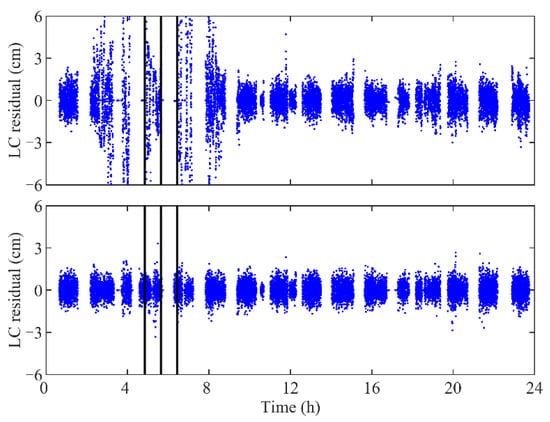
Figure 9.
LC residuals of BDS2-based POD for TH-2A without maneuver estimation (top panel) and those with maneuver estimation (bottom panel) on DOY 314, 2019. The vertical bars denote the centers of thrust execution periods. Residuals beyond ±6 cm are not shown in the top panel.
Table 2 shows the average RMS of the residuals for the GPS- and BDS2-based POD. It can be found that the LC residuals for the POD with maneuver estimation are significantly reduced compared with those without maneuver estimation. Moreover, such values for the TH-2A with maneuver estimation are comparable with those for the TH-2B, whose thrusters did not fire during the test periods. Similar to the LC residuals, the ionosphere-free linear pseudorange combination (PC) residuals for the POD can also be reduced with maneuver handling. These results indicate that the impact of thrusts on the POD results of the LEOs can be eliminated by maneuver handling, and their orbit precision is on par with that of the maneuver-free LEOs.

Table 2.
Average RMS of PC and LC residuals of GPS- and BDS2-based POD for TH-2A (without maneuver estimation), TH-2A (with maneuver estimation), and maneuver-free TH-2B.
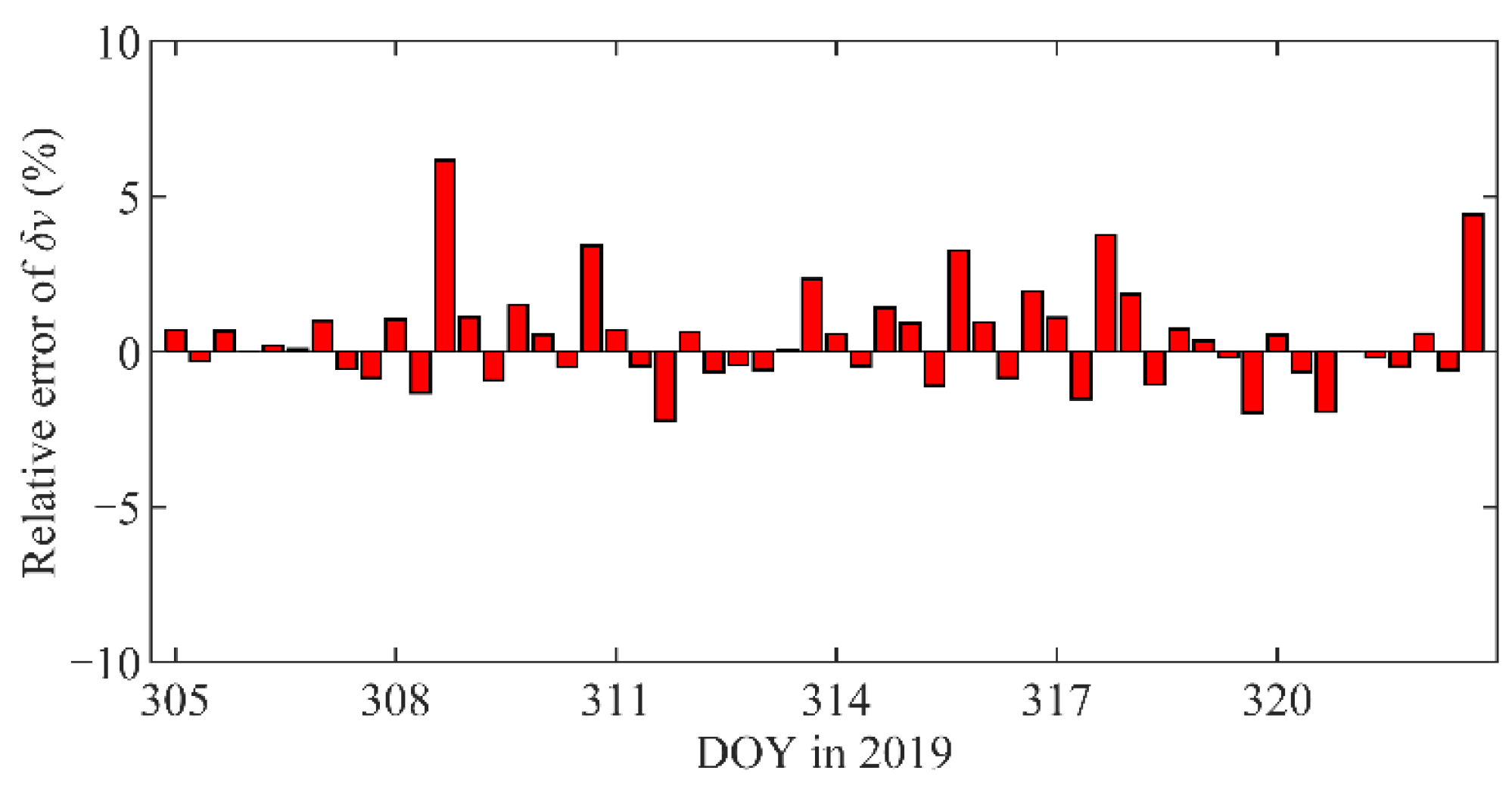
The maneuver accelerations derived from the GPS data have proven to be in good agreement with the onboard telemetry data [21]. Therefore, the GPS-derived results can be treated as references to evaluate the maneuver estimations by the BDS2-based POD. Figure 10 shows the relative errors of velocity changes obtained by the BDS2-based POD with respect to those obtained by the GPS-based POD, which are less than 7.0%, and the mean relative error is 1.2%. The result indicates that the maneuver estimations of the LEOs derived from the regional BDS2 data are on par with those derived from the global GPS data.
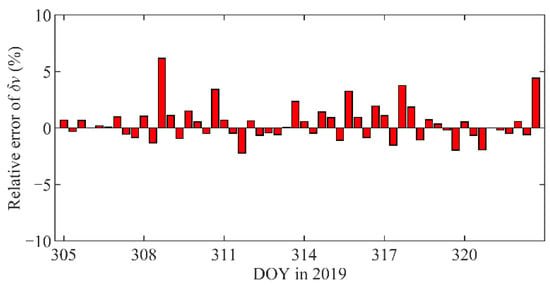
Figure 10.
Relative errors of velocity changes obtained by BDS2-based POD wrt those by GPS.
4.2. POD Performance of Single GNSS
As an internal consistency assessment method for the POD, overlap comparison is utilized to evaluate the orbit precision of the GPS-based POD for the TH-2. Table 3 shows the average RMS of 6 h overlap comparisons in the radial, along-track, and normal direction for the GPS-based POD solutions. The 3D RMS statistics are given in the most right column. Since the two satellites are equipped with the same type of receiver, the RMS of the overlap comparisons for the TH-2A are close to that for the TH-2B. The along-track components of the overlap errors are larger than the radial and normal components, which is attributed to the weaker constraint of the reduced-dynamic model in this direction [49]. The result indicates that the GPS-based POD of the TH-2 has a good internal consistency, with 0.7 cm in 3D RMS.

Table 3.
Average RMS of overlap comparisons for GPS-based orbit solutions for TH-2A and TH-2B.
For the BDS2-based POD, the average 3D RMS of the overlap comparisons are 5.49 and 6.36 cm for the TH-2A and TH-2B, respectively. Compared with the GPS-based orbits, the internal consistency of the BDS2-based orbits is weaker due to the poor viewing geometry. Table 4 shows the statistics of the orbit comparisons between the BDS2- and GPS-based POD in different regions. It may be noted that the along-track and normal components of the RMS errors in the Asia-Pacific region are smaller than those in the other areas. Since most BDS2 satellites are located in the Asia-Pacific region, the regional constellation results in a 3D RMS error of 7 cm in this region, which is slightly better than that of 9 cm in other regions.

Table 4.
Average RMS of orbit differences between BDS2- and GPS-based POD in different regions.
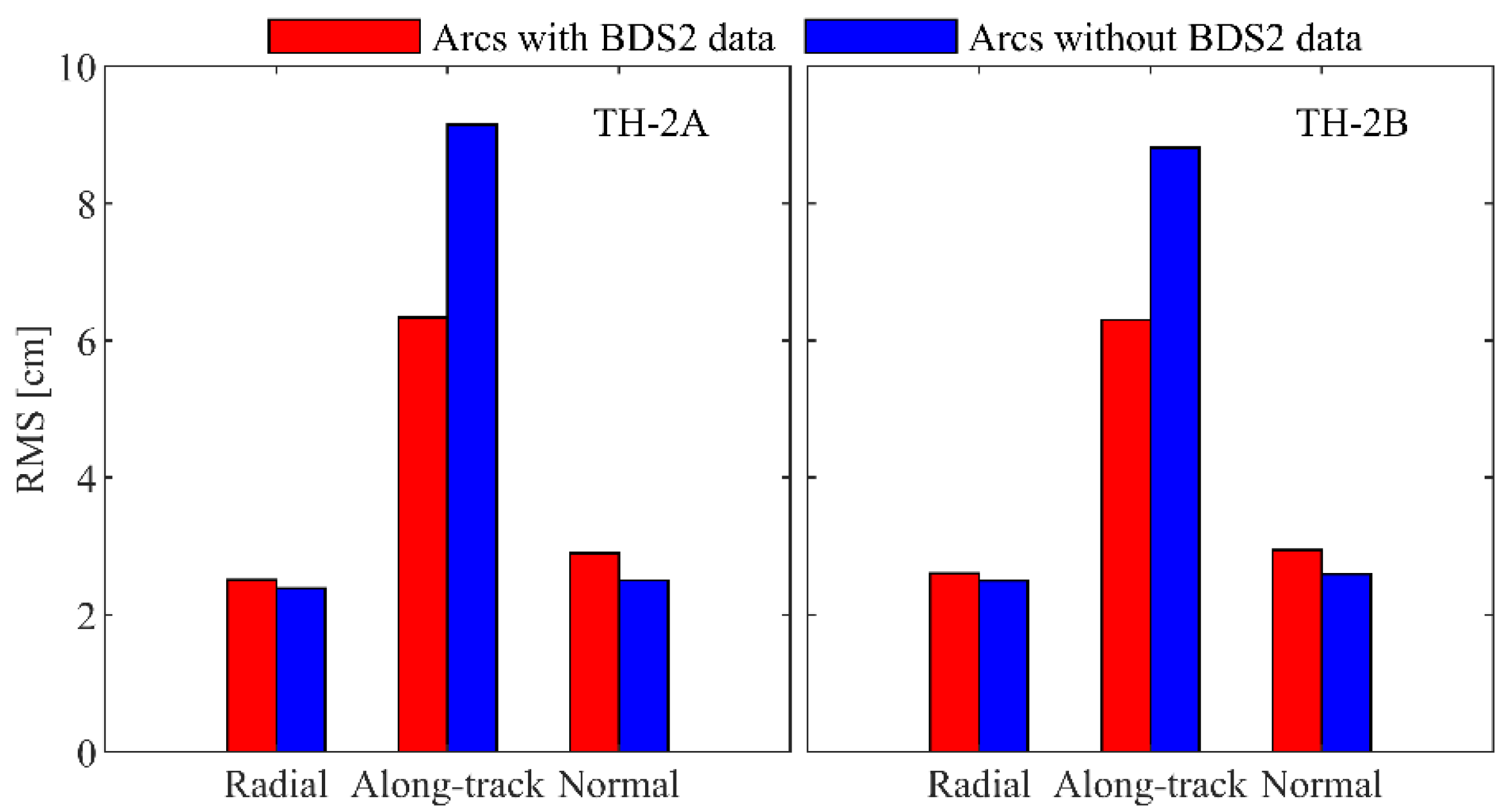
There are about 2.0 h with no available BDS2 IGSOs/MEOs per day. Figure 11 shows the orbit differences between the BDS2- and GPS-based POD during the arcs with and without the BDS2 data. The orbit accuracy with/without the BDS2 data in the radial and normal direction is 2–3 cm. However, the orbit accuracy in the arcs of no BDS2 data in the along-track direction significantly degrades by 42.1% on average.
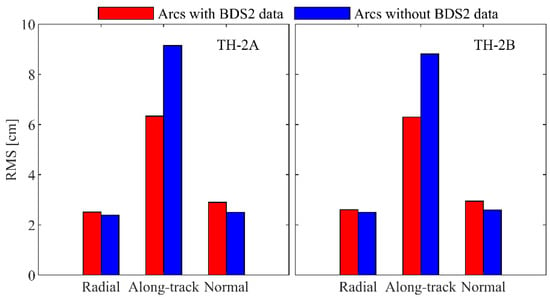
Figure 11.
Orbit differences between BDS2- and GPS-based POD during the arcs with and without BDS2 data.
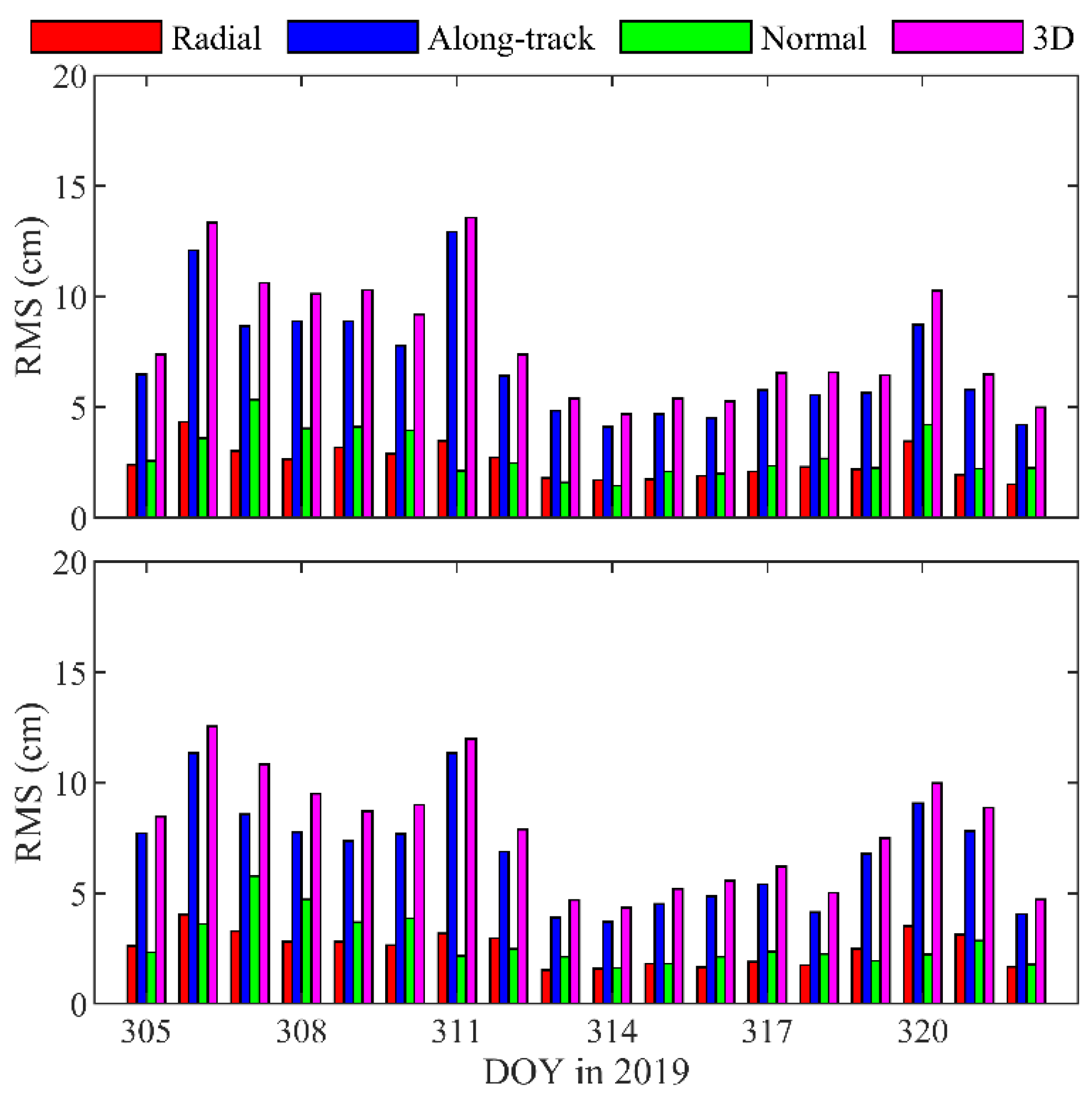
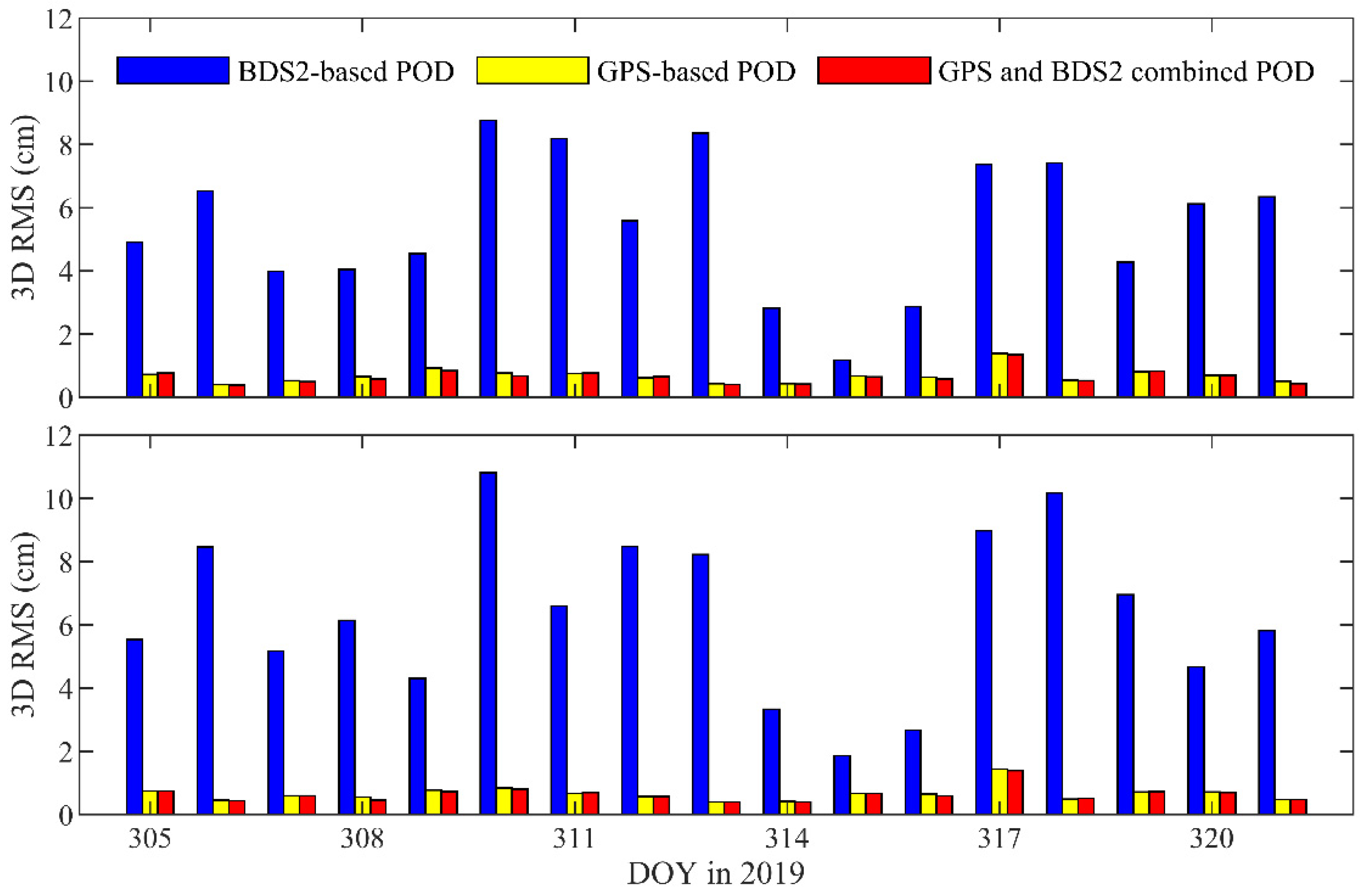
Figure 12 shows the daily RMS of the orbit differences between the BDS2- and GPS-based POD. The along-track components of the RMS errors are larger than the radial and normal components for each arc. The 3D RMS of orbit differences are all smaller than 15 cm, and the average values are 7.99 and 7.83 cm for the TH-2A and TH-2B, respectively. These results indicate that the precision of the BDS2-based orbits of the TH-2 can achieve a subdecimeter level and satisfies the InSAR mission requirement.
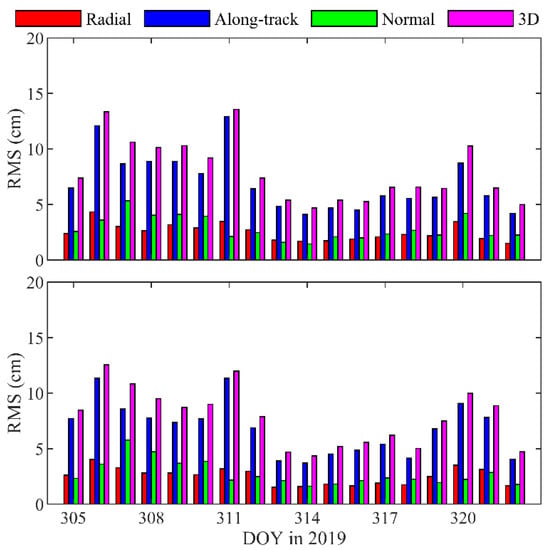
Figure 12.
Orbit differences between BDS2- and GPS-based POD in radial, along-track, normal, and 3D directions for TH-2A (top panel) and TH-2B (bottom panel).
4.3. GPS and BDS2 Fused Results
The combination of multi-GNSS provides a better observation geometry and achieves a more robust positioning ability than a single navigation system. Therefore, it is necessary to analyze the results of the GC combined processing for the TH-2. In addition, as with the BDS2-based POD, we exclude the BDS2 GEO observations so to ensure the precision of the combined processing results.
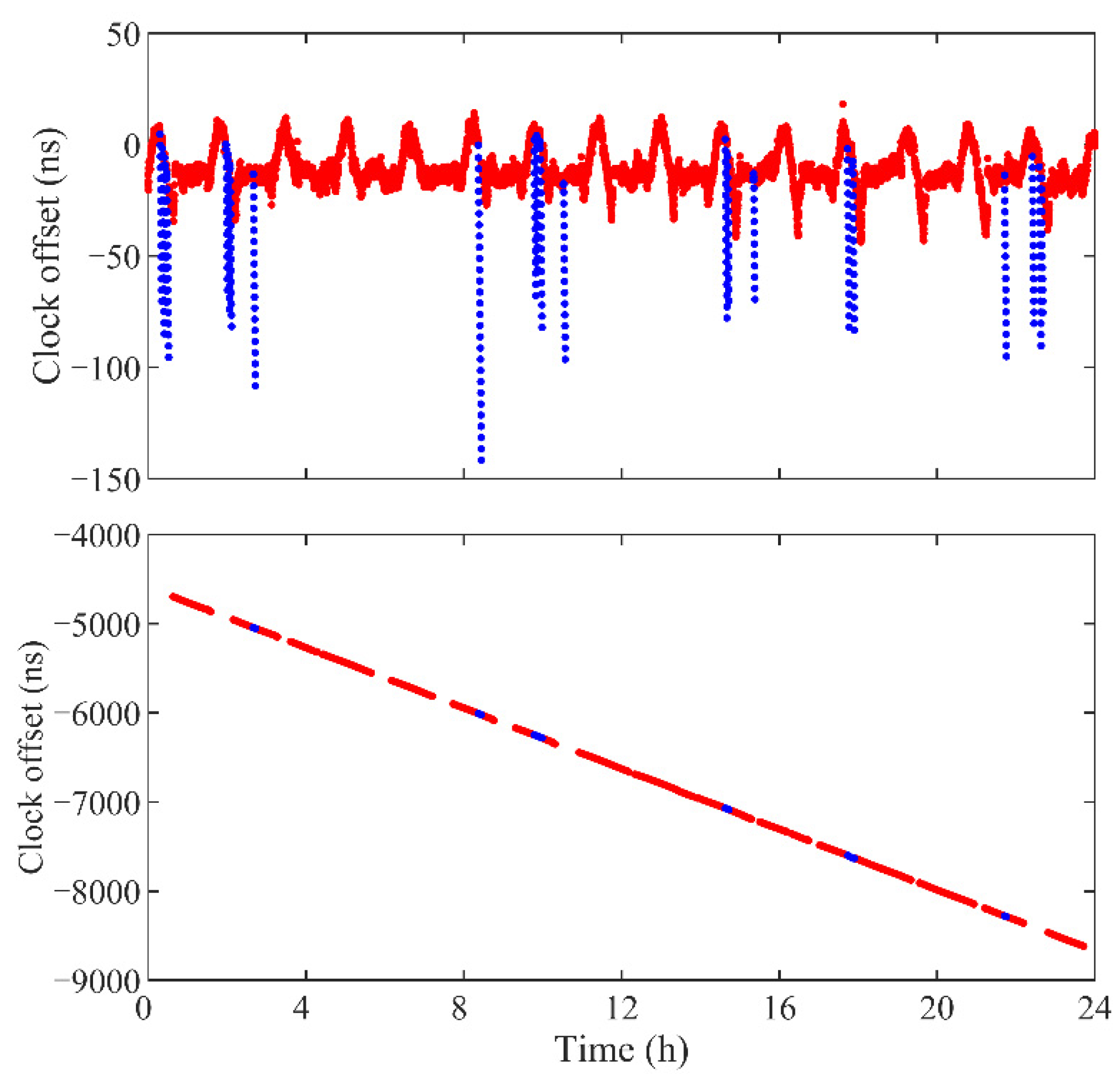
In multi-GNSS data processing, the characteristics of the receiver must be taken into account when estimating the ISB. As introduced in Section 2.1, the time tag corrections of the receiver to the raw GPS and BDS2 observations are different when the GPS is used for positioning, which are a time-varying value and a constant, respectively. Thus, the clock offsets derived by the GPS- and BDS2-based POD are different from each other, as shown in Figure 13. For the GPS, most clock offsets are within 40 ns. However, several large deviations can be noticed due to the suspension of time calibration during the radar operating period. As the velocity of the GPS satellite is about 4 km/s, −150 ns of receiver clock offset will lead to about 0.6 mm error in the distance when calculating the satellite position from the ephemeris. Such a position error will cause a similar magnitude of deviation for the receiver positioning [50]. Therefore, the influence of the deviations on the precision of the GPS-based POD is insignificant. For the BDS2, the clock offsets are accumulated, which is attributed to the fact that the differences between the pseudorange offsets and constant corrections are accumulated in the observations. In addition, the limited available BDS2 satellites results in the periodic gaps of the clock offsets. Since the time tag corrections cannot be obtained, and the accumulation of the BDS2 receiver clock offset increases the orbit errors, we correct the raw BDS2 data by using clock offsets obtained from the first BDS2-based POD. Due to the discrepancies in the data processing strategy, the ISB between GPS and BDS2 is not a constant. Therefore, the independent clock offsets for GPS and BDS2 should be estimated respectively in the GC combined processing of the TH-2.
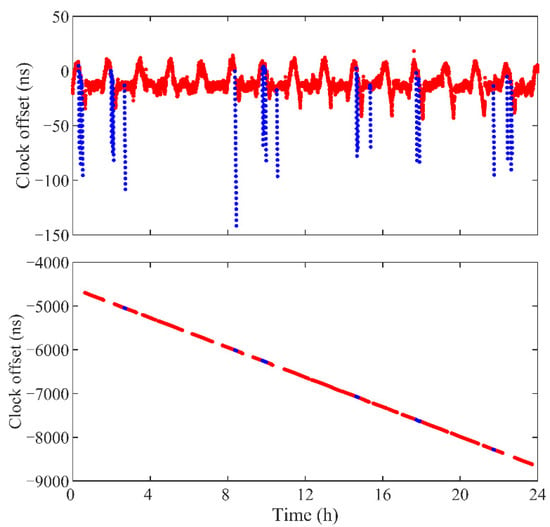
Figure 13.
Clock offsets of TH-2A (on DOY 308, 2019) obtained from POD based on GPS observations (top panel) and BDS2 observations without correction (bottom panel). Blue and red points show the estimated clock offsets when radar is in operation and powered off, respectively.
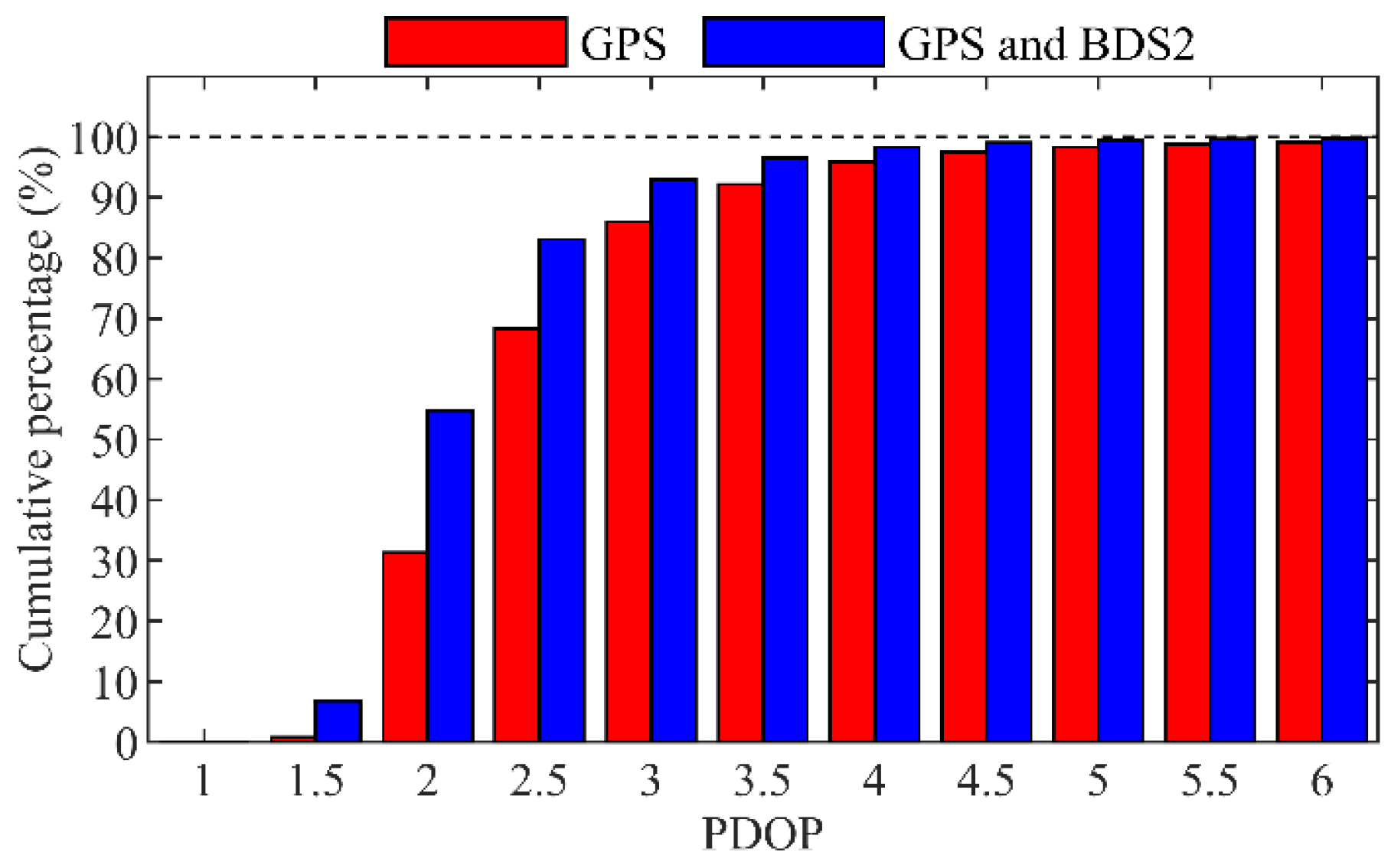
The observation geometry has a significant impact on the orbit accuracy, whose characteristics can be reflected by the PDOP values. Figure 14 shows that about 86% of the epochs with the PDOP values of GPS less than three along the trajectories of the TH-2. When the BDS2 IGSO and MEO observations are added, more than 90% of the epochs have PDOP values of GPS + BDS2 less than three. The average PDOP values of GPS + BDS2 and GPS-only are 2.1 and 2.5, respectively, which means a better observation geometry for the GC combined processing.
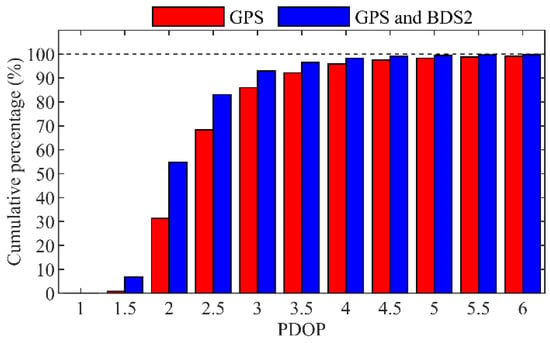
Figure 14.
Cumulative percentages of the PDOP values of GPS-only and GPS + BDS2 along the trajectories of TH-2A.
As an important navigation method in real-time satellite orbit determination, single point positioning (SPP) can be used to evaluate the contribution of BDS2 to the LEO orbit determination. By using the GFZ precise ephemeris, the SPP solutions are obtained based on the ionosphere-free pseudorange observations. Table 5 shows the statistics of the orbit differences of the GPS-only and GC combined SPP solutions with respect to the GPS-based POD. The SPP error in the radial is larger than that in the along-track or normal direction due to the uneven distribution of the viewing GNSS satellites in space (i.e., GNSS satellites in the nadir direction cannot be observed). Compared with the GPS SPP solutions, the precision of the GC combined SPP solutions is improved by more than 6% in 3D RMS.

Table 5.
Average RMS of orbit differences of GPS-only and GC combined SPP solutions with respect to GPS-based POD for TH-2A and TH-2B.
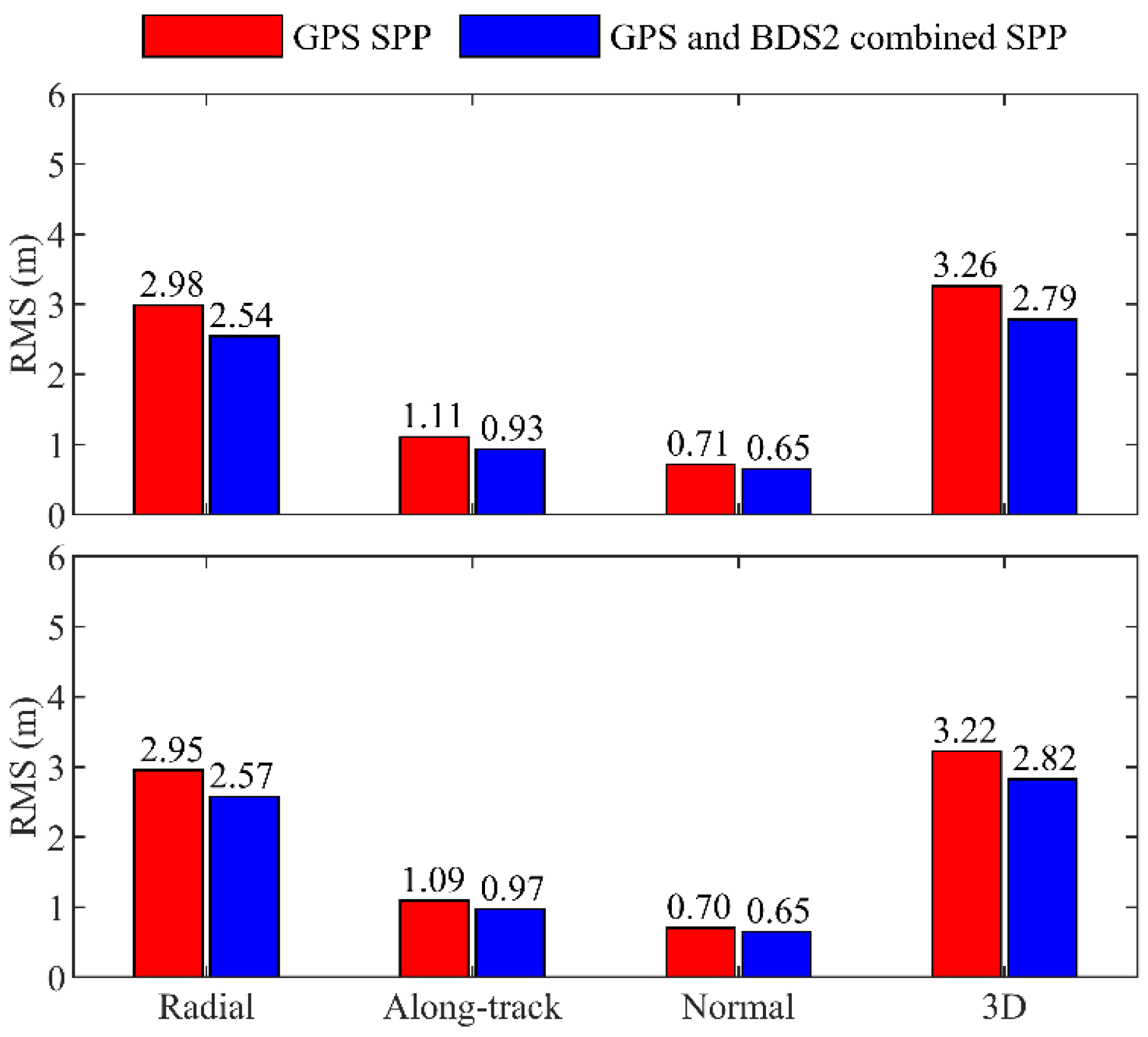
For a single GNSS system, the PDOP values usually amount to 2–3 under open sky [51]. A larger PDOP value means a weaker observation geometry, thereby degrading the precision of the orbits. Figure 15 shows the precision of the GPS and GC combined SPP solutions when the PDOP values of GPS exceed three. Compared with the GPS-only, the precision of the GC combined SPP solutions is improved by 14.4% and 12.4% for the TH-2A and TH-2B in 3D RMS, respectively. Since the PDOP values of GPS + BDS2 are smaller than those of GPS-only, the GC combined solutions can achieve a better accuracy in those regions with poor GPS viewing geometry.
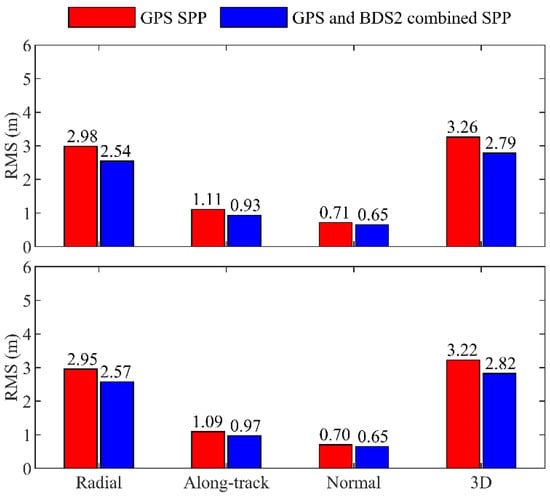
Figure 15.
Differences of GPS and GC combined SPP solutions with respect to GPS-based POD when the PDOP values of GPS exceed 3. (top panel) is TH-2A and (bottom panel) is TH-2B.
The contribution of the BDS observations for the combined POD is analyzed in this section. The residuals and overlap comparisons are used to assess the orbit precision. Table 6 shows that the values of the residual RMS of the combined POD are close to those obtained by the GPS- and BDS2-only POD, as listed in Table 2. The overlap comparisons of the GC combined POD are smaller than those of the single BDS- and GPS-based POD. Figure 16 indicates that the daily 3D RMS of the overlap differences of the GC combined POD are less than those of the BDS2-only. The overlap comparisons of the GC combined solutions are on average 0.65 and 0.64 cm (3D RMS) for the TH-2A and TH-2B, respectively. Compared with the GPS-based orbits, the precision of the GC combined solutions is only improved by 3–4% in 3D, which is hampered by the precision of the BDS2 precise orbit and clock products [36].

Table 6.
Average RMS of PC and LC residuals of GC combined POD.
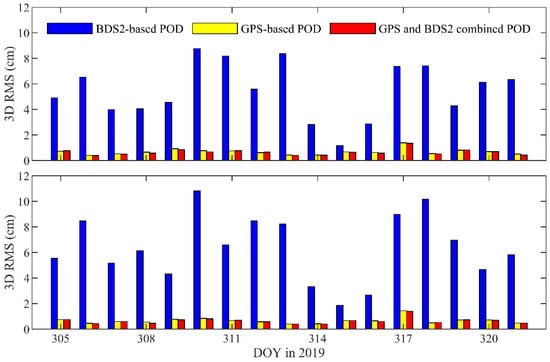
Figure 16.
3D RMS of overlap comparisons of BDS2-only, GPS-only, and GC combined POD for TH-2A (top panel) and TH-2B (bottom panel).
5. Discussion
Orbital maneuvers can change the accelerations of the LEOs and therefore have an important impact on the accuracy of LEO orbits. Our results show that the maneuver handling based on the spaceborne BDS2 data can eliminate the influence of thrusts to the TH-2 orbits, and the accuracy of the BDS2-based orbits of the TH-2 is at the same level as other missions, such as the Fengyun-3C [9], Fengyun-3D [11], and CSES [12]. After the correction of the pseudorange data, the RMS of the pseudorange multipath for BDS2 is less than that for GPS. Therefore, the BDS2 pseudorange measurements exhibit a smaller PC RMS than the GPS. The LC RMS of the BDS2-based POD is larger than that of the GPS for the TH-2A without maneuver estimation, which may be attributed to the lower precision of the BDS2-based orbits. By using the observations from only six BDS2 IGSOs and three MEOs, the maneuver estimations are on par with those based on global GPS. With the completion of the BDS3, more BDS3 satellites can be used for the POD of LEOs and the further investigation of maneuver estimation. Meanwhile, considering that the BDS3 orbit and clock products are significantly improved, more research is needed on the contribution of BDS3 to the POD of LEOs.
In the GPS and BDS2 combined processing, due to the differences of the time tag corrections for the GPS and BDS data, we found that it is necessary to estimate the independent receiver clock offsets for each system. The results show that the GPS and BDS2 combined SPP and POD solutions have better precision than the corresponding GPS-only results. However, the combined POD solutions are only assessed by the observation residuals and overlap comparisons, which are both internal evaluation methods. If independent external validations are performed in the future, like satellite laser ranging measurements, it would be good for orbit quality evaluation. In addition, the ISB is usually estimated as a constant in the previous combined POD of LEOs. Such a strategy is effective for GNSS receivers using both the GPS and BDS2 to perform in-orbit positioning [16]. For the GNSS receiver under a single GNSS positioning mode, if the time tag corrections for the different system are inconsistent, the independent clock offsets for each system should be estimated in combined processing.
6. Conclusions
We analyzed the orbit determination and maneuver estimation of the TH-2 satellite system based on spaceborne GPS and BDS2 observations. The analysis of the data quality shows that the spaceborne receiver of the TH-2 has a stable data tracking ability and a good observation quality.
The assessments of the maneuver handling show that the residuals of the POD for the maneuvering TH-2A are comparable to those of the maneuver-free TH-2B. Maneuver handling can avoid the precision degradation of the GPS- and BDS2-based POD caused by thrusts. The GPS-based POD solutions have good accuracy, which are better than 0.7 cm in 3D RMS. The orbit precision of the BDS2-based POD is smaller than 8 cm compared with the GPS-based orbits. This result indicates that the precision of the BDS2-based orbits achieves the subdecimeter level and satisfies the accuracy requirement of 1 m for the TH-2. In addition, the relative error of velocity changes between the GPS- and BDS2-based POD is less than 7.0%, which indicates that the maneuver estimation by using regional BDS2 data can be on par with using global GPS data.
In the fusion of the GPS and BDS observations, we found that the independent receiver clock offsets need to be estimated for each system due to the different time tag corrections for the GPS and BDS2 data obtained by the TH-2. Compared with the GPS-only solutions, the precision of the GPS and BDS2 combined SPP solutions is improved by 12–14% when the PDOP values of GPS exceed three. For the GPS and BDS2 combined POD, the 3D RMS of the overlap comparison is 0.64–0.65 cm. Nevertheless, due to the weaker consistency of the BDS2 precise ephemerides, the orbit precision of the combined POD is only improved by 3–4% compared with the GPS-only orbits.
Author Contributions
Conceptualization, H.Z. and B.J.; data curation, Z.H.; formal analysis, H.Z., B.J. and K.S.; funding acquisition, X.D.; writing—original draft, H.Z.; writing—review and editing, D.G., B.J., K.S. and B.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Key R&D Program of China (2020YFA0713502) and the National Natural Science Foundation of China (41874028, 11771450, and 61803018).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used to support the findings of this study are available from the corresponding author upon request.
Acknowledgments
We are very grateful to the GFZ for providing the GPS and BDS2 precise orbit and clock products. We would like to thank Qianghua Yu, Ran Ding, and Mohan Chen for the valuable information about the receiver.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yang, C. LM-4B sends Tianhui 2 satellite into orbit. Aerosp. China 2019, 20, 59. [Google Scholar]
- Lou, L.; Liu, Z.; Zhang, H.; Qian, F.; Huang, Y. TH-2 satellite engineering design and implementation. Acta Geod. Car-Tographica Sin. 2020, 49, 1252–1264. [Google Scholar] [CrossRef]
- Qian, F.; Chen, G.; Lu, J.; Chen, X.; Lou, L.; Jiang, T.; Liu, W.; Wang, S. Correcting method of slant-range error for the TH-2 satellites. Remote. Sens. Lett. 2021, 12, 142–149. [Google Scholar] [CrossRef]
- Birmingham, W.P.; Miller, B.L.; Stein, W.L. Experimental Results of Using the GPS for Landsat 4 Onboard Navigation. Navigation 1983, 30, 244–251. [Google Scholar] [CrossRef]
- Kang, Z.; Tapley, B.; Bettadpur, S.; Ries, J.; Nagel, P.; Pastor, R. Precise orbit determination for the GRACE mission using only GPS data. J. Geod. 2006, 80, 322–331. [Google Scholar] [CrossRef]
- Ijssel, J.V.D.; da Encarnacao, J.T.; Doornbos, E.; Visser, P. Precise science orbits for the Swarm satellite constellation. Adv. Space Res. 2015, 56, 1042–1055. [Google Scholar] [CrossRef]
- Moon, Y.; Koenig, R.; Michalak, G.; Rothacher, M. Precise orbit and baseline determination for TerraSAR-X and TanDEM-X. In Proceedings of the 2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008. [Google Scholar]
- Arnold, D.; Montenbruck, O.; Hackel, S.; Sośnica, K. Satellite laser ranging to low Earth orbiters: Orbit and network validation. J. Geod. 2018, 93, 2315–2334. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Li, W.; Shi, C.; Jiang, K.; Guo, X.; Dai, X.; Meng, X.; Yang, Z.; Yang, G.; Liao, M. Precise orbit determination of the Fengyun-3C satellite using onboard GPS and BDS observations. J. Geod. 2017, 91, 1313–1327. [Google Scholar] [CrossRef] [Green Version]
- Xiong, C.; Lu, C.; Zhu, J.; Ding, H. Orbit determination using real tracking data from FY3C-GNOS. Adv. Space Res. 2017, 60, 543–556. [Google Scholar] [CrossRef]
- Li, X.; Zhang, K.; Meng, X.; Zhang, Q.; Zhang, W.; Li, X.; Yuan, Y. LEO–BDS–GPS integrated precise orbit modeling using FengYun-3D, FengYun-3C onboard and ground observations. GPS Solut. 2020, 24, 48. [Google Scholar] [CrossRef]
- Qing, Y.; Lin, J.; Liu, Y.; Dai, X.; Lou, Y.; Gu, S. Precise Orbit Determination of the China Seismo-Electromagnetic Satellite (CSES) Using Onboard GPS and BDS Observations. Remote Sens. 2020, 12, 3234. [Google Scholar] [CrossRef]
- Lou, Y.; Zheng, F.; Gu, S.; Wang, C.; Guo, H.; Feng, Y. Multi-GNSS precise point positioning with raw single-frequency and dual-frequency measurement models. GPS Solut. 2015, 20, 849–862. [Google Scholar] [CrossRef]
- Zhao, W.; Chen, H.; Gao, Y.; Jiang, W.; Liu, X. Evaluation of Inter-System Bias between BDS-2 and BDS-3 Satellites and Its Impact on Precise Point Positioning. Remote Sens. 2020, 12, 2185. [Google Scholar] [CrossRef]
- Zeng, A.; Yang, Y.; Ming, F.; Jing, Y. BDS–GPS inter-system bias of code observation and its preliminary analysis. GPS Solut. 2017, 48, 1573–1581. [Google Scholar] [CrossRef]
- Cai, Y.; Bai, W.; Wang, X.; Sun, Y.; Du, Q.; Zhao, D.; Meng, X.; Liu, C.; Xia, J.; Wang, D.; et al. In-orbit performance of GNOS on-board FY3-C and the enhancements for FY3-D satellite. Adv. Space Res. 2017, 60, 2812–2821. [Google Scholar] [CrossRef]
- Jäggi, A.; Montenbruck, O.; Moon, Y.; Wermuth, M.; König, R.; Michalak, G.; Bock, H.; Bodenmann, D. Inter-agency comparison of TanDEM-X baseline solutions. Adv. Space Res. 2012, 50, 260–271. [Google Scholar] [CrossRef]
- Allende-Alba, G.; Montenbruck, O.; Ardaens, J.-S.; Wermuth, M.; Hugentobler, U. Estimating maneuvers for precise relative orbit determination using GPS. Adv. Space Res. 2017, 59, 45–62. [Google Scholar] [CrossRef]
- Beutler, G.; Jäggi, A.; Hugentobler, U.; Mervart, L. Efficient satellite orbit modelling using pseudo-stochastic parameters. J. Geod. 2006, 80, 353–372. [Google Scholar] [CrossRef] [Green Version]
- Yoon, Y.; Montenbruck, O.; Kirschner, M. Precise maneuver calibration for remote sensing satellites. In Proceedings of the 19th international symposium on space flight dynamics, Kanazawa, Japan, 4–11 June 2006; pp. 607–612. [Google Scholar]
- Ju, B.; Gu, D.; Herring, T.A.; Allende-Alba, G.; Montenbruck, O.; Wang, Z. Precise orbit and baseline determination for maneuvering low earth orbiters. GPS Solut. 2015, 21, 53–64. [Google Scholar] [CrossRef] [Green Version]
- Woo, K. Optimum Semi-Codeless Carrier Phase Tracking of L2. NAVIGATION. J. Inst. Navig. 2000, 47, 82–99. [Google Scholar] [CrossRef]
- Montenbruck, O.; Garcia-Fernandez, M.; Williams, J. Performance comparison of semicodeless GPS receivers for LEO satellites. GPS Solut. 2006, 10, 249–261. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, Y.; Li, J.; Yang, C. Progress and performance evaluation of BeiDou global navigation satellite system: Data analysis based on BDS-3 demonstration system. Sci. China Earth Sci. 2018, 61, 614–624. [Google Scholar] [CrossRef]
- Teunissen, P.J.; Kleusberg, A. GPS for Geodesy; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Zhang, X.; Wu, M.; Liu, W.; Li, X.; Yu, S.; Lu, C.; Wickert, J. Initial assessment of the COMPASS/BeiDou-3: New-generation navigation signals. J. Geod. 2017, 91, 1225–1240. [Google Scholar] [CrossRef]
- Wanninger, L.; Beer, S. BeiDou satellite-induced code pseudorange variations: Diagnosis and therapy. GPS Solut. 2015, 19, 639–648. [Google Scholar] [CrossRef] [Green Version]
- Pan, L.; Guo, F.; Ma, F. An Improved BDS Satellite-Induced Code Bias Correction Model Considering the Consistency of Multipath Combinations. Remote Sens. 2018, 10, 1189. [Google Scholar] [CrossRef] [Green Version]
- Montenbruck, O.; Kroes, R. In-flight performance analysis of the CHAMP BlackJack GPS Receiver. GPS Solut. 2003, 7, 74–86. [Google Scholar] [CrossRef]
- Wu, S.C.; Yunck, T.P.; Thornton, C.L. Reduced-dynamic technique for precise orbit determination of low earth satellites. J. Guid. Control. Dyn. 1991, 14, 24–30. [Google Scholar] [CrossRef]
- Gu, D.; Ju, B.; Liu, J.; Tu, J. Enhanced GPS-based GRACE baseline determination by using a new strategy for ambiguity resolution and relative phase center variation corrections. Acta Astronaut. 2017, 138, 176–184. [Google Scholar] [CrossRef]
- Tian-Yi, H.; Qing-Lin, Z. Adams-Cowell integrator with a first sum. Chin. Astron. Astrophys. 1993, 17, 205–213. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, L. The comparison between Adams-Cowell method and KSG integrator. Publ. Purple Mt. Obs. 1998, 17, 19–27. [Google Scholar]
- Prince, P.; Dormand, J. High order embedded Runge-Kutta formulae. J. Comput. Appl. Math. 1981, 7, 67–75. [Google Scholar] [CrossRef] [Green Version]
- Jäggi, A.; Dach, R.; Montenbruck, O.; Hugentobler, U.; Bock, H.; Beutler, G. Phase center modeling for LEO GPS receiver antennas and its impact on precise orbit determination. J. Geod. 2009, 83, 1145–1162. [Google Scholar] [CrossRef] [Green Version]
- Steigenberger, P.; Montenbruck, O. Consistency of MGEX Orbit and Clock Products. Engineering 2020, 6, 898–903. [Google Scholar] [CrossRef]
- Li, X.; Zhu, Y.; Zheng, K.; Yuan, Y.; Liu, G.; Xiong, Y. Precise Orbit and Clock Products of Galileo, BDS and QZSS from MGEX Since 2018: Comparison and PPP Validation. Remote Sens. 2020, 12, 1415. [Google Scholar] [CrossRef]
- Uhlemann, M.; Gendt, G.; Ramatschi, M.; Deng, Z. GFZ Global Multi-GNSS Network and Data Processing Results. In Gravity, Geoid and Height Systems; Springer: Singapore, 2015; pp. 673–679. [Google Scholar]
- Rebischung, P.; Schmid, R. IGS14/igs14.atx: A new framework for the IGS products. In Proceedings of the American Geo-physical Union Fall Meeting 2016, San Francisco, CA, USA, 12–16 December 2016. [Google Scholar]
- Dilssner, F.; Springer, T.; Schönemann, E.; Enderle, W. Estimation of satellite antenna phase center corrections for BeiDou. In Proceedings of the IGS Workshop, Pasadena, CA, USA, 23–27 June 2014. [Google Scholar]
- Wu, J.-T.; Wu, S.C.; Hajj, G.A.; Bertiger, W.I.; Lichten, S.M. Effects of antenna orientation on GPS carrier phase. In Proceedings of the AAS/AIAA Astrodynamics Conference, Hilton Head, SC, USA, 10–12 August 1992; pp. 1647–1660. [Google Scholar]
- Wang, N.; Yuan, Y.; Li, Z.; Montenbruck, O.; Tan, B. Determination of differential code biases with multi-GNSS observations. J. Geod. 2016, 90, 209–228. [Google Scholar] [CrossRef]
- Ries, J.C.; Eanes, R.; Kang, Z.; Ko, U.; McCullough, C.; Nagel, P.; Bettadpur, S.; Pie, N.; Poole, S.; Richter, T.; et al. The Devel-opment And Evaluation of The Global Gravity Model GGM05; Center for Space Reseach of University of Texas: Austin, TX, USA, 2016. [Google Scholar]
- Petit, G.; Luzum, B. IERS Conventions (2010). IERS Tech. Note 2010, 36, 1. [Google Scholar]
- Standish, E.M. JPL Planetary and Lunar Ephemerides, DE405/LE405. Interoffice Memorandum IOM 312, F-98-048. Jet Propulsion Laboratory, Pasadena. 1998. Available online: https://www.iers.org/IERS/EN/Publications/TechnicalNotes/tn36.html (accessed on 2 September 2021).
- Jacchia, L.G. Revised Static Models of the Thermosphere and Exosphere with Empirical Profiles; Smithsonian Astrophysical Observatory: Cambridge, MA, USA, 1971. [Google Scholar]
- Li, X.; Zhang, K.; Meng, X.; Zhang, W.; Zhang, Q.; Zhang, X.; Li, X. Precise Orbit Determination for the FY-3C Satellite Using Onboard BDS and GPS Observations from 2013, 2015, and 2017. Engineering 2019, 6, 904–912. [Google Scholar] [CrossRef]
- Wang, L.; Xu, B.; Fu, W.; Chen, R.; Li, T.; Han, Y.; Zhou, H. Centimeter-Level Precise Orbit Determination for the Luojia-1A Satellite Using BeiDou Observations. Remote Sens. 2020, 12, 2063. [Google Scholar] [CrossRef]
- Montenbruck, O.; van Helleputte, T.; Kroes, R.; Gill, E. Reduced dynamic orbit determination using GPS code and carrier measurements. Aerosp. Sci. Technol. 2005, 9, 261–271. [Google Scholar] [CrossRef]
- Van Diggelen, F. Method and Apparatus for Time-Free Processing of GPS Signals. U.S. Patent No. 6,417,801, 9 July 2002. [Google Scholar]
- Montenbruck, O.; Steigenberger, P.; Hauschild, A. Comparing the ‘Big 4′-A User’s View on GNSS Performance. In Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, OR, USA, 20–23 April 2020; pp. 407–418. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).