Explainable Boosting Machines for Slope Failure Spatial Predictive Modeling
Abstract
:1. Introduction
2. Background
2.1. Explainable Machine Learning
2.2. Slope Failure Mapping and Modeling
3. Methods
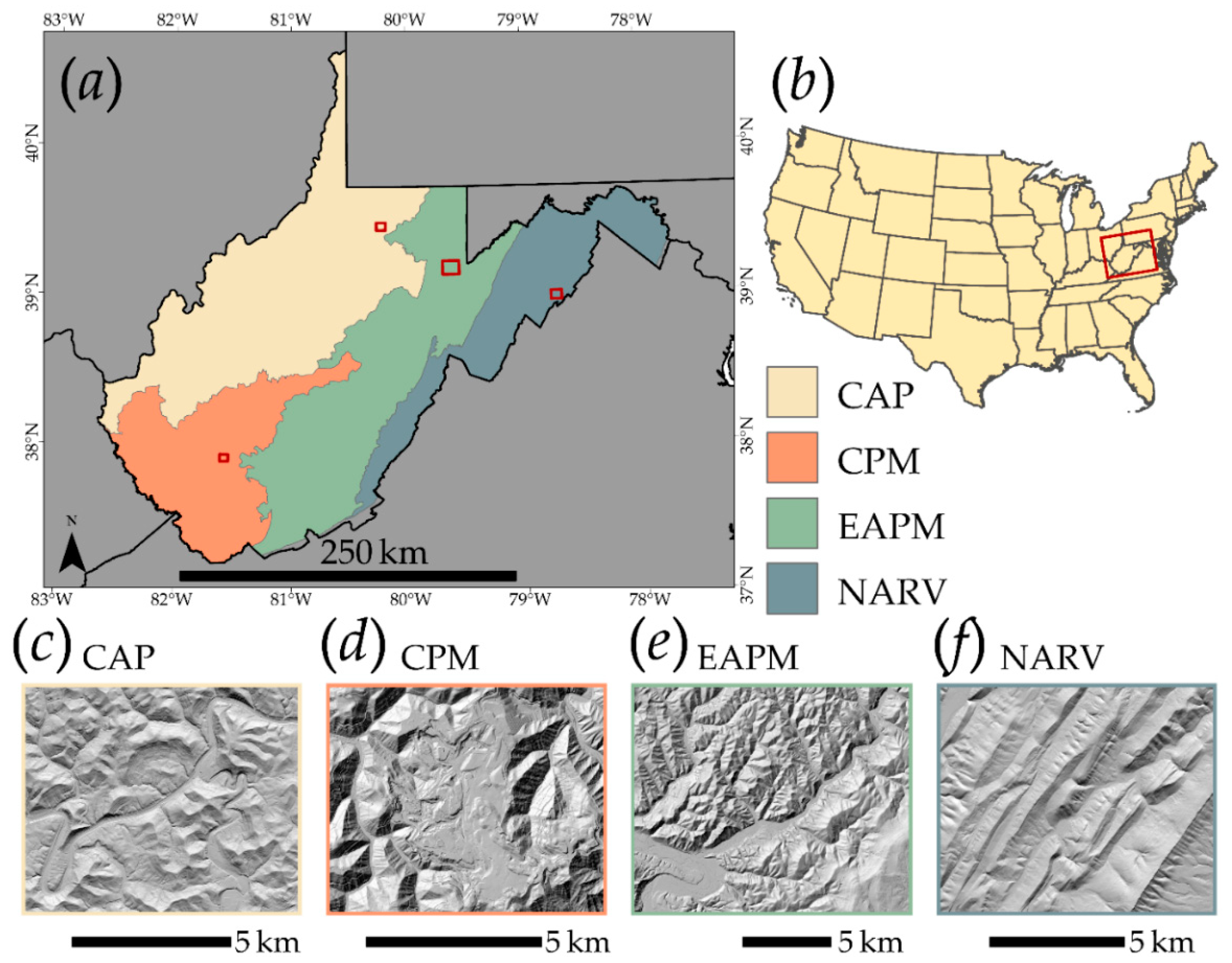
3.1. Study Areas and Slope Failure Data
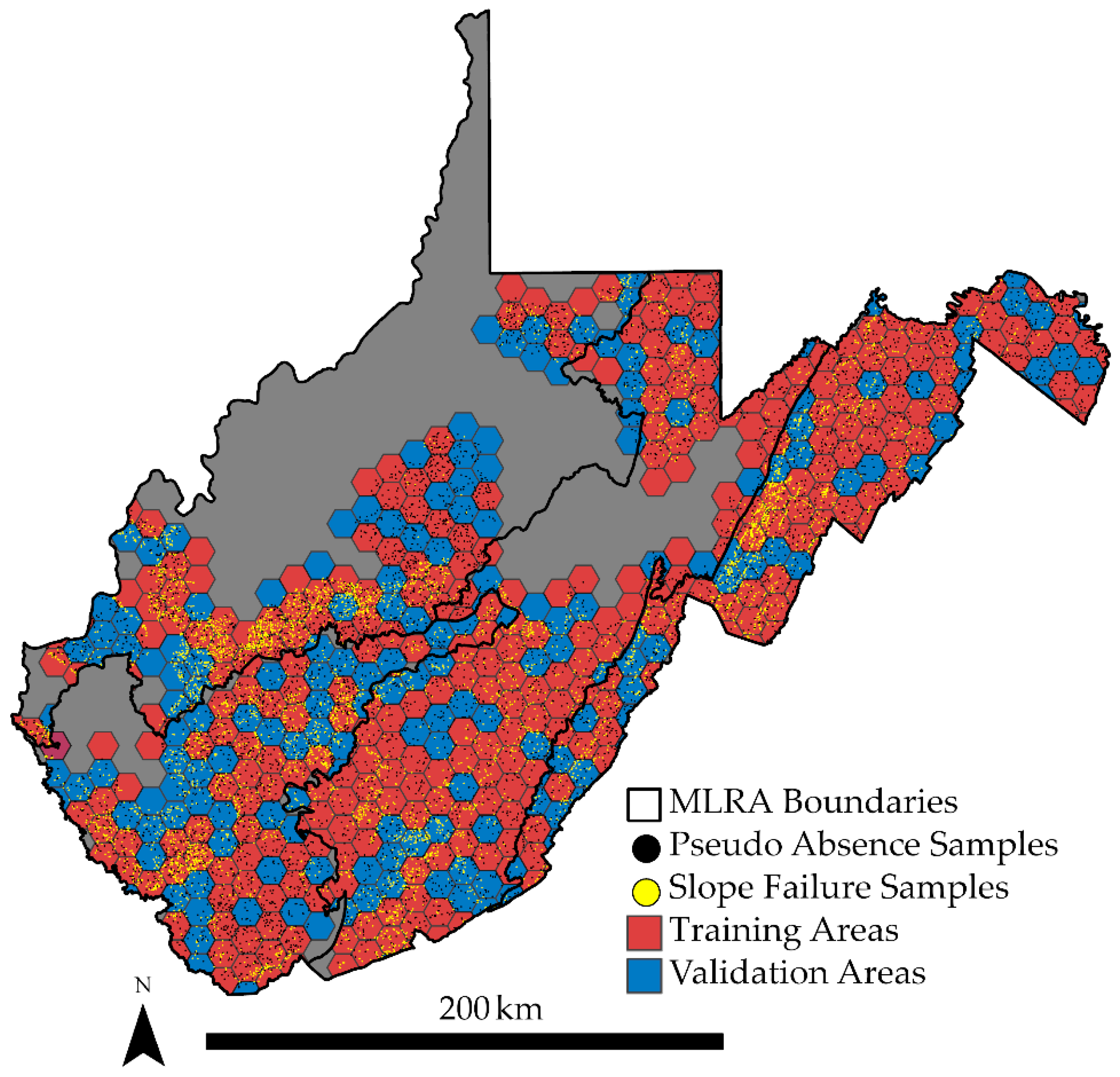
3.2. Training Data and Predictor Variables
3.3. Model Traning
3.4. Model Assessment
4. Results
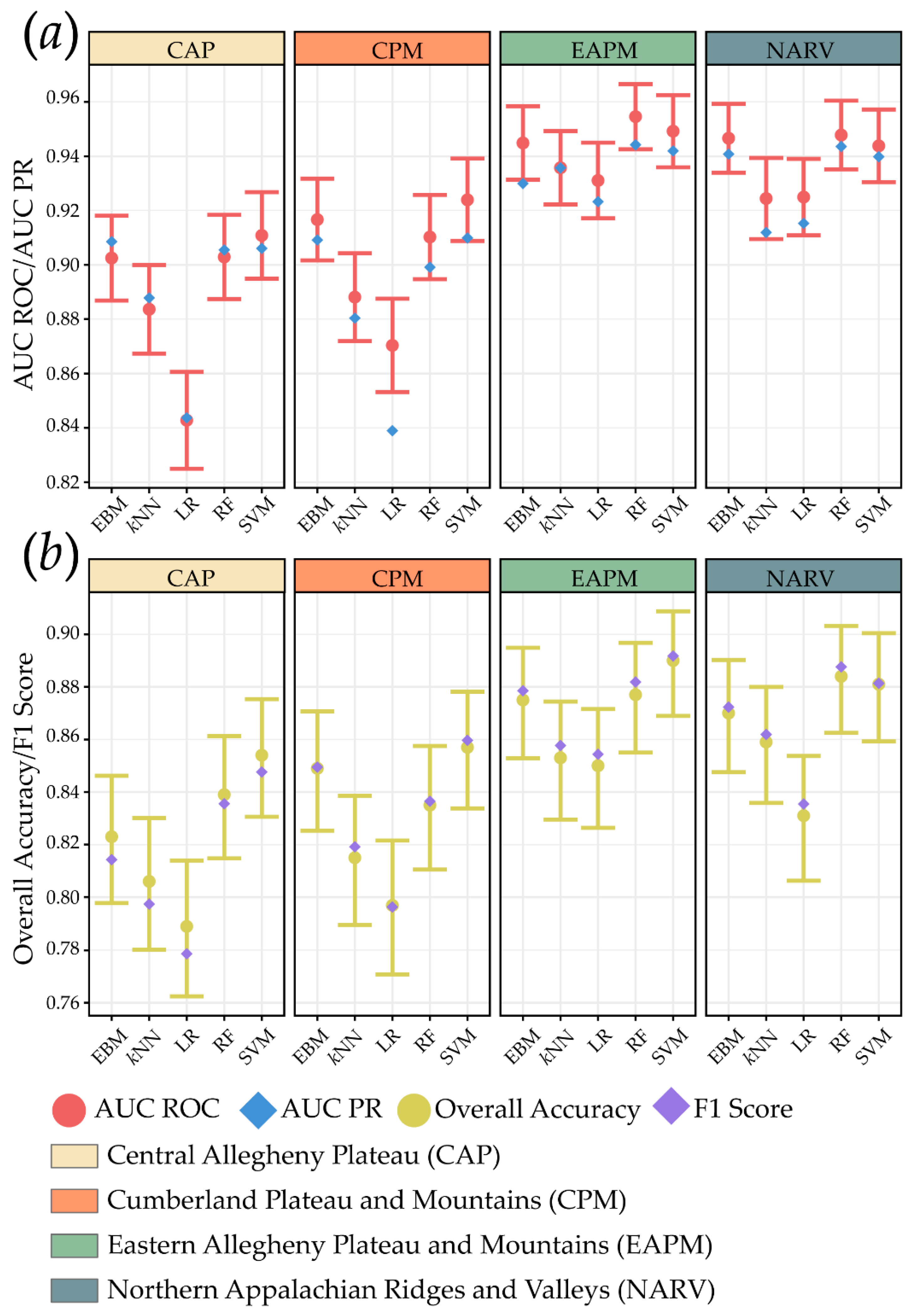
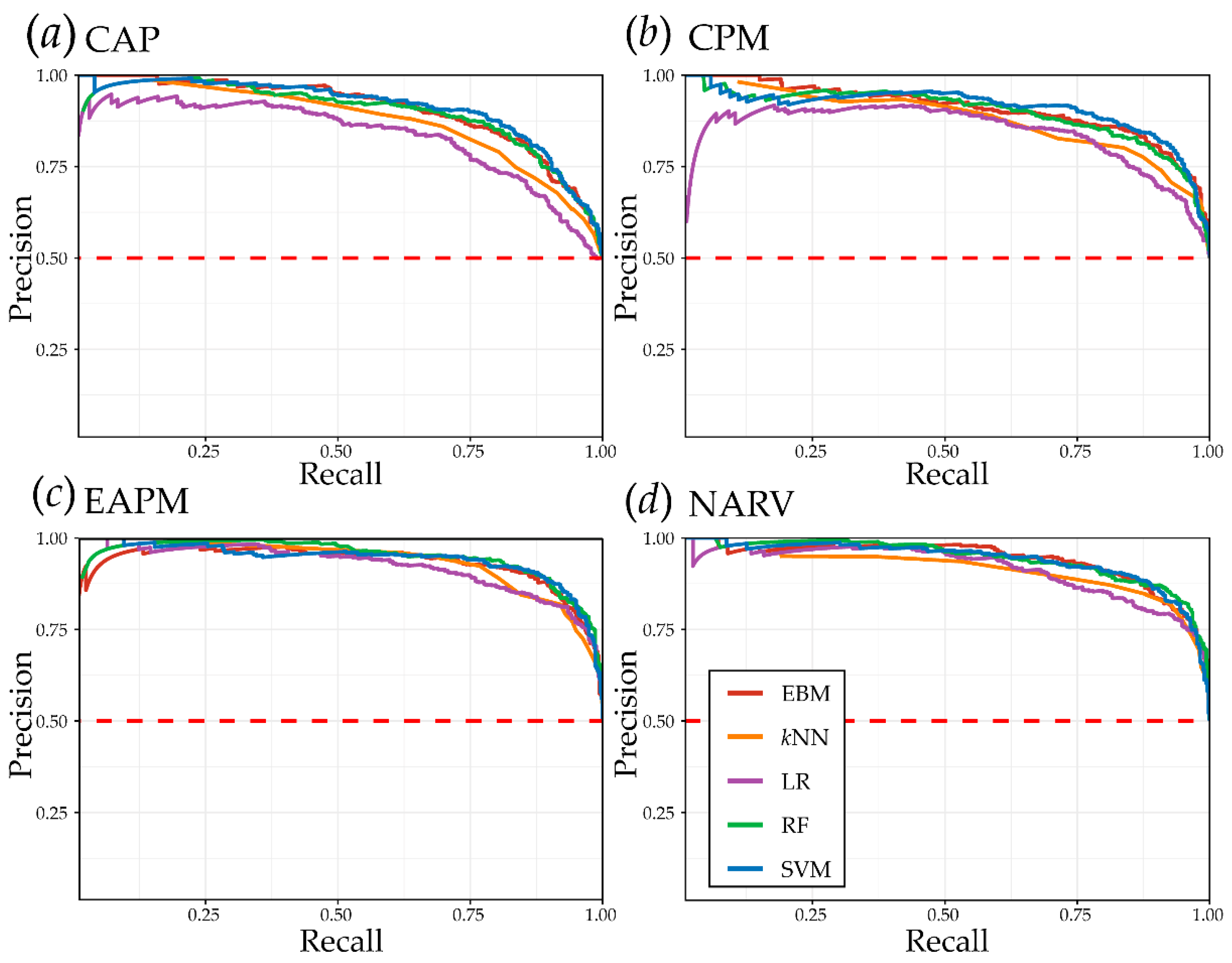
4.1. Algorithm Comparisons
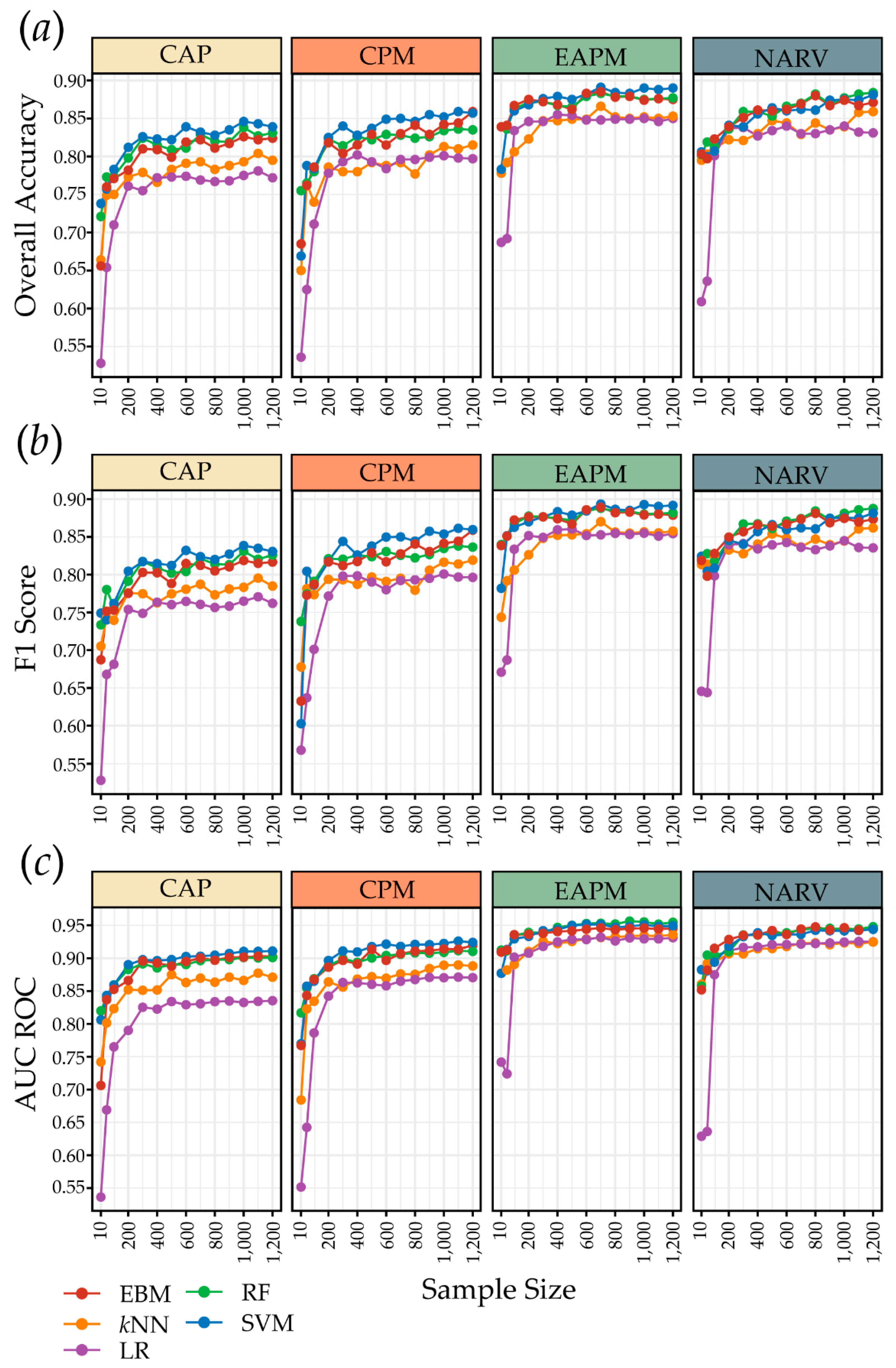
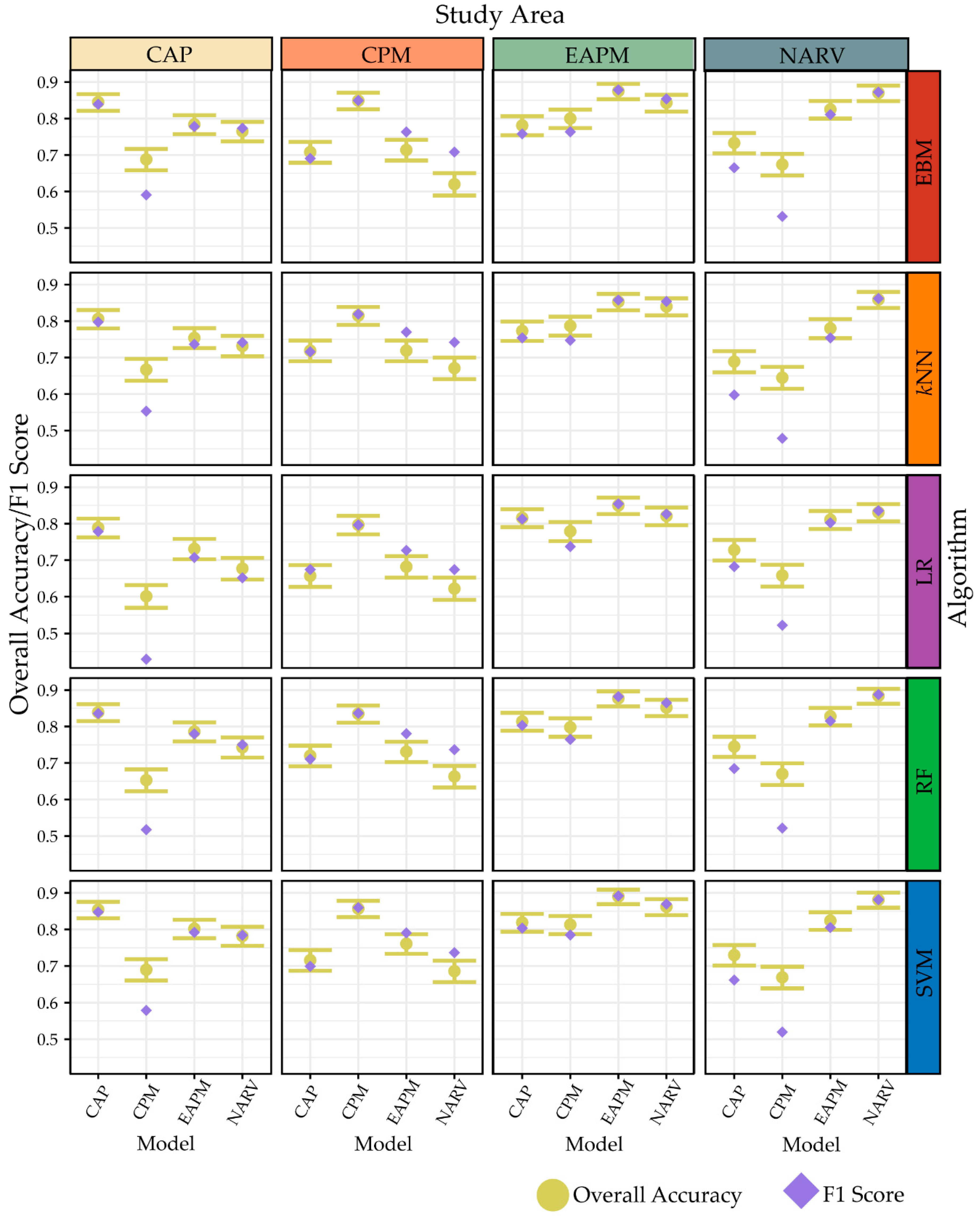
4.2. Sample Size and Model Generalization
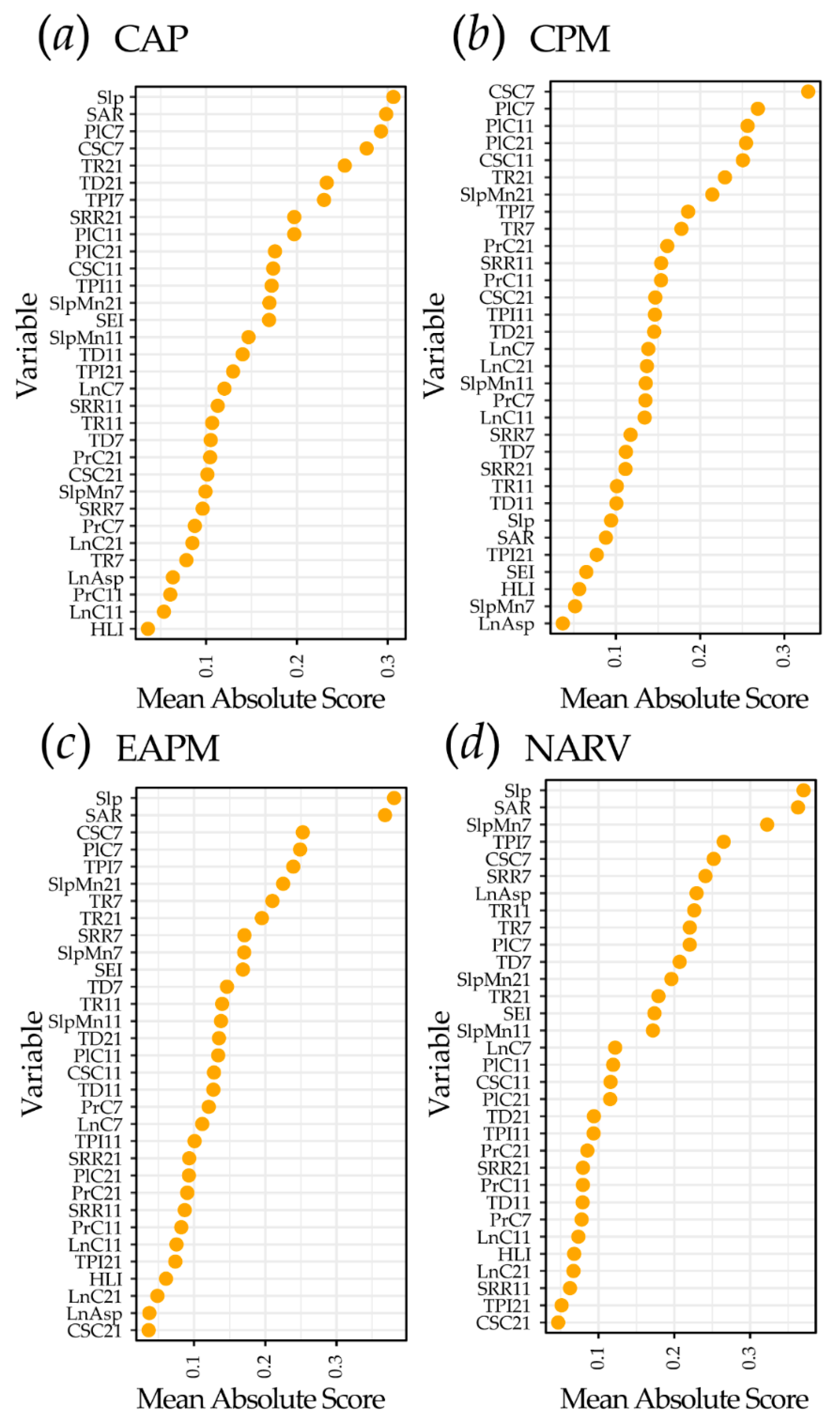
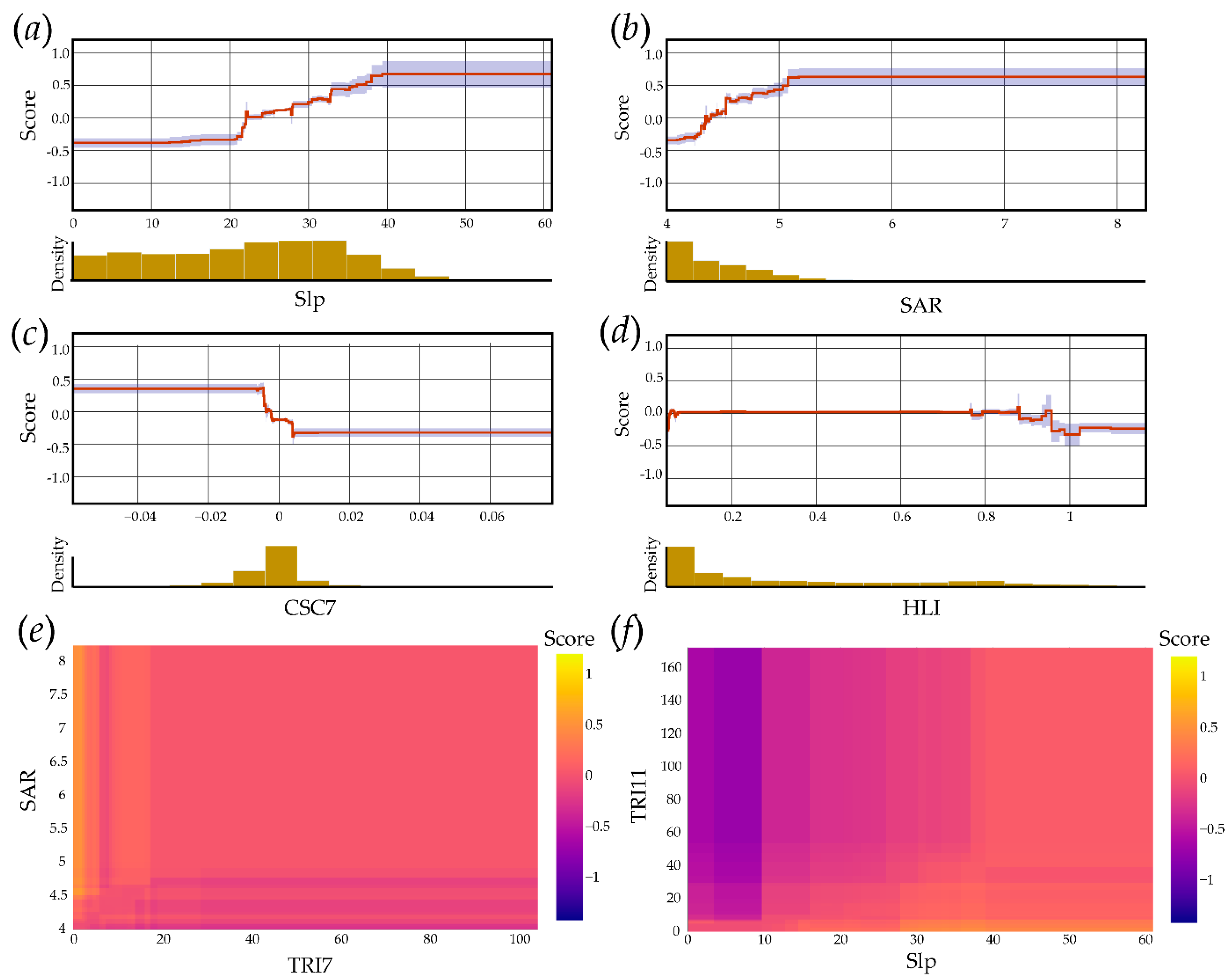
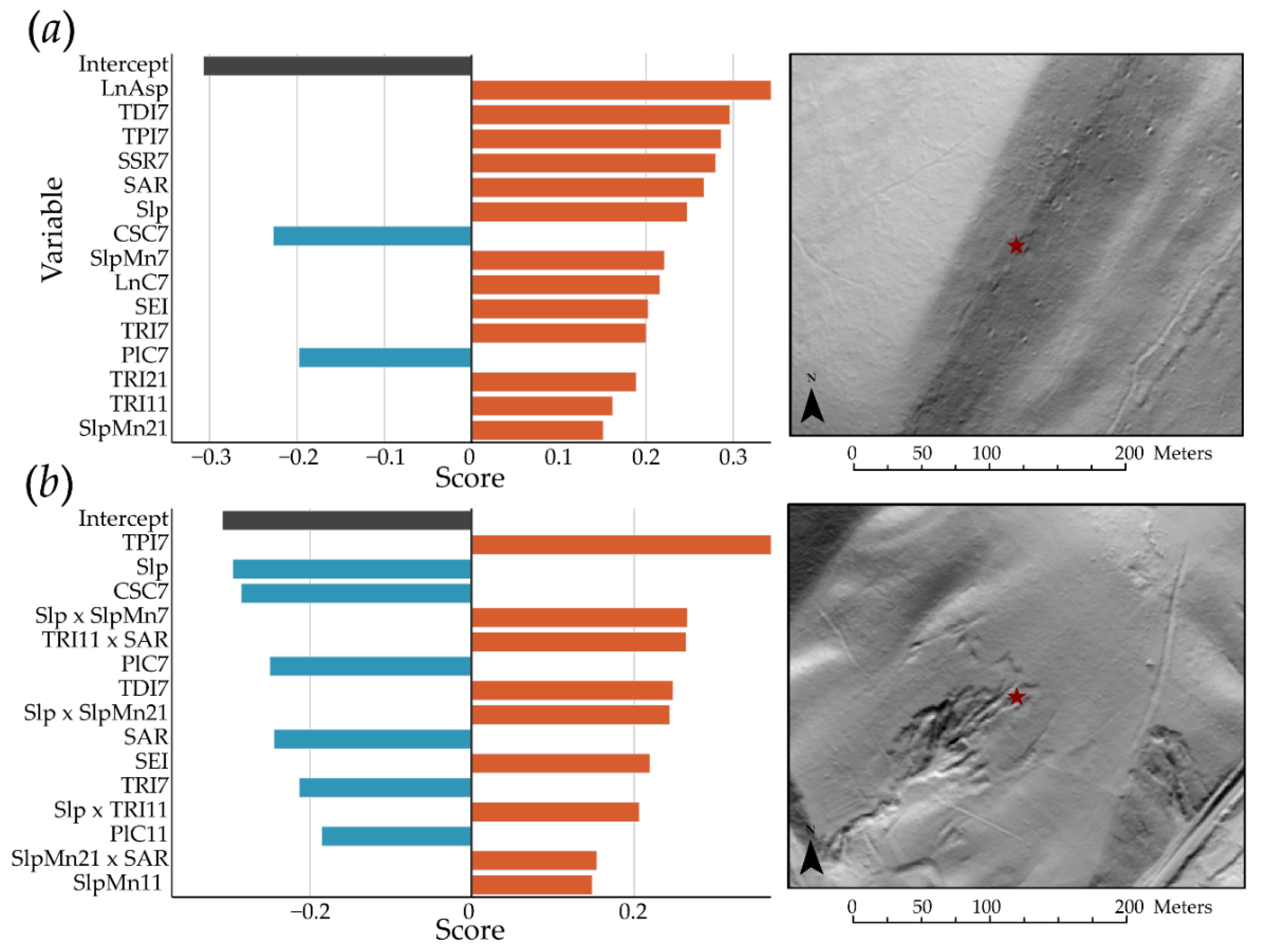
4.3. Exploration of EBM Results
5. Discussion
5.1. Algorithm Performance Comparison and EBM Interpretability
5.2. Future Research Needs
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Maxwell, A.E.; Warner, T.A.; Fang, F. Implementation of Machine-Learning Classification in Remote Sensing: An Applied Review. Int. J. Remote Sens. 2018, 39, 2784–2817. [Google Scholar] [CrossRef] [Green Version]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: Berlin/Heidelberg, Germany, 2013; Volume 112. [Google Scholar]
- Mountrakis, G.; Im, J.; Ogole, C. Support Vector Machines in Remote Sensing: A Review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Rudin, C. Stop Explaining Black Box Machine Learning Models for High Stakes Decisions and Use Interpretable Models Instead. Nat. Mach. Intell. 2019, 1, 206–215. [Google Scholar] [CrossRef] [Green Version]
- Papernot, N.; McDaniel, P.; Goodfellow, I.; Jha, S.; Celik, Z.B.; Swami, A. Practical Black-Box Attacks against Machine Learning. In Proceedings of the 2017 ACM on Asia Conference on Computer and Communications Security, Abu Dhabi, United Arab Emirates, 2–6 April 2017; pp. 506–519. [Google Scholar]
- Nori, H.; Jenkins, S.; Koch, P.; Caruana, R. InterpretML: A Unified Framework for Machine Learning Interpretability. arXiv 2019, arXiv:1909.09223. [Google Scholar]
- Lou, Y.; Caruana, R.; Gehrke, J.; Hooker, G. Accurate Intelligible Models with Pairwise Interactions. In Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Chicago, IL, USA, 11–14 August 2013; pp. 623–631. [Google Scholar]
- Maxwell, A.E.; Sharma, M.; Kite, J.S.; Donaldson, K.A.; Thompson, J.A.; Bell, M.L.; Maynard, S.M. Slope Failure Prediction Using Random Forest Machine Learning and LiDAR in an Eroded Folded Mountain Belt. Remote Sens. 2020, 12, 486. [Google Scholar] [CrossRef] [Green Version]
- Maxwell, A.E.; Sharma, M.; Kite, J.S.; Donaldson, K.A.; Maynard, S.M.; Malay, C.M. Assessing the Generalization of Machine Learning-Based Slope Failure Prediction to New Geographic Extents. ISPRS Int. J. Geo. Inf. 2021, 10, 293. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R. Generalized Additive Models: Some Applications. J. Am. Stat. Assoc. 1987, 82, 371–386. [Google Scholar] [CrossRef]
- Nori, H.; Caruana, R.; Bu, Z.; Shen, J.H.; Kulkarni, J. Accuracy, Interpretability, and Differential Privacy via Explainable Boosting. arXiv 2021, arXiv:2106.09680. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why Should i Trust You?” Explaining the Predictions of Any Classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar]
- Lundberg, S.M.; Nair, B.; Vavilala, M.S.; Horibe, M.; Eisses, M.J.; Adams, T.; Liston, D.E.; Low, D.K.-W.; Newman, S.-F.; Kim, J.; et al. Explainable Machine Learning Predictions to Help Anesthesiologists Prevent Hypoxemia during Surgery. bioRxiv 2017. [Google Scholar] [CrossRef] [Green Version]
- Lundberg, S.M.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 4768–4777. [Google Scholar]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Strobl, C.; Boulesteix, A.-L.; Kneib, T.; Augustin, T.; Zeileis, A. Conditional Variable Importance for Random Forests. BMC Bioinform. 2008, 9, 307. [Google Scholar] [CrossRef] [Green Version]
- Strobl, C.; Hothorn, T.; Zeileis, A. Party on! A New, Conditional Variable Importance Measure Available in the Party Package. R J. 2009, 1, 14–17. [Google Scholar] [CrossRef]
- Kursa, M.B.; Jankowski, A.; Rudnicki, W.R. Boruta—A System for Feature Selection. Fundam. Inform. 2010, 101, 271–285. [Google Scholar] [CrossRef]
- Kursa, M.B.; Rudnicki, W.R. Feature Selection with the Boruta Package. J. Stat. Softw. 2010, 36, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Rudnicki, W.R.; Wrzesień, M.; Paja, W. All Relevant Feature Selection Methods and Applications. In Feature Selection for Data and Pattern Recognition; Springer: Berlin/Heidelberg, Germany, 2015; pp. 11–28. [Google Scholar]
- Tonekaboni, S.; Joshi, S.; McCradden, M.D.; Goldenberg, A. What Clinicians Want: Contextualizing Explainable Machine Learning for Clinical End Use. In Proceedings of the Machine Learning for Healthcare Conference PMLR, Ann Arbor, MI, USA, 9–10 August 2019; pp. 359–380. [Google Scholar]
- Lundberg, S.M.; Nair, B.; Vavilala, M.S.; Horibe, M.; Eisses, M.J.; Adams, T.; Liston, D.E.; Low, D.K.-W.; Newman, S.-F.; Kim, J.; et al. Explainable Machine-Learning Predictions for the Prevention of Hypoxaemia during Surgery. Nat. Biomed. Eng. 2018, 2, 749–760. [Google Scholar] [CrossRef]
- Holzinger, A.; Biemann, C.; Pattichis, C.S.; Kell, D.B. What Do We Need to Build Explainable AI Systems for the Medical Domain? arXiv 2017, arXiv:1712.09923. [Google Scholar]
- Tjoa, E.; Guan, C. A Survey on Explainable Artificial Intelligence (Xai): Toward Medical Xai. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 4793–4813. [Google Scholar] [CrossRef]
- Bibal, A.; Lognoul, M.; De Streel, A.; Frénay, B. Legal Requirements on Explainability in Machine Learning. Artif. Intell. Law 2021, 29, 149–169. [Google Scholar] [CrossRef]
- Bussmann, N.; Giudici, P.; Marinelli, D.; Papenbrock, J. Explainable AI in Fintech Risk Management. Front. Artif. Intell. 2020, 3, 26. [Google Scholar] [CrossRef]
- Bussmann, N.; Giudici, P.; Marinelli, D.; Papenbrock, J. Explainable Machine Learning in Credit Risk Management. Comput. Econ. 2021, 57, 203–216. [Google Scholar] [CrossRef]
- Deeks, A. The Judicial Demand for Explainable Artificial Intelligence. Columbia Law Rev. 2019, 119, 1829–1850. [Google Scholar]
- Rodríguez Oconitrillo, L.R.; Vargas, J.J.; Camacho, A.; Burgos, Á.; Corchado, J.M. RYEL: An Experimental Study in the Behavioral Response of Judges Using a Novel Technique for Acquiring Higher-Order Thinking Based on Explainable Artificial Intelligence and Case-Based Reasoning. Electronics 2021, 10, 1500. [Google Scholar] [CrossRef]
- Ghiringhelli, L.M. Interpretability of Machine-Learning Models in Physical Sciences. arXiv 2021, arXiv:2104.10443. [Google Scholar]
- Dramsch, J.S. 70 Years of Machine Learning in Geoscience in Review. Adv. Geophys. 2020, 61, 1. [Google Scholar]
- Roscher, R.; Bohn, B.; Duarte, M.; Garcke, J. Explain it to Me—Facing Remote Sensing Challenges In The Bio-and Geosciences with Explainable Machine Learning. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 3, 817–824. [Google Scholar] [CrossRef]
- Brenning, A.; Schwinn, M.; Ruiz-Páez, A.; Muenchow, J. Landslide Susceptibility near Highways Is Increased by 1 Order of Magnitude in the Andes of Southern Ecuador, Loja Province. Nat. Hazards Earth Syst. Sci. 2015, 15, 45–57. [Google Scholar] [CrossRef] [Green Version]
- Goetz, J.N.; Brenning, A.; Petschko, H.; Leopold, P. Evaluating Machine Learning and Statistical Prediction Techniques for Landslide Susceptibility Modeling. Comput. Geosci. 2015, 81, 1–11. [Google Scholar] [CrossRef]
- Goetz, J.N.; Guthrie, R.H.; Brenning, A. Integrating Physical and Empirical Landslide Susceptibility Models Using Generalized Additive Models. Geomorphology 2011, 129, 376–386. [Google Scholar] [CrossRef]
- Kim, J.-C.; Lee, S.; Jung, H.-S.; Lee, S. Landslide Susceptibility Mapping Using Random Forest and Boosted Tree Models in Pyeong-Chang, Korea. Geocarto Int. 2018, 33, 1000–1015. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Kerle, N. Random Forests and Evidential Belief Function-Based Landslide Susceptibility Assessment in Western Mazandaran Province, Iran. Environ. Earth Sci. 2016, 75, 185. [Google Scholar] [CrossRef]
- Youssef, A.M.; Pourghasemi, H.R.; Pourtaghi, Z.S.; Al-Katheeri, M.M. Landslide Susceptibility Mapping Using Random Forest, Boosted Regression Tree, Classification and Regression Tree, and General Linear Models and Comparison of Their Performance at Wadi Tayyah Basin, Asir Region, Saudi Arabia. Landslides 2016, 13, 839–856. [Google Scholar] [CrossRef]
- Chen, W.; Pourghasemi, H.R.; Kornejady, A.; Zhang, N. Landslide Spatial Modeling: Introducing New Ensembles of ANN, MaxEnt, and SVM Machine Learning Techniques. Geoderma 2017, 305, 314–327. [Google Scholar] [CrossRef]
- Marjanović, M.; Kovačević, M.; Bajat, B.; Voženílek, V. Landslide Susceptibility Assessment Using SVM Machine Learning Algorithm. Eng. Geol. 2011, 123, 225–234. [Google Scholar] [CrossRef]
- Yao, X.; Tham, L.G.; Dai, F.C. Landslide Susceptibility Mapping Based on Support Vector Machine: A Case Study on Natural Slopes of Hong Kong, China. Geomorphology 2008, 101, 572–582. [Google Scholar] [CrossRef]
- Tien Bui, D.; Pradhan, B.; Lofman, O.; Revhaug, I. Landslide Susceptibility Assessment in Vietnam Using Support Vector Machines, Decision Tree, and Naïve Bayes Models. Math. Probl. Eng. 2012, 2012, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Ayalew, L.; Yamagishi, H. The Application of GIS-Based Logistic Regression for Landslide Susceptibility Mapping in the Kakuda-Yahiko Mountains, Central Japan. Geomorphology 2005, 65, 15–31. [Google Scholar] [CrossRef]
- Lee, S. Application of Logistic Regression Model and Its Validation for Landslide Susceptibility Mapping Using GIS and Remote Sensing Data. Int. J. Remote Sens. 2005, 26, 1477–1491. [Google Scholar] [CrossRef]
- Lee, S.; Ryu, J.-H.; Won, J.-S.; Park, H.-J. Determination and Application of the Weights for Landslide Susceptibility Mapping Using an Artificial Neural Network. Eng. Geol. 2004, 71, 289–302. [Google Scholar] [CrossRef]
- Yilmaz, I. Landslide Susceptibility Mapping Using Frequency Ratio, Logistic Regression, Artificial Neural Networks and Their Comparison: A Case Study from Kat Landslides (Tokat—Turkey). Comput. Geosci. 2009, 35, 1125–1138. [Google Scholar] [CrossRef]
- Trigila, A.; Iadanza, C.; Esposito, C.; Scarascia-Mugnozza, G. Comparison of Logistic Regression and Random Forests Techniques for Shallow Landslide Susceptibility Assessment in Giampilieri (NE Sicily, Italy). Geomorphology 2015, 249, 119–136. [Google Scholar] [CrossRef]
- Ghorbanzadeh, O.; Blaschke, T.; Gholamnia, K.; Meena, S.R.; Tiede, D.; Aryal, J. Evaluation of Different Machine Learning Methods and Deep-Learning Convolutional Neural Networks for Landslide Detection. Remote Sens. 2019, 11, 196. [Google Scholar] [CrossRef] [Green Version]
- Ghorbanzadeh, O.; Meena, S.R.; Blaschke, T.; Aryal, J. UAV-Based Slope Failure Detection Using Deep-Learning Convolutional Neural Networks. Remote Sens. 2019, 11, 2046. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Wu, L. Geological Disaster Recognition on Optical Remote Sensing Images Using Deep Learning. Procedia Comput. Sci. 2016, 91, 566–575. [Google Scholar] [CrossRef] [Green Version]
- Carrara, A.; Cardinali, M.; Detti, R.; Guzzetti, F.; Pasqui, V.; Reichenbach, P. GIS Techniques and Statistical Models in Evaluating Landslide Hazard. Earth Surf. Process. Landf. 1991, 16, 427–445. [Google Scholar] [CrossRef]
- Carrara, A.; Sorriso-Valvo, M.; Reali, C. Analysis of Landslide Form and Incidence by Statistical Techniques, Southern Italy. Catena 1982, 9, 35–62. [Google Scholar] [CrossRef]
- Catani, F.; Lagomarsino, D.; Segoni, S.; Tofani, V. Landslide Susceptibility Estimation by Random Forests Technique: Sensitivity and Scaling Issues. Nat. Hazards Earth Syst. Sci. 2013, 13, 2815–2831. [Google Scholar] [CrossRef] [Green Version]
- Taalab, K.; Cheng, T.; Zhang, Y. Mapping Landslide Susceptibility and Types Using Random Forest. Big Earth Data 2018, 2, 159–178. [Google Scholar] [CrossRef]
- Dou, J.; Yunus, A.P.; Tien Bui, D.; Sahana, M.; Chen, C.-W.; Zhu, Z.; Wang, W.; Thai Pham, B. Evaluating GIS-Based Multiple Statistical Models and Data Mining for Earthquake and Rainfall-Induced Landslide Susceptibility Using the LiDAR DEM. Remote Sens. 2019, 11, 638. [Google Scholar] [CrossRef] [Green Version]
- Hong, H.; Liu, J.; Bui, D.T.; Pradhan, B.; Acharya, T.D.; Pham, B.T.; Zhu, A.-X.; Chen, W.; Ahmad, B.B. Landslide Susceptibility Mapping Using J48 Decision Tree with AdaBoost, Bagging and Rotation Forest Ensembles in the Guangchang Area (China). Catena 2018, 163, 399–413. [Google Scholar] [CrossRef]
- Colkesen, I.; Sahin, E.K.; Kavzoglu, T. Susceptibility Mapping of Shallow Landslides Using Kernel-Based Gaussian Process, Support Vector Machines and Logistic Regression. J. Afr. Earth Sci. 2016, 118, 53–64. [Google Scholar] [CrossRef]
- Mahalingam, R.; Olsen, M.J.; O’Banion, M.S. Evaluation of Landslide Susceptibility Mapping Techniques Using Lidar-Derived Conditioning Factors (Oregon Case Study). Geomat. Nat. Hazards Risk 2016, 7, 1884–1907. [Google Scholar] [CrossRef]
- Chang, K.-T.; Merghadi, A.; Yunus, A.P.; Pham, B.T.; Dou, J. Evaluating Scale Effects of Topographic Variables in Landslide Susceptibility Models Using GIS-Based Machine Learning Techniques. Sci. Rep. 2019, 9, 12296. [Google Scholar] [CrossRef] [Green Version]
- Brock, J.; Schratz, P.; Petschko, H.; Muenchow, J.; Micu, M.; Brenning, A. The Performance of Landslide Susceptibility Models Critically Depends on the Quality of Digital Elevation Models. Geomat. Nat. Hazards Risk 2020, 11, 1075–1092. [Google Scholar] [CrossRef]
- United states Department of Agriculture (USDA). Major Land Resource Area (MLRA). NRCS Soils. Available online: https://www.nrcs.usda.gov/wps/portal/nrcs/detail/soils/survey/geo/?cid=nrcs142p2_053624 (accessed on 28 February 2021).
- WVGES. Homeowner’s Guide to Geologic Hazards. Available online: http://www.wvgs.wvnet.edu/www/geohaz/geohaz3.htm (accessed on 7 November 2019).
- Strausbaugh, P.D.; Core, E.L. Flora of West Virginia; West Virginia University Bulletin; West Virginia University: Morgantown, WV, USA, 1952. [Google Scholar]
- WVGES. WV Physiographic Provinces. Available online: https://www.wvgs.wvnet.edu/www/maps/pprovinces.htm (accessed on 14 November 2019).
- Ross, M.R.V.; McGlynn, B.L.; Bernhardt, E.S. Deep Impact: Effects of Mountaintop Mining on Surface Topography, Bedrock Structure, and Downstream Waters. Environ. Sci. Technol. 2016, 50, 2064–2074. [Google Scholar] [CrossRef] [Green Version]
- Maxwell, A.E.; Strager, M.P. Assessing Landform Alterations Induced by Mountaintop Mining. Nat. Sci. 2013, 05, 229–237. [Google Scholar] [CrossRef] [Green Version]
- Wickham, J.; Wood, P.B.; Nicholson, M.C.; Jenkins, W.; Druckenbrod, D.; Suter, G.W.; Strager, M.P.; Mazzarella, C.; Galloway, W.; Amos, J. The Overlooked Terrestrial Impacts of Mountaintop Mining. BioScience 2013, 63, 335–348. [Google Scholar] [CrossRef]
- Chang, K.-T. Geographic Information System. In International Encyclopedia of Geography; American Cancer Society: Atlanta, GA, USA, 2017; pp. 1–9. ISBN 978-1-118-78635-2. [Google Scholar]
- ESRI. ArcGIS Pro 2.2. 2018. Available online: https://www.esri.com/en-us/arcgis/products/arcgis-pro/resources (accessed on 6 December 2021).
- Evans, J.S. Jeffreyevans/GradientMetrics. 2020. Available online: https://github.com/jeffreyevans/GradientMetrics (accessed on 6 December 2021).
- Stage, A.R. An Expression for the Effect of Aspect, Slope, and Habitat Type on Tree Growth. For. Sci. 1976, 22, 457–460. [Google Scholar] [CrossRef]
- Lopez, M.; Berry, J.K. Use Surface Area for Realistic Calculations. GeoWorld 2002, 15, 25. [Google Scholar]
- Reily, S.J.; DeGloria, S.D.; Elliot, R.A. Terrain Ruggedness Index That Quantifies Topographic Heterogeneity. Intermountain. J. Sci. 1999, 5, 23. [Google Scholar]
- Jacek, S. Landform Characterization with Geographic Information Systems. Photogramm. Eng. Remote Sens. 1997, 63, 183–191. [Google Scholar]
- Evans, I.S. General Geomorphometry, Derivatives of Altitude, and Descriptive Statistics. In Spatial Analysis in Geomorphology; Taylor: Hoboken, NJ, USA, 1972; pp. 17–90. [Google Scholar]
- Pike, R.J.; Evans, I.S.; Hengl, T. Geomorphometry: A Brief Guide. In Developments in Soil Science; Hengl, T., Reuter, H.I., Eds.; Elsevier: Amsterdam, The Netherlands, 2009; Volume 33, pp. 3–30. [Google Scholar]
- Pike, R.J.; Wilson, S.E. Elevation-Relief Ratio, Hypsometric Integral, and Geomorphic Area-Altitude Analysis. GSA Bull. 1971, 82, 1079–1084. [Google Scholar] [CrossRef]
- Ironside, K.E.; Mattson, D.J.; Arundel, T.; Theimer, T.; Holton, B.; Peters, M.; Edwards, T.C.; Hansen, J. Geomorphometry in Landscape Ecology: Issues of Scale, Physiography, and Application. Environ. Ecol. Res. 2018, 6, 397–412. [Google Scholar] [CrossRef]
- McCune, B.; Keon, D. Equations for Potential Annual Direct Incident Radiation and Heat Load. J. Veg. Sci. 2002, 13, 603–606. [Google Scholar] [CrossRef]
- Wood, J. Geomorphometry in LandSerf. In Developments in Soil Science; Hengl, T., Reuter, H.I., Eds.; Elsevier: Amsterdam, The Netherlands, 2009; Volume 33, pp. 333–349. [Google Scholar]
- Wood, J. The Geomorphological Characterisation of Digital Elevation Models. Ph.D. Thesis, University of Leicester, Leicester, UK, 1996. [Google Scholar]
- Module Morphometric Features—SAGA-GIS Module Library Documentation (v2.2.5). Available online: http://www.saga-gis.org/saga_tool_doc/2.2.5/ta_morphometry_23.html (accessed on 14 November 2019).
- SAGA—System for Automated Geoscientific Analyses. Available online: http://www.saga-gis.org/en/index.html (accessed on 14 November 2019).
- Kuhn, M. Building Predictive Models in R Using the Caret Package. J. Stat. Softw. Artic. 2008, 28, 1–26. [Google Scholar] [CrossRef] [Green Version]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S; Springer: New York, NY, USA, 2002. [Google Scholar]
- Liaw, A.; Wiener, M. Classification and Regression by RandomForest. R News 2002, 2, 6. [Google Scholar]
- Karatzoglou, A.; Smola, A.; Hornik, K.; Zeileis, A. Kernlab—An S4 Package for Kernel Methods in R. J. Stat. Softw. 2004, 11, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Welcome to Python.Org. Available online: https://www.python.org/ (accessed on 27 September 2021).
- InterpretML—Alpha Release. InterpretML. 2021. Available online: https://github.com/interpretml/interpret (accessed on 6 December 2021).
- Tharwat, A. Classification Assessment Methods. Appl. Comput. Inform. 2020, 17, 168–192. [Google Scholar] [CrossRef]
- Clopper, C.J.; Pearson, E.S. The use of confidence or fiducial limits illustrated in the case of the binomial. Biometrika 1934, 26, 404–413. [Google Scholar] [CrossRef]
- Beck, J.R.; Shultz, E.K. The Use of Relative Operating Characteristic (ROC) Curves in Test Performance Evaluation. Arch. Pathol. Lab. Med. 1986, 110, 13–20. [Google Scholar] [PubMed]
- Bradley, A.P. The Use of the Area Under the ROC Curve in the Evaluation of Machine Learning Algorithms. Pattern Recogn. 1997, 30, 1145–1159. [Google Scholar] [CrossRef] [Green Version]
- DeLong, E.R.; DeLong, D.M.; Clarke-Pearson, D.L. Comparing the Areas under Two or More Correlated Receiver Operating Characteristic Curves: A Nonparametric Approach. Biometrics 1988, 44, 837–845. [Google Scholar] [CrossRef]
- Robin, X.; Turck, N.; Hainard, A.; Tiberti, N.; Lisacek, F.; Sanchez, J.-C.; Müller, M. PROC: An Open-Source Package for R and S+ to Analyze and Compare ROC Curves. BMC Bioinform. 2011, 12, 77. [Google Scholar] [CrossRef]
- Saito, T.; Rehmsmeier, M. The Precision-Recall Plot Is More Informative than the ROC Plot When Evaluating Binary Classifiers on Imbalanced Datasets. PLoS ONE 2015, 10, e0118432. [Google Scholar] [CrossRef] [Green Version]
- Grau, J.; Grosse, I.; Keilwagen, J. PRROC: Computing and Visualizing Precision-Recall and Receiver Operating Characteristic Curves in R. Bioinformatics 2015, 31, 2595–2597. [Google Scholar] [CrossRef] [PubMed]
- Kuhn, M.; Vaughan, D. RStudio Yardstick: Tidy Characterizations of Model Performance. 2020. Available online: https://yardstick.tidymodels.org/ (accessed on 6 December 2021).
- Evans, J.S.; Cushman, S.A. Gradient Modeling of Conifer Species Using Random Forests. Landsc. Ecol. 2009, 24, 673–683. [Google Scholar] [CrossRef]
- Rather, T.A.; Kumar, S.; Khan, J.A. Using Machine Learning to Predict Habitat Suitability of Sloth Bears at Multiple Spatial Scales. Ecol. Process. 2021, 10, 1–12. [Google Scholar] [CrossRef]
- Strager, M.P.; Strager, J.M.; Evans, J.S.; Dunscomb, J.K.; Kreps, B.J.; Maxwell, A.E. Combining a Spatial Model and Demand Forecasts to Map Future Surface Coal Mining in Appalachia. PLoS ONE 2015, 10, e0128813. [Google Scholar] [CrossRef]
- Lawrence, R.L.; Moran, C.J. The AmericaView Classification Methods Accuracy Comparison Project: A Rigorous Approach for Model Selection. Remote Sens. Environ. 2015, 170, 115–120. [Google Scholar] [CrossRef]
- Steger, S.; Brenning, A.; Bell, R.; Petschko, H.; Glade, T. Exploring Discrepancies between Quantitative Validation Results and the Geomorphic Plausibility of Statistical Landslide Susceptibility Maps. Geomorphology 2016, 262, 8–23. [Google Scholar] [CrossRef]
- Palmer, M.A.; Bernhardt, E.S.; Schlesinger, W.H.; Eshleman, K.N.; Foufoula-Georgiou, E.; Hendryx, M.S.; Lemly, A.D.; Likens, G.E.; Loucks, O.L.; Power, M.E.; et al. Mountaintop Mining Consequences. Science 2010, 327, 148–149. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Debeer, D.; Strobl, C. Conditional Permutation Importance Revisited. BMC Bioinform. 2020, 21, 307. [Google Scholar] [CrossRef]


| MLRA | Abbreviation | Land Area in WV | Number of Slope Failures Mapped |
|---|---|---|---|
| Central Allegheny Plateau | CAP | 22,281 km2 | 29,637 |
| Cumberland Plateau and Mountains | CPM | 11,644 km2 | 20,712 |
| Eastern Allegheny Plateau and Mountains | EAPM | 18,071 km2 | 12,518 |
| Northern Appalachian Ridges and Valleys | NARV | 10,320 km2 | 1997 |
| Variable | Abbreviation | Description | Window Radius (Cells) |
|---|---|---|---|
| Slope Gradient | Slp | Gradient or rate of maximum change in Z as degrees of rise | 1 |
| Mean Slope Gradient | SlpMn | Slope averaged over a local window | 7, 11, 21 |
| Linear Aspect | LnAsp | Transform of topographic aspect to linear variable | 1 |
| Profile Curvature | PrC | Curvature parallel to direction of maximum slope | 7, 11, 21 |
| Plan Curvature | PlC | Curvature perpendicular to direction of maximum slope | 7, 11, 21 |
| Longitudinal Curvature | LnC | Profile curvature intersecting with the plane defined by the surface normal and maximum gradient direction | 7, 11, 21 |
| Cross-Sectional Curvature | CSC | Tangential curvature intersecting with the plane defined by the surface normal and a tangent to the contour—perpendicular to maximum gradient direction | 7, 11, 21 |
| Slope Position | TPI | Z–Mean Z | 7, 11, 21 |
| Topographic Roughness | TRI | Square root of standard deviation of slope in local window | 7, 11, 21 |
| Topographic Dissection Index | TDI | 7, 11, 21 | |
| Surface Area Ratio | SAR | 1 | |
| Surface Relief Ratio | SRR | 7, 11, 21 | |
| Site Exposure Index | SEI | Measure of exposure based on slope and aspect | 1 |
| Heat Load Index | HLI | Measure of solar insolation based on slope, aspect, and latitude | 1 |
| Reference Data | ||||
|---|---|---|---|---|
| True | False | 1—Commission Error | ||
| Classification Result | True | TP | FP | Precision |
| False | FN | TN | NPV | |
| 1—Omission Errors | Recall | Specificity | ||
| Study Area | Algorithm | OA | Precision | F1 Score | Recall | Specificity | NPV | AUC ROC | AUC PR |
|---|---|---|---|---|---|---|---|---|---|
| CAP | EBM | 0.823 | 0.857 | 0.814 | 0.776 | 0.870 | 0.795 | 0.903 | 0.909 |
| CAP | kNN | 0.806 | 0.834 | 0.797 | 0.764 | 0.848 | 0.782 | 0.884 | 0.888 |
| CAP | LR | 0.789 | 0.819 | 0.779 | 0.742 | 0.836 | 0.764 | 0.843 | 0.844 |
| CAP | RF | 0.839 | 0.854 | 0.836 | 0.818 | 0.860 | 0.825 | 0.903 | 0.905 |
| CAP | SVM | 0.854 | 0.886 | 0.848 | 0.812 | 0.896 | 0.827 | 0.911 | 0.906 |
| CPM | EBM | 0.849 | 0.847 | 0.849 | 0.852 | 0.846 | 0.851 | 0.917 | 0.909 |
| CPM | kNN | 0.815 | 0.801 | 0.819 | 0.838 | 0.792 | 0.830 | 0.888 | 0.880 |
| CPM | LR | 0.797 | 0.799 | 0.796 | 0.794 | 0.800 | 0.795 | 0.870 | 0.839 |
| CPM | RF | 0.835 | 0.829 | 0.836 | 0.844 | 0.826 | 0.841 | 0.910 | 0.899 |
| CPM | SVM | 0.857 | 0.844 | 0.860 | 0.876 | 0.838 | 0.871 | 0.924 | 0.910 |
| EAPM | EBM | 0.875 | 0.854 | 0.879 | 0.904 | 0.846 | 0.898 | 0.945 | 0.930 |
| EAPM | kNN | 0.853 | 0.831 | 0.858 | 0.886 | 0.820 | 0.878 | 0.936 | 0.936 |
| EAPM | LR | 0.850 | 0.830 | 0.854 | 0.880 | 0.820 | 0.872 | 0.931 | 0.923 |
| EAPM | RF | 0.877 | 0.848 | 0.882 | 0.918 | 0.836 | 0.911 | 0.955 | 0.944 |
| EAPM | SVM | 0.890 | 0.878 | 0.892 | 0.906 | 0.874 | 0.903 | 0.949 | 0.942 |
| NARV | EBM | 0.870 | 0.857 | 0.872 | 0.888 | 0.852 | 0.884 | 0.947 | 0.941 |
| NARV | kNN | 0.859 | 0.845 | 0.862 | 0.880 | 0.838 | 0.875 | 0.924 | 0.912 |
| NARV | LR | 0.831 | 0.814 | 0.835 | 0.858 | 0.804 | 0.850 | 0.925 | 0.915 |
| NARV | RF | 0.884 | 0.861 | 0.888 | 0.916 | 0.852 | 0.910 | 0.948 | 0.944 |
| NARV | SVM | 0.881 | 0.879 | 0.881 | 0.884 | 0.878 | 0.883 | 0.944 | 0.940 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maxwell, A.E.; Sharma, M.; Donaldson, K.A. Explainable Boosting Machines for Slope Failure Spatial Predictive Modeling. Remote Sens. 2021, 13, 4991. https://doi.org/10.3390/rs13244991
Maxwell AE, Sharma M, Donaldson KA. Explainable Boosting Machines for Slope Failure Spatial Predictive Modeling. Remote Sensing. 2021; 13(24):4991. https://doi.org/10.3390/rs13244991
Chicago/Turabian StyleMaxwell, Aaron E., Maneesh Sharma, and Kurt A. Donaldson. 2021. "Explainable Boosting Machines for Slope Failure Spatial Predictive Modeling" Remote Sensing 13, no. 24: 4991. https://doi.org/10.3390/rs13244991
APA StyleMaxwell, A. E., Sharma, M., & Donaldson, K. A. (2021). Explainable Boosting Machines for Slope Failure Spatial Predictive Modeling. Remote Sensing, 13(24), 4991. https://doi.org/10.3390/rs13244991






